摘要:研究非牛顿流体转捩问题, 可为调控非牛顿流体动力特性提供理论基础. 相对于牛顿流体转捩问题, 非牛顿流体转捩研究较少, 缺乏转捩雷诺数精细预报方法. 论文以格子Boltzmann方法为核心求解器, 以典型非牛顿流体幂律模型为例, 开展了幂律流体二维顶盖驱动流转捩模拟, 给出剪切变稀和剪切增稠流体的第一转捩雷诺数, 并分析了转捩雷诺数附近流场时频域特性及模态分布. 结果表明, 剪切变稀流体和剪切增稠流体的第一转捩雷诺数与牛顿流体差异显著, 且在转捩临界雷诺数附近监控点处速度分量均呈现周期性变化趋势. 通过对流场速度和涡量的本征正交分解发现, 不同类型的流体在转捩临界雷诺数附近, 前两阶模态均为流场的主模态, 能量占比超过95%, 且同类型流体不同雷诺数的主模态间具有相似的结构.
关键词: 幂律流体/
转捩/
格子Boltzmann方法/
顶盖驱动流

English Abstract

全文HTML

--> --> -->

顶盖驱动流是计算流体力学中经典物理模型之一, 被广泛应用于层流流动、流动转捩等问题的研究^[1-4]. 研究流动转捩问题, 可为界定流场状态和调控流体动力特性提供理论依据, 具有重要学术意义. 转捩问题涉及多种流动状态, 属复杂流体力学问题, 已有大量****开展过相关研究. 例如, Peng等^[5]采用有限差分法研究了顶盖驱动流的转捩雷诺数, 并给出临界雷诺数附近流场的时频域特性. Bruneau和Saad^[6]进一步提高网格分辨率, 改进对流项差分格式, 佐证了Peng等^[5]、Auteri等^[7]、Sahin和Owens^[8]关于第一转捩雷诺数在8000附近的结论. 需要指出的是, 上述研究均是以牛顿流体为研究对象.
非牛顿流体的剪应力与剪切应变率之间为非线性关系, 会表现出剪切增稠^[9]、剪切变稀^[10]等不同于牛顿流体的运动行为. 非牛顿流体广泛存在于自然界和工业生产中, 如化工中的聚乙烯、聚氯乙烯, 食品中的淀粉液, 人体内的血液等. 非牛顿流体种类众多, 其中具有代表性的是幂律流体. 幂律流体按照幂律指数主要分为剪切变稀流体、剪切增稠流体. 作为特例, 牛顿流体可视为指数为1的幂律流体. ****们开展了大量的幂律流体实验与仿真的研究, 如Johnston等^[11]发现相比于牛顿流体, 用幂律流体模拟血液流动, 可获更精准的壁面切应力; Zhao等^[12]模拟了幂律流体在微通道中的电渗流动; Hojjat等^[13]通过实验研究了含纳米颗粒流体的剪切变稀行为. 但是, 关于幂律流体转捩问题的鲜有研究报道.
与有限差分和有限体积等传统方法不同, 格子Boltzmann方法(lattice Boltzmann method, LBM)^[14]通过对分布函数进行碰撞和迁移处理, 可实现宏观流场时空演化过程的模拟, 具有并行性高, 边界处理简单等优势, 已在牛顿流体仿真领域取得大量研究成果^[15-17]. 近年来, 也有****将LBM拓展至非牛顿流体模拟, 如Boyd等^[18]在LBM框架下实现了幂律流体中速度导数的快速求解; Wang和Ho^[19]在LBM的框架下模拟了剪切变稀的血液流动; Chen等^[20]模拟了幂律流体通过多孔介质的流动. 然而, 将LBM应用于幂律流体转捩问题研究仍有待探索.
基于此, 本文以二维顶盖驱动流为物理模型, 以格子Boltzmann方法为核心求解器, 采用非牛顿流体幂律模型, 开展了非牛顿流体二维顶盖驱动流转捩模拟, 并借助快速傅里叶变换、本征正交分解(proper orthogonal decomposition, POD)等方法, 分析了转捩点附近的流场时频域特性及模态分布.

2

-->

2.1.物理模型

顶盖驱动流模型如图1所示, 上顶板为运动壁面, 速度为U₀, 其余3个壁面均为静止无滑移壁面. 模型水平和竖直方向上长度分别为L_x和L_y, 且L_x = L_y = L₀, L₀为特征长度. 图1中, 坐标原点O位于底面与左壁面交点处. 为定量表征流场状态与雷诺数(Reynolds number, Re)之间的关系, 选取监控点坐标为(0.6L₀, 0.6L₀).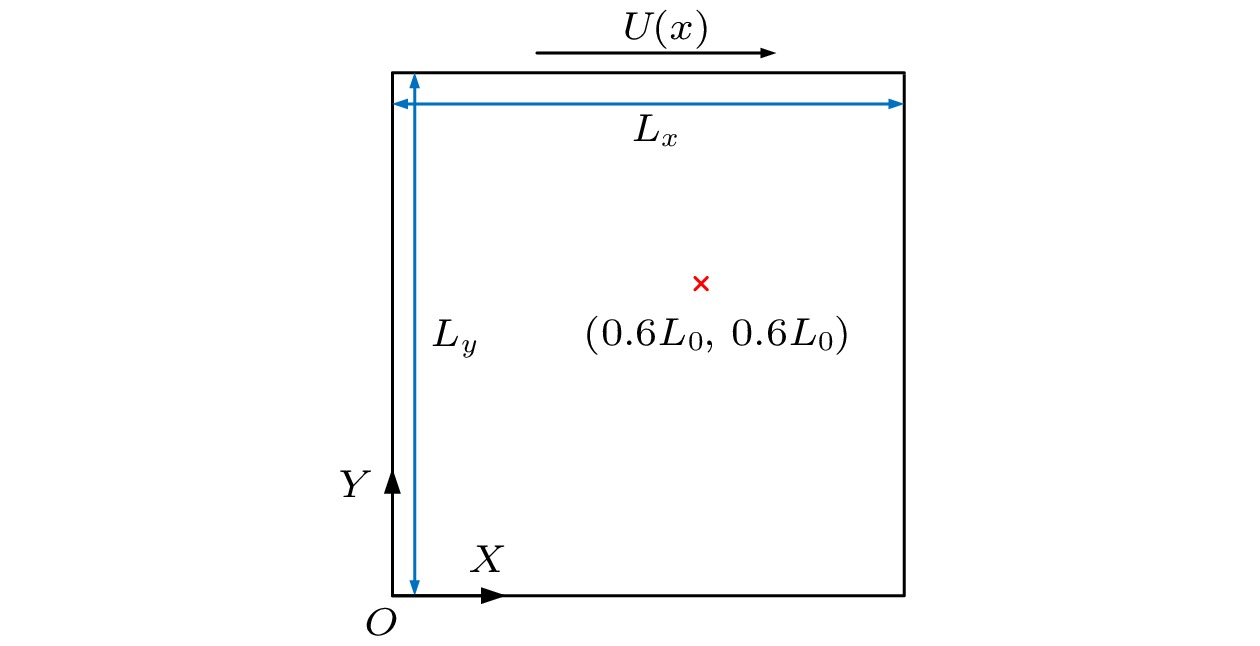
图 1 算例模型示意图
Figure1. Schematic diagram of calculation model.

幂律流体运动黏性系数的计算公式如下:

$\left\{ {\begin{aligned}&{{\boldsymbol{S}} = \frac{1}{2}\left( {{\bf{\nabla}} {\boldsymbol{u}} + {\bf{\nabla}} {{\boldsymbol{u}}^{\rm{T}}}} \right),}\\&{\dot \gamma = \sqrt {2{\boldsymbol{S}}:{\boldsymbol{S}}},}\\&{\nu = m{{\left( {\dot \gamma } \right)}^{n - 1}},}\end{aligned}} \right.$

式中, S为流场中格点处应变率张量, $ \dot{\gamma } $为剪切率, n为幂律指数, $ \nu $为运动黏性系数, m为幂律系数(与Re有关的常量). 当n = 1时为牛顿流体; n < 1为剪切变稀流体; n >1时为剪切增稠流体.
雷诺数的定义为^[21]

$ Re = {{{{U}}_{ {0}}^{\left( {2 - {n}} \right)}{L}_{ {0}}^{n}}}/{m}. $

2 -->

2.2.数值方法

采用LBM多松弛时间模型^[22], 并使用基于统一计算设备构架的显卡并行加速技术^[23]来提高计算速度. 其中, 多松弛时间模型表达式为

$ \begin{split} &f\left( {\boldsymbol{x} + {\boldsymbol{e}_i}{\text{δ}}t,t + {\text{δ}}t} \right) - f\left( {\boldsymbol{x},t} \right) \\ =\;& - \left( {{{\boldsymbol{M}}^{ - 1}}{{\boldsymbol{\varLambda}} ^f}{\boldsymbol{M}}} \right)\left[ {f\left( {\boldsymbol{x},t} \right) - {f^{{\rm{eq}}}}\left( {\boldsymbol{x},t} \right)} \right], \end{split} $

式中, $ f(\boldsymbol{x}, t) $为t时刻流场中坐标位置为x处的分布函数, $ {\boldsymbol{e}}_{i} $为离散速度, $\text{δ}t$为时间步长, M为从速度空间向矩空间进行转换的矩阵, $ {f}_{i}^{\mathrm{e}\mathrm{q}} $为平衡态分布函数.
针对文中研究的二维顶盖驱动流, 选用经典D2Q9模型^[24], 离散速度$ {\boldsymbol{e}}_{i} $为

$ {\boldsymbol{e}_i} = \begin{cases} (0,0), & i = 0, \\(\cos [(i-1) \pi/2], \sin [(i-1){\rm{\pi }}/2]), & i= 1—4,\\\sqrt2(\cos [(i-5){\rm{\pi }}/2 + {\rm{\pi }}/4],& \\ ~~\sin [( i - 5){\rm{\pi }}/2 + {\rm{\pi }}/4]), & i = 5—8. \end{cases} $

LBM平衡态分布函数采用不可压模型^[25], 其表达式为

$ f_i^{{\rm{eq}}} = \left\{ {\begin{aligned} &{{\rho _0} - \left( {1 - {w_i}} \right)\frac{p}{{c_{\rm{s}}^2}} - \frac{{{w_i}}}{{2c_{\rm{s}}^2}}{u^2},\,\;\;\;\;\;\;\;\;\;\;\;\;\;i = 0,}\\ &{\frac{{{w_i}p}}{{c_{\rm{s}}^2}} + {w_i}\left( {\frac{{{\boldsymbol{e}_i}\boldsymbol{u}}}{{c_{\rm{s}}^2}} + \frac{{{{\left( {{\boldsymbol{e}_i}\boldsymbol{u}} \right)}^2}}}{{2c_{\rm{s}}^4}} - \frac{{{u^2}}}{{2c_{\rm{s}}^2}}} \right),\;\;i = 1—8,} \end{aligned}} \right. $

式中, $ {\rho }_{0} $为不可压流体的密度; $ p $为压强; $ \boldsymbol{u}$为格点处的速度; 权系数$ {w}_{i} $的取值为$ {w}_{0}=4/9 $, ${w}_{1-4}= 1/9$, $ {w}_{5-8}=1/36 $; $ {c}_{\mathrm{s}} $为格子声速. 松弛参数对角矩阵选为${\boldsymbol{\varLambda }}^{f}=[1.0, \;1.1, \;1.0, \;1.0, \;1.2, \;1.0, \;1.2,\; 1/\tau,\; 1/\tau]$, 松弛时间$ \tau $与运动黏性关系为$\nu =(\tau - 0.5) {c}_{\mathrm{s}}^{2}\text{δ}t$.
流场中宏观速度与压强的求解公式为

$\boldsymbol{u}=\frac{1}{{\rho }_{0}}\sum {f}_{i}{\boldsymbol{e}}_{i}, $

$p=\frac{{\rho }_{0}{c}_{\mathrm{s}}^{2}}{1-{w}_{0}}\bigg(\sum\limits_{i\ne 0}{f}_{i}-\frac{{w}_{0}{u}^{2}}{2{c}_{\mathrm{s}}^{2}}\bigg). $

为保证流场时空分辨率, 本文最终选用的网格分辨率为512 × 512, 计算时间总长2000T₀ (T₀为参考时间), 即1600万个格子时间步长. 静壁边界采用半步长反弹格式^[26], 动壁采用动量补偿格式^[27]. 为防止运动黏性系数过大或者过小造成计算结果发散, 这里设置运动黏性系数上限和下限^[28]分别为$ 20{\nu }_{0}, \; {\nu }_{0}/20 $. 不失一般性, 文中取n = 0.75, 1.25分别代表剪切变稀流体和剪切增稠流体. 具体模拟流程如图2所示.
图 2 LBM与幂律模型耦合计算流程示意图
Figure2. Diagram of coupling calculation process between LBM and power law model.

2 -->

2.3.POD方法

POD^[29,30]是一种广泛应用于流场降阶模型中的方法, 可用于流场特征信息的提取. 以速度POD为例, 已知N个时刻流场速度信息$ {\boldsymbol{u}}(\boldsymbol{x}, {t}_{i}) $, i = 1—N, 则有

$ {\boldsymbol{u}}\left(\boldsymbol{x},{t}_{i}\right)=\bar{\boldsymbol{u}}\left(\boldsymbol{x}\right)+{\boldsymbol{u}}'\left(\boldsymbol{x},{t}_{i}\right), $

$ \bar{\boldsymbol{u}}\left(\boldsymbol{x}\right)=\frac{1}{N}\sum _{i=1}^{N}\boldsymbol{u}\left(\boldsymbol{x},{t}_{i}\right), $

$ {\boldsymbol{D}} = [{\boldsymbol{u}}'\left(\boldsymbol{x},{t}_{1}\right) \; {\boldsymbol{u}}'\left(\boldsymbol{x},{t}_{2}\right)\cdots {\boldsymbol{u}}'\left(\boldsymbol{x},{t}_{N}\right)] = \boldsymbol{\varPhi }\boldsymbol{\varSigma }{\boldsymbol{C}}^{\mathrm{T}}. $

式中, $ \bar{\boldsymbol{u}}\left(\boldsymbol{x}\right) $为N个时刻流场的平均值, $ {\boldsymbol{u}}'\left(\boldsymbol{x}, {t}_{i}\right) $为对应的波动量, D为速度相关矩阵. 通过对D进行奇异值分解, 可获得POD模态矩阵$ \boldsymbol{\varPhi } $、奇异值对角矩阵$ \boldsymbol{\varSigma } $以及时间演化系数矩阵$ \boldsymbol{C} $, 其中, $ \boldsymbol{\varPhi } $和$ \boldsymbol{\varSigma } $为正交矩阵.
另外, $ \boldsymbol{\varSigma }=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}({\sigma }_{1}, {\sigma }_{2}, \cdots {\sigma }_{i}, \cdots ) $中各$ {\sigma }_{i} $模长的平方可用来表征对应模态的“能量”. 按照模态能量的大小进行排序即可得到流场的主要模态.
2 -->

2.4.第一转捩雷诺数计算

在顶盖驱动流中, 随着Re增加, 呈现出的流动状态往往是从层流逐步过渡到湍流, 并存在Hopf分岔现象. 通过在流场的特定位置处设置监控点的方法^[5,31], 可以研究Hopf分岔现象. 开始产生分岔现象时的雷诺数, 即第一转捩雷诺数可以通过如下的方式计算:

${A}_{\mathrm{m}\mathrm{p}}=\mathrm{m}\mathrm{a}\mathrm{x}\left[u\right(t\left)\right]-\mathrm{m}\mathrm{i}\mathrm{n}\left[u\right(t\left)\right], $

其中$ \mathrm{m}\mathrm{a}\mathrm{x}\left[u\right(t\left)\right] $与$ \mathrm{m}\mathrm{i}\mathrm{n}\left[u\right(t\left)\right] $分别为流场充分发展后, 监控点处水平速度u的最大值与最小值. 鉴于$ {A}_{\mathrm{m}\mathrm{p}}^{2} $与Re成正比关系, 因此可以通过计算不同雷诺数下的$ {A}_{\mathrm{m}\mathrm{p}}^{2} $, 使用最小二乘法线性拟合出$Re\text{-} $$ {A}_{\mathrm{m}\mathrm{p}}^{2}$图. 拟合所得的直线与$ {A}_{\mathrm{m}\mathrm{p}}^{2}=0 $的交点, 即流场从稳定向周期态转变的第一转捩临界雷诺数.

2

-->

3.1.算例验证

为了验证计算的准确性, 这里首先给出了牛顿流体顶盖驱动流模拟结果. 图3为Re = 5000时, 方腔中心线上的速度分布与Peng等^[5]结果的对比, 其中X-v曲线显示的是竖直方向上方腔的中心线上速度分量分布, 即纵坐标y/L = 0.5上的X和v之间的对应关系; Y-u曲线显示的是水平方向上的中心线上速度分量分布, 即横坐标x/L = 0.5上的Y和u之间的关系. Peng等^[5]在牛顿流体顶盖驱动流转捩问题研究中, 使用的是限差分法, 本文的计算结果与Peng等^[5]对比良好. 值得注意的是Peng等^[5]求解对流项使用的是七阶迎风格式, 扩散项使用的是六阶中心差分格式.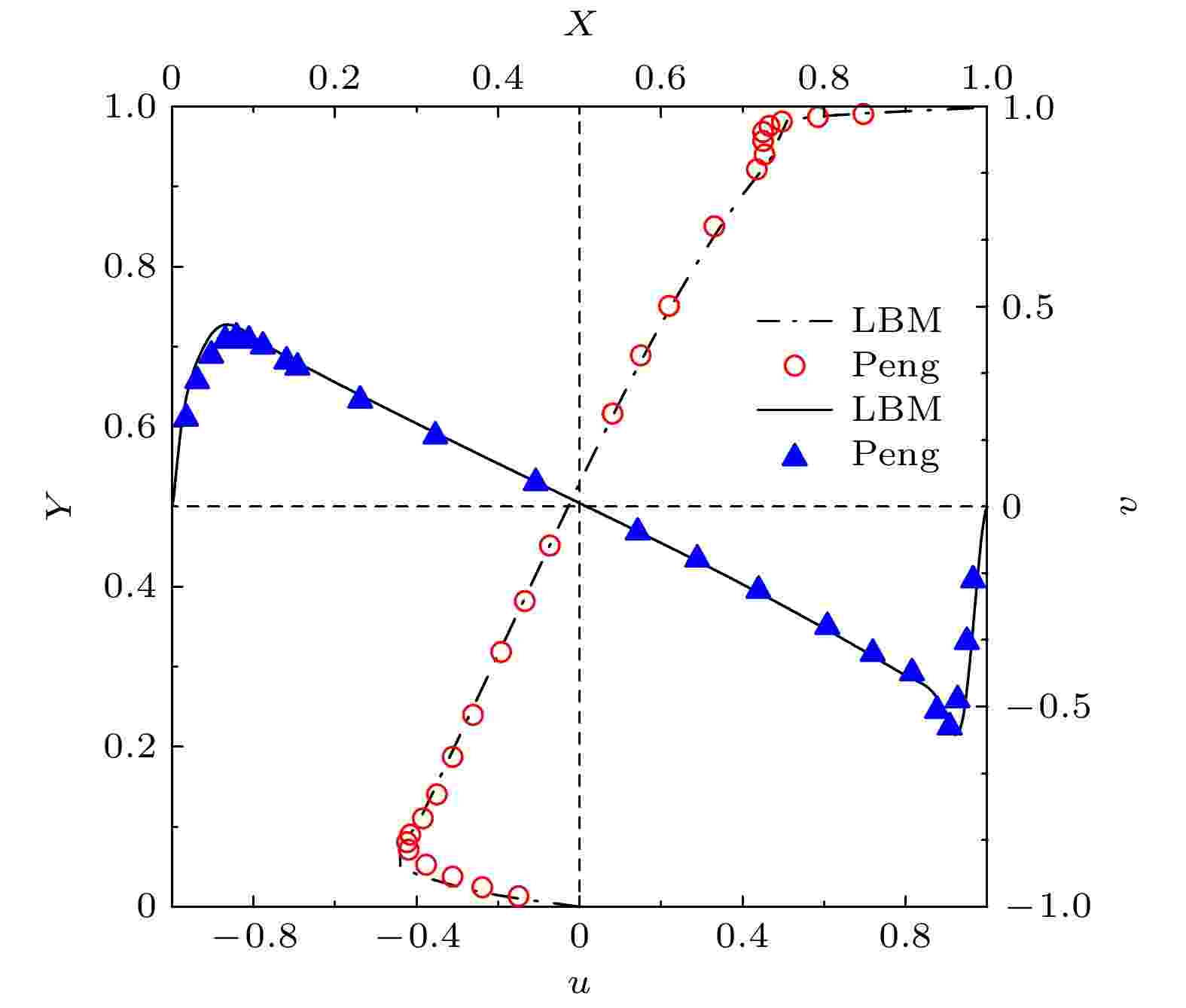
图 3 顶盖驱动流在中心线处的速度分布
Figure3. Velocity distribution at center line of lid-driven flow.

2 -->

3.2.第一转捩雷诺数

按照文中2.4节的方法得到牛顿流体、剪切变稀流体和剪切增稠流体的第一转捩雷诺数依次为7835, 5496和11546, 结果如图4所示.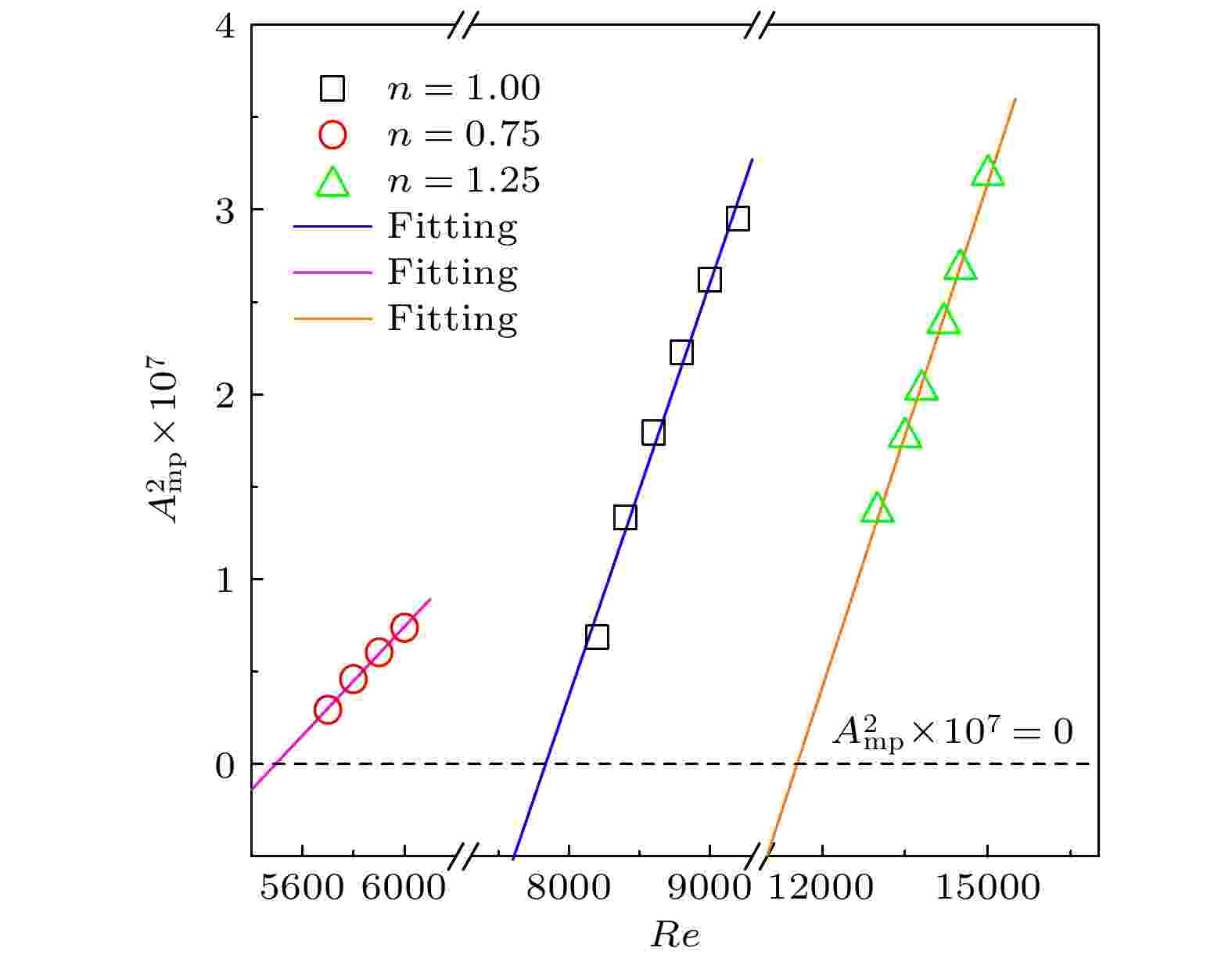
图 4 转捩临界雷诺数
Figure4. Transition critical Reynolds number.

将本文计算的牛顿流体转捩雷诺数与文献的结果进行比对, 如表1所列, 可以看出, 本文计算的牛顿流体转捩临界雷诺数相对于Peng等^[5]和Poliashenko与Aidu^[32]的计算结果而言较大, 而相对于Cazemier等^[31]和Bruneau与Saad^[6]的计算结果而言较小, 但是从总的相对误差的值来看, 误差上限不超过5%, 可以看出本文计算可靠性较高.

	转捩临界雷诺数
本文	7835
Peng等[5]	7704
Poliashenko和Aidu[32]	7763 × (1% ± 2%)
Cazemier等[31]	7819
Bruneau和Saad[6]	8000—8030

表1牛顿流体转捩临界雷诺数计算结果的对比
Table1.Comparison of calculation results of critical Reynolds number for Newtonian fluid transition.

相比于牛顿流体, 剪切变稀流体的转捩雷诺数较低, 即剪切变稀流体更容易从定常状态向周期态转变. 而由剪切变稀流体本身的定义可知, 剪切速率越大, 其黏性会越低, 流动状态也越容易发生转变, 这与计算结果表现出的性质是相符合的. 与牛顿流体相比, 剪切增稠流体的转捩临界雷诺数较高, 即剪切增稠流体更不易从定常状态向周期态转变. 而根据剪切增稠流体本身的定义可知, 剪切速率越大, 其黏性会越大, 流动状态也越不易发生转变.
2 -->

3.3.速度监控点时频域特性

选取三类流体在转捩雷诺数附近的流场, 进行时频域分析. 图5给出了三类流体在转捩雷诺数附近, 速度监控点处的时频域特性图. 其中图5(a)—(c)给出了三类流体在转捩前后, 水平方向速度随时间的变化, 可以看出, 三类流体在转捩发生前的定常流动状态下, 速度为一水平直线, 在转捩雷诺数附近, 速度均呈现周期性变化的特点, 在转捩后湍流状态下, 速度有明显的大幅度波动. 对水平速度作快速傅里叶变换得图5(d)—(f), 在发生转捩前, 由于其直流部分即$ f=0 $为其主要分量, 在频谱图上显示为一点, 在转捩雷诺数附近, 水平速度均存在一个主频$ {f}_{1} $与谐频$ {f}_{2} $, 且满足$ {f}_{2}=2{f}_{1} $, 但不同类型流体的$ {f}_{1} $值并不相同, 在转捩后湍流状态下, 出现了明显的多频现象. 图5(g)—(i)为三类流体在转捩雷诺数附近, 水平速度u与竖直方向速度v之间形成的速度相图. 可以发现不同类型的流体的速度相图的变化范围并不相同, 但均为单一光滑封闭曲线.
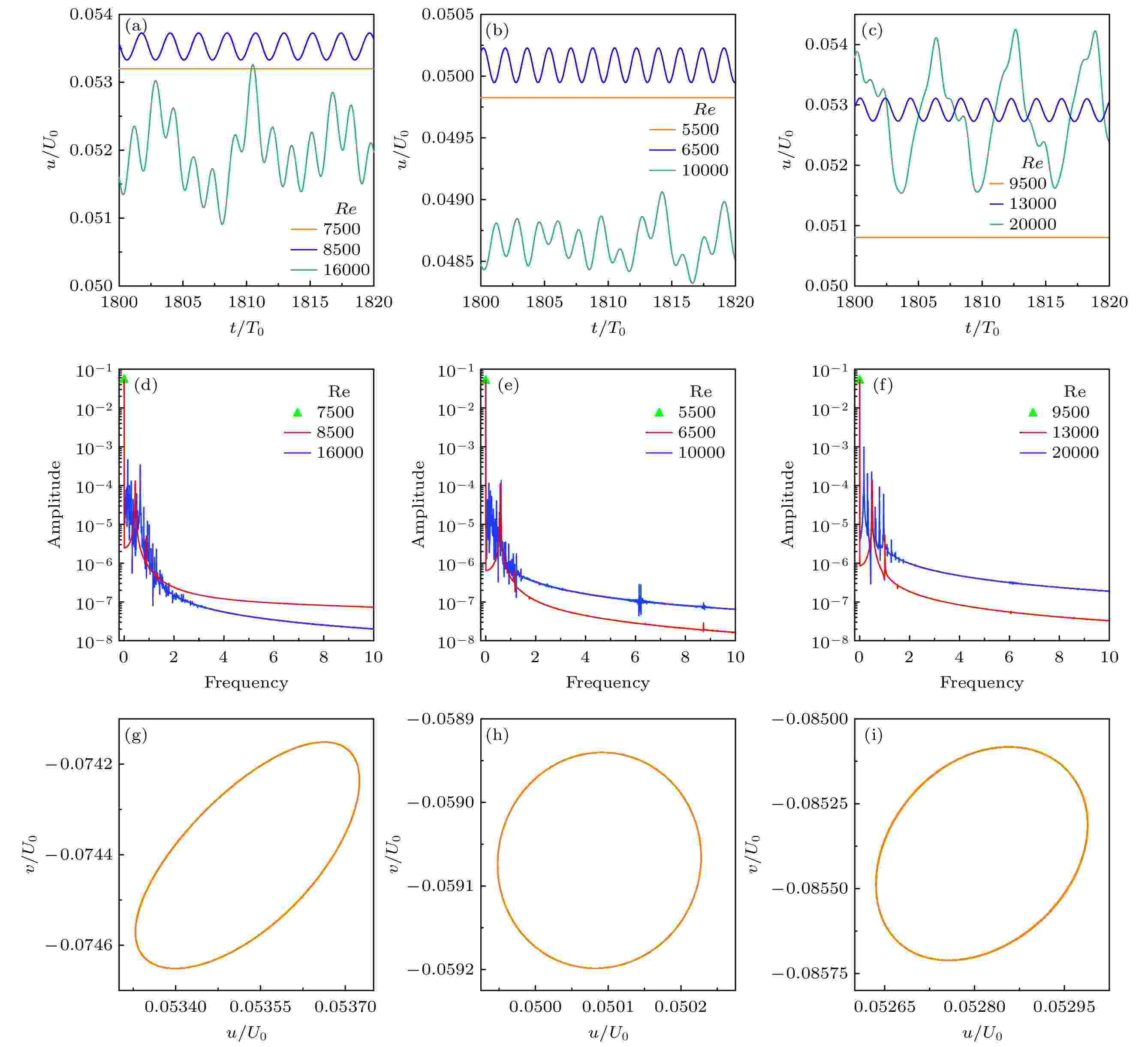图 5 三类流体在速度监控点处的时频域特性　(a), (d) n = 1, Re = 7500, 8500, 16000; (g) n = 1, Re = 8500; (b), (e) n = 0.75, Re = 5500, 6500, 10000; (h) n = 0.75, Re = 6500; (c), (f) n = 1.25, Re = 9500, 13000, 20000; (i) n = 1.25, Re = 13000
Figure5. Time-frequency spectrum characteristics at the velocity monitoring point for three types of fluids: (a), (d) n = 1, Re = 7500, 8500, 16000; (g) n = 1, Re = 8500; (b), (e) n = 0.75, Re = 5500, 6500, 10000; (h) n = 0.75, Re = 6500; (c), (f) n = 1.25, Re = 9500, 13000, 20000; (i) n = 1.25, Re = 13000.

图6为监控点处牛顿流体、剪切变稀与剪切增稠流体在不同雷诺数情况下的速度相图, 各封闭曲线中心点用虚线进行连接. 图6(a)为牛顿流体在不同雷诺数下的速度相图, 其中Re = 7500, 8000时, 速度波动极小, 在相图上呈现的是1个点, 而在Re = 8500—9500时, 相图为光滑封闭曲线, 曲线整体向右上方移动且包围的面积在不断增加. 图6(b)为剪切变稀流体在不同雷诺数下的速度相图, 在Re = 5500时, 速度相图为1个点, 而Re = 5700—6000时, 速度相图为封闭曲线, 随着Re增加向上方移动, 且包围的面积在不断增加. 图6(c)为剪切增稠流体在不同雷诺数下的速度相图, 其中Re = 11500, 12000, 12500时, 速度相图为单一点, 而Re = 13000—15000时, 速度相图为光滑封闭曲线. 速度相图整体变化趋势为先向右再向左上方移动, 向右移动的过程中, 竖直方向上速度v几乎没有变化, 而向左上方移动的过程中, 封闭曲线包围的面积逐渐增大, 有较为明显的变化规律.
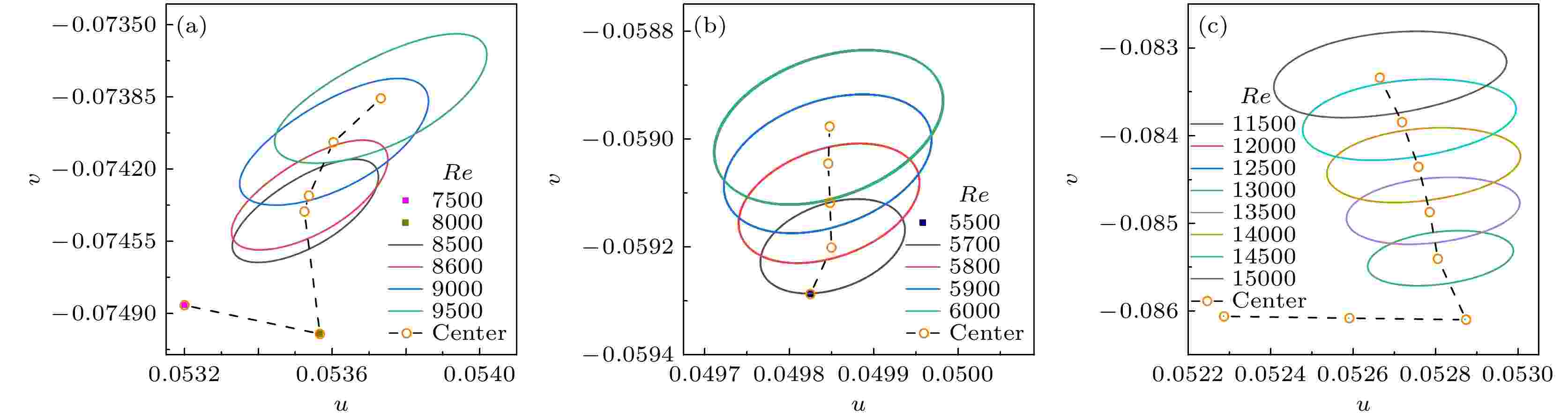图 6 在监控点处的速度相图　(a) 牛顿流体; (b) 剪切变稀流体; (c) 剪切增稠流体
Figure6. Velocity phase diagrams at the monitoring point: (a) Newtonian fluid; (b) shear-thinning fluid; (c) shear-thickening fluid.

2 -->

3.4.流场模态分析

进一步使用POD对牛顿流体、剪切变稀和剪切增稠流体的流场速度、涡量和黏性进行处理, 结果如图7和图8所示. 图7(a)—(c)分别为牛顿流体、剪切变稀流体和剪切增稠流体的水平速度POD能量占比图. 从图7可以发现, 不同类型的流体在第一临界转捩雷诺数附近且发生转捩后, 均呈现前两阶模态能量占主导地位的特点, 能量占比超95%, 且前两阶模态能量占比接近. 在图7(a) Re = 10500时, 出现了多模态的结果, 这里的流场可能是进入Hopf第二分岔第二模式中^[5]. 在图7(c) Re = 11500, 12500时, 一阶模态能量占比大幅度高于二阶模态的能量占比, 但结合图6(c)可以发现, 此时流场速度波动量较小几乎为定常流场, 一阶模态与二阶模态相对于平均流场几乎可以忽略.
图 7 速度u的各阶模态的能量占比　(a) 牛顿流体; (b) 剪切变稀流体; (c) 剪切增稠流体
Figure7. Energy share of each order of mode for velocity u: (a) Newtonian fluid; (b) shear thinning-fluid; (c) shear-thickening fluid.

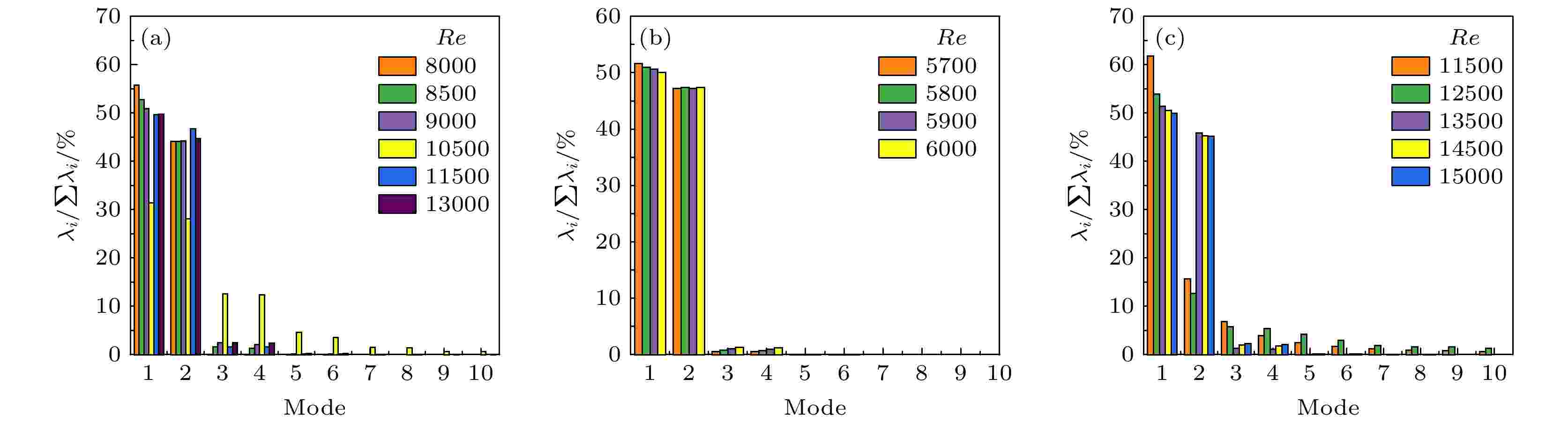图 8 涡量的各阶模态的能量占比　(a) 牛顿流体; (b) 剪切变稀流体; (c) 剪切增稠流体
Figure8. Vortex energy share of each order of mode: (a) Newtonian fluid; (b) shear-thinning fluid; (c) shear-thickening fluid.

图8(a)—(c)分别为牛顿流体、剪切变稀流体和剪切增稠流体的涡量POD能量占比图. 涡量POD能量占比与水平速度POD能量占比结果相比, 同种流体在同一雷诺数下, 涡量POD一阶模态的占比略高于水平速度POD能量占比, 涡量POD中前两阶模仍占主导地位.
图9为牛顿流体在不同雷诺数下各阶模态的流场模态的速度场云图, 图9(a)和图9(d)分别为Re = 8500与Re = 9000时平均水平速度场云图, 图9(b)和图9(e) 分别为Re = 8500与Re = 9000时水平速度一阶模态云图, 图9(c)和图9(f) 分别为Re = 8500与Re = 9000时水平速度二阶模态云图. 从速度平均场来看, Re = 8500与Re = 9000的结果相近; 从一阶模态的云图来看, 峰值区域均靠近壁面, 且峰值区域的形状相似; 从二阶模态的云图来看, 二阶模态的结果相近, 且峰值主要分布在壁面处.
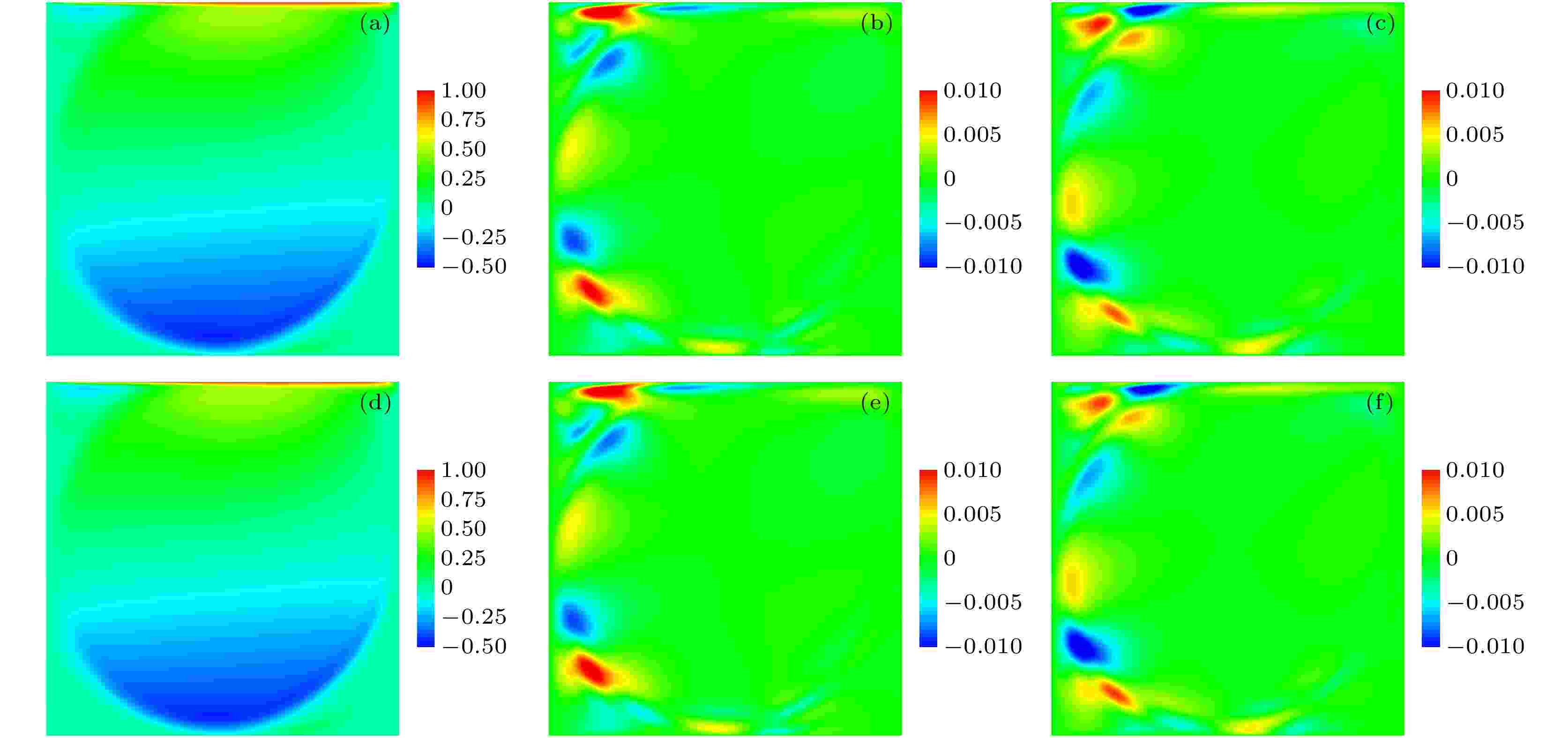图 9 牛顿流体的水平速度的各阶模态图　(a), (b), (c) Re = 8500时, 平均场、一阶模态与二阶模态; (d), (e), (f) Re = 9000时, 平均场、一阶模态与二阶模态
Figure9. Modal diagrams of horizontal velocity of Newtonian fluid: (a), (b) and (c) The mean field, the first and second modes when Re = 8500; (d), (e), (f) mean field, first-order mode and second-order mode when Re = 9000

图10为剪切变稀流体在不同Re下各阶模态的流场模态的速度场云图, 图10(a)和图10(d)分别为Re = 5700与Re = 6000时平均速度场云图, 图10(b)和图10(e)分别为Re = 5700与Re = 6000时速度一阶模态云图, 图10(c)和图10(f)分别为Re = 5700与Re = 6000时速度二阶模态云图. 从平均场的结果来看, Re = 5700与Re = 6000结果相近; 从一阶和二阶模态的结果来看, 模态峰值分布区域集中在壁面附近, 峰值分布区域的形状相似, 但峰值分布区的模态值相反.
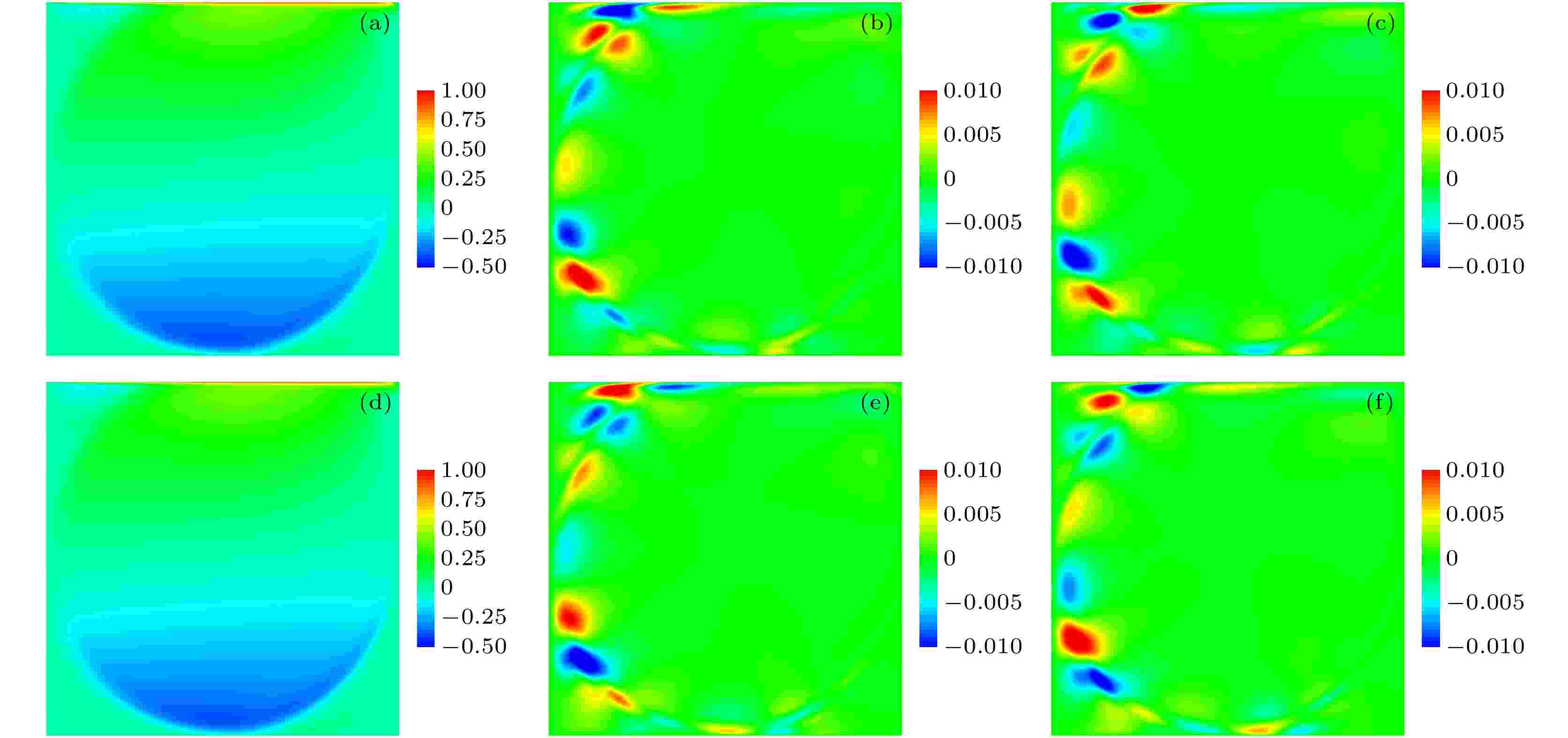图 10 剪切变稀流体的水平速度的各阶模态图　(a), (b), (c) Re = 5700时, 平均场、一阶模态与二阶模态; (d), (e), (f) Re = 6000时, 平均场、一阶模态与二阶模态
Figure10. Modal diagrams of horizontal velocity of shear-thinning fluid: (a), (b), (c) The mean field, the first and second modes when Re = 5700; (d), (e), (f) mean field, first-order mode and second-order mode when Re = 6000.

图11为剪切增稠流体在不同Re下各阶模态的流场模态的速度场云图, 图11(a)和图11(d)分别为Re = 13000与Re = 13500时平均速度场云图, 图11(b)和图11(e)分别为Re = 13000与Re = 13500时速度一阶模态云图, 图11(c)和图11(f)分别为Re = 13000与Re = 13500时速度二阶模态云图. 从平均场的结果来看, Re = 13000与Re = 13500结果相近; 从一阶和二阶模态的结果来看, 峰值分布区域集中在壁面附近, 且峰值分布区域的形状相似, 这与牛顿流体和剪切变稀流体的结果是类似的. 剪切增稠流体一阶和二阶模态峰值分布区的模态值相反.
图 11 剪切增稠流体的水平速度的各阶模态图　(a), (b), (c) Re = 13000时, 平均场、一阶模态与二阶模态; (d), (e), (f) Re = 13500时, 平均场、一阶模态与二阶模态
Figure11. Modal diagrams of horizontal velocity of shear-thickening fluid: (a), (b), (c) The mean field, the first and second modes when Re = 13000; (d), (e), (f) mean field, first-order mode and second-order mode when Re = 13500.

论文针对典型的非牛顿流体—幂律流体, 利用格子Boltzmann的计算框架, 以顶盖驱动流为物理模型, 研究得到幂律指数在0.75和1.25时的第一临界转捩Re分别为5496和11546. 在转捩Re附近且发生转捩后, 流场监控点的速度随时间呈周期性变化, 存在一个主频与谐频. 与转捩前速度相图为单一点不同, 转捩后速度相图为光滑封闭曲线, 且随着Re增加, 曲线中心点朝一定的方向移动且包络面积不断增加, 但不同流体中心点移动的方向不相同. 流场的速度、涡量POD分解的结果均表明, 流场在转捩临界雷诺数附近, 其前两阶模态为其主要模态, 能量占比超95%. 从模态云图的结果看, 一阶模态与二阶模态速度峰值分布区域主要在壁面附近, 且同种流体不同Re下的平均场结果相近, 一阶模态与二阶模态的峰值分布区域形状相似.