摘要:CdS/CdMnTe异质结是具有集成分立光谱结构的叠层电池的“核芯”元件, 是驱动第三代太阳能电池发展的核心引擎, 其界面相互作用对大幅度提高太阳能电池的转换效率至关重要. 本文采用基于密度泛函理论的第一性原理计算构建CdS (002), CdMnTe (111)表面模型及Mn原子占据不同位置的CdS/CdMnTe异质结界面结构模型, 分析CdS (002), CdMnTe (111)表面及异质结界面的电子性质和光学性质. 晶格结构分析表明, CdS/CdMnTe异质结的晶格失配度约为3.5%, 弛豫后原子位置与键长均在界面处发生一定程度的变化. 态密度分析发现异质结界面的费米能级附近不存在界面态, 并且界面处的Cd, S, Te原子之间的轨道杂化可增强界面的结合能力. 差分电荷密度分析显示, 界面处发生了电荷的重新分配, 电子由CdMnTe转移到CdS侧. 光学分析显示, CdS/CdMnTe异质结主要吸收紫外光, 吸收系数可达10⁵ cm^–1, 但不同Mn原子位置的异质结光学性质也稍有差别. 在200—250 nm范围, Mn原子位于中间层的异质结的吸收系数更大, 但在250—900 nm范围内, Mn原子位于界面层的异质结吸收峰更高. 本文合理构建了CdS/CdMnTe异质结模型, 计算分析了其界面光电性能, 可为提高叠层电池的光电转换效率提供一定的理论参考, 为实现多带隙异质结的实验研究提供一定的理论依据.
关键词: CdS/CdMnTe异质结/
第一性原理计算/
态密度/
光学性质

English Abstract

全文HTML

--> --> -->

随着科学技术的进步和化石燃料消耗峰值的到来, 人类能源结构将发生根本性变革, 预计到2050年, 可再生能源占总一次能源的比例将大于50%^[1]. 太阳能既是可再生能源, 又是清洁能源, 因此, 研究太阳能电池符合世界范围能源与环境的发展趋势^[2-5]. 晶硅太阳能电池研究最早, 工艺最成熟, 在太阳能电池领域占据主导性地位. 但是, 由于晶硅材料进一步降低成本的空间很小和世界硅年产量不足等原因, 世界各国一直高度重视薄膜太阳能电池的开发和利用^[6,7], 一方面因为其材料消耗低而有利于降低成本, 另一方面因为薄膜太阳能电池能制备成大面积组件而有利于规模化生产. 因此, 薄膜太阳能电池的研发在一个较长的历史阶段代表着光伏科学与技术的发展方向^[8,9].
提高太阳能电池的转换效率是光伏工作者不懈的追求, 目前非晶硅、碲化镉和铜铟镓硒等单结薄膜电池的实际效率已接近理论效率(20%), 这是因为吸收层有一个确定的带隙宽度, 所以理论转换效率受到了限制^[10-12]. 具有更高效率(20%—40%)的薄膜太阳能电池可以通过双结或多结叠层电池来实现^[13]. 研究表明^[14,15], 对于高转换效率的双结叠层电池, 所需的顶层电池材料的理想禁带宽度为1.7 eV左右. 碲锰镉(CdMnTe)薄膜材料在太阳光谱范围内具有高吸收系数、高电子传输性能、高化学稳定性等特点, 其禁带宽度在1.45—2.85 eV之间连续可调, 是制备叠层太阳能电池顶层电池的理想材料^[16-18]. 关于CdMnTe太阳能电池薄膜生长实验和理论方面的研究已取得一定的进展. 2004年, Wang等^[19]采用磁控溅射法成功制备出CdMnTe单异质结薄膜太阳能电池, 并分析了氯化处理对其光电转换效率的影响, 发现在390—430 ℃时, H₂ + Ar气氛下加入CdCl₂ + MnCl₂(10%)进行退火, CdMnTe电池的效率可提高100倍. 2010年, 侯泽荣等^[20]在用化学沉积法制备CdMnTe的实验中发现, CdS/CdMnTe异质结界面附近可能存在由于原子互扩散而形成的中间层, 这个中间层可以降低晶格失配度和界面态, 从而改善p-n结的光电性能. 2019年, Chander和Dhaka^[16]采用近空间升华法制备了CdMnTe薄膜太阳能电池, 探索了高光电转换效率的制备条件和退火工艺条件. 2020年, Olusola等^[21]采用双电极沉积技术在不同阴极电位下成功制备出p型和n型导电的CdMnTe薄膜, 研究结果表明, 不管使用何种电位, 生长的CdMnTe薄膜在退火后均为p型导电, 这为获得光电质量良好的p型CdMnTe薄膜提供了途经. 相比于薄膜生长实验, 理论方面的研究鲜见报道, 并且主要集中于对单层材料本身的计算. 2014年, Shafaay^[22]采用广义梯度近似(GGA-PBE)理论对CdS窗口层的结构进行优化, 并计算出其禁带宽度为2.66 eV. 2016年, Gueddim等^[23]通过密度泛函理论对CdMnTe吸收层的电子结构与光学性质进行了研究, 计算并分析了不同Mn含量的CdMnTe晶体的能带结构与吸收光谱. 2020年, Ilchuk等^[24]在赝势框架内, 进行了CdMnTe动力学理论研究, 通过改变电子系统参数, 结合Kramers-Kronig方程, 得到了与实验数据相符的介电磁导率、反射指数与反射光谱.
CdS/CdMnTe异质结的界面电子形态对提高CdMnTe薄膜太阳能电池的性能至关重要, 但实验研究难以在原子尺度上观察界面的显微结构并揭示其微观机理, 因此需要对界面性质进行理论研究. 本文瞄准CdS/CdMnTe异质结界面原子的相互作用, 通过第一性原理从头计算的方法, 研究CdS, CdMnTe表面以及异质结界面的光学性质, 分析CdS/CdMnTe界面态、Mulliken电荷和差分电荷等电学性质. 旨在通过异质结模型的合理构建及界面附近电子性质的分析计算, 对CdS/CdMnTe界面的光电性能有更深入的了解, 对提高CdMnTe薄膜顶层电池的光电转换效率有所裨益.

CdMnTe是Mn原子部分取代CdTe晶格中的Cd而形成的三元化合物. 在建立表面模型前对CdTe和CdS的晶格结构进行了研究, 计算得到的晶格常数如表1所列. 对比表中的数据可以看出, 本文的计算结果与文献结果^[25-27]符合较好.

	CdTe	CdS	*CdTe[25]	*CdS[25]	#CdTe[26]	#CdS[27]
a/?	6.642	4.214	6.646	4.212	6.481	4.140
b /?	6.642	4.214	6.646	4.212	6.481	4.140
c /?	6.642	6.850	6.646	6.858	6.481	6.720
注: *为理论值, #为实验值.

表1CdTe和CdS晶格参数优化结果
Table1.Optimal lattice parameters of CdTe and CdS.

本研究采用基于密度泛函理论(DFT)的Material Studio软件的CASTEP模块进行计算. 计算过程中采用投影缀加平面波(PAW)方法描述赝势^[28-30], 广义梯度近似(GGA-PBE)泛函确定交换关联能^[31]. 平面波基的截止能量设置为400 eV, 布里渊区的Monkhorst-Pack网格设置为4 × 4 × 1. 由于Mn原子的存在, 计算过程中考虑了自旋轨道耦合(SOC)因素^[32]. 所有原子均采用Broyden-Fletcher-Goldfarb-Shanno (BFGS)方法进行几何优化, 直到每个原子上的离子力小于0.02 eV/A, 总能量变化小于1.0 × 10^–6 eV.

2

-->

3.1.CdS (002)和CdMnTe (111)表面模型和电子性质

3 -->

3.1.1.CdS(002)和CdMnTe(111)表面模型

薄膜生长实验发现^[33,34], CdMnTe薄膜太阳能电池的CdS和CdMnTe的择优生长面分别为(002)和(111)晶面, 因此计算中选取(2 × 2)-CdS (002)表面(如图1(a)所示)和($ \sqrt{3} $ × $ \sqrt{3} $)-CdMnTe (111)表面(如图1(b)和图1(c)所示)进行匹配. 由于超胞大小的限制, 在建立CdMnTe表面模型时设计了两种Mn原子位置的模型, 即Mn原子替换表面层(Layer 1)中的Cd原子形成的A₁模型和Mn原子替换中间层(Layer 2)中的Cd原子形成的B₁模型. 两种模型中Mn含量均为原子百分比6.67%, 符合薄膜生长实验中典型的Mn含量要求. 为使表面模型有足够的厚度以模拟体相特性, CdS (002), CdMnTe (111)-A₁和B₁表面模型均包含5个双原子层. 其中表面两层自由弛豫, 下面三层原子冻结以模拟体相原子, 并添加20 ?的真空层以消除周期性边界条件对表面模型的影响.
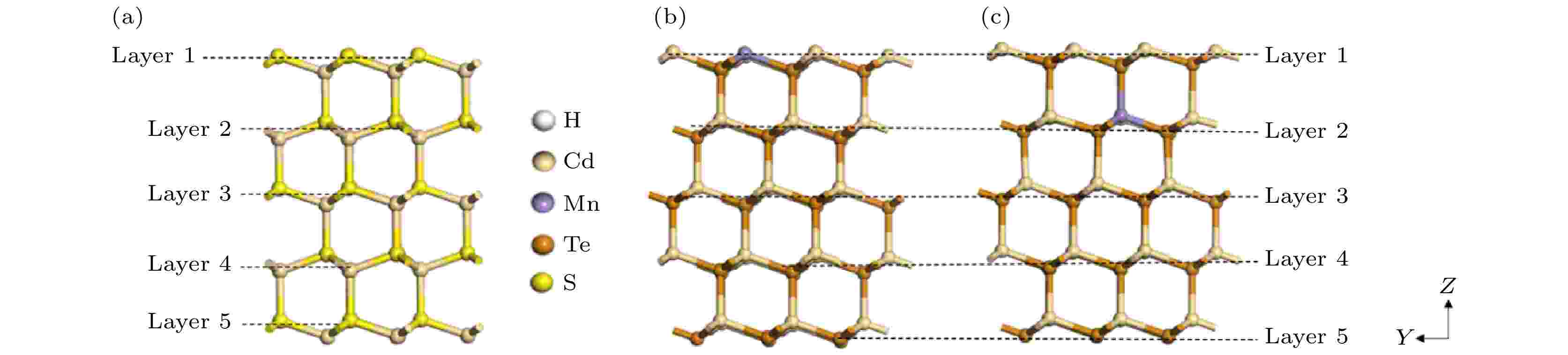图 1 表面模型的建立　(a) CdS (002)表面模型; (b) CdMnTe (111)-A₁表面模型; (c) CdMnTe (111)-B₁表面模型
Figure1. Building of the surface models: (a) Model of the CdS (002) surface; (b) A₁ surface model of CdMnTe (111); (c) B₁ surface model of CdMnTe (111).

结构弛豫后的CdS (002)和CdMnTe (111)表面原子位置和键长的变化如图2所示. 图2(a)中CdS (002)表面的Cd原子沿z轴向上移动了0.035 ?, S原子沿z轴向下移动了0.052 ?. 图2(b)中CdMnTe (111)-A₁表面的Cd原子沿z轴向下移动了0.021 ?, Te原子沿z轴向上移动了0.013 ?. 图2(c)中B₁表面模型的Cd原子沿z轴向下移动了0.073 ?, Te原子沿z轴向上移动了0.040 ?. 层间距离大小和层间距离变化的计算结果见表2. 从表2中的数据可以看出, 弛豫后第1层与第2层, 第2层与第3层之间的原子键长与层间距离的变化比第3层与第4层, 第4层与第5层之间的变化大, 说明层间收缩或扩张主要发生在表面, 内部原子键长与层间距离基本保持不变.
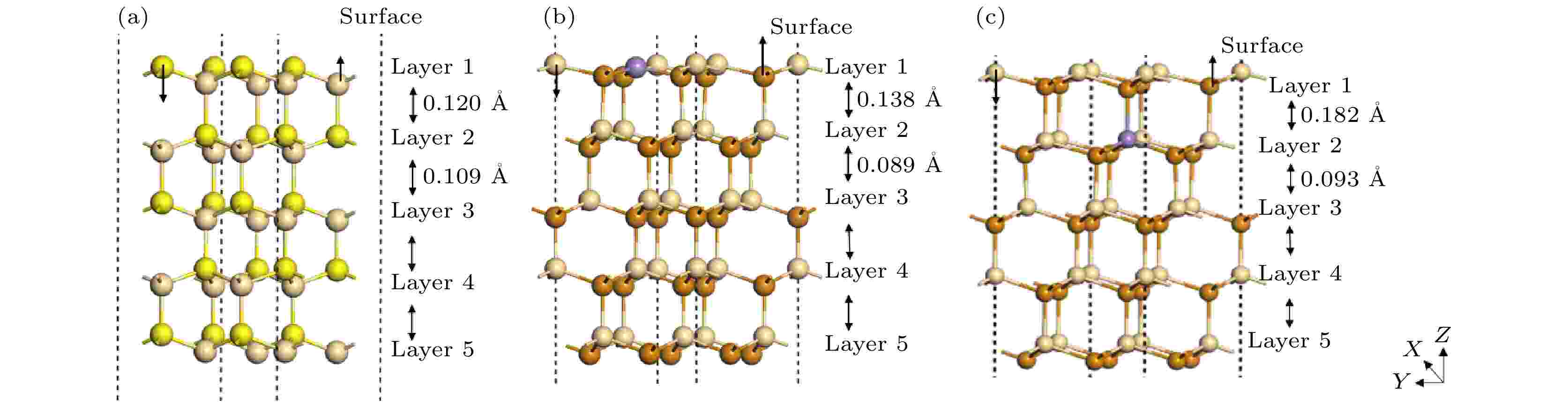图 2 弛豫后的表面原子位置和层间距离的变化　(a) CdS (002)表面模型; (b) CdMnTe (111)-A₁表面模型; (c) CdMnTe (111)-B₁表面模型
Figure2. Variations of atomic positions and interlayer spacing after relaxation: (a) Model of the CdS (002) surface; (b) A₁ surface model of CdMnTe (111); (c) B₁ surface model of CdMnTe (111).

Surface	items	d1-2/?	d2-3/?	d3-4/?	d4-5/?
CdMnTe-A1	dCd-Te	2.829	2.837	2.831	2.831
	dMn-Te	2.605
	?d	0.138	0.089	0.000	0.000
CdMnTe-B1	dCd-Te	2.791	2.841	2.831	2.831
	dMn-Te		2.697
	?d	0.182	0.093	0.000	0.000
CdS	dCd-S	2.534	2.538	2.536	2.536
	?d	0.120	0.109	0.000	0.000

表2弛豫后CdMnTe (111)和CdS (002)表面层间距离的变化
Table2.Variations of interlayer spacing of CdMnTe (111) and CdS (002) surfaces after relaxation.

3 -->

3.1.2.CdS (002)和CdMnTe (111)表面的电子性质

CdS (002)和CdMnTe (111)表面模型的总态密度及其第1层和第5层的局域态密度如图3所示. 图3(a)所示的CdS (002)表面模型总态密度中费米能级附近出现了额外的电子态, 即表面态, 从第1层和第5层的局域态密度可知, 该表面态主要是由CdS表面第1层中S-3p, Cd-4p, Cd-5s轨道引起的. 第5层由于距离表面较远, 受到表面的影响较小, 表现出较好的体相特性. 表面态出现的主要原因是表面原子结构的周期性遭到破坏, 未能形成成对电子而导致电子密度的增加. 这些新的表面电子态对CdS表面的光学性质具有一定的影响.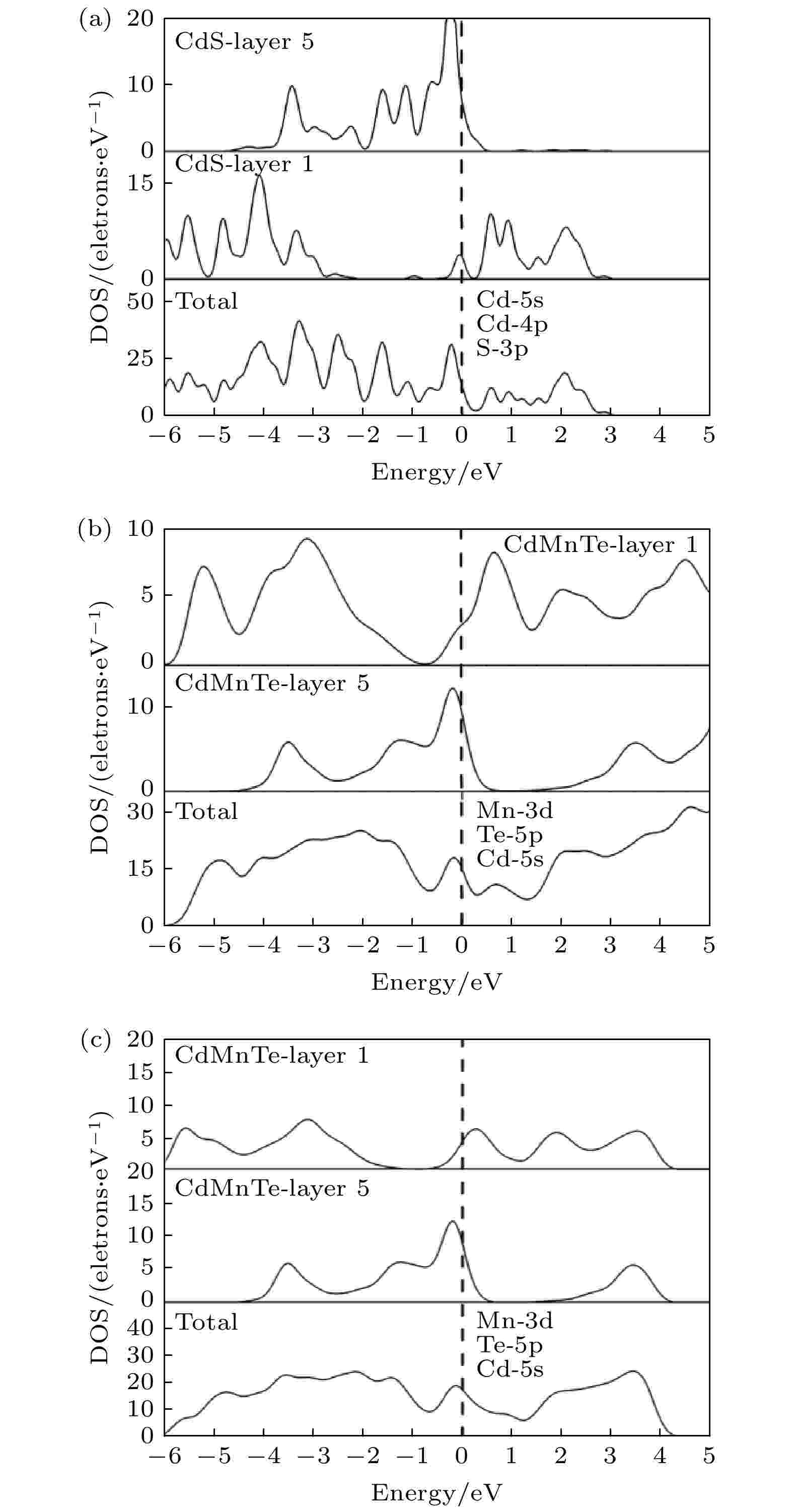
图 3 表面模型总态密度和第1层及第5层局域态密度　(a) CdS (002); (b) CdMnTe (111)-A₁; (c) CdMnTe (111)-B₁
Figure3. Total density of states and the local density of states of the first layer and the fifth layer: (a) CdS (002); (b) A₁ of CdMnTe (111); (c) B₁ of CdMnTe (111).

图3(b)代表了CdMnTe (111)-A₁表面模型的总态密度和局域态密度, 其总态密度中费米能级附近也出现了新的表面态. 该表面态是由CdMnTe表面第1层中Mn-3d和Te-5p引起的, 远离表面的内部在费米能级附近没有出现新的电子态. 图3(c)所示的B₁表面模型中总态密度的费米能级附近也出现了由第1层中Mn-3d和Te-5p轨道引起的表面态, 但其峰值略低.
2 -->

3.2.CdS/CdMnTe异质结模型和电子性质

3 -->

3.2.1.CdS/CdMnTe异质结模型

由CdS (002)和CdMnTe (111)表面模型构建的CdS/CdMnTe异质结模型如图4所示, 模型A₂为Mn原子位于界面层(Layer 1)的异质结模型(Mn原子位置同模型A₁), B₂为Mn原子位于中间层(Layer 2)的异质结模型(Mn原子位置同模型B₁). 异质结包含77个原子, 化学式为H₇S₁₈Cd₃₄MnTe₁₅, 晶格参数为a = b = 8.15 ?, 晶格失配度约为3.5%. 同样在第5层外添加20 ?的真空层以减小周期性边界条件对异质结模型的影响, 采用氢原子钝化最外层原子的悬挂键以减小表面态对异质结界面的影响. 另外, 令界面两端第1, 2原子层自由弛豫, 第3—5原子层固定. 采用单点能量计算方法来获得合适的界面距离, 如图5所示. 可以看出, 当界面距离为2.26 ?时, 模型A₂系统总能量最低; 当界面距离为2.55 ?时, 模型B₂系统总能量最低.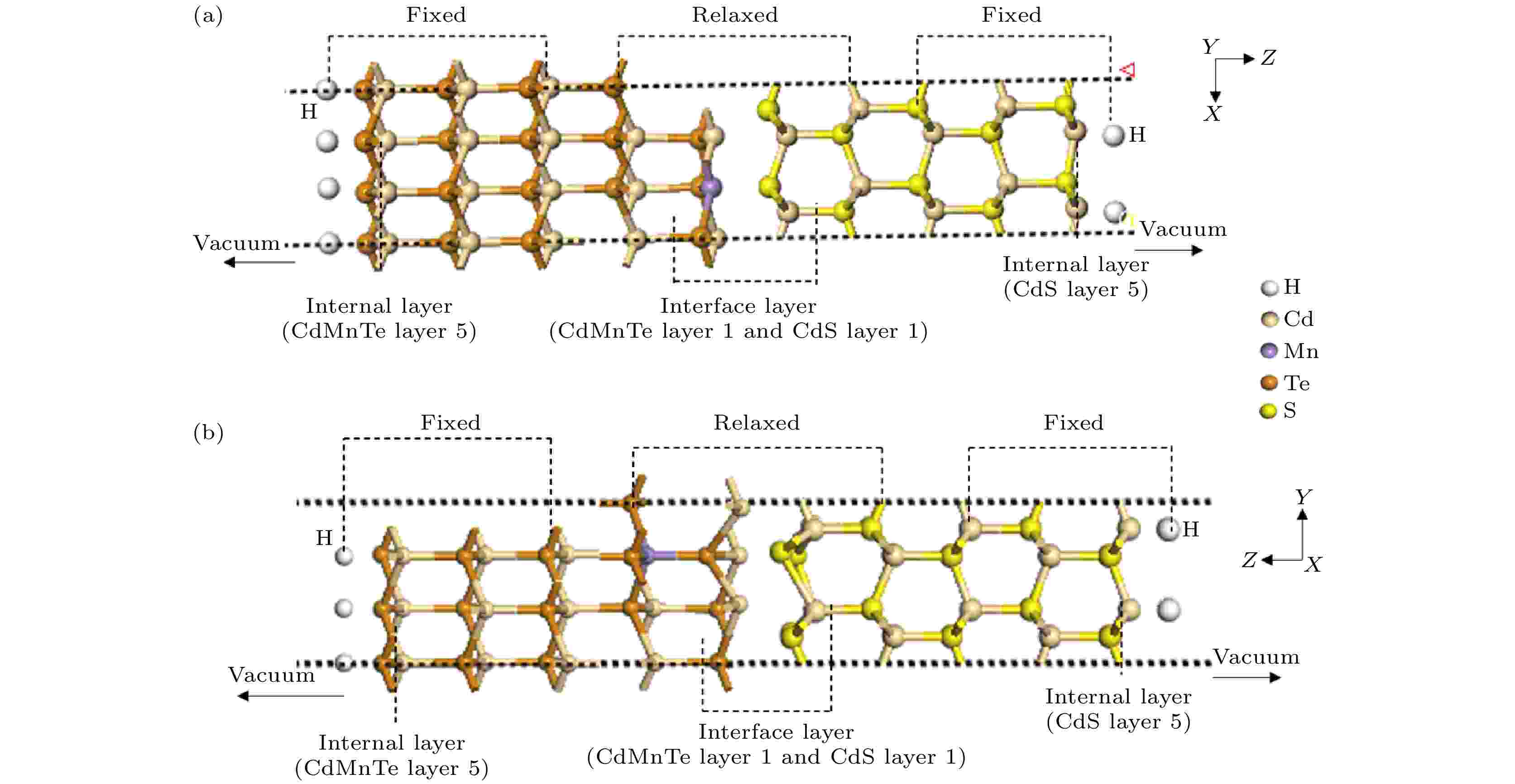
图 4 CdS/CdMnTe异质结模型　(a) Mn原子位于界面层的异质结模型(模型A₂); (b) Mn原子位于中间层的异质结模型(模型B₂)
Figure4. CdS/CdMnTe heterojunction models: (a) Mn atom being in the interface layer (model A₂); (b) Mn atom in the internal layer (model B₂).

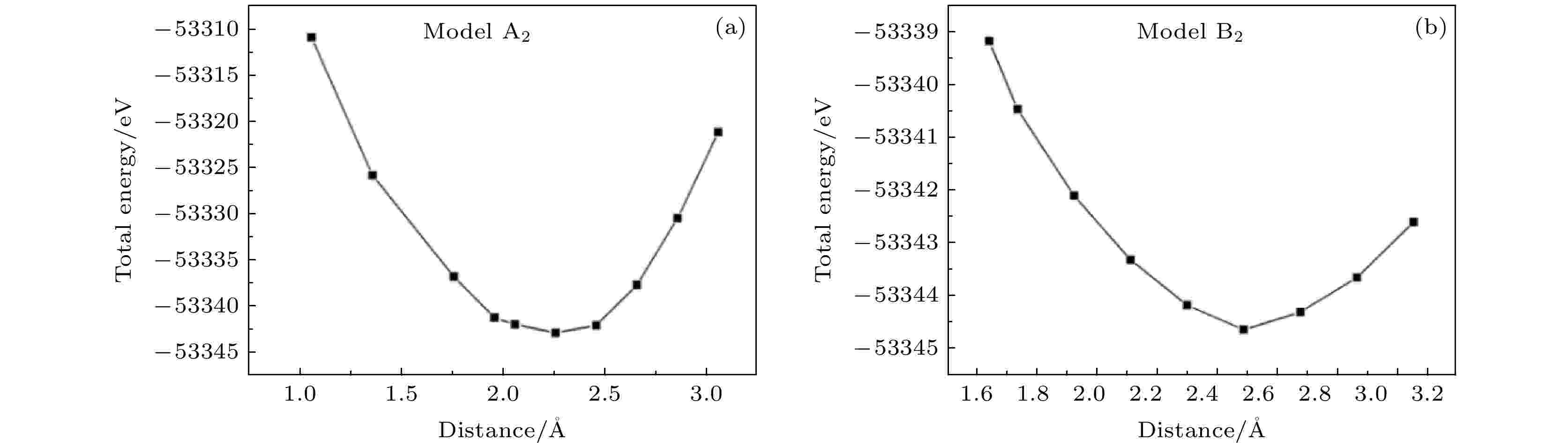图 5 模型A₂和B₂的总能量随界面间距的变化
Figure5. Variation of total energy dependent on the interface distance of the models A₂ and B₂, respectively.

采用BFGS方法分别对两种模型进行结构优化, 优化后的模型如图6所示. 图6(a)和图6(b)分别表示模型A₂弛豫前后原子键长的变化, 模型A₂弛豫后界面上原子键长为d_Cd—Te = 2.902—2.994 ?(弛豫前2.871 ?), d_Mn—Te = 2.740—2.720 ? (弛豫前2.651 ?), d_Cd—S = 2.531—2.666 ?(弛豫前2.497 ?); 界面附近原子键长为d_Cd—Te = 2.841—2.852 ?(弛豫前2.969 ?), d_Cd—S = 2.502—2.547 ? (弛豫前2.542 ?), 远离界面处的原子键长和位置基本保持不变. 图6(c)和图6(d)分别表示模型B₂弛豫前后原子键长的变化, 弛豫后界面上的原子键长为d_Cd—Te = 2.871—2.942 ?(弛豫前2.832 ?), d_Cd—S = 2.541—2.579 ?(弛豫前2.503 ?); 界面附近原子的键长为d_Cd—Te = 2.813—2.814 ?(弛豫前2.906 ?), d_Mn—Te = 2.696 ?(弛豫前2.661 ?), d_Cd—S = 2.543—2.584 ?(弛豫前2.759 ?), 同样远离界面处的原子键长和位置也基本保持不变.
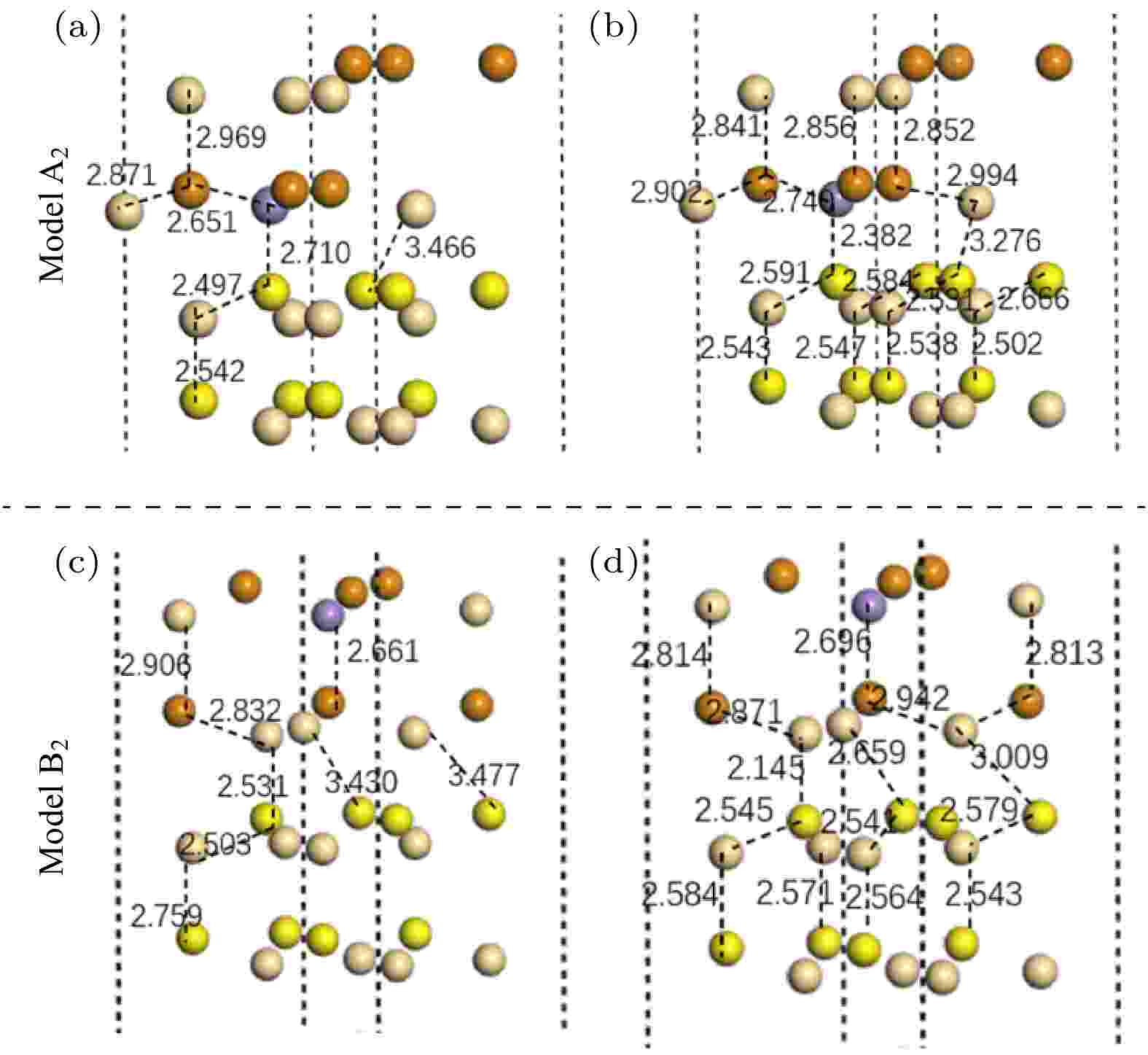图 6 弛豫前后界面及其附近原子键长的变化　(a)弛豫前的模型A₂; (b)弛豫后的模型A₂; (c)弛豫前的模型B₂; (d)弛豫后的模型B₂
Figure6. Bond lengths in/near of the interface before and after relaxation: (a) Before relaxation of A₂; (b) after relaxation of A₂; (c) before relaxation of B₂; (d) after relaxation of B₂.

弛豫前后界面上原子键长的变化是由界面处原子的种类和结构的差异造成的. 在两种异质结模型中, 模型B₂弛豫前后界面附近原子键长变化的幅度偏大, 说明模型B₂界面处原子间作用力较大, 界面原子的结合更加稳定, 更益于形成稳定的界面.
根据CdS/CdMnTe异质结界面结合能的大小可以判断其结构的稳定性, 若结合能为负值, 则异质结模型是稳定的, 且负值越大模型越稳定^[35,36]. 界面结合能的计算公式为

$\begin{split}{E_{{\rm{ads}}}}\big( {{\rm{eV}}/{{\text{?}}^2}} \big) =\;& \left[ {E_{{\rm{CdS}}/{\rm{CdMnTe}}}}\left( {{\rm{eV}}} \right) - {E_{{\rm{CdS}}}}\left( {{\rm{eV}}} \right) \right.\\&\left.-{E_{{\rm{CdMnTe}}}}\left( {{\rm{eV}}} \right) \right]/2S \end{split}$

其中, E_CdS/CdMnTe是弛豫后系统的总能量, E_CdS和E_CdMnTe是弛豫后CdS (002)和CdMnTe (111)表面的总能量. 计算结果显示, 模型A₂的结合能为–0.51 J/m², 模型B₂的结合能为–0.53 J/m², 根据负值越大越稳定来判断, 模型B₂的结构更加稳定, 这一结论与模型B₂弛豫后原子键长的变化偏大的结论一致.
3 -->

3.2.2.CdS/CdMnTe异质结的电子性质

下面通过异质结的总态密度、局域态密度、原子的分态密度和差分电荷密度研究异质结的电子性质. 图7(a)和图7(b)分别表示模型A₂和B₂的总态密度和局域态密度, 可以看出, 异质结A₂和B₂在费米能级附近约–0.15—0.20 eV范围内均出现了新的电子态, 即界面态, 并且模型A₂中费米能级附近出现了更高的界面态. 界面态在载流子传输过程中可以充当俘获中心, 阻止光生载流子通过费米能级, 导致带隙减小, 开路电压和短路电流降低. 局域态密度分析发现, 异质结的界面态主要是由CdMnTe (111)第5层引起的, 而CdS (002)和CdMnTe (111)第1层的费米能级附近均没有界面态. 也就是说, 这两个异质结界面不会捕获载流子, 避免了费米能级在界面处被钉扎. 这可能是因为界面处原子的紧密结合促进了共价键的形成, 消除了界面悬挂键而使电子达到了饱和状态, 故CdS/CdMnTe异质结界面处不显示界面态.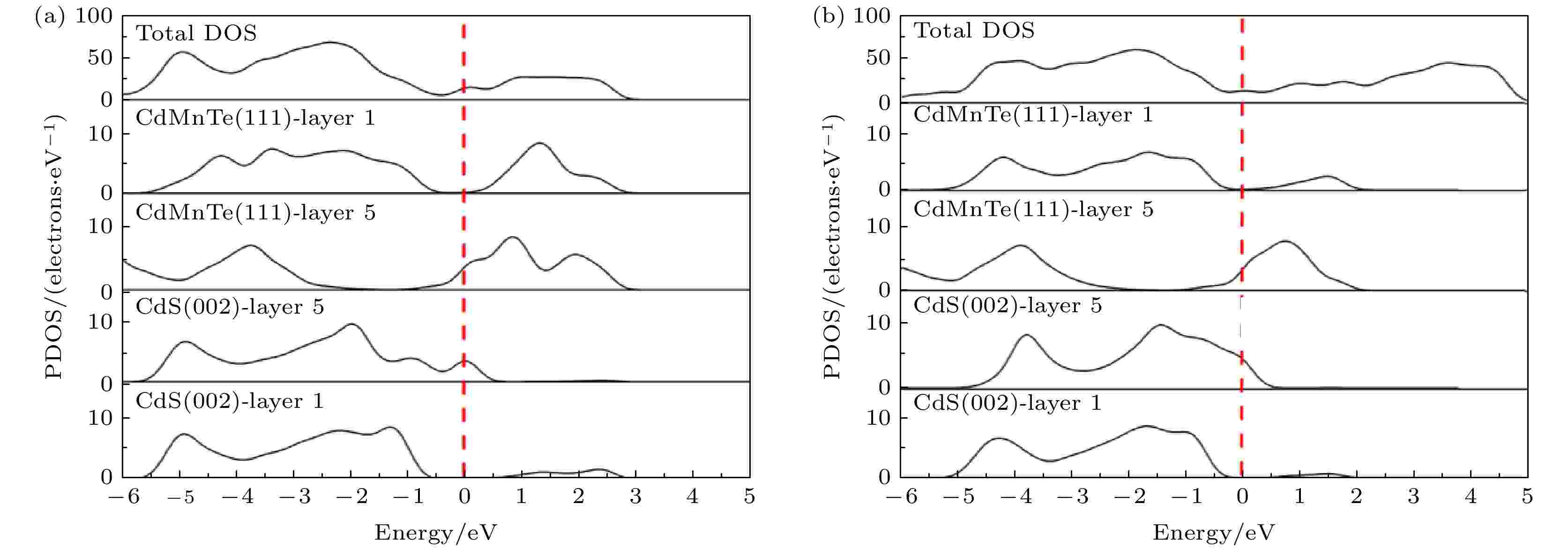
图 7 CdS/CdMnTe异质结总态密度与局域态密度　(a)模型A₂; (b)模型B₂
Figure7. Total density of states and local density of states of the CdS/CdMnTe heterojunction: (a) Model A₂; (b) model B₂.

图8表示CdS/CdMnTe异质结界面处原子的分态密度, 图8(a)说明模型A₂界面处所有的原子在费米能级附近均没有其他电子态. 在–5 eV附近, Mn-3 d和Te-5p轨道发生微弱杂化, 在0.5—1.5 eV处, Mn-3p和Te-5p轨道也发生了较弱的杂化, 在–3—–1 eV处, Mn-3p与Cd-3p轨道发生部分杂化, 在1.5 —2.5 eV处, Mn-4s, Cd-3p与S-3s电子发生较小的轨道杂化. 这些原子轨道的杂化作用促进了界面处Mn与Te, Mn与S, S与Cd原子之间的成键. 对于模型B₂, 如图8(b)所示, 在–5—–4.5 eV与–3.5—–1.5 eV处, Te-5p和S-3p发生强烈的轨道杂化, 在1—2 eV处, Cd-4p和S-3s轨道发生杂化, 在–5 eV附近, Cd-5s和S-3p轨道发生微弱的杂化. 此外, H原子1s轨道在费米能级处出现了界面态, 说明H原子的加入对CdS/CdMnTe异质结有不利的影响.
图 8 CdS/CdMnTe异质结界面处原子的分态密度　(a)模型A₂; (b)模型B₂
Figure8. Part density of states of different atoms in the CdS/CdMnTe interface: (a) Model A₂; (b) model B₂.

界面上原子轨道杂化能力的强弱是影响界面结合程度的关键因素, 异质结B₂具有比异质结A₂更强的界面原子轨道杂化能力, 说明异质结B₂具有更加稳定的结构.
异质结沿z轴方向的电荷密度差可以由下式表示:

$\Delta \rho = {\rho _{{\rm{CdS}}/{\rm{CdMnTe}}}} - {\rho _{{\rm{CdS}}}} - {\rho _{{\rm{CdMnTe}}}}{{,}}$

其中, ρ_CdS/CdMnTe为异质结系统的总差分电荷密度, ρ_CdS和ρ_CdMnTe分别为系统中CdS (002)和CdMnTe (111)表面的差分电荷密度.
垂直于z轴方向的电荷重新分布如图9所示, 图中蓝色区域表示电荷累积, 黄色区域表示电荷耗尽. 从图9(a)和图9(c)所示的差分电荷示意图中可以看出, 电荷的重新分配主要发生在CdS/CdMnTe界面处, 这是由于界面处原子轨道的杂化作用促进了界面的结合, 远离界面处的原子由于CdMnTe与CdS两相之间的相互作用较弱几乎没有电荷转移. 沿z轴方向的平面平均电荷密度差代表电荷的重新分布, 正值表示电子累积, 负值表示电子耗尽. 通过界面处偶极矩变化的定量计算, 表明电子主要通过界面从CdMnTe侧转移到CdS侧. 此外, 通过Mulliken电荷计算出异质结A₂电荷转移量为0.89, 异质结B₂电荷转移量为0.91, 此结果表明异质结B₂具有较强的电荷转移能力.
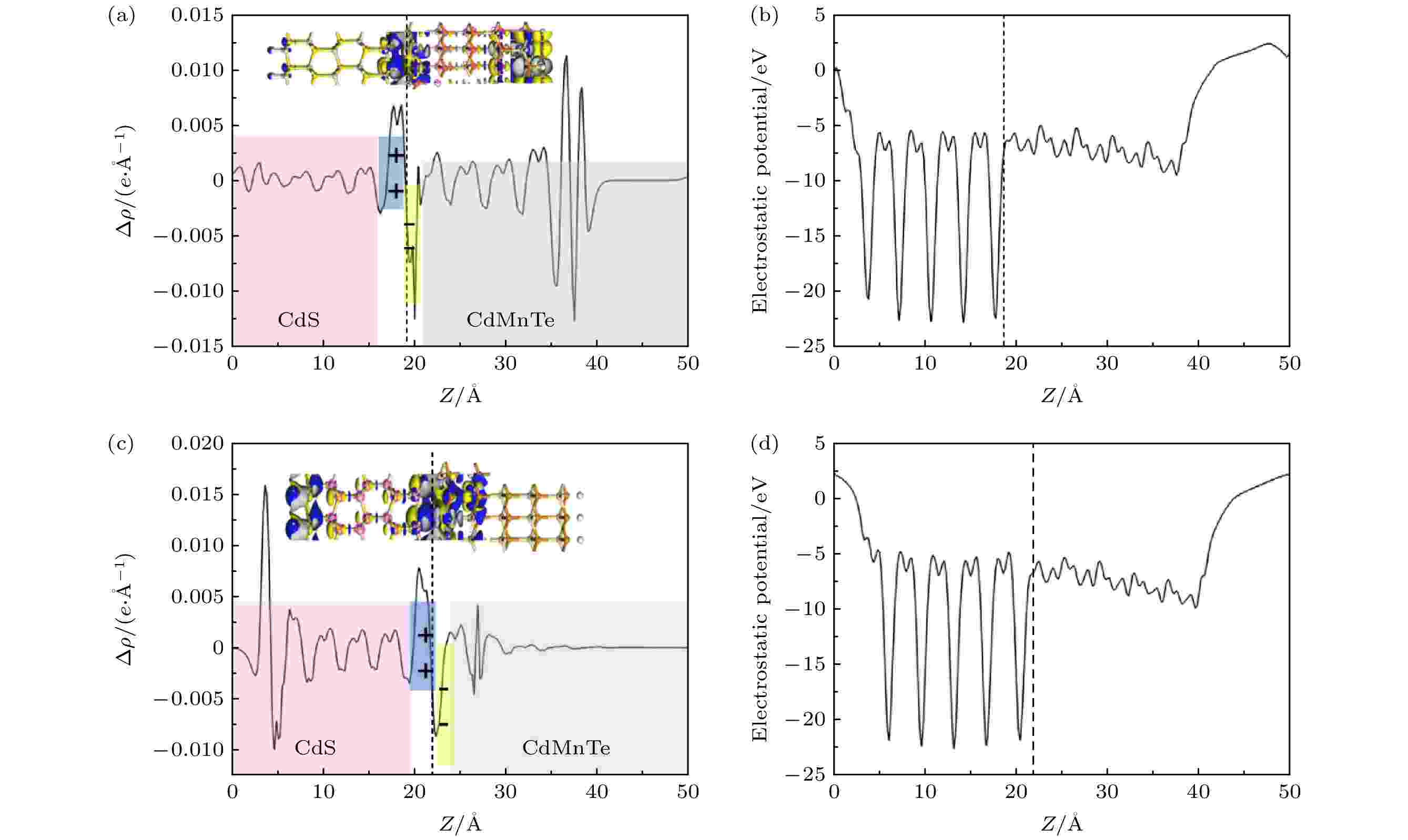图 9 电荷重新分布图 (a), (c)异质结A₂与B₂的差分电荷示意图和相应平面差分电荷密度曲线, 黄色区域代表电荷消耗, 蓝色区域代表电荷积累, 等值面值为0.00103 e/?³; (b), (d) A₂与B₂沿z轴方向的平均静电势
Figure9. Distribution diagram of charges: (a), (c) Charge density difference and the corresponding planar differential charge density curve of the A₂ model and B₂ model, respectively. The yellow region represents charge depletion, the bule region indicates charge accumulation, the isosurface value is 0.00103 e/?³. (b), (d) the average electrotactic potential difference of the A₂ model and B₂ model, respectively, along the direction of z axis.

图9(b)和图9(d)分别表示CdS/CdMnTe异质结A₂和B₂模型界面间的静电势. 计算结果显示, 异质结B₂在界面处的电位更低, 表明电子更容易在此界面区域转移和积累. Guo Y等^[37]研究表明, 在CdS/CdMnTe异质结界面处将发生载流子的有效分离, 较大的导带偏移有助于增强电子注入CdS层的能力. 因为异质结B₂具有更高的界面结合能和更强的电荷转移能力, 这将有助于减小CdS/CdMnTe价带偏移而增加导带偏移, 对促进载流子的分离具有积极的意义.
2 -->

3.3.CdS (002), CdMnTe (111)表面及其异质结的光学性质

研究CdS (002), CdMnTe (111)表面及其异质结的光学性质对于扩展多结串联电池的光谱响应范围具有重要意义^[38]. 介电函数$ \varepsilon \left(\omega \right) $和吸收系数$ \alpha \left(\omega \right) $的表示如下^[39-41]:

$ \varepsilon \left(\omega \right)={\varepsilon }_{1}\left(\omega \right)+{{\rm{i}}\varepsilon }_{2}\left(\omega \right){,} $

$ \alpha \left(\omega \right)=\sqrt{2}\omega {\left[\sqrt{{{\varepsilon }_{1}\left(\omega \right)}^{2}\!+\!{{\varepsilon }_{2}\left(\omega \right)}^{2}}\!-\!{\varepsilon }_{1}\left(\omega \right)\right]}^{1/2}=2\omega k{.} $

(1)式和(2)式中的介电函数虚部$ {\varepsilon }_{2}\left(\omega \right) $由(3)式确定. 实部$ {\varepsilon }_{1}\left(\omega \right) $可以通过Kramers-Kronig变换, 获得如(4)式的表达式^[42].

$\begin{split}{\varepsilon _2}\left( \omega \right) =\;& \frac{{4{e^2}{\pi ^2}}}{\varOmega }\mathop {{\rm{lim}}}\limits_{q \to 0} \frac{1}{{{q^2}}}\sum\limits_{c,v,k} 2 {w_k}\delta \left( {{\varepsilon _{ck}} - {\varepsilon _{vk}} - \omega } \right)\\& \times \left\langle {{u_{ck}} + {e_{{\rm{\alpha }}q}}|{u_{vk}}} \right\rangle \left\langle {{u_{ck}} + {e_{{\rm{\beta }}q}}|{u_{vk}}} \right\rangle ,\\[-10pt]\end{split}$

${\varepsilon }_{1}\left(\omega \right)=1+\frac{2}{\rm{\pi }}P{\int }_{0}^{\infty }\frac{{\varepsilon }_{2}\left({\omega }'\right){\omega }'}{{\omega }^{{'}2}-{\omega }^{2}+{\rm{i}}\eta }{\rm{d}}{\omega }'{.}$

图10(a)为CdS (002)表面、CdMnTe (111)-B₁模型与异质结CdS/CdMnTe-B₂模型的吸收光谱. 可以看出, CdS (002)表面模型具有深紫外吸收峰, 在160 nm处的最大吸收系数达1.58 × 10⁵ cm^–1. CdMnTe (111)-B₁模型与异质结B₂模型的吸收系数具有相似的变化趋势, 但异质结B₂模型的吸收系数却相对较低, 这是因为两种材料组合成异质结时, 界面处的周期性结构被破坏形成了不饱和悬挂键. 接着分析了异质结A₂与B₂模型的吸收光谱(图10(b)), 异质结B₂在200—250 nm范围的吸收系数远高于异质结A₂, 而在250—900 nm范围内, 异质结A₂具有更高的吸收系数. 两种异质结的光学性质略有差异, 这可能与异质结中的界面态有关, 也可能是受到Cd-4p, S-3s和Te-5p电子轨道杂化的影响.
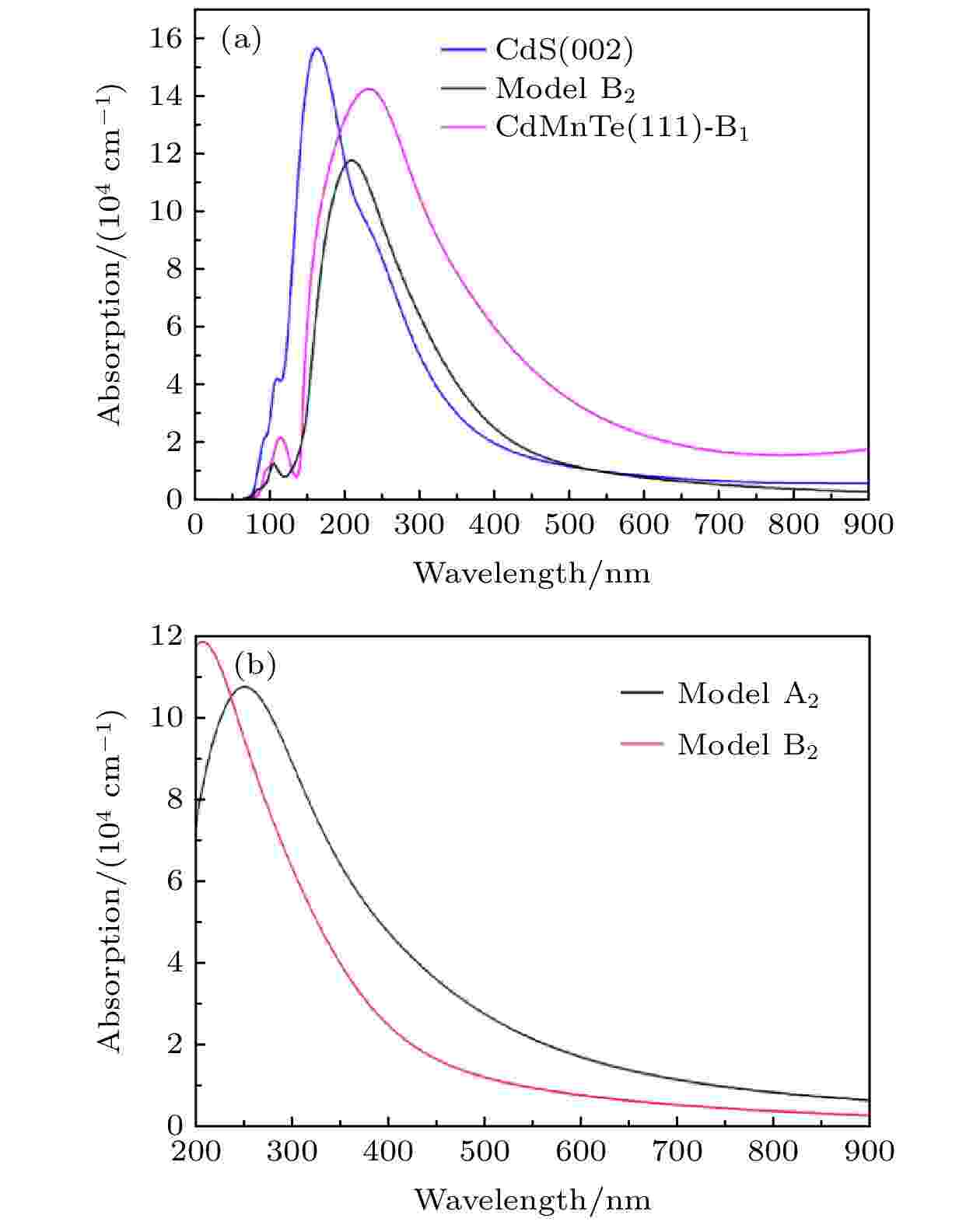图 10 表面模型和异质结模型的吸收光谱　(a) CdS (002), CdMnTe (111)-B₁表面和异质结B₂模型; (b)异质结A₂和B₂模型
Figure10. Absorption spectra of surface models and heterojunction models: (a) Surface CdS (002), surfaces of CdMnTe (111)-B₁, and B₂ model of CdMnTe/CdS heterojunction model; (b) heterojunction A₂ model and B₂ model.

CdMnTe薄膜太阳能电池的性能取决于窗口层CdS与吸收层CdMnTe的电子结构与界面性质. 本文采用第一性原理计算了CdS (002)和CdMnTe (111)表面以及CdS/CdMnTe异质结的界面结构与光电性质. 通过构建两种不同Mn原子位置的CdS/CdMnTe异质结模型及其结构优化, 得到了Mn原子位于中间层的较为稳定的异质结模型B₂, 其界面结合能为–0.53 J/m². 计算分析发现, CdS/CdMnTe异质结界面处Cd, S和Te原子之间的轨道杂化作用增强, 提高了界面结合能力, 界面处费米能级附近不存在界面态, 这有利于提高电池的导电性. 异质结B₂拥有更强的电荷转移能力, 这对增大界面处导带偏移, 促进载流子的有效分离, 提高载流子运输具有积极的意义. 计算结果还发现, 异质结B₂在200—250 nm范围内具有更高的吸收系数.