摘要: 钾掺杂钨合金是一种典型的弥散强化钨基材料, 钾掺入在提高钨材料抗冲击能力的同时, 也引入大量缺陷, 这些缺陷会对合金在服役过程中氢原子和氦原子的存在形态以及演变产生影响. 本文使用正电子湮没谱学方法从微观角度研究辐照后钨钾合金中的缺陷信息, 通过对氢氦相关缺陷的正电子湮没参数进行模拟, 发现氢原子对正电子寿命的影响比氦原子小, 弥散在位错或晶界中的氢、氦原子会影响正电子湮没区域, 而单个钾原子的存在对氢氦相关缺陷的正电子寿命影响甚微; 结合扫描电镜与正电子湮没寿命谱和慢正电子束多普勒展宽谱, 测试结果确认了钨钾合金中钾泡以及其钉扎的位错等缺陷对氢原子和氦原子的影响, 与纯钨相比, 在纯H和H+6%He中性束辐照下钾泡等缺陷会促进氢原子的释放, 同时成为氦原子的捕获中心, 促使其形成氦-空位复合体, 并在此成核, 生长为尺寸更大的氦泡, 在应力和温度梯度的作用下促进其从表面释放, 有利于相关缺陷的恢复, 降低其损伤程度.
关键词: 正电子湮没谱学 /
中性束辐照 /
钨钾合金 /
钾掺杂 English Abstract Defects in H/He neutral beam irradiated potassium doped tungsten alloy by positron annihilation technique He Wei-Di 1 ,Zhang Pei-Yuan 1 ,Liu Xiang 2 ,Tian Xue-Fen 1 ,Fu Xin-Ge 1 ,Deng Ai-Hong 1 1.College of Physics, Sichuan University, Chengdu 610065, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11675114)Received Date: 08 March 2021Accepted Date: 05 April 2021Available Online: 07 June 2021Published Online: 20 August 2021Abstract: Pure tungsten (W) is a primary plasm-facing material (PFM) candidate because of its superior properties, but it still has some drawbacks. In order to solve these problems, various methods have been used to improve the performances of tungsten-based materials. Potassium (K) doping, as one of the typical dispersion-strengthening methods for W materials, improves low temperature brittleness, reduces the ductile-brittle transition temperature, and suppresses the recrystallization. Meanwhile, it also improves the thermal shock resistance and fracture toughness of the material by introducing nano-sized K bubbles. However, this method brings a large number of defects inevitably. In fact, the K bubbles and the dislocations which are pinned by these K bubbles can affect the morphology and evolution of hydrogen (H) and helium (He) atoms in the alloys. As a very sensitive method to detect vacancy-type defects in materials, positron annihilation spectroscopy is used to study the irradiation damage caused by H and He atoms in this paper. The calculation of positron lifetime shows that positrons are more sensitive to the vacancy-type defects. Bounding of H and He with vacancies reduces the positron lifetime because of the increase of valence electron density. Combining the calculated results with the positron annihilation lifetime spectrum (PLAS) results shows that the W-K alloy is easier to promote the H atoms to release. Besides, it also more likely to form larger He bubbles which can be estimated by positron lifetime values. The result is also confirmed by the measurements from the scanning electron microscope (SEM) and slow positron Doppler broadening spectroscopy (DBS). The defects in the W-K alloy such as K bubbles and their pinned dislocations can act as diffusion channels to promote the H atoms to release, which gives rise to a smoother surface under the pure H irradiation. Meanwhile, under the condition of the H+6%He irradiation, the K bubbles and their pinned dislocations in the W-K alloy become the capture center of He atoms, promote their nucleation and grow into larger He bubbles. Moreover, under the action of stress and temperature gradient, some of the He bubbles migrate to the surface and release, this process is conducive to the recovery of related defects and the reduction of radiation damage.Keywords: positron annihilation spectroscopy /neutral beam irradiation /potassium-tungsten alloy /potassium doping 全文HTML --> --> --> 1.引 言 钨由其熔点高、导热性好、溅射系数低、氚保留率低、蒸汽压低和光学反射率高等优越性能, 被选作最具有潜力的面向等离子体材料(plasma-facing materials, PFMs)[1 ] . 但在实际应用当中, 钨还存在低温脆性、高韧脆转变温度[2 -6 ] 以及再结晶引起的脆化[7 ,8 ] 等潜在缺陷. 因此, 为了解决这些问题, 大量研究人员通过晶粒细化[9 ] 、弥散强化[10 ] 和合金化[11 ,12 ] 等手段对钨进行改性. 其中钾掺杂作为一种常见的弥散强化方法也得到研究者们的广泛关注. 钾掺杂钨最早用于强化钨丝, 在照明行业有着悠久的历史[13 ] . 近年来Nogami等[14 ] 研究了钾掺杂对钨合金拉伸性能以及抗冲击性能的影响, 发现钾掺杂细化了钨晶粒尺寸, 增强了其抗冲击性能, 同时提高钨材料的低温脆性, 降低韧脆转变温度, 抑制再结晶. Huang等[15 ] 对不同含量钾掺杂钨合金进行了力学、热学以及抗热冲击性能的研究, 结果表明, 随着钾含量的增加, 合金热导率降低, 断裂韧性增加, 而钾的质量分数为8.2 × 10–5 的钨钾样品具有最高的抗拉强度和抗热冲击性能. 同时他们认为通过制备工艺引入的纳米尺度气泡对材料断裂韧性的影响不同于大孔隙, 小尺寸球化封闭孔隙能够偏转和钝化裂纹, 有助于增强材料的断裂韧性. 为了探究钾掺杂钨合金在聚变堆中的实际应用前景, Feng等[16 ] 对不同钨基材料(纯W, W-K和W-Y2 O3 )进行高能氢/氦中性束辐照, 以研究锻造弥散强化钨合金在边缘等离子体条件下的辐照性能. 研究表明, 虽然弥散强化钨合金比纯钨更容易形成针孔结构, 但W-K合金比纯W具有更高的强度, 能更好地抑制裂纹的萌生和扩展. 但是目前对钨钾合金在聚变堆中应用前景的研究主要集中于宏观性能, 缺少对于其辐照后钾泡对氢原子和氦原子存在形式及演变影响的研究. 因此, 从微观角度探究氢氦相关缺陷在钨钾合金中的演化情况是十分必要的. 正电子湮没谱学(positron annihilation spectroscopy, PAS)是一种无损检测材料中微观缺陷的方法. 通过正电子湮没参数可以反映出材料中正电子所处位置的电子密度或电子动量分布信息, 对原子尺度上开空间晶格缺陷(空位、空位团、位错、晶界等)十分敏感. 其中正电子湮没寿命谱(positron annihilation lifetime spectrum, PALS)主要用于定性和半定量研究缺陷尺寸和浓度[17 ] . 基于慢正电子束流技术的多普勒展宽(Doppler broadening spectroscopy, DBS)可以通过调节正电子注入能量探测样品内部缺陷随深度的变化情况[18 ] .2.模拟与实验 22.1.样品制备 2.1.样品制备 选用通过粉末冶金制备的纯钨(PW)和硅酸钾(ASK)掺杂方式制备的钾的质量分数为8 × 10–5 的商用钨钾合金(WK), 纯度均大于99.9 wt.%. 分别将两种样品切割成尺寸为20 mm × 12 mm × 6 mm的长方体, 经过仔细抛光将其表面粗糙度控制在0.5 μm以下, 在1000 ℃下真空退火5 h以消除样品在成型和加工过程中的内应力, 依次使用酒精-丙酮-酒精进行超声波清洗, 后焊接到CuCrZr热沉部件上.2.2.高能H/He中性束辐照 -->2.2.高能H/He中性束辐照 样品在德国马普等离子物理研究所的高热流测试设备GLADIS上进行高功率稳态中性束流辐照[19 ] , 选用10 MW/m2 的纯H和8 MW/m2 的H+6%He中性束, 循环注入40到80个20 s的脉冲束流模拟准稳态加载条件, 具体辐照条件如表1 所列, 实验中氢原子能量取其在该加速电压下的平均值为15 keV[20 ] , 氦原子能量为28 keV. 由于热通量呈高斯分布, 钨钾合金样品和纯钨样品对称放置以使辐照条件一致. 采用双色高温计和红外相机对样品的表面温度进行监测. 注入过程中使用流速10 m/s、温度20 ℃的冷却水保证稳定传热.编号 样品 功率–2 ) 入射 加速电 注量/24 m–2 表面温 WK1 WK 10 H 29 3.4 1000 PW1 PW 10 H 29 3.4 1000 WK2 WK 8 H+6%He 27 6.7 800 PW2 PW 8 H+6%He 27 6.7 800
表1 中性束辐照条件Table1. Conditions of neutral beam irradiation.2.3.样品表征 -->2.3.样品表征 借助武汉大学的快-快符合正电子寿命谱仪(PALS)在室温下对辐照样品进行正电子寿命谱测试. 采用22 Na正电子源和塑料闪烁体γ光子探测器, 谱仪的时间分辨率约220 ps, 每个谱的累积计数约2 × 106 , 以减小不必要的统计误差, 保证实验结果的准确. 利用PATFIT程序对寿命谱解析, 在去除源成分后得到长短不同的两个寿命及其对应的强度.22 Na作为正电子放射源, 高纯Ge探测器垂直于光束方向, 通过改变样品架上的负高压控制正电子束的注入深度. 通常用S 参数和W 参数对正电子湮没光谱进行表征, 其中S 参数定义为511 keV峰中央的面积(510.2—511.8 keV)与峰总计数(499.5—522.5 keV)的比值, 反映了低动量价电子或传导电子的动量信息. 而W 参数定义为峰两侧计数(513.6—516.9 keV和505.1—508.4 keV)与总计数的比值, 反映了高动量芯电子的动量信息. 通过改变入射正电子能量, 可以得到S 参数和W 参数的深度分布, 反映不同深度缺陷的演化情况. 正电子的平均注入深度由入射能量定义, 其关系式为[21 ] Z (E )为注入深度, 单位为nm; ρ 为样品密度, 单位为kg/m3 ; E 为注入能量, 单位为keV.2.4.模拟方法 -->2.4.模拟方法 为了了解不同氢氦相关缺陷的正电子寿命值, 使用Puska 和 Nieminen提出的原子叠加法(atomic superposition, AT-SUP)[22 ] 对包含各种相关缺陷的钨晶格进行正电子寿命计算. 在AT-SUP近似中, 固体的电子密度$ {n}_{\_}\left(\boldsymbol{r}\right) $ 和库伦势$ {V}_{\mathrm{c}}\left(\boldsymbol{r}\right) $ 分别通过单个原子电荷密度和库伦势的叠加来计算[23 ] :$ {n}_{\_}^{\mathrm{a}\mathrm{t}}\left(\boldsymbol{r}\right) $ 是自由电子密度; $ {\boldsymbol{R}}_{\boldsymbol{i}} $ 是被原子占据的点位; $ {V}_{\mathrm{a}\mathrm{t}} $ 是电子密度和原子核产生的原子库仑势. 在密度泛函理论(density functional theory, DFT)中原子基态电子构型的密度和电势是自洽的.$ {V}_{+}\left(\boldsymbol{r}\right) $ 由$ {V}_{\mathrm{c}}\left(\boldsymbol{r}\right) $ 和正电子-电子交换能$ {V}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}\left({n}_{\_}\right(\boldsymbol{r}\left)\right) $ 共同决定:$ {V}_{\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{r}}\left({n}_{\_}\right(\boldsymbol{r}\left)\right) $ 由局部密度近似得到[24 -26 ] . 用松弛法[27 ] 求解离散$ \mathrm{S}\mathrm{c}\mathrm{h}\mathrm{r}\ddot{\mathrm{o}}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{e}\mathrm{r} $ 方程得到正电子波函数及其能量特征值. 因此正电子的湮没率, 由正电子和电子密度的积分得到:$ {r}_{0} $ 是经典电子半径; c 是真空中的光速; $ {n}^{+}\left(\boldsymbol{r}\right) $ 是正电子密度; $ \gamma \left(\boldsymbol{r}\right) $ 是增强因子, 也由局部近似给出[24 -26 ] . 正电子的寿命与湮没率互为倒数, 因此可得到相关的正电子寿命.[28 ] . 采用超软赝势来近似电子和离子间的相互作用[29 ] . 交换关联泛函选用Perdew-Burke-Ernzerhof (PBE)形式的广义梯度近似(generalized gradient approximation, GGA)[30 ,31 ] . 平面波截断能设置为300 eV. 使用Monkhorst-Pack法[32 ] 选取k 点. 构建尺寸为9a 0 × 9a 0 × 9a 0 具有周期性边界条件的体心立方结构(body-centered cubic, BCC)钨超胞, 钨晶格常数为3.1652 ?. 在几何优化过程中, 钨超胞使用3 × 3 × 3均匀k 点网格进行布里渊区积分, 对于位错模型选用了刃位错和螺旋位错, 晶界模型选用倾斜晶界, 具体参数如表2 和表3 所列. 对结构进行弛豫, 使每个原子的受力小于0.01 eV/?, 能量差小于5.0 × 10–6 eV/atom, 晶体中最大应力不超过0.02 GPa, 最大原子位移小于0.0005 ?. 优化后, 无缺陷超胞中氦、氢原子占据四面体间隙处或八面体间隙处; 当存在空位时, 氢、氦原子会被空位捕获, 单空位中占据的氢、氦原子数目有极限, 多余的氢、氦原子则会停留在空位周围的四面体间隙或八面体间隙处.Dislocation Type Slip plane(z ) Bugers vector[b ] Dislocation line[y ] b -y Angle/(°)Intact/ps Vac.1/ps SCREW ($\bar{1}01$) (111)/2 ($\bar{1}2\bar1$) 90 106.5 196.4 EDGE ($\bar{1} 01$) (111)/2 (111) 0 133.9 197.2
表2 位错模型参数Table2. Detailed parameters of dislocations models.GB Type Σ GB Plane Rotation axis Angle/(°) Intact/ps Vac.1/ps TILT 5 {$0\bar{1} 5$} x (100)22.61 142.2 204.8
表3 晶界模型参数Table3. Detailed parameters of grain boundary model.3.结果与分析 23.1.样品表面形貌分析 3.1.样品表面形貌分析 图1 给出不同辐照条件下四组样品的表面形貌图. 图1(a) 和图1(b) 分别是未辐照WK和PW样品的表面形貌图, 表面均较为平整. 图1(c) 和图1(d) 纯H辐照下样品WK1和PW1的形貌图, 样品WK1表面较为平整, 并且出现少许孔状结构和明显晶界. 而样品PW1表面较为粗糙且未出现明显针孔结构. 这表明, 在纯H辐照条件下, 钨钾合金中钾掺入引入的钾泡等缺陷会成为氢的扩散通道, 促进氢原子的释放; 另外弥散强化粒子会细化晶粒增加晶界密度, 氢原子更容易在这些晶界处汇聚[16 ] , 因此出现明显晶界结构. 对比图1(e) 和图1(f) 发现, 在H+6%He辐照下, 两种样品均出现明显针孔结构, 表明氦原子会造成比氢原子更为严重的损伤. Temmerman等[33 ] 也发现类似现象, 其研究表明该形貌主要是由近表面区域氦泡引起. 通过局部放大图可以看出样品WK2的针孔结构较样品PW2略大, 表明钨钾合金更容易形成尺寸更大的氦泡, 其原因将在后文进行详细讨论.图 1 样品SEM图 (a) 未辐照WK样品; (b) 未辐照PW样品; (c) 辐照样品WK1; (d) 辐照样品PW1; (e) 辐照样品WK2 (右上角为红框区域局部放大图); (f)辐照样品PW2(右上角同(e))Figure1. SEM images: (a) nonirradiated Sample of WK; (b) nonirradiated Sample of PW; (c) sample WK1; (d) sample PW1; (e) sample WK2 (The upper right corner is a partial enlargement of the red box area); (f) sample PW2 (The same as (e)).3.2.正电子湮没寿命谱分析 -->3.2.正电子湮没寿命谱分析 33.2.1.正电子湮没寿命模拟 -->3.2.1.正电子湮没寿命模拟 图2 给出了钨超胞中不同类型缺陷的湮没分布图, 模拟结果表明, 正电子对空位型缺陷更加敏感, 当钨晶格中只存在位错缺陷时, 正电子湮没区域包含整个位错区域; 当位错中存在空位时, 正电子只在空位处湮没, 并且寿命值与完整晶格中空位处湮没寿命相同约为197 ps(单空位). 当位错区域弥散有氢、氦原子时, 氢、氦原子的存在会影响其所在位置的电子密度, 形成一个更高的势垒, 正电子会避开该区域. 同样若存在空位, 则正电子更倾向于在空位中湮没, 并且湮没区域包含被空位捕获的氢、氦原子. 因此正电子寿命由相关的空位型缺陷决定而不是位错, 这与Staikov和Djourelov[34 ] 的结论一致. 晶界处的湮没情况与位错类似, 如图2(e) 和图2(f) 所示, 图中黄色区域的正电子湮没区域实际是指正电子电荷密度分布于电子密度的重叠部分. 在对含钾原子的模拟中发现: 钾原子的掺入不会表现出钾的寿命特征, 正电子湮没区域会避开钾原子[35 ] , 只反映空位中包含的信息, 如图2(d) 所示. 因此在分析辐照后钨钾样品的正电子湮没寿命谱时不考虑钾.图 2 正电子湮没分布 (a)位错; (b)位错中弥散有氢原子; (c)位错中存在一个空位; (d)空位中存在一个钾原子; (e)晶界; (f)晶界中存在一个空位Figure2. Positron annihilation distribution: (a) dislocation; (b) hydrogen atoms are scattered in the dislocation; (c) dislocation with a vacancy; (d) vacancy with a potassium at dislocation; (e) grain boundary; (f) grain boundary with a vacancy.图3 和图4 分别给出了与氢、氦相关的不同空位型缺陷的正电子寿命模拟结果. 计算结果表明, 游离于间隙位的氢原子和氦原子对钨的寿命值基本无影响. 钨中单空位的正电子寿命值约为197 ps, 并且随氢、氦原子占据数量的增多而下降, 氢、氦原子的占据导致空位型缺陷的有效开空间体积减小[36 ] , 并且氢、氦引入的电子密度会导致价电子密度增加[34 ] , 因此正电子寿命降低. 氦原子对正电子寿命的影响比氢原子大, 当空位中包含一个氢原子时, 正电子寿命值下降至约168 ps, 当包含一个氦原子时则下降至约155 ps, 这是由于氦原子体积大于氢原子, 使空位团簇中电子密度更大[37 ] . 氢、氦原子在空位的数量有极限, 当占据数量过多时会从空位中脱离, 停留在空位附近的四面体或八面体间隙处. 当空位中氢原子数目达到6个时, 含氢单空位寿命值降至极限约为126 ps, 而当氦原子达到7个时降至极限约104 ps, 该结果与Troev等[38 ] 计算的结果相符. 多空位的正电子寿命变化趋势与单空位一致, 占据原子为氢时, 双空位的极限正电子寿命值约为116 ps, 当空位数为9时, 虽然在本文模拟的氢原子数目范围内未达到极限, 但在氢原子数量为35时已有平缓趋势, 估计其极限值约为168 ps; 占据原子为氦时, 空位数为2和9的极限正电子寿命值分别约为116 和145 ps. 正电子寿命与缺陷有效开空间体积也有关, 空位团簇的正电子寿命随空位尺寸增大而增大[38 ] .图 3 钨中氢相关缺陷的正电子寿命Figure3. Positron lifetime of H-related defects in tungsten.图 4 钨中氦相关缺陷的正电子寿命Figure4. Positron lifetime of He-related defects in tungsten.3.2.2.正电子寿命谱测试结果分析 -->3.2.2.正电子寿命谱测试结果分析 为了探究辐照后样品中氢氦相关缺陷的演化, 对纯H和H+6%He中性束辐照的钨钾样品和纯钨样品进行正电子湮没寿命测试, 结果如表4 所列, 利用PATFIT软件对正电子湮没寿命谱进行解谱, 在去除源成分后得到短寿命$ {\tau }_{1} $ 和长寿命$ {\tau }_{2} $ 两个分量. 其中$ {\tau }_{1} $ 是约化正电子体寿命, $ {\tau }_{2} $ 是缺陷态寿命. $ {\tau }_{1}^{\mathrm{c}\mathrm{a}\mathrm{l}} $ 通过(9 )式计算得到.编号 $ {\tau }_{1} $/ps $ {I}_{1} $/% $ {\tau }_{2} $/ps $ {I}_{2} $/% $ {\tau }_{m} $/ps $ {\tau }_{1}^{\mathrm{c}\mathrm{a}\mathrm{l}} $/ps WK1 133.0 ± 1.8 62.1 ± 1.0 325.1 ± 3.5 38.0 ± 1.0 205.9 ± 2.4 92.79 WK2 132.1 ± 1.3 70.6 ± 0.7 360.4 ± 3.5 29.4 ± 0.7 199.2 ± 1.9 95.23 PW1 123.1 ± 1.3 70.8 ± 0.7 343.3 ± 3.3 29.2 ± 0.7 187.4 ± 1.8 94.22 PW2 144.0 ± 1.8 66.2 ± 1.0 340.4 ± 4.1 33.8 ± 1.0 210.3 ± 2.6 95.75
表4 辐照样品正电子寿命Table4. Positron lifetime of irradiated samples.[39 ] :$ {n}_{\mathrm{b}}\left(t\right), {n}_{\mathrm{d}}\left(t\right) $ 分别为t 时刻正电子在体态和缺陷态的数目; $ {\lambda }_{\mathrm{b}}, {\lambda }_{\mathrm{d}} $ 为正电子体态和缺陷态的湮没率; κ 为缺陷的捕获率. 上式的初始条件为${n}_{\mathrm{b}}\left(0\right)= $ $ {N}_{0}$ , $ {N}_{0} $ 为t = 0时刻正电子的总数目. 其解即正电子的衰变谱:κ 为μ 为正电子捕获系数.$ {\tau }_{1} $ 与计算得到的$ {\tau }_{1}^{\mathrm{c}\mathrm{a}\mathrm{l}} $ 发现结果差异较大, 表明样品中不只存在一种缺陷, 可能有与体寿命相近的缺陷对其分量造成影响. 前文对相关缺陷的正电子寿命模拟计算结果以及其他研究人员的研究结果表明[38 ,40 ] , 寿命值在100—160 ps间的缺陷类型较多, 包括氢-空位复合体、氦-空位复合体以及氢-氦-空位复合体等, 这些缺陷类型均可能为$ {\tau }_{1} $ 贡献一定强度. 对比纯钨在两种辐照下的寿命情况, 样品PW2的短寿命值$ {\tau }_{1} $ 为144.0 ps而PW1为123.1 ps, 表明在H+6%He混合束辐照条件下, 出现更多寿命值较大的缺陷. 结合正电子寿命模拟计算可推测在纯H辐照下, $ {\tau }_{1} $ 所包含的缺陷主要为空位数较小的饱和氢-空位复合体(正电子寿命值约125—137 ps), 而在混合束辐照条件下, 氦原子会造成比氢原子更为严重的损伤, 出现空位体积更大的氦-空位复合体(约145 ps左右), 因而$ {\tau }_{1} $ 值增大. 而对于钨钾合金, 一方面钾原子与钨原子体积差异较大, 钾原子的引入会导致样品体缺陷增加, 使得纯H辐照下样品WK1的$ {\tau }_{1} $ 值增加. 另一方面钾掺入带来的钾泡会阻碍位错环、氦空位团簇的迁移合并[41 ] ; 除此之外, 钾泡以及其钉扎的大量位错会成为氢原子的扩散通道, 使样品中氢原子的数量下降, 形成氦原子占主导的复合体(约139 ps左右), 使正电子寿命下降. 二者的共同作用导致钨钾样品在两种辐照条件下的短寿命值$ {\tau }_{1} $ 相差不大且位于纯钨样品之间.表4 长寿命分量发现, 4组样品的$ {\tau }_{2} $ 值均大于320 ps, 超过前文计算复合体寿命值, 这表明在两种辐照后形成了大尺寸缺陷如空位型团簇、气泡或孔洞等[38 ,42 ] . 对比测试结果, 在纯H辐照下样品WK1较PW1长寿命$ {\tau }_{2} $ 值更小而强度$ {I}_{2} $ 更大, 表明纯钨样品中缺陷尺寸更大, 钨钾样品会促进氢原子的释放. 而在H+6%He混合束辐照条件下则相反, 样品WK2的长寿命$ {\tau }_{2} $ 值更大而强度$ {I}_{2} $ 更小, 表明钨钾样品中缺陷尺寸更大, 其原因可能来自两方面: 其一高能的氦氢粒子注入造成了大量的离位损伤, 产生大量的空位, 氢原子由于其结合能较低容易从这些缺陷中释放出去, 而氦原子则会通过冲出位错环机制产生位错[43 ] , 并在此成核, 生长为氦泡; 其二在钨钾合金中钾原子与基体之间存在巨大相界, 氦原子更容易在此聚集形成氦泡[16 ] . 因此钨钾合金中更容易存在大尺寸的氦泡导致$ {\tau }_{2} $ 值更大. 根据正电子表面态模型[44 ] 可以对氦泡尺寸进行估算, 结合正电子寿命谱测试结果可确定两种样品中氦泡生长情况. 该模型认为正电子在气泡中的正电子寿命主要由表面金属电子的恒定湮没率和气泡中气体原子浓度决定的, 因此钨中正电子寿命$ {\tau }_{2} $ 和泡内氦原子浓度$ {n}_{\mathrm{H}\mathrm{e}} $ 的关系式为[45 ] , 钨钾中由于少量钾掺杂对寿命基本没有影响, 因此不考虑钾原子的作用. 假设样品中总的氦浓度$ {N}_{\mathrm{H}\mathrm{e}} $ 均分布于氦泡中, 且氦泡为球体, 则可以得到氦泡半径r 和总浓度的关系:$ {C}_{\mathrm{B}} $ 是气泡浓度; κ 气泡捕获速率; μ 是比捕获率. 比捕获率取决于缺陷半径和温度, 根据大量实验有如下经验公式[46 ] :A = 9.07 × 1015 ?–1 ·s–1 , B = 3.3 × 1014 ?–2 ·s–1 . 结合(13 )式—(16 )式可以得到尺寸方程:17 )变为只与D 相关的二次方程:18 )得到${D}_{{\rm{WK}}}$ 为18.6、${D}_{{\rm{PW}}}$ 为15.8, 则由式(19 )可知钨钾合金中氦泡尺寸更大. 因此, 钨钾合金中, 钾引入带来的钾泡以及其钉扎的位错等缺陷会成为氢的扩散通道, 促进氢原子的释放, 形成以小尺寸氢-空位复合体为主的缺陷; 而对于氦原子, 钾泡等缺陷会成为氦原子的捕获中心, 促进氦原子成核并在此生长为更大尺寸的氦泡.3.3.慢正电子束多普勒展宽谱分析 -->3.3.慢正电子束多普勒展宽谱分析 33.3.1.SRIM模拟分析 -->3.3.1.SRIM模拟分析 图5 和图6 分别给出了氢原子和氦原子注入纯钨和钨钾合金中损伤和粒子浓度随深度的分布. 选用TRIM程序中的“序中的“氢原子和 Calculation with full amage Cascades”辐照模式进行模拟. 设置钨的离位能为 90 eV, 表面能和结合能为 0 eV, 钾的离位能 25 eV, 得到氢、氦原子随深度的分布. 计算中采用的纯钨样品密度约 19.2 g/cm3 , 钨钾合金样品的密度约 19.0 g/cm3 , 相应的原子密度约为6.338 × 1022 atoms/cm3 . 具体结果由输出文件给出. 从图5 和图6 可以看出, 两种样品的离位损伤和粒子浓度分布差距较小, 这是由于SRIM软件创建的钨钾模型中钾原子均匀分布在钨晶格中, 并且含量很低, 对粒子注入过程中产生的损伤影响极小. 两种模型中, 氢原子的损伤分布主要集中在0—130 nm范围内; 而氦原子产生的损伤比氢原子稍深, 主要分布在20—190 nm范围内.图 5 SRIM 模拟H/He中性束辐照纯钨和钨钾的辐照损伤分布Figure5. Profiles of damage in PW and WK irradiated with pure H and H+6%He neutral beam calculated with SRIM.图 6 SRIM 模拟H/He中性束辐照纯钨和钨钾的粒子浓度分布Figure6. Profiles of particle concentration in PW and WK irradiated with pure H and H+6%He neutral beam calculated with SRIM.3.3.2.慢正电子束多普勒展宽谱分析 -->3.3.2.慢正电子束多普勒展宽谱分析 图7 给出了纯钨和钨钾合金在纯H和H+6%He中性束辐照后的S-E 分布和VEPFIT拟合结果, 图8 是拟合得到的4种样品的S 参数随深度的分层图. 从图7 可以看出, 在纯H辐照下, 样品PW1和WK1无明显损伤区域, S 参数拟合分为2层: 表面层和体层. 其原因可能是本实验中纯氢束辐照温度较高(1000 ℃), 氢在样品中的扩散较剧烈更容易从样品中释放, 并且高温也会使缺陷有所恢复[18 ] . 值得注意的是, 样品WK1的S 参数明显小于PW1, 表明钨钾合金中缺陷浓度或尺寸减小. 钨钾合金中弥散强化粒子会增加晶界密度[16 ] , 促进氢原子的释放; 钾泡以及其钉扎的位错等缺陷也会成为氢的释放通道, 降低样品中氢的滞留. 与SEM结果以及正电子寿命谱结果相符. 另外在模拟中发现, 弥散在位错中的氢原子会影响正电子的湮没, 因此当正电子被位错等缺陷捕获后, 由于弥散的氢原子对电子密度的影响, 正电子与高动量电子的湮没概率增加, 也会导致S 参数下降. 在H+6%He中性束辐照条件下, 样品PW2和WK2均有明显损伤区域, S 参数分为3层: 表面层、损伤层和体层. 从图8 可以看出, 样品WK2的损伤深度小于PW2, 这可能是钾泡阻碍了空位团簇和位错等缺陷的迁移和合并. 并且样品WK2的损伤程度更低, 其可能是钨钾本身的缺陷成为氦的成核点, 促进氦空位复合体的形成, 并通过合并或吸收氦原子不断长大, 形成氦泡, 在应力和温度梯度的作用下促进氦泡迁移到表面破裂并释放了部分氦氢原子[47 ] ; 另外间隙位错环从氦泡中冲出迁移也会使缺陷有所恢复[47 ] .图 7 纯钨和钨钾合金H/He中性束辐照后S-E 分布和拟合曲线Figure7. S-E distribution and fitting curve of irradiatered PW and W-K.图 8 VEPFIT拟合H/He中性束辐照样品的S 参数随注入深度的变化Figure8. Fitted S parameters versus VEPFIT for irradiated samples.S 参数和W 参数有以下关系式:S d 为缺陷态S 参数; S b 为体态S 参数; W d 为缺陷态W 参数; W b 为体态W 参数; R 为S , W 参数斜率, 只与缺陷类型有关. 因此S-W 曲线反映了正电子的湮没机制, 曲线之间各斜率的差异反应了正电子在不同类型缺陷中湮没, 根据聚集区或者转折可以判断缺陷类型的变化. 图9 给出了四种样品的S-W 拟合曲线, 从图中可以看出样品WK1的S-W 点基本分布在一条直线上, 说明样品WK1的缺陷较为单一, 推测其可能是钨钾合金中钾泡等缺陷会成为氢的扩散通道, 促进氢原子的释放, 形成小尺寸的氢空位复合体, 与正电子寿命谱测试结果相符. 样品PW1, WK2和PW2的S-W 点分布较为集中, 出现转折和聚集区, 说明缺陷类型复杂. 分析发现样品PW1与WK2及PW2在较深处S-W 点重合, 并且其斜率与样品WK1接近, 表明此缺陷类型相同, 为小型氢空位复合体, 在高温作用下, 一部分从表面释放, 另一部分迁移到样品深处. 斜率的细微差异由复合体中氢与空位占比不同引起. 该三种样品的的S-W 分布都出现转折, 表明其缺陷类型发生变化. 其中样品PW2和WK2的S-W 分布基本重合, 而与样品PW1不同, 表明此缺陷变化与氦原子的掺入有关, 在H+6%He中性束辐照条件下, 氦相关缺陷如氦空位复合体以及氦泡等向表面区域迁移, 而氢原子由较高的辐照温度从邻近表面区域释放.图 9 辐照后纯钨和钨钾合金样品S-W 参数变化Figure9. S-W plots for irradiated PW and WK samples.4.结 论 本文使用正电子湮没谱学对纯H和H+6%He中性束辐照的纯钨和钨钾合金样品中氢氦相关缺陷进行研究. 通过对钨超胞中正电子湮没参数进行模拟, 发现弥散在位错和晶界中的氢、氦原子会影响正电子的湮没区域, 但当位错和晶界中存在空位时, 氢、氦原子会被空位捕获, 并且正电子也会湮没于该空位中; 正电子湮没寿命计算结果表明, 氢原子对其寿命的影响比氦原子小; 另外单个钾原子的引入对氢、氦相关缺陷正电子寿命值基本无影响. 结合正电子寿命谱测试结果发现钨钾合金中钾泡以及其钉扎的位错等缺陷会成为氢的扩散通道, 促进氢原子的释放, 形成较小的饱和氢-空位复合体; 而对于氦原子, 这些缺陷会成为氦原子的捕获中心, 促进其成核并生长为尺寸更大的氦泡. 扫描电镜和慢正电子束多普勒展宽测试结果验证了钾泡等缺陷的作用, 与纯钨相比, 在纯H辐照下钨钾合金表面更加平整, 样品中缺陷尺寸和浓度更低; 而在H+6%He中性束辐照中, 这些缺陷促进了氦泡的长大, 并在应力和温度梯度的作用下促使其迁移至表面区域释放, 从而有利于相关缺陷的修复, 降低了辐照损伤程度. 正电子湮没谱学主要是通过对空位型缺陷的信息进行分析, 间接研究钨钾合金中钾泡等缺陷对氢氦相关缺陷演化的影响, 后续可结合透射电子显微镜等测试技术进行更加直观的研究, 为相关材料性能的优化方向提供参考. 












 图 1 样品SEM图 (a) 未辐照WK样品; (b) 未辐照PW样品; (c) 辐照样品WK1; (d) 辐照样品PW1; (e) 辐照样品WK2 (右上角为红框区域局部放大图); (f)辐照样品PW2(右上角同(e))
图 1 样品SEM图 (a) 未辐照WK样品; (b) 未辐照PW样品; (c) 辐照样品WK1; (d) 辐照样品PW1; (e) 辐照样品WK2 (右上角为红框区域局部放大图); (f)辐照样品PW2(右上角同(e))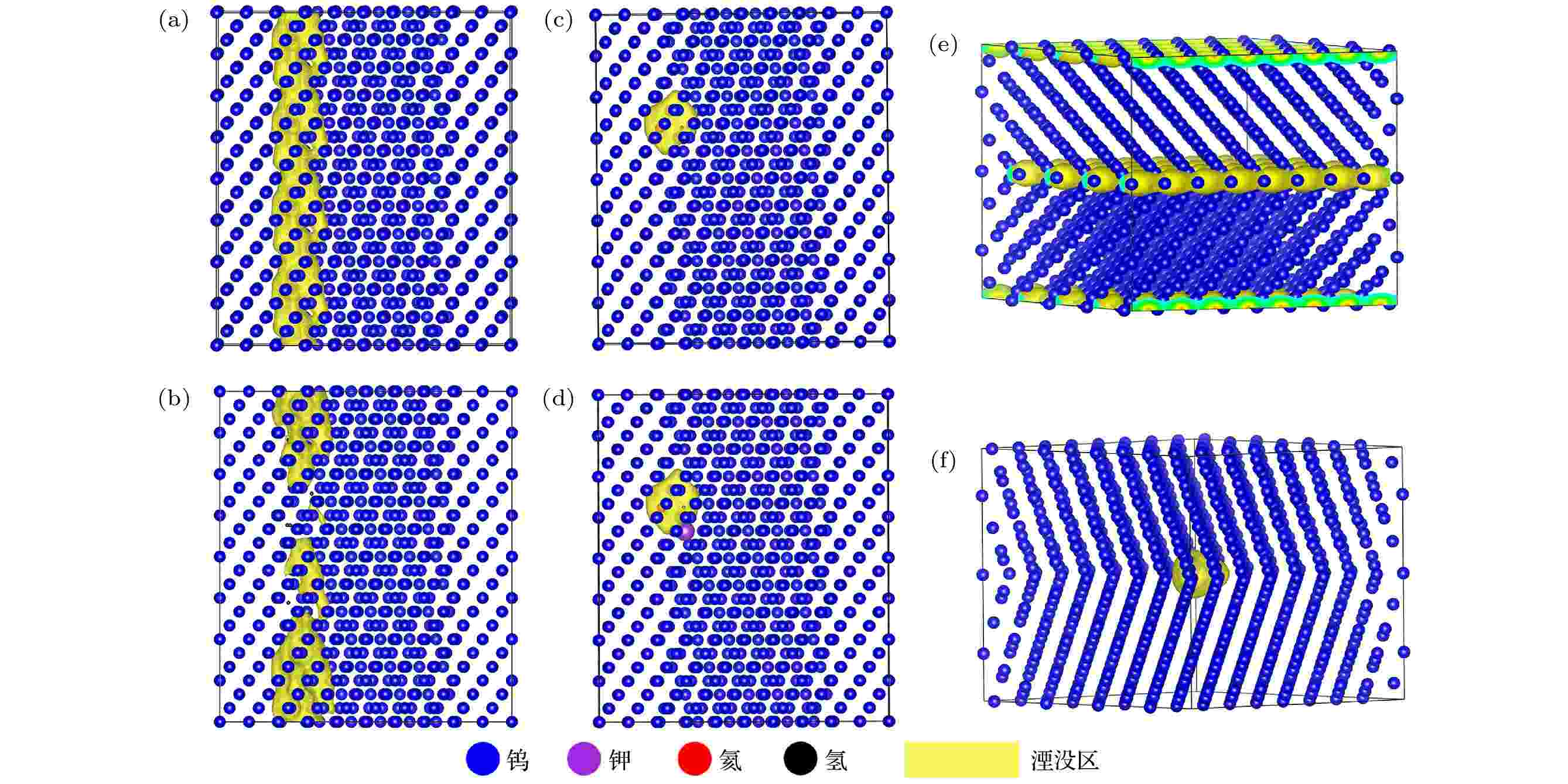 图 2 正电子湮没分布 (a)位错; (b)位错中弥散有氢原子; (c)位错中存在一个空位; (d)空位中存在一个钾原子; (e)晶界; (f)晶界中存在一个空位
图 2 正电子湮没分布 (a)位错; (b)位错中弥散有氢原子; (c)位错中存在一个空位; (d)空位中存在一个钾原子; (e)晶界; (f)晶界中存在一个空位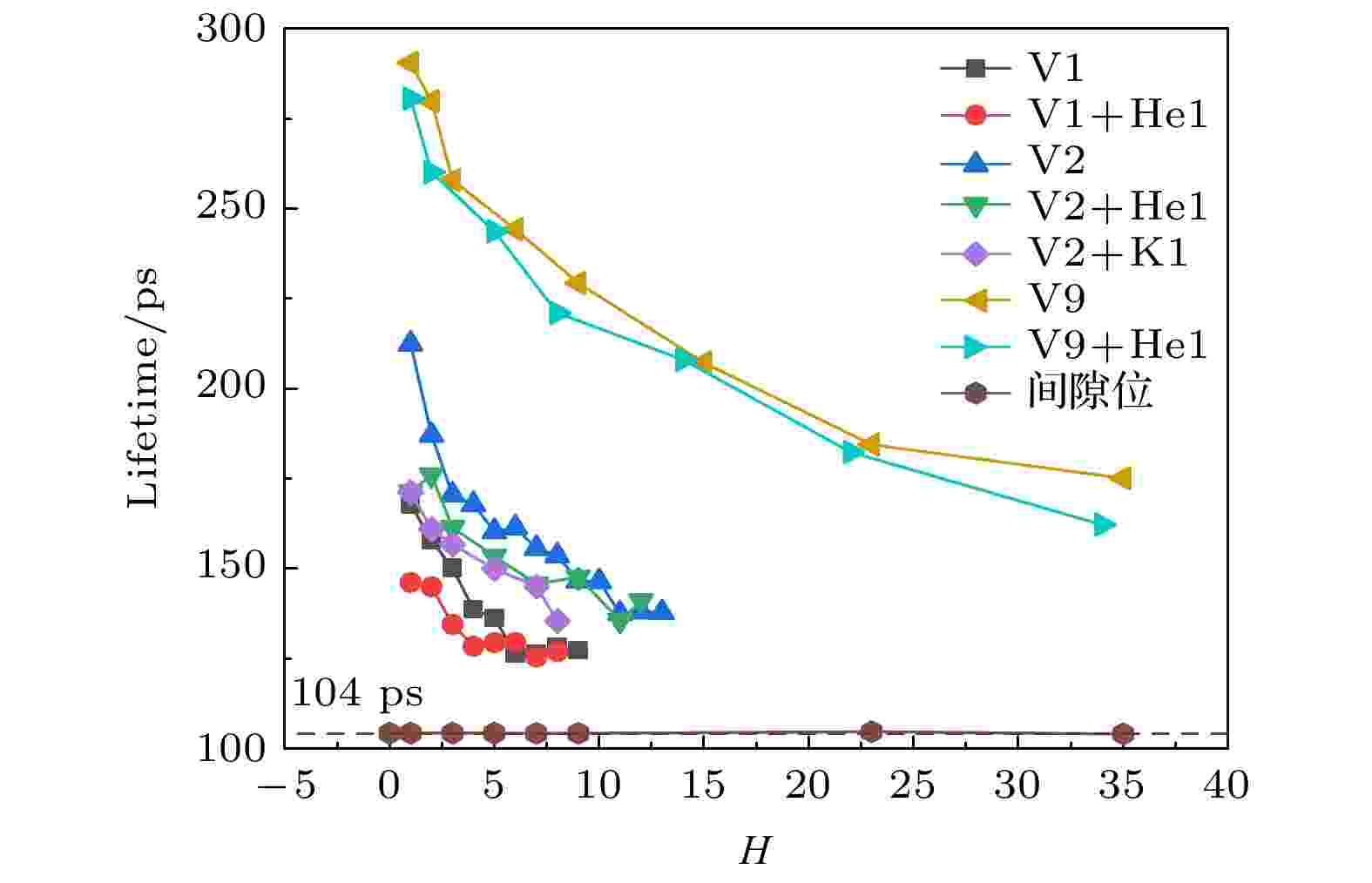 图 3 钨中氢相关缺陷的正电子寿命
图 3 钨中氢相关缺陷的正电子寿命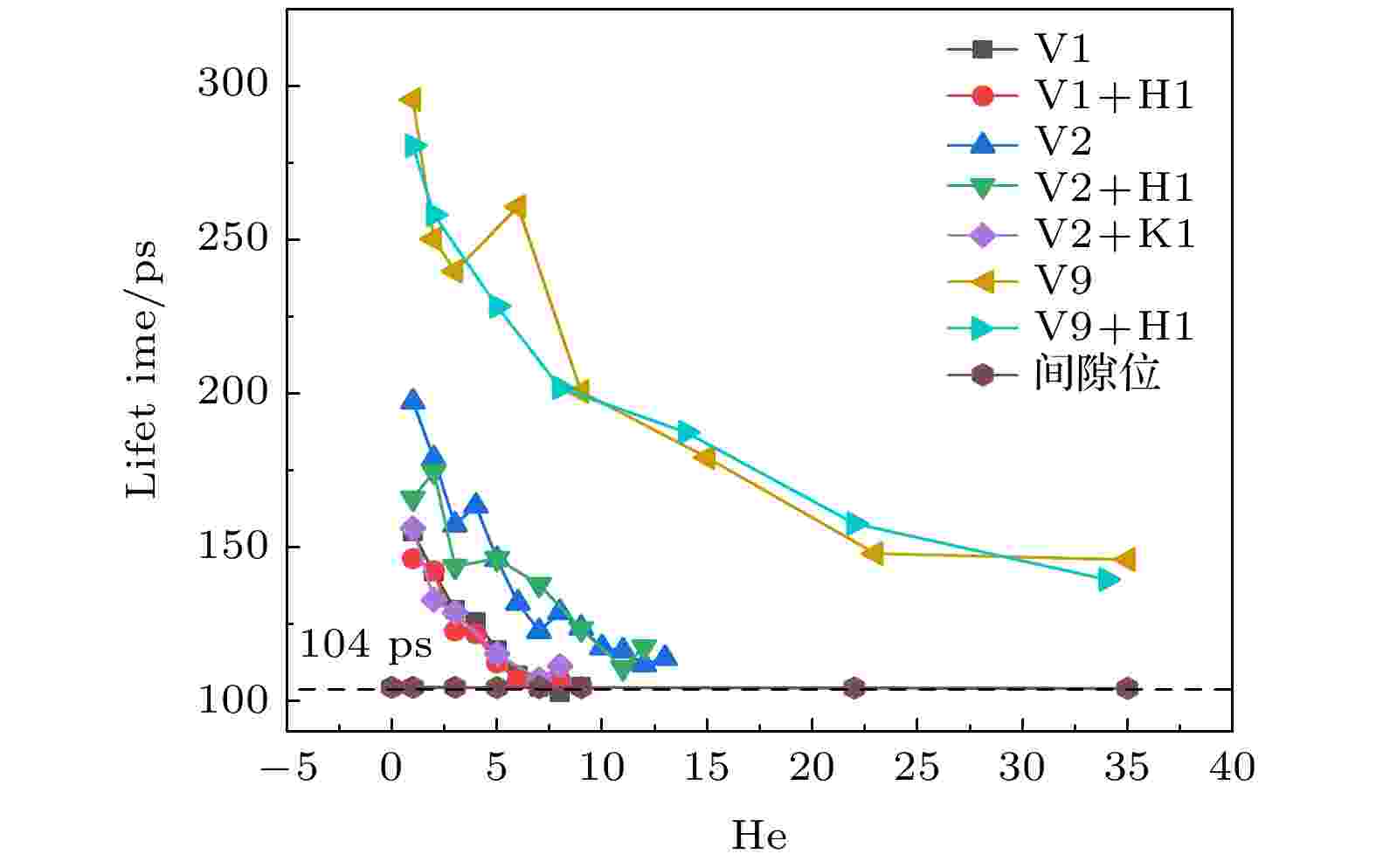 图 4 钨中氦相关缺陷的正电子寿命
图 4 钨中氦相关缺陷的正电子寿命

































































































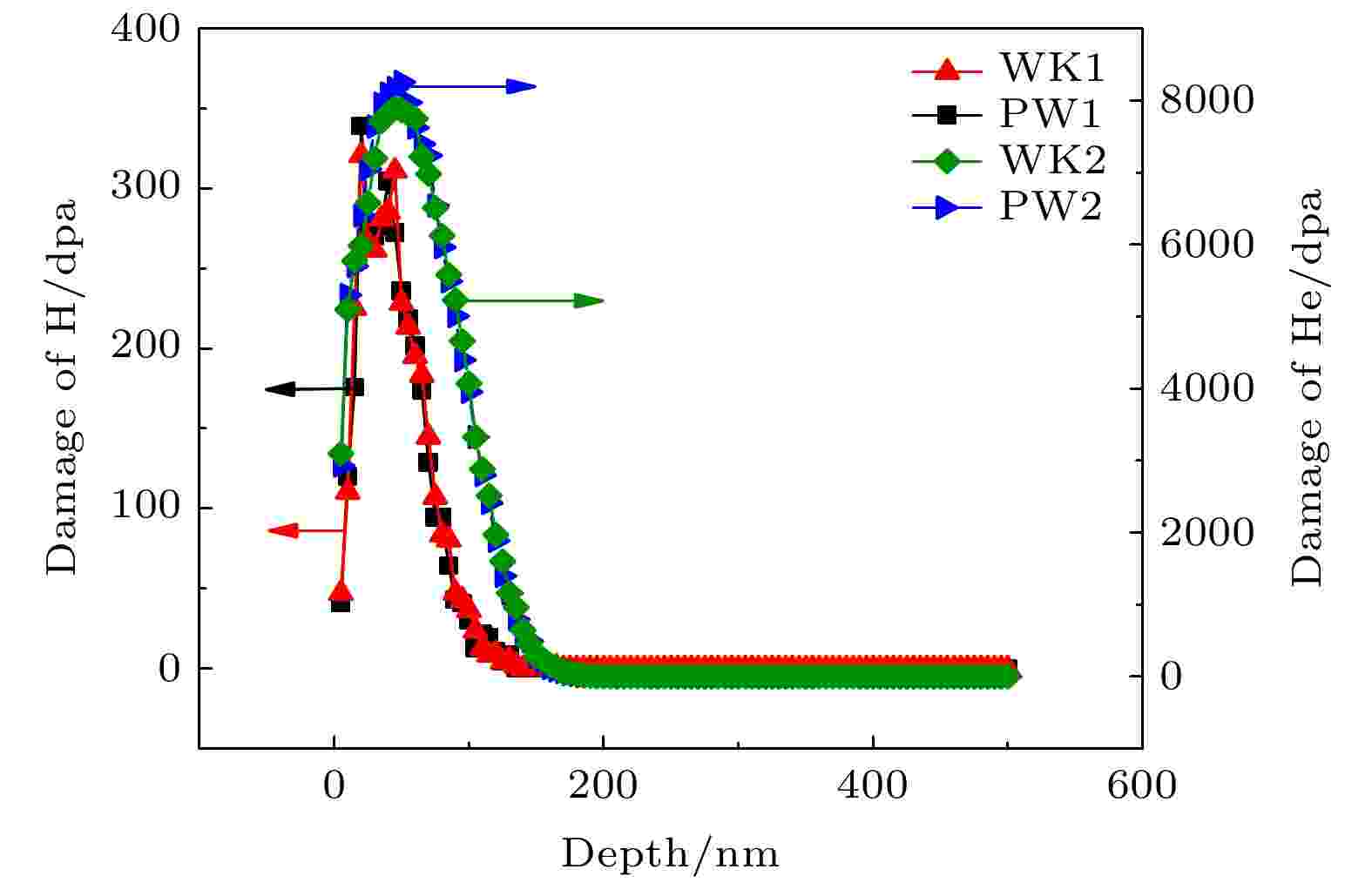 图 5 SRIM 模拟H/He中性束辐照纯钨和钨钾的辐照损伤分布
图 5 SRIM 模拟H/He中性束辐照纯钨和钨钾的辐照损伤分布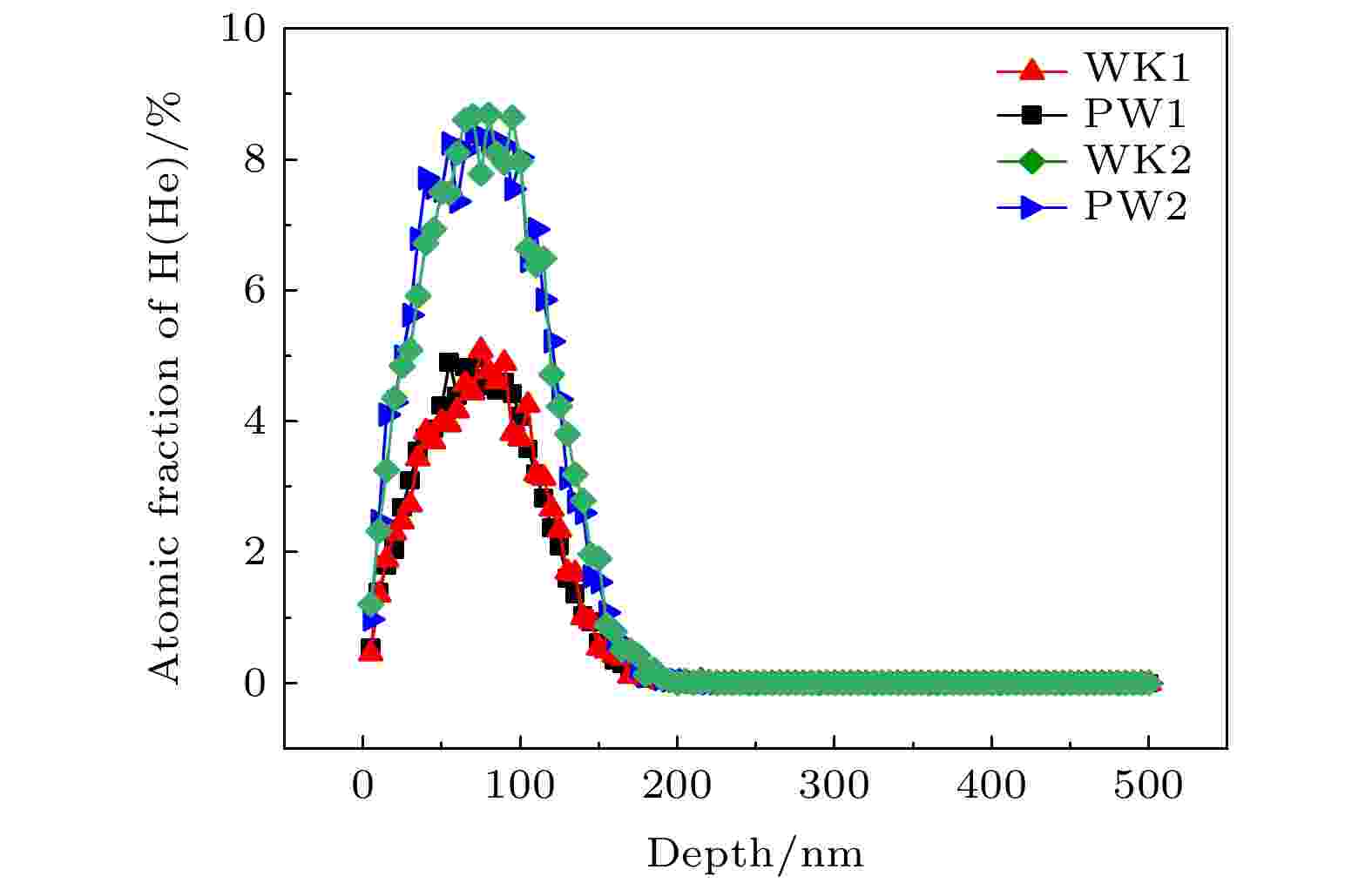 图 6 SRIM 模拟H/He中性束辐照纯钨和钨钾的粒子浓度分布
图 6 SRIM 模拟H/He中性束辐照纯钨和钨钾的粒子浓度分布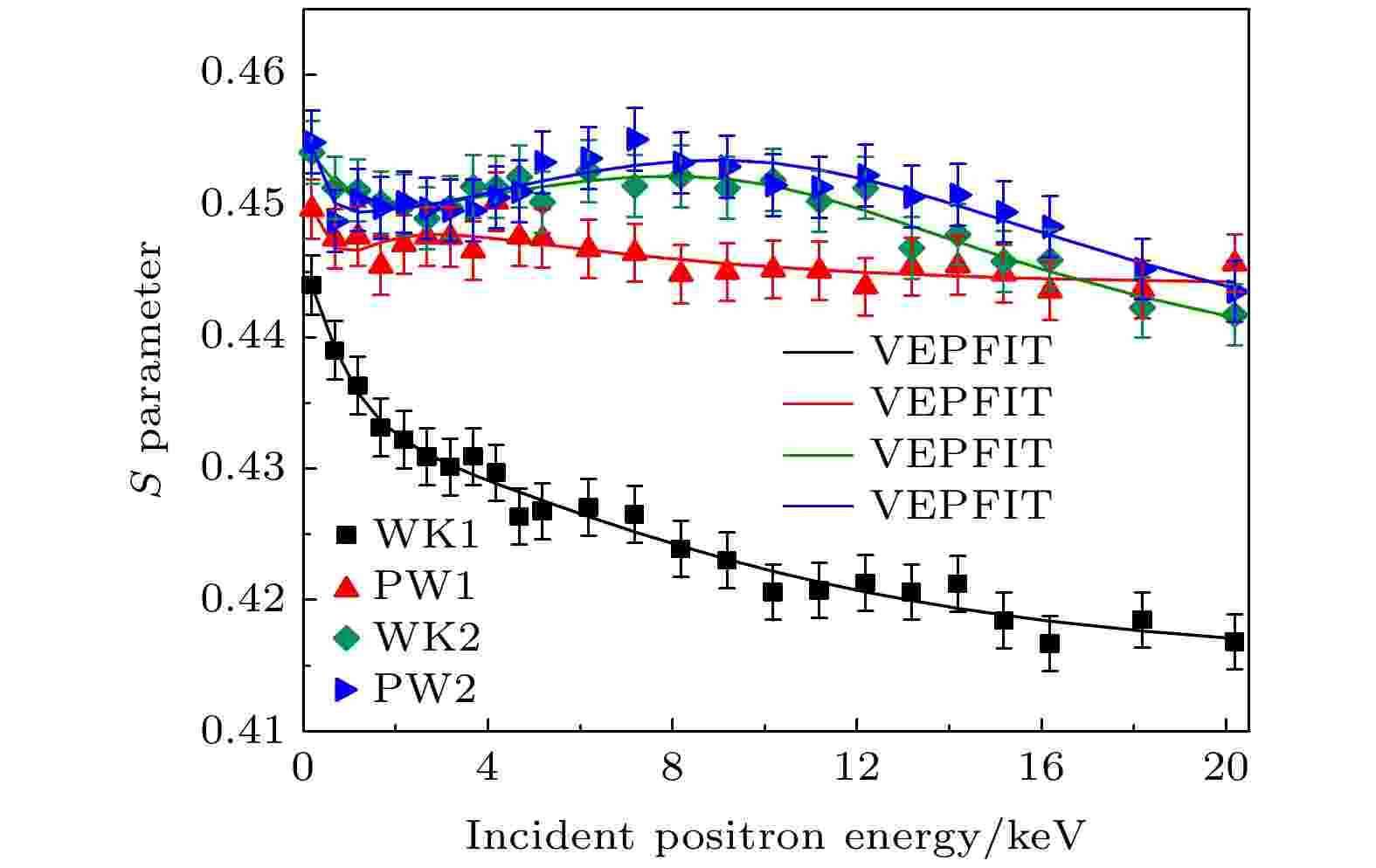 图 7 纯钨和钨钾合金H/He中性束辐照后S-E分布和拟合曲线
图 7 纯钨和钨钾合金H/He中性束辐照后S-E分布和拟合曲线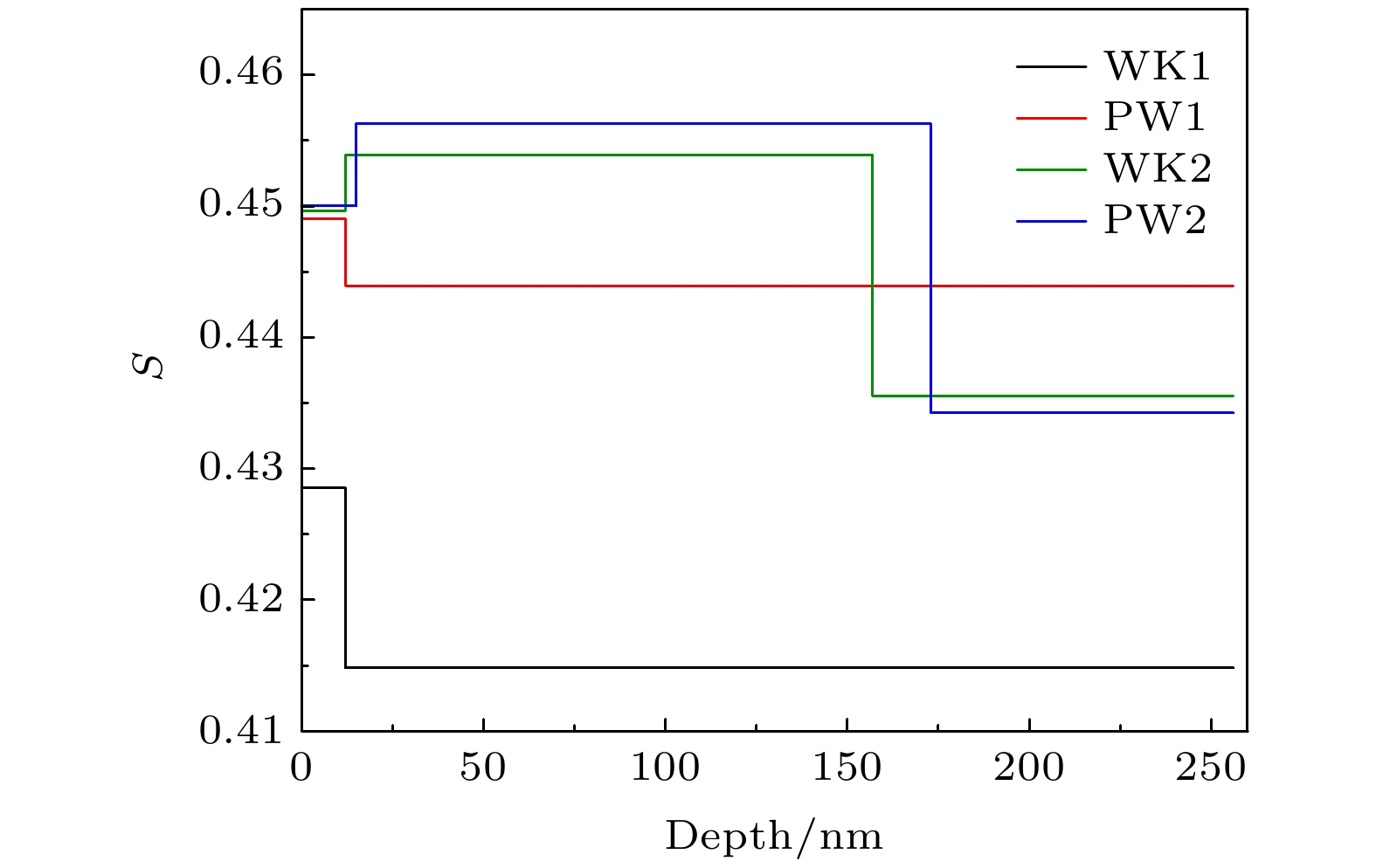 图 8 VEPFIT拟合H/He中性束辐照样品的S参数随注入深度的变化
图 8 VEPFIT拟合H/He中性束辐照样品的S参数随注入深度的变化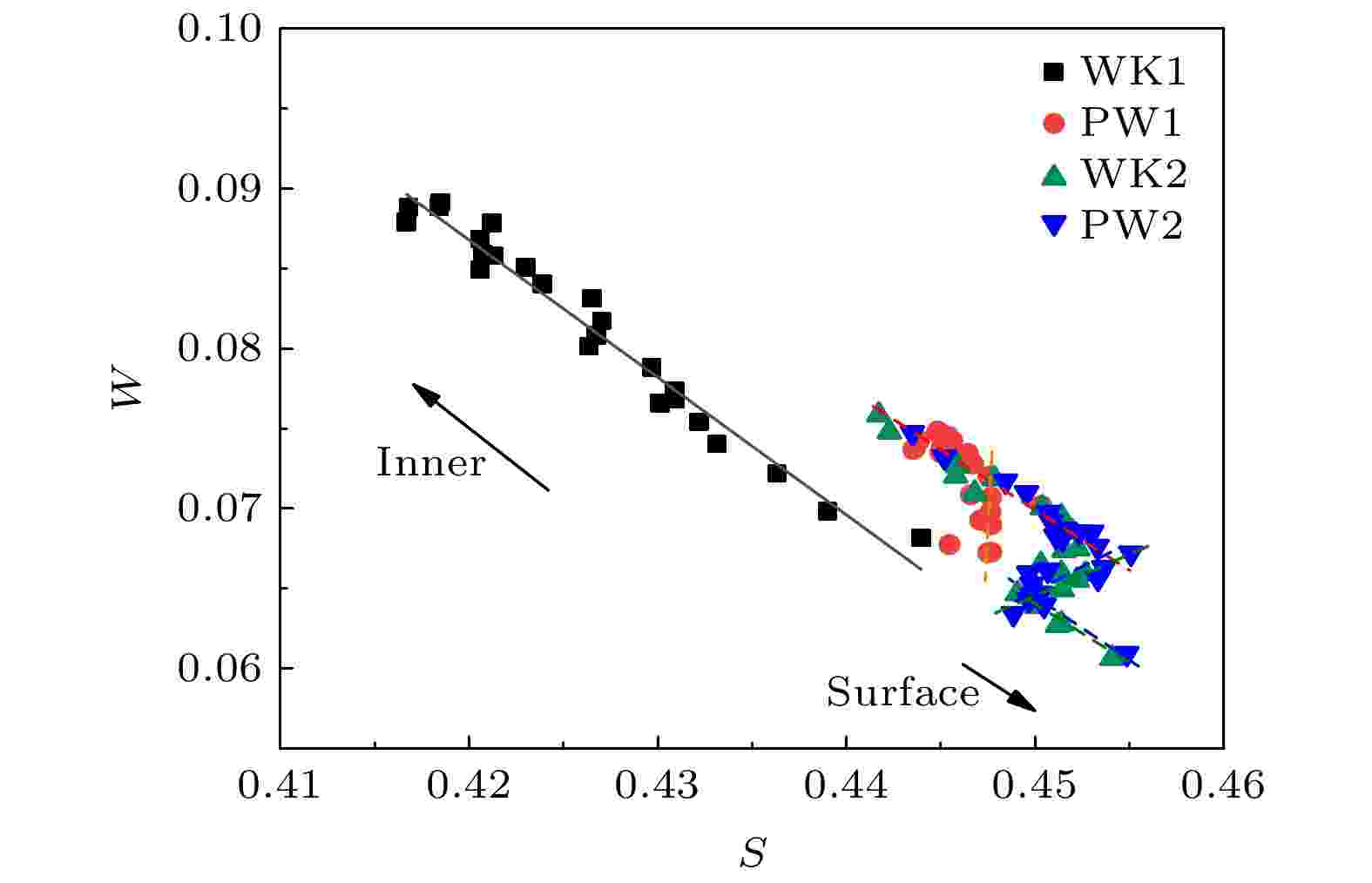 图 9 辐照后纯钨和钨钾合金样品S-W参数变化
图 9 辐照后纯钨和钨钾合金样品S-W参数变化