摘要:构造了一种多腔型基本单元, 由该基本单元构成的声学超构材料能够实现声场增强效应. 此功能的实现是由基本单元的声腔和系统结构之间的相互耦合作用产生的单极子Mie共振引起. 本文通过对多个基本单元进行不同形式的排列组合构造了对称型超构材料和非对称型超构材料, 这两类超构材料可用于实现不同效果的声场增强. 研究表明, 由于对称型超构材料结构的高度对称, 其声场增强效应的实现不受入射声波方向的影响; 而非对称型超构材料的声场增强效应具有较强的方向依赖性, 声波从不同侧入射时, 超构材料对声场的增强效果也不同. 本文关于这两类超构材料的研究将在隔声、声传感器、声通信、非对称性声学器件方面具有潜在的应用前景.
关键词: Mie共振/
对称型超构材料/
非对称型超构材料/
声场增强效应

English Abstract

全文HTML

--> --> -->

近年来, 在空气声中实现声波分量的局域增强这项研究工作逐渐受到关注. 若声场能够被大幅度增强, 这将会发掘许多有价值的潜在应用, 例如声传感器、声通信等. 在自然界中, 由于声能具有很低的能量密度, 空气中声场局域增强效应的实现通常比较困难. 因此, 探索新的物理机制和方法去实现声场增强具有重要的意义.
声学超构材料作为一种人工专门设计的复合结构, 可通过局域共振机理来调控弹性波的能带结构, 从而获得自然材料所不具备的物理特性, 如负等效体积模量^[1,2]、负等效质量密度^[3-5]、零折射率^[6]等. 超构材料在对声波传播方式的调控方面起重要作用, 目前, 基于亥姆霍兹共振器^[7]和腔谐振器^[8,9]的局域共振机理设计的超构材料已经实现了声场增强效应. Yuan等^[10,11]分别通过优化亥姆霍兹共振器底部和颈部结构来降低声学粘性损耗, 实现了低频声波的局域增强效应. Song^[12]等设计了一种新型声腔型双壁超构材料, 其能够在亚波长的空气隙内发生强烈的局域声场增强效应. 此外, 近年来, 超构材料的声学Mie共振得到越来越多的关注, 相比局域共振, Mie共振具有更为丰富的共振模式, 如单极子、偶极子、四极子等更高的多极子共振模式. 利用声学Mie共振的不同共振模式可分别实现不同效果的局域声场增强. Zhu等^[13]提出一种偶极子共振的亚波长尺度下的指向性传感结构, 结构内声压增幅与卷曲空间外壳的折叠程度相关. Zhao等^[14]设计了一种简并Mie共振的亚波长壳结构, 在不改变声源方向性的前提下, 可以实现单级源和多级源的声波增强发射. 上述方法都通过不同共振形式和结构实现了声场增强效应.
另外, 近年来利用声学超构材料设计实现的非对称声传输开始受到研究者的高度重视^[15-17]. 研究人员已经通过非线性效应^[18,19]、近零折射率材料特性^[20,21]、超构表面的表面消逝波等原理实现了非对称声传输. Jin等^[18]和Liang等^[19]利用非线性介质和一维声子晶体相结合的方法提出了一种声整流模型. Li等^[22]提出了一种由近零折射率超构材料设计而成的声学棱镜模型, 其利用近零折射率材料对入射声波角度的高度依赖性, 实现了声波单向传输. Shen等^[23]利用该原理, 通过采用梯度折射率超构表面和近零折射率超构表面组合而成的双层复合结构, 产生了强非对称声传输效应. Song等^[24]基于超构表面的表面消逝波实现了非对称声传输效果. 若能将声场增强和非对称声传输这两种功能在一个系统中同时实现, 则有望实现具有非对称性质的声场增强效应, 其将在隔声、非对称声学器件等方面具有重要的应用价值.
基于此, 本文构建了一种多腔型基本单元结构, 利用其组成不同形状的超构材料, 并使每种超构材料都含有丰富的Mie共振特性. 声场增强效应是基于基本单元的声腔和系统结构之间相互耦合产生的单极子Mie共振来实现. 由于设计的超构材料对声波入射方向具有依赖性, 利用这一特性可以实现声场的非对称增强. 研究表明, 对称型超构材料的声场增强效应不受声波入射方向的影响, 而非对称型超构材料的声场增强效应具有较强的方向依赖性.

本文设计的多腔型基本单元的结构如图1(a)所示, 该基本单元的外部形状是1个圆形, 其由1个圆形中心腔和12个谐振腔共同组成, 可以分为4个相同的部分, 其中12个谐振腔以3个为一组围绕中心腔的四周均匀分布. 中心腔和谐振腔内填充的媒质均为空气, 腔壁选取的材料为环氧树脂. 腔壁的厚度为t, 中心腔的开口宽度均为a, 谐振腔的开口宽度均为w, 圆形中心腔的半径为r₁, 基本单元的外部圆形的半径为R₁. 所有的结构参数分别为t = 3 mm, a = 5 mm, w = 4 mm, r₁ = 2.7 cm和R₁ = 5 cm. 环氧树脂的材料参数分别为密度${\rho _1} = 1050\;{\rm{ kg/}}{{\rm{m}}^3}$、杨氏模量E = 5.08 GPa和泊松比v = 0.35; 背景媒质空气的密度和声速分别为ρ₀ = 1.21 kg/m³和c₀ = 343 m/s. 本文在r₁和R₁之间引入两个具有相同场的虚拟层, 基于声散射理论可以计算出多腔型基本单元的各阶Mie共振所对应的共振频率. 将入射声源视为平面波${p_{{\rm{in}}}} = {p_0}{{\rm e}^{{{\rm i}}(kr\cos \phi - \omega t)}}$, 其中${p_0}$为声压振幅, i表示虚部, k是空气中的波数, $\omega $是角频率, $\phi $是相位, r是半径. 声压分布可以用Bessel (J_m)函数和Hankel (H_m)函数表示:
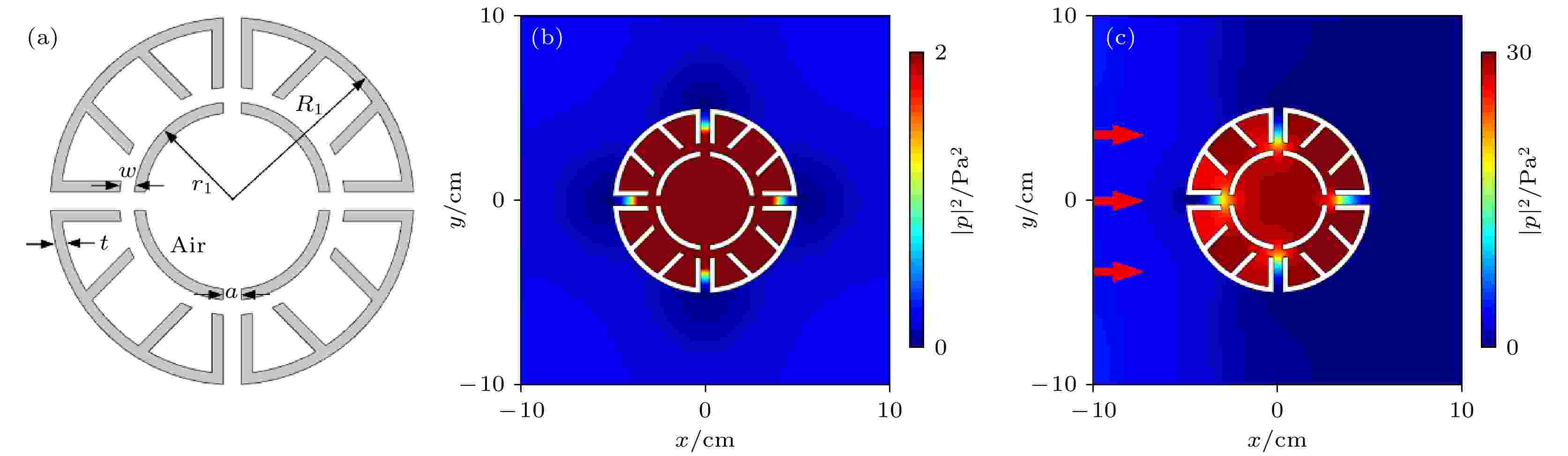图 1 (a)多腔型基本单元的结构示意图; (b)特征频率为672 Hz时, 基本单元在单极子Mie共振模式下的声强分布图; (c)当频率为672 Hz的声波从结构左侧垂直入射时, 多腔型基本单元的声强分布图
Figure1. (a) Structural diagram of multiple-cavity unit; (b) sound intensity distribution of the unit in monopole Mie resonance mode at the characteristic frequency of 672 Hz; (c) sound intensity distribution of the unit when the sound wave with frequency of 672 Hz is normally incident from the left side.

$\begin{align}& p = \\& \begin{cases}\displaystyle \sum\limits_m {[{C_m}{{\rm{J}}_m}({k_0}r) + {D_m}{{\rm{H}}_m}({k_0}r)]} {{\rm{e}}^{{\rm{i}}m\theta }}, & r > {R_1},\\\displaystyle\sum\limits_m {[{E_m}{{\rm{J}}_m}({k'}r) + {F_m}{{\rm{H}}_m}({k'}r)]} {{\rm{e}}^{{\rm{i}}m\theta }}, \\\qquad {r_1} < r < {r_2} = {r_1} + ({R_1} - {r_1})\delta {\rm{ }},\\\displaystyle\sum\limits_m {{G_m}} {{\rm{J}}_m}({k_0}r){{\rm{e}}^{{\rm{i}}m\theta }}, & r < {r_1} ,\end{cases}\end{align}$

其中$\delta = {{4 w} / {2{\text{π}}{R_1}}}$是四通道圆的占空比, ${k_0} = {\omega / {{c_0}}}$是空气中的波数, ${k'}$是基本单元的等效波数, ${C_m}—{G_m}$是各层m阶的展开系数. 当$\left| {{{{D_m}} / {{C_m}}}} \right|$为1时, 代表散射声场达到最大, 此时可以求得第m阶Mie共振模式的共振频率. 当m = 0时, 单极子Mie共振模式所对应的共振频率可以近似地表示为${f_{\rm{R}}} \approx \dfrac{{{c_0}}}{{{\text{π}}{\eta _{\rm{r}}}}}\sqrt {\dfrac{{2\delta }}{{{r_1}({R_1} - {r_1})}}}$^[25], 其中${\eta _{\rm{r}}}$为基本单元的折射率, 根据反演法^[26]求得基本单元的等效折射率${\eta _{\rm{r}}}$约等于2.1, 则理论计算得到该基本单元的单极子Mie共振模式所对应的共振频率为666 Hz. 当m为其他正整数时, 可以得到其他共振模式所对应的共振频率.
采用有限元仿真软件COMSOL的声固耦合模块对多腔型基本单元的声学特性进行仿真验证. 在Mie共振单元结构中通过调整空气通道内声波的相位可实现单极子共振、偶极子共振以及其他多重Mie共振. 其中在单极子共振模式下, 声能能够聚集在结构内部, 且内部中心处的声强大小是入射声波的数倍, 因此本文将采用多腔型基本单元的单极子Mie共振在结构内部实现声场增强效应^[27]. 图1(b)显示了特征频率为672 Hz时所对应的单极子Mie共振模式下的声强分布, 与上述利用Mie散射理论所得的单极子共振频率(666 Hz)基本一致, 可以明显观察到多腔型基本单元结构内部出现声场增强的现象, 且声压大小远比结构外部的大, 这也证实了该多腔型基本单元可用于实现声场增强效应. 图1(c)是频率为672 Hz的平面波从左侧垂直入射到基本单元后的声强分布图, 其中入射平面波的声压振幅为1 Pa. 观察此图可以发现, 声能主要集中在该基本单元的内部, 且其内部中心点处的声场强度可高达30 Pa², 但这个增强的声场沿着圆形中心腔的径向衰减, 单元外部的强度均接近于0. 因此, 设计多腔型基本单元具有良好的声场增强效应.

2

-->

3.1.基于多腔型基本单元的对称型超构材料

基于该多腔型基本单元, 设计了一系列由多个基本单元组成的复合结构, 用以实现复合结构的单极子共振. 如图2(a)所示, 将8个相同的多腔型基本单元组成了一个外部形状为正方形的对称型超构材料, 基本单元的结构参数与图1(a)的相同, 相邻两个基本单元中心点之间的距离d为15 cm. 图2(b)给出了该对称型超构材料在特征频率为669 Hz时所对应的复合单极子Mie共振模式下的声强分布. 在该频率点处, 设计的正方形对称型超构材料处于单极子共振模式, 可以将声能集中在系统的中心区域, 实现声场增强效应.
图 2 (a)由8个多腔型基本单元组成的正方形系统示意图; (b)特征频率为669 Hz时, 正方形系统在复合单极子Mie共振模式下的声强分布图
Figure2. (a) Schematic diagram of a square system composed of eight multiple-cavity units; (b) sound intensity distribution of the square system in the compound monopole Mie resonance mode at the characteristic frequency of 669 Hz.

上述的研究通过使用特征频率分析求得该正方形系统的单极子Mie共振模式所对应的共振频率为669 Hz. 图3(a)和图3(b)分别是频率为669 Hz的平面波从该正方形系统的左侧和右侧垂直入射时系统的声强分布图, 可以发现, 该正方形系统的复合单极子共振模式在669 Hz频率处被激发, 声场增强效应在此频率处实现. 同时, 声波从左侧和右侧垂直入射时声强的分布均相同, 说明该系统具有良好的对称性. 为了与多腔型基本单元作对比, 与其样品同尺寸同分布的8个硬边界圆形结构被放置在相同位置, 相应的声强分布如图3(c)所示. 通过对比图3(a)、图3(b)与图3(c), 可以发现在相同入射声波的情况下, 正方形对称型超构材料样品内部中心点处的声强明显比硬边界圆形结构的要大, 这意味着超构材料样品具有更好的声能聚焦效果, 有效地体现了该对称型超构材料在复合单极子共振模式下实现的声场增强效应.
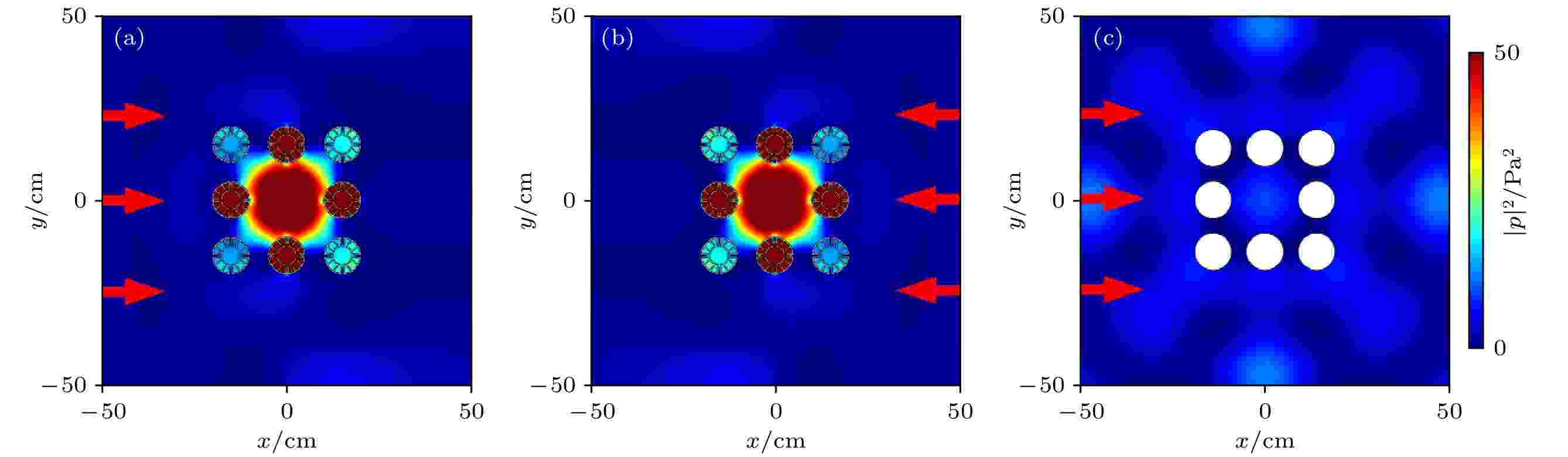图 3 声波从(a)左侧和(b)右侧垂直入射到8个多腔型基本单元组成的正方形系统时的声强分布图; (c)声波从左侧垂直入射到由8个硬边界圆形结构组成的系统时的声强分布
Figure3. Sound intensity distributions of the square system composed of eight multiple-cavity units when the sound wave is normally incident from (a) the left side and (b) the right side, respectively; (c) sound intensity distribution of the system composed of eight hard boundary circular structures when the sound wave is normally incident from the left side.

除此之外, 还可以利用该多腔型基本单元组成了其他不同形状的对称型超构材料, 验证不同的对称结构是否存在声场增强效应. 结构设计分别如图4(a)—(c)所示, 利用不同数量的多腔型基本单元设计了外部形状分别为圆形、矩形、正六边形的对称型超构材料. 其中圆形对称型超构材料的半径为d₁ = 18 cm, 矩形和正六边形对称型超构材料中相邻两个基本单元中心点之间的距离分别为d₂ = 16 cm和d₃ = 20 cm, 并且这些多腔型基本单元的结构参数与图1(a)中的完全一致. 对于这3个系统, 圆形、矩形和正六边形超构材料对应的复合单极子Mie共振模式所对应的共振频率分别为648, 629和621 Hz. 在共振频率处, 当声波以1 Pa的强度从左侧垂直入射到这3个超构材料系统时的声强分布分别如图4(d)—(f)所示, 声场增强效应均存在于这3个对称型超构材料的中心区域, 其内部中心点处的声场强度分别达到了15, 20和20 Pa². 由此可以推断, 由该多腔型基本单元构成的不同形状的对称型超构材料均可以实现声场增强效应, 这种灵活可调的声场增强系统可应用于许多特定场景, 例如声通信、声源或噪声定位等.
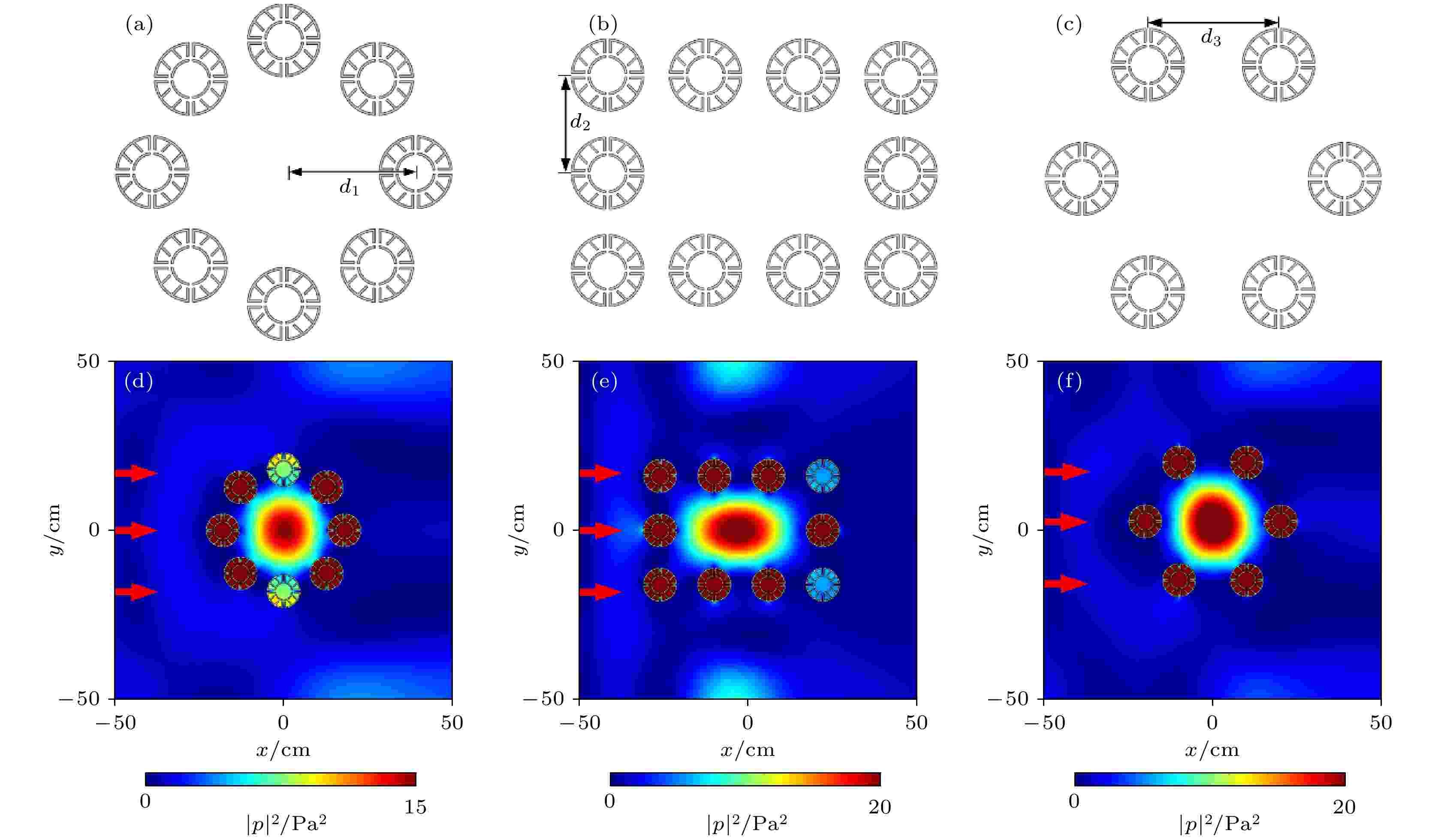图 4 由多腔型基本单元组成的(a)圆形、(b)矩形和(c)正六边形对称型超构材料的结构示意图; 在复合单极子Mie共振模式下, (d)圆形超构材料、(e)矩形超构材料和(f)正六边形超构材料的声强分布图, 对应的工作频率分别为648, 629, 621 Hz
Figure4. Schematic diagram of the (a) circular, (b) rectangular and (c) regular hexagonal symmetric metamaterials composed of multiple-cavity units. Sound intensity distributions of the (d) circular metamaterial, (e) rectangular metamaterial and (f) regular hexagonal metamaterial under the compound monopole Mie resonance mode with the working frequencies of 648, 629 and 621 Hz, respectively.

2 -->

3.2.基于多腔型基本单元的非对称型超构材料

除了利用该多腔型基本单元设计对称型超构材料, 本文还利用该基本单元构造了左右非对称超构材料. 如图5(a)所示, 设计了一个形状为等边三角形的左右非对称型的超构材料, 在此结构中相邻两个基本单元中心点之间的距离均为d₄ = 28 cm. 如图5(b)所示, 频率为637 Hz的平面波以1 Pa的强度从左侧垂直入射, 该非对称型超构材料实现了声场的局部增强效应, 声能集中在系统内部的中心区域, 中心点处声强可高达100 Pa², 实现了较强的声场增强效应. 为了探究该非对称型超构的声场增强效应是否受入射声波角度的影响, 绘制了结构内部点A处的声强随入射声波角度的变化情况. 如图5(c)所示, 点A处的声强分布关于0°对称, 当入射声波的角度趋于–90°和90°时, 点A处的声强趋于0 Pa². 而当声波从左侧垂直入射时($\theta {\rm{ = }} {\rm{0}}^\circ $), 点A处的声强达到最大值, 随着角度的逐渐增大, 点A处的声强也随之减小, 因此, 该非对称型超构材料内部的声场增强效应与入射声波的角度有密切关系. 从图5(a)的几何图形可以发现, 当平面波沿着该非对称超构材料左侧以60°入射时, 相当于平面波从右侧垂直入射. 结合图5(b)的声强分布可知, 平面波从左侧垂直入射的情况下, 结构内部中心点处的声强约为100 Pa², 而由图5(d)可知, 当平面波从右侧垂直入射的情况下, 结构内部中心点处的声强仅为10 Pa². 因此, 设计的非对称超构材料对侧向垂直入射声波实现了高效的非对称声场增强效应, 且通过调节该等边三角形的倾角可对声场增强效应进行调控.
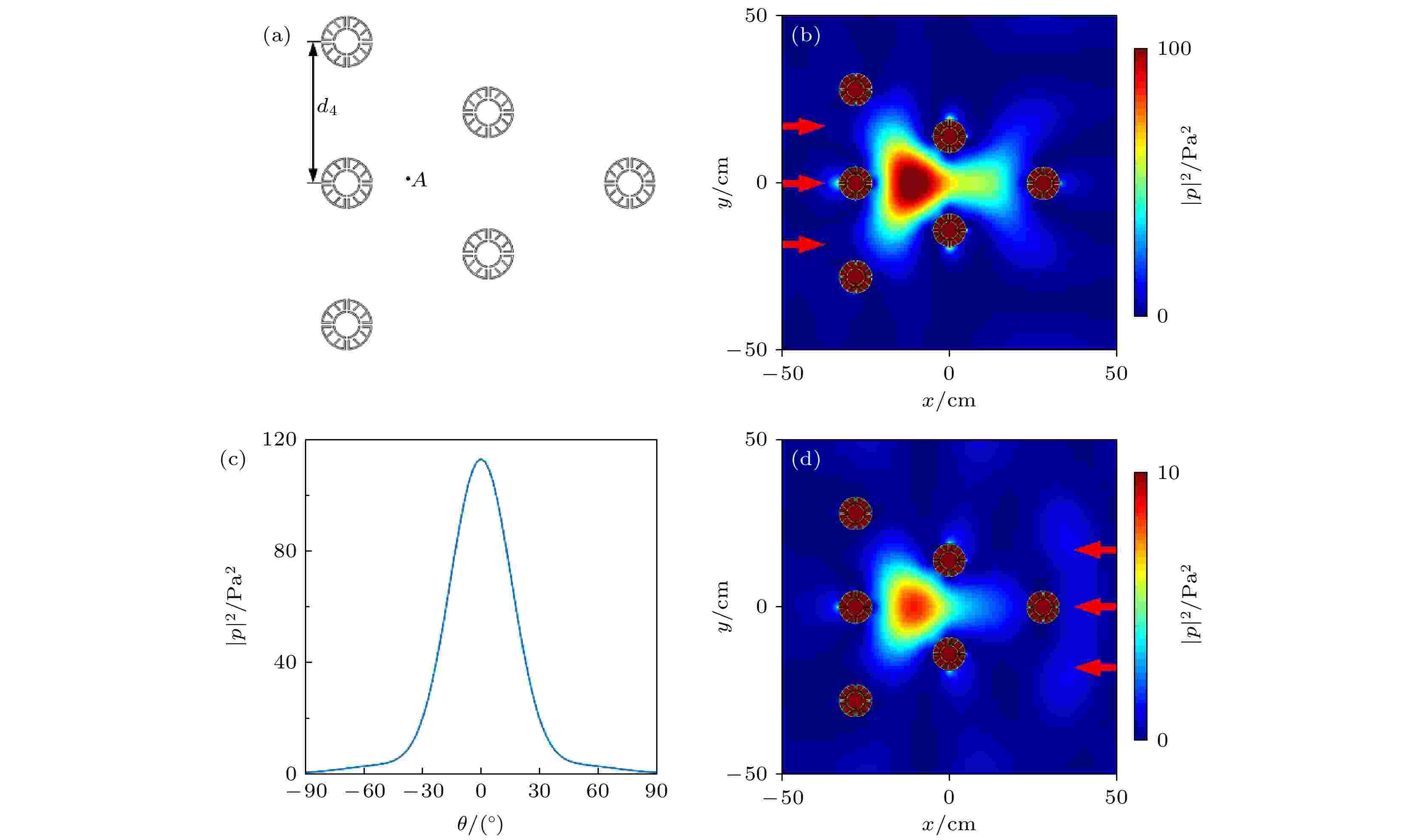图 5 (a) 6个多腔型基本单元组成的等边三角形非对称型超构材料的结构示意图; (b) 当频率为637 Hz的声波从结构左侧垂直入射时, 非对称超构材料的声强分布图; (c) 非对称超构材料内部点A处的声强随入射声波角度的变化情况; (d) 当频率为637 Hz的声波从结构右侧垂直入射时, 非对称超构材料的声强分布图
Figure5. (a) Structural diagram of the equilateral triangular asymmetric metamaterial composed of six multiple-cavity units; (b) sound intensity distribution of the asymmetric metamaterial when the sound wave with frequency of 637 Hz is normally incident from the left side; (c) acoustic intensity curve at the center point A of the asymmetric metamaterial with different angles of incident wave; (d) sound intensity distribution of the asymmetric metamaterial when the sound wave is normally incident from the right side with frequency of 637 Hz.

通过对该非对称型超构材料的研究, 可以发现, 声波入射方向不同, 声场增强效应也不同. 对于本文设计的左右非对称系统而言, 当声波从结构左侧垂直入射时, 能够在系统内部实现声场增强效应, 而当声波从结构右侧垂直入射时, 其中心点处的声强将大大减小, 声能聚集于各个多腔型基本单元中. 由此可知, 由该基本单元所设计的非对称型超构材料, 具有较强的方向依赖性, 利用该特性通过设计由多腔型基本单元组成的非对称结构可实现非对称声场增强效应, 进而实现隔声、声传感等方面的应用.

本文利用多腔型基本单元构造了不同结构的超构材料, 研究声波入射方向、激发频率、结构对称性等因素对声场增强效应的影响. 结果表明, 不同的结构在外部声波激励下, 有着不同效果的声场增强效应. 对称型超构材料的声场增强效应不受入射方向的影响, 这一特性使其在声通信、声源或噪声定位等方面有重要的应用价值. 非对称型超构材料具有较强的方向依赖性, 声波入射方向不同, 系统中心点处的声强也不同. 利用该多腔基本单元组成非对称型超构材料能够实现非对称声场增强, 甚至单向声场增强, 这一特性使其在隔声、声传感等方面具有潜在的应用价值.