<script type="text/javascript" src="https://cdn.bootcss.com/mathjax/2.7.2-beta.0/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script> <script type='text/x-mathjax-config'>MathJax.Hub.Config({tex2jax: {inlineMath: [['$','$'], ['\\(','\\)']]},"HTML-CSS": {linebreaks: { automatic: true},scale: 100}});</script> 摘要:物理学在机器学习中的应用以及两者的交叉融合正引起广泛关注, 尤其是在波动系统和扩散系统中. 本文重点关注波动与扩散物理系统和机器学习之间的内在联系以及对机器学习算法和物理实现的推进作用, 综述了波动系统和扩散系统中的机器学习研究, 介绍了部分最新研究成果. 文中首先讨论了监督学习的波动系统实现, 包括神经网络的波动光学实现、量子搜索的波动实现、基于波动系统的递归神经网络以及神经形态的非线性波动计算. 接着, 文中继续讨论了受扩散系统启发的机器学习算法, 如基于扩散动力学的分类算法, 基于热扩散的数据挖掘和信息过滤, 以及基于群体扩散的搜索优化等. 波动系统以其天然的并行性、高效、低能耗等优势, 通过丰富的波动力学和波动物理现象进行计算或算法模拟, 正成为机器学习的新型物理载体. 扩散系统中的物理机制可以启发构建高效的机器学习算法, 用于复杂系统和物理学研究中的分类、优化等问题. 期望通过对波动、扩散物理系统与机器学习内在联系的讨论, 能够为开发物理启发的新算法和硬件实现甚至软硬一体化带来抛砖引玉的启示.
关键词: 波动系统/
扩散系统/
机器学习/
人工神经网络

English Abstract

全文HTML

--> --> -->

机器学习与人工智能被认为是这个时代的突破性技术之一, 应用领域广泛^[1-4]. 机器学习主要用大量数据训练结构, 以此模拟人类的学习行为, 进而对复杂事件作出推理和决策. 这与物理系统的思维方式十分接近. 因为任一物理系统都可视作将输入信息映射到输出结果的一种信息处理方式, 于是机器学习能够作为物理学研究的工具^[5]. 但是机器学习与物理学的交叉互融不仅限于此, 物理学也可以促进机器学习. 物理学中的波动系统和扩散系统可以构建更高效的机器学习硬件平台和算法, 从而满足人们日益增长的对计算机算力的需求.
自从20世纪80年代机器学习成为一个独立的研究方向以来, 各种机器学习算法被大量提出, 但是如何直接利用硬件设备实现更高效的机器学习仍是一个值得探索的命题. 尽管电子器件的发展使机器学习在集成电路上能达到令人满意的效果, 这种方式需要比较高的能耗和带宽. 同时, 通过传统的电子设备实现机器学习通常需要大量时间和较大尺寸的硬件设备. 这使得我们在处理复杂问题和边缘计算时将会十分困难^[6]. 波动系统实现监督学习(如实现人工神经网络), 具有天然的优势. 它保证了大规模的并行性^[7,8]和片上集成后较小的设备尺寸. 信息将以非常快的速度传输, 例如光速, 并且这种传输方式极大地减少了能耗, 甚至能够达到零能耗^[9]. 另一方面, 物理学和机器学习都试图分析数据的规律来建立模型, 从而预测系统的行为, 两者之间存在着一些本质联系. 可以用物理学的机制来理解和构建机器学习方法, 例如基于扩散系统实现分类、信息过滤、优化等无监督算法.
物理学和机器学习的交叉互融具有悠远的历史和广泛的应用, 涉及范围十分宽广. 更多有关机器学习与物理学的讨论可以参考《Review of Modern Physics》以及《Physics Reports》的两篇综述文章^[5,10], 它们更一般地回顾了机器学习技术在物理学的各大领域的典型应用. 由于能力和篇幅限制, 本文主要基于课题组自身的研究积累, 尝试从波动与扩散动力学的物理视角, 来统一地阐述和理解机器学习相关研究. 特别地, 本文重点关注波动、扩散物理系统对物理实现的推进作用, 以及机器学习算法启发, 主要讨论波动物理作为人工神经网络的硬件平台以及两者之间的内在联系, 以及受扩散物理启发的分类、优化等机器学习算法. 扩散与波动过程是物理学中的基本动力学过程, 我们希望通过这一独特的切入点, 为后续物理启发的机器学习研究带来新的思路.

根据训练数据是否已经被人为标记, 可以将机器学习算法大致地分为两类—监督学习和无监督学习(图1(a)). 监督和无监督学习算法不仅能成为解决物理系统中特定问题的机器学习工具, 波动物理系统和扩散物理系统还可以反过来为机器学习提供硬件实现平台和启发新的算法.
图 1 (a) 监督学习与无监督学习; (b) 一个单隐藏层神经网络的基本结构, 各层神经元根据权重系数相互连接; (c)利用无监督学习进行社交网络分析
Figure1. (a) Supervised learning and unsupervised learning; (b) the structure of a single hidden-layer neural network, where neurons are connected by weight coefficients; (c) unsupervised learning can be applied in social network analysis.

物理学中的波动系统既能实现监督学习, 也能实现无监督学习^[11,12]. 然而随着近年来计算机视觉等领域的发展, 波动系统执行推理任务的能力尤为重要, 于是波动系统被频繁地与一些监督学习算法联系在一起. 在监督学习中, 假设有n个数据样本, 用$ {X}_{i}(i={1, 2}, \cdots, n) $来表示这些数据的特征向量. 同时, 各数据样本的标记是已知的, 用${Y}_{i}(i=1, $$ 2, \cdots, n)$表示. 监督学习的目标是建立一个函数f, 使$ f\left({X}_{i}\right) $尽可能地接近$ {Y}_{i} $. 过去二十年间, 人工神经网络^[13]成为最热门的监督学习方法之一. 1982年, 美国科学家Hopfield^[14]提出了适应于集成电路的人工神经网络, 引起了巨大的反响. 图1(b)展示了一个单隐藏层神经网络的基本结构. 其中$ {{W}}_{1} $, $ {{W}}_{2} $代表权重矩阵, $ {{b}}_{1} $, $ {{b}}_{2} $代表偏差. 隐藏层和输入层之间的连接满足如下关系: ${{H}}={{W}}_{1}{{X}}+ $$ {{b}}_{1}$. 神经网络之所以区别于传统的线性回归, 并具有更强的计算能力的原因之一在于, 神经网络包含了非线性激活元. 若以$ \sigma \left(\cdot \right) $来表示非线性激励函数, 则输出结果为$ {{Y}}=\sigma ({{W}}_{2}\cdot \sigma \left({{H}}\right)+{{b}}_{2}) $. Farhat等^[15]于1985年提出Hopfield模型可以在光学系统中实现, 奠定了波动系统实现人工神经网络的基础.
物理学中的扩散现象描述了大量粒子集体运动的统计结果. 对物理学中的扩散机制的研究和深入了解启发了新的机器学习算法的诞生, 尤其是一些改进的无监督学习算法. 与监督学习不同, 无监督学习的训练样本是没有已知标记的. 因此, 无监督学习不再依赖于“经验”, 而是更注重数据样本的内在模式和统计规律, 这与物理学中的扩散机制存在本质联系. 传统的无监督学习方法包括聚类—k-means算法^[16]和EM算法^[17]等, 以及数据降维—主成分分析(PCA)^[18]和流形学习^[19,20]等方法. 基于对物理学中的热传导扩散和概率扩散等系统的研究, 逐渐开发出各种改进的机器学习算法. 例如, 基于扩散动力学实现数据降维, 并根据数据的内在规律进行分类^[21]; 基于热传导扩散实现数据挖掘, 建立推荐模型并应用于社交网络分析^[22](图1(c)); 以及基于全局扩散搜索算法建立优化模型, 实现材料搜索和结构预测, 等等.
下面将分别介绍波动系统中的监督学习, 包括神经网络的波动光学实现、波动系统的递归神经网络、神经形态的非线性波动计算, 以及基于扩散系统的无监督学习, 包括基于扩散动力学的分类模型、基于热传导扩散的推荐模型、基于全局和局部扩散搜索算法的优化模型.

数学上, 波在自由空间中的传播可以用菲涅耳-基尔霍夫衍射积分公式来描述, 它相当于对场进行卷积. 在实际应用中, 这种卷积行为可以通过傅里叶光学实现. 输入场通过特定的透镜进行傅里叶变换, 与光学元件的振幅和相位的按元素相乘. 这就完成了输入场与元素的傅里叶逆变换的卷积. 于是, 波在自由空间和不同介质中的传播可以高速、低能耗地实现卷积、矢量-矩阵乘法等运算(图2)^[6], 从而在波动系统中实现线性回归^[23]等, 乃至更复杂的计算. 我们的宇宙简直就是一个天然的计算器.
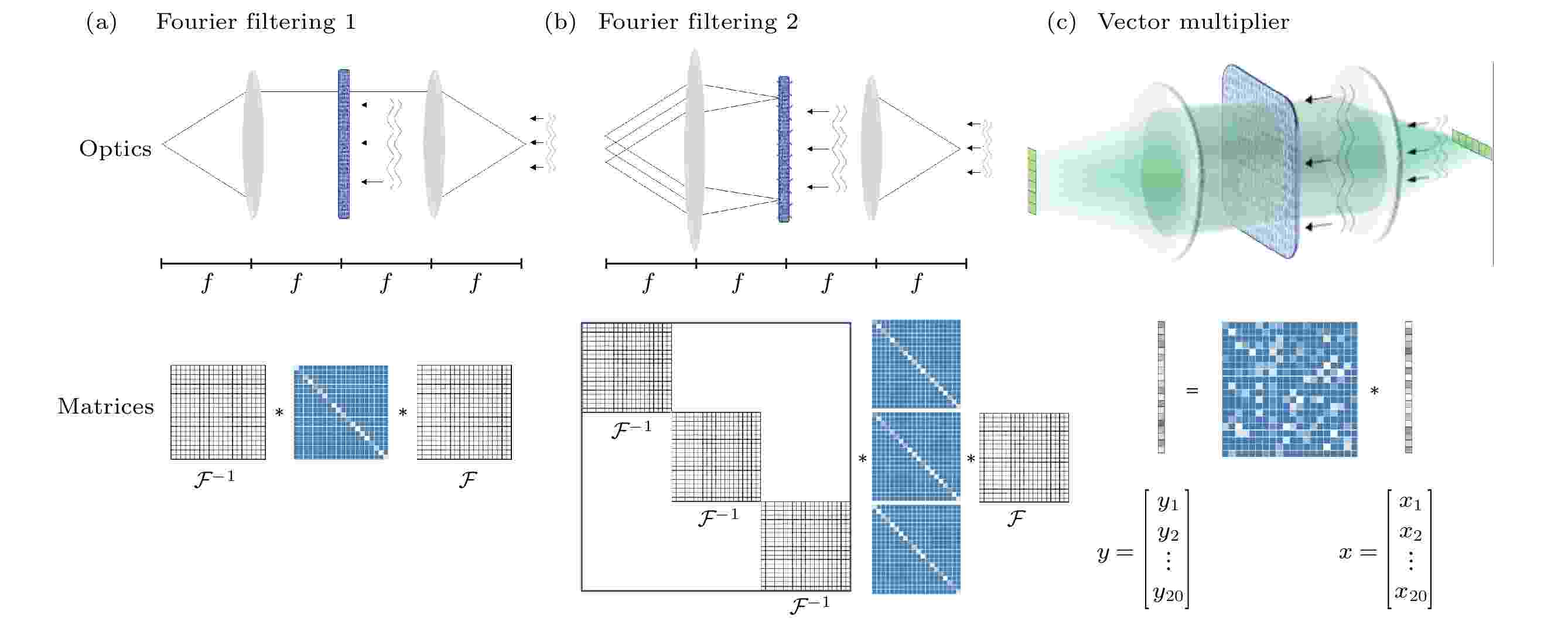图 2 波在不同介质中的传播以及相应的线性矩阵运算　(a) 传统光学4f系统在傅里叶空间中实现乘法, 对应于在原空间中的卷积. 两个透镜分别实现傅里叶变换和傅里叶逆变换, 散射层对应于核矩阵, 场与薄散射层的相互作用相当于与对角矩阵的乘积; (b) 改进后的4f系统可以用光栅多次复制输入场, 并用不同的核矩阵进行卷积; (c) 通过类似4f的系统可以实现矢量-矩阵乘法, 实现一维行向量与稠密矩阵相乘, 得到一位列向量^[6]
Figure2. Wave propagation through different media and the corresponding linear matrix operations: (a) A traditional optical 4f system realizes multiplication in Fourier space, which corresponds to the convolution in the original space; (b) modified 4f systems can copy the input field with a grating and use different kernels for convolution; (c) a 4f-type system can implement the vector–matrix multiplication^[6].

随着深度学习的兴起, 近年来人们更关注人工神经网络的波动物理实现. 人工神经网络需要在矩阵乘法运算的基础上引入非线性激活函数, 这在波动系统中是个挑战. 如何用波的传输模拟神经元中的信息传输, 如何控制权重也是亟待解决的问题. 接下来, 简要介绍近期与波动系统中的神经网络有关的部分工作.
2

-->

3.1.神经网络的波动光学实现

对于最常见的全连接神经网络, 输出层中的每个元素都可以视作输入层中所有元素的加权和. 这种矢量-矩阵乘法的运算, 可以通过马赫-曾德干涉仪在光学领域实现^[24]. 随着近年来光子集成电路的迅速发展, 科学家用一个可编程纳米光子处理器来实现基于相干光和全光学矩阵乘法的硅光子神经形态电路(图3(a))^[25]. 光子神经形态计算的另一个重要方法是基于相变材料和器件的整合. 最近一项研究中, 科学家利用微米级环型谐振器将输入信息调制成不同波长, 并通过相变材料实现权重调节(图3(b)). 这种方式通过相变材料和环型谐振器的耦合来实现非线性激活, 最终在光子集成系统中构建出了脉冲神经网络^[12,26], 有效地减小了光子芯片的体积.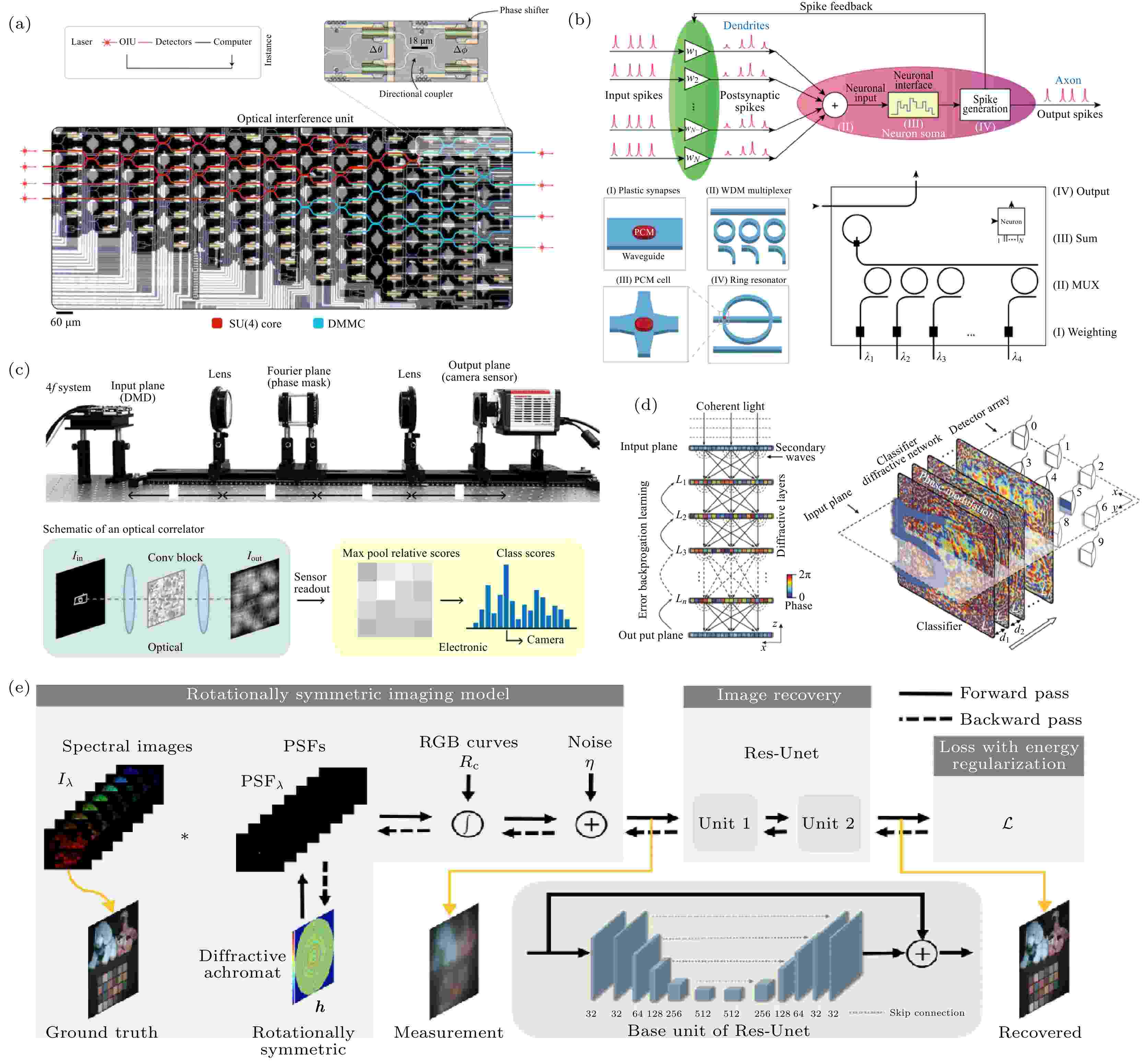
图 3 (a) 基于相干光和全光学矩阵乘法的硅光子神经形态电路可用于实现元音分类^[25]; (b) 基于波分复用(WDM)的分层结构构成的全光脉冲神经网络, 能够实现图像和语言识别^[12]; (c) 改进的光学4f系统实现卷积神经网络, 提高图像分类性能^[27]; (d) 全光衍射深度神经网络实现数字分类^[29]; (e) 光学衍射元件与图像处理算法端对端协同设计^[32]
Figure3. (a) Nanophotonic circuits based on coherent light and all-optical matrix multiplication is capable for vowel recognition^[25]; (b) image and language recognition are achieved by an all-optical spiking neural networking with wavelength division multiplexing (WDM)^[12]; (c) a design for an optical convolutional layer using a modified optical 4f system^[27]; (d) an all-optical diffractive deep neural network that implements the digit classification^[29]; (e) end-to-end learning paradigms of diffractive optics and processing algorithms^[32].

除了光子集成电路, 还可以利用波通过透镜的传播来构建神经网络. Chang 等^[27]提出了一种光电混合的卷积神经网络, 即在电子计算之前加入一层光学卷积层, 减小电子计算成本和处理时间, 同时提高处理图像分类任务的性能(图3(c)). 这种方式是分离地在光计算层进行线性计算, 在电子计算层实现非线性激活函数, 但是光电转换过程的效率就成为主要瓶颈. 构建全光神经网络可以解决这一问题, 即神经网络中的线性和非线性操作都在波动系统中实现. 例如, 用空间光调制器和傅里叶透镜实现线性操作, 电磁诱导透明的激光冷却原子实现非线性光学激活函数^[28].
衍射层可以用来代替透镜调节与波的相互作用, 在缩小系统外形的前提下构建更高效的全光神经网络. 衍射层上的每个点透射或反射入射波, 并通过波的衍射连接到下一衍射层. 根据惠更斯-菲涅耳原理, 输入波经过衍射层上各个点的透射或反射后成为次波源, 次波源的振幅和相位由输入波与该点的复数透射或反射系数的乘积决定. 因此, 衍射层上各点的透射或反射系数可被视作神经网络的权重, 通过设计固定结构的多层衍射层形成全光神经网络, 实现手写数字分类(图3(d))^[29]. 类似的衍射神经网络还可以用来执行光学逻辑运算, 实现小型化的光学逻辑门^[30]. 为了进一步提高核心计算模块的训练速度和能量效率, 科学家们提出了一种原位光学学习结构. 通过这种结构, 可以在光学系统中实现衍射神经网络的训练过程^[31]. 衍射光学元件与计算成像结合, 有望实现轻薄的高性能成像系统. 同济大学程鑫彬课题组^[32]提出基于同心圆环分解的成像模型计算降维理念, 成功地将衍射光学元件和图像处理算法端到端设计框架的内存需求降低了一个数量级, 有助于发展基于衍射光学元件的轻薄计算成像系统(图3(e)).
除此之外, 衍射神经网络也可以在声学超构材料^[33]或者傅里叶空间中^[34]实现. 已有研究在声波系统中利用超材料控制声波的相位和透射率进行模拟计算^[35], 可以实现空间上的微分、积分和卷积^[36,37]以及常微分方程的求解^[38,39]等. Weng等^[33]从理论上提出并实验证明了一个纯粹的被动神经网络, 由于它的超材料单元产生深亚波长相移, 该声学神经网络能够通过分析声散射实时识别复杂物体(图4(a)). 特别地, 由于线性波动系统本身具有并行运算能力, 即两个或多个波包的传播不互相影响, 利用波动系统构建机器学习算法时还可以考虑结合量子算法进一步提升计算速度^[40]. 例如, 以波元的振幅代表量子态的概率幅, 波元的相位代表量子态的相位, 可以实现有别于经典搜索的量子搜索算法. 对于一个包含有N个数据的数据库而言, 找到一个指定数据, 经典算法成功搜索一个数据需要根据搜索条件在数据库中逐一进行比对, 平均需要$ N/2 $次迭代计算, 其量级正比于N. 而Grover量子搜索算法成功搜索数据所需的迭代次数$ {r}_{f} $为: ${r}_{f}=\dfrac{\pi }{4}\sqrt{N}-\dfrac{1}{2}$. 显然, 当数据库足够大时, Grover算法所需迭代次数$ {r}_{f} $正比于$ \sqrt{N} $, 远小于$ N/2 $. 具体到波动系统中(图4(b))^[40], 可以利用超材料调节波的传播波速和方向以实现相对应的量子逻辑门操作. 如果将经典波动系统中实现量子算法的思路与机器学习算法相结合, 可以进一步提升受到经典计算机算力限制的机器学习算法的性能.
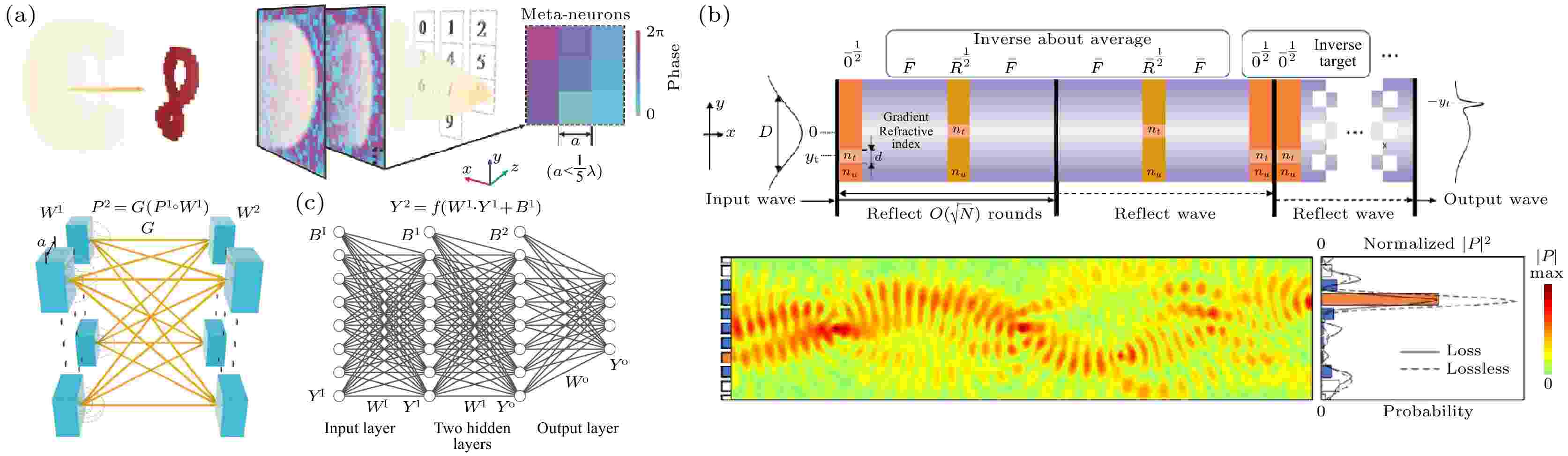图 4 (a) 基于声学超构神经网络的被动目标识别^[33]; (b) 利用声表面波系统实现量子搜索算法, 实现与量子逻辑门相似的操作^[40]
Figure4. (a) Passive object recognition with acoustic meta-neural-network^[33]; (b) realize quantum search algorithm with acoustic system, achieving operations similar to quantum logic gates^[40].

2 -->

3.2.波动系统的递归神经网络

波的动力学与递归神经网络(recurrent neural network, RNN)之间具有强烈的映射关系(图5)^[41]. 包括声学和光学在内的波动物理可以自然地为时变信号构建模拟处理器. 如图5(a)所示, 递归神经网络中的更新过程可以描述为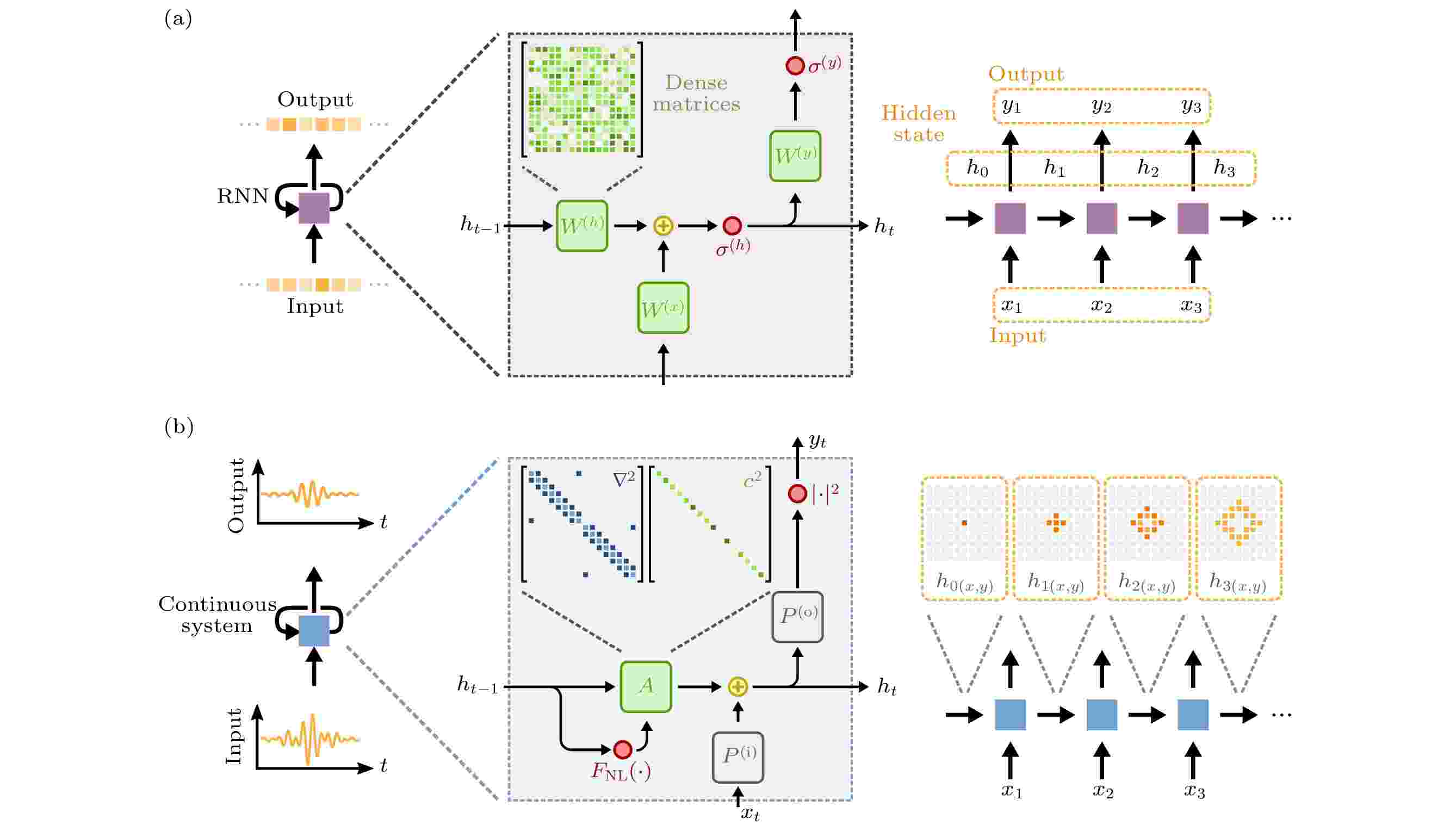
图 5 标准RNN和波物理的对比　(a)具有离散的输入、输出序列的RNN的更新过程; (b) 具有连续输入、输出序列的波动系统系统的更新过程^[41]
Figure5. Comparison of a standard RNN and a wave system: (a) The update process of an standard RNN with discrete input and output sequence; (b) the update process of a wave-based physical system with continuous input and output sequence^[41].

${{h}}_{t+1}={\sigma }^{\left(h\right)}\big({{W}}^{(h)}\cdot {{h}}_{t}+{{W}}^{{(}x)}\cdot {{x}}_{t+1}\big),$

${{y}}_{t+1}={\sigma }^{\left(y\right)}({{W}}^{(y)}\cdot {{h}}_{t+1}),$

其中$ {{x}}_{t} $, $ {{h}}_{t} $, $ {{y}}_{t} $分别代表t时刻的输入向量、隐藏态向量和输出向量; $ {{W}}^{\left(h\right)} $, $ {{W}}^{{(}x)} $, $ {{W}}^{\left(y\right)} $代表权重矩阵, 上标$ \left(h\right) $, $ \left(x\right) $, $ \left(y\right) $分别对应于隐藏层, 输入层和输出层; $ {\sigma }^{\left(h\right)}(\cdot ) $和$ {\sigma }^{\left(y\right)}(\cdot ) $代表非线性激励函数.
波场分布$ u(x, y, z) $可以由二阶偏微分方程表示:

$\frac{{\partial }^{2}u}{\partial {t}^{2}}-{c}^{2}\cdot {\nabla }^{2}u=f,$

其中$ {\nabla }^{2} $是拉普拉斯算子; $ c=c(x, y, z) $表示波速的空间分布; $ f=f(x, y, z) $表示源. 对(3)式进行有限差分, 得到递归关系:

$\frac{{u}_{t+1}-2{u}_{t}+{u}_{t-1}}{?{t}^{2}}-{c}^{2}\cdot {\nabla }^{2}{u}_{t}={f}_{t}.$

将(4)式写成矩阵形势:

$\begin{split}\left[ {\begin{array}{*{20}{c}}{{u_{t + 1}}}\\{{u_t}}\end{array}} \right] =\;& \left[ {\begin{array}{*{20}{c}}{2 + \Delta {t^2} \cdot {c^2} \cdot {\nabla ^2}}&{ - 1}\\1&0\end{array}} \right]\\&\times \left[ {\begin{array}{*{20}{c}}{{u_t}}\\{{u_{t - 1}}}\end{array}} \right] + \Delta {t^2} \cdot \left[ {\begin{array}{*{20}{c}}{{f_t}}\\0\end{array}} \right].\end{split}$

波系统的隐藏态定义为当前时刻和前一时刻的场分布相连$ {{h}}_{t}\equiv {\left[{u}_{t}, {u}_{t-1}\right]}^{\rm{T}} $, 对应于RNN中的隐藏态向量$ {{h}}_{t} $, 于是波动方程的更新过程可写作:

${{h}}_{t+1}=A\left({{h}}_{t}\right)\cdot {{h}}_{t}+{{P}}^{\left({\rm{i}}\right)}\cdot {{x}}_{t+1},$

${{y}}_{t+1}={\big|{{P}}^{\left({\rm{o}}\right)}\cdot {{h}}_{t+1}\big|}^{2}.$

见(图5(b)). 显然, (6)式和(7)式有与(1)式和(2)式一样的形式, 其中$ {{h}}_{t} $都是隐藏态向量, $ {{y}}_{t+1} $都是输出向量. 类比于标准RNN中的权重矩阵$ {{W}}^{{(}x)} $, $ {{W}}^{\left(y\right)} $, 波动方程的隐藏态与输入输出之间的关系也由线性算子$ {{P}}^{\left({\rm{i}}\right)} $, $ {{P}}^{\left({\rm{o}}\right)} $给出. 但不同之处在于, $ {{P}}^{\left({\rm{i}}\right)} $, $ {{P}}^{\left({\rm{o}}\right)} $式只在波源的入射处和输出波的测量处为1, 其余位置为0的矩阵. 于是通过$ {{P}}^{\left({\rm{i}}\right)}\cdot {{x}}_{t+1} $将输入向量$ {{x}}_{t+1} $编码成空间内特定位置入射的波源$ {f}_{t} $, 对应于(1)式中的$ {{W}}^{{(}x)}\cdot {{x}}_{t+1} $. 稀疏矩阵$ {{A}}\left({{h}}_{t}\right) $描述了无源条件下波场$ {u}_{t} $的更新, 对应于(1)式中的隐藏态权重矩阵$ {{W}}^{\left(h\right)} $. 在线性波中, A实际上不依赖于$ {{h}}_{t} $. 为了实现(1)式中的非线性激励函数$ {\sigma }^{\left(h\right)}(\cdot ) $, 可以进一步引入非线性波, $ {{A}}\left({{h}}_{t}\right) $中的波速的形式为$ c={c}_{\rm{lin}}+{u}_{t}^{2}\cdot {c}_{\rm{nl}} $, $ {c}_{\rm{nl}} $对应非线性响应区域. 这种形式的非线性在各种各样的波物理中都会遇到, 包括水波、非线性光学材料、气泡流体和软材料中的声学. 而通过测量波的强度得到输出结果时, (7)式中的$ {\left|\cdot \right|}^{2} $自然地完成了(2)式中的非线性操作$ {\sigma }^{\left(y\right)}(\cdot ) $.
通过这种递归神经网络与波动物理的映射表明, 神经网络学习时间数据中的复杂特征, 可以通过特定的波动物理系统来实现. 例如, 通过波在非均匀介质中的散射和传播实现对音频信号的元音分类, 实现了与递归神经网络的标准数字实现相当的性能^[41]. 除此之外, 在小型硬件构成的神经网络上加入非线性动力学特征, 如振荡和同步, 可以实现特殊的分类任务, 例如训练一个由四个自旋转矩纳米振荡器组成的硬件网络, 通过自动实时学习规则调整语音元音的频率来识别语音元音^[42]. 另外, 波在非均匀纳米光子介质中的散射也可以实现连续无分层的方式的人工神经网络计算. 非均匀介质通过变换波前来实现复杂的计算任务, 如图像识别. 这些计算介质可以小到几十个波长, 并提供超高的计算密度, 这种方式利用亚波长散射体来实现复杂的输入/输出映射, 超越了传统纳米光子器件的能力^[43]. 除了经典的时间序列学习, 波动系统有望应用于更复杂的系统学习, 如厦门大学赵鸿^[44]提出的利用时序数据的自演化学习机, 可以解决“黑箱”系统周期动力学, 甚至混沌动力学的推断问题, 并有望推广到复杂耦合体系的系统重构^[45].
2 -->

3.3.神经形态的非线性波动计算

神经网络计算同样可以通过非线性波实现. Marcucci等^[46]最近研究了非线性波具有进行神经形态计算的潜力. 非线性波, 如孤子、冲击波和怪波的发散行为能够提供足够的复杂度来进行机器学习, 它们被有效地应用到储蓄池计算中. Marcucci等^[46]提出了一个由非线性偏微分方程驱动的计算模型, 称为单波层前馈网络(single wave-layer feed-forward network, SWFN)(图6(a)). SWFN结构由三层组成: 编码层, 将输入向量编码成波的初始振幅或相位; 储蓄层, 波按照非线性波动方程演化; 读出层, 通过波动演化后, 从最终状态读出结果. 由于该网络是储蓄池计算网络, 只需对读出层的权值进行训练. 除了该系统中用到的非线性薛定谔方程, 其他任何非线性波动微分方程都可用于波的演化. 事实上, 任何具有非线性波动动力学特征的系统都可以用来建立神经形态的非线性波动网络. 研究人员用不同的编码方法实现了三种具体应用: 近似计算一维函数(图6(b)), 学习一个八维数据集(图6(c)), 实现布尔逻辑门(图6(d)). 三个例子中, SWFN都能与传统神经网络一样. 这说明了SWFN的通用性, 它能够用于近似计算任意函数和学习高维数据集. 这项基础工作阐明了非线性波与机器学习之间的联系, 为电子学、光子学、自旋电子学、流体力学、玻色-爱因斯坦凝聚等领域的各种非线性波现象用作神经形态计算打开了大门.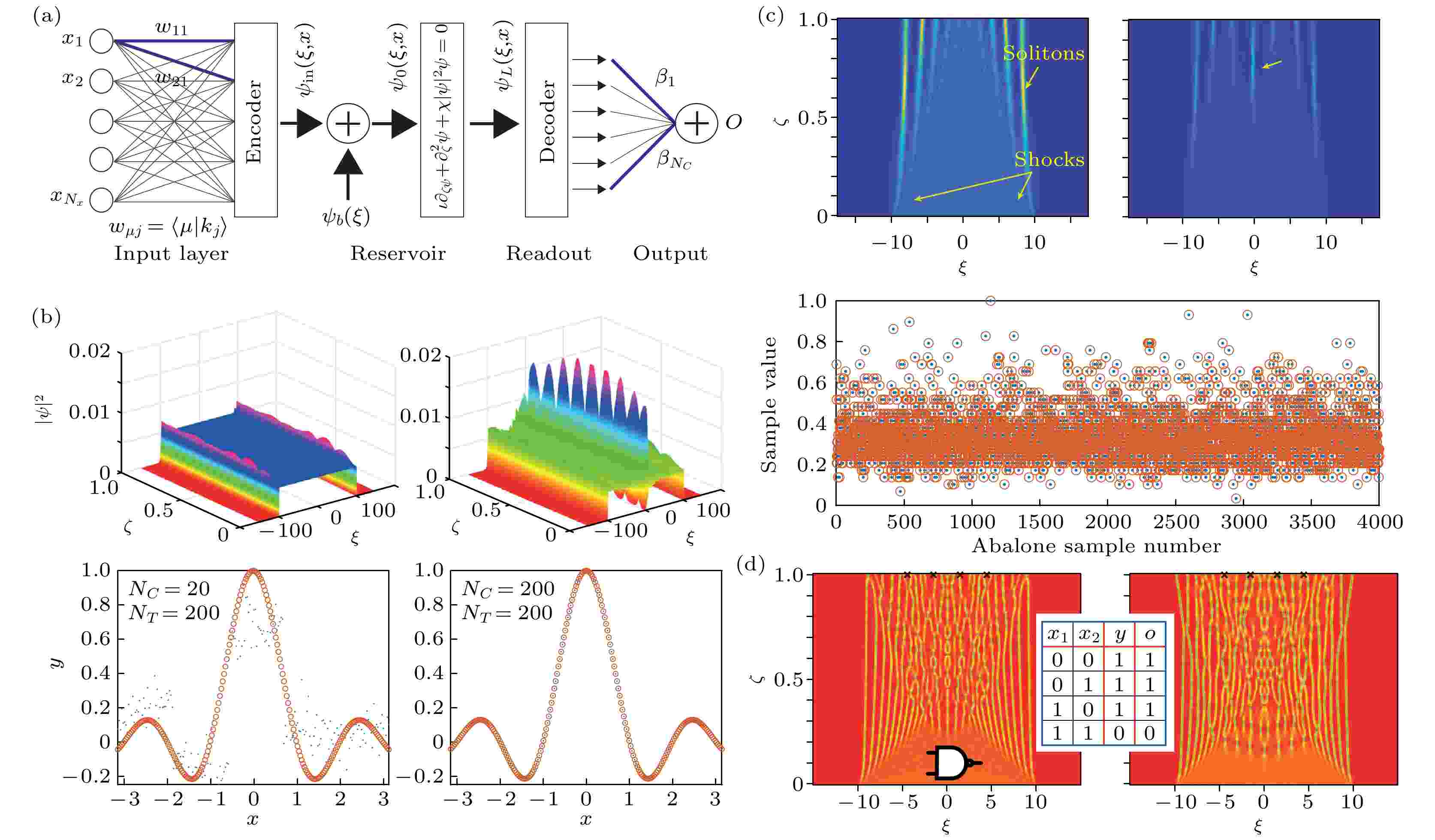
图 6 神经形态的非线性波动网络　(a) 单波层前馈网络(SWFN)包含编码层、储蓄层和读出层, 其中波按照非线性偏微分方程演化; (b) 偏差$ {\psi }_{b} $的演化、波的演化以及近似计算一维函数$ y={\rm{sin}}\left({\text{π}}x\right)/\left({\text{π}}x\right) $的结果; (c) SWFN用于学习鲍鱼数据集; (d) 用孤子训练通用的布尔逻辑门^[46]
Figure6. Neuromorphic computing by nonlinear waves: (a) Single wave-layer feed forward neural network (SWFN) with input layer, reservoir and readout layer, where the wave evolves according to a nonlinear partial differential equation; (b) the bias and wave evolution and results of learning the function $ y={\rm{sin}}\left({\text{π}}x\right)/\left({\text{π}}x\right) $; (c) results of learning the abalone dataset; (d) training a universal logic gates by soliton gases^[46].

储蓄池计算^[47,48]是一类特殊的人工神经网络, 其作为中间层的储蓄层是随机生成的, 且生成后就保持不变, 只需要训练输出层. 科研工作者提出了一个多功能的基于孤子的计算系统^[49], 使用离散孤子链作为储蓄池, 通过利用其可调的控制动力学, 证明了足够强的非线性动力学能够实现对非线性可分离数据集执行精确的回归和分类任务. 由于近年来科研工作者们才关注到非线性波中的机器学习, 相关的工作还很少. 但是基于非线性波实现储蓄池计算, 通过储蓄层中的波传输携带大量信息, 能够学习更大尺度的数据集, 并且这种方式往往不需要严格控制传播介质, 因此该方向值得深入的研究探索.

扩散过程是物理学的经典过程之一. 微观上是粒子无规则运动而导致了宏观迁移. 根据傅里叶定理, 单位时间内通过垂直于扩散方向的单位面积截面的扩散热量, 与扩散物质的温度梯度成正比. 因此, 物质总趋向于由高势能区域流向低势能区域, 一段时间后达到稳态. 扩散系统在给定初始条件和边界条件的情况下, 根据自身的规律进行演化, 最终呈现稳定的分布, 这启发了许多新的无监督机器学习算法. 这些算法通过计算、分析扩散过程稳态时的概率分布实现对数据的分类、评级等功能. 下面介绍若干扩散系统用于开发无监督学习算法的示例, 包括概率扩散用于数据降维和分类, 热扩散用于数据挖掘与社会网络推荐机制, 以及基于多体扩散的扩散搜索算法用于结构搜索和材料预测.
2

-->

4.1.基于扩散动力学的分类模型

分类是机器学习的重要任务之一. 流形学习能够将真实世界中的高维数据映射到一个低维特征空间, 从而根据数据的内在规律进行分类. 但是对于非线性流形, 传统的线性映射方法并不可行, 因此科学家们提出了扩散映射^[50,51]. 扩散映射的基本思想是在数据图上定义一个扩散行为, 通过一段时间的扩散, 逐渐滤除数据集中不重要的信息, 并得到数据之间的相似度关系.
在具有N个数据点的数据集$ {\left\{{x}_{n}\right\}}_{n=1}^{N} $, ${x}_{n}\in {\mathbb{R}}^{p}$上定义一个Markov随机行走, 则任意两个数据点$ {x}_{i} $和$ {x}_{j} $之间的距离为

${A}_{i,j}={A}_{\varepsilon }\left({x}_{i},{x}_{j}\right).$

A定义为对应参数$ \varepsilon $的核矩阵, 常选用${\rm{exp}}{\Big(-\tfrac{{||{x}_{i}-{x}_{j}||}^{2}}{2\varepsilon }\Big)}$ 的形式. 定义对角矩阵${{D}}= $$ {\rm{diag}} ([{D}_{1}\cdots {D}_{N}])$, 其中${D}_{j} \!=\! \sum\limits_{i=1}^{N}{A}_{i, j} \!=\! \sum\limits_{i=1}^{N}{A}_{\varepsilon }({x}_{i}, {x}_{j})$. 本征方程为

$ {{{AD}}^{ - 1}}\left| \psi \right\rangle = \lambda \left| \psi \right\rangle {\text{~或~}}{{P}}\left| \psi \right\rangle = \lambda \left| \psi \right\rangle , $

其中$ {{P}}={{A}}{{{D}}}^{-1} $是对核矩阵进行列归一化之后的转移矩阵, 用来描述扩散图上的随机行走, $ \lambda $是本征值, $ \left| \psi \right\rangle $是本征右矢. 经过一个时间步长$ \varepsilon $, 数据点$ {x}_{j} $到$ {x}_{i} $的扩散概率为

$\begin{split}&p\left({x}^{t+\varepsilon }={x}_{i}|{x}^{t}={x}_{j}\right)={P}_{i,j}=\frac{{A}_{\varepsilon }\left({x}_{i},{x}_{j}\right)}{{D}_{j}}\\&\qquad\;\;\;\;=\frac{{A}_{\varepsilon }\left({x}_{i},{x}_{j}\right)}{\displaystyle\sum\nolimits _{i=1}^{N}{A}_{\varepsilon }\left({x}_{i},{x}_{j}\right)}.\end{split}$

经过n个步长后, 从数据点$ {x}_{j} $出发到终点y的扩散概率为

$p\left(t=n\varepsilon,\;y|{x}_{j}\right) \!=\! p\left({x}^{t}=y|{x}^{0}={x}_{j}\right)\!=\! {{P}}^{n}{{e}}_{j} ,$

其中$ {{e}}_{j} $是一个仅在$ {j}^{\rm th} $处为1, 其余位置为0的列向量. 转移矩阵P可转化为对称矩阵 ${{P}}_{\rm{s}}= $$ {{{D}}}^{-1/2}{{P}}{{{D}}}^{1/2}$, P和$ {{P}}_{\rm{s}} $具有M个相同的本征值, 定义$ {{P}}_{\rm{s}} $的本征矢为$ \left| {{\varphi _k}} \right\rangle $是列向量, 则转移矩阵P的第k个本征左矢和本征右矢分别为

$\left\langle {{\phi _k}} \right| = {\left| {{\varphi _k}} \right\rangle ^{\rm{T}}}{{{D}}^{ - \tfrac{1}{2}}},\;\left| {{\psi _k}} \right\rangle = {{{D}}^{\tfrac{1}{2}}}\left| {{\varphi _k}} \right\rangle .$

$\left\langle {{\phi _k}} \right|$和$\left| {{\varphi _k'}} \right\rangle $是双正交的, 即:

$\left\langle {{\phi _k}|{\psi _{k'}}} \right\rangle = {\delta _{k,k'}}.$

经过时间t后, 从点x扩散到y的概率为

$ p\left( {t, {{y}}|x} \right) = \left\langle {{{y}}|{\psi _0}} \right\rangle + \mathop \sum \limits_{k \geqslant 1} \left\langle {{{y}}|{\psi _k}} \right\rangle \lambda _k^t\left\langle {{\phi _k}|{x}} \right\rangle , $

其中$\left\langle {{y}} \right|$和$ \left| {{y}} \right\rangle $分别是表示N个数据点的行向量和列向量, 仅在y处为1, 其余处为0. $\left| {{\psi _0}} \right\rangle $是特征值$ {\lambda }_{0}=1 $对应的P矩阵的本征右矢, $\left\langle {{x_i}|{\psi _0}} \right\rangle = $$ {D_{i, i}}/\mathop \sum \nolimits_j {D_{j, j}}. \;{\lambda }_{k}^{n}$是矩阵$ {P}^{n} $的第k个本征值. 数据点$ {x}_{i} $和$ {x}_{j} $之间的扩散距离定义为

$d_t^2\left( {{x_i},{x_j}} \right) = \mathop \sum \limits_{{{y}} = {{{x}}_1}}^{{x_N}} \frac{{{{\left( {p\left( {t,{{y}}|{x_j}} \right) - p\left( {t,{{y}}|{x_i}} \right)} \right)}^2}}}{{\left\langle {{{y}}|{\psi _0}} \right\rangle }}.$

将(14)式代入(15)式, 并结合(12)式和(13)式中的关系, 扩散距离(15)式等于扩散空间中的欧氏距离:

$d_t^2\left( {{x_i},{x_j}} \right) = \mathop \sum \limits_{k = 1}^{M - 1} \lambda _k^{2n}{\left( {\left\langle {{\phi _k}|{x_j}} \right\rangle - \left\langle {{\phi _k}|{x_i}} \right\rangle } \right)^2}.$

通过扩散, 原空间中的高维数据被映射到k个特征向量上, 扩散距离的大小代表着数据之间的相似度大小(图7(a)). 经过长时间的演化, 数据自然地进行聚类, 并在数据分布图和势能绘景图上显示出分类信息(图7(b)).
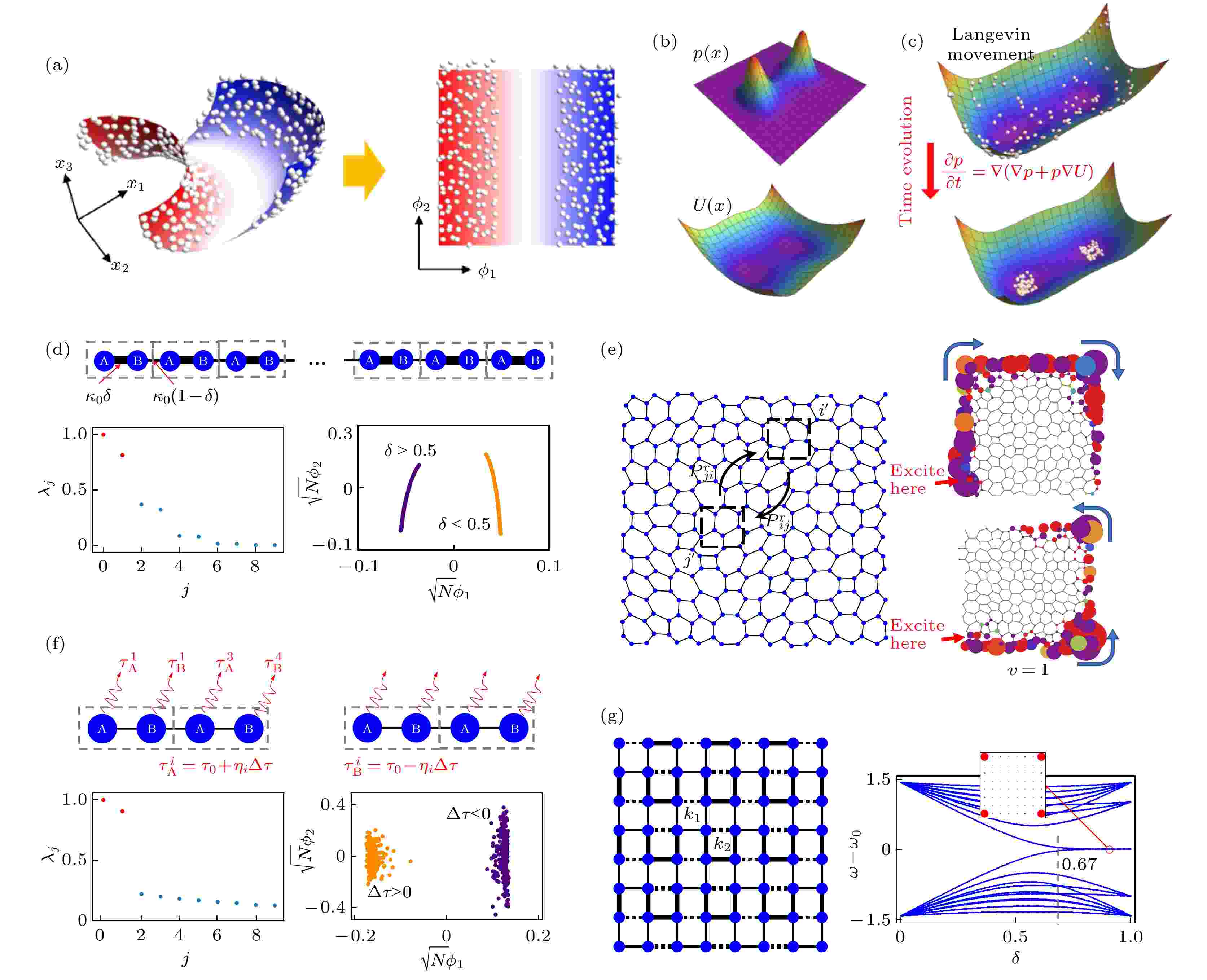图 7 利用扩散映射实现典型声子系统中的流形聚类　(a) 流形空间降维; (b) 流形空间的样本数据分布与势能绘景; (c) 流形空间的扩散与凝聚, 稳态显示出天然的聚类; (d)随机耦合的无序Su-Schrieffer-Heeger(SSH)声子链; (e) 无序非晶态声子的拓扑分类; (f) 一维非厄米声子链; (g) 高阶拓扑声子^[21]
Figure7. Diffusion mapping in typical phononic systems to realize manifold clustering: (a) Dimension reduction in manifold space; (b) the probability distribution of samples and the effective landscape; (c) along with evolution, the samples diffuse and finally concentrate on positions with minimum local potentials, which indicates the clustering; (d)–(g) applications in disordered photonic SSH chain, amorphous topological phononics, 1D non-Hermitian phononic chain, high-order topological phononics^[21].

最近, 同济大学声子学课题组通过扩散映射, 实现了基于实空间动力学性质相似性的拓扑声子无监督流形聚类(图7)^[21]. 用一个$ L\times L $阶的对角矩阵$ \widehat{{P}} $描述声子系统谐振子之间的相互作用, 对应的核矩阵为${A}_{\varepsilon }\left(i, j\right)={\rm{exp}}\bigg(-\dfrac{{||{\widehat{P}}_{i}-{\widehat{P}}_{j}||}^{2}}{2\varepsilon {L}^{2}}\bigg)$. 拓扑不变量v是关于几何参数构型$ \widehat{{P}} $的函数, 所以可以根据构型$ \widehat{{P}} $的差异对拓扑性质$v\big(\widehat{{P}}\big)$进行分类. 这种聚类方法只需要定义矩阵$ \widehat{{P}} $和核矩阵$ {{{A}}}_{\varepsilon }\left(i, j\right) $, 不需要针对具体系统定义特定的拓扑不变量, 因此可用于不同的拓扑声子系统, 包括随机耦合的一维Su-Schrieffer-Heeger声子链(图7(d))、不规则声子拓扑绝缘体(图7(e))、随机耗散的非厄米声子链(图7(f))和具有高阶声子拓扑态(图7(g)).
基于扩散动力学的分类算法有很强的可适应性, 通过定义式(8)式中的核矩阵$ {A}_{i, j}={A}_{\varepsilon }\left({x}_{i}, {x}_{j}\right) $的具体形式, 能够快速转变成适合不同物理情境的分类算法. Rodriguez-Nieva和Scheurer^[52]提出了基于扩散映射的无监督机器学习算法, 能够对二维XY模型的样品进行卷绕数分类, 并捕获Berezinskii-Kosterlitz-Thouless跃迁(图8(a)). 这种方法也可以应用于伊辛规范理论, 从而通过扩散图进行拓扑分类, 实现了对物质奇异相的完全无监督研究. 继我们的工作之后^[21], Scheurer 和Slager^[53]将扩散映射算法用于搜索哈密顿量之间的绝热路径, 从而根据它们的拓扑性质对它们进行聚类. Lustig等^[54]将类似的方法应用于从实验数据中识别拓扑相变, 分析了经历拓扑相变的光学系统的实验数据, 证明了即使数据来源于系统的一小部分甚至不包括边缘态, 扩散映射也能识别拓扑相变(图8(b)). Lidiak和Gong^[55]提出了适用于量子系统中的扩散映射算法, 作为学习各种量子相位和相变的通用工具(图8(c)). 这种方法可以在单一基础上测量局部可观测值, 例如测量单个方向上的所有自旋, 因此很容易应用于许多实验量子模拟器. 另外, Che等^[56]提出了适用于动量空间的扩散映射方法, 成功识别拓扑特征, 并且在动量空间中的典型Su-Schrieffer-Heeger模型、Qi-Wu-Zhang模型和淬火Su-Schrieffer-Heeger模型上证明了这种方法.
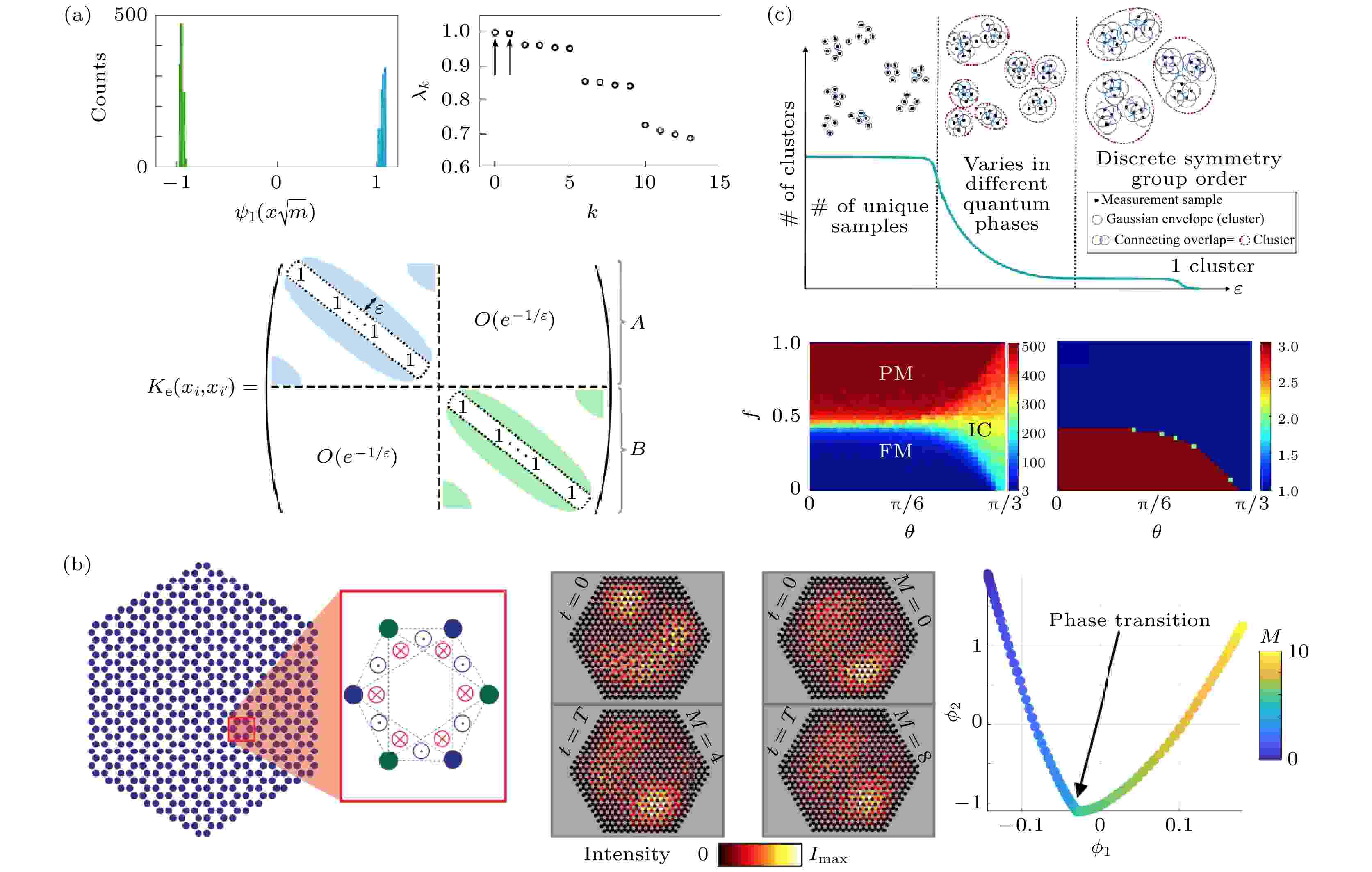图 8 基于扩散映射的无监督学习方法适用于解决不同物理系统中的拓扑分类问题　(a) 一维XY模型拓扑序的检测^[52]; (b) 扩散映射能够不借助边缘态, 识别Haldane模型描述的拓扑相变点^[54]; (c) 量子系统中的扩散映射算法, 能够无监督地识别$ {\mathbb{Z}}_{3} $横场伊辛模型的量子相^[55]
Figure8. The unsupervised learning with diffusion map is applied to solve topology identification in different physical systems: (a) Identifying the topological order in 1-dimensional XY model^[52]; (b) detection of the phase transition for the Haldane model without the edge states^[54]; (c) diffusion maps in learning quantum phases with a $ {\mathbb{Z}}_{3} $ transverse field Ising model^[55].

2 -->

4.2.基于热传导扩散的推荐模型

除了基于概率扩散的机器学习算法, 热传导扩散也启发了新的机器学习算法. 热传导系统中, 由于介质与介质之间存在温度差而产生传热, 使能量从物体的高温部分传至低温部分, 经过一段时间后形成稳定的温度分布. 热传导机制能够有效地应用于建立社会网络中的信息挖掘和推荐模型. 这种方法通过用户已选择的偏好项目(高温部分)推测出用户可能选择的其他项目(低温部分). 例如淘宝网通过用户已购买的产品推荐其他类似的产品. 基于物理学中的热传导^[57,58], 科研工作者们提出了可以处理个性化边界条件的推荐模型, 用于处理社会网络中庞大的数据信息.
物理学中的热传导过程可以用偏微分方程:

$ - \kappa {\nabla ^2}T\left( {{r}} \right) = {{\nabla}} \cdot {{J}}\left( {{r}} \right),$

描述, 其中$ \kappa $为导热系数; $ T\left({{r}}\right) $为温度; $ {{J}}\left({{r}}\right) $为热流密度. 将包含N个项目的推荐网络视作一个含有N个节点的热传导模型, 定义R表示N个节点的温度向量, 已知的高温节点处温度为1, 低温节点处温度为0, 我们的目标是得到热平衡状态时其余节点的温度. 节点之间的连接关系由对称邻接矩阵A给出(图9): 若两个项目直接相关, 即两个节点之间直接相连, 则元素$ {A}_{ij}= $1, 反之$ {A}_{ij}= $0. 构建转移矩阵$ {{P}}={{{D}}}^{-1}{{A}} $, 其中D是表示权重的对角矩阵. 这个网络中的离散拉普拉斯算子${{L}}={\hat{{{I}}}}- {{P}}$ 类似于(17)式中的$ -\kappa {\nabla }^{2} $, 其中$ \hat{{{I}}} $是单位矩阵. 于是只需要求解
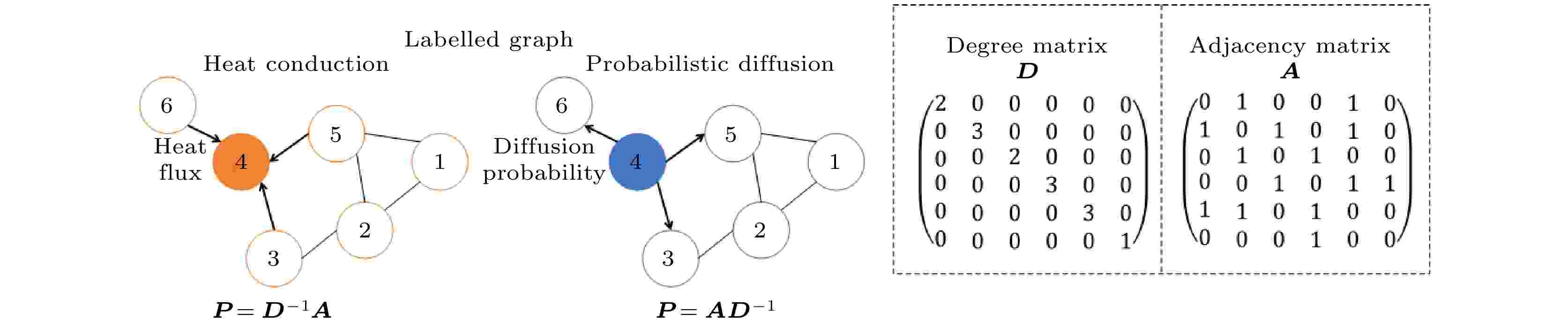图 9 标号图表明6个点(项目)之间的连接关系, 右侧是对应的权重矩阵和邻接矩阵
Figure9. Labelled graphs show the connection of 6 points (items), and the corresponding degree matrix and adjacency matrix are on the right side.

${{LR}}{\rm{ = }}{{f}}{{.}}$

(18)式与(17)式相类似, 其中f是表示外部热源的向量, f对应于$ {{\nabla}} \cdot {{J}}\left( {{r}} \right) $; 温度向量R对应于$ T\left({{r}}\right) $.
格林函数可以用来处理图上的扩散型问题^[22]. 在推荐模型中, 温度向量R即用户对项目的评级向量, $ {R}_{i}\ne 0 $代表用户对第i个项目的评级, 对应于热传导模型中已知的节点温度, 若该用户未对该项目进行过评级, 则$ {R}_{i}=0 $, 对应于热传导模型中待确定的节点温度. 所有已评级的项目($ {R}_{i}\ne 0 $)是这个系统的边界条件. 将用户的已知评级(边界条件)和未知评级分别用$ {R}_{\rm{B}} $和$ {R}_{\rm{U}} $表示, 则(18)式可展开成:

$ \left( {\begin{array}{*{20}{c}} {{{R}_{\rm{B}}}}\\ {{{R}_{\rm{U}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{P}_{{\rm{BB}}}}}&{{{P}_{{\rm{BU}}}}}\\ {{{P}_{{\rm{UB}}}}}&{{{P}_{{\rm{UU}}}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{R}_{\rm{B}}}}\\ {{{R}_{\rm{U}}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {f}\\ 0 \end{array}} \right). $

只需要求解

$ {R}_{\rm{U}}={P}_{{\rm{U}}{\rm{B}}}{R}_{\rm{B}}+{P}_{{\rm{U}}{\rm{U}}}{R}_{\rm{U}}+0. $

预测得到的评级向量为

$ {R}_{\rm{U}}={\big(\hat{{{I}}}-{P}_{{\rm{U}}{\rm{U}}}\big)}^{-1}{P}_{{\rm{U}}{\rm{B}}}{R}_{\rm{B}}. $

经过n个时间步长之后, (21)式的解为

$ {R}_{\rm{U}}=\left(\hat{{{I}}}+{P}_{{\rm{U}}{\rm{U}}}+{P}_{{\rm{U}}{\rm{U}}}^{2}+\cdots +{P}_{{\rm{U}}{\rm{U}}}^{n-1}\right){P}_{{\rm{U}}{\rm{B}}}{R}_{\rm{B}}. $

因为${P}_{{\rm{U}}{\rm{U}}} $的特征值小于1, 所以${P}_{{\rm{U}}{\rm{U}}}^{n} $很快收敛, 于是经过几个步长之后就能得到稳定解. 这种方式避免了对评级矩阵R的迭代求解, 而是将已知信息作为边界条件直接得到最终稳态解, 从而减少计算时间. 其中${P}_{{\rm{U}}{\rm{B}}} $代表着已知评级节点到未知评级节点的转移矩阵, ${P}_{{\rm{U}}{\rm{U}}} $代表着未知评级节点之间的转移矩阵. 已知评级${R}_{\rm{B}} $即热传导过程中的热源, 未知评级${R}_{\rm{U}} $即其余节点平衡态时的温度.
热传导扩散和概率扩散都能应用于机器学习. 值得注意的是, 热传导模型中, 定义行归一化的转移矩阵$ {{P}}={{{D}}}^{-1}{{A}} $. 拉普拉斯矩阵${{L}}=\hat{{{I}}}-{{{D}}}^{-1}{{A}}$表示该点的温度变化仅与汇入的净总热流有关. 例如图9中, 节点4的温度变化量仅与相连的节点3, 5, 6流入节点4的净热流的算术平均值有关, $\dfrac{{\partial {T_4}}}{{\partial t}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{3}}&{\dfrac{1}{3}}&{\dfrac{1}{3}} \end{array}} \right]{\left[ {\begin{array}{*{20}{c}} {{J_1}}&{{J_2}}&{{J_3}} \end{array}} \right]^{\rm{T}}}$, J为流入的净热流. 而在概率扩散过程中, 定义列归一化的转移矩阵 $ {{P}}={{{A}}{{D}}}^{-1} $, 拉普拉斯矩阵${{L}}=\hat{{{I}}}-{{{A}}{{D}}}^{-1}$表示扩散概率守恒. 例如图9中, 当时间步长$ ?t $很短时, 假设仅从节点4扩散到节点3, 5和6, 那么这四个节点概率之和为1.
2 -->

4.3.基于全局和局部扩散搜索算法的优化模型

扩散搜索算法能够在庞大的数据集中, 通过随机且分布均匀的搜索方式实现信息的最优化处理, 被广泛的应用于结构搜索^[59-61]. Pickard和Needs^[62]将随机扩散与第一性原理相结合, 提出了从头算随机结构搜索算法(ab initio random structure searching, AIRSS). 该算法以最随机的方式生成初始结构, 为了提高效率可以考虑引入基于化学、实验或对称性的偏置条件, 然后在保持实验和对称约束的同时演化起始结构. AIRSS的计算量集中在演化大量不同的初始结构, 直到多次获得相同的最低能量结构, 以确保该结构的势能面位于全局最小值.
粒子群优化算法(particle swarm optimization, PSO)^[63]模拟自然界中鸟群的捕食行为, 它不同于普通的单一粒子扩散行为, 群体中每个粒子的扩散搜索不仅受到自身个体极值影响, 还受到整个粒子群的当前全局最优解影响, 最终实现全局或局部扩散搜索最优解(图10(a)). 利用PSO进行晶体结构搜索, 吉林大学马琰铭教授团队^[64,65]开发了CALYPSO, 全称为基于粒子群优化算法的晶体结构分析(crystal structure analysis by particle swarm optimization). 该方法只需要给定材料的化学成分和外部条件, 如压力, 就能预测材料稳定或亚稳结构, 大大减少了第一性原理密度泛函计算的计算量 (图10(b)). CALYPSO算法的开发启发了很多原创性工作, 在设计各种材料方面具有广泛应用, 为功能驱动的材料设计打开了大门, 具体内容可以参考《Journal of Physics: Condensed Matter》, 《Computational Materials Science》以及《Chinese Physics B》上的相关综述文章^[66-68].
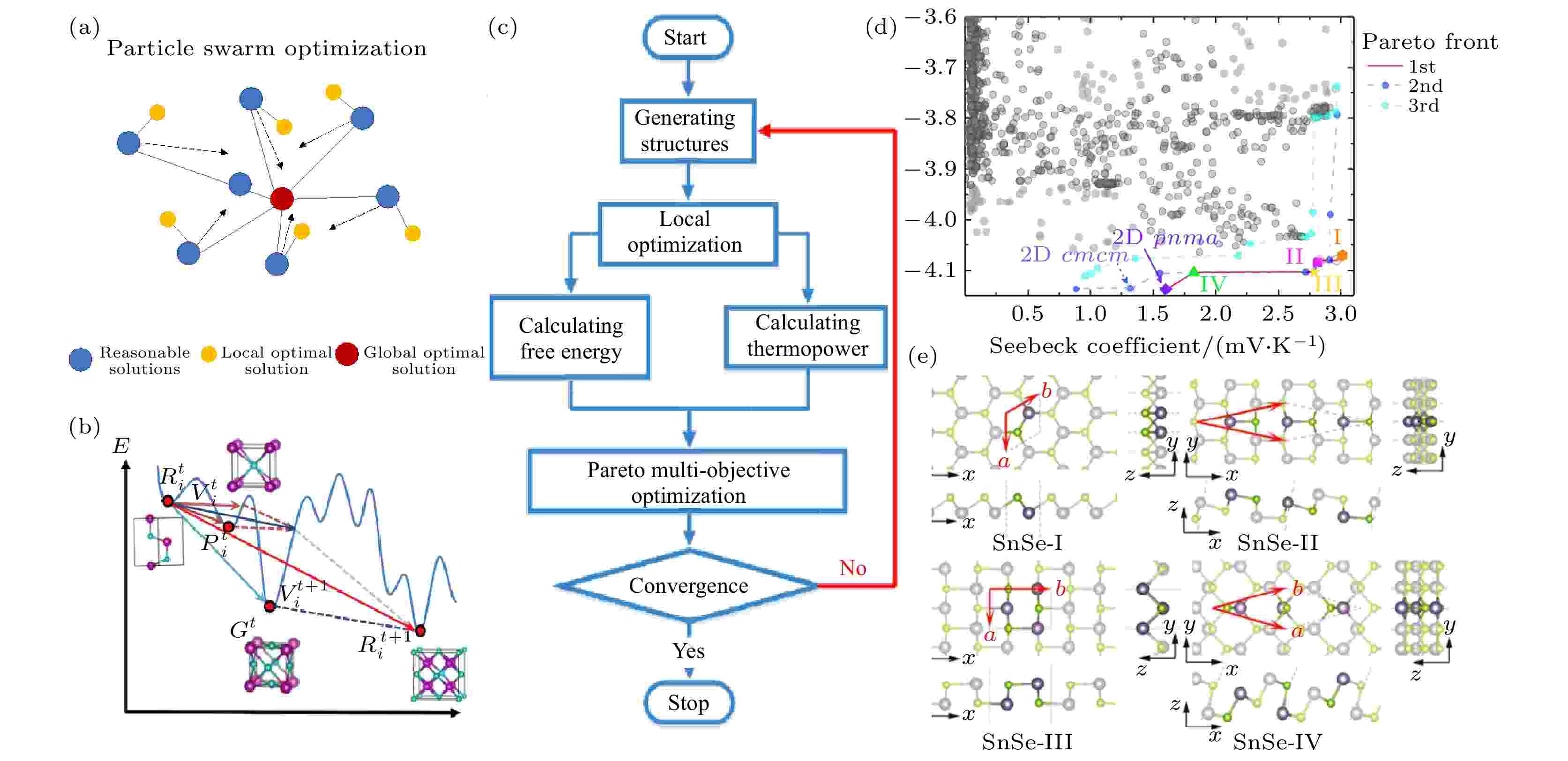图 10 (a) 全局及局部粒子群优化算法示意图; (b) 粒子群优化算法中速度及位置更新示意图^[68]; (c) 多目标优化的二维SnSe材料定向设计工作流程图; (d) 室温下(300 K), 二维SnSe材料单层结构的自由能; (e) 图(d) 中第一Pareto前沿(红线)上的四种新型单层结构的三视图, 深灰色和绿色的球分别表示Sn原子和Se原子^[70]
Figure10. (a) The diagram of PSO; (b) The schematic diagram of the velocity and position updates in PSO^[68]; (c) workflow of the multi-objective optimization for 2D SnSe materials design; (d) thermopower landscape at room temperature (300 K) versus the free energy of 2D SnSe materials; (e) four 2D SnSe structures on the first Pareto front, where the dark gray and green balls denote Sn and Se atoms, respectively^[70].

Gao等^[69] 通过晶体结构搜索, 找到了三种新型的具有平面内负泊松比的氧化硅结构, 并且确认了二维氧化硅结构的全局最小自由能, 这在纳米力学和纳米电子学中有巨大的潜在应用. 基于PSO的扩散搜索也可以是多目标的, 多目标约束下功能材料的定向设计是一个很大的挑战, 其中性能和稳定性是由不同物理因素的复杂关联决定的. 闫申申等^[70]基于帕累托最优和粒子群优化方法的多目标优化方法, 对新型功能材料进行定向设计. 该工作利用第一性原理结合多目标优化算法同时预测了具有低自由能和高热电势的多种新型二维硒化锡(图10(c)—(e)), 并且揭示了这些新型二维材料高热电势来源于其费米面附近能带的多简并度. 基于粒子群扩散的多目标优化方法能为未来多目标、多功能材料的一体化设计提供一个新的思路.
除此之外, 物理学中的扩散机制可以延伸到更为宽泛的领域, 比如利用极小值跳跃^[71]和微分演化^[72]进行材料结构预测也可视作广义上的扩散过程. 扩散搜索算法有望应用于更多凝聚态物理学领域, 比如解决文章^[73]中提到到的光子拓扑态逆设计问题, 以及文章^[74]中提到的分子热流分束问题.

针对波动和扩散系统中的机器学习研究方兴未艾. 近年来人们关注该领域两个重点内容: 其一是在利用丰富的波物理现象作为实现机器学习的硬件平台, 以实现波动系统中的人工神经网络为主; 另一个是扩散系统启发新的机器学习算法, 通过物理中的扩散机制分析数据的内在规律, 从而实现分类、优化等. 本文围绕着这两个方面简要介绍了相关的进展以及一些前沿工作.
首先, 本文介绍了波动系统中的神经网络实现, 包括线性的光学、声学系统以及非线性波系统. 一系列相关工作说明了依赖于波的并行性和快速传输性, 波动系统中的神经网络具有高效、低能耗、高带宽的特点. 本文重点介绍了几个示例, 凸显出波动系统在推断视觉任务、时序任务或大数据集任务时的优越性. 波动系统作为人工神经网络硬件载体具有巨大潜力, 为下一代芯片的开发提供了启发性的思路. 再者, 本文介绍了由扩散系统启发的无监督机器学习算法. 扩散系统中物质根据一定规律扩散, 最终达到稳态分布, 这一机制开发了许多机器学习算法, 解决了许多具有类似特点的实际问题. 例如, 基于概率扩散的分类算法, 基于热传导的社会网络推荐模型, 以及基于群体扩散的结构搜索算法.
尽管这个方向的研究已经取得巨大的进展, 但是仍处于初步阶段, 一些重要的基本问题尚未解决. 首先, 如何在波动系统中实现非线性激励函数仍是个重要的问题. 考虑到波动系统实现非线性激励函数的复杂度和局限性, 在波动系统中实现神经网络是否优于传统方法(如线性回归)值得商榷^[23]. 另外, 在光学系统中可以通过有效的电光转换机制进行信号恢复^[75]避免散粒噪声, 但是在其他的波动系统中如何避免噪声还不明确. 除此之外, 现有的研究主要通过波动系统实现人工神经网络, 突破经典硬件平台的限制, 或是根据扩散机制分析数据的内在规律, 从而实现无监督学习. 二者之间的交叉结合却鲜有讨论, 扩散物理是否能与人工神经网络相结合, 从而进一步实现扩散系统中的深度学习, 以及如何实现硬件和软件的结合优化, 这些都是值得继续深入研究的问题. 最后, 在经典波动系统或者经典扩散系统中实现类量子或量子启发算法模拟也是一个重要的研究方向.