摘要: 为了提高分布式结构声源的声场重建精度, 本文提出了基于单元辐射叠加法的结构声源声场重建方法. 该方法首先利用声场叠加原理和结构振声传递特性, 建立了结构声源表面振动与辐射声场之间的振声传递关系解析表达式, 得到便于快速计算的振声传递矩阵, 能够解决连续分布、相干结构噪声源的声传播模型精细化表征问题. 然后利用振声传递矩阵作为传递算子进行声场重建, 并与迭代加权算法相结合. 通过将基于单元辐射叠加法的声场预报结果与解析法预报结果进行比较, 验证了单元辐射叠加法具有较高的准确性. 并将基于单元辐射叠加法的声场重建方法与传统等效源法近场声全息和迭代加权等效源法相比较, 通过仿真分析与矩形板声场重建实验证明了基于单元辐射叠加法的声场重建方法能够改善结构声源的声场重建精度并增大近场声全息的有效测试距离范围.
关键词: 结构声源 /
单元辐射叠加法 /
近场声全息 /
声场重建 English Abstract Sound field reconstruction of structural source based on element radiation superposition method Shi Sheng-Guo 1,2,3 ,Gao Yuan 3 ,Zhang Hao-Yang 1,2,3 ,Yang Bo-Quan 3 1.Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 61701133)Received Date: 23 November 2020Accepted Date: 15 February 2021Available Online: 21 June 2021Published Online: 05 July 2021Abstract: In order to improve the sound field reconstruction accuracy of distributed structural source, a new near-field acoustic holography is established based on the element radiation superposition method (ERSM). In the proposed method, the surface of structural source is divided into several regular pistons. The sound field of structural source is considered as the superposition of sound field of pistons. Firstly, we compare the sound field calculated by ERSM with that by Rayleigh's integral. It is proved that ERSM is quite accurate in sound field prediction. Based on ERSM, a vibration acoustic transfer (VAT) function is derived. The VAT function has computable analytical expression and embodies the transfer relationship between the structural source surface and the radiated sound field. The VAT function can precisely characterize the acoustic propagation of continuous distributed coherent sources. Subsequently, we employ the VAT function to replace the Green's function, and apply the VAT function to sound field reconstruction. Different with the equivalent source method (ESM) which is widely used in sound field reconstruction, ERSM directly divides the piston-sources on the surface of structural source rather than constructing the equivalent point-sources on a plane behind the structural source. Furthermore, we introduce a weight matrix into ERSM and iteratively calculate the vibration velocity for a more accurate result, and we call the proposed method as iterative weighted ERSM (IWERSM). In this paper, the simulations and experiment of sound field reconstruction of a rectangular plate are performed. In the proposed method, the rectangular plate is divided into several rectangular pistons. The reconstruction results of ERSM and IWERSM are compared with that of ESM and iterative weighted ESM (IWESM) respectively. The reconstruction accuracies at different distances between the plate and array (test distances) are analyzed. The simulation results show the accuracy of ERSM and IWERSM are better than that of ESM and IWESM respectively. With the increase of test distance, the phenomenon is more obvious, and IWERSM even shows a good reconstruction accuracy while the test distance is more than half a wavelength. The experiment results also validate that ERSM and IWERSM have better reconstruction accuracy than ESM and IWESM respectively at the same test distance. In a word, the simulations and experiments demonstrate that the proposed method can improve the sound field reconstruction accuracy of regular structural source and expand the valid test distance of near-field acoustic holography.Keywords: distributed structural source /element radiation superposition method /near-field acoustic holography /sound field reconstruction 全文HTML --> --> --> 1.引 言 近场声全息是一种常用的基于阵列测量的声场重建技术, 由于其利用了包含声源细节信息的倏逝波成分, 可获得不受波长限制的高分辨率[1 ] . 但声源的倏逝波成分随距离的增大急剧衰减, 因此利用近场声全息方法重建声场通常要求测量阵列距离声源半个波长以内, 甚至更近. 但对于较大型的分布式结构声源, 近距离测试可能会带来较大的实施难度. 基于等效源法(equivalent source method, ESM)的近场声全息近年来已广泛应用于结构声源的识别与声场重建. ESM的主要思想是将声源的辐射声场由其内部一系列等效源产生的声场叠加代替, 等效源的源强可通过匹配声源表面的法向振速得到. 该方法适用于任意形状声源, 同时避免复杂的插值运算、奇异积分处理和解的非唯一性等问题, 计算效率和精度都大大提高. 毕传兴等[2 -4 ] 在国内提出将ESM引入近场声全息, 并在提高声源分辨率和声场重建精度方面做了一系列研究. Pinho[5 ] 以无限大障板中的简支板为例分析了等效源的数目、布置位置和测量误差等因素对ESM重建声场的影响. Valdivia和Williams[6 ] 以圆柱壳为目标, 对ESM和边界元法的柱壳辐射声场重建精度进行了比较. Zhang[7 ] 采用质点振速作为输入数据, 降低了ESM的声场重建结果对测量误差的灵敏度. 等效源源强的求解是ESM能否精确重建声场的关键, Oudompheng等[8 ] 将包含声源先验信息的加权矩阵引入源强的最优化问题求解, 提高了声场重建精度; Xu等[9 ] 采用迭代加权等效源法(iterative weighted ESM, IWESM)显著提高了声源识别的分辨率; 蔡鹏飞[10 ] 将迭代加权最小二乘法引入等效源强的求解中, 通过迭代运算保留了声源强度中幅值较大的部分, 能够提高稀疏声源的识别和声场重建精度; Ping等[11 ] 将IWESM与宽带声全息相结合, 提高了低频声源的分辨率和声场重建精度. 近年来, 许多****将压缩感知与ESM相结合, 并涌现出了许多在稀疏框架下建立的声场重建算法[12 -14 ] . 由于基于压缩感知原理建立的ESM对声源的稀疏性有一定要求, 对于较复杂振动结构的声场重建精度仍有待改善. 目前所有基于ESM的声场重建方法都是采用点源Green函数传递算子, 对于连续分布的结构声源, 点源传播模型可能存在一定的局限性, 影响算法的声场重建性能.[15 ,16 ] . 而结构声源的声辐射计算与表征则是提升结构声源声场重建精度的关键. 模态分析法[17 ,18 ] 是一种常用的解析计算方法, 通过分析各阶模态的声辐射阻抗和声辐射效率来确定辐射声场, 常用于分析矩形板、球壳或有限长圆柱壳等特殊规则结构的振动声辐射问题. 在实际应用中, 随着分析频率的提高, 参与振动的模态越来越多, 计算量巨大. 因此模态分析法仅适用于简单结构的中低频振动声辐射分析. 有限元法[19 ] 是目前理论计算弹性结构声辐射较为常用的数值计算方法, 但因涉及有限元网格划分, 其计算能力受到分析频率、结构尺寸及声场计算距离的严重限制. 为提升辐射声场的计算效率, 王斌等[20 ] 提出了一种新的辐射声场近似计算方法—单元辐射叠加法(element radiation superposition method, ERSM), 其核心是采用规则障板表面活塞的辐射声场去近似实际障板表面活塞的辐射声场, 直接建立结构声源表面振动与辐射声场之间的传递关系, 并对表面振速进行加权、求和得到结构声源辐射声压. 该方法避免了求解Helmholtz表面积分方程及其逆矩阵, 在计算速度上明显优于边界元等其他数值积分方法, 没有非唯一性、奇异积分及高维矩阵求逆等问题的困扰, 且具有较大的频率适用范围.2.单元辐射叠加法理论研究 本节将基于单元辐射叠加法, 获得反映结构声源传递特性、便于快速计算的振声传递矩阵. 并以矩形板为例, 将基于单元辐射叠加法的矩形板声场预报结果与解析法预报结果相比较, 以验证单元辐射叠加法的准确性.$ {{p}}_{\rm{S}} $ 与法向振速向量$ {{v}}_{\rm{S}} $ 的关系:N 为声源表面离散单元数, 矩阵A B [20 ] . 在(1 )式两边同时左乘矩阵A Z r 点处的辐射声压表达式为C D [20 ] . 将(2 )式代入(3 )式可得到4 )式表明, 辐射声压可根据向量${{G}} = [G_1, $ $ G_2,\; \cdots,\; G_N]$ 对表面振速加权、求和得到, 向量G $ {{v}}_{\rm{S}} = [1,\; 0, \;\cdots, \;0]^{\rm{T}} $ , 并代入(4 )式可得$ p_1 = G_1 $ ; 令$ {{v}} _{\rm{S}} = [0,\; 1, \;0, \;\cdots, \;0]^{\rm{T}} $ , 则可得到$ p_2 = G_2 $ ; 最终依次得到$ p_i = G_i, \; i = 1,\; 2,\; \cdots,\; N $ . 则振声传递向量的表达式变为$ p_i $ 为第i 个离散单元以单位速度振动、其他单元振速为零时的辐射声压. 因此, 振声传递向量中各项元素等于辐射面共形障板表面所对应的刚性活塞面以单位速度振动时的辐射声压. 进一步可构建振声传递矩阵图1 所示, 其表面矩形活塞的辐射声压可由无限大平面障板表面矩形活塞的远场辐射声压表达式近似计算[20 ] :图 1 平面障板及其表面活塞示意图Figure1. Plane baffle and corresponding pistonsR 为活塞中心到声场一点的距离, θ 为对应俯仰角, φ 为对应方位角, $ L_x $ , $ L_y $ 分别为矩形活塞的长与宽; j为虚数单位, ρ 为介质密度, c 为介质中的声速, k 为声波波数, v 表示活塞法向振速, ${{\rm{J}}_0}(\cdot)$ 为零阶球贝塞尔函数. (7 )式适用于矩形活塞的远场, 按照近-远场判距公式$r_{\rm g} = ({L_x}/2)^{2}/\lambda$ , λ 为结构辐射波长[21 ] , (7 )式能够应用于大于$r_{\rm g}$ 处的声场预报和重建. 因此, 可通过调节活塞尺寸来改变$r_{\rm g}$ , 使(7 )式适用的下限距离远小于整个障板的结构辐射波长λ , 则(7 )式能够应用在障板的近场范围内. 以上限频率2 kHz为例, 取活塞尺寸$ L_x\approx0.147\lambda $ (下文中仿真参数), 则计算得到$r_{\rm g}\approx $ $ 0.0054\lambda$ . 下面以矩形板声源为例, 通过仿真对比基于ERSM的声场预报结果和解析法预报结果(瑞利积分公式计算[17 ,18 ] ), 以验证ERSM的准确性, 具体的研究参数如表1 所列.仿真参数 数值/单位 仿真参数 数值/单位 矩形板长度 1 m 弹性模量 $ 2.1\times10^{11}\;{\rm{N}}/{\rm{m}}^{2}$ 矩形板宽度 0.8 m 泊松比 0.3 矩形板厚度 0.0036 m 损耗因子 0.002 矩形板密度 $ 7800\;{\rm{kg}}/{\rm{m}}^{3}$ 简谐力幅值 1 N 空气密度 $ 1.29\;{\rm{kg}}/{\rm{m}}^{3}$ 激励点位置 矩形板中心 空气声速 340 m/s 参考声压 $ 2\times10^{-5}\;{\rm{Pa}}$ 矩形活塞长 0.025 m 矩形活塞宽 0.02 m
表1 仿真参数Table1. Parameters of simulations图2 和图3 分别为在100和1000 Hz振动频率下的矩形板辐射声场预报结果, 预报距离分别取距板面0.005λ , 0.3λ , 0.6λ , 0.9λ , 1.2λ , 图例中SPL为声压级. 从图2 和图3 可以看到, 随着振动频率的增加, 辐射声场的复杂性也在提高, 而无论100 Hz还是1000 Hz, ERSM的预报结果与解析法预报结果都基本一致. 在预报距离0.005λ 和1.2λ 处, 取y = 0的一条切线, 对比不同振动频率下的声压, 结果如图4 和图5 所示, 可见无论是在接近活塞近场的距离处还是在超过一倍波长的距离处, 基于ERSM的预报结果均与解析法预报结果有较高的符合度.图 2 不同距离处的声场预报结果(100 Hz) (a) 解析法; (b) 单元辐射叠加法Figure2. Sound field prediction at 100 Hz: (a) Analytical value (theoretical); (b) ERSM图 3 不同距离处的声场预报结果(1000 Hz) (a) 解析法; (b) 单元辐射叠加法Figure3. Sound field prediction at 1000 Hz: (a) Analytical value (theoretical); (b) ERSM图 4 100 Hz预报声压切线对比图 (a) 0.005λ ; (b) 1.2λ Figure4. Pressure profiles at 100 Hz: (a) 0.005λ ; (b) 1.2λ 图 5 1000 Hz预报声压切线对比图 (a) 0.005λ ; (b) 1.2λ Figure5. Pressure profiles at 1000 Hz: (a) 0.005λ ; (b) 1.2λ $ \|\cdot\|_2 $ 表示取2范数, $ |\cdot| $ 表示取幅值, ${{p}}_{\rm ersm}$ 为单元辐射叠加法预报的声压, ${{p}}_{\rm t}$ 为解析法所预报的声压(理论值), 预报距离为0.005λ . 图6 为单元辐射叠加法预报声压随频率变化的误差曲线, 频率为10—2000 Hz. 可以看到, 除开极个别频率点, 误差基本都控制在${5{\text{%}}}$ 以内. 出现误差峰值的原因可能有两个: 一是该频率正好为某一阶振动模态的固有频率, 矩形板在该频率处的响应幅值会有较大变化, 因此进行声场预报的误差可能会增加; 二是在矩形板的边缘处, (7 )式在某些频率处的误差会有所增大. 综合以上对比结果, 可以验证基于单元辐射叠加法的建模方法具有较高的准确性.图 6 0.005λ 预报距离处的声压误差曲线Figure6. Error-frequency curve of ERSM at 0.005λ 3.基于单元辐射叠加法的近场声全息 现有的声场重建算法都是将点源Green函数作为传递算子来对目标声场进行重建. 本文提出将ERSM引入近场声全息, 并采用振声传递矩阵${{G}}_{\rm vat}$ 作为传递算子, 建立适用于结构声源声场重建的振声传递模型, 实现声源表面振动到声场空间的传递. 同时引入迭代加权算法, 进一步提高结构声源的声场重建精度和声全息阵列测试距离.3.1.ERSM声场重建基本理论 3.1.ERSM声场重建基本理论 传统等效源法将目标声场看成由一系列等效点源辐射声场的叠加, 通过计算等效源强来重建声场. 本节基于ERSM, 将结构声源表面划分成若干规则活塞, 声源的外部辐射声场可看成由一系列活塞的辐射声场叠加而成, 则基于ERSM的全息面测点声压可表示为$ {{p}}_{\rm{H}} = [p(r_{{\rm{H}}1}),\; p(r_{{\rm{H}}2}) , \;\cdots, \;p(r_{{\rm{H}}M})]^{\rm{T}} $ 为全息面上所测声压向量, M 为全息测点数, T表示转置; $ {{r}}_{\rm{H}} $ , $ {{r}}_{\rm{S}} $ 分别表示全息面测点位置和声源表面活塞位置, $ {{v}}_{\rm{S}} = [v(r_{{\rm{S}}1}),\; v(r_{{\rm{S}}2}) , \;\cdots,\; v(r_{{\rm{S}}N})]^{\rm{T}} $ 为全部活塞的振速向量, N 为活塞个数; $ {{G}} _{\rm vat}({{{r}}_{\rm{H}}}, {{{r}}_{\rm{S}}}) $ 为结构声源表面到全息面的振声传递矩阵, 表示为9 )式是不适定的, 为求解全部活塞的振速向量$ {{v}}_{\rm{S}} $ , 引入Tikhonov正则化技术, 求解$ {{v}}_{\rm{S}} $ 的过程可转变为最优化如下函数:β 为正则化参数, 本文采用Bayesian准则[22 ] 来获取最佳参数值. 在活塞数多于测量点数的情况下$ (M<N) $ , (11 )式的最优解可表示为$ [\cdot]^{\rm{H}} $ 表示转置共轭, I $ {{v}}_{\rm{S}} $ 与振声传递矩阵来重建声场:$ {{p}}({{r}}) $ 为声场重建声压, ${{G}}_{\rm vat}({{{r}}}, {{{r}}_{\rm{S}}})$ 为声源表面到声场空间的振声传递矩阵, r 3.2.迭代加权的ERSM -->3.2.迭代加权的ERSM 本小节通过在约束项中引入加权矩阵而加强对(11 )式中最优化问题的解的约束, 则引入迭代加权的ERSM (IWERSM)声场重建最优化问题可表示为$ {{G}}_{\rm vat} $ 为结构声源表面到全息面的振声传递矩阵(省略位置向量), 权矩阵W W $ {{WW}}^{-1} = {{I}} $ . 定义$ {\widetilde{{v}}}_{\rm{S}} = {{W}}{{v}}_{\rm{S}} $ , 代入(14 )式得15 )式可视为标准的Tikhonov泛函问题, 其解为${\widetilde{{G}}}_{\rm vat} = {{G}}_{\rm vat}{{W}}^{-1}$ , 对其进行奇异值分解$ {\widetilde{{U}}} $ 为左奇异向量矩阵, $ {\widetilde{{V}}} $ 为右奇异向量矩阵, $ {\widetilde{{S}}} $ 为奇异值矩阵. 将(17 )式代入(16 )式得$ r_N $ 为第N 个活塞中心到阵列中心的距离. 在求解出初始振速向量后, 继续以迭代的方式构造权矩阵, 定义$ i = 1, \;2, \;\cdots $ 为迭代次数. 当满足如下收敛条件时迭代终止:$ \|\cdot\|_1 $ 表示取1范数; τ 为收敛阈值, 通常取值在0.01—0.1之间, 即两次迭代的振速幅值相差小于一定值时可终止迭代. 迭代计算时采用Bayesian正则化准则确定正则化参数β . 利用IWERSM来重建声场的步骤可表示如下:20 )式定义权矩阵初始值$ {{W}}_0 $ ;18 )式与(19 )式, 得到初始振速向量$ {{v}}^{(0)}_{\rm{S}} $ ;21 )式重新定义权矩阵$ {{W}}_i $ , 且${{W}} = $ $ {{W}}_{0}{{W}}_{i}$ ;18 )式与(19 )式, 输出$ {{v}}^{(i)}_{\rm{S}} $ ;22 )式计算收敛条件, 若满足收敛条件, 迭代终止;13 )式可重建声场声压.4.矩形板声场重建研究 本节进行矩形板声场重建仿真分析, 重建算法包括传统等效源法近场声全息(ESM)、迭代加权等效源法(IWESM)、基于单元辐射叠加法的近场声全息(ERSM)、以及迭代加权单元辐射叠加法(IWERSM). 其中, ESM和IWESM的传递算子为自由场点源Green函数; ERSM和IWERSM的传递算子为振声传递矩阵${{G}}_{\rm vat}$ , 其元素由(7 )式求得.表1 所列. 图7 是声场重建示意图, 全息面的阵列孔径为$ 1\; {\rm{m}}\times1\; {\rm{m}} $ , 阵元间距0.05 m, 重建面距板面0.01 m, ESM和IWESM的等效源面距板面0.05 m, ERSM和IWERSM则在板面划分矩形活塞. 在此以解析解(瑞利积分公式计算)为理论值, 计算各算法重建声压与理论值之间的误差, 定义误差计算公式为图 7 声场重建示意图Figure7. Diagram of sound field reconstruction${{p}}_{\rm r}$ 为算法重建声压, ${{p}}_{\rm t}$ 为重建面声压理论值.图8 是测试距离为0.5λ 的各算法重建声压误差, 频率为100—2000 Hz, 频率间隔为50 Hz. 可以看到, 各算法的误差随频率变化而波动起伏, 重建误差关系为ERSM < ESM, IWERSM < IWESM. 重点分析不同阵列测试距离情况下的各算法声场重建精度, 矩形板振动频率分别取500, 1000和1500 Hz, 阵列分别设置在距板面0.1λ —1λ 之间的各位置, 图9 为500, 1000, 1500 Hz振动频率下的重建误差随测试距离的变化曲线.图 8 声场重建误差 (d = 0.5λ )Figure8. Errors of sound field reconstruction (d = 0.5λ )图 9 重建声压误差随测试距离变化曲线 (a) 500 Hz; (b) 1000 Hz; (c) 1500 HzFigure9. Curves of pressure error with different test distances: (a) 500 Hz; (b) 1000 Hz; (c) 1500 Hz图10 为500 Hz振动频率下测试距离为$ 0.1\lambda $ , 0.5λ , $ 1\lambda $ 的各算法重建面声压横向切线图, 切线取在重建面中间位置. 结合图9(a) 可得: 在$ 0.1\lambda $ 处, 各算法的重建误差都很低且重建结果与理论值高度符合. 随着测试距离的增大, 各算法的重建误差也在增大. 其中, ESM的重建误差增大最明显, 在$ 0.5\lambda $ 处, 边缘处的重建声压与理论值相比已有较大差距. ERSM与IWESM在$ 0.5\lambda $ 处的重建误差都要低于ESM且重建结果与理论值大致相符, 但在$ 1\lambda $ 处误差增大明显. IWERSM的重建误差随距离的变化增加最小, 在$ 0.5\lambda $ 和$ 1\lambda $ 处的误差都要低于其他算法, 在$ 1\lambda $ 处也能大致重建出真实声压分布. 综合可得各算法的重建精度关系为ERSM > ESM, IWERSM > IWESM.图 10 500 Hz不同测试距离处的重建声压切线 (a) $ 0.1\lambda $ ; (b) $ 0.5\lambda $ ; (c) $ 1\lambda $ Figure10. Pressure profiles with different test distances at 500 Hz: (a) $ 0.1\lambda $ ; (b) $ 0.5\lambda $ ; (c) $ 1\lambda $ 图11 为1000 Hz振动频率下的重建声压切线结果. 结合图9(b) 可得: $ 0.1\lambda $ 处各算法的误差都很低且能准确重建声压分布. 当测试距离增大, ESM的重建误差增大仍是最明显的, 在0.5λ 处误差已达40%. ERSM, IWESM在0.5 λ 处的重建误差较ESM要低, 除边缘处外大致符合理论声压分布. 但在$ 1\lambda $ 处误差增大同样明显, 已不能准确重建出声压分布. IWERSM的重建误差增加最小, 在$ 1\lambda $ 处的重建结果也相对准确, 重建精度为各算法中最高的, 通过图9(b) 可更直观地得出结论, 各算法重建精度关系为ERSM > ESM, IWERSM > IWESM. 究其原因, 迭代加权能让重建结果更精确, 同时ERSM采用振声传递矩阵作为传递算子, 考虑了矩形板固有的传递特性, 能更好地对板结构声源进行识别, 进一步提高其声场重建精度, 在测试距离增大的情况下也能具有较小误差, 从而可增大近场声全息的有效测试距离范围.图 11 1000 Hz不同测试距离处的重建声压切线 (a) $ 0.1\lambda $ ; (b) $ 0.5\lambda $ ; (c) $ 1\lambda $ Figure11. Pressure profiles with different test distances at 1000 Hz: (a) $ 0.1\lambda $ ; (b) $ 0.5\lambda $ ; (c) $ 1\lambda $ 图12 为1500 Hz振动频率下的重建声压切线图. 结合图9(c) 可得: 在1500 Hz振动频率下, $ 0.1\lambda $ 处的各算法误差较前两个频率要高, 但仍能较准确地重建出声压分布. 在其他测量距离处, 测量精度的高低依次是: IWERSM > ERSM > IWESM > ESM, 足以看出基于ERSM的算法能够提升对结构声源的声场重建精度. 在测试距离大于$ 0.5\lambda $ 时, 各算法的误差普遍都有较大增加, 但IWERSM将振声传递模型与迭代加权相结合, 能够改善IWESM对分布式板结构声源的声场重建性能, 在测试距离接近$ 1\lambda $ 的情况下, 重建误差也能基本控制在30%左右.图 12 1500 Hz不同测试距离处的重建声压切线 (a) $ 0.1\lambda $ ; (b) $ 0.5\lambda $ ; (c) $ 1\lambda $ Figure12. Pressure profiles with different test distances at 1500 Hz: (a) $ 0.1\lambda $ ; (b) $ 0.5\lambda $ ; (c) $ 1\lambda $ 5.实验研究 本节将通过实验进一步验证基于ERSM的声场重建方法的有效性. 实验装置连接示意图如图13 所示, 信号源发出单频周期信号, 通过功率放大器将信号放大再输入激振器, 激振器作用于钢板下表面几何中心, 钢板振动向外辐射噪声. 传声器线阵在钢板正上方, 与Y 轴平行, 可沿X 轴方向左右滑动进行扫描, 垂直高度上下可以调节. 传声器接收声压信号, 并通过程控滤波器进行滤波放大, 然后用采集器进行信号采集, 最后用计算机通过第三 节所述方法对信号进行处理, 实现声场重建. 实验现场如图14 所示, 矩形钢板长1 m, 宽0.8 m, 厚0.0036 m, 其他参数与仿真条件一致. 传声器为17元线阵, 阵元间距0.05 m, 实验中移动线阵进行扫描,并选取与钢板孔径一致的$ 21\times17 $ 元阵列数据进行处理, 阵列到钢板的垂直距离分别取0.04, 0.14, 0.29, 0.54 m. 本实验选取0.04 m处测量的声压作为理论值, 分别用ESM, ERSM, IWESM, IWERSM这4种算法在其他距离重建0.04 m处的钢板辐射声压, 并对比各算法的重建精度. 钢板振动频率取100, 200, 400 Hz. 图15 所示为各算法在100, 200, 400 Hz振动频率下不同测试距离处的重建误差, 误差计算公式如(23 )式所示. 图16 —图18 分别为100, 200, 400 Hz振动频率下各算法的声场重建结果.图 13 实验装置连接示意图Figure13. Diagram of measurement图 14 实验现场图 (a) 矩形钢板; (b) 传声器阵列Figure14. Experimental facilities: (a) Rectangular steel plate; (b) microphones array图 15 不同距离处的重建声压误差 (a) 100 Hz; (b) 200 Hz; (c) 400 HzFigure15. Reconstruction error with different test distances: (a) 100 Hz; (b) 200 Hz; (c) 400 Hz图 16 不同测试距离的实验重建声压(100 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)Figure16. Experimental acoustic pressure reconstruction at 100 Hz: (a) Theoretical; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM(0.54 m); (e) ERSM (0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM(0.54 m); (k) IWERSM (0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)图 18 不同测试距离的实验重建声压(400 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)Figure18. Experimental acoustic pressure reconstruction at 400 Hz: (a) Theoretical; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM(0.54 m); (e) ERSM (0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM(0.54 m); (k) IWERSM (0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)图15(a) 和图16 可以看出: 在100 Hz振动频率下, 随着测试距离的增大, 重建误差在增加, 声压重建精度依次降低. 在相同测试距离的情况下, 各算法的重建误差关系为: ERSM < ESM, IWERSM < IWESM. 在0.14 m处, ERSM和IWERSM能较准确地重建真实的声压分布; ESM和IWESM的误差主要来自声压幅值较大的区域. 在0.29 m处, 各算法的误差进一步扩大, ESM已无法分辨左右两块幅值较大的区域, 但ERSM 和IWERSM仍能大致重建出真实的声压分布. 在0.54 m处, IWERSM还能保持50%以下的误差, 与ESM和IWESM在0.29 m处的误差结果近似.图15(b) 和图17 可以看出: 在200 Hz振动频率时, 相同测试距离下的各算法重建误差关系为: ERSM < ESM, IWERSM < IWESM. 在0.14 m处, ERSM和IWERSM能较准确地重建真实的声压分布, 误差主要来自板的中心区域; ESM没有完整地重建出部分辐射声压较弱的区域; IWESM的重建误差略微低于ESM. 在0.29 m处, ERSM和IWERSM仍能大致重建出真实的声压分布; ESM和IWESM的重建结果与理论分布相比有较明显的缺失或不一致. 在0.54 m处, 随着测试距离的增大, 受实际测量因素等影响较大, 各算法的误差都明显增大, ERSM和IWERSM的优势无法充分体现.图 17 不同测试距离的实验重建声压(200 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)Figure17. Experimental acoustic pressure reconstruction at 200 Hz: (a) Theoretical; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM(0.54 m); (e) ERSM (0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM(0.54 m); (k) IWERSM (0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)图15(c) 和图18 可以看出: 在400 Hz振动频率时, 相同测试距离下的各算法重建误差关系为: ERSM < ESM, IWERSM < IWESM. ERSM和IWERSM在0.14 m处能够较准确地重建出真实声压分布, 随着测试距离的增大, 重建精度在0.29 m处下降, 但与实际声压分布仍大致相符. ESM和IWESM在0.14和0.29 m处的声场重建精度均不如ERSM和IWERSM. 在0.54 m处, 各算法重建误差都明显增大.6.结 论 为了提高结构声源的声场重建精度, 本文首先利用声场叠加原理和结构振声传递特性, 获得了结构声源表面振动到辐射声场的振声传递矩阵. 该矩阵与表面法向振速无关, 而与振动频率、结构声源形状、活塞划分大小等有关, 反映了结构声源固有的传递特性. 进一步提出了基于ERSM的近场声全息, 该方法利用结构声源的振声传递矩阵代替传统点源Green函数作为传递算子进行声场重建, 并引入迭代加权算法. 通过与解析法的预报结果进行比较, 证明了ERSM具有较高的准确性. 通过矩形板的声场重建仿真证明了在相同测试距离下, ERSM和IWERSM的重建误差要分别低于ESM和IWESM, 且随着测试距离的增大, 该现象更加明显. 其中IWERSM在接近1倍波长的测试距离时, 误差基本能控制在30%以下. 通过钢板空气实验同样验证了在相同测试距离下, ERSM和IWERSM具有更低的重建误差, 并能在适当范围内提升阵列测试距离. 所提出的声场重建方法适用于特殊规则结构声源的声场重建, 根据已知其他规则曲面结构表面活塞(柱面活塞、球冠活塞等)的辐射声场表达式, 该方法还有望应用于柱壳、球壳等结构声源的声场重建, 为空气中或水下的大型结构声源精准声场重建提供参考. 









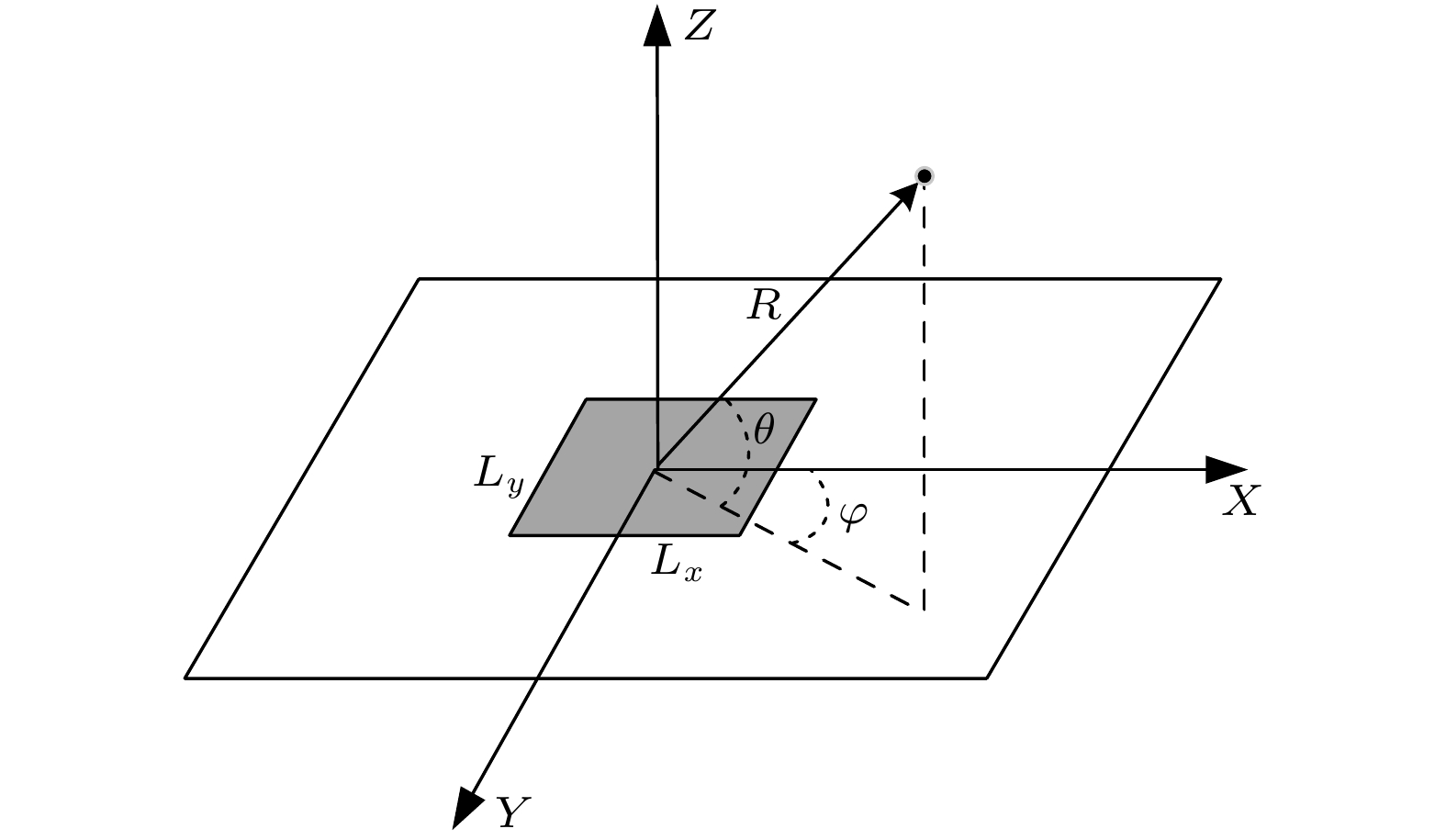 图 1 平面障板及其表面活塞示意图
图 1 平面障板及其表面活塞示意图










 图 2 不同距离处的声场预报结果(100 Hz) (a) 解析法; (b) 单元辐射叠加法
图 2 不同距离处的声场预报结果(100 Hz) (a) 解析法; (b) 单元辐射叠加法 图 3 不同距离处的声场预报结果(1000 Hz) (a) 解析法; (b) 单元辐射叠加法
图 3 不同距离处的声场预报结果(1000 Hz) (a) 解析法; (b) 单元辐射叠加法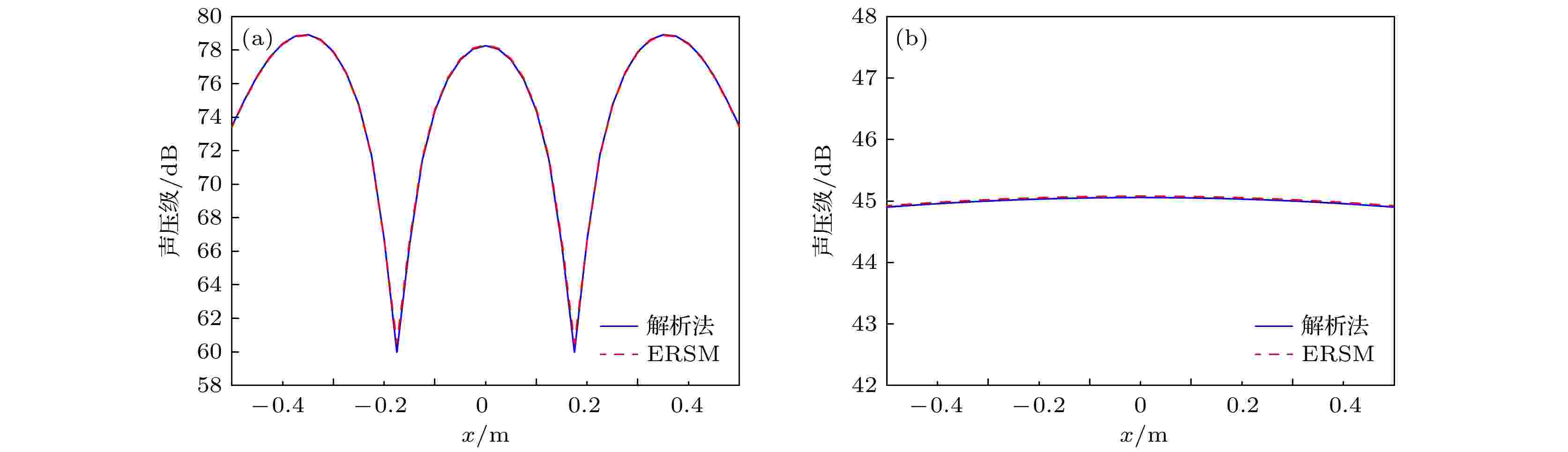 图 4 100 Hz预报声压切线对比图 (a) 0.005λ; (b) 1.2λ
图 4 100 Hz预报声压切线对比图 (a) 0.005λ; (b) 1.2λ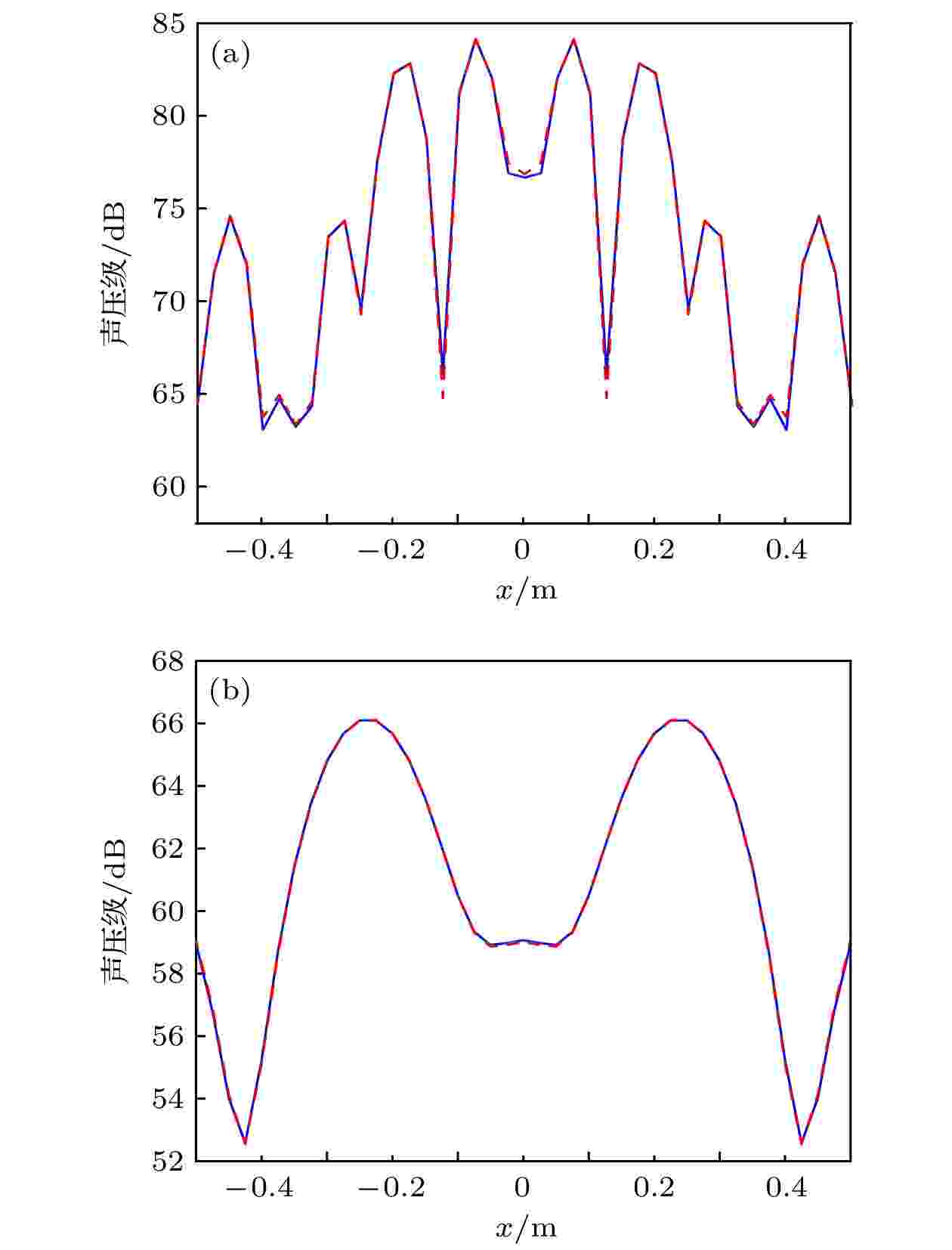 图 5 1000 Hz预报声压切线对比图 (a) 0.005λ; (b) 1.2λ
图 5 1000 Hz预报声压切线对比图 (a) 0.005λ; (b) 1.2λ




 图 6 0.005λ预报距离处的声压误差曲线
图 6 0.005λ预报距离处的声压误差曲线
































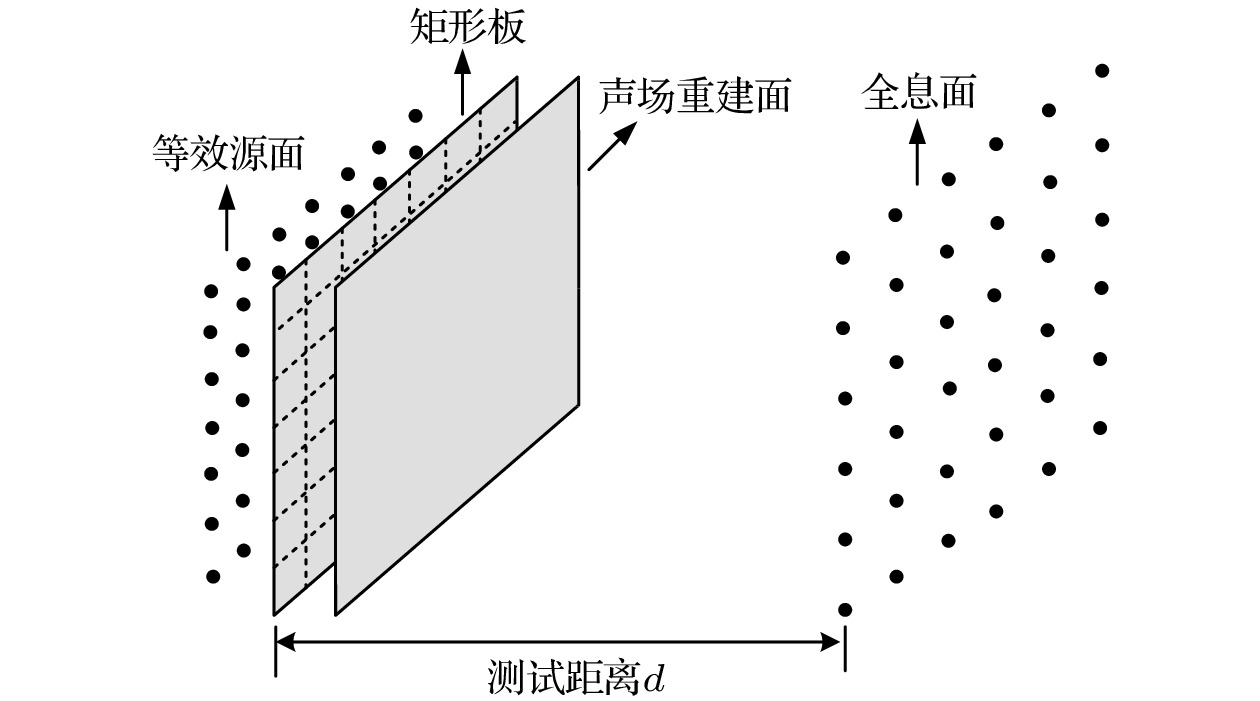 图 7 声场重建示意图
图 7 声场重建示意图

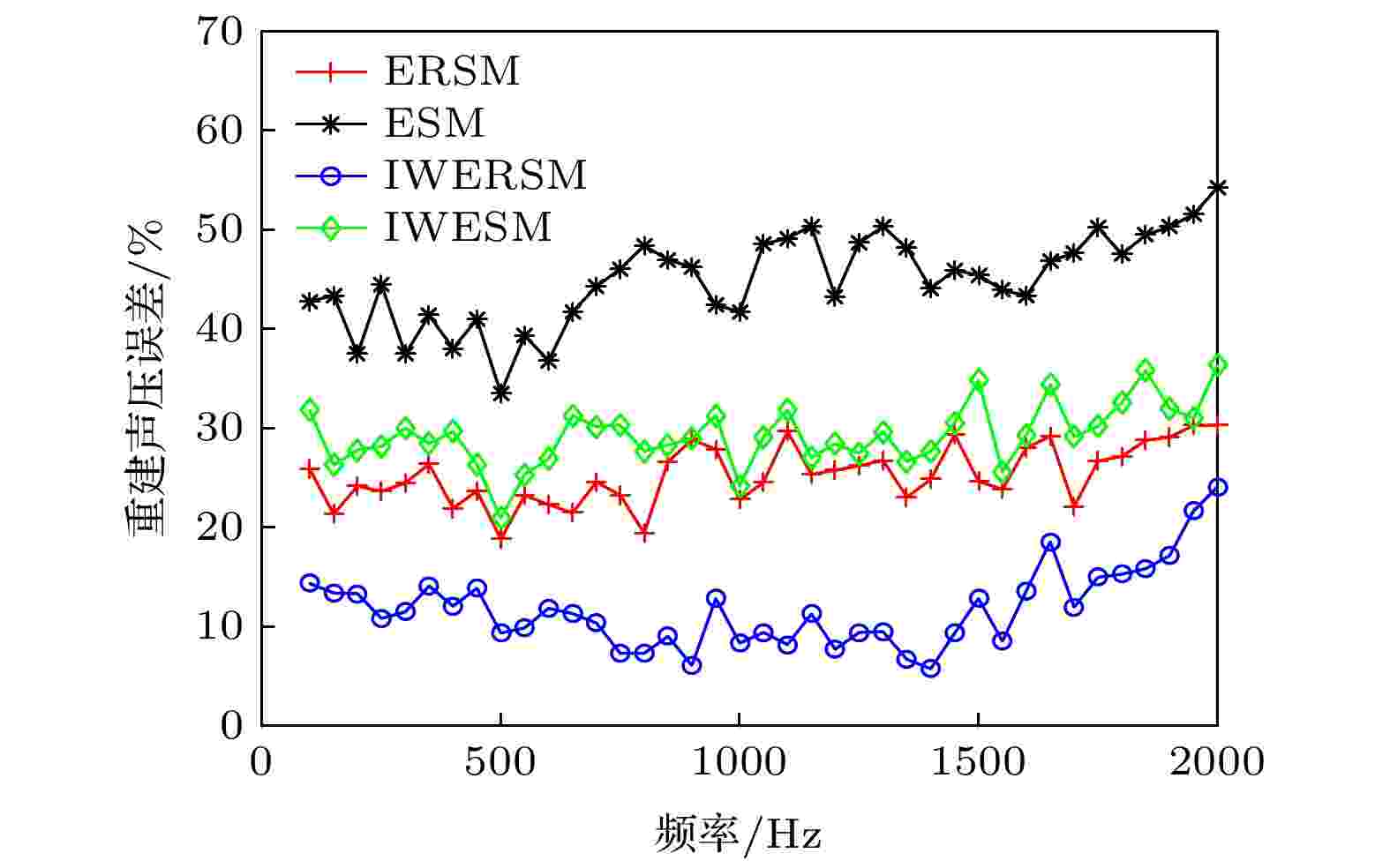 图 8 声场重建误差 (d = 0.5λ)
图 8 声场重建误差 (d = 0.5λ) 图 9 重建声压误差随测试距离变化曲线 (a) 500 Hz; (b) 1000 Hz; (c) 1500 Hz
图 9 重建声压误差随测试距离变化曲线 (a) 500 Hz; (b) 1000 Hz; (c) 1500 Hz




























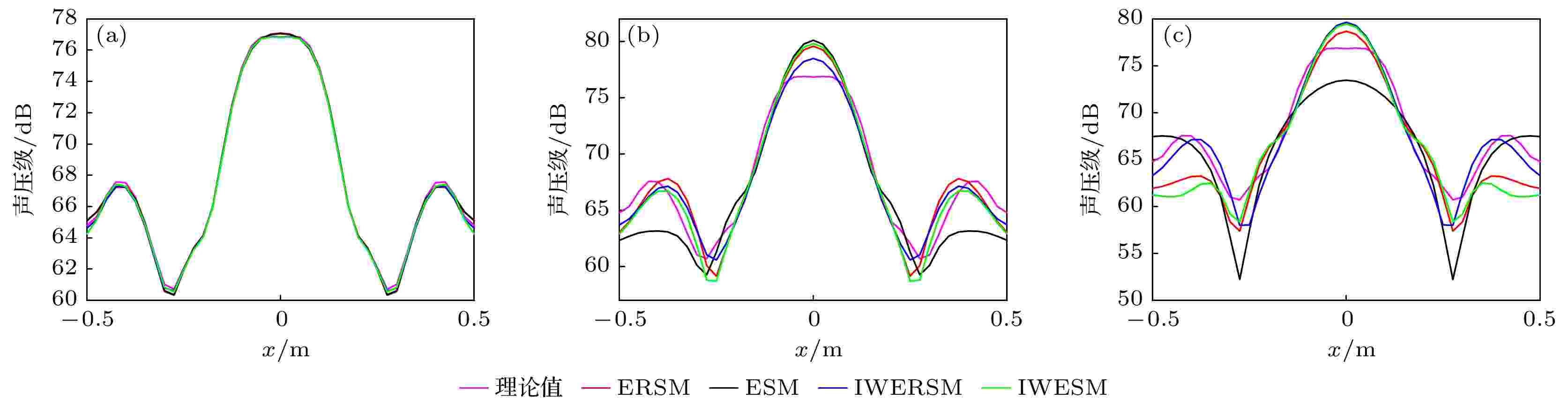 图 10 500 Hz不同测试距离处的重建声压切线 (a)
图 10 500 Hz不同测试距离处的重建声压切线 (a) 










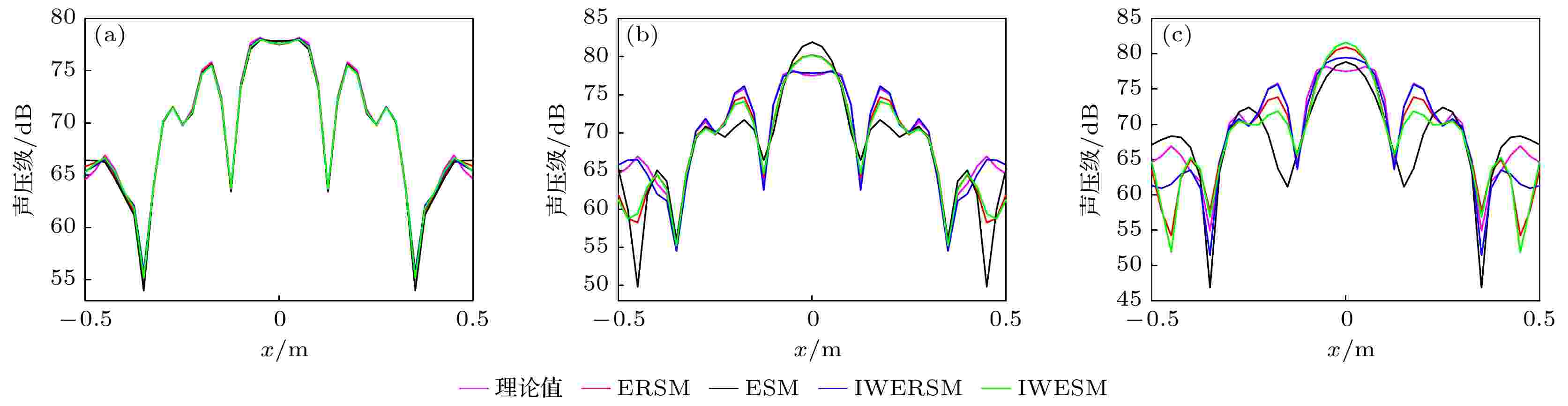 图 11 1000 Hz不同测试距离处的重建声压切线 (a)
图 11 1000 Hz不同测试距离处的重建声压切线 (a) 








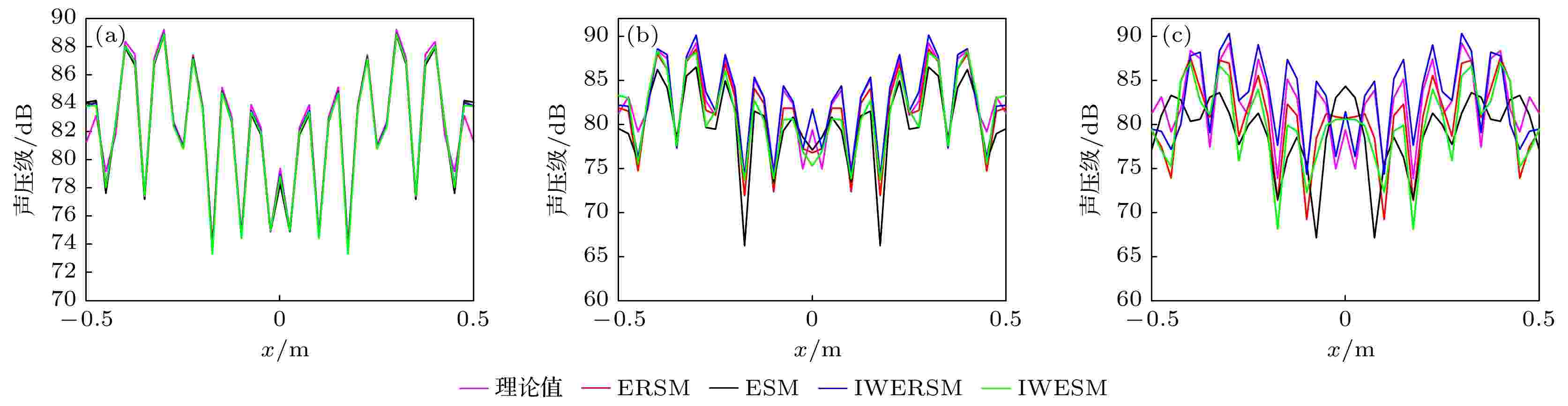 图 12 1500 Hz不同测试距离处的重建声压切线 (a)
图 12 1500 Hz不同测试距离处的重建声压切线 (a) 






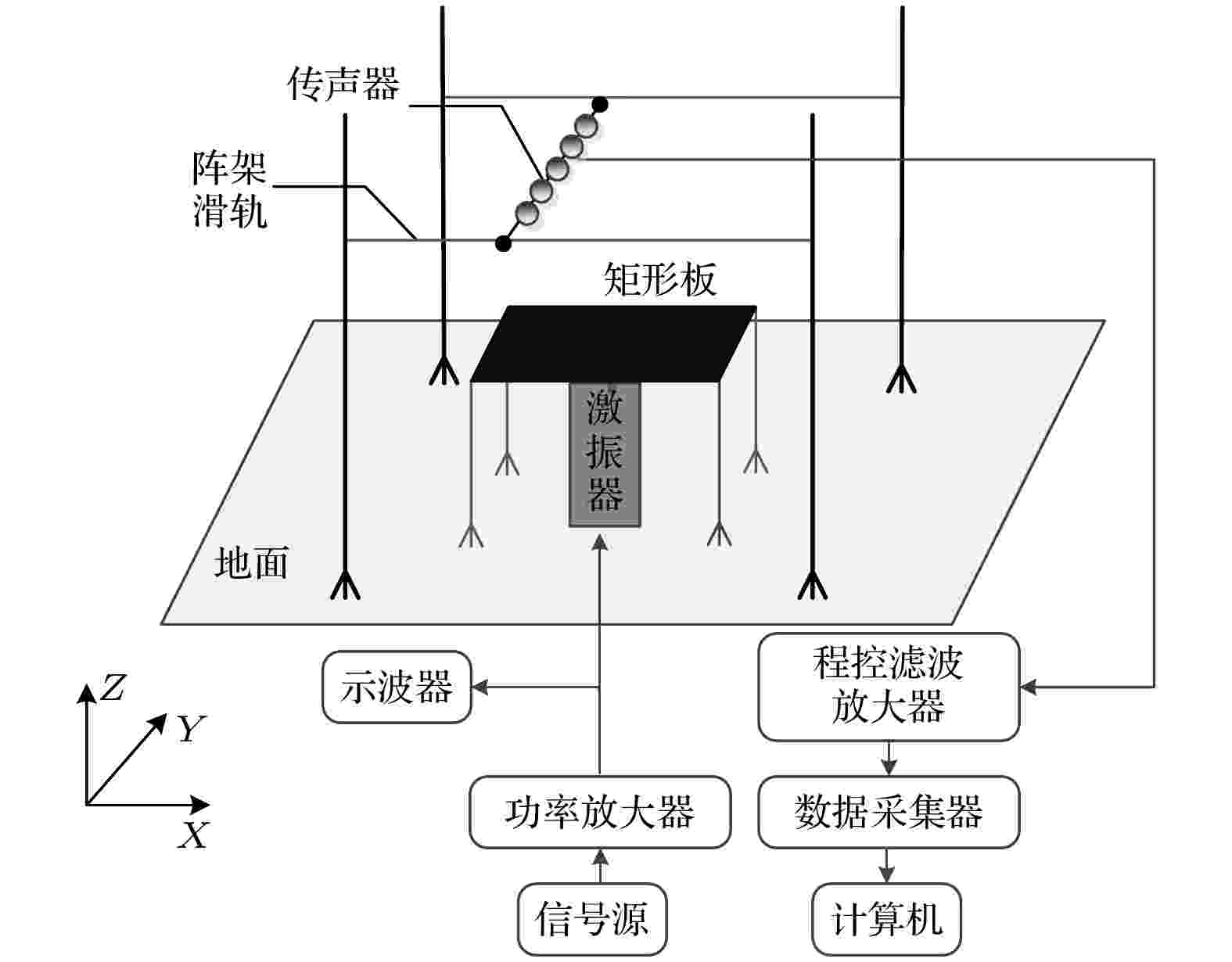 图 13 实验装置连接示意图
图 13 实验装置连接示意图 图 14 实验现场图 (a) 矩形钢板; (b) 传声器阵列
图 14 实验现场图 (a) 矩形钢板; (b) 传声器阵列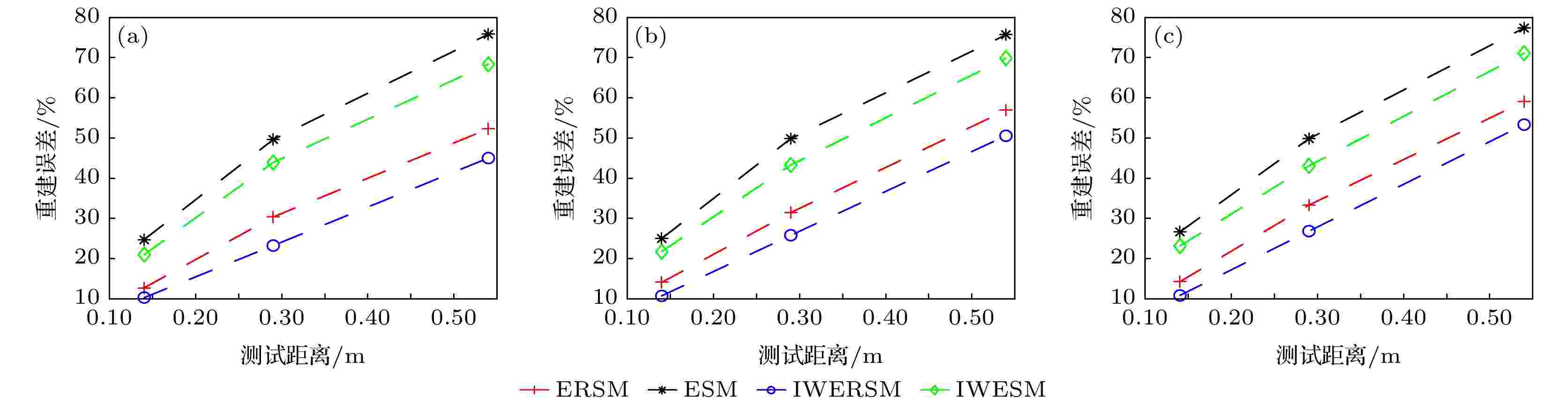 图 15 不同距离处的重建声压误差 (a) 100 Hz; (b) 200 Hz; (c) 400 Hz
图 15 不同距离处的重建声压误差 (a) 100 Hz; (b) 200 Hz; (c) 400 Hz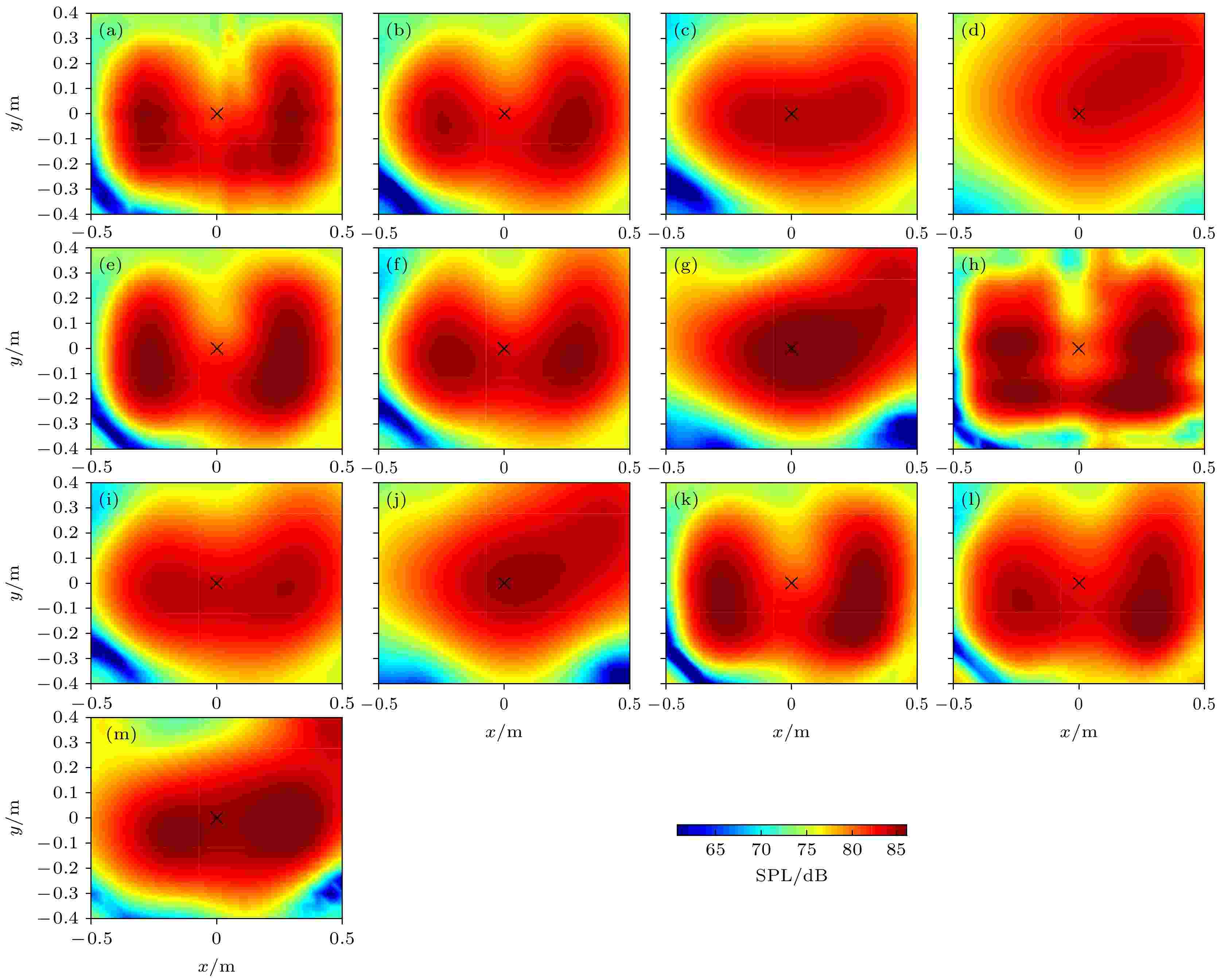 图 16 不同测试距离的实验重建声压(100 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)
图 16 不同测试距离的实验重建声压(100 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)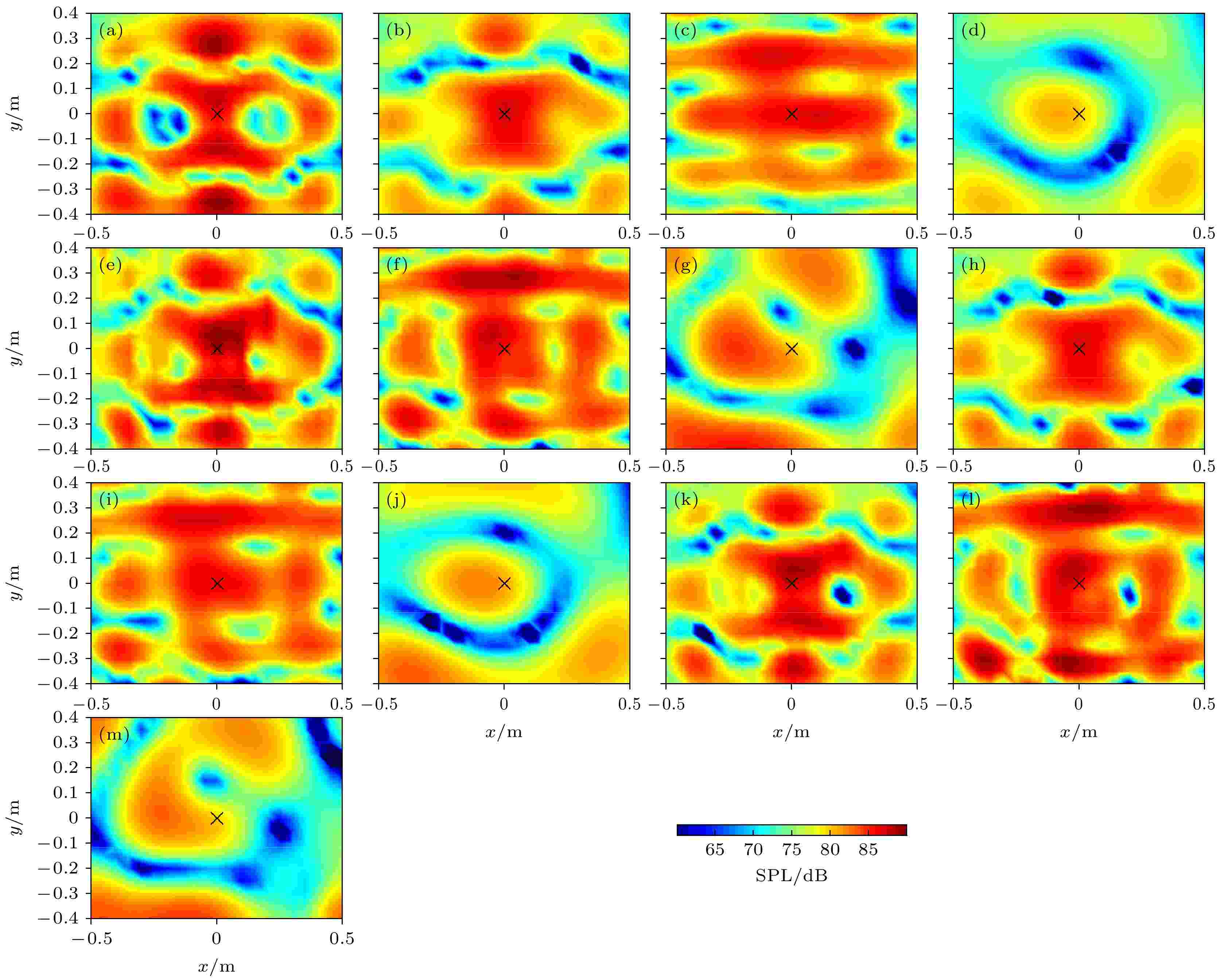 图 18 不同测试距离的实验重建声压(400 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)
图 18 不同测试距离的实验重建声压(400 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m) 图 17 不同测试距离的实验重建声压(200 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)
图 17 不同测试距离的实验重建声压(200 Hz) (a) 理论值; (b) ESM (0.14 m); (c) ESM (0.29 m); (d) ESM (0.54 m); (e) ERSM(0.14 m); (f) ERSM (0.29 m); (g) ERSM (0.54 m); (h) IWESM (0.14 m); (i) IWESM (0.29 m); (j) IWESM (0.54 m); (k) IWERSM(0.14 m); (l) IWERSM (0.29 m); (m) IWERSM (0.54 m)