全文HTML
--> --> -->前人研究限于铝沸石周期骨架里的铷簇或合金铷簇在低温下自发磁化强度和磁化率以及其居里温度的观测, 而对常温或较高温度下的铷元素的孤立自由原子簇的磁矩大小的研究内容还未见报道. 针对这种状况, 在光磁共振吸收光谱分析的基础上, 本文对铷元素三相点(312.41 K)附近的300—328 K温度下孤立自由铷原子簇87Rbn的磁矩进行了深入研究, 通过实验和理论计算分别得到了密闭容器内充有约1333.3 Pa (10 Torr)缓冲气体氮气的饱和铷蒸馏汽样品中含有的孤立原子簇的自发磁矩的具体数值, 并证实其磁矩大小与其含有的5s电子个数n存在的依赖关系; 分析了铷簇磁矩的形成与5s电子自旋排列的相互耦合的相关性. 这些研究内容是进一步探索铷原子簇的物化性能所必需的理论基础, 对于未来多原子分子磁矩的研究具有很重要的推进作用.
2.1.实验过程
近20年作者在测量大量铷蒸馏气体样品中单原子分子87Rb1的朗德因子及其磁矩时, 逐步发现了其他14种簇粒子(87Rb)
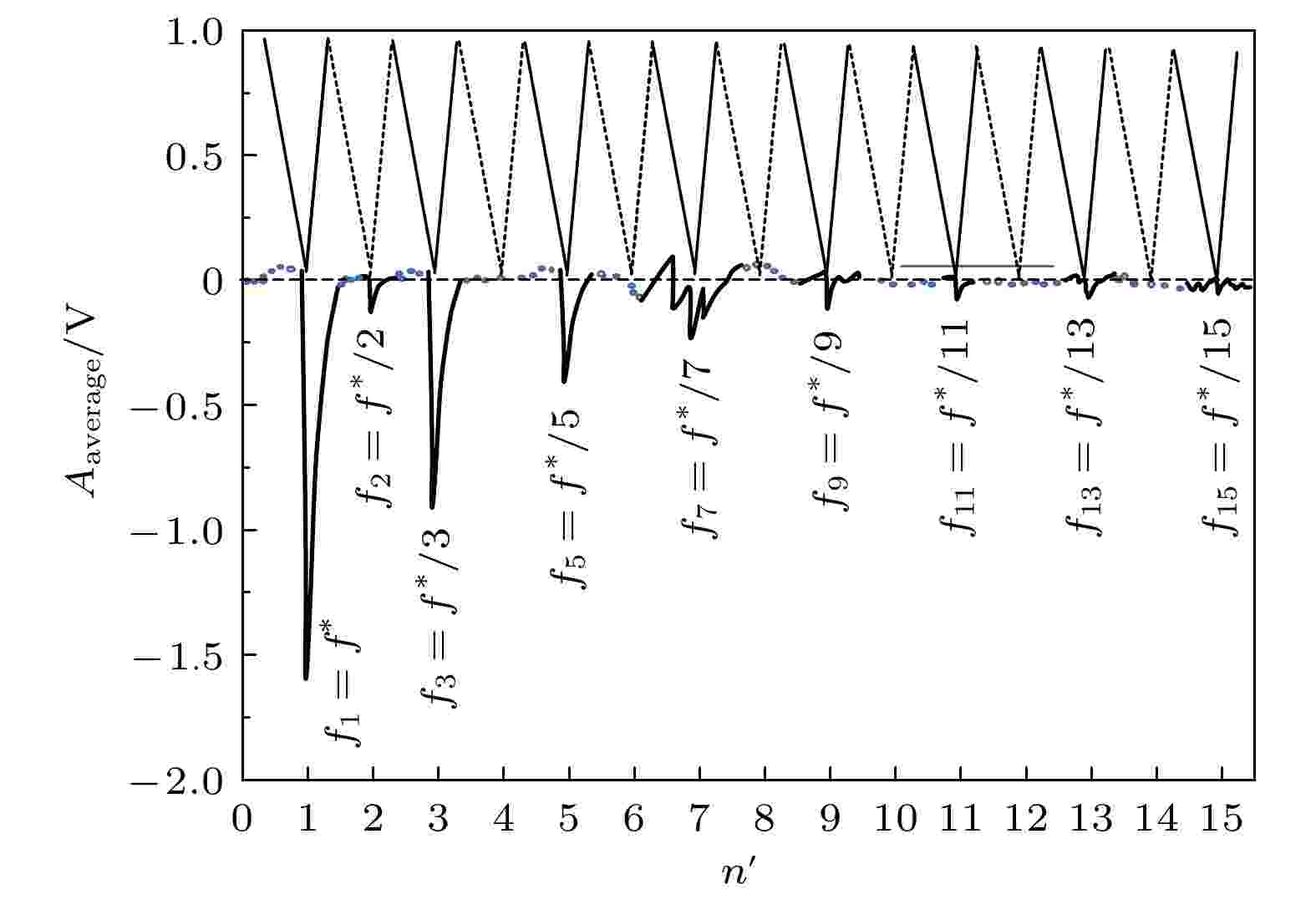 图 1 实验测量的
图 1 实验测量的
Figure1. Schematic illustration of the resonance spectral amplitudes and shape of the 1?15 kinds of Rb cluster particles derived from experiments.
2
2.2.实验现象
对样品进行光磁共振实验检测发现, 固定一水平磁场值, 改变水平磁场方向与扫场及地磁场水平分量方向相同或相反, 两个方向上均能出现除了单原子分子87Rb1一对共振光谱以外的其他相对弱小的14对相似共振光谱. 通过对这些共振光谱信息进行大量采样、比对、分析, 逐渐准确捕捉到了这些共振光谱的频率、振幅大小、形态等特征. 获得了包括87Rb1光谱在内的15对共振光谱振幅形态示意图如图1所示.从图1可以看出光谱规律如下:
1)同一外场下, 除87Rb1以外的14对共振光谱的频率f














2)当










3)当















2
2.3.样品表征
考虑到样品工作温度为300—328 K, 该温度在铷元素三相点314.14 K附近, 而且饱和蒸馏气体中的碱金属铷原子分子经过多次加热与冷却制作过程, 在不可避免的铷原子分子相互碰撞中, 它们会像其他碱金属元素钠、钾一样很容易簇起来[14,15,16]. 相关文献中曾证实在碱金属单原子分子蒸汽中发现含有稳定的双原子分子的现象[14]. 为确定本文所用的单原子分子铷蒸汽样品中含有多原子个数的原子簇粒子, 对本文用的75%样品进行了SEM和TEM检测, 检测结果如图2所示.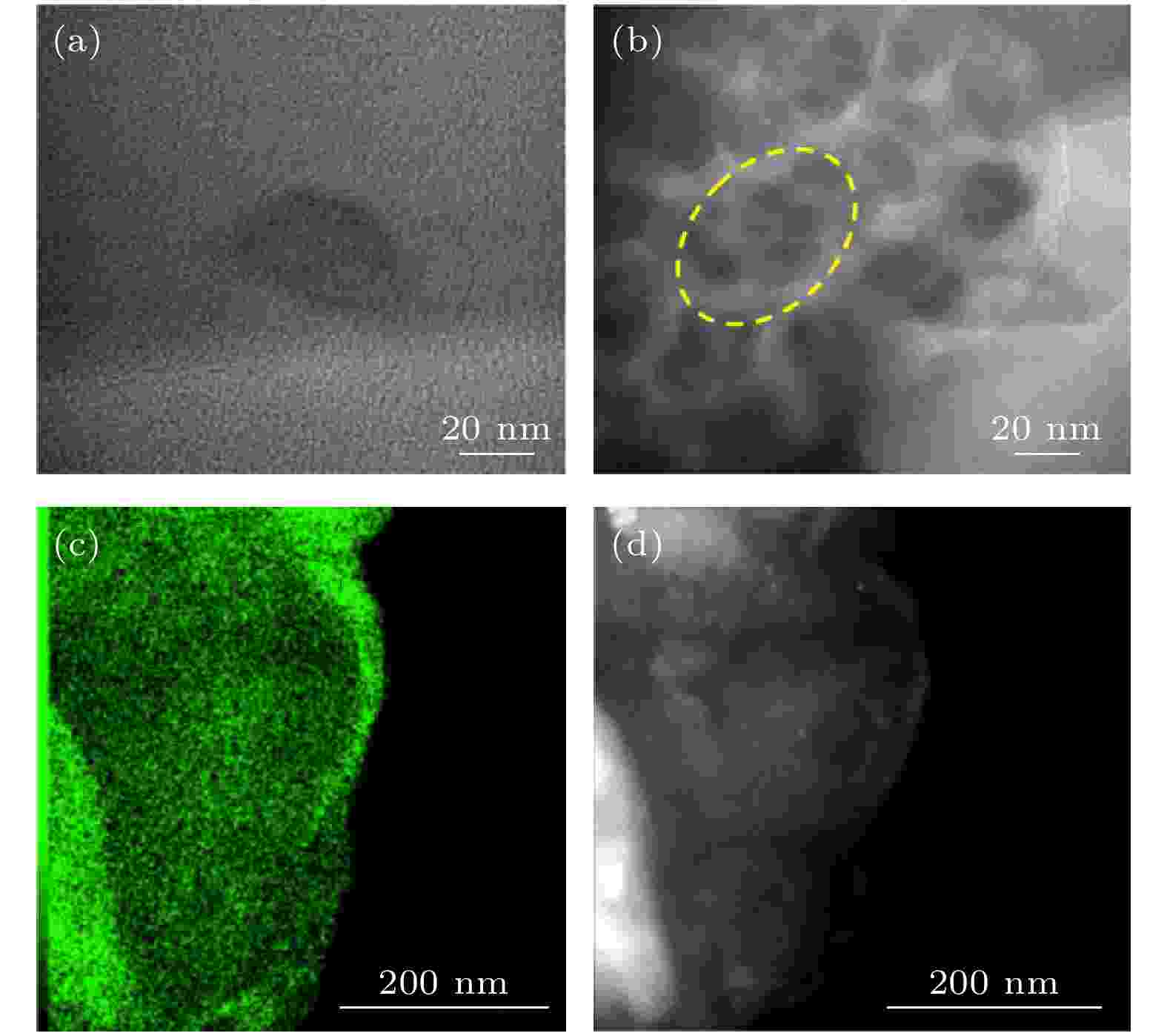 图 2 (a), (b)铷簇颗粒的TEM图片; (c), (d)铷元素分布图
图 2 (a), (b)铷簇颗粒的TEM图片; (c), (d)铷元素分布图Figure2. (a), (b) TEM images of the Rb cluster particles; (c), (d) the distribution of rubidium by EDS mappings.
由文献[17,18]可知, 两个铷原子簇分子的最小核间距为0.495 nm, 依据Na15的结构形状[19], 估算87Rb15簇的直径为2 × 0.495 = 0.99 nm, 约等于1 nm. 图2(a)中的黑色团簇是直径约为20 nm的簇粒子, 估算大约上百个铷原子簇的大小, 图2(b)中黄色圆圈内的黑色团簇是多个直径不等的纳米级粒子, 图2(c)和图2(d)是固态样品中相互对照的实物粒子与铷原子的绿色点状分布图(EDS mapping). 由此可见铷蒸馏气体样品中确实存在簇粒子, 共振光谱图1是铷蒸馏气体含有的多种自由原子簇粒子(87Rb)

3.1.实验数据与结果
用87Rb1, (87Rb)2′, ···, (87Rb)15′符号分别代表实验中测到的包含87Rb1在内

将(2)式与(3)式相加, 并令




























截取补充材料SB, SC, SD中各簇粒子相应的朗德因子、磁矩、振幅的平均值



| ${n'} $为奇数粒子 | ${n'} $ | ${\bar g_{n'}}$ | $\bar \mu {}_{n'}$/μB | ${\bar A_{n'}}$/mV | ${n'} $为偶数粒子 | ${n'} $ | ${\bar g_{n'}}$ | $\bar \mu {}_{n'}$/μB | ${\bar A_{n'}}$/mV | |
| 87Rb1 | 1 | 0.494337 | 0.494337 | 1574.50 | (87Rb)2′ | 2 | 0.246984 | 0.246984 | 105.75 | |
| (87Rb)3′ | 3 | 0.164598 | 0.164598 | 883.07 | (87Rb)4′ | 4 | 0 | 0 | 0 | |
| (87Rb)5′ | 5 | 0.098789 | 0.098789 | 383.47 | (87Rb)6′ | 6 | 0 | 0 | 0 | |
| (87Rb)7′ | 7 | 0.070635 | 0.070635 | 188.70 | (87Rb)8′ | 8 | 0 | 0 | 0 | |
| (87Rb)9′ | 9 | 0.054953 | 0.054953 | 84.92 | (87Rb)10′ | 10 | 0 | 0 | 0 | |
| (87Rb)11′ | 11 | 0.044975 | 0.044975 | 48.62 | (87Rb)12′ | 12 | 0 | 0 | 0 | |
| (87Rb)13′ | 13 | 0.038060 | 0.038060 | 31.55 | (87Rb)14′ | 14 | 0 | 0 | 0 | |
| (87Rb)15′ | 15 | 0.032978 | 0.032978 | 12.63 |
表1实验获得的(87Rb)




Table1.The




再利用补充材料SB中表SB1—SB8和补充材料SC中表SC1的

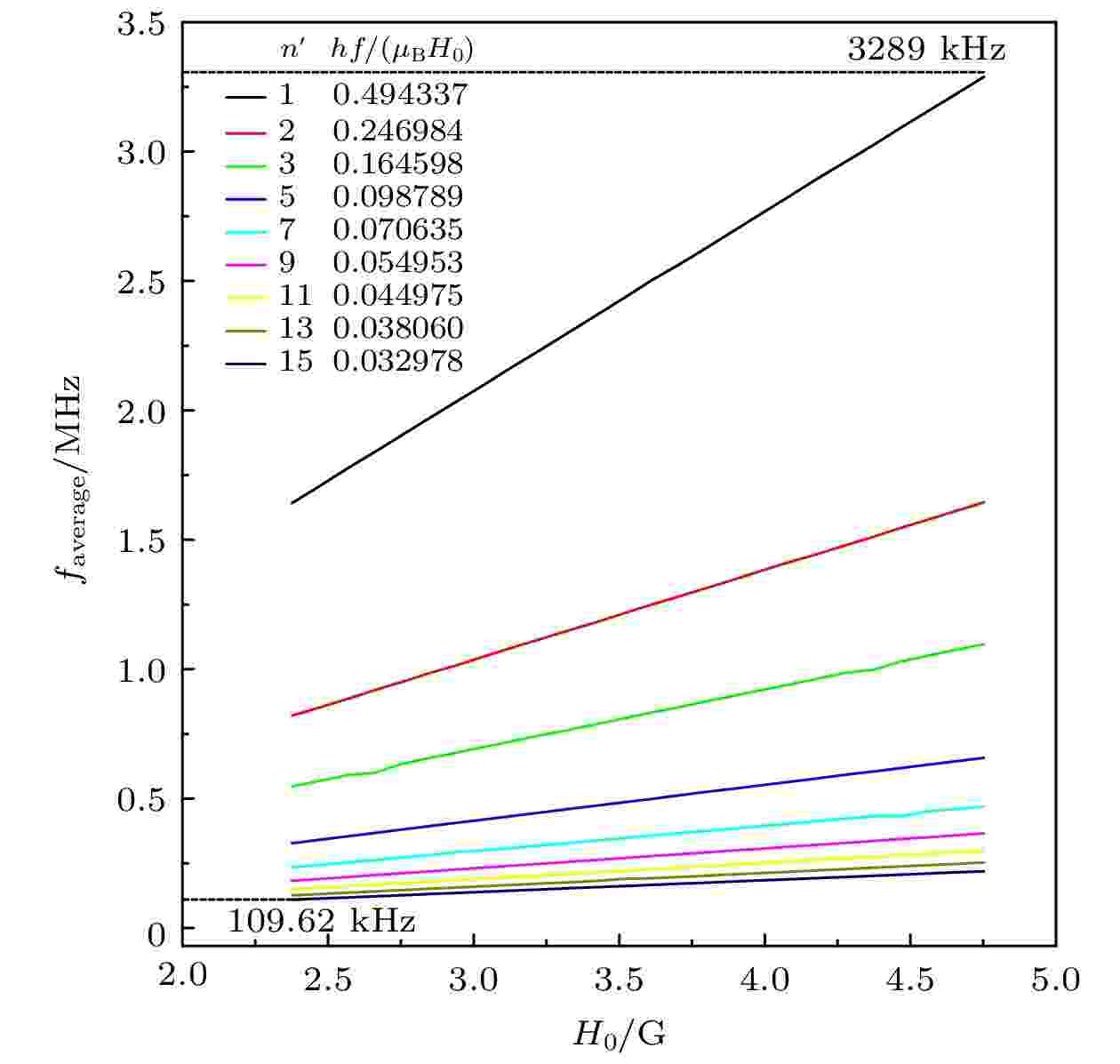 图 3 实验测得的 (87Rb)
图 3 实验测得的 (87Rb)


Figure3. Magnetic field strength H0 dependence of resonance frequency



2
3.2.实验结果与讨论
由图3可以看出, 9种簇粒子的共振频率





实验获得的

















因



















实验还证明了, 对于本文中磁矩值不为0的除87Rb1以外的8种簇粒子, 其由稳定分子态跃迁到相邻塞曼能级时, 一定产生了簇粒子解离成单原子的现象[14,22], 才能在光磁共振检测中看到图1所示的因共振吸收射频子后又吸收单原子光谱7948 ?的D1σ+光的共振光谱.
在铷蒸汽中的簇粒子是属于大核间距的簇分子, 基态或最低激发态的簇分子内的原子之间只有介于金属键与范德瓦耳斯键力之间的作用力[14,22], 限于范德瓦耳斯力使其势能曲线在颇大核间距上有一个很小的极小值, 这些簇分子也叫范德瓦耳斯分子, 在328 K左右, 当kT (0.028 eV)近于离解热(87Rb2离解热最大为0.49 eV)小于3.5 eV[14,22], 在低气压(P (1333.3 Pa) 小于0.02个大气压)条件下, 热碰撞就可能使簇分子离解成单原子. 因此在本实验中, 具有跃迁概率组元不为0的簇分子, 在原子光谱7948 ?的D1σ+光辐照下, 由稳定的簇分子态吸收射频能量后, 跃迁到簇分子的相邻塞曼能级的分子态. 因为对于一个簇分子能检测出的稳定态很稀少[14], 跃迁后的这个相邻塞曼子能级的分子态或是不稳定预离解态或是在激发到这个稳定态的过程中, 由于D1σ+原子光谱的辐照或多体碰撞, 如I2, Hg2一样由于原子光谱辐照而解离为I, Hg单原子, 铷簇分子同样地解离为87Rb1原子, 从而使解离后的单原子吸收了7948 ? 的D1σ+原子光谱, 发生了簇分子的塞曼跃迁共振解离为原子而原子又吸收原子光谱的现象[14]. 但

本文依据表1中(87Rb)





4.1.各簇分子的核间距大小及Hund耦合属性的判断
根据相关文献估算


2
4.2.87Rbn–1 + 87Rb1原子簇分子的电子组态和项型构建及其稳定性的判断
本研究引用Nan + Na1原子簇构建模式[19], 即用87Rbn = 87Rbn–1 + 87Rb1逐一添加一个原子构建原子簇的模式, 构造出原子数逐渐增多、化学意义上的2—15个原子组成的87Rbn的14个簇分子. 在每个簇分子中含有由原子的原子核和核外KLMNspd的闭壳层电子组建成的封闭的大分子实, 即不论由几个原子形成的团簇, 它们都可以粗略地看成由不同个封闭的原子实凑近构成封闭的大分子实, 大分子实外开壳价电子在5s与4d壳层或更高层发生分子轨态顺序重排(也就是通常所说的5s与4d轨道杂化), 这些价电子不再属于某一个固定原子, 而是按着大核间距大壳层分子的泡利原理原则, 尽可能优先填入能量最低的分子轨态.用一个新的视角去看原子簇分子, 将其看作是由双分子构成的簇分子即87Rbn = 87Rbn–1 + 87Rb1. 再将双分子87Rbn–1 + 87Rb1簇比照双原子分子; 用双分子87Rbn–1 + 87Rb1的分子实中心连线轴即87Rbn–1的分子实中心与87Rb1的核心连线(以后称作实间轴, a spindle connecting the real centers of two molecules), 比照双原子分子的核间轴; 再用双分子87Rbn–1 + 87Rb1的任一价电子i的轨道角动量在分子实中心连线轴上的分量量子数





















按照分子轨态方法[14], 参考文献[14]中的表29、表33、表34以及图157界定相关条件, 并结合具体簇分子的核间距大小和Hund(a)情形, 写出了表2中87Rbn的大壳层双原子分子的各簇分子基态电子组态和分子态项型. 并按着只将基态中一个电子跃迁到较高轨态的Hund(a)情形的激发原则, 即遵从





| 团簇分子, 参考分子 | 基态电子组态和分子态及$ {\lambda }_{\text{合}}$和S | 最低激发电子组态及其$ {\lambda }_{\text{合}}$和S (Hund(a) 情形跃迁规则$\Delta \lambda =0, \pm 1$, $g\;\, \leftrightarrow u$, $ \Delta n = 0, \;\; \pm 1, ~\Delta S = 0$ | 基态X与最低激发态A 稳定性比较${P_{\rm{a}}} - {P_{\rm{b}}}$ |
| 87Rb1 | $ {\rm{KLMN}}_{\rm{spd}}(\sigma {}_{\rm{g}}\rm{5}\rm{s})$ ${}^2{\Sigma _{\rm{u} } },$${\lambda }_{\text{合} }=0,$$S = 1/2$ | $ {\rm{KLMN}}_{\rm{spd}}({\text{π}}{}_{\rm{u}}{4}{\rm{d}})$ ${}^2{\Pi _{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1/2$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1/2$ |
| 87Rb2 85Rb2[14] | ${({\rm{\sigma } }{}_{\rm{g} }5{\rm{s} })^2},$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$ ${\lambda }_{\text{合} }=0,$$S = {{0}}$或 [${\rm{(\sigma } }{}_{\rm{g} }{\rm{5s} })({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} } ,$ ${}^3{ {\Sigma } }_{\rm{u} }^{ + },$${\lambda }_{\text{合} }=0 ,$$S = {{1}}$] | ${\rm{(\sigma }}{}_{\rm{g}}{\rm{5 s}})({{\text{π}}_{\rm{u}}}{\rm{4 d)}},$ ${}^1{{\Pi}_{\rm{u}}},$$ {\lambda }_{\text{合}}=1,$$S = {{0}}$或 [${\rm{(\sigma } }{}_{\rm{u} }{\rm{5s} })({ {\text{π} }_{\rm{u} } }{\rm{4 d)} },$${}^3{{\Pi}_{\rm{g}}},$${\lambda }_{\text{合} }=1,$$S = {{1}}$] | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 1 - 0 = 1$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = 1 - 0 = 1$ [X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1/2 - 1/2 = { {0} }$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1/2 - 1/2 = { {0} }$] |
| 87Rb3 | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s} })^{ {2} } }({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} } ,$ ${}^2{{\Sigma } }_{\rm{u} }^ +,$${\lambda }_{\text{合} }=0,$$S = 1/2$ | ${\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)(} }{ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)(} }{ {\text{π} }_{\rm{u} } }{\rm{4 d)} },$ ${}^2{ {\Pi}_{\rm{g} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1 - 1/2 = 1/2$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1 - 1/2 = 1/2$ |
| 87Rb4 | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s)} }^{ {2} } }{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^{ {2} } },$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = {{0}}$ | ${\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)(} }{ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s} }{ {\rm{)} }^{ {2} } }{\rm{(\pi } }{}_{\rm{u} }{\rm{4 d)} },$ ${}^1{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = {{0}}$ | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 1 - 1 = 0$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = 1 - 1 = 0$ |
| 87Rb5 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} } ,$ ${}^2{{\Sigma } }_{\rm{g} }^ + ,$${\lambda }_{\text{合} }=0,$$S = 1/2$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^1},$ ${}^2{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1\frac{1}{2} - 1 = 1/2$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 1\frac{1}{2} - 1 = 1/2$ |
| 87Rb6 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2},$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = {{0}}$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)(} }{ {\text{π} }_{\rm{u} } }{\rm{4 d)} },$ ${}^1{ {\Pi}_{\rm{u} } } ,$${\lambda }_{\text{合} }=1,$$S = {{0}}$ | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 2 - 1 = 1$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = 2 - 1 = 1$ |
| 87Rb7 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}({ {\text{π} }_{\rm{u} } }{\rm{4 d)} },$ ${}^2{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^1}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^2} ,$ ${}^2{ {\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = 1/2$; ${}^2{ { {\Delta } }_{\rm{g} } },$ ${\lambda }_{\text{合} }=2, S =1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 2\frac{1}{2} - 1 = 1\frac{1}{2}$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 2\frac{1}{2} - 1 = 1\frac{1}{2}$ |
| 87Rb8 | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^2},$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = {{0}}$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^1}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^3},$ ${}^1{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = {{0}}$ | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 3 - 1 = 2$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = 3 - 1 = 2$ |
| 87Rb9 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^3},$ ${}^2{ {\Pi}_{\rm{u} } } ,$${\lambda }_{\text{合} }=1,$$S = 1/2$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^1}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4},$ ${}^2{{\Sigma } }_{\rm{g} }^ + ,$${\lambda }_{\text{合} }=0,$$S = 1/2$; ${}^2{ { {\Delta } }_{\rm{g} } },$ ${\lambda }_{\text{合} }=2, S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 3\frac{1}{2} - 1 = 2\frac{1}{2}$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 3\frac{1}{2} - 1 = 2\frac{1}{2}$ |
| 87Rb10 | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4},$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = {{0}}$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^1}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^1},$ ${}^1{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = {{0}}$ | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 4 - 1 = 3$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = {\rm{4 - 1}} = {\rm{3}}$ |
| 87Rb11 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^1},$ ${}^2{ {\Pi}_{\rm{g} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^1}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^2},$ ${}^2{{\Sigma } }_{\rm{u} }^ + ,$${\lambda }_{\text{合} }=0,$$S = 1/2$; ${}^2{ { {\Delta } }_{\rm{g} } },$${\lambda }_{\text{合} }=2,$ $S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 4 - 1\frac{1}{2} = 2\frac{1}{2}$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 4 - 1\frac{1}{2} = 2\frac{1}{2}$ |
| 87Rb12 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^2} ,$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = {{0}}$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^1}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^3},$ ${}^1{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = {{0}}$ | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 4 - 2 = 2$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = {\rm{4 - 2}} = {{2}}$ |
| 87Rb13 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^3},$ ${}^2{ {\Pi}_{\rm{g} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^1}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^4},$ ${}^2{ {\Pi}_{\rm{u} } } ,$${\lambda }_{\text{合} }=1,$$S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 4 - 2\frac{1}{2} = 1\frac{1}{2}$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 4 - 2\frac{1}{2} = 1\frac{1}{2}$ |
| 87Rb14 | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^4},$ ${}^1{{\Sigma } }_{\rm{g} }^ +,$${\lambda }_{\text{合} }=0,$$S = {{0}}$ | ${ {\rm{(\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^3} ({ {\rm{\sigma } }_{\rm{u} } }{\rm{4 d)} },$ ${}^1{ {\Pi}_{\rm{u} } },$${\lambda }_{\text{合} }=1,$$S = {{0}}$ | X: ${P_{\rm{a}}} - {P_{\rm{b}}} = 4 - 3 = 1$ A: ${P_{\rm{a}}} - {P_{\rm{b}}} = 4 - 3 = 1$ |
| 87Rb15 | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^4}({ {\rm{\sigma } }_{\rm{u} } }{\rm{4 d)} },$ ${}^2{{\Sigma } }_{\rm{u} }^ +,$${\lambda }_{\text{合} }=0,$$S = 1/2$ | ${({\rm{\sigma } }{}_{\rm{g} }{\rm{5 s} })^2}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{5 s)} }^2}{({ {\rm{\sigma } }_{\rm{g} } }{\rm{4 d)} }^2}{({ {\text{π} }_{\rm{u} } }{\rm{4 d)} }^4}{({ {\text{π} }_{\rm{g} } }{\rm{4 d)} }^3}{({ {\rm{\sigma } }_{\rm{u} } }{\rm{4 d)} }^2},$${}^2{ {\Pi}_{\rm{g} } },$${\lambda }_{\text{合} }=1,$$S = 1/2$ | X: ${P_{\rm{a} } } - {P_{\rm{b} } } = 4-3\frac{1}{2} = \frac{1}{2}$ A: ${P_{\rm{a} } } - {P_{\rm{b} } } = 4-3\frac{1}{2} = \frac{1}{2}$ |
| 注: 表中电子组态仅87Rb1的基态和激发态标出了闭壳层KLMNspd, 其他粒子没有重复标出闭壳层KLMNspd. | |||
表215种原子簇分子87Rbn的基态和最低激发态的电子组态和分子态项型表
Table2.Electron configuration and molecular state of the ground state and the lowest excited state of 15 kinds of cluster particles 87Rbn.
2
4.3.簇分子的项态结果与讨论
从表2各簇分子的项态可知:1)稳定性: 表2中15种分子的各自相应的基态X与最低激发态A的





2)简并性:










3)磁性: 对于有磁性的


































4)塞曼效应可见性: 对于






2
4.4.簇分子平均磁矩的公式计算
将双原子分子在磁场H0(z)方向上的磁矩分量的平均值











































| n为奇数 的簇分子 | n为奇数的 分子项 | 5s价电子 个数 | $\bar \mu {}_n$/μB | ${\bar g_n}$ | n为偶数 的簇分子 | n为偶数的 分子项 | 5s价电 子个数 | $\bar \mu {}_n$/μB | ${\bar g_n}$ | |
| 87Rb1 | ${}^2{\Pi _{\rm{u}}}$ | 1 | $1/2$ | $1/2$ | 87Rb2 | ${}^2{\Pi _{\rm{g}}}$ | 2 | $1/4$ | $1/4$ | |
| 87Rb3 | ${}^2{\Pi _{\rm{g}}}$ | 3 | $1/6$ | $1/6$ | 87Rb4 | ${}^2{\Pi _{\rm{u}}}$ | 4 | 0 | 0 | |
| 87Rb5 | ${}^2{\Pi _{\rm{u}}}$ | 5 | $1/10$ | $1/10$ | 87Rb6 | ${}^2{\Pi _{\rm{u}}}$ | 6 | 0 | 0 | |
| 87Rb7 | ${}^2{\Pi _{\rm{u}}}$ | 7 | $1/14$ | $1/14$ | 87Rb8 | ${}^1{\Pi _{\rm{u}}}$ | 8 | 0 | 0 | |
| 87Rb9 | ${}^2{\Pi _{\rm{u}}}$ | 9 | $1/18$ | $1/18$ | 87Rb10 | ${}^2{\Pi _{\rm{u}}}$ | 10 | 0 | 0 | |
| 87Rb11 | ${}^2{\Pi _{\rm{g}}}$ | 11 | $1/22$ | $1/22$ | 87Rb12 | ${}^2{\Pi _{\rm{u}}}$ | 12 | 0 | 0 | |
| 87Rb13 | ${}^2{\Pi _{\rm{g}}}$ | 13 | $1/26$ | $1/26$ | 87Rb14 | ${}^2{\Pi _{\rm{u}}}$ | 14 | 0 | 0 | |
| 87Rb15 | ${}^2{\Pi _{\rm{g}}}$ | 15 | $1/30$ | $1/30$ |
表387Rbn簇的磁距


Table3.Theoretical calculation results of


2
4.5.各原子簇分子的共振光谱振幅值理论评估
粗略认为所有簇粒子共振光谱的平均振幅





| 团簇 87Rbn | n | $\bar \mu {}_n$/μB | 团簇 (87Rb)${}_{n'} $ | $n'$ | $\bar \mu {}_{n'}$/μB | 磁矩的相对误差% | ${\bar A_{n'} }$/mV | ${\bar A_{n'}}$与${\bar A_n}$ 比较 |
| 87Rb1 | 1 | $1/2$ | 87Rb1 | 1 | 0.494337 | 1.1326 | 1574.50 | 一致 |
| 87Rb2 | 2 | $1/4$ | (87Rb)2′ | 2 | 0.246984 | 1.2063 | 105.75 | 线性分子简并态 |
| 87Rb3 | 3 | $1/6$ | (87Rb)3′ | 3 | 0.164598 | 1.2411 | 883.07 | 一致 |
| 87Rb4 | 4 | 0 | (87Rb)4′ | 4 | 0 | 0 | 0 | 0 |
| 87Rb5 | 5 | $1/10$ | (87Rb)5′ | 5 | 0.098789 | 1.2110 | 383.47 | 一致 |
| 87Rb6 | 6 | 0 | (87Rb)6′ | 6 | 0 | 0 | 0 | 0 |
| 87Rb7 | 7 | $1/14$ | (87Rb)7′ | 7 | 0.070635 | 1.1042 | 188.70 | 一致 |
| 87Rb8 | 8 | 0 | (87Rb)8′ | 8 | 0 | 0 | 0 | 0 |
| 87Rb9 | 9 | $1/18$ | (87Rb)9′ | 9 | 0.054953 | 1.0843 | 84.92 | 一致 |
| 87Rb10 | 10 | 0 | (87Rb)10′ | 10 | 0 | 0 | 0 | 0 |
| 87Rb11 | 11 | $1/22$ | (87Rb)11′ | 11 | 0.044975 | 1.0556 | 48.62 | 一致 |
| 87Rb12 | 12 | 0 | (87Rb)12′ | 12 | 0 | 0 | 0 | 0 |
| 87Rb13 | 13 | $1/26$ | (87Rb)13′ | 13 | 0.038060 | 1.0467 | 31.55 | 一致 |
| 87Rb14 | 14 | 0 | (87Rb)14′ | 14 | 0 | 0 | 0 | 0 |
| 87Rb15 | 15 | $1/30$ | (87Rb)15′ | 15 | 0.032978 | 1.0658 | 12.63 | 一致 |
| 15种簇粒子(87Rb)${}_{n'} $与87Rbn的磁矩相对误差均值为: 0.6765% | ||||||||
| 9种磁矩不为0的簇粒子(87Rb)${}_{n'} $与87Rbn的磁矩相对误差均值为: 1.1275% | ||||||||
表487Rbn与 (87Rb)

Table4.Comparison of average magnetic moment and amplitude of 87Rbn and (87Rb)

由表4可以看出, 当n =

















基于分子轨态法理论分析和计算得到了87Rbn的朗德因子值







当n =



















