摘要: 利用双色双光子阿秒干涉光谱可以在阿秒量级上精确测量光电子从原子、分子以及固体中的电离时间, 为人们理解激光辅助单光子电离中的光电子超快发射过程提供了前所未有的推动作用. 理解光电子发射时间依赖于物理模型, 而目前的模型在预测光电子发射时间上有很大的偏差. 于是, 本文对之前的程函近似模型进行了改进. 与之前的程函近似模型相比, 本文模型使用了更准确的末态波函数, 并且在计算光电子传播过程中累积的相位时, 更准确地计算了光电子轨迹, 因而可以更准确地预测光电子发射时间. 对比得到的数值模拟结果表明, 改进后的程函近似模型比以前的理论模型更加接近含时薛定谔方程的结果, 加深了我们对光电子发射超快过程的理解.
关键词: 双色双光子 /
阿秒干涉 /
含时薛定谔方程 /
程函近似模型 English Abstract An eikonal approximation model for two-color two-photon attosecond interferometric spectrum Tu Qian Chen You-Long Liu Kai Wang Feng Zhang Xiao-Fan Yang Yi Tang Fu-Ming Liao Qing Hubei Key Laboratory of Optical Information and Pattern Recognition, Wuhan Institute of Technology, Wuhan 430205, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11674257, 11604248, 11874019, 11947096, 11904269), the President’s Fund of Wuhan Institute of Technology, China, the Program for Distinguished Middle-aged and Young Innovative Research Team in Higher Education of Hubei Province, China (Grant No. T201806), and the Natural Science Foundation of Hubei Province, China (Grant No. 2020CFA082)Received Date: 27 October 2020Accepted Date: 29 December 2020Available Online: 20 May 2021Published Online: 05 June 2021Abstract: The emission time of photoelectrons from atoms, molecules and solids can be accurately measured on an attosecond scale by using two-color two-photon attosecond interferometric spectroscopy, which helps us to understand the ultrafast electronic dynamics in laser-assisted single photoionization. Understanding the photoelectron emission time depends on the physical model, and the relevant theoretical model provides a better physical explanation and numerical prediction for the photoemission time delay. Although the numerical solution of the time-dependent Schr?dinger equation can accurately predict the photoelectron emission time, but it cannot provide a physical explanation. Although some other current theoretical models can provide a more reasonable corresponding physical process, the quantitative prediction of the photoemission time delay has a large deviation. Therefore, we improve the exisating eikonal approximation model. Comparing with the existing eikonal approximation model, we use a more accurate final state wave function and calculate the photoelectron trajectory more accurately when calculating the phase accumulated in the photoelectron propagation process, so we can predict the photoemission time delay more accurately. By comparing our numerical simulation results, we find that when the final kinetic energy of photoelectron is low, the calculated results from the existing theoretical model are greatly different from those from the time-dependent Schr?dinger equation, reaching tens of attoseconds. The resultsfrom the existing theoretical model are closer to those from the time-dependent Schr?dinger equation with the increase of final kinetic energy of photoelectron. However, no matter what the final kinetic energy of the photoelectron is, the difference between the calculation result from the improved eikonal approximation model and that from the time-dependent Schr?dinger equation is always very small. Therefore, our improved eikonal approximation model is closer to the results from the time-dependent Schr?dinger equation than the existing theoretical model, which greatly deeps our understanding of the ultra-fast process of photoelectron emission.Keywords: two-color two-photon /attosecond interference /time-dependent Schr?dinger equation /eikonal approximation model 全文HTML --> --> --> 1.引 言 从高次谐波中获得阿秒脉冲的时间特性是阿秒脉冲应用中的一个重要问题. Paul等[1 ] 和Muller[2 ] 利用双光子干涉的阿秒拍频重构法(reconstruction of attosecond beating by interference of two-photon transitions, RABITT)第一次获得了阿秒脉冲的时间特性. RABITT利用了泵浦探测原理来探索光电子超快动力学过程. 泵浦光为极紫外(extreme ultraviolet, XUV)阿秒脉冲, 探测光为红外(infrared, IR)脉冲, 基态的电子可以通过吸收不同能量的XUV光子而发生电离, 形成一系列主峰, 接着吸收或放出一个IR光子, 这两种通道由于具有相同的能量会发生干涉, 从而在相邻两个主峰之间形成边带峰(sideband, SB). SB光电子信号会随着XUV脉冲与IR脉冲之间的延时周期性振荡, 通过这种振荡就可以提取出光电子发射时间[1 ,3 ] .[4 -6 ] 、分子[7 ,8 ] 以及固体[9 -12 ] 中的发射时间, 为人们认识光电子超快动力学过程起到了很好的推动作用. 相关理论模型为光电子发射时间提供了较好的物理解释和数值预测. 通过数值求解含时薛定谔方程(time-dependent Schr?dinger equation, TDSE)[13 -15 ] 虽然可以准确预测光电子发射时间, 但是不能提供物理解释. 其他一些理论模型[3 ,16 ,17 ] 虽然可以提供比较合理的对应物理过程, 但是对光电子发射时间的定量预测偏差很大. 本文对之前的程函近似(eikonal approximation, EA)模型做出了大幅度改进, 对光电子发射时间随激光波长的变化做了一个系统的数值模拟, 与其他理论模型相比, 在定量预测上得到了明显的提高, 加深了我们对激光辅助单光子电离过程的物理理解.ω 为基频的高次谐波, 相邻谐波之间相差2ω . 当XUV脉冲作用到氢原子上时, 处于基态的电子会吸收一个XUV光子而发生电离, 形成一系列主峰, 再与IR脉冲作用, 吸收或放出一个IR光子并发生干涉, 相邻主峰之间就会出现SB峰. 本文就是对这些SB峰的光电子发射时间延迟进行数值计算.2.理论模型 22.1.数值求解含时薛定谔方程 2.1.数值求解含时薛定谔方程 量子力学中描述粒子或系统的状态都是用波函数表示的, 波函数满足含时薛定谔方程:H 表示系统的哈密顿量. 如果带电粒子受到外加电场的影响, 则完整的哈密顿量可表示为(除非特殊说明, 本文始终使用原子单位)P E $ V\left({{r}}\right) $ 表示库仑势能. 本文模拟的是氢原子, 故库仑势能为$ V\left({{r}}\right)=-1/r $ , 在球极坐标系中系统的哈密顿量可写为H 是指作用在约化波函数$\varPhi =r\psi $ 上的哈密顿量, 记为约化哈密顿量, 其中, L 2 为系统的总角动量算符, E ${{r}} \cdot {{E}}=r[{E}_{\mathrm{I}\mathrm{R}}(t)\!+\!{E}_{\mathrm{X}\mathrm{U}\mathrm{V}}(t)]\mathrm{cos}\theta$ , $ {E}_{\mathrm{I}\mathrm{R}}\left(t\right) $ , $ {E}_{\mathrm{X}\mathrm{U}\mathrm{V}}\left(t\right) $ 分别代表IR激光场与XUV激光场, 它们分别为:E L , E X 分别为IR场和XUV脉冲的振幅, t tau 为IR场和阿秒脉冲链之间的延时, T 1 , T 2 分别为IR场和XUV脉冲的光周期, ω 为IR场的频率, $ {\omega }_{2 n+1} $ 为XUV场的频率, 2n +1 (n 为整数)表示高次谐波的阶次. 波函数随时间步长Δt 向前演化的表达式为A 和B , $ {\mathrm{e}}^{A+B}\ne {\mathrm{e}}^{A}{\mathrm{e}}^{B} $ , 但是利用分裂算符[18 ,19 ] 的方法可以以最小误差逼近演化算子[20 ] , 于是利用分裂算符的方法将(3 )式代入(6 )式中, 可以得到:t 的三阶误差项. 通过将(7 )式中的算符依次作用在初始波函数Ψ (t = 0)上, 可以得到在连续时间增量上的波函数Ψ (t + Δt ). 不断地重复上述过程, 就能得到末态波函数ψ (r t = T ).ψ (r , t = ∞)投影到散射态$ {\varPsi }_{k}^{\left(-\right)}\left(r\right) $ :k 表示光电子动量. 光电子能量分布为2.2.EA模型 -->2.2.EA模型 由于我们使用的是线偏振脉冲, 在这里只考虑光电子沿正Z 方向(θ = 0)的轨迹, 因为只有沿着这个方向运动的光电子才能在与激光场偏振平行的方向发射出去($ {\theta }_{k} $ = 0)[21 ] .ψ i ψ k k 为光电子渐近动量, 考虑库仑势和探测场(红外脉冲)共同作用在光电子上, 光电子末态波函数可写为${a_k}\left( {r, t} \right)$ 表示振幅. ${A}_{\mathrm{I}\mathrm{R}}(t)$ 表示红外脉冲的矢势, 它与电场矢量之间的关系为: ${A_{{\rm{IR}}}}\left( t \right) = - {\rm{ }}\displaystyle\int {{E_{{\rm{IR}}}}\left( t \right)} {{\rm{d}}}t$ ; ${S}_{k}(r,t)$ 表示局域相位, 它是由加入的红外脉冲电场与库仑场耦合引起的.$ {S}_{k}\left(r, t\right) $ 可写为${S}_{k}^{\mathrm{E}\mathrm{A}}\left(r, t\right)= $ $ {S}_{k}^{\mathrm{S}\mathrm{F}\mathrm{A}}\left(t\right)+{S}_{k}^{\mathrm{C}\mathrm{L}}\left(r, t\right)$ , $ {S}_{k}^{\mathrm{S}\mathrm{F}\mathrm{A}}\left(t\right) $ 表示强场近似(strong field approximation, SFA)中的Volkov相位, ${S}_{k}^{\mathrm{S}\mathrm{F}\mathrm{A}}\left(t\right)=k\displaystyle\int _{t}^{\infty }\mathrm{d}{t}'{A}_{\mathrm{I}\mathrm{R}}\left({t}'\right)$ .t 时刻的r 位置出发, 在势能V (r ${r}'\left({t}', t, r\right)=r+k\left({t}'-t\right)$ 计算的:${\Delta }r\left(t, {t}'\right)=\displaystyle\int _{t}^{{t}'}\mathrm{d}{t}''{A}_{\mathrm{I}\mathrm{R}}\left({t}''\right)$ 修正. 于是, 在加红外场的情况下, 自由电子经典轨迹为${r}_{\mathrm{L}}\left({t}', t, r\right)= $ $ {r}'\left({t}', t, r\right)+{\Delta }r\left(t, {t}'\right)$ .17 ]中的EA模型的描述, 而在本文改进后的EA模型中, 我们更加准确地描述了光电子的运动轨迹, 从而更加准确地获得了光电子的相位, 因此, 这种改进能够更加准确地预测光电子发射时间. 在库仑场和探测场的共同作用下, 光电子在任意时刻的动量$ k\left(t\right) $ 与到达探测器的末态动量$ {k}_{\mathrm{f}} $ 之间运用能量守恒原理存在某种近似解析的对应关系, 如下式所示:$t' = t + n{{\rm{d}}}t''$ . 用$ {r}_{\mathrm{L}} $ 代替(12 )式中的${r}'$ , 就可以得到库仑场和探测场(Coulomb-laser, CL)耦合作用的相位[17 ,22 -25 ] :${\psi _i}\left( {r, t} \right) \approx {\psi_i}\left( r \right){{\rm{e}}^{ - {\rm{i}}{\varepsilon_B}t}}$ , 并对光电子末态波函数ψ k $P(W\!=\!{k}^{2}/2, {t}_{\mathrm{t}\mathrm{a}\mathrm{u}})\!=\! {|{T}_{k}^{\mathrm{E}\mathrm{A}}({t}_{\mathrm{t}\mathrm{a}\mathrm{u}})|}^{2}$ .2.3.二阶微扰模型 -->2.3.二阶微扰模型 利用二阶微扰理论, 研究了双光子电离的跃迁矩阵, 包括吸收一个谐波光子$ {\omega }_{\mathrm{H}} $ 和一个红外光子ω , 电子从初态ψ i ψ k $ {{\epsilon}} $ 表示XUV场和IR场共同的偏振矢量, $ {\mathrm{\epsilon}}_{i} $ , $ {\mathrm{\epsilon}}_{n} $ 分别表示初态能量和中间态能量.${Y_{\ell 0}}$ 表示球谐函数, ${C_{\ell 0}}$ 表示对应的角度系数, ${\eta _\ell }$ 表示末态的散射相位. 径向双光子跃迁矩阵元$T_a^{\left( 2 \right)}\left( k \right)$ 可以表示为[26 ,27 ] 19 )式的右侧, 引入了与波数${k_a}$ 有关的摄动波函数${\rho _{{k_{a1}}}}$ , 为${R_{k\ell }}$ 为具有渐近性质的实数:$-\dfrac{\ell}{2}\mathrm{\pi }$ 产生于离心力势, ${\rm{ln}}\left( {2 kr} \right){\rm{/}}k$ 为一个修正项. 利用(18 )式—(21 )式可以得到$M_a^{\left( 2 \right)}\left( k \right)$ 的一个近似表达式:$z = 1/{k_a} - 1/k$ . 通过计算不同XUV与IR脉冲相对延时下的光电子跃迁振幅, 可以得到RABITT谱, 进而得到不同光电子末态动能下的光电子发射时间延迟.3.结果与讨论 本文运用基于图形处理器的计算程序数值求解含时薛定谔方程[28 ] , 所选取的角量子数L = 19, 阿秒脉冲链和IR脉冲的包络均为高斯包络, 阿秒脉冲链的强度为5 × 1011 W/cm2 , IR脉冲的强度为5 × 109 W/cm2 . 为了保证结论的普遍性, 计算了同一能量范围内不同IR波长条件下的光电子发射时间延迟随光电子末态动能的变化. 图1 为IR波长λ IR = 600 nm时的光电子能谱图, 所使用的时间步长Δt = 0.0068, 空间步长Δr = 0.0824, 空间范围R = 1350, 空间角度θ 取0—π, XUV脉冲由9, 11, 13, 15, 17, 19, 21, 23, 25, 27阶高次谐波组成, 也就是在n 取4—13.图 1 (a), (c) IR波长为600 nm时, 用TDSE和改进后EA得到的光电子能谱图, 显示了光电子跃迁几率随两个脉冲之间的延时和光电子末态动能的变化分布, 其中显示了10个主峰和9个SB; (b), (d)积分处理过的12阶, 16阶和24阶SB峰Figure1. (a), (c) The photoelectron spectrograms obtained by TDSE and improved EA at the IR wavelength of 600 nm, respectively; (b), (d) the integral 12, 16 and 24 order SB peaks from (a) and (c).图1(a) 和图1(c) 是IR波长为600 nm时, TDSE和改进后EA计算得到的光电子能谱图. 横坐标为XUV脉冲和IR脉冲之间的相对延时, 纵坐标为高次谐波的阶次, 两图表明了光电子跃迁几率随阿秒脉冲链和IR脉冲之间的相对延时和电子末态动能的变化分布, 可以看到主峰之间出现了9个SB峰, 这9个SB峰出现明暗交替的变化. 图1(b) 和图1(d) 分别对应图1(a) 和图1(c) 中的第12, 16和24阶SB峰, 横坐标为XUV脉冲与IR脉冲之间的相对延时, 纵坐标为SB峰的强度. 对图1(b) 和图1(d) 中的SB峰进行归一化处理(SB峰除以其最大值), 并将归一化后的SB峰按余弦型函数$ s\left({t}_{\mathrm{t}\mathrm{a}\mathrm{u}}\right)=\alpha +\beta \mathrm{cos}\left[2\omega \left({t}_{\mathrm{t}\mathrm{a}\mathrm{u}}-{\tau }_{\mathrm{I}}\right)\right] $ 进行拟合就可以提取出光电子发射时间延迟$ {\tau }_{\mathrm{I}} $ .图2(a) 为TDSE, EA, 改进后的EA和二阶微扰模型计算得到的光电子发射时间延迟随光电子末态动能的变化. 其中, 蓝色星号表示TDSE模型的计算结果, 红色虚线表示EA模型的计算结果, 紫色虚线表示改进后EA模型的计算结果, 绿色点划线表示二阶微扰模型的计算结果. 从图2(a) 可以看出, 在光电子末态动能较低(小于20 eV)时, EA模型和二阶微扰模型的计算结果与TDSE相差较大, 达到了几十阿秒. 随着光电子末态动能的增加, EA模型和二阶微扰模型的计算结果越来越接近TDSE. 然而, 在光电子末态动能从5 eV变化到40 eV时, 改进后EA模型的计算结果与TDSE计算的结果一直相差很小. 这是因为, 在光电子末态能量较低时, 改进的EA模型使用了更加准确的光电子运动轨迹, 从而得到了更准确的光电子相位, 因此, 获得了更加准确的光电子发射时间. 可见, 相比于EA和二阶微扰模型的计算结果, 改进后EA模型的计算结果与TDSE更加符合. 为了验证结论的普遍性, 图2(b) —图2(d) 计算了IR波长为800, 1200和1600 nm下的结果. 从图2(b) —图2(d) 可见, 当IR波长从800 nm增加到1600 nm时, 改进后EA模型的计算结果均比EA和二阶微扰模型的计算结果更符合TDSE. 比较图2 中的四幅图可以看到, 随着波长的增加, 改进的EA模型在低能部分与TDSE的偏差越来越大, 而在高能部分与TDSE一直符合得很好. 这是因为, 不同波长在计算光电子相位, 即对光电子的运动轨迹进行积分时出现了差异, 在短波长情况下进行积分时, 更高的频率使得积分时的抵消效应更加明显, 更好地符合(13 )式. 对于改进的EA模型在低能和高能部分与TDSE符合得不一样这个问题, 我们做过一个系统的研究. 先给定光电子的末态动能E 1 , 逆推出初始动量; 再由初始动量出发, 应用(13 )式去求解光电子的末态动能E 2 , 通过对比, 发现E 1 与E 2 之间的相对偏差同时依赖于光电子的末态动能和矢势的振幅. 当光电子的末态动能较大并且矢势的振幅较小时, 相对偏差可以忽略, 由(13 )式确定的$ k\left(t\right) $ 也就可以近似地看成真实动量. 在矢势的振幅已经确定的情况下, 光电子的末态动能越大, (13 )式就越加贴近实际情况, 所得到的光电子发射时间也就越符合TDSE.图 2 TDSE(蓝色星号)、EA(红色虚线)、改进的EA(紫色虚线)和二阶微扰模型(绿色点划线)四种模型计算的不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) λ IR = 600 nm; (b) λ IR = 800 nm; (c) λ IR = 1200 nm; (d) λ IR = 1600 nmFigure2. The photoemission time delays calculated by TDSE (blue stars), EA (red dotted line), improved EA (purple dotted line) and second order perturbation model (green dotted line) with the IR wavelengths of (a) λ IR = 600 nm, (b) λ IR = 800 nm, (c) λ IR = 1200 nm, (d) λ IR = 1600 nm.图3 是不同IR波长下光电子发射时间延迟随光电子末态动能的变化. 图3(a) 和图3(b) 分别是TDSE和改进后EA计算得到的结果. 其中, 蓝色线表示600 nm的结果, 红色线表示800 nm的结果, 绿色线表示1200 nm的结果, 紫色线表示1600 nm的结果. 从图3 可以看到, 在同一IR波长下, 光电子发射时间延迟随光电子末态动能的增加而减小. 在相同光电子末态动能下, IR波长越长, 光电子发射时间延迟越大. 这是因为在同一IR波长下, 当末态动能越大时, 初始速度越大, 电离电子在电场中运动时离原子核的位置越远, 库仑势的影响就会越小, 光电子发射时间延迟也就越小. 而在相同光电子末态动能下, IR波长越长, IR场的频率越小, 库仑势的影响就越大, 光电子发射时间延迟也就越大.图 3 不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) TDSE结果; (b)改进后EA结果Figure3. The photoemission time delays calculated by TDSE and improved EA with different IR wavelengths: (a) TDSE; (b) the improved EA models.4.结 论 本文对EA模型进行了改进, 并验证了其准确性. 分别使用了TDSE, EA, 改进后EA和二阶微扰模型四种方法计算了氢原子在不同波长同一能量范围内光电子发射时间延迟随末态动能变化的曲线, 并对所得曲线进行对比. EA模型的改进使得我们能够更加准确地描述光电子的运动轨迹, 从而更加准确地获得了光电子的相位, 因此, 这种改进能够更加准确地预测光电子发射时间. 通过对比TDSE, EA, 改进后EA和二阶微扰模型的计算结果, 发现当IR波长从600 nm变化到1600 nm时, 改进后EA模型的计算结果比EA模型和二阶微扰模型更符合TDSE的结果, 同时, 随着波长的增加, 改进的EA模型在低能部分与TDSE的偏差越来越大, 而在高能部分与TDSE一直符合得很好. 由此可见, 改进的EA模型还有需要改进的空间, 可以对(13 )式进行改进, 这项工作还有待今后进一步研究. 此外还发现, 在相同IR波长下, 光电子发射时间延迟随光电子末态动能的增加而减小; 而在光电子末态动能下, IR波长越长, 光电子发射时间延迟越大. 












































 图 1 (a), (c) IR波长为600 nm时, 用TDSE和改进后EA得到的光电子能谱图, 显示了光电子跃迁几率随两个脉冲之间的延时和光电子末态动能的变化分布, 其中显示了10个主峰和9个SB; (b), (d)积分处理过的12阶, 16阶和24阶SB峰
图 1 (a), (c) IR波长为600 nm时, 用TDSE和改进后EA得到的光电子能谱图, 显示了光电子跃迁几率随两个脉冲之间的延时和光电子末态动能的变化分布, 其中显示了10个主峰和9个SB; (b), (d)积分处理过的12阶, 16阶和24阶SB峰


 图 2 TDSE(蓝色星号)、EA(红色虚线)、改进的EA(紫色虚线)和二阶微扰模型(绿色点划线)四种模型计算的不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) λIR = 600 nm; (b) λIR = 800 nm; (c) λIR = 1200 nm; (d) λIR = 1600 nm
图 2 TDSE(蓝色星号)、EA(红色虚线)、改进的EA(紫色虚线)和二阶微扰模型(绿色点划线)四种模型计算的不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) λIR = 600 nm; (b) λIR = 800 nm; (c) λIR = 1200 nm; (d) λIR = 1600 nm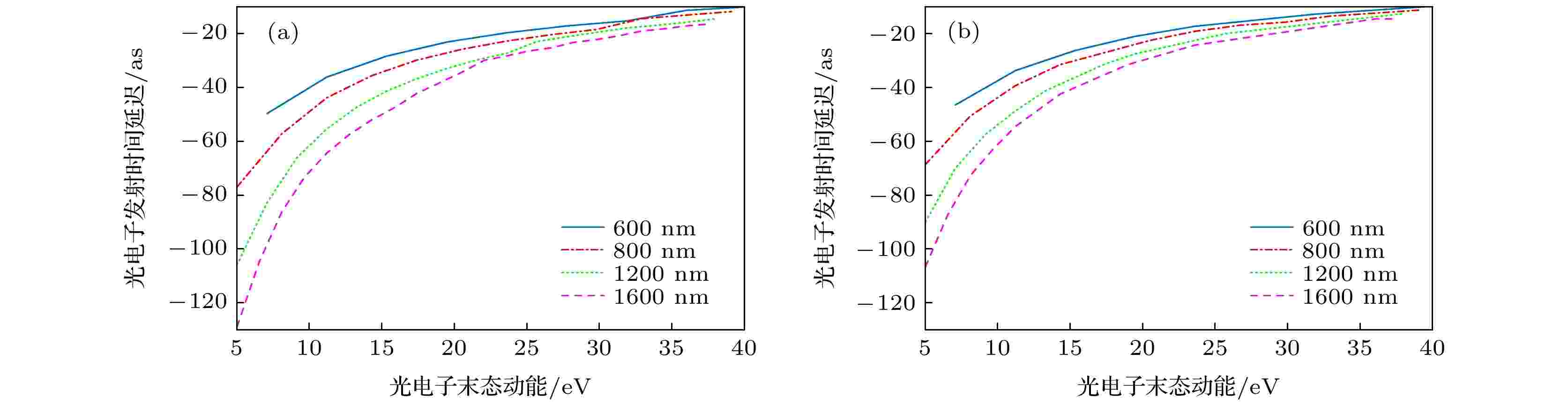 图 3 不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) TDSE结果; (b)改进后EA结果
图 3 不同IR波长下光电子发射时间延迟随光电子末态动能的变化 (a) TDSE结果; (b)改进后EA结果