摘要: 纳米激光器作为未来实现光集成的重要光学元件, 成为了近年来的研究热点之一, 相应的结构工程及输出特性受到了广泛的关注. 然而, 纳米激光的非线性动力学方向上的研究却少有报道. 本文基于纳米激光器的单模速率方程, 应用排列熵复杂度量化工具分析了光反馈及光注入下的混沌纳米光源不可预测程度, 并通过自相关函数进行时延表征. 结果表明: 增加线宽增强因子
α 、偏置电流
I dc 、减小增益饱和因子
ε 、自发辐射增强因子
F 、自发辐射耦合因子
β 都有利于提升混沌的不可预测性并抑制时延特征. 而通过光反馈方式产生的混沌光源进一步注入到另一个纳米激光器, 会带来额外的光场非线性作用, 进一步地增强混沌激光的复杂度特性. 此外, 基于绘制频率失谐及注入强度下激光器输出的二维复杂度空间分布, 确定了获取高不可预测度纳米激光混沌信号的参数范围. 这对于实现低成本、小尺寸、高品质混沌光源的研究有重要推动作用.
关键词: 纳米激光 /
混沌 /
不可预测性 /
时延 English Abstract Time delay concealment and unpredictability enhancement of nanolasers under external cavity regulation Jiang Pei 1,2 ,Zhou Pei 1,2 ,Li Nian-Qiang 1,2 ,Mu Peng-Hua 3 ,Li Xiao-Feng 1,2 1.School of Optoelectronic Science and Engineering, Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University, Suzhou 215006, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 62004135, 62001317, 61875143), the Natural Science Research Project of Jiangsu Higher Education Institutions, China (Grant No. 20KJA416001), the Startup Funding of Soochow University, China (Grant No. Q415900119), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20180042), and the Superior Discipline Construction Project of Jiangsu Higher Education Institutions, ChinaReceived Date: 10 January 2021Accepted Date: 28 January 2021Available Online: 29 May 2021Published Online: 05 June 2021Abstract: As an important optical element of the optical integration in the future, nanolasers has been a research hotspot in recent years, and the corresponding structural engineering and output characteristics have been widely investigated. However, the nonlinear dynamical performances of nanolasers are rarely reported. Only some preliminary analyses of the dynamic behavior under the optical feedback, optical injection and mutual injection can be found. Some researches pointed out the future prospect of nanolasers, however, some chaos-based applications have not been explored. Therefore, we numerically investigate chaos dynamics in a nanolaser subjected to optical feedback and in another nanolaser subjected to chaotic injection from the former structure by using single mode rate equation, which includes the Purcell cavity-enhanced spontaneous emission factor F and spontaneous emission coupling factor β . The F denotes the ratio of the spontaneous emission rate into the cavity mode to the total spontaneous emission rate in the bulk medium in the absence of a cavity and β represents the fraction of spontaneous emitted photons which are coupled into cavity mode. Specifically, chaos time delay signature (TDS) and unpredictability are evaluated by the peak size of autocorrelation function (ACF) and permutation entropy (PE) respectively. Such kinds of calculations have the advantage of fast operation speed and anti-noise robustness. The results show that the increasing of bias current and the decreasing of gain saturation factor ε , F and β are beneficial to improving the unpredictability and suppressing TDS because the weak damping of the relaxation oscillation leads to strong oscillation. Large linewidth enhancement factor α will increase the number of laser oscillating modes, sideband modes, the spectral components, and enhance the dispersion effect, which will also weaken the information about outer cavity and improve the complexity of chaos. In addition, the above-mentioned chaos properties can be enhanced by injecting the chaos output from a nanolaser subjected to optical feedback into another (slave) nanolaser, which is due to the nonlinear interaction between the driving chaotic signal and the internal electric field of the slave nanolaser. Finally, two-dimensional maps depicting high unpredictability and TDS concealment in the parameter space of the frequency detuning and the injection strength are obtained. It can be found that unpredictability degree can be enhanced by choosing high detuning frequency and intermediate injection strength in the non-injection locking area. The numerical results pave the way for generating the high-quality chaotic sources on a chip or the photonic integrated circuits based on novel semiconductor nanolaser and its related applications.Keywords: nanolasers /chaos /unpredictability /time delay signature 全文HTML --> --> --> 1.引 言 在过去几十年里, 半导体激光器的非线性动力学受到了人们的广泛关注. 其中, 激光混沌由于具有时间维度上的长期不可预测性, 被广泛地应用于保密通信[1 ,2 ] , 高速物理随机数的产生[3 ,4 ] , 以及混沌激光雷达[5 ,6 ] 等方面. 而混沌的产生方式也有很多种, 大致可分为光反馈、光注入、光电反馈、电流调制等几大类[2 ] . 其中, 由于具有结构简单、可控性强等特点, 光反馈半导体激光器装置产生光学混沌的方案被广泛地应用到研究中[7 ] . 然而, 在该条件下产生的混沌与引入的光反馈外腔有关, 表现出一定的周期性, 被称为时延特征(time delay signature, TDS)[8 ] . 如果以这种带有时延特征的混沌信号作为信息载体, 关键参数的相关信息泄漏风险会增大, 窃听者可能重构混沌吸引子并对有用信息进行预测, 这会对混沌通信系统的安全性构成威胁[9 ] . 因此, 必须提高混沌信号质量, 再进一步地实现相关应用.[10 ] 、样本熵[11 ] 、动态熵(Kolmogorov-Sinai entropy, KS)[12 ] 和排列熵(permutation entropy, PE)[13 ] 等. 其中, PE是引入的与时间序列相关的参数, 可通过比较相邻两个值大小而得到具体结果, 用于解决其他量化工具在加入无法避免的噪声后易失效的问题, 更适合评估高维度的动态系统时间序列的复杂度特性. 此外, 它还具有简单、运算速度快等优点. 因此, PE广泛地适用于量化混沌激光系统所产生混沌信号的不可预测程度(unpredictability degree, UD). 例如, Xiang课题组[14 -16 ] 探究了垂直腔面发射激光器(vertical-cavity surface-emitting laser, VCSEL)在固定偏振及可变偏振条件下, 偏振角度、反馈强度、反馈延时、偏置电流等因素对不可预测度的影响, 并将产生的混沌应用于保密性增强并且高度同步的通信系统中. 此外, 该课题组分析了单注入[17 ] 、双注入[17 ] 、互注入[18 ] , 以及多延时下的双反馈[19 ] 、环形网络[20 ] 等装置下相应的不可预测性. Li等[21 ] 则发现在单注入下, 增加线宽增强因子有利于抑制强度及相位中的时延特征, 还探究了具有较好集成度的半导体环形激光的混沌不可预测程度[22 ] . 然而, 它们中的大多数都是由传统半导体激光器和辅助元件构成的复杂结构. 未来做大规模集成就必须要突破有源器件面临的瓶颈—大尺寸. 而半导体纳米激光器展现了模体积小、阈值低、量子效率高、响应速度快等优势, 具备在紧凑型光子集成电路中的应用潜力, 因此在近些年备受关注.[23 ] 提出基于表面等离激元效应, 并通过补偿由于金属带来的高损耗, 从而制备出了近红外波段有效输出的纳米级尺寸激光. 由于纳米激光器的模体积小于衍射极限, 具有明显的局域场增强特性. 因此, Lau等[24 ] 于2009年提出在传统的激光器速率方程中引入了自发辐射特征增强因子F 与自发辐射耦合因子$ \beta $ , 建立了纳米激光器速率方程. 在此基础上, Shore等分析了纳米激光在电流调制[25 ] 、光反馈[26 ,27 ] 、光注入[28 ] 、光反馈及光注入共同作用[29 ] , 以及互注入作用下[30 ] 的动力学行为. 此外, 纳米激光器由于具有高调制、低阈值等优势也被认为是混沌源的候选元件. 2018年, Elsonbaty等[31 ] 从强度及相位自相关角度入手, 与普通光反馈、相位共轭光反馈(phase conjugated feedback, PCF)及光栅镜面光反馈下产生的混沌特性做了比较, 证实了采用全光和电光混合反馈的方案可以更好地抑制时延特征, 并将产生的混沌光源用于图像加密. 2019年, Xiang课题组[32 ] 发现受到来自两个主纳米激光器双混沌注入的从纳米激光器输出在宽参数范围内具备了低时延特征. 本课题组则在先前的工作中报道了基于单注入产生优质混沌光源, 并将其作为载波实现信息的安全传输[33 ] . 这些详细的研究阐明了纳米激光进入混沌的路径, 不同系统下的时延特性, 也为混沌的应用奠定了理论基础.F 、自发辐射耦合因子$ \beta $ 、偏置电流、增益饱和因子、线宽增强因子、反馈强度、注入强度、频率失谐等关键参数对纳米激光器混沌光源不可预测程度的影响.2.理论模型 通过外腔附加自由度, 带来额外的光波扰动, 与激光器形成的光场发生拍频效应, 就可以使激光器输出在时域上呈现出周期、类周期、混沌的多种波形. 这是研究激光器非线性动力学最常见的方式. 本文主要介绍在光反馈及光注入两种常规外部扰动下的纳米激光混沌特性. 对应公式如下[32 ] :$ I(t) $ 为随时间变化的光子数, $ N(t) $ 为载流子数, $\varphi \left( t \right)$ 为对应的相位, 下标m, s分别代表主激光器与从激光器, F 为珀塞尔腔增强自发辐射因子, $ \beta $ 为自发辐射耦合因子, $ {I_{{\rm{dc}}}} $ 为注入电流, $ {I_{{\rm{th}}}} $ 为阈值电流, $ \alpha $ 为线宽增强因子, $ \varepsilon $ 为增益饱和因子, $ \varGamma $ 为局限因子, $ {V_{\rm{a}}} $ 为活性层体积, $ {\tau _{\rm{p}}} $ 为光子寿命, $ {\tau _{\rm{n}}} $ 为载流子寿命, $ {g_{\rm{n}}} $ 为微分增益, e 为单位电荷量, $ {N_0} $ 为透明电流密度. 光反馈条件下, 在(1 )式、(2 )式中分别有一个反馈延时项, 包含了反馈延时$ {\tau _{\rm{d}}} $ , 反馈强度$ {k_{\rm{d}}} $ , 这项参数可表示为[26 ] f 表示反馈耦合因子, R 表示纳米激光器的腔面反射率, $ {R_{{\rm{ext}}}} $ 表示的是镜面反射率, c 代表着真空中光速, n 是激光介质的折射率, L 代表反馈腔长. 而通过光反馈产生的混沌光源会被进一步注入到从激光中, 在(1 )式、(2 )式中都存在一个注入延时项, 包含注入强度$ {k_{\rm{r}}} $ , 注入延时$ {\tau _{\rm{r}}} $ . 此外, 主激光与从激光之间会存在频率失谐$ \Delta f = ({f_{\rm{m}}} - {f_{\rm{S}}}) $ , 其中$ {f_{\rm{m}}} $ , $ {f_{\rm{S}}} $ 分别为主从激光的工作频率, 与波长$ {\lambda _{\rm{0}}} $ 有关.1 )—(5 )式进行数值求解. 如无特别说明, 所用参数如下[32 ] : $ F = 14 $ , $\beta = 0.05, ~~\alpha = 5,$ $\varepsilon = 2.3 \times {10^{ - 17}}\; $ $ {\rm{c}}{{\rm{m}}^3},$ ${\tau _{\rm{d}}} \!=\! $ $ 0.2\;{\rm{ns}},\; {\tau _{\rm{r}}} \!=\! 0\;{\rm{ns}}, \;\varGamma \!=\! 0.645$ , ${g_{\rm{n}}} \!=\! 1.64 \!\times\! {10^{ - 6}}\; {\rm{c}}{{\rm{m}}^3} /{\rm{s}}$ , ${V_{\rm{a}}} \!=\! {\rm{3}}{\rm{.96}} \!\times\! {\rm{1}}{{\rm{0}}^{{\rm{ - 13}}}}\;{\rm{c}}{{\rm{m}}^{\rm{3}}}$ , ${\tau _{\rm{p}}} \!=\! {\rm{0}}{\rm{.36}}\;{\rm{ps}}$ , ${\tau _{\rm{n}}} \!=\! 1\;{\rm{ns}}$ , $ n = 3.4 $ , $ {I_{{\rm{th}}}} = 1.1\;{\rm{mA}} $ , ${I_{{\rm{dc}}}} = 2{I_{{\rm{th}}}},\; {N_0} = 1.1 \times $ $ {10^{18}}\;{\rm{c}}{{\rm{m}}^{ - 3}}$ , ${\lambda _0} = $ $ 1.591\;$ μm, $ R = 0.85 $ , $ {R_{{\rm{ext}}}} = 0.95 $ , $ L = 1.39\; $ μm.[13 ] . 即对于一个时间序列{x t t = 1, ···, T }, 通过相空间重建的方法来构造d 维向量, $ X_t = (x(t), $ $ x(t + \tau_{\rm e}), \cdots, x (t+ (d - 1) \tau_{\rm e}))$ , d 为嵌入维数, τ e 为嵌入时延, T 为序列长度[34 ,35 ] . 将序列X t $x(t+(r_1 - 1)\tau_{\rm e}) \leqslant $ $ x(t \!+\! (r_2 - 1) \tau_{\rm e}) $ $ \leqslant x(t \!+\! (r_{\rm d} - 1)\tau_{\rm e})$ 时, 如果$r_{t1} \!\leqslant\! r_{t2}$ , 则按照$x(t+(r_{t1} - 1) \tau_{\rm e}) \leqslant x(t+ (r_{t2} - 1) \tau_{\rm e})$ 进行排列. 在这种情况下, 序列X t d ! 种排列方式, 都可能会被映射到相应的排列顺序π = {r 1 , r 2 , ···, r d }, 而给定排列的概率P = {p (π )}, 对应式如下:p (π)表示特定的排列分布所对应的可能性, 用于进一步计算熵值. 往往不同排列下的概率分布越均衡表示事件越随机, 熵值会越大. 将得到的概率进行如下计算, 就得到了归一化熵值为H [P ]介于0—1之间, 如果值越大, 则表示不可预测程度越高, 相应的序列越接近于完全随机序列. 这里, 选择了维数$ d = 5 $ , T = 105 , ${\tau _{\rm{e}}} = {\tau _{\rm{d}}}/{\varOmega _{\rm{s}}} = $ $ {10^3}({\varOmega _{\rm{s}}} = 0.2\;{\rm{ps}})$ 进行熵值计算[21 ] , 采样率$ {\varOmega _{\rm{s}}} $ 刚好对应Runge-Kutta的积分步长. 此外, 可利用自相关函数(auto correlation function, ACF)对时滞下混沌随机序列的时间延迟信号进行评估[36 ,37 ] . ACF也称为序列相关, 是一个信号与自身在不同时间点下相似度的比较. 利用该函数可以找出重复模式, 即被噪声掩盖的周期信号, 对分析混沌信号的伪随机特性具有重要意义. 此外, 该技术具有计算效率高、鲁棒性强、不受白噪声影响等优点. 具体公式如下:$\left\langle {\;} \right\rangle $ 为时间序列的平均值, $\Delta t $ 为滞后时间. 我们取ACF函数相对应在时间窗口$t \in [{\tau _{\rm{d}}} - \kappa \times {\tau _{\rm{d}}}, $ $ {\tau _{\rm{d}}} + \kappa \times {\tau _{\rm{d}}}]~{\rm{ns}}$ 范围内的峰值, $ \kappa $ = 10%进行TDS的衡量. 混沌随机序列在越低自相关值下, 往往对应越高的不可预测性, 表示越难以提取出有用信息.3.结果与讨论 首先, 分析在不同反馈强度下纳米激光混沌输出的时延及不可预测特性. 图1 显示了在反馈耦合因子f 分别为0.02和0.06下的时序, ACF及PE变化情况. 此时的激光工作在混沌状态, 时序具有类噪声波形, 无法看出明显的特征信息. 然而, 当采用ACF表征相关信息时, 会发现在反馈延时附近具有明显的峰值. 此外, PE曲线中对应延迟时间的位置, 熵值出现了明显的下降. 这说明采用两种方式都能表征出延时特征. 反馈延时附近对应特征峰值越大, 熵值下降得越多, 表示延时特征越明显. 而在这两种不同反馈强度下, 这个特征都明显地存在, 这是由于镜面光反馈只能提供局部光反馈, 反馈回来的光与特定时刻的激光输出具有强相关性, 导致了所产生混沌的随机性较差. 只有通过调节反馈强度与偏置电流, 使弛豫振荡周期与反馈延时相接近, 才可能有效地抑制住这种时延特征[8 ] . 因此, 需要采用其他有效的方式, 例如增加反馈腔的数量或利用非线性装置代替镜面减弱相关性, 提升混沌的不可预测程度并实现时延隐藏, 进而确保信息的安全传输.图 1 (a1), (a2)光反馈下的纳米激光器时序; (b1), (b2) ACF曲线; (c1), (c2) PE曲线. 反馈耦合因子: (a1)—(c1)$f = 0.02$ ; (a2)—(c2)$ f = 0.06$ Figure1. (a1), (a2) Time series; (b1), (b2) ACF curve; (c1), (c2) PE curve of a nanolaser under optical feedback. The feedback coupling fraction: (a1)–(c1) $ f = 0.02 $ ; (a2)–(c2) $ f = 0.06 $ .$ \varepsilon $ 与线宽增强因子$ \alpha $ 对混沌信号复杂度的影响. $ \alpha $ 是表征非线性相移、频率啁啾效应和因载流子浓度变化引起线宽展宽的一项重要参数. 图2(a) 展示了随着$ \alpha $ 增大后所对应的时延特征值变化, 曲线呈下降趋势表示TDS会逐渐减弱, 但不能得到完全消除, 即时延特征值始终大于0.2, 在这种条件下时延信号无法在背景噪声中得到有效地隐藏. 主要原因是增加$ \alpha $ 导致了激光振荡模式及边带模式数量的增加, 光谱成分增多, 色散效应增强, 从而削弱了外腔的信息, 减小混沌的周期性. 图2(b) 则展示了不可预测度的变化趋势, 与时延特征值的变化刚好相反, 所对应的HP值会逐渐增加并趋近于1. 此外, 固定$ \alpha $ 值, 发现随着$\varepsilon $ 减小, 经过光反馈产生混沌输出信号的不可预测程度会得到提升, 时延特征峰值则有所减弱. 其物理原因可能是增益饱和效应会抑制激光强度的剧烈波动, 即增益饱和因子较大时, 对激光器的弛豫振荡会起到很好的阻尼作用, 因此时序上表现为小幅度的振荡, 此时激光输出处于弱混沌状态. 而基于最大李雅普诺夫指数、KS动态熵和KY维数(Kaplan-Yorke dimension)等技术对有无增益饱和因子下的非线性动力学分析中也已经指出了增大$ \varepsilon $ 会导致复杂度的减弱[38 ] . 综上所述, 较小的$ \varepsilon $ 及较大的$ \alpha $ 有利于增强纳米激光器混沌输出的随机特性, 并降低时延特征值.图 2 光反馈纳米激光器 (a) TDS与 (b) H [P ]随着$ \alpha $ , $ \varepsilon $ 的变化Figure2. (a) TDS and (b) H [P ] of a nanolaser subjected to optical feedback as functions of $ \alpha $ , $ \varepsilon $ .F , $ \beta $ )对于混沌输出复杂度的影响也是具有意义的. 研究单模激光的混沌输出特性时, F 表示单位时间内进入相应模式的瞬态辐射率与无腔介质中总自发辐射率之比; $ \beta $ 表示自发辐射光子耦合进入腔模所占的比例. 如图3 所示, 反馈耦合因子f 在0.005—0.080内变化. 随着反馈增加, 时延特征值会达到相应的波谷位置, 此时激光输出的扰动效果加剧, 使混沌序列随机性增强, 混沌的时延峰值减小, 在反馈耦合因子又逐渐增大进入强反馈区域后, 激光会形成稳定的外腔运行模式, 即外部反馈光占据主导, 因此不可预测性又有所减弱, 时延特征再次变得明显, 这与在传统的半导体激光器得到的时延特征演变趋势一致[8 ] . 特别说明当固定$ \beta = 0.1 $ , F 值的变化范围在10—30时, 只有极小的阈值电流波动, 并不会影响计算过程中发现的一般性趋势, 因此这里都采用阈值电流$ {I_{{\rm{th}}}} = 1.1\;{\rm{mA}} $ [30 ] . 相应的结果表明了增加F 会导致混沌输出的随机性减弱, 对应时延特征变得明显. 其次, 固定F 值, 改变$ \beta $ 值会得到同样的变化趋势, 即$ \beta $ 增加后, 时延特征会更明显. 这归结于自发辐射增强会导致激光器启动延迟的降低, 引发的强阻尼在激光器的动力学转化过程中产生长尾效应, 从而影响纳米激光输出的非线性动力学行为及特性.图 3 光反馈纳米激光器 (a) TDS与 (b) H [P ] 随着$ F $ 的变化Figure3. (a) TDS and (b) H [P ] of a nanolaser subjected to optical feedback as functions of $ F$ .图4 所示. 定义$ {I_{{\rm{dc}}}} = {\it{q}}{I_{{\rm{th}}}} $ , q 是电流的量化因子. 发现在低反馈强度下, 不同偏置电流对应的H [P ]值及时延特征无明显差异. 但是当反馈强度进一步增大, 更高的偏置电流条件下所对应不可预测度会增加, 时延特征值则减小. 因为在光反馈条件下, 更高的偏置电流会使输出的激光更强, 带来的扰动更剧烈, 此时激光输出进入混沌所需的反馈阈值则越小, 混沌输出的随机性也会越好. 并且随着反馈强度增加, 不同偏置下反馈光强的差异会明显增加, 这导致了混沌随机性及时延特征值的差异更为明显.图 4 光反馈纳米激光器 (a) TDS与 (b) H [P ] 随着偏置电流的变化Figure4. (a) TDS and (b) H [P ] of a nanolaser subjected to optical feedback as functions of the bias current.[21 ] . 我们知道基于一定的频率失谐可以更好地抑制时延特性, 这里以频率失谐$ \Delta f = 25\;{\rm{GHz}} $ , 反馈耦合因子f = 0.02为例, 具体结果如图5 所示. 可以看到, 在嵌入延时位置的H [P ]值从0.90提高至0.95以上, 时延特征值也变得更小. 而对比两种不同的注入强度下所得到的结果, 发现$ {k_{\rm{r}}} = 100\;{\rm{n}}{{\rm{s}}^{ - 1}} $ 时的混沌不可预测程度更高, 对应时延特征则可以得到彻底消除. 此时的从激光器没有被主激光器注入锁定, 相互之间的扰动加剧, 通过拍频作用会产生高频振荡输出. 由外腔反馈所形成的混沌光注入到从纳米激光器后, 所形成的输出可以作为一个增强的混沌源. 当进一步提升注入强度$ {k_{\rm{r}}} = 200\;{\rm{n}}{{\rm{s}}^{ - 1}} $ 时, 从激光器的输出会被主激光器锁定, 从而呈现出与主激光器一致的输出. 主激光器只在单一光反馈结构下实现混沌输出, 所对应随机性较弱, 因此强光注入下的从纳米激光器输出时延特征会再次变得明显.图 5 混沌光注入下从纳米激光器的 (a1), (a2)时序; (b1), (b2)ACF曲线; (c1), (c2) PE曲线. 注入强度(a1)—(c1)$ {k_{\rm{r}}} = 100\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ; (a2)—(c2)$ {k_{\rm{r}}} = 200\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ; $ \Delta f = 25\;{\rm{GHz}} $ Figure5. (a1), (a2) Time series; (b1), (b2) ACF curve; (c1), (c2) PE curve of the slave nanolaser under chaotic optical injection. The injection strength (a1)–(c1) $ {k_{\rm{r}}} = 100\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ; (a2)–(c2) $ {k_{\rm{r}}} = 200\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ;$ \Delta f = 25\;{\rm{GHz}} $ .图6 所示, 显示了从激光在反馈延时位置的H [P ]值随注入强度$ {k_{\rm{r}}} $ 和频率失谐$ \Delta f $ 的变化, 不同颜色表示了不同的H [P ]值, 对应$20\;{\rm{n}}{{\rm{s}}^{ - 1}} \leqslant {k_{\rm{r}}} \leqslant 300\;{\rm{n}}{{\rm{s}}^{ - 1}}$ , $- 30\;{\rm{GHz}} \leqslant \Delta f \leqslant $ $ 30\;{\rm{GHz}}$ . 为清晰起见, H [P ]=0.99作为分界线, 相应的值越高表示混沌输出越难以预测, 时延可以更好地被抑制. 从图6 中可以看出以下几个特征: 首先是处于高不可预测度的激光混沌输出参数范围(深红色部分, H [P ] $\geqslant $ 0.99)容易在适当注入, 以及一定的频率失谐下得到. 正如在描述图5 时所提到的, 随着注入强度增加, 从激光器会被主激光器注入锁定, 不可预测度会明显下降, 此时需要更高的频率失谐减弱锁定效应. 因此在图6 中, 该范围展现了“V”型效果. 然而, 由于$ \alpha $ 不等于零, 展现的形状关于频率失谐变化又不完全对称. 其次, 在较高的注入强度下, 增大正频率失谐会使主从激光器之间产生的拍频效果更明显, 进而使输出不可预测性得到提升. 而对比不同F , β 和偏置电流下复杂度的二维分布效果, 发现从激光器混沌输出处于高不可预测程度的范围会随着F 和β 值增大而减小. 另外, 通过对比${I_{{\rm{dc}}}} = 2{I_{{\rm{th}}}} $ 和$ {I_{{\rm{dc}}}} = 4{I_{{\rm{th}}}} $ 的结果图, 可以观察到在选择合适的F 和β 条件下, 增大偏置电流会带来更剧烈的扰动效果, 该范围也会被进一步扩大.图 6 在不同F , β 及偏置电流下, 从纳米激光器混沌输出的H [P ]随失谐频率及注入强度变化的二维映射 (a1)—(a3)${I_{{\rm{dc}}}} = $ $ 2{I_{{\rm{th}}}}$ ; (b1)—(b3)$ {I_{{\rm{dc}}}} = 4{I_{{\rm{th}}}} $ . (a1), (b1)F = 14, β = 0.05; (a2), (b2)F = 14, β = 0.1; (a3), (b3)F = 30, β = 0.1Figure6. Two-dimensional maps of H [P ] in the parameter space of the frequency detuning and injection strength under different values of F , β and injection current for the slave nanolaser: (a1)–(a3) $ {I_{{\rm{dc}}}} = 2{I_{{\rm{th}}}} $ ; (b1)–(b3) $ {I_{{\rm{dc}}}} = 4{I_{{\rm{th}}}} $ . (a1), (b1) F = 14, β = 0.05; (a2), (b2) F = 14, β = 0.1; (a3), (b3) F = 30, β = 0.1.$ \alpha $ 增加, 会产生更宽的混沌有效区间; 在连续光注入条件下使从纳米激光器工作在非稳态, 其动力学路径也会发生变化[28 ] . 在动力学行为变化的同时, $ \alpha $ 变化必然会影响纳米激光器混沌输出特性. 如图7(a1) 和图7(b1) 所示, 具备高不可预测度与时延隐藏(对应深蓝色区域, C ≤ 0.2)的激光混沌输出参数范围相对较小. 主要原因是在较大的注入强度下从纳米激光器容易被注入锁定, 即此时的混沌特性会由主激光器所主导. 通过将图7(a2) 和图7(b2) 、图7(a3) 和图7(b3) 与图7(a1) 和图7(b1) 进行对比, 发现当增大$ \alpha $ 时, 从纳米激光器混沌输出可在更宽的注入参数范围内实现高不可预测度和时延隐藏. 如图7(a3) 和图7(b3) , H [P ]较高的区域占据了大部分的参数空间, 此时注入锁定的条件就变得严苛, 所对应混沌特性得到提升, 因为增大$ \alpha $ 会增强光场中幅度和相位的耦合程度, 从而得到了更为复杂的激光混沌输出. 同理, 减小增益饱和因子也会使从纳米激光器的输出非线性得到增强, 达到不可预测性提升与时延抑制的效果, 这里就不一一赘述.图 7 在不同线宽增强因子下, 从纳米激光器混沌输出的 (a1)—(a3)H [P ]及(b1)—(b3)时延特征峰值随失谐频率及注入强度变化的二维映射. (a1), (b1)$ \alpha=4 $ ; (a2), (b2)$ \alpha=5 $ ; (a3), (b3)$ \alpha=6 $ Figure7. Two-dimensional maps of (a1)–(a3) H [P ] and (b1)–(b3) TDS in the parameter space of the frequency detuning and injection strength under different values of the linewidth enhancement factor for the slave nanolaser. (a1), (b1) $ \alpha=4 $ ; (a2), (b2) $ \alpha=5 $ ; (a3), (b3) $ \alpha=6 $ .4.结 论 本文基于纳米激光器的单模速率方程, 在一定的光反馈条件下实现混沌输出, 并基于光注入进一步提升混沌激光的动力学特性, 对输出信号的时延及不可预测程度做了系统分析, 详细探究了反馈参数和注入参数对纳米激光器混沌输出不可预测程度演化的影响. 数值仿真结果表明, 增加线宽增强因子$ \alpha $ 、偏置电流$ {I_{{\rm{dc}}}} $ , 以及减小增益饱和因子$ \varepsilon $ 、自发辐射增强因子F 与自发辐射耦合因子$ \beta $ 都有利于光反馈及光注入下纳米激光器混沌输出不可预测性的提升以及时延特征的抑制. 此外, 通过绘制从纳米激光器的混沌输出随着注入强度与失谐频率的演化图, 发现在正频率失谐与中等注入强度的参数条件下, 从纳米激光器混沌输出的复杂度会提升. 上述发现对实现高品质物理随机数发生器及保密性增强的混沌光通信应用具有重要意义. 



























































 图 1 (a1), (a2)光反馈下的纳米激光器时序; (b1), (b2) ACF曲线; (c1), (c2) PE曲线. 反馈耦合因子: (a1)—(c1)
图 1 (a1), (a2)光反馈下的纳米激光器时序; (b1), (b2) ACF曲线; (c1), (c2) PE曲线. 反馈耦合因子: (a1)—(c1)













































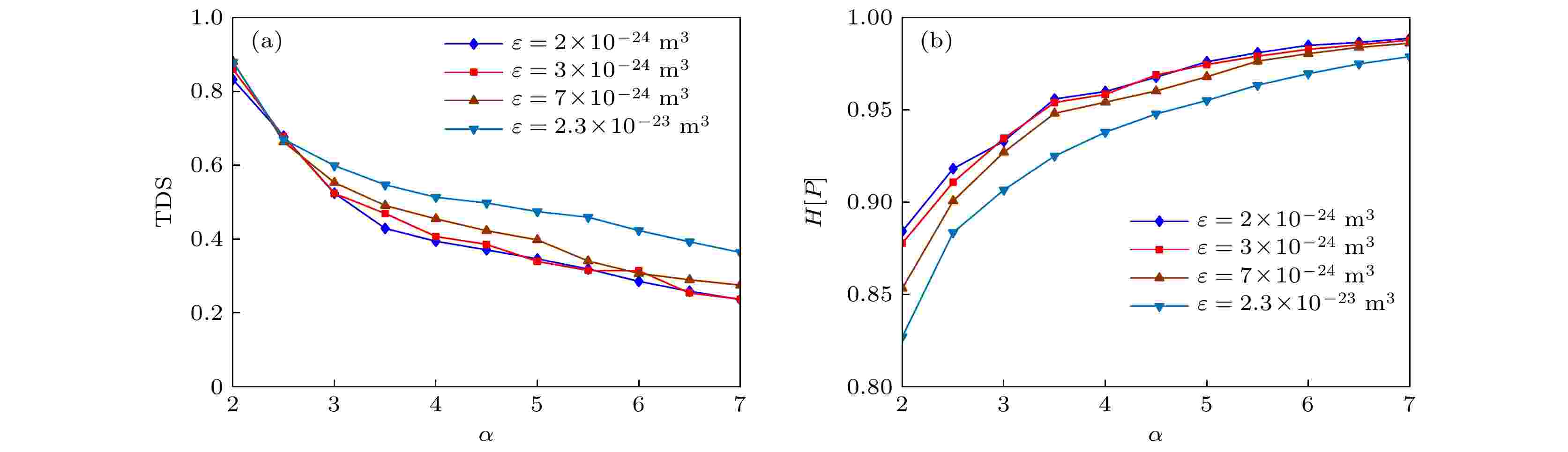 图 2 光反馈纳米激光器 (a) TDS与 (b) H[P ]随着
图 2 光反馈纳米激光器 (a) TDS与 (b) H[P ]随着





















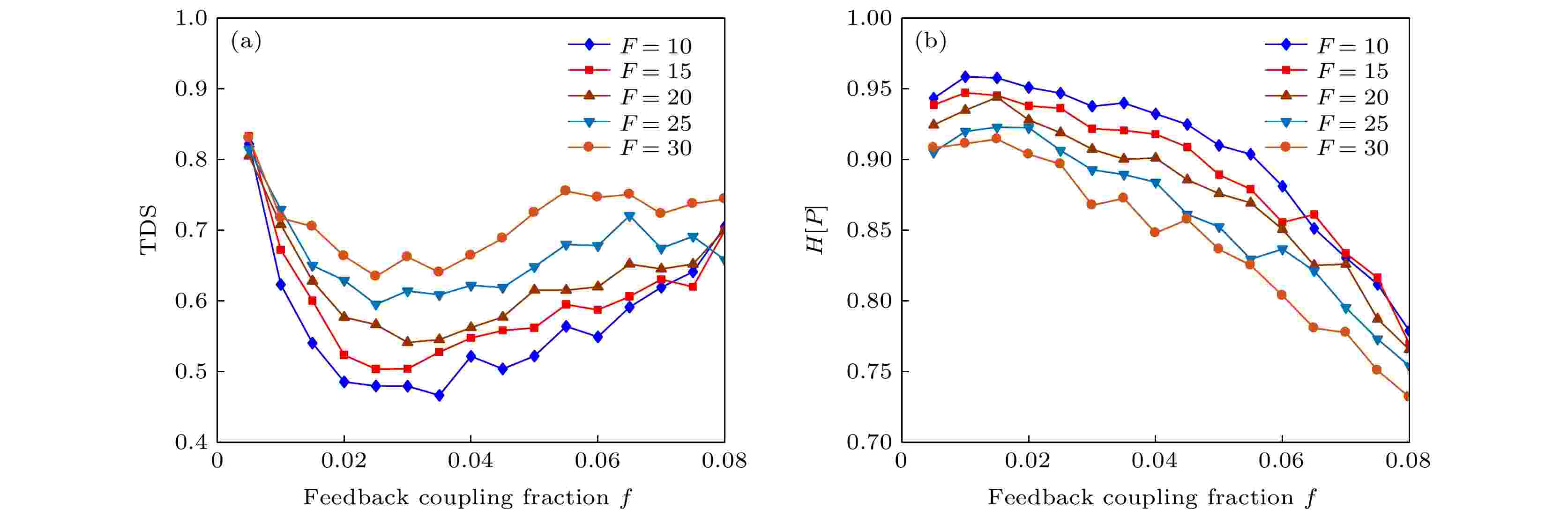 图 3 光反馈纳米激光器 (a) TDS与 (b) H[P] 随着
图 3 光反馈纳米激光器 (a) TDS与 (b) H[P] 随着


 图 4 光反馈纳米激光器 (a) TDS与 (b) H[P] 随着偏置电流的变化
图 4 光反馈纳米激光器 (a) TDS与 (b) H[P] 随着偏置电流的变化


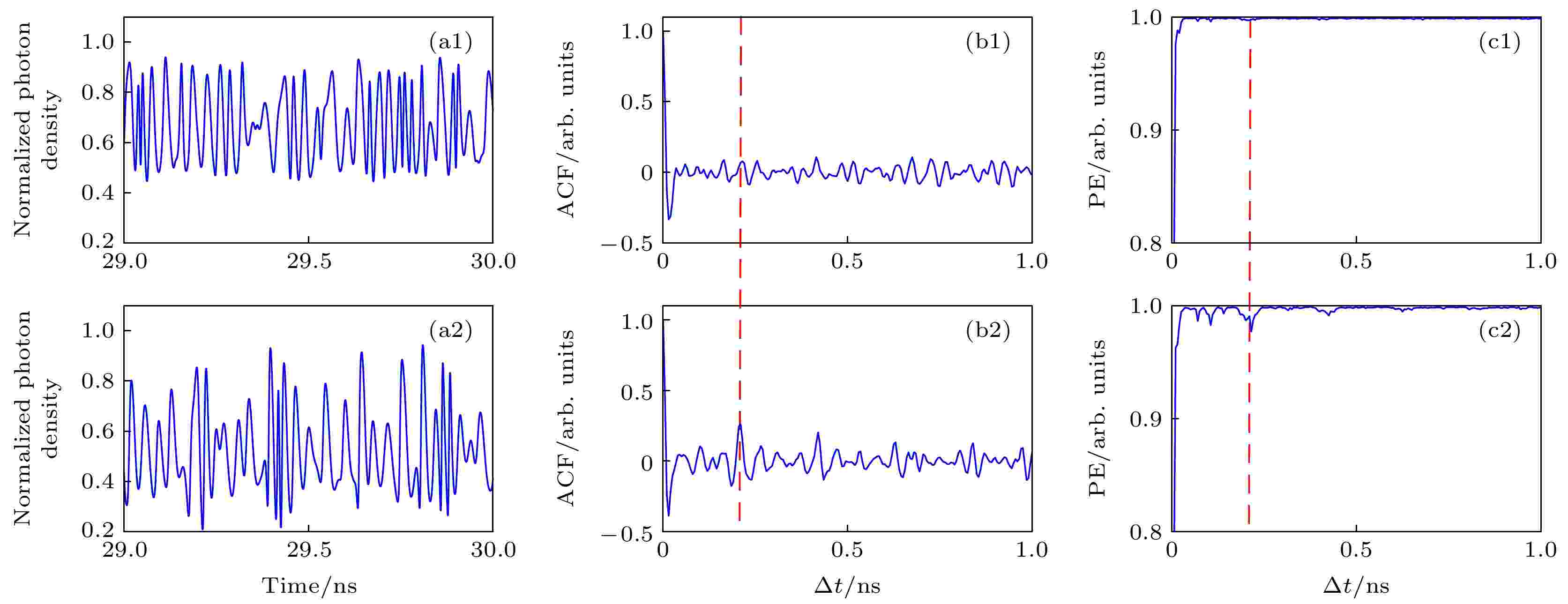 图 5 混沌光注入下从纳米激光器的 (a1), (a2)时序; (b1), (b2)ACF曲线; (c1), (c2) PE曲线. 注入强度(a1)—(c1)
图 5 混沌光注入下从纳米激光器的 (a1), (a2)时序; (b1), (b2)ACF曲线; (c1), (c2) PE曲线. 注入强度(a1)—(c1)














 图 6 在不同F, β及偏置电流下, 从纳米激光器混沌输出的H[P ]随失谐频率及注入强度变化的二维映射 (a1)—(a3)
图 6 在不同F, β及偏置电流下, 从纳米激光器混沌输出的H[P ]随失谐频率及注入强度变化的二维映射 (a1)—(a3)




















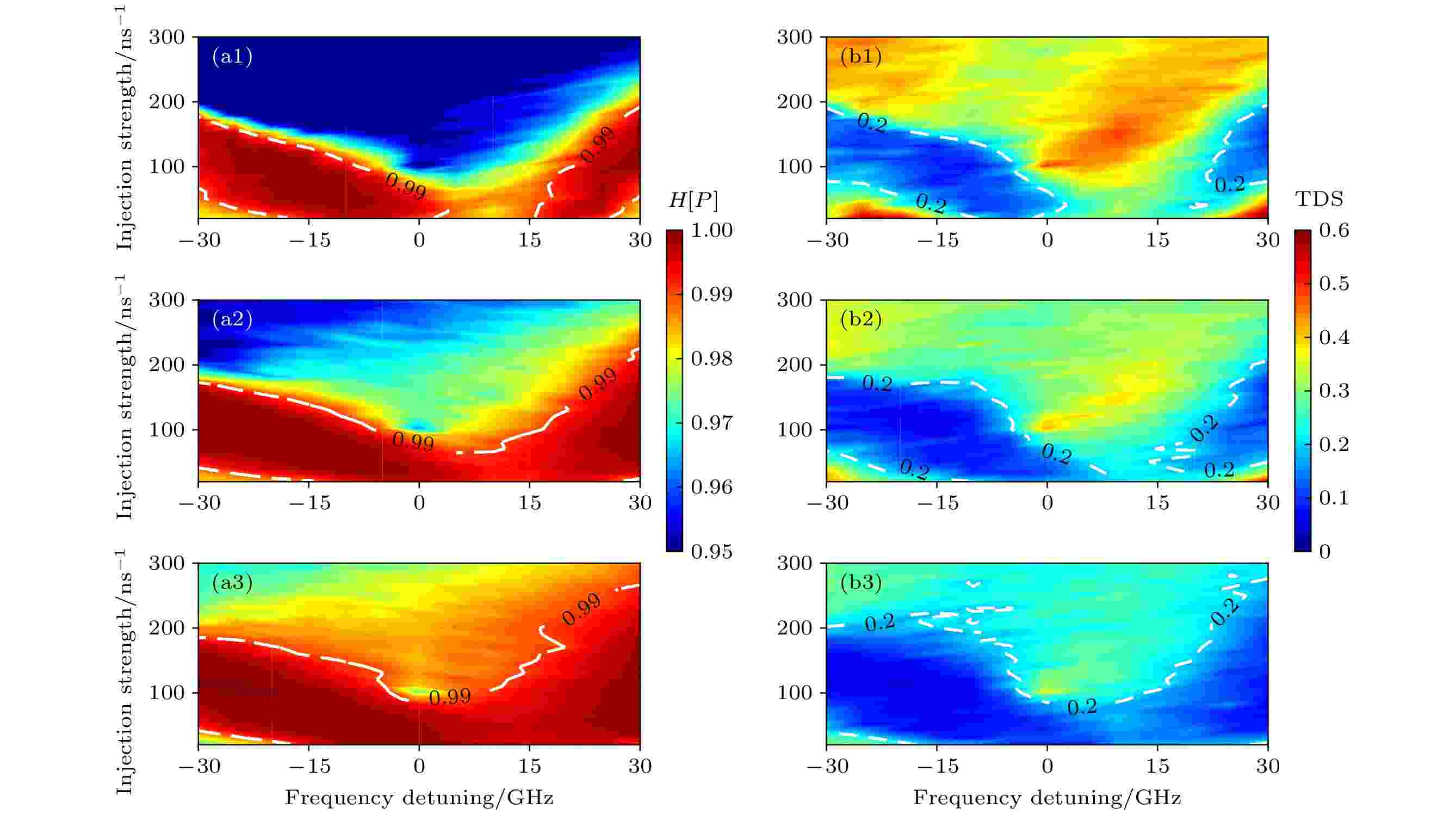 图 7 在不同线宽增强因子下, 从纳米激光器混沌输出的 (a1)—(a3)H[P ]及(b1)—(b3)时延特征峰值随失谐频率及注入强度变化的二维映射. (a1), (b1)
图 7 在不同线宽增强因子下, 从纳米激光器混沌输出的 (a1)—(a3)H[P ]及(b1)—(b3)时延特征峰值随失谐频率及注入强度变化的二维映射. (a1), (b1)









