摘要: 按照章等[Zhang Y Z, Liu Z Y, Mahajan S M, Xie T, Liu J
2017 Phys. Plasmas 24 122304 ]发展的漂移波-带状流理论, 将多重尺度导数展开法应用到电子漂移动理学方程, 零级为描述微观尺度捕获电子模的线性本征模方程, 一级为介观尺度受带状流调制的捕获电子模的包络方程. 其中线性本征模方程已经在谢等[Xie T, Zhang Y Z, Mahajan S M, Wu F, He Hongda, Liu Z Y
2019 Phys. Plasmas 26 022503 ]的研究中被求解, 利用该文得到的捕获电子模的本征值和二维模式结构计算包络方程中的群速度. 径向群速度由托卡马克磁场的测地曲率贡献, 极向群速度来自逆磁漂移速度和法向曲率, 它们仅是极向角的函数, 后者给出极向角到时间的映射. 径向群速度作为时间的函数, 其周期在毫秒量级, 具有快速过零的特征. 这为研究捕获电子模驱动带状流提供了充实的理论基础.
关键词: 托卡马克 /
捕获电子模 /
群速度 /
带状流 English Abstract Group velocity in spatiotemporal representation of collisionless trapped electron mode in tokamak Liu Zhao-Yang 1 ,Zhang Yang-Zhong 2 ,Xie Tao 3 ,Liu A-Di 1 ,Zhou Chu 1 1.School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. U1967206, 11975231, 11805203, 11775222), the National MCF Energy R & D Program, China (Grant Nos. 2018YFE0311200, 2017YFE0301204), and the Key Research Program of Frontier Sciences, Chinese Academy of Sciences (Grant No. QYZDB-SSW-SYS004)Received Date: 27 November 2020Accepted Date: 19 January 2021Available Online: 29 May 2021Published Online: 05 June 2021Abstract: The multiple scale derivative expansion method is used to manipulate the electron drift kinetic equation, following the theoretical framework of drift wave–zonal flow system developed by Zhang et al. [Zhang Y Z, Liu Z Y, Mahajan S M, Xie T, Liu J 2017 Phys. Plasmas 24 122304 ]. At the zeroth order it is the linear eigenmode equation describing the trapped electron mode on a mirco-scale. At the first order it is the envelop equation for trapped electron mode modulated by the zonal flow on a meso-scale. The eigenmode equation has been solved by Xie et al. [Xie T, Zhang Y Z, Mahajan S M, Wu F, He Hongda, Liu Z Y 2019 Phys. Plasmas 26 022503 ] to obtain the eigenvalue and two-dimensional mode structure of trapped electron mode. These are essential components in calculating group velocities contained in the envelop equation. The radial group velocity arises from the geodesic curvature of magnetic field in tokamak. The poloidal group velocity stems from the normal curvature and diamagnetic drift velocity, which yields the mapping between the poloidal angle and time. Since the radial group velocity is also a function of poloidal angle, it is mapped to a periodic function of time with a period of milliseconds. The numerical results indicate the rapid zero-crossing, which is significant in the drift wave – zonal flow system and provides a sound foundation for studying zonal flow driven by trapped electron mode.Keywords: tokamak /trapped electron mode /group velocity /zonal flow 全文HTML --> --> --> 1.引 言 托卡马克低-高约束模(L-H)转换的物理机制是长期困扰学术界的难题之一, 目前被普遍接受的观点是带状流在其中扮演关键角色[1 -3 ] . 尽管大部分理论基于本征模方法讨论漂移波湍流激发带状流的问题[4 -6 ] , 然而如何正确地计算两个非线性量: 雷诺协强和漂移波群速度仍然是一个开放问题. 文献[7 ]以弱上下不对称气球理论[8 ,9 ] 为基础, 采用非线性始值方法求解了流体框架下的离子温度梯度模-低频带状流系统, 结果表明带状流在纯相位调制(没有线性不稳定性)下也能增长, 漂移波的群速度在其中起重要作用, 它描述了受带状流调制的漂移波包络的运动模式, 对理解托卡马克的漂移波-带状流系统有关键意义[7 ] . 该文描述漂移波-带状流系统的基本方程是在时空表象中, 包含群速度的包络方程和包含雷诺协强的带状流方程. 这种方法不仅需要知道色散关系, 还需要知道模式的二维结构. 本文的目的是从电子漂移动理学方程出发, 按文献[7 ]所建议的方法计算无碰撞捕获电子模[10 ] 在时空表象中的群速度.[11 ] , 对满足色散关系$\omega = \omega \left( k \right)$ 的波包, 其群速度为${V_g} \equiv \partial \omega /\partial k$ , 这里$\omega $ 和k 分别表示波的频率和波数. 目前, 几乎所有关于托卡马克漂移波的理论都是按照朗道的方法定义群速度[4 ,6 ,12 -15 ] . 然而, 按文献[7 ]发展的漂移波-带状流理论, 却有意回避傅氏表象, 这里有一个重要思考. 托卡马克中的漂移波是附属在有理面附近的局部模, 服从自然边界条件(由方程自身给出的边界条件, 而非外加的边界条件). 然而, 傅氏表象要求外加的周期边界条件, 这与自然边界条件相矛盾. 在平板模型中漂移波是以每个有理面为中心的单模, 通过磁场曲率与多个相邻有理面的单模耦合形成环形模. 这类模在求出模结构之前并不知道“径向边界”的具体位置, 甚至确切定义, 使得傅氏表象应用在径向缺乏坚实基础. 而弱上下不对称气球理论恰恰可以给出待求的, 满足自然边界条件的二维模式结构[8 ,9 ] . 另一方面, 按文献[7 ]的方法计算群速度在时空表象中的公式, 当应用于简单几何, 其结果与采用色散关系方法所得的结果一致.[16 -18 ] 出发, 采用导数展开法[19 ] 计算托卡马克无碰撞捕获电子模的群速度. 第2 节给出受带状流调制的电子漂移动理学方程, 对其作导数展开后, 零级即描述微观尺度捕获电子模的线性本征模方程, 一级为介观尺度的包络方程. 第3 节利用文献[20 ]求得的捕获电子模的本征值和扰动电势, 计算扰动密度和扰动压强的二维模式结构, 代入包络方程计算捕获电子模的群速度. 第4 节是总结和讨论.2.捕获电子模的多重尺度导数展开法 22.1.受带状流调制的电子漂移动理学方程 2.1.受带状流调制的电子漂移动理学方程 本文所讨论的无碰撞捕获电子模建立在大环状比、上下对称、同心圆磁面的托卡马克平衡之上, 出发点是对静电扰动线性化的电子漂移动理学方程[16 -18 ] :f 是扰动分布函数, $\varphi $ 是扰动电势, ${{{v}}_{\rm{de}}} \equiv $ $ - \left[ {c{m_{\rm{e}}}/(eB)} \right]\left( {v_{//}^2 + v_ \bot ^2/2} \right){{b}} \times {{\kappa }}$ 是电子曲率漂移速度, ${v_{//}}$ 和${v_ \bot }$ 分别是电子的平行和垂直速度, ${{b}} \equiv $ $ {{B}}/B$ 是沿着磁场方向的单位矢量, ${{\kappa }} \equiv {{b}} \cdot \nabla {{b}}$ 是磁场曲率, ${F_{\rm{M}}} \equiv {n_{\rm{e}}}{\left[ {{m_{\rm{e}}}/(2{\text{π}} {T_{\rm{e}}})} \right]^{3/2}}\exp \left[ { - {m_{\rm{e}}}{v^2}/(2{T_{\rm{e}}})} \right]$ 是平衡电子麦克斯韦分布函数, ${v^2} = v_{/\!/} ^2 + v_ \bot ^2$ , ${m_{\rm{e}}}$ , ${n_{\rm{e}}}$ 和${T_{\rm{e}}}$ 分别是电子质量, 平衡密度和温度, e 是单位电荷, c 是光速.$\left( {r, \vartheta, \zeta } \right)$ 分别代表径向、极向和环向坐标, 扰动电势归一化到电子热能: $e\varphi /{T_{\rm{e}}} \to $ $ \varphi$ , 平衡分布函数归一化到电子密度: ${F_{\rm{M}}}/{n_{\rm{e}}} \to {F_{\rm{M}}}$ , 平行和垂直速度归一化到电子热速度: ${v_{\rm{te}}} \equiv $ $ \sqrt {2{T_{\rm{e}}}/{m_{\rm{e}}}}$ , ${\hat v_{/\!/}} \equiv {v_{/\!/} }/{v_{\rm{te}}}$ , ${\hat v_ \bot } \equiv {v_ \bot }/{v_{\rm{te}}}$ . 定义$y \equiv r\vartheta $ , 曲率频率算子:$\sin \vartheta $ 和$\cos \vartheta $ 分别代表磁场的测地和法向曲率; R 是托卡马克大半径. 逆磁频率算子${L_n} \equiv - {\left( {\partial \ln {n_{\rm{e}}}/\partial r} \right)^{ - 1}}$ 表示密度梯度长度, ${\eta _{\rm{e}}} \equiv $ $ {\rm{d}}\ln {T_{\rm{e}}}/{\rm{d}}\ln {n_{\rm{e}}}$ . 考虑带状流的多普勒频移调制作用, 电子漂移动理学方程(1 )式可写为$\bar {{\upsilon}} \equiv \left[ {c{T_{\rm{e}}}/(eB)} \right]{{b}} \times \nabla \bar \varphi \equiv \bar \upsilon {{{e}}_\vartheta }$ 表示(沿着极向${{{e}}_\vartheta }$ )带状流, $\bar \varphi $ 是带状电势, 它具有环向和极向对称, 径向波长在介观尺度的特征[3 ] .2.2.由导数展开法得到的零级和一级方程 -->2.2.由导数展开法得到的零级和一级方程 多重尺度问题(微观和介观尺度)可以采用导数展开法[19 ] :${\varepsilon _{\rm{E}}} \ll 1$ 是小量标签; $\left( {t, r, y} \right)$ 表示慢尺度变量(具轴对称性, 环向模数$n = 0$ ); $\left( {\tilde t, \tilde r, \tilde y, \tilde \zeta } \right)$ 表示快尺度变量(高环向模数: $n \gg 1$ ), 扰动分布函数和电势包含两个部分: 受带状流调制的(介观尺度)慢变包络和(微观尺度)快变函数:f 对速度空间积分后就是扰动密度, 一个简单假设是其受带状流调制的包络满足绝热关系: $\bar f\left( {t, r, y} \right) = $ $ \bar \phi \left( {t, r, y} \right)$ . 后面将看到这是导数展开法给出的零级方程恰是描述捕获电子模的漂移动理学方程的充分条件.${\upsilon _*} \equiv {\rho _{\rm{s}}}{c_{\rm{s}}}/{L_n}$ , ${c_{\rm{s}}} \equiv $ $ \sqrt {{T_{\rm{e}}}/{m_{\rm{i}}}}$ 是离子声速, ${\rho _{\rm{s}}} \equiv {c_{\rm{s}}}/{\omega _{\rm{ci}}}$ 是电子温度下的离子拉莫尔半径; ${\omega _{\rm{ci}}} \equiv eB/(c{m_{\rm{i}}})$ 是离子回旋频率, ${m_{\rm{i}}}$ 是离子质量; q 是安全因子.4 )式导数展开的过程中, 带状流作为小量处理$\bar \upsilon \to {\varepsilon _{\rm{E}}}\bar \upsilon $ , 得到$\bar f\left( {t, r, y} \right) = \bar \phi \left( {t, r, y} \right)$ 条件下, 零级方程即描述捕获电子模的漂移动理学方程:12 )式即文献[20 ]中的(1 )式.$\hat v_{/\!/} ^2 \ll \hat v_ \bot ^2 \approx {\hat v^2}$ . 对高n 模, $\tilde \varphi \left( {r, y, \zeta } \right) = {\tilde \varphi _m}\left( {r, \vartheta } \right) \cdot $ ${{\rm{e}}^{{\rm{i}}n\zeta - {\rm{i}}m\vartheta }}$ , $\tilde h( r, y, \zeta; $ $ {v_{/\!/} }, {v_ \bot } ) = {\tilde h_m}\left( {r, \vartheta;{v_{/\!/} }, {v_ \bot }} \right){{\rm{e}}^{{\rm{i}}n\zeta - {\rm{i}}m\vartheta }}$ , ${k_\vartheta } \equiv m/{r_j}$ , m 表示中心极向模数, ${r_j}$ 是有理面位置, 对局部模有$r \approx {r_j}$ .13 )式对速度空间积分, ${\hat v_{/\!/} }$ 的矩量为零, 因为在大回弹频率近似下, 捕获电子的平行速度在一个回弹周期内平均为零. 速度$\hat v$ 的零次和二次矩量分别对应非绝热扰动密度${\tilde n_m}\left( {r, \vartheta } \right) = $ $ {\tilde \varphi _m}\left( {r, \vartheta } \right) + {\tilde n_{{\rm{na}}}}\left( {r, \vartheta } \right)$ . 另一方面, 捕获电子模在有理面附近被激发, 离开有理面将受到磁剪切阻尼[21 ] , 它在径向是驻波, 还需要对径向快尺度求平均[7 ] . 由此得到受带状流调制的捕获电子模的包络方程:18 )式中${\tilde \varphi _m}$ , ${\tilde n_m}$ 和${\tilde \varepsilon _m}$ 分别代表电势、密度和热能的涨落, 这些量是物理观测量. 从测量角度而言, 单纯测量这些量的本身仅可能是实量, 但在本征模理论构架中这些量的虚部也有物理意义. 在托卡马克输运的准线性理论中, 包括计算粒子流和热流, 涉及密度、压强和电势极向导数的乘积, 后者与电势有90o的相差, 而(18 )式所计算的平均中并没有上述的90o相差问题. 最终需要计算的量是群速度, 保留这些量的虚部将导致群速度存在虚部, 这在物理上没有意义, 因为群速度是可观测量, 它代表波包传播速度. 注意到本文计算的群速度是介观尺度量, 而捕获电子模的线性增长时间在微观尺度, 其在介观尺度时间内已经达到饱和. 另一方面, 托卡马克是一个开放系统, 外部因素如加热、加料等, 使得引起不稳定性的自由能总是存在. 因此本文假设线性二维模式结构在进入饱和阶段后没有重要变化, (18 )式中的扰动电势、密度和压强作为可观测量仅取实部, 这保证了所计算的群速度是实的.3.捕获电子模的群速度 23.1.捕获电子模的二维模式结构 3.1.捕获电子模的二维模式结构 由第2 节可以看到, 按照文献[7 ]的方法在时空表象中计算捕获电子模的群速度需要知道其二维模式结构. 电子漂移动理学方程(12 )式已经在文献[20 ]中采用弱上下不对称气球理论[8 ,9 ] 求解, 这里直接引用该文的结果, 选取的托卡马克装置的基本平衡参数如表1 所列.R /ma /m${r_j}/a$ ${T_{\rm{e}}}$/eV ${\tau _{\rm{e}}}$ q B /T$\hat s$ ${L_n}/R$ ${\eta _{\rm{e}}}$ ${\eta _{\rm{i}}}$ n 1.65 0.4 0.41 250 10 1 1.35 1 0.1 1 0 –44
表1 基本平衡参数Table1. Basic equilibrium parameters.$\hat \omega \equiv \omega /{\omega _{*{\rm{e}}}} = $ $ 0.4215 + 0.1133{\rm{i}}$ , ${\omega _{*{\rm{e}}}} \equiv - {k_\vartheta }{\upsilon _*}$ . 捕获电子模扰动电势的二维模式结构如图1 , 这里${\tilde \varphi _n}\left( {r, \vartheta } \right) \equiv $ $ {\tilde \varphi _m}\left( {r, \vartheta } \right){{\rm{e}}^{ - {\rm{i}}m\vartheta }}$ , $\rho \equiv r/a$ . 由图1 可以看到二维模式结构的中心相对赤道面几乎没有偏移, 但存在较小的上下不对称性, 其径向关联长度约为极向的2—3倍.图 1 (a) 捕获电子模扰动电势${\tilde \varphi _n}\left( {r, \vartheta } \right)$ 实部的等高线图; (b) 坏曲率区的放大图Figure1. (a) Level contours of the real parts of the perturbed electrostatic potential ${\tilde \varphi _n}\left( {r, \vartheta } \right)$ for trapped electron mode; (b) the close-up view in bad curvature region.20 ]的方法, 可以得到捕获电子模的整体本征值和扰动电势, 现在利用该结果计算扰动密度和扰动压强的二维模式结构. 出发点是捕获电子模的非绝热响应分布函数(文献[20 ]中的(A10)式):$\left\langle {\cdots} \right\rangle \equiv \dfrac{\displaystyle\oint {{\rm{d}}\vartheta } ( {\cdots} )/{v_{/\!/} }}{\displaystyle\oint {{\rm{d}}\vartheta } /{v_{/\!/} }}$ (${v_{/\!/} } \!\sim\!\! \sqrt {{\kappa ^2} \!-\! {{\sin }^2}\!\left( {\vartheta}/{2} \right)}$ , ${\kappa ^2} \equiv {\sin ^2}\left( {{\vartheta _r}/2} \right)$ , ${\vartheta _r}$ 是捕获电子转向点${v_{/\!/} } = 0$ 处的极向角)表示对捕获电子的回弹周期求平均. 对捕获电子的速度空间积分可写为(文献[20 ]中的(9)式)$\varepsilon \equiv r/R$ , $\kappa _{\min }^2 \equiv {\sin ^2}\left( {\vartheta /2} \right)$ . 将(19 )式和(20 )式代入(14 )式得到非绝热扰动密度的表达式:$q\left( r \right) \approx q\left( {{r_j}} \right) + $ $ x/n$ , $m = nq\left( {{r_j}} \right)$ , $x \equiv {k_\vartheta }\hat s\left( {r - {r_j}} \right)$ , $\hat s$ 表示磁剪切,$\zeta _{\rm{e}}^2 \equiv \omega /\left\langle {{\omega _{\rm{de}}}} \right\rangle $ , $Z\left( {{\zeta _{\rm{e}}}} \right) \equiv {{\text{π}} ^{ - 1/2}}\displaystyle\int_{\rm{L}} {{\rm{d}}\hat v} \exp( { - {{\hat v}^2}} )/( \hat v - {\zeta _{\rm{e}}} )$ 是等离子体色散函数. 将前面计算得到的扰动电势${\tilde \varphi _n}\left( {r, \vartheta } \right)$ 代入(21 )式, 数值积分得到扰动密度的二维模式结构如图2 , 这里$\tilde n\left( {r, \vartheta } \right) \equiv {\tilde n_m}\left( {r, \vartheta } \right){{\rm{e}}^{ - {\rm{i}}m\vartheta }}$ .图 2 (a) 捕获电子模扰动密度$\tilde n\left( {r, \vartheta } \right)$ 实部的等高线图; (b) 坏曲率区的放大图Figure2. (a) Level contours of the real parts of the perturbed density $\tilde n\left( {r, \vartheta } \right)$ for trapped electron mode; (b) the close-up view in bad curvature region.19 )式和(20 )式代入(15 )式得到扰动压强的表达式:图3 , 这里$\tilde \varepsilon \left( {r, \vartheta } \right) \equiv {\tilde \varepsilon _m}\left( {r, \vartheta } \right){{\rm{e}}^{ - {\rm{i}}m\vartheta }}$ .图 3 (a) 捕获电子模扰动压强$\tilde \varepsilon \left( {r, \vartheta } \right)$ 实部的等高线图; (b) 坏曲率区的放大图Figure3. (a) Level contours of the real parts of the perturbed pressure $\tilde \varepsilon \left( {r, \vartheta } \right)$ for trapped electron mode; (b) the close-up view in bad curvature region.3.2.捕获电子模的径向和极向群速度, 径向群速度的时间结构 -->3.2.捕获电子模的径向和极向群速度, 径向群速度的时间结构 将3.1 节计算得到的${\tilde \varphi _m}\left( {r, \vartheta } \right)$ , ${\tilde n_m}\left( {r, \vartheta } \right)$ 和${\tilde \varepsilon _m}\left( {r, \vartheta } \right)$ 的实部代入(18 )式, 数值积分得到两个平均量如图4 . 它们在好曲率($\vartheta \sim 0$ )和坏曲率($\vartheta \sim $ $ \pm {\text{π}} $ )区都有快速变化, 而在其他区域相对比较光滑.图 4 (18 )式定义的两个平均量 (a)$\bar E\left( \vartheta \right)$ ; (b)$\bar \varPhi \left( \vartheta \right)$ Figure4. Two average quantities and defined in Equation (18 ): (a) $\bar E\left( \vartheta \right)$ ; (b) $\bar \varPhi \left( \vartheta \right)$ .17 )式计算得到捕获电子模的径向和极向群速度分别如图5(a) 和图5(b) . 从图5(a) 和图5(b) 可以看到, 径向群速度来自磁场的测地曲率, 极向结构基本是一次正弦$ \sim \sin \vartheta $ . 极向群速度主要来自逆磁漂移速度$ \sim {\upsilon _*}$ , 而法向曲率$ \sim \cos \vartheta $ 的贡献较小. 按照一阶偏微分方程的特征线解法, (16 )式中的极向特征线为${\rm{d}}\vartheta /{\rm{d}}t = {\upsilon _{\rm{gy}}}\left( \vartheta \right)/{r_j}$ , 它提供了极向角到时间的映射$t = \displaystyle\int_0^\vartheta {{r_j}{\rm{d}}\vartheta '} /{\upsilon _{\rm{gy}}}\left( {\vartheta '} \right)$ , 这里积分常数设为$\vartheta (t = 0) $ $ = 0$ . 这样径向群速度可以写为时间的函数, 如图5(c) 所示. 从图5(c) 可见径向群速度是时间的周期函数, 周期约为1.5 ms, 在t = 0 ms向上过零, 而在t = 0.7 ms向下过零, 前者过零快于后者.图 5 捕获电子模的 (a) 径向群速度${\upsilon _{\rm{gr}}}\left( \vartheta \right)$ , (b) 极向群速度${\upsilon _{\rm{gy}}}\left( \vartheta \right)$ 和(c) 径向群速度随时间的变化${\upsilon _{\rm{gr}}}\left( t \right)$ Figure5. (a) Radial group velocity ${\upsilon _{\rm{gr}}}\left( \vartheta \right)$ , (b) poloidal group velocity ${\upsilon _{\rm{gy}}}\left( \vartheta \right)$ , and (c) radial group velocity versus time ${\upsilon _{\rm{gr}}}\left( t \right)$ for trapped electron mode.4.总 结 从电子漂移动理学方程出发, 采用多重尺度导数展开法, 零级为描述微观尺度捕获电子模的线性本征模方程, 一级为介观尺度的包络方程. 利用文献[20 ]中求得的捕获电子模的线性本征值和扰动电势, 计算了扰动密度和扰动压强的二维模式结构. 代入包络方程对速度空间积分和径向快尺度求平均, 得到捕获电子模的径向和极向群速度. 径向群速度由磁场的测地曲率贡献, 极向结构基本是一次正弦$ \sim \sin \vartheta $ . 极向群速度包含两项: 逆磁漂移速度${\upsilon _*}$ 和法向曲率$ \sim \cos \vartheta $ , 二者相比$ \sim R/{L_n}$ , 因此前者占主导地位. 包络方程描述了捕获电子模包络的传播行为, 它是一阶偏微分方程, 其极向特征线给出极向角到时间的映射$\vartheta \left( t \right)$ . 因此径向群速度可以写为时间的周期函数, 其周期在毫秒量级, 具有快速过零的特征. 为简化计算本文采用的是圆截面位形, 对实际的托卡马克放电的非圆截面位形, 拉长比和三角形变等几何因子将导致测地和法向曲率由一次正弦和余弦结构变为更复杂的角向结构, 可以预见它们将对径向和极向群速度产生重要的定量修正.7 ]的理论构架, 仅计算时空表象中的群速度, 对无磁剪切平板漂移波, 容易证明它与采用色散关系方法所得的结果一致, 但对有剪切的环形系统, 两种途径的比较不是本文探讨的对象; 2) 环形效应对捕获电子模的径向群速度非常重要, 其极向结构来自磁场测地曲率的贡献; 3) 在计算群速度的过程中仅取扰动电势、密度和压强的实部, 以保证所计算的群速度是实的. 这里假设了线性二维模式结构在进入饱和阶段后没有重要变化, 其非线性演化问题留待将来研究.[7 ] ), 这可能与很多托卡马克实验观测到的阵发现象有关. 文献[7 ]中还指出由于径向群速度周期性过零, 低频带状流也会周期性地振荡, 这可能解释实验和模拟中看到的低频带状流的频率. 瞬子在径向群速度过零时开始形成, 随后其本身, 以及对应的频率快速增长, 如果其瞬时频率达到约20 kHz, 能够共振激发测地声模[22 ] , 这为解释测地声模的阵发性激发和传播特性提供了理论基础, 对其详细讨论将由另文论述. 




































































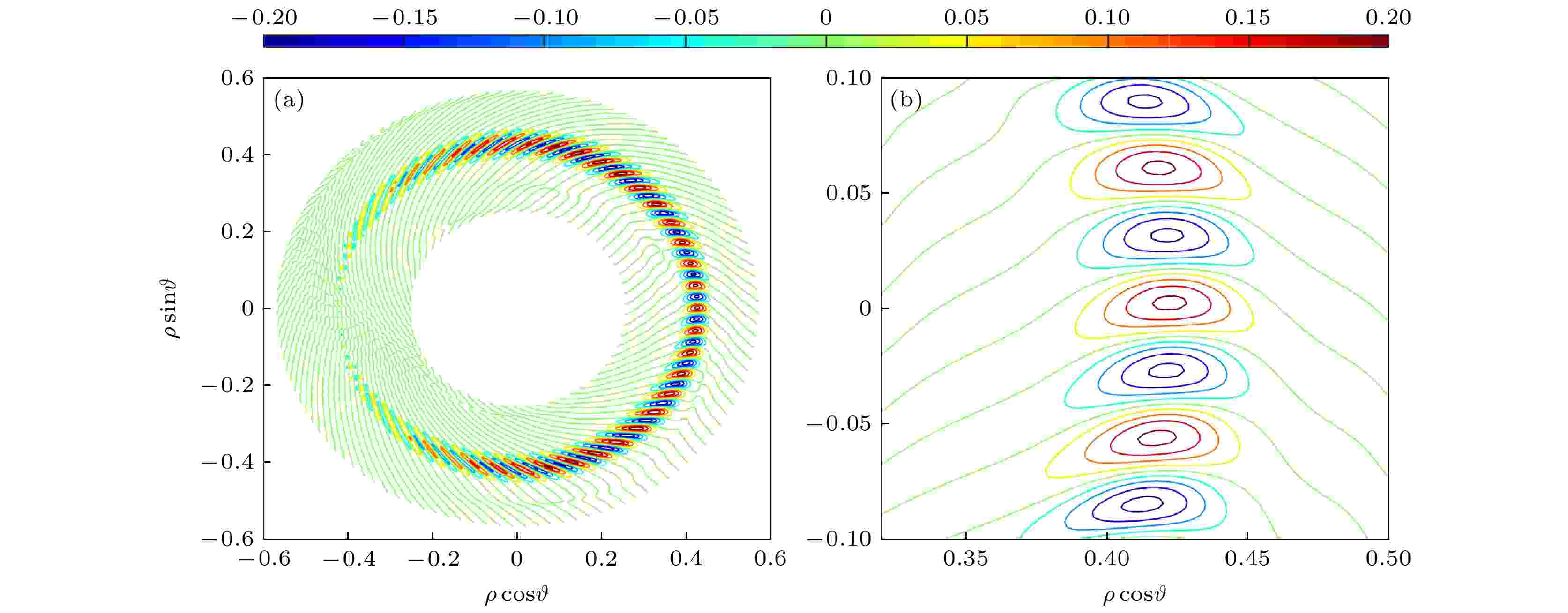 图 1 (a) 捕获电子模扰动电势
图 1 (a) 捕获电子模扰动电势

















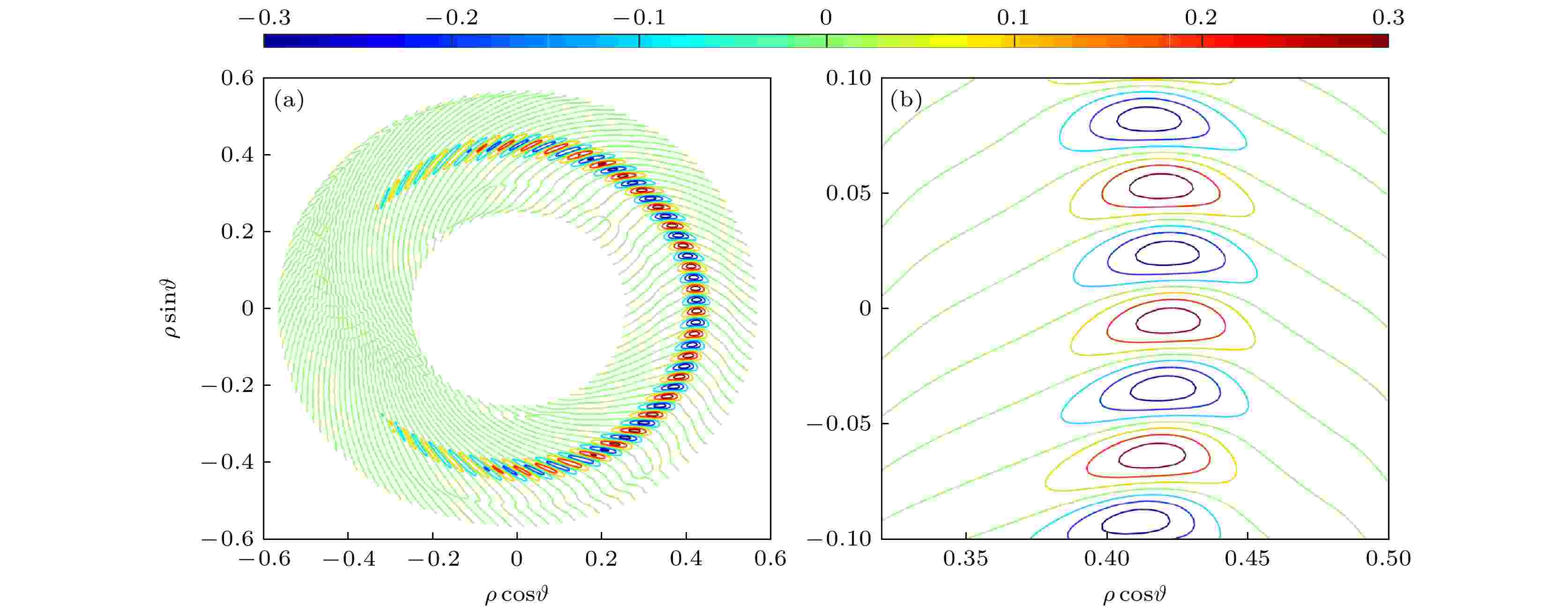 图 2 (a) 捕获电子模扰动密度
图 2 (a) 捕获电子模扰动密度


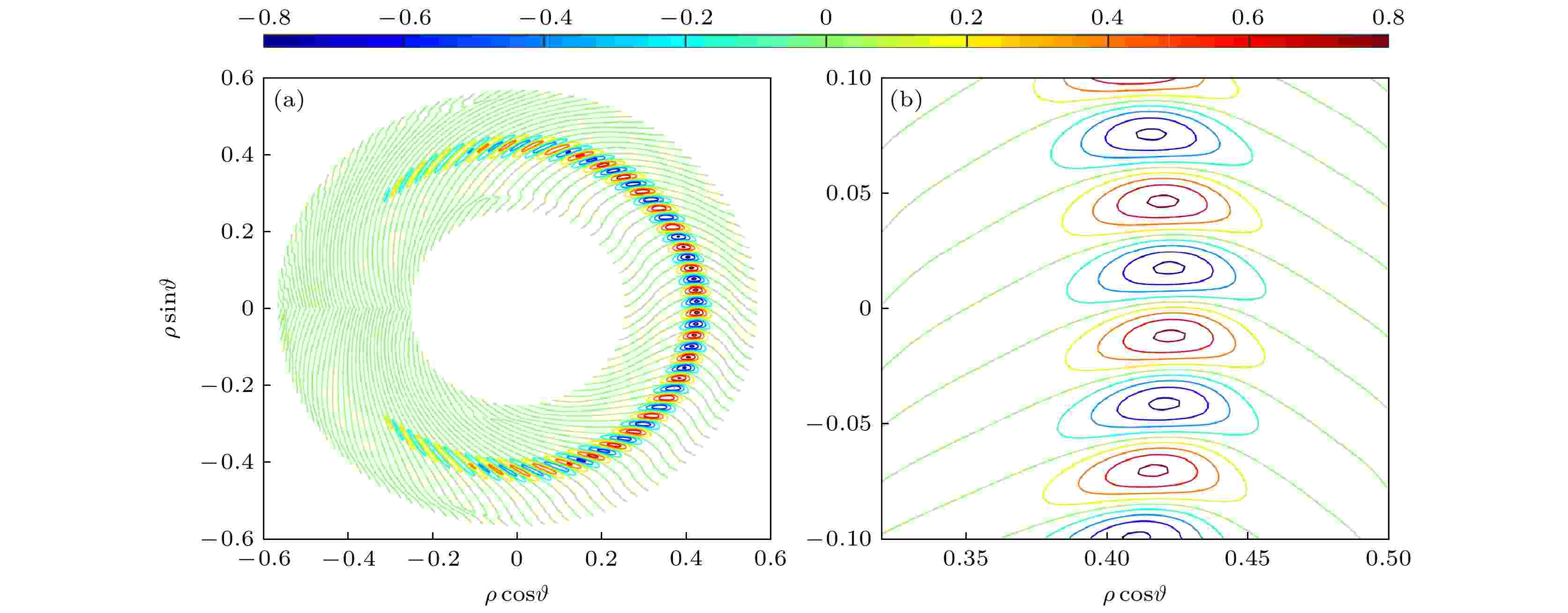 图 3 (a) 捕获电子模扰动压强
图 3 (a) 捕获电子模扰动压强







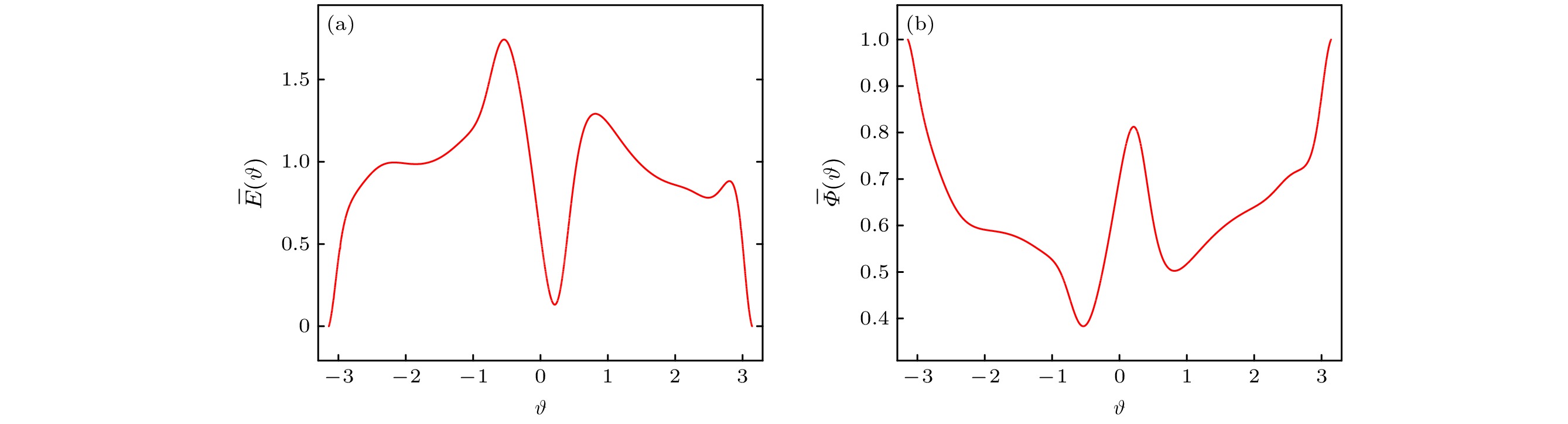 图 4 (18)式定义的两个平均量 (a)
图 4 (18)式定义的两个平均量 (a)










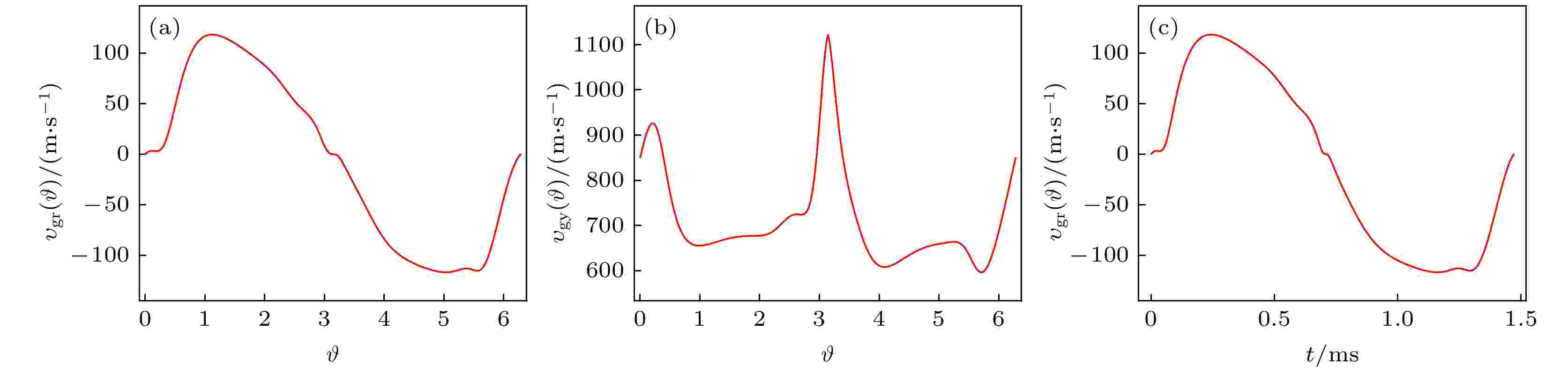 图 5 捕获电子模的 (a) 径向群速度
图 5 捕获电子模的 (a) 径向群速度










