删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

二维材料<i>X</i>Te<sub>2</sub> (<i>X</i> = Pd, Pt)热电性能的第一性原理计算

本站小编 Free考研考试/2021-12-29
摘要:利用密度泛函理论结合玻尔兹曼输运方程, 预测了二维层状热电材料XTe2 (X = Pd, Pt)的热电性质. 两种材料都具有较低的热导率, 材料的晶格热导率随温度的升高而降低, 且表现出各向异性. 而电子热导率随温度的升高而升高. 在较低温时, 晶格热导率对总热导率的贡献占据主导地位. 较高的载流子迁移率、电导率及塞贝克系数也对材料的热电转换效率产生极大的影响, 展现出较为优异的电输运性能. 对比分析PdTe2和PtTe2两种材料的ZT值, 发现两种材料的热电性能以p型掺杂为主. PtTe2单层的ZT值高于PdTe2单层, 并且PtTe2单层在常温下的ZT峰值可达到2.75, 是一种极具潜力的热电材料.
关键词: 第一性原理计算/
输运性质/
热电效应/
电导及热导

English Abstract


全文HTML

--> --> -->
1.引　言
能源危机日益严重, 驱使着新能源领域发展. 作为新型能源材料, 热电材料对环境友好, 能直接将废热、余热转换为电能. 近年来, 热电材料独特的性质引发了人们的关注. 热电转换装置具有体积小、可靠性高、适应温度范围广等优点, 可以将其用于军事、航天、医疗、通信、可穿戴设备等领域. 目前热电装置已初步运用到汽车的废热回收和垃圾燃烧余热发电等方面[1]. 遗憾的是热电材料的转换效率仍受制于热电优值(ZT ). 探索高性能热电材料和提升材料热电性能是研究的两大重点. 提高材料热电性能, 除了可以通过提高功率因子改善材料的电学性质, 还可以通过降低材料的导热系数提高材料的ZT值[2-5]. 二维材料的量子局域效应可以有效提高材料的功率因子, 同时层间的多种界面散射可以增加声子散射, 降低声子热导率[6]. 因此, 二维材料是极具潜力的热电材料, 探究其热电性能已成为科学界的一个热门话题[7,8]. 过渡金属硫化物是典型二维热电材料, 但材料的ZT值并不理想[9-12]. 近年来, 人们对带有S和Se原子的贵金属(如Pd和Pt)化合物进行了大量的理论和实验研究, PdSe2正交结构的热电性质明显优于其六角结构[8,13-18]. Pt基化合物的性能优异, 目前已有实验合成了PbTe-PtTe2的纳米粒子, 增强了材料热电性能[3]. Wang等[19]制备出了具有高导电性的层状PtTe2 鳞片, 但关于层状有序结构XTe2材料的理论研究还比较匮乏. 本文利用第一性原理计算的方法对二维材料XTe2 (X = Pd, Pt)的热电输运性质展开了研究.
2.计算方法
本文采用第一性原理计算软件包VASP来计算材料的晶体结构[20-24]. 计算的结构基于已被实验制备的稳定三维材料PdX2[25,26]. 选取三维材料其中一层作为研究对象, 为避免层间相互作用, 将真空层厚度设定20 ? (1 ? = 0.1 nm). 使用广义梯度近似(GGA)下的Perdew-Burke-Ernzerhof (PBE)来处理交换关联[23]. 平面波基组的截断能设定为 500 eV, 在结构优化和自洽计算中采用布里渊区15 × 15 × 1的k网格点[27]. 为了保证计算的精度, 总能的收敛精度达到10–7 eV, 原子间力的收敛标准为0.001 eV/?. 对于热输运性质, 通过求解玻尔兹曼声子输运方程获得晶格热导率[28,29]. 构建5 × 5 × 1的超胞, 采用有限位移法进行声子谱计算, 进而确定二阶原子间力常数[30], 采用4 × 4 × 1的超胞计算了三阶力常数. 基于玻尔兹曼输运理论获得热电输运参数[27]. 为了得到更准确的热电输运参数, 采用45 × 45 × 1的密集k点网格对倒空间采样进行自洽计算. 弛豫时间τ, 有效质量m*及载流子迁移率μ由Bardeen-Shockley形变势理论得到[31,32]:
$\tau =\frac{\mu {m}^{*}}{e}, $
$\mu =\frac{e{\hbar}^{3}{C}_{2\rm{D}}}{{k}_{\rm{Β}}{T}{m}^{*}{m}_{\rm{d}}{E}_{\rm{l}}{}^{2}},$
其中C2D, m*, md和El分别对应有效弹性模量、输送方向有效质量、平均有效质量及形变势常量, e为电子电量. 用形变势理论来估算弛豫时间是一种可靠的方法, 目前已经成功运用在多种二维层状或三维块体热电材料中[32-34].
3.结果与讨论
二维层状XTe2 (X = Pd, Pt)材料, 空间群为P2_1/c, 具有和石墨烯类似的褶皱结构. 图1展示了XTe2 (X = Pd, Pt)层状材料的晶体结构, 2个X (X = Pd, Pt)原子和3个Te原子, 构成5边网格状. 计算得到的晶格参数信息如表1所示, PdTe2优化后的晶格常数a为6.145 ?, 与已有研究结果6.147, 6.14 ?相吻合[8]. PtTe2的晶格常数a为6.423 ?, 与已有结果6.44 ?相吻合[35]. X (X = Pd, Pt)独立原子坐标为(0.5, 0.5, 0.5/0, 0, 0.5); Te原子独立坐标为(0.62, 0.13, 0.54/0.12, 0.37, 0.46).
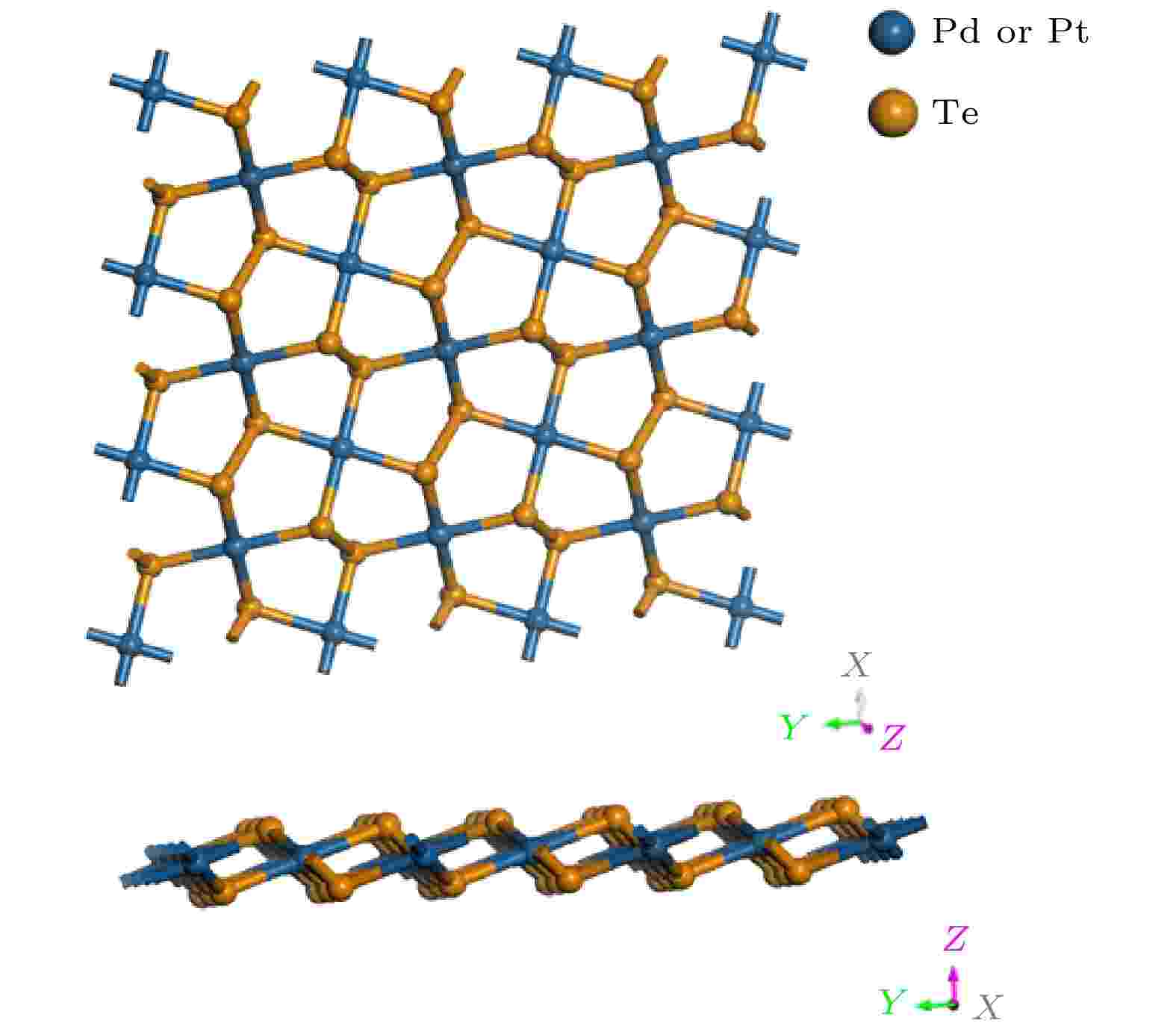图 1 XTe2 (X = Pd, Pt)单层结构的顶视图和侧视图
Figure1. Top and side views of XTe2 (X = Pd, Pt) monolayers

MaterialsResultsa/?b/?
PdTe2Present6.4376.145
Calc.6.44[8], 6.439[35]6.14[8], 6.147[35]
PtTe2Present6.4236.12
Calc.6.44[36]—


表1XTe2 (X = Pd, Pt) 单层的晶格常数(a, b)
Table1.The optimized lattice parameters (a, b) of XTe2 (X = Pd, Pt) monolayers.

XTe2 (X = Pd, Pt)的声子色散图如图2所示. XTe2单层的声子谱在高对称方向上没有虚频, 说明优化后的结构具有热力学稳定性. PdTe2和PtTe2单层声子振动的最高频率分别为6.33, 5.82 THz, 与已有结果6.09, 5.24 THz相吻合[16,36]. PdTe2, PtTe2单层的声子振动最高频率低于常见热电材料PdS2和PdSe2的声子振动频率. 两种材料的声子振动最高频率较低, 则声学分支频率也相应较低. 由于晶格热导率依赖于声学分支, 表明这两种材料的晶格热导率可能低于其他常见热电材料. PtTe2的声子振动频率低于PdTe2的声子振动频率, 这是因为元素Pt的原子质量比Pd更大, 会抑制声学支频率. 这意味着PtTe2可能比PdTe2有更低的晶格热导率, 更优异的热电性能. XTe2 (X = Pd, Pt)材料的能带结构如图3 (a), (b)所示. 层状PdTe2, PtTe2属于间接带隙半导体材料, 价带顶部的能带相比导带底部的能带来说更为陡峭. 计算得到的带隙值分别为1.24, 1.38 eV, 与已有PdTe2的计算结果1.24 eV吻合[8].
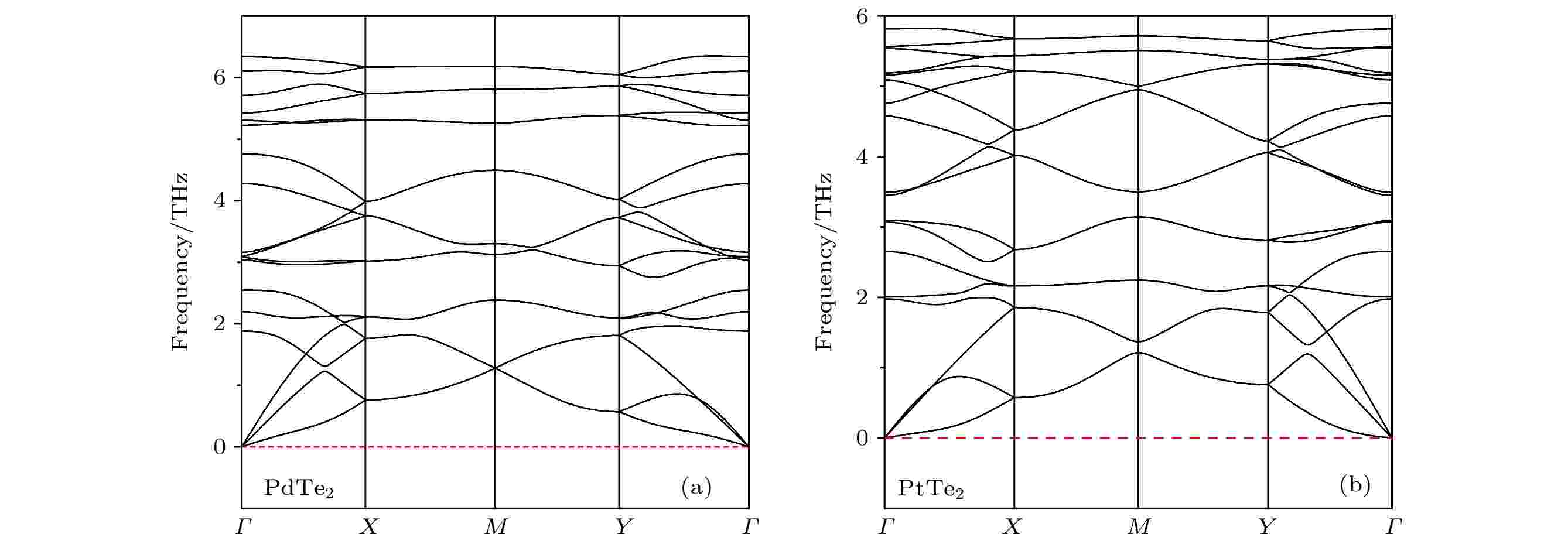图 2 PdTe2 (a)和PtTe2 (b)的声子色散图
Figure2. Calculated phonon dispersion curves of PdTe2 (a)and PtTe2 (b).

图 3 PdTe2 (a)和PtTe2 (b)单层沿布里渊区高对称方向的能带结构
Figure3. Calculated energy-band structure of layered PdTe2 (a) and PtTe2 (b) along high-symmetry directions of the Brillouin zone.

晶格热导主要源于声子间的非谐效应, 是声子模式热导贡献的总和. 每一支声子模式的热导与声子群速度有关, 与声子群速度的平方成正比. 通过声子谱计算了声子群速度, 如图4所示. 图4展示了声学分支3种模式: LA (纵声学支), TA (横声学支)和ZA (平面外的声学支)的声子群速度. 声子群速度ZA分支小于TA和LA分支. 对于层状结构, ZA分支的频率依赖于波矢, 二次声子分支在许多非应变二维材料中普遍存在, 是ZA支靠近Г点时非线性离散的可能原因[37].
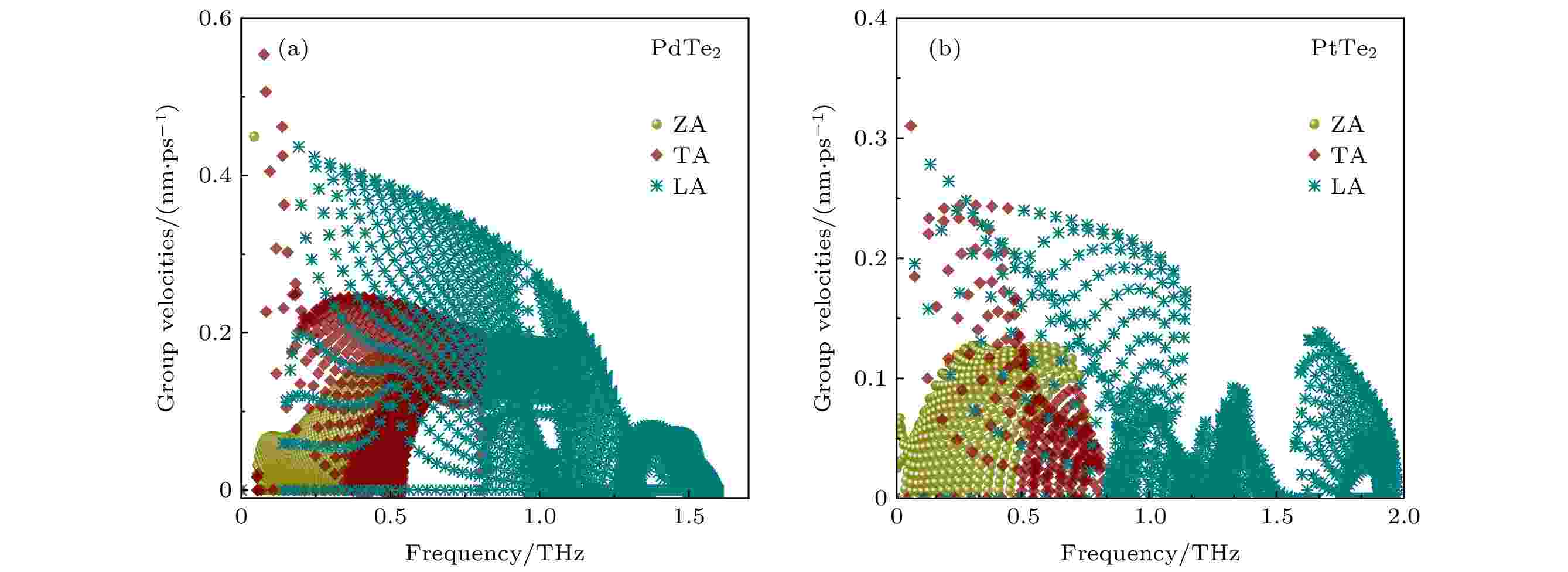图 4 单层PdTe2 (a)和PtTe2 (b)群速度的三支声学分支(LA, TA 和ZA)随频率的变化
Figure4. Variation of group velocity of three acoustic branches (ZA, TA, LA) with the frequency of PdTe2 (a) and PtTe2 (b) monolayers.

通常来说, 具有褶皱结构的二维材料打破了平面外的对称性, 增加了非谐声子的散射, 进而降低晶格热导[38]. 温度为300 K时, PdTe2和PtTe2总声子散射率随频率的变化如图5所示. 当声子频率较低时, ZA, TA和LA声学分支的声子散射率随声子频率的增大而增大, ZA分支的声子色散率最小. 高频部分的光学分支散射范围较大, 3个声学支声子散射率远远小于光学支的声子散射率. PtTe2的声子散射率比PdTe2的更大, 更离散, 导致了PtTe2的声子寿命比PdTe2更短, 进而可能导致PtTe2的晶格热导相对较小.
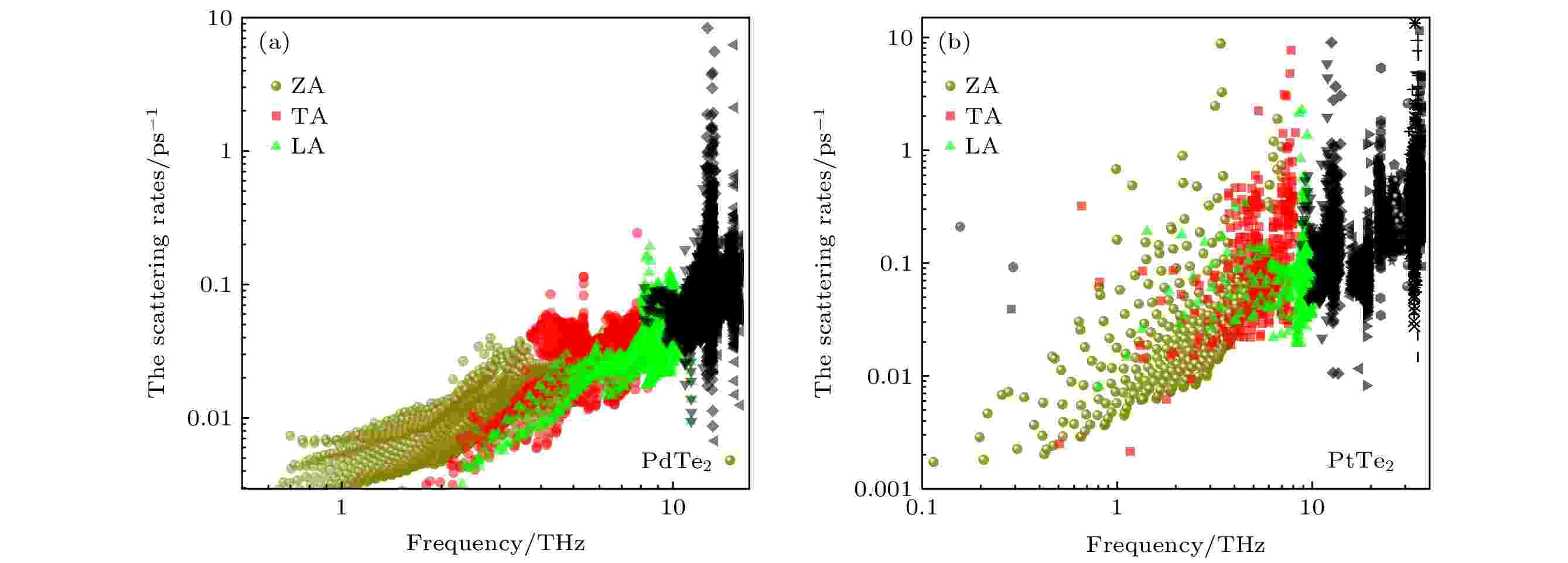图 5 室温下PdTe2 (a)和PtTe2 (b)单层的声子色散率随频率的变化关系, LA, TA 和ZA为三支声学分支
Figure5. Phonon scattering rates of PdTe2 (a) and PtTe2 (b) monolayers at room temperature, where ZA, TA and LA are acoustic branches.

热导率是影响材料热电性能的重要因素, 热电性能表现优异的材料通常具有较低的热导率. 通过求解玻尔兹曼输运方程可以得到PdTe2和PtTe2材料的热导率[28]. 材料的晶格热导率随温度的变化率如图6 (a)所示. 随着温度的升高, 声子的平均自由程会大幅减小, 晶格热导率随温度的升高而降低, 同时表现出x, y方向的各向异性. 在300 K时, PdTe2在x, y方向晶格热导率分别为3.95和2.70 W/(m·K). PtTe2单层在x, y方向晶格热导率分别为3.27和1.04 W/(m·K), PtTe2的晶格热导率低于PdTe2. 由Wiedemann-Franz 定律可以得到电子热导率. 我们对比了PdTe2和PtTe2晶格热导率及电子热导率, 展示了总热导率随温度变化的情况, 如图6 (b), (c)所示. 随着温度升高, 自由电子运动加快, 热电子扩散迅速, 电子热导率升高. 电子热导率随温度升高而增大, 与晶格热导率随温度的变化关系呈相反的趋势. 计算出来的总热导率情况表明, 低温时, 晶格热导率对总热导率的贡献占据主导地位. PdTe2 和PtTe2在300 K的总热导率分别为4.22和2.2 W/(m·K). 对比发现, PtTe2具有更低的热导率, 可能具有比PdTe2更优异的热电性能.
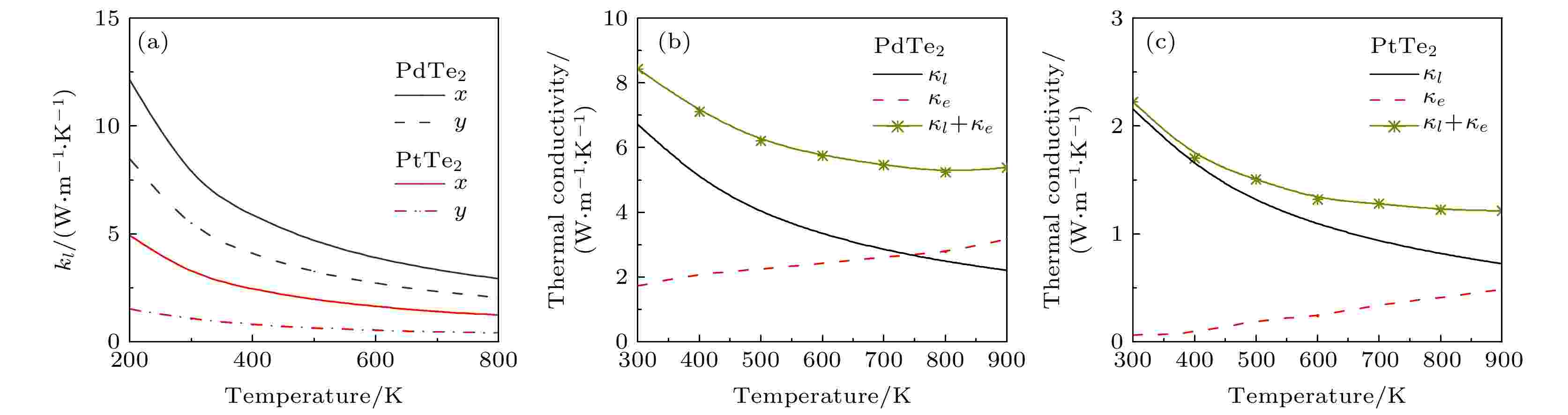图 6 (a) PdTe2和PtTe2层状材料的晶格热导率沿x, y方向随温度的变化率; PdTe2 (b)和PtTe2 (c) 晶格热导率, 电子热导率及总热导率随温度变化的关系
Figure6. (a) Calculated lattice thermal conductivity of monolayer PdTe2 and PtTe2 along the x (dark dashed line) and the y (red dashed line) directions and from 200 K to 800 K with the interval of 100 K; thermal conductivity of PdTe2 (b) and PtTe2 (c) at different temperatures, where ke is electron thermal conductivity, kl is lattice thermal conductivity, and ke + kl is total thermal conductivity.

在热电材料中, 载流子和声子之间的散射被认为是主要的散射机制, 其弛豫时间依赖于散射机制. 采用形变势理论计算得到的有效弹性模量C2D、输送方向有效质量m*、形变势常量El、弛豫时间τ及载流子迁移率μ, 如表2所示. p型掺杂时, PdTe2在x, y方向的形变势常量El分别为3.6, 3.2 eV; n型掺杂时分别为5.5, 4.6 eV. 跟已有结果(p型) 3.972, 2.631 eV (n型) 5.286, 4.081 eV吻合[35]. 结果显示, XTe2 (X = Pd, Pt)的弛豫时间具有较强的各向异性, 并且p型掺杂时的弛豫时间高于n型掺杂时, 这很可能导致两种掺杂方式的热电性能有所差异. 载流子迁移率的结果也可以说明这个情况, 空穴迁移率比电子迁移率更大, 更可观. 因此材料p型掺杂时的热电性能可能更为优异.
PdTe2xyPtTe2xy
pnpnpnpn
C2D/(eV·?–2)4.863.904.755.84
El/eV3.65.53.24.62.653.833.96.4
m*/me0.880.580.880.580.440.330.460.29
μ/(cm2·V–1·s–1)16215716818311501071630546
τ/(10–14 s)8.25.38.56.128.920.316.68.9


表2温度为300 K时, PdTe2和PtTe2的有效弹性模量C2D、形变势常量El、有效质量m*、载流子迁移率μ及弛豫时间τ
Table2.Calculated elastic modulus C2 D, DP constant El, effective mass (m*), carrier mobility (μ), and relaxation time (τ) at 300 K of PdTe2 and PtTe2 monolayers.

通过求解电子玻尔兹曼输运方程[27], 我们计算了XTe2 (X = Pd, Pt)的电输运参数, 如: 电导率与弛豫时间的比值(σ/τ), Seebeck系数(S)等. 电导率与弛豫时间的比值随载流子浓度及时间的变化如图7所示. σ/τ 的值随载流子浓度的增大而增大, 也随温度的升高而增大, 温度变化对σ/τ 变化率的贡献远小于载流子浓度的贡献. 对于PdTe2单层, p型掺杂时, 各向异性对σ/τ 的影响不明显; n型掺杂时, σ/τ 沿x方向上的值远大于y方向的值. 对于PtTe2单层, p型掺杂时, 各向异性对σ/τ 的影响同样不明显; n型掺杂时, σ/τ 沿y方向上的值大于x方向的值.
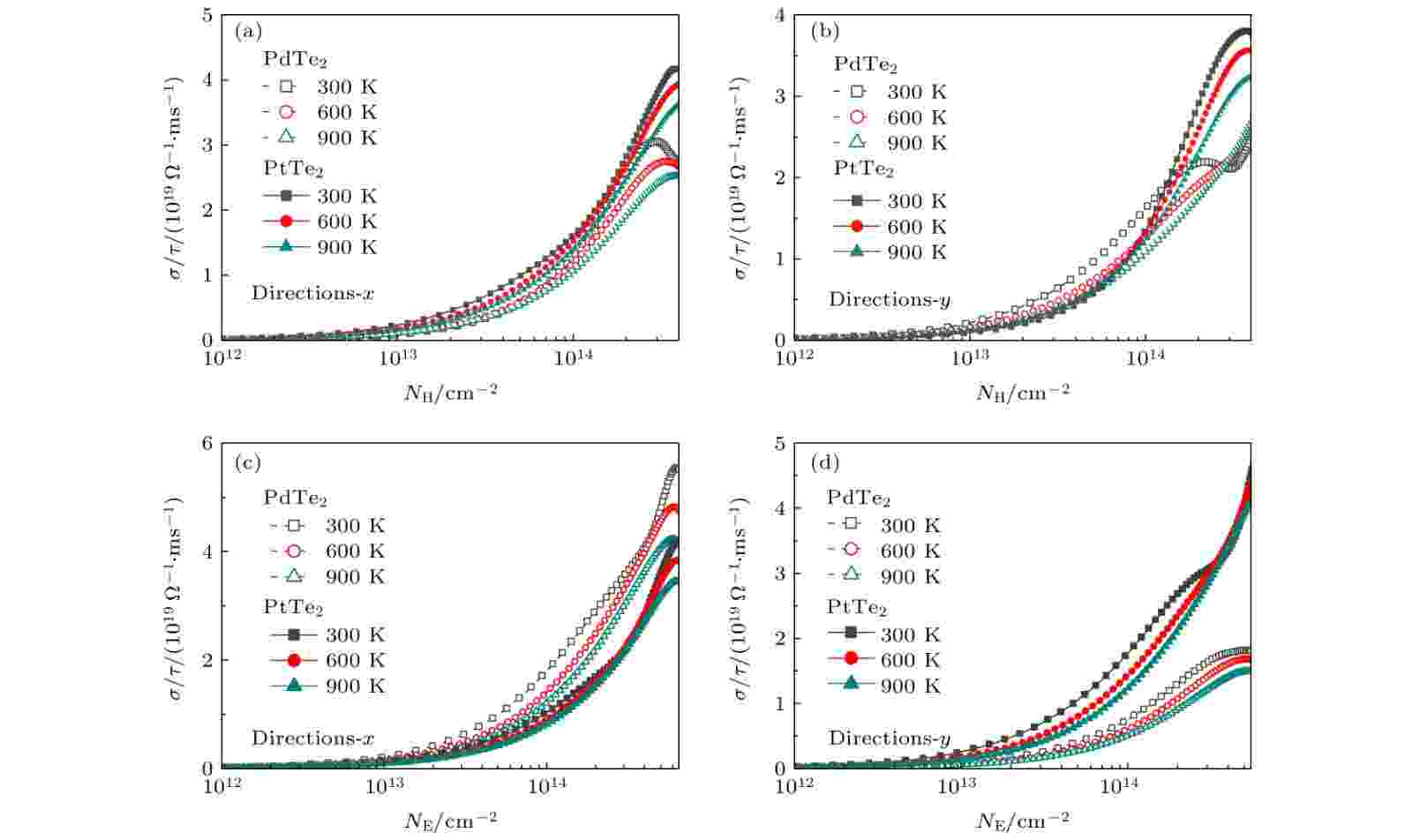图 7 p型掺杂时, PdTe2 (a)和PtTe2 (b)两种材料在不同温度下沿x, y两个方向σ/τ 随载流子浓度的变化. n型掺杂时, PdTe2 (c)和PtTe2 (d)两种材料在不同温度下沿x, y两个方向σ/τ 随载流子浓度的变化
Figure7. Calculated electrical conductivity of p-type (a), (b) and n-type (c), (b) monolayer PdTe2 and PtTe2 along the x and the y directions from 300 K to 900 K with the interval of 300 K.

不同温度下塞贝克系数S随载流子浓度变化的关系如图8所示, S随载流子浓度的增加而减小, 随温度的增加而增大. 温度变化对S的影响较小. 从表1结果中可以看出, 不同方向的有效质量相差较大, 但不同传输方向的塞贝克系数却相差较小, 说明XTe2 (X = Pd, Pt)在电子输运性质上表现较弱的各向异性. 当温度为300 K时, p和n型掺杂的PdTe2 单层S值最大值分别可以达到694, 728 μV/K; p和n型掺杂的PtTe2 单层S值最大值可以达到706, 681 μV/K. 塞贝克系数和电导率对材料转换效率有极大的影响.
图 8 p型掺杂时, PdTe2 (a)和PtTe2 (b)两种材料在不同温度下沿x, y两个方向的塞贝克系数S随载流子浓度的变化. n型掺杂时, PdTe2 (c)和PtTe2 (d)两种材料在不同温度下沿x, y两个方向的塞贝克系数S随载流子浓度的变化
Figure8. Calculated Seebeck coefficient S of p-type (a), (b) and n-type (c), (d) monolayer PdTe2 and PtTe2 along the x and the y directions from 300 to 900 K with the interval of 300 K.

热电材料的转换效率由ZT值来定量描述, 可以根据计算公式
$ZT = \frac{{{S^2}\sigma T}}{{{k_{\rm{e}}} + {k_{\rm{l}}}}}$
得到, 其中S代表塞贝克系数, σ代表电导率, T为温度, ke为电子热导率, kl 为晶格热导率. ZT值是一个无量纲参数, 具有大ZT值的材料是高效的TE材料. PdTe2和PtTe2两种材料在不同温度下沿x, y两个方向的ZT值随载流子浓度的变化如图9所示. ZT值随载流子浓度的增大而增大, 达到一个峰值后开始随浓度增大而减小. p型掺杂时, PdTe2和PtTe2两种材料在不同温度下沿x, y两个方向的ZT值随载流子浓度的变化如图9 (a), (b) 所示. 当温度为300 K时, PdTe2单层在x, y方向的ZT峰值分别为0.83, 0.72, 此时载流子浓度分别为3.2 × 1017 cm–2, 1.47 × 1017 cm–2, PtTe2单层的ZT峰值分别为2.75, 0.92, 此时载流子浓度分别为2.18 × 1016 cm–2, 1.71 × 1016 cm–2. n型掺杂时, PdTe2和PtTe2两种材料在不同温度下沿x, y两个方向的ZT值随载流子浓度的变化如图9 (c),(d) 所示. 当温度为300 K时, PdTe2单层在x, y方向的ZT峰值分别为0.87, 0.57, 此时载流子浓度均为3.8 × 1017 cm–2, PtTe2单层在x, y方向的ZT峰值分别为2.07, 0.85, 此时载流子浓度分别为4.64 × 1016 cm–2, 9.5 × 1016 cm–2. 从结果来看, PtTe2是比PdTe2更优异的热电材料. 从ZT值的结果来看, 两种材料p型掺杂时的热电性能优于n型掺杂, 这点也可以从电子能带结构图(图3)中可以看出, 两种材料的价带顶部的能带相比导带底部的能带来说更为陡峭.
图 9 p型掺杂时PdTe2 (a)和PtTe2 (b)两种材料在不同温度下沿x, y两个方向ZT值随载流子浓度的变化. n型掺杂时PdTe2 (c)和PtTe2 (d)两种材料在不同温度下沿x, y两个方向ZT值随载流子浓度的变化
Figure9. Calculated ZT values of p-type (a), (b) and n-type (c), (d) monolayer PdTe2 and PtTe2 along the x and the y directions from 300 K to 900 K with the interval of 300 K.

4.结　论
基于密度泛函理论, 得到了PdTe2和PtTe2两种层状材料稳定的晶格参数信息, PdTe2和PtTe2单层属于间接带隙半导体材料. 通过求解玻尔兹曼输运方程得到了二维材料XTe2 (X = Pd, Pt)的热电性质. 相比常规热电材料, 层状材料表现出优异的热电性能, 具有较强的实用性能. 具体结论如下.
从热输运性能方面来说. 声学支振动对晶格热导率产生主要影响. 元素Pt的原子质量比Pd大, 抑制了声学支频率; PtTe2的色散率比PdTe2更大, 更离散, PtTe2单层的声子寿命比PdTe2更短. 这两个原因使得PtTe2具有更低的晶格热导率. PdTe2和PtTe2单层的晶格热导率随温度的升高而降低, 且表现出x, y 方向的各向异性. 电子热导率随温度升高而增大, 与晶格热导率随温度的变化关系呈相反的变化趋势, 这是由于温度升高后, 自由电子运动加快, 热电子扩散变得迅速. 从结果来看, 低温时, 晶格热导率对总热导率做主要贡献, PtTe2的总热导率也低于PdTe2, PtTe2具有更为优异的热电性能.
从电输运性能方面来说. 两种材料的电导率与弛豫时间的比值σ/τ、塞贝克系数S等具有各向异性. 较高的载流子迁移率、电导率及塞贝克系数值, 展示出材料较优异的热电性能. 材料p型掺杂的热电性能优于n型掺杂. 对比PdTe2和PtTe2单层的ZT值, 发现PtTe2的ZT值更高, 当温度为300 K时, PtTe2的ZT峰值可以达到2.75. 因此PtTe2是比PdTe2更优异的热电材料, 热电转换效率非常可观.
相关话题/材料 计算 电子 结构 声学
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 准二维湿颗粒体系融化过程中的结构与缺陷
    摘要:研究颗粒体系中的结构与缺陷对于研究固-液融化的物理机制具有重要的价值.本文实验研究了垂直振动下单层湿颗粒在固-液融化过程中的结构与缺陷.根据实验及理论分析构建了湿颗粒体系的接触模型,量化了准二维湿颗粒体系融化过程中颗粒的结构变化.然后以颗粒为点建立Voronoi图对颗粒体系的“相”转变进行研究 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 纳米光子学结构对GaInAsSb p-n结红外光电性能的调控
    摘要:GaInAsSb在红外光电领域具有重要应用价值,但是窄带隙材料较高的本征载流子浓度和俄歇复合系数使其室温暗电流密度较高,需要进行制冷才能获得满足应用要求的光电性能.本文利用表面宽带隙半导体纳米柱阵列和背面高反射率金属对GaInAsSbp-n结有源区进行双面光调控,将光限制在较薄的有源区进行吸收 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 微分相位衬度计算机层析成像的感兴趣区域重建方法
    摘要:基于光栅干涉仪系统的X射线微分相位衬度计算机层析成像,不仅可以重建物体的线性衰减系数,还可以重建物体的相移系数和线性散射系数.在实际应用时,大面积光栅不易获得,常常遇到样品大于光栅的情况.当用小于样品的光栅对样品进行扫描时,样品超出光栅成像视野的部分会导致微分相位投影信息被截断.本文针对微分相 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于纳米发电机的触觉传感在柔性可穿戴电子设备中的研究与应用
    摘要:柔性可穿戴电子设备因其在人工智能、健康医疗等领域的应用而受到了人们的极大关注.然而,如何降低功耗或实现自供能一直是阻碍其广泛应用的瓶颈.随着纳米发电机与自驱动技术的兴起,尤其以摩擦纳米发电机(TENG)与压电纳米发电机(PENG)代表的研究,为解决可穿戴传感器电源的问题提供了可行的方案.TEN ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 周期性分流微通道的结构设计及散热性能
    摘要:微通道散热器在集成电路中具有重要应用,但目前传统的长直微通道散热过程导致温度不均匀,散热效率较低.本文设计了一种周期性分流微结构并与传统微通道进行集成,实现了一种高效率的周期性分流微通道散热器.基于以上周期性分流微通道,系统研究了单根微通道内微结构数目、微结构的排布方式及结构参数对其散热性能的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 含钨难熔高熵合金的制备、结构与性能
    摘要:高熵合金(high-entropyalloys,HEAs)作为一种新型多主元合金,原子排列有序、化学无序,具有高熵、晶格畸变、缓慢扩散、“鸡尾酒”等四大效应,表现出优异的组合性能,有望作为新型高温结构材料、耐磨性材料、抗辐照材料应用于航空航天、矿山机械、核聚变反应堆等领域.本文介绍了目前含钨H ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 超电容储能电极材料的密度泛函理论研究
    摘要:由于量子限域效应和态密度的限制,石墨烯、硅烯等二维材料的量子电容在费米能级附近趋近于零.基于密度泛函理论的第一性原理研究发现,掺杂和吸附使石墨烯等二维电极材料的电子结构得以有效的调制,它促进狄拉克点附近局域电子态的形成和/或费米能级的移动,从而使量子电容得到了提高.比较Ti(Au,Ag,Cu, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种具有“1111”型结构的新型稀磁半导体(La<sub>1–<i>x</i></sub>Sr<sub><i>x</i&g
    摘要:利用高温固相反应法,成功合成了一种新型块状稀磁半导体(La1–xSrx)(Zn1–xMnx)SbO(x=0.025,0.05,0.075,0.1).通过(La3+,Sr2+)、(Zn2+,Mn2+)替换,在半导体材料LaZnSbO中分别引入了载流子与局域磁矩.在各掺杂浓度的样品中均可观察到铁磁 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 非热等离子体材料表面处理及功能化研究进展
    摘要:等离子体技术在现代材料制备和表面处理过程中起着重要的作用.本文聚焦于非热等离子体(NTP)材料表面处理及功能化应用,重点综述NTP在材料表面处理及功能化过程中的最新研究进展,包括激励产生等离子体的等离子体源、NTP材料表面处理及功能化工艺以及具体应用.其中,激励产生等离子体的等离子体源包括感应 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 容性耦合等离子体中电子加热过程及放电参数控制
    摘要:容性耦合等离子体放电因在工业界有重要的应用价值而受到广泛关注.对于容性耦合等离子体放电的研究主要集中于对等离子体参数的控制,以实现更好的工艺效果,例如高深宽比刻蚀等.而关于等离子体参数的调控主要分为气体、腔室以及源这三个方面.改变这些外部参数,可以直接影响鞘层的动力学过程以及带电粒子的加热过程 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.