全文HTML
--> --> -->总界面电容(CT)[4,5]可以通过下述公式来表示: 1/CT = 1/CQ + 1/CD, 其中CQ和CD分别表示量子电容、双电层电容, 可看出总界面电容同时受CQ和CD两个物理量的制约, CT < min(CQ, CD). 由于量子限域效应和较小态密度的限制, 石墨烯、硅烯等二维电极材料在对体系充电时, 需要显著移动费米能级才能使材料积累一定数量的载流子. 如果把这个过程与外部电路做对比, 它就是量子电容, 也可以当作一个串联的电容. 石墨烯等二维电极材料在费米能级附近量子电容接近于零. 相对于双电层电容, 量子电容有很大的提升空间. 可以通过掺杂, 引入缺陷等显著移动费米能级或增加费米能级附近的电子局域态以提高量子电容. 一直以来科研工作者们对CQ贡献的忽视造成了部分实验现象无法得到解释, 也缺少在微观机制方面对提高总界面电容的理解.
因为大家经常忽略量子电容的贡献, 因此提高石墨烯基材料中的总界面电容不能仅通过提高比表面积的方式来实现, 前期中双电层超级电容器的储能与其比表面积呈线性增加的趋势, 随之就出现了瓶颈问题[6]. N掺杂是石墨烯改性中最常见的掺杂元素并导致了总界面电容的提高, 但微观机理不清晰, 普遍认为双电层电容的增加是由于石墨烯在经过N掺杂后同电解液中的碱金属原子之间键能的增强, 因此更多的碱金属离子被吸引过来, CD的提升是促成CT提高的主要原因, 并未提及量子电容的贡献[7-9]. 然而, 基于第一性原理计算发现, 石墨烯费米能级的位置可通过N掺杂而得到改变, 同时可以有效地提升量子电容, 但是在有机离子电解液中N掺杂对双电层电容的贡献几乎为零[10], 因此量子电容是改善总界面电容的主要因素.
二维电极材料近年来发展迅猛, 石墨烯、硅烯、锗烯、二硫化钼和MXene等典型的二维层状材料受到了人们的极大关注. 硅烯、锗烯具有类似于石墨烯的六角单层结构, 是二维量子材料中冉冉升起的新星. 目前, 硅烯、锗烯已经以多种形式在实验中被成功制备[11,12]. 但是研究硅烯、锗烯的量子电容方面的内容还鲜有报道. 根据以往研究发现, 作为类石墨烯材料的硅烯、锗烯也是双电层超级电容器潜在的电极材料[13,14]. 相对石墨烯而言, 硅烯和锗烯的质量比量子电容和面积比量子电容中谁具有明显的优势还存在一些未知. 本文旨在研究双电层超级电容器能量密度低的问题, 拟对二维双电层电极材料进行结构优化设计. 对比三种典型二维电极材料石墨烯、硅烯和锗烯的量子电容, 并拟合了3-N掺杂单空位石墨烯的总界面电容. 研究发现, 改善二维电极材料的量子电容是开发高性能双电层超级电容器的设计思路.
在公式μF = eΦ中, μF为电化学电势, e是一个电子的电量, Φ为局部电势, 其中μF与Φ成正比关系. (1)式可表示电极上的多余电荷密度[14]:
在本征锗烯(硅烯、石墨烯)上吸附金属原子, 以锗烯为例, 其吸附能由下式定义:
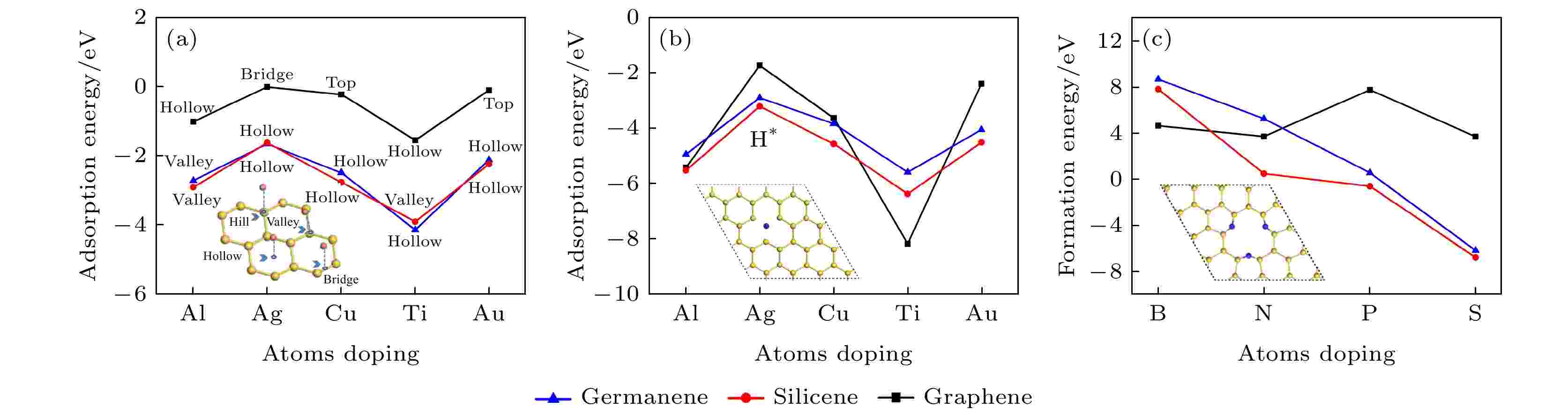图 1 (a), (b) 金属原子分别在本征和单空位锗烯(硅烯, 石墨烯)上的最稳定吸附位置的吸附能, 掺杂浓度为3.1%; (c) 单空位锗烯(硅烯, 石墨烯)掺杂3-B (N, P, S)原子的形成能, 掺杂浓度9.3%Figure1. (a), (b) The adsorption energies of adsorbing metal atoms in the strongest position on pristine and single-vacancy germanene (silicene, graphene) with thedoping concentration of 3.1%; (c) the formation energy of single-vacancy germanene (silicene, graphene) doped with triple-B (N, P, S) with the doping concentration of 9.3%.
| System ΔEad (eV) | Hill | Valley | Bridge | Hollow | H* | |
| Graphene | Al | –0.888 | — | –0.902 | –1.012 | –5.399 |
| Ag | 0.035 | — | –0.001 | 0.011 | –1.695 | |
| Cu | –0.220 | — | –0.217 | –0.057 | –3.599 | |
| Ti | –1.075 | — | –0.827 | –1.544 | –8.159 | |
| Au | –0.096 | — | –0.082 | –0.073 | –2.359 | |
| Silicene | Al | –2.794 | –2.907 | — | –2.573 | –5.502 |
| Ag | –0.991 | –1.313 | –1.244 | –1.616 | –3.182 | |
| Cu | –1.549 | –2.368 | — | –2.764 | –4.538 | |
| Ti | –3.694 | –3.907 | — | –3.893 | –6.348 | |
| Au | –1.843 | — | –1.933 | –2.238 | –4.486 | |
| Germanene | Al | –1.815 | –2.716 | — | –2.520 | –4.908 |
| Ag | –0.984 | –1.322 | — | –1.650 | –2.869 | |
| Cu | –1.377 | –2.091 | — | –2.489 | –3.812 | |
| Ti | –3.569 | –3.968 | — | –4.144 | –5.565 | |
| Au | –1.636 | –1.700 | –1.818 | –2.113 | –4.020 | |
表1在本征和单空位石墨烯、硅烯、锗烯上分别以不同位置吸附Al, Ag, Cu, Ti和Au金属原子的吸附能
Table1.The adsorption energy of Al, Ag, Cu, Ti, Au adsorbed on pristine and single-vacancy graphene (silicene, germanene) with different configurations.
| System ΔEf (eV) | B | N | P | S |
| Graphene | 4.663 | 3.735 | 7.773 | 3.708 |
| Silicene | 7.825 | 0.503 | –0.590 | –6.759 |
| Germanene | 8.684 | 5.256 | 0.575 | –6.149 |
表2在单空位石墨烯、硅烯、锗烯上掺杂3-B(N, P, S)原子的形成能
Table2.The formation energy of triple-B (N, P, S) doped single-vacancy graphene (silicene, germanene).
我们还考虑了单空位石墨烯、硅烯、锗烯掺杂3-B(N, P, S)的情况, 如图1(c)所示, 对硅烯和锗烯进行掺杂, 形成能的变化趋势相似, S是最稳定的掺杂原子. 对于石墨烯来说, 几种不同掺杂原子的形成能几乎相近, S掺杂的形成能最低.
图2显示了本征锗烯、硅烯、石墨烯的量子电容随电势变化的关系图. 根据图2(b)可知, 锗烯和硅烯面积比量子电容的增减趋势几乎同步, 还发现, 在低电势|Φ|范围内, 锗烯和硅烯的量子电容近乎是石墨烯量子电容的两倍. 但是, 质量比电容与面积比电容的变化趋势不同, 如图2(a)所示. 硅的相对原子质量是碳的两倍, 只有锗的二分之一. 根据碳、硅、锗的原子间距不同, 可计算出石墨烯、硅烯、锗烯的比表面积分别为2630 m2/g, 2738 m2/g和1148 m2/g. 从而得出三者的质量比电容大小关系为: 硅烯 > 锗烯 > 石墨烯, 如图2(a)所示. 当电势小于–0.5 V时, 硅烯和锗烯的量子电容急剧增加, 这与石墨烯变化趋势有所不同, 在狄拉克点附近发现它们的量子电容趋近于零, 量子电容随着电势|Φ|的增加而增加, 其归因于在狄拉克点附近的线性色散. 另外, 根据公式CQ∝υF–2, 量子电容随着费米速度的增大而减小. 由于石墨烯的费米速度是大于硅烯和锗烯[19], 所以根据上述公式可知, 石墨烯的量子电容远小于硅烯和锗烯的量子电容.
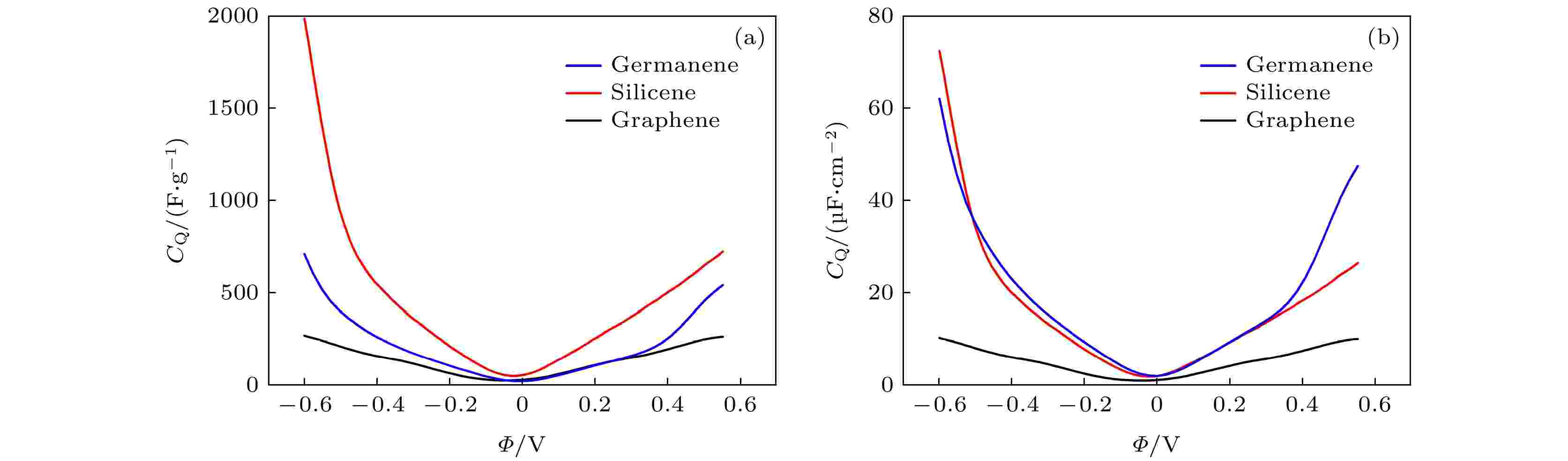图 2 (a), (b)分别为本征石墨烯、硅烯、锗烯的质量比量子电容, 面积比量子电容(锗烯: 1 μF/cm2 = 11.48 F/g, 硅烯: 1 μF/cm2 = 27.37 F/g, 石墨烯: 1 μF/cm2 = 26.3 F/g)Figure2. (a), (b) calculated specific quantum capacitance (CQ), areal CQ vs. potential drop of pristine graphene, siliceneand germanene. (For germanene 1 μF/cm2 = 11.48 F/g, silicene 1 μF/cm2 = 27.37 F/g, and graphene 1 μF/cm2 = 26.3 F/g).
计算了单空位石墨烯、硅烯、锗烯吸附金属原子Ti, Cu, Au, Ag和Al的量子电容, 如图3(a)—(c)所示, 通过对比发现Cu吸附石墨烯的量子电容最高, Ti吸附硅烯和锗烯后, 量子电容显著提升. 同时, 还计算了单空位石墨烯、硅烯和锗烯掺杂3-B (N, P, S)的量子电容, 通过对比, 发现3-N掺杂单空位石墨烯的量子电容最高, 如图3(d)—(f)所示.
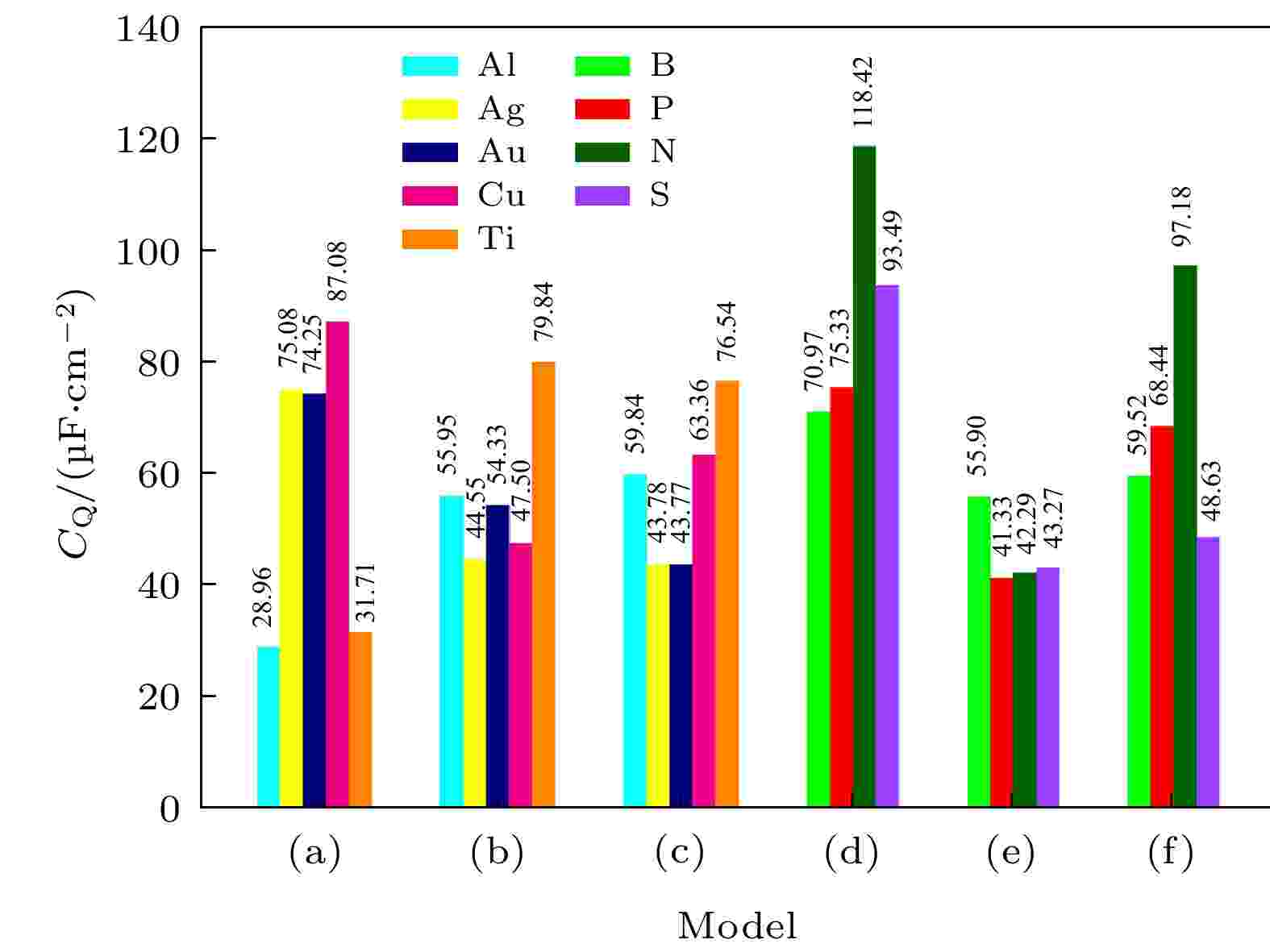图 3 (a)?(c) 单空位石墨烯(硅烯, 锗烯)吸附Ti (Cu, Au, Ag, Al)和(d)?(f) 3-B (P, N, S)掺杂单空位石墨烯(硅烯, 锗烯)量子电容最大值的变化趋势图Figure3. (a)?(c) Change trend chart of the maximum value of CQ for Ti (Cu, Au, Ag and Al) adsorbed single-vacancy grapheme (silicene, germanene), and (d)?(f) 3-B (P, N, S)-doped single-vacancy grapheme (silicene, germanene).
在单空位石墨烯(硅烯, 锗烯)分别吸附Ti, Au, Ag, Cu, Al体系中, 拟合了其中最高的量子电容与电势的关系图, 分别为Cu吸附单空位石墨烯和Ti吸附单空位硅烯和锗烯, 量子电容分别为87.08 μF/cm2, 79.84 μF/cm2和76.54 μF/cm2, 如图4(a)所示. 分析量子电容提高的原因, 以Ti吸附单空位硅烯为例, 从图5(a) Ti掺杂单空位硅烯浓度的态密度(DOS)和局域态密度(LDOS)图可看出, Ti的吸附导致硅烯费米能级附近引入局域态, 导致硅烯能带发生劈裂, Ti的3d轨道导致态密度自旋向上和自旋向下态之间的对称性在费米能级附近被破坏, Ti的3d轨道的能级与局域缺陷态的能级比较匹配. 从Ti吸附单空位硅烯, 我们可看出, 量子电容得到了提高归因于费米能级附近局域态的形成.
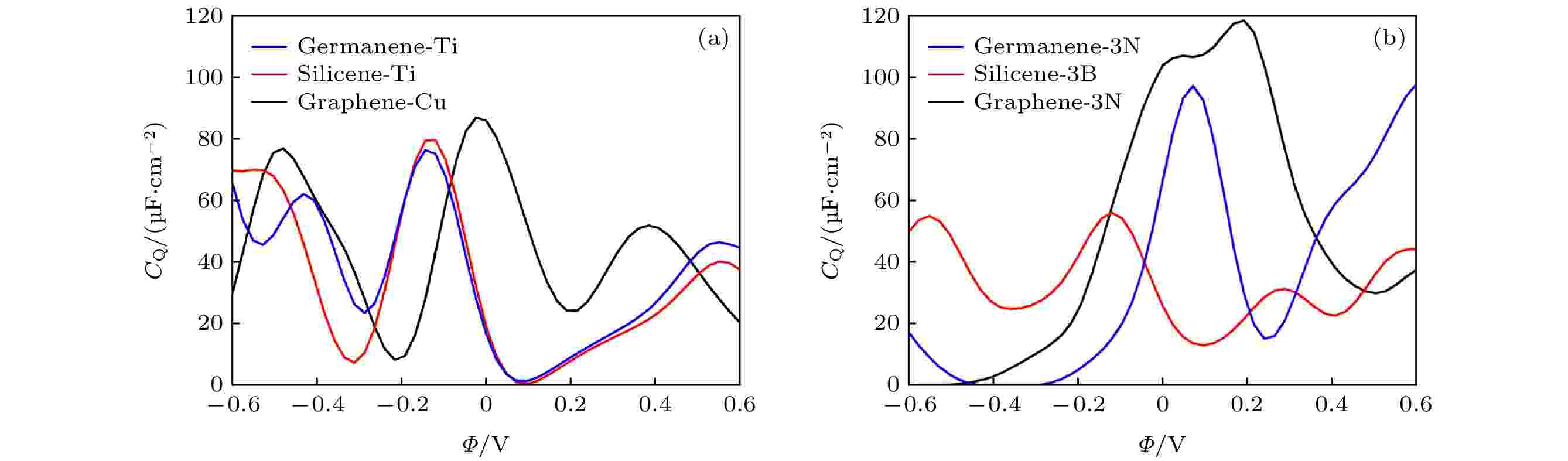图 4 (a) 单空位石墨烯(硅烯, 锗烯)吸附Ti, Au, Ag, Cu, Al体系中, 最高的量子电容与电势的关系图, 掺杂浓度为3.1%; (b) 单空位石墨烯(硅烯, 锗烯)掺杂三个B, N, P, S原子体系中, 最高的量子电容-电势关系图, 掺杂浓度为9.3%Figure4. (a) Under the condition of doping concentration of 3.1%, the calculated quantum capacitance of single-vacancy grapheme (silicene, germanene) adsorbed withTi, Au, Ag, Cu, Al with the best properties, as a function of local electrode potential (Φ); (b) CQ of single-vacancy germanene (silicene, graphene) doping with triple-B (N, P, S)with the best properties, under the condition of doping concentration of 9.3%.
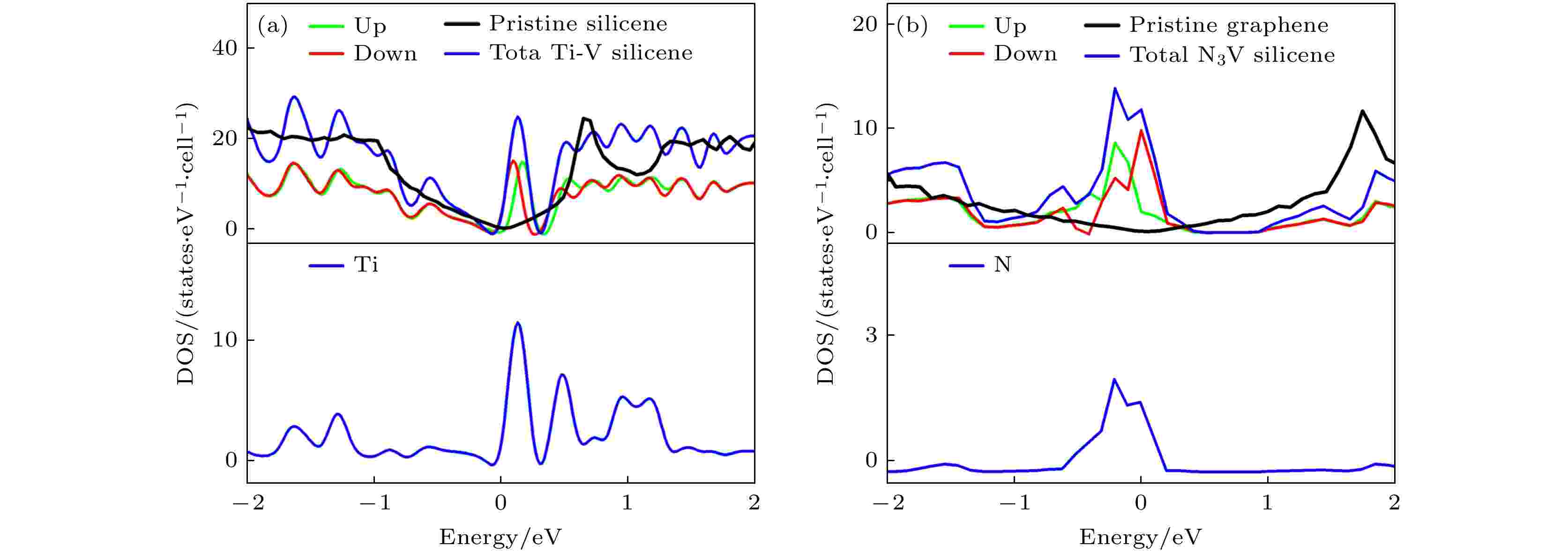图 5 (a) Ti掺杂单空位硅烯浓度的态密度(DOS)和局域态密度(LDOS)图, 掺杂浓度为3.1%; (b) 3-N原子掺杂单空位石墨烯的态密度(DOS)和局域态密度(LDOS)图, 掺杂浓度为9.4%Figure5. Density of states (DOS) and local density of states (LDOS) of adsorbed Ti atoms on single-vacancy silicene with Ti concentration3.1%, and (b) triple N-doping single-vacancy grapheme with N concentration 9.4%.
单空位石墨烯(硅烯, 锗烯)分别掺杂三个B, N, P, S原子体系中, 最高的量子电容-电势关系图, 分别为3-B掺杂单空位硅烯, 3-N掺杂单空位石墨烯、锗烯. 其中3-N掺杂单空位石墨烯量子电容最高, 达118.42 μF/cm2 (0.21 V), 如图4(b)所示, 分析此体系量子电容提升的原因, 从态密度(DOS)和局域态密度(LDOS)图5(b)中可看出, 由于三个相邻的N原子的耦合, N原子的孤对电子态被破坏, N原子的贡献导致费米能级附近形成了局域电子态, 从而导致量子电容的提高.
采取调整石墨烯超胞中C原子与3-N + 空位比例的方法来改变N掺杂的浓度. 根据模型图1(c)可知, 掺杂的N原子两两相邻. N原子之间发生的耦合会促使孤对电子态被破坏, 局域电子态于费米能级附近形成, 提高了量子电容. 当N原子的掺杂浓度为1.85%时, 量子电容的最大值为47.38 μF/cm2; 当掺杂浓度增加到16.7%时, 量子电容增加到142.8 μF/cm2. 由图6(a)可知, 量子电容的增加是由于小电势范围内局域电子态的形成. 图6(b)为石墨烯掺杂N原子的不同浓度的表面电荷密度-电势关系图. 由图6可知, 在正电势下电荷密度明显提高. 我们也研究了3-N掺杂单空位硅烯的浓度效应, 如图6(c)所示, 量子电容的局部最小值对应的电势随着N掺杂浓度的增加移动了约0.3—0.5 V. 当N掺杂浓度为4.2%时, 量子电容的最大值为15.94 μF/cm2; 当浓度增加到37.5%, 零电势附近的量子电容也增至58.68 μF/cm2. 这是由于在小电势范围内, 费米能级的下移和附近的能带重组促使了量子电容的提升. 图6(d)代表不同浓度的硅烯掺杂N原子的表面电荷密度-电势的关系图, 可看出正电势下电荷密度明显增强. 图6(e)和图6(f)分别为单空位锗烯掺杂3个N原子的关系图, 随着浓度从6%增加到37.5%, 量子电容的极大值分别从58.7 μF/cm2 (0.144 V)增加到168.3 μF/cm2 (0.408 V). 显然, 局域态导致了低电势下量子电容的增加. N掺杂在正电势下整体电荷积累效果最佳.
图 6 (a)?(f)不同掺杂浓度的单空位石墨烯(硅烯, 锗烯)掺杂三个N原子的量子电容以及表面电荷密度-电势的关系图Figure6. (a)?(f)Calculated quantum capacitance and surface charge vs. potential drop of 3 N-doping single-vacancy grapheme (silicene, germanene) with different concentration, as a function of local electrode potential (Φ).
通过对比图3, 发现3-N掺杂单空位石墨烯的量子电容最高, 因此选择3-N掺杂单空位石墨烯电极材料做进一步的研究, 如图7所示. 3-N掺杂单空位石墨烯和本征石墨烯的总界面电容CT与CQ和CD之间存在这样一个关系, 1/CT = 1/CQ + 1/CD, 通过在1 M NaCl的水溶液中利用经典分子动力学模拟计算获得了双电层电容CD[20], 通过上面的串联公式拟合出CT, 得到了CT与电势的关系图, 与CT曲线相对比, 本征石墨烯的CT曲线是U字形. 而3-N掺杂单空位石墨烯的CT
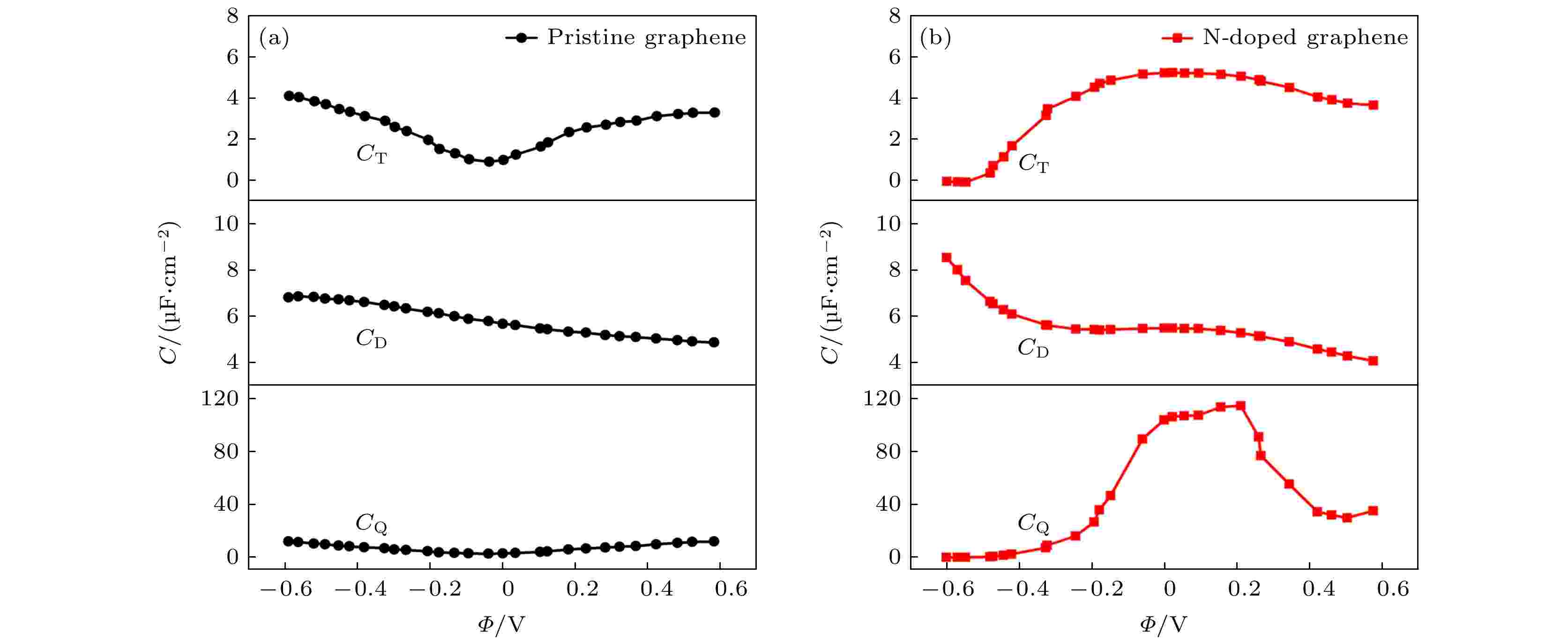图 7 本征石墨烯和石墨烯掺杂3-N原子的总界面电容, 双电层电容以及量子电容. 双电层电容是根据经典分子动力学模拟获得, 模拟条件为1 M NaCl水性电解液[20]Figure7. The capacitance of triple-N doped with graphene and pristine grapheme, including quantum capacitance (CQ), electric double-layer capacitance (CD) and total interfacial capacitance(CT).The CD is obtained by classical MD simulation under the condition of 1 M NaCl aqueous electrolyte[20].
