摘要:微通道散热器在集成电路中具有重要应用, 但目前传统的长直微通道散热过程导致温度不均匀, 散热效率较低. 本文设计了一种周期性分流微结构并与传统微通道进行集成, 实现了一种高效率的周期性分流微通道散热器. 基于以上周期性分流微通道, 系统研究了单根微通道内微结构数目、微结构的排布方式及结构参数对其散热性能的影响. 结果表明, 引入的分流微结构可增大换热面积、打破原有层流边界层、促进冷/热冷却液混合、显著改善微通道散热性能. 在100 W/cm²的热流密度下, 入口端冷却液流速为1.18 m/s时, 单根微通道内引入9组微结构后, 其最高温度下降约24 K, 热阻下降约44%, 努塞尔数增大约124%, 整体传热性能(PEC)达1.465. 进一步地, 微结构采用交错渐变的周期排布方式, 沿流动方向逐渐变宽的扰流元使得冷却液被充分利用, 减少了高/低温区的存在且缓解了散热面沿流动方向存在的温度梯度, 压降损失相较于均匀排布也有一定程度的降低, 有效提升了散热效率. 本文提出的周期性分流微通道将在大功率集成电路及电子冷却领域中具有广阔的应用前景.
关键词: 微通道/
散热结构/
周期性分流

English Abstract

全文HTML

--> --> -->

如今, 微电子技术发展迅猛, 电子芯片朝着小尺寸、高集成度的方向发展^[1]. 也意味着在有限的体积内, 越来越多的电子元器件集成其中^[2]. 在电子芯片性能提高的同时, 也产生了更多的热量, 使芯片温度升高.
温度对电子芯片的性能及可靠度有着直接影响. 10 ℃法则表明: 在室温附近温度每提高10 ℃, 电子元件使用寿命将减少一半; 在70—80 ℃时, 温度升高1 ℃则会导致电子器件可靠性下降5%^[3]. 因此, 材料与器件的传热及散热问题成为了微电子领域不可忽视的问题之一. 对于材料的传热, 当下更多****着重于对微尺度传热以及固液界面传热领域的研究. 对微尺度传热领域, Zhang等^[4]总结了低维纳米材料中与尺寸有关传热行为的最新研究, 讨论了各种重要尺寸的相关热传输行为, 且提出了几种重要的热传递行为和独特的潜在物理机制. Xu等^[5]总结了导电聚合物及其复合材料中热传递的基本原理, 以及调节其导热性的最新进展. 对于此类问题的研究完善了热传递的理论体系, 加深了人们对微尺度传热的理解, 但仍然存在诸多特性及理论等待人们去探索及完善. 对于固液界面传热, Ma等^[6]研究了界面电荷修饰对石墨烯和水之间的卡皮察热阻的影响, 发现与不进行电荷修饰的情况相比, 卡皮察热阻降低幅度达97%. Dmitry等^[7]使用分子动力学模拟研究了多层石墨烯与水之间的卡皮察热阻, 并通过施加整体横断面压力和改变石墨烯的疏水性, 控制了微流体和纳米流体系统中的散热. 对此类问题的研究大大推动了对跨固-液界面传热及散热问题的研究及发展, 同时对于电子冷却领域具有一定程度的借鉴意义.
与此同时, 在电子冷却领域, 更多****关注于散热方法的研究以及散热结构的设计. 于是, 各种芯片散热技术应运而生, 主要包括自然对流、强制风冷以及微通道散热器等^[8], 其中微通道散热器因为具有优异的散热性能, 自1981年被Tuckerman和Pease^[9]首次提出后就备受关注. 在过去的几十年中, 有大量的研究人员对其进行研究, 致力于微通道散热器的完善和发展. 部分****对微通道散热器的材料进行研究, 裘腾威等^[10,11]采用多孔铜作为衬底制备出的微通道散热器散热能力优异. Qi等^[12]制备出的金刚石微通道散热器具有优异的传热系数. 还有****将不同种类^[13]以及不同颗粒形状^[14]的纳米流体代替水作为冷却剂以此增强换热. 但此类方式大大增加了微通道的制造难度及材料成本且材料导热性能发展有极限, 更多的研究着重于对微通道散热器的结构进行改进. 有****受仿生学的启发, 对微通道的整体结构进行设计以改善其热性能. Rubin-Jimenez等^[15]及俞炜等^[16]设计了ψ型微通道并研究了其流动机理; Ghaedamini等^[17]对树形微通道进行研究; 还有部分****用蜂巢结构对微通道进行设计^[18]. 除此之外, 还有****同样对微通道的整体结构进行设计改进, Abo-Zahhad等^[19]设计出的菱形微通道、Wang等^[20]设计出的肋间断微通道以及Bhandari和Prajapati^[21]设计出的混合微通道均较大程度改善了换热性能. 但由于此类结构往往较为复杂, 制备难度较大, 大部分还停留在理论及数值仿真阶段. 还有****以传统矩形长直微通道为基础, 着重于微通道内局部微结构的设计^[22], Xia等^[23]在微通道侧壁加入周期性三角形的凹穴, 但热性能提升较小; 有****在长直微通道中加入周期性矩形^[24]、水滴形^[25]扰流元, 提升了热性能但造成了较大压降损失. Xie等^[26]将不同形状微针鳍引入微通道中; 文献[27, 28]在传统矩形微通道中加入垂直以及Y形分叉; Li等^[29]在微通道中加入散热片以及空腔; 还有****将设计的双分裂圆柱体引入微通道中^[30]. 此类方式相比于材料的更换以及微通道整体结构的设计对微通道的热性能改善更大, 且节约了成本、制造难度低, 成为了最具前景的微通道散热器性能提升方式. 但往往由于微结构对冷却液流动的阻碍导致压降损失升高, 以致牺牲了较大的能耗, 且微结构的均匀排布使得基底上沿流动方向出现明显的温度梯度或局部高/低温区, 温度分布的不均匀将导致系统稳定性降低. 所以如何降低压降损失以及保证温度的均匀性成为了提升此类微通道散热器热性能的关键.
针对微结构的引入造成压降损失较大的问题, 本研究系统设计与仿真了一种周期性分流微结构, 发现其在提升散热效率的同时, 避免微结构处通道过窄而产生较大压降的损失. 进一步针对微通道散热器温度分布不均的问题, 打破原有微通道内微结构的均匀排布方式, 通过考虑分流微结构在微通道内的排布方式以及结构参数的变化, 设计与仿真了一种交错渐变分流微通道, 发现此排布方式在进一步提升热性能的同时避免了换热面上沿流动方向出现的温度梯度, 减少了换热面上的高/低温区, 使换热面温度变得更加均匀. 此设计将为高集成电路芯片散热问题提供一种新的高效散热结构.

2

-->

2.1.长直微通道散热器

图1为矩形长直微通道散热器示意图, 将作为对照组出现在之后的研究中. 其由40根截面为矩形的微通道组成, 等距排列于20 mm × 20 mm的基底上. 在本文的计算中, 热源的最大功率为400 W(100 W/cm²), 换热面为其底面(下表面). 假定每根微通道内部高H_c为400 μm, 宽W_c为300 μm, 微通道上下壁厚T_c均为50 μm, 侧壁厚T_w为100 μm. 所以, 单根微通道的整体高度H便为500 μm, 宽度W_a为500 μm, 两根微通道之间的壁厚为200 μm.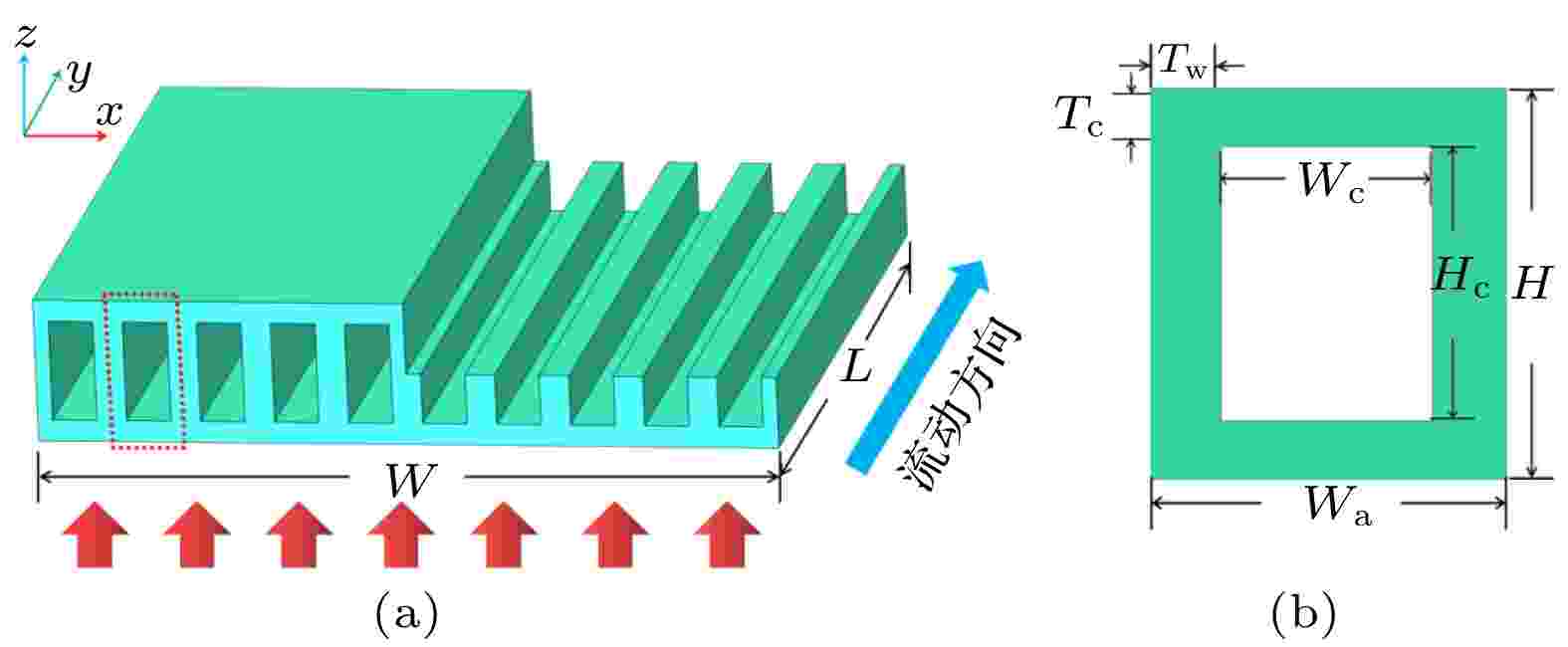
图 1 长直微通道散热器结构示意图　(a)长直微通道散热器; (b)单根微通道截面
Figure1. Schematic diagram of the long straight microchannel heat sink: (a) Long straight microchannel heat sink; (b) cross section of a single microchannel

2 -->

2.2.分流微通道

为提高微通道的散热性能, 基于矩形长直微通道, 本文提出了一种具有分流微结构(在下文中简称为微结构)的微通道散热器, 其示意图如图2所示. 微结构由两部分组成, 其一是微通道中间的长方体扰流元, 其二是微通道侧壁的凹穴结构. 由于微通道间的壁厚限制, 考虑将凹穴的深度c设置为75 μm, 为尽量减少扰流元对流体流动的阻碍, 本文将扰流元的宽度b设置为75 μm. 同时, 将凹穴的长度d设置为800 μm, 为保证冷却液在通道中的流动畅通, 将扰流元的长度a设置成3/5 d即480 μm.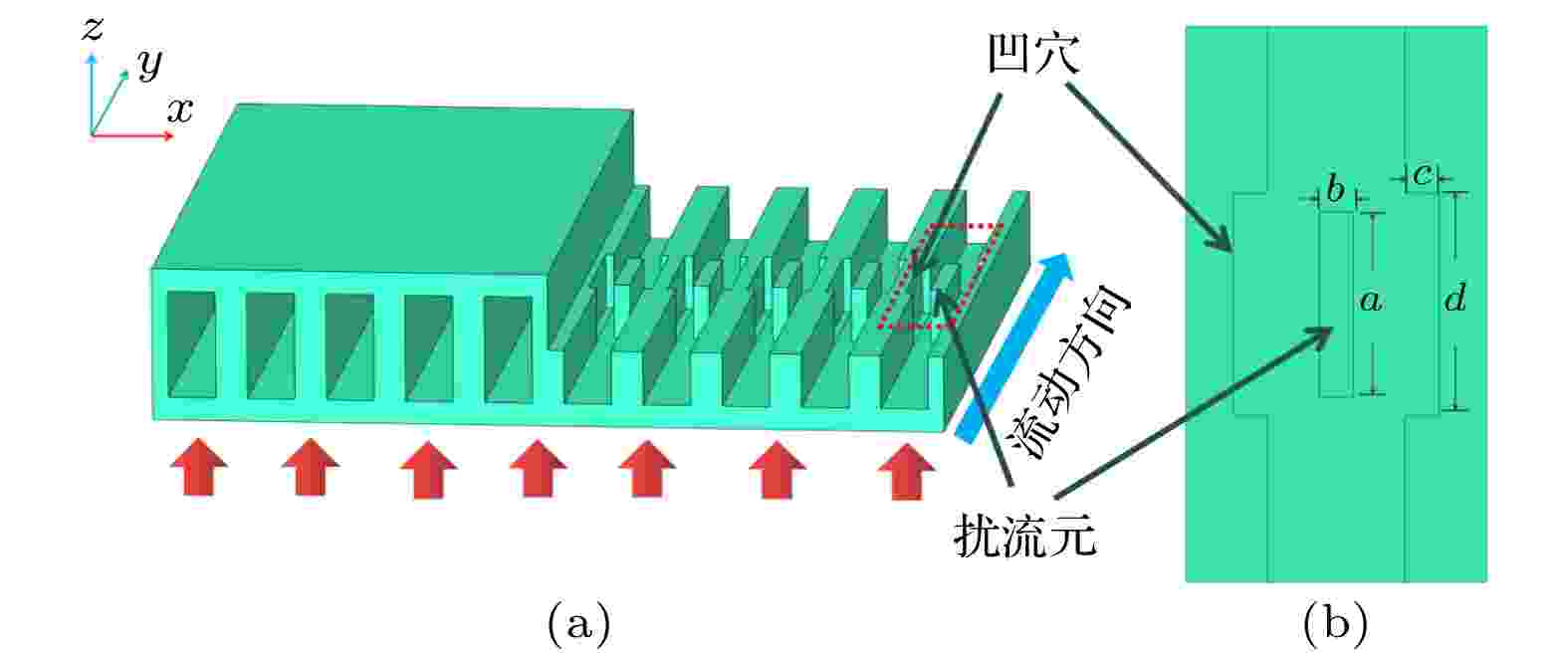
图 2 分流微通道结构示意图　(a)分流微通道散热器; (b)分流微结构局部俯视图
Figure2. Schematic diagram of the split-flow microchannel structure: (a) Split-flow microchannel heat sink; (b) Partial top view of the split-flow microstructure

2 -->

2.3.周期性分流微通道

基于矩形微通道以及分流微通道, 本文设计了一种具有周期性微结构的周期性分流微通道. 其结构是将分流微结构周期性排布于每根矩形微通道上(除入口端). 为探究每根分流微通道上分流微结构的个数对微, 道散热器散热性能的影响, 将单根微通道上微结构的数目分别设置为0, 3, 9, 15个, 并将其等距分布于每根微通道中, 单根微通道的结构示意图如图3中SM1—SM4所示.
图 3 含有不同数量及排布方式微结构的单/双根微通道示意图: SM1 (0组); SM2 (3组); SM3 (9组); SM4 (15组); DM1 (交错排布); DM2 (渐密排布); DM3 (渐变排布); DM4(交错渐变排布)
Figure3. Schematic diagram of single/double microchannels with different numbers and arrangements of microstructures: SM1 (0 group); SM2 (3 groups); SM3 (9 groups); SM4 (15 groups); DM1 (staggered arrangement); DM2 (gradually arranged); DM3 (gradient arrangement); DM4 (staggered gradient arrangement)

为改善微通道散热面温度分布不均的状况, 本研究设计了四种不同的排布方式, 如图3中DM1—DM4所示. DM1为交错排布, 即在单根微通道内微结构仍为等距排布, 但对于相邻的两根微通道, 微结构交错分布. DM2为渐密排布, 从微通道的入口端至出口端, 两组微结构之间的间距逐渐变小, 微结构越来越密集. 而DM3则在等距排列的基础上, 沿流动方向逐渐加宽了扰流元的宽度b, 在此称之为渐变排布. DM4将DM1与DM3的排布方式进行结合, 即交错渐变排布. 将微结构数量均设置成9组.
基于集成电路的基材大都为硅, 因此在本文中选用硅作为微通道散热器的基底材料. 考虑水为最常用的散热流体, 本文中水被选作为冷却介质.

2

-->

3.1.流体流动模型

在本研究中, 由于流体流的克努森数小于10^–3, 因此假定所有微通道散热器中的流体流都是连续的. 对于连续流体, 在单位时间内流经单位体积空间输入与输出的质量差与其内部质量变化的代数和等于零. 同时, 假设本研究中的冷却液为不可压缩流体, 单位时间单位体积空间内流入与流出的液体体积之差等于零, 所以模型的质量守恒方程如下^[31]:

$\rho \nabla \cdot \left(u\right)=0,$

其中$ \rho $为物质密度; $ u $代表流体速度; $ \nabla u $代表速度梯度.
纳维-斯托克斯(Navier-Stokes)方程是普遍用于描述黏性不可压缩流体动量守恒的运动方程, 适用于此分析. 同时, 计算中做出如下假设: (a)流体内部的体积力被忽略; (b)流体为层流; (c)流体为不可压缩且稳定; (d)考虑黏性耗散项, 冷却液的动力学黏度如表1所列. 所以流体的动量守恒可做如下表示^[31]:

温度 T/K	密度 ρ/ (kg·m–3)	恒压热容 cp/ (J·kg–1·K–1)	导热系数 κ/ (W·m–1·K–1)	动态黏度 μ/ (10–4 Pa·s)
293.15	998.2	4186.9	0.59423	10.093
303.15	995.62	4179.7	0.61055	7.96
313.15	992.2	4176.5	0.62516	6.51
323.15	988.05	4176.8	0.6381	5.47
333.15	983.22	4180.2	0.64942	4.70
343.15	977.78	4186.3	0.65916	4.10
353.15	971.78	4194.8	0.66738	3.59
363.15	965.3	4205.4	0.67413	3.17
373.15	958.39	4218.2	0.67944	2.82
383.15	958.39	4233	0.68337	2.53

表1不同温度下水的物理参数
Table1.Physical parameters of water at different temperatures

$\rho \left(u\cdot \nabla \right)=-p\nabla +\nabla (\mu \cdot \nabla u),$

其中, $ \mu $代表动力学黏度; p为流体静压.
在本研究中, 模型的边界条件如下:
1)对于流场, 认为入口速度是均匀的, 温度为室温(293.15 K);

$\begin{split}& y=0,~~ u={u}_{0}=0.88\sim \frac{1.88~\mathrm{m}}{s},\\ & {T}_{\mathrm{f}}={T}_{0}=293.15~\mathrm{K},\end{split}$

其中, $ {u}_{0} $为冷却液入口端流速; $ {T}_{\mathrm{f}} $代表流体温度; $ {T}_{0} $代表入口端流体温度.
2)在出口处施加了一定的压力条件(1 atm (1 atm=101325 Pa)):

$y=20000\;\mathrm{u}\mathrm{m},{P}_{\mathrm{f}}={P}_{\mathrm{o}\mathrm{u}\mathrm{t}}=1\;\mathrm{a}\mathrm{t}\mathrm{m},$

其中, $ {P}_{\mathrm{f}} $代表流体静压; $ {P}_{\mathrm{o}\mathrm{u}\mathrm{t}} $为流体出口端静压.
在以上的边界条件下, 通过对方程(1)以及方程(2)进行求解便可以求得三维模型中的速度场以及压力场.
2 -->

3.2.流/固体传热模型

广义传热方程(能量守恒方程)可用于描述热传导过程. 本研究涉及流体以及固体传热, 在流体域中, 热量主要通过流体对流传热以及热传导进行传播, 为简化计算, 忽略对传热影响较小的黏性发热项、压力功项以及累积项. 同时, 冷却液的物性会随着温度的变化而变化, 如表1所列^[32], 所以流体域中的能量守恒方程如下:

$ \rho {c}_{\mathrm{p}}u\cdot \nabla T-k{\nabla }^{2}T=Q,$

其中$ \rho $为物质密度; ${c}_{\mathrm{p}}$为材料比热容; T代表温度, $ \nabla T $代表温度梯度; k代表导热系数.
在固体域中, 只考虑热传导项, 同时, 假设材料物性不随时间及温度的变化而变化, 如表2所列^[32], 能量守恒方程如下:

材料 物性	密度ρ/ (kg·m–3)	恒压热容 cp/ (J·kg–1·K–1)	导热系数k/ (W·m–1·K–1)
硅	2329	700	130

表2硅的物理参数
Table2.Physical parameters of silicon.

$ {k\nabla }^{2}T=0,$

其边界条件设定如下:
1)底面施加100 W/cm²的广义向内热通量边界条件:

$z=0,\; {q=q}_{\mathrm{m}}=-k\nabla T,\; {q}_{\mathrm{m}}=1000000~\mathrm{W}/{\mathrm{m}}^{2},$

其中, $ {q}_{\mathrm{m}} $为换热面上的热通量.
2)侧壁使用对称边界条件:

$x=0,\; x=500~\text{μ}\mathrm{m},\;{q=q}_{\mathrm{s}}=-k\nabla T,~{q}_{\mathrm{s}}=0 ,$

其中, $ {q}_{\mathrm{s}} $为侧壁上的热通量.
3)其余外表面均为热绝缘状态

$q={q}_{\mathrm{f}}=-k\nabla T,\; {q}_{\mathrm{f}}=0,$

其中, $ {q}_{\mathrm{f}} $为其余表面的热通量.
将以上边界条件以及层流模块求出的速度场结果代入能量守恒方程进行求解, 便可求得模型固体以及流体域中的温度场. 温度场同时也将作为自变量对材料的物性造成影响, 在此形成双向耦合关系. 计算中考虑将流/固体传热模块进行耦合, 通过稳态方程求解在稳定工作状态下的压力场、流体速度场、流/固体温度场分布.
本文所涉及的基材物理参数及散热流体参数从用表1与表2参数.
2 -->

3.3.流体参数

雷诺数是一种表征流体流动情况的无量纲数, 在管道流中, 雷诺数小于2300的流动为层流. 微通道入口端雷诺数由以下公式定义:

$ Re=\frac{\rho {u}_{0}D}{\mu },$

其中, Re代表雷诺数, D是水力直径, 在本文中, 假设流体为层流, 计算过程中, 入口端雷诺数取200—600.
通过模型压力场计算结果可以求得冷却液在微通道内的压降损失, 压降是流体流动前后的压力差, 代表了流体流动过程中能量损失的大小, 由以下公式定义:

$\Delta P={P}_{0}-{P}_{\mathrm{o}\mathrm{u}\mathrm{t}},$

其中, $ \Delta P $代表压降, $ {P}_{0} $为冷却液入口端平均压力, $ {P}_{\mathrm{o}\mathrm{u}\mathrm{t}} $为冷却液出口端平均压力.
通过压降损失的计算结果, 以及流体速度场的求解结果可以通过(12)式和(13)式求得系统所需泵送功率的大小以及达西摩擦因子的大小. 其中泵送功率决定了系统的能耗, 摩擦因子反映了微通道对流体流动的阻力.
泵送功率:

$P=V\cdot \Delta P={n}_{0}\cdot {u}_{0}\cdot {A}_{\mathrm{a}}\cdot \Delta P, $

其中, P代表泵送功率, $ {A}_{\mathrm{a}} $是通道的入口横截面积, $ {n}_{0} $是微通道的数量, $ {u}_{0} $是流体在通道入口处的平均速度.
摩擦因子:

$f=\frac{\Delta P}{2\rho {u}_{0}^{2}}\cdot \frac{D}{L},$

其中, f代表泵送功率, D为通道长度.
通过流/固体温度场的求解结果可以通过(14)式和(15)式求得模型的总热阻以及平均努塞尔数. 其中热阻反映了模型传热能力的大小, 努塞尔数反映了对流换热的强烈程度.
散热器的总热阻:

$R=\frac{{T}_{\mathrm{m}}-{T}_{\mathrm{a}}}{q\cdot A},$

其中, R代表热阻, $ {T}_{\mathrm{m}} $是换热面最高温度, $ {T}_{\mathrm{a}} $是上游流体温度, $ A $是换热面面积.
微通道的平均努塞尔数^[33]:

${Nu}=\frac{q\cdot A\cdot D}{k{n}_{0}{A}_{\mathrm{b}}\left({T}_{\mathrm{b}}-{T}_{\mathrm{m}}\right)},$

其中, $ {Nu} $为平均努塞尔数, $ k $是导热率, A_b是每个通道的计算表面面积, T_b是通道壁表面的平均温度, T_m代表冷却液的平均温度.
在此基础上, 采用整体传热性能(performance evaluation criterion, PEC)来比较周期性分流微通道与传统微通道之间传热性能及流动阻力的提高^[34].

$\mathrm{P}\mathrm{E}\mathrm{C}=\frac{{Nu}/{{Nu}}_{0}}{f/{f}_{0}},$

其中, $ {{Nu}}_{0} $为SM1的平均努塞尔数, $ {f}_{0} $为SM1的达西摩擦因子. 若PEC > 1, 则表示周期性分流微通道的整体传热性能优于传统长直微通道.
2 -->

3.4.网格设置

本文的模拟仿真主要采用基于有限元方法进行仿真计算的COMSOL软件进行. 有限元方法的核心是通过网格划分的方式将复杂的几何实体离散成有限个规则的几何单元. 网格的质量以及数量直接决定了计算结果的准确性, 使用常见的单根矩形长直微通道(SM1)进行网格独立性测试, 对流体域部分采用质量较高的六面体结构化网格进行划分, 对于剩余固体域部分, 采用自由四面体网格进行划分. 并使用6种不同数量的网格来检查网格独立性, 网格数目分别为893083, 1128905, 1414841, 1702482, 1916125, 3475672. 入口速度固定为1.18 m/s. 表3列出了以3475672个网格为基准的计算结果.

	网格1893083	网格21128905	网格31414841	网格41702482	网格51916125	网格63475672
压降损失($ \Delta P $)	4195.0	4287.0	4341.2	4379.9	4409.6	4406.1
最高温度(Tm)	353.05	352.65	352.32	351.94	351.88	351.87
误差	4.8%; 0.33%	2.7%; 0.22%	1.47%; 0.13%	0.59%; 0.020%	0.079%; 0.0028%	基准

表3网格独立性研究
Table3.Grid independence research

如表3中所示, 随着网格逐渐细化, 计算结果中压降以及最高温度的误差逐渐变小, 对于网格5, 其最高温度和压降的误差很小, 可以忽略不计. 因此, 兼顾计算准确性与效率, 选择网格5所对应的网格划分方式及大小进行后续所有仿真计算.

基于以上物理及数学模型与网格设置, 分别计算了 SM1—SM4以及DM1—DM4的压力场、速度场以及温度场特性. 通过压力特性、流动特性以及温度特性三方面对设计的不同微通道散热器进行分析, 以验证微结构对微通道热性能提升的有效性. 同时, 探究了微结构数目对其热性能的影响, 探索其最优微结构数目. 此外, 也研究了不同的排布方式及结构参数对微通道散热器热性能的影响.
2

-->

4.1.压力特性

图4(a)给出了在入口流速为1.18 m/s的情况下, SM1~SM4 四种情况下在流体流动方向上的压力变化曲线. 其中SM1在流体进入微通道直至流出微通道的过程中, 压力下降稳定. 可以预料到, 如果流动是层流且流动充分展开, 则通常的平滑通道内的压降会由于通道壁面对流体的阻力显示出线性下降, 这与图4(a)所示的结果相接近. 在引入微结构后, 流体压力在呈现线性下降的基础上出现了波动. 图5给出了SM2中流体流经微结构附近时的压力分布云图. 可以看到, 流体在途经微结构区域前压力分布均匀, 流体流经微结构时首先进入突扩段, 即微通道突然变宽段, 突扩型通道中流体在流动过程中遇到管道截面突然变宽, 流体具有一定速度, 不能立即随通道形状的变化而变化, 从而产生局部紊流, 造成阻力增大. 同时, 由于扰流元侧壁对流体流动的阻碍作用, 压力升高. 之后流体被分为两束流入左右两侧凹穴后继续向前流动, 此时微通道宽度较无微结构段略宽, 由于壁面摩擦阻力使得压力迅速下降. 经过扰流元后流体再次进入突扩段, 产生局部紊流, 同时受到微通道左右凹穴边缘的阻碍导致压力再次上升, 随后进入突缩段, 即微通道突然变窄段, 此时被打破的层流边界层正处于恢复阶段, 且由于流出微结构后流体流动方向与微通道侧壁不平行, 存在一定夹角, 导致低压区出现, 使得流体局部压力迅速下降. 随后, 层流边界层恢复, 层流压力再次呈现线性下降, 这与图4(a)中SM2—SM4所示的流体沿流动方向流经任意一组微结构时压力出现的先升高, 再降低, 再升高, 再降低的趋势一致.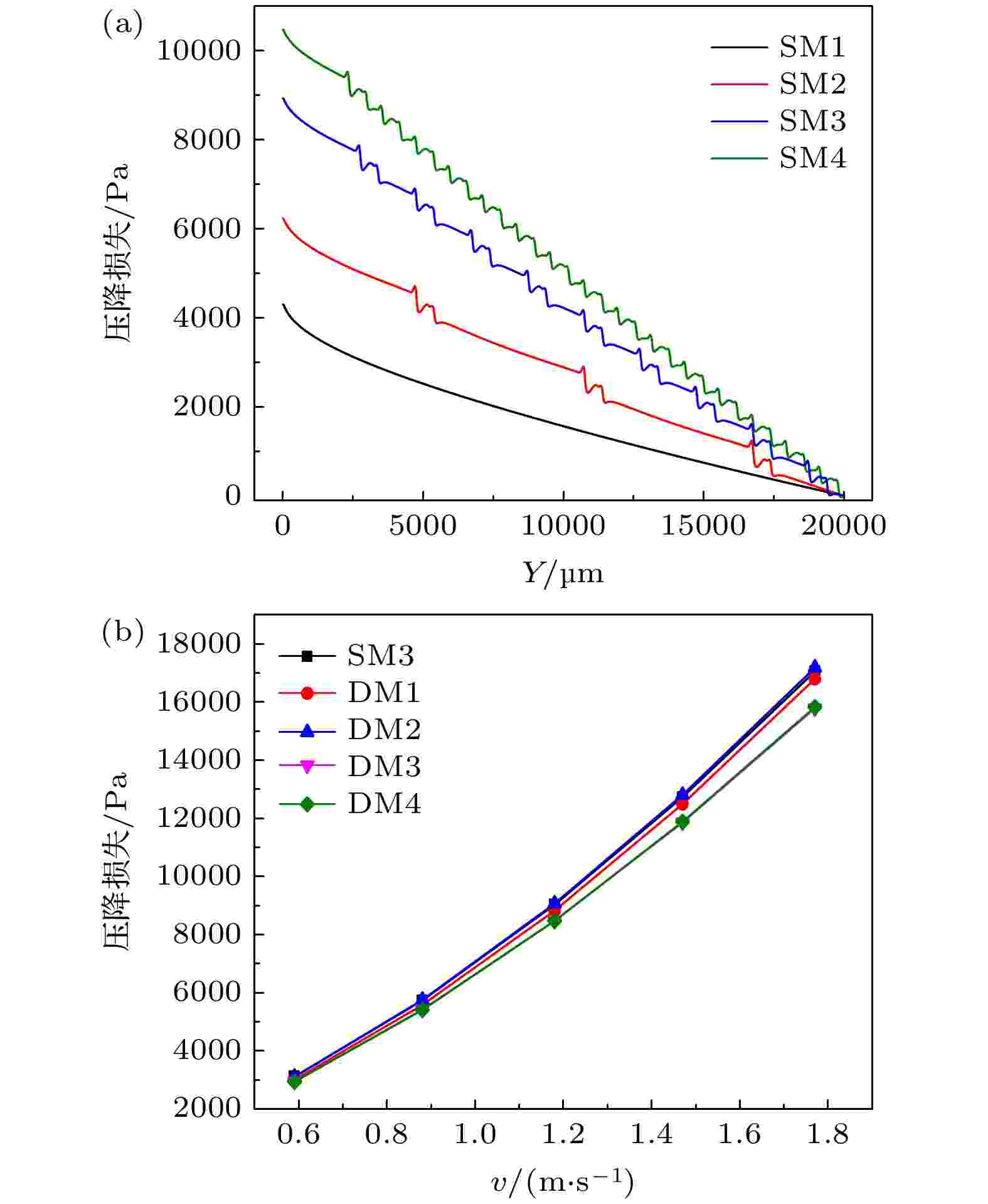
图 4 (a) SM1—SM4微通道内主流线方向流体的压力变化; (b) SM3及DM1—DM4在不同入口端流速下的压降损失
Figure4. (a)Pressure change of the fluid in the direction of the main flow line in the SM1–SM4 microchannel; (b) the pressure drop loss of SM3 and DM1–DM4 at different inlet flow rates.

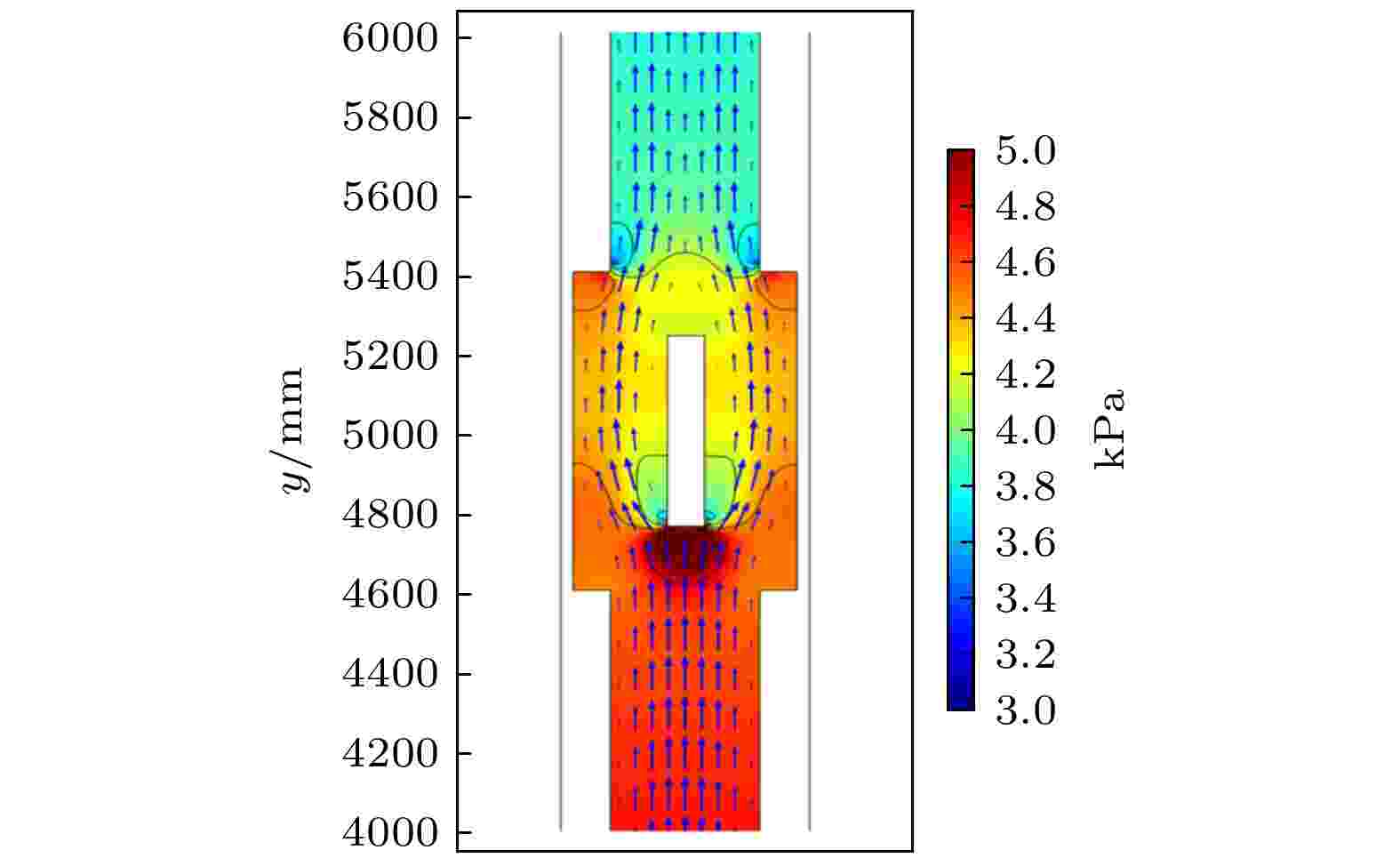图 5 SM2中微结构附近局部流体的压力变化切面云图
Figure5. Cross-sectional cloud diagram of pressure change of local fluid near the microstructure in SM2

由图4(a)可知, 由于微结构的引入使得分流微通道相较于传统长直微通道的压降损失更大, 也产生了更多的压力突变区, 使系统稳定性产生一定程度的降低, 这也是在所难免的. 随着微结构数量增加产生了更大的压降损失, 但压降损失的增长速度越来越慢, 这是由于流体在流经微结构时原本层流的边界层被打破, 经过微结构后又逐渐恢复, 但随着微结构数量增加, 两组微结构之间距离变短, 层流边界层在未完全恢复时就已经到达下一组微结构处, 减少了每组微结构所产生的压力损失, 但总体来说仍然是更多组的微结构产生更大的压降损失. 图4(b)给出了5种微结构数量相同但排布方式不同的微通道在不同入口端流速情况下的压降损失. 对于SM3, DM1及DM2, 虽然3种情况下压力的波动变化有所差异, 但3种不同的微结构排布方式的总压降损失十分接近. 可以得出在微结构数目相同的情况下, 不同的微结构排布方式对微通道整体的压降损失没有明显的影响. 但对于DM3及DM4, 压降损失出现了减少, 在入口端流速为1.88 m/s时最为明显, 压降减小了1200 Pa左右, 这是由于减薄了部分扰流元宽度, 降低了其对流体流动的阻碍所导致的.
压降的增加将会提高微通道散热器所需的泵送功率. 泵送功率越高, 能耗越大, 微通道系统的稳定性就越低. 图6(a)给出了SM1—SM44种情况下的泵送功率与总热阻之间的关系. 结果表明, 整体热阻随着泵送功率的增加而减小. 对于给定的泵送功率, 微结构的存在会导致整体热阻下降, 且微结构数量越多, 热阻越低, 这表明了微结构对于提升微通道热性能的有效性. 但是, 从图6(a)可以看到, 当微结构到达9组后, 继续增加微结构数目, 相同泵送功率下的热阻变化变得微小, 不能继续提升微通道的散热性能, 初步确定9组为单根微通道内的最佳组元数目. 在微结构数目相同但排布方式及结构参数不同的情况下, DM1—DM4相同泵送功率下的热阻几乎相同, 且均优于SM3, 其中DM4的热阻最低, 如图6(b)所示. 换言之, 在几种情况热阻相同时, 交错渐变式排布微通道所需的泵送功率更低, 能耗损失更小, 系统具有更高的稳定性.
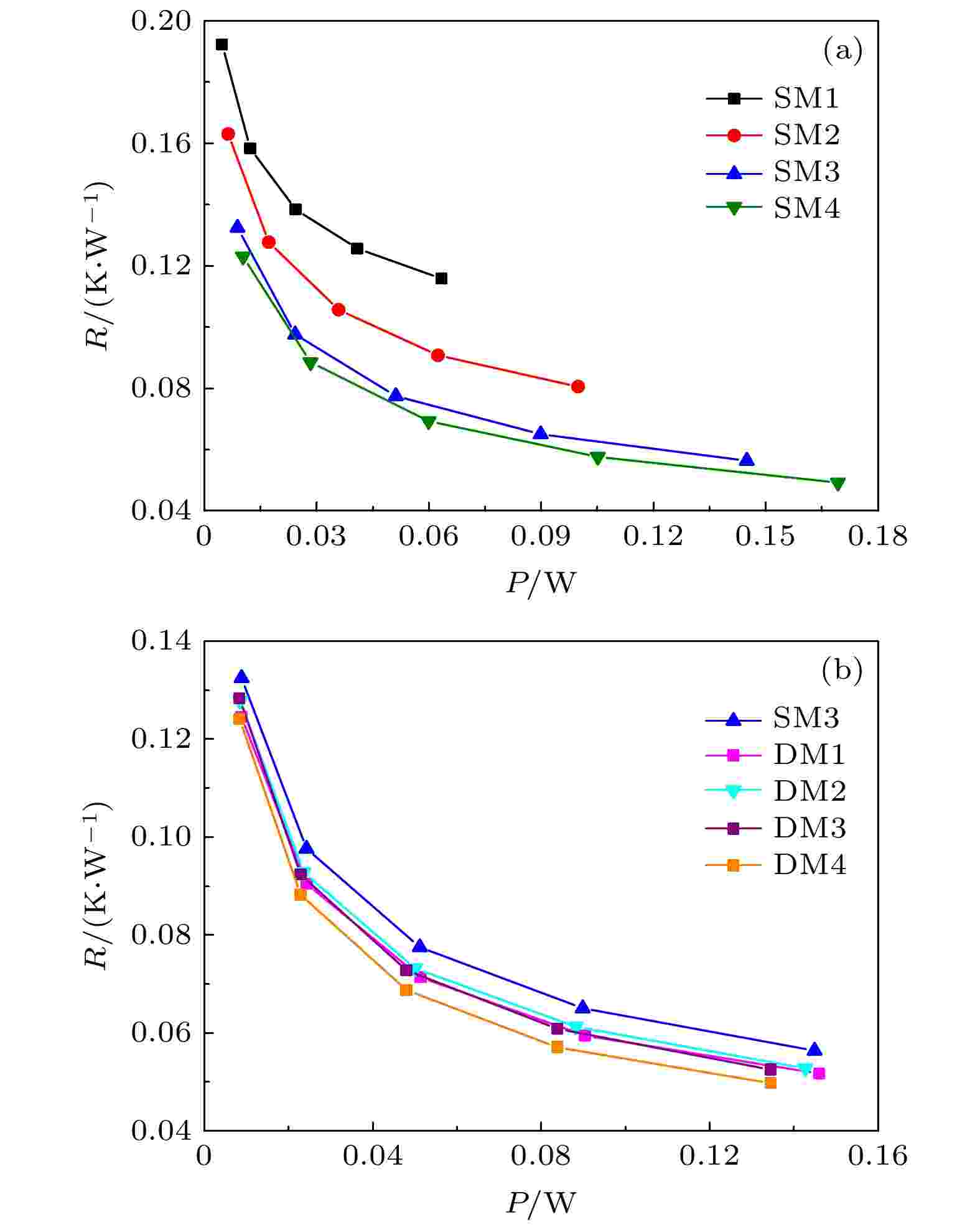图 6 整体热阻与泵送功率的关系　(a) SM1—SM4; (b) SM3, DM1—DM4
Figure6. Relationship between overall thermal resistance and pumping power: (a) SM1–SM4; (b) SM3, DM1–DM4

2 -->

4.2.流动特性

图7所示为SM2中流体在流经微结构前后(x–y)平面中的局部速度变化. 可以看到, 微通道入口与进入微结构之前的位置流体速度相对稳定, 流体的流动由于壁面的摩擦, 均呈现沿流动方向外侧流速变慢而内部流动变快的趋势, 如图7(a)所示. 但是如图7(b)所示, 微结构的引入改变了微通道内的冷却液流动, 流体在流经微结构时内部扰流元的存在可以有效地促进边界层的生长, 在流体中间部分产生新的边界层, 且在局部位置产生了较低流速的二次流及回流区, 促进了冷却液的混合, 相应地增强热传递. 流场在离开微结构后开始逐渐恢复到其原始状态, 如图7(c)所示, 速度逐渐趋于稳定且中间的边界层逐渐消失.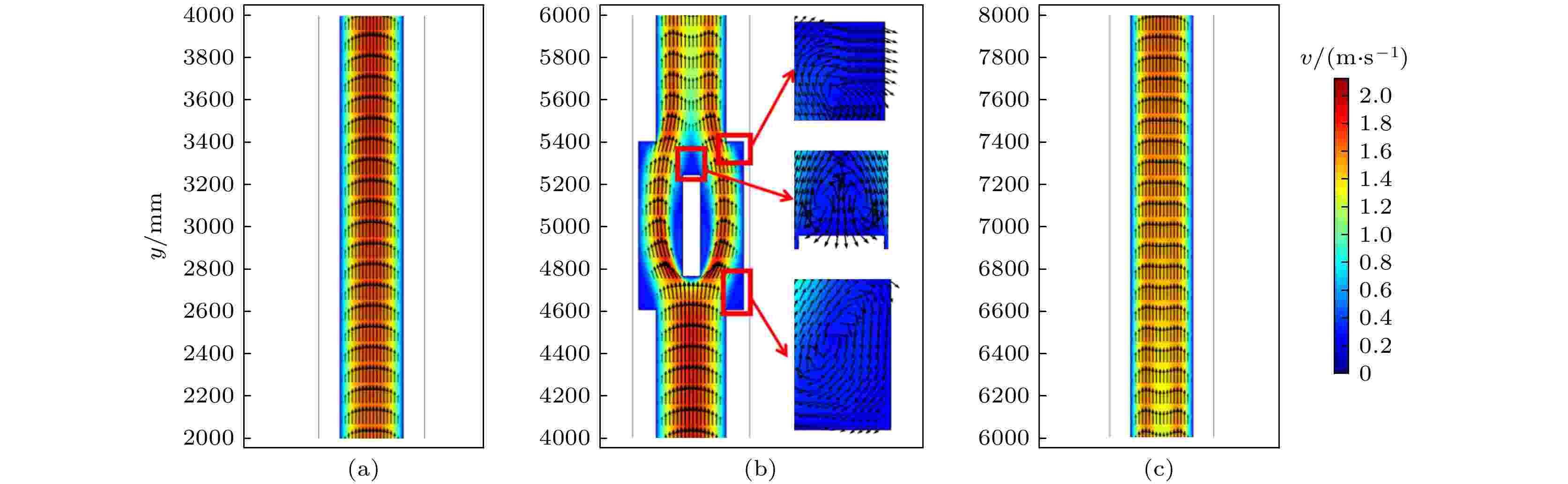
图 7 流体在SM2微通道内不同位置的流速分布
Figure7. Flow velocity distribution of fluid at different positions in the SM2 microchannel

图8更加直观给出了流体流经微结构前后边界层生长与恢复的过程, 当流体进入微结构区域但未到达扰流元时, 其流速切面如图8(b)所示. 此时, 由于受到扰流元的干扰, 中间流体开始向左右两侧流动, 新的层流边界层开始在中间位置产生. 在流体经过扰流元后, 如图8(c)所示, 左右两侧流体开始向中间方向流动, 中部边界层开始逐渐消失. 在边界层生长与消失的过程中, 冷却液的横向流动也促进了微通道内冷/热冷却液的混合, 促进了热交换.
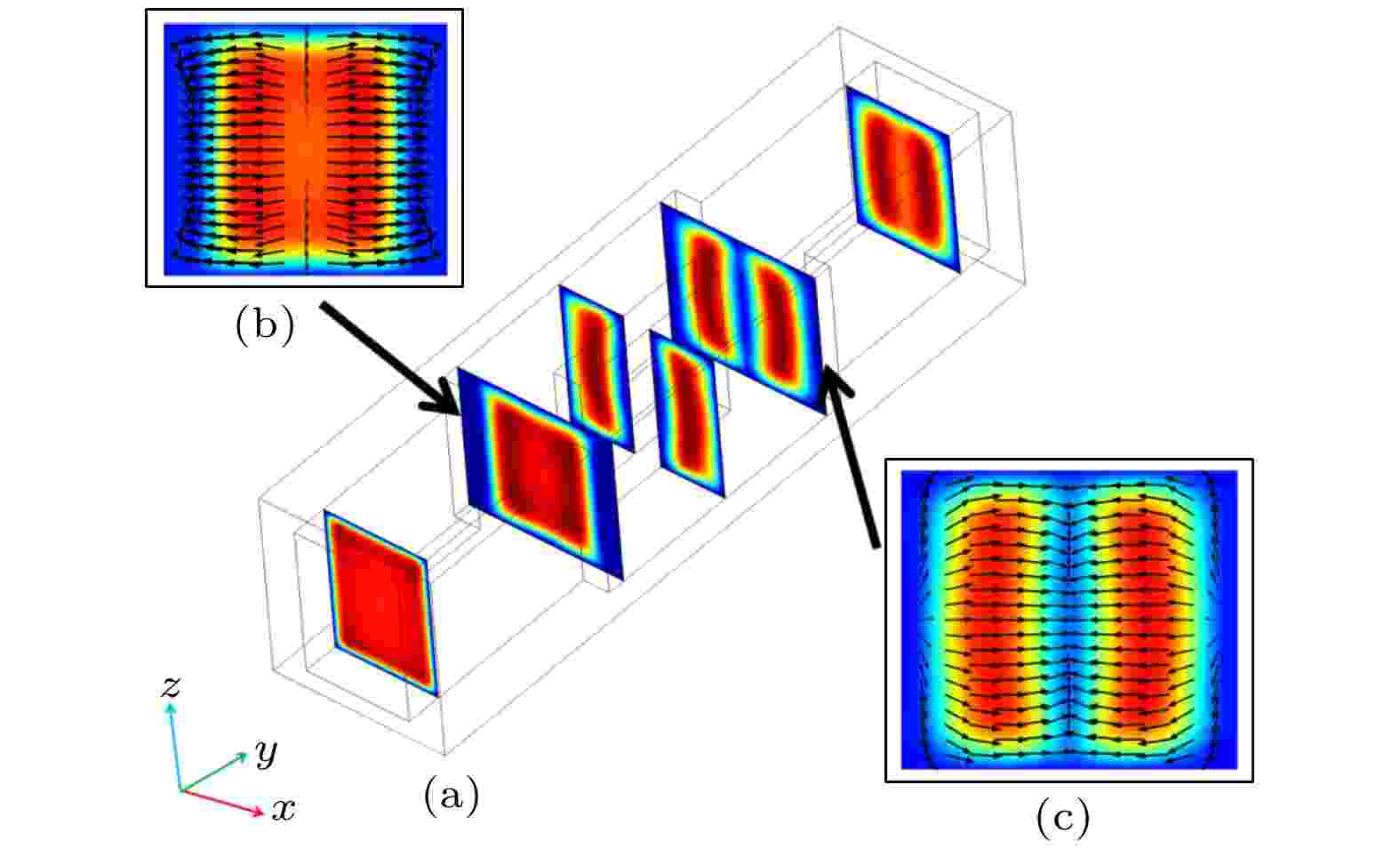图 8 不同位置流速切面图
Figure8. Cross-sectional view of flow velocity at different locations

2 -->

4.3.温度特性

微通道底面的最高温度与入口端流速之间的关系如图9(a)所示. 无论是否引入微结构, 通过改变入口端冷却液的流速均可对其表面最高温度进行控制. 冷却液流速越大时, 散热器的表面最高温度越低. 而在相同的流速下, 微结构的引入使微通道底面的最高温度得以下降, 这直观证明了微结构改善微通道散热器热性能的有效性. 此外, 拥有更多组微结构的微通道散热器表面最高温度更低. 在入口端流速为1.18 m/s时, SM2比SM1的最高温度下降了13.1 K, SM3同样比SM2最高温度下降11.26 K, 而继续增加微结构数量时, 最高温度的降低变得缓慢. 对于5种微结构数量相同但排布方式不同的情况, DM1~DM4的底面最高温度均略低于均匀排布(SM3), 其中DM4最高温度最低, 在不同流速下相比SM3均下降了3~5 K. 这也证明了交错渐变排布方式有利于进一步降低散热器表面结温.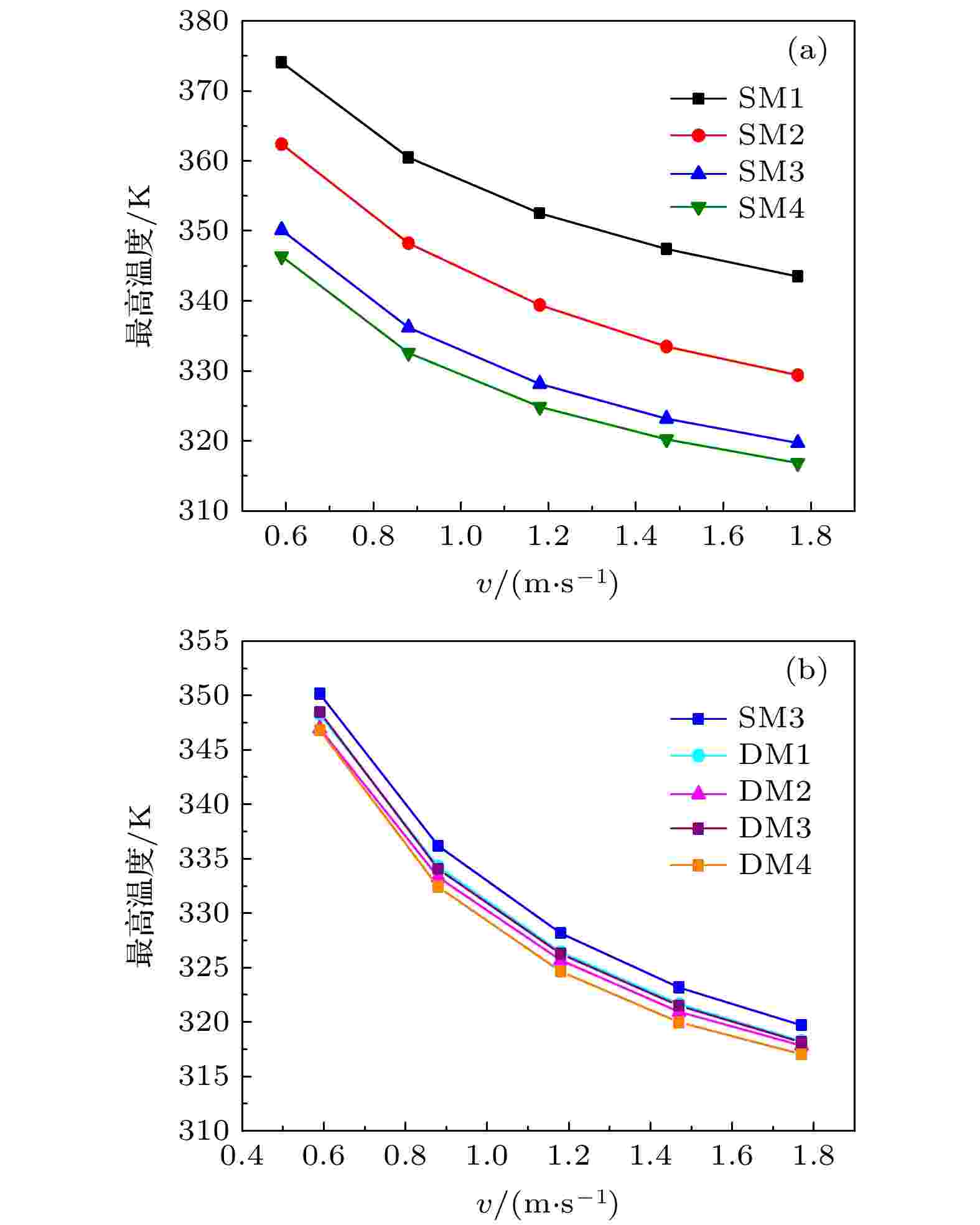
图 9 微通道底面最高温度与入口端流速的关系　(a) SM1—SM4; (b) SM3及DM1—DM4
Figure9. Relationship between the maximum temperature on the bottom of the microchannel and the flow rate at the inlet: (a) SM1–SM4; (b) SM3 and DM1–DM4

图10(a)给出了SM1~SM4了在入口速度为1.18 m/s的情况下, 沿着主流动方向的微通道底部中心线上的温度分布. SM1的底面温度沿着流动方向呈现持续上升的趋势, 这是由于冷却液在流动过程中与微通道壁面进行热交换, 外部流体被逐渐降温, 导致换热效果下降所致. 而引入微结构后温度则呈现出周期性变化的趋势, SM2—SM4底面温度沿流动方向在微结构处出现波动, 呈现先下降再上升的波动, 延缓了温度的持续上升. 这主要是由于微结构的引入打破了流体的边界层, 增大了换热面积及促进了冷/热冷却液的混合所导致的. 但微结构在提高微通道散热性能的同时, 也使其温度分布变得不均匀. 如图11所示, SM1—SM4基底出现多处低温区, 且换热面均沿流动方向出现较大的温度梯度, 温度分布的不均匀将产生热应力, 使系统稳定性降低.
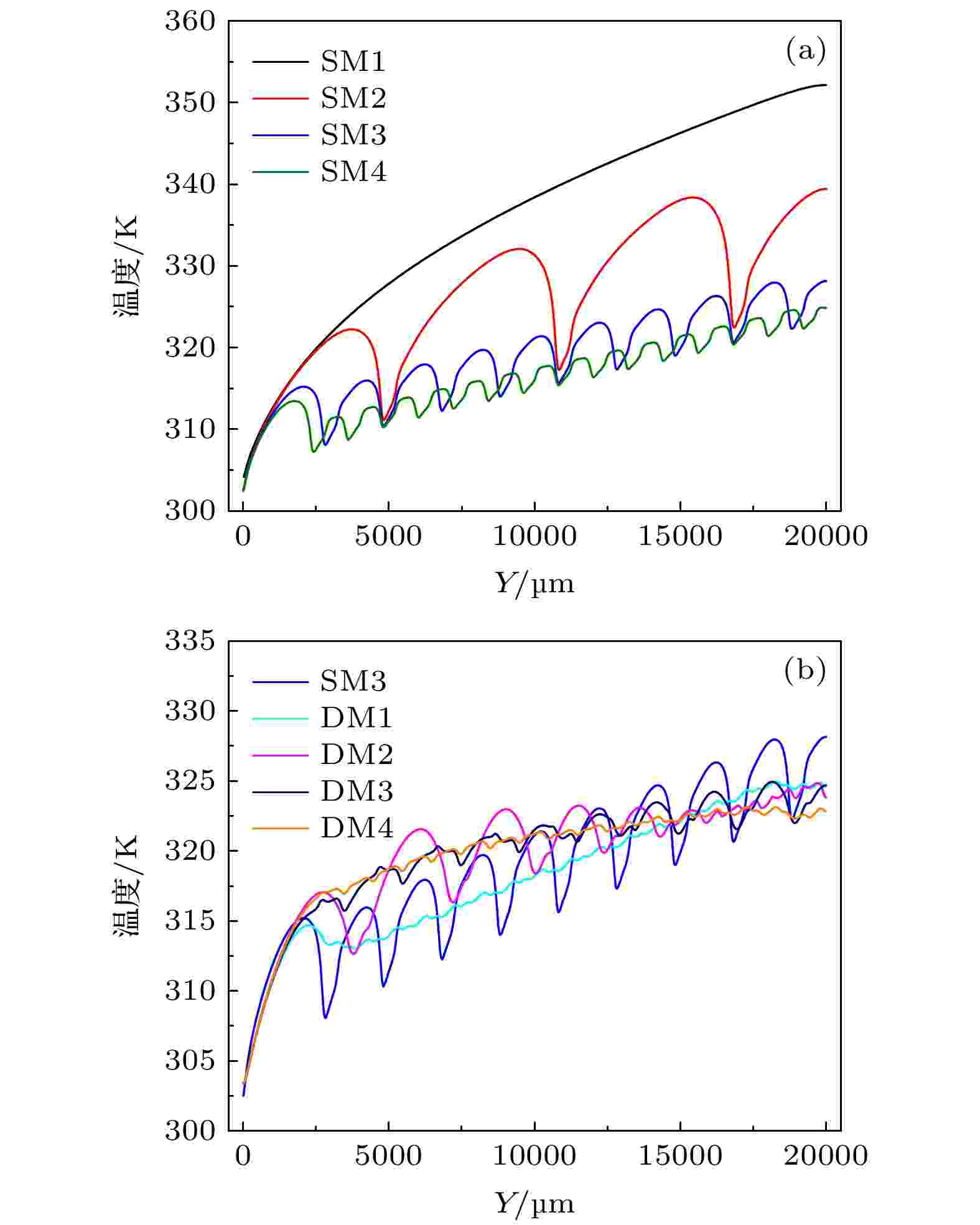图 10 不同情况下底面上沿主流动方向上温度变化　(a) SM1—SM4; (b) SM3及DM1—DM4
Figure10. Temperature changes along the main flow direction on the bottom surface under different conditions: (a) SM1–SM4; (b) SM3 and DM1–DM4.

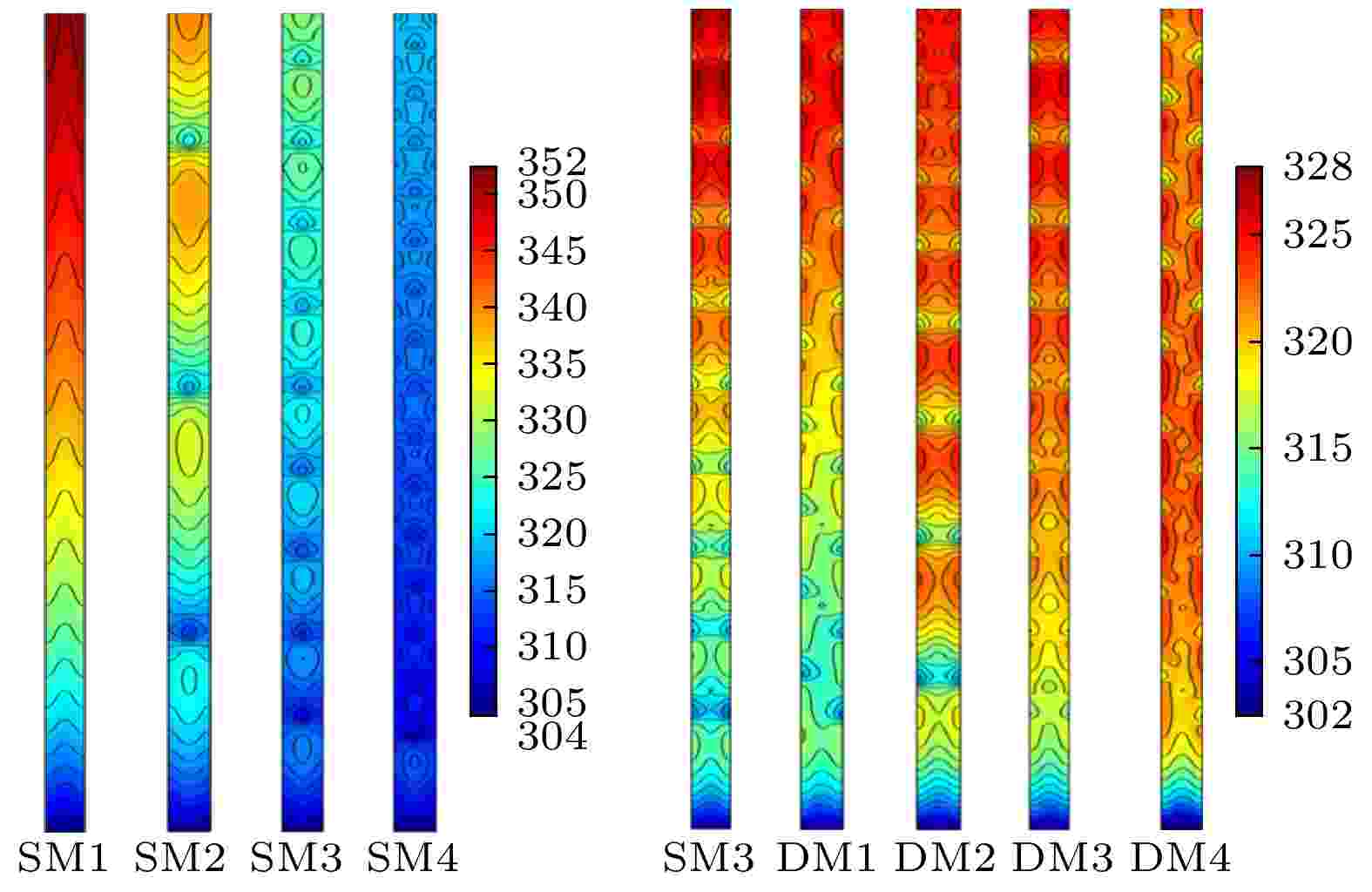图 11 不同情况下换热面温度分布云图
Figure11. Cloud diagram of temperature distribution of heat exchange surface under different conditions.

从图11可以发现, 不同的微结构排布方式对微通道的温度分布有较大影响. 对于DM2, 由于入口一端微结构排布稀疏, 导致其散热面沿流动方向上温度变化波动性较大, 散热面温度均匀性较低, 这也是不难想象的. 此难以避免的缺点也是建立对照组时并未将其与其他排布方式进行结合并进行分析的原因. 但对于DM1及DM4由于采用了交错式排布, 避免了在两组微结构中间出现长距离的无微结构段, 在一定程度上避免了高/低温区的产生. 在图10(b)中可以更直观地看出DM1及DM4在主流动方向上的温度波动变得微小. 且对于DM4, 其沿流动方向逐渐变宽的扰流元使得冷却液被充分利用, 换热面上除入口段外沿流动方向温度始终维持于较小范围内, 说明渐变的排布方式使微通道散热面上的温度变得较为均匀, 减少了高/低温区域、减小了温度梯度, 使系统变得更加稳定. 综上所述, DM4的温度特性最优.
图12给出了不同情况下入口雷诺数与整体热阻之间的关系. 显然, 不同情况下的热阻均随着雷诺数的增加而减小. 这是由于流量的增加导致雷诺数增加, 改善了微通道的热性能. 在雷诺数相同的情况下, 引入了微结构的微通道的整体热阻明显低于传统长直微通道. 且随着微结构数量的增加热阻逐渐降低. 对于入口端雷诺数为400的微通道, 相比于SM1, SM2热阻下降约25%, SM3热阻下降了约44%. 这表明微结构大大提高了微通道散热器的传热能力, 但在超过9组时, 微结构数量的增加对其热阻的减小变得缓慢. 同时, 在数目相同的情况下改变排布方式其热阻也会有一定程度的降低, 其中DM4热阻最低, 相比于SM3下降了12%左右, 也证明了交错渐变排布方式的微通道具有更优的传热能力.
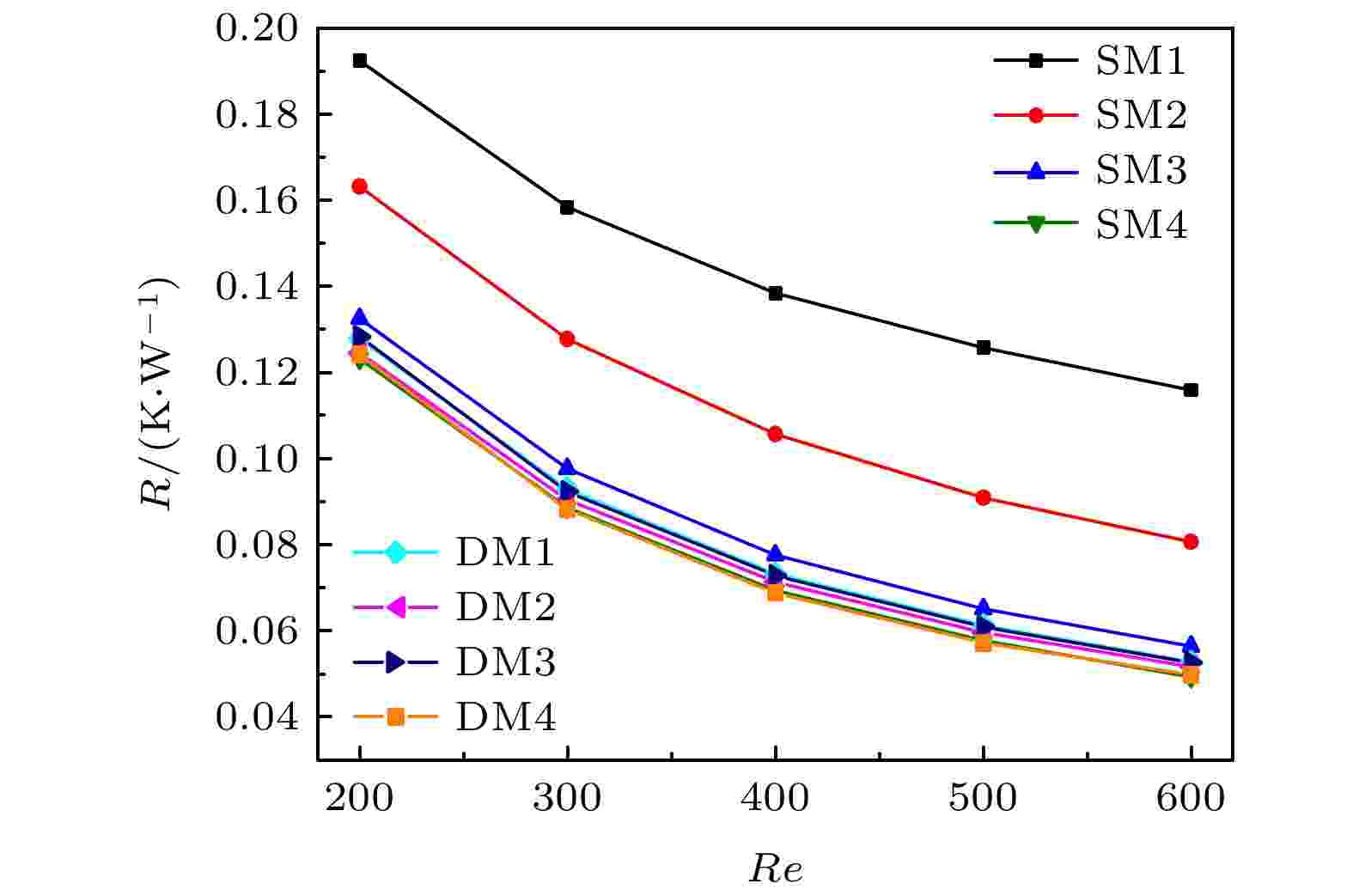图 12 微通道散热器整体热阻与入口雷诺数的关系
Figure12. The relationship between the overall thermal resistance of the microchannel radiator and the entrance Reynolds number.

图13(a)给出了8种情况下平均努塞尔数与雷诺数的关系. 在所有情况下, 努塞尔数均随进口雷诺数的增加而增加. 内部包含微结构的微通道的努塞尔数均高于矩形长直微通道(SM1), 表明微结构的引入将增强微通道内的对流换热. 且微结构数目为9组时努塞尔数的提升最为明显. 在改变微结构的排布方式时, 从图13(a)可以发现, 采取不同的排布方式努塞尔数有着不同程度的提升, 其中DM4努塞尔数最高, 相比均匀排布的SM3努塞尔数提高约5%, 故其内部对流换热最为剧烈.
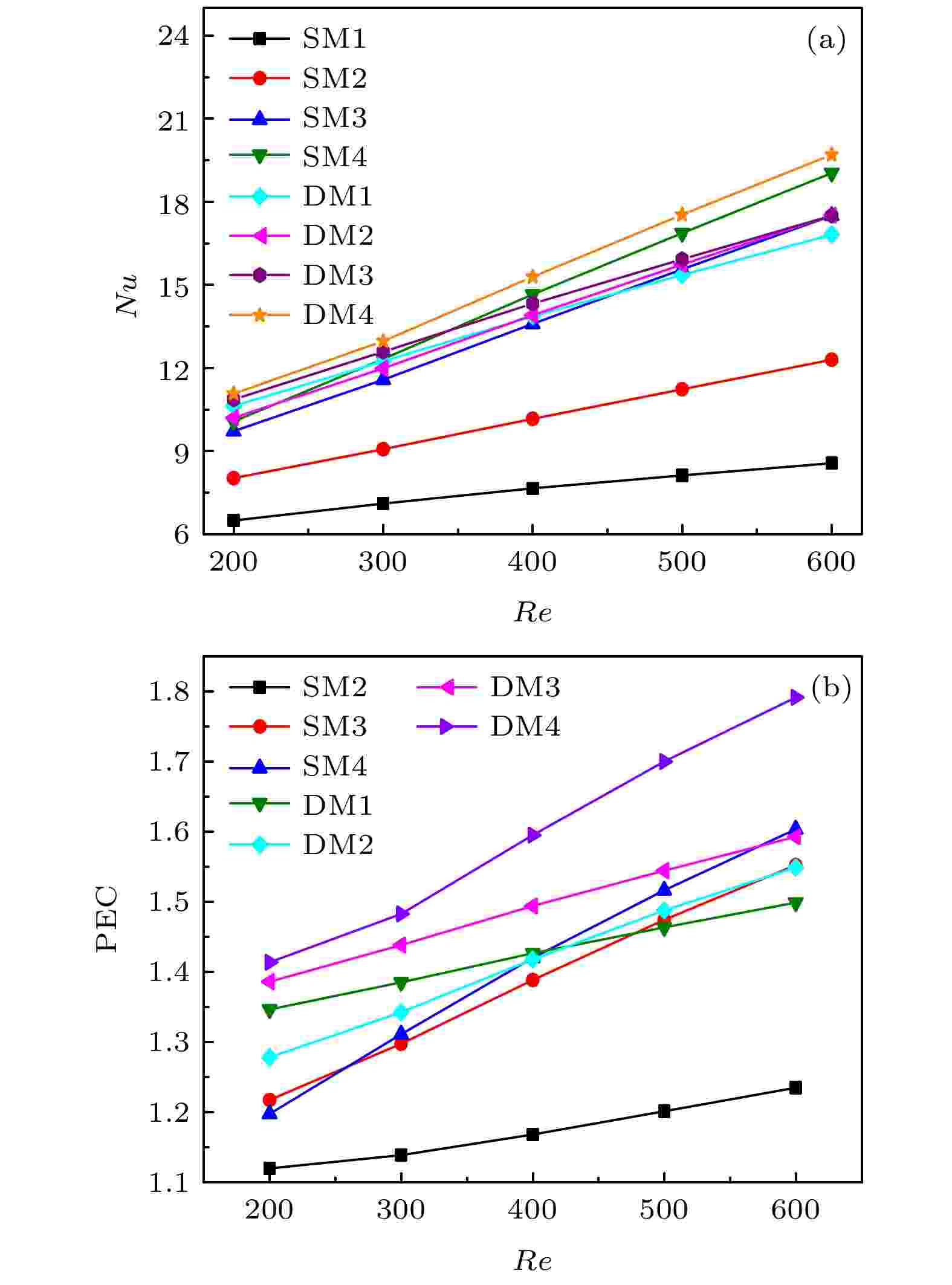图 13 (a)不同情况下努塞尔数与入口端雷诺数的关系; (b)不同情况PEC与入口雷诺数的关系
Figure13. (a) The relationship between Nusselt number and inlet Reynolds number under different conditions; (b) the relationship between performance evaluation criterion and inlet Reynolds number under different conditions.

从图13(b)可以发现, 在不同的入口端雷诺数下, 包含微结构的微通道散热器的整体传热性能(PEC)均大于1, 证明了微结构对综合热性能提升的有效性. 其中微结构采用交错渐变方式排布的DM4 PEC值最高, 在微结构数量为9组、雷诺数为700时达到1.79, 展现出最优的综合热性能.

本文基于周期性分流微通道的结构设计及其散热仿真, 系统研究了微结构数量及微结构排布方式对其压降、流动及传热性能的影响, 主要结论如下:
1)分流微结构的引入可增加微通道内部换热面积, 打破原有层流边界层且局部产生二次流动, 增强冷/热冷却液的混合, 降低散热面上最高结温, 有效提升微通道散热器的散热性能.
2)微结构的数量对微通道的散热性能有着直接的影响, 综合考虑微通道散热器的热性能、压降损失以及系统稳定性, 最终确定9组为单根微通道内最佳微结构数目. 在入口流速为1.18 m/s时, 相较于传统长直微通道散热器基底表面最高结温下降24.5 K左右, 热阻下降44 %左右, 努塞尔数增大约124 %, 整体传热性能(PEC)达1.465.
3)优化排布方式对微通道散热器的热性能有进一步的提高, 其中采用交错渐变的微结构排布方式对微通道热性能提升最为明显, 在微结构数量为9组, 入口端流速为1.18 m/s时, 相比于微结构均匀排布的微通道散热器, 其压降损失降低约500 Pa; 表面最高结温下降约3.5 K; 热阻下降约12 %; PEC提升15 %左右.
4)微结构采用交错渐变的周期排布方式避免了两组微结构间的长距离无微结构段, 沿流动方向逐渐变宽的扰流元使得冷却液被充分利用, 从而减少微通道散热器换热面上的高/低温区域, 降低沿流动方向出现的温度梯度, 使散热面上温度分布均匀, 减少热应力的产生, 一定程度上提高了冷却效率以及系统稳定性.
本文提出的周期性分流微通道散热结构, 为高密集电路的高效散热问题提供了新的解决思路与方法, 有望用于超大规模集成电路芯片的高效散热基底.