摘要: 多焦点结构光照明显微镜(multifocal structured illumination microscopy, MSIM)能在50 μm的成像深度内实现2倍于衍射极限分辨率的提升, 但在对厚样品成像时, 散射光和离焦光限制了其层析能力和图像衬度. 双光子多焦点结构光照明显微镜(two-photon MSIM, 2P-MSIM)克服了样品组织散射的影响, 进一步提高了MSIM的成像深度和成像特性. 然而, 现有的2P-MSIM通常采用振镜扫描成像, 系统复杂, 灵活性差. 为了解决上述问题, 本文提出了一种基于高速相位型空间光调制器(spatial light modulator, SLM)的双光子多焦点结构光照明超分辨显微成像系统, 通过在SLM上同时加载生成多焦点阵列的相位图和线性相位光栅的相位图, 实现了多焦点阵列的产生和在样品面上的高精度的并行数字随机寻址扫描和激发成像, 结合像素重定位和反卷积技术实现了三维双光子多焦点结构光超分辨成像, 解决了扫描振镜在2P-MSIM成像中的机械惯性问题, 同时降低了系统的复杂性, 提升了灵活性. 在此基础上, 利用搭建的2P-MSIM开展了小鼠肾组织切片和铃兰根茎双光子超分辨成像实验, 验证了该方法的三维超分辨成像能力, 对于2P-MSIM的发展具有重要的意义.
关键词: 多焦点结构光照明显微技术 /
双光子 /
荧光显微镜 /
空间光调制器 English Abstract Two-photon multifocal structured light microscopy based on high-speed phase-type spatial light modulator Yu Huan-Huan Zhang Chen-Shuang Lin Dan-Ying Yu Bin Qu Jun-Le Key Laboratory of Optoelectronic Devices and Systems of Ministry of Education and Guangdong Province, College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61975131, 61775144, 61835009), the Natural Science Foundation of Guangdong Province, China (Grant No. 2018A030313362), the Scientific and Technological Innovation (Key) Projects of Department of Education of Guangdong Province, China (Grant No. 2016KCXTD007), and the Shenzhen Basic Research Project, China (Grant Nos. JCYJ20170818141701667, JCYJ20170818144012025, JCYJ20170412105003520, JCYJ20180305125649693)Received Date: 29 October 2020Accepted Date: 24 November 2020Available Online: 20 April 2021Published Online: 05 May 2021Abstract: Multifocal structured illumination microscopy (MSIM) can achieve a doubled improvement in the resolution of the diffraction limit within an imaging depth of 50 μm. But when imaging thick samples, scattered light and defocused light limit its optical sectioning capability and image contrast. Two-photon MSIM (2P-MSIM) overcomes the influence of sample tissue scattering and further improves the imaging depth and imaging characteristics. However, the existing 2P-MSIM usually adopts galvanometer based scanning mirrors for precisely scanning imaging, which is a complicated and poor flexibility system. Here we propose a simpler 2P-MSIM. Two-photon multifocal scanning imaging can be realized by a spatial light modulator (SLM) with a high frame rate (< 845 Hz). The phase map of generating multi-focus array and linear phase grating loaded on the SLM simultaneously, high-precision parallel digital random address scanning and excitation imaging on the sample surface can be realized. The mechanical inertia problem of the galvanometer scanner in multifocal imaging can be solved by the proposed method while reducing the complexity of the system and improving flexibility. We finally realize two-photon multifocal imaging of mouse kidney tissue slices and lily of the valley rhizome by this system, which verifies the three-dimensional super-resolution imaging capability of this method. It is of great significance in developing the 2P-MSIM.Keywords: multifocal structured illumination microscopy /two-photon /fluorescence microscope /spatial light modulator 全文HTML --> --> --> 1.引 言 近年来, 多种突破光学衍射极限限制的超分辨显微技术蓬勃发展, 如: 受激发射损耗(stimulated emission depletion, STED)显微技术[1 ] 、光激活定位显微技术[2 ] 、随机光学重构显微成像技术(stochastic optical reconstruction microscopy, STORM)[3 ] 及结构光照明显微成像技术(structured illumination microscopy, SIM)[4 ] 等, 已达到了纳米量级的空间分辨率, 实现了对细胞内精细结构的观察, 极大地推动了生命科学等诸多领域的发展. 尽管STED显微技术能对较厚的生物组织进行高分辨率成像, 但需要特定荧光标记的样品及高能量的损耗光, 后者一定程度地造成了光漂白和光损伤, 限制了该技术的进一步应用. STORM虽能提供更高分辨率成像, 但其不仅仅受到荧光染料种类的限制, 宽场的激发方式和稀疏化的发光模式进一步限制了其成像深度和成像速度. 与此同时, SIM虽然仅仅能提供2倍的分辨率提升, 但由于其具有成像时不受荧光染料的限制, 不需要高的激发光功率, 以及快的成像速度等优势, 在活细胞成像方面获得广泛的应用. 令人遗憾的是, 传统的宽场结构光照明显微成像技术仅仅能实现对比较薄的样品(< 10 μm)超分辨成像, 限制了其发展. 图像扫描显微镜(image scanning microscopy, ISM)[5 ] 被认为是一种点扫描照明显微成像技术, 这种超分辨技术的出现大大提高了结构光照明显微成像技术的成像深度. 然而, 单个聚焦点的扫描方式限制了ISM的成像速度, 于是多焦点结构光照明显微镜(multifocal structured illumination microscopy, MSIM)[6 ] 被提出, 采用多点并行扫描的方式, 大大提高了单点扫描结构光照明显微镜的成像速度.[7 ] 、微透镜阵列[8 -10 ] 、衍射光学元件[11 ,12 ] 及空间光调制器(spatial light modulator, SLM)[13 -15 ] 等. 目前, 在2P-MSIM[10 ] 中, 主要采用微透镜阵列与扫描振镜相结合的方式实现双光子点阵的激发和扫描, 但其双光子激发点阵是固定的, 灵活性差. 而基于SLM的多焦点产生技术在点阵的均匀性、效率及随机性方面都具有较大的优势. 利用SLM生成点阵的算法主要有基于相位恢复(Gerchberg-Saxton, GS)算法[16 ] 、广义自适应加法算法[17 ] 、直接搜寻算法[18 ] 、以及加权相位恢复(weighted GS, WGS)算法[19 ,20 ] 等. 在这些算法中, WGS算法生成的点阵具有更好的均匀性和效率. 直到目前, 几乎所有的多焦点多光子结构光照明显微成像系统都需要振镜来实现扫描成像, 系统具有较大的复杂性且受机械惯性的影响, 灵活性差. 为了解决上述问题, 本文提出并搭建了一种基于高速相位型SLM的2P-MSIM, 仅通过在SLM上加载生成点阵和线性相位光栅的合成相位图, 就同时实现了点阵产生和在样品面上高精度并行数字随机寻址扫描激发, 结合像素重定位和反卷积技术实现了三维双光子多焦点结构光超分辨成像. 利用搭建的系统完成了对小鼠肾切片、铃兰根茎及荧光珠的双光子超分辨成像, 具有较好的成像效果, 验证了该方法的三维超分辨成像能力.2.2P-MSIM原理与方法 22.1.2P-MSIM成像理论 2.1.2P-MSIM成像理论 2P-MSIM被认为是一种并行的2P-ISM, 其实现超分辨的原理与2P-ISM一致. 在ISM[5 ] 中, 一个面阵探测器替换了激光共聚焦扫描显微镜中的点探测器. 探测器探测到的图像不仅仅与激发点的位置有关, 同时也与探测器上的像素点的位置有关, 因此, 在不考虑系统放大倍率的情况下, 在样品面扫描位置r s [5 ,21 ] $c({{r}}')$ 表示荧光分子分布, $E\left( {{{r}}'} \right)$ 表示在扫描位置为r $U\left( {{{r}} + {{s}}} \right)$ 表示探测位置为r s ${E_0}\left( {{r}} \right)U\left( {{{r}} + {{s}}} \right)$ , 其中${E_0}\left( {{r}} \right) = {E^2}\left( {{r}} \right)$ , 表示在扫描位置为r ${\sigma _{{\rm{in}}}}$ 和${\sigma _{\det }}$ , 那么双光子激发下, 系统有效的点扩散函数可重新表示为[22 ] G 表示高斯函数, ${U_{{\rm{eff}}}}$ 表示有效的点扩散函数.${\sigma _{{\rm{2 P \text{-} in}}}} = {{{\sigma _{{\rm{ex}}}}} / {\sqrt 2 }}$ , 其中${\sigma _{{\rm{ex}}}}$ 为单光子激发下, 系统激发点扩散函数的标准差. 在双光子激发过程中, 分子吸收两个光子经过斯托克斯位移后自发辐射出单个光子, 则双光子激发波长${\lambda _{{\rm{ex}}}}$ 与探测波长${\lambda _{\det }}$ 的比值$1 < k < 2$ , 其中$k = {{{\lambda _{{\rm{ex}}}}} / {{\lambda _{\det }}}}$ . 所以系统激发点扩散函数和系统探测点扩散的标准差之间的关系变为${\sigma _{{\rm{ex}}}} = k{\sigma _{\det }}$ , 因此, 双光子激发点扩散函数的标准差与系统探测点扩散函数标准差之间关系为${\sigma _{{\rm{2 P\text-in}}}} = {{k{\sigma _{\det }}} / {\sqrt 2 }}$ .2 )式, 则2P-ISM的有效点扩散函数${U_{{\rm{2 P \text- eff}}}}$ 可以描述为$I\Big( {{r}} - \dfrac{{{k^2}}}{{{k^2} + 2}}{{s}}, {{s}} \Big)$ 对s 1 )式, 2P-MSIM有效图像可重新表示为6 )式可以看出, 有效图像包含的频谱范围是宽场照明得到$({{{k^2} + 2}})/{{{k^2}}}$ , 所以, 通过像素重定位(pixel reassignment)和反卷积(deconvolution)处理, 理论上2P-MSIM相比于宽场显微镜能实现$({{{k^2} + 2}})/{{{k^2}}}$ 倍分辨率的提升.2.2.系统光路设计 -->2.2.系统光路设计 2P-MSIM是基于尼康显微镜实现的(Nikon ECLIPSE Ti-U). 一台波长为1036 nm、功率为1 W、脉宽为145 fs的激光从光纤激光器发出(安扬, FemotoYL-6), 首先通过一个可用来调节激光出射功率的半波片(Thorlabs, AHWP05M-980)和偏振分光棱镜对; 从偏振分光棱镜出射的P偏振光再次经过半波片(Thorlabs, AQWP10M-980), 用来调整飞秒光在通过SLM之前的偏振方向. 然后, 光束被一对包含焦距为25 mm (Thorlabs, AC127-025-B-ML)以及焦距为80 mm (Thorlabs, AC254-080-B-ML)的透镜对扩束; 经扩束后的光束通过一个可调光阑照射在一个高速相位型SLM (Meadowlark Optics, 像元数为1920 × 1152, 像素尺寸为9.2 μm × 9.2 μm)上; 通过在SLM上加载生成点阵和线性相位光栅的合成相位图, 能够实现多个聚焦点阵列在其傅里叶面上的扫描移动; 经SLM调制的激发光经过一个焦距为300 mm的透镜(Thorlabs, AC508-300-B)后照射在显微镜的管镜上; 为了满足SLM采光面大小与物镜后孔径面大小尽可能匹配, 将原来的管镜替换成焦距为300 mm, 尺寸为2英寸的透镜(Thorlabs, A508-300-AB-ML), 与前一个透镜构成一个无扩束的4f 系统; 为了只让SLM的一级光通过系统, 在4f 系统两个透镜间放置一个可调光阑用来滤除SLM的其他衍射级的光; 光束经过管镜后又经过水浸物镜(Nikon, 60 ×, NA 为1.27)在样品面上形成多个聚焦点; 样品被激发后产生的荧光信号经二向色镜与发射片后由sCMOS相机(滨松, ORCA-Flash4.0 v3)接收. 整个光路的示意图如图1 所示.图 1 2P-MSIM系统光路示意图Figure1. Schematic diagram of 2P-MSIM system.2.3.点阵产生和扫描相位图设计 -->2.3.点阵产生和扫描相位图设计 32.3.1.点阵相位图设计原理 -->2.3.1.点阵相位图设计原理 整个相位图的设计分成3步: 1)点阵相位图的设计; 2)用于点阵扫描的线性相位光栅的设计; 3)将两个相位图进行叠加生成最终的复合相位图.[20 ] , 即当WGS算法迭代几次后, 一直保持频谱面的相位不变, 用作下一次的迭代, 直至算法收敛. 利用这种方式大大减少了迭代次数, 加快了收敛速度. 在传统的WGS算法中, 初值相位可以设置成分布范围为–π—π的随机矩阵, 当算法执行第i 次迭代时, 傅里叶平面的振幅和相位可以根据输入平面的振幅$\sqrt {I\left( x \right)} $ 和相位${\varPhi _i}\left( x \right)$ 经过二维傅里叶变换得到. 保持傅里叶面的相位${\varPsi _i}\left( u \right)$ 不变, 振幅${B_i}\left( u \right)$ 用目标振幅$\varGamma \left( u \right)$ 乘以一个不均匀性矫正的加权系数${g_i}\left( u \right)$ 来替换. ${g_i}\left( u \right)$ 可以表达为${\langle {B_i}\left( u \right)\rangle _M}$ 表示计算得到的M 个点的振幅平均值, $\delta \left( u \right)$ 表示的是狄拉克函数, ${g_0}\left( u \right)$ 设置为1.${A_{i + 1}}\left( x \right)$ 和相位${\varPhi _{i + 1}}\left( x \right)$ , 通过这种方式不断迭代下去, 最后就能得到均匀性好的点阵的输入相位. 但是当用传统的WGS算法生成点阵时, 我们发现在迭代过程中用$\sqrt {I\left( x \right)} $ 替换${A_{i + 1}}\left( x \right)$ 使${g_i}\left( u \right)$ 在矫正均匀性时很难有较大的改善, 往往需要较长的时间才能实现较好的矫正效果. 主要原因是对于输入平面的傅里叶变换, 振幅的替换引入了一个相位改变量$\text{δ}{\varPsi _i}\left( u \right)$ , 这个改变量要比加权系数改变量$\text{δ}{g_i}\left( u \right)$ 大得多, 所以导致了${g_i}\left( u \right)$ 在矫正不均匀性方面很难有比较好的效果. 值得注意的是, 通过对后续的i +1次迭代的相位改变施加影响, 能有效地移除相位改变量$\text{δ}{\varPsi _i}\left( u \right)$ . 具体做法是在WGS算法执行N 次迭代达到目标调制效率后, 保持后续迭代中傅里叶平面的相位不变, 即${\varPsi _i}\left( u \right) = {\varPsi _N}\left( u \right)$ . 利用这种方法, 算法可以在很少的迭代次数就完成了收敛, 且最终生成了一个均匀性好、效率高的多焦点阵列. 算法的执行过程可以通过图2(a) 来表示, 图2(b) 和图2(c) 分别表示利用该算法得到的相位图和点阵图.图 2 (a) WGS算法流程图; (b)得到的相位图; (c)生成的点阵图Figure2. (a) Flow chart of WGS algorithm; (b) generated phase map; (c) generated multi-focus array.2.3.2.线性相位光栅的设计 -->2.3.2.线性相位光栅的设计 线性相位光栅的相位表达式可以表示为k 表示光栅的频率, r 表示SLM面的坐标.$\exp \left( {{\rm{i}}2{\text{π}}kr} \right)$ , 从频率空间来考虑, 其傅里叶变换为$\delta \left( {u - k} \right)$ . 考虑到光学的傅里叶变换和数学上傅里叶变换的坐标变换关系, 相位光栅对应的傅里叶面的复振幅分布为$\delta \left( {\dfrac{u}{{f\lambda }} - k} \right)$ , 其中f 表示透镜的焦距, λ 表示激光器的波长. 再令$k = \dfrac{\rho }{{f\lambda }}$ , 则该复振幅表达式变为$\delta \left( {\dfrac{{u - \rho }}{{f\lambda }}} \right)$ . 假设生成的点阵对应的复振幅为${B_i}\left( u \right){\varPsi _i}\left( u \right)$ 且激光器的波长带宽很窄, 考虑到空域内的复振幅的乘积对应频域内的复振幅的卷积, 则相应的叠加相位图对应傅里叶面的复振幅分布为${B_i}\left( {\dfrac{{u - \rho }}{{f\lambda }}} \right){\varPsi _i}\left( {\dfrac{{u - \rho }}{{f\lambda }}} \right)$ . 从这个表达式上看, 点阵的位置被移动了ρ .23 ], 相位光栅能实现的扫描精度为${{{\delta _{\rm{f}}}} / {{k_{\max }}}}$ , 这里${\delta _{\rm{f}}} = {{f\lambda }}/{D}$ , D 表示物镜的通光孔径; ${k_{\max }}$ 表示相位光栅产生位移在$ j{\delta }_{\mathrm{f}} $ —$ {\delta }_{\mathrm{f}} $ 的最大可实现个数, ${k_{\max }}$ 可以表示为N 为产生的相位光栅在SLM上所占的像素个数, g 为是SLM的灰度级. 综合以上的分析, 利用线性相位光栅可实现亚纳米级的扫描步长.2.4.2 P-MSIM数据获取与分析 -->2.4.2 P-MSIM数据获取与分析 为了实现同步扫描同步记录的目的, 用LABVIEW软件分别控制纳米位移台(Pi, E-709)、相机和空间光调制器. 实验中, 纳米位移台每上升一步, 就用SLM和相机完成一层的成像. SLM每加载一张图片, 相机同时曝光记录一次, 直至成像完成整个二维平面. 根据每一层的图像信息能够完成对荧光样品的三维重构.[6 ] 相类似, 2P-MSIM超分辨图像也可以通过像素重定位技术, 即: 多焦激发(multifocal-exciting)、数字高斯针孔(pinholing)滤波、图像缩放(scaling)、求和(summing) 4个图像处理步骤来重建超分辨图像(multifocal-exciting pinholing scaling summing, MPSS), 再经过Richardson-Lucy (RL)反卷积来进一步提升图像的分辨率, 获得2倍分辨率提升的2P-MSIM图像. 考虑到激发点大小的改变和波长的差异, 实际的处理过程需要对实验室已有程序[24 ] 略微加以改进, 即可获得近似2倍分辨率提升的双光子超分辨图像.3.结果与讨论 23.1.荧光珠成像 3.1.荧光珠成像 为了测试系统的空间分辨率, 首先对尺寸100 nm, 中心发射波长为580 nm的荧光珠进行成像, 由于所选荧光珠尺寸小于该成像系统的理论分辨率, 所以实验分析时未考虑荧光珠直径对测量的半高全宽的影响. 对得到的2P-MSIM原始数据进行了重构, 分别获得了点阵激发图通过添加高斯数字针孔再叠加(pinholed+summed)的初步降噪的宽场图像(pinholed widefield, Pinholed WF)、像素重定位的MPSS图像及MSIM图像, 结果如图3 所示. 图3(a) —(c) 分别表示荧光珠在经过这3个过程后得到的图像, 大的虚线框内的荧光珠为小的虚线框内的荧光珠的放大, 可以明显观察到在PinholedWF图像中原本分不开的荧光珠图像在MPSS和MSIM图像中能明显地分开. 图3(d) 为图3(a) —(c) 中黄色实线所在像素的值的大小与对应的像素所占的宽度作的曲线拟合, 每条曲线都经过了归一化处理. 为了能标定系统的分辨率, 也对视场范围内10颗荧光珠的图像进行高斯曲线拟合, 并进行统计平均, 得到了系统的平均分辨率, 如图3(e) 所示. 经过对单个荧光珠的PinholedWF, MPSS和MSIM图像拟合, 得到荧光珠的半高全宽值分别是(360 ± 15) nm, (207 ± 15) nm和(148 ± 13) nm, 与系统的宽场分辨率相比基本实现了近似2倍的分辨率提升.图 3 100 nm荧光珠成像 (a) PinholedWF图像; (b) MPSS图像; (c) MSIM图像; (d)图(a)—(c)中黄色实线所在像素值的大小与对应像素所占宽度的拟合曲线; (e)单个荧光珠的高斯拟合曲线Figure3. 100 nm fluorescent bead imaging: (a) PinholedWF image; (b) MPSS image; (c) MSIM image; (d) fitting curves of the size of the pixel value of the yellow solid lines in panel (a)-(c) vs. the width of corresponding pixel; (e) Gaussian fitting curves of a single fluorescent bead.3.2.小鼠肾切片三维成像 -->3.2.小鼠肾切片三维成像 2P-MSIM相比于1P-MSIM在成像深度方面有明显的提升, 具有良好的三维层析成像能力. 为了测试2P-MSIM的三维成像能力, 对商用的小鼠肾切片进行成像. 为了尽可能提高成像速度, 同时保证超分辨成像质量, 避免图像出现伪影及点阵信号之间的串扰. 设置点阵间隔为3250 nm, 点阵数量为8 × 8, 横向的扫描步长为130 nm, 整幅图像的成像时间是6.25 s, 成像区域大小为26.1 μm × 26.1 μm. 通过控制纳米位移台, 实现了同一个小鼠肾切片的不同厚度的成像, 分别是0, 5, 10 μm, 如图4 所示. 可以明显地观察到小鼠肾切片在不同深度结构的改变, 同时MSIM处理后的图像的分辨率具有显著的提高.图 4 小鼠肾切片的不同厚度层成像图Figure4. Images of different thickness layers of mouse kidney section.图5 所示, 重构出的三维超分辨小鼠肾切片图像实现了近似2倍的分辨率提升.图 5 小鼠肾切片三维成像图 (a) PinholedWF图像; (b) MSIM图像Figure5. Three-dimensional image of mouse kidney section: (a) PinholedWF image; (b) MSIM image.3.3.铃兰根茎成像 -->3.3.铃兰根茎成像 为了进一步测试2P-MISM的成像能力和分辨率, 对铃兰根茎进行了成像. 和前文描述的方法一样, 对铃兰根茎的不同深度的区域完成了成像, 成像深度分别是0, 12, 24 μm, 如图6 所示. 可以看出原本无法观测到的铃兰根茎内部结构变化在超分辨处理后能较清晰地观测到, 进一步验证了所搭建2P-MSIM的成像能力.图 6 铃兰根茎不同厚度层成像图Figure6. Images of different thickness layers of lily of the valley rhizome.4.结 论 本文提出和搭建了一套新的双光子多焦点结构光超分辨显微成像系统. 利用了一个高速相位型空间光调制器同时完成了多焦点阵列的生成及点阵在样品面上的高精度扫描移动, 实现了双光子多焦点成像的目的, 解决了扫描振镜在多焦点成像中的机械惯性问题, 同时降低了系统的复杂性, 提高了灵活性. 另外, 为了进一步提高双光子多焦点成像的分辨率, 把点扫描结构光成像和双光子成像结合在一起, 实现了双光子多焦点结构光照明的超分辨成像, 将双光子多焦点的成像分辨率提高了近2倍. 最后, 利用该系统完成了小鼠肾切片和铃兰根茎的三维超分辨成像, 证实了该系统具有优异的成像特性, 为进一步开展活体细胞及组织的超分辨成像打下了基础. 





















 图 1 2P-MSIM系统光路示意图
图 1 2P-MSIM系统光路示意图



























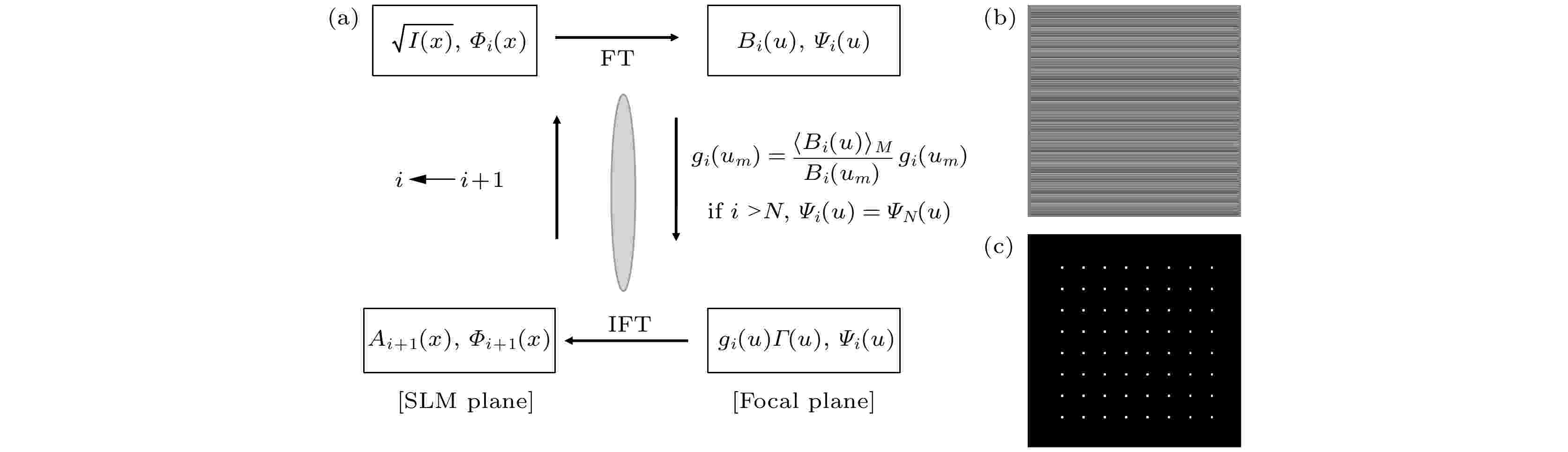 图 2 (a) WGS算法流程图; (b)得到的相位图; (c)生成的点阵图
图 2 (a) WGS算法流程图; (b)得到的相位图; (c)生成的点阵图














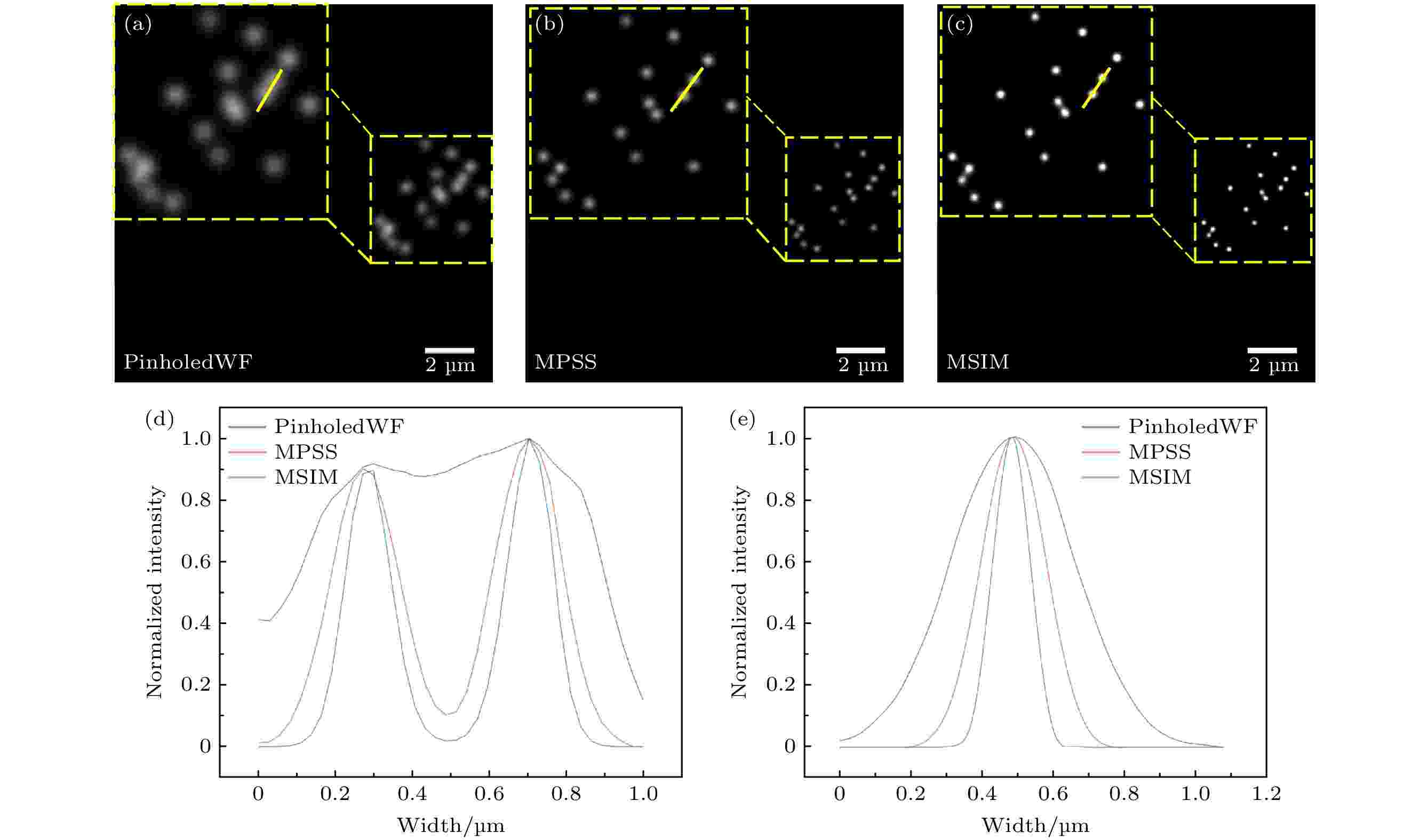 图 3 100 nm荧光珠成像 (a) PinholedWF图像; (b) MPSS图像; (c) MSIM图像; (d)图(a)—(c)中黄色实线所在像素值的大小与对应像素所占宽度的拟合曲线; (e)单个荧光珠的高斯拟合曲线
图 3 100 nm荧光珠成像 (a) PinholedWF图像; (b) MPSS图像; (c) MSIM图像; (d)图(a)—(c)中黄色实线所在像素值的大小与对应像素所占宽度的拟合曲线; (e)单个荧光珠的高斯拟合曲线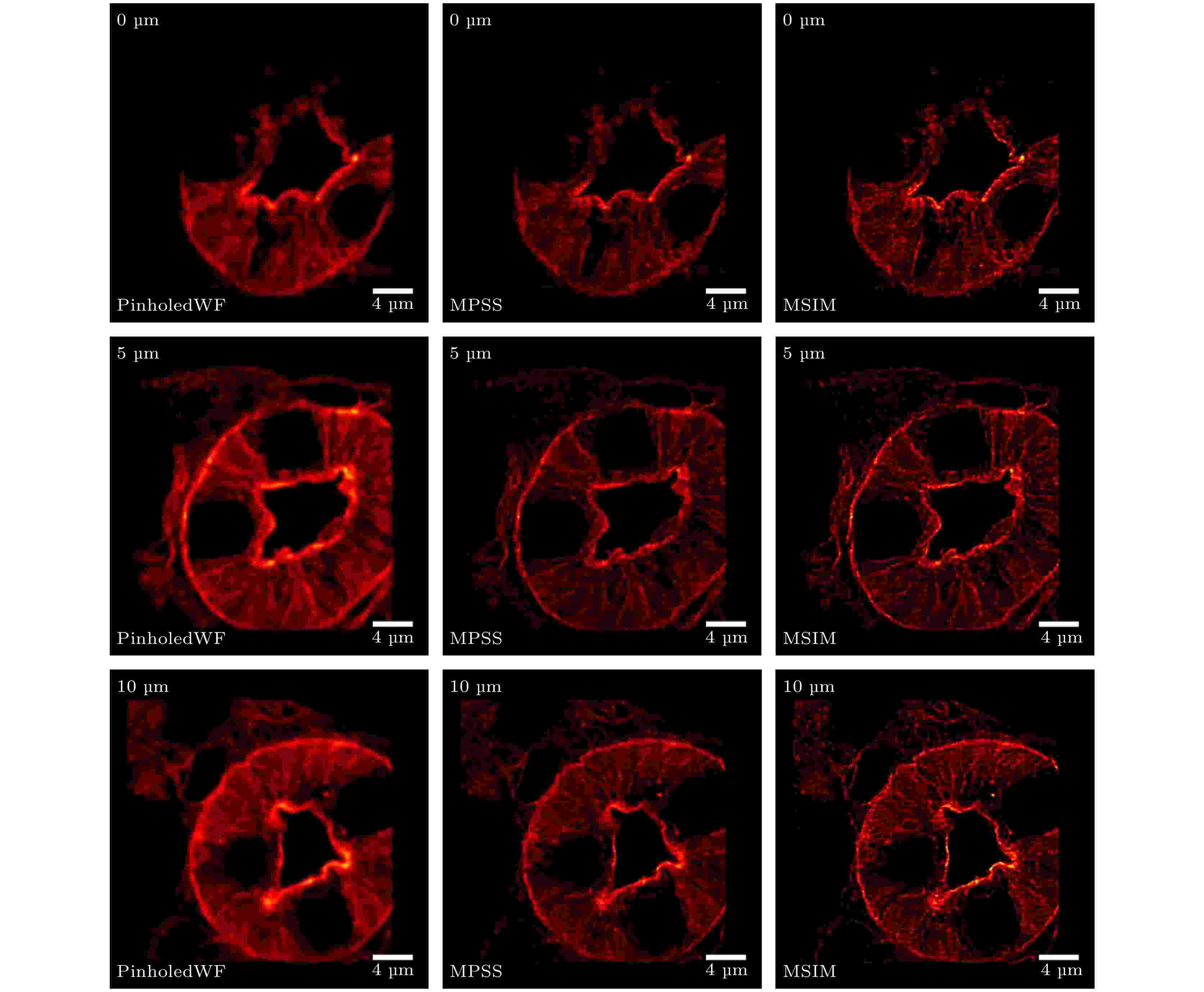 图 4 小鼠肾切片的不同厚度层成像图
图 4 小鼠肾切片的不同厚度层成像图 图 5 小鼠肾切片三维成像图 (a) PinholedWF图像; (b) MSIM图像
图 5 小鼠肾切片三维成像图 (a) PinholedWF图像; (b) MSIM图像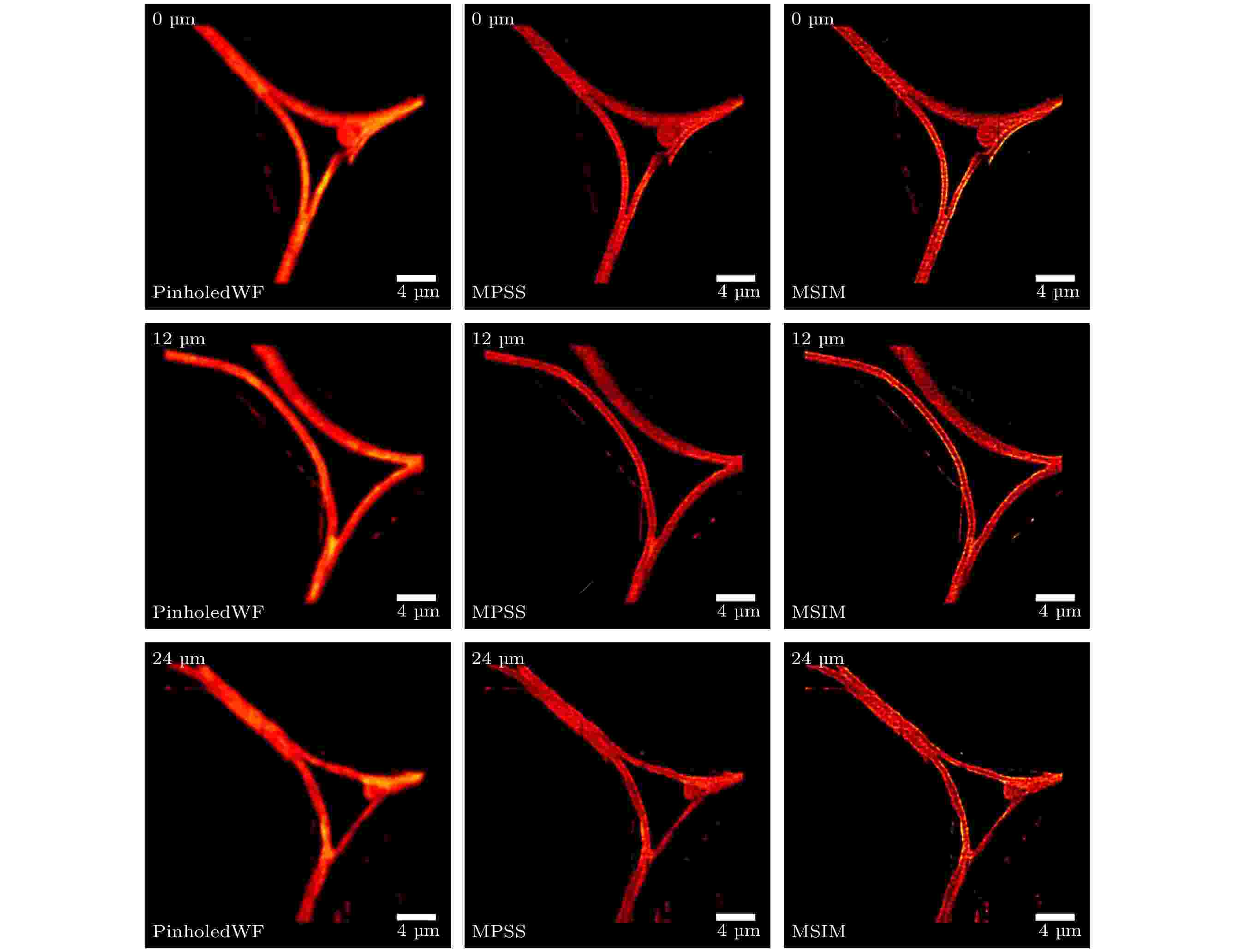 图 6 铃兰根茎不同厚度层成像图
图 6 铃兰根茎不同厚度层成像图