摘要:应用固体与分子经验电子理论系统地研究液态金属池Na||Sb-Pb-Sn电极的价电子结构与热、电性能. 研究结果表明: 电极合金的价电子结构与其性能密切关联. 阴极合金Na_1–xIA_x (IA = K, Rb, Cs)的晶格电子随着掺杂量的增加而减少, 诱发合金的熔点、结合能随掺杂量的增加而降低. Na离子输运到阳极, 与阳极Sb-Sn-Pb形成产物NaSb₃, NaSn, Na₁₅Sn₄, NaPb. 其理论熔点与实验相符. NaSb₃的平均晶格电子数最少, 开路电压最高. 研究表明: 对于Na||Sb-Pb-Sn液态金属电池体系而言, 晶格电子扮演重要的角色, 可以调控电极的热、电性能.
关键词: 固体与分子经验电子理论/
液态金属电池/
价电子结构/
开路电压

English Abstract

全文HTML

--> --> -->

可再生能源技术的快速发展, 要求研究低成本、长寿命和大容量储能系统, 以增强电网的稳定性、可靠性和安全性^[1]. 传统的储能系统主要采用铅酸电池蓄电, 但电池循环寿命短, 充放电速度慢, 且对环境污染大; 锂离子电池具有高储存能量密度, 但制造成本较高, 充、放电性能差, 电池均一性和安全性差; 液流电池结构比较复杂, 需要对电解液、离子交换膜等关键材料进行深入的技术开发; 钠硫电池所采用的固体电解质的热稳定性较差、安全性差^[2-5]. 这些电化学储能电池的主要问题是使用寿命短、成本高, 无法满足市场需求. 针对这一问题, 美国麻省理工学院的Sadoway教授提出“液态金属电池(liquid metal battery)”的新概念^[6,7]. 实验研究表明: 液态金属电池具有成本低廉、寿命长、放电速率高、储能密度大等优点, 可以使用15年以上, 满足大规模静态储能的要求^[8-12]. 液态金属电池的电极材料和电解质均为液态, 工作温度范围为500—700 ℃, 阴极选用活性较高的液态碱金属或碱土金属^[13]. 由于液态金属电池电极的工作温度比较高, 适用性受限. 通过元素的添加, 使金属电极合金化, 可以降低电极的熔点, 进而降低运行成本和工作温度^[14]. 钠与锂同族, 具有与锂相似的物理和化学性能, 钠在地壳中含量丰富、成本低. 因此, 选取金属Na作为阴极材料, 并设计在Na电极中添加熔点低的IA碱金属元素K, Rb, Cs等元素来降低工作温度^[15,16]. 阳极选择Sb, 设计添加低熔点的IV族金属Pb和Sn, 实现阳极熔点的降低. 本文设计的液态金属电池的体系是Na||Sb-Pb-Sn. 应用理论研究电池合金化后的电子结构和物理性能.
随着计算材料科学的发展, 材料的理论研究有助于材料成分设计及其性能的提高^[17-19]. 固体与分子经验电子理论在材料的电子结构和性能研究方面, 具有丰富的研究成果, 涉及材料的力学性能、热性能、电磁性能和光特性等方面. 性能的理论计算与实验相符^[20-22]. 其优势在于: 理论模型简单, 没有涉及复杂的微积分及数理方程计算, 而且计算参数少.
本文应用固体与分子经验电子理论研究液态金属电池Na||Sb-Pb-Sn, 并通过价电子结构的分析和热、电性能(电极熔点, 结合能, 电势, 开路电压)计算, 揭示电池性能与电子结构的关联性.

固体与分子经验电子理论是基于能带理论和Pauling的价键理论基础之上, 研究物质性能与其价电子结构的关联性^[23-30]. 计算物理性能包括熔点、结合能、磁矩、居里温度、超导转变温度及光吸收带宽等^[20,21,31], 性能的理论值与实验相符. 理论包括三种假设及一种分析方法(键距差法).
2

-->

2.1.价电子结构的三种假设

3 -->

2.1.1.双态的假设

电子结构存在两种基本的状态: 能量低的稳态(h态)及能量高的激发态(t态), 双态分布着各种各样的电子, 如: s, p, d轨道上的价电子n_s, n_p, n_d; 共价电子n_c; 晶格电子n_l; 哑对电子n_Y; 磁电子m^3d及总电子n_T.
3 -->

2.1.2.杂化态叠加的假设

依据量子力学态叠加原理, 物质的电子结构是由h态和t态成分比例分数C_h和C_t的叠加. 其比例分数C_h和C_t是不连续的, 呈现量子化. 其计算公式为

${C_{\rm{h}}} = 1 - {C_{\rm{t}}},\;\;\;{C_{{\rm{t}} }}= \frac{1}{{1 + {K^2}}},$

在h态, C_t = 0, K = $ {\infty } $. t态时, C_t = 1, K = 0. 在给定原子杂化状态下, K的取值为

$ K\!=\!\frac{{{\tau }}'{l}'\!+\!{m}'\!+\!{n}'}{\tau l+m+n}\!\sqrt{\frac{{\tau }'+{m}'+{n}'}{l+m+n}}\frac{l\pm \sqrt{3m}\pm \sqrt{5n}}{{l}'\pm \sqrt{3{m}'}\pm \sqrt{5{n}'}},$

其中, l, m, n, l', m', n'分别表示h态和t态中的s, p, d价电子和晶格电子数. 当(2)式h态的价电子全部是晶格电子时不适用, 即l + m + n = 0, (2)式无意义. 此时的K公式修正为

$K=\frac{{l}'+{m}'+{n}'}{l}\frac{{l}'+{m}'+{n}'}{{l}'\pm \sqrt{3{m}'}\pm \sqrt{5{n}'}}. $

各种电子数可以通过h态和t态成分比例分数计算. 并通过双态的加权平均方法计算出各种电子数, 这些电子数与其电子态(又称杂化态)一起组成元素的价电子结构的杂化表. 本文研究的阴、阳极金属元素的杂化表, 见附录A.
3 -->

2.1.3.键距方程

对于晶胞内任何两个相邻的u和v原子所形成的u—v键, 其键矩可以根据Pauling提供的键距计算公式:

$\begin{split}{D_{{\rm{uv}}}}\left( {{n_\alpha }} \right) =\;& {R_{\rm{u}}}\left( 1 \right) + {R_{\rm{v}}}\left( 1 \right) - \beta {\rm{lg}}{n_\alpha }, \\&(\alpha = A,B,C, \cdots,N),\end{split}$

其中, D_uv(n_α)为键距, n_α是共价电子对数, R_u(1)和R_v(1)分别代表u, v原子的单键半矩. 参数β取值如下:

$\beta \! =\!\! \left\{ {\begin{aligned}&{0.710\;\text{?} ,}\qquad\quad{{n^{\rm{M}}}< 0.250~{\text{或}}~{n^{\rm{M}}} > 0.750,}\\&{0.600\;\text{?},}\quad\qquad{0.300 \leqslant {n^{\rm{M}}} \leqslant 0.700,}\\&{0.710 \!-\! 2.2\varepsilon \;\text{?},}\;\;{{n^{\rm{M}}} \!=\! 0.250 + \varepsilon\, {\text{或}}\,{n^{\rm{M}}} \!=\! 0.750 \!-\! \varepsilon ,}\end{aligned}} \right.$

其中, $ \varepsilon $是偏离量, 取值范围0 < $ \varepsilon $ < 0.050; $ {n}^{\mathrm{M}} $是共价电子对数n_α中的最大值.
2 -->

2.2.键距差方法^[20,21]:

第1条键:

${D}_{\mathrm{uv}}\left({n}_{A}\right)={R}_{\mathrm{u}}\left(1\right)+{R}_{\mathrm{v}}\left(1\right)-\beta \mathrm{lg}{n}_{A}. $

第i条键:

${D}_{\mathrm{uv}}\left({n}_{i}\right)={R}_{\mathrm{u}i}\left(1\right)+{R}_{\mathrm{v}i}\left(1\right)-\beta \mathrm{lg}{n}_{i}. $

(7)式–(6)式则有:

${{\Delta }D}_{i}={{\Delta }R}_{i}-\beta \mathrm{lg}{\gamma }_{i},$

其中: $ {{\Delta D}}_{i}={D}_{\mathrm{uv}}\left({n}_{A}\right)-{D}_{\mathrm{uv}}\left({n}_{i}\right) $; ${{\Delta }R}_{i}={R}_{\mathrm{u}}\left(1\right)+ $$ {R}_{\mathrm{v}}\left(1\right){-R}_{\mathrm{u}i}\left(1\right)-{R}_{\mathrm{v}i}\left(1\right)$; ${\gamma }_{i}= {{n}_{A}}/{{n}_{i}}$. 由(8)式得

${\gamma }_{i}={10}^{\tfrac{{{\Delta }R}_{i}-{{\Delta }D}_{i}}{\beta }},~~~ (i=A, B, \cdots, N) .$

晶胞中总的共价电子数n_c:

${n}_{\mathrm{c}}=\sum\limits_{i}^{n}{n}_{\mathrm{c}i}. $

总的共价电子数也是所有等价键上的共价电子对数之和:

${n}_{\mathrm{c}}=\sum\limits_{\alpha =A}^{N}{n}_{\alpha }{I}_{\alpha } ={n}_{A}\sum\limits_{\alpha =A}^{N}{\gamma }_{\alpha }{I}_{\alpha },$

$ {n}_{A}=\frac{\displaystyle\sum\nolimits_{i}^{n}{n}_{ci}}{\displaystyle\sum\nolimits_{\alpha =A}^{N}{\gamma }_{\alpha }{I}_{\alpha }},\;\; {n}_{\alpha }={\gamma }_{\alpha }{n}_{A},$

其中, I_α是等价键数, 其与结构式中的原子个数$ {I}_{\mathrm{M}} $, 原子配位数$ {I}_{\mathrm{S}} $及成键原子的异同因子$ {I}_{K} $有关($ {I}_{K} $的取值: 对于同类原子取1, 异类原子取2). 计算公式如下:

$ {I}_{\alpha }={I}_{\mathrm{M}}{I}_{\mathrm{S}}{I}_{K}.$

将(12)式代入(4)式, 则可以计算出u, v原子之间的理论键距$ {\bar{D}}_{\mathrm{uv}}\left({n}_{\alpha }\right) $.

$\begin{split}{\bar{D}}_{\mathrm{uv}}\left({n}_{\alpha }\right)=\;&{R}_{\mathrm{u}}\left(1\right)+{R}_{\mathrm{v}}\left(1\right)-\beta \mathrm{lg}{n}_{\alpha }, \\& ( \alpha =A, B, C, \cdots, N) .\end{split}$

理论值与实验值之差$\Delta D$ = ${\bar{D}}_{\mathrm{uv}}\left({n}_{\alpha }\right)- $$ {D}_{\mathrm{uv}}\left({n}_{\alpha }\right)$作为价电子态的选择判据, 在一级近似下, $|\Delta D| \leqslant 0.05~\text{?}$.
2 -->

2.3.性能计算模型

根据价电子结构参数, 建立结合能理论模型. 能量由四项组成: 键能、晶格电子电位能、磁能及内壳层电子的内聚能. 结合能$ {\bar{E}}_{\mathrm{C}} $的计算公式如下:

${\bar{E}}_{\mathrm{C}}=b\left\{\sum\nolimits_{\alpha }\frac{{I}_{\alpha }{n}_{\alpha }}{{D}_{\mathrm{uv}}\left({n}_{\alpha }\right)}f+\frac{{n}_{l}}{\bar{D}}{f}^{'}+\alpha {m}^{3\mathrm{d}}-CW\right\}, $

其中: b是电子对核电荷的屏蔽系数, 取值为b = 313.95/(n – 0.36·$ \delta $) kJ·$\text{?}$/mol, n和δ是由于原子的内层电子的屏蔽、电子的库仑、交换及关联作用对键能影响的总效应, n = 1, 2, 3, 4, 5, 7, 13, $ \delta $ = 2, 1, 0; f是成键因子; $ {n}_{\mathrm{l}} $是晶格电子数; ${f}{'}$为晶格电子的成键因子; $\bar{D}=\dfrac{\displaystyle\sum {I}_{\alpha }{D}_{uv}\left({n}_{\alpha }\right)}{\displaystyle\sum {I}_{\alpha }}$为等效键距; $ \alpha $ = 0.1542; $ {m}^{3\mathrm{d}} $是原子的磁电子数; C = 0.907P, P的取值对应于B亚族的V, VI, VII各族, 第VII族的Fe, Co, Ni, 以及IB和IIB族元素分别依次为6, 5, 4, 3, 2, 1和0 (0对应IB和IIB族); $W=\dfrac{{\text{哑对电子}}+{\text{磁电子}}}{{\text{外壳电子总数}}}$^[25]. 由于研究的电极金属都是主族金属元素, 没有过渡簇金属元素, 因此, 结合能只有前两项.
熔化模型: 热声子能量随着温度的升高增加. 当达到温度达到临界值(熔点$ {T}_{\mathrm{m}} $)时, n摩尔的热声子能量刚好与最强键的能量$ {E}_{\mathrm{s}} $相等. 即

$\frac{3}{2}nR{T}_{\mathrm{m}}={E}_{\mathrm{s}}.$

高于该温度, 最强键将被打断. 理论熔点$ {\bar{T}}_{\mathrm{m}} $计算公式为

${\bar T_{\rm{m}}} = \frac{b}{{3/2nR}}\left\{ {\frac{{{n_A}}}{{{D_{uv}}\left( {{n_\alpha }} \right)}}f + \frac{{{n_l}f'}}{{{I^\delta }\bar D}} - \frac{{CW}}{{{I^\delta }}}} \right\} \times {10^3}\;{\rm{K,}}$

其中, ${I}^{\delta }=\displaystyle\sum {I}_{\alpha }{r}_{\alpha }$, R = 8.31 J/mol, 式中因子$ {10}^{3} $是由于R和b的单位关系引入的.
开路电压V: 对于液态金属电池而言, 开路电压等于阳、阴电极的电势差. 应用阳、阴电极的电位能差除以其总的晶格电子数$ {n}_{\mathrm{l}} $后获得, 如(18)式所示.

$V=\frac{{b}_{\mathrm{a}}{f}_{\mathrm{a}}'}{e\bar{{D}_{\mathrm{a}}}}-\frac{{b}_{\mathrm{c}}{f}_{\mathrm{c}}'}{e{I}^{\delta }\bar{{D}_{\mathrm{c}}}}, $

其中, e为电子电量, 下标a与c分别对应阳极和阴极.

2

-->

3.1.阴极的价电子结构与热电性能计算

为了降低电池阴极的熔点, 在阴极Na金属中添加熔点低的IA族碱金属元素K, Rb, Cs形成Na_1–xIA_x合金电极(x ≤ 0.05). Na具有体心立方结构, 空间群为$ Im\bar{3}m $, IA族碱金属元素的微量掺杂不影响Na的晶体结构, 等效于Na的固溶体合金. 由于原子半径的差异, 掺杂会引起Na的点阵常数变化. 应用平均原子模型计算合金的点阵常数:

$a=\left(1-x\right) \cdot {a}_{\mathrm{Na}}+x \cdot {a}_{\mathrm{IA}}, $

其中: $ {a}_{\mathrm{Na}} $和$ {a}_{\mathrm{IA}} $分别代表Na及其他IA族的点阵常数. 合金的共价电子数$ {n}_{\mathrm{c}} $、晶格电子数$ {n}_{\mathrm{l}} $及平均的单键半矩R(1)分别可以通过Na和添加IA簇金属按成分加权平均的方法获得, 如下所示:

${n}_{\mathrm{c}}=x{n}_{\mathrm{c}}^{\mathrm{Na}}+(1-x){n}_{\mathrm{c}}^{\mathrm{IA}}, $

${n}_{\mathrm{l}}=x{n}_{\mathrm{l}}^{\mathrm{Na}}+(1-x){n}_{\mathrm{l}}^{\mathrm{IA}}, $

$R\left(1\right)=x{R}^{\mathrm{Na}}\left(1\right)+(1-x){R}^{\mathrm{IA}}\left(1\right),$

其中: $ {n}_{\mathrm{c}}^{\mathrm{Na}} $, $ {n}_{\mathrm{l}}^{\mathrm{Na}} $, $ {R}^{\mathrm{Na}}\left(1\right) $, $ {n}_{\mathrm{c}}^{\mathrm{IA}} $, $ {n}_{\mathrm{l}}^{\mathrm{IA}} $和$ {R}^{\mathrm{IA}}\left(1\right) $分别为Na和添加IA金属的共价电子, 晶格电子及单键半距. 应用键距差方法计算阴极Na合金中理论键距, 理论键距与实验值相符, 最大的|?D| < 0.0175 ${\text{?} }$. 计算结果见表1.

Na1–xIAx	$ {I}_{\alpha } $	$ {D}_{\mathrm{uv}}\left({n}_{\alpha }\right) $/?	${\bar{D}}_{\mathrm{uv}}\left({n}_{\alpha }\right) $/?	$ {n}_{\rm{A}}$	$ { I}_{\alpha } $	$ {D}_{\mathrm{uv}}\left({n}_{\alpha }\right) $/${ \text{?} }$	${\bar{D} }_{\mathrm{uv} }\left({n}_{\alpha }\right)/{ \text{?} }$	$ {n}_{\alpha } $	|?D|/${\text{?} }$
Na	8	3.7296	3.7502	0.05160	6	4.3004	4.3210	0.00810	0.0206
Na0.99K0.01	8	3.7381	3.7538	0.05220	6	4.3103	4.3260	0.00820	0.0157
Na0.99Rb0.01	8	3.7430	3.7572	0.05220	6	4.3157	4.3300	0.00820	0.0143
Na0.99Cs0.01	8	3.7454	3.7628	0.05220	6	4.3187	4.3361	0.00810	0.0175
Na0.98K0.02	8	3.7465	3.7574	0.05290	6	4.3202	4.3310	0.00823	0.0108
Na0.98Rb0.02	8	3.7564	3.7643	0.05290	6	4.3310	4.3389	0.00820	0.0079
Na0.98Cs0.02	8	3.7611	3.7755	0.05290	6	4.3370	4.3513	0.00817	0.0143
Na0.97K0.03	8	3.7550	3.7610	0.05348	6	4.3301	4.3361	0.00829	0.0060
Na0.97Rb0.03	8	3.7697	3.7713	0.05351	6	4.3463	4.3479	0.00825	0.0016
Na0.97Cs0.03	8	3.7769	3.7881	0.05354	6	4.3552	4.3665	0.00821	0.0113
Na0.96K0.04	8	3.7635	3.7647	0.05411	6	4.3399	4.3411	0.00834	0.0012
Na0.96Rb0.04	8	3.7831	3.7785	0.05415	6	4.3616	4.3570	0.00829	0.0047
Na0.96Cs0.04	8	3.7926	3.8009	0.05419	6	4.3735	4.3818	0.00824	0.0082
Na0.95K0.05	8	3.7719	3.7684	0.05474	6	4.3498	4.3463	0.00840	0.0036
Na0.95Rb0.05	8	3.7965	3.7856	0.05479	6	4.3769	4.3661	0.00834	0.0109
Na0.95Cs0.05	8	3.8084	3.8136	0.05484	6	4.3918	4.3971	0.00827	0.0052

表1Na_1–xIA_x合金键距计算
Table1.Calculation of bond distances of Na_1–xIA_x alloy.

Na_1–xIA_x合金的价电子结构计算结果如表2所示. 基体金属Na取第2杂阶, 掺杂金属K, Rb, Cs取第4杂阶. 随着IA族元素的掺杂量的增加, 共价电子数n_c, s与p价电子数n_s与n_p趋于增加, 晶格电子数n_l减少. 将这些价电子结构参数代入计算性能模型, 计算合金的热、电性能. 计算结果见表3.

Na1–xIAx	nc	ns	np	nl	R(1)
Na	0.4614	0.4606	0.0008	0.5386	1.4181
Na0.99K0.01	0.4668	0.4660	0.0008	0.5332	1.4217
Na0.98K0.02	0.4722	0.4713	0.0008	0.5278	1.4254
Na0.97K0.03	0.4776	0.4767	0.0009	0.5224	1.4290
Na0.96K0.04	0.4830	0.4821	0.0009	0.5170	1.4327
Na0.95K0.05	0.4884	0.4875	0.0009	0.5116	1.4363
Na0.99Rb0.01	0.4668	0.4660	0.0008	0.5332	1.4235
Na0.98Rb0.02	0.4722	0.4713	0.0008	0.5278	1.4289
Na0.97Rb0.03	0.4776	0.4767	0.0009	0.5224	1.4343
Na0.96Rb0.04	0.4830	0.4821	0.0009	0.5170	1.4397
Na0.95Rb0.05	0.4884	0.4875	0.0009	0.5116	1.4451
Na0.99Cs0.01	0.4668	0.4660	0.0008	0.5332	1.4263
Na0.98Cs0.02	0.4722	0.4713	0.0008	0.5278	1.4345
Na0.97Cs0.03	0.4776	0.4767	0.0009	0.5224	1.4428
Na0.96Cs0.04	0.4830	0.4821	0.0009	0.5170	1.4510
Na0.95Cs0.05	0.4884	0.4875	0.0009	0.5116	1.4592

表2Na阴极合金的价电子结构
Table2.Valence electron structures of cathode Na based alloy.

掺杂量x	原子	杂阶	掺杂	杂阶	$ \bar{T}_{\rm{m}} $/K	$ {E}_{\mathrm{c}} $/(eV·atom–1)	$ {\bar{E}}_{\mathrm{c}} $/(eV·atom–1)	$\left| { {\Delta E}_{\mathrm{c} } }/{ {E}_{\mathrm{c} } }\right|/{\%}$	电势/V
0	Na	3	—	—	336.76	1.113	1.165	4.67	0.1482
0.01	Na	2	K	4	336.64	1.111	1.164	4.77	0.1481
0.01	Na	2	Rb	4	336.45	1.110	1.163	4.77	0.1480
0.01	Na	2	Cs	4	336.02	1.103	1.161	5.26	0.1478
0.02	Na	2	K	4	336.64	1.109	1.163	4.39	0.1481
0.02	Na	2	Rb	4	336.14	1.108	1.161	4.78	0.1478
0.02	Na	2	Cs	4	335.29	1.110	1.158	4.32	0.1475
0.03	Na	2	K	4	336.60	1.103	1.162	5.35	0.1480
0.03	Na	2	Rb	4	335.85	1.109	1.159	4.51	0.1476
0.03	Na	2	Cs	4	334.58	1.108	1.154	4.15	0.1471
0.04	Na	2	K	4	336.57	1.107	1.162	4.97	0.1479
0.04	Na	2	Rb	4	335.57	1.103	1.157	4.90	0.1474
0.04	Na	2	Cs	4	333.88	1.109	1.151	3.79	0.1467
0.05	Na	2	K	4	336.55	1.108	1.161	4.78	0.1478
0.05	Na	2	Rb	4	335.30	1.107	1.156	4.43	0.1472
0.05	Na	2	Cs	4	333.20	1.108	1.147	3.52	0.1463

表3阴极Na_1–xIA_x合金的熔点、结合能与电势
Table3.Melting point, cohesive energy, and electric potentials of cathode Na_1–xIA_x alloy.

计算结果表明: 阴极合金Na_1–xIA_x的熔点与结合能随着IA族原子掺杂量x的增加趋于降低; Cs原子掺杂降低更显著. 其电位能和熔点变化与结合能变化情况相似, 随着K, Rb, Cs原子掺杂量的增加而降低. 当掺杂量相同时, Cs的E_c最低, K时E_c最高. 阴极合金的电势变化情况与熔点和结合能一致. 计算结合能与实验值相符. 实验值由Na和IA族元素的单质的内聚能^[32]按成分比例平均获得:

${E}_{\mathrm{C}}=(1-x) \cdot {E}_{\mathrm{Na}}+x \cdot {E}_{\mathrm{IA}}. $

金属电极的性能与价电子结构密切相关联, 阴掺杂IA族元素形成合金Na_1–xIA_x可以调控阴极的电子结构, 进而影响性能. 图1展示阴极熔点与电子结构及掺杂量之间的关联性. 随着掺杂量的增加, 在Na_1–xRb_x和Na_1–xCs_x合金的熔点降低, Cs掺杂的合金降低更明显. 阴极合金的价电子结构的变化直接反应其相关性, 随着掺杂量的升高, 晶格电子数n_l明显降低, 共价电子n_c和s价电子数n_s呈现增加的趋势. 由于总电子数恒定, 晶格电子数的减少, 共价电子数的增加. 等效于晶格电子向价电子的转化. 根据熔化模型, 熔点的降低主要源于第二项晶格电子贡献的降低. 说明热声子优先破坏非成键的晶格电子在晶格空间的分布, 降低其电位能. 阴极合金的结合能也表现出相同的现象, 如图2所示, 随着掺杂量的增加, 三种合金的结合能都明显下降. Cs掺杂合金降幅更大. 从价电子结构变化看: 随着掺杂量的升高, 晶格电子数n_l明显降低. 说明晶格电子电位能的降低是主要原因. 阴极合金电势的变化与前两者相同, 呈现下降的趋势, 如图3所示. 主要原因还是晶格电子的减少, 共价电子的增加.
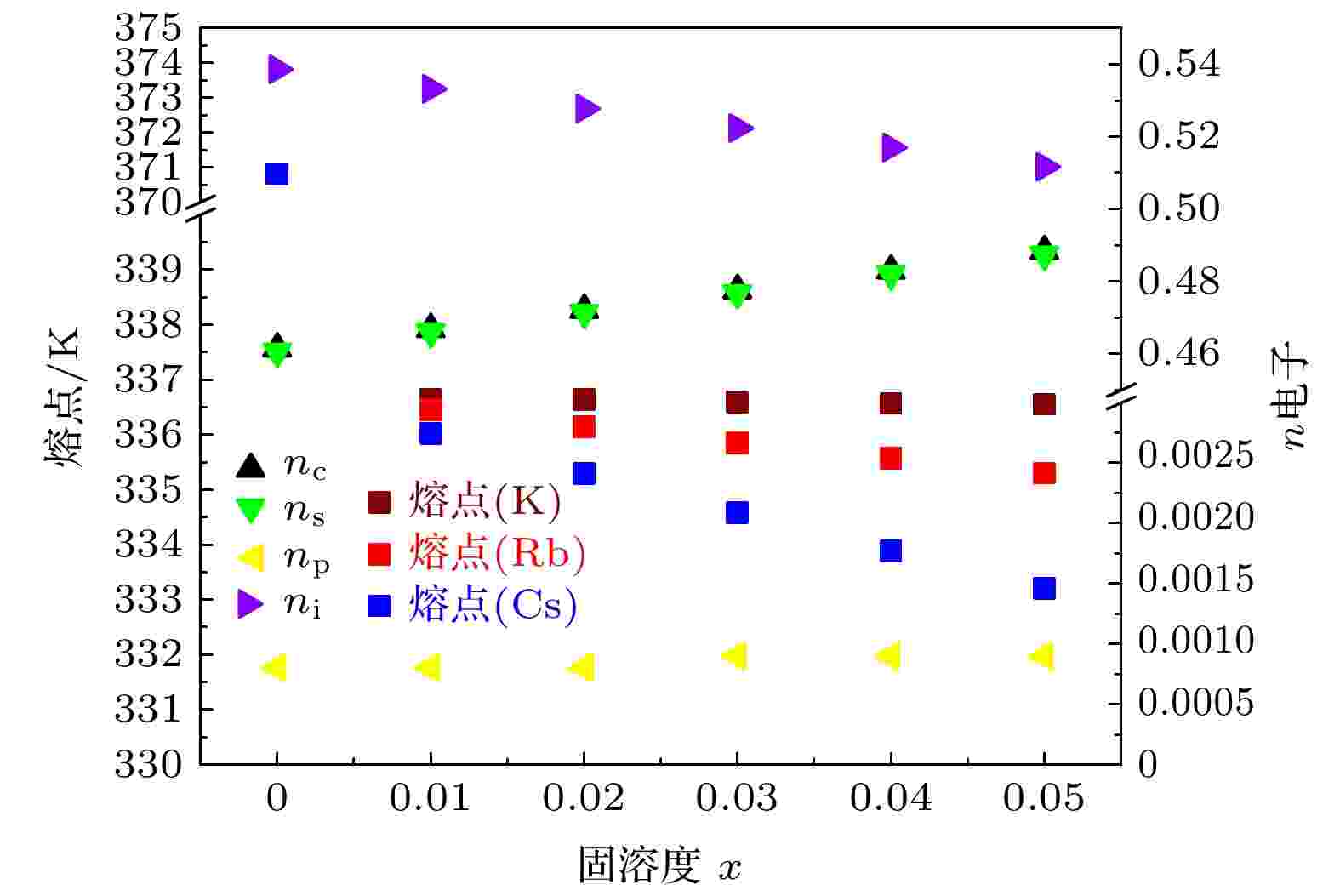图 1 阴极Na_1–xIA_x合金的n电子数与熔点的关联图
Figure1. Correlations between various electron numbers and melting points of Na_1–xIA_x cathode alloys.

图 2 阴极Na_1–xIA_x合金的各种电子数与结合能的关联图
Figure2. Correlations between various electrons and cohesive energy of Na_1–xIA_x cathode alloys.

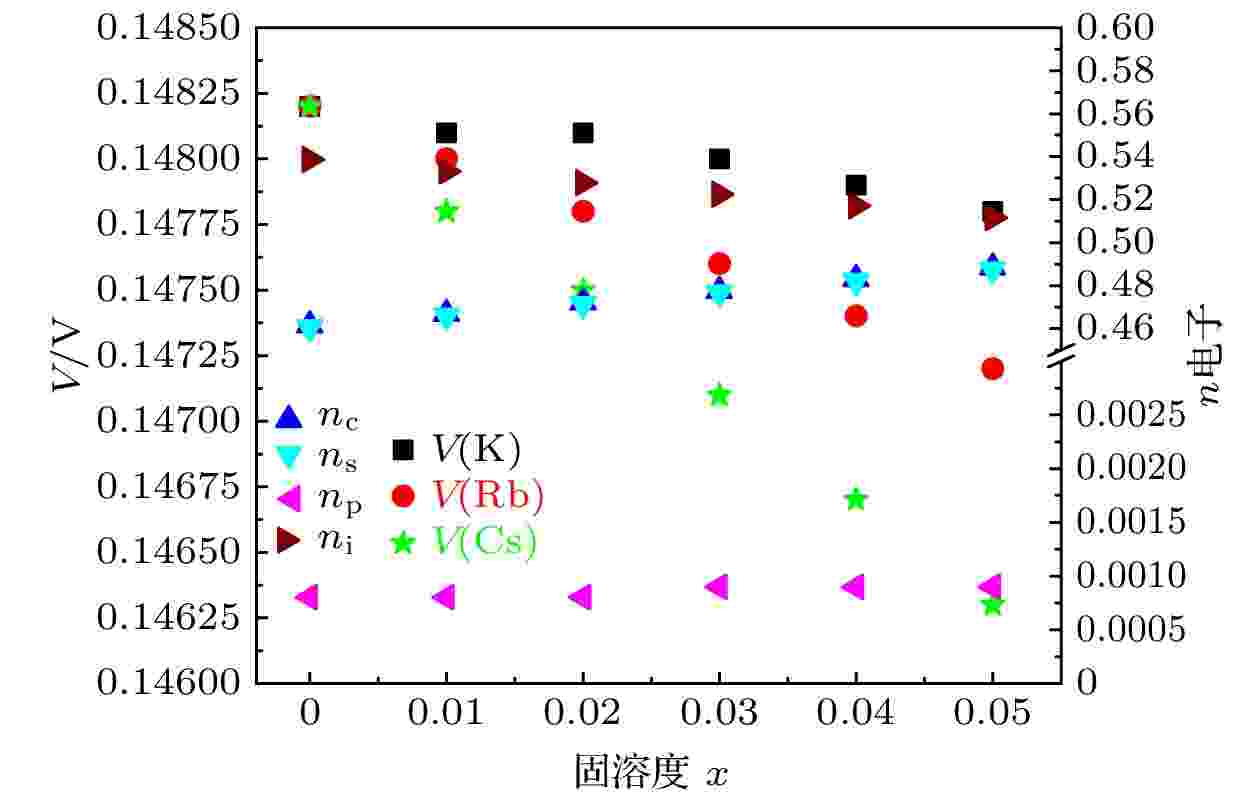图 3 阴极Na_1–xIA_x合金的各种电子数与电势的关联图
Figure3. Correlations of various electrons and electric potentials for Na_1–xIA_x anode alloys.

2 -->

3.2.正极合金价电子结构与热、电性能计算

本文选择Pb, Sb, Sn三种元素来设计液态金属电池的阳极合金; Sn, Pb, Sb相对于其他金属, 具有较高的电负性, 适合作为液态金属电池正极材料^[33-34]. Na离子输运到阳极, 与阳极金属Pb, Sb, Sn反应形成阳极产物(合金化合物): Na₃Sb, NaSn, Na₁₅Sn₄, NaPb. 四种合金化合物的晶体结构, 见表4.

合金	空间群	a/$\text{?}$	b/$\text{?}$	c/$\text{?}$	原子	占位	x	y	z
					Sb	2c	0.3333	0.6666	0.2500
Na3Sb	P63mmc (194)	5.355	5.355	9.496	Na1	2b	0	0	0.2500
					Na2	4f	0.3333	0.6666	0.5830
NaSn	I41/acd (142)	10.460	10.460	17.390	Sn	32g	0.0696	0.1260	0.9362
					Na1	16f	0.6258	0.8758	0.1250
					Na2	16e	0.8724	0	0.2500
					Sn	16c	0.2083	0.2083	0.2083
Na15Sn4	I43d (220)	13.140	13.140	13.140	Na1	12a	0.3750	0	0.2500
					Na2	48e	0.1270	0.1548	0.9670
					Pb	32g	0.0696	0.1186	0.9383
NaPb	I41/acd (142)	10.580	10.580	17.746	Na1	16e	0.2500	0.1250	0.5000
					Na2	16f	0.1250	0.3750	0.6250

表4正极合金的晶体结构
Table4.Crystal structures of anode alloys.

应用键距差方法计算这四种合金化合物中的所有键距, 计算值与实验相符, 最大键距差都满足判据: |ΔD| ≤ 0.05 ?. 计算结果见表5.

合金	键序	成键原子	$ {I}_{\alpha } $	$ {D}_{\mathrm{uv}}\left({n}_{\alpha }\right) $/$\text{?}$	$ {\bar{D}}_{\mathrm{uv}}\left({n}_{\alpha }\right)/$$\text{?}$	$ {n}_{\alpha } $	|ΔD|/$\text{?}$
Na3Sb	1	Sb-Na2	6	3.0975	3.0910	0.39055	0.0065
	2	Sb-Na1	4	3.1685	3.1620	0.19416	0.0065
	3	Na1-Na2	4	3.1780	3.1715	0.18030	0.0065
	4	Na1-Na1	6	3.4769	3.4704	0.03738	0.0065
	5	Sb-Na1	12	3.4813	3.4748	0.05846	0.0065
	6	Na2-Na1	12	3.4813	3.4748	0.05630	0.0065
	7	Na2-Na1	12	4.4310	4.4245	0.00147	0.0065
	8	Na2-Na2	2	4.7575	4.7510	0.00064	0.0065
NaSn	1	Sn-Sn	2	2.9748	3.0201	0.42650	0.0453
	2	Sn-Sn	4	2.9925	3.0378	0.39849	0.0453
	3	Na1-Sn	4	3.3355	3.3808	0.07506	0.0453
	4	Na1-Sn	4	3.3592	3.4045	0.06854	0.0453
	5	Na2-Sn	4	3.3974	3.4427	0.13064	0.0453
	6	Na2-Sn	4	3.4231	3.4684	0.11837	0.0453
	7	Na1-Sn	4	3.4870	3.5323	0.04197	0.0453
	8	Na2-Sn	2	3.5225	3.5678	0.08083	0.0453
	9	Na2-Sn	4	3.5482	3.5935	0.07324	0.0453
	10	Na1-Na2	4	3.6148	3.6601	0.03985	0.0453
	11	Na1-Na2	4	3.6658	3.7111	0.03277	0.0453
	12	Na1-Na1	1	3.7218	3.7671	0.01197	0.0453
	13	Sn-Sn	2	3.7406	3.7859	0.02257	0.0453
	14	Sn-Sn	2	4.3780	4.4233	0.00196	0.0453
	15	Na1-Na2	4	4.4919	4.5372	0.00138	0.0453
	16	Na1-Sn	4	4.6674	4.7127	0.00045	0.0453
	17	Na2-Na2	1	4.7095	4.7548	0.00132	0.0453
Na15Sn4	1	Sn-Na2	24	3.2378	3.2854	0.20850	0.0476
	2	Na2-Na2	24	3.2624	3.3100	0.19499	0.0476
	3	Na1-Na2	24	3.3425	3.3901	0.11017	0.0476
	4	Na2-Na2	12	3.3468	3.3944	0.14830	0.0476
	5	Sn-Na2	24	3.4049	3.4525	0.12127	0.0476
	6	Sn-Na2	24	3.4189	3.4665	0.11589	0.0476
	7	Na1-Na2	24	3.5026	3.5502	0.06555	0.0476
	8	Sn-Na1	24	3.5482	3.5958	0.05582	0.0476
	9	Na2-Na2	24	3.8138	3.8614	0.03261	0.047
	10	Na2-Na2	24	3.9794	4.0270	0.01906	0.0476
	11	Na2-Na2	12	4.1712	4.2188	0.01023	0.0476
NaPb	1	Pb-Pb	2	3.1464	3.1452	0.33477	0.0013
	2	Pb-Pb	4	3.1618	3.1606	0.31556	0.0013
	3	Pb-Na2	4	3.3653	3.3641	0.19895	0.0013
	4	Pb-Na1	4	3.3888	3.3876	0.08237	0.0013
	5	Pb-Na2	4	3.4215	3.4203	0.16035	0.0013
	6	Pb-Na2	4	3.4847	3.4835	0.12582	0.0013
	7	Pb-Na1	4	3.4929	3.4917	0.05524	0.0013
	8	Pb-Na1	4	3.5549	3.5537	0.04354	0.0013
	9	Pb-Na1	4	3.6172	3.6160	0.03428	0.0013
	10	Pb-Pb	2	3.6418	3.6406	0.05001	0.0013
	11	Na1-Na2	8	3.6967	3.6955	0.03479	0.0013
	12	Na2-Na2	1	3.7406	3.7394	0.06488	0.0013
	13	Pb-Pb	2	4.4008	4.3996	0.00272	0.0013
	14	Na1-Na2	4	4.5455	4.5443	0.00134	0.0013
	15	Pb-Na2	4	4.7513	4.7501	0.00097	0.0013

表5阳极合金的键距
Table5.Bond distances of the anode alloy.

四种阳极合金的价电子结构计算结果如表6所示. Na₃Sb合金化合物: 2c晶位的Sb取第2杂阶, 只提供价电子; 2b晶位的Na取4杂阶, 只提供价电子; 4f晶位的Na取第2杂阶, 提供晶格电子. NaSn合金化合物: 晶格电子由16e晶位的Na及32g晶位的Sn所提供. Sn也提供价电子, 然而位于16f晶位的Na只提供价电子. Na₁₅Sn₄合金化合物: 晶格电子由16c晶位的Sn及48e晶位的Na所提供, 位于12a晶位的Na只提供价电子. NaPb合金化合物: 位于32g晶位的Pb提供价电子和晶格电子; 16e晶位的Na只提供价电子; 位于16f晶位的Na只提晶格电子.

合金	原子	杂阶	nc	ns	np	nl	R(1)
Na3Sb	Sb	2	3.0000	0.5694	2.4306	0	1.4279
	Na1	4	1.0000	0.9982	0.0018	0	1.3070
	Na2	2	0.4614	0.4606	0.0008	0.5386	1.4181
NaSn	Sn	1	2.0000	0	2.0000	2.0000	1.3990
	Na1	1	1.0000	0.9982	0.0018	0	1.3070
	Na2	4	0	0	0	1.0000	1.5133
Na15Sn4	Sn	4	3.6638	0.8319	2.8319	0.3362	1.3990
	Na1	4	1.0000	0.9982	0.0018	0	1.3070
	Na2	3	0.5350	0.5340	0.0010	0.4650	1.4029
NaPb	Pb	2	2.0962	0.0481	2.0481	1.9038	1.4300
	Na1	4	1.0000	0.9982	0.0018	0	1.3070
	Na2	1	0	0	0	1.0000	1.5133

表6阳极产物的价电子结构
Table6.Valence electron structures of anode products

依据电子结构参数, 计算阳极合金化合物的热、电性能, 理论熔点与实验相符. 计算结果由表7所示. 计算结果表明: 四种阳极合金化合物的熔点的范围在604.89—1142.96 K之间, NaPb的熔点最低, Na₃Sb的熔点最高. 然而电势, Na₃Sb最高1.152 V, NaSn的最低0.7343 V.

合金	Tm/K [35]	$ \bar{T}_{\rm{m}} $/K	|${\Delta {T}_{\mathrm{m} } }/{ {T}_{\mathrm{m} } }$|/%	电势/V	n	β	Ec/(eV·atom–1)
Na3Sb	1129	1142.96	1.2	1.1520	4	0.60	1.766
NaSn	851	813.16	4.4	0.7343	5	0.60	2.103
Na15Sn4	681	746.16	9.6	0.9074	3	0.71	1.318
NaPb	645	630.68	2.2	0.8263	6	0.60	1.559

表7正极合金的熔点、结合能与电势
Table7.Melting point, cohesive energy, and electric potentials of anode alloy.

2 -->

3.3.液态金属电池的开路电压

应用开路电压(18)式系统地计算阴、阳电极之间的开路电压. 表8列出金属电极及其开路电压值. 计算结果表明: Na||Sb电极之间的开路电压最高略高于1 V. Na||Sn电极的开路电压低, 约为前者的一半. 开路电压与平均每原子的晶格电子数成反比, 平均晶格电子数最低的Na₃Sb(0.2693), 其开路电压最高; 而平均晶格电子最高的NaSn, 其开路电压则最低.

Na1–xIAx	开路电压/V
	Na3Sb	NaSn	Na15Sn4	NaPb
Na	1.0038	0.5861	0.7592	0.6781
Na0.09K0.01	1.0039	0.5862	0.7593	0.6782
Na0.98K0.02	1.0039	0.5862	0.7593	0.6782
Na0.97K0.03	1.0040	0.5863	0.7594	0.6783
Na0.96K0.04	1.0041	0.5864	0.7595	0.6784
Na0.95K0.05	1.0042	0.5865	0.7596	0.6785
Na0.99Rb0.01	1.0040	0.5863	0.7594	0.6783
Na0.98Rb0.02	1.0042	0.5865	0.7596	0.6785
Na0.97Rb0.03	1.0044	0.5867	0.7598	0.6787
Na0.96Rb0.04	1.0046	0.5869	0.7600	0.6789
Na0.95Rb0.05	1.0048	0.5871	0.7602	0.6791
Na0.99Cs0.01	1.0042	0.5865	0.7596	0.6785
Na0.98Cs0.02	1.0045	0.5868	0.7599	0.6788
Na0.97Cs0.03	1.0049	0.5872	0.7603	0.6792
Na0.96Cs0.04	1.0053	0.5876	0.7607	0.6796
Na0.95Cs0.05	1.0057	0.5880	0.7611	0.6800
nl/atom	0.2693	1.2500	0.3645	1.0682

表8电池的开路电压
Table8.Open gate voltages of the battery.

应用固体与分子经验电子理论研究了Na||Sb-Pb-Sn液态金属电池电极的价电子结构、熔点、结合能、电势及开路电压. 研究表明: 阴极合金Na_1–xIA_x的熔点、结合能与电势都随着掺杂量x的增加而降低. 理论的结合能与实验相符. 其价电子结构研究揭示: 合金性能的变化与价电子结构密切相关, 随着掺杂量的升高, 晶格电子数n_l明显降低, 这说明热声子优先破坏非成键的晶格电子在晶格空间的分布, 降低其电位能, 进而降低其对于阴极合金的熔点、结合能的贡献. 对于阳极产物, 理论熔点与实验一致. 由于其晶体结构复杂, 多种原子占位, 不同于结构简单的阴极合金. 其性能不是与单独某种电子相关, 而是与共价电子和晶格电子相关联. 开路电压与晶格电子密切相关, 与平均每原子的晶格电子数成反比, 平均晶格电子数最低的Na₃Sb(0.2693)的开路电压最高, 而平均晶格电子最高的NaSn的最低. 对于Na||Sb-Pb-Sn液态金属电池体系而言, 晶格电子扮演重要的角色, 可以调控电极的热、电性能.

σ		1	2	3	4
Chσ		1	0.5386	0.4650	0
Ctσ		0	0.4616	0.5350	1
nTσ		1	1	1	1
nlσ		1	0.5386	0.4650	0
ncσ		0	0.4616	0.5350	1
Rσ(1)	H	0.3708	0.3289	0.3222	0.2800
	Li	1.3260	1.2089	1.1440	0.9860
	Na	1.5133	1.4551	1.4308	1.3070
	K	1.9628	1.8794	1.8601	1.7820
	Rb	2.0870	2.0270	2.0175	1.9570
	Cs	2.2140	2.2260	2.2279	2.2400
注: $ l, \; m, \;n, \; \tau $: 1 0 0 0 　 $l{'}, \; m{'}, \;n{'}, \; \tau {'}$: 0.9982 0.0018 0 0

表A1IA族元素的乙种杂化表
TableA1.B type hybrid table of IA group

σ		1	2	3	4
Chσ		1	0.5694	0.1983	0
Ctσ		0	0.4306	0.8017	1
nTσ		3 or 5	3 or 5	3 or 5	3 or 5
nlσ		0	0	0	0
ncσ		3 or 5	3 or 5	3 or 5	3 or 5
Rσ (1)	N	0.7000	0.7517	0.7973	0.8200
	P	1.0980	1.1173	1.1343	1.1428
	As	1.1800	1.2390	1.2911	1.3170
	Sb	1.3560	1.4279	1.4919	1.5230
	Bi	1.3990	1.4455	1.5044	1.5290
注: $ l, \; m, \; n, \; \tau $: 1 2 0 1; $ l{'}, \; m{'}, \; n{'}, \; \tau {'} $: 0 3 0 1

表A2VA族元素的甲种杂化表
TableA2.A type hybrid table of VA group

σ		1	2	3	4	5	6
Chσ		1	0.9502	0.8320	0.1681	0.0481	0
Ctσ		0	0.0498	0.1680	0.8319	0.9519	1
nTσ		4	4	4	4	4	4
nlσ		2	1.9040	1.6640	0.3360	0.0960	0
ncσ		2	2.0960	2.3360	3.6640	3.9040	4
Rσ(1)	C	0.7630	0.7630	0.7630	0.7630	0.7630	0.7630
	Si	1.1700	1.1700	1.1700	1.1700	1.1700	1.1700
	Ge	1.2230	1.2230	1.2230	1.2230	1.2230	1.2230
	Sn	1.3990	1.3990	1.3990	1.3990	1.3990	1.3990
	Pb	1.4300	1.4300	1.4300	1.4300	1.4300	1.4300
注: $ l, \; m, \; n, \; \tau $; 2 2 0 0; $ l{'}, \; m{'}, \; n{'}, \; \tau {'}; $ 1 3 0 1

表A3IVA族元素的甲种杂化表
TableA3.A type hybrid table of IVA group