摘要: 获得覆盖较宽温度和压力范围内的等离子体热力学和输运性质是开展等离子体传热和流动过程数值模拟的必要条件. 本文通过联立Saha方程、道尔顿分压定律以及电荷准中性条件求解等离子体组分; 采用理想气体动力学理论计算等离子体热力学性质; 基于Chapman-Enskog方法求解等离子体输运性质. 利用上述方法计算了压力为0.1, 1.0和10.0 atm (1 atm = 101325 Pa), 电子温度在300—30000 K范围内, 非局域热力学平衡(电子温度不等于重粒子温度)条件下氩-氮等离子体的热力学和输运性质. 结果表明压力和非平衡度会影响等离子体中各化学反应过程, 从而对氩-氮等离子体的热力学及输运性质有较大的影响. 在局域热力学平衡条件下, 计算获得的氩-氮等离子体输运性质和文献报道的数据符合良好.
关键词: 氩-氮等离子体 /
热力学和输运性质 /
非局域热力学平衡 English Abstract Calculation of two-temperature thermodynamic and transport properties of argon-nitrogen plasma Pan Zi-Han Chen Xian-Hui Wang Cheng Xia Wei-Dong School of Engineering Science, University of Science and Technology of China, Hefei 230022, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11675177,11875256)Received Date: 02 December 2020Accepted Date: 15 December 2020Available Online: 08 April 2021Published Online: 20 April 2021Abstract: The thermodynamic and transport properties of plasmas over a wide range of temperature and pressure are necessary to model the heat transfer and flow processes in plasma. In this study, the plasma composition is solved by simultaneous Saha equation, Dalton's partial pressure law and charge quasi-neutral equation. The thermodynamic properties of plasma computation are based on the kinetic theory for ideal gas. While the calculation of transport properties is based on the solution of Boltzmann’s equation by the Chapman-Enskog method. The thermodynamic and transport properties of argon-nitrogen plasma at pressures of 0.1, 1.0 and 10.0 atm, electron temperatures ranging from 300 to 30000 K, and non-local thermodynamic equilibrium (NLTE), where the electron temperature is not equal to the temperature of heavy particles,, are investigated by using the above method. The results show that the value of non-equilibrium parameter has a great influence on the properties of the argon-nitrogen mixture. With the increase of non-equilibrium parameter, the dissociation reaction requires a higher electron temperature, which leads the dissociation peak to shift to a higher electron temperature. The ionization and dissociation reaction will enter into the high temperature region due to the increase in pressure. This change will affect the peak position and value of the specific heat, viscosity, thermal conductivity and electrical conductivity of plasma. In addition, since the electronic translational thermal conductivity and electrical conductivity mainly depend on the electron number density, when non-equilibrium parameter and pressure increase, the electron number density will increase at high electron temperature, thus improving the electronic translational thermal conductivity and electrical conductivity. Under the condition of local thermodynamic equilibrium, the transport properties of argon-nitrogen plasma obtained by calculation are in good agreement with previously reported data.Keywords: argon-nitrogen plasma /thermodynamic and transport property /non-local thermodynamic equilibrium plasma 全文HTML --> --> --> 1.引 言 氮气等离子体具有高焓值、良导热性能等优点, 通常按照一定比例混合在氩气等离子体中以提高焓值和加强传热. 此外, 在氮气等离子体氛围下, 可以形成氮化颗粒、氮化涂层, 以及合成氨气和实现氮掺杂石墨烯等工艺过程[1 -5 ] . 由于等离子体恶劣的热环境、非平衡特性以及反应时间短等, 上述工艺过程中涉及的流动、传热传质和化学反应等过程往往难以开展相关的实验诊断. 因此, 构建数学物理模型进行数值模拟是一种非常有效的研究方法. 而准确的氩-氮等离子体组分、热力学和输运性质数据是可靠数值模拟的先决条件.[6 ] : 假设各个粒子的速度分布函数是处于Maxwell分布的一阶微扰逼近, 将分布函数展开成Sonine多项式的有限级数, 对Boltzmann方程进行线性化处理, 最终将输运性质表达成一系列碰撞积分的线性组合. 此方法在局域热力学平衡(LTE)等离子体中得到了广泛的研究, 文献中报道了一些常用的纯气体和混合物的计算结果[7 -11 ] .[12 ] 发展的简化理论, 忽略了重粒子和电子之间的碰撞耦合, 这种方法假定电子和重粒子之间完全解耦, 从而使得与电子有关的输运性质只是电子温度的函数, 与重粒子有关的输运性质只是重粒子温度的函数; Rat等[13 ] 认为电子与重粒子之间的碰撞耦合不能被忽略, 基于这种思想发展出一套全耦合输运性质计算方法. 值得注意的是, 除了某些寻常扩散系数外, 电子和重粒子之间的耦合并不会导致计算的NLTE等离子体输运性质发生显著的变化[14 ] . 在NLTE等离子体中, 利用简化理论对纯气体和混合物的输运性质进行了计算[15 -20 ] ; Rat等[21 -26 ] 的方法在等离子体输运性质的计算中已有报道. 而关于氩-氮混合物在NLTE状态下的热力学和输运性质的数据尚未见到报道.27 ]对LTE等离子体的组分计算方法扩展到NLTE等离子体中, 获得了不同压力下, 电子温度范围300—30000 K内氩-氮等离子体的热力学和输运性质随非平衡度的变化情况, 并对其变化趋势进行了讨论和分析. 此外还将LTE条件下计算的等离子体输运性质计算结果与文献报道的数据进行了对比, 结果符合良好.2.等离子体组分及热力学性质 等离子体组分的确定是计算其热力学性质和输运性质的前提, 通过Saha方程、道尔顿分压定律以及电荷准中性条件求解等离子体中每种粒子的数密度. 在NLTE等离子体系统中, 由于电子与重粒子低频率的碰撞, 电子温度与重粒子温度存在差异, 采用非平衡度$ \theta ={T}_{\rm{e}}/{T}_{\rm{h}} $ 定义体系中的偏离热力学平衡的程度, 其中$ {T}_{\rm{e}} $ 和$ {T}_{\rm{h}} $ 分别为电子温度和重粒子温度.1 )式为van de Sanden等[28 ] 提出的电离过程的化学平衡方程, (2 )式为Ghorui等[18 ] 提出解离过程的化学平衡方程, 对于电离反应, 其反应特征温度为$ {T}_{\rm{e}} $ , 对于解离反应, 其反应特征温度为$ {T}_{\rm{h}} $ . 式中$ {n}_{i} $ 为第i 种粒子的数密度, $ {Q}_{i}^{\rm{tr}} $ 和$ {Q}_{i}^{\rm{int}} $ 分别是第i 种粒子的平动配分函数和内配分函数, $ {Z}_{i} $ 是第i 种粒子的电荷数, k 是玻尔兹曼常数, p 为压力, $ {E}_{i} $ 是第i 种粒子的形成能, 下标a(z )和m分别表示带z 个电荷的离子和分子. 在本文中忽略了潘宁放电和三体复合反应.$ {\rm{Ar}} $ , $ {\rm{Ar}}^{+} $ , $ {\rm{Ar}}^{++} $ , $ {\rm{Ar}}^{+++} $ , 对于氮气有$ {{\rm{N}}}_{2\;}, \;{\rm{N}} $ , $ {\rm{N}}_{2}^{+} $ , $ {{\rm{N}}}^{+} $ , $ {\rm{N}}^{++} $ , $ {\rm{N}}^{+++} $ . 用于评价原子和离子配分函数的电子能级的数据以及电离和解离能数据从NIST数据库[29 ] 中获得, 用于计算分子配分函数的数据从JANAF表中得到[30 ] .[27 ] 提出的方法来求解上述非线性方程组, 该算法适用于LTE等离子体的组分计算, 在本工作中扩展到NLTE等离子体. 在高温条件下(在计算程序中高温达到100000 K), 假设当系统的基系为$ {\rm{Ar}}^{+++} $ , $ {\rm{N}}^{+++} $ 以及e时, 用基系粒子表示非基系粒子(例如$ {{\rm{N}}}^{+} $ ), 可以写出如下方程:$ {T}_{\rm{e}} $ . 当非基系粒子为分子时(例如$ {{\rm{N}}}_{2} $ ), 反应方程为$ {T}_{\rm{h}} $ , 离子参与的反应特征温度为$ {T}_{\rm{e}} $ , 故上述反应的特征温度需要重新确定. 其特征温度T 确定方法如下. 根据氮气的基本反应:13 )式 × (12 )式 × (11 )式]2 × (9 )式, 可得到反应(7 )式. 此时, 反应(7 )式的特征温度表示为$ {{\rm{N}}}_{2} $ 先离解为$ {\rm{N}} $ 原子($ {T}_{\rm{h}} $ ), 随后$ {\rm{N}} $ 原子电离成$ {\rm{N}}^{+++} $ ($ {T}_{\rm{e}} $ ), 这分别对应不同的特征温度. 对于非基系分子$ {\rm{N}}_{2}^{+} $ , 同理, 其反应温度项表示为$ {T}_{\rm{e}} $ . 当所有反应的特征温度全部确定时, 通过牛顿迭代便可得到所有粒子的数密度.$ \theta $ 条件下, 50%$ {\rm{Ar}} $ 和50%$ {\rm{N}}_{2} $ 混合物的化学平衡组分随电子温度的变化如图1 所示. 在LTE条件下, 大约在7000 K, $ {\rm{N}}_{2} $ 的解离达到最大, Ar (15.76 eV)和N (14.5 eV)的一次电离能较为接近, 在15000 K左右时一次电离达到最大值. 随着$ \theta $ 的提高, 高电子温度所对应解离反应的特征温度($ {T}_{\rm{h}} $ )依旧很低, 因此氮的解离需要更高的电子温度, 从而导致氮原子浓度的降低. 在电离发生之前, 体系压力(1 atm)主要由$ {\rm{N}}_{2} $ 和Ar决定, 即$ p=({n}_{\rm{Ar}}+{n}_{{\rm{N}}_{2}})k{T}_{\rm{h}} $ , 所以$ \theta $ 的增大会提高$ {\rm{N}}_{2} $ 和Ar的数密度. 电子数密度随着$ \theta $ 的增大而增大, 这一趋势对于和电子有关的输运系数有着重要影响.图 1 不同非平衡度下50%$ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物中各粒子数密度随电子温度的变化(1 atm)Figure1. Electron temperature dependence of composition of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter (1 atm).图2 给出了LTE条件下氩-氮混合物的化学平衡组分随电子温度和压力的变化, 其中图2(c) 的结果与图1 中实线结果($ \theta =1 $ )一致, 都是处于1 atm时, LTE条件下等离子体组分随电子温度的变化. 等离子体中粒子总数密度随着温度的升高而减少, 随着压力的增大而增加. 电离温度随压力的增大而升高是勒夏特列原理的结果[10 ] . 当压力增大时, 一次和二次电离反应会转移到更高的电子温度.图 2 LTE条件下50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物中各粒子数密度随电子温度的变化 (a) 0.1 atm; (b) 0.5 atm; (c) 1.0 atm; (d) 10.0 atmFigure2. Electron temperature dependence of composition of 50% argon-50% nitrogen mixtures under LTE condition: (a) 0.1 atm; (b) 0.5 atm; (c) 1.0 atm; (d) 10.0 atm.$ {m}_{i} $ 是第i 种粒子的质量.$ \theta $ 和压力下, 50%$ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物的质量密度、焓值以及比热随电子温度的变化如图3 所示. 密度随$ \theta $ 和压力的增大而增大, 这是由于各个粒子的数密度提高导致的. 焓值随$ \theta $ 增大而降低. 此外, 随着压强的增大, 焓值随着温度的升高而增长变慢, 这是因为电离反应向更高温度转移. 氩-氮混合物的总比热表现为$ {\rm{N}}_{2} $ 解离峰($ {T}_{\rm{h}} $ ≈ 7000 K)和Ar, N($ {T}_{\rm{e}} $ ≈ 15000 K)及其离子的电离峰($ {T}_{\rm{e}} $ ≈ 28000 K). 由于解离反应受重粒子温度控制, 当$ \theta $ 增大时, 它们向更高的电子温度偏移. 对于$ \theta =3 $ , $ {\rm{N}}_{2} $ 解离峰到达了发生第一次电离的温度范围($ {T}_{\rm{e}} $ ≈ 15000 K), 导致电离向更高电子温度方向偏移. 此外, 随着$ \theta $ 增大, 一次电离发生在较窄的电子温度范围内, 从而产生较高的总比热峰, 随着压力的增大, 解离反应和电离反应需要更高的电子温度, 比热的峰值也转移到更高的电子温度, 由于压力的增大, 焓值随温度的升高而增长变慢, 所以比热的峰值较低.图 3 不同压力和非平衡度下50%$ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物热力学性质随电子温度的变化Figure3. Electron temperature dependence of thermodynamic properties of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure.3.碰撞积分 输运性质的表达式依赖于碰撞积分. 第i 种与第j 种粒子的相互作用的碰撞积分定义为[23 ] $ x={\mu }_{ij}{g}^{2}/2 k{T}_{ij}^{2} $ 是约化相对速度, ${\mu }_{ij}= $ $ {m}_{i}{m}_{j}/\left({m}_{i}{+m}_{j}\right)$ 是约化质量, $ {T}_{ij}^{*} $ 是碰撞的有效温度, 定义为$ {Q}_{i, j}^{\left(l\right)} $ 的定义如下:$ \chi $ 和b 分别是碰撞偏转角和碰撞参数.3.1.中性粒子之间的相互作用 3.1.中性粒子之间的相互作用 表1 总结了中性粒子之间碰撞积分的计算方法和作用势的数据来源.相互作用 方法 文献 Ar-Ar HFDTCS2势 [31 ] N2 -N2 Exponential势 [32 ] N2 -N Exponential势 [32 ] N-N 碰撞积分表 [33 ] N2 -Ar ESMV势 [34 ] $ {\rm{Ar}} $-N Lennard-Jones势 [34 ]
表1 中性粒子之间相互作用Table1. Data source of neutral-neutral interaction3.2.中性粒子与离子的相互作用 -->3.2.中性粒子与离子的相互作用 对于离子与中性粒子的相互作用, 考虑两种过程, 一是纯弹性碰撞过程, 二是有电荷交换的非弹性碰撞过程. 当l 为奇数时, 后者在确定碰撞积分$ {\tilde {Q}}_{i, j}^{\left(l, s\right)} $ 中起重要作用. 考虑到弹性和非弹性过程, 采用Murphy之前的方法[9 ] , 根据经验混合规则估计总碰撞积分:g 是相对速度, A 和B 为实验常数. 弹性碰撞和非弹性碰撞的数据源如表2 所示.相互作用 弹性碰撞 文献 非弹性碰撞 文献 Ar+ -Ar 2 ∑1/2u Morse势[35 ] ∑ 电荷转移 [35 ] 2 ∑1/2g Exponential势[35 ] Π 电荷转移 [35 ] 2 Π3/2g Morse势[35 ] 2 Π3/2u Exponential势[35 ] 2 Π1/2g Morse势[35 ] 2 Π1/2u Exponential势[35 ] ${\rm{N}}_2^+ $-N2 极化势 积分输运截面 [36 ] ${\rm{N}}_2^+ $-N 极化势 N+ -N2 极化势 积分输运截面 [36 ] N+ -N2 碰撞积分表 [37 ] 碰撞积分表 [37 ] Ar+ -N2 极化势 Ar+ -N 极化势 ${\rm{N}}_2^+ $-Ar 极化势 N+ -Ar 3 ∑– Morse势[38 ] 3 Π Morse势[38 ] Xn + -X , Y n ≥ 2) 极化势
表2 中性粒子与离子相互作用Table2. Data source of neutral-ion interaction.3.3.电子与中性粒子之间的相互作用 -->3.3.电子与中性粒子之间的相互作用 电子与中性粒子的碰撞积分通过(19 )式对碰撞截面$ {Q}_{i, j}^{\left(l\right)} $ 直接数值积分得到. 表3 总结了电子与中性粒子碰撞积分的计算方法和作用势的数据来源.相互作用 方法 文献 e-N2 积分输运截面 [39 ] e-N 积分输运截面 [40 ] e-Ar 积分输运截面 [26 ]
表3 电子与中性粒子相互作用Table3. Data source of electron-neutral interaction3.4.带电粒子之间的相互作用 -->3.4.带电粒子之间的相互作用 带电粒子之间的相互作用采用屏蔽Coulomb电势计算:$ {\lambda }_{\mathrm{D}} $ 为德拜长度, $ {Z}_{i} $ 和$ {Z}_{j} $ 分别是粒子i , j 的电荷数, $ {\epsilon }_{0} $ 是真空介电常数. 屏蔽库仑势的碰撞积分由文献[41 ]给出.4.等离子体输运性质 24.1.热导率 4.1.热导率 热导率可分为平动热导率、反应热导率和内部热导率. 由于内部热导率所占比例很小, 本文忽略对其计算[16 ] . 最终热导率可以写成:$ {q}^{mp} $ 通过相应的碰撞积分计算得到, 见文献[12 ].N 是粒子的数量. $ {q}_{hk}^{mp} $ 通过相应的碰撞积分计算得到, 见文献[42 ].[17 ] :$ {F}^{ij} $ 是矩阵$ {{F}}_{{ij}} $ 的代数余子式, 它的定义为[26 ] 报道:n 是总数密度, $ {g}_{ij} $ 表达式为$ {\theta }_{ji}={T}_{j}/{T}_{i} $ . 通过寻常扩散系数来定义双极扩散系数:$ \alpha $ 和$ \beta $ 可以用粒子的电荷、质量、数密度、温度及相关的寻常扩散系数表示为$ {\Delta }{h}_{\mathrm{r}} $ 为反应的焓值, 对于各个粒子分压力对$ {T}_{\rm{e}} $ 和$ {T}_{\rm{h}} $ 的偏导数见文献[43 ].$ \theta $ , 总反应热导率由下式计算:图4 为1 atm下, 50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物在不同$ \theta $ 下的反应热导率. 总反应热导率显示了3个峰值, 分别为$ {\rm{N}}_{2} $ 的解离峰($ {T}_{\rm{h}} $ ≈ 7000 K), Ar, N($ {T}_{\rm{e}} $ ≈ 15000 K)以及$ {\rm{N}}^{+} $ , $ {\rm{Ar}}^{+} $ 的电离峰($ {T}_{\rm{e}} $ ≈ 28000 K). 当$ \theta =1 $ 时, 3个峰值有明显区别, 值得注意的是, 当$ \theta $ 提高时, 解离峰的位置转向更高的电子温度. 电子反应热导率曲线在电离反应发生时出现峰值, 而重粒子反应热导率曲线在解离反应发生时出现峰值. 随着$ \theta $ 的增大, 重粒子反应热导率峰值逐渐增大, 这是由于粒子数密度的急剧变化造成的[44 ] . 此外, 电子反应热导率峰值随着$ \theta $ 的增大而提高, 其原因可以结合前面给出的电子数密度随$ \theta $ 的变化趋势来解释, 由于电子数密度随$ \theta $ 的增大而增大, 电离复合反应释放出来的能量更多, 从而导致电子反应热导率峰值上升.图 4 不同非平衡参数下50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物反应热导率随电子温度的变化 (a)电子反应热导率; (b) 重粒子反应热导率; (c) 总反应热导率(1 atm)Figure4. Electron temperature dependence of reactive thermal conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter: (a) Reactive thermal conductivity of electrons; (b) reactive thermal conductivity of heavy particles; (c) total reactive thermal conductivity(1 atm).$ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物在不同$ \theta $ 和压力下的总热导率如图5 所示. 由于压力的提高, 电离反应及解离反应的温度区间向高温移动, 所以对应的热导率的峰值也随之向高温区移动. 在解离和电离发生的温度范围内, 反应热导率占主要地位, 而对于高温情况下, 电子平动热导率占据主导作用. 随着压力的增大, 电子数密度提高, 而电子平动热导率随电子数密度增大而增大, 如图6 所示, 这就解释了在较高的温度下, 热导率增大的原因.图 5 不同压力和非平衡度下50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物热导率随电子温度的变化, 符号$ \times $ 代表Murphy和Arundelli[9 ] 计算结果Figure5. Electron temperature dependence of total thermal conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure, the symbol $ \times $ shows results of Murphy and Arundelli[9 ] .图 6 不同压力和非平衡度下50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物电子平动热导率随电子温度的变化Figure6. Electron temperature dependence of electron translational thermal conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure.4.2.黏 度 -->4.2.黏 度 黏度的计算方法见文献[17 ].图7 显示了不同$ \theta $ 和压力下50% Ar和50% $ {\rm{N}}_{2} $ 混合物黏度随电子温度的变化. 黏度与气体动量输运相关. 由于气体粒子速度随温度的升高而增大, 导致气体的黏度增大, 直至电离开始. 当气体发生电离反应, 长程库仑相互作用随电离强度增强而增大, 并导致黏度值下降. 随着$ \theta $ 的增大, 重粒子温度下降, 所以黏度的峰值向更高的电子温度偏移. 图7 还表明压力对氩-氮等离子体黏度有着较大影响, 当压力提高时, 等离子体中重粒子的数密度提高, 而黏度主要由于重粒子碰撞导致的, 这就导致了黏度的峰值提高, 此外, 由于压力的提高, 电离反应需要更高的电子温度, 这就导致了黏度的峰值随之向高温区移动.图 7 不同压力和非平衡度下50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物热导率随电子温度的变化, 符号$ \times $ 代表Murphy和Arundelli[9 ] 计算结果Figure7. Electron temperature dependence of viscosity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure, the symbol $ \times $ shows results of Murphy and Arundelli[9 ] .4.3.电导率 -->4.3.电导率 电导率的计算方法见文献[17 ].图8 显示了不同$ \theta $ 和压力下50% Ar和50% $ {\rm{N}}_{2} $ 混合物电导率随电子温度的变化. 在电子温度较低时, 随着$ \theta $ 的增大, 气体的电导率降低, 这是因为解离反应向更高的电子温度转移. 在高$ \theta $ 和高电子温度下, 一旦解离开始, 电导率随着电子温度的升高而迅速增大. 因此, 在较高的$ \theta $ 下, 可以注意到图中$ \sigma $ -$ {T}_{\rm{e}} $ 曲线较陡. 当电子温度升高时, 电导率随$ \theta $ 增大而增大, 由于电导率与电子数密度密切相关, 从图1 中可以看出电子数密度随$ \theta $ 的增大而增大, 从而引起电导率的增大, 此外, 随着压力的提高, 电离反应向着高温区移动, 导致此转折温度提高(当压力为0.1, 1.0和10.0 atm时, 转折温度分别为14000, 15000和19000 K). 当压力为0.1 atm, $ {T}_{\rm{e}} $ ≈ 20000 K时, 电导率的数值略有下降, 原因在于二次电离结束后, 在恒压下, 随着温度的升高, 电子数密度减小, 导致电导率降低, 文献[17 ]报道的氮氧等离子体也有类似的现象. 随着压力的提高, 电导率降低, 温度随之提高, 这是因为电离反应需要更高的电子温度, 当压力高于10 atm时, 观察不到明显的下降趋势.图 8 不同压力和非平衡度下50% $ {\rm{Ar}} $ 和50% $ {\rm{N}}_{2} $ 混合物电导率随电子温度的变化, 符号$ \times $ 代表Murphy和Arundelli[9 ] 计算结果Figure8. Electron temperature dependence of electrical conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure, the symbol $ \times $ shows results of Murphy and Arundelli[9 ] .5.总 结 本文研究了不同压力下、电子温度范围在300—30000 K内, NLTE条件下氩-氮等离子体的热力学和输运性质, 在LTE条件下, 与先前文献报道的结果符合较好[9 ] , 验证了本文程序的可靠性. 本工作填补了氩-氮混合物在非平衡条件下热力学和输运性质数据的不足, 为以后相关的等离子体的数值模拟提供了基础.27 ]思想推广到NLTE等离子体热力学和输运性质计算. 结果表明, 非平衡度对氩-氮混合物的性能影响很大. 随着$ \theta $ 的增大, 解离反应需要更高的电子温度, 导致解离峰向更高的电子温度推移, 由于压力的提高, 会导致电离和解离反应向高温区转移. 这种变化会对等离子体的比热、黏度、热导率以及电导率的峰位置及峰值产生影响. 此外, 由于电子平动热导率以及电导率主要取决于电子数密度, 当$ \theta $ 以及压力提高时, 在高温条件下会提高电子数密度, 从而提高了电子平动热导率和电导率. 






































































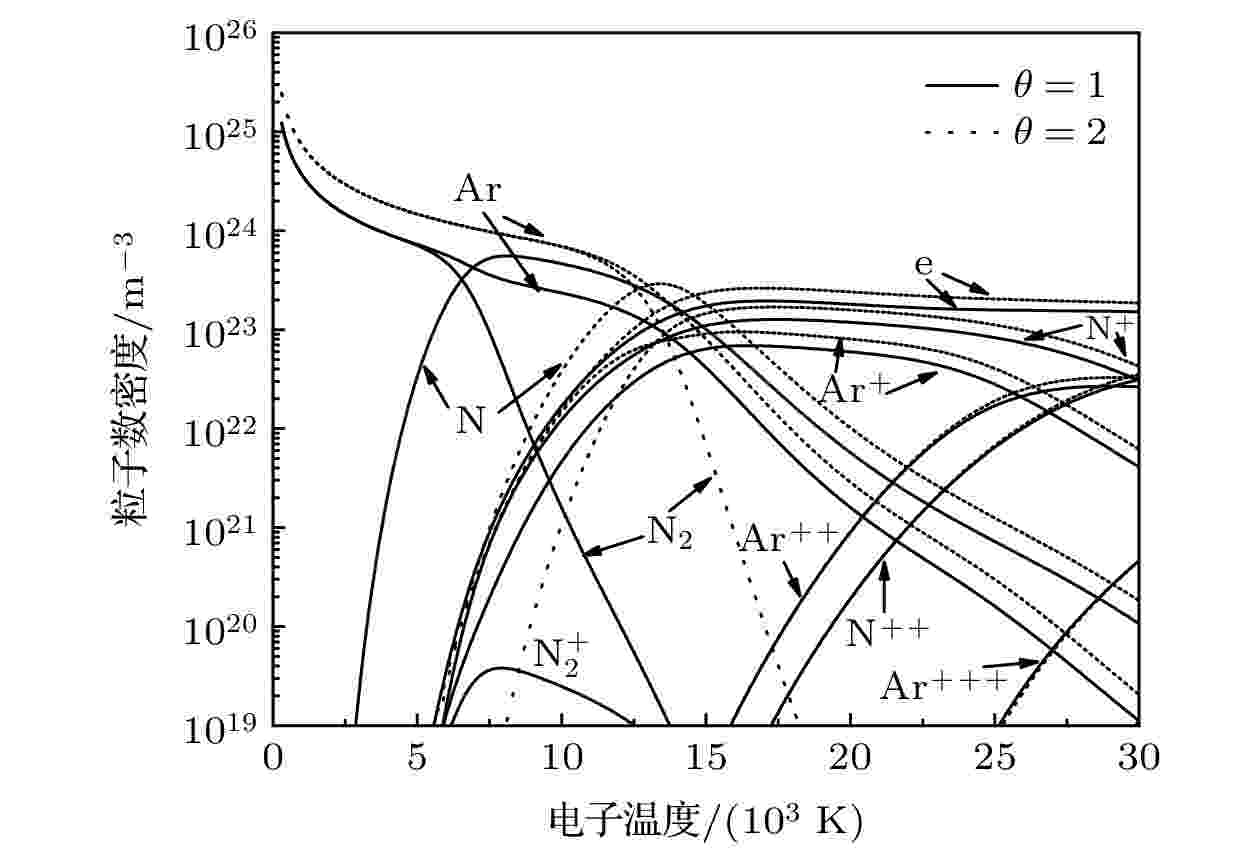 图 1 不同非平衡度下50%
图 1 不同非平衡度下50%


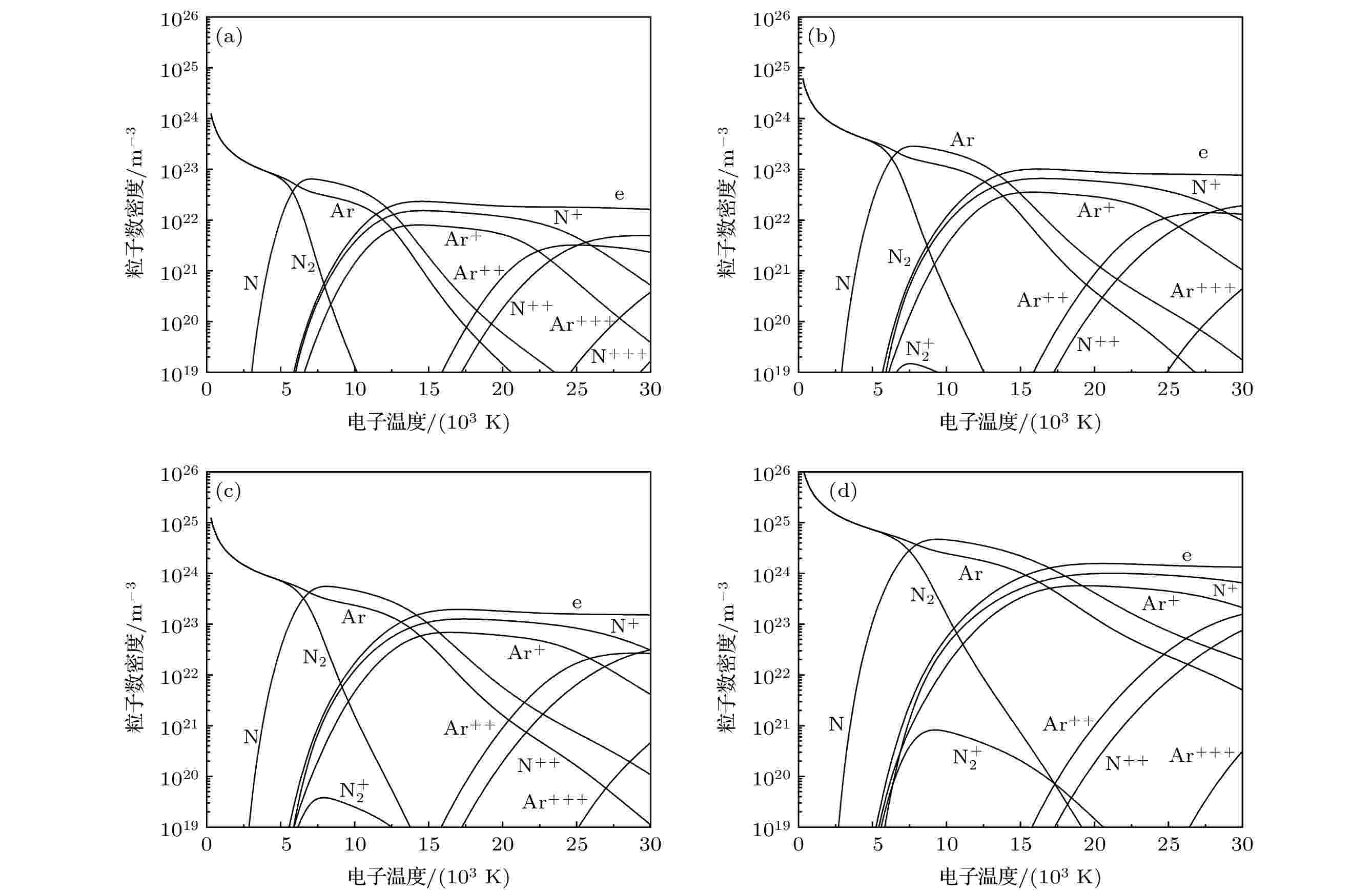 图 2 LTE条件下50%
图 2 LTE条件下50% 
















































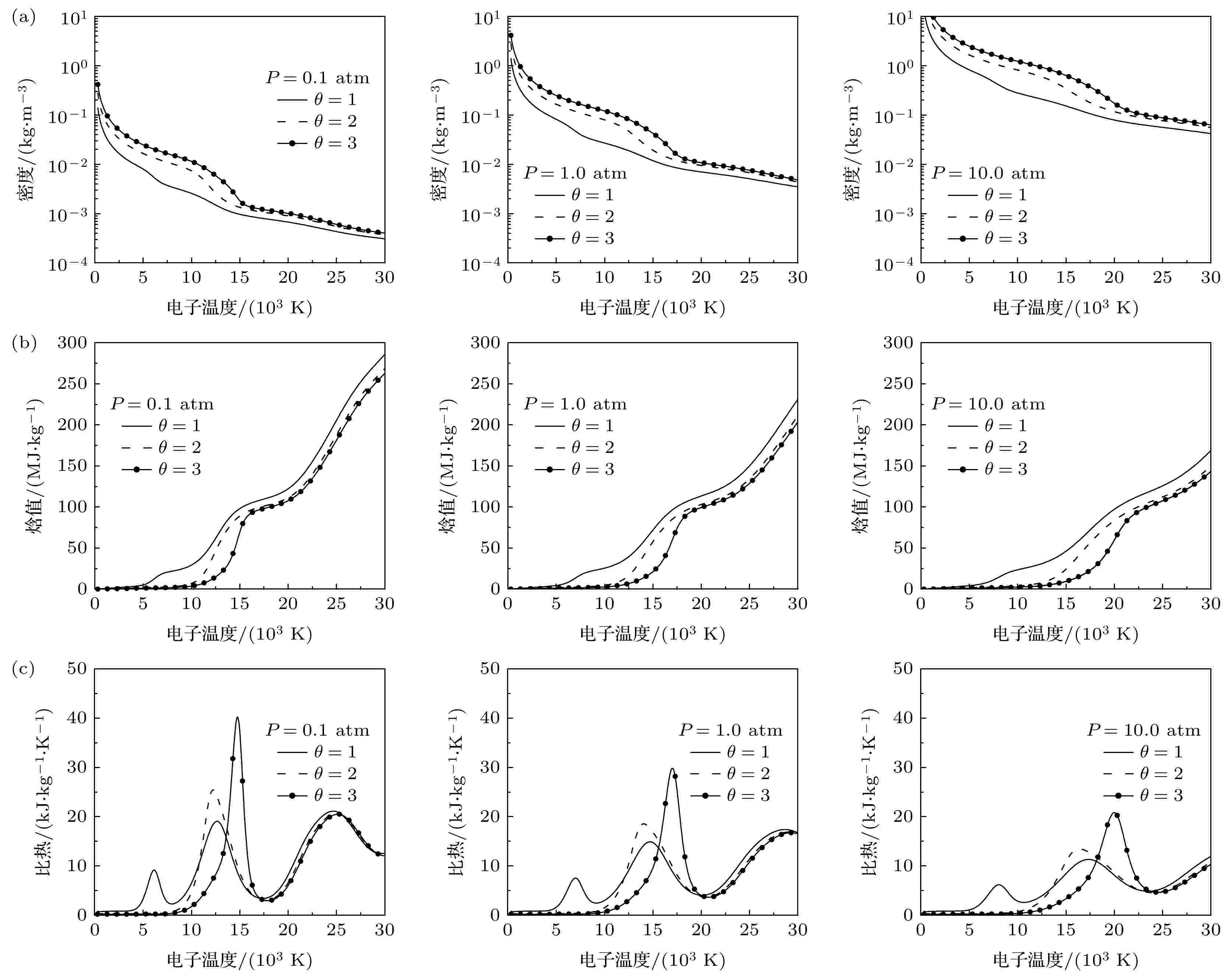 图 3 不同压力和非平衡度下50%
图 3 不同压力和非平衡度下50%










































































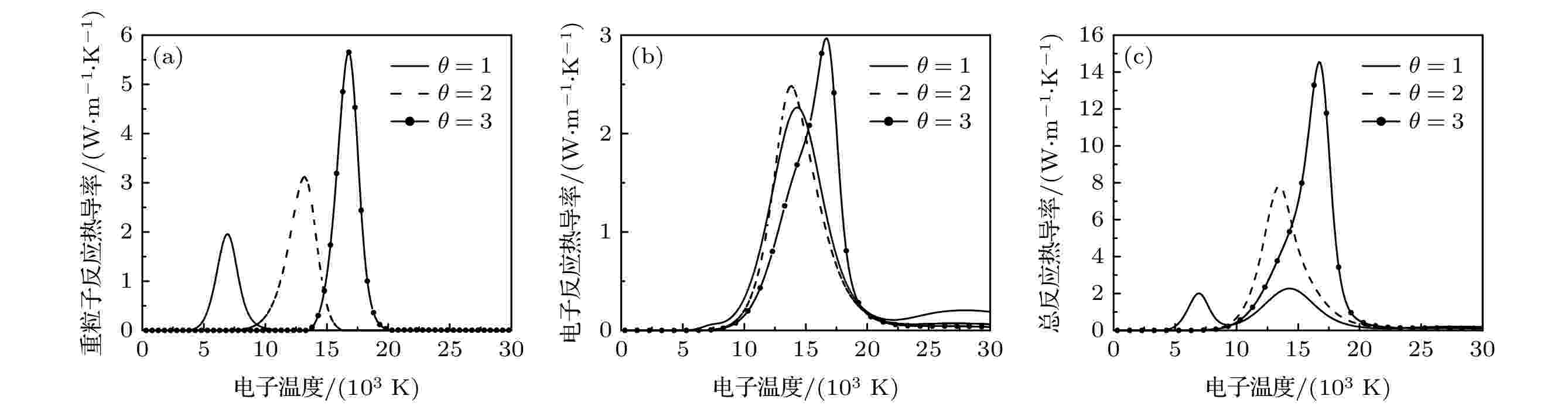 图 4 不同非平衡参数下50%
图 4 不同非平衡参数下50% 




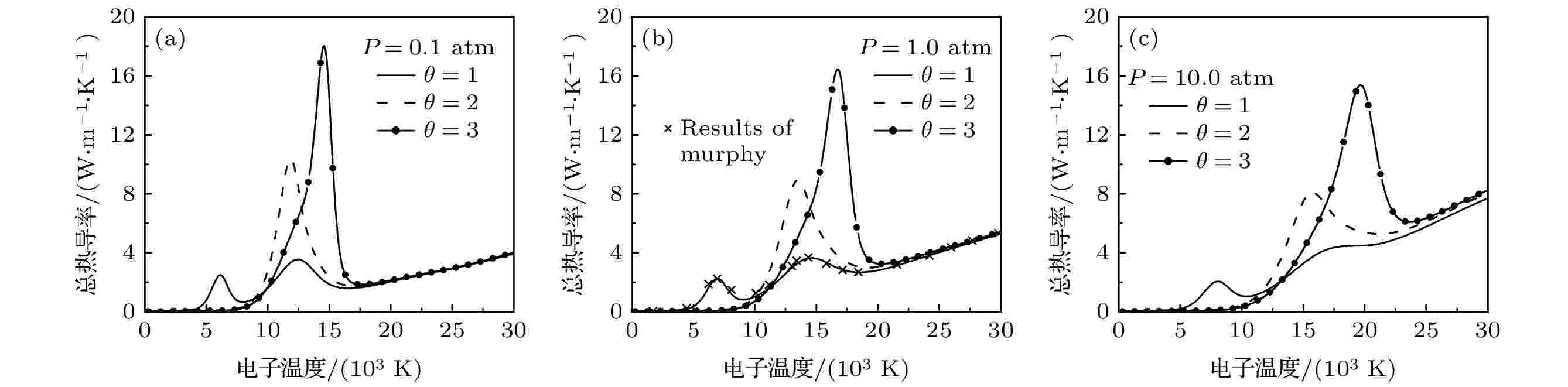 图 5 不同压力和非平衡度下50%
图 5 不同压力和非平衡度下50% 



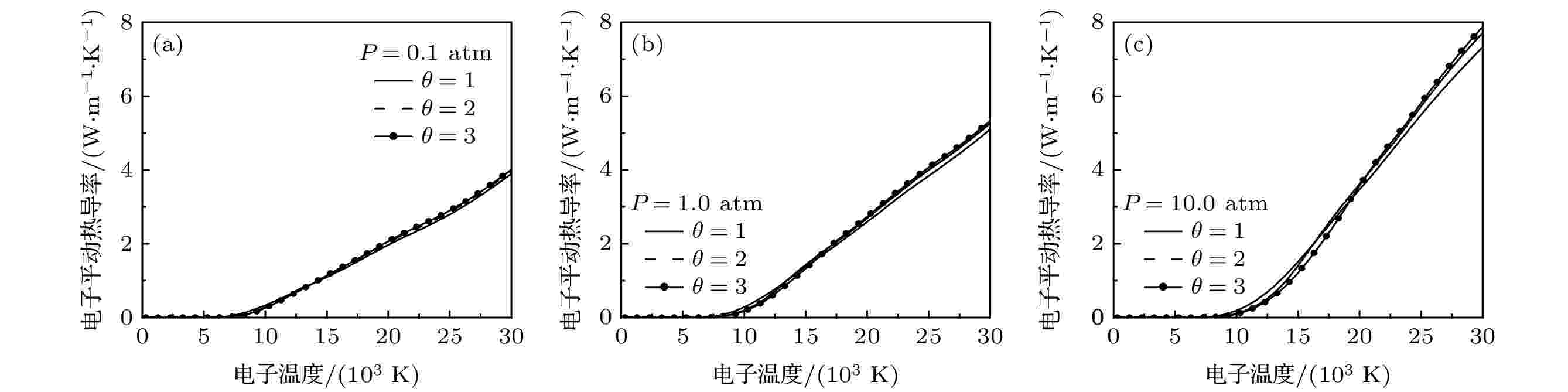 图 6 不同压力和非平衡度下50%
图 6 不同压力和非平衡度下50% 






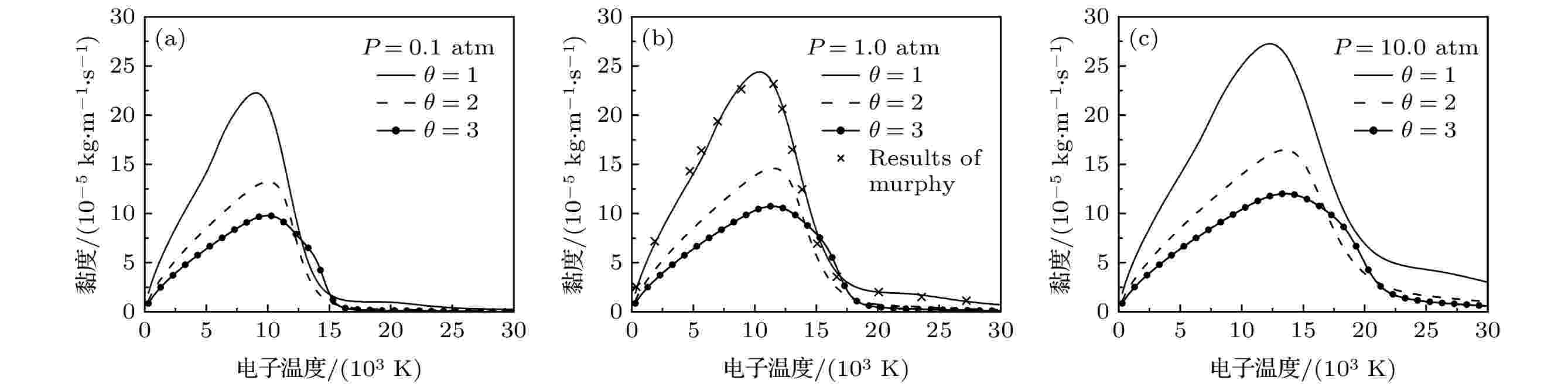 图 7 不同压力和非平衡度下50%
图 7 不同压力和非平衡度下50% 













































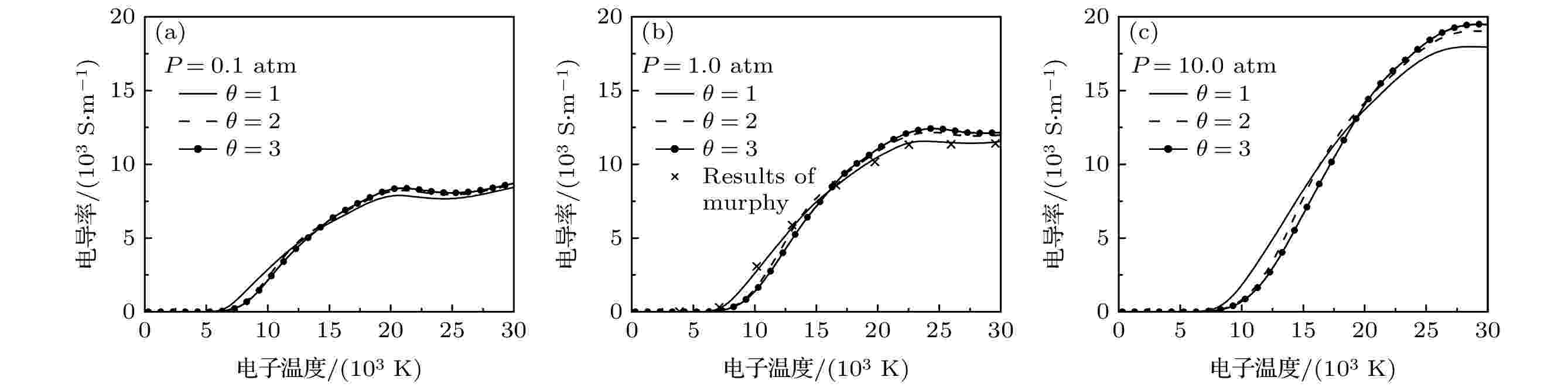 图 8 不同压力和非平衡度下50%
图 8 不同压力和非平衡度下50% 







