全文HTML
--> --> -->基于原子制造先进合成技术, 目前可以实现原子数目精确可控的纳米团簇或纳米颗粒的批量制造[1]. 纳米团簇相比于纳米颗粒而言, 可以在单原子精度下控制其尺寸和组成. 而近年来, 随着纳米团簇研究体系变大, 纳米颗粒研究体系变小, 两者之间的差异越来越小. 纳米团簇的存在最早可以追溯到宇宙成形时就已经稳定存在的富勒烯C60[2,3]. 在20世纪50年代和60年代, 人们利用质谱仪中的强烈分子束在低温下通过超音速膨胀开始制备纳米团簇[4,5]. 自20世纪80年代起, 过渡金属、难熔金属纳米团簇以及二元和三元的半导体元素及化合物纳米团簇也逐渐诞生. 纳米团簇因其尺寸受限、成分可控而同时具有非比寻常的物理和化学性质. 譬如在纳米团簇中, 金属性元素可以转变为绝缘性; 半导体性元素可以转变为金属性; 非磁性材料可以转变为磁性材料; 不透明材料可以变为透明材料; 惰性材料可以变得有活性[5]. 此外, 还可以通过设计和合成不同尺寸、组成的团簇使其具有类原子的电子性能[6]. 纳米团簇不仅是原子、分子、纳米颗粒、块体材料之间的桥梁, 也是物理学、化学、材料科学、生物学、药学和环境科学之间的重要桥梁. 随着纳米科技的发展, 目前已经有很多新型的纳米材料或纳米结构用于催化、电子器件、能量转化和存储等领域[7]. 纳米团簇的使役条件多样且复杂, 不仅局限于真空室温, 还往往常用于高温条件、气氛条件、液相条件甚至不同条件之间的组合等. 不同的外界条件会导致纳米团簇的结构和性质发生动态的变化, 而纳米团簇的尺寸、形状、成分和结构是决定器件整体功能性的关键. 因此, 对纳米团簇和颗粒的三维定量表征, 即在三维尺度确定每个原子的种类和位置, 是极其重要也极具挑战的.
高空间分辨表征材料三维化学元素分布的技术之一是三维原子探针, 它利用原子探针场离子显微镜, 可以在原子精度进行原子探针层析[8]. 它的特点是化学灵敏度高、可以对材料中的不同化学元素在单原子尺度解析, 缺点是原子位置的精度不够, 因此无法准确给出材料的晶体结构信息. 此外, 样品条件相对苛刻, 一般需要被测样品是导体且需要制备针形的样品[9], 不适合分析单个纳米团簇或颗粒.
随着球差校正等先进电子显微学技术的进步[10], 已经可以在原子尺度对材料进行二维表征, 并衍生出一系列对复杂材料结构在三维尺度上进行全面分析和表征的技术[11]. 透射电子显微镜(transmission electron microscope, TEM)可以提供关于材料内部结构的原子级信息, 例如原子位置、元素组成、化学键合、化学价态, 可以解析单个原子柱, 测量它们的位置, 可以精确到皮米精度[12,13]. 应用透射电子显微学分析材料原子尺度结构信息的原理是利用高能电子自样品上方入射, 与材料相互作用, 发生散射, 在像平面上形成不同的衬度. 电子沿某一特定方向入射至样品, 得到的衬度是沿该入射方向样品内部结构信息的叠加. 因此, 传统TEM二维投影的成像模式不能够直接反映三维尺度上材料内部的结构信息. 精确了解材料中的每个原子的三维位置有助于分析任何复杂化学物质[14]. 发展高空间分辨率和高灵敏度的原子尺度成像和谱学测量方法来理解材料的构性关系是实现精准原子制造的物理基础.
磁性纳米颗粒和纳米薄膜材料被广泛应用于靶向治疗、生物医药、信息存储、大数据等国民经济和国家安全中的各个领域. 伴随着原子制造技术对所合成材料的精准控制, 越来越多的科研工作者和工程师在实际应用中需要在纳米尺度甚至原子尺度上了解这些磁性材料内部不同区域内不同元素的定量磁矩信息. 实现自旋构型与材料结构的高空间分辨协同定量表征, 是理解、预测与调控原子制造磁性材料的物理性能的关键.
高空间分辨磁成像领域的前沿技术是自旋极化扫描隧道显微术[15,16]和磁交换力显微术[17]等扫描探针技术. 它们可实现原子尺度空间分辨测量材料表面原子的净磁矩. 然而这些磁性测量的方法仅对材料的表面信息敏感, 难以测量材料内部或表面不平整的纳米颗粒的磁矩信息. 当关注纳米材料内部磁学性能时, 上述方法就无法应用. 而高空间分辨磁谱学领域的前沿技术是同步辐射光源X射线磁圆二色谱(X-ray magnetic circular dichroism, XMCD), 其原理是磁性材料在左旋圆偏振X射线和右旋圆偏振X射线的照射下, 其X射线吸收谱在磁性元素的电离边处不同, 两个谱图之差即为磁圆二向色谱信号. 应用加和定则可从XMCD谱中定量计算出材料的轨道磁矩和自旋磁矩. XMCD技术具有优异的能量分辨率和信噪比, 当与光电子发射显微术(photoelectron emission microscopy, PEEM)结合时, 其磁衬度的空间分辨率决定于元素特征吸收峰处偏振X射线的束斑尺寸[18], 受限于X射线波长与成像透镜的像差, 目前国际上最好能达到约15 nm[19,20]; 结合X射线叠层成像(X-ray ptychography)技术, 空间分辨率可进一步提高至7 nm[21], 但还是有限. 由于XMCD技术探测深度约为5 nm, 所以可用来测量靠近材料表面的内部信息. 目前像差校正透射电子显微镜已经可以实现原子尺度解析材料的结构与成分信息, 而基于电子显微学的磁性表征技术也相比一般磁性表征技术有着更高的空间分辨率. 因此, 利用电子显微学手段可以实现高空间分辨定量表征材料磁矩, 实现原子尺度结构和性能的协同表征.
原子表征作为原子制造的物理基础之一, 对于深入研究原子水平操控材料物性具有非常重要的意义. 因此, 本文将着重介绍利用电子显微学方法对纳米团簇/颗粒结构在原子尺度进行三维定量表征的诸多方法与实例, 尤其是对于存在无序/有序结构的纳米颗粒、使役条件下纳米团簇/颗粒结构演变, 以及纳米颗粒/晶粒结构-成分-磁性协同定量表征等复杂体系中三维定量表征方面的突破进行总结和归纳.
2
2.1.单一图像强度定量分析
应用像差校正高空间分辨透射电子显微术, 可在入射电子方向上得到材料原子排布的二维投影信息. 基于二维投影像中的强度定量分析, 可获取沿入射电子方向即样品厚度方向上的原子种类与数目, 实现对材料的三维结构的定量表征. 主要的成像模式有两种: 一种是高角环形暗场扫描透射电子显微(high-angle annular dark-field scanning transmission electron microscopy, HAADF STEM)成像[22], 另一种是负球差成像(negative spherical aberration coefficient imaging, NCSI)技术[23].考虑到所观测的原子柱的HAADF STEM图像强度随其原子序数和原子数量的增加在一定范围内呈单调递增的趋势[22], 2008年李自由课题组及合作者[24]利用像差校正扫描透射电子显微成像及图像模拟方法, 对于特定大小的Au纳米团簇的尺寸、三维形状、取向和原子排列进行原子分辨精确表征. 他们通过结合分子动力学模拟、HAADF STEM像定量分析及图像模拟技术, 可以确定软着陆(soft-landing)的Au纳米团簇的尺寸、形状、结构和取向.
李自由课题组及合作者[24]针对特定大小的AuN (N = 309 ± 6)纳米团簇进行验证, 因为309是纳米团簇可能的幻数(magic number)之一. 他们结合Au309纳米颗粒的三张高空间分辨HAADF STEM图像, 由3个不同投影方向观测Au纳米颗粒分别呈五边形、四边形和六边形. 每一个团簇图像衬度的变化反映了不同团簇形貌对应的不同原子柱排列情况. 通过分析一系列特定大小(N = 55—1500原子)的Au纳米团簇HAADF STEM图像积分强度, 可以获得不同尺寸团簇对应的平均原子柱衬度与包含特定原子数N的团簇之间的函数关系, 其积分强度会随着组成团簇原子数目的增加而线性增加. 这种线性关系表明, 在团簇尺寸较小时, 团簇内的原子对HAADF探测器收集到的总的散射电子信号的贡献是均等的. 依据该线性函数关系, 可以将每个原子柱所对应的原子数目计算出来, 并相应地分析出原子团簇的三维原子密度分布和三维模型. 值得注意的是, 由于纳米团簇与电子束极易发生相互作用, 在拍摄同一颗粒的不同照片时, 会发现团簇有时会少量移动或旋转, 有时其结构也会发生变化, 特别是表面原子会发生变化. 但若和时间分辨的成像技术结合, 该方法有潜力提供原子团簇结构变化的动态分析结果, 而这将更有利于理解催化反应过程中所发生的变化. 2012年, Bals课题组和Lievens课题组[25]通过连续采集100帧单帧时间为0.1 s的图像对Ge原子团簇在高能电子束下的动态行为进行定量表征. 该工作虽未达到极高的时间分辨率, 但对半导体纳米团簇的三维动态演变的研究做出了有意义的探索. 总体而言, 从沿单一投影方向的一张HAADF STEM图像可以获得沿深度方向的定量原子数量信息, 并实现原子尺度三维团簇结构定量表征, 且该方法的优势之一是对于团簇稳定性要求不高.
除了HAADF STEM成像技术, 应用NCSI技术同样可以实现从单一投影图像获得沿深度方向的原子数量信息, 从而定量表征材料三维原子构型. 应用透射电子显微术对物体进行高空间分辨成像时会受到透镜系统像差的限制, 尤其是物镜球差系数(spherical aberration coefficient, CS)的影响. 球差校正器的出现[10]使得人们可以调整由物镜和校正器组成的系统的球差系数至一个特定的值, 其范围是从仪器本身未被校正时的球差系数调整至零甚至是负值[26]. 为了尽可能减小衬度离域效应, 研究者常常应用球差校正技术将CS调整到接近于0. 2003年, Urban课题组[23]指出将CS调整为负值, 结合恰当的过焦条件可以得到高信噪比的图像衬度和信号强度, 开创性地提出了NCSI方法, 在SrTiO3和YBa2Cu3O7中直接观察到了散射能力很弱的氧的原子柱. 2014年贾春林等[27]通过对单张MgO晶体的高分辨NCSI图像进行定量拟合, 实现了对平行于电子束方向的原子柱中的二元组分的原子数量的定量分析. 即使对于在晶体表面尤其是顶部或底部表面的O这类散射能力较弱的轻元素, 也可以达到单原子分析精度. 基于NCSI技术获得的图像, 可以实现在平面内x和y方向上对晶体材料的原子柱位置进行皮米精度测量, 同时通过强度的定量分析拟合可以获得z方向上每个原子柱中每个原子的种类、数量和排布, 对原子柱内化学占比实现几个原子百分比精度水平上的定量测量, 从而获得二元MgO晶体的三维原子构型.
综上所述, 无论是基于高空间分辨HAADF STEM成像还是NCSI技术, 都可以对单张二维投影像的强度进行定量分析来解析纳米团簇或纳米材料的三维原子构型.
2
2.2.“大爆炸”原子分辨电子断层成像术
2012年Van Dyck和陈福荣等人[28]发展了“大爆炸”(big bang)原子分辨电子断层成像术, 该方法基于单一投影方向上的系列欠焦高分辨透射电子显微图像和出射波重构技术, 辅以特定的三维重构算法, 可以实现在原子尺度上获得材料三维结构信息. 这一方法的原理是: 电子束经过原子散射后按球面波传播, 若考虑出射波的空间傅里叶变换, 其各个分量的相位随傅里叶分量的平方是线性变化的, 而斜率则是焦距, 即原子至出射波平面的距离, 那么基于出射波重构技术[29-33], 可以获得每一个原子的出射波在重构面上的振幅和相位信息, 从而可以推得该原子的出射波传播到重构面时所经过的距离, 即得到了原子在电子束传播纵深方向上的位置. 应用此方法可以解出双层石墨烯的三维结构, 其重构结果中展现出两层碳原子面的层间距为3.28 ?, 与理论预测的3.35 ?接近[34].基于出射波重构技术的“大爆炸”原子分辨电子断层成像术的另一优点是, 它可以有效地结合低剂量(low dose)电子显微学, 避免破坏材料原有的表面和内部结构. 由于材料的表面以及缺陷往往对电子束辐照比较敏感, 所以如何在图像采集过程中保证材料表面和缺陷结构不发生变化是一个实验上的难点. 常规的高分辨图像采集需要在记录单张图片的过程中提供足够的辐照剂量以满足信噪比的要求, 而出射波重构技术可以将总辐照剂量平均分配到系列欠焦像中每一张图像上[35,36]. 较之于常规的采集方法, 可以有效地降低单位时间内单张图片的辐照剂量, 从而最大程度地避免对材料的损伤. 在TEM成像过程中, 高能电子会与纳米团簇或颗粒相互作用, 导致纳米团簇或颗粒发生转动、重排、迁移、长大或缩小等动态变化[37-40]. “大爆炸”方法原子分辨电子断层成像术是一种使用电子束剂量相对较小的三维成像方法, 可以在观测过程中维持晶体颗粒初始结构不发生显著变化. 该方法不仅可以定量确定每个原子柱中原子数量并达到单原子灵敏度, 而且可以通过定量确定欠焦量即原子柱到公共参考平面的距离来确定原子柱的位置, 沿电子束方向的距离可达到原子级精度. 结合这两方面的信息, 就可以重构出晶体颗粒的三维结构. 特别值得注意的是, 这种重构方法可实现在低电子剂量下采集图像, 并且保持成像过程中材料结构的完整性, 且不会影响原子尺度空间分辨率和单原子灵敏度. 目前使用这种方法采集图像时的电子剂量率已经可以降低至6 e·?–2·s–1的水平[14], 可以用于分析材料中对电子束辐照较敏感的缺陷结构, 比如位错、孪晶界.
2016年陈福荣等[14]用纳米Au样品进行实验验证. 采用物理气相沉积法在Ge上生长Au样品, 生长过程结束后, 再把Ge基底刻蚀掉以得到底部平坦、顶部圆润的自支撑金属样品(图1(a))[14]. 该样品中包含孪晶和位错, 以验证前述提到的方法对于缺陷的分析也是适用的. 图1(a)中所示样品图像是在真空区域采集的, 支撑膜在视场内不可见. 实验过程中采用液氮以维持镜筒内良好的真空环境, 并且实验过程中并未发现有明显气体分子附着在样品表面. 实验条件下的电子计量为46 e·?–2·s–1. 图1(a)为纳米Au样品的同轴全息图, 是利用沿[110]方向以2 nm欠焦步长和CS为零的35张系列欠焦像重构得到的出射波相位. 图1(a)中有孪晶界, 在3个孪晶界交汇处有一个位错核心, 用红色箭头表示. 图1(a)所示相位图中许多原子柱成“甜甜圈”形状是因为原子柱原子数量和离焦量的信息已被卷积. 图1(b)和图1(c)所示的是纳米Au样品的三维表面形貌和原子构型图. 在获取高分辨率TEM图像时, 电子束剂量越高, Au晶体的表面将改变得越快. 从暴露的多个外表面为(111)面可以推断, 这个动态变化过程使得Au晶体所暴露的表面变成了热力学上更加稳定的表面. 这种原子重构是以低表面能γAu(111)为驱动力的. 图1(b)和图1(c)所示的三维模型是从60 s内连续采集的系列欠焦像中解析出的平均晶体结构. 即便电子束剂量已经较低, 但不同图像之间的晶体表面都一直在变化. 若使用更高的电子束剂量会继续增加相位变化的误差, 进一步会影响三维结构解析的可靠性.
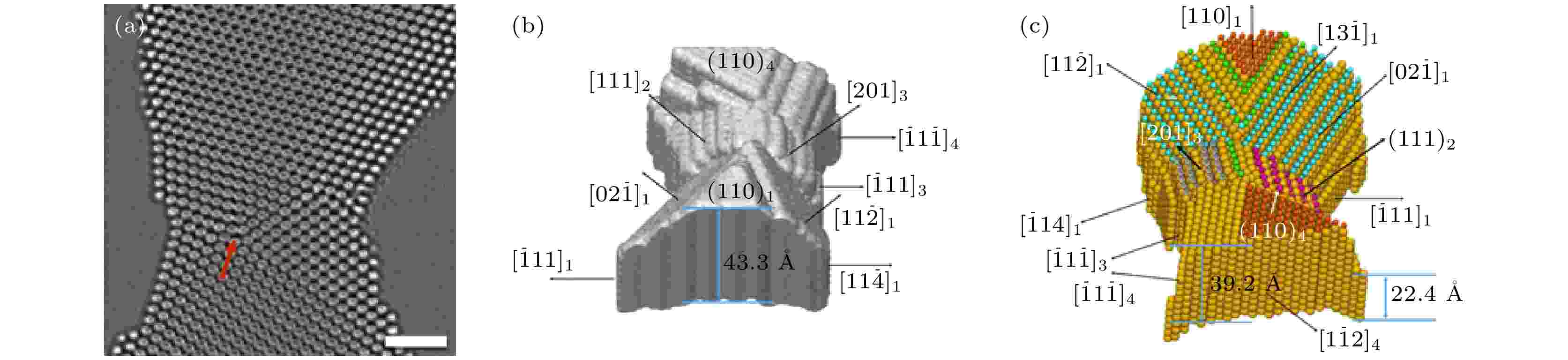图 1 (a)加速电压为300 kV下的纳米金样品同轴全息图, 标尺为1 nm, 图中在3个孪晶的交接处用红色箭头标出了位错; 纳米金样品的三维(b)表面形貌和(c)原子构型, 并用不同的颜色标出不同晶体学取向的表面[14]Figure1. (a) In-line holograms of a nanosized Au sample at the acceleration voltage of 300 kV. Scale bar is 1 nm. It is noteworthy that there are edge-on twin boundaries present in the imaged gold sample. At the intersection of three twin boundaries, a present end-on dislocation marked by the red arrow. (b) Surface morphology and (c) atomic structure views of the nanosized Au sample in three dimensions. The facets with different crystallographic orientations are highlighted with different colors[14].
“大爆炸”原子分辨电子断层成像术通常可以利用在较低电子束剂量下连续采集20张TEM图像重构得到. 因此, 它可以有效控制总电子束剂量和剂量率, 将电子束对样品的损伤控制到很低程度, 可应用于电子束辐照敏感的材料, 如纳米团簇和软物质材料等. 综上所述, 该方法的优点是可以使用低电子束剂量, 减少在图像采集过程中电子束辐照所导致的样品结构变化, 尽可能保持材料结构在电子束辐照下的稳定性, 实现对材料真实三维结构的定量解析, 可用于在原子尺度上分析材料的三维表面结构与缺陷分布.
2
2.3.原子级电子断层成像术
电子断层扫描术是一种三维定量表征纳米团簇和纳米颗粒的常见方法. 经典的电子断层扫描术是通过获取样品不同取向条件下的一系列图像, 利用三维重构算法如背投影算法从系列投影像中分析出样品的三维形貌. 电子断层成像术于1968年首先应用于生物样品, 通过重构来获得其三维结构[41-43]. De Rosier和Klug[41]描述了利用螺旋对称性从单一投影对生物大分子结构进行重构. Hoppe等[42]展示了非对称性物体可以通过足量的投影像重构其三维结构. Hart[43]表明通过多张系列倾转图像重构计算, 可以有效提升所解析的生物结构的信噪比. 随后电子断层扫描术也逐渐应用于材料科学中, 随着透射电镜自动化、新的重构算法和新的断层成像模式的发展, 目前已在各类材料特别是纳米团簇和纳米颗粒中得到广泛使用[11].2005年, Arslan课题组及合作者[44]利用扫描透射电子显微成像模式下Z衬度断层扫描术确定约5 nm大小的包埋于材料内部的量子点纳米颗粒的完整三维尺寸和形状, 且能达到1 nm × 1 nm × 1 nm 的三维空间分辨率. 通过在尽可能大的角度范围内沿着倾转轴每隔相同角度如1°—2°记录图像, 再对系列倾转像进行背投影三维重构, 可以获得量子点的三维形貌. 应用系列倾转三维电子显微学方法可以获得材料的立体形貌信息, 而人们同样关心的是如何从三维的表界面结构中获得与材料性能密切相关的定量结构参数, 比如催化剂粒子表面的低配位原子数所占比例或者氧化物界面的粗糙度. 随后钟虓?课题组和柯小行课题组[45]通过纳米颗粒特定晶体学取向与实空间方向的对应关系建立了三维尺度下晶体学坐标系与实空间坐标系的转换矩阵, 将具有凹陷结构的纳米催化剂颗粒表面定量指标化, 计算得到整个催化剂颗粒表面中仅有68%的表面原子配位数为8, 即完美立方结构晶体表面原子的配位数, 而高达32%的表面原子具有低于8的配位数. 该结果对定量理解低配位表面原子与纳米颗粒的催化反应活性之间的关系奠定了实验基础. 此外钟虓?等[46,47]还实现了定量计算材料内部界面三维尺度化学粗糙度, 从三维界面结构三维定量表征的层次上加深了对氧化物界面互掺杂导致的界面导电机理的理解.
2011年安特卫普大学的Van Aert等[48]结合像差校正扫描透射电子显微术、 统计参数估计理论和离散断层成像术, 通过在两个投影方向上采集并分析HAADF STEM图像, 在原子尺度获得纳米团簇的三维模型. 离散断层成像术是一种可使用较少投影方向比如两个投影方向的图像来实现三维重构的方法, 它需要利用对原子的离散性质及其晶格结构的预先知识在重构迭代过程中做限定来解析三维结构. Van Aert等[48]利用镶嵌在Al基底中的Ag纳米团簇证实了这种方法的可行性, 并定量获得Ag纳米团簇的原子尺度三维构型.
缪建伟课题组十多年来一直致力于发展AET来解析纳米颗粒的原子尺度三维结构信息. 有别于传统TEM电子断层成像术中的等角度采集STEM图像进行重构的方式, 他们用等斜率方式来采集系列倾转环形暗场(annular dark-field, ADF) STEM像, 图2所示即为原子级电子断层成像示意图[49]. 该方法是通过将电子束聚焦在一个小点上并在样品上扫描以形成二维图像, 每个扫描位置的积分信号由ADF探测器记录. 绕倾转轴旋转样品并在不同的倾转角度下测量一系列二维图像. 随后将系列倾转图像经过预处理和对中后, 再通过分数傅里叶变换 (fractional Fourier transform, FrFT) 将系列倾转图像转换为傅里叶片层. 最后用傅里叶迭代算法进行三维重构. 通过三维重构, 可以跟踪和细化单个原子的坐标, 从而生成样品的三维原子模型. 2012年, 缪建伟课题组及合作者结合同步辐射X射线断层扫描中等斜率断层成像术(equally sloped tomography, EST)的迭代重建算法, 发展了AET方法对Au纳米颗粒进行三维重构, 其三维空间分辨率可达到2.4 ?, 且该方法对结晶性没有要求[50]. 2013年, 缪建伟课题组同合作者[51]应用AET方法针对多重孪晶Pt纳米颗粒进行三维成像, 在原子尺度观察到了孪晶界处的三维原子台阶以及刃位错和螺位错的三维核芯结构, 实现了纳米颗粒中三维缺陷构型的原子分辨定量表征. 2015年, 他们同合作者进一步利用AET技术定量测量出钨针尖样品端部每个原子的3D坐标[52]. 应用EST算法将实验采集的62张像差校正ADF STEM像重构并估计出每个原子的三维强度分布, 利用原子追踪方法获得针尖处3769个原子的三维坐标. 原子位置在x、y、z方向上精度分别为10.5、15和5.5 pm, 即在三维空间中的坐标精度约19 pm.
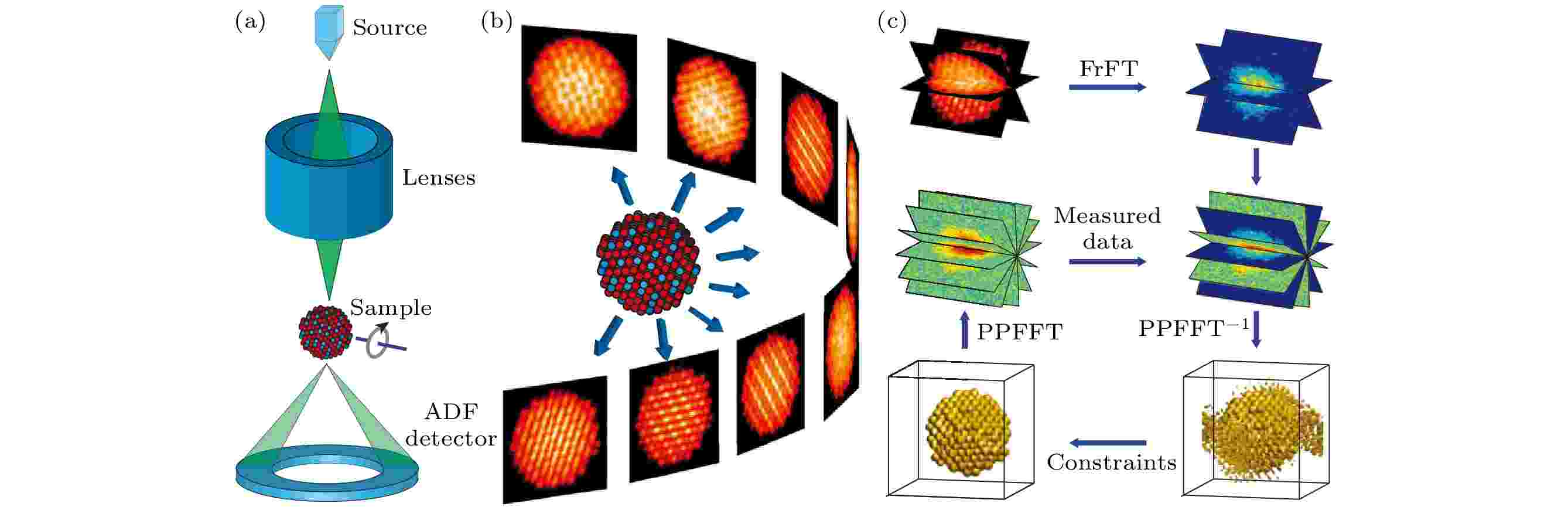图 2 原子级电子断层成像术示意图 (a)电子束聚焦在一个小点上并在样品上扫描以形成二维图像. 每个扫描位置的积分信号由环形暗场(ADF)探测器记录. (b)通过绕倾转轴旋转样品, 并在不同的倾转角度下测量一系列二维图像. (c)经过预处理和对中后, 通过分数傅里叶变换(FrFT)将系列倾转图像转换为傅里叶片层. 三维重构是通过傅里叶迭代算法来计算的. 通过三维重构, 可以跟踪和细化单个原子的坐标, 从而生成样品的三维原子模型[49]Figure2. Schematic layout of atomic electron tomography (AET): (a) An electron beam is focused on a small spot and scanned over a sample to form a 2D image.The integrated signal at each scanning position is recorded by an annular dark-field (ADF) detector. (b) By rotating the sample around a tilt axis, a series of 2D images is measured at different tilt angles. (c) After preprocessing and alignment, the tilt series is inverted to Fourier slices by the fractional Fourier transform (FrFT). A 3D reconstruction is computed by using a Fourier-based iterative algorithm. From the 3D reconstruction, the coordinates of individual atoms are traced and refined to produce the 3D atomic model of the sample[49].
前面这些例子中都是应用AET方法对单组分体系的纳米颗粒进行三维定量分析. 2017年缪建伟课题组及合作者[53]研究了包含6569个Fe和16627个Pt的FePt纳米颗粒, 并确定了每个原子的种类和三维坐标, 并在原子尺度上将化学有序/无序和晶体缺陷与材料性能相关联. 金属间化合物FePt是有序的面心四方(L10)相, 是新一代磁存储介质和永磁铁应用的候选. 刚合成的FePt纳米颗粒是一种无序的面心立方相(A1相). 当在较高温度退火时, 纳米颗粒会依据化学组成的不同由A1相转变为L10或者有序的面心立方(L12相). L10相具有极大的磁晶各向异性能. 应用AET方法, 利用一个通用傅里叶迭代重建算法(a generalized Fourier iterative reconstruction algorithm, GENFIRE)对68张系列倾转像进行三维重构. 针对三维重构结果, 通过原子追踪和分类的方法, 依据Fe和Pt的局部强度分布来确定每一个Pt原子和Fe原子的坐标, 其坐标精确度可达到22 pm. 基于所建立的三维原子模型进行ADF STEM图像模拟, 并与实验图像相对比进行验证. 利用三维结构中所有相的短程有序参数(short-range order parameter, SROP)对FePt的三维化学有序/无序程度进行分类. FePt颗粒可分成几个不同的相的晶粒, 并且所有原子位点上的SROP都可以测量出来. 通过AET方法, 在三维尺度上可以精确确定二元金属间化合物纳米颗粒中原子尺度的有序/无序结构.
综上所述, 本节论述了三类不同的TEM方法, 包括单一图像强度定量分析、“大爆炸”原子分辨电子断层成像术和原子级电子断层成像术, 以及如何定量解析纳米团簇和颗粒在三维空间中的原子坐标、种类和数量, 获得局部区域的原子尺度的晶体学信息和缺陷构型. 这些前沿的TEM表征方法对于深入理解由先进“原子制造”合成技术得到的数目精确可控的纳米团簇和颗粒的三维结构信息非常关键.
2
3.1.加热过程中纳米团簇/颗粒三维结构演变
基于原子制造精准合成的纳米团簇的结构及其动力学行为是由团簇的多维势能面(potential energy surface, PES)决定的. 很多理论计算试图找出纳米体系中特别是纳米团簇中同分异构体的基态结构和能量差异. 了解同分异构体之间的能量差异, 不仅对于材料的原子制造精准设计至关重要, 而且可以理解它们在原位加热过程中如何发生结构演变. 譬如, 如果一个特定结构的同分异构体是不稳定的, 那么在高温下它就会倾向于转变成基态, 从而改变这个系统的特征. 而这些信息与纳米团簇的应用, 比如催化、药物运输、化学传感都是密切相关的.虽然如第2节所述, 目前已经可以实现团簇原子结构的三维定量表征, 但是因为团簇在形成过程中非常容易发生变化, 所以拍摄图像时所捕捉到的很可能是众多团簇同分异构体中的一种, 并且极有可能不是其热力学平衡态. 因此, 需要从实验的角度得到不同温度下团簇的三维原子构型及其PES的关键参数. 因为Au团簇在催化领域的普遍应用[54], 所以受到很多****的关注和研究. 2018年Palmer课题组及合作者[55]应用像差校正扫描透射电子显微术针对软着陆在非晶氮化硅上的Au561团簇的同分异构体在不同温度下的结构进行定量原位研究.
图3所示为Au561团簇的HAADF STEM像及其对应的多片层法模拟像[55]. 图3(a)和图3(b)分别对应在20 ℃下采集的面心立方结构和十面体构型的团簇. 图3(c)和图3(d)分别对应在500 ℃下采集的fcc和同轴十面体构型的团簇. 通过统计分析在不同温度下亚稳态Ino十面体构型与稳态fcc构型的团簇数量分布, 可定量获得Au561团簇的PES关键参数, 即Dh构型比fcc构型的能量仅高出(0.040 ± 0.020) eV. 图3中HAADF STEM像提供的是在不同温度下团簇的二维结构信息. 更进一步, 2019年Palmer课题组及合作者[56]利用球差校正电镜原位观察碳膜上直径在2—5 nm的Au纳米团簇的原子尺度表面熔化过程. 实验发现, 在较高温度下, Au纳米颗粒会形成内部液体芯-固体壳的结构. 团簇表面熔化温度显示出与尺寸相关的熔点抑制效应, 且团簇内部的熔化温度比依据现存的自由团簇模型预测的熔化温度要高.
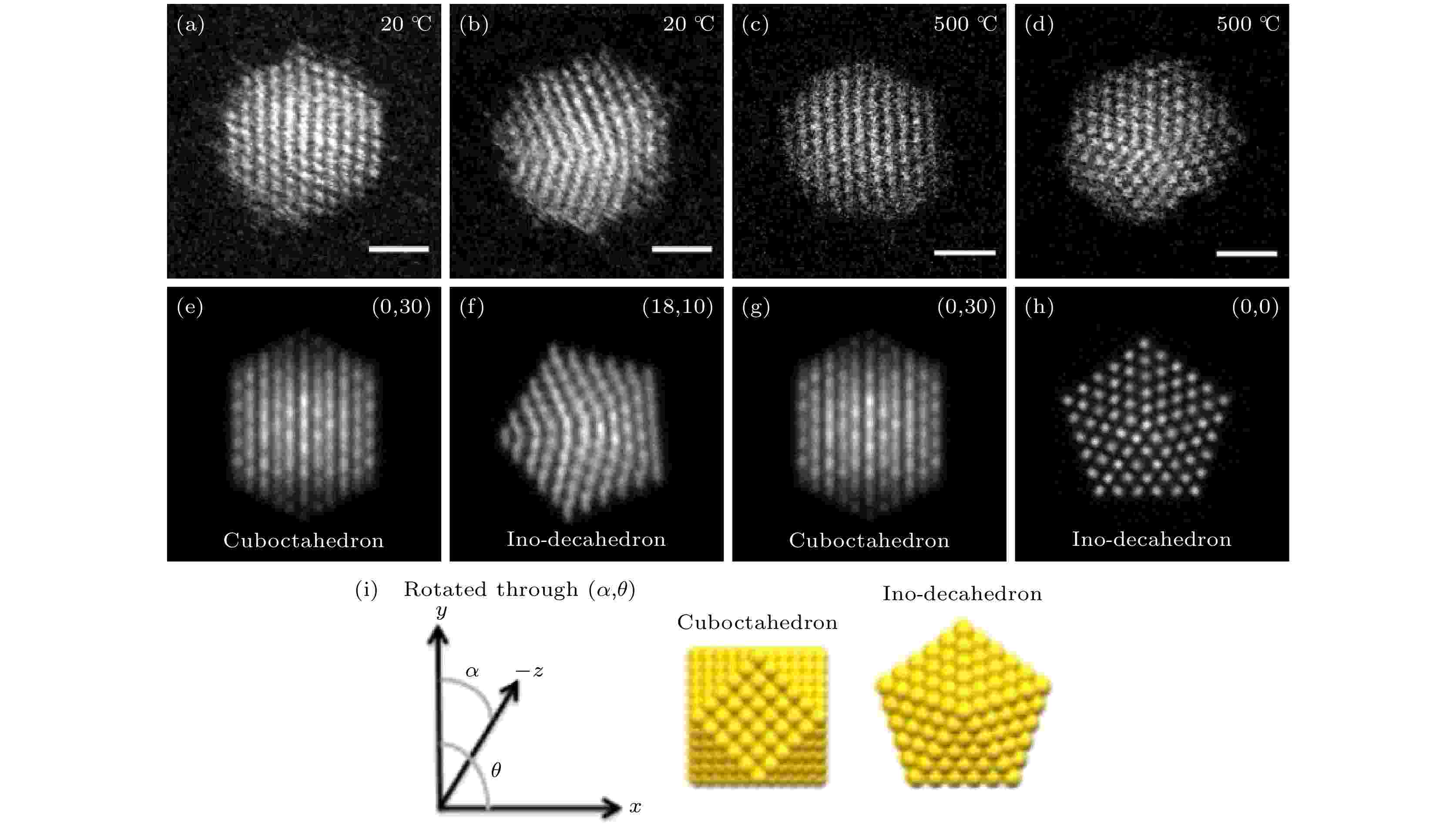图 3 20 ℃和500 ℃下的Au561团簇的高角环形暗场扫描透射显微(HAADF STEM)图像 (a)—(d) Au561团簇HAADF STEM图像和(e)—(h)对应的不同带轴下立方八面体和Ino十面体的多片层法模拟像; (a), (b)在20 ℃下记录的实验像; (c), (d)在500 ℃下记录的实验像; (i)立方八面体和Ino十面体的几何构型及其旋转角度示意[55]Figure3. High-angle annular dark-field scanning transmission electron microscopy (HAADF STEM) images of Au561 clusters at 20 ℃ and 500 ℃: (a)–(d) HAADF STEM images of Au561 clusters and (e)–(h) matching multi-slice electron scattering simulations of the cuboctahedron and Ino-decahedron at different orientations; (a), (b) experimental images recorded at 20 ℃; (c), (d) images recorded at 500 ℃; (i) rotation angle of the cuboctahedron and Ino-decahedron geometries[55].
2019年缪建伟课题组及合作者[57]应用AET研究了单个FePt纳米颗粒的原子尺度三维构型随加热退火时间增加而产生的结构演变, 实现四维尺度表征, 即空间的3个维度与时间维度. 为了得到同一FePt纳米颗粒早期形核过程的四维模型, 在形核过程中的不同退火时间点获取系列倾转HAADF STEM像, 通过AET方法进行重构、原子追踪、原子鉴定和优化等程序[53], 确定同一颗粒在不同加热时间点所对应的三维原子坐标和原子种类. FePt颗粒在退火9, 16和26分钟的3个三维原子构型的原子总数目在退火过程中发生细微的改变, 这是由于在退火过程中发生了原子的扩散. 退火时间在9和16分钟时原子数目十分相近, 但是从16分钟到26分钟时发生了变化. 表面和亚表面上的一部分原子重组并形成L10相, 但是纳米颗粒富Pt的核心没有发生变化. 这个现象可以由退火过程中空位诱导原子扩散来解释, 因为从能量角度在表面和界面产生空位比在颗粒核心处产生空位容易得多. 退火后的FePt颗粒由A1, L12和L10三相组成, 根据短程有序参数对它们进行定量分析, 发现L10相、Fe富集的A1相、Pt富集的A1相、Fe富集的L12相和Pt富集的L12相等在这一纳米颗粒中形核, 其中L10相的比例相对最高. 每一个相在形核早期有一至多个最大有序度的核心, 即形核位点. 形核位点在颗粒中的三维分布和退火时间是密切关联的. 当退火16和26分钟时, 大部分形核点位于颗粒表面、边界或者角落. 而当退火9分钟时, 在颗粒亚表面存在更多形核点, 其形核相对较大并延伸至纳米颗粒内部. 在加热退火过程中颗粒的三维原子构型演变证实了形核过程是异质形核, 比均质形核在能量上更低. 考虑到L10 相FePt纳米颗粒在技术上有很好的应用前景, 把加热退火过程中颗粒的三维构型扩充到其材料数据库, 将为原子尺度上建立四维尺度结构演变提供直接的实验证据, 这将加深对于通过原子制造合成的作为磁存储媒介和催化剂的纳米颗粒构性关系的理解.
2
3.2.气相反应中纳米颗粒三维结构演变
原子制造精准合成的纳米团簇或颗粒在催化领域有广阔的应用前景. 而仅仅在静态真空条件下获得纳米颗粒的三维构型不足以理解其在高温和不同反应气氛下的结构演变和性质变化. 很多原位TEM研究工作表明纳米颗粒在氧化-还原反应过程中会发生形貌变化, 大都是纳米颗粒的二维投影像[58]. 在催化过程对纳米颗粒的结构演变和表面分布进行三维结构实验表征非常具有挑战性, 也是未来对理解和调控纳米催化材料结构性能的重要表征工具. 因此, 为获取优异性能需要在原位加热气氛条件下针对精确设计原子制造的纳米催化材料进行三维构型的定量表征.2019年, Bals课题组及合作者[59]实现了在300 ℃不同气氛下纳米颗粒原子尺度的三维定量表征. Pt纳米颗粒是常见的负载型催化剂材料, 其催化活性强烈地受到其三维表面构型、接触界面以及反应环境的影响. 他们以Pt纳米颗粒为例, 研究其在300 ℃下H2和O2两种不同气氛的反应过程中的三维构型演变. 因此, 可以在不同原位气氛条件下以原子分辨率量化Pt纳米颗粒表面上刻面的重新排布(refacet). 在H2气氛中观察到{100}和{111}刻面占主导的整个颗粒形貌, 轮廓较为清晰; 在O2气氛中{100}和{111}刻面数量急剧减小, 高指数晶面数目显著增加, 使得整个颗粒形貌变得接近圆球. 虽然在2.1节中阐明用较高信噪比的HAADF STEM图像可以直接得到纳米颗粒中每个原子柱的原子数目, 但是在气相环境中这是不可行的. 主要原因之一是进行原位气氛实验时Pt纳米颗粒需要放至两层厚度约为30 nm的非晶氮化硅窗口中间密封起来, 而这两层氮化硅的存在大大降低了HAADF STEM图像质量, 且在气体存在时这种影响更为显著. 另一原因是扫描畸变, 这种畸变会降低定量分析的可靠度. 该研究中应用基于深度卷积神经网络的方法, 通过神经网络训练对图片进行畸变的探测和校正, 然后再对校正过的图像进行每个原子柱原子数目的定量分析. 根据这个结果, 可以得到平行于电子束的方向上原子柱上的原子组成. 通过分子动力学模拟, 对上述初步的三维模型进行弛豫, 就可以得到相应的纳米颗粒的三维模型. 图4(a)所示为基于上述方法获得的真空中纳米颗粒的三维原子构型. 原位实验均在300 ℃的条件下进行, 而图4(b)—(e)所示是相似的纳米颗粒在不同的气氛条件下的三维构型, 图4(b)是先通入1 bar (1 bar = 105 Pa)气压含有5% H2的Ar气时, 图4(c)是切换并通入1 bar气压O2气氛时, 图4(d)是再切换并通入1 bar气压含有5% H2的Ar气时, 图4(e)是最终切换并通入1 bar气压O2气氛时, 这与氧化还原反应中常规反应所使用的典型条件是一致的. 在不同气体的反应阶段, 结构中的平均总原子数目基本保持不变, 误差为0.9%. 这表明反应过程中没有发生显著的原子数量减少. 从图4(a)—(e)的三维原子构型的变化可以明显看出气氛会影响纳米颗粒的表面形貌. 在真空中纳米颗粒的外貌是截角立方体, 在H2气氛中是截角八面体, 在O2气氛中形貌变得接近圆球. 通过对比真空中升温至300 ℃前后的颗粒形状, 发现图4中的三维表面构型演变是由气氛变化而非温度变化引起的. 随着对H2或O2的吸附, 颗粒表面能会相应发生变化, 导致某些晶面更加稳定, 进而影响颗粒表面结构. 在反应气氛下定量解析纳米颗粒三维表面构型变化对于理解原位气相催化过程中催化剂的结构演变、催化活性与反应机理非常重要.
图 4 Pt纳米颗粒在不同条件下的三维结构演变形貌 (a) 在真空中; (b), (d) 300 ℃下通入含5% H2的Ar气; (c), (e) 300 ℃下通入O2; 颗粒表面上不同晶面族的原子用不同颜色表示, 蓝色对应{100}, 粉色对应{110}, 紫色对应{111}, 灰色对应高指数面[59]Figure4. Three dimensional morphology of structural evolution of Pt nanoparticles under different environmental conditions: (a) In vacuum; (b), (d) in 5% H2 in Ar at 300 °C; (c), (e) in O2 at 300 °C. The atoms are presented in different colors, according to the type of surface facet: blue = {100}, pink = {110}, purple = {111}, gray = higher index[59].
2
3.3.液相环境中纳米颗粒三维结构演变
在液相环境中纳米颗粒三维结构、生长机制与相互作用一直是人们较为关心的课题. 了解胶体纳米晶体生长机制对于合成具有特定物性的纳米团簇或颗粒至关重要. 精确掌握纳米颗粒在不同配体液相环境中的三维结构动态演变对于调控纳米颗粒生长并实现更好的催化性能与表面活性具有重要意义. 1944年Abrams和McBain[60]就设计了用于液相电子显微学的封闭样品腔. 1970年Swift和Brown[61]在TEM中实验获得了液态环境下微生物的图像. 近十多年来, 随着微机电系统技术应用于TEM样品杆和样品托设计, 使得液体可以封闭在微米尺度的液体腔中而不破坏真空系统[62], 这极大程度地促进了液相电子显微学的发展, 实现了在TEM中观察纳米颗粒在液相中的结构和行为.2009年Dahmen课题组和Alivisatos课题组[62]使用原位液相透射电子显微镜, 表明铂纳米颗粒可以通过溶液中的单体附着或颗粒碰撞融合而生长. 通过这两个过程的组合, 初始较宽泛的颗粒尺寸分布可以自发地缩小为几乎单分散的尺寸分布. 他们提出胶体纳米晶体根据其大小和形态依赖内部能量会采取不同的生长途径. 这项研究表明液相环境中颗粒间的相互作用起着重要作用, 而传统的单分散纳米晶体生长的经典模型假定为离散成核阶段, 然后是单体附着生长, 但忽略了粒子与粒子的相互作用. 2012年Alivisatos课题组及合作者[63]进一步利用原位液相电子显微术研究了纳米颗粒在较低扩散极限情况下实时形成阵列结构的过程. 同年, Lee课题组、Zettl课题组和Alivisatos课题组[64]发展了一种基于石墨烯液体腔的原位液相电子显微成像方法, 其原理是将所观察液体封闭在石墨烯层间形成的液体腔中. 常规TEM液体腔壁由至少10 nm厚的非晶氮化硅薄膜构成, 而石墨烯液体腔的腔壁由石墨烯构成, 腔壁厚度超薄、原子序数低、由腔壁所引入的背景强度会极大程度地降低, 非常有利于实现液体中材料的原子级分辨率成像. 他们在实验中利用石墨烯液体腔来探索胶体Pt纳米颗粒的生长机制, 在电子束辐射下仍可实现接近现实条件的液体环境, 原子分辨率成像能够直接观测纳米颗粒生长过程中的关键步骤. 2014年郑海梅课题组及合作者[65]应用液相透射电子显微术方法实现在液相环境中Pt纳米颗粒生长的动态高空间分辨成像. 研究表明, 除{100}面外所有低指数面会持续生长直至形成纳米立方体且增长率接近, 而{100}面却停止增长. 理论计算发现{100}面上配体的低移动性是{100}面生长受阻的主要原因, 这揭示了液相中纳米颗粒形貌控制机制.
上述液相电子显微学工作中获得的纳米颗粒结构信息是二维投影信息. 2015年Alivisatos课题组[66]综合了石墨烯液体腔、高分辨率透射电子显微术、直接电子探测器和应用于生物样品的单粒子三维重构算法发展了石墨烯液体腔电子显微学纳米颗粒结构解析(structure identification of nanoparticles by graphene liquid cell electron microscopy, SINGLE)方法, 实现在液体环境中解析Pt纳米颗粒的三维结构并接近原子分辨率. 从单个纳米颗粒在溶液中自由旋转时沿不同投影方向的一系列图像中, 应用单粒子三维重构算法得到三维结构. 因此, 该方法可以分析在溶液中合成的每一个独立的纳米颗粒, 并在原子尺度上观测其三维结构的异同. 2020年Ercius课题组、Elmlund课题组和Park课题组[67]通过SINGLE方法研究了六种不同尺寸的Pt纳米颗粒, 以4号纳米颗粒为例, 图5给出了该颗粒的三维原子构型、密度分布、沿着
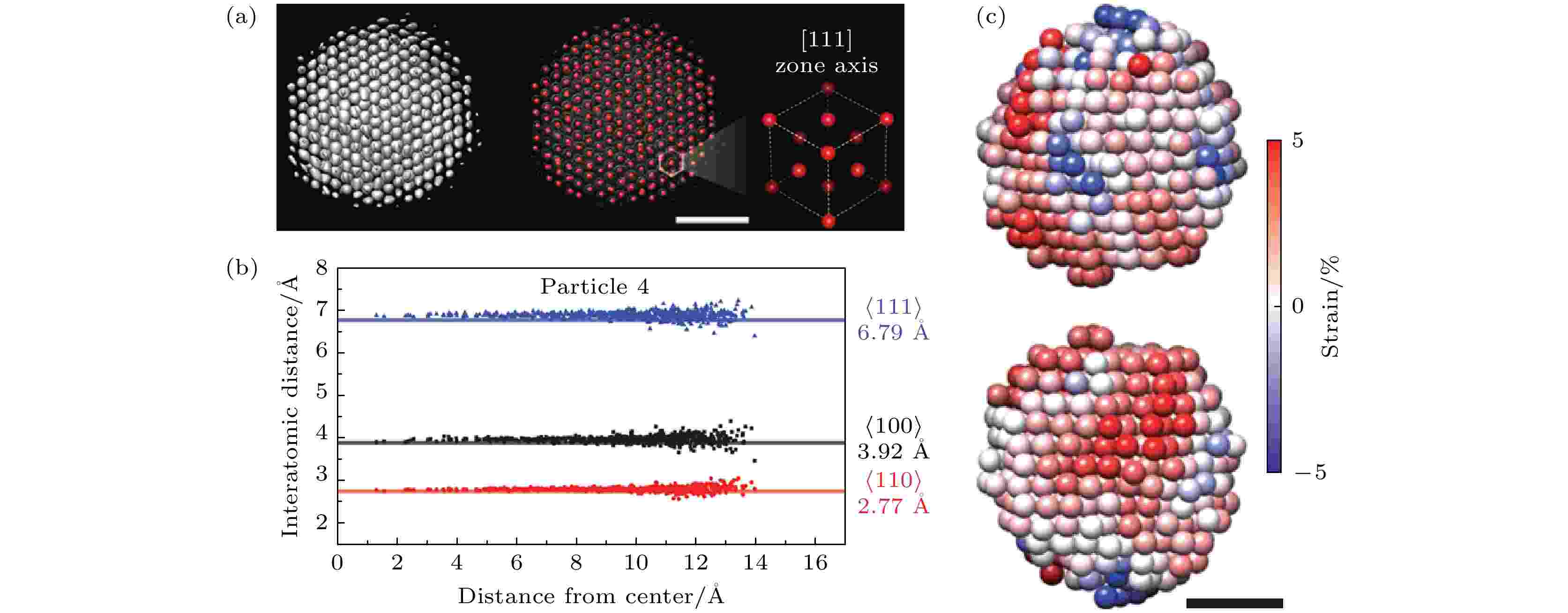图 5 使用原子级电子断层成像术表征FePt颗粒中四维原子运动 (a)—(c) FePt纳米颗粒在累计退火时间为9、6和26分钟时的三维原子模型(Fe是红色、Pt是蓝色); (d)—(f) 在三种不同退火时间下富Pt的核心保持不变, 模型下方的浅灰色和深灰色投影分别显示了整个纳米颗粒及其核心; (g)—(i) 在3个退火时间沿 [010] 方向相同的纳米颗粒内部原子构型(Fe原子为红色, Pt原子为蓝色), 其中表面原子和亚表面的一小部分原子重新排列形成L10相(由椭圆形标出), 标尺为1 nm; (j)—(l) 颗粒形核点在退火时间为9、16和26分钟的分布, 其中点的颜色越淡代表其离表面越近, 颜色越暗表明其越靠近内部, 
Figure5. Capturing four-dimensional atomic motion with atomic electron tomography. (a)–(c) Three-dimensional atomic models (Fe in red and Pt in blue) of an FePt nanoparticle with an accumulated annealing time of 9, 16 and 26 min, respectively. (d)–(f) The Pt-rich core of the nanoparticle (shown here) remained the same for the three annealing times. The light and dark grey projections below the models show the whole nanoparticle and the core, respectively. (g)–(i) The same internal atomic layer of the nanoparticle along the [010] direction at the three annealing times (Fe in red and Pt in blue), where a fraction of the surface and subsurface atoms had rearranged to form L10 phase (ellipses). Scale bar is 1 nm. (j)–(l) Distribution of the nucleation sites (dots) in particle with an accumulated annealing time of 9, 16 and 26 min, respectively, where the lighter colored dots are closer to the front side and the darker dots are closer to the back side of the nanoparticle. The
此外, 值得注意的是TEM中高能电子与液体溶剂(比如水)会产生直接作用, 比如水的解离, 从而有可能导致TEM原位观测纳米颗粒在液相的行为会与在未经电子束辐照下的情形大为不同. 2014年, Sutter等[68]利用液相电子显微术观察Ag纳米颗粒和Pt离子水溶液之间的Galvanic还原反应, 原位TEM观察Ag纳米颗粒转变为空心Ag-Pt纳米颗粒的动态过程. 对比未经电子束辐照的实验, 在电子束辐照下反应速率要提高很多. 2017年陈福荣课题组和Kundu课题组及合作者[69]发现电子束辐照含有有机分子的水溶液会产生大量H2纳米气泡. 随后陈福荣、隋曼龄课题组及合作者[70]又发现原本不溶于水的CeO2纳米颗粒在电子束辐照的辅助下可以溶于水溶液. 因此, 需要特别注意电子束对液相中纳米颗粒结构和行为的影响, 优化实验条件控制电子束剂量[71], 并与非电子束辐照条件下的情形进行系统比对, 才能更准确地理解纳米颗粒在液相中化学反应与结构演变规律.
基于透射电子显微学的磁性谱学表征手段为电子能量损失磁手性二色谱(energy-loss magnetic chiral dichroism), 也称电子磁圆二色谱(electron magnetic circular dichroism, EMCD)[72]. EMCD技术的基本物理原理与XMCD技术相类似. XMCD中左旋圆偏振X射线与右旋圆偏振X射线的偏振矢量表达式分别为
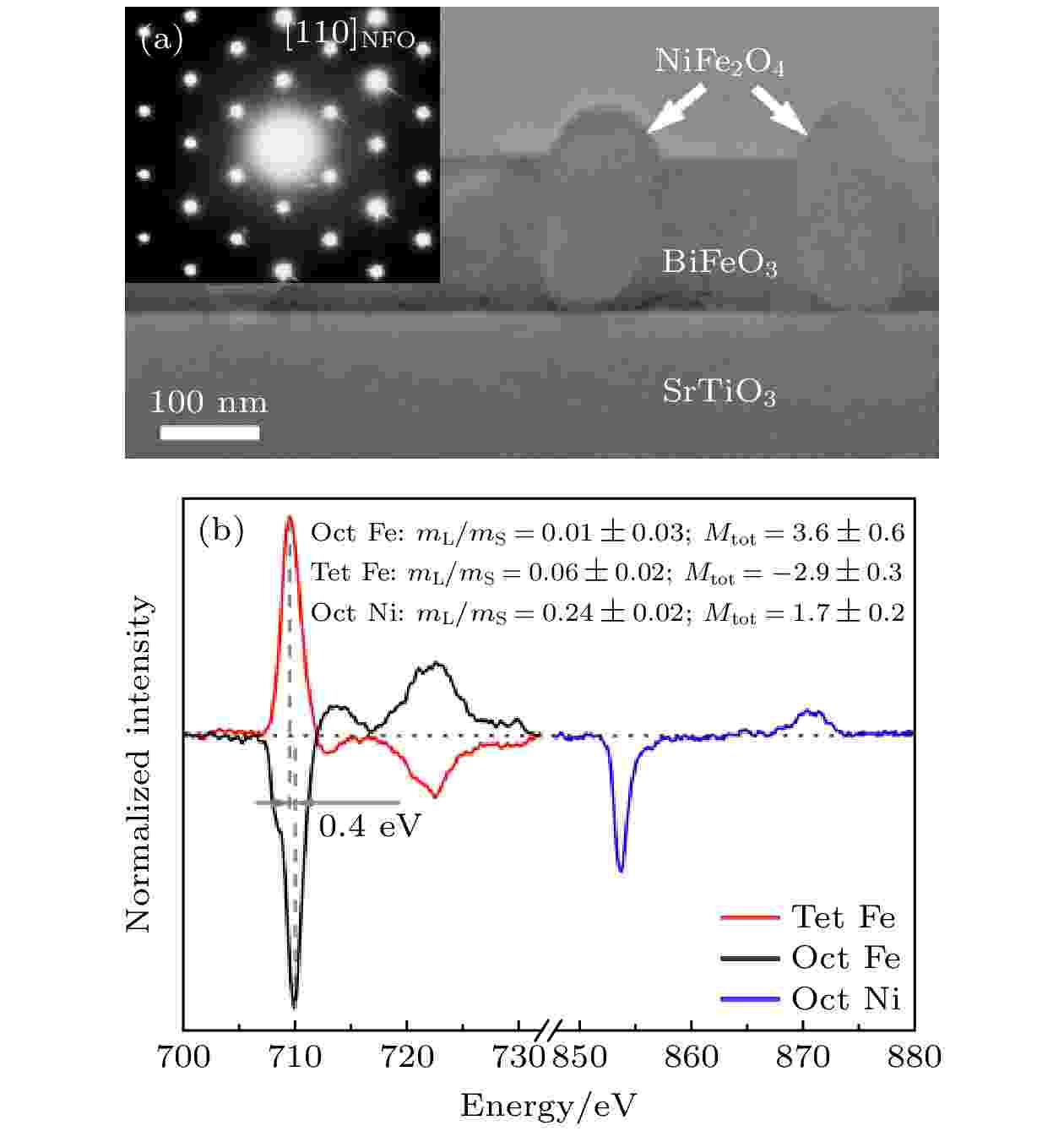图 6 纳米尺度协同测量单一NiFe2O4纳米晶粒的晶体结构、元素成分与定量磁矩 (a) 复合薄膜截面样品的透射电子显微(TEM)图像和选区衍射 (SAED) 花样, 在SrTiO3基底上异质外延生长的钙钛矿BiFeO3纳米晶粒和尖晶石NiFe2O4纳米晶粒的截面样品的低倍TEM图像, NiFe2O4纳米晶粒柱在[110]带轴下的单晶SAED花样; (b) 八面体Fe (Oct Fe)、八面体Ni (Oct Ni)、四面体Fe (Tet Fe)的占位分辨的磁圆二色谱; Oct Fe和Tet Fe之间的0.4 eV的化学位移差别反映了不同占位对称性上的差异, mL/mS为轨道自旋磁矩比, MOct, Fe, MTet, Fe和MOct, Ni 是Oct Fe, Tet Fe和Oct Ni的总磁矩, 单位为μB/atom[73]Figure6. Nanoscale co-located measurement of crystallographic structure, elemental composition and quantitative magnetic moments of single NiFe2O4 nanograin: (a) Transmission electron microscopy (TEM) image and selected area electron diffraction (SAED) patterns of cross-sectional composite films. Low-magnification TEM image for cross-section sample of hetero-epitaxial composite thin films formed by perovskite BiFeO3 and spinel NiFe2O4 nanograins on SrTiO3 substrates. The single-crystalline SAED patterns are acquired from one NiFe2O4 nanograin along the [110] zone axis. (b) Site-specific magnetic circular dichroism spectra for Fe atoms at octahedral sites (Oct Fe), Ni atoms at octahedral sites (Oct Ni) and Fe atoms at tetrahedral sites (Tet Fe). A chemical shift of 0.4 eV between oct Fe peak and Tet Fe peak reveals the chemical shift for different site symmetries. mL/mS refers to the orbital to spin magnetic moment ratio. MOct, Fe, MTet, Fe and MOct, Ni are the total magnetic moments (the sum of spin and orbital magnetic moments) of Oct Fe, Tet Fe and Oct Ni in the units of μB/atom[73].
随着对EMCD理论的深入理解以及实验方法的进步, 近年来人们在不断探 索提高EMCD空间分辨率[79-81]的方法. 在STEM模式下EMCD的空间分辨率主要决定于电子束斑尺寸. 然而随电子束斑减小, 会聚角增大, 电子磁圆二色谱的信噪比急剧降低, 因此在会聚束照射模式下应用大会聚角的亚埃尺度束斑采集电子磁圆二色谱把空间分辨率推进到原子尺度非常困难. 国际材料学界长期关注如何实现在原子尺度上测量材料的磁矩, 但这一方法与技术始终难以突破.
2018年钟虓?课题组及合作者[82,83]基于前期的实验积累, 提出在平行束照射模式下利用色差校正技术在能量色散平面实现实空间和能量损失空间原子尺度协同成像(图7), 发展了原子面分辨电子磁圆二色谱技术. 以双钙钛矿结构的Sr2FeMoO6为模型材料验证了实验设计, 建立了一套普适的具有原子面分辨的磁圆二色谱测量方法(图7), 实现了在原子尺度下对材料的原子构型、化学成分与自旋排布的协同表征, 并定量测量原子尺度的轨道自旋磁矩比. 通过原子面分辨电子磁圆二色谱技术可实现材料内部原子尺度的自旋探测, 结合原子尺度的HAADF STEM像、能量色散X射线谱和电子能量损失谱, 可将材料的轨道自旋磁矩分布磁信息与其原子构型、元素组成、化学键合等结构信息在原子层次上一一对应, 这将有助于在原子尺度真正理解原子制造材料功能基元的物理起源.
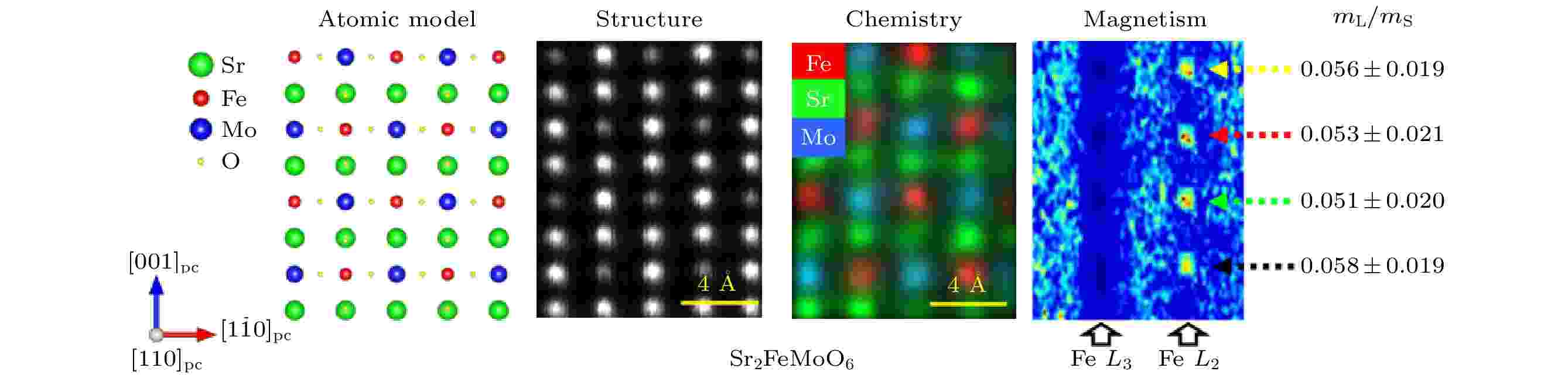图 7 原子尺度协同测量Sr2FeMoO6的晶体结构、元素成分与定量磁矩(mL/mS为轨道自旋磁矩比)[82,83]Figure7. Atomic scale co-located measurement of crystal structure, elemental composition and quantitative magnetic moment of Sr2FeMoO6. mL/mS refers to the orbital to spin magnetic moment ratio[82,83].
电子全息是TEM中另外一种常见的高空间分辨磁成像技术, 基于电子波之间的相互干涉. 干涉产生条纹的相位和振幅受到局域结构的调控. 尽管已经有很多形式的电子全息, TEM中最常用的还是离轴电子全息技术, 它可以记录相位的信息. 电子波的相位与材料电势和磁势之间的关系可以表示为
2016年Alemeida等[84]利用高空间分辨离轴电子全息术研究单个Fe3O4纳米颗粒的热磁行为, 即在原位加热条件下定量观测纳米颗粒内剩余磁化强度分布变化. 他们研究了在温度在20—550 ℃(仅略微低于居里温度)范围内20个Fe3O4纳米颗粒的磁感应强度分布的变化过程. 图8(a)中的明场像给出了长对角轴约为150 nm的菱形Fe3O4纳米颗粒的形貌及其对应的单晶电子衍射图. 图8(b)所示是在室温20 ℃下经饱和磁化后的剩余磁感应强度分布图, 是一个典型的伪单畴态. 图8(c)是从室温加热到400 ℃后其剩余磁感应强度分布图, 和室温下的结果非常相似, 因此推测从室温加热到400 ℃磁化强度的大小和方向几乎未发生明显改变并且十分稳定. 然而伪单畴态在升温至500 ℃时发生显著变化, 如图8(d)所示, 相位等高磁轮廓线沿长对角轴缩小且对齐, 并弯曲远离颗粒顶部和底部的该轴. 室温和400 ℃下具有涡旋结构的磁轮廓线密度比500 ℃下的磁轮廓线密度要低. 因此认为室温下大部分磁化分量是朝面外方向, 而在500 ℃时转到面内方向. 温度进一步升高至550 ℃时会导致相位等高磁轮廓线的进一步扩大, 与长对角轴更紧密地对齐. 降温至500 ℃时, 磁感应强度分布回到图8(d)中的状态; 继续降温至400 ℃时, 恢复伪单畴态, 磁感应强度分布接近于图8(c)中的状态; 继续冷却至20 ℃时, 磁感应强度分布与未加热前的初始态非常相似. 随后在一个较大的纳米颗粒中进行了同样的升降温原位实验. 较之于小颗粒, 大颗粒的伪单畴热稳状态更稳定, 一直保持涡旋状态和杂散场直到550 ℃. 较大纳米颗粒热稳性的提高是因为颗粒体积增大, 在可能的伪单畴状态间具有更高的能量壁垒. 而纳米颗粒尺寸对于剩余磁化强度的影响在400 ℃以下时都非常小, 只有畴结构的强度受到影响. 而这一系列电子全息实验结果表明在变温过程中单个纳米颗粒的结构与磁性可以在纳米尺度协同表征.
图 8 原位观测伪单畴的Fe3O4纳米颗粒的热磁行为 (a) 长对角轴的长度约为 150 nm的Fe3O4纳米颗粒的明场像以及对应的电子衍射花样; (b)—(h)依次在(b) 20 °C以及原位反应过程中加热到(c) 400 °C, (d) 500 °C和(e) 550 °C, 以及随后降温到 (f) 500 °C, (g) 400 °C和(h) 20 °C时记录的全息图重构出的磁感应强度分布图(标有FD字样的红色箭头代表诱导产生剩磁的外加饱和磁场的面内分量方向, 蓝色箭头表示为计算平均内势能而施加的额外的外磁场的方向); 所有磁感应强度分布图的等高磁轮廓线间距为 0.098 rad, 磁化方向使用箭头显示, 如色轮中所示; v代表漩涡的中心[84]Figure8. Visualization of the thermomagnetic behavior of a small pseudo-single-domain Fe3O4 grain. (a) Bright-field transmission electron microscopy image of the individual Fe3O4 grain (about 150 nm in length across its long-diagonal axis), with associated electron diffraction pattern inset. (b)–(h) Magnetic induction maps reconstructed from holograms taken at (b) 20 °C (with the red arrow, labeled FD, showing the direction of the in-plane component of the applied saturating field to induce magnetic remanence, whereas the blue arrow shows the additional direction the field was applied for the calculation of the mean inner potential); during in situ heating to (c) 400 °C, (d) 500 °C, and (e) 550 °C; upon subsequent cooling to (f) 500 °C, (g) 400 °C, and (h) 20 °C. The contour spacing is 0.098 rad for all the magnetic induction maps, and the magnetization direction is shown using arrows, as depicted in the color wheel. v, center of the vortex[84].
此外, Alemeida等[85]结合环境透射电子显微镜和离轴电子全息术, 定量观测了单个Fe3O4纳米颗粒在高温氧化转变为γ-Fe2O3后晶体结构、元素价态、配位环境和磁性能的变化, 来理解氧化过程如何影响磁存储方向和磁化强度, 即化学剩余磁化态. 图9(a)所示为一个直径约为200 nm表面光滑的Fe3O4纳米颗粒的TEM明场像与相应的SAED图. 图9(b)所示是同一Fe3O4颗粒在700 ℃和9 mbar的O2氛围中曝光8小时的TEM明场像. 样品表面的退化非常明显, 相应的SAED花样显示仍是单相结构并出现了一些由于退火引起的纳米颗粒轻微扭转所导致的衍射增强. 图9(e)对比了氧化处理前后的Fe的EELS近边精细结构. 在高温氧化后纳米颗粒的EELS谱中L3边出现小的边前峰且L2边处出现较明显劈裂, 如红色箭头所示, 显示了γ-Fe2O3的特征, 而原始样品的L2边具有典型的混合价态占位的化合物的特征, 三处具有不同强度的小特征分别对应Fe3O4中的四面体Fe3+, 八面体Fe2+和八面体Fe3+, 如黑色箭头所示. 图9(c)是原始样品的磁感应强度分布图, 可以看出, 从表面到颗粒中心均匀间隔的相位等高磁轮廓线逆时针方向流动(用箭头表示), 呈现出涡流状态的特征. 图9(d)是高温氧化后纳米颗粒的磁感应强度分布图, 其间距变大, 尤其是在靠近颗粒边缘的位置处, 且仍以逆时针方向流动. 图9(f)定量表征了随着Fe3O4氧化成γ-Fe2O3, 纳米颗粒的总剩余磁化强度相应降低. 用同样的方法, 他们也证实了高温氧化过程会改变单个纳米颗粒磁化方向. 由此可见, 透射电子显微镜可以实现在高温氧化前后单个伪单畴Fe3O4纳米颗粒晶体结构、电子结构与磁性的纳米尺度协同表征, 可用于定量评估颗粒氧化程度对化学剩余磁化态的影响, 直接建立颗粒氧化态与其磁记录保真程度之间的相互关系.
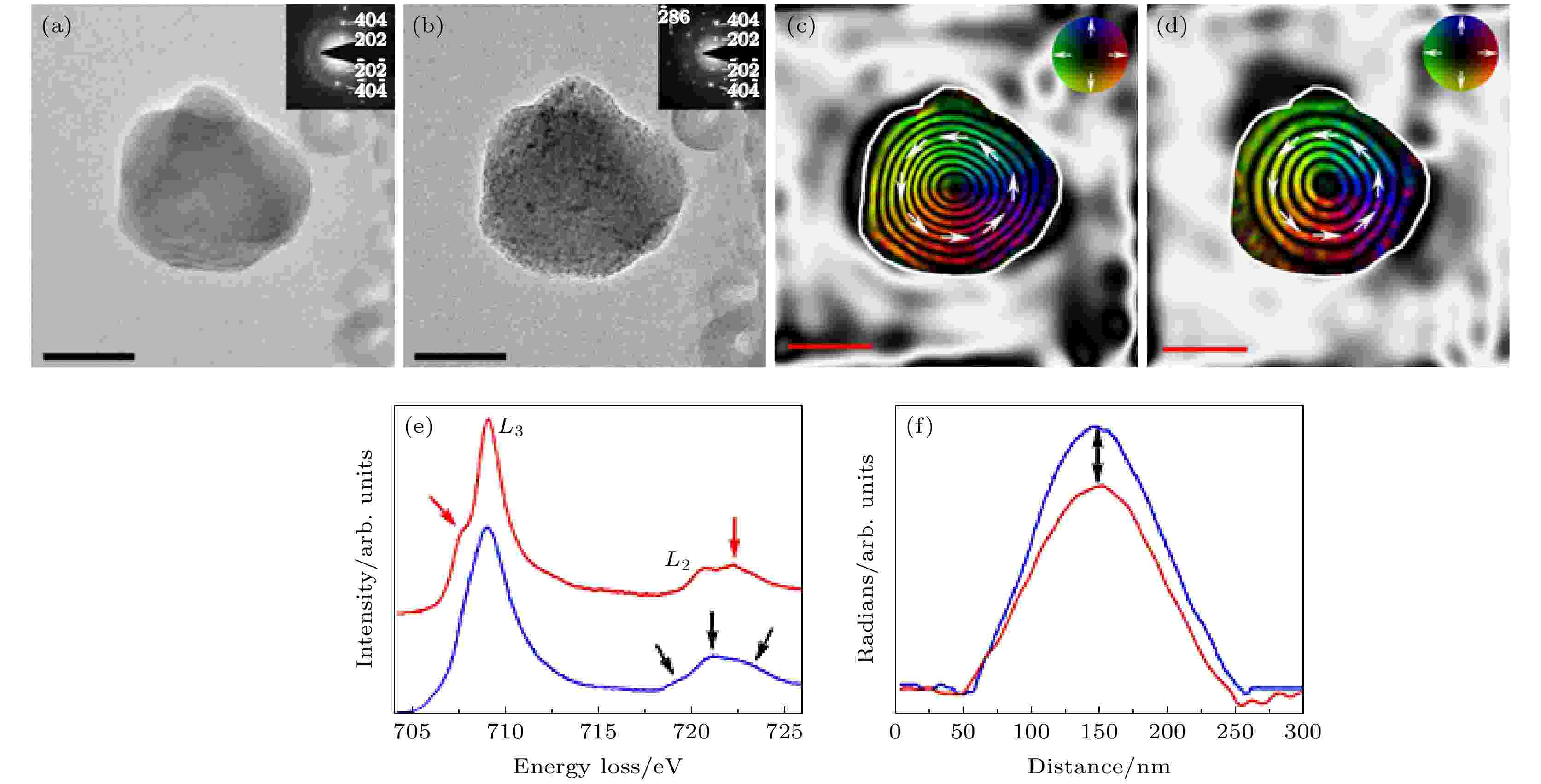图 9 原位观测氧化态对等轴Fe3O4纳米颗粒磁性的影响, 其中, (a)和(b)图分别是在原位加热至700 ℃ (a)之前和(b)之后的明场透射电子显微像, 原位加热过程是在9 mbar的O2的环境下在环境透射电镜中加热8小时, 插图为对应纳米颗粒的选区电子衍射花样; 从原位加热(c)之前和(d)之后采集的全息图重构出的相位变化信息中获得的磁感应强度分布图, 展示出纳米颗粒的磁涡旋本征态, 等高磁轮廓线的间距是0.79 rad, 磁场方向用箭头表示, 与色轮对应; (e) Fe3O4 颗粒在环境透射电镜中退火前(蓝色, γ-Fe2O3)和退火后(红色, Fe3O4)对应的电子能量损失谱中的Fe 2p的L2, 3边, 黑色箭头表明了Fe3O4 中的三种混合价态, 红色箭头强调了边前峰和边后峰的形成并表明样品在朝着γ-Fe2O3态氧化; (f)退火前(蓝色, γ-Fe2O3)和退火后(红色, Fe3O4) 颗粒中沿颗粒中心至边缘的剩余磁化强度分布, 黑色箭头表明了退火后整体剩磁的减少[85]Figure9. Visualized effect of oxidation on the magnetization of an equiaxed Fe3O4 particle. Bright-field transmission electron microscopy images acquired (a) before and (b) after in situ heating to 700 ℃ under 9 mbar of O2 for 8 h in an environmental transmission electron microscope (ETEM), with associated selected area electron diffraction patterns inset. (c), (d) Magnetic induction maps determined from the magnetic contribution to the phase shift, reconstructed from holograms taken (c) before and (d) after in situ heating, revealing the vortex nature of the particle. The contour spacing is 0.79 rad for both magnetic induction maps. The magnetization direction is shown using arrows, as depicted in the color wheel. (e) Associated electron energy-loss spectra of the Fe 2p L2, 3 edge acquired from the Fe3O4 particle before (blue) and after (red) annealing within the ETEM. Black arrows emphasize three differing intensities from the mixed-valence compound of Fe3O4, while the red arrows highlight formation of pre- and post-peaks that indicate oxidation towards γ-Fe2O3. (f) Line profiles across their centers of magnetic contribution of nanoparticles before (blue) and after (red) annealing. Black arrows in (f) illustrate the loss in overall magnetic remanence[85].
