摘要: 作为马约拉纳费米子的“凝聚态版本”, 马约拉纳零能模是当前凝聚态物理领域的研究热点. 马约拉纳零能模满足非阿贝尔统计, 可以构建受拓扑保护的量子比特. 这种由空间上分离的马约拉纳零能模构建的拓扑量子比特不易受局域噪声的干扰, 具有长的退相干时间, 在容错量子计算中具有重要的应用前景. 半导体/超导体纳米线是研究马约拉纳零能模和拓扑量子计算的理想实验平台. 本文综述了高质量半导体纳米线外延生长、半导体/超导体异质结制备以及相应的马约拉纳零能模研究方面的进展, 并对半导体/超导体纳米线在量子计算中的应用前景进行了展望.
关键词: 半导体/超导体纳米线 /
马约拉纳零能模 /
非阿贝尔统计 /
量子计算 English Abstract From high-quality semiconductor/superconductor nanowires to Majorana zero mode Wen Lian-Jun 1,2 ,Pan Dong 1,2,3 ,Zhao Jian-Hua 1,2,3,4 1.State Key Laboratory of Superlattices and Microstructures, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China Fund Project: Project supported by the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB28000000), the National Natural Science Foundation of China (Grant No. 61974138), the Natural Science Foundation of Beijing, China (Grant No. 1192017), and the Youth Innovation Promotion Association of Chinese Academy of Sciences, China (Grant No. 2017156)Received Date: 21 October 2020Accepted Date: 18 November 2020Available Online: 25 February 2021Published Online: 05 March 2021Abstract: As the version of Majorana fermions in condensed matter physics, the research of Majorana zero modes is one of the most interesting topics in physics currently. Majorana zero modes obey the non-Abelian statistics and can be used for constructing the topologically protected qubits. This kind of qubit constructed from spatially separated Majorana zero modes is immune to local noise, and has a long decoherence time, which makes it show important application prospects in fault-tolerant quantum computation. The semiconductor/superconductor nanowires are one of the most ideal experimental platforms for studying Majorana zero modes and topological quantum computation. This work reviews the research progress of the epitaxial growth of high-quality semiconductor nanowires, the fabrication of semiconductor/superconductor heterostructure nanowires, and Majorana zero modes in semiconductor/superconductor nanowires. The application prospects of semiconductor/ superconductor nanowires in quantum computation is also prospected finally.Keywords: semiconductor/superconductor nanowire /Majorana zero mode /non-Abelian statistics /quantum computation 全文HTML --> --> --> 1.引 言 1937年, 意大利物理学家埃托雷·马约拉纳(Ettore Majorana)求解狄拉克方程时发现, 在纯虚数构建的狄拉克矩阵表示下(即马约拉纳表象), 狄拉克方程存在实数解. 该粒子的产生算符$ {\gamma }^{\dagger } $ 和湮灭算符γ 相等, 即其反粒子为自身, 粒子呈电中性, 这类自旋1/2的粒子被称为马约拉纳费米子. 在粒子物理领域中, 呈电中性的中微子曾被预言是马约拉纳费米子, 但该观点至今尚未得到相关实验数据的支持[1 ] . 在凝聚态物理的固体宇宙世界中, 虽然主要的研究对象是电子, 但是晶体材料中特殊的场激发有可能产生具有部分马约拉纳费米子特性的准粒子. 电中性和自共轭($ {\gamma }^{\dagger }=\gamma $ )特性是马约拉纳费米子具有的基本特性, 超导体可能是制备马约拉纳准粒子的理想材料. 超导体的激发态是电子和空穴的叠加态, 如果电子和空穴以等比例进行叠加, 那么就可以得到电中性的准粒子[2 ] . 2001年, Kitaev[3 ] 从理论上推导出在一维无自旋p波超导链两端存在满足自共轭条件的拓扑型激发, 即马约拉纳零能模(Majorana zero mode). 利用这对空间上分离的马约拉纳零能模可以定义量子比特, 并且这种由非局域的费米子态构建的量子比特可以抗局域噪声的干扰, 具有长的退相干时间, 因此相比于一般的量子计算机, 基于马约拉纳零能模构建的拓扑量子计算机在硬件层次上具有更佳的容错特性[4 ,5 ] . 此外, 不同于经典的玻色子和费米子, 马约拉纳零能模满足非阿贝尔统计, 这意味着仅通过交换马约拉纳零能模的位置就可以改变量子态, 相当于量子计算中的量子门操作[4 ] . 这些优异且独特的性质使马约拉纳零能模研究成为当前凝聚态物理领域中的研究热点之一. 目前, 理论上预言的可承载马约拉纳零能模的材料体系包括: p波超导体[6 ] 、5/2分数量子霍尔态[7 ] 、拓扑绝缘体/超导体异质结[8 ] 、磁性原子链[9 ] 和半导体/超导体纳米线[10 -12 ] 等. 本文主要关注半导体/超导体纳米线体系的材料制备以及输运研究进展, 其相关的基础理论以及其他材料体系的综述可以参考文献[2 ,13 -19 ].[10 -12 ] 独立提出了基于半导体/超导体异质结纳米线体系的理论方案: 当具有强自旋轨道耦合的半导体纳米线与s波超导体形成异质结时, 在外加磁场B m *, μ , α 和$E_{\rm{Z}}~(=1/2g{\mu }_{\rm{B}}{{B}}$ , g 和$ {\mu }_{\rm{B}}$ 分别为朗德因子和玻尔磁子)分别表示半导体纳米线中电子的有效质量、化学势、自旋轨道耦合强度和塞曼能. σy σz Δ 为超导体在半导体纳米线中诱导出的超导能隙. 当体系满足${E}_{\rm{Z}}^{2}\geqslant {\mu }^{2}+{\varDelta }^{2}$ 的相变条件时, 半导体/超导体纳米线将从平庸的超导态进入到非平庸的拓扑超导态, 并在其两端形成一对马约拉纳零能模[10 -12 ] . 利用这对马约拉纳零能模可以构建一个零能费米态, 该费米态的占据数“0”和“1”用于定义量子计算中的基本单元—量子比特[20 ,21 ] . 从(1 )式的哈密顿量以及上述的相变条件可以看出, 为了在实验上更好或更容易制备拓扑超导态, 在材料的选择上通常要求半导体纳米线具有强的自旋轨道耦合以及足够大的朗德g 因子, 要求超导体具有相对大的超导能隙. 大的朗德g 因子保证在相对小的外加磁场下就可以打开足够大的塞曼能隙, 使半导体/超导体纳米线在超导态被破坏前可以进入到拓扑超导态. 具有强的自旋轨道耦合以及大的朗德因子的InAs和InSb纳米线是当前研究的热点材料, 超导体通常使用Al和Nb[22 -27 ] . 本文将详细介绍高质量InAs和InSb纳米线外延生长、高质量半导体/超导体异质结的制备、马约拉纳零能模的低温输运实验进展和马约拉纳零能模的编织方案.2.高质量半导体纳米线的外延生长 纳米线通常是指径向宽度被限制在百纳米以内, 而轴向长度可达数微米甚至更长的一种准一维纳米结构. 一般来讲, 实现纳米线结构的方法可以划分成两大类: “自上而下”和“自下而上”技术. 其中“自上而下”是通过使用各种刻蚀技术将较大尺寸的材料刻蚀成一维纳米线的一种技术. 该技术具有相对成熟的制备工艺, 但易在刻蚀过程中引入表面缺陷, 使制备的纳米线性能大幅降低. “自下而上”是指组分原子自动有序排列并形成纳米线的技术, 在形成纳米线的过程中, 可以人为地调控纳米线的结构与性质. 由于纳米线具有小的直径, 在外延生长中更容易释放晶格应力, 因而可以在晶格失配大的衬底上进行高质量半导体纳米线的外延生长.[28 -37 ] . 图1(a) 是利用气-液-固生长模式进行纳米线生长的过程示意图. 一定温度下, 在衬底表面上沉积金属薄膜并形成催化剂的小液滴, 由于液体表面比固体表面有更大的粘附系数, 组分原子会优先溶入液滴形成合金液滴. 一旦组分原子在液滴中达到过饱和, 就会在衬底与液滴的界面处析出晶核, 开始纳米线的生长. 基于该原理, 可以较为容易地制备各种具有高纵横比的半导体纳米线. 从材料生长的角度看, 纳米线的外延生长除了需要实现对其形貌和生长方向的控制外, 还需保证制备的纳米线具有高的晶体质量(无位错、堆垛层错和孪晶等缺陷). 事实上, 对于III-V半导体纳米线, 由于形成闪锌矿和纤锌矿结构所需的能量相近, 纳米线常表现为闪锌矿与纤锌矿的混合相, 且纳米线中常存在大量的堆垛层错及孪晶等缺陷(如InAs纳米线)[28 -31 ] . 制备高质量半导体纳米线一直是材料生长领域中的研究重点与难点. 从马约拉纳零能模低温输运研究的角度看, 纳米线中的这些缺陷会极大地降低器件的电学性能, 并可能会成为平庸信号的起源(无序诱导的零偏压电导峰), 干扰人们对输运结果的解读与判断[38 ] . 成熟的高质量半导体纳米线制备技术对马约拉纳零能模研究以及最终实现拓扑量子计算机都极为重要. 如图1(b) 和图1(c) 所示, 我们课题组选用Ag作为金属催化剂, 通过对纳米线直径的调控, 成功在Si衬底上实现了纯纤锌矿结构InAs纳米线的外延生长[28 ] . 相较于InAs, InSb具有更大的晶格常数, 与常用的Si衬底和GaAs衬底晶格失配更大, 直接在衬底上外延生长高质量InSb纳米线仍是一个巨大的挑战[37 ] . 换源工艺是当前制备纯相InSb纳米线的主要手段[32 -36 ] , 即通过气-液-固的生长方式, 首先在衬底上预生长其他III-V纳米线, 然后切换生长源材料, 实现III-V/InSb轴向异质结纳米线的制备. 基于换源工艺, 我们也成功实现了高质量InAs/InSb轴向异质结纳米线的外延生长(见图1(d) ), InSb纳米线为纯闪锌矿结构的单晶(见图1(e) )[36 ] .图 1 (a) 纳米线的气-液-固生长过程示意图; (b), (c) Si衬底上Ag辅助生长的纯纤锌矿InAs纳米线[28 ] ; (d), (e) Si衬底上Ag辅助生长的InAs/InSb轴向异质结纳米线[36 ] ; (f) 利用电子束曝光技术, 对InP衬底进行图形化处理, 定义纳米线的生长位置[45 ] ; (g) InP衬底上Au辅助生长的InAs纳米线阵列[45 ] Figure1. (a) The schematic diagram of the nanowires grown with a vapor-liquid-solid manner; (b), (c) Ag-assisted growth of pure wurzite InAs nanowires on Si substrates[28 ] ; (d), (e) Ag-assisted growth of InAs/InSb axial heterojunction nanowires on Si substrates[36 ] ; (f) nanowire growth position is defined by electron beam lithography on InP substrates[45 ] ; (g) Au-assisted growth of InAs nanowire arrays on InP substrates[45 ] .[39 -49 ] . 一般来讲, 利用气-液-固生长模式实现半导体纳米线交叉结构的方法可以划分成两大类. 第一类方法主要通过调节实验参数(如生长温度、束流和催化剂成分)来控制半导体纳米线生长方向, 让具有不同生长方向的相邻纳米线形成交叉结构[40 -43 ] . 例如, 实验中可利用原位退火工艺首先让纳米线顶部的催化剂液滴向纳米线的侧壁转移, 随后利用催化剂液滴引导纳米线水平生长, 最后优化纳米线的生长时间可使相邻纳米线形成交叉结构[40 ] . 另一类方法是通过对衬底的图形化处理并利用衬底和半导体纳米线生长方向之间的外延依赖关系来实现交叉结构的制备[44 -49 ] . 如图1(f) 和图1(g) 所示[45 ] , 该方法可以对纳米线交叉的位置、形貌和密度等参数实现高精度的人为控制. 此外, 该方法也容易实现更复杂的纳米线网状结构[49 ] .[50 -56 ] . 面内纳米线网络的选区外延生长过程可大致分为两步: 首先, 利用电子束曝光技术以及相关刻蚀技术对衬底做图形化处理, 设计出合适的纳米线网络的生长沟道; 其次, 在沟道内实现半导体纳米线网络的选择性生长. 该技术可利用III-V族元素在图形化衬底表面上不同区域的脱附速率差异来实现半导体纳米线网络的选区外延: 在掩模上, III-V族元素脱附速率足够高; 而在沟道内, III-V族元素脱附速率相对较低. 常用的掩模有SiOx x y [50 -56 ] . 对于化学束外延技术和金属有机化学气相沉积技术, 纳米线网络制备所用的源材料为III族金属有机气态源, 该材料不容易聚集在掩模表面(SiOx x y [57 ] , 这种选择性使得半导体纳米线网络的选区外延具有较大的生长区间[54 ,56 ] . 对于分子束外延技术, 半导体纳米线网络制备所用的源材料为固态单质源, 其选区外延除了需要考虑III-V族元素在衬底表面上的脱附速率之外还需考虑元素在衬底表面上的扩散. 为避免III族元素在掩模上聚集形成液滴, 常要求III族元素具有较大的扩散长度. 如图2(a) 所示, 利用分子束外延技术制备的InAs纳米线网络具有良好的重复性以及优异的选择性[55 ] . 为了在分子束外延系统中实现InSb纳米线网络的异质外延生长, Aseev等[53 ] 提出了基于金属播种(metal-sown)纳米线网络的选区生长模型: 首先在InP (111)B衬底上的沟道内沉积In液滴, 其次利用Sb束流饱和In液滴形成InSb种子层, 最后同时供应In和Sb可在InSb种子层上实现InSb纳米线网络的选择性生长(见图2(b) ).图 2 (a) InP (111)B衬底上InAs纳米线网络的选区生长[55 ] ; (b)基于金属播种方法制备的InSb纳米线网络[53 ] ; (c)立式InAs/Al纳米线的高分辨透射电子显微图像[58 ] ; (d)面内InAs/Al纳米线网络的截面高分辨透射电子显微图像[55 ] Figure2. (a) The selective area growth of InAs nanowire networks on InP (111)B substates[55 ] ; (b) the fabrication of InSb nanowire networks via a metal-sown selective area growth technique[53 ] ; (c) the high-resolution transmission electron microscope image of the free-standing InAs/Al nanowire[58 ] ; (d) the cross-sectional high-resolution transmission electron microscope image of the in-plane InAs/Al nanowire network[55 ] .3.高质量半导体/超导体异质结的制备 目前, 高质量InAs和InSb纳米线的低温输运研究结果已表明这些材料具有强的自旋轨道耦合和大的朗德因子等优异性质[22 -27 ,58 -68 ] , 适用于马约拉纳零能模研究. 同时, 也为高质量半导体/超导体异质结的制备创造了条件. 早期的半导体/超导体纳米线器件的制作方法简单方便, 即首先将生长的InAs或InSb半导体纳米线转移至干净衬底上, 然后基于非外延的方式直接将超导体选择性地沉积到纳米线上, 从而构成半导体/超导体纳米线器件[25 -27 ] . 在该类器件中, 半导体与超导体之间的界面无序所导致的软能隙(soft gap)问题常使得超导能隙中存在子能隙态. 这些态可以在超导输运中贡献非零的零偏压电导峰[69 ] , 使实验上难以确认观测到的零偏压电导峰的起源. 为了解决这一难题, 对半导体/超导体异质结界面进行优化是材料制备方面主要的突破方向[38 ,69 ] . 2015年, Krogstrup等[66 ] 发展了低温分子束外延技术(生长温度约–30 ℃), 成功在InAs纳米线侧壁上原位外延生长了Al. 由于InAs与Al存在大的晶格失配, 在InAs纳米线侧壁上Al倾向于岛状生长, 实验中需要通过超低的生长温度来降低Al的扩散长度, 从而实现连续且平整的超导层的外延生长. 2017年, Kang等[58 ] 采用相同的低温外延技术, 在InAs (001)衬底上也实现了InAs/Al的生长. 从图2(c) 中可以看出, InAs与Al之间具有平整的界面, 并且超导输运结果表明该体系具有硬超导能隙(hard gap)[58 ] . 低温分子束外延技术成功解决了由界面无序诱发的软能隙问题[58 ,69 -71 ] . 基于低温分子束外延技术, 人们也实现了面内InAs/Al纳米线网络的选区生长(见图2(d) )[55 ] . 值得一提的是, 所有半导体纳米线制备技术中, 目前仅分子束外延技术可以实现超导层的低温外延生长.4.马约拉纳零能模的输运特征 当半导体/超导体纳米线从拓扑平庸态进入到拓扑超导态时, 马约拉纳零能模的形成使该体系存在一系列独特的、标志性的输运特征. 量子化的零偏压电导峰是马约拉纳零能模的标志性特征之一[71 -77 ] . 实验上测量零偏压电导峰的器件结构示意图如图3(a) 所示. 当半导体/超导体纳米线从拓扑平庸的超导态进入到拓扑超导态时, 费米面上将产生零能的边缘电子态[10 -12 ,21 ] . 这种受拓扑保护的边缘电子态在输运上可引起共振Andreev反射, 导致零偏压电导峰的出现[27 ,74 -76 ,78 ] . 在足够低的温度下, 零偏压电导峰表现为量子化电导值(约2e 2 /h ), 如图3(b) 所示[78 ] . 在早期的零偏压电导峰测量实验中[25 -27 ] , 虽然观察到了随磁场变化的零偏压电导峰, 但其零偏压电导峰值远低于理论预期, 并且该实验中由半导体/超导体纳米线的界面无序引发的软超导能隙也可解释这一现象[69 ] . 随着对半导体/超导体异质结界面以及器件结构的优化, 最近张浩等[73 ] 已在InSb/Al纳米线中观测到了量子化零偏压电导峰, 但目前该实验仍难以排除Andreev 束缚态等平庸态的影响.图 3 (a)半导体/超导体纳米线隧穿电导测量的器件示意图, 其中底栅控制整个半导体纳米线的化学势, 超导栅调控半导体/超导体异质结区域的化学势, 隧穿栅控制异质结与电极之间的耦合; (b)半导体/超导体纳米线器件的微分电导G 随塞曼能E Z 和偏压V 变化的示意图[78 ] ; (c)约瑟夫森电流I (φ )随超导相位差φ 变化的示意图[12 ] ; (d)仅考虑Rashba自旋轨道耦合时, 半导体/超导体纳米线中x 方向上的自旋极化分布[81 ] Figure3. (a) The schematic diagram of semiconductor/superconductor nanowire device for detecting zero-energy conductance peaks: The super-gate and global back-gate are respectively used for controlling the chemical potential of the semiconductor/superconductor heterojunction and the semiconductor nanowire, and the tunnel-gate is used for tuning the coupling between the semiconductor/superconductor heterojunction nanowire and the lead; (b) the schematic diagram of the differential conductance G varing with Zeeman energy E Z and bias voltage V [78 ] ; (c) the schematic plot of Josephoson current I (φ ) as a function of the superconducting phase difference φ[12 ] ; (d) the spin polarization distribution along the x direction in semiconductor/superconductor nanowire with Rashba spin-orbit coupling[81 ] .[3 ,12 ] . 如图3(c) 所示[12 ] , 对于由常规超导体构成的约瑟夫森结, 其约瑟夫森电流随超导相位差φ 呈2π的振荡周期(红色曲线), 即$ I\propto {\rm{sin}}\varphi $ ; 当由两个拓扑超导体构成约瑟夫森结时, 流过该结的约瑟夫森电流将随两拓扑超导体的相位差呈现出4π的振荡周期(蓝色曲线), 即$I\propto {\rm{sin}}\dfrac{\varphi }{2}$ . 这种输运行为上的差异表明两种约瑟夫森结存在不同的微观输运机制. 对于普通的约瑟夫森结, 超导相位差φ 诱导库珀对隧穿产生超导电流; 对于由拓扑超导体构成的约瑟夫森结, 其基态存在奇数占据态, 单电子的相干隧穿过程可诱导产生分数化的约瑟夫森电流. 目前, Laroche等[79 ] 已成功在InAs/Al纳米线中观测到分数化的约瑟夫森效应.[21 ,23 ,39 ,80 ] . 充电能对应的哈密顿量为E C , N , C g 和V g 分别表示充电能、库仑岛上电荷数、栅电容和栅电压. 对于s波超导体, 基态由大量的库珀对构成, 费米面上不允许单电子态的存在, 因此N 总是取偶数值; 对于拓扑超导体, 由于马约拉纳零能模的存在, 基态除了库珀对还允许单电子态的存在, 此时N 既可以取偶数值也可以取奇数值[21 ,39 ] . 因而, 在实验上可通过测量电导G 随栅电压以及外加磁场的变化来分析马约拉纳库仑岛器件是否存在拓扑相变. 在低磁场下, 电导G 随栅电压V g 呈现2e 的周期性振荡; 当磁场高于拓扑相变的临界磁场时, 电导G 将随栅电压V g 表现出e 的周期性振荡[23 ] .[81 ] . 假设位于x -y 平面内的半导体/超导体纳米线沿x 方向放置, 磁场沿z 方向垂直于纳米线. 当半导体/超导体纳米线处于拓扑平庸态时, 纳米线两端自旋极化的x 和y 分量都为零, 自旋沿z 方向排列. 当半导体/超导体纳米线从拓扑平庸态进入到拓扑超导态后, 由于纳米线两端形成了马约拉纳零能模, 其自旋结构(spin texture)会产生明显的变化. 仅考虑Rashba自旋轨道耦合时, 纳米线左右两端的自旋极化分别为k 为常数, $ \phi $ 与异质结的化学势和塞曼能有关[81 ] . (3 )式和(4 )式表明对处于拓扑超导态的半导体/超导体纳米线, 其两端自旋极化的x 分量不为零(见图3(d) ). 相变前后显著的自旋结构变化为证实马约拉纳零能模的存在提供了重要的理论依据, 利用自旋极化的STM测量有可能在实验上证实这一方案[81 ] .5.马约拉纳零能模的编织方案 在实验上寻找马约拉纳零能模输运证据的同时, 理论科学家们也在思考如何实现拓扑量子比特构建和操纵[20 ,39 ,49 ,50 ,82 -84 ] . 在量子计算中, 一套普适的量子门是实现量子信息处理的核心[85 ] . 对于拓扑量子计算, 由于马约拉纳零能模满足非阿贝尔统计, 量子信息处理可以通过交换马约拉纳零能模之间彼此的空间位置(编织)来实现. 马约拉纳零能模的编织操作等价于量子门, 这也是马约拉纳零能模体系适于量子计算机研发的关键因素之一[1 -4 ,20 ,39 ] .[20 ] . 利用库仑阻塞效应, 在T型结中实现马约拉纳零能模编织的示意图如图4(a) —图4(d) 所示[39 ] . 该方案中利用栅电压控制马约拉纳库仑岛之间以及马约拉纳库仑岛与超导电极之间的耦合, 进而实现马约拉纳零能模的移动和交换. 如图4(a) 所示, 水平分支上的两个马约拉纳库仑岛分别与左右超导电极耦合(此时栅电压对应的状态定义为“开”态), 形成两对马约拉纳零能模: γ 1 γ 2 和γ 3 γ 4 (马约拉纳库仑岛与超导电极之间的耦合可以降低马约拉纳库仑岛上的有效充电能, 使体系回到简并的基态). 垂直分支上的马约拉纳库仑岛与超导电极之间存在高的隧穿势垒(此时栅电压对应的状态定义为“关”态), 强的库仑相互作用使得该马约拉纳库仑岛两端不能形成马约拉纳零能模. 使水平分支左端和垂直分支上所有栅极处于开态, 可以将γ 2 移动至垂直分支上(见图4(b) ). 随后使γ 1 与γ 2 之间的栅极处于关态并同时使γ 3 处的栅极处于开态, 从而将γ 3 移动到左边的马约拉纳库仑岛上(见图4(c) ). 最后使垂直分支上以及γ 2 与γ 4 之间的栅极都处于关态, 将γ 2 移动到水平分支右端, 从而实现马约拉纳零能模γ 2 和γ 3 在空间位置上的交换(见图4(d) ), 即基于上述过程实现了马约拉纳零能模的一次编织.图 4 (a)?(d) T型结中马约拉纳零能模的编织过程[39 ] ; (e)马约拉纳干涉仪[82 ] ; (f)基于投影测量的马约拉纳零能模编织过程[82 ] ; (g)马约拉纳零能模网络, 其中紫色区域R t )代表Kekule涡旋[83 ] Figure4. (a)?(d) The braiding of Majorana zero modes in a T-junction[39 ] ; (e) Majorana interferometer[82 ] ; (f) the measurement-based braiding of Majorana zero modes[82 ] ; (g) the network of Majorana zero modes: the Kekule vortex represented by R t )[83 ] .[86 ,87 ] . 在这一理论方案中, 通过对马约拉纳双线性算子iγ 1 γ 2 的本征值测量(iγ 1 γ 2 有两本征态: $ |?\pm \rangle_{12},?{\rm i}\gamma_1\gamma_2| \pm\rangle_{12}?=?\pm ?|\pm\rangle_{12}) $ 取代了物理上的移动马约拉纳零能模. 马约拉纳干涉仪是投影测量中使用的一种装置, 如图4(e) 所示[82 ] . 在外磁场的作用下, 器件的电导将随磁通Ф 呈h /e 的周期性变化. 在$ | \pm \rangle_{12} $ 基下, 通过对电导的测量可得到马约拉纳双线性算子的本征值(见图4(e) ). 基于该原理, 对由多对马约拉纳零能模构成的马约拉纳干涉仪, 可以通过设计一系列合理的投影测量步骤来等效地实现对体系初态做幺正变换(见图4(f) )[82 ] , 即实现了没有真实物理移动的编织操作.[83 ] . 如图4(g) 所示, 理论上假定六角蜂窝状的半导体/超导体纳米线网络的所有分支都进入拓扑超导态, 则每一分支上都存在两个马约拉纳零能模. 在每个Y型结处, 三个马约拉纳零能模可相互耦合产生一个有效马约拉纳零能模. 利用栅电压控制这些位于Y型结上的有效马约拉纳零能模进行耦合, 在适当的条件下可以形成一系列Kekule涡旋(见图4(g) 中的紫色区域R t )), 并在每个涡旋中心产生一个逻辑马约拉纳零能模. 这些逻辑马约拉纳零能模也满足非阿贝尔统计特性, 可以用于定义拓扑量子比特. 逻辑马约拉纳零能模的移动可以通过施加随时间变化的栅电压来实现, 在这个过程中, 处于第一层的马约拉纳零能模并未移动. 该方案中完全可以通过程序化的设定栅电压来控制逻辑马约拉纳零能模的移动, 提供了一种有可能直接验证非阿贝尔统计的方法.6.新型二维半导体纳米结构 除了上述基于一维半导体/超导体纳米线的实验方案, 近年来, 高质量二维立式半导体纳米材料的出现也为马约拉纳零能模研究提供了机遇[36 ,88 -91 ] . 利用高质量的立式二维单晶半导体纳米片并结合原位阴影生长技术制备的材料, 有望用于下一代新型量子器件研究[89 ] . 2016年, 我们课题组利用纳米线的两种典型生长模式: 气-液-固生长模式和气-固生长模式, 在一维InAs纳米线顶端成功外延生长出了二维高质量InSb纳米片(见图5(a) —图5(c) )[36 ] . InSb纳米片的长宽可达数微米, 厚度可薄至10 nm(见图5(c) ). InSb纳米片具有高的晶体质量, 为纯闪锌矿单晶, 其结构中观察不到堆垛层错及孪晶等缺陷(见图5(d) )[36 ,92 ] . 低温磁输运结果表明InSb纳米片中存在明显的SdH振荡以及量子霍尔效应, 这为InSb纳米片中电子的二维输运行为提供了直接证据[93 -95 ] . 此外, 利用AgIn合金催化剂偏析[88 ,96 ] , 还在实验上实现了InAs纳米结构的维度调控, 成功制备了立式高质量纯纤锌矿结构的单晶InAs纳米片(见图5(e) 和图5(f) [88 ] ). 低温磁输运研究证实了InAs纳米片中电子的二维输运行为[97 ] . 这些新型的二维InAs和InSb纳米结构与超导体相结合, 可能会在未来的拓扑量子器件中扮演重要角色.图 5 (a)?(c) InSb纳米片的扫描电子显微图[36 ] ; (d) InSb纳米片的高分辨透射电子显微图[36 ] ; (e) InAs纳米片的扫描电子显微图[88 ] ; (f) InAs纳米片的高分辨透射电子显微图[88 ] Figure5. (a)?(c) Scanning electron microscope images of InSb nanosheets[36 ] ; (d) the high-resolution transmission electron microscope image of the InSb nanosheet[36 ] ; (e) the scanning electron microscope image of InAs nanosheets[88 ] ; (f) the high-resolution transmission electron microscope image of the InAs nanosheet[88 ] .7.总结与展望 本综述介绍了高质量半导体纳米线以及高质量半导体/超导体异质结的制备方法、表征马约拉纳零能模的特征性实验以及马约拉纳零能模的编织方案. 随着对材料以及器件结构的不断优化, 人们已在实验上观察到量子化零偏压电导峰[73 ] 、分数约瑟夫森效应[79 ] 和电子隐形传态[23 ] 等输运特征, 这为确认马约拉纳零能模的存在提供了必要但还不够充分的证据. 从近期来看, 仍需要进一步对半导体/超导体纳米线的生长条件以及相应的器件结构进行优化, 以期获得更多的实验证据来进一步证实纳米线两端存在马约拉纳零能模, 并排除其他平庸的信号来源(如Andreev束缚态). 从长期来看, 马约拉纳零能模非阿贝尔统计性质的验证依旧是拓扑量子计算领域中最为关键的一步. 因此, 对半导体/超导体纳米线网络进行结构设计以及晶体质量的优化将对可扩展拓扑量子计算机的实现具有重要意义. 
图 1 (a) 纳米线的气-液-固生长过程示意图; (b), (c) Si衬底上Ag辅助生长的纯纤锌矿InAs纳米线[28]; (d), (e) Si衬底上Ag辅助生长的InAs/InSb轴向异质结纳米线[36]; (f) 利用电子束曝光技术, 对InP衬底进行图形化处理, 定义纳米线的生长位置[45]; (g) InP衬底上Au辅助生长的InAs纳米线阵列[45]
图 2 (a) InP (111)B衬底上InAs纳米线网络的选区生长[55]; (b)基于金属播种方法制备的InSb纳米线网络[53]; (c)立式InAs/Al纳米线的高分辨透射电子显微图像[58]; (d)面内InAs/Al纳米线网络的截面高分辨透射电子显微图像[55]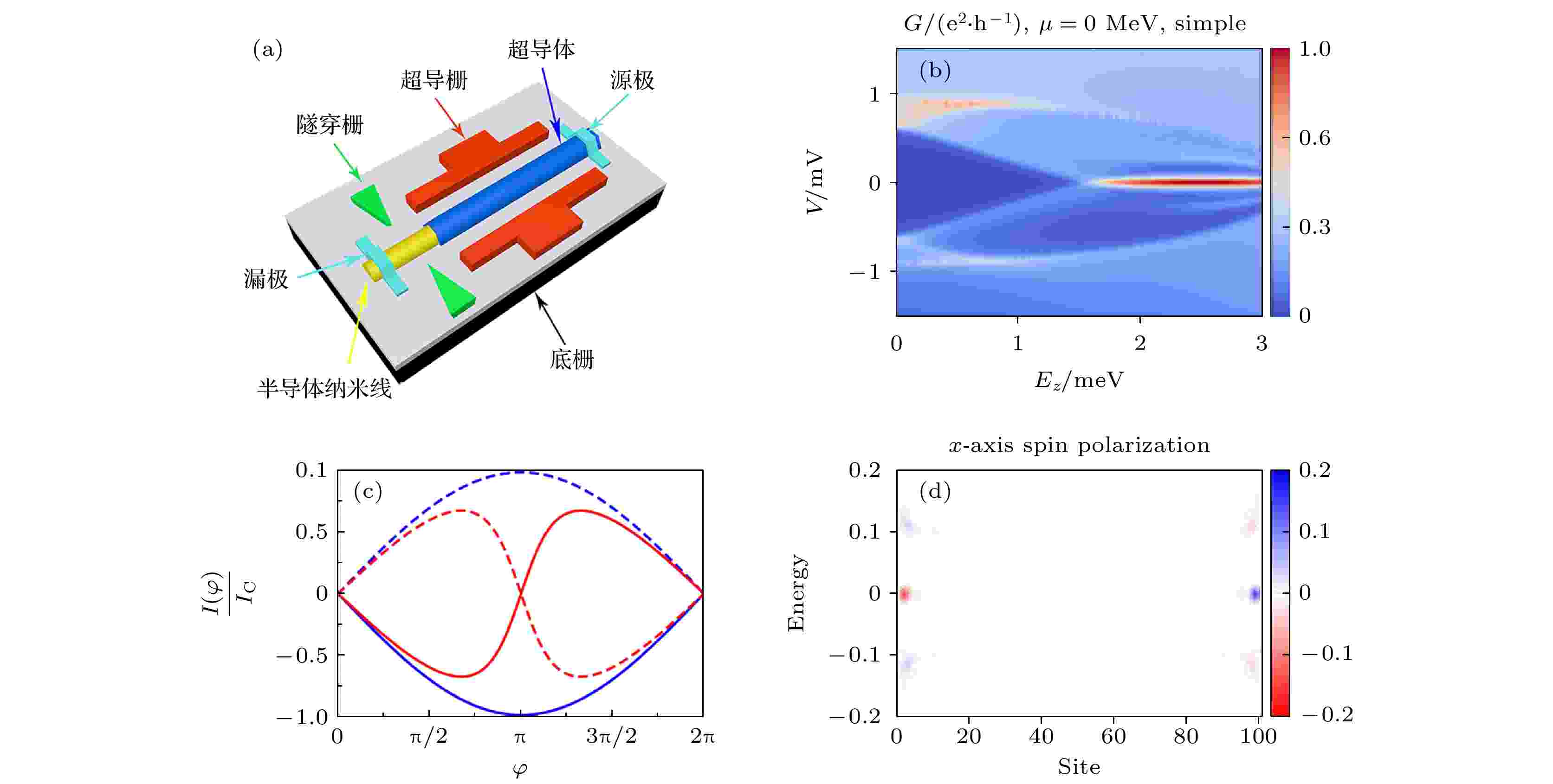
图 3 (a)半导体/超导体纳米线隧穿电导测量的器件示意图, 其中底栅控制整个半导体纳米线的化学势, 超导栅调控半导体/超导体异质结区域的化学势, 隧穿栅控制异质结与电极之间的耦合; (b)半导体/超导体纳米线器件的微分电导G随塞曼能EZ和偏压V变化的示意图[78]; (c)约瑟夫森电流I(φ)随超导相位差φ变化的示意图[12]; (d)仅考虑Rashba自旋轨道耦合时, 半导体/超导体纳米线中x方向上的自旋极化分布[81]
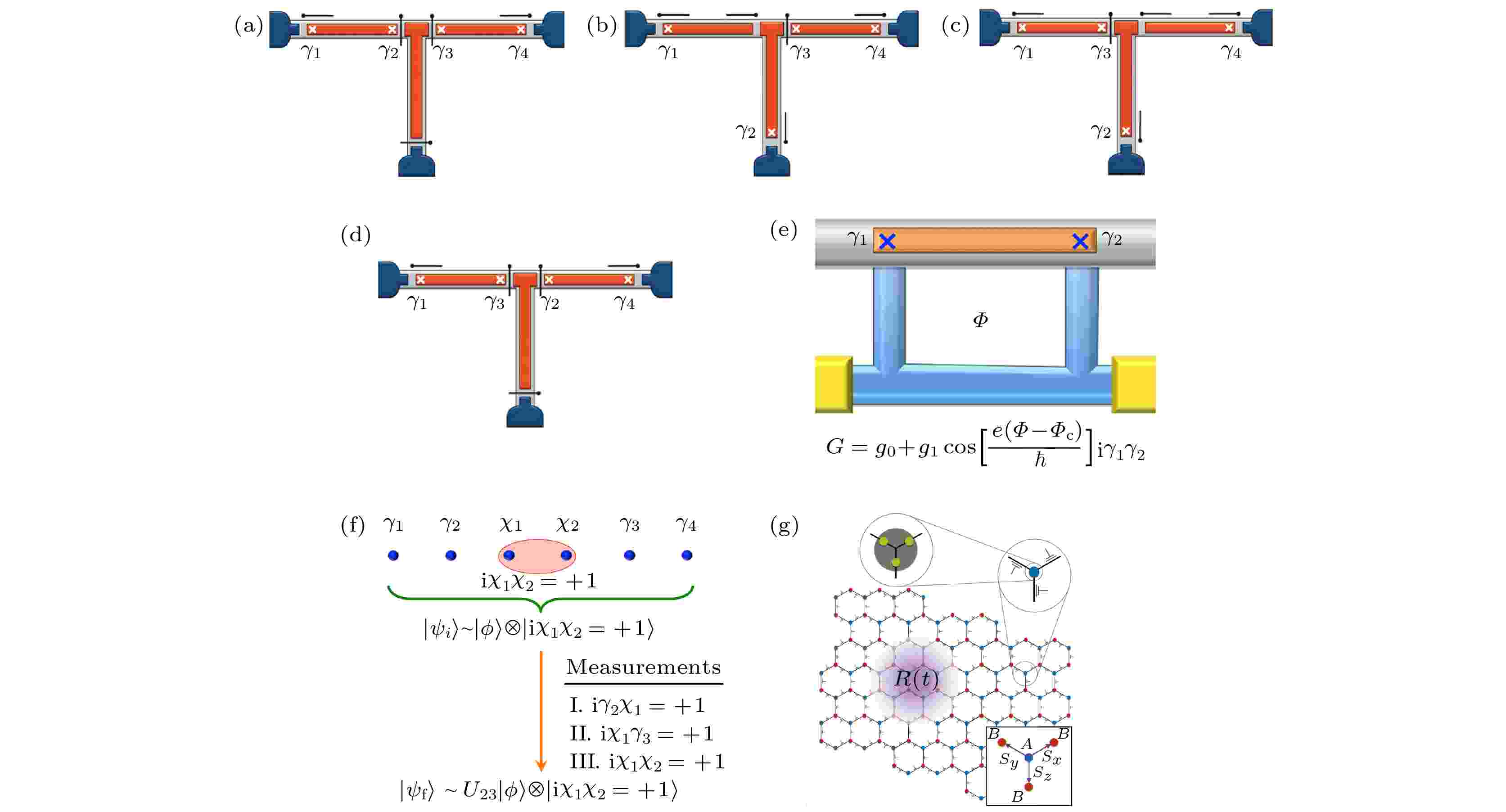图 4 (a)?(d) T型结中马约拉纳零能模的编织过程[39]; (e)马约拉纳干涉仪[82]; (f)基于投影测量的马约拉纳零能模编织过程[82]; (g)马约拉纳零能模网络, 其中紫色区域R(t)代表Kekule涡旋[83]
图 5 (a)?(c) InSb纳米片的扫描电子显微图[36]; (d) InSb纳米片的高分辨透射电子显微图[36]; (e) InAs纳米片的扫描电子显微图[88]; (f) InAs纳米片的高分辨透射电子显微图[88]