全文HTML
--> --> -->经典的布尔网络各节点的更新机制是确定的, 通常由一个外部时钟控制网络中各个节点同时更新状态, 这种更新机制为同步更新, 或者由一个选择设备指定各节点的更新顺序, 使各节点按照一定的更新顺序更新状态, 这种更新机制为异步更新. 在这种确定性的更新机制的布尔网络中, 网络状态是离散的有限的. 自治布尔网络是没有设备控制各节点的更新时间和更新顺序, 各节点的更新由节点本身的特性所定, 与确定的更新机制中网络的节点在指定的时间点发生突变不同, 自治更新的网络中节点的状态是连续变化的, 网络输出更加复杂. 2009年, Zhang等[10]在实验室实现了硬件系统自治布尔网络, 并在实验中观察到改变电压可以改变网络输出状态为有序状态和混沌状态, 其混沌带宽可达吉赫(GHz)(–10 dB), 与现有电学混沌相比具有较大优势, 并推测其原因为逻辑器件的供电电压不同时使得器件引起的各种特征时间发生变化引起的, 如传输延时和器件上升沿下降沿时间. 该自治布尔网络硬件系统是仅由逻辑器件经导线相互连接构成的数字电路, 具有电路结构简单、功耗低、易于集成的优点. 自治布尔网络硬件系统的实现为在实验室进行多种基于自治布尔模型的系统模拟实验提供了非常有利的条件. 目前, 自治布尔网络硬件系统提出以来已在随机数产生[11-15]、储备池计算[16-17]、基因调控[18-19]、不可克隆函数[20]等许多领域获得了成功应用.
自治布尔网络的输出可以在周期和混沌之间转换, 目前, 已有研究****对自治布尔网络输出不同状态的影响因素进行了分析研究. 2010年Cavalcante等[21]分析了简单自治布尔网络中输出为混沌的原因, 研究表明网络节点间链路延时的不一致性、器件的滤波效应和延时对输入和历史状态的依赖性均对网络输出混沌状态有影响. 2014年Rosin等[22]通过实验和仿真研究了节点间链路延时参数对耦合自治布尔网络同步的影响, 研究表明在单向耦合网络和双向耦合网络中该延时参数均可以调节耦合强度从而改变网络输出及其同步效果. 2014年Rosin等[23]进一步研究了超过100个节点的大网络中, 不同节点间由随机初始状态到达同步状态之前的暂态传输过程存在非常复杂的动态行为, 该暂态传输的平均时间随着网络节点数量增长呈指数增长. 2016年D'Huys等[24]研究了自治布尔网络的链路延时对网络的影响, 表明链路延时越大网络输出到达稳态之前的暂态传输状态时间越长. 2019年Gong等[25]分析了电路中噪声对自治布尔网络输出的影响, 证明噪声使网络输出状态不可预测. 综上所述, 目前的研究多基于对具有稳定状态的自治布尔网络, 研究节点数量、链路延时对网络到达稳态之前的瞬态传输的时序的影响. 对于可以产生混沌的自治布尔网络只是初步探索了产生混沌的影响因素, 并没有详细研究各因素变化对网络输出的影响.
本文研究了自治布尔网络中器件响应特性的变化对网络输出的影响, 逻辑器件是构成自治布尔网络的核心器件, 实际中有多种类型的逻辑器件, 其响应特性各不相同, 本文的研究对自治布尔网络在不同应用领域中器件的选择具有重要意义. 首先通过单变量布尔模型分析数学模型中参数对器件响应特性的表征性能. 然后以小型自治布尔网络为研究对象, 仿真研究器件响应特性变化对自治布尔网络输出状态的调控效果, 观察了器件响应特性和链路延时时间二维参数空间上自治布尔网络输出状态的分布情况, 分析了两个参数之间的相互影响. 进一步观察和分析了变量间器件响应特性的不一致性对自治布尔网络输出状态的影响.
2.1.单节点异或非逻辑门模型
图1为异或非逻辑门示意图, u1, u2为输入信号, yout为输出信号. 实际逻辑器件中, 异或非逻辑门无法对输入信号做瞬时响应, 当输入信号u1, u2维持时间较短时, 异或非逻辑门将不能完全响应, yout不能产生对应的输出波形, 本文称这一特性为逻辑器件响应特性, 在本文的研究中, 对任一给定的信号维持时间为?tu的输入信号, 输出信号脉冲幅值和脉冲宽度的不同表征了器件响应特性的不同, 输出信号幅值越大、脉冲宽度越宽表明器件响应越快, 能响应更窄的输入信号.
图 1 异或非逻辑门示意图Figure1. The schematic illustration of the XNOR logic gate.
图1中异或非逻辑门的数学模型如(1)式—(3)式所示, 式中微分项dx/dt能够模拟器件响应过程, 由于微分项的存在, 使输出不可能发生突变, 能够模拟实际器件中器件不能对输入信号做瞬时响应的特性. 因此微分项是模拟器件响应特性的核心, τlp为器件响应特性参数, 改变τlp可以改变模型中微分过程的时间长短, 从而调节逻辑器件响应特性. u1(t), u2(t)为输入信号, yout(t)为输出信号, “⊙”表示异或非运算, U1(t), U2(t)为量化的输入信号, Yout(t)为量化的输出信号, uth = yth = 0.5 V为阈值电压, τlp为一阶微分项的常系数, 改变τlp可以调节异或非逻辑门的响应特性.
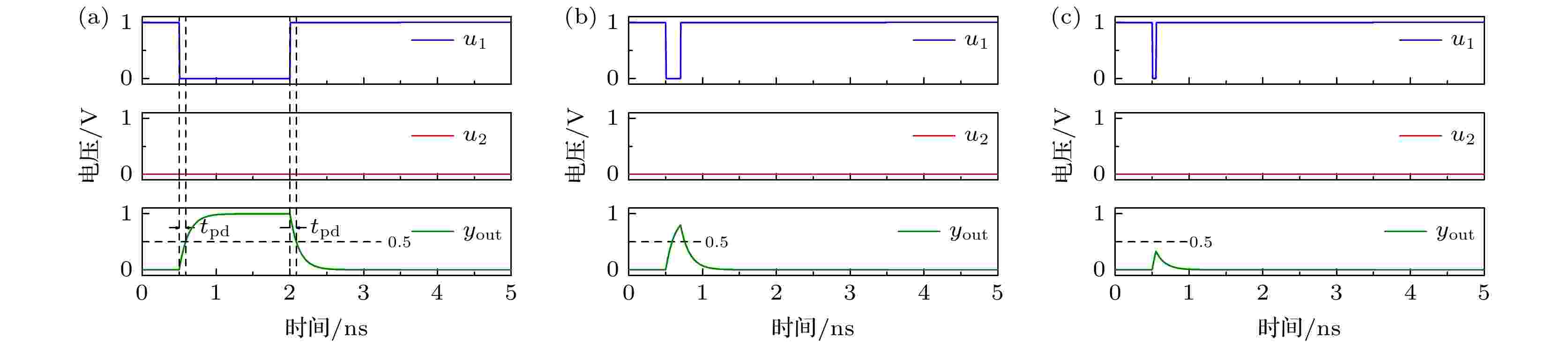图 2 异或非逻辑门输入输出响应波形图 (a) 完全响应波形图; (b) 不完全响应波形图; (c) 非正确响应波形图Figure2. I/O response waveform of XNOR logic gate: (a) Full response waveform; (b) incomplete response waveform; (c) incorrect response waveform.
(1)式—(3)式中τlp是器件输入输出延时tpd的常数倍, τlp = tpd/ln(2), tpd表示器件从接收到输入信号的变化开始响应到穿越阈值电压的时间[26]. 实际器件中tpd受制造工艺、环境温度、工作电压的影响, 不同器件之间差异较大, 相同器件之间也不能完全相同. 如图3所示, 图3(a)为输入信号, u2(t)为恒定低电平0 V, u1(t)初始为高电平1 V, 在0.50—0.75 ns处有一脉冲宽度?tu = 0.25 ns的低电平脉冲, yout(t)初始为低电平, 根据逻辑运算, 当u2(t)低电平脉冲出现时yout(t)应响应为高电平脉冲, 图3(b)中红色曲线为器件输出信号yout(t), 曲线峰值为输出脉冲幅值ymax, 蓝色曲线为输出信号yout(t)经过(2)式量化后的信号Yout(t), 如图所示, 蓝色曲线为矩形脉冲, 其脉冲宽度即为输出信号脉冲宽度?tY. 对比图中不同τlp取值的输出信号可以看出, 随着τlp增大, yout(t)的幅值ymax减小, 脉冲宽度?tY减小, 表明τlp增大器件响应速度变慢, 对于相同的输入信号, 其输出幅值减小脉冲宽度变窄, τlp为0.4 ns时脉冲宽度减小为0 ns. 此时器件响应速度太慢, 不能响应维持时间为0.25 ns的输入信号.
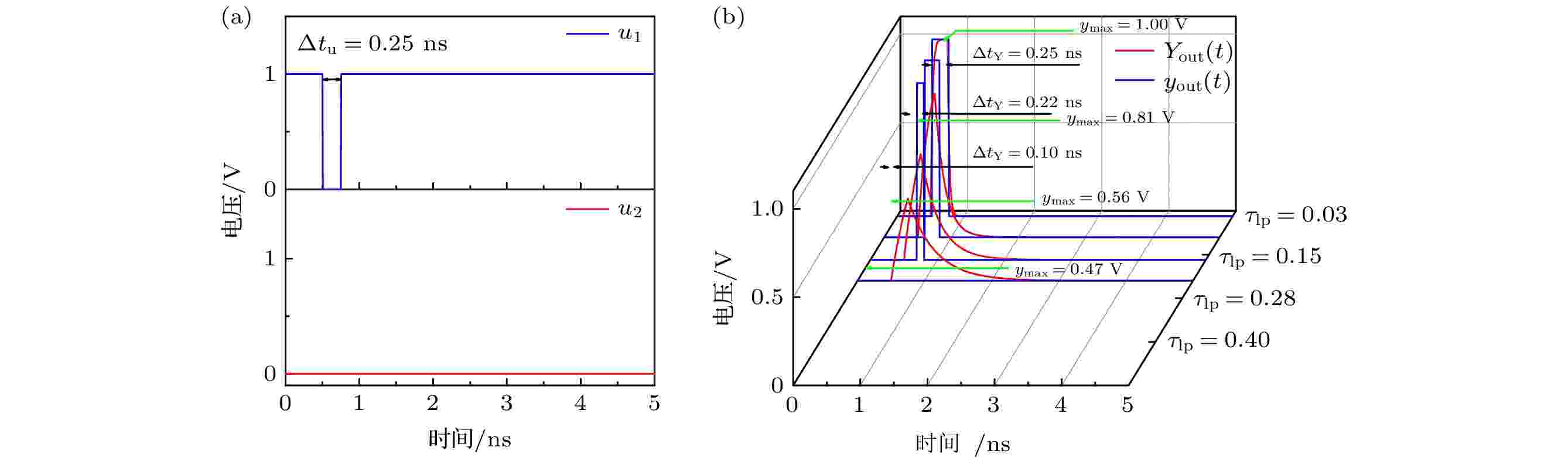图 3 异或非逻辑门输入相同, τlp = 0.03, 0.15, 0.28, 0.40时输出波形 (a)输入波形; (b)输出波形Figure3. Output waveforms of XNOR logic gate for τlp = 0.03, 0.15, 0.28, 0.40 when inputs are the same: (a) Input waveform; (b) output waveform.
为了更详细直观地观察输出波形随器件响应特性的变化规律, 选取5个输入信号, 如图4(a)所示, u2完全相同均为低电平0 V, u1, j表示u1的j种不同波形, 其低电平0 V保持时间分别为0.1, 0.2, 0.3, 0.4, 0.5 ns. 观察τlp从0.01 ns增大至5.00 ns时输出脉冲的幅值ymax和宽度?tY的变化, τlp调节步进为0.05 ns. 如图4(b)所示为ymax随τlp的变化曲线, 曲线有明显凹点, 凹点之前ymax随着τlp的变大迅速减小, 且减小的速度越来越快, 凹点之后减小的速度降低曲线趋于平缓. 图4(c)为?tY随着τlp的变化曲线, 可以看出, 对于同一个输入信号随着参数τlp的增大响应脉冲宽度?tY逐渐减小, 最终降为0 ns, 表明此时逻辑器件不能输出正确的响应(此例中为高电平). 仿真结果表明模型参数τlp能够对逻辑器件的响应特性进行连续调节, 因此本文中将参数τlp称为器件响应特性参数, 下文中通过调节τlp研究逻辑器件响应特性对自治布尔网络输出的影响.
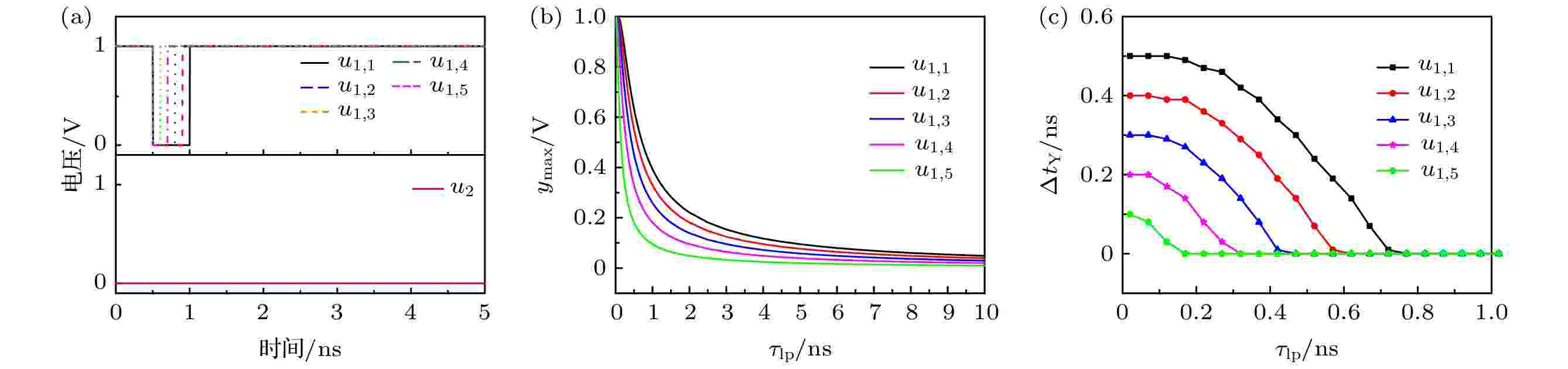图 4 异或非逻辑门输出脉冲幅值和宽度随τlp变化曲线 (a) 输入波形图; (b) 输出脉冲幅值ymax随τlp变化曲线; (c) 输出脉冲宽度?tY随τlp变化曲线Figure4. Output pulse amplitude and width as a function of τlp : (a) Input waveform; (b) output pulse amplitude as a function of τlp; (c) output pulse width as a function of τlp.
2
2.2.自治布尔网络模型
选取文献[10]中提出的三节点小型自治布尔网络作为研究对象, 如图5所示. 节点2为异或非逻辑门, 节点1, 3为异或逻辑门, 连接线箭头方向为信号传输方向, τij表示节点j到i的链路延时.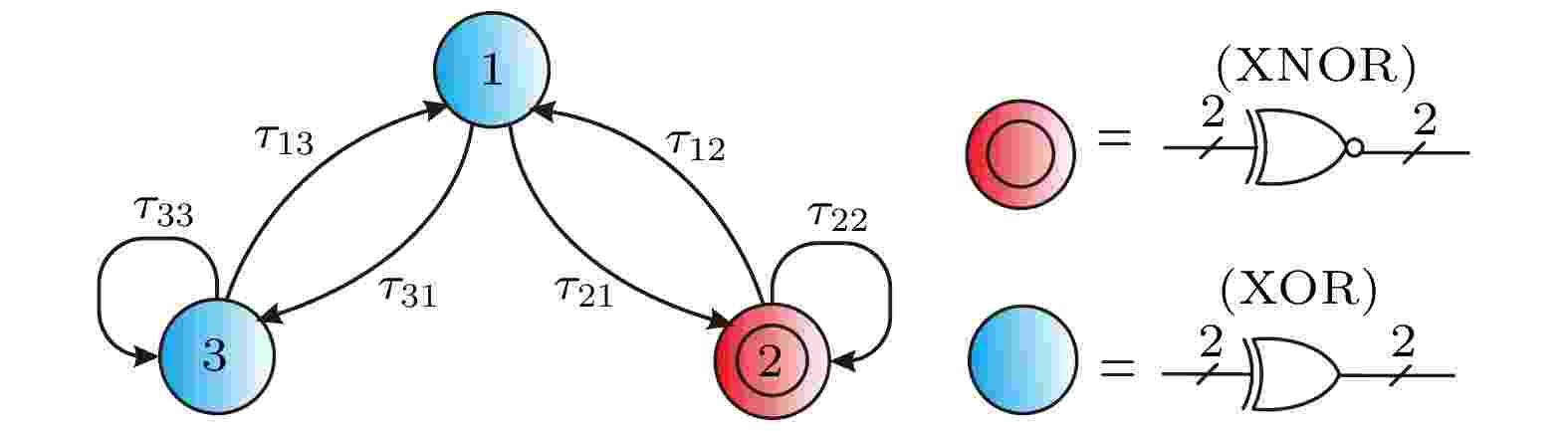
图 5 自治布尔网络示意图Figure5. Schematic illustration of autonomous Boolean network.
自治布尔网络的数学模型如 (4) 式和(5) 式所示, 对比模型(1) 式和(2)式可见, 三节点模型为3个模型(1)式中单节点模型相互连接, 网络中节点1, 2, 3的器件模型中仍然用微分项dx1/dt, dx2/dt, dx3/dt模拟器件响应输入信号的时间过程, 模型(1) 式和(2)式不同的地方是模型(2)式中各器件的输入信号来自其他器件或者件自身的输出信号, 而模型(1)式中输入信号为外部指定的. 因此多节点模型中微分项系数τlp,i能够调节器件响应特性, τlp,i减小器件响应速度更快, 使器件能够响应维持时间更短的输入信号. (4)式中“
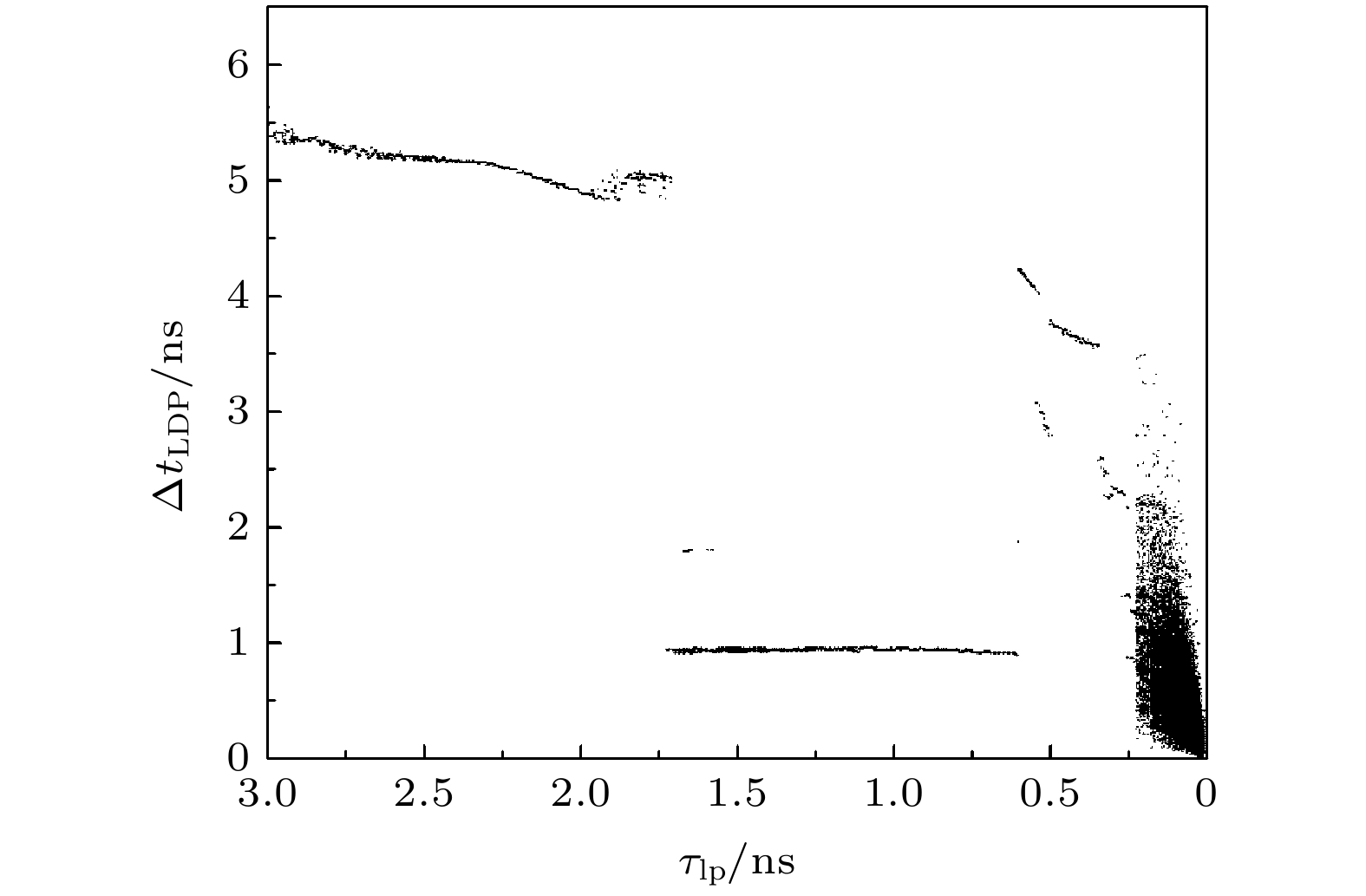图 6 自治布尔网络分岔图Figure6. Bifurcation diagram of the autonomous Boolean network.
图7为τlp = 0.630 ns, 0.305 ns和0.050 ns时网络输出时序、频谱、?tLDP序列相图. 图7(a1),(b1)和(c1)表明 τlp = 0.63 ns时的输出为周期时序, 对应的频谱中有尖峰, 此时?tLDP序列相图可以看出, 存在两个相近的?tLDP, 分别为0.89 和0.92 ns, 表明一个周期内有2次上升沿和下降沿; 图7(a2), (b2), (c2)表明τlp = 0.305 ns时输出时序比图7(a1)复杂程度更高, 但仍有周期; 图7(a3), (b3), (c3)表明τlp = 0.05 ns时输出为频谱平坦的混沌.
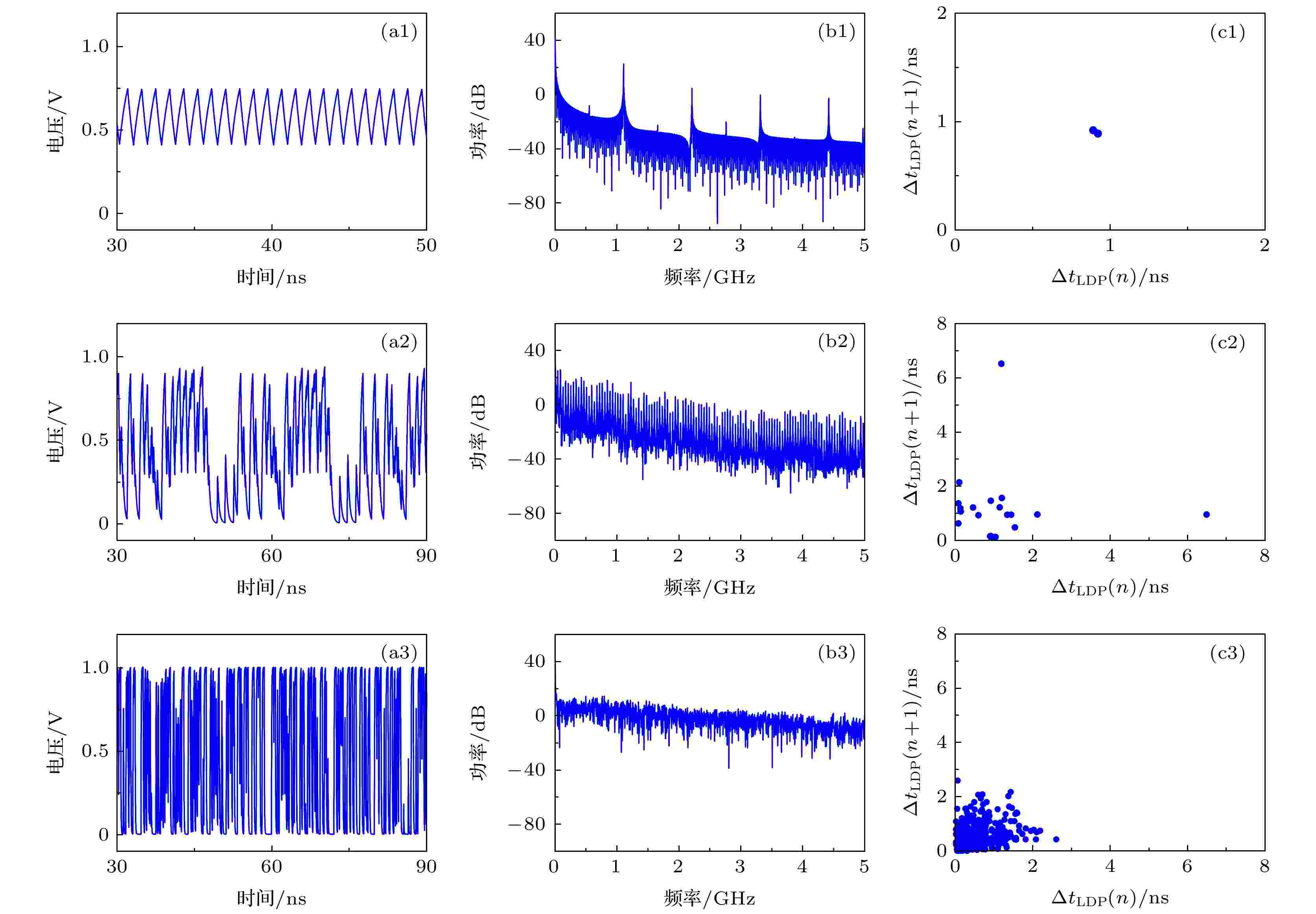图 7 自治布尔网络在τlp = 0.630, 0.305, 0.050 ns的模拟结果 (a1)?(a3) 时序; (b1)?(b3) 频谱; (c1)?(c3) ?tLDP序列相图Figure7. Simulation results of the autonomous Boolean network for τlp = 0.630, 0.305, 0.050 ns: (a1)?(a3) Time-evolution; (b1)?(b3) power spectra; (c1)?(c3) phase diagrams of ?tLDP series.
节点之间的链路延时τij是自治布尔网络的另一个重要参数, 不失一般性地, 假设τij和τlp两个参数在调节过程中会相互影响, 为了研究响应特性参数τlp,i和链路延时参数τij之间的相互作用, 本文对自治布尔网络输出的复杂程度在参数τlp,i和τij二维空间上的分布情况进行了研究. 排序熵是常用的混沌表征方法, 可以衡量序列的复杂程度, 具有计算简单快速的优点[27,28]. 固本文中应用排序熵H表征输出序列的复杂程度, 排序熵计算如下:
图8所示为自治布尔网络输出的排序熵在参数τlp (τlp = τlp,1 = τlp,2 = τlp,3)和τij二维空间上的分布, 图中颜色表示不同的排序熵值, 红色区域的排序熵值较高, 观察可见红色区域主要分布在图中右下三角区域, 表明τij越大τlp越小时布尔网络输出排序熵值越高序列复杂程度越高, 此外, 图中有零散的小面积红色区域分布, 猜测其分布规律可能与τij的取值有关. 本文定义序列排序熵值H > 0.95为高复杂序列, 图中黑色曲线为H = 0.95的等值线, 随着τlp减小, τij轴方向H > 0.95等值线内区域范围逐渐变宽, 表明τlp减小可以增大τij参数空间中高复杂序列的分布范围, 有利于高复杂混沌的稳定产生. 观察比较图中相同列的两幅排序熵分布, 图8(a),(d)、图8(b),(e)具有相似的分布, 表明节点i, j相互传输的两个延时τij和τji具有一致的调控效果.
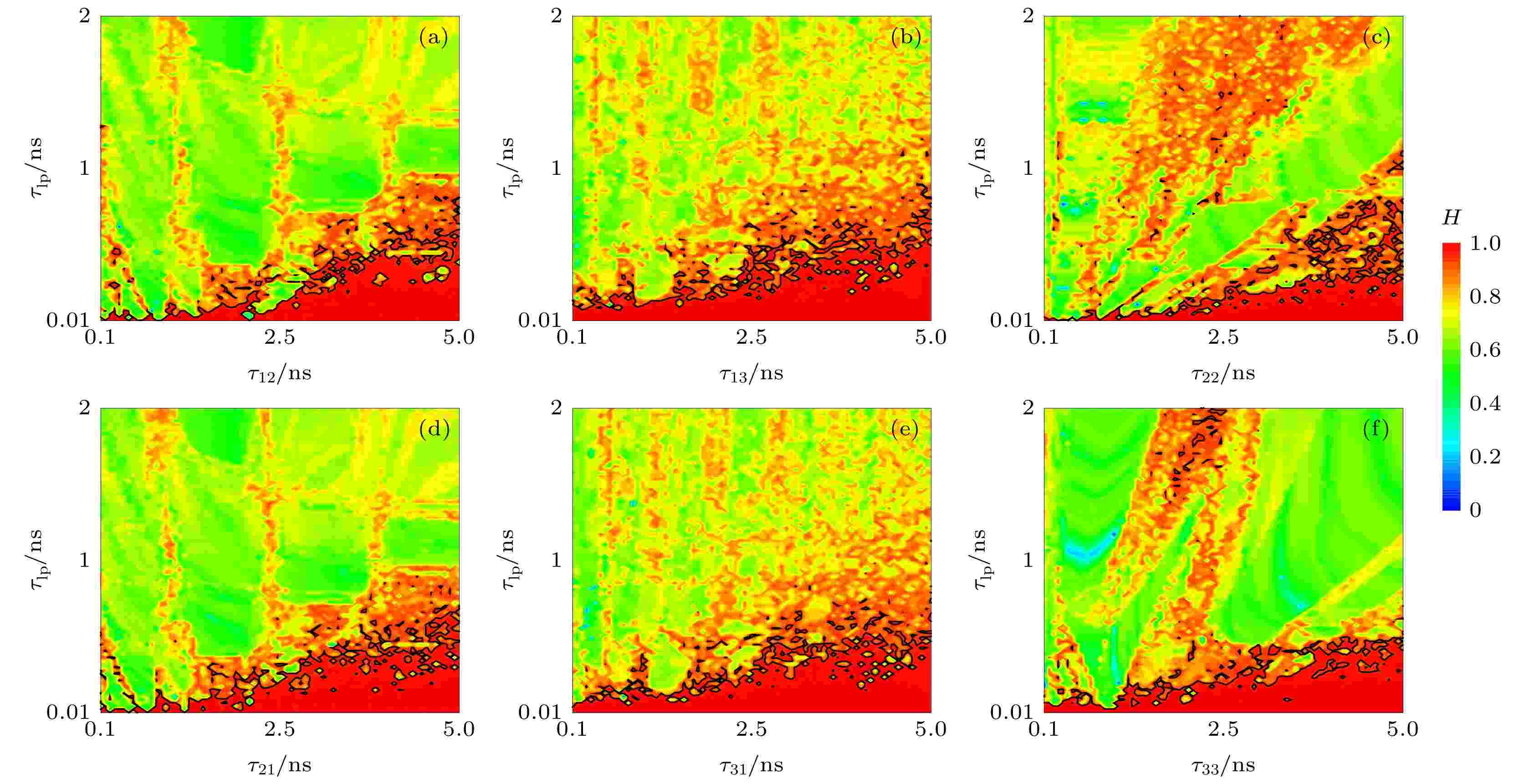图 8 排序熵值在二维参数空间τlp和τij上的分布图 (a) τij = τ12; (b) τij = τ13; (c) τij = τ22; (d) τij = τ21; (e) τij = τ31; (f) τij = τ33Figure8. Two dimensional maps of H in the parameter space of τlp and τij: (a) τij = τ12; (b) τij = τ13; (c) τij = τ22; (d) τij = τ21; (e) τij = τ31; (f) τij = τ33.
进一步研究了自治布尔网络中不同节点处逻辑器件响应特性单独变化对输出的影响. 图9(a)—(c)分别为固定τlp,1, τlp,2, τlp,3时, 输出排序熵值在(τlp,1, τlp,2), (τlp,1, τlp,3), (τlp,2, τlp,3)的二维参数空间中的分布图. 通过比较第1行、第2行、第3行可以发现, 第1行图中高排序熵区域较大, 表明任意单个节点τlp,i减小都有利于高排序熵序列的产生. 图9(b1)的红色区域显著高于其他分布图, 可以表明τlp,2的减小对网络输出的高排序熵空间增强效果最大, 可有效促进高排序熵序列的产生.
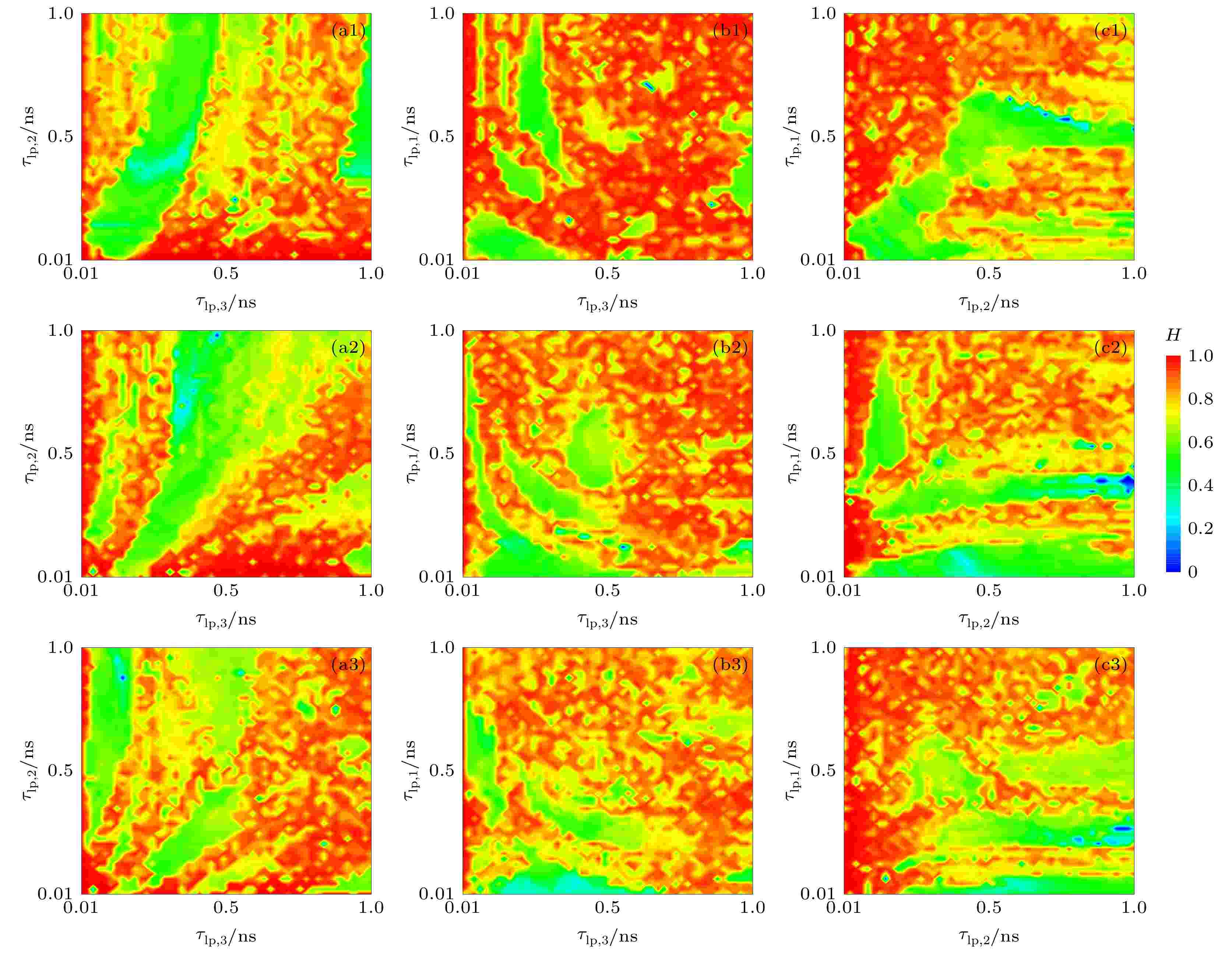图 9 排序熵值在二维参数空间(τlp,i, τlp,j)上的分布图 (a1)?(a3) τlp,1 = 0.1, 0.3, 0.5 ns且(τlp,i, τlp,j) = (τlp,2, τlp,3); (b1)?(b3) τlp,2 = 0.1, 0.3, 0.5 ns且(τlp,i, τlp,j) = (τlp,1, τlp,3); (c1)?(c3) τlp,3 = 0.1, 0.3, 0.5 ns且(τlp,i, τlp, j) = (τlp,1, τlp,2)Figure9. Two dimensional maps of H in the parameter space of (τlp,i, τlp,j): (a1)?(a3) τlp,1 = 0.1, 0.3, 0.5 ns and (τlp,i, τlp,j) = (τlp,2, τlp,3); (b1)?(b3) τlp,2 = 0.1, 0.3, 0.5 ns and (τlp,i, τlp,j) = (τlp,1, τlp,3); (c1)?(c3) τlp,3 = 0.1, 0.3, 0.5 ns and (τlp,i, τlp,j) = (τlp,1, τlp,2).
本文研究成果对自治布尔网络各应用领域器件的选择具有重要意义, 根据不同的应用需求选择不同响应特性的器件, 如在随机数的应用中, 随机数是信息加密过程中的关键组成部分, 随机数的产生速率和不可预测性是信息加密安全性的重要保障, 应用本文的研究结论, 选择器件响应特性快的器件可以提高序列复杂程度, 增强高复杂序列空间, 促进高复杂混沌序列的稳定产生, 进而提高随机数产生速率和不可预测性.
