摘要:心电图(electrocardiogram, ECG)诊断心脏疾病的严格标准, 要求有效地消除噪声并准确地重建ECG信号. 经验模式分解(empirical mode decomposition, EMD)方法重建ECG信号中, 模式混叠及重建采用模式分量的识别以经验为基础, 导致重建ECG信号准确度降低, 且方法不具有自适应和通用性. 本文首先基于积分均值定理提出一种改进的EMD方法—积分均值模式分解(integral mean mode decomposition, IMMD)方法, 经5000个高斯白噪声样本的蒙特卡罗法验证, IMMD方法比EMD具有更优多分辨率分析能力, 能够有效地缓解模式混叠. 其次, 基于ECG信号内固有心动物理特征量识别重建ECG信号所采用的模式分量, 具有现实物理意义, 因此, 方法具有自适应和通用性. 经验证, 提出方法重建47例ECG信号与原ECG信号的相关系数中: 31例优于变分模式分解方法; 33例优于Haar小波软阈值法; 42例优于集总经验模式分解方法; 45例优于EMD方法. 相关系数均值为0.8904, 方差为0.0071, 表现稳定且最优.
关键词: 心电信号/
重建/
心率/
积分均值模式分解

English Abstract

全文HTML

--> --> -->

心电图(electrocardiogram, ECG)记录的是心脏生理电活动信号, ECG检查一般通过ECG中P, QRS, T特征波波形、时长及幅值识别诊断各种心脏疾病. 例如P波形状高尖, 且振幅 ≥ 0.25 mV判断为右房肥大; P, R间期延长 > 0.21 s存在房室传导阻滞等^[1]. 因此, ECG信号轻微失真, 也可能导致心脏疾病误诊. 然而, ECG信号是一种非线性、非平稳弱信号, 极易被噪声污染. 噪声一般包括两类: 50 Hz (在一些国家为60 Hz)电源线工频及由呼吸、电极或人体运动引起的基线漂移(baseline wander, BW)等窄带噪声; 主要由肌肉收缩引起的肌电干扰(muscle artifact, MA)等宽带噪声^[2]. 两种噪声常常叠加引起ECG信号畸变, 严重影响ECG诊断评估心脏病准确性, 甚至导致诊断失效. 严格的ECG检查标准量以及ECG信号的噪声特点, 要求有效消除噪声后重建的ECG信号具有高准确度.
窄带噪声频谱与ECG信号频谱不重叠, 常见线性和非线性信号处理方法都可有效校正^[3-5], 而宽带噪声全频域污染ECG信号, 导致严重特征波失真, 成为ECG信号消噪重点. 迄今为止, 已有多种非线性信号处理方法应用于消除宽带噪声并重建ECG信号, 但各种方法均存在缺点, 重建准确度不令人满意. 其中, 自适应滤波需要额外地采集噪声相关参考信号^[6]; 奇异值分解(singular value decomposition, SVD)^[7]和小波阈值法^[8,9]中, 阈值过小消噪不理想, 过大将导致波形严重畸变, 并且阈值不能自适应噪声水平的波动^[10].
经验模式分解(empirical mode decomposition, EMD)是一种自适应且数据驱动的非线性信号处理方法^[11], 可以克服SVD 和小波阈值法缺乏自适应的缺点, 成为近年来生理信号^[12]、医学图像^[13]、特别是ECG信号重建的研究热点. 然而, EMD域内重建ECG信号存在两个问题: 1)瞬时模态分量(intrinsic mode function, IMF)之间的模式混叠, 导致ECG信号重建不准确. 集总经验模式分解(ensemble empirical mode decomposition, EEMD)^[14]以及变分模式分解(variational mode decomposition, VMD)^[15]能够缓解模式混叠, 并已应用于ECG信号消噪和重建^[16,17]. 然而, 严格意义上, 对每一个ECG信号, EEMD都需要预先多次测试并选择合适的辅助噪声幅度和数量; VMD同样需要预先多次测试并选择合适的分解层数、平衡参数、噪声松弛等参数, 因此, 两种方法都不属于自适应且不具有通用性. 2) 重建ECG信号采用的模式分量基于工作者经验识别^[18,19], 不具有通用性. 采用IMF的香农熵、平均值、方差等统计特征量的阈值识别IMF, 阈值也基于经验设置^[20].
极值域模式分解(extremum field mean mode decomposition, EMMD)^[21]是一种改进的EMD方法. EMMD采用积分均值定理(integral mean value theorem, IMVT)求信号均值, 能够增强分解信号能力, 但EMMD算法分解信号存在过分解问题. 为了在EMD域内进一步提高重建ECG信号准确度, 同时保证重建方法具有自适应和通用性, 本文提出一种重建ECG信号新方法. 新方法首先改进EMMD, 保留IMVT均值方法并解决算法导致的过分解问题. 为了区别于EMMD, 本文将改进的EMMD称为积分均值模式分解(integral mean mode decomposition, IMMD). 经验证可以发现, IMMD比EMD具有更优的多分辨率分解能力, 并且可以有效地缓解IMF之间的模式混叠. 其次, 心电活动或心肌细胞的除极、复极过程对应一个完整的心动周期, 因此, ECG信号呈现心动的周期性波动, 其IMF分量同样表现出心动物理周期特征. 本文采用心动物理周期特征识别属于ECG信号的IMF, 识别方法符合ECG信号的物理本质, 并保证重建ECG信号方法的自适应及通用性.

2

-->

2.1.IMMD方法

设 $x_i(t) ~(t_i\leqslant t \leqslant t_{i+1}, i= 1,2,\cdots, n-1)$为信号$ x?(t) $相邻两个极值$ x(t_i) $和$ x(t_{i+1}) $之间的局部, IMVT求信号局部$ x_i(t) $的均值为

${m_i}(t) = \frac{1}{{{t_{i + 1}} - {t_i}}}\sum\limits_{{t_i}}^{{t_{i + 1}}} {{x_i}(t)} . $

m_i(t)固定于局部中点$t = \dfrac{1}{{{t_i} + {t_{i + 1}}}}$. 基于(1)式求出所有局部均值点后, 三次样条插值所有均值点构建均值曲线m(t).
原型模式函数(proto mode function, PMF)^[22] 即为

$ \mathrm{PMF}(t) = x(t) - m(t) . $

上述过程称为一次均值筛选^[11], PMF记为PMF₁. PMF₁作为一个新信号, 迭代重复均值筛选过程k (k = 2, 3, ···)次, 得到PMF_k. 当PMF_k满足柯西筛选停止准则^[11]:

$\begin{split}\mathrm{SD} \!=\!\;& \!{\sum\limits_{t = 0}^{T}\!{\left[ {{\left| \mathrm{PM}{{\mathrm{F}}_{k -1}}(t) \!-\! \mathrm{PM}{{\mathrm{F}}_{k}}(t) \right|}^{2}} \!\right]}}\bigg/{\sum\limits_{t = 0}^{T}\!{\left[ \mathrm{PMF}_{k \!-\! 1}^{2}(t) \right]}}\; \\&< 0.2—0.3 , \\[-10pt]\end{split}$

筛选停止, PMF_k即为IMF1. 将剩余分量${r_1}(t) = $ x(t) – IMF1作为新信号, 重复上述所有过程得到IMF2. 同理, 可得其余IMF分量及剩余分量r(t).
除局部均值外, EMMD方法利用相邻两个局部均值m_i(t)和m_i+1(t)加权求取二者之间极值点t_i+1处均值, 即:

$m({t_{i + 1}}) = h({t_i}){m_i}(t) + h({t_{i + 1}}){m_{i + 1}}(t), $

其中,

$h({t_i}) = \frac{{{t_{i + 1}} - {t_i}}}{{{t_{i + 2}} - {t_i}}},~~{\rm{ }}h({t_{i + 1}}) = \frac{{{t_{i + 2}} - {t_{i + 1}}}}{{{t_{i + 2}} - {t_i}}}.$

然而, m(t_i+1)携带数据信息是m_i(t)和m_i+1(t)所携信息的重复. 并且均值点数增加, 极易导致样条插值构造均值曲线的不平滑, 最终造成信号过分解. 因此, IMMD方法仅采用局部均值经三次样条插值构建均值曲线.
2 -->

2.2.IMMD方法的多分辨率分解信号能力

文献[23]研究了EMD分解5000个长度N = 512, 均值为0, 方差为1的高斯白噪声数据样本, 得到如下结论: EMD类似于小波变换Mallat算法, 等效于一个恒定品质因子Q的二分(或二进)滤波器组, 具有多分辨率分解信号能力. 本节将采用同样方法, 分析IMMD分解高斯白噪声特性, 以此说明方法分解信号的性能.
IMMD分解每个高斯白噪声样本, 得到至少10个IMF. 对所有样本相应阶数IMF求平均傅里叶功率谱, 结果见图1(a). IMF1相当于一个高通滤波器, 其余IMF等效于一组重叠带通滤波器, 且后一IMF等效带通滤波器中心频率约是前一 IMF等效带通滤波器中心频率的2/3. IMMD方法分解高斯白噪声等效于滤波器组, 且具有三分特性.
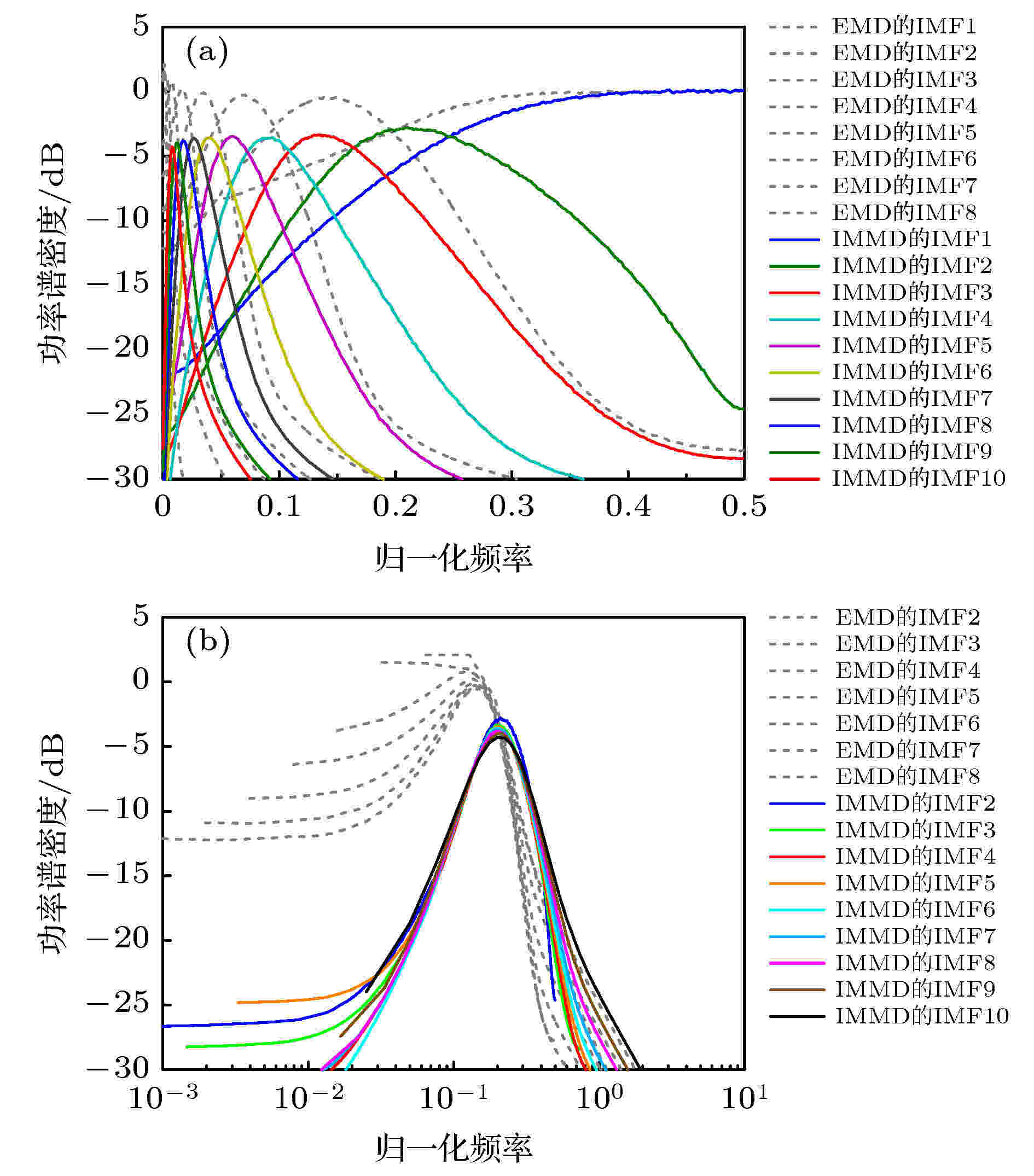图 1 IMMD和EMD方法分解高斯白噪声的等效滤波器组特性　(a) IMMD (实线)和EMD (虚线)的IMF分量的平均功率谱; (b) 基于(5)式, IMMD (实线)和EMD (虚线)的IMF分量的平均功率谱坍缩重合
Figure1. Equivalent filter banks of IMMD and EMD decomposing Gauss white noises: (a) Averaged power spectra of IMFs from IMMD (solid curves) and EMD (dotted curves); (b) collapse and coincidence of the average power spectrum of IMFs from IMMD (solid curves) and EMD (dotted curves) based on Eq. (5).

除IMF1外, 后一IMF等效带通滤波器频带宽度大致是前一IMF的2/3, 所以等效带通滤波器组具有恒Q性质. 因此, IMFs的功率谱存在自相似性^[23]:

${S_{k'}}(f) = {S_k}({\rho ^{k' - k}}f) , $

其中${S_{k'}}(f)$是第$k'$个IMF的功率谱(${S_k}(f)$是第k个IMF的功率谱), $k' > k \geqslant 2$; ρ是常数, 对于IMMD, $\rho = 3/2$, 对于EMD, $\rho = 2$. 基于(5)式对平均功率谱标准化, 所有带通IMF的功率谱坍缩并重合为一条曲线. 对于EMD, 带通滤波器混叠较多低频成分, 关于中心频率对称度差, 窄带特性差, 需要适当调整ρ值为2.01^[24]. 对于IMMD, 等效带通滤波器关于中心频率对称度及窄带特性明显优于EMD, 两套等效带通滤波器组的平均功率谱标准化结果如图1(b)所示.
IMMD分解高斯白噪声等效滤波器组具有三分特性, 等效滤波器个数多于EMD (图1), 滤波器组窄带特性及恒Q性质优于EMD, 因此, 具有更好的多分辨率分析能力. 除上述5000个高斯白噪声样本数据的蒙特卡罗方法实验外, 本课题组基于大量数据实验, 验证得到: 相比EMD, IMMD具有更好的多分辨率分析能力, 可以有效地缓解IMF分量之间模式混叠.
2 -->

2.3.心动物理特征识别IMF

ECG信号是记录人体心脏电活动信号, 具有心动物理周期特性, 其IMF分量将呈现心动周期或心率(heart rate, HR)特征.
任一个IMF分量可表达为^[25]

$\mathrm{IMF} = a(t)\cos (\varphi (t)) , $

其中$\varphi (t)$为IMF频率调制, $a(t)$为IMF振幅调制. 心动周期特征通过两种模式作用于IMF分量: 1) 属于ECG信号的低阶IMF, 心动周期特征作用于调幅$a(t)$. 此时, IMF分量的包络具有心动周期特性, 包络的频谱中最大幅值对应频率等于HR. 2) 属于ECG信号的高阶IMF, 心动周期特征作用于调频$\varphi (t)$. 此时, IMF具有周期性心动的谐波特性, 频谱中最大幅值对应频率为HR的整数倍(通常为1—3倍). 噪声属性IMF分量不能表现上述两种心动周期特性.
2 -->

2.4.IMMD域内心动物理特征识别模式分量重建ECG方法

1) 含噪ECG信号经IMMD分解为一套IMFs分量集合;
2) 求出每一个IMF的上包络功率谱, 若谱中最大幅值对应频率等于HR, 则IMF被识别为ECG信号分量;
3) 对步骤2中未被识别为ECG信号分量的IMF, 求出每一个IMF功率谱, 若谱中最大幅值对应频率等于HR整数倍, 则IMF也被识别为ECG信号分量;
4) 采用上述所有被识别为ECG信号分量的IMF重建ECG信号.

2

-->

3.1.105 ECG信号^[26]实验

选取MIT-BIH心律失常数据库中105 ECG、压力测试数据库中BW和MA噪声^[27], 叠加构成含噪105 ECG信号, 采样频率为360 Hz, 采样长度为3.6 × 10³, HR等于1.4 Hz, 如图2所示. 可见, 原105 ECG信号的噪声污染程度较低, 便于本节下述实验中的定量分析.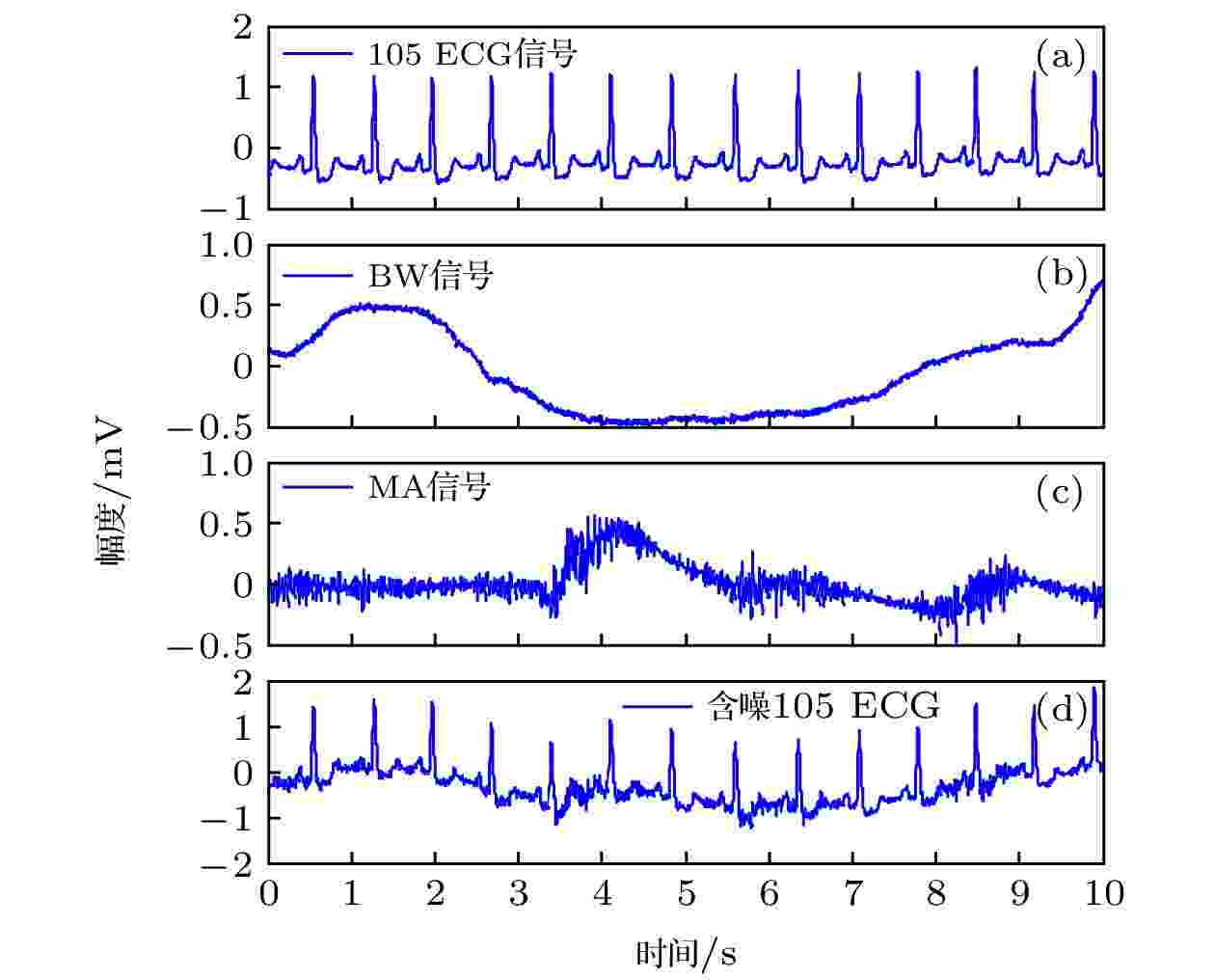
图 2 实验采用信号波形　(a) 105 ECG信号; (b) BW信号; (c) MA信号; (d)含噪105 ECG信号
Figure2. Waveform of signals used in experiment: (a) No. 105 ECG signal; (b) BW signal; (c) MA signal; (d) the noisy No. 105 ECG signal.

IMMD分解含噪105 ECG信号得到IMF分量及其包络如图3所示, 对应频谱如图4所示. IMF1和IMF2及其包络的频域中, 幅值最高点处频率不等于1.4 Hz, 因此没有表现出心动周期特征作用IMF的两种模式(详见2.3节), 被识别为MA噪声高频分量; IMF3—8包络的频域中, 幅值最高点对应频率等于心率1.4 Hz, 符合心动周期特征作用IMF的第一种模式; IMF9—12的频域中, 幅值最高点对应频率分别等于心率的3, 3, 2, 1倍, 识别为ECG信号谐波分量, 符合心动周期特征作用IMF的第二种模式; IMF13—r没有表现出心动周期特征作用IMF的两种模式, 统一归类为低频噪声. 产生的原因包括: MA噪声低频分量, BW噪声分量, IMMD方法端点效应以及原105 ECG信号的非零均值. 经上述心动物理周期特征识别, IMF3—12为ECG信号分量, IMF1和IMF2为高频噪声, IMF13—r为低频噪声.
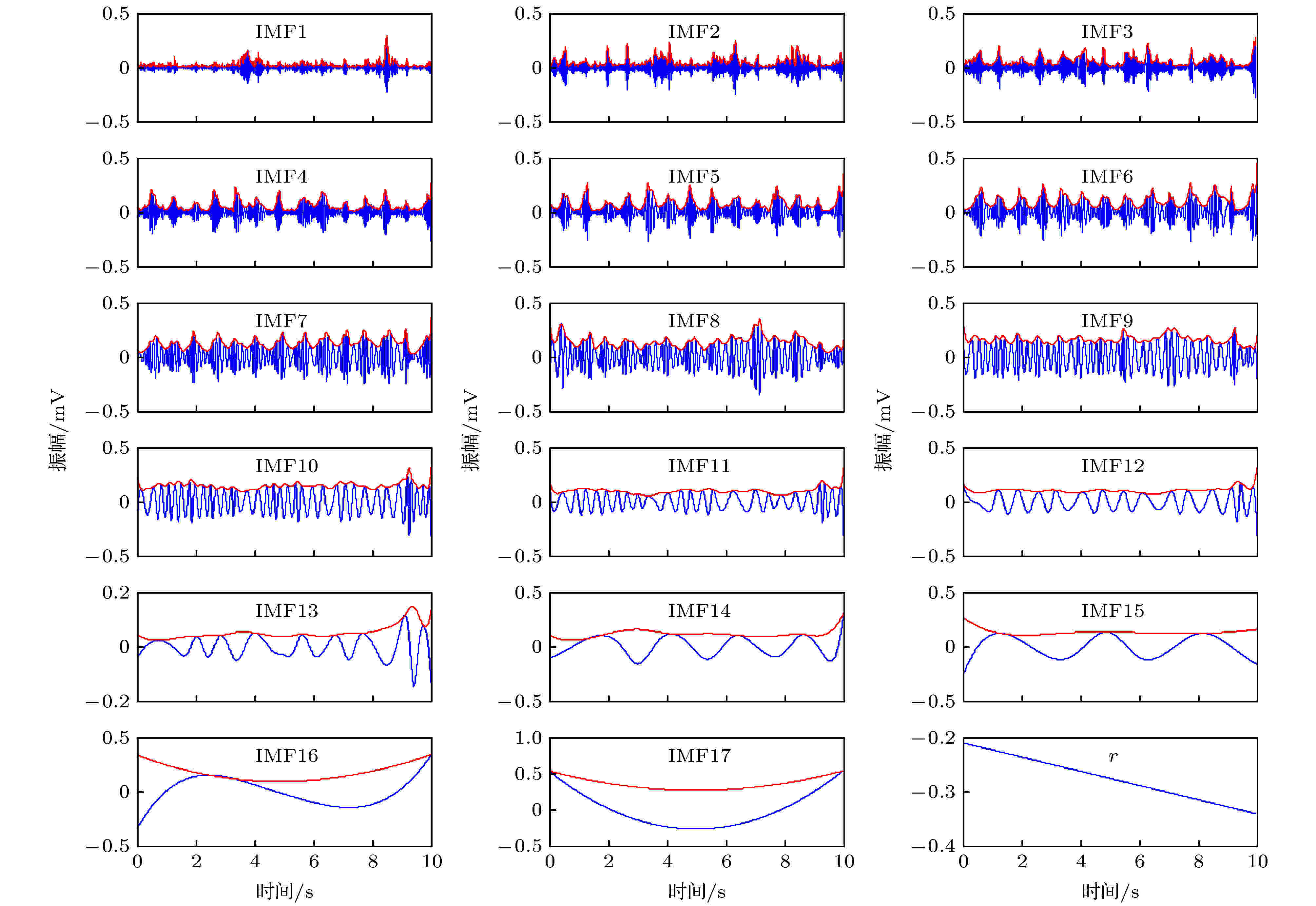图 3 含噪105 ECG信号的IMF (蓝色曲线)及其包络(红色曲线)
Figure3. IMF envelopes (red curves) and IMFs (blue curves) of noisy No. 105 ECG signal.

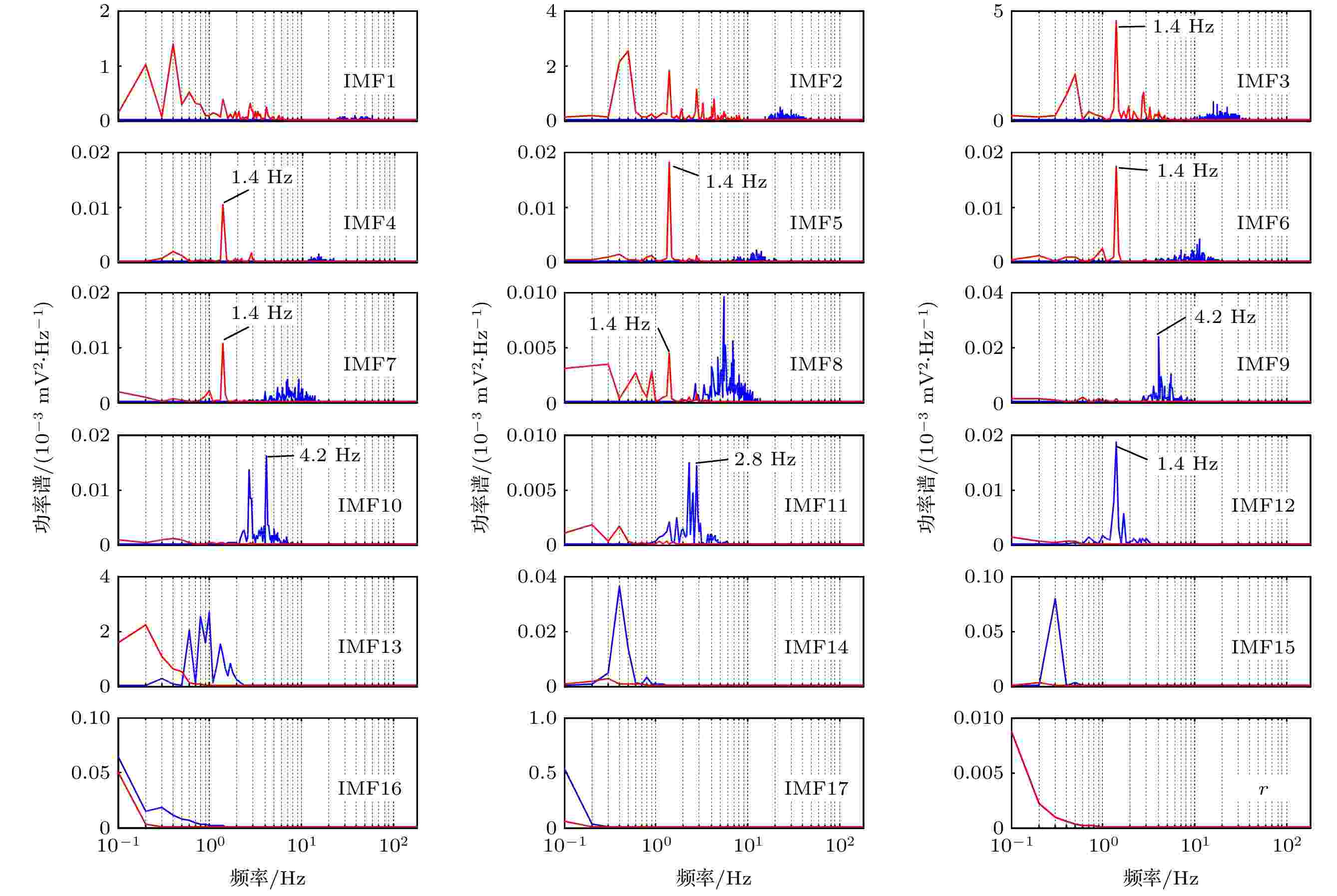图 4 含噪105 ECG信号IMFs的功率谱(蓝色曲线), 及IMFs包络的功率谱(红色曲线)
Figure4. Power spectra of envelopes of IMFs (red curves) and of IMFs (blue curves) of noisy No. 105 ECG signal.

为了显示所提出方法的能力, 将本文方法同近年来常用VMD、小波软阈值法、EEMD以及EMD重建105 ECG信号进行对比, 利用这五种方法重建的105 ECG信号如图5所示. 由图5可见, 五种方法都很好地消除了BW噪声. 由于MA噪声宽频特性, 五种方法重建ECG信号中仍然存在少量MA噪声分量, 特别是Harr小波软阈值方法. EMD方法重建ECG信号畸变最为严重, 其次是EEMD. 实际中, EEMD对含噪105 ECG信号的多次重建结果之间都有轻微不同, 这是由辅助白噪声的随机性引起的^[28]. 另外, VMD方法中特征R波的峰值失真比本文提出方法严重, 例如, 图5(b)中第10个R波波峰峰值损失14.5%, 本文方法为3.2%.
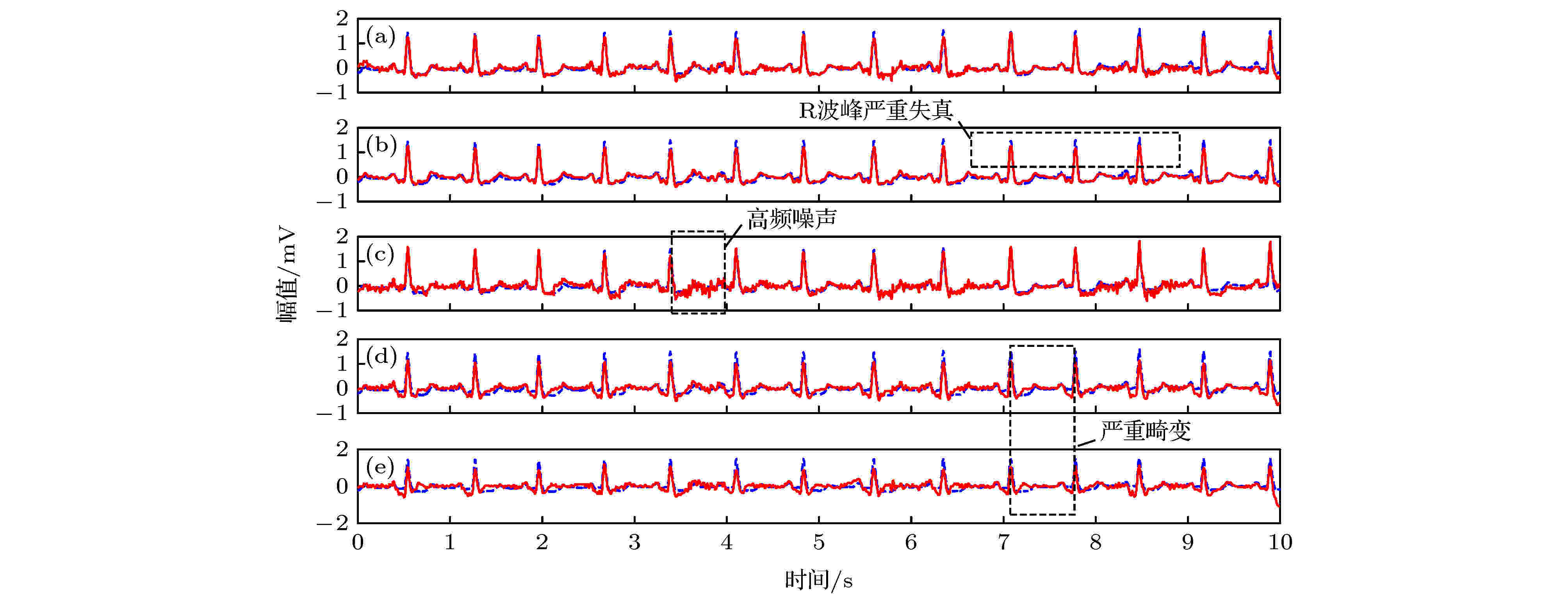图 5 原105 ECG信号(蓝色点虚线)与由五种方法重建的105 ECG信号(红色实线)　(a) 本文方法; (b) VMD; (c) Haar小波软阈值; (d) EMMD; (e) EMD
Figure5. Original No. 105 ECG signal (blue dotted curves) and the No. 105 ECG signals (red solid curves) reconstructed by 5 methods: (a) The proposed method; (b) VMD; (c) Haar wavelet with soft threshold; (d) EEMD; (e) EMD.

采用重建ECG与原ECG信号的相关系数R定量描述重建准确度, 信噪比(signal-to-noise ratio, SNR)及均方误差(mean square error, MSE)定量描述消噪能力, 五种方法重建105 ECG信号R, SNR, MSE的值如表1所列. 可见, 提出方法的R和SNR值最大, MSE值最小, 重建105 ECG信号和消噪能力最优.

重建方法	R	SNR/dB	MSE/mV2
本文方法	0.9577	10.7740	0.0076
VMD	0.9572	10.6602	0.0078
Haar	0.9434	9.0070	0.0114
EEMD	0.9204	8.1126	0.0140
EMD	0.7638	3.6982	0.0388

表1五种方法重建105 ECG信号的特征量值
Table1.Characteristic values of No. 105 ECG signals reconstructed by 5 methods.

2 -->

3.2.47例含噪ECG信号实验

为了进一步验证提出方法的有效性以及普遍适用性, 选取MIT-BIH心律失常数据库中其余ECG信号(心律失常ECG信号对应类型见表2), 分别叠加BW和MA噪声, 构成47例含噪ECG信号(除去周期性极差的232号), 并采用上述五种方法重建47例原ECG信号.

心律失常类别	ECG索引号
房性早搏	100, 232
P波峰值和 起搏心搏	102, 104, 107, 217
心房颤动	201, 203, 210, 219, 221
预激综合征	230
左束支传导阻滞	109, 111, 214
右束支传导阻滞	118, 124, 207, 212, 231, 232
室性早搏	119, 200, 203, 207, 208, 210, 214, 221, 233

表2实验采用的部分ECG信号对应心律失常类型
Table2.Type of arrhythmia corresponding to some ECG signals used in the experiment.

由于大多数原ECG信号本身含有一定量的低频和高频噪声, 严重影响SNR和MSE值的准确度, 因此, 仅采用相关系数R对五种方法进行对比评估. 利用五种方法重建5组47例ECG信号与原ECG信号的相关系数柱状图如图6所示. 其中, 本文提出方法有31例R值优于VMD, 33例R值优于Haar小波, 42例R值优于EEMD, 45例R值优于EMD.
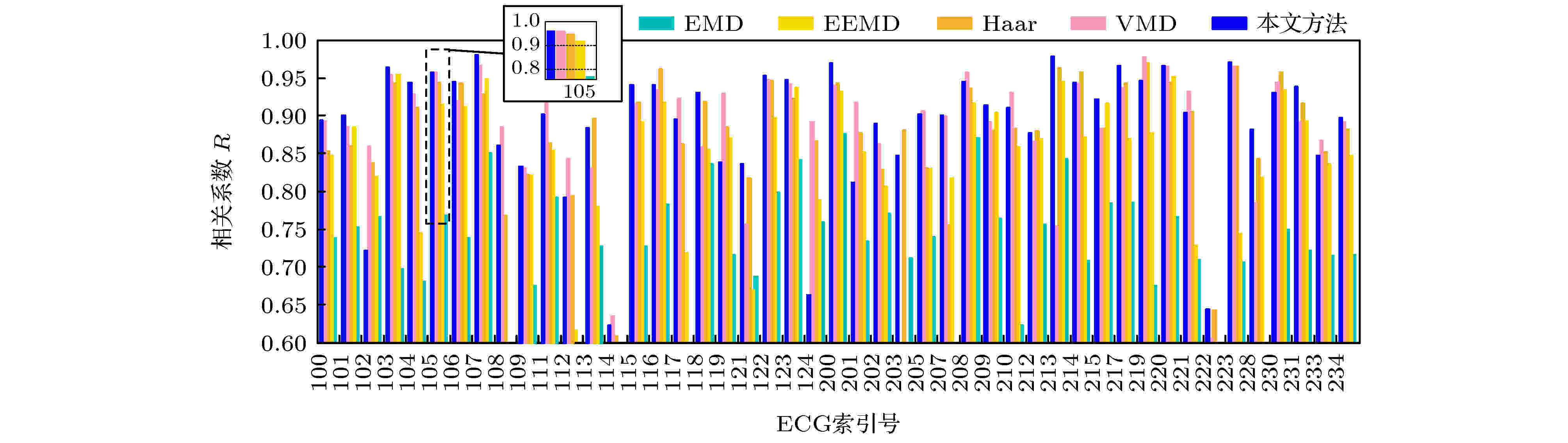图 6 采用五种方法重建47个ECG信号的R值柱状图
Figure6. Histogram of R values of 47 ECG signals reconstructed by 5 methods.

采用五种方法重建47个ECG信号的相关系数R值的统计盒形图如图7所示, 平均值及方差见表3. 表3中, 本文提出方法对应相关系数均值最高, 方差仅大于小波阈值. 由图7可见, 本文提出方法明显优于其余四种方法. 本文提出方法重建ECG信号最为稳定、准确, 其次为VMD, Haar小波阈值法, EEMD, EMD.

重建方法	均值	方差
本文方法	0.8904	0.0071
VMD	0.8826	0.0081
Haar	0.8804	0.0058
EEMD	0.8222	0.0166
EMD	0.7100	0.0143

表3五种方法重建47个ECG信号的R值的均值与方差
Table3.Means and variances of R values of 47 ECG signals reconstructed by 5 methods.

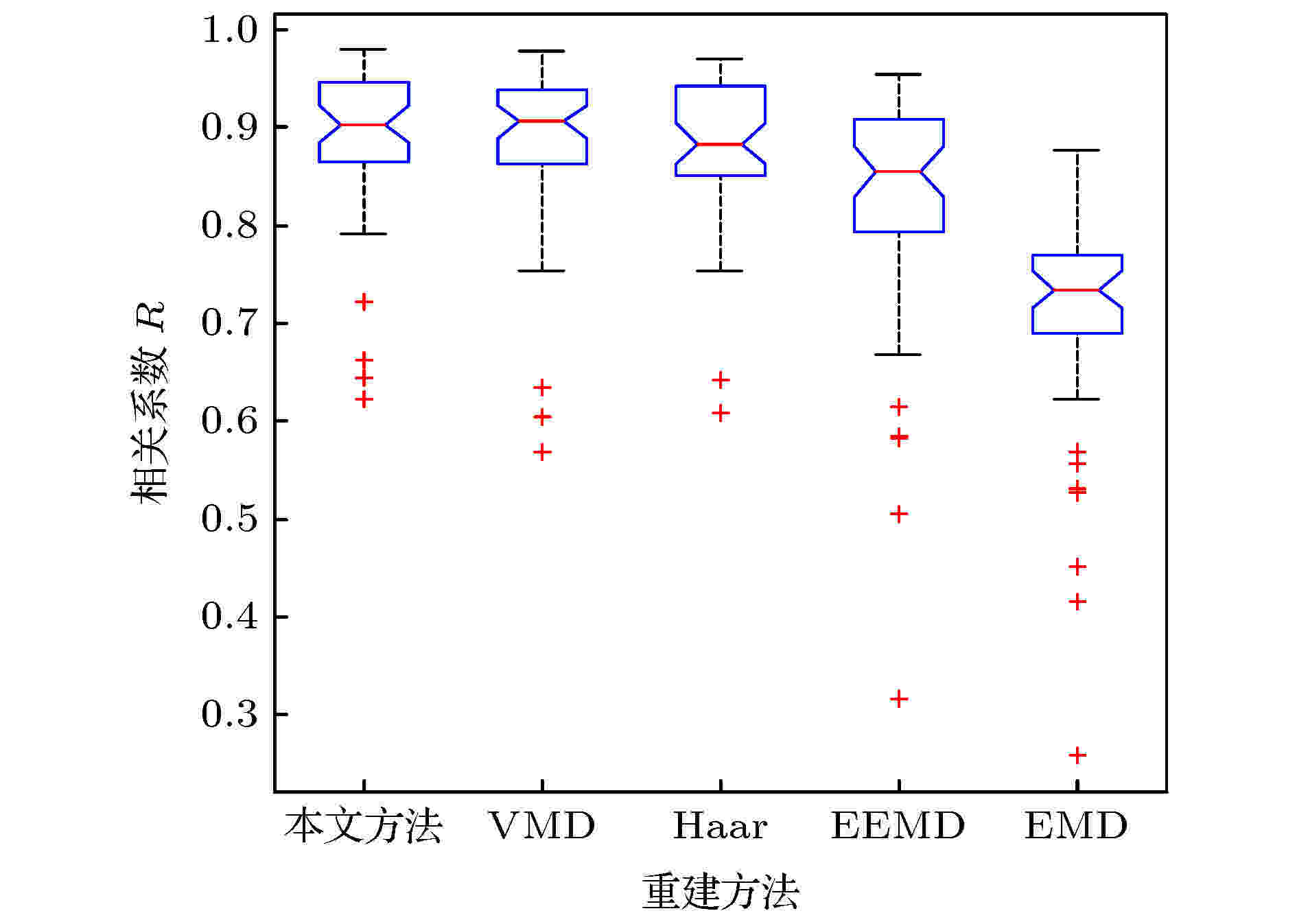图 7 采用五种方法重建47个ECG信号的相关系数R值的统计盒子图
Figure7. Five box-plots of R values of 47 ECG signals reconstructed by 5 methods.

相比经验性包络相减法求均值(EMD, EEMD方法内), 本文提出的IMMD方法采用IMVT求均值, 具有严格的均值数学基础, 因此, IMF能够从信号中被准确地筛选剥离. 经5000个高斯白噪声样本的蒙特卡罗法统计验证, IMMD方法具有比EMD, EEMD (同EMD方法一样, EEMD具有恒Q二分滤波器组特性^[29])更优的多分辨率分解信号能力, 可以有效缓解IMF之间的模式混叠.
另外, ECG信号具有心动周期、心率等波动物理特征, ECG信号的IMF分量同样具有心动周期或HR的特性. 因此, 本文方法中使用心动周期或HR识别ECG信号的IMF分量, 符合ECG的物理本质特性. EMD, EEMD和VMD域内ECG重建一般采用QRS特征波经验性识别IMF, 适用于时域中具有显著QRS波动的IMF识别(例如图3中IMF4). 如果存在: 1) 时域中QRS波动不显著但属于ECG信号的低阶IMF (例如图3中IMF3); 2) 时域完全没有QRS特征但属于ECG信号的高阶IMF (例如图3中IMF12), 该方法识别错误. 小波阈值法中固定阈值不能自适应小波系数不同局部内噪声水平波动, 因此, 重建ECG信号可能存在局部消噪不理想(例如图5(c)). 所以, 本文提出方法, 能够比上述四种方法进一步提高ECG信号重建准确度, 且方法具有自适应和通用性. 经47例ECG信号实验验证, 提出的方法重建ECG与原ECG信号相似度平均值为0.8904, 方差为0.0071, 且有31例相似度值优于VMD, 33例相似度值优于Haar小波, 42例相似度值优于EEMD, 45例相似度值优于EMD. 本文提出方法重建ECG信号能力体现了物理特征或现象在生物电信号处理中具有重要作用.
本方法中, 建议通过含噪ECG信号IMF分量包络频谱图, 经验确定HR. HR可以通过严格的RR波间隔得到, 但需要大量算法实现. 实际上, 人心率一般为1—1.7 Hz (60—100次/min). 对于采集良好的ECG信号, 其IMF分量包络的频谱图中, 1—2 Hz之间的幅度最大值对应频率即为HR, 并且它常常出现在多个IMF分量包络的频谱中, 容易辨别(如图4所示). 本文选取的47个ECG信号, 都是基于上述经验方法确定HR.
提出的方法具有一定局限. 对于极其特殊的232 ECG信号(窦性心动过缓、一级房室传导阻滞和频繁异位心房运动, ECG信号停顿持续长达6 s)重建, 本文提出方法失效. 关于心动周期特性极差的ECG信号重建, 以及从物理现象本质探索ECG信号处理, 是本课题组下一步的工作.