摘要:衍射光栅已在波导中得到广泛应用, 能将光束或图像从耦入端传输并在预定位置耦合输出, 不过在应用于诸如增强现实/虚拟现实等大视场角(field of view, FOV)、彩色光源时会存在FOV不匹配、视场缺失、出射不均匀等问题. 故从这些物理问题出发, 推导出衍射波导的FOV上限、视场完整的理论边界公式, 在此基础上再分别针对单色波和复色波进行深入研究. 得出单层衍射波导在常规高折射率n = 1.75条件下, 支持单色波FOV理论上限约48°, 支持复色波颜色系数q = 1.3的FOV理论上限26.4°, 更大FOV就需要配置更高折射率和更小q值. 视场完整性的边界条件表明, 减小长波的最大衍射角和减薄波导厚度就能解决视场缺失的问题, 实用最大衍射角一般不超过75°, 波导层厚度根据FOV大小一般在0.5—1.0 mm之间. 最后提出将各全内反射视场展开为光线追迹图的方法和瞳孔均摊接收各角度光能的分布函数, 就此可求解光栅耦出区的最佳位置, 并利用分布函数的倒数来约束投射光的角分布或者光栅效率的角分布, 以在任意位置都能接收均匀出射视场: 单色波导的均匀性从0.27提高到0.15, 单光栅复色波导中长波均匀性从0.40提高到0.28. 这些研究结果有助于解决衍射波导用于大FOV和复色光的难题.
关键词: 衍射光栅/
平面波导/
视场角/
全内反射

English Abstract

全文HTML

--> --> -->

光波导是将光能从一个地方传输到另一个地方的器件, 由于光束被限制在封闭范围内, 能量传输利用率高, 故得到广泛应用, 比如光纤通信、LCD背光和光学互联等^[1-3]. 光波导包括三部分: 1)耦入端将光耦合到波导介质中; 2)光线在光纤、平面玻璃等透明介质内通过全内反射(total internal reflection, TIR)进行传输; 3)输出端将光耦合输出. 根据耦入耦出方式不同, 可分为基于折射和反射原理的波导和基于光栅原理的衍射波导. 随着增强现实(augmented reality, AR)和虚拟现实(virtual reality, VR)等投影显示技术的应用和发展^[4-6], 具备小体积、大视场、轻薄便捷等优势的衍射波导越来越获得学术界和工业界的青睐^[7,8]. 衍射是自然界中美丽的现象, 菲涅耳、夫琅禾费等科学家很早就将其带入到大众视野和工业应用中, 自20世纪80年代起有用于近眼显示的衍射波导研究, 从最初单色、单角度, 到现在多色、大视场, 衍射波导被推向了时代前沿^[9-11]. 表面浮雕光栅或全息体光栅等都能做衍射波导, 其研究主要包括两方面, 一是入射视场角和衍射波导参数的匹配优化, 二是优化光栅的轮廓或倾斜来达到目标衍射效率. 1995年, 以色列Amitai等^[12]提出了基于衍射光栅的波导方案, 2000年初, Levola^[13]在视场角(field of view, FOV)和出瞳方面开展了深入研究并提出用表面浮雕光栅实现二维扩瞳, 微软的Kress团队^[14]研发了基于衍射波导的HoloLens AR眼镜, 两代产品的双眼水平FOV从30°提高到43°. 国内自2000年后开始在头盔显示上进行研究, 包括北京理工大学、浙江大学、东南大学、中国航空工业集团公司洛阳电光设备研究所(洛阳613所)、中国科学院长春光学精密机械与物理研究所等科研院所^[15-19], 以及鲲游光电、三极光电科技(苏州)有限公司、歌尔股份有限公司等企业瞄准产品开发应用^[20]. 总的来看, 百花齐放的研究已覆盖了衍射波导的各方面, 不过在如何获得更大FOV、如何获得更均匀出瞳效果上仍缺乏明确的物理指导和优化方案, 这正是本工作的研究内容.
衍射光栅能以不同的轮廓和倾斜角将单色、固定入射角的光束以最大效率耦合到波导中^[21,22], 同时也能多次、多方向耦合输出以方便扩瞳, 这也在之前使用透射光栅时被发现过^[23]. 本文针对多色、大FOV入射在衍射波导中各种边界条件的物理问题进行研究. 首先推导并给出波导支持FOV的理论上限公式并分别针对单色波和复色波进行了详细计算分析, 提出了颜色系数q值对FOV的影响. 其次, 研究如何优化设置光栅耦合输出区和入射分布函数, 使得瞳孔在任意位置都能接收到尽量均匀的各入射角光能. 推导出视场完整的边界条件, 用于约束最大衍射角和波导厚度; 提出了将各级全内反射视场展开为光线追迹三角图的方法, 并就此能在图中追溯最佳的光栅耦出区的设置; 用两个实例来优化入射光角分布函数, 提高了耦合输出的均匀性, 无疑有利于大FOV和复色光波导. 因此, 本文研究内容及相关结果能为衍射波导的应用提供指导方向.

2

-->

2.1.数理关系定义

为便于后续论述清晰, 本节先对衍射波导相关数理关系进行约定. 由于无色散0级在波导内不能发生全内反射, 耦入时只有高级次衍射光才有可能在波导内全内反射传输, 故通常使用+1或–1级作为传输波. 以波导界面法线为基准, 入射和衍射关系采用常见的光栅方程公式:

${n_1}\sin {\theta _{{\rm{in}}}} = {n_2}\sin {\theta _m} + m\frac{\lambda }{d}, $

式中, 入射角为θ_in, 入射若是空气则折射率n₁近似为1, 波导介质折射率n₂记为n, m是衍射级次标号, 衍射角为θ_m, λ为波长, d为光栅常数. (1)式对于耦入和耦出光栅均适用. 由于衍射级标号可正可负, 衍射角也可正可负(相对界面法线), 统一起见, 入射角为正时, 相对θ_in居于法线异侧的衍射角为正, 否则记为负. 级次正负则以0级为参考, 比0级角度大的m为负级次, 否则记为正级次. 此外对于衍射波导来说, 耦入和耦出光栅面既可同侧也可异侧, 物理上并无区别, 考虑采用透射耦出的AR/VR眼镜一般配置异侧较为实用, 故绘制图1作为衍射波导耦入、传输和耦出的概略示意图. 图1设光源O在此方向FOV范围为[0, θ], 左边蓝色和绿色光线表示是以T_–1作为传输波, 右边红色和淡蓝色光线表示以T₁作为传输波, 两者在耦出光栅区都是T₁级次输出到人眼. 无论采用T_–1或T₁, 都要使得整个FOV视场光线耦入后, 衍射角都要大于全内反射临界角θ_c = arcsin(1/n). 两者差别在于: 由(1)式可知T_–1对应光栅常数d接近波长即可, T₁由于反向偏折较多要求光栅常数d更小, 也即光栅线更精细; 此外不同槽型斜光栅的T_–1/T₁的耦入效率也有差别, 故可根据实用来选择使用哪一级.
图 1 波导使用不同衍射级次耦入的简示图
Figure1. Schematic diagram of waveguide coupling using different diffraction orders.

2 -->

2.2.介质折射率与入射FOV

不失一般性, 以下分析针对图1左边T_–1耦入进行考察, 右边T₁耦入只是正负号有所变化, 能获得类似公式和边界约束, 后续不再赘述. 令L, R标记为视场的左、右边缘光线, 入射角记为θ_L和θ_R, 则FOV即为θ_R–θ_L, 将m = –1代入(1)式并移项, 得到衍射关系为

$\left\{ \begin{aligned} &n\sin {\theta _{ - 1,{\rm{L}}}} = \sin {\theta _{\rm{L}}} + {\lambda }/{d}, \\& n\sin {\theta _{ - 1,{\rm{R}}}} = \sin {\theta _{\rm{R}}} + {\lambda }/{d}. \end{aligned} \right.$

显然左光线必须要发生全内反射(即θ_{–1, L} > θ_c), 右光线必须要存在(即θ_{–1, R} < 90°), 是衍射波导的边界条件:

$\frac{\lambda }{{n - \sin {\theta _{\rm{R}}}}} < d < \frac{\lambda }{{1 - \sin {\theta _{\rm{L}}}}}.$

若波导用于复色光比如R, G, B三波长, 设波长上下限为λ_max, λ_min, 则有:

$\frac{{{\lambda _{\max }}}}{{n - \sin {\theta _{\rm{R}}}}} < d < \frac{{{\lambda _{\min }}}}{{1 - \sin {\theta _{\rm{L}}}}}.$

(3)式、(4)式分别作为单色和多色耦入时, 光栅常数d要满足的限定条件, 显然如果FOV过大, 与波导介质折射率n不匹配的话, 则很可能无解. 故波导能支持耦入的FOV大小, 取决于不等式(4)式的右端大于左端的关系:

$\frac{{{\lambda _{\max }}}}{{n \!-\! \sin {\theta _{\rm{R}}}}} < \frac{{{\lambda _{\min }}}}{{1 \!-\! \sin {\theta _{\rm{L}}}}} \Rightarrow \frac{{{\lambda _{\max }}}}{{{\lambda _{\min }}}}\left( {1 \!-\! \sin {\theta _{\rm{L}}}} \right) < n \!-\! \sin {\theta _{\rm{R}}}.$

只要满足(5)式, 就能从单色波(3)式或复色波(4)式计算选定合适光栅常数d. (5)式表明衍射波导支持的微投(微型投影仪)FOV角范围与d无关, 仅与波长和介质折射率相关, 无疑是有意思的结论, 可以说已经规约到很简单的数学解. 下面针对单色和多色入射, 来进一步解析(5)式限定的含义和边界条件.
2 -->

2.3.单色光波导分析

此时λ_max = λ_min, 令θ_avg = (θ_R + θ_L)/2为视场中心光线入射角, 由(5)式有

$1 \!-\! \sin {\theta _{\rm{L}}} < n \!-\! \sin {\theta _{\rm{R}}} \Rightarrow 2\sin \left( {\frac{{{\rm{FOV}}}}{2}} \right)\cos \left( {{\theta _{{\rm{avg}}}}} \right) < n \!-\! 1.$

故单色光条件下, 波导能传输的最大FOV与波长无关, 仅与中心光线角和折射率相关如表1所示, 这无疑也是一个很有意义的结论. 分析(6)式, 若θ_avg = 0即中心光线垂直波导界面, 衍射波导允许的FOV满足公式:

${\rm{FOV}} < 2 \times \arcsin [ (n - 1)/2].$

中心光 线角/(°)	介质折 射率n	FOVmax/(°)	介质折 射率n	FOVmax/(°)
10	1.5	29.41	1.75	44.76
15	1.5	30.00	1.75	45.68
20	1.5	30.85	1.75	47.03
25	1.5	32.02	1.75	48.88
30	1.5	33.55	1.75	51.31

表1不同中心光线角和波导介质折射率支持耦入的最大FOV
Table1.Support maximum FOV by different configurations.

由于双眼AR/VR左右两边各有一个微投, 设计上能将左右图像正好投射到两眼轴的左边和右边如图2所示, 双眼合成FOV等效于两微投FOV之和, 故此方向双眼FOV理论最大为2倍单微投的FOV_max. 此配置下, 某边缘光线会垂直界面、中心光线角满足|θ_avg| = FOV/2, 代入(6)式得到单微投FOV为
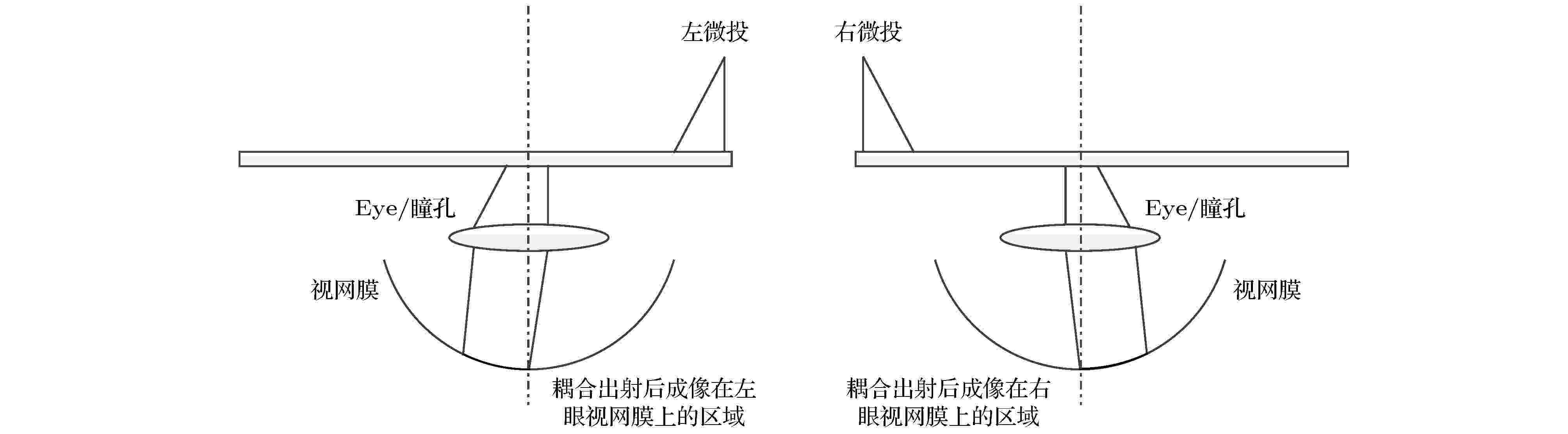图 2 左右微投发光经波导耦合输出到人眼, 重叠视场正好为0的理想情况
Figure2. The left and right micro-projector output light to the human eye by waveguide, where the overlapping field of view is exactly 0

${\rm{FOV}} < \arcsin \left( {n - 1} \right).$

不过左右图像大部分情况会配置成有重叠, 故双眼在此方向FOV为

${\rm{FO}}{{\rm{V}}_{{\rm{2eyes}}}} = 2 \times {\rm{FOV}} - {\theta _{{\rm{ov}}}}, $

式中θ_ov是重叠FOV, 参考人眼成像模型, 最大约为单微投FOV的一半. 举例(考察θ_ov = 0的情况): 当n = 1.5时, 支持单微投FOV_max是30°, 合成视场FOV_{2 eyes}最大可到60°; 当n = 1.75时, 单微投FOV_max约48.6°, 合成视场FOV_{2 eyes}将达到97°; 当n = 2时, 单微投FOV_max能达理论最大值90°, FOV_{2 eyes}将能到180°.
考虑最大折射率n到2, 图3计算显示θ_avg = FOV/2, 衍射波导支持的单微投最大FOV角、光栅常数d与介质折射率n之间的关系. 由此可见, 对于单色光或者窄带光的VR/AR眼镜来说, 使用常规折射率n为[1.50—1.75]的材料, 能轻松支持单微投30°—48°的FOV. 如果需要支持更大FOV, 必然要选择更高折射率的介质材料, 用(6)式或其特例(7)式、(8)式, 以及(3)式来解析相应的n, FOV和d的配置.
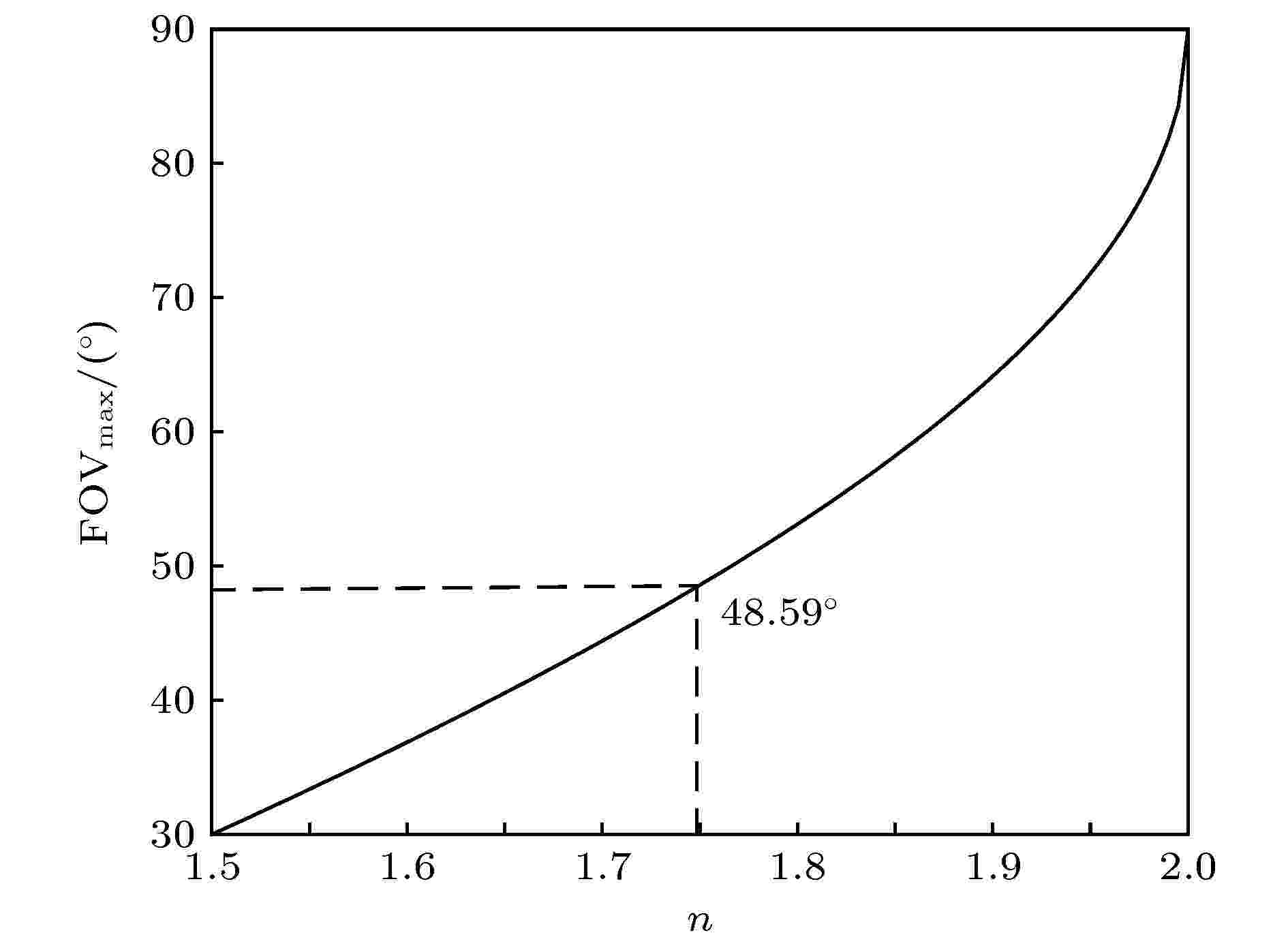图 3 单微投θ_avg = FOV/2时, 衍射波导支持的最大FOV角度与折射率关系
Figure3. Relationship between the maximum FOV and the refractive index when θ_avg = FOV/2.

2 -->

2.4.复色光波导分析

彩色图像投射是更吸引人的. 为改善最终在出瞳位置的颜色均匀性、减小彩虹效应, 当前眼镜大都简单采用3层光栅波导, 每一层分别耦合传输R, G, B三个分量的光. 该方案的优点是每层只需考虑单色光, 故根据2.3节所述, 采用常规折射率材料即可. 不过衍射波导的3倍成本、匹配组装的工艺难度以及3层波导的厚度增大, 是规避不了的问题.
本节计算分析单光栅波导用于复色波的边界条件, 从源头展示如何用一层光栅作用于RGB三色、并实现最大FOV. 无论是micro-LED还是激光束扫描的微投, 都能用三色光来合成白光效果, 比如R = 633 nm, G = 532 nm, B = 450 nm, 则λ_max = 1.41λ_min, 不妨令λ_max = qλ_min, 则q相当于光源的单色性. 依据微投的发光配置方式, q取值范围在1.30—1.75之间. 将q代入(5)式中定义, 有

$\begin{split} & \sin {\theta _{\rm{R}}} - q\sin {\theta _{\rm{L}}} < n - q \\\Rightarrow&\; 2q\cos ({\theta _{{\rm{avg}}}})\sin \left( {{{{\rm{FOV}}}}/{2}} \right) \\&- (q - 1)\sin {\theta _{\rm{R}}} < n - q.\\[-10pt]\end{split}$

由(10)式可知, 为尽可能支持大视场多色光波导, 介质折射率n应该越大越好, 颜色系数即单色性q越小越好, 不过两者总是有边界的, 这也就制约了单光栅能支持最大复色光波导FOV的能力. 类似上一节分析, 先考察微投中心光线垂直于界面的情况, 即θ_avg = 0, 此时θ_R = FOV/2, 故(10)式简化为

${\rm{FOV}} < 2 \times \arcsin \left( {\frac{{n - q}}{{1 + q}}} \right).$

q取可行的小值, 如1.3 (R = 620 nm, B = 475 nm). 当n = 1.5时, FOV_max约为9.97°; 当n = 1.75时, FOV_max约为22.56°; 当n = 2时, FOV_max约为35.43°. 可见微投中心光线垂直波导表面时, 支持多色FOV_max很小, 即使用n = 2超高折射率玻璃, 理论最大也就35°.
考察两微投左右投射各半图像到双眼中的情况, 此时|θ_avg| = FOV/2, θ_R = FOV, 故(10)式简化为

${\rm{FOV}} < \arcsin \left( {n - q} \right), $

当q = 1单色光时, (11)式和(12)式分别归约到(7)式和(8)式; q > 1多色光进入时, 所能支持的最大FOV相对就小. 举例: n = 1.5, q = 1.3时, FOV_max约为11.5°; n = 1.75, q = 1.3时, FOV_max约为26.4°; n = 2, q = 1.3时, FOV_max约为44.4°. 图4(a)更详细地显示了q = 1.3条件下, 单光栅能支持多色波导最大FOV角与折射率n的关系; 或固定折射率n = 1.75, FOV随光源单色性q的关系如图4(b)所示.
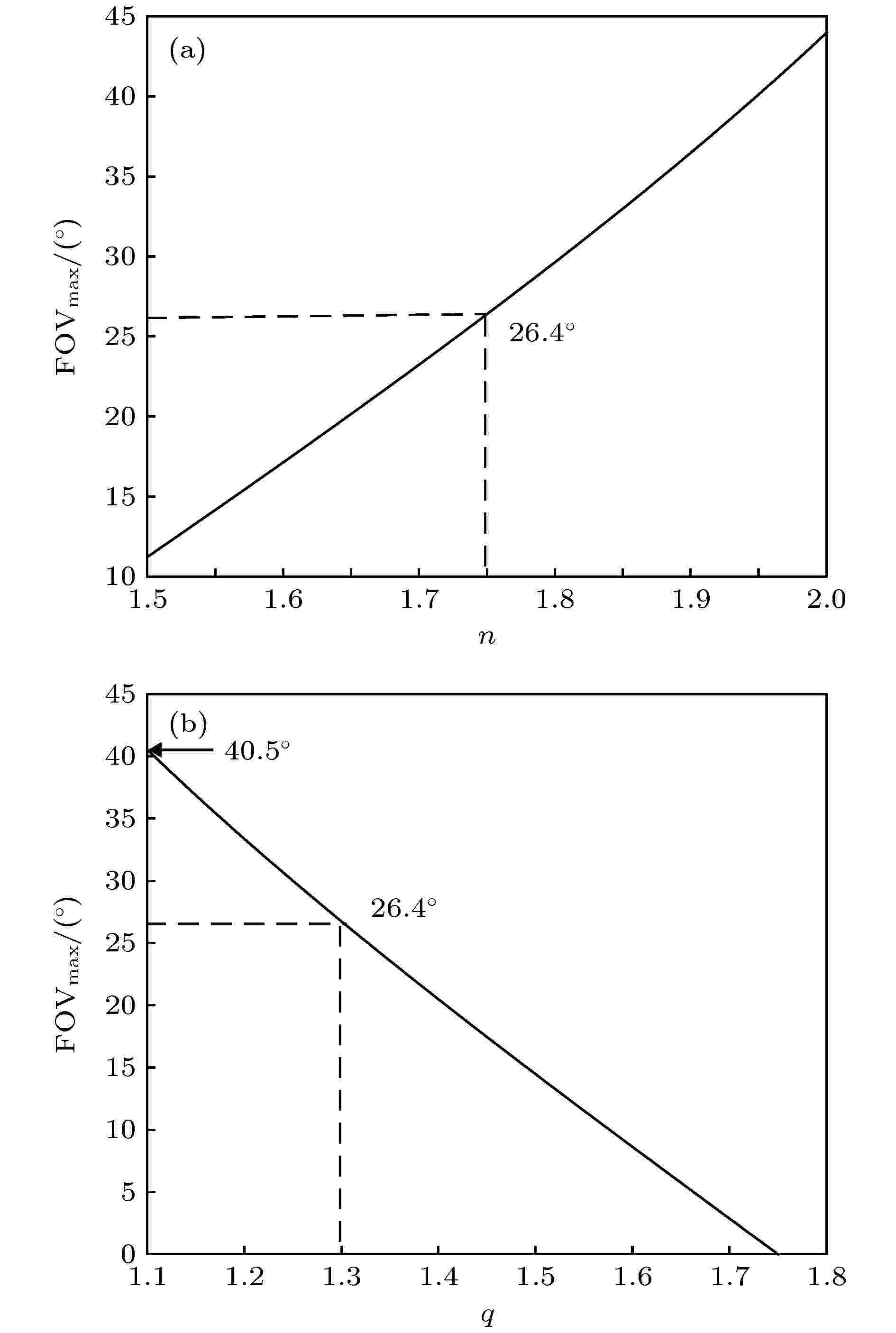图 4 单微投θ_avg = FOV/2时　(a) 固定q = 1.3, 单光栅支持多色光波导的FOV角度随n变化曲线; (b)固定n = 1.75, 单光栅支持多色光波导的FOV角度随q变化曲线
Figure4. When θ_avg = FOV/2: (a) q = 1.3, the relation curve between multi-color FOV and n supported by single grating; (b) n = 1.75, the relation curve between multi-color FOV and q.

考察实际应用, 比如要求大FOV的VR眼镜, 双眼FOV到100°, 计入一定重合量则单眼FOV_max需要达到65°—70°, 从图4来看单光栅波导是无解的. 考虑人眼聚焦和舒适度, AR眼镜对FOV要求相对较小、通常双眼在40°—50°区间, 上述当n = 1.75, q = 1.3时, 单光栅波导能支持FOV_max约26.4°, 代入(9)式并计入一定重合量后, 双眼FOV预计能到45°左右.
既然单层光栅用于复色波导, 受限于上述边界条件, 可折衷考虑多做一层来满足更大FOV的耦入需求. 就颜色发光模型来说, 蓝光和绿光波长相对接近, 红光偏大很多, 故采用两层光栅波导来做彩色也是可行方向: 第一层针对蓝光和绿光设计(比如G = 520 nm, B = 475 nm, 则此层q = 1.1), 第二层针对红光就为2.3节单色波情况. 由图4(b)来看, n = 1.75、蓝绿q = 1.1, 采用两层光栅波导, 双眼三色FOV预计能做到60°—70°; 提高折射率n = 2, 则单眼FOV最大64.2°, 预计能接近VR双眼100°的要求.
上述(11)式、(12)式是θ_avg = 0, FOV/2的特殊情况公式, 当左右图像要有一定重合时, 视场中心角必然是一般值. 比如人类单眼水平视角约150°, 双眼合计水平视角约190°, 重合角θ_ov约110°. 因此不同应用投射图像不一定正好贴合眼轴, 可能会有所重叠、也可能会错开, 则两微投的中心光线角度也要随之改变, 形成所需投射效果. 故再考虑θ_avg为变量, 将θ_R = θ_avg + FOV/2代入(10)式:

$\begin{split}&2q\cos ({\theta _{{\rm{avg}}}})\sin \left( { {{{\rm{FOV}}}}/{2}} \right) \\&- (q - 1)\sin \left( {{\theta _{{\rm{avg}}}} + {{{\rm{FOV}}}}/{2}} \right) < n - q.\end{split}$

采用变量代换以及正余弦公式, 经过一系列数学推导解得:

${\rm{FOV}} < 4 \arctan \left[ {\frac{{a - \sqrt {{a^2} \!-\! (n \!-\! q \!+\! b)(n \!-\! q \!-\! b)} }}{{n - q - b}}} \right], $

其中a = (q + 1)cos(θ_avg), b = (q － 1)sin(θ_avg), 显然根号内数值必须大于0才有解, 它限定了n, q, a, b的边界条件. 故设置各微投中心光线角θ_avg后, 再结合n, q等参数, 由(14)式来计算具体配置下, 单层波导能支持多色波的最大FOV.

不同于传统波导只需针对单色、固定角度的应用, 衍射波导用于眼镜有天然难度, 一是光线入射FOV范围大, 二是彩色波长范围很宽. 因衍射色散导致介质内各传输光线的角度差异非常大, 使得波导介质内不同入射角和不同颜色光线的全反射角和次数有很大差异, 导致各光线在光栅耦合端输出次数/光能密度就有很大差异, 瞳孔接收的光能和颜色分量等均匀性较差, 甚至会无法接收到某些视场区域, 出现类似文献[20]描述的彩虹和缺块效应, 这对扩瞳来说是不利的. 实际上, 只要结合理论计算和设计, 这些问题都可以规避或者弱化.
2

-->

3.1.耦合输出全视场的边界条件

图5所示衍射波导传输图中, 记光栅耦合输入为表面1, 光栅耦合输出为对面的表面2, 微投点光源到表面1的距离为s, 其视场左、中、右光线在光栅耦合输入面的交线为紫色L、绿色和红色R, 波导介质厚度为t. x轴以O为原点, 沿衍射传输方向为正方向, 定义k表示某一次全内反射, 图中k₂表示表面2的全内反射视场, k₁表示表面1的全内反射视场, 显然本图中k₂为奇数、k₁为偶数. 因衍射色散强烈依赖于光线的入射角和波长, 故小衍射角的紫光线反射次数最多, 大衍射角的红光线反射次数最少, 比如图5分别有4紫、3绿、2红的光线耦合输出到人眼视网膜上, 意味着进入人眼的光能不均匀. 每次表面发生全反射, 图像沿x方向都有一定范围, 不妨用x_L, x_R表示, 则输入面微投视场的左右边界光线x坐标为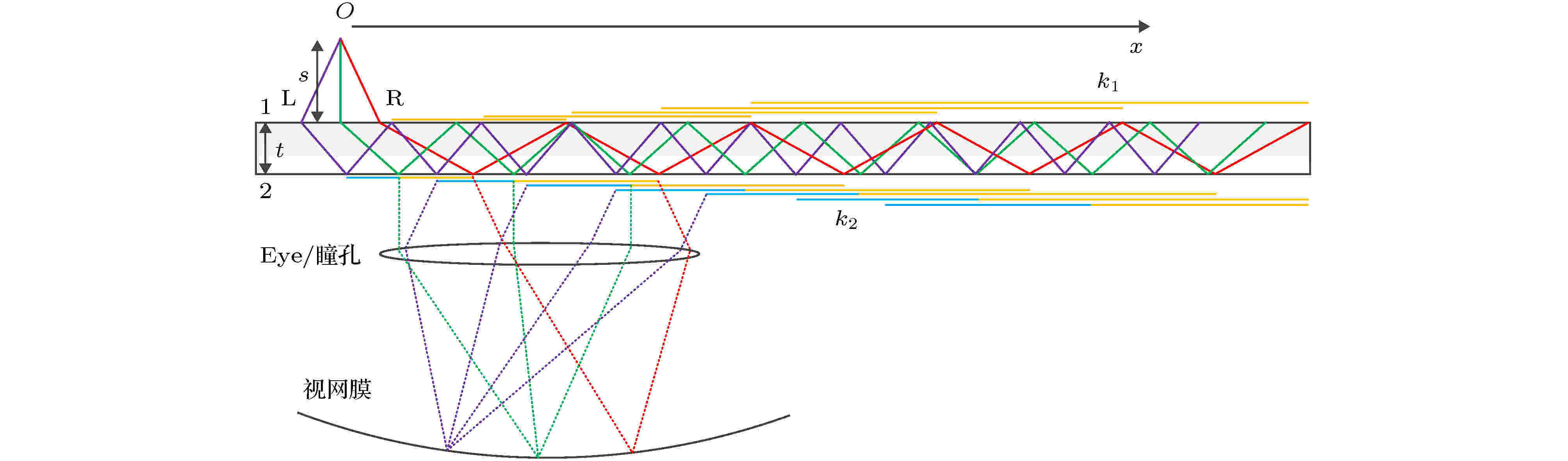
图 5 衍射波导的光线传输以及全反级次视场标记
Figure5. Light transmission of diffraction waveguide and FOV marker of TIR.

$\left\{ \begin{aligned}& x_{\rm{L}}^{\rm{0}} = s \cdot \tan ({\theta _{\rm{L}}}), \\& x_{\rm{R}}^{\rm{0}} = s \cdot \tan ({\theta _{\rm{R}}}). \end{aligned} \right.$

两边界光线衍射角分别记为β_L和β_R, 复色波时β_L对应短波左边界光线、β_R对应长波右边界光线. 每发生一次全内反射, 视场左端和右端的x坐标增量分别为

$\left\{ \begin{aligned}& \Delta {x_{\rm{L}}} = t \cdot \tan ({\beta _{\rm{L}}}), \\& \Delta {x_{\rm{R}}} = t \cdot \tan ({\beta _{\rm{R}}}), \\ \end{aligned}\right.$

第k次全内反射视场的左右两端x坐标为

$\left\{ \begin{aligned} &x_{\rm{L}}^k = x_{\rm{L}}^0 + t \cdot \tan ({\beta _{\rm{L}}}), \\ &x_{\rm{R}}^k = x_{\rm{R}}^0 + t \cdot \tan ({\beta _{\rm{R}}}), \end{aligned} \right.$

则第k次全内反射视场的x方向宽度为

${L^k} = x_{\rm{R}}^k - x_{\rm{L}}^k = \left( {x_{\rm{R}}^0 - x_{\rm{L}}^0} \right) + kt\left[ {\tan ({\beta _{\rm{R}}}) - \tan ({\beta _{\rm{L}}})} \right].$

由于耦合衍射角β_L < β_R, 故Δx_L < Δx_R, 因此随着k增大, 视场右端x坐标增量要快于左端x坐标增量, 导致L_k不断增大, 图5表面1用橙色标注每个k₁的视场, 下表面2用蓝+橙标注每个k₂的视场(中心绿光线为一半视场的分界), 更形象展示出右端增长速度远快于左端, 无法在固定位置放置耦合输出光栅. 这正是用于大FOV、复色光的衍射波导设计难度所在: 因无法兼顾所有不同入射角/颜色的光线, 而导致耦合输出视场出现明暗(各FOV光强不均匀)和彩虹(颜色不均匀)问题.
令眼睛瞳孔尺寸为l, 显然当L^k > l时, 出现l无法覆盖第k次视场的情况, 不过此处瞳孔仍能接收其他级次的部分视场, 故只要设计得当, 就能在人眼中输出完整视场, 否则就必然会出现视场缺失问题. 由图5及(16)式可知, 最右端衍射光线在下表面2上相邻两次全内反射的最短间距是2Δx_R, 若用激光扫描会有一定线宽w, 则此间距能更窄一点, 故由此得到必要的边界条件: 瞳孔尺寸l不小于该间距才能看到所有入射图像, 否则就出现部分视场光线无法进入瞳孔的问题, 即

$2t \times \tan ({\beta _{\rm{R}}}) - w \leqslant l.$

因此, 减薄波导厚度t与减小最大衍射角β_R是有利的, β_R与最大入射角、光栅常数和波长相关, 多色波导时β_R为长波的最大衍射角, 显然光栅常数d尽可能大则β_R就能尽量小, 如前所述实用时β_R一般控制不超过75°.
2 -->

3.2.光栅耦出区域的优化设计

本节优化光栅耦合输出区域的位置和宽度, 将图5所示k级全内反射视场的x方向坐标和宽度, 展开为如图6所示的光线追迹三角图, 紫线对应最小衍射角、红线对应最大衍射角, 蓝线为耦入光栅面, 后续橙线为在表面2上每次全反射的视场, 那么蓝橙线间距为波导厚度t, 橙线间距为两倍厚度即2t. 故耦合输出面的级次k都是奇数, 相邻视场左右端的x坐标增量即为2Δx_L和2Δx_R. 自图6来看, 全内反射视场右端能快速进入光栅区, 而其左端缓慢进入光栅区, 定义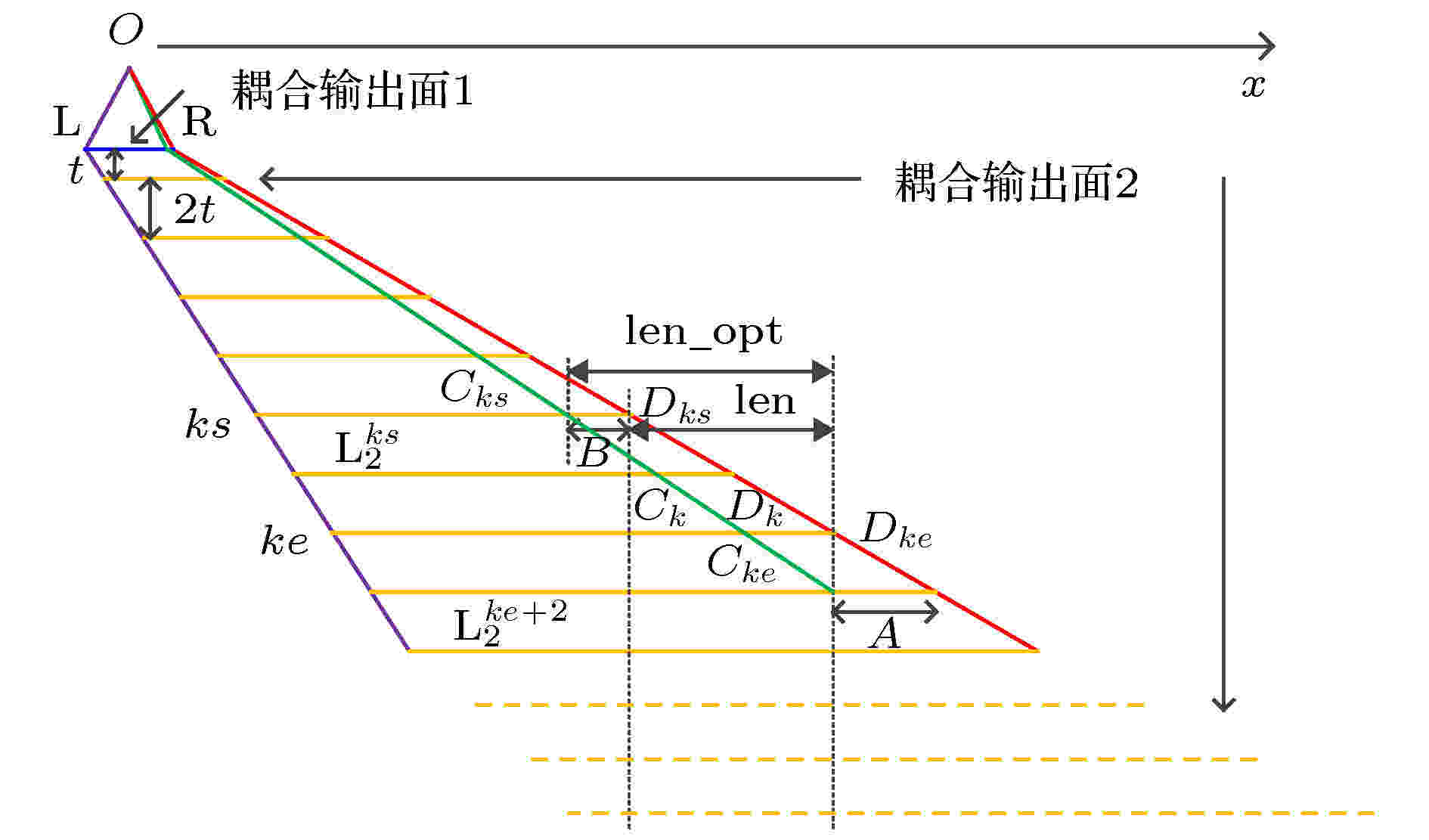

$\begin{split} &{\rm{fastTimes}} = \dfrac{{k{e_{{\rm{last}}}} - k{e_{{\rm{first}}}}}}{2} + 1, \\& {\rm{slowTimes}} = \dfrac{{k{s_{{\rm{last}}}} - k{s_{{\rm{first}}}}}}{2} + 1, \end{split} $

其中, 下标last表示最后一次在光栅区, first表示首次进光栅区, ks, ke分别表示初次进入和最后一次离开的视场级次, 均能由光源到光栅区x方向距离和全内反射视场两端增量(16)式对应计算出. fastTimes是最大衍射角所需耦合输出次数, slowTimes是最小衍射角的耦合输出次数.
图 6 各视场的光线追迹展开图
Figure6. Expanded ray-tracing of FOV.

图6以最大衍射角输出fastTimes = 3为例, 令D_k是第k级橙线与红线交点, 假设光栅区初始位置是D_ks和D_ke之间(即图中长虚线区域), 光栅区初始宽度为len = 4Δx_R. 令C_k为图中绿线与橙线的交点, C_ks左侧视场必能至少耦合输出3次(长虚线往下覆盖橙线各FOV的次数), 而第ke + 2视场的右端A部分(对应长虚线内每条橙线C_k到D_k之间那部分视场)只能耦合输出2次, 故光栅区宽度优化要么往右包含A (不含右端点D_ke+2), 要么往左到图中B部分, 才能使得视场所有光线都至少能耦合输出3次. 考虑到A区较宽, 会使得其他小衍射角耦合输出次数增多, 故本文选用往左优化至图中对应宽度较窄的B部分, 是为最佳, 由于A宽度为2Δx_R, 可简单采用份额比例来近似求解len_B有

${\rm{le}}{{\rm{n}}_B} = \dfrac{{L_2^{ks}}}{{L_2^{ke}}} \times 2\Delta {x_{\rm{R}}}, $

则优化光栅区宽度为

${\rm{len\_opt}} = {\rm{len}} + {\rm{le}}{{\rm{n}}_B} = \left( {{\rm{fastTimes}} \!-\! 1 \!+\! \frac{{L_2^{ks}}}{{L_2^{ke}}}} \right) \times 2\Delta {x_{\rm{R}}}.$

由此, 光栅区优化设置为: 终止x坐标为第ke级视场右端, 光栅区x方向宽度len_opt由(22)式算得.
2 -->

3.3.单色光耦合输出与输入亮度的优化

虽然耦出光栅能在刻蚀深浅变化上做出优化^[13,14], 不过深度变化仅能调整瞳孔在不同位置的整体亮度, 而无法在同一位置调节瞳孔接收不同角度光线的均匀性. 故将扩瞳均匀输出的压力都让光栅承担也并不现实, 还得在微投入射源做相应优化, 才能获得不错结果. 本节先考察单色波不同入射角的耦合输出, 参数为: θ_avg = 18.5°, FOV = 37°, 波长λ = 620 nm, n = 1.75, s = 2 mm, t = 0.95 mm, d = 618 nm, w = 0.5 mm, 瞳孔l = 4 mm, 容易算得满足边界条件(19)式, 故瞳孔在任意位置都能接收视场所有光线. 若要求光栅区起始x坐标(到光源距离)不低于16 mm, 最大衍射角光线耦合输出次数fastTimes = 5, 由(16)式、(20)式和(22)式算得到光栅区终止x坐标约为38.7 mm和len_opt约19.7 mm, 光栅区x坐标为[19.0, 38.7] mm. 继续由(20)式算得光栅区覆盖左端慢速级次slowTimes = 15次, 也就意味最大衍射角与最小衍射角的耦合输出次数相差3倍. 图7(a)显示了光栅区内所有入射光线在光栅区的全反射次数, 显然若按倒数关系约束微投图像中x方向入射角的光能分布如图7(b), 就能使得视场所有角度的光线在光栅区形成均匀的全反射光能覆盖, 故本例算得投射图像0°到边缘37°的光强要差3倍.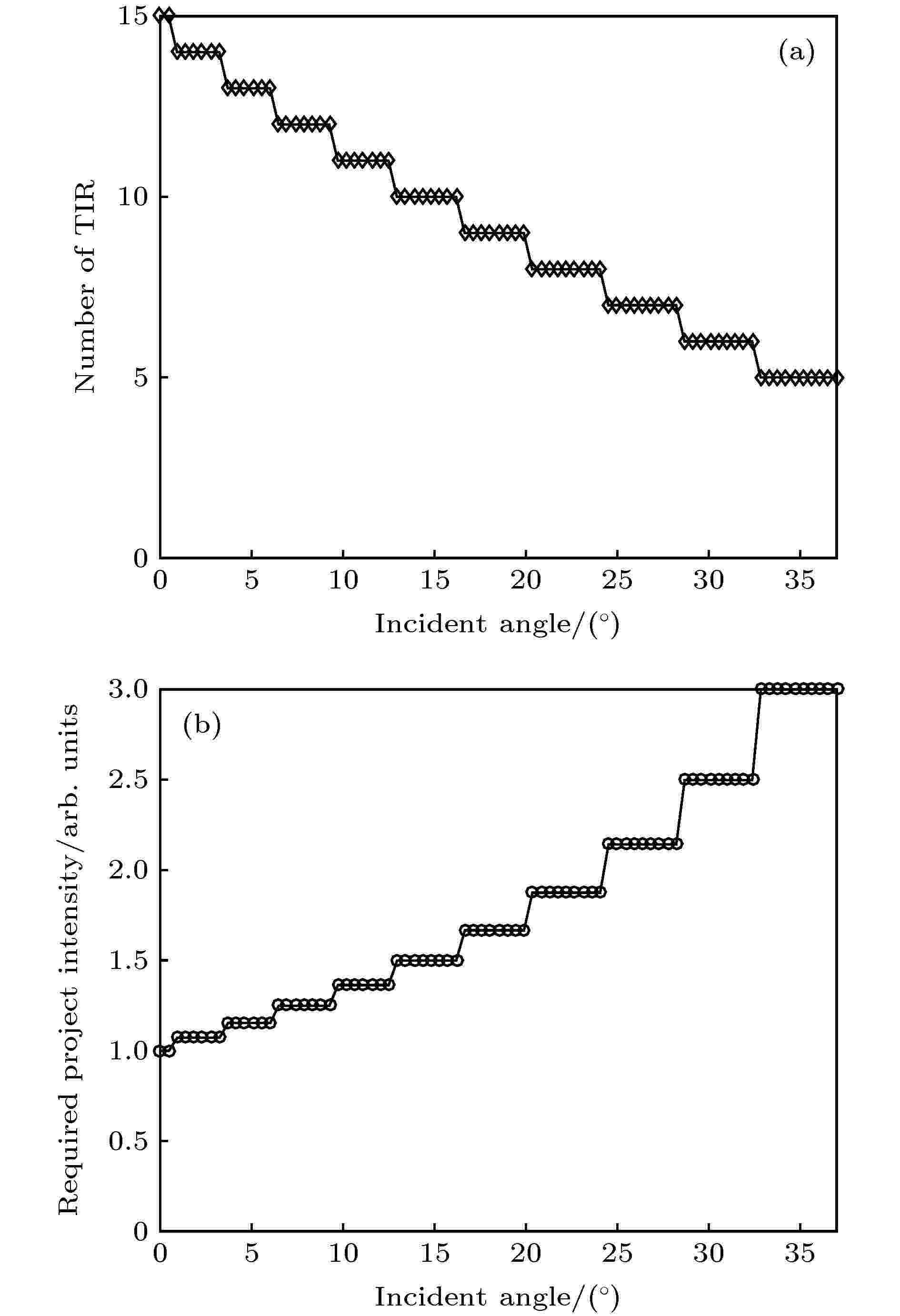
图 7 (a)各角度光线在光栅区的全内反射次数; (b)微投在x方向归一化光能的投射曲线
Figure7. (a) Number of TIR at various incident angles in the grating area; (b) required projection curve of micro-projecter normalized light energy along the x direction.

深入研究发现, 一方面光栅区每次全内反射耦合输出光能后必然影响后续的耦合输出, 另一方面瞳孔只占整个光栅区的小部分, 故要考虑这两方面对瞳孔接收光强均匀性的影响. 显然优化fastTimes和slowTimes差距是最先想到的方案, 不过一旦d和FOV固定后, 衍射色散效应也就定下来, 单纯调节波导厚度t无法消除此差距, 利用稍复杂的薄膜分层可以缩短此差距^[13]. 不过幸运的是, 实际瞳孔区域l一般只有4 mm左右, 其所能收集的视场光能, 对应到最大衍射角耦合输出一般是1次、最小衍射角耦合输出一般是2次, 其他FOV耦合输出在1—2次之间, 故被瞳孔接收视场的明暗差距最多是2倍, 这无疑是有利的. 简单起见, 令光栅区对所有角度光线都输出相同效率η = 20%, 整个光栅区x方向按3.2节优化的坐标为[x_L, x_R], 对于光栅区扩瞳输出来说, 瞳孔位置是随机的, 故考虑均摊或者说平均效果为佳, 可将瞳孔在[x_L, x_R]内按间距d_s滑动计算每个宽l窗口接收的各角度光线强度, 一共滑动nBlocks次:

${d_s} = \frac{{{\rm{len\_opt}} - l}}{{{\rm{nBlocks}} - 1}}.$

依次统计每个l窗口接收的光能情况, 再对这nBlocks个结果做平均, 即得瞳孔在光栅区期望接收到的视场各入射角的光能分布记为avgE:

$\begin{split} &{\rm{enEye}}{({\theta _{{\rm{in}}}})_m} = I({\theta _{{\rm{in}}}}) - I({\theta _{{\rm{in}}}},{\rm{prev}}) - I({\theta _{{\rm{in}}}},{\rm{after}}), \\ &{\rm{avgE}}({\theta _{{\rm{in}}}}) = {\rm{average}}\left[ {{\rm{enEye}}({\theta _{{\rm{in}}}})} \right],\\[-10pt] \end{split} $

式中, I(θ_in)是入射场耦入到波导中的光能分布函数, 简单设定为单位平面波, I(θ_in, prev)表示瞳孔左侧已经耦合输出的光能, I(θ_in, after)表示瞳孔右边剩余光能, 减掉后两者就是在瞳孔区耦合输出的光能分布函数enEye(θ_in)_m, 下标m表示瞳孔在光栅区的第m个位置, 随后对nBlocks个求平均即得avgE函数. 因此若沿x方向角约束投射亮度为avgE的倒数, 就能期望瞳孔在光栅区任意位置都能接收到尽量均匀的视场. η = 20%, nBlocks = 8条件下求得avgE, 按其倒数关系设置微投x方向入射角的光能分布如图8(a)所示, 其二次曲线拟合最小值1.1, 最大值1.58, 即亮度差1.4倍, 在预期1—2倍范围内, 再将此曲线乘以初始I(θ_in) 作为新的投射源, 重新计算avgE, 如图8(b)所示, 故瞳孔内光能分布均匀性得到显著提高, 各角度耦合输出光能曲线从下降趋势变为水平, 数值均匀性pv指标从0.272提高到0.152, 此指标定义为
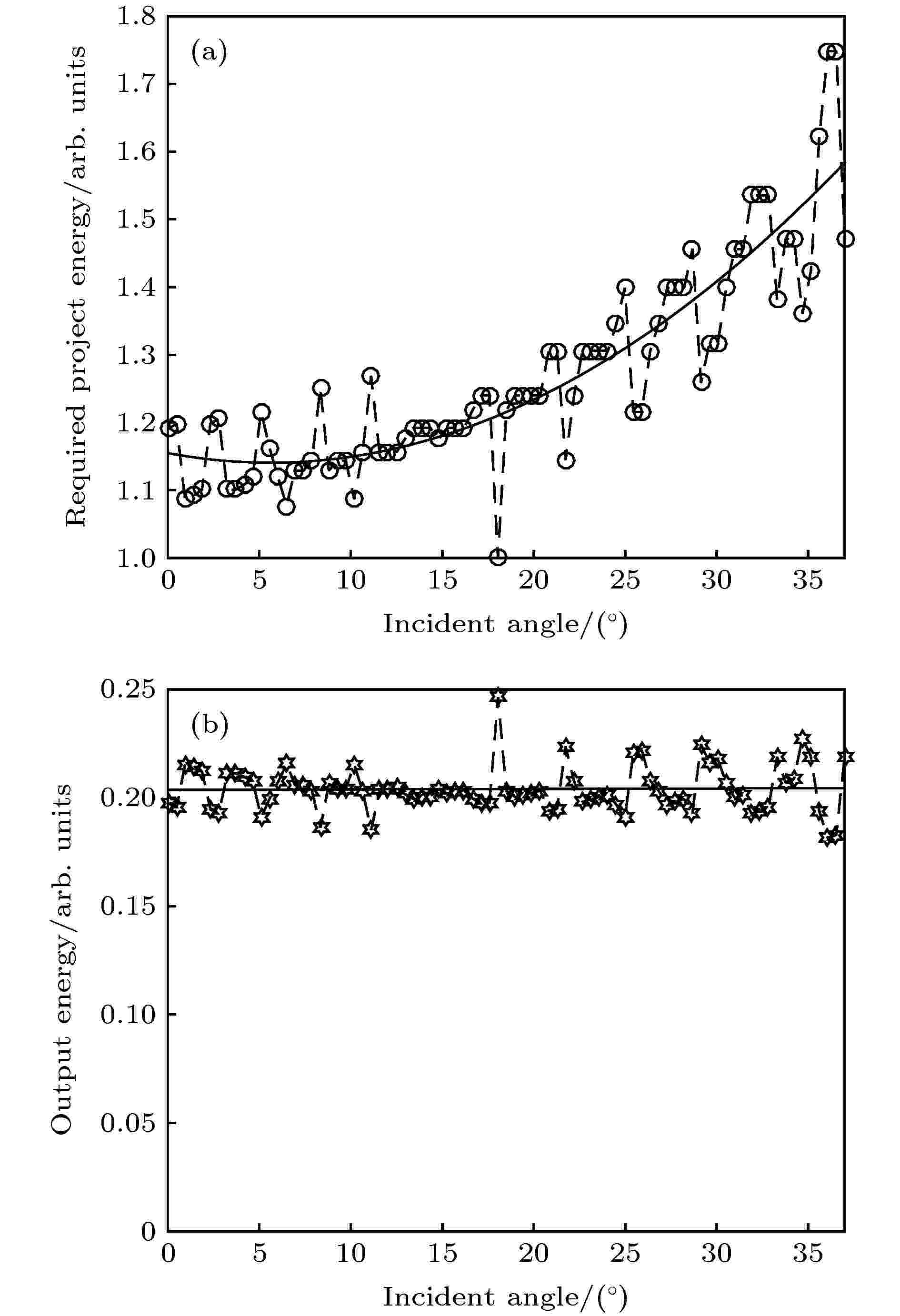图 8 (a) 微投在x方向归一化光能的投射曲线; (b) 按(a)图对投射端优化后的重新计算结果
Figure8. (a) Required projected angular light energy distribution function along the x direction; (b) recalculated results after optimizing the projection by (a).

${\rm{pv}} = ({{{I_{\max }} - {I_{\min }}}})/({{{I_{\max }} + {I_{\min }}}}), $

式中, 下标max/min表示各角度最大/最小光强, 显然pv越小表明均匀性越好.
2 -->

3.4.复色光耦合输出与输入亮度的优化

单光栅用于复色波导(R = 620 nm, G = 520 nm, B = 475 nm), 2.4节表明θ_avg > 0时能理论支持FOV_max为26.4°, 如前所述最大衍射角应不超75°, 故参数选为: 中心光线θ_avg = 11.5°, FOV = 23°, n = 1.75, s = 2 mm, d = 473 nm, w = 0.5 mm, 为使得红绿蓝三色都满足边界条件(19)式, 设置波导厚度为t = 0.54 mm. 再由上述优化光栅区的终止x坐标和len_opt的相关公式(以红光最大衍射角fastTimes = 5为目标), 算得光栅区位置约[18.9, 39.1] mm, 即尺寸约20.2 mm. 类似3.3节分析, 设三色光耦出η都是20%, 计算瞳孔接收三色在8个位置耦合输出均值avgE后, 按倒数关系设置微投图像x方向入射角的各色光能如图9(a)所示, 就能期望瞳孔在不同位置都能接收到尽量均匀的耦合输出如图9(b). 可见蓝绿光几乎无需优化投射角分布函数, 而红光必须要处理, 自拟合优化曲线来看, 最大约1.76倍, 最小约1.15倍. 红绿蓝三色在瞳孔内的均匀性, 自优化前pv_R = 0.404, pv_G = 0.144, pv_B = 0.162, 改进为: pv_R = 0.283, pv_G = 0.142, pv_B = 0.160, 可见红光均匀性得到大幅提高. 考虑θ_ov = [0°, 11°]的重叠, 则双眼综合FOV为[35°, 46°], 能满足一般应用需求.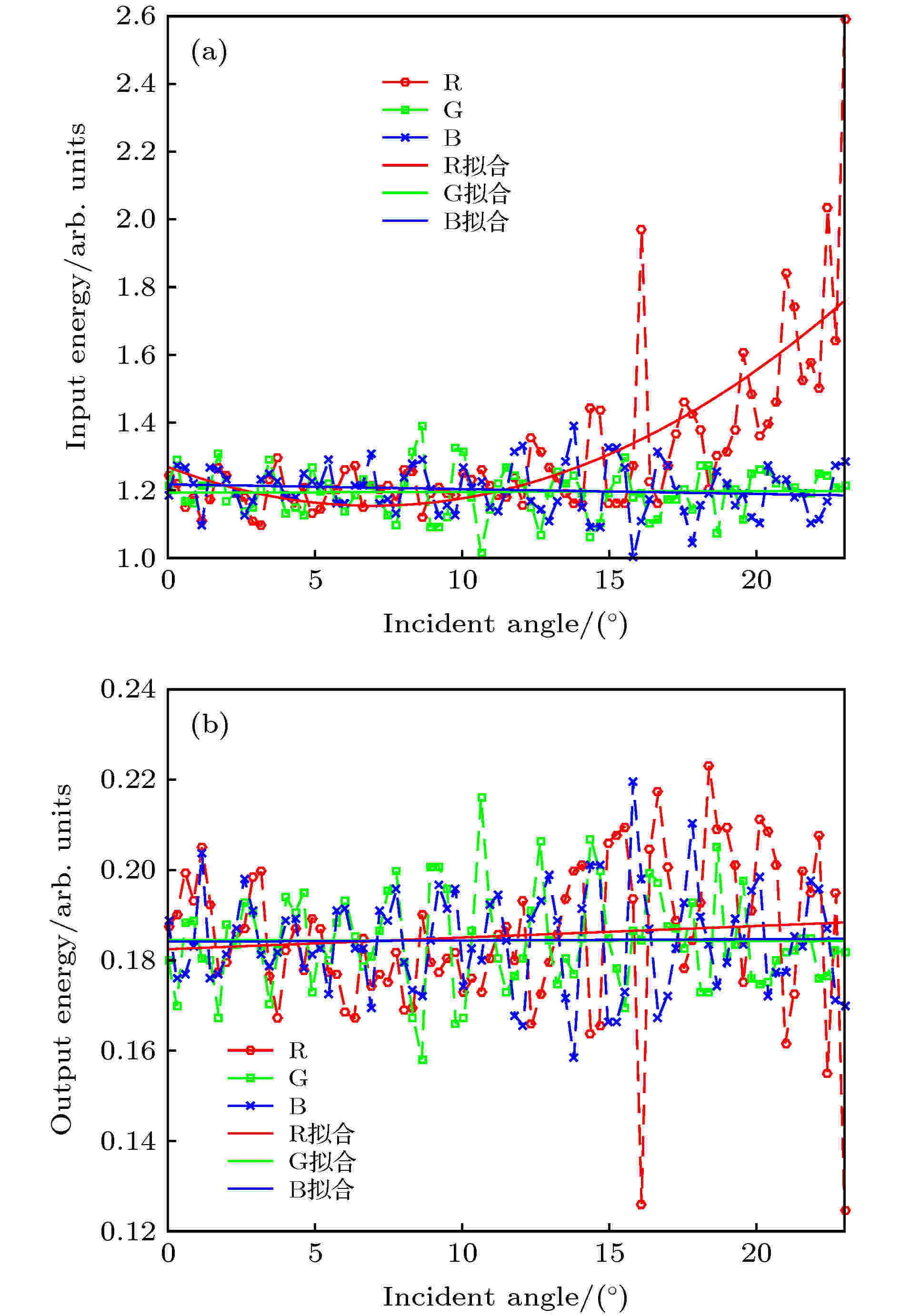
图 9 (a) 微投在x方向RGB三色光随FOV归一化光能的投射曲线; (b) 按(a)图对投射端优化后的重新计算结果
Figure9. (a) Required projected angular light energy distribution function of RGB along the x direction; (b) recalculated results after optimizing the projection by (a).

上一实例可见蓝绿光输出效果相对接近, 故无法获得更高折射率波导介质时, 采用两块光栅波导来做更大彩色FOV是可选方案, 其一针对蓝绿光, 另一单独针对红光如3.3节所述. 因图4(b)中q = 1.1支持最大FOV = 40.5°, 实用要偏小一点, 故设置为: 中心光线角θ_avg = 18.5°, FOV = 37°, n = 1.75, s = 2 mm, d = 473 nm, w = 0.5 mm. 为使得蓝、绿光都能满足边界条件(19)式, 设置t = 0.54 mm, 并优化算得光栅区位置约[19.5, 39.6] mm即尺寸约20.1 mm. 类似得到下述图10(a)所示按avgE倒数关系设置的各入射角光能及相应拟合曲线, 随后依据此设计的亮度分布函数, 重新耦合输出到瞳孔的光能, 如图10(b)所示, 各角度耦合输出的光能曲线变为水平一致. 可见, 蓝光相对平稳几乎无需优化投射角分布函数, 而绿光大角度需投射更多光能才行, 自优化前的pv_G = 0.301, pv_B = 0.125, 改进为pv_G = 0.178, pv_B = 0.116, 故绿光均匀性得到大幅提高. 考虑比如θ_ov = [0°, 18°]的重叠, 则双眼综合视场角为[56°, 74°].
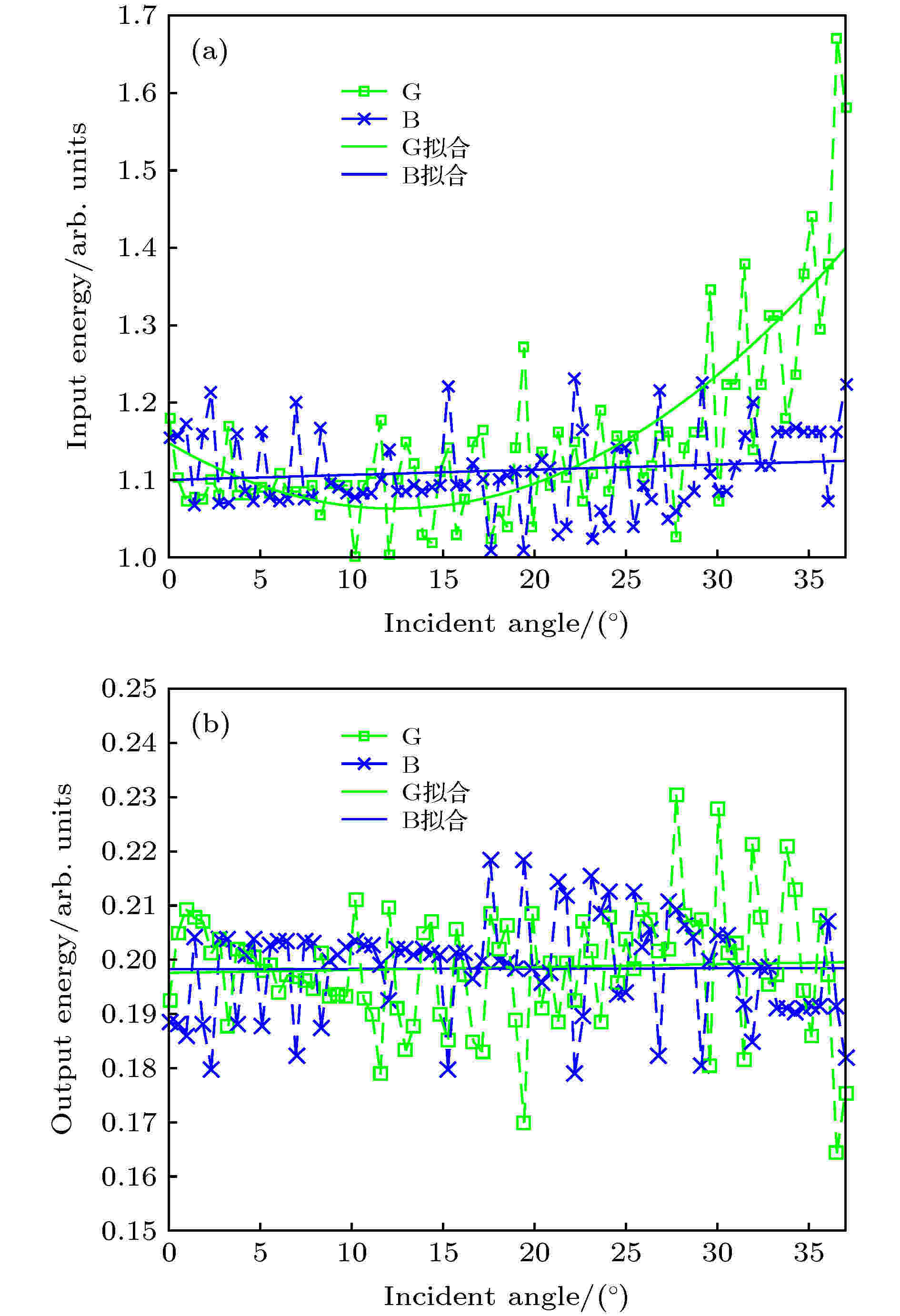图 10 (a) 微投在x方向GB两色光随视场角度归一化光能的投射曲线; (b) 按(a)图对投射端优化后的重新计算结果
Figure10. (a) Required projected angular light energy distribution function of GB along the x direction; (b) recalculated results after optimizing the projection by (a).

本文第2节开展衍射波导与入射视角关系的研究, 给出波导支持视场角范围与d无关、仅与波长和介质折射率相关的(5)式, 随后分别针对单色波和复色波进行了详细计算分析. 单色波入射时, 波导传输的最大视场角与波长无关, 仅与中心光线角和折射率相关, 由(6)式、(7)式、(8)式获得的参数配置优化能适应任意单色波长; 常规高折射率n = 1.75材料能支持单眼视场角约48°, 极高折射率n = 2能支持到理论最大角90°. 复色波入射时, 受光源颜色系数q值的约束, 归纳出(11)式、(12)式、(14)式来求解视场角上限, 在n = 1.75, q = 1.3条件下, 单眼视场角约26.4°, 远低于单色波. 实用还要考虑最大衍射角一般不超过75°, 此时FOV会比理论最大值稍小一点, 因此如果要做出双眼FOV ≥ 50°的单光栅多色衍射波导, 只能往两方向努力: 一是制备折射率更大的光学玻璃或聚合物, 如n到2 (美国康宁公司、德国肖特集团等厂家在推动); 二是弱化彩色分量范围, 将光源多色q值降低, 如低到1.2. 或者折中采用双层光栅波导, 更能达到双眼FOV约70°的目标. 此外, 因激光q值几乎接近1, 故多层光栅波导使用激光光源将有更好的视场角表现.
第3节研究如何优化设置光栅耦合输出区和入射分布函数, 使得瞳孔在任意位置都能接收到尽量均匀的各入射角光能. 首先给出了视场完整的基本边界条件(19)式, 一旦不满足此条件, 无论做出效率多高、分布多完美的光栅, 耦合输出到瞳孔中的图像都会出现部分缺失的问题. 其次就各全内反射级次视场两端增长快慢的不同, 提出将沿传输方向的全内反射视场坐标和宽度展开为光线追迹三角图的方法, 推导出(20)式、(21)式来对光栅区位置和尺寸进行优化设置, 使得最大衍射角光线至少能输出, 如3—5次. 发现减薄波导厚度t与减小最大衍射角β_R, 或者利用薄膜夹层使得各衍射角分层发生全内反射, 都能提高耦合输出均匀性. 随后引入均摊的瞳孔接收各角度光能分布函数avgE, 利用其倒数来约束投射光的角分布, 提高瞳孔接收不同角度光线的均匀性. 最后, 对单层波导分别用于三色和双色的两个实例, 进行计算和优化设计, 逆向获得的分布函数I(θ_in), 不仅可用于投射光源角分布的约束, 实际上也能用于光栅耦入/耦出角效率分布的约束, 甚至纳入后者再进行深入优化的可能.

本文先给出了单层波导支持单色和复色光视场角的理论上限, 便于选择合适的衍射波导参数, 以满足不同需求, 尤其在常规折射率区间n = [1.50, 1.75]和极高折射率n = 2, 以及复色光系数q值等方面进行了深入挖掘, 以便不同大小FOV应用时选取合适的n和q值, 或者反过来说固定n和q时知晓波导能支持的最大FOV角. 随后开展光栅耦出区域优化以及提高瞳孔接收各角度光线均匀性的研究, 利用边界条件阐明了如何规避视场缺失问题, 提出利用角向分布函数约束微投亮度角分布来提高出瞳均匀性, 给出单层波导三色视场角约40°到双层波导视场角约70°的两个计算实例(双眼), 为衍射波导用于各类视场角指出了方向, 也为耦入/耦出光栅结构设计的角向效率提出了约束条件, 这也是今后要进一步开展的研究方向.