摘要: 波导中模式耦合是一种普遍的现象. 在光纤通信中不同导模之间的耦合会引起串扰, 导模和辐射模的耦合会降低导模的功率. 另一方面, 利用模式耦合现象能设计出具有特定功能的耦合器和分束器等光学器件. 模式耦合在光纤通信和光纤传感中也具有广泛应用. 因此, 分析研究波导模式如何耦合具有重要的应用价值. 模式耦合理论是研究波导中模式耦合的常用方法, 不仅提供了一种直观的物理图景来描述光学模式如何杂化, 而且还对相关模式如何杂化给出定量评估. 近年来, 以宇称时间对称性结构为代表的非厄米波导成为研究热点, 但传统模式耦合理论在这种情况下不再适用. 本文简述了模式耦合理论的发展历史, 详细介绍了构造互易波导模式耦合理论的关键概念和方法, 进一步回顾了在波导模式耦合理论方面的一系列代表性工作, 尤其是手征对称模式耦合理论以及广义模式耦合理论, 总结了这些模式耦合理论和传统模式耦合理论之间的联系, 最后简单介绍了它们在宇称时间对称波导及各向异性波导中的应用.
关键词: 波导 /
模式 /
耦合 /
互易 English Abstract Reciprocal waveguide coupled mode theory Chen Yun-Tian 1,2 ,Wang Jing-Wei 1 ,Chen Wei-Jin 1 ,Xu Jing 1,2 1.School of Optical and Electronic Information, Huazhong University of Science and Technology, Wuhan 430074, China Received Date: 09 February 2020Accepted Date: 22 April 2020Available Online: 15 May 2020Published Online: 05 August 2020Abstract: Mode coupling is a common phenomenon in waveguides. The mode coupling among different guided modes in fiber-optic communication can cause crosstalk, and the mode coupling of guided mode and radiated mode can reduce the power of the guided mode. Application of mode coupling can guide the design of optical devices such as couplers and beam splitters with specific functions, which have been widely used in fiber optic communication and fiber sensing. So it is important to analyze how waveguide modes are coupled. The coupled-mode theory is a common method of studying mode coupling in waveguides. It provides not only an intuitive picture of how the photonic modes are hybridized, but also a quantitative assessment of how the hybridization among those relevant modes evolves. In recent years, non-Hermitian waveguides, represented by parity-time symmetrical structures, have become a research hotspot. However the conventional coupled-mode theory no longer works in this case. In this review, we briefly summarize the development history of coupled-mode theory and introduce the representative work in reciprocal waveguide coupled-mode theory in detail. Then the relationship among several coupled-mode theories is analyzed and their applications are briefly introduced.Keywords: waveguide /mode /coupling /reciprocity 全文HTML --> --> --> 1.引 言 模式耦合理论是分析设计光学器件不可或缺的工具, 在波导、光学腔以及许多光学子领域都有深远的影响和应用. 模式耦合理论是一种理论框架, 其将具有特定时空分布的每个单独的光学模式视为一个对象, 随着光学系统参数(例如折射率或者光学结构尺寸)的变化, 一种模式可以和另一种模式耦合. 作为一个简单理论模型, 模式耦合理论不仅提供了光学模式如何耦合的直观物理图景, 而且还提供定量评估这些模式耦合演化的技术手段. 因此, 模式耦合理论被广泛用于研究分析设计波导、光学腔等光电器件. 此外, 光子晶体中广泛使用的${ K} \cdot { P}$ 方法也是一种线性模式耦合理论.$\beta$ 决定. 波导系统可用本征值方程${\cal{H}} {{\phi}}_i = \beta_i {{\phi}}_i$ 描述, 其中${\cal{H}}$ 是波导系统的哈密顿算符, 可由麦克斯韦方程组推导而来, ${{\phi}}_i$ 是系统的本征模式, $\beta_i$ 为该模式对应的本征值, 即本征传播常数. ${{\phi}}_i$ 又称为哈密顿算符${\cal{H}}$ 的右矢. 在一定微扰${\cal{H}} + \varDelta$ 下, 构造波导耦合方程需要三步: 1) 微扰下波导场用模式集$[{{\phi}}_i]$ 展开${{\phi}}^{\rm{new}} = \sum a_i {{\phi}}_i$ . 其中${{\phi}}^{\rm{new}}$ 为耦合场, $a_i$ 为耦合系数. 2) 微扰系统的本征方程可以被修改为残差形式$R \!=\! ({\cal{H}} \!+\! \varDelta){{\phi}}^{\rm{new}} \!-\! \beta {{\phi}}^{\rm{new}}$ , 其中$\varDelta$ 为微扰项, $\beta$ 为微扰后系统的本征值. 再用哈密顿算符${\cal{H}}$ 的左矢${{\psi}}_j$ 作为测试函数去测试残差. 3) 在一定条件下, 展开函数${{\phi}}_i$ 和测试函数${{\psi}}_j$ 具有一定联系, 由此可以建立耦合方程. 这里测试是指用${{\psi}}_j$ 左乘R , 并使其等于0, 即$\displaystyle\iiint { \psi} _j \cdot R{\rm{d}}v = 0$ , 这时模式耦合问题就转化为了泛函的极值问题, 通过求解上式, 便能得到模式展开系数$a_i$ . 重要的是, 测试函数的模式集$[{{\psi}}_j]$ 的完备性保证了上述方法与变分原理等效. 将一个物理问题用变分法化为求泛函极值问题, 就称为该物理问题的变分原理. 在模式耦合理论中, 变分原理由麦克斯韦方程组推出, 在理论上是完备的.2.波导模式耦合理论的发展历程 模式耦合的概念可以追溯到20世纪50年代, 最初应用于微波领域, 后在许多人的贡献下逐渐发展. 首先由Pierce[1 ] 将模式耦合理论应用于微波分析, 随后Gould[2 ] 将模式耦合理论应用于背向波振荡器, 之后模式耦合理论被用于分析微波中的参量放大器、振荡器和变频器[3 ] . Miller[4 ] 首先将模式耦合理论引入微波波导和无源器件的分析和设计中. 在20世纪60年代, 模式耦合理论得到进一步发展, 被用于研究微波波导[5 ,6 ] 和周期性波导结构[7 ] 中各种不规则结构引起的模式杂化. 这些模式耦合理论并没有进行严格的理论推导.[8 ] 从麦克斯韦方程组出发, 将耦合场用一组基模展开, 严格推导出了模式耦合方程. 1958年, Haus[9 ] 结合变分原理, 也得到相同的模式耦合方程. 随后, Marcuse[10 ,11 ] , Snyder[12 ,13 ] , Yariv和Taylor[14 ,15 ] 及Kogelnik[16 ] , McIntyre和Snyder[17 ] 将模式耦合理论应用于光波导. 20世纪70年代, 模式耦合理论已成功地应用于各种光波导和光纤器件的建模和分析, 例如光纤[18 -21 ] 、光栅波导和耦合器[22 -26 ] . 此时模式耦合理论使用正交基展开耦合场, 因此也称为正交模式耦合理论(orthogonal coupled mode theory, OCMT). Hardy和Streifer[27 ] , Haus等[28 ] , 以及Chuang[29 ] 将模式耦合理论扩展到非正交情况, 用于展开耦合场的基底无需正交, 因此也称为非正交模式耦合理论(non-orthogonal coupled mode theory, NCMT). OCMT和NCMT统称为传统模式耦合理论(CCMT). 通过正交化方法, NCMT可以退化为OCMT. 无论OCMT还是NCMT, 都需要整个系统满足能量守恒条件.[30 -44 ] , PT对称系统加入了增益和损耗介质, 系统算符为非厄米算符, 在非厄米性较弱时本征值近似为实数, 但当系统的非厄米性变强时, 本征值从实数变为复数. PT对称结构具有许多新特性, 例如基于PT相变的完美相干吸收, 利用这些新特性可以设计激光器、光开关等光学器件. 其中PT对称系统的模式耦合的研究方法普遍基于数值仿真或实验的经验模型[45 ] . 而经验模型并不具备严格的理论基础.[30 ] 从归一化薛定谔方程出发, 结合拉格朗日量, 得到本征值$\beta$ 为实数时的耦合场, 即该方法仅在$\beta$ 为实数时是有效的. 2015年Xu和Chen[46 ] 从作用量守恒原理出发, 利用手征对称性, 构建耦合方程, 得到了GCMT. GCMT不仅具有严格的理论推导, 而且能得到PT对称系统较为精确的耦合模式. 当PT对称系统中本征值由实数变为复数时, GCMT仍然有效. 随后, Wu, Liu等[47 -49 ] 成功将GCMT应用于光学腔、波导链以及波导阵列. 2017年Xiong等[50 ] 证明了在时间反演对称、宇称对称等其他对称条件下波导的后向传播模式可由前向传播模式得到. 2019年, Chen等[51 ] 同样从作用量守恒原理出发, 证明了在双正交内积下互易波导自伴随特性, 且原始系统模式和伴随系统模式正交. 以原始系统模式集合和伴随系统模式集合为展开函数和测试函数, 构建耦合模方程, 得到了广义模式耦合理论(GCMF). GCMF能够解决任意互易波导耦合问题, 包含厄米及非厄米波导系统. 本文将GCMT和GCMF统称为互易波导模式耦合理论.[52 ] 、光子晶体[53 ,54 ] 等. 理论上, 本文讨论的互易波导模式耦合理论也能够处理非平移对称性波导结构, 但需进一步地完善和发展, 才能应用于复杂结构的波导, 如周期性波导等. 对于结构更为复杂的波导的模式计算, 则主要使用数值仿真方法, 例如时域有限差分和有限元[55 -57 ] 等方法.${\cal{H}}$ 是厄米算符, 因此左矢可由右矢得到, 并且沿着传播方向能量积分是守恒的. 类似地, 只要波导介质是互易的, 并且满足作用量守恒, 就可以通过对右本征态${{\phi}}_i$ 的场分量执行转置运算和相应操作来获得双正交积中的左本征态${{\psi}}_j$ . 当波导存在增益/损耗, 沿着波导传播方向上的能量积分不是守恒的, 因此Xu和Chen[46 ] 提出了基于双正交内积的模式耦合理论来分析增益损耗平衡的PT对称波导, 即GCMT. 本质上, 互易波导模式耦合理论是对CCMT的发展, 因此在传统波导中互易性或作用量守恒也是成立的, 用双正交内积代替了厄米内积是可行的. 另外, 在双正交内积下, 如果波导材料是各向同性或者仅在平面内各向异性, 模式耦合理论很容易降维, 将波导模式耦合问题从三维降为二维, 这能够极大减少计算量.3.波导的一般本征值问题 23.1.原始波导系统的一般本征值问题 3.1.原始波导系统的一般本征值问题 考虑一般双各向异性波导, 其本构关系为[58 ] D B E H ${{\bar{{{\varepsilon}}}}} = \varepsilon_0 {{\bar{{{\varepsilon}}}}}_{\rm r}$ (${\bar{ \mu}} = \mu_0 {\bar{ \mu}}_{\rm r}$ ) 为介电(磁导率)张量. ${{\bar{ \chi}}}_{eh} = \sqrt{\varepsilon_0 \mu_0}{{\bar{ \chi}}}_{{\rm r}, eh}$ 和${{\bar{ \chi}}}_{he} = \sqrt{\varepsilon_0 \mu_0}{{\bar{ \chi}}}_{{\rm r}, he}$ 为磁电耦合常数. 更具体地,z 轴具有平移对称性的无限长波导, 在时谐关系${\rm{e}}^{{\rm{i}}\omega t}$ 下, 波导模式能够通过解麦克斯韦方程得到, 即$\nabla \!\times\! {{{E}}} \!=\! -{\rm{i}}\omega\left({\bar{{{\mu}}}}{{{H}}}+{\bar{{\chi}}}_{he}{{{E}}}\right)$ , $\nabla \!\times\! {{{H}}} = {\rm{i}}\omega\left({\bar{{{\varepsilon}}}}{{{E}}}+{\bar{{\chi}}}_{eh}{{{H}}}\right)$ , 其中${\rm{i}} = \sqrt{-1}$ . 将电场强度和磁场强度归一化, 即${{e}} = {{{E}}}$ 和${{h}} = \sqrt{\dfrac{\mu_0}{\varepsilon_0}} {{{H}}}$ , 能建立如下所示的麦克斯韦方程:$k_0 = \omega \sqrt{\varepsilon_0 \mu_0}$ . 在沿z 轴平移对称性条件下, 可以将归一化的电磁场分离为横向项和纵向项[51 ] , 即$\beta$ 为传播常数. 纵向项可以表示为2 )式化为四分量矩阵方程, 如下所示:${{\phi}} = [e_x, e_y, h_x, h_y]^{\rm{T}}$ , T为转置算符, $e_x$ 和$e_y$ 为归一化电场e x 轴分量和y 轴分量, $h_x$ 和$h_y$ 为归一化磁场h x 轴分量和y 轴分量. 其中,3 )式能得到传播常数为$\beta_i = n_{\rm{eff}} ^i k_0$ 的一系列模式, 其中i 表示第i 个模式.4 )式与哈密顿量${\cal{H}}$ 关系为${\cal{H}} = {\bar{{B}}}^{-1}{\bar{{L}}}$ . 用$({\bar{{L}}}, {\bar{{B}}})$ 和${\cal{H}}$ 来描述波导系统本质上是等价的. 波导的哈密顿量${\cal{H}}$ 给出了波导简明扼要的描述[59 ] , 但难以解释元素之间的复杂关系. 相对地, 一般本征值问题$({\bar{{L}}}, {\bar{{B}}})$ 中元素之间的关系更加简单. 可以证明${\bar{{B}}}$ 是一个反对称矩阵, 即${\bar{{B}}}^{\rm{T}} = -{\bar{{B}}}$ . $({\bar{{L}}}, {\bar{{B}}})$ 和${\cal{H}}$ 在描述波导系统时物理上等效但各有数学形式上的优势, 后面将在合适的情况下分别使用它们二者来描述波导系统.3.2.左矢和双正交内积 -->3.2.左矢和双正交内积 在量子力学中, 所有的物理规律在一个希尔伯特空间中表示, 这个希尔伯特空间可以称为右矢空间. 在右矢空间中, 可选取一组线性独立且完备的基矢量, 也称基元函数. (3 )式定义了$({\bar{{L}}}, {\bar{{B}}})$ 的右矢, 即${{\phi}}_i$ 是右矢空间的完备展开集合的基元函数. 类似地, 左矢${{\psi}}_j$ 可以定义为${{\psi}}_j$ 和${{\phi}}_i$ 相同维度, 但是${{\psi}}_j$ 是左矢空间的完备展开集合的基元函数. 在矩量法和有限元法中, ${ {{\phi}}}_i$ 又被称为展开函数, ${{\psi}}_j$ 被称为测试函数.${\cal{H}}$ 并不满足厄米内积下的厄米算符定义式, 因此需要引入其他内积来描述哈密顿量${\cal{H}}$ 和左矢${{\psi}}_j$ 、右矢${{\phi}}_i$ 之间的关系. ${ {{\phi}}}_i$ 和${{\psi}}_j$ 的双正交内积[60 ,61 ] 定义为6 )式称为第一类内积. 接下来介绍第二类内积, 其定义为${\bar{\sigma}}$ 的维度同${\bar{{B}}}$ . 若${\bar{\sigma}}$ 是单位矩阵, 则第二类内积可以化为第一类内积. 第二类内积也称为B $({\bar{{L}}}, {\bar{{B}}})$ , B ${\cal{H}}$ 一起使用.3.3.伴随波导系统 -->3.3.伴随波导系统 在波导模式耦合理论中, 通常需要寻找与原始波导系统相关的伴随波导系统, 将伴随波导系统的本征模作为测试函数. 原始波导中本征值问题使用${\cal{H}} {{\phi}}_i = \beta_i {{\phi}}_i$ 来描述. 类似地, 可以定义伴随系统${\cal{H}}^{\rm{a}}$ 满足${\cal{H}}^{\rm{a}}{{\psi}}_j = \beta_j {{\psi}}_j$ . 类似${\cal{H}} = {\bar{{B}}}^{-1}{\bar{{L}}}$ , 有${{\cal{H}}^{\rm{a}}} = ({{\bar{{B}}}^{\rm{a}}})^{-1} {{\bar{{L}}}^{\rm{a}} }$ , 因此伴随系统${\cal{H}}^{\rm{a}}$ 的一般本征值问题可以写为5 )式和(8 )式有相同的形式, 可知${\bar{{B}}}^{\rm{a}} \!=\! {\bar{{B}}}^{\rm{T}} \!=\! -{\bar{{B}}}$ . 应当指出的是, (8 )式中${\bar{{L}}}^{\rm{a}}$ 和(5 )式中${\bar{{L}}}^{\rm{T}}$ 并不一定相等.${\cal{H}}$ 和伴随波导系统${\cal{H}}^{\rm{a}}$ 之间伴随关系用B ${{\phi}}_i$ 和${{\psi}}_j$ 都满足B B 7 )式, 可得(9 )式的右边等于$\left[({\bar{{B}}}^{\rm{a}})^{\rm{T}}\right]^{-1} = {\bar{{B}}}^{-1}$ , 所以可证明(9 )式给出的伴随关系可以化为以下关系式:10 )式表明$({\bar{{L}}}, {\bar{{B}}})$ 和$({\bar{{L}}}^{\rm{a}}, {\bar{{B}}}^{\rm{a}})$ 之间的伴随关系可以简化为${\bar{{L}}}$ 和${\bar{{L}}}^{\rm{a}}$ 之间的伴随关系. 值得指出的是, 此处伴随算符${\bar{{L}}}^{\rm{a}}$ 仅仅是抽象形式, ${\bar{{L}}}^{\rm{a}}$ 的具体形式将在下一节给出.4.互易性波导 24.1.波导的互易性和正交关系 4.1.波导的互易性和正交关系 原始波导问题对应的算符${\bar{{L}}}$ 由(4 )式描述. ${\bar{{L}}}$ 和${\bar{{L}}}^{\rm{a}}$ 都是对波导问题的描述, 因此${\bar{{L}}}^{\rm a}$ 具有和${\bar{{L}}}$ 相似的形式:10 )式的伴随关系, 能够直接证明伴随波导的介质参数满足[51 ] ${\bar{{{\varepsilon}}}} _{\rm r} ^{\rm{a}} = {\bar{{{\varepsilon}}}} _{\rm r} ^{\rm{T}}$ , ${\bar{ \mu}} _{\rm r}^{\rm{a}} = {\bar{ \mu}} _{\rm r} ^{\rm{T}}$ , ${\bar{ \chi}}_{{\rm r}, he}^{{\rm{a}}} = - \left( {\bar{ \chi}}_{{\rm r}, eh} \right)^{\rm{T}}$ , 和${\bar{ \chi}}_{{\rm r}, eh}^{{\rm{a}}} = - \left({\bar{ \chi}} {_{{\rm r}, he}} \right)^{\rm{T}}$ . 对于互易性波导, 介质参数满足互易性条件, 即${{\bar{{{\varepsilon}}}}}_{\rm r} \!=\! \left({{\bar{{{\varepsilon}}}}}_{\rm r}\right)^{\rm{T}}$ , ${\bar{ \mu}}_{\rm r} \!=\! \left( {\bar{ \mu}}_{\rm r} \right)^{\rm{T}}$ ,${\bar{ \chi}}_{{\rm r}, he} = -\left({\bar{ \chi}}_{{\rm r}, eh} \right)^{\rm{T}}$ , 可以得到$ {\bar{{L}}} $ 是自伴随算符:${\bar{{L}}} $ 自伴随性也是介质参数满足互易性条件的充要条件, 因此称(12 )式为波导的互易性关系.3 )式和伴随系统(8 )式, 即$\iint \left[{{\psi}}_j\cdot (3)- (8)\cdot{{\phi}}_i \right] {\rm{d}}x{\rm{d}}y$ , 可以直接证明得到以下等式[62 -64 ] :13 )式和(10 )式可得到${{\phi}}_i$ 和${{\psi}}_j$ 之间的关系为$\beta_i \neq \beta_j$ , 易证$\iint{ {{\psi}}_j^{\rm{T}} {\bar{{B}}}{{\phi}}_i \, {\rm{d}}x{\rm{d}}y} = 0$ . 通过适当的归一化, 可以得到$\delta_{ij}$ 为克罗内克$\delta$ 函数. (15 )式称为原始场${{\phi}}_i$ 和伴随场${{\psi}}_j$ 之间的B [65 ] . 用角标i 和j 表示原始场和伴随场, 写出${{\phi}}_i$ 和${{\psi}}_j$ 具体形式, 能发现[66 ] . 要注意的是, 正交性不是必须的, 但是正交关系(15 )式为求解模式展开系数$a_i$ 提供了很大的便利.4.2.互易性波导的前向和后向传播模式间的对称关系 -->4.2.互易性波导的前向和后向传播模式间的对称关系 通过伴随算符的定义, 能够证明无论${\bar{{L}}} $ 是否为自伴随, 用$({{\bar{ L}}}^{\rm{a}}, {\bar{{B}}}^{\rm{a}})$ 和$({{\bar{ L}}}, {\bar{{B}}})$ 描述的互为伴随的两个波导模式有相同的本征值$\beta$ (证明见附录A ), 该结论称为同$\beta$ 推论. 同$\beta$ 推论用以下等式描述:$\left[\beta_i, \ {{\phi}}_i\right]$ 和伴随系统本征解$\left[\beta_i, \ {{\psi}}_i\right]$ 有相同的$\beta_i$ .${{\bar{ L}}} = {{\bar{ L}}}^{\rm{a}}$ 和${\bar{{B}}}^{\rm{a}} = -{\bar{{B}}}$ , (16b )式可以化为16a )式, (17 )式给出了相较原始本征解$\left[\beta_i, {{\phi}}_i\right]$ 不同的本征解$\left[-\beta_i, \ {{\psi}}_i\right]$ . 这两个本征解都和$({{\bar{ L}}}, {\bar{{{B}}}})$ 直接相关. 两不同的本征解对应的本征值的绝对值相同, 都为$|\beta_i|$ , 但符号相反[67 ] , 故此结论称为双$\beta$ 推论. 双$\beta$ 推论也适用于互易波导的伴随算符$({{\bar{ L}}}^{\rm{a}}, {\bar{{{B}}}}^{\rm{a}})$ , 意味着如果$\left[\beta_i, {{\psi}}_i\right]$ 是$({{\bar{ L}}}^{\rm{a}}, {\bar{{{B}}}}^{\rm{a}})$ 的本征解, 那么一定存在一个不同于原始本征解但满足${{\bar{ L}}}^{\rm{a}}{{\phi}}_i = -\beta_i {\bar{{{B}}}}^{\rm{a}} {{\phi}}_i$ 的本征解.表1 中, 对于互易波导, 简明地总结了由同$\beta$ 推论和双$\beta$ 推论决定的对称模式关系. 表1 中每列对应的原始系统和伴随系统的本征值相同, 都为$\beta_i$ , 即为同$\beta$ 推论. 每行对应的同一系统的两个本征值反号, 但绝对值相同, 都为$|\beta_i|$ , 即为双$\beta$ 推论. 上面主要讨论了表1 中对称关系的严格数学证明过程,下面简单讨论该对称关系对应的物理含义, 及其在模式耦合理论构建过程中的意义. 对于给定的$\beta_i$ , 即对应于前向传播模式$\beta_i > 0$ . $\left[\beta_i, {{\phi}}_i\right]$ 和$\left[-\beta_i, {{\psi}}_i\right]$ 给出的配对模式实际上是前向和后向传播模式. 由配对${\beta}$ 参数可知, 前向和后向传播模式的${\beta}$ 的绝对值相同.$\beta_i$对应的模式 $-\beta_i$对应的模式 $({\bar{{L}}}, {\bar{{B}}})$ $\left[\beta_i, {{\phi}}_i\right]$ $\left[-\beta_i, {{\psi}}_i\right]$ $({\bar{{L}}}^{\rm{a}}, {\bar{{B}}}^{\rm{a}})$ $\left[\beta_i, {{\psi}}_i\right]$ $\left[-\beta_i, {{\phi}}_i\right]$
表1 当$\beta_i > 0$ 时, 互易波导中原始场和伴随场之间的对称关系Table1. Symmetric relation of original field and adjoint field in the reciprocal waveguides with $\beta_i > 0$ $\left[\beta_i, {{\phi}}_i\right]$ 和$\left[-\beta_i, {{\psi}}_i\right]$ 与用$({{\bar{ L}}}, {\bar{{{B}}}})$ 定义的原始波导有关. 模式场$\left[-\beta_i, {{\phi}}_i\right]$ 和$\left[\beta_i, {{\psi}}_i\right]$ 也是$({{\bar{ L}}}^{\rm a}, {\bar{{{B}}}}^{\rm a})$ 的解. $({{\bar{ L}}}^{\rm a}, {\bar{{{B}}}}^{\rm a})$ 的伴随本征解能够从$({{\bar{ L}}}, {\bar{{{B}}}})$ 的已知本征解推得, 对一般双各向异性波导构建耦合方程有很大帮助.${{\phi}}_i$ 和${{\psi}}_i$ 不一定相关. 在一些特殊情况下, 前向和后向传播模式能够利用对称操作相互转换[50 ] . 对称操作及关系如表2 所示. 表2 中, 列出了三种类型的对称操作, 包括手征对称、时间反演对称和宇称对称, 也列出了不同对称操作相应的介质参数的约束. 三种对称性示意图如图1 所示, $\beta$ 向右和向左分别表示前向和后向传播模式, E H A 代表横截面的参考平面上一点, 对于后向传播模式, $A^{\prime}$ 代表参考平面上相应的点. 在图1(a) 和图1(b) 中, A 和$A^{\prime}$ 在x -y 平面上有相同的坐标, 即${{r}}_A (x, y) = {{r}}_{A^{\prime}}(x, y)$ . 而在图1(c) 中, A 和$A^{\prime}$ 关于中心对称, 即${{r}}_A(x, y) = -{{r}}_{A^{\prime}}(x, y)$ . 手征对称可用于波导介质张量没有非对角项的情况, 请参见表2 中的介质参数的约束. 图1(a) 直观地展示了手征(chiral)对称性, 其中横向电场方向相同而横向磁场方向相反. 当介质不包含任何损耗或增益时(即介质参数为实数)满足时间反演对称性, 如图1(b) 所示, 电磁场满足${{{E}}}^+ = {({{{E}}}^-)}^\ast$ 和${{{H}}}^+ = -{({{{H}}}^-)^\ast}$ . 图1(c) 所示为宇称对称性成立的情况, 其中电磁场满足以下关系式: ${{{E}}}^+({{r}}) = {{{E}}}^-(-{{r}})$ , ${{{H}}}^+({{r}}) = -{{{H}}}^-(-{{r}})$ . 前向和后向传播模式关系的具体细节请参见附录B .图 1 前向和后向传播模式之间对称关系 (a) 手征对称; (b) 时间反演对称; (c) 宇称对称Figure1. Symmetry relations between the forward and backward propagating modes: (a) Chiral symmetry; (b) time reversal symmetry; (c) parity symmetry.对称关系 算符 对称性关系 约束条件 手征对称 ${\sigma}$ ${{{\psi}}}_i({{r}}) = {\bar{\sigma}}{{{\phi}}}_i({{r}})$ ${{{\varepsilon}}}_{\rm r}^{zt} = {{{\varepsilon}}}_{\rm r}^{tz} = 0$, ${{{\mu}}}_{\rm r}^{zt} = {{{\mu}}}_{\rm r}^{tz} = 0$和${\bar{ \chi}} = 0$ 时间反演对称 ${\cal{T}}$ ${{{\psi}}}_i({{r}}) = {\bar{\sigma}}({{{\phi}}}_i({{r}}))^*$ ${\bar{{{\varepsilon}}}}_{\rm r}$, ${\bar{{{\mu}}}}_{\rm r}$和${\bar{ \chi}}$是实数 宇称对称 ${\cal{P}}$ ${{{\psi}}}_i({{r}}) = {\bar{\sigma}}{{{\phi}}}_i(-{{r}})$ ${\bar{{{\varepsilon}}}}_{\rm r}({{r}}) = {\bar{{{\varepsilon}}}}_{\rm r}(-{{r}})$, ${\bar{{{\mu}}}}_{\rm r}({{r}}) = {\bar{{{\mu}}}}_{\rm r}(-{{r}})$和 ${\bar{ \chi}}({{r}}) = -{\bar{ \chi}}(-{{r}})$
表2 互易波导中原始场和伴随场之间的对称关系Table2. Symmetry relations of original field and adjoint field in the reciprocal waveguides.${{\psi}}_i$ 和${{\phi}}_i$ 组合起来, 作为构建模式耦合方程的完备模式集. 这是在构建广义模式耦合理论时除了守恒量的变化之外的另一个关键之处. 例如, 在原始波导中, 存在$2+2$ 的本征解, 即两个前向传播模式${{\phi}}_1$ , ${{\phi}}_2$ , 两个后向传播模式${{\psi}}_1$ , ${{\psi}}_2$ . 微扰系统的展开函数和测试函数可近似表示为${\beta}$ 和${-\beta}$ . 未知的耦合系数$a_j$ 和$b_j$ 没有确切的关系. 应当注意, 完备模式集本应包含导模和辐射模, 但在模式耦合理论中, 通常认为耦合模仅由波导的导模线性叠加[28 ] , 忽略了辐射模的影响. 这是因为辐射模和导模耦合重叠积分很小, 辐射模对耦合模的贡献十分微弱, 即使忽略, 对模式耦合理论的精确性也并无太大影响, 因此本文完备模式集也不考虑辐射模.4.3.通过微扰构建一般波导耦合理论 -->4.3.通过微扰构建一般波导耦合理论 通过微扰, 利用前向传播模式和后向传播模式构成的完备模式集来构建一般波导耦合方程. 在小微扰下, ${\bar{{L}}} ^{\#} = {\bar{{L}}} + \Delta {\bar{{L}}}$ , 微扰波导$({\bar{{L}}} ^{\#}, {\bar{{B}}})$ 的本征模式${{\varPhi}}$ 可以用没有微扰前的波导$({\bar{{L}}}, {\bar{{B}}})$ 的本征模式${{\phi}}_i$ 展开. 具体而言, 微扰波导的模式可写为${{\varPhi}} = \sum a_i {{\phi}}_i$ , 其中$a_i$ 是要确定的耦合系数, 系统本征值由已知的$\beta_i$ 变为未知的$\beta$ . 在微扰下, 原始系统(3 )式可以写为微扰的本征方程${{{{\bar{ L}}}}^\# }{{\varPhi}} = \beta {{\bar {{{B}}}}}{{\varPhi}}$ . 能够证明微扰算符${{\bar{ L}}} ^{\#}$ 和原始算符${{\bar{ L}}}$ 都满足波导的互易性. 由${{\bar{ L}}} ^{\#}$ 的定义, 公式$\left\langle {{{{\psi}}_j}, {\bar{{L}}} {{\varPhi}} } \right\rangle$ 可写为$\left\langle {{{\psi}}_j}, [{\bar{{L}}} ^{\#} - \Delta{\bar{{L}}}] {{\varPhi}} \right\rangle$ . 将$\left\langle {{{{\psi}}_j}, [{\bar{{L}}} ^{\#} -\Delta{\bar{{L}}}] {{\varPhi}} } \right\rangle$ 代入(12 )式, 并写到等式左右两边, 可以推得$\left\langle {{{{\psi}}_j}, {\bar{{L}}} ^{\#} {{\varPhi}} } \right\rangle - \left\langle {{{\bar{{L}}}}{{\psi}}_j, {{\varPhi}} } \right\rangle = \left\langle {{{{\psi}}_j}, \Delta{\bar{{L}}} {{\varPhi}} } \right\rangle$ . 忽略微扰项$\left\langle {{{{\psi}}_j}, \Delta{\bar{{L}}} {{\varPhi}} } \right\rangle$ 得到互易关系:${{\psi}}_j$ 是波导$({\bar{{L}}}, -{\bar{{B}}})$ 的伴随模式, 模式集$[{{\psi}}_j]$ 能够由已知的本征解${{\phi}}_i$ 推得.13 )式的构建过程, 能得到一般波导耦合理论, 如下所示:${b_{ij}}$ 为${p_{ij}}$ 为$k_{ij}$ 包含三项, 即$k_{ij} = k^1_{ij}+k^2_{ij}+k^3_{ij}$ . 第一项$k^1_{ij}$ 为横向电场引起的微扰,$k^2_{ij}$ 来自磁电耦合,$k^3_{ij}$ 来自横向场分量和纵向场分量之间的耦合,20 )式中$b_{ij}$ 可由其他参量表示, 消去$b_{ij}$ , (20 )式化为$\beta$ 是传播常数, $a_j$ 是模式展开系数. 前向传播模式和后向传播模式一起作为展开模式集包含在(21 )式中. 在$p_{ij}$ 和$k_{ij}$ 的求解中, 前面提到的正交性对计算简化起到了很大作用.5.波导模式理论的对比 CCMT, GCMT和GCMF三者是一脉相承而又有所发展, 其具体联系与区别如表3 所列.模式耦合理论 传统模式耦合理论(CCMT) 手征对称模式耦合理论(GCMT) 广义模式耦合理论(GCMF) 耦合模式展开式形式 $\varPhi =\displaystyle \sum a_i\phi _i$ $\varPhi = \displaystyle\sum a_i\phi _i$ $\varPhi = \displaystyle\sum a_i\phi _i ^+ +b_i \psi _i ^-$ 守恒量 光功率守恒 作用量守恒 作用量守恒 测试函数 $\phi _j ^{\ast} $ $\sigma \phi _j$ $ \psi _j ^+$, $\psi _j ^-$ 本征方程 ${\bar{{L}}}{{\phi}}_i = \beta_i {\bar{{B}}}{{\phi}}_i $ ${\bar{{L}}}{{\phi}}_i = \beta_i {\bar{{B}}}{{\phi}}_i $ ${\bar{{L}}}{{\phi}}_i = \beta_i {\bar{{B}}}{{\phi}}_i$ 测试函数进行测试 $\displaystyle\iiint \phi _j ^{\ast} [{\bar{{L} } }{{\phi} }_i-\beta_i {\bar{{B} } }{{\phi} }_i]{\rm{d} }v \!=\! 0$ $\displaystyle\iiint \sigma \phi _j [{\bar{{L} } }{{\phi} }_i-\beta_i {\bar{{B} } }{{\phi} }_i]{\rm{d} }v \!=\! 0$ $\displaystyle\iiint \psi _j \cdot [{\bar{{L} } }{{\phi} }_i \!-\! \beta_i {\bar{{B} } }{{\phi} }_i]{\rm{d} }v \!=\! 0$
表3 CCMT, GCMT和GCMF之间比较Table3. Comparison between CCMT, GCMT and GCMF.${ {\phi}}_i$ )作为展开函数, 而GCMF使用正向和反向传播模式(${ {\phi}}_i^+$ 和${ {\phi}}_i^-$ )一起作为展开函数. 这是因为在模式耦合发展的早期阶段, 所使用的波导介质较为简单, 正向与反向传播模式之间没有发生耦合, 而随着波导的复杂化以及各向异性、双各项异性介质的应用, 前向与后向模式之间的耦合已经不可忽略[68 ] , 因此必须考虑正反向模式共同构成的完备集合$[{ {\phi}}_i^+]$ 和$[{ {\phi}}_i^-]$ .表2 ), 因此其测试函数各不相同. 接下来具体分析为什么系统的对称性会决定展开函数与测试函数之间的正交性. 由(15 )式可知, 系统的原始场(即展开函数)与伴随场(由表3 得伴随场即为反向传播场)正交, 而表2 中的对称性决定了正向场(即原始场或展开函数)与其对应的反向传播场的关系; 因此本质上是对称性决定了展开函数与测试函数的正交性关系. 换言之, 波导系统的结构与光学参数的选取决定了测试函数的选择. 需要注意的是GCMF中的测试函数包含了表1 中伴随场模式的全体, 本质是基于互易波导理论得到的, 是无需满足任意对称性的. 值得指出的是非正交耦合模是存在的, 不过在这三种耦合模中, 只考虑正交耦合模.${\bar{ L}}$ 中材料的光学参数需要满足各自的对称性条件(见表2 ). 总之, 三种模式耦合理论的差异来自于前向传播模式和后向传播模式间的不同对称条件, 以及复杂介质所带来的完备性要求.6.互易波导模式耦合理论的应用 图2 为CCMT应用的一个简单例子, 它由两个具有相同几何尺寸且彼此靠近放置的波导组成. 两个耦合核心层被空气包围, 尺寸分别为$h = 0.2\lambda,\; w = 0.3\lambda,\; d = 0.03\lambda,\; {{\varepsilon}} _0 = 10, \lambda _0$ 是真空波长. 图2(a) 中纤芯1相对介电常数为${{\varepsilon}} = {{\varepsilon}}_0 + \Delta {{\varepsilon}}$ , 纤芯2相对介电常数为${{\varepsilon}} = {{\varepsilon}}_0 + \Delta {{\varepsilon}}$ . 图2(b) 中纤芯1相对介电常数为${{\varepsilon}} = {{\varepsilon}}_0 + \Delta {{\varepsilon}}$ , 纤芯2相对介电常数为${{\varepsilon}} = {{\varepsilon}}_0 - \Delta {{\varepsilon}}$ . 蓝色圆圈代表GCMT的计算结果, 红色叉代表CCMT计算结果. 灰色实线代表商业软件包COMSOL MULTIPHYSICS计算结果, 该结果被认为是正确结果. 很明显, 图2 的波导结构是厄米波导, 因此满足CCMT的使用条件, 即系统整体满足能量守恒条件, 且系统有时间反演对称性. 因为有效折射率虚部为零, 图2 仅给出了实部部分. 图2 中给出了由CCMT以及GCMT计算出的色散关系, 可以看到两者都和灰色线给出的全波模拟完美匹配, 这是由于该结构也满足GCMT的使用条件, 即手征对称性.图 2 有效折射率$n_{\rm{eff}}$ 实部与$\Delta {{\varepsilon}} $ (a) 纤芯1 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ , 纤芯2 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ ; (b) 纤芯1 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ , 纤芯2 相对介电常数为${{\varepsilon}}= {{\varepsilon}}_0 - \Delta {{\varepsilon}} $ Figure2. Real part of effective mode indices $n_{\rm{eff}}$ versus $\Delta {{\varepsilon}} $ : (a) ${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ in core layer 1 and ${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ in core layer 2; (b) ${{\varepsilon}}= {{\varepsilon}}_0 + \Delta {{\varepsilon}} $ in core layer 1 and ${{\varepsilon}}= {{\varepsilon}}_0 - \Delta {{\varepsilon}} $ in core layer 2.图2 中纤芯1和纤芯2的相对介电常数变为复数, 即纤芯1相对介电常数变为${{\varepsilon}} = {{\varepsilon}}_0 + {\rm{i}}\Delta {{\varepsilon}}$ , 纤芯2相对介电常数变为${{\varepsilon}} = {{\varepsilon}}_0 - {\rm{i}}\Delta {{\varepsilon}}$ . $d = 0.03\lambda$ (蓝色实心圆, 绿色空心圆)或$0.05\lambda$ (红色菱形, 品红色十字架), 其他结构参数同图2 结构. 原波导系统变为PT对称波导, 即图3 所示结构, 该结构的波导依旧满足手征对称. 但由于纤芯相对介电常数具有虚部, 波导具有了增益或损耗, CCMT不再适用. 图3(a) 和图3(b) 中 GCMT的结果与全波模拟计算结果匹配得非常好, 但图3(c) 和图3(d) 中CCMT的结果便不再正确.图 3 有效折射率$n_{\rm{eff}}$ 实部与虚部及$\Delta {{\varepsilon}} $ (a), (c) 有效折射率$n_{\rm{eff}}$ 实部; (b), (d) 有效折射率$n_{\rm{eff}}$ 虚部Figure3. Real part and imaginary part of effective mode indices $n_{\rm{eff}}$ versus $\Delta {{\varepsilon}} $ : (a), (c) Real part of effective mode indices $n_{\rm{eff}}$ ; (b), (d) imaginary part of effective mode indices $n_{\rm{eff}}$ .图4(a) 所示为各向异性介质波导, 其截面是各向异性电介质椭圆, 被长轴$a = \lambda _0$ 和短轴$b = 0.5 \lambda _0$ 的理想电导体包围, 其中$\lambda _0$ 是真空波长. 波导芯的介电张量为各向异性的, 即图 4 各向异性波导 (a) 椭圆波导示意图; (b) 使用有限元法进行全波计算得到的有效折射率$n_{\rm{eff}}$ 实部(红线)和虚部(黑线)与${{\varepsilon}}_{\rm{r}}$ 函数关系; (c)有效折射率$n_{\rm{eff}}$ 实部; (d) 有效折射率$n_{\rm{eff}}$ 虚部; (e)—(h) 图(b)中黑色实心圆标记点前向/后向传播模式$\phi$ 的$E_x$ 分量的实部/虚部Figure4. Anisotropic waveguide: (a) The schematic of elliptical waveguide; (b) the real (red line) and imaginary (black line) part of effective modal indices, calculated from fullwave simulation using finite element method, as a function of ${{\varepsilon}}_{\rm{r}}$ ; (c) real part of effective mode indices $n_{\rm{eff}}$ ; (d) imaginary part of effective mode indices $n_{\rm{eff}}$ ; (e)?(h) the real/imaginary part of $E_x$ obtained from fullwave simulation is shown for the modes $\phi$ ${{\varepsilon}}_{\rm r}^{zz} = 0.8$ , 以确保当仅存在前向传播模式和后向传播模式耦合时波导仅有单模. 图4(b) 中, 波导的色散, 即有效折射率的实部和虚部(分别由红线和红线标记)是由商业软件包COMSOL MULTIPHYSICS计算得到. 图4(b) 表明前向与后向模式之间的耦合已经不可忽略. 在两条紫色虚线之间选择一个有限区域, 即范围为${{\varepsilon}}_{\rm r} = -0.5— 0.4$ , 其中包含有效折射率从实数到复数的分界点(EP点), 在该区域用GCMF预测的有效折射率$n_{\rm{neff}}$ 与全波模拟仿真结果进行比较.$\Delta {{\varepsilon}}$ 为扰动的强度, 表明非对角项中的各向异性大小. 从图4(c) 和图4(d) 可以看出, GCMF (红色圆圈)获得的色散与全波模拟的数值结果(灰色实线)具有很好的一致性, 但GCMT (蓝色方块)获得的色散有很大差异. 通过全波模拟计算的前向和后向传播模式如图4(e) —(h) 所示, 其中图4(e) 和图4(f) 绘制了前向传播模式$\phi$ 的$E_x$ 分量的实部和虚部. 图4(g) 和图4(h) 绘制了后向传播模式$\psi$ 的$E_x$ 分量的实部和虚部. 图4(e) —(h) 绘制的示意图对应图4(b) 中黑色实心圆标记点. 图4(e) —(h) 表明, 前向传播模式和后向传播模式之间失去了确定的关系, 这导致仅存在单个传播模式时CCMT及GCMT失效, 只有用前向和后向传播模式共同作为展开函数, 才能得到正确的结果.7.总 结 互易波导模式耦合理论突破了传统模式耦合理论的限制, 不再要求波导系统满足光功率守恒, 适用于任意互易波导模式耦合问题, 为互易波导中的模式耦合提供了统一的描述. 互易波导模式耦合理论中, 证明了互易波导在双正交内积下是自伴随的, 继而建立原始波导系统的本征模和伴随系统的本征模间的相互联系. 在一定的对称性条件下, 伴随系统的本征模可由原始系统本征模得到, 即测试函数在对称性条件下可由展开函数得到, 这大大简化了模式耦合的计算. 通过比较三种具体的模式耦合理论, 发现互易波导模式耦合理论和传统模式耦合理论有相同的形式, 在一定的条件下互易波导模式耦合理论可以退化为传统模式耦合理论, 这也表明互易波导模式耦合理论是对传统波导模式耦合的完善与补充. 对比三种模式耦合理论的不同之处, 能够发现互易波导模式耦合理论之所以能适用于任意互易波导, 是因为其选用了完备的模式集作为展开函数和测试函数. 在互易波导模式耦合理论提出之前, 只能通过经验模型或者数值仿真计算来分析各向异性和双各向异性介质波导模式耦合问题, 这些方法不仅缺少严格的理论推导, 而且不能为波导模式耦合分析提供直观的描述.[69 -71 ] . 互易波导模式耦合理论不仅为各向异性和双各向异性介质波导模式耦合提供了新的分析方法, 而且也为超材料波导的设计提供了理论依据.附录A.同$\beta$ 推论的证明 考虑由两个方程描述的波导系统:$\beta_1$ 和$\beta_2$ 的关系, 以双正交基$[{{{\phi}}_i}]$ , $[{{{\psi}}_j}]$ 作为基底来表示上述微分算子. 通过应用标准的伽辽金矩阵法, 以$[{{{\phi}}_i}]$ , $[{{{\psi}}_j}]$ 为基底, 可以计算出算符对应的矩阵元素,$\bar{ \bar { L}}$ , $\bar{ \bar { L}}^{\rm{a}}$ , $\bar{ \bar {{{B}}}}$ , $\bar{ \bar {{{B}}}}^{\rm{a}}$ 为矩阵形式. 对(10 )式转置, 可得到$\bar { \bar {{L}}}_{ij}$ 是标量, 可以不改变数值的情况下进行转置,A2 )式、(A3 )式和(A5 )式三个等式, 得到$\bar { \bar {{L}}}_{ji} = {\bar{\bar{ L}}}^{\rm{a}}_{ij}$ , 可以得到对称关系$\bar {{{\bar{ L}}}}^{\rm{a}} = \big(\bar {{\bar{ L}}}\big)^{\rm{T}}$ . 对于算符${\bar{{B}}}$ , 易得$\bar { \bar {{B}}}^{\rm{a}} = \big(\bar { \bar {{B}}}\big)^{\rm{T}} = -\bar { \bar {{B}}}$ .A1 )和(A2 )写为矩阵形式, 能得到A6 )式和(A7 )式的本征值等式为$|\bar {{\bar{ L}}}-\beta_1\bar { \bar {{{B}}}} | = 0$ 和$|(\bar {{\bar{ L}}})^{\rm{T}}+ \beta_2 \bar { \bar {{{B}}}}| = 0$ . 对$|(\bar {{\bar{ L}}})^{\rm{T}}+\beta_2 \bar { \bar {{{B}}}}| = 0$ 进行转置后便能得到$\beta_1 = \beta_2$ .附录B.互易波导前向/后向传播模式的对称性 首先给出描述一般双各向异性波导问题的本征方程:${\cal{H}}$ 为哈密顿量, 有关${\cal{H}}$ 的具体形式, 参见文献[50 ]. $\varPsi$ 为本征模式, $\beta$ 为本征值. 接下来使用本征方程和三种对称性, 即手征对称、时间反演对称、宇称对称, 来分别推导出前向/后向传播模式在三种对称性下的约束关系.${{\sigma}}$ 作用于模式$\varPsi$ 时, 横向磁场反号, 而横向电场符号不变, 又因为坡印亭矢量P ${{P}} = {{E}}\times{{H}}$ , 所以手征操作${{\sigma}}$ 作用于模式后会改变能量的传播方向, 因而建立起了前向/后向传播模式之间的关系. 引入手征对称对光学参数的约束条件[50 ] : $\bar {{{\varepsilon}}} _{\rm r}^{zt}$ , $\bar {{{\varepsilon}}} _{\rm r}^{tz}$ , $\bar {{{\mu}}} _{\rm r}^{zt}$ , $\bar {{{\mu}}} _{\rm r}^{tz}$ 和${\bar{ \chi}}$ 都为0, 则${\cal{H}}$ 满足如下手征对称性关系: ${{\sigma}}^{ - 1} {\cal{H}}{{{\sigma}}} = - {\cal{H}}$ . 将其代入(B1 )式, 得到反向传播场的方程:$\beta$ 的本征模式$\varPsi$ (见(B1 )式), 则该波导也一定存在传播常数为$-\beta$ 的本征模式${{\sigma}}\varPsi$ (见(B3 )式). 即对于给定的前向传播模式, 则一定存在后向传播模式, 并且前向和后向传播模式可通过对称操作${{\sigma}}$ 相互转换.${\cal{T}}:\hat{p}\rightarrow -\hat{p}, {\rm{i}}\Rightarrow -{\rm{i}}$ , 其中$\hat{p}$ 是动量算符[30 ,72 ] . 通常该算符可以表示为${\cal{T}} = { {UK}}$ , 其中U K [73 ] . 在手征对称操作中算符${{\sigma}}$ 也是幺正矩阵, 这里可用来代替U ${\cal{T}} = {{\sigma}} K$ . 当算符K B1 )式中介电常数张量${{\bar{{{\varepsilon}}}}}_{\rm r}$ , 磁导率张量${\bar{ \mu}}_{\rm r}$ 和$\bar{{\chi}}$ 取复共轭. 如果波导在时间反演操作下是不变的, 那么需要介质参数的所有元素为实数, 即${{\bar{{{\varepsilon}}}}}_{\rm r}$ , ${\bar{ \mu}}_{\rm r}$ 和$\bar{{\chi}}$ 为实数, 那么将有${\cal{T}}^{ - 1} {\cal{H}}{{\cal{T}}} = -{\cal{H}}$ . 然后将其代入(B1 )式, 并考虑${\cal{T}}$ 的定义式, 得到:$\beta$ 的本征模式$\varPsi$ (见(B1 )式), 则该波导也一定存在传播常数为$-\beta^*$ 的本征模式${{\sigma}}\varPsi^*$ (见(B4 )式). 即对于给定的前向传播模式, 如果满足时间反演对称条件, 则一定存在后向传播模式, 并且前向和后向传播模式可通过对称操作${\cal{T}}$ 相互联系.${\cal{P}}$ , ${{r}}\rightarrow-{{r}}$ , $\hat{p}\rightarrow -\hat{p}$ , 其中r $(x, y)$ . 波导的光学性质基本由空间相关的介电常数${\bar{{{\varepsilon}}}}_{\rm r}\left({{r}} \right)$ 和磁导率$ {\bar{{{\mu}}}}_{\rm r}\left({{r}} \right) $ . 在$\bar{{\chi}}$ = 0的情况下, (B1 )式可写为${\cal{H}}$ 中的第一个r r ${\cal{P}}$ 也包含一个幺正矩阵${{\sigma}}$ 和反转坐标的算符. 将${\cal{P}}$ 算符作用于(B5 )式的哈密顿量, 能得到以下等式:${\cal{P}}$ 操作不变, 即满足宇称对称条件${\bar{{{\varepsilon}}}}_{\rm r}\left(-{{r}} \right) = {\bar{{{\varepsilon}}}}_{\rm r}\left({{r}} \right)$ , ${\bar{{{\mu}}}}_{\rm r}\left(-{{r}} \right) = {\bar{{{\mu}}}}_{\rm r}\left({{r}} \right)$ , 可以得到宇称对称关系${\cal{P}}{\cal{H}}\left({{r}}, {\bar{{{\varepsilon}}}}_{\rm r}\left({{r}} \right), {\bar{{{\mu}}}}_{\rm r}\left({{r}} \right)\right){\cal{P}}^{-1} = -{\cal{H}}\left({{r}}, {\bar{{{\varepsilon}}}}_{\rm r}\left({{r}} \right), {\bar{{{\mu}}}}_{\rm r}\left({{r}} \right)\right)$ . 与之前步骤类似, 考虑${\cal{P}}$ 的定义与(B1 )式, 可以得到反向传播模式满足的方程:$\beta$ 的本征模式$\varPsi$ (见(B1 )式), 则该波导也一定存在传播常数为$-\beta$ 的本征模式${{\sigma}}{\bf{\varPsi}}(-{{r}})$ (见(B7 )式). 即对于给定的前向传播模式, 如果满足宇称对称条件, 则一定存在后向传播模式, 并且前向和后向传播模式可通过对称操作${\cal{P}}$ 相互联系. 当$\bar{{\chi}}$ 不能被忽略时, 只要满足${\bar{ \chi}}\left({{r}}\right) = -{\bar{ \chi}}\left(-{{r}}\right)$ 宇称对称性的结论依旧成立. 




























































































































































































































































































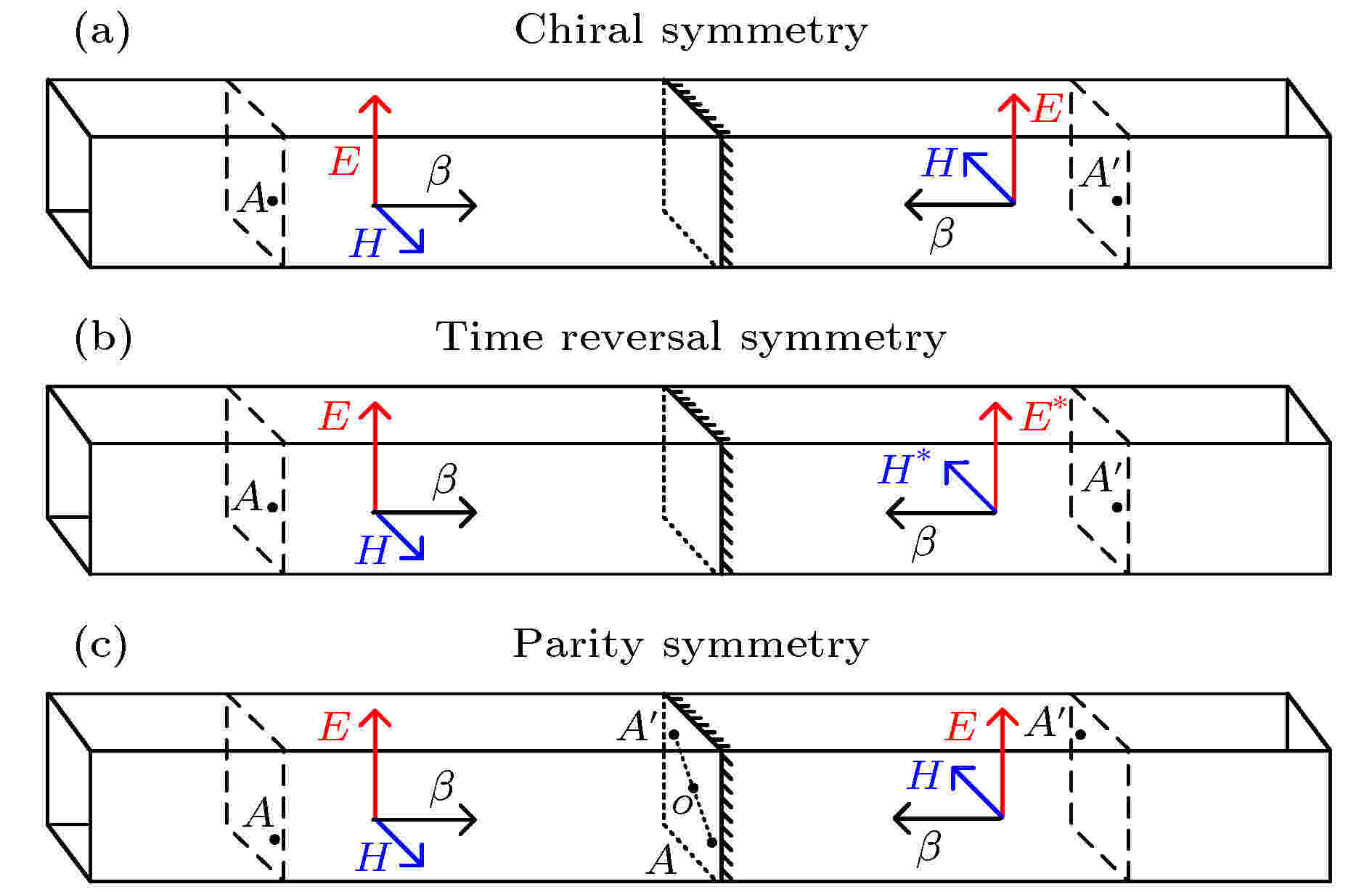 图 1 前向和后向传播模式之间对称关系 (a) 手征对称; (b) 时间反演对称; (c) 宇称对称
图 1 前向和后向传播模式之间对称关系 (a) 手征对称; (b) 时间反演对称; (c) 宇称对称


































































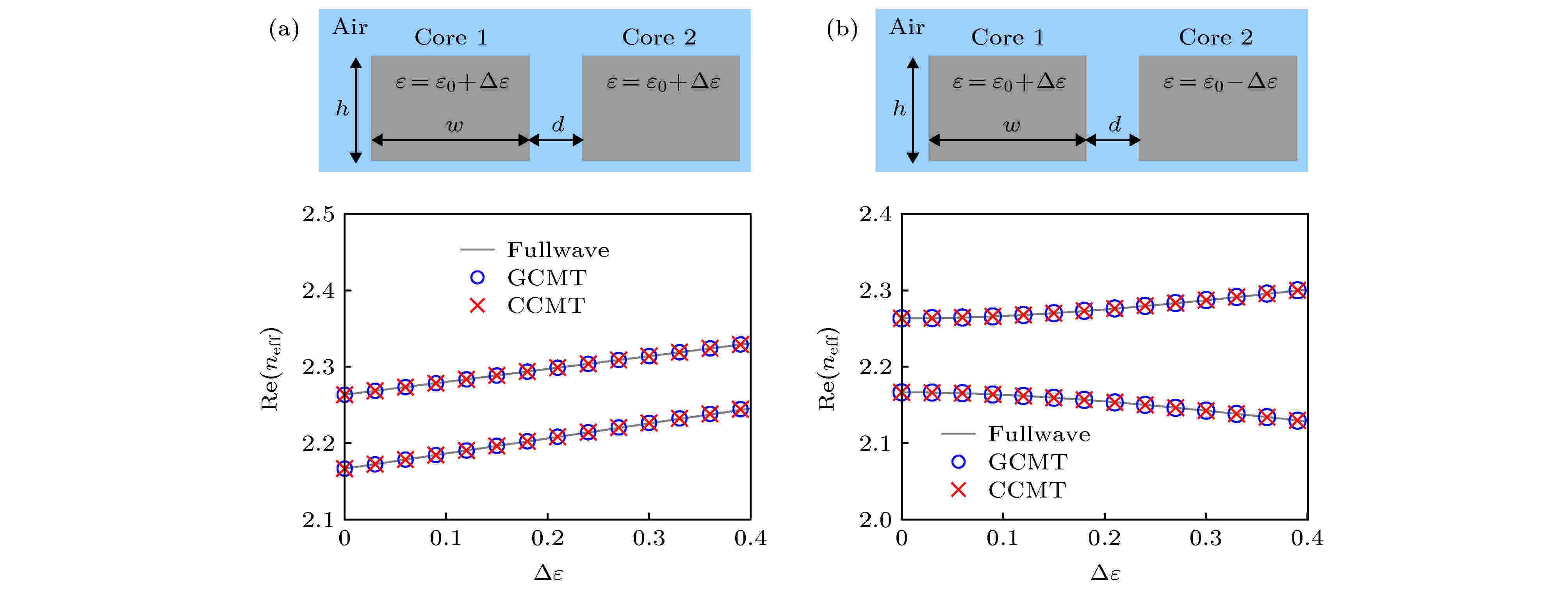 图 2 有效折射率
图 2 有效折射率























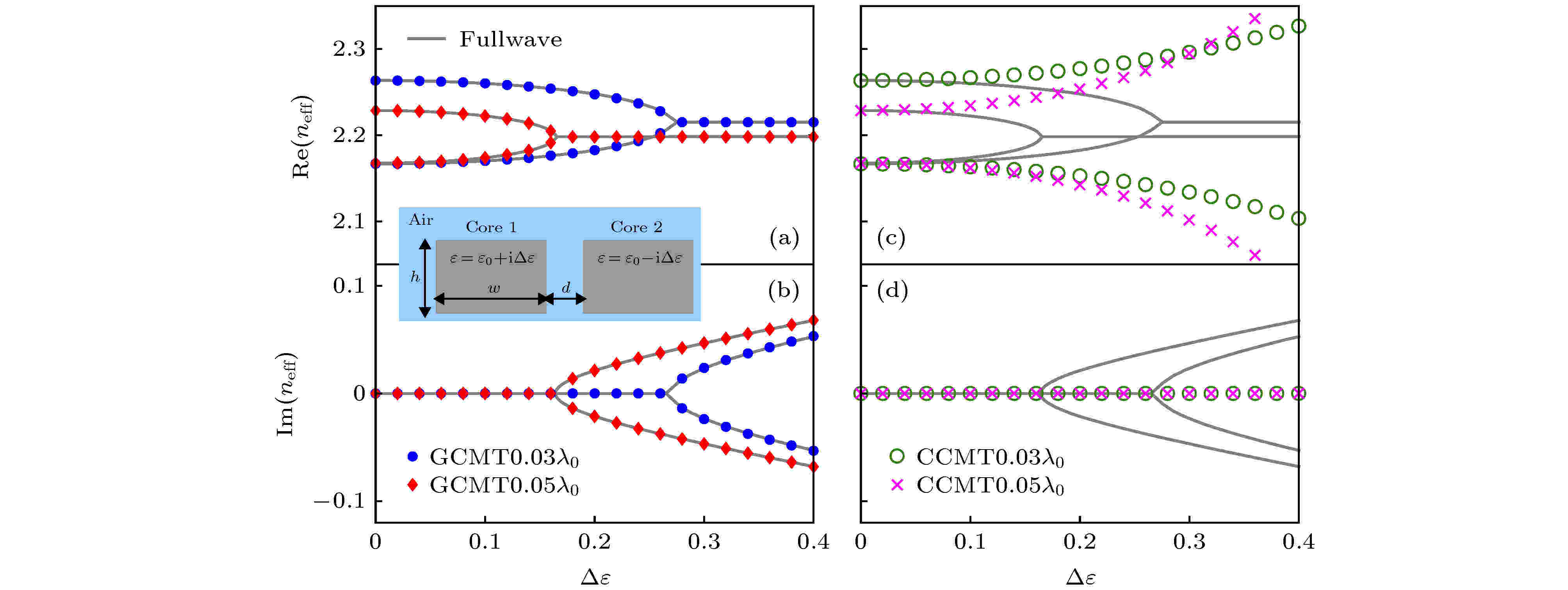 图 3 有效折射率
图 3 有效折射率






















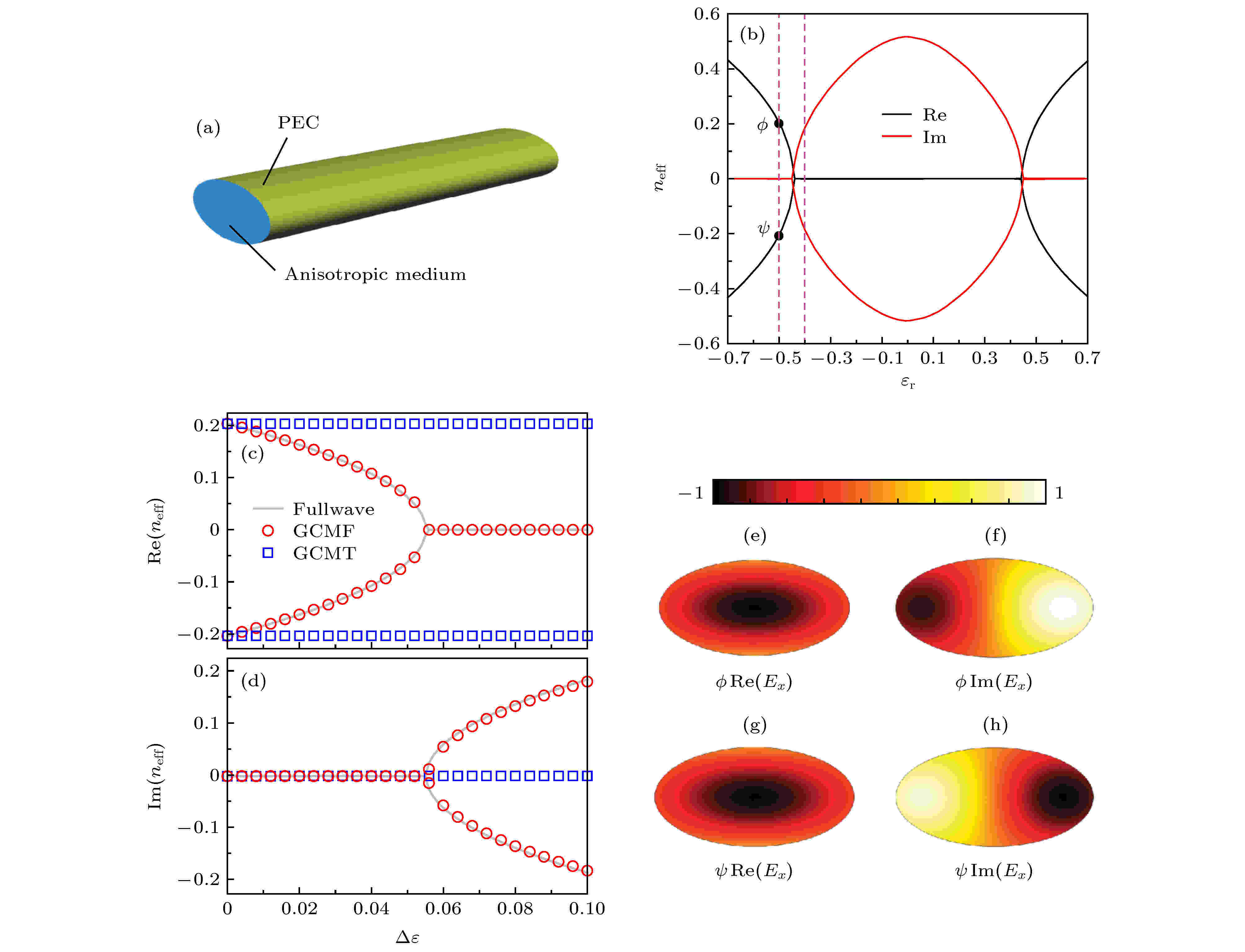 图 4 各向异性波导 (a) 椭圆波导示意图; (b) 使用有限元法进行全波计算得到的有效折射率
图 4 各向异性波导 (a) 椭圆波导示意图; (b) 使用有限元法进行全波计算得到的有效折射率































































































































