摘要:光学超构材料是一种人工设计的微结构材料, 它的出现打破了传统材料设计思维的局域性, 为在微纳尺度上人为调控电磁波提供了新的范式, 实现了具有超越自然界常规材料的光学性质. 尤其是超构材料具有将光和电磁辐射耦合到亚波长尺度的能力, 满足了高速发展的现代科学技术对光学元器件的高性能、微型化以及集成化的新要求. 因此, 基于超构材料的光子芯片带来很多令人鼓舞的应用, 如突破衍射极限的完美成像、多功能的集成光学器件等. 更有意思的是, 超构材料光子芯片还可以用来模拟一些广义相对论的现象, 尤其是探索一些尚未被实验证实的与引力相关的现象. 本文从不同类型的超构材料芯片出发, 简要介绍了在光学超构材料芯片上开展的类比引力的研究, 最后对其发展现状、优势与面临的挑战进行了相应的总结与展望.
关键词: 光学超构材料/
光子芯片/
类比引力

English Abstract

全文HTML

--> --> -->

近年来, 超构材料迎来了极为快速的发展, 由于具有超越于传统材料的物理特性, 它在力学、热学、光学、电磁学以及声学等领域中大放光彩. 超构材料引起大家的兴趣最早源于左手材料^[1]的提出. 这种奇异的媒质之所以被称为左手材料是因为它的介电常数和磁导率都为负值, 同时麦克斯韦方程组计算发现电磁波在这种材料中传播时, 电场矢量、磁场矢量和波矢遵循反常的左手螺旋定律. 进一步研究发现, 电磁波在左手材料中传播时能流矢量与相速度方向相反, 从而导致负折射现象. 更有意思的是, 这种奇异的左手材料带来了很多与自然界传统材料截然不同的物理现象, 譬如逆斯涅耳定律、逆多普勒效应等. 由于这种左手材料在自然界中不是天然存在的, 所以它被提出时仅仅是理论预测, 无法在实验上被验证, 因此很长时间内没有引起普遍的关注. 超构材料真正引起人们广泛兴趣是人工金属劈裂环共振器^[2](split-ring resonator, SRR)的提出. 1999年, 英国科学家Pendy等^[2]研究发现, 当电磁波与SRR相互作用时, 电磁波的磁场分量可以使SRR结构产生感应电流, 进而产生磁偶极共振. 进一步研究发现, 以SRR为单元的周期性排列的超构材料可以实现负的磁导率.正是基于Pendry等^[2]的开创性工作, Shelby等^[3]利用SRR结构在微波波段第一次实验证实了Veselago的预言. 负折射率材料的出现带来一个重要的应用是完美透镜^[4]. 理论研究发现, 当携带信息的电磁波在负折射率超构材料中传播时, 衰减的倏逝电磁波会被放大, 传播的电磁波会因为负折射而产生波前聚焦, 因此, 倏逝波和传播的电磁波所携带的信息都会被汇聚到一个焦点, 进而打破衍射极限, 完美成像. 2005年, Fang等^[5]首次在实验上证实了打破衍射极限的近场完美成像, 该实验利用银膜放大倏逝波的信号, 实现了紫外波段约为波长六分之一的线宽成像. 2007年, Liu等^[6]利用银和三氧化二铝交替生长的多层膜结构组成的双曲超透镜, 同样在紫外波段实验上实现了远场的超分辨率成像. 随着超构材料的发展, 尤其是电磁隐身斗篷的出现, 科学界掀起对超构材料研究新的高潮. 受到广义相对论的启发, 2006年, 在同期的《科学》杂志上, Pendry等^[7]和Leondart^[8]分别独立地提出了变换光学的理论. 研究发现, 借助超构材料高效地调控等效电磁参数, 可以实现电磁波按照理论设计的路径进行传播. 电磁隐身斗篷就是其中一个最经典的案例, 可以让电磁波绕过障碍物体传播而没有任何的反射和散射. 2006年, Schurig等^[9]首次在微波波段利用SRR结构的电磁超构材料实现了隐身斗篷. 但SRR共振实现的隐身斗篷只能工作在很窄的频率范围内, 同时Pendry最早设计的隐身方案对超构材料的电磁参数空间分布有着苛刻的参数要求, 为了克服这些缺点, Li和Pendry^[10]提出了地毯隐身的方案. 2009年, Smith研究组^[11]和崔铁军研究组^[12]在微波波段通过连续改变亚波长的SRR结构构造的非共振超构材料实现了宽波段的地毯隐身衣. 紧接着, 在近红外以及可见光宽波段的地毯隐身^[13-15]在实验上也被一一实现. 更有意思的是, 可见光波段宏观物体的隐身衣^[16,17]利用天然方解石晶体也在实验上被证实. 陈红胜等^[18]在实验中使用折射率高的透明玻璃材料实现了在自然环境下生物活体的隐身. 除此之外, 电磁波的隐身斗篷也可以拓展到其他不同类型波, 譬如物质波隐身斗篷^[19]、弹性波隐身斗篷^[20]、声波隐身斗篷^[21-24]以及热流隐身斗篷^[25-27]. 除了突破衍射极限的完美成像和具有想象力的隐身斗篷外, 超构材料还带来了很多富有创造力的功能器件. 马云贵等^[28]利用超构材料在微波波导内实现了电磁波180°转弯. 陈焕阳和陈子亭^[29]提出利用超构材料可以实现能对电磁波的场分布进行任意旋转的器件. 赖耘等^[30]提出利用超构材料来实现幻觉功能的器件, 即利用超构材料将物体本身的影像消除, 并重构出另外一个新的幻觉影像. Liu等^[31]提出利用超构材料对电磁波阻抗和偏振进行控制, 实现了电磁波在横电(transverse electric, TE)模式与横磁(transverse magnetic, TM)模式间无损耗地相互转换, 进一步构建了电磁波的赝磁场^[32], 实现了类比电子的自旋霍尔效应. 关于超构材料和变换光学相结合的工作, 在陈子亭与合作者^[33]的综述文章中有较为系统的总结.
另一方面, 未来信息技术对集成芯片提出了更高的要求, 譬如传输速度更快、信道容量更大以及集成度更高. 通常信息的载体有光子和电子, 电子集成技术近些年来发展迅猛, 而光子作为自然界传播信息最快的载体在芯片集成技术上却相对落后. 基于超构材料对电磁波的高效调控, 光子集成设计方法与超构材料结合可以在一个微小的光学芯片上对光子进行高效的调控, 由此带来很多功能性很强的器件. Rahm等^[34]和Roberts等^[35]在理论上提出在电磁波导中利用超构材料技术可实现光束各种角度的拐弯、分束、扩束以及聚焦等光学功能器件. 在光子集成技术中, 金属表面等离激元是一种自由电子在电磁波作用下集体振荡产生极化波, 能将电磁波压缩到亚波长的尺寸. 因此金属表面等离激元可以作为未来高度集成光子芯片的信息载体. 2010年, 两个研究组^[36,37]利用变换光学原理并结合超构材料技术在芯片上实现了可见光波段的金属表面等离激元传播的调控. 当金属表面等离激元传播遇到障碍物时, 其能量有很强的散射损失, 如果将理论设计的超构材料包裹在障碍物上, 金属表面等离激元可以越过障碍物而没有任何散射, 这种特殊的芯片设计方法极大地提高了光子传输对杂质的免疫能力. 正是基于这种方法, 张翔研究组^[38]利用灰度电子束曝光方法制备了光子芯片, 实现了近红外波段金属表面等离激元传输的调控, 如可以将金属表面等离激元进行几乎没有能量损失的聚焦. 这种方法也实现了近红外波段多功能的光子芯片^[39], 即一块光子芯片同时具有对金属表面等离激元进行聚焦和扩束的功能.
早期, 人们尝试在凝聚态物质中模拟广义相对论效应. 这种研究方法源于类比思想, 是物理学研究中一个重要的思想方法. 以电动力学早期发展为例, 电磁、磁场及其规律是类比流速场及其规律, 例如涡旋、源、汇等概念的引入. 这对于推动电磁学的发展至关重要. 基于相同的思想, 凝聚态体系也被用来研究一些由于天文观测手段限制而无法观测的广义相对论现象, 其中最突出的例子就是霍金^[40]提出黑洞辐射不久, 安鲁^[41]在1981年提出了类比引力的声学黑洞模型, 其直观的物理图像是用流体中的声波来类比弯曲时空中的电磁波. 对于以一定速度逆流而上的声波, 当流体的速度超过声速时, 声波被流体拖曳会困在该流体超声的区域. 这个超声区域可以类比视界, 从而可进一步在声学视界上观测声子的霍金辐射. 当声学黑洞模型被提出后, 人们在超导电子线路^[42]、简并的Fermi气体^[43]、³He超流体^[44]、玻色-爱因斯坦凝聚体^[45-47]以及离子阱^[48]等多个体系中模拟研究了霍金-安鲁效应. Philbin等^[49]在光纤体系中利用光纤介质的克尔效应在实验上实现了类比视界, 并观测到视界附近的蓝移现象. 实验上类比视界是利用超快脉冲改变光纤介质的折射率, 随后注入弱的探测光. 由于探测光的速度稍快, 当它靠近脉冲光时, 光纤折射率因克尔效应增大, 从而导致其速度减小, 直至相对脉冲光静止. 最近, 同样在光纤体系中, 人们成功观测到类霍金的受激自发辐射^[50]. Berliorno等^[51]在熔融的二氧化硅玻璃中注入激光脉冲也在实验上实现了类霍金的自发辐射. Yu和Hu^[52]在综述文章中对不同的物理体系模拟霍金-安鲁效应进行了较为系统的总结. 除了霍金辐射之外, Bekenstein等^[53]利用非线性晶体的热效应研究了引力场的非线性动力学效应, 并观测到由于电磁波包与引力场相互作用而产生的引力红移和蓝移. Roger等^[54]同样利用非线性晶体的热效应模拟了玻色子恒星的演化. 正是基于类比思想, 很多被广义相对论所预言但是很难被观察到的现象可以在实验室环境下被重复细致地研究.
最近十多年来, 超构材料作为一种人工可调控的微结构材料, 也被拓展到类比引力的研究中. Smolyaninov等^[55,56]提出利用双曲超构材料可以模拟时空结构的改变. 双曲超构材料是电磁超构材料的一个重要分支, 其有着特殊的色散关系: $(k_x^2 + k_y^2)/{\varepsilon _{zz}} + k_z^2/{\varepsilon _ \bot } = k_0^2$, 其中${k_0}$是真空波矢的大小, ${{ k}_x}$, ${{ k}_y}$, ${{ k}_z}$分别为x, y, z方向上的波矢, 这里假设光轴沿z方向, ${\varepsilon _{zz}}$是沿着光轴方向上的介电参数, ${\varepsilon _ \bot } = {\varepsilon _{xx}} = {\varepsilon _{yy}}$是垂直于光轴方向上的介电参数, 同时满足${\varepsilon _{zz}}$与${\varepsilon _ \bot }$的符号相反(${\varepsilon _{zz}} > 0$, ${\varepsilon _ \bot } < 0$或者${\varepsilon _{zz}} < 0$, ${\varepsilon _ \bot } > 0$). 由于双曲超构材料沿着光轴方向或者垂直光轴方向的介电常数为负, 因此电磁场方程中在该方向的二阶导数项的系数为负, 而在其他方向上保持系数为正的性质不变. 基于克莱因-高登方程与双曲超构材料中电磁波传播的亥姆霍兹方程在数学上的类似性, 介电常数为负的方向可以看作是一个等效的时间方向. 因此可以用电磁波在双曲超构材料中的演化来模拟时间演化的方向性^[57], 甚至模拟宇宙大爆炸以及宇宙暴涨过程^[58]. Greenleaf等^[59]在理论上提出利用超构材料调控介电常数和磁导率以构造外界电磁场不可探测的电磁通道来模拟电磁虫洞. Narimanov和Kildishev^[60]通过理论计算发现利用超构材料构造人工黑洞可以对电磁波进行全方向捕获. 随后崔铁军研究组^[61]利用SRR为结构单元的超构材料在微波波段实现了这种人工“电磁黑洞”, 其不仅可以吸收周围的电磁波, 而且对电磁波的吸收率可达到99%以上. Genov等^[62]也从拉格朗日光学出发, 在理论上提出通过在高电磁介质中填充不均匀空气的点阵能构造出各向同性的可见光波段的黑洞, 可以模拟天体在引力场运动, 譬如轨道运动、奇异吸引子和混沌运动等. 陈焕阳等^[63]在理论上提出利用电磁参数各向异性的超构材料可以构造满足施瓦西度规的黑洞. Li等^[64,65]在理论上计算了德西特时空中电磁场的Casimir能量与视界的尺度的关系, 发现这种关系与全息暗能量的形式相同, 并进一步提出可以利用超构材料模拟德西特时空. Mackay和Lakhtakia^[66]提出可利用电磁参数为含时变化的超构材料来实现引力波的模拟. Ginis等^[67]同样基于含时变化的超构材料模拟了宇宙膨胀导致的引力红移. Hu和Yu^[68]利用非线性的超构材料模拟了宇宙弦时空的光锥涨落.
本文介绍了不同类型的超构材料光子芯片的特点和利用其特点开展的类比引力的研究. 这种类比研究的基本思路是从超构材料中的电磁波方程出发, 根据材料的电磁参数与时空度规的等价性, 利用超构材料控制电磁参数在空间的分布来模拟弯曲时空. 最后对在超构材料芯片上类比引力研究进行了相应的总结与展望.

渐变光学波导芯片通过对光学波导尺寸的调控来实现对电磁波的绝热连续的控制. Smolyaninov等^[69]通过将镀上金属膜的非球面透镜放置在金属平板上构建的绝热变化的波导来实现各向异性的介电常数和磁导率的分布(图1(a)), 实现了在可见光波段大于100倍波长尺寸的宽波段的电磁隐身斗篷. Stockman^[70]通过理论计算发现, 利用金属锥可以实现可见光波段表面等离激元波导的纳米聚焦, 当局域在金属/空气界面上的表面等离激元沿着轴向向金属锥的尖端传播时, 金属表面等离激元会在尖端产生汇聚, 其场强有超过10³倍的增强. 研究获得在金属锥上传播的表面等离激元的色散关系为
图 1 (a) 绝热变化的波导实现的隐身斗篷; (b) 绝热变化的透镜实现打破衍射极限的远场成像; (c) 金属微球夹在金属/介质/金属的三明治结构之间实现黑洞的模拟; (d) 具有奇异点的金属结构对表面等离激元的纳米聚焦; (e) 具有一些奇异点表面等离激元结构模拟紧致空间
Figure1. (a) Tapered waveguide acting as an optical cloak; (b) far-field imaging with breaking diffraction limitation using plasmonic lens with adiabatic change structure; nanofocusing using tapered plasmonic waveguides; (c) the emulation of black hole using a silver microsphere sandwiched by a metal-insulator-metal structure; (d) nanofocusing using metallic nanoparticle with structure singularity; (e) a transformation compacts three dimensions into two dimensions.

$n(R) \approx \dfrac{1}{{{k_0}R}}\sqrt { - \dfrac{{2{\varepsilon _{\rm{d}}}}}{{{\varepsilon _{\rm{m}}}}}} {\left[ {\ln \sqrt { - \dfrac{{4{\varepsilon _{\rm{d}}}}}{{{\varepsilon _{\rm{m}}}}}} - \gamma } \right]^{ - 1}},$

其中R是金属锥的半径, ${k_0} = 2{\text{π}} /\lambda $, $\lambda $是空气中激发的表面等离激元的波长, ${\varepsilon _{\rm{m}}}$和${\varepsilon _{\rm{d}}}$分别是金属和空气的介电常数, γ是欧拉常数. 从色散关系可以看出, 金属表面等离激元在金属锥尖端的等效折射率趋向无穷大, 同时可以无散射地汇聚到金属锥的尖端, 绝热地转换为局域等离激元. Choi等^[71]也通过V字形金属槽在近红外波段实验验证了金属表面等离激元的纳米聚焦, 研究发现, 激发的金属表面等离激元会向槽的尖端汇聚, 并将电磁场的空间大小压缩到波长的1/40, 且这种V形槽的纳米聚焦能力随着其尖端宽度的减小而增大. 由于入射的金属表面等离激元被压缩成线状而不是点, 因此实验上仅仅观测到10倍的增强. Yablonovitch研究组^[72]在实验上使用锥形的金属/介质/金属波导实现了金属表面等离激元的三维纳米聚焦. 理论计算研究发现, 可以将波长为830 nm的表面等离激元深度压缩到尺寸大小仅为2 nm × 5 nm的区域, 最重要的是损耗低于3 dB, 场强获得3.0 × 10⁴的增强. 进一步在双光子荧光增强的实验中验证了锥形的金属/介质/金属波导对金属表面等离激元的纳米聚焦能力, 将金属表面等离激元汇聚到尺寸为14 nm × 80 nm的区域, 同时有400倍的场强增强. 除了纳米聚焦之外, 这种渐变光学波导还可以用来作为超高分辨率绝热成像透镜. Cang等^[73]在一个金属面上放置一个金属球, 并且二者之间有几纳米的空气间隙, 这种结构可以看作一个金属/介质/金属渐变波导结构. 当在二者间隙处激发的金属表面等离激元从球的底部向顶部传播时, 金属表面等离激元被压缩到几纳米间隙处的电磁信息会被绝热放大到远场. 理论计算发现这种绝热成像透镜可以实现在可见光波段下50 nm超高分辨率的成像. Pendry等^[74-77]将变换光学的方法拓展到亚波长尺寸金属纳米颗粒的设计. 根据保角变换, 具有结构奇异点的金属纳米颗粒可以实现可见光宽波段范围内对金属表面等离激元深度的纳米聚焦. 激发的表面等离激元会向结构奇异点汇聚, 同时波包传播的群速度减小甚至完全到零, 因此表面等离激元的场强得到绝热的增强(图1(d)). 这种方法最近被提出来还可以模拟弦论里的空间紧致化^[78], 如图1(e)所示, 可将三维无限大具有周期性金属表面等离激元结构压缩到具有奇异点结构的金属超表面中.
渐变光学波导除了可实现纳米聚焦和超高分辨率成像以外, 还可以展开类比引力现象的研究. Sheng等^[79]在理论上提出, 将金属微球嵌在金属/介质/金属波导的结构中 (图1(c))可以实现可见光波段各向同性黑洞的模拟, 这里是利用金属球与底层金属板之间的间隙实现了黑洞的势场. 在理论数值计算中, 观测到当金属表面等离激元的入射半径小于黑洞光子球尺寸时, 金属表面等离激元会被黑洞捕获并聚焦. 由于金属表面等离激元在传播过程中有着很强的欧姆损耗, 在实验上观测到这种金属表面等离激元的黑洞存在挑战. 为了克服金属表面等离激元的损耗, 渐变聚合物介质波导被用来模拟可见光波段的人工黑洞. 首先从均匀的平板波导出发, 在二氧化硅基底上镀上一层金属银膜, 再旋涂上一层聚合物介质(polymethyl methacrylate, PMMA). 从计算的平板波导的色散关系可以看出, 对于任一激发的波长, 这种平板波导的等效折射率跟介质层的厚度有关. 在一定的厚度范围内, 随着介质层厚度的增加, 等效折射率从空气的折射率绝热增加介质本身的折射率, 因此实验上可以连续改变介质层的厚度来调控等效折射率的分布, 从而实现模拟广义相对论的弯曲时空. 在Sheng等^[80]的工作中, 在实验上使用旋涂加热工艺制备了渐变的介质波导芯片, 利用聚合物与微球之间的表面张力效应(图2(b))构造出介质层的厚度按照中心对称形式非均匀变化的波导, 实现了类似黑洞引力场的等效势场. 这种类比黑洞势场的微腔可以很好地模拟光子在黑洞引力场中传播时由于引力而产生的弯曲(图2(c)). 与此同时, 这种人工黑洞的光学微腔与普通的共振光学微腔相比具有宽波段捕获光子的能力, 在宽波段的激光光源、光电探测以及光伏器件等领域有着潜在的应用价值.
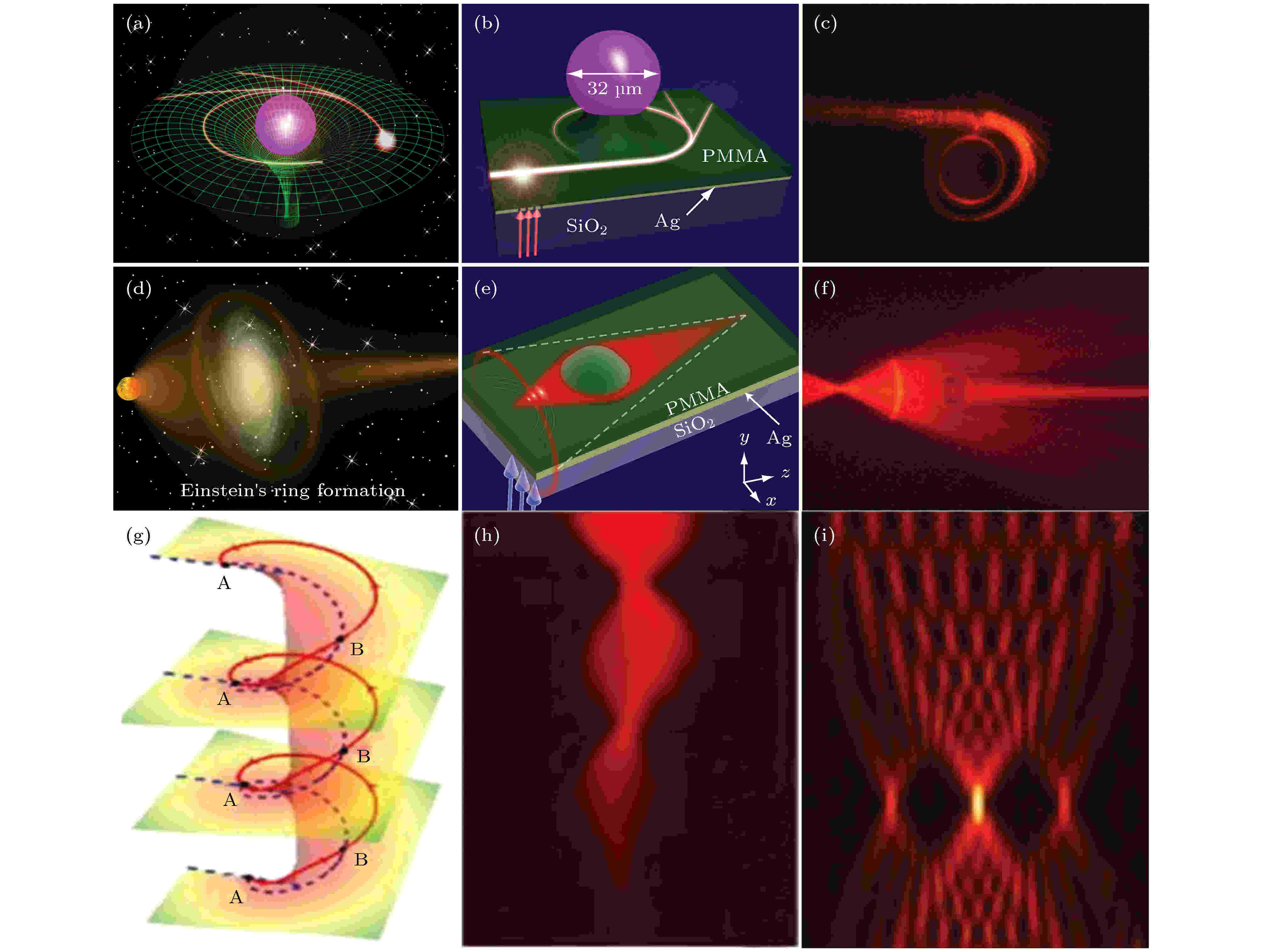图 2 (a) 引力透镜的效应的示意图; (b) 在渐变的介质波导芯片中模拟黑洞的引力透镜效应的示意图; (c) 人工黑洞对光子的捕获; (d) 爱因斯坦环的示意图; (e) 渐变的介质波导芯片中模拟爱因斯坦环的示意图; (f) 模拟爱因斯坦环的实验结果图; (g) 在黎曼曲面上光线的传播; (h)共形Talbot效应的实验结果; (i)利用共形Talbot效应演示的数字编码的传输
Figure2. (a) The schematic of gravitational lensing effect; (b) the emulation of the gravitational lensing of the black hole using adiabatic change dielectric waveguides on a photonic chip; (c) the light trapping of an artificial black hole; (d) the schematic of Einstein ring; (e) the emulation of Einstein ring using adiabatic change dielectric waveguides on a photonic chip; (f) the experiment result of the emulation of Einstein ring; (g) the light propagation on Riemann’s space; (h) the experimental result of conformal Talbot effect; (i) digital coding using the conformal Talbot effect.

渐变介质波导光子芯片除了可以模拟黑洞对光子的捕获, 还可以模拟一些广义相对论预测的罕见天文现象, 譬如爱因斯坦环. 它的形成原因同样来源于大质量天体的引力透镜效应. 当遥远天体发出的光经过大质量天体附近时会由于引力透镜效应产生汇聚, 观测者能在大质量天体附近观测到遥远天体的一系列环状成像(图1(d)). Sheng等^[81]通过液滴的表面张力效应, 制备出了一种模拟天体中心引力场的聚合物波导(图2(e)). 实验中激发弧形光栅模拟遥远天体所需要的球面波的波前, 当发散的光经过“天体”时会由于引力透镜效应而重新聚焦. 进一步在实验中采用可见光波段的量子点荧光成像技术直接观测到爱因斯坦环的形成过程, 测量了重新聚焦的光束宽度与传播距离的关系如图2(f)所示, 同时比较实验所得的结果与爱因斯坦所预测环的角尺寸大小, 二者符合得很好. 这种渐变的介质波导芯片除了模拟弯曲时空中广义相对论的现象, 还可以对电磁波的波前进行调控, 譬如在线性重力场中实现高斯波包与非衍射的艾里波包的相互转换^[82]. Wang等^[83]利用共形变换光学理论, 将麦克斯韦鱼眼透镜通过指数共形变换映射到物理空间, 并结合黎曼页支割线分析(图2(g)), 得到了Mikaelian透镜. 借助于聚合物溶液表面张力自组织过程, 利用这种渐变光学波导制备出了Mikaelian透镜, 并且演示了几何光学条件下的自聚焦特性和类正弦曲线. 同时在芯片上实现了非衍射的Talbot效应, 如图2(h)所示, 可以将图像无损耗地传递到远方. 通过进一步研究, 该器件可以将数据编码无衍射地长距离传输, 因此在信息编码传递方面有着潜在的应用价值. 除了透镜功能之外, 这种渐变的光学波导芯片被实验证明可以实现大角度的光束拐弯^[84].

最近兴起的二维超构材料—超表面^[85]为人们高效调控电磁波提供了新途径. 传统的超构材料通过电磁波在体块中传播来改变相位, 而超表面仅仅在亚波长的传播范围内高效地改变电磁波的波前, 因此超表面极大地克服了超构材料被发现以来所遇到的损耗问题. 除此之外, 超表面是二维材料的特性降低了对微加工技术的要求, 同时也极大地减少了样品的加工时间. 超表面对于电磁波辐射的远场调控有大量报道, 譬如以超表面为单元的平面光学元件^[86-89]以及全息成像^[90,91]等. 更有意思的是, 张翔研究组^[92]采用超表面调控入射电磁波的波前, 实现了可见光波段的皮肤隐身衣, 如图3(a)所示, 且该皮肤隐身衣的厚度仅为80 nm. 与此同时, 超表面对电磁波近场辐射的调控也有相关报道. 譬如Sun等^[93]在理论和实验上实现了微波波段自由空间的电磁波到束缚的表面波的高效转换(图3(b)). Liu和Zhang^[94]在理论上提出超表面可以对表面等离激元的波前进行高效调控. 该理论方案利用可见光波段的双曲超表面在实验上被予以证实^[95](图3(c)). Gomez-Diaz等^[96]在理论上提出在石墨烯超表面中调控等离激元的色散, 可以实现色散从封闭的椭圆到开放的双曲线的拓扑相变(图3(d)). Xu等^[97]在理论上以及实验上将超表面和微波波导相结合, 实现了不对称的电磁波传输(图3(e)). Li等^[98]不仅在近红外波段实现了超表面波导的非对称传输, 还实现了波导模式和偏振模式的调控(图3(f)).
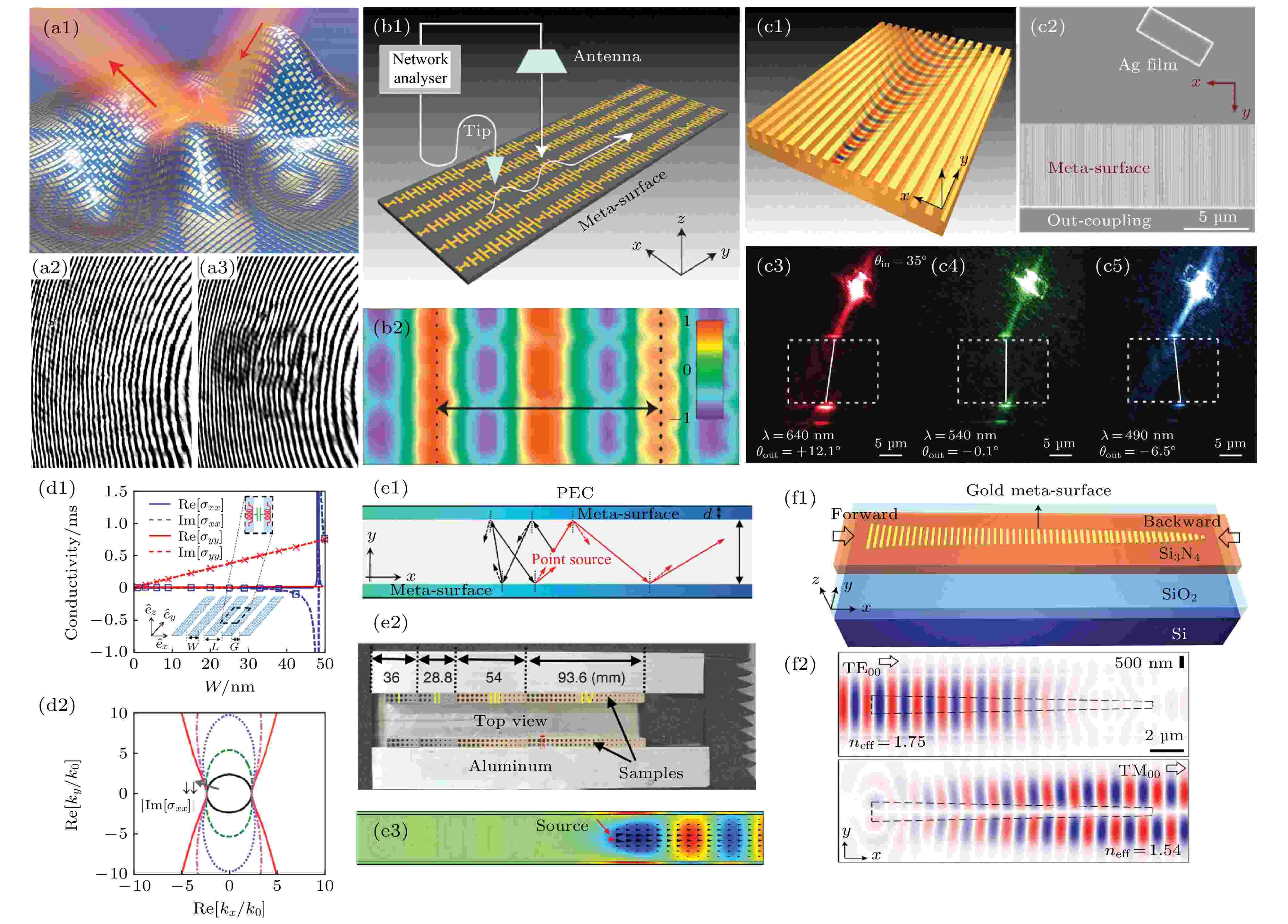图 3 (a1)?(a3) 皮肤隐身衣, 其中(a1) 利用超表面实现皮肤隐身衣的示意图, (a2)有隐身衣时的效果, (a3) 没有隐身衣时的效果; (b1), (b2) 渐变超表面实现电磁波从远场到近场的高效转换, 其中(b1) 渐变超表面波导的示意图; (b2) 近场扫描的实验结果; (c1)?(c5) 超表面波导对表面等离激元的高效调控, 其中(c1) 超表面的表面等离激元波导的示意图, (c2) 超表面的表面等离激元波导的样品图, (c3)?(c5) 在超表面的表面等离激元波导上实现正折射、零折射、负折射; (d1), (d2) 石墨烯超表面实现表面等离激元色散的拓扑相变, 其中(d1) 石墨烯超表面对电导率的调控, (d2) 石墨烯超表面实现表面等离激元色散; (e1)?(e3)超表面波导实现不对称的电磁传输, 其中(e1)超表面波导的示意图, (e2)实验样品图, (e3)实验结果; (f1), (f2) 超表面波导实现电磁模式的转换, 其中(f1) 渐变超表面波导示意图; (f2)电磁模式转换的实验结果
Figure3. (a1)?(a3) Skin cloaking: (a1) Schematic of skin cloaking using metasurfaces; (a2) the reflection case with skin cloaking; (a3) the reflection case without skin cloaking. (b1), (b2) A gradient-index metasurface used to convert a freely propagating wave to a surface wave: (b1) Schematic picture describing the near-field scanning technique; (b2) the experimental result using near-field scanning. (c1)?(c5) Metasurface waveguide for manipulating surface plasmons: (c1) Schematic illustration of a metasurface made of periodic metallic gratings; (c2) a scanning electron microscope image of a device; (c3)?(c5) images of SPP refraction at metasurface waveguides. (d1), (d2) Topological transitions for surface plasmon propagation using grapheme metasurface: (d1) Effective conductivity tensor of the uniaxial metasurface waveguide; (d2) isofrequency contours of grapheme metasurface waveguides. (e1)?(e3) The asymmetric propagation of electromagnetic waves using metasurface waveguide: (e1) Schematic diagram of a metasurface waveguide; (e2) the fabricated sample; (e3) the experimental result. (f1), (f2) The manipulation of waveguide modes using a metasurface waveguide: (f1) Schematic of a working device; (f2) the experimental result demonstrates mode converts.

基于超表面对表面波的高效调控, 超表面波导光子芯片也可以被用来展开类比引力的研究^[99]. 理论学家认为宇宙从大爆炸诞生、演化到现在, 随着温度的降低, 宇宙时空经过了一系列量子相变过程, 这种相变会导致时空真空场的对称性破缺, 而在宇宙中留下各种拓扑缺陷, 例如磁单极子和宇宙弦等. 通过探测这些时空的拓扑缺陷, 人们不但可以追溯早期宇宙的诞生过程, 还能观测量子引力效应, 研究时空的本质. 虽然人们已经开始尝试寻找时空拓扑缺陷, 但由于探测技术的局限, 目前尚未成功. Sheng等^[100]制备了一种二维弯曲超材料, 如图4(a)和图4(b)所示, 实现了一种新型的具有轴向旋转对称的超构材料光子芯片, 其旋转对称中心可以模拟一维时空拓扑缺陷—宇宙弦. 虽然宇宙弦不会像其他质量的天体那样在周围时空中直接产生引力场, 但是会造成周围时空拓扑结构的改变, 导致时空角度的缺损或盈余, 光在这种拓扑时空中传播时, 无论光子的入射位置、传播方向、波长以及偏振方向如何, 都会产生一个确定的偏转角$\varDelta \theta = 4{\text{π}}G\mu /(1 - 4 G\mu )$(这里G是引力常数), 散射的角度只跟宇宙弦的质量密度$\mu $相关, 这是由宇宙弦拓扑时空鲁棒特性所确定的. 对于质量密度为负的宇宙弦$\mu < 0$, 散射角度$\Delta \theta < 0$, 光线会被宇宙弦所排斥(图4(a)和图4(c)); 对于质量密度为正的宇宙弦$\mu > 0$, 散射角度为$\Delta \theta > 0$, 光线会被宇宙弦所吸引(图4(a)和图4(d)). 实验通过调节结构参数, 制备得到了对应负质量和正质量密度的宇宙弦的光学芯片, 并通过显微荧光探针技术直接观察到了光束经过拓扑缺陷产生的偏折, 实验测量的偏折角度具有时空拓扑保护的鲁棒特性, 与入射光束的位置以及方向等因素都无关. 普通的光学介质在对光场进行操控时, 总会改变光场的部分性质, 让光场携带的信息丢失, 例如最简单的光学反射会翻转光场的左右分布, 普通天体引力透镜会导致光场的形变和发散, 而宇宙弦拓扑时空中光场的传递具有很好的鲁棒性, 光场的分布被整体地保护起来, 光信息的传递基本没有损失.
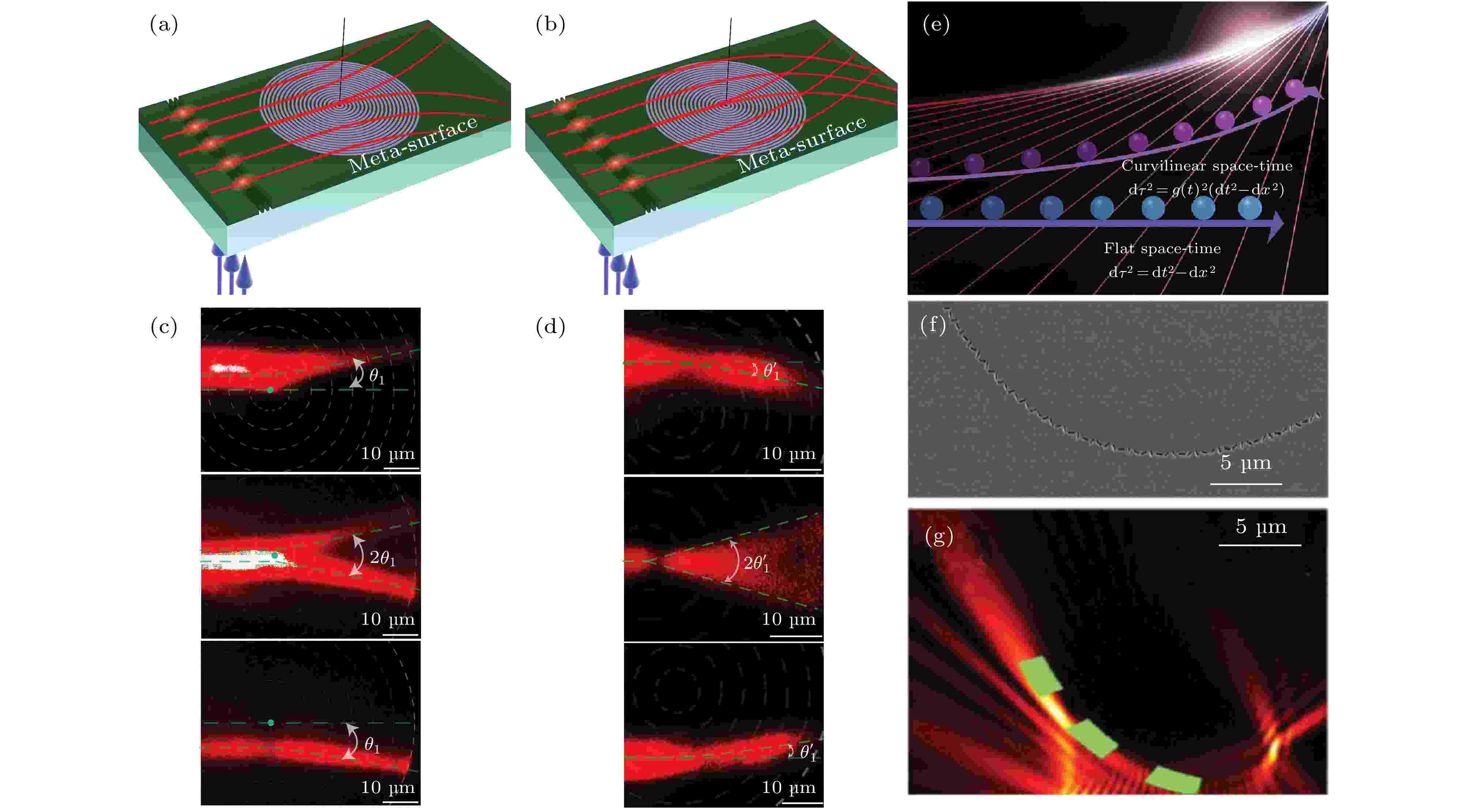图 4 (a) 由超表面波导构造的负质量密度宇宙弦的示意图; (b) 由超表面波导构造的正质量密度宇宙弦的示意图; (c)负质量密度宇宙弦对电磁波散射的实验结果图; (d)正质量密度宇宙弦对电磁波散射的实验结果图; (e) 由超表面波导模拟加速空间中的粒子运动与轫致辐射的示意图; (f) 实验样品照片; (g) 实验测量的等离激元波束
Figure4. (a) Schematic of cosmic string with negative mass density using metasurace waveguides; (b) the electromagnetic scattering in the spacetime of cosmic string with positive mass density; (c) the experimental results to emulate negative cosmic string; (d) the experimental results to emulate positive cosmic string; (e) the schematic of mimicking Bremsstrahlung radiation of moving particles; (f) the scanning electron microscope image of a sample; (g) the experimental result of surface plasmon rays.

除了模拟时空拓扑缺陷—宇宙弦, 超表面波导光子芯片还可以用来模拟弯曲时空中粒子轫致辐射. 根据量子力学理论, 粒子具有内禀自由度, 并且会与外部空间相互作用从而产生很多丰富可观测的效应, 譬如弯曲空间的自旋霍尔效应. 光子是自旋为1的玻色子. Zhong等^[101]将光自旋引入超构材料光学芯片, 通过同时改变超构材料整体的弯曲形状和结构单元局域的旋转角度, 调控时空中自旋光子态的几何相位模拟弯曲时空中粒子的加速运动和轫致辐射(图4(e)). 在实验中采用聚焦离子束技术, 制备了超表面/介质/金属板的光学结构(图4(f)). 超表面由金属纳米孔作为结构单元, 纳米孔与金属板之间的耦合可以产生强的局域磁共振, 以便增强等离激元的激发效率. 实验中在一块具体样品中设计和构造了广义相对论中的伦德勒时空, 模拟了加速坐标系中的轫致辐射, 实现了自由空间的自旋光子到超表面光子芯片上伦德勒等离激元光束的转化. 理论上研究了不同弯曲时空度规之间的的广义协变, 发现了一系列满足广义协变等价的弯曲超构材料, 并在实验上予以证实. 相比较传统变换光学方法通过改变材料的电磁参数的方式, 这种通过调控光自旋子几何位相的方法具有更大的自由度, 而且更容易通过实验实现.

在1981年, Dacosta^[102]从单电子运动的薛定谔方程出发, 研究发现当电子被限定在一个弯曲的曲面上运动时, 电子的运动跟曲面的拓扑曲率有关. 在曲面上波包的运动也被拓展到光学体系中, 当电磁波受限在一个弯曲曲面上的光波导中运动时, 电磁波包的演化同样感受到曲面的拓扑曲率的影响. Batz等^[103-105]在理论上和实验上研究了不同的曲面曲率对电磁波演化的影响. 当电磁波在球形曲面上的电磁波导中传播时, 曲率为正的弯曲表面使得电磁波呈现周期性的聚焦或非衍射的传播(图5(a)). 而当电磁波在马鞍形曲面上的电磁波导中传播时, 曲率为负的弯曲表面导致电磁波以指数形式速率衍射(图5(b)). 该研究组^[106]还进一步研究了在球面以及马鞍形曲面上的Hanbury-Brown-Twiss干涉, 如图5(d)所示, 通过强度干涉的g (2)系数来甄别弯曲空间的曲率. Bekenstein等^[107,108]在实验上和理论上研究了非衍射加速的电磁波包在弯曲表面的演化, 如图5(c) 所示, 非衍射加速波包的轨迹不满足测地线传播, 这意味着其传播轨迹不是最短路径. 这个研究说明弯曲曲面对于电磁波来说相当于一个势场. Xu等^[109]研究了弯曲曲面上的测地线透镜(如图5(g)所示), 譬如广义的麦克斯韦透镜; 同时通过保角变换建立了光在曲面上的传播与在折射率非均匀分布的透镜中传播的等价关系. 并进一步基于保角变换建立了锥形旋转曲面(图5(h))与折射率拓扑缺陷的关系^[110], 研究了该缺陷对电磁波的定向散射(图5(i)和图5(j)). 除此之外, 弯曲曲面上的波导还可以拓展到弯曲空间的广义相对论的模拟. Bekenstein等^[111]将黑洞的Schwarzschild度规投影到了Flamm形曲面上, 如图5(e)所示, 从理论上研究了电磁波在这种曲面上传播的群速度的变化, 在实验上通过3D打印方式制备出按理论设计的Flamm形曲面, 在实验测量上通过高斯光束宽度的变化获得了波包的群速度大小的变化, 进一步观测到电磁波包在黑洞视界附近的隧穿效应(图5(f)). Xu等^[112]研究了在二维旋转曲面上传播电磁波的Gouy相位与旋转曲面的曲率的关系. Zhu等^[113]利用3D打印方式制备模拟了虫洞的弯曲曲面的波导结构, 在弹性波波段模拟了虫洞的隧穿效应. Libster-Hershko等^[114]通过研究在弯曲曲面上表面等离激元的传播, 发现了空间曲率对量子波包演化的影响.
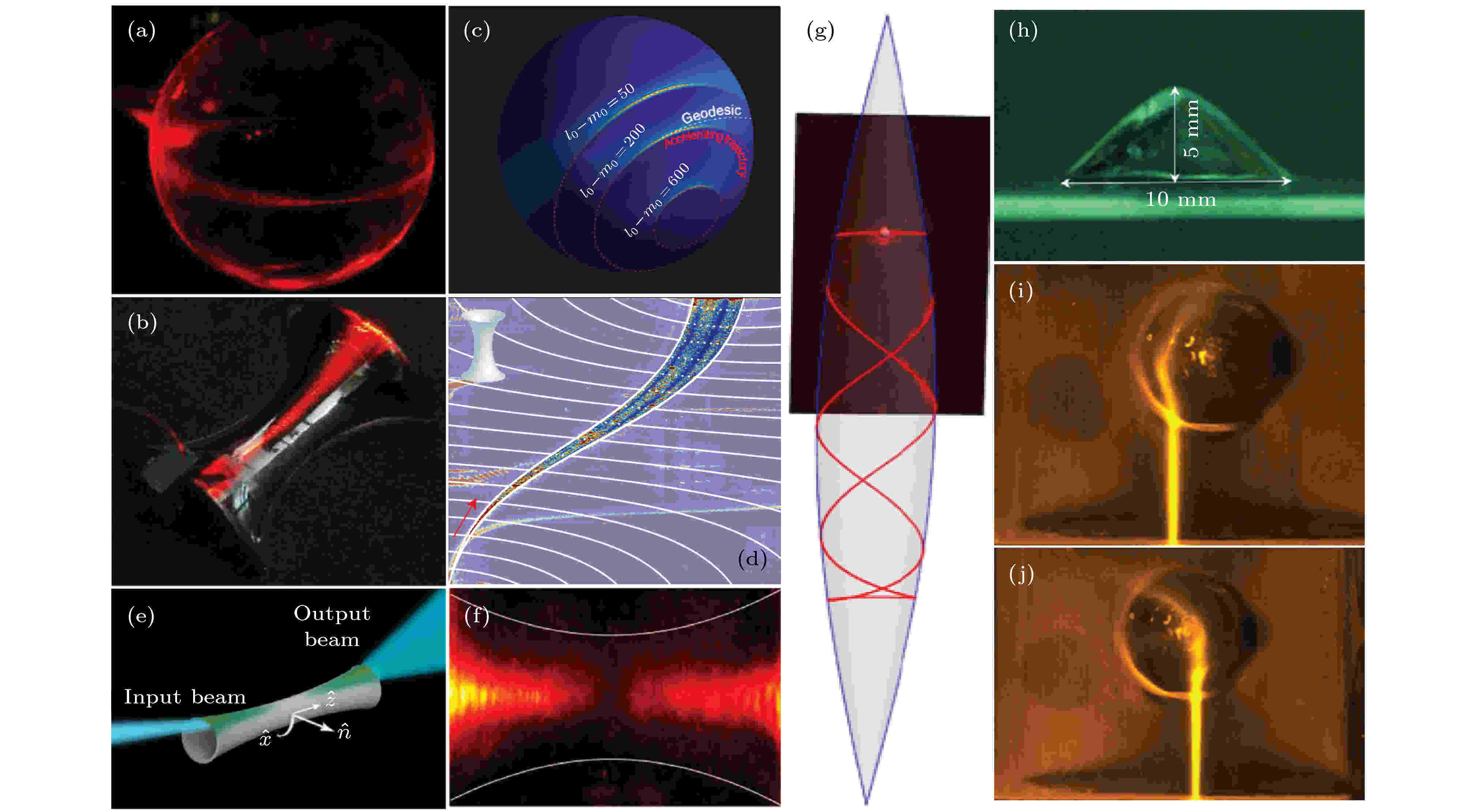图 5 (a) 在球面上电磁波导的传播; (b) 在马鞍面上电磁波导的传播; (c) 加速波包在球面上远离测地线的传播; (d) 在马鞍面上电磁波导传播的干涉; (e) 电磁波在Flamm形曲面传播的示意图; (f) 空间曲率对弯曲波导衍射的影响; (g) 弯曲曲面上的测地线透镜; (h) 实验制备的旋转锥形结构; (i), (j) 旋转锥形结构对曲面上电磁波的散射
Figure5. (a) Propagating electromagnetic waves on a sphere waveguide; (b) the propagating electromagnetic waves on a saddle waveguide; (c) the observation of accelerating wave packets on a sphere waveguide; (d) the interference of electromagnetic waves on a sphere waveguide; (e) schematic of the coupling scheme of the light to the paraboloid waveguide; (f) curvature effects on diffraction; (g) the geodesic lens on a curved space; (h) the side view of experimental cone structure; (i), (j) the experimental results of electromagnetic waves scattered by the cone structure.

光学波导阵列由结构分立的、尺寸大约是波长量级的导波光学器件所组成. 相比较体块的光学介质, 光学波导阵列周期性的特点带来了各种截然不同的物理现象, 因此在集成光学、量子光学领域有着广泛的应用. 电磁波在波导阵列的演化方程满足傍轴近似的Helmholtz方程^[115]:

$\begin{split}& {\rm i}\lambda \frac{\partial }{{\partial z}}E(x,y,z)= \\\;& - \bigg[ \frac{{{\lambda ^2}}}{{2{n_0}}}\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}}\!+\!\frac{{{\partial ^2}}}{{\partial {y^2}}}} \right) \!+\! \Delta n(x,y,z) \bigg] E(x,y,z),\end{split}$

其中, $E(x, y, z)$是电磁波的强度, $x, y, z$是空间坐标, ${n_0}$是体块折射率, $\Delta n = {n_0} - n(x, y, z)$是波导的折射率差, $\lambda $是约化波长.
在量子力学中描述单电子波函数演化的薛定谔方程是

$\begin{split}& {\rm i}\hbar \frac{\partial }{{\partial t}}\varPsi (x,y,z) =\\ & - \bigg[ \frac{{{\hbar ^2}}}{{2m}}\left( {\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {y^2}}}} \right) - V(x,y,z) \bigg)\varPsi (x,y,z),\end{split}$

其中, $\varPsi (x, y, z)$是波函数, t是时间, m是质量, $\hbar $是普朗克常数, $V(x, y, z)$是势场. 比较(1)式和(2)式, 电磁波在波导阵列的演化方程可以与单电子演化的薛定谔方程进行类比, 只需将电磁波的传播方向z取代时间t, 约化波长$\lambda $相当于普朗克常数$\hbar $, 体块折射率${n_0}$相当于质量m, 波导的折射率差异${{\Delta }}n$相当于势场V. 正是基于波导中电磁波演化方程与薛定谔方程的类似性, 波导阵列可以看作是研究凝聚态物理、原子物理和粒子物理现象的一个很好的人工实验平台, 譬如固体物理中由于电子和晶格发生散射而无法观测到的量子相干效应, 粒子原理中在强磁场下才存在的量子场效应等. 由于波导阵列与其他物理系统的动力学演化方程类似, 可以通过这个平台去研究那些物理过程发生很快、物理条件苛刻的难以观测的实验现象. 而且随着光学微加工技术的飞速发展, 多种光学波导阵列可以制备出来, 譬如基于SOI技术的硅波导阵列、铌酸锂波导阵列以及飞秒激光直写的波导阵列. 在这些波导阵列中, 人们可以精确地控制波导的形状、传播常数以及耦合参数等. 正是通过精确操控的波导阵列, 人们可以等效模拟在凝聚态物理、原子物理和粒子物理等体系中不容易观测实现的物理现象, 譬如量子Bloch振荡^[116-119]、Bloch-Zener效应^[120,121]、安德森局域化^[122,123]以及量子的随机行走^[124,125]等.
除此之外, 波导阵列还可以用来研究广义相对论的现象. Szameit研究组^[126]利用飞秒激光直写技术制备出了一维双组元的波导阵列, 研究发现, 波导阵列在布里渊区带边处的色散关系与广义相对论下自由粒子的能量-动量关系相同, 同时在布里渊区带边处波导阵列的演化方程与一维狄拉克方程是类似的, 更有意思的是, 在这种波导阵列中观察到了狄拉克粒子正负能量对相互干涉而产生的Zitterbewegung效应(图6(a)). 进一步, 该研究组^[127]利用弯曲的波导模拟交变电场, 从而在这种弯曲的一维双组元波导阵列中模拟量子电动力学真空中正负能量粒子对的产生 (图6(b)). 除此之外, 这种弯曲的波导阵列还可以模拟零质量狄拉克粒子波函数的特殊演化^[128]. 同时该研究组^[129]还利用飞秒直写的波导阵列模拟了天使粒子—Majorana费米子 (图6(c)). Marini等^[130]利用上下两层垂直放置的双组元的波导阵列, 通过调控波导阵列的等效折射率实现了不同质量狄拉克费米子演化方程的耦合, 从而模拟了中微子的振荡 (图6(d)). 以上这些波导阵列的工作都是模拟了平直时空的量子场论的效应. Koke等^[131]利用波导阵列模拟量子场论的现象, 研究从平直时空拓展到弯曲时空, 通过将弯曲时空的狄拉克方程与耦合波导阵列建立联系, 研究弯曲时空中正负粒子对的产生以及相对论的Zitterbewegung效应.
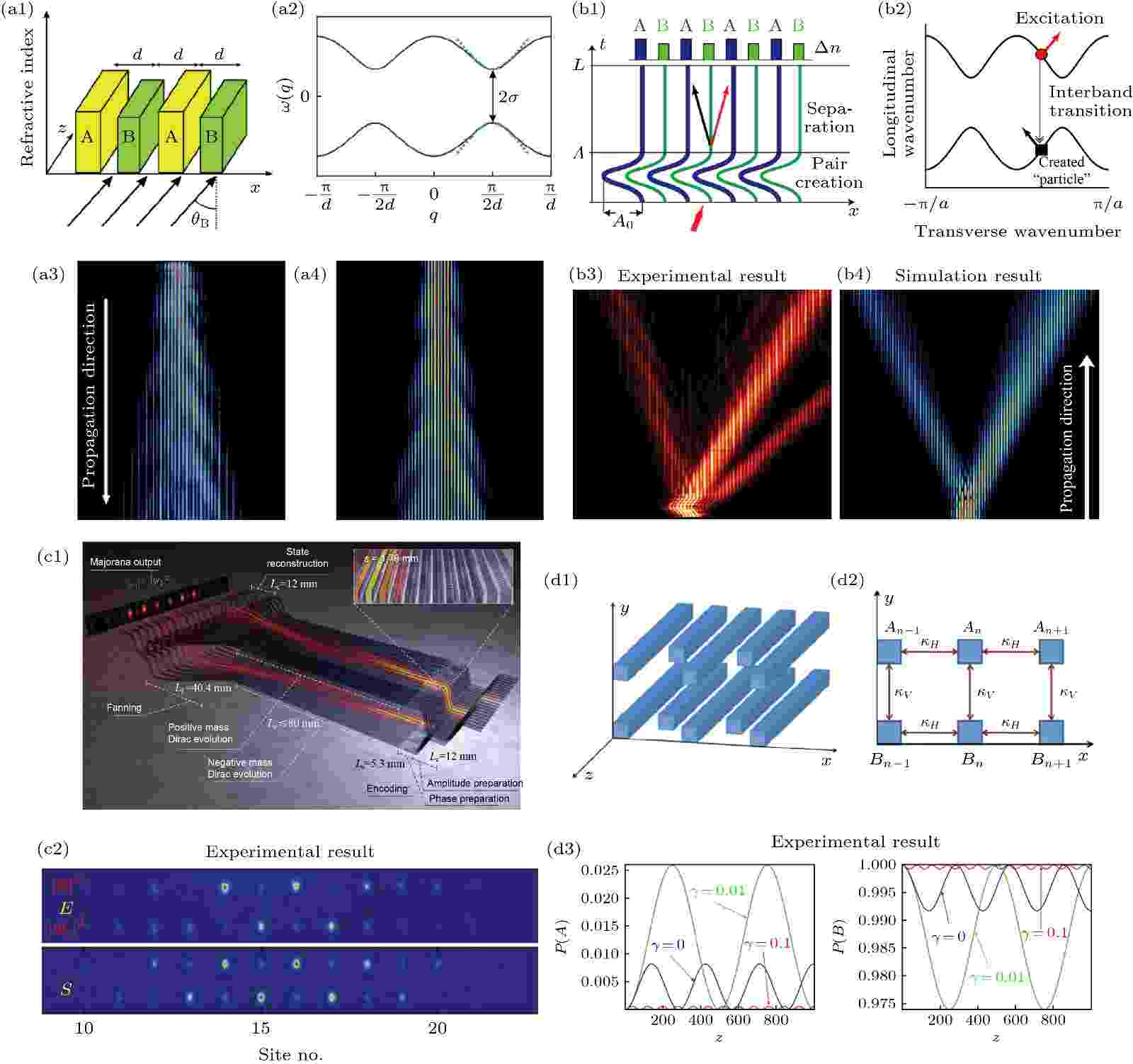图 6 (a1)?(a4) 一维双组元波导阵列模拟广义相对论的Zitterbewegung效应, 其中(a1) 波导阵列的示意图, (a2) 波导阵列的色散, (a3) 实验结果图, (a4) 理论模拟图; (b1)?(b4) 一维弯曲的双组元波导阵列模拟正负粒子对的产生, 其中(b1) 波导阵列的示意图, (b2) 波导阵列的色散, (b3) 实验结果图, (b4) 理论模拟图; (c1), (c2) 波导阵列模拟Majorana费米子, 其中(c1) 波导阵列的示意图, (c2) 实验结果图; (d1)?(d3) 两层垂直放置的双组元的波导阵列模拟中微子振荡, 其中(d1) 波导阵列的示意图; (d2) 波导阵列耦合系数的设置; (d3) 实验结果图
Figure6. (a1)?(a4) Simulation of relativistic zitterbewegung using the one dimensional binary waveguide system: (a1) Schematic of the one dimensional binary waveguide system; (a2) the dispersion relation of the waveguide; (a3) the experimental results; (a4) the simulation results. (b1)?(b4) Simulation of pair production in vacuum using the curved waveguides: (b1) Schematic of the one dimensional curved waveguide; (b2) the dispersion relation of the waveguide; (b3) the experimental results; (b4) the simulation results. (c1), (c2) Simulation of Majorana fermions: (c1) Schematic of the waveguide system; (c2) the experimental results. (d1)?(d3) Simulation of neutrino oscillations: (d1) Schematic of two vertically displaced binary waveguides; (d2) transverse section of the structure; (d3) the experimental results.

除此之外, Lustig等^[132]研究了弯曲表面上离散波导阵列的演化, 如图7(a)所示, 将一维波导阵列放置在弯曲的曲面上, 发现了由于空间弯曲而产生的拓扑边界态(图7(b)). Wang等^[133]研究了黑洞视界附近正负粒子对的产生, 首先从1 + 1维施瓦西黑洞在视界附近处的度规出发, 考虑到无质量的弯曲时空的狄拉克方程, 理论计算获得了正负能量对的狄拉克粒子在黑洞视界附近的量子演化(图7(c)), 即正能粒子加速逃逸视界而负能粒子朝向视界运动, 最后在视界附近静止而被黑洞捕获. 为了在波导阵列光子芯片中模拟弯曲时空中的量子效应, 首先将连续弯曲时空的狄拉克方程离散化, 获得对应波导阵列耦合系数的关系. 实验中将单光子注入该理论设计的双层波导阵列中, 如图7(e)所示, 成功地观测到具有正能量的单光子波包逃逸而负能量的单光子波包被视界捕获的过程(图7(f)). 这个过程很好地对应了霍金辐射的部分过程. 除了单光子, 这个体系还可以拓展全同的双光子以及纠缠光子对在弯曲时空中的演化, 可以研究弯曲时空对量子干涉以及量子纠缠的影响.
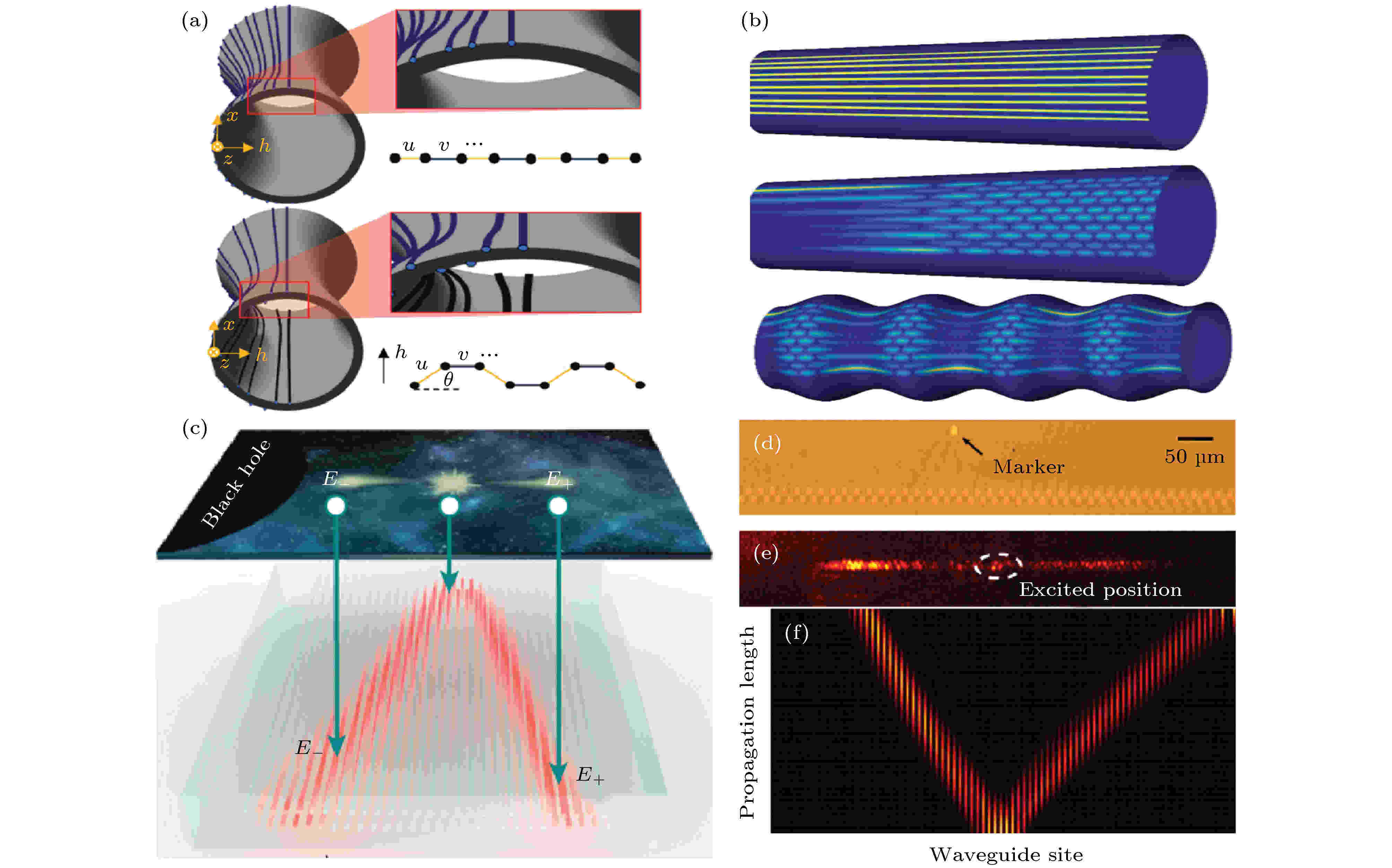图 7 (a) 弯曲曲面上的波导阵列; (b) 弯曲的曲率对波导阵列中电磁波演化的影响; (c) 黑洞视界附近正负能量粒子对的产生的示意图; (d) 飞秒直写波导阵列的样品图; (e) 实验结果图; (f) 正负能量粒子对的演化
Figure7. (a) Waveguide sites on the curved space; (b) the waveguide evolutions related with curvature of space; (c) the schematic of pair production near the event horizon of black hole; (d) a sample fabricated by femtosecond direct writing method; (e) the experimental result; (f) the evolution of the pair production.

探索和理解光与物质相互作用的机理, 进而在此基础上实现对光的任意调控及其应用必将极大推动人类社会的发展. 以对电磁波的调制技术为例, 其在信息通信、信息存储、显示成像、天文以及医疗等领域都扮演着不可或缺的重要角色. 超构材料的兴起与发展为在微纳尺度上人为调控电磁波提供了新的范式, 实现了具有超越自然界常规材料的光学性质. 尤其是超构材料具有将光和电磁辐射耦合到亚波长尺度的能力, 满足了高速发展的现代科学技术对光学器件提出的高性能、微型化以及集成化的新要求, 各种基于超构材料的新颖光学器件已经被提出或者在实验上实现了, 譬如完美透镜、无色差的成像器件等. 除此之外, 以超构材料为基础的集成光子芯片还能作为研究广义相对论弯曲时空现象的实验平台, 可以在实验可控的环境下去研究一些理论上被预测但未被观测到、或者难以重复细致研究的与引力相关的宇观现象. 以前基于超构材料光子芯片的类比引力工作, 大多数聚焦于研究弯曲时空中的经典现象, 如果将量子光学技术与超构材料光子芯片结合, 类比引力的研究可以拓展到一些更加具有挑战性的工作, 譬如弯曲时空量子场论的研究等. 众所周知, 光子本身就是一个很好的量子系统, 可以被构造出一些丰富光量子态, 最典型的例子就是不同类型的光子纠缠态. 一方面, 超构材料光子芯片可以构造出各种不同类型的弯曲时空, 譬如德西特以及反德西特时空. 丰富的光量子态与超构材料光子芯片相结合可以用来研究一些与引力相关的量子现象, 譬如研究加速坐标系中纠缠态的退相干问题以及额外时空维度对光量子态演化的影响等. 另一方面, 弯曲时空的量子场论不涉及引力量子化, 而是把引力场或背景时空当作经典场来处理. 如何将引力量子化, 是现代物理学的一个巨大的挑战, 尽管弦论、圈量子引力等理论被提出, 但是这些理论还存在一些问题, 不能自洽地统一广义相对论与量子力学, 或许在超构材料光子芯片中开展类比引力相关量子效应的研究可以为在理论上探索引力本质提供一些有意义的思考.