摘要:光子晶体中的拓扑相变源自于其能带结构中带隙的打开-闭合-再打开, 其中伴随着能带结构中带序(或本征态)之间的交换. 本文探讨了偏置磁场方向对磁性光子晶体能带结构的影响, 它在构建拓扑边界态中的作用以及对边界态特性的影响. 结果表明: 反转偏置磁场方向会导致能量不同但宇称相同的本征态之间的交换, 这种交换为构造不同特性的拓扑边界态(如多重边界态等)提供了更多选择性. 根据边界两侧光子晶体能带结构的相对关系, 可以预测在边界上是否出现拓扑边界态以及边界态的主要特性.
关键词: 磁性光子晶体/
偏置磁场方向/
拓扑能带结构/
边界态

English Abstract

全文HTML

--> --> -->

近十年来有关光子晶体中光子拓扑态的研究迎来了极为快速的发展. 光子拓扑态源于凝聚态物质拓扑相的物理学研究, 由于光子晶体具有与固态电子系统相似的数学特征, 因此凝聚态中的拓扑相同样会出现在光子系统中^[1]. 凭借其独特的性能, 例如完全背散射抑制和缺陷免疫的单向输运的边界态等^[1-6], 光子晶体中拓扑相的研究吸引了人们极大的关注. 此外, 光学系统具有比固态电子系统更高的自由度来设计能带结构, 它为诸如拓扑相变和选择性传输等研究提供了一个良好的工作平台.
与电子系统相似, 光子晶体中同样具有多种拓扑相, 如量子霍尔相^[2-11]、量子自旋霍尔相^[12-16]和量子谷霍尔相^[17-24]等. Raghu和Haldane^[2,3]最早在理论上预见了当打破时间反演对称性后, 二维光子晶体带隙会具有非零拓扑不变量, 它类比为电子系统中的量子霍尔效应. 这一思想很快由Wang等^[4,5]利用二维磁性光子晶体在微波频段进行了实验验证, 观测到了具有鲁棒性单向传输特征的边界态. 之后, 各种关于光子晶体的量子霍尔相及其应用被不断地提出或得到实验验证^[7-11].
人们发现带隙拓扑性质的改变总伴有能带带序上的反转, 而带序的变化可以由能带上本征态的模式分布加以确定, 故而光子晶体中的拓扑相可以通过构建特定的能带带序结构加以实现. 例如, 在时间反演对称性保持不变的体系中, 人们发现打破赝时间反演对称性可以实现具有1/2赝自旋态的光学量子自旋霍尔相. 打破赝时间反演对称性使得能带带序发生反转, 实现了从光学绝缘相到量子自旋霍尔相的转变^[12-16]. 这种方案最早由Wu等^[12]提出, 它通过改变蜂窝结构的半径来打破赝时间反演对称性. 这种方法在微波频段下得到了实验证实^[13], 观测到了光子晶体板边缘存在与赝自旋相关的单向边界态. 这类光子拓扑绝缘相的拓扑性质对光子晶体边缘的晶格完整性敏感, 故在投影能带中的边界态并不是严格无带隙的^[1,12-16]. 类似地, 研究人员发现在蜂窝结构中打破空间反演对称性可以实现量子谷霍尔相. 打破空间反演对称性使得能带带序在K和K′ 能谷处发生反转, 从而实现了两种量子谷霍尔相的相互转换, 这两种量子谷霍尔相具有相反的谷陈数${C_{k(k')}} = \pm 1/2$^[17-24]. 当连接两个具有不同谷陈数的光子晶体结构时, 拓扑保护的边界态出现在带隙中. 利用能带带序的反转还可以在光子晶体中实现多种不同的拓扑相和不同相之间的转变, 例如, 在磁性光子晶体中可以实现量子自旋霍尔相和光子绝缘体相之间的相变转换^[16], 量子霍尔相和量子谷霍尔相的相变转换^[23,24]. 因此, 构建不同类型的能带带序在研究光子拓扑相和设计边界态中都有着举足轻重的作用.
对于磁性光子晶体而言, 改变能带带序的办法可以是改变偏置磁场大小或光子晶体结构. 本文讨论了偏置磁场的方向对磁性光子晶体能带结构, 特别是带序结构的影响. 结果表明: 改变偏置磁场的方向会使得能量不同但宇称相同的本征态之间发生交换, 从而使得能带结构中出现带序交换. 利用这一特点, 可以在两个光子晶体的边界上构建出不同特性的拓扑边界态并调控边界态的传输特性. 在边界上是否出现拓扑保护的边界态及边界态的主要特性可以用边界两侧光子晶体体能带的相对关系直接判断. 利用偏置磁场方向改变能带带序的方法将有助于加深我们对能带结构的理解, 构建出所需要的拓扑边界态.

考虑如图1(a)所示的二维磁性光子晶体结构, 基元是由六根铁氧体柱(YIG)组成的六角集群, 其中铁氧体柱的半径r = 2 mm, R为铁氧体柱到基元中心的距离. 基元以六角晶格的形式排列, 晶格常数$a = 10\sqrt 3$ mm. 图1(a)中的虚线框显示了光子晶体的原胞单元. YIG的电磁参数如下: 相对介电常数${\varepsilon _{\rm{r}}} = 15.26$, 饱和磁化强度${M_{\rm{s}}} = 1884{\rm{G}}$ (1 G = 10^–4 T), 磁损耗系数$\alpha = 0.007$^[9,11]. 当偏置磁场H₀沿着z轴并且处于饱和磁化时, 铁氧体材料具有张量形式的磁导率^[25]:
图 1 (a)二维光子晶体示意图, 其中黄色的圆表示空气背景中的铁氧体柱, 黑色六边形表示阵列结果中的一个基元; (b) H = 0和R = a/3时的能带结构, 在Γ点具有一个四重简并点; (c) H ≠ 0和R = a/3时的能带结构(由于打破时间反演对称性, 能带结构中出现了完全带隙, 并在Γ点出现了两个双重简并点); (d) H ≠ 0和R ≠ a/3时的能带结构
Figure1. (a) Schematic of two-dimensional magnetic photonic crystal fabricated by ferrite rods (denoted by yellow circles) embedded in air background. The black hexagon denotes the basis of the array. (b) Band structure at H = 0 and R = a/3. A four-fold degeneracy point shows at the Γ point. (c) Band structure at H ≠ 0 and R = a/3. A full bandgap presents in the band structure because of time reverse symmetry broken, and two doubly degeneracy points present at Γ point. (d) Band structure at H ≠ 0 and R ≠ a/3.

$[{{{\mu}} _{\rm{r}}}] = \left[ {\begin{array}{*{20}{c}} {{\mu _m}}&{ \pm {\rm{j}}{\mu _k}}&0 \\ { \mp {\rm{j}}{\mu _k}}&{{\mu _m}}&0 \\ 0&0&{{\mu _{\rm{C}}}} \end{array}} \right],$

式中, ${\mu _m} = 1 + {\omega _m}({\omega _0} + {\rm{j}}\alpha \omega )/[{({\omega _0} + {\rm{j}}\alpha \omega )^2} - {\omega ^2}]$, ${\mu _k} = {\omega _m}\omega /[{({\omega _0} + {\rm{j}}\alpha \omega )^2} - {\omega ^2}]$和${\mu _{\rm{C}}} = 1$, 其中${\omega _0} = {\mu _0}\gamma {H_0}$, ${\omega _m} = {\mu _0}\gamma {M_{\rm{s}}}$, γ = 1.759 × 10¹¹ C/kg, 非对角元素${\mu _k}$前的“$ \pm $”符号对应于偏置磁场分别沿+z方向和–z方向.
由于晶格结构的C₆对称性, 在布里渊区中心点$ \varGamma $处的本征态有2个二维不可约表示: E₁和E₂. 每种不可约表示有两个态, 它们分别是对应于E₁的两个具有奇宇称的偶极子态$({p_x}, {p_y})$和对应于E₂的两个具有偶宇称的四极子态$({d_{xy}}, {d_{{x^2} - {y^2}}})$. 两个p(d)态可以组合成模拟自旋向上的态${p_ + } = {p_x} + {\rm{j}}{p_y}\left( {{d_ + } = {d_{{x^2} - {y^2}}} + {\rm j}{d_{xy}}} \right)$和自旋向下的态${p_{\rm{ - }}} = {p_x} - {\rm{j}}{p_y}\left( {{d_{\rm{ - }}} = {d_{{x^2} - {y^2}}} - {\rm{j}}{d_{xy}}} \right)$, 它们被称为赝自旋态. 本征态的±符号表示其轨道角动量的方向, 它们可以由本征态的电场相位分布或者坡印亭矢量来确定, 比如正(负)的轨道角动量对应着本征态中电场相位分布或者坡印亭矢量沿着z轴逆(顺)时针旋转, 如图2所示. 利用COMSOL软件计算了图1中光子晶体的能带结构. 图1(b)展示了偏置磁场为零时的能带结构, 当R = a/3时, p态和d态会在$ \varGamma $点处简并形成双狄拉克锥. 若施加偏置磁场打破时间反演对称性, p态和d态将分裂形成两个双重简并点, 同时出现一个全带隙, 如图1(c)所示. 简并点分别是由d_－与p₊简并, p_－与d₊简并形成的. 进一步改变R的大小, 打破赝时间反演对称性, 两个双重简并点再次分裂, 最后形成独立的四个态. 图1(d)显示了R减小时Γ点处本征态的次序, 按频率从低到高的次序是$[{d_ - }, {d_ + }, {p_ + }, {p_ - }]$, 此时全带隙频率范围内光子晶体处于量子自旋霍尔相^[12]. 通常全带隙两侧的本征态的次序确定了带隙的拓扑特性^[16]: 次序$[{d_ - }, {p_ + }, {p_ - }, {d_ + }]$对应于量子霍尔相, $[{d_ - }, {d_ + }, {p_ + }, {p_ - }]$对应于量子自旋霍尔相, $[{p_ + }, {p_ - }, {d_ - }, {d_ + }]$对应于光学绝缘相.
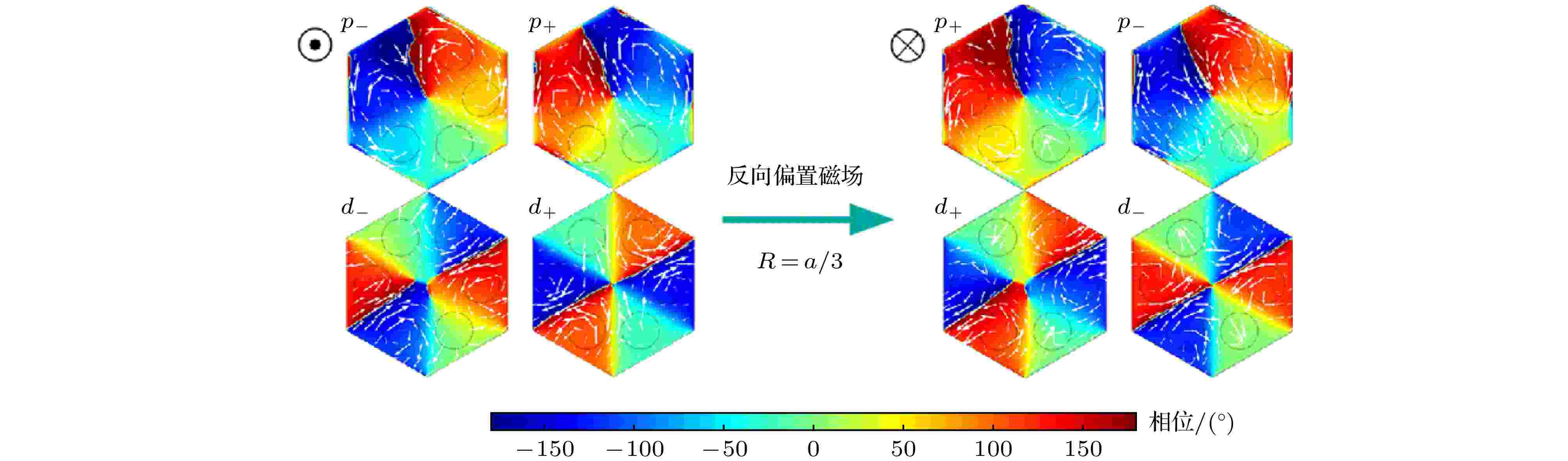图 2 正向和反向偏置磁场时, Г点处四个本征态的电场相位分布和磁场(反转偏置磁场的方向将使得本征态的电场相位和磁场在形式上出现p₊和p_－, d₊和d_－之间的交换)
Figure2. Magnetic fields and the phase of electric fields for the eigenstates p₊, p_－, d₊, d_－ at the Г point. Reversing the direction of bias magnetic field causes the exchange in the profiles of electric phase and magnetic field.

考虑横向电场(TE)极化的电磁波(即交变电场沿z方向), 电磁场可表示为: ${{E}} \!=\! (0, 0, {E_z}){{\rm{e}}^{ - {\rm{j}}{{k}} \cdot {{r}}}}$, ${{H}} = ({H_x}, {H_y}, 0){{\rm{e}}^{ - {\rm{j}}{{k}} \cdot {{r}}}}$, 其中${{r}}$表示位置矢量, ${{k}}$表示波矢. 将波矢分解成${k_x} = k\cos \theta $和${k_y} = k\sin \theta $, $\theta $是波矢${{k}}$与x轴的夹角. 根据麦克斯韦方程, 可以得到下面的解^[26]:

$\frac{{{H_x}}}{{{H_y}}} = \frac{{{k^2}\sin \theta \cos \theta }}{{{k^2}{{\sin }^2}\theta - k_0^2{\varepsilon _{\rm{r}}}{\mu _m}}} \pm {\rm{j}}\frac{{k_0^2{\varepsilon _{\rm{r}}}{\mu _k}}}{{{k^2}{{\sin }^2}\theta - k_0^2{\varepsilon _{\rm{r}}}{\mu _m}}},$

其中±符号取决于偏置磁场的方向. (2)式表明当偏置磁场方向改变时H_x的相位可以超前或者滞后于H_y的相位, 这会导致磁场绕着z轴右旋或左旋. 如果将电场E_z用磁场分量H_x和H_y表示, 则

${E_z} = \sqrt {\frac{{{\mu _0}}}{{{\varepsilon _0}{\varepsilon _{\rm{r}}}}}\frac{{{\mu _m}^2 - {\mu _k}^2}}{{{\mu _m}}}} ({H_x}\sin \theta - {H_y}\cos \theta ).$

(3)式表明电场的相位会随着磁场旋转方向的改变相应地发生变化, 表现为相位随时间的变化为右旋或左旋, 也就是改变了轨道角动量的方向. 图2给出了偏置磁场反向前后本征态的磁场矢量和电场相位的变化, 可以看到偏置磁场反向后$ \varGamma $点处相应本征态的本征频率未发生变化, 但是其轨道角动量与反向前刚好相反. 具体表现为: 逆时针的p₊(d₊)电场分布变为顺时针的p_－(d_－), 而顺时针的p_－(d_－)电场分布则变为逆时针的p₊(d₊). 这表明本征态的正负符号发生交换, 从而能带带序也发生了交换.
图3给出了在正反磁场两种情形下p态和d态次序是如何随着R发生改变的. 图3(a)给出了位于$ \varGamma $点的p态和d态的本征频率随参数a/R的变化, 在计算过程中始终保持偏置磁场为H₀ = 800 Oe $\Big(1\;{\rm{Oe}} = \dfrac{1}{{4{\text{π}} \times {\rm{1}}{{\rm{0}}^{ - 3}}}}\;{\rm{A/m}}\Big)$. 当改变R值时, 带隙经历了闭合和重新打开, 这暗示着时间反演对称性和赝时间反演对称性之间的竞争使得磁性光子晶体发生了从量子自旋霍尔相到量子霍尔相, 再到光学绝缘相的转变. 不同光子相的典型能带结构如图3(b)—(d)所示, 图中还内嵌了$ \varGamma $点处相应本征态的场结构. 这些图片清楚地显示了本征态在带隙两侧的交换, 从而导致了磁性光子晶体不同的拓扑相变.
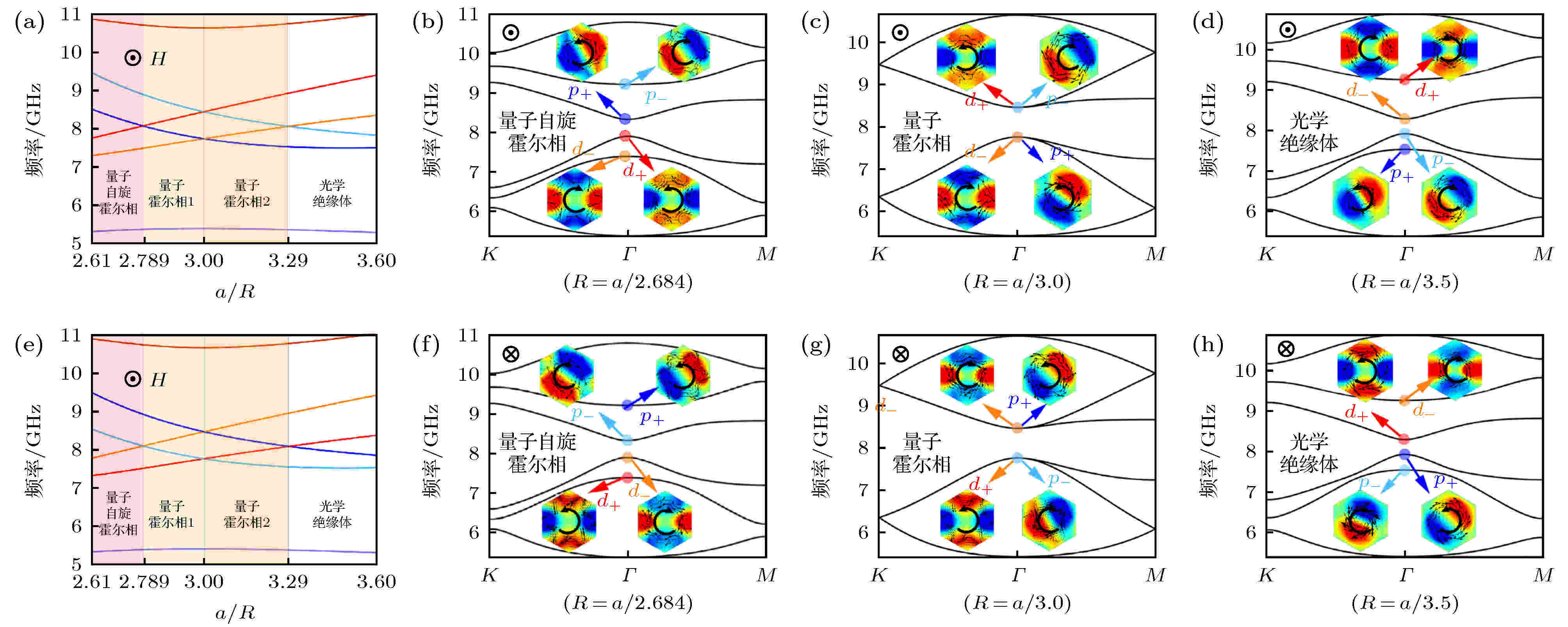图 3 (a)当偏置磁场沿着+z方向时, Г点的p态和d态的本征频率随参数a/R的变化(随着a/R的增加, Г点处发生能带带序反转, 并伴随着拓扑相变; 不同颜色的阴影显示三种不同的拓扑相); (b)?(d)分别是当光子晶体处于量子自旋霍尔相(R = a/2.684)、量子霍尔相(R = a/3)和光学绝缘相(R = a/3.5)时的能带结构; 图中的插图是能带结构对应点上的场模式图, 其中黑色箭头表示坡印亭矢量; (e)?(h)是当偏置磁场沿着–z方向时, 本征频率随a/R的变化, 以及三种典型的拓扑相的能带结构和场模式
Figure3. (a) Evolution of p and d eigenstates at point Г as a function of the radio of a/R with the bias magnetic field in the +z direction. As a/R increases, the band order exchange takes place where phase transition happens. Three types of phases are shaded in different colors. (b)?(d) Typical band structures of quantum spin-Hall (QSH) phase (R = a/2.684), quantum Hall (QH) phases (R = a/3), and conventional insulator (CI) phase (R = a/3.5). (e)?(h) The same as (a)?(d), but the bias magnetic field is in the –z direction. The insets of the panels (b)?(d) and (f)?(g) are the profile of eigenstates at the corresponding dots on the band structure of the panels, where the black arrow indicates the Poynting vectors.

图3(e)展示了偏置磁场反向时, 能带结构在$ \varGamma $点处的变化. 可以看到磁性光子晶体也经历了拓扑相变, 但是拓扑相的能带带序不同于图3(a). 图3(f)—(h)给出了三种典型拓扑相的能带结构和$ \varGamma $点处的本征态. 比较图3(a)和图3(e), 可以看到磁场方向反转后本征态p₊和p_–发生了交换, d₊和d_–发生了交换. 相似的结果也可以从图3(f)—(h)得知. 偏置磁场的方向对能带带序的改变在以往的研究中是被忽视的^[12-16].

光子拓扑绝缘体最主要的特征是出现拓扑保护的边界态. 根据“体边”对应理论^[27], 当两个具有不同拓扑指数的结构组合在一起时, 它们的边界上必然存在拓扑保护的边界态. 假设磁性光子晶体被分成如图1所示的左右两个区域, 它们分别被命名为域I和域II. 通过独立地调整两个区域各自的参量R使它们处于不同的拓扑相, 那么在区域边界上将出现拓扑保护的边界态.
边界态的特性不仅取决于域所处的拓扑相, 还取决于边界两侧拓扑相能带的相对关系. 考虑两个区域都处于量子霍尔相, 但它们的参量R分别是a/2.93和a/3.09, 并且偏置磁场方向相同. 此时, 两个区域的共同带隙两侧虽然有不同的能带带序(见图3(a)), 但是在域边界上并没有出现边界态(见图4(a)). 如果改变域I中偏置磁场方向, 其能带带序将从$[{d_ - }, {p_ + }, {d_ + }, {p_ - }]$转变为$[{d_ + }, {p_ - }, {d_ - }, {p_ + }]$, 边界态将会出现在两个域的共同带隙中. 图3(d)给出了此时的投影能带结构, 可以看到带隙中出现了两条边界, 并且它们几乎是简并的. 由于两个边界态之间的耦合作用, 边界态中会出现一个微小的间隙. 需要指出的是这两条边界态对应的电磁模式具有不同的轨道角动量. 作为证明, 模拟了边界态在8 GHz时电磁波的传输特性. 图4(e)和图4(f)给出了TE极化电磁波沿着边界传播时的场分布图, 图中S₊和S_–分别表示轨道角动量为正和负的激发源, 它们是由具有${{\text{π}} / 2}$相位差的面内磁场${S_ \pm } = {H_0}({e_x} \mp {\rm{j}}{\kern 1 pt} {e_y})$激发. 结果显示具有正和负轨道角动量的激励源都激发起了沿同一方向传播的单向波. 这一现象在以往边界态的研究中尚未涉及到. 作为对比, 图4(b)和图4(c)给出了在同向磁场下的模拟结果, 可以看到不同轨道角动量的激发源在域边界上都不能激发起边界模式的波. 以上结果表明, 我们能够通过改变区域的偏置磁场方向来调控边界态, 从而实现对光信息的控制.
图 4 偏置磁场方向对边界态的影响(区域I和II均处于量子霍尔相, 但结构参量R分别是a/2.93和a/3.09)　(a)两个区域施加同向偏置磁场时的投影能带结构; (b)和(c)分别用激发源S₊和S_–激发时的场分布; (d)两个区域施加反向偏置磁场时的投影能带结构; (e)和(f)分别用激发源S₊和S_–激发时的场分布, 其中的放大图展示了电磁波的轨道角动量特性, 图中箭头表示坡印亭矢量(当两个区域施加反向偏置磁场时, S₊和S_–都可以激发沿同一方向传播的单向波); (a)和(d)图中的插图给出了两个区域中能带结构的对应关系, 两块域中相同的本征态连线连的交叉点出现在共同带隙中时将出现拓扑边界态
Figure4. Influence of the direction of bias magnetic field on the edge states when two domains are in the QH phase but have different geometric structure (R = a/2.93 and R = a/3.09). (a) The projected band structure when two domains are applied by the same direction of bias magnetic field. (b) and (c) Electrical field distribution at 8 GHz excited by S₊ and S_–, respectively. No edge mode is excited. (d) The projected band structure when two domains are applied by the opposite direction of bias magnetic field. (e) and (f) Electric field distribution corresponding to (d) at 8 GHz excited by S₊ and S_–. The waves propagate unidirectional. The inset enlarges the field details which shows the orbital angular momentum of the wave. The inserts of (a) and (d) show the schematic of the relationship of the topological edge state and eigenstates in the two domains.

上述例子表明了边界态的出现与光子晶体边界两侧共同带隙附近能带带序的相对关系有关. 为了简单起见, 考虑如图5所示的情况. 如果固定域II的拓扑相不变, 使域I发生拓扑相变, 那么在两个区域的边界上必定会经历带隙的闭合以中和拓扑指数, 然后重新打开带隙. 由于域I的拓扑相变是由域中的能带带序交换引起的, 连接两个域中相同本征态将会在两个区域的共同带隙中出现交叉, 它和边界态形成过程中的能带闭合再打开过程一致. 因此, 在共同带隙中的交叉点预示着在域边界上会出现边界态. 图5给出了上述拓扑边界态出现的示意图. 当域I的拓扑相发生相变时, 连接两个域中相同的本征态的连线在它们的共同带隙中经历了分离(图5(b))、闭合(图5(c))、交叉(在带隙内出现交叉点, 如图5(d)), 重现了不同拓扑指数的光子绝缘体在其边界上经历的过程. 因此, 可以通过带隙内是否出现交叉点以及交叉点的个数来判断在边界上是否出现边界态以及边界态的数量. 图4(a)中的插图给出了两个区域在同向磁化时的能带相对关系, 由于边界两侧相同本征模式之间的连线在共同带隙中不存在交叉点, 故投影能带结构中没有边界态. 而在图4(d)插图中, 两个能带的相对关系确定了在共同带隙中存在两个交叉点, 所以在投影带结构中有两条边界态. 除此以外, 还可以通过能带相对关系示意图获得其他关于边界态的信息. 例如, 图4(d)中的两个交叉点分别由正的轨道角动量(d₊, p₊)模式和负的轨道角动量(d_–, p_–)模式相互连接构成, 所以这两条边界态分别具有正的和负的轨道角动量. 进一步, 当d₊(p_–)从左下方连接到右上方, 而p₊(d_–)从左上方连接到右下方时, 边界态会具有负的群速度. 在表1列出了四种边界态的基本情况, 其他复杂情况都可以从这四种边界态推导得出.

本征态	连接方式	轨道角动量	群速度
d+	从左下方到右上方	正	负
p+	从左上方到右下方
p–	从左下方到右上方	负	负
d–	从左上方到右下方
d–	从左下方到右上方	负	正
p–	从左上方到右下方
p+	从左下方到右上方	正	正
d+	从左上方到右下方

表1由本征态连接方式决定边界态的轨道角动量和群速度
Table1.Orbital angular momentums and group velocities determined by the linked manner of eigenstates.

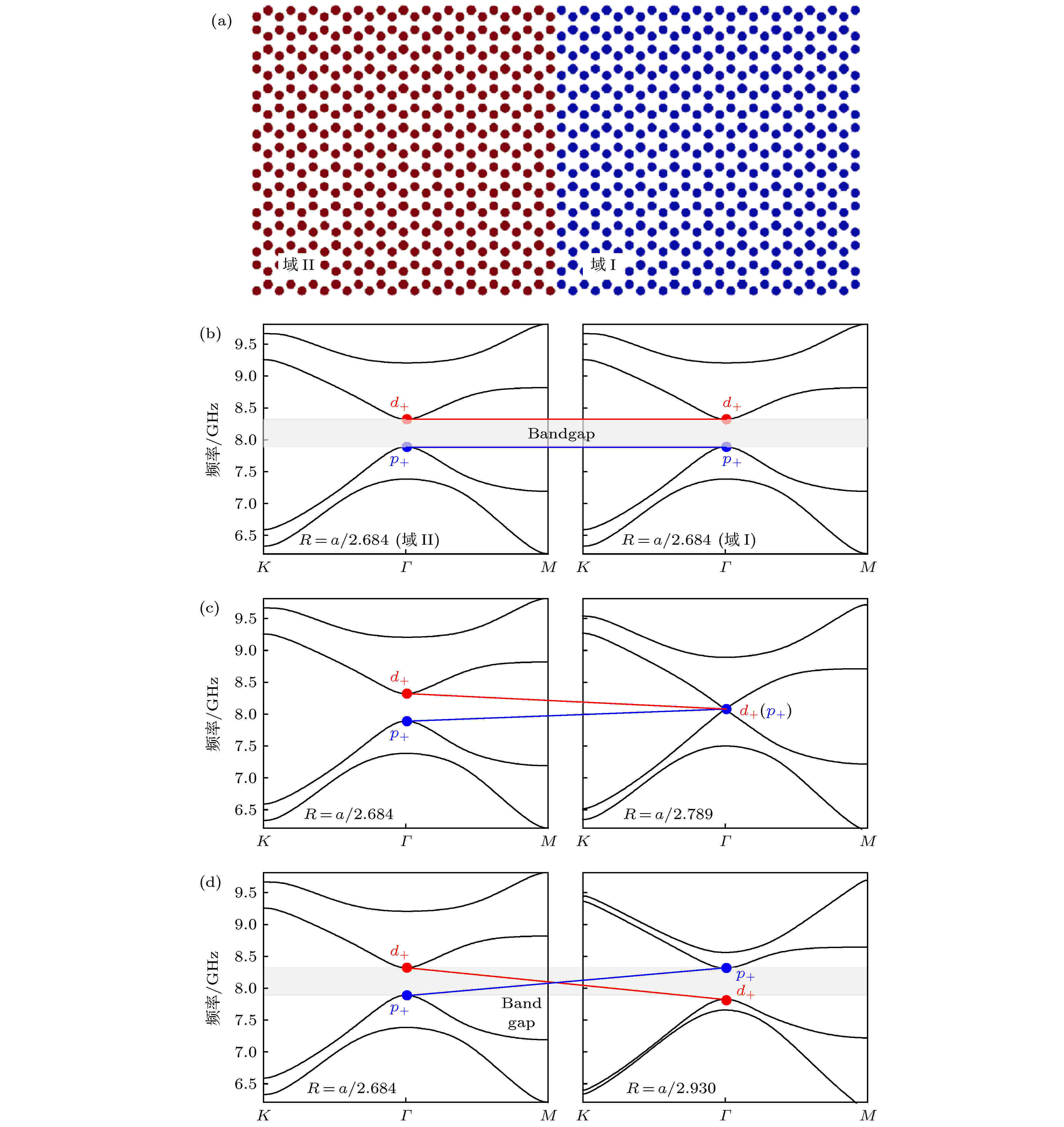图 5 (a)由两个具有不同拓扑指数的域组合在一起形成的域边界(假设保持域II固定在量子自旋霍尔相); (b)?(d)域I从量子自旋霍尔相转变到量子霍尔相时, 域边界出现拓扑边界态的过程示意图
Figure5. (a) Schematics of the domain boundary created by two domains with distinct topological index. Supposing the domain II keeps in QSH phase. (b)?(d) The procedure of the topological edge state creation when domain I takes place the phase transiting from QSH phase to QH phase.

对于更加一般的情况, 如两个区域分别处于量子自旋霍尔相(R = a/2.684)和光学绝缘相(R = a/3.50), 并施加方向相同的偏置磁场. 图6(a)中的插图给出了此时的能带相对关系示意图. 两个交叉点分别由正的轨道角动量(d₊, p₊)的模式和负的轨道角动量(d_–, p_–)的模式连接构成, 所以在边界上存在着两条轨道角动量相反的边界态. 这个结论和图6(a)中的投影能带是一致的. 不同于图4(d), 此处的两条边界态具有相反的群速度和轨道角动量^[12-16], 这将会产生与量子自旋霍尔效应相似的赝自旋单向波. 当域II中的偏置磁场反向时, 无论交叉点的个数还是本征态的连接方式都没有改变(见图6(b)插图), 所以边界态的轨道角动量和群速度保持不变. 作为进一步的证明, 图6(c)和图6(d)分别展示了在边界上用正和负的轨道角动量的源激发的电场分布情况, 结果显示不同角动量波将会沿不同的方向传播. 而用线电流源S激发时, 具有正和负的轨道角动量的电磁波会被分开, 然后分别沿着不同的边界传播, 如图6(e)所示. 对其他用不同拓扑相以及磁场方向变化导致的带序变化构建的边界态的情况, 读者可仿照上述方法自行分析, 在此就不再一一赘述. 需要指出当域I和域II的磁化方向相同时, 共同带隙两侧光子晶体能带带序的组合是不完全的. 如果再引入磁场方向作为参量, 则可以实现所有可能的组合, 从而实现更多可能的拓扑边界态. 如何实现上述由磁场方向导致的拓扑态, 在实验上还存在着挑战. 一种可能的方法是采用永磁体来实现对偏置磁场方向的控制^[28], 但是它可能会带来非均匀磁化的问题.
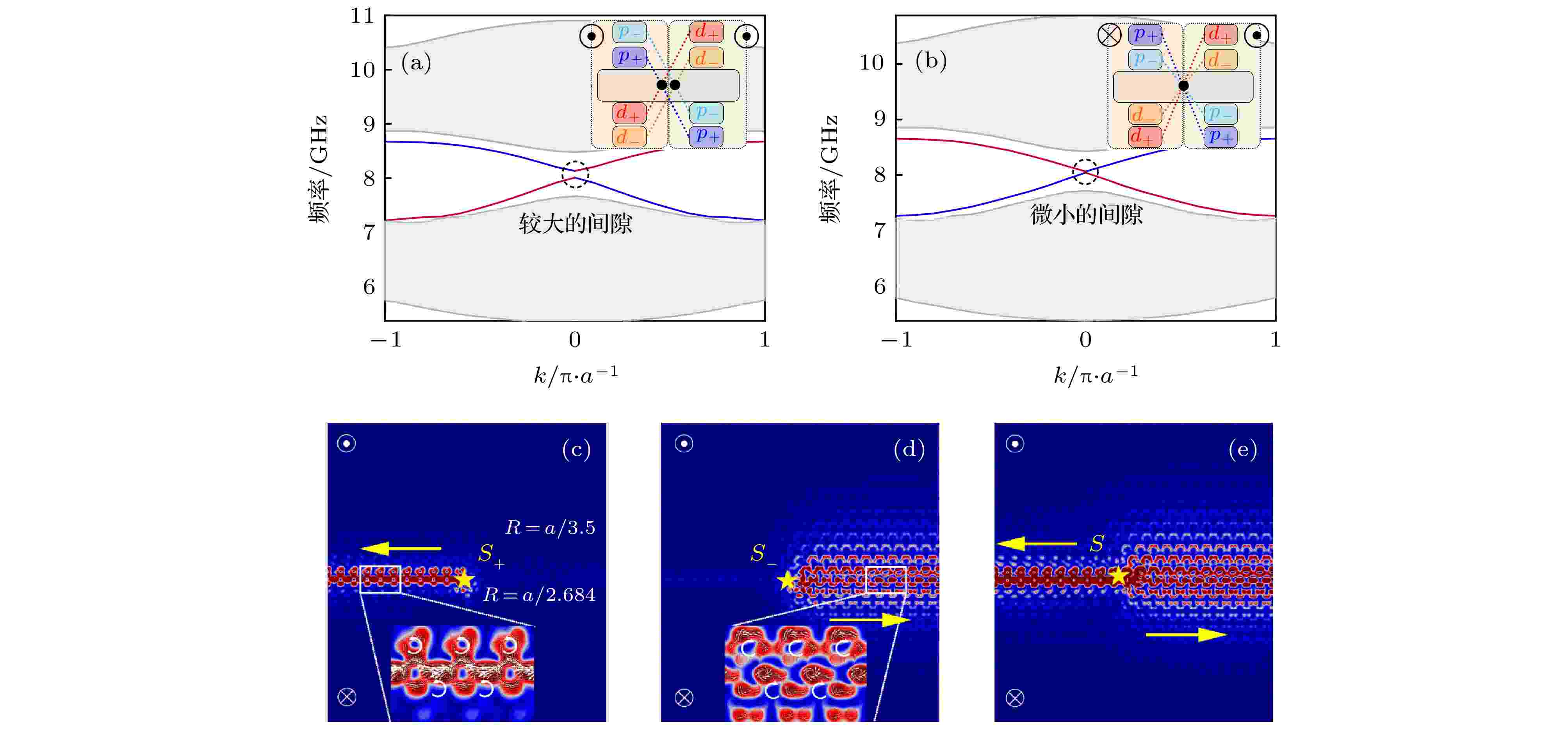图 6 区域I和II分别处于量子自旋霍尔相和量子霍尔相时, 偏置磁场方向对边界态的影响　(a)同向偏置磁场和(b)正反向偏置磁场时的投影能带结构(两条边界态具有相反的群速度和轨道角动量, 在边界上形成与量子自旋霍尔效应相似的赝自旋单向波; 采用正反向偏置磁场可以有效地减小边界态的间隙); (c) S₊激发源可以实现向左边传播的单向传播; (d) S_–激发源可以实现向右边传播的单向传播; (e)当S被激发时, TE波沿着两个方向传播
Figure6. Influence of the direction of bias magnetic field on the edge states when two domains are the QSH phase and the CI phases, respectively. (a), (b) The projected band structure for the two domains are respectively applied by the same and the opposite direction of bias magnetic field. The edge states localized at the boundary lead to a pseudo-spin dependent one-way propagation. The application of using opposite direction of bias magnetic field in the two domain reduces the gap of edge states. (c) Unidirectional wave propagation localized at domain interface excited by S₊. (d) Unidirectional wave propagation excited by S_–. (e) TE wave propagates along with opposite side when it is excited by S.

值得注意的是, 改变边界两侧偏置磁场的方向会明显地改变边界态电磁波的传输特性. 计算了图7(a)所示光子晶体的传输效率. 传输效率T为磁性光子晶体下方的出射电磁波功率p_out和光子晶体上方的入射功率p_in之比, 采取对数刻度可表示为$T\; = 10 \lg({P_{{\rm{out}}}}/{P_{{\rm{in}}}})$. 图7(b)给出了在边界两侧施加不同方向的偏置磁场时的传输效率. 可以看到在左右两侧光子晶体的共同带隙频率范围内(灰色阴影区域), 由于存在边界态的缘故光子晶体的传输效率得到较大的提高. 图中红色和蓝色的曲线分别对应于图6(a)和图6(b)偏置状态下的效率. 对比传输效率可以发现: 当两个区域的偏置磁场相反时, 传输曲线的趋势保持不变, 但传输效率有了明显的提高. 这证明了边界两侧能带的相对关系不但影响到边界态的形成, 还会影响其传输效率.
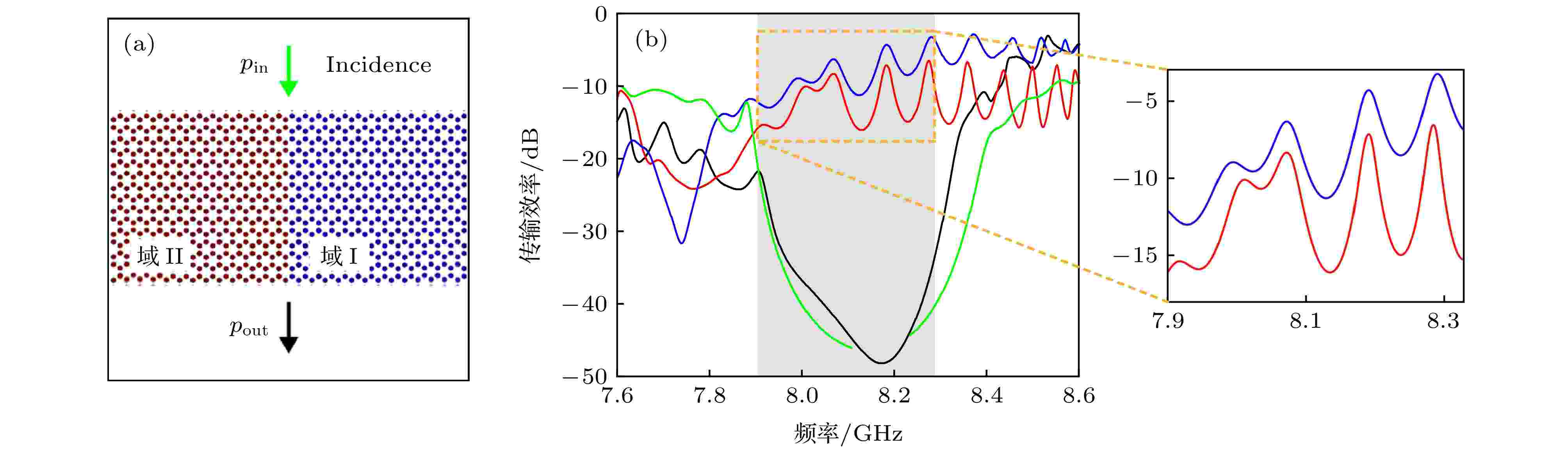图 7 (a)传输效率计算示意图; (b)与图6对应的传输效率(红线和蓝线相应于边界两侧同向和正反向偏置磁场时边界态的传输效率, 绿线和黑线是左侧光子晶体(R = a/2.684)和右侧光子晶体(R = a/3.5)单独存在时的传输效率, 阴影区为两侧光子晶体的共同带隙)
Figure7. (a) Schematic of the computational transmission efficiency. (b) The transmission efficiency corresponding to the Fig. 6. The transmission efficiency of the edge state under the condition of applying bias magnetic field with the same (red curve) or opposite direction (blue curve) in the two domains. The transmission efficiency of the full photonic crystals of the left domain is shown in green curve and the right domain in black curve. The shadow region indicates the common band gaps.

本文系统地研究了偏置磁场向对磁性光子晶体能带结构的影响. 反转偏置磁场的方向会使得能带结构中宇称相同的能带之间发生交换, 从而使得能带结构中的带序发生改变. 探讨了这种带序交换在构建拓扑边界态中的作用以及它对边界态特性的影响. 这种作用和影响可以利用边界两侧, 光子晶体共同带隙附近能带结构的相对关系加以判断. 带序交换为构造不同特性的拓扑边界态提供了更多选择性, 比如多重拓扑保护的边界态等. 利用这种带序交换可以极大地减小边界态的间隙, 从而提高边界态上电磁波的传输效率. 本文的工作将有助于加深对与光子晶体拓扑带隙相关的能带结构的理解, 构造出具有实际应用价值的边界态, 它们在诸如赝自旋分束器和无反射单向光开关等器件中具有潜在的应用前景.