全文HTML
--> --> -->另一方面, 二维材料也可能呈现出许多不同的多态结构相, 并且可能会很大程度地改变其物理和化学性质, 例如, MoS2在2H和1T结构相分别为半导体和金属[12,13]. 因此, 预测所报道的二维材料的稳定同素异形体是寻找具有物理意义的功能材料的关键技术和重要方法. 最近, 一种以正方形和八边形环为重复单元构成的四方晶格, 也称为haeckelites结构[14], 在大量不同种类的二维材料中被广泛地研究. 四方石墨烯是一种有费米面的半金属[15-17]. 单层过渡金属硫族化合物MX2 (M = Mo, W; X = S, Se, Te)的四方同素异形体具有量子自旋霍耳效应和狄拉克费米子[18-21]. 单层四方V族元素(P, As, Sb, Bi)是具有不同带隙的[22]的半导体或者较大带隙[23]的拓扑绝缘体. 因此, 二维四方材料为探索二维材料的独特物理性质提供了一个很好的机会. 据我们所知, 迄今为止, 由矩形环构成的二维III族金属硫族化合物MX (M = Al, Ga, In; X = S, Se, Te)还尚未研究. 因此, 全面分析这些化合物和多态结构相对于探索它们的新特性和拓展它们的实际应用是非常重要的.
本文设计了一类新型的单层III族金属单硫族化合物MX (M = Al, Ga, In; X = S, Se, Te)的二维四方同素异形体. 通过第一性原理计算, 我们系统地研究了这些化合物的结构和电学性能. 此外, 还探讨了应变对其电学性能的影响. 预测到这些结构具有丰富的电子结构性质和可调的带隙, 有可能被用于未来纳米电子学领域.
3.1.原子结构与稳定性
图1(a)和图1(b)给出了优化后的二维四方III族金属硫族化合物MX单层的原子结构. 二维四方MX的晶格是在x和y方向的四边环和八边环重复单元构成, 每个单元由8个M和8个X原子构成. 二维四方MX由4个原子层按X-M-M-X的顺序堆叠而成, 如图1(b)所示. 计算获得的晶格常数(a和b)汇总列于表1中. 从表1中数据可以看出, 由于随着VI族元素在周期表中纵向列位置从上往下的改变, 其原子半径随着而增加, 导致给定阳离子(MIII)的化合物MX的晶格常数(a和b)随着阴离子(XVI)的原子序数的增加而增加.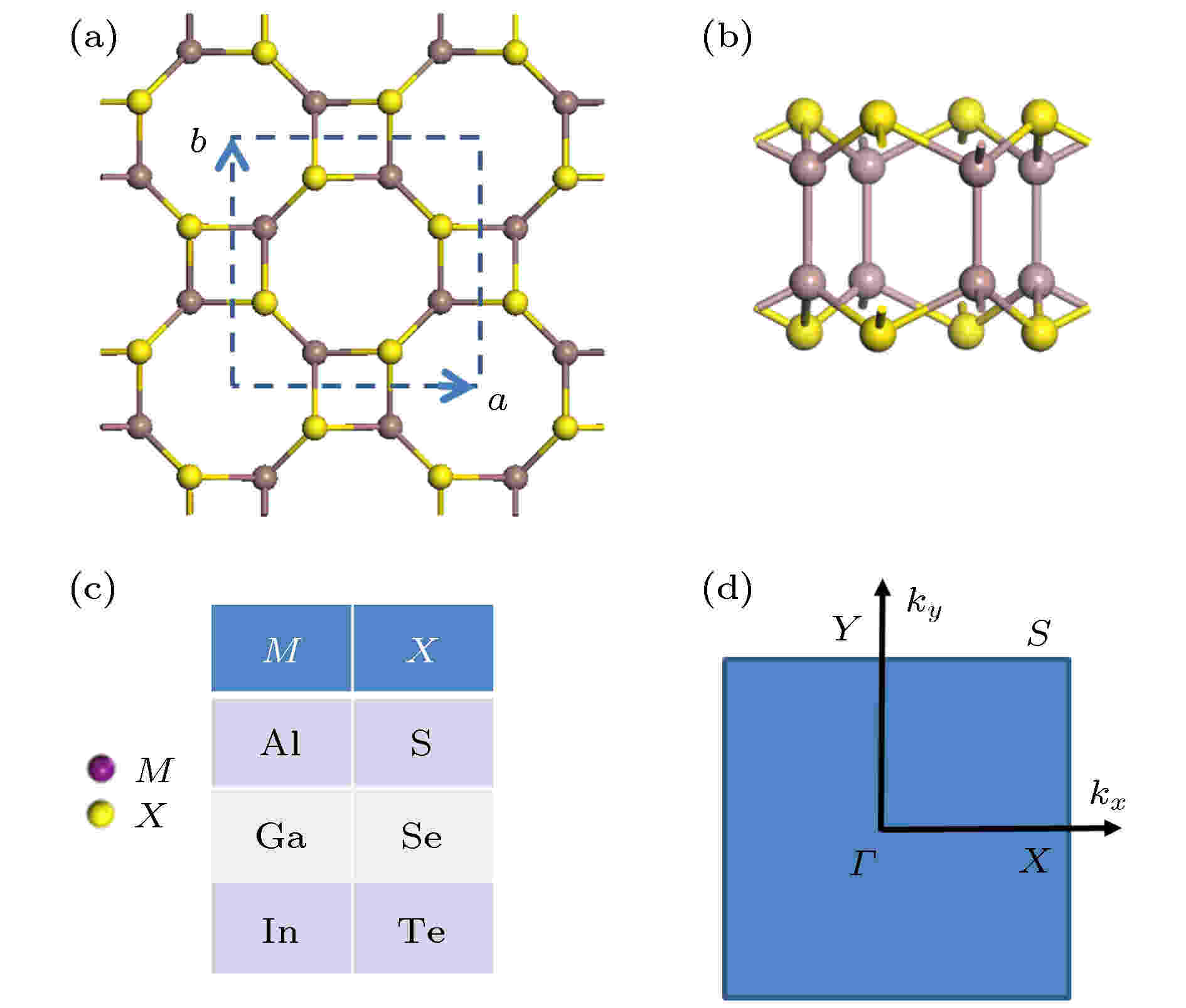
图 1 四方III族金属硫族化合物MX的几何结构 (a), (b) 分别对应原子结构的俯视图和侧视图; (c) 体系计算中选择的各种组成成分; (d) 体系的第一布里渊区, 其中字母标出了能带计算时的特殊点和路径Figure1. The geometric structures of tetragonal group III monochalcogenide MX: (a) and (b) Top-view and side-view of the structure; (c) considered systems with various choice of compositions; (d) the first Brillouin zone of structure with letters designating special points and the lines for band-structure calculation.
| MX | a/? | b/? | EC/eV | EC(2H)/eV | EgPBE/eV | EgHSE/eV | Eg(2H)PBE/eV |
| AlS | 7.07 | 7.06 | 4.44 | 4.54 | 2.28 | 3.08 | 2.10 |
| AlSe | 7.43 | 7.45 | 3.98 | 4.07 | 2.34 | 3.03 | 1.99 |
| AlTe | 8.07 | 8.08 | 3.48 | 3.55 | 2.07 | 2.70 | 1.84 |
| GaS | 7.16 | 7.15 | 3.78 | 3.89 | 2.21 | 3.24 | 2.35 |
| GaSe | 7.51 | 7.53 | 3.42 | 3.52 | 1.70 | 2.61 | 1.77 |
| GaTe | 8.12 | 8.15 | 3.03 | 3.11 | 1.50 | 2.23 | 1.43 |
| InS | 7.76 | 7.75 | 3.49 | 3.59 | 1.55 | 2.42 | 1.64 |
| InSe | 8.08 | 8.09 | 3.18 | 3.27 | 1.29 | 2.07 | 1.37 |
| InTe | 8.64 | 8.67 | 2.83 | 2.91 | 1.23 | 1.88 | 1.29 |
表1计算得到的二维四方III族金属硫族化合物MX (M = Al, Ga, In; X = S, Se, Te)的结构和电学性质: 晶格参数a和b, 结合能(EC)和分别用PBE和HSE06泛函计算得到的带隙(EgPBE和EgHSE), 表中同时给出了六方结构的结合能(EC(2H))和带隙(Eg(2H)PBE)
Table1.The calculated structural and electronic properties of 2D tetragonal group III monochalcogenides MX (M = Al, Ga, and In, X = S, Se, and Te): Lattice parameters a and b, cohesive energy (EC), band gap calculated using PBE and HSE06 functional (EgPBE and EgHSE, respectively). For comparison, the cohesive energy (EC(2H)) and band gap (Eg(2H)PBE) of the hexagonal MX are also given.
预测结构是否可以存在, 可以通过计算体系的结合能EC来评估. 体系结合能EC的计算公式如下, EC = [(NMEM + NXEX) – EMX]/(NM + NX), 其中EMX是系统的总能量, 而EM和EX是组成元素M和X的单原子能, 其中M和X分别代表第III和第VI主族原子. NM (NX)是原胞中M (X)的原子个数. 计算结果汇总列于表1中. 结合能均为正值, 同时其大小相对于实验上已经被合成的六方III-VI族MX单层要小一些(大约为0.07—0.10 eV)[32], 意味着所有的III-VI族四方MX单层是可以存在的.
为了揭示二维III-VI族四方化合物MX的键合特性, 计算了电荷密度的等值面. 计算的总电荷密度等值面如图2所示. 在所有化合物中, 电荷密度等值面显示出电子很大程度地局域在X和M原子所处的位置上, 这表明M—X键是离子性的. 此外, 当改变化合物的组分时, 把M原子从Al改变为Ga, 再改变成In或把X原子从S改变为Se, 再改变成Te, M和M原子之间的电子局域化程度有很大的改变, 并呈现出特定的规律. 例如, 对于给定的阴离子X, 当把M原子从Al改变为Ga, 再改变成In时, 电子局域在M与M原子之间的程度先增大后减小(如AlTe < InTe < GaTe), 从而导致M与M原子之间共价键强度的增加顺序为: Al < In < Ga. 化合物AlTe, GaSe, GaTe, InSe和InTe中两种元素的电负性差分别为0.49, 0.74, 0.29, 0.77和0.32. 由于不同化合物的电负性不同, 这些化合物的总电荷密度分布也不同. 对于给定阴离子X, 局域在MX化合物阳离子M和M之间的电荷密度随着X和M原子电负性差的增大而增大. 例如: AlTe, InTe和GaTe三个化合物, 电负性分别为0.49, 0.29和0.32, 相应的局域在M和M间的电荷密度大小为: AlTe < InTe < GaTe.
图 2 四方MX的总电荷密度等值面的俯视图和侧视图 (a) AlTe; (b) GaSe; (c) GaTe; (d) InSe; (e) InTe. 选择的总电荷密度等值面的值为0.05 electrons/?3Figure2. Top view and side view of the total charge density isosorfaces of tetragonal MX: (a) AlTe; (b) GaSe; (c) GaTe; (d) InSe; (e) InTe. Isosurface value is 0.05 electrons/?3.
为了进一步验证这些单层化合物的稳定性, 还计算了体系的振动声子谱. 图3给出了所有二维四方MX的声子谱. 可以发现, 声子谱在整个布里渊区中基本上都没有虚频, 这意味着这些化合物是动力学稳定的, 是可以稳定独立存在的二维晶体. 化合物AlS, AlSe, GaS和InS的声子谱在Γ点附近的“U”形特征是体系的弯曲声学模特性, 而不是不稳定特性. 这主要来源于计算的数值收敛难实现, 这是二维材料第一性原理计算中的一个常见问题[32-34].
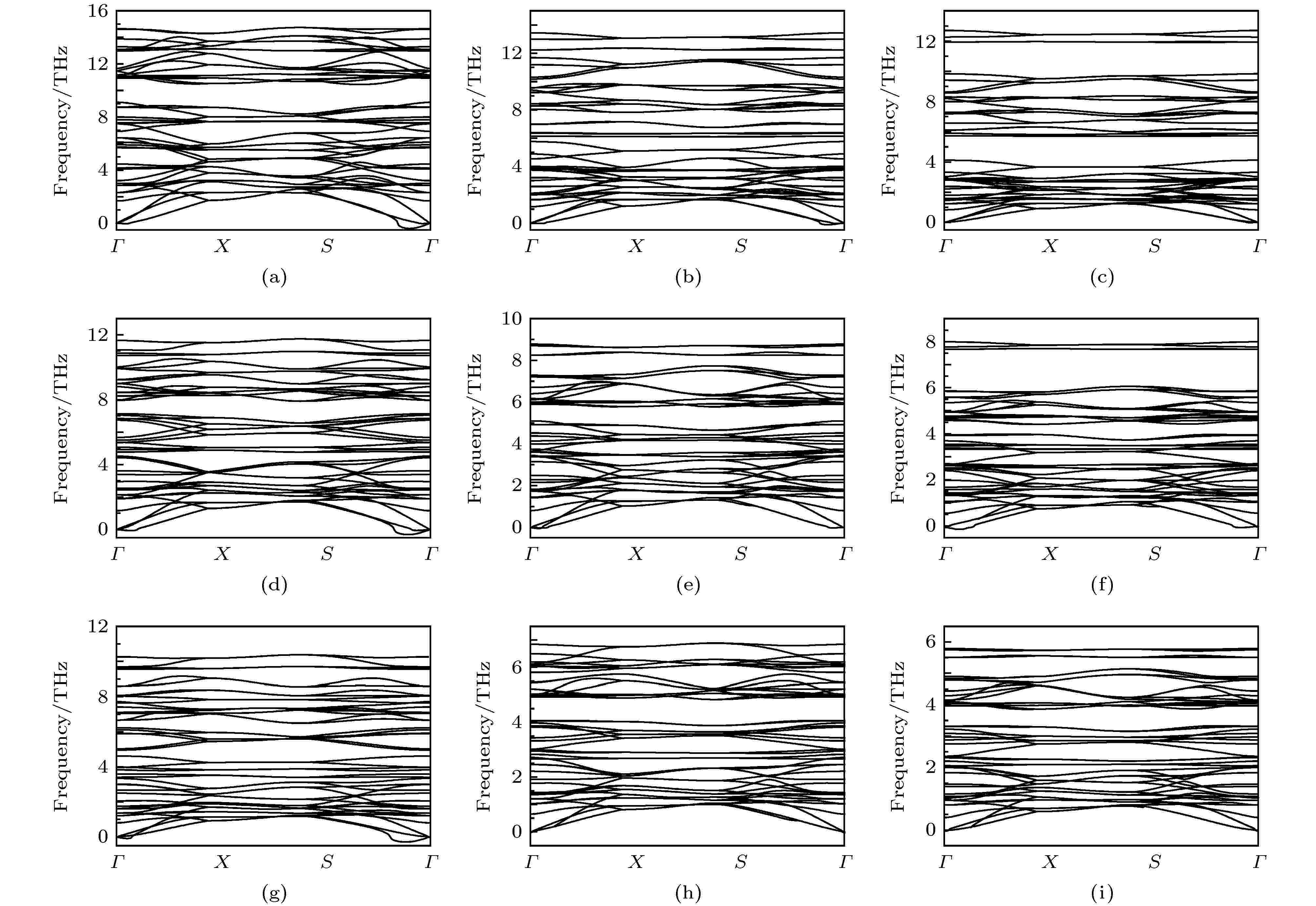图 3 单层haeckelites结构III族金属硫族化合物沿着二维布里渊区高对称方向的振动声子谱 (a) AlS; (b) AlSe; (c) AlTe; (d) GaS; (e) GaSe; (f) GaTe; (g) InS; (h) InSe; (i) InTeFigure3. Vibrational phonon spectra of group III monochalocogenide haeckelites monolayers along the high symmetry directions in the 2D Brillouin zone: (a) AlS; (b) AlSe; (c) AlTe; (d) GaS; (e) GaSe; (f) GaTe; (g) InS; (h) InSe; (i) InTe.
2
3.2.电子结构
图4为优化好的四方MX单层采用PBE和HSE06泛函计算获得的能带结构. 所有化合物采用PBE和HSE泛函获得的带隙总结在表1中. PBE泛函给出的带隙范围是1.23—2.28 eV, 而HSE泛函给出的带隙范围是1.88—3.08 eV. 对于四方MX来说, 用PBE泛函计算得到的带隙要比HSE泛函的小0.65—1.00 eV. 除InTe外, 大部分四方MX为宽带隙半导体, 它们的带隙值均大于2.0 eV. 这些材料适用于与紫外光相关的应用, 例如光电探测器和紫外光检测[35]. 我们还发现AlS, AlSe和GaS的带隙分别为3.08, 3.03和3.24 eV, 它们都大于2.8 eV, 适用于光学透明器件[36]. 此外, 对于给定阳离子M (或阴离子X)时, 当X (或M)位置的离子从S变为Se再变为Te(或Al变为Ga再变为In)时, 四方MX的带隙基本都会随着减小, 例如InS, InSe和InTe的带隙分别为2.42, 2.07, 1.88 eV. 同时发现选择不同的交换关联泛函, 不会影响计算得到的能带结构的形状. PBE和HSE泛函计算的能带结果显示, 四方III族金属硫族化合物MX单层都是间接带隙半导体, 其中导带底(CBM)位于Γ点, 价带顶(VBM)位于Γ-X(或Γ-Y)之间.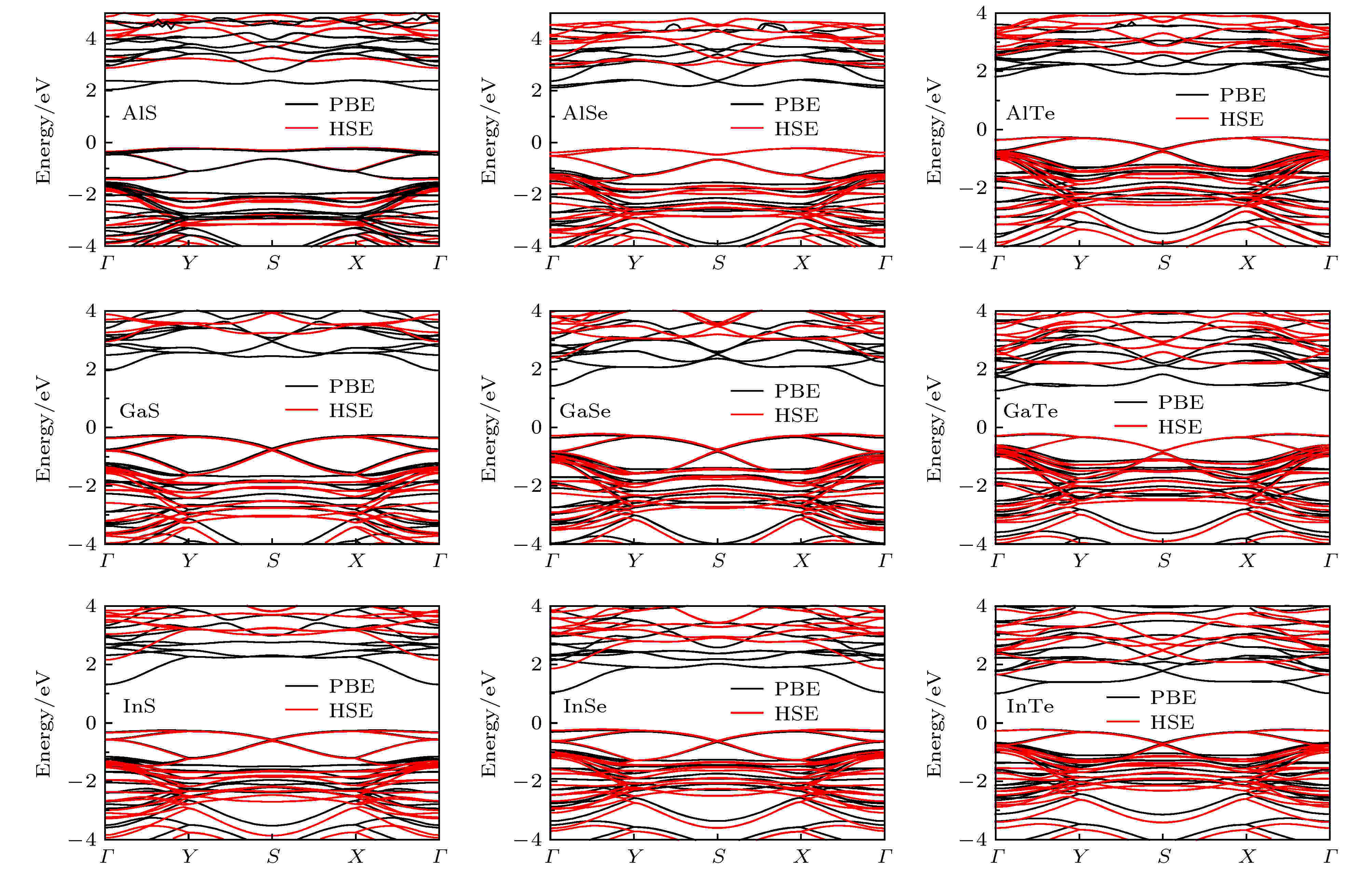
图 4 PBE和HSE泛函给出的四方MX单层的能带结构, 所有化合物都是间接带隙半导体Figure4. The PBE and HSE band structures for tetragonal MX monolayers. All the compounds are indirect band gap semiconductors.
此外, 为了比较四方和六方两种结构在电学性能的上的差异, 把六方结构的带隙(Eg(2H)PBE)和四方结构MX带隙(EgPBE)的值都列于表1中. 由计算知道, 选择HSE06泛函不会改变得到能带的形状, 仅仅扩大带隙, 所以这里我们只对PBE泛函给出的结果进行对比, 就可以体现出两种结构电学性能的差异. 从表1可以看出以下特点: 1) 随着构成成分M和X原子的改变, 对于AlX (X = S, Se, Te)两种结构对应的带隙值相差较大, 大约在0.18—0.35 eV, 对于GaX和InX (X = S, Se, Te)两者相差不大, 大约为0.06—0. 14 eV; 2) 我们发现两种结构带隙的大小没有统一的规律, 例如, 对AlS, EgPBE = 2.28 eV大于Eg(2H)PBE = 2.10 eV, 而对于InS, EgPBE = 1.55 eV大于Eg(2H)PBE = 1.64 eV.
2
3.3.机械应变的影响
众所周知, 机械应变是调节材料物理性能的重要手段. 此外, 由于合成环境和应用环境的影响, 应变效应是不可避免的. 在这里, 我们考虑双轴应变对预测体系的影响, 双轴应变定义为ε = (a–a0)/a0, 其中a0和a分别为应变前和应变后的晶格常数. ε的正负值对应于拉伸应变和压缩应变. 施加的双轴应变范围为–0.10至+0.10. 图5给出了带隙与应变ε的依赖关系. 对于GaSe, InS, InSe和InTe, 它们的带隙随ε的增大而减小, 并且几乎呈线性变化. 对于AlS, AlSe, 带隙有两种线性变化趋势. 例如, 当ε > 0.025时, AlSe的带隙随ε的增大而减小; 当ε < 0.025时, AlSe的带隙随ε的减小而减小. 当ε > 0.025时, 随着ε的增大Al和Se原子的距离也增大, 使得Al和Se原子的电子波函数交叠或杂化变小, 进而导致带隙变小; 当ε < 0.025时, 随着ε的减小, 同一个平面亚层内的Al和Al原子的距离变得很近, 使得Al和Al原子的内层电子波函数交叠或杂化变大, 进而导致带隙变小. 对于AlTe, GaS和GaTe, 它们的带隙随ε的增大而减小, 并呈现出两种线性变化趋势. 也就是说, 在ε<0.025时的带隙变化趋势比在ε>0.025时的带隙变化趋势更为平缓.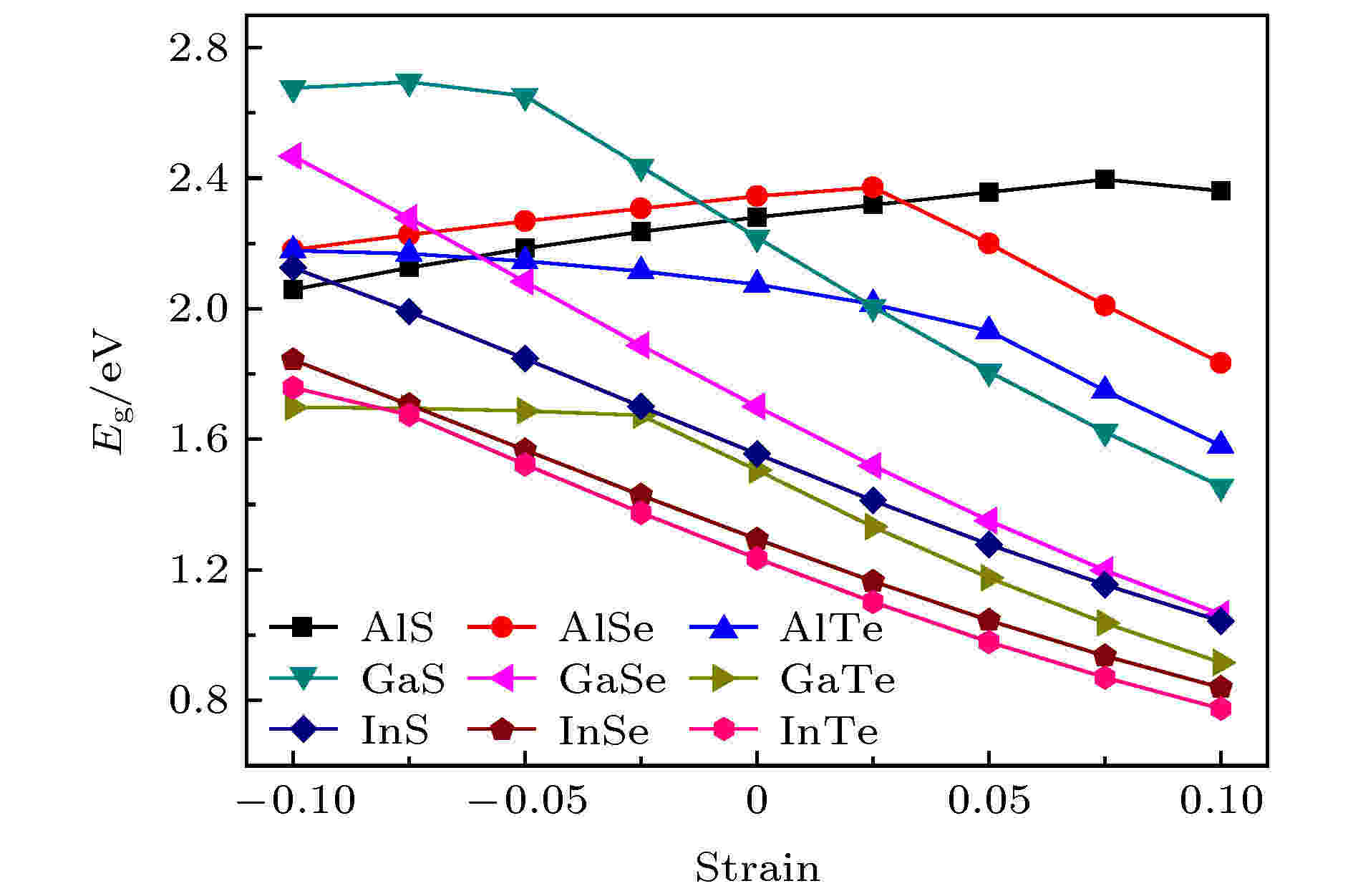
图 5 四方MX在不同的层内应变强度(–0.10—0.10)下的电子带隙Figure5. The electronic band gaps for tetragonal MX as a function of the in-layer strain from –0.10 to 0.10.
接下来, 探讨一下应变对四方MX的带隙类型(由直接(间接)到间接(直接))改变的影响. 不同应变强度下GeSe的能带结构如图6所示. 可以发现, 层内应变虽然能显著改变带隙Eg 大小, 但不能将四方GaSe从间接带隙半导体转变为直接带隙半导体.
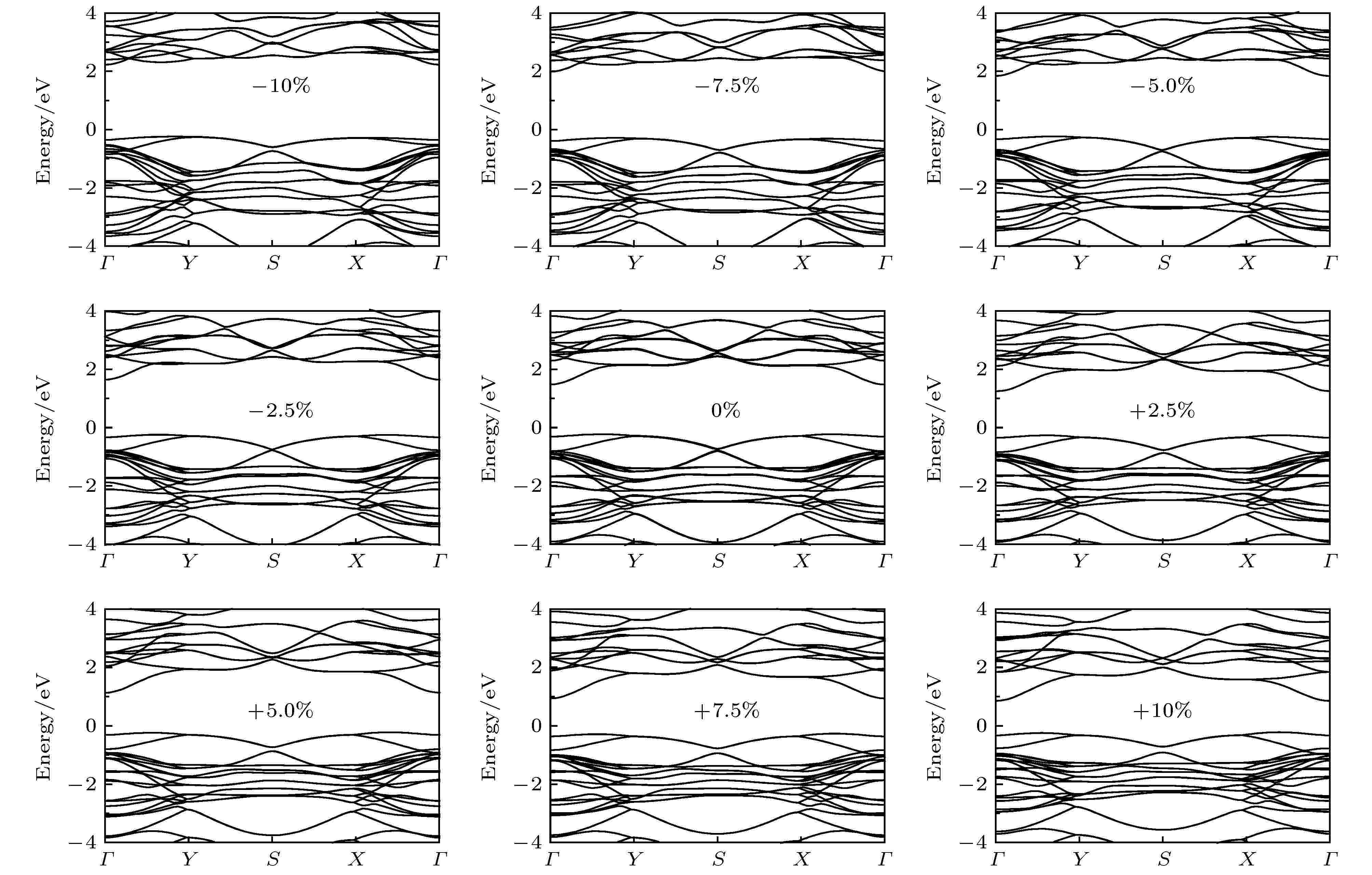图 6 二维四方GaSe在不同应变下的电子能带结构, 其中费米能级设为零Figure6. Electronic band structure of 2D tetragonal GaSe under different strains. The Fermi level is set to zero.
感谢国家超级计算机天津中心天河一号(Tianhe-1A)为本文提供的计算资源.
