摘要: 针对低磁雷诺数方法的适用性问题, 分析了当前低磁雷诺数条件应用上存在分歧以及全磁流体力学方法在高超声速领域局限性产生的原理. 在低磁雷诺磁流体力学控制数值模拟方法的基础上, 基于感应电流积分计算磁矢量势, 考虑截断因子对计算域的缩减, 提出了一种考虑感应磁场修正的低磁雷诺数磁流体力学计算方法, 并加以验证. 结合RAM-C钝锥体试验飞行状态数值模拟, 分析了“忽略感应磁场”造成的计算偏差, 探讨了“低磁雷诺数假设”在高超声速领域的使用原则. 研究表明: 1)本文建立的修正计算方法, 突破低磁雷诺数条件的限制, 拓展了低磁雷诺数方法在高超声速领域的适用性和应用范围, 数值模拟结果可信度高, 同时通过积分区域限制等方法使计算效率得到了较大的提升; 2)高超声速流动过程中感应磁场的影响, 在宏观上表现为对外加磁场的削弱和扭曲, 一定程度上降低了磁控效果; 本文计算条件下, “
Re m < 0.1”的低磁雷诺数条件可能过于保守, 建议取为
Re m < 1.0, 同时其特征电导率和特征尺度应综合考虑实际的等离子体分布.
关键词: 磁流体动力学 /
低磁雷诺数条件 /
等离子体 /
数值模拟 English Abstract An improved low magnetic Reynolds magnetohydrodynamic method based on computing induced magnetic vector potential by integrating induced current Ding Ming-Song Jiang Tao Liu Qing-Zong Dong Wei-Zhong Gao Tie-Suo Fu Yang-Aoxiao Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China Received Date: 14 January 2020Accepted Date: 25 March 2020Available Online: 09 May 2020Published Online: 05 July 2020Abstract: Aming at the applicability of low magnetic Reynolds number method, in this paper we analyze the differences in the application of low magnetic Reynolds number condition and the limitation of full MHD method when it is applied to hypersonic flow. According to the low magnetic Reynolds number magneto-hydrodynamic control numerical simulation method, computing magnetic vector potential through integrating induced current, and considering the reduction of computation domain caused by truncation factors, we propose a low magnetic Reynolds number MHD computation method which is adjusted by the induced magnetic field, and the validation of this method is also presented. Through the numerical simulation of RAM-C blunt cone in flight test condition, we analyze the discrepancy caused by “neglecting induced magnetic field”, and also discuss the principle of the application of low magnetic Reynolds number assumption of hypersonic flow. The obtained results are as follows. (1) The adjusted computation method developed in this paper breaks through the limit of low magnetic Reynolds number, and expands the application range of low magnetic Reynolds number method to hypersonic flow, the numerical simulation result is reliable; Compared with direct integration of Biot-Savart law, the computation efficiency is considerably improved. (2) In the hypersonic flow, the influence of induced magnetic field is presented, thus weakening and distorting the applied magnetic field macroscopically, as a result weakening the effect of magnetic control to some extent. Under the condition of this paper, the low magnetic Reynolds number condition “Rem < 0.1” is probably too conservative, and it is better to adopt Rem < 1.0, and the characteristic conductivity and characteristic length should be chosen according to the actual plasma distribution.Keywords: magnetohydrodynamic /low magnetic Reynolds number condition /plasma /numerical simulation 全文HTML --> --> --> 1.引 言 早在二十世纪五六十年代, 人们就开始了磁流体力学(magnetohydrodynamic, MHD)的研究. 上世纪九十年代以来, 随着高超声速飞行技术、计算机技术和便携磁体制造业的发展, 高超声速磁流体力学控制掀起了新的研究热潮. 在飞行器不同部位加载合适的磁场发生装置, 通过动量和能量的输运对高超声速飞行器周围的流动状态进行控制, 显著地改进和提升飞行器的气动力/热特性、电磁通信性能、隐身与突防特性等, 这就是高超声速磁流体力学控制[1 ] . 高超声速磁流体控制技术已经成为一个多学科交叉融合的重要研究方向, 其应用前景十分广泛, 可用于飞行器气动热环境管理、气动力操控、等离子体电子数密度控制、流速控制和边界层控制等多个方面[2 ] . 由于它具备不改变飞行器外部结构、无需机械传动、响应快速准确、兼容性强等优点, 因而受到世界各国高度重视.[1 ,3 ] : 全MHD方法和低磁雷诺数MHD方法(或简称低磁雷诺数方法).[4 ,5 ] 是通过广义欧姆定律和安培环路定理消去流动控制方程和麦克斯韦方程组中电场E 和感应电流J , 然后将流动控制方程和磁扩散方程(由法拉第定律得到)联立构成全MHD方程组, 求解该方程组得到磁流体流场和感应磁场分布. 在此基础上, 可通过求解电流连续性方程和广义欧姆定律, 得到电场和电流分布. 全MHD方法理论上适用于各类磁流体的数值计算分析, 但在高超声速飞行器流场(尤其是外流场)MHD数值模拟方面存在很大困难[1 ,2 ] .[6 ] 、Otsu[7 ] 、Fujino等[8 ] 和Takahashi等[9 ] , 美国的Bisek等[10 ,11 ] 和Lee等[12 ] , 意大利的Cristofolini等[13 ,14 ] , 国内的李开等[15 ,16 ] 、姚霄等[17 ] 、潘勇[2 ] 、张向洪[3 ] 、何淼生等[18 ] 、陈刚等[19 ] 以及孙晓辉[20 ] 等, 在针对“低磁导率、低电导率特征”气体的数值模拟时, 也几乎都采用低磁雷诺数MHD方法.2.低磁雷诺数MHD方法适用性分析 采用低磁雷诺数MHD方法, 忽略了感应磁场的影响, 必须满足低磁雷诺数近似条件, 即$R{e_{\rm{m}}} \equiv {\mu _{\rm{e}}}\sigma U{L_{\rm{p}}} \ll 1$ . 这就对磁导率${\mu _{\rm{e}}}$ 、电导率$\sigma $ 、速率U 以及电磁流动相互作用区域${L_{\rm{p}}}$ 等多个方面的流体特征提出了要求, 客观上限制了低磁雷诺数MHD方法的应用范围.[21 ] 开展了钝体飞行器磁流体力学控制研究, 认为$R{e_{\rm{m}}} = 3$ 时感应磁场可以忽略, 可采用低磁雷诺数MHD方法; 2007年, Fujino等[22 ] 开展了再入飞行器磁控技术研究, 认为$R{e_{\rm{m}}} < 1$ 时可采用低磁雷诺数MHD方法; Khan等[23 ] 采用定电导率方法开展了磁场对边界层速度分布影响的研究, 探讨了低磁雷诺数MHD方法的适用性, 发现当$R{e_{\rm{m}}} = 2.5$ 时低磁雷诺数MHD方法基本失效, 并给出了低磁雷诺数条件$R{e_{\rm{m}}} < 0.125$ , 在此基础上开展了二维钝锥体$R{e_{\rm{m}}} = 0.179$ 时的磁流体数值模拟, 发现采用低磁雷诺数MHD方法, 对计算结果的影响小于2.02%. 2008年, MacCormack[24 ] 开展了强磁场下的磁流体力学控制数值模拟, 认为$R{e_{\rm{m}}} < 1$ 时可采用低磁雷诺数MHD方法, 并开展了$R{e_{\rm{m}}} = 0.17$ 时磁流体加速装置研究, 发现采用低磁雷诺数MHD方法对轴线速度造成的计算偏差很小; 同期, 田正雨[1 ] 基于国外的低磁雷诺数条件的研究, 给出了较为保守的低磁雷诺数条件$R{e_{\rm{m}}} < 0.1$ ; 2009年, Kim[25 ] 对高超声速流动的低磁雷诺数条件进行了探讨, 认为当气体电离度小于1%时可应用低磁雷诺数MHD方法; 2010年, Bocharov[26 ] 综合了Khan等[23 ] 和MacCormack[24 ] 等在低磁雷诺数MHD方法适用性方面的研究, 给出低磁雷诺数条件$R{e_{\rm{m}}} < 0.5$ ; 2013年, Fujino和Ishikawa [8 ] 开展了再入返回器大钝体外形的磁流体数值模拟, 计算状态64 km时, 磁雷诺数$R{e_{\rm{m}}} = 29.12$ (${L_{\rm{p}}}$ 取钝体尺寸0.4 m), 感应磁场最大仅相当于外加磁场的5.4%, 采用低磁雷诺数MHD方法(忽略感应磁场)对流场结构和表面热流的影响很小, 其偏差基本可以忽略.$R{e_{\rm{m}}} < 0.1$ . 但对于高超声速流动, 由于其流速较高, 很容易就接近或超出这一条件. 例如, 对于特征电导率500 S/m、特征长度1 m和特征速度6 km/s的磁流体状态, 其特征磁雷诺数高达3.768.[7 ] 在开展钝体磁流体数值模拟研究时采用低磁雷诺数MHD方法, 其磁雷诺数$R{e_{\rm{m}}} = 3.26$ (特征电导率取400 S/m); 2007年, Yoshino等[27 ] 在开展沿再入轨道的磁流体数值模拟时采用低磁雷诺数MHD方法, 飞行高度75 km时磁雷诺数为12.66. 2012年, Nagata等[6 ] 在开展钝柱体磁流体力学控制阻力特性研究时采用低磁雷诺数MHD方法, 其磁雷诺数$R{e_{\rm{m}}} = 2.04$ (特征电导率取250 S/m); 2015年, Takahashi等[9 ] 在开展了火星探测器磁流体研究, 经测算其磁雷诺数$R{e_{\rm{m}}}$ 高达196.9 (特征电导率取波后峰值电导率1600 S/m), 数值模拟时仍采用低磁雷诺数MHD方法; 2016年, 国内****在开展返回舱OREX磁控热防护系统时采用低磁雷诺数MHD方法[28 ] , 经本文测算其数值模拟状态的磁雷诺数$R{e_{\rm{m}}}$ 高达11.6.${\nu _{\rm{e}}}{\nabla ^2}{{B}}$ , 其磁扩散率${\nu _{\rm{e}}} = 1/(\sigma {\mu _{\rm{e}}})$ , 这里${{B}}$ 为磁场磁感应强度. 由于高超声速流动的气体磁导率${\mu _{\rm{e}}}$ 、电导率$\sigma $ 一般较低, 磁扩散率高, 其磁扩散项大, 甚至高出磁扩散方程中其他项几个数量级, 此时方程存在巨大的刚性, 极大地影响了计算的稳定性和收敛性. 尤其是高超声速流场中很多区域气体电导率接近于零, 其磁扩散项趋近于无穷大, 全MHD方程组几乎无法直接求解, 需要进行近似处理.[1 ,2 ] 可知, 在等离子体电磁流体相互作用过程中, 电磁场对流场动量输运F ${E_{\rm{M}}}$ 分别为:${{U}}$ 为气流速度. 可见, 电流${{J}}$ 和电场${{E}}$ 在电磁流体相互作用过程中, 占据极其重要的地位, 直接表征了电磁场对流动的干扰. 而在全MHD方法中电流${{J}}$ 和电场${{E}}$ 由磁场的变化得到[4 ] :$\nabla \!\times\! {{B}}$ 的计算很容易出现数值误差. 而对于地球大气, 磁导率非常小${\mu _{\rm{e}}} \approx 4{\text{π}} \times {\rm{1}}{{\rm{0}}^{ - 7}}{\rm{ h/m}}$ . 当磁场${{B}}$ 的一阶偏导数由于某种原因(如数值误差、迭代中间差量等)出现较小的非物理扰动时, 该扰动反映在电流${{J}}$ 和电场${{E}}$ 上就会被放大106 倍甚至更高. 尤其是低电导率或零电导率时, 电场${{E}}$ 就面临着“极小值除以极小值”甚至“零除以零”的极端情况. 结合(1 )式可以看出, 这将直接影响电磁流动核心的动量与能量传输过程. 可见, 全MHD方法“以磁场的变化表征电场、电流变化”基本思路, 在低磁导率、低电导率的高超声速飞行领域存在缺陷, 这将极大地影响计算的稳定性和有效性.[29 ] :${{{H}}_2}, {{{H}}_1}$ 分别为界面两边的磁场强度矢量, ${{{B}}_2}, {{{B}}_1}$ 分别为界面两边的磁感应强度矢量, ${j_{\rm{s}}}$ 为界面电流密度, ${{n}}$ 为界面方向矢量. 由于界面电流很难有效确定, 真实的磁场交界面的切向分量很难直接给出. 因此全MHD方法磁场气固界面一般都采用近似条件[1 -3 ] : 对于完全导体界面${\rm{d}}{{B}}/{\rm{d}}{{n}} = 0$ ; 对于绝缘壁面${{B}} = {{{B}}_{\rm{w}}}$ . 对比(3 )式可知, 这两种边界均不能完全涵盖分界面电磁场的连续性条件. 磁场边界的不准确, 将可能引入非物理的数值模拟误差.[30 ] 采用全MHD方法开展钝体磁流体数值模拟, 得到的结论是磁场使头部区域热流上升; 2006年, Khan等[31 ] 采用全MHD方法开展钝体磁流体数值模拟, 其中部分状态磁雷诺数仅为0.01, 此时感应(诱导)磁场远小于外加磁场, 但其计算结果与低磁雷诺数MHD方法结果存在明显差异, 这一计算结果的有效性也值得商榷; 2009年, 国内****采用全MHD方法开展了RAM-C磁流体数值模拟[32 ] , 得到的结论同样是磁场使头部热流上升. 事实上, 在飞行器头部加载一定的磁场可以有效降低驻点热流, 这一点在试验中已经得到了验证. 例如意大利航天中心开展了钝体磁控热防护试验, 磁场可使表面热流下降46%[13 ,28 ] . 近两年国防科技大学柳军等开展了钝体的磁控热防护试验研究, 试验结果也表明外加磁场能有效地降低端头热流.[12 ,23 ,24 ,30 ,31 ,33 ] 时, 气体电导率计算多采用定电导率方法.2 —103 S/m量级, 其他流场绝大部分区域电导率均小于10 S/m, 甚至接近于0. 其等效等离子体特征电导率远小于流场中峰值电导率, 等效的等离子体特征厚度远小于飞行器特征尺度(如球头半径等), 且这两者的直接提取相对困难. 此时, 如果采用流场中峰值电导率和飞行器特征尺度计算磁雷诺数, 就会使计算得到的磁雷诺数远远大于真实的等效结果.$R{e_{\rm{m}}} < 0.1$ )来判断低磁雷诺数MHD方法是否适用, 其必要性仍有待商榷. 反之, 如果完全忽视低磁雷诺数条件的限制, 则有可能由于感应磁场不可忽略, 引入较大的计算偏差. 而常用的考虑“感应磁场”的全MHD方法在高超声速领域存在较大的局限性, 影响了计算的有效性. 因此, 有必要建立适用于高超声速领域的考虑感应磁场的磁流体数值模拟方法.3.修正方法的建立 由于低磁雷诺数MHD方法在流动控制方程方面没作任何简化, 其形式与完整的磁流体力学方程组[1 ,2 ] 中的流动方程一致. 因此如果在低磁雷诺数MHD方法中, 进一步考虑感应磁场的影响, 那么这种方法就能从理论上突破低磁雷诺数条件的限制, 在更大程度上反映完整磁流体力学方程的物理本质, 因此适用范围更加广泛.${{{B}}_{{\rm{ext}}}}$ 为外加磁场, 由机载磁场发生装置产生; ${{{B}}_{\rm{in} }}$ 为感应磁场(或称诱导磁场), 由等离子体中感应电流诱导产生. 对于高超声速磁流体力学控制来说, 磁场对流场动量和能量的输运需要时间的累积, 因此其控制过程一般可近似为定常(或准定常)状态. 此时其收敛状态的流场中感应电流${{J}}$ 和感应磁场${{{B}}_{\rm{in} }}$ 的分布不随(或近似不随)时间变化, 满足(或近似满足)电流稳恒和静磁条件. 因此${{r}}$ 处的感应磁场${{{B}}_{\rm{in} }}$ 可由毕奥-萨伐尔定律积分给出:${{r'}}$ 和$V'$ 为体积积分的位置矢量和区间.[29 ] , 因此基于感应电流磁诱导积分得到的${{{B}}_{\rm{in} }}$ , 自动满足了安培环路定理和磁场高斯定律. 此时, 按照磁场唯一性原理[29 ] , 这一${{{B}}_{\rm{in} }}$ 应与直接求解麦克斯韦方程中安培环路定理和磁场高斯定律等同, 这从理论上说明了该方法的可行性.${{{B}}_{\rm{in} }}$ , 在省去了繁琐的磁扩散方程或磁矢量势泊松方程组离散与迭代求解过程的同时, 还可以考虑边界处可能存在的面电流影响(可将其直接列入积分), 避免磁场边界或磁矢量势边界难以确定的问题. 因此其物理意义更加明确, 计算更加简便.N 个微元, 那么每一步迭代耦合的计算量将会达到N 2 量级. 随网格量增大, 计算量将迅速增加. 对于高超声速复杂流动问题, 计算网格很容易达到千万(107 )量级, 此时计算量将高达1014 量级, 一般的计算机系统很难承受.$\nabla \cdot {{{B}}_{\rm{in} }} = 0$ , 引入磁矢量势${{{A}}_{\rm{in} }}$ 的概念:5 )式变形可得:$\nabla $ 是对${{r}}$ 的微分算符, 与${{r'}}$ 无关, 有恒等式:7 )式可写为${{{A}}_{\rm{in} }}$ 可写为10 )式得到磁矢量势, 然后就可由(6 )式得到感应磁场${{{B}}_{\rm{in} }}$ 分布. 相比于(5 )式, (10 )式的积分计算要简单得多, 计算量也要小得多.${{{B}}_{\rm{in} }}$ 时, 可以根据磁流体流动特征对计算范围进行缩减, 进一步减小计算量.${{{B}}_{\rm{in} }}$ 的区域${{{B}}_{\rm{in} }}$ , 图1(a) 给出了文献[34 ]计算的流场电导率, 可以看出很大区域的电导率趋近于零. 当流场某区域气流的电导率很低甚至接近于零时, 流体几乎不受常规磁场的宏观作用, 此时该区域感应磁场存在与否, 对流动干扰很小. 换句话说, 如果某区域的流体受常规磁场的影响很小, 那么该区域的感应磁场可以不用计算. 由于磁相互作用数可以在一定程度上表征磁场与流动耦合作用的整体效果, 这里引入单位磁相互作用数${Q'_{\rm{m}}}$ 的概念, 令磁相互作用数中的特征磁感应强度和特征长度分别为1 T和1 m, 即有${Q'_{\rm{m}}} = \sigma /\rho u$ , 这里$\rho, \;u$ 为气体密度和速度大小. 因此, 需要计算感应磁场${{{B}}_{\rm{in} }}$ 的区域, 可以通过气体电导率或者单位磁相互作用数高于某个值进行判定:图 1 流场中电导率和环形感应电流分布[34 ] (a)电导率; (b)电流密度Figure1. Distribution of electronic conductivity and annular electric current: (a) Conductivity; (b) current.${\sigma _{\rm{c}}}$ 或者截断单位磁相互作用数${Q_{\rm{c}}}$ 应取值恰当. 例如对于高超声速流动, 其激波后电导率为102 —103 S/m, ${\sigma _{\rm{c}}}$ 可取为0.1—1.0 S/m或者更小. 为了减小不同计算状态的人为干预, 这里引入截断因子$\eta $ :${\sigma _0}$ 为磁流体作用区域典型电导率, ${Q'_{{\rm{m0}}}}$ 为磁流体作用区域典型单位磁相互作用数. 在迭代初期, 截断因子$\eta $ 可选用较大的值, 如$\eta = {10^{ - 1}}—{10^{ - 3}}$ , 以减小计算量, 加快收敛; 在迭代后期, $\eta $ 可选用较小的值, 如$\eta = {10^{ - 4}}—{10^{ - 6}}$ , 以提高计算精度.${{{B}}_{\rm{in} }}$ 所需要的感应电流积分区域图1(b) 可以看出, 高超声速流场中感应电流主要集中于流场与电磁场相互作用的小部分区域, 很大区域电流趋近于零. 因此, 也可以引入类似于(11 )式和(12 )式的条件, 来判别计算感应磁场${{{B}}_{\rm{in} }}$ 时需要积分的空间区域:${J_{\rm{c}}}$ 为截断电流密度大小, ${J_0}$ 为磁相互作用区典型电流密度.5 )式还可以看出, 由电流微元产生的感应磁场与距离的平方呈反比关系. 可见由稳恒(或近似稳恒)的感应电流产生的磁场, 其主要作用区域应该为有限的空间, 将其定为${L_{\rm{c}}}$ 为磁流体作用区域的特征尺度; L 为感应磁场作用区间尺度, 超出L 流场空间, 不参与该外加磁场作用区域的感应磁场计算; $\lambda $ 为放大因子, 可结合具体的物理实际进行设置, 本文数值模拟时$\lambda = 5$ .4.数值计算分析 24.1.无限长直流导线产生磁场 4.1.无限长直流导线产生磁场 为了保证电流数值离散积分过程的正确性, 首先对电流积分计算磁场的程序模块进行校验, 这是本文低磁雷诺数MHD方法修正的基础.I 的无限长直导线, 导线外距离为r 的任意一点的磁场${{B}}$ 由安培环路定理计算: $\displaystyle\int_L {{{B}} \cdot {\rm{d}}{{l}}} =\! \displaystyle\iint_S {(\nabla \times {{B}}) \cdot {\rm{d}}{{S}}} =\! \displaystyle\iint_S {{\mu _{\rm{e}}}}{{J}} \cdot {\rm{d}}{{S}}=\! {\mu _{\rm{e}}}I,$ 这里L 为半径为r 的圆周, S 为圆面, 圆面方向为电流方向. 由于对称性$\displaystyle\int_L {{{B}} \cdot {\rm{d}}{{l}}} = 2{\text{π}}rB$ , 因此有磁感应强度大小$B = {\mu _{\rm{e}}}I/2{\text{π}}r$ , 其方向符合右手系.$I = 1.0\; {\rm{A}}$ . 假设电流在导线截面内均匀分布, 则电流密度约为$J = 3.18 \times {\rm{1}}{{\rm{0}}^5}~{\rm{ A/}}\;{{\rm{m}}^{\rm{2}}}$ , 这与图1(b) 流场感应电流密度在同一数量级. 为了保证“无限长”的假设近似成立, 本文取直导线长为100 m. 采用圆柱形网格, 网格点设为$10001 \times 51 \times 181$ , 沿导线长方向的网格点均匀分布, 其他两个方向非均匀分布.图2 给出了不同位置的磁场感应强度与理论值的比较. 由图2(a) 可以看出, 在导线的端头(x = 0.0 m)附近, 数值积分的磁感应强度明显小于理论值, 这是因为$x < 0.0 \;{\rm{m}}$ 的部分被人为截断, 没有参与数值积分, 因此不满足“近似无限长条件”. 随着x 增大, 这种“人为截断”产生影响逐渐减小, 数值结果逐渐趋近于理论值, 长直导线中点(x = 50.0 m), 数值结果几乎与理论值完全重合. 图2(b) 中也有类似的现象: 当r 较小时, 数值结果与理论值几乎完全重合, 随r 进一步增大, r 逐渐接近甚至大于导线的长度, 此时“人为截断”产生的影响逐渐增大, 不再满足“近似无限长条件”, 数值结果与理论值偏离.图 2 不同位置的磁感应强度 (a) $r = 1.0\; {\rm{m}}$ ; (b) $x = 50.0 \;{\rm{m}}$ Figure2. Magnetic induction intensity in different locations: (a) $r = 1.0 \;{\rm{m}}$ ; (b) $x = 50.0 \;{\rm{m}}$ 4.2.三维钝柱体外形考虑感应磁场修正的磁流体数值模拟 -->4.2.三维钝柱体外形考虑感应磁场修正的磁流体数值模拟 为了进一步校验本文修正计算方法的有效性, 开展钝柱体外形高超声速磁流体数值模拟, 该算例有低磁雷诺数方法和全MHD方法计算结果[33 ] . 计算外形头部半径0.01 m, 柱体长0.075 m. 计算来流为混合电离气体, 来流温度9000.0 K, 来流压力7726.0 Pa, 来流密度0.01429 kg/m3 , 来流速度6710.0 m/s, 壁面温度12000.0 K. 采用偶极子磁场, 磁场中心位于头部球心, 磁特征感应强度${B_0} = 4.0 \;{\rm{T}}$ , 磁场特征长度为0.01 m. 采用固定电导率方法, 全场混合气体电导率均为4800 S/m, 特征磁相互作用数为69.图3 和图4 分别给出了本文计算的外加磁场和感应磁场分布, 并与文献[33 ]给出的结果进行对比, 图中数值乘以$\sqrt {{\mu _{\rm{e}}}} $ 转化为以特斯拉为单位的量. 由图可以看出, 本文修正方法计算得到的感应磁场, 相对于外加磁场量值较小; 除局部细节外, 整体分布变化规律和量值均与全MHD方法的结果[33 ] 相符合, 这说明本文修正方法能较好计算磁流体流动过程中的感应磁场分布.图 3 外加磁场 (a)本文BXF; (b)文献BXF; (c)本文BYF ; (d)文献BYFFigure3. Externally applied magnetic field: (a) BXF of this paper; (b) BXF[33 ] ; (c) BYF of this paper; (d) BYF[33 ] .图 4 感应磁场 (a)本文BX; (b)文献BX; (c)本文BY; (d)文献BYFigure4. Induced magnetic field: (a) BX of this paper; (b) BX[33 ] ; (c) BY of this paper; (d) BY[33 ] .图5 给出了不同计算方法得到的流场压力分布. 可以看出, 在磁场作用下本文计算得到的流场压力分布规律与文献[33 ]基本一致, 但本文给出的激波脱体距离明显大于文献结果. 这是由于文献[33 ]没有给出混合电离气体的成分, 也没有明确气体状态计算方法, 而本文采用的等效比热比的气体计算方法, 可能与文献[33 ]中的气体模型不一致. 事实上, 文献[33 ]给出的该状态磁场使激波脱体距离增大的倍数并不确定, 为3—7.5倍[33 ] , 图2 —图5 中文献结果为增大3倍的结果, 而本文计算结果为磁场使激波脱体距离增大约4—5倍. 本文计算激波脱体距离较远, 导致了感应磁场分布细节上的差异.图 5 不同方法计算的流场压力分布 (a)文献低磁雷诺数MHD方法; (b)文献全MHD方法; (c)本文低磁雷诺数MHD方法; (b)本文修正方法Figure5. Distribution of pressure in the flow computed by different method: (a) Low Re m method[33 ] ; (b) full MHD method[33 ] ; (c) low Re m method of this paper; (d)improved method of this paper.图5 还可以看出, 本文修正方法计算得到的压力与一般的低磁雷诺数MHD方法模拟结果, 除局部细节外的分布规律基本一致, 与文献[33 ]“低磁雷诺数MHD方法和全MHD方法结果之间的差异”类似. 这里以磁场尺度和来流速度为特征量, 计算磁雷诺数$R{e_{\rm{m}}} \approx 0.4$ . 可见, 此时采用低磁雷诺数假设忽略感应磁场, 对流场结构的影响不大, 这与图3 和图4 显示的“感应磁场相对于外加磁场的量值较小”相互印证.4.3.Ram-C钝锥“忽略感应磁场”对磁流体数值模拟影响的分析 -->4.3.Ram-C钝锥“忽略感应磁场”对磁流体数值模拟影响的分析 文献[35 ]为了分析电导率模拟准确性问题, 基于低磁雷诺数方法探讨了国内外常见的多种电导率模型差异及其影响, 其中采用电导率模型M6时, 流场中峰值电导率高达6000 S/m, 其磁雷诺数远高于0.1, 低磁雷诺数方法的适用性有待商榷. 本文结合这一典型飞行状态与计算条件, 开展一般低磁雷诺数方法和本文修正方法的数值对比计算, 分析“忽略感应磁场”对磁流体控制数值模拟的影响, 探讨低磁雷诺数条件适用性.[35 ,36 ] , 计算飞行高度71 km, 飞行速度7650 m/s, 等温壁面条件, 壁面温度1500 K, 完全非催化壁面条件. 磁场配置采用磁偶极子磁场, 磁感应特征强度${B_0} = 0.5 \;{\rm{T}}$ , 特征长度${r_0} = 0.1524$ m, 磁偶极子方向为直角坐标横轴负方向. 采用电导率模型M6[35 ] , 其形式为$\sigma = 1.56 \times {10^{ - 2}}{T^{1.5}}/\ln (1.23 \times {10^7}{T^{1.5}}/n_{\rm{e}}^{0.5})$ , T 为温度, n e 为电子数密度. 采用11组分Park反应模型计算等离子体分布.图6 给出了采用M6模型计算得到的流场中电导率分布, 图6(a) 为采用一般低磁雷诺数MHD方法模拟得到的流场电导率分布云图, 图6(b) 为采用修正方法和一般低磁雷诺数MHD方法计算得到的驻点线电导率分布比较. 可以看出, 在磁场作用下流场峰值电导率可达5000 S/m, 但取得峰值电导率的等离子区域厚度较薄, 波后较大区域内气体电导率仅为1000 S/m左右. 采用不同方法计算, 磁场对激波脱体距离的外推效果存在差别, 采用修正方法得到的激波脱体距离, 比采用一般低磁雷诺数MHD方法结果稍小.图 6 采用电导率模型M6计算的流场电导率分布 (a)全场云图; (b)驻点线参数分布Figure6. Distribution of electronic conductivity using M6: (a) Full contour map; (b) parameters along stagnation line.图7 给出了修正方法计算得到的感应磁场分布. 对比图4 可以看出, 感应磁场的整体分布与4.2 节钝柱体的感应磁场分布大体相似, 但二者又有明显的差异. 造成差异的原因可能有两个方面: 一是计算外形差别; 二是电导率分布存在差别, 尤其是激波波前位置, 4.2 节采用定电导率方法, 其流场波前气体电导率为4800 S/m, 此时波前流动也会产生较强的环形感应电流; 而本节状态的流场波前电导率接近于零, 波前环形电流也接近于零. 这种感应电流分布的差异必然影响感应磁场的分布.图 7 修正方法计算的钝锥RAM-C感应磁场 (a) ${B_x}$ 分量; (b) ${B_y}$ 分量Figure7. Induced magnetic field of RAM-C using improved method: (a) Component ${B_x}$ ; (b) component ${B_y}$ .图8 进一步给出了外加磁场分布和全磁场分布, 这里全磁场是外加磁场与感应磁场叠加的结果. 结合图7 可以看出, 除局部细节外, 感应磁场方向大体上与外加磁场相反, 感应磁场的影响在某种程度上相当于对外加磁场作用效果的削弱. 这是符合磁电阻扩散基本原理的, 由楞次定律可知, 具有导电性的等离子体在磁场中运动时, 其感应磁场方向总是对抗磁通量的变化方向, 因此整体上表现为对原磁场的某种削弱, 整体影响幅度不大, 其x 分量最大值相当于外加磁场x 方向最大值的7.9%左右, 其y 分量最大值相当于外加磁场y 方向最大值的4.6%左右.图 8 钝锥RAM-C外加磁场和修正方法计算的全磁场分布 (a)全磁场${B_x}$ 分量; (b)全磁场${B_y}$ 分量; (c)外加磁场${B_x}$ 分量; (b)外加磁场${B_y}$ 分量Figure8. Total magnetic field computed using improved method and externally applied magnetic field of RAM-C: (a) Total ${B_x}$ ; (b) total ${B_y}$ ; (c) externally ${B_x}$ ; (c) externally ${B_y}$ .表1 给出了不同条件或方法计算得到的阻力系数, 可以看出, 采用修正方法计算得到的阻力系数与一般低磁雷诺数MHD方法计算结果的差异在1%左右, 其磁控效果没有本质差别.计算方法或条件 总阻力系数 增大比例 No Mag. 0.292 — 一般低$R{e_{\rm{m}}}$方法 0.991 239% 修正方法 0.980 234%
表1 钝锥RAM-C阻力系数Table1. Drag coefficient of RAM-C.图9 进一步给出了不同计算方法得到的表面热流分布. 由图可以看出, 采用修正方法计算得到的热流与采用一般低磁雷诺数MHD方法的结果局部存在差异, 但整体分布趋于一致, 这说明磁控热防护效果没有本质差异. 在X = 0 m附近, 两者差异稍大, 采用修正方法的热流的磁控热防护效率比一般低磁雷诺数MHD方法的下降不到10%. 可见, 考虑感应磁场影响在一定程度上降低了局部区域的磁控热防护效果.图 9 修正方法和一般低磁雷诺数MHD方法计算得到的热流分布比较Figure9. Heat flux computed using Low Re m method or improvbed method.$R{e_{\rm{m}}} \approx 7.3$ , 此时不符合低磁雷诺数条件要求. 如果以波后较大区域电导率1000 S/m和头部等离子体层厚度0.1 m为特征量, 则磁雷诺数$R{e_{\rm{m}}} \approx 0.96$ . 两者差异较大, 后者综合考虑了等离子体的实际分布特征、磁扩散方向以及电磁相互作用区间, 因而更加准确, 但其结果仍然比保守的低磁雷诺数条件($R{e_{\rm{m}}} \leqslant 0.1$ )高得多. 结合图8 和表1 “忽略感应磁场对计算结果影响较小”的结论可以看出, 对于本文这种不含人工电离的高超声速空气流场计算状态, “$R{e_{\rm{m}}} < 0.1$ ”的低磁雷诺数条件过于保守, 可扩展为$R{e_{\rm{m}}} < 1.0$ , 同时其特征电导率和特征尺度应综合考虑实际的等离子体分布.图10 进一步给出两种修正方法计算得到的热流和残差收敛曲线. Modified Method 1为直接积分计算毕奥-萨伐尔定律积分的方法, Modified Method 2为基于电流积分计算磁矢量势同时考虑截断因子对计算区域进行缩减的方法. 由图可以看出, 这两种方法计算得到的热流几乎完全重合, 计算精度相当. 本文Modified Method 2的计算时间较短, 效率较高.图 10 采用不同修正方法计算得到的热流和残差收敛曲线 (a)热流; (b)残差Figure10. Heat flux and residual error computed using different modified method: (a) Heat flux; (b) residual error.5.结 论 (1)本文在详细探讨低磁雷诺数方法适用性以及全MHD方法局限性及其原理的基础上, 基于感应电流积分计算磁矢量势得到感应磁场, 提出了一种低磁雷诺数MHD修正计算方法, 突破了“低磁雷诺数假设”的限制, 增强了低磁雷诺数MHD方法的适用性, 拓宽了应用范围. 考核验算表明, 该方法可较为准确地计算模拟磁流体流动中的感应磁场, 数值模拟结果与理论分析及文献结果相符, 具有较高的可信度.35 ]采用常规的低磁雷诺数MHD方法“忽略感应磁场”造成的计算偏差, 对其计算结论的取得不构成实质性影响; 3)相比于全域直接积分计算毕奥-萨划尔定律, 本文基于电流积分计算磁矢量势同时考虑截断因子对计算区域进行缩减的耦合计算方法, 在计算时间和效率方面具有明显优势; 4)本文计算条件下, “$R{e_{\rm{m}}} < 0.1$ ”的低磁雷诺数条件过于保守, 建议取为$R{e_{\rm{m}}} < 1.0$ , 同时其特征电导率和特征尺度应综合考虑实际的等离子体分布. 
























































































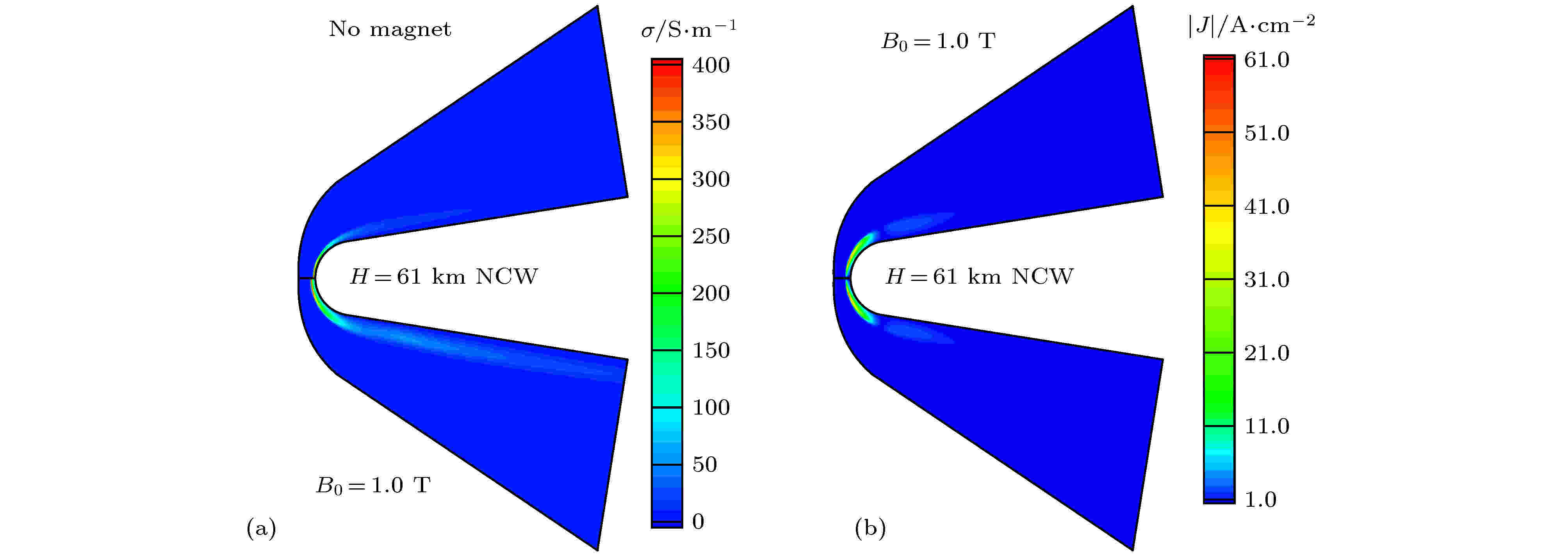 图 1 流场中电导率和环形感应电流分布[34] (a)电导率; (b)电流密度
图 1 流场中电导率和环形感应电流分布[34] (a)电导率; (b)电流密度




























 图 2 不同位置的磁感应强度 (a)
图 2 不同位置的磁感应强度 (a) 





 图 3 外加磁场 (a)本文BXF; (b)文献BXF; (c)本文BYF; (d)文献BYF
图 3 外加磁场 (a)本文BXF; (b)文献BXF; (c)本文BYF; (d)文献BYF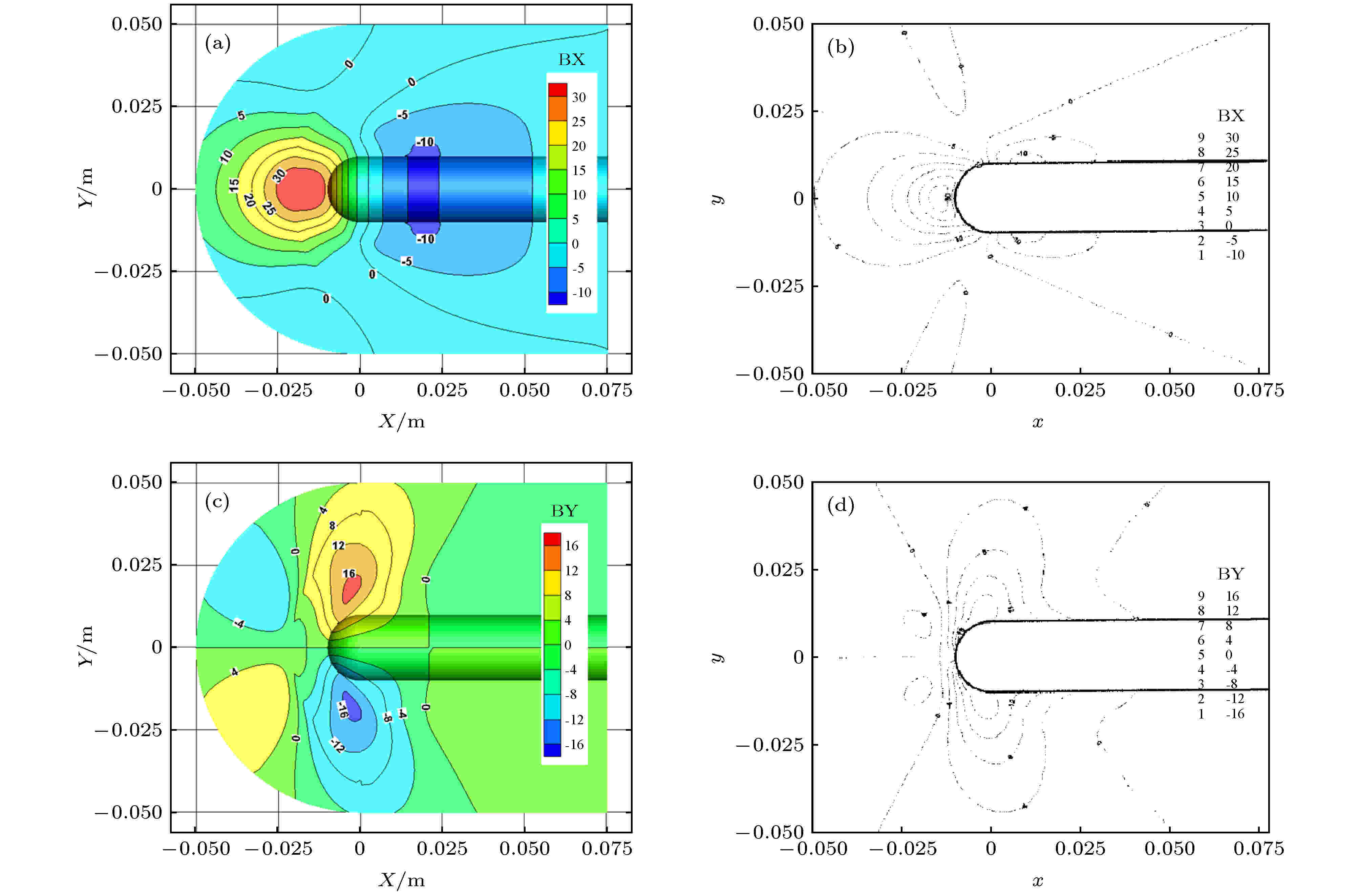 图 4 感应磁场 (a)本文BX; (b)文献BX; (c)本文BY; (d)文献BY
图 4 感应磁场 (a)本文BX; (b)文献BX; (c)本文BY; (d)文献BY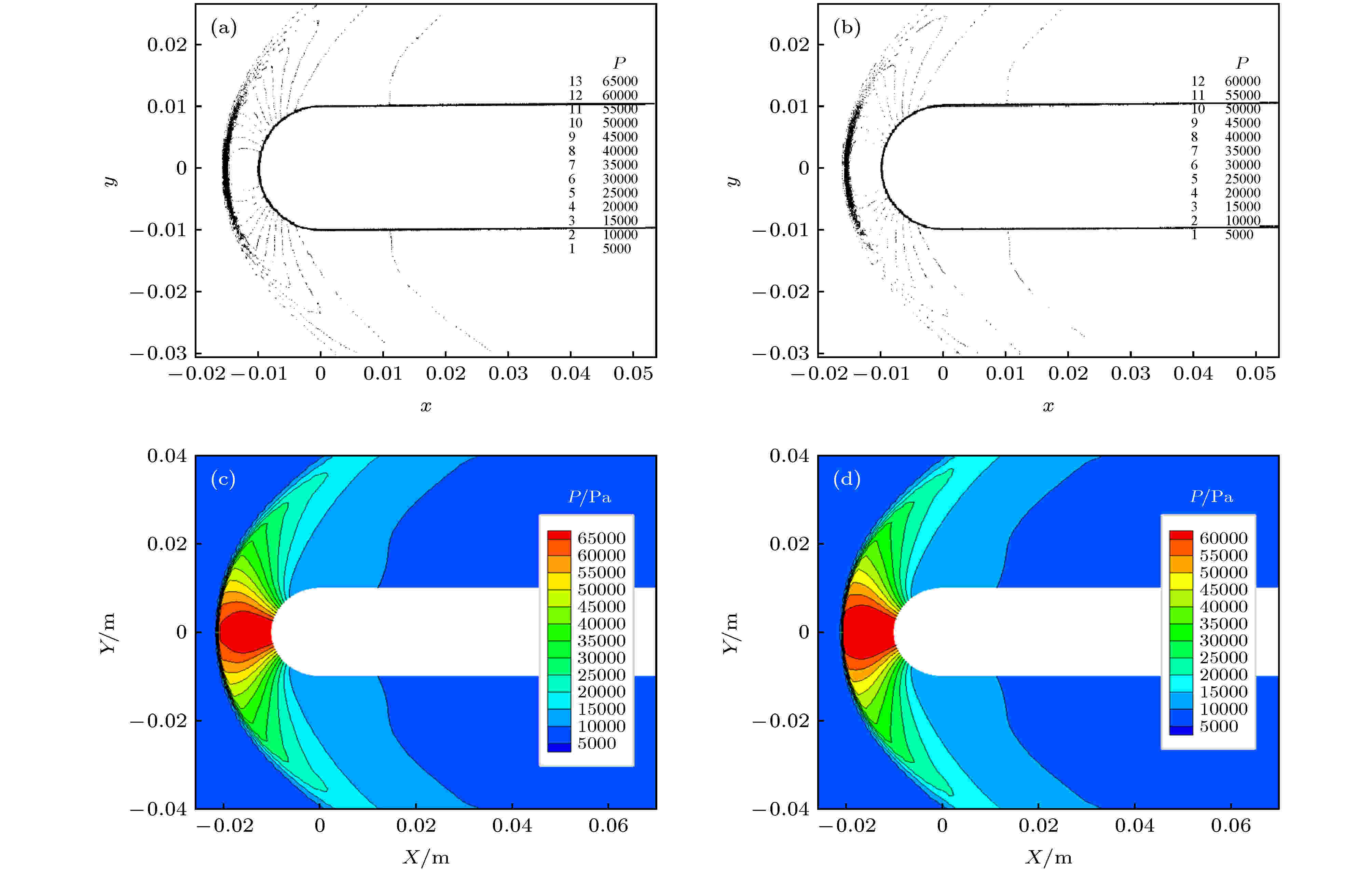 图 5 不同方法计算的流场压力分布 (a)文献低磁雷诺数MHD方法; (b)文献全MHD方法; (c)本文低磁雷诺数MHD方法; (b)本文修正方法
图 5 不同方法计算的流场压力分布 (a)文献低磁雷诺数MHD方法; (b)文献全MHD方法; (c)本文低磁雷诺数MHD方法; (b)本文修正方法



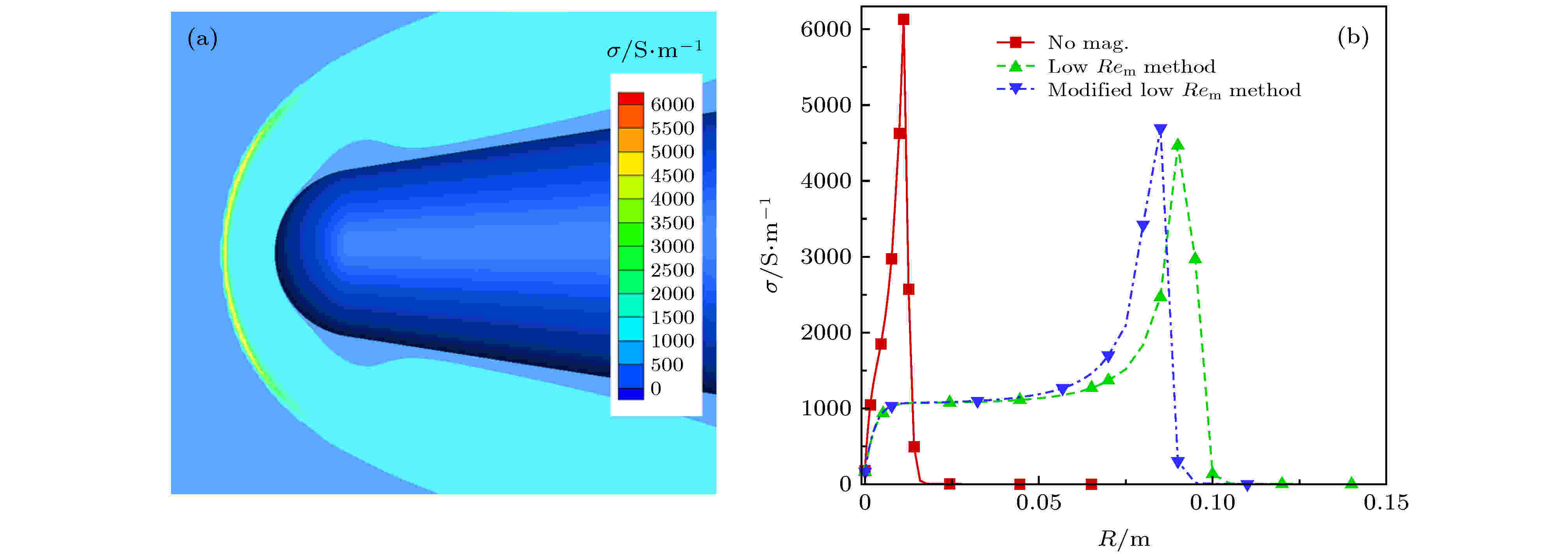 图 6 采用电导率模型M6计算的流场电导率分布 (a)全场云图; (b)驻点线参数分布
图 6 采用电导率模型M6计算的流场电导率分布 (a)全场云图; (b)驻点线参数分布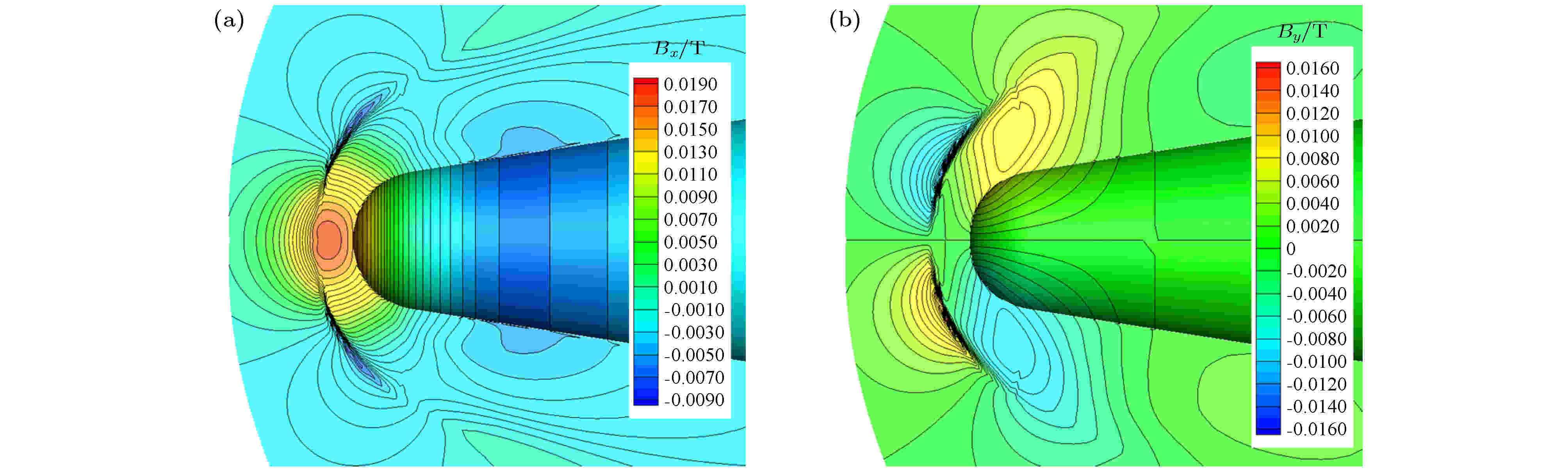 图 7 修正方法计算的钝锥RAM-C感应磁场 (a)
图 7 修正方法计算的钝锥RAM-C感应磁场 (a) 



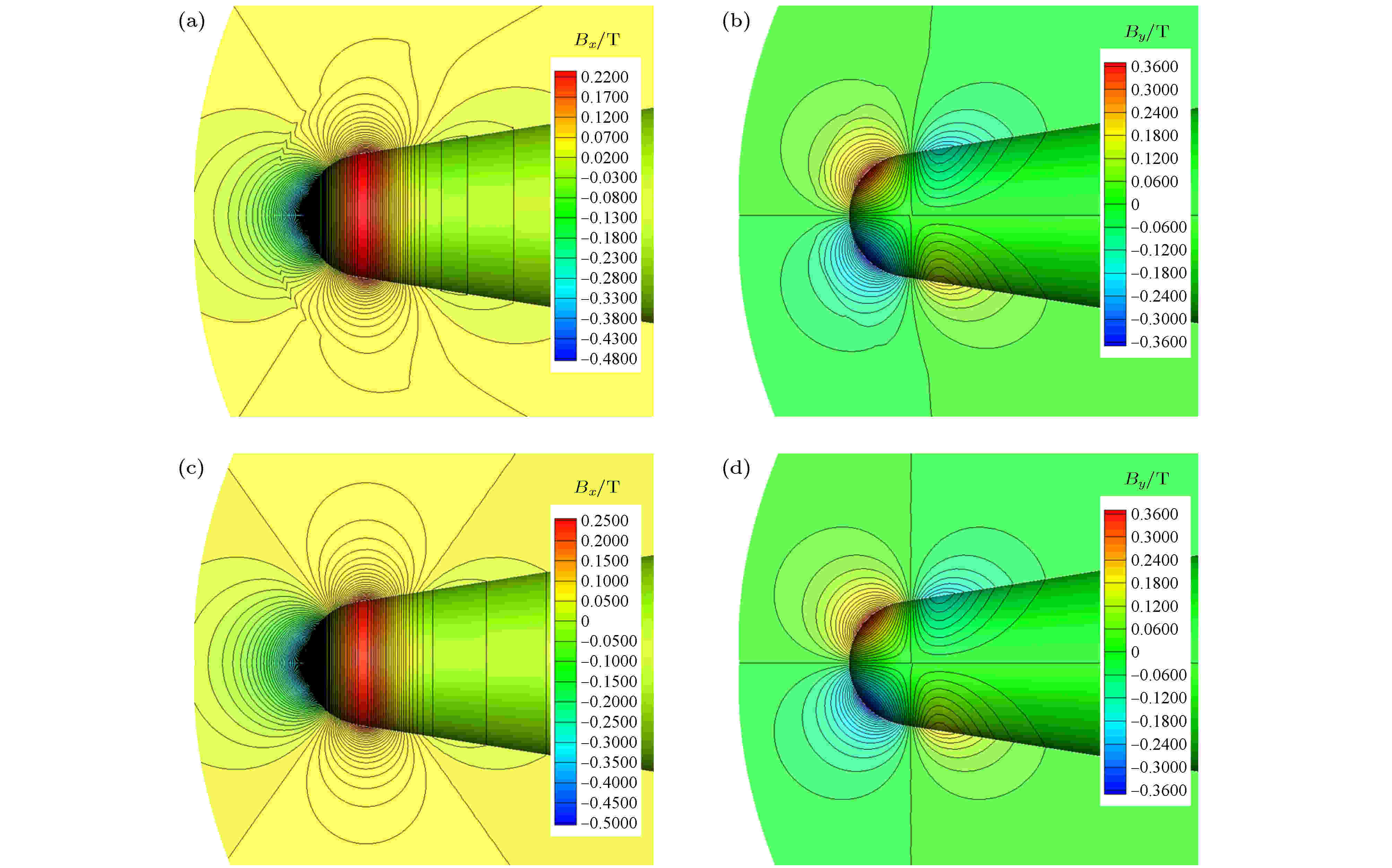 图 8 钝锥RAM-C外加磁场和修正方法计算的全磁场分布 (a)全磁场
图 8 钝锥RAM-C外加磁场和修正方法计算的全磁场分布 (a)全磁场















 图 9 修正方法和一般低磁雷诺数MHD方法计算得到的热流分布比较
图 9 修正方法和一般低磁雷诺数MHD方法计算得到的热流分布比较




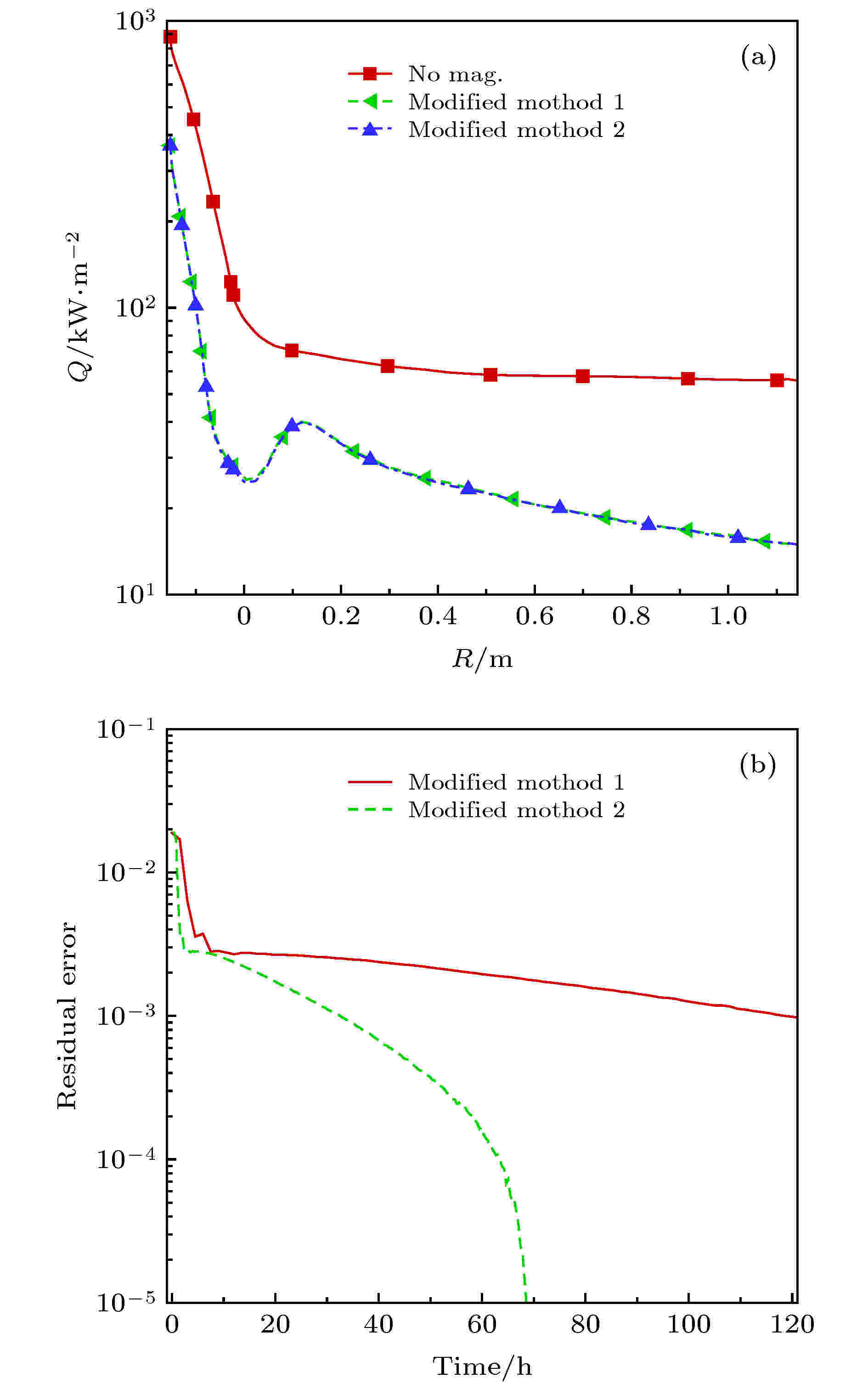 图 10 采用不同修正方法计算得到的热流和残差收敛曲线 (a)热流; (b)残差
图 10 采用不同修正方法计算得到的热流和残差收敛曲线 (a)热流; (b)残差

