全文HTML
--> --> -->将石墨烯切割成纳米带是一种能够实现量子限制作用的有效方法. Kheirabadi和Shafiekhani[19]发现石墨烯纳米片的尺寸对电子带隙影响很大, 通过增加纳米石墨烯的尺寸可以使电子能带带隙变窄, 特别是通过改变纳米带的宽度能够控制能带带隙. 石墨烯的痕量替位掺杂会打破石墨烯两个子晶格的对等性, 也能够使电子能带形成带隙. Ajeel等[20]对石墨烯纳米带进行磷掺杂研究, 证明掺杂石墨烯纳米带中的电子结构依赖于掺杂原子的几何位置. Mohammed[21]报道了在石墨烯纳米带中的替位掺杂BN, 证明碳原子排列反演对称性的破坏亦会使石墨烯形成电子带隙. 然而, 在实验中很难实现为了调控石墨烯能带及电导特性而进行的均匀周期性掺杂. 最近有文献报道了关于反点排列(antidot pattern)石墨烯纳米结构-石墨烯纳米网的最新实验和理论研究, 采用嵌段共聚物光刻方法或结合纳米印刷光刻与高分辨纳米模板绘图自组装技术能够制作出漏孔周期排列在石墨烯片层上的纳米结构[22-24]; 使用圆柱体塑造二嵌段共聚物模板也可以成功制成纳米多孔石墨烯材料[25]; 结合电子束光刻和氧气反应离子刻蚀技术能够高效地制作结构可调的石墨烯超晶格[26]. 纳米穿孔石墨烯材料石墨烯纳米网的实验研究结果证明规则图案石墨烯能够应用于纳米器件的可行性. 由石墨烯纳米网制成的具有超高开/关比的场效应管可以承载比石墨烯纳米带晶体管高一百多倍的电流, 表明石墨烯纳米网在纳米电子器件领域具有很高的潜在的应用价值[20]. 进一步探索石墨烯纳米网的用途和价值, 亟待全面理解和认识规则排列多孔反点阵对电子特性的调控作用. 实际上石墨烯纳米网可以被看作由规则排列的碳原子空位构成的石墨烯超晶格, 会使Born-von Karman边界条件发生相应的改变[27,28]. 石墨烯上的圆形空洞在实验上比较容易实现, 并且这些圆形孔形成以后制成的石墨烯纳米网仍然保持原始石墨烯的六角对称和子晶格对等性, 与一般通过打破反演对称性产生电子能带带隙的方法不同[23-26], 表明保持反演对称性的石墨烯纳米结构仍然可以形成能带带隙. 因此研究石墨烯超晶格能带带隙的产生和变化机理对于基础科学研究和实际应用都具有重要意义.
本文按照基于密度泛函理论的赝势平面波第一原理计算方法, 通过计算电子结构研究了规则网孔排列的石墨烯纳米网电导特性随超晶格对称性和磁特性的变化机理. 根据网孔之间Y形结点的结构特征和拓扑磁性将石墨烯纳米网的网孔分为三种类型. 通过能带结构对比分析石墨烯超晶格和石墨烯纳米网的电子能带在布里渊区中心点的四重简并和分裂, 考察反演对称性和超胞尺寸对形成能带带隙的作用. 本文重点研究了磁性石墨烯纳米网的反铁磁耦合和磁性网孔边缘氢钝化对狄拉克锥点产生带隙的作用机理, 揭示了石墨烯纳米网能带带隙的形成机理, 为石墨烯纳米结构的实验研究提供了理论依据.
3.1.石墨烯纳米网孔形状及磁耦合
在石墨烯碳原子平面上构建规则排列的六角形纳米孔洞形成的石墨烯纳米网结构如图1(a)所示, 由晶格矢量A和B表示的周期性重复单元为石墨烯纳米网的六角形超胞, 每个超胞包含一个六角网孔. 石墨烯纳米网还可以被看作由Y形结点连接的网络结构. 根据Y形连接结点的原子排列结构和磁矩分布将石墨烯纳米网分为三类, 如图1(b)所示, 分别用G60, G42, G84表示(石墨烯平面去除包含n个碳原子的D6h六角对称石墨烯纳米片段后构建石墨烯纳米网Gn), 其中G60不具有磁性, 而G42和G84分别产生相邻原子反铁磁耦合和相邻磁性团簇反铁磁耦合. 因此本文将此三种石墨烯纳米网的周期性有序排列网孔分别简称为非磁(non-magnetic, NM)、磁性原子(magnetic atom, MA)和磁性团簇(magnetic clusters, MC)网孔. MC石墨烯纳米网孔洞边缘上有3个相连的碳原子通过铁磁耦合形成磁性团簇, 而MA与MC网孔不同, 其磁矩局域分布在单个碳原子上.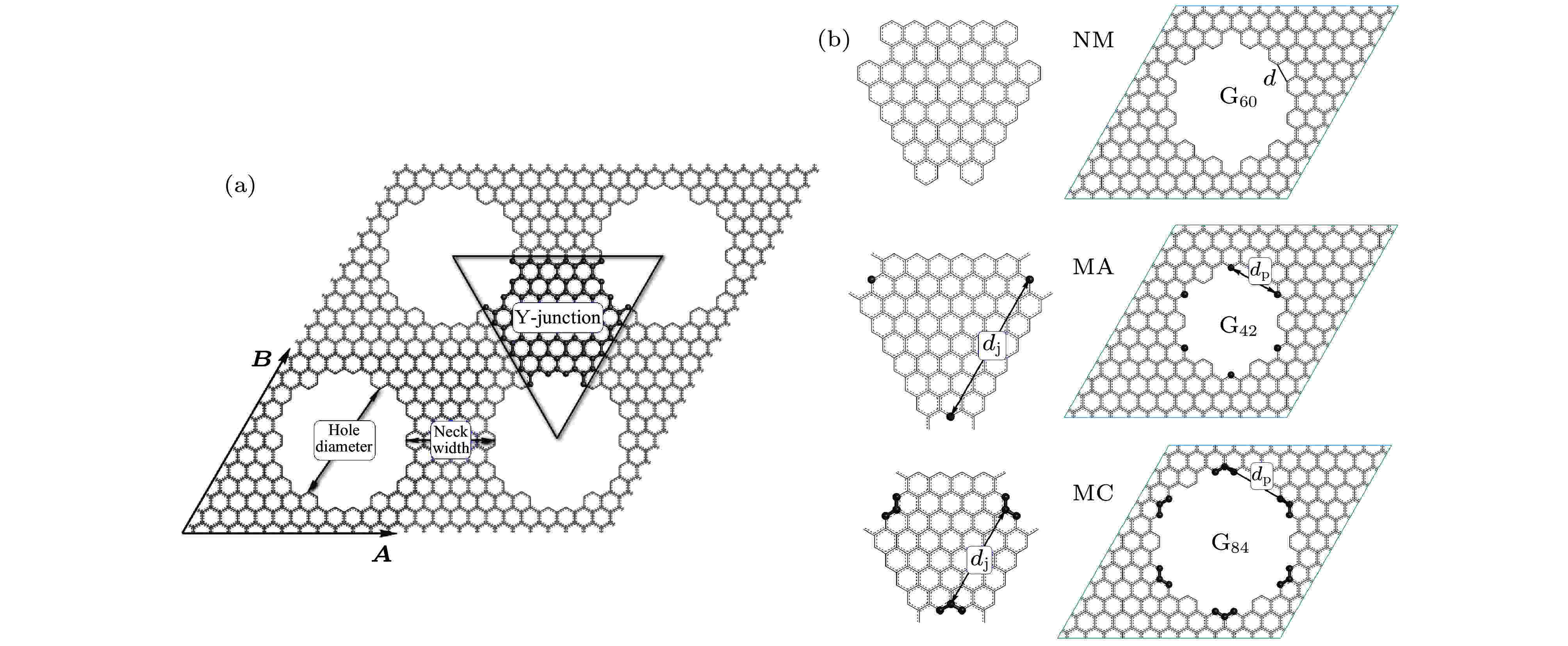
图 1 (a) 网孔周期性有序排列的石墨烯纳米网示意图; (b) 不同磁分布的三种类型石墨烯纳米网的空孔超晶格胞结构(左)和Y形结点连接部分(右), 黑色小球表示G42 (MA) 和G84 (MC) 网孔边缘上具有净自旋磁矩分布的碳原子Figure1. (a) Schematic structure of graphene nanomesh with periodically patterned holes; (b) the supperlattice cells (left) and Y-junction connection areas (right) for three types of vacant holes with different magnetic distributions, black beads represent carbon atoms distributed with net spin moment at the edge of G42 (MA) and G84 (MC) holes in graphene nanomeshes.
磁耦合强度决定于Y形结点拐角处的磁性原子(团簇)之间的距离dj以及网孔边缘上相邻两个磁性原子(团簇)之间的距离dp(图1(b)). 分别计算铁磁态与反铁磁态的MA和MC网孔石墨烯纳米网的总能量, 并对网孔和超胞尺寸对两种磁有序状态之间能量差ΔE(铁磁态能量减去反铁磁态能量)的影响进行比较分析. 由于G6(MA)网孔边缘上相邻磁性原子间距离dp = 2.8 ?较小, 所以ΔE = 480 meV相对较大; 并且除了dj特别小的石墨烯纳米网以外, G42和G84因dp较大而使ΔE明显降低. 由于MA有序网孔石墨烯纳米网结点边缘的磁性原子间距dp相对较大(G6除外), 因此dj决定了磁耦合的强度大小. Y形结点上磁性原子之间的铁磁耦合会削弱网孔边缘上相邻磁性原子之间的反铁磁耦合作用, 所以dj减小会使ΔE降低, 特别是当MA石墨烯纳米网的网孔间距较小时(dj < 7.4 ?), 甚至铁磁态比反铁磁态的能量更低. MC石墨烯纳米网网孔边缘的磁性原子团簇间能够形成较强的磁耦合作用, 因此ΔE主要决定于dp, 基本不随dj变化.
2
3.2.非磁性石墨烯纳米网
为了研究网孔周期性排列的石墨烯纳米网的电子特性, 首先以G60为例通过第一原理计算对NM石墨烯纳米网的电子结构进行分析. 为了简化描述, 本文用(M, N)来表示晶格矢量A = Ma, B = Nb (a和b分别表示石墨烯原胞的两个晶格矢量)的石墨烯纳米网超晶格. G60 (N, N)石墨烯纳米网(N = 10—20)的电子结构计算结果如图2(a)所示, 网孔中缺失碳原子使费米能级降低到了石墨烯K位置狄拉克点以下0.4—0.7 eV处, 当N = 3n (n为整数)时, 能带结构形成带隙. 在石墨烯的能带工程应用中, 一般采用打破石墨烯子晶格的对等性来产生和调节能带带隙, 而石墨烯纳米网的子晶格仍然保持对等, 虽然N ≠ 3n的石墨烯纳米网能带结构中没有开口带隙, 但N = 3n的石墨烯纳米网却形成了能带带隙, 因此石墨烯纳米网的能带带隙产生机理与通过打破晶格反演对称性来产生能带带隙的机理不同. 为了研究石墨烯纳米网能带带隙的产生原因, 对相同胞尺寸的纯石墨烯超晶格进行同样的计算并比较能带结构, 结果发现(3m,3n) (m, n为整数)的石墨烯超晶格能带结构在布里渊区中心Γ点的费米能级处产生四重简并(图3). 石 墨烯中空位原子或原子团如石墨烯纳米网的网孔使Γ点的四重简并态发生分裂, 从而形成开口带隙.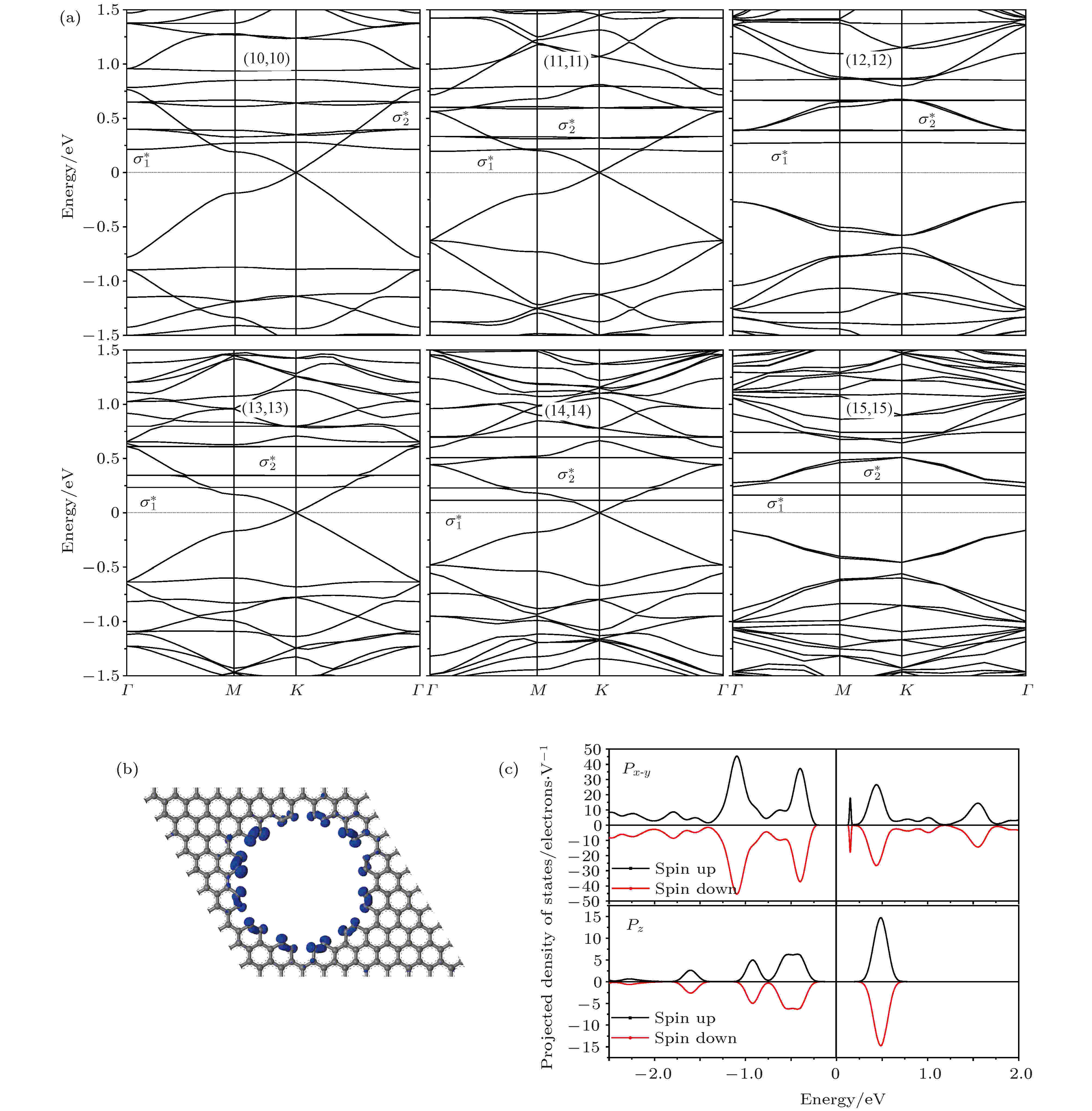
图 2 G60石墨烯纳米网的电子结构计算结果 (a)超晶格(N, N)胞尺寸N = 10 – 15的G60纳米网能带结构; (b) N = 12的G60纳米网在布里渊区K点σ*态的电子密度空间分布(电子态能量～0.2 eV); (c) N = 12网孔边缘碳原子的投影能态密度. 费米能级为参考能量零点(竖直虚线)Figure2. Calculated electronic structures of G60 patterned graphene nanomeshes: (a) Energy band structures of the G60 nanomeshes with supplattice cell (N, N) (N = 10 – 15); (b) the electron density distribution of the σ* state at K point in the energy ～0.2 eV for N = 12; (c) the projected density of states on the carbon atoms of hole edge for N = 12. The reference energy zero is set as Fermi energy level indicated with horizontal dot line.
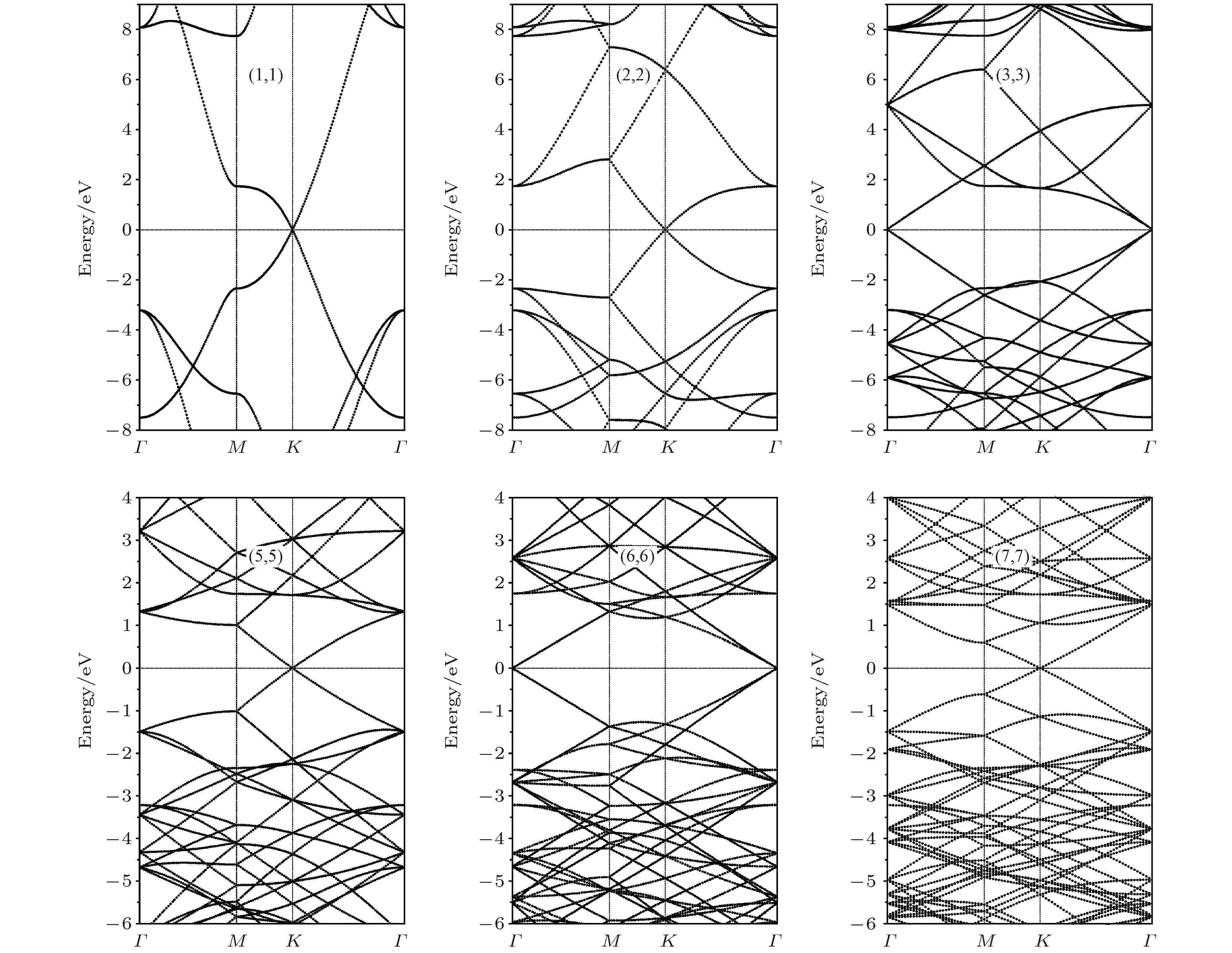图 3 石墨烯超晶格的能带结构, 超胞尺寸从(1, 1)至(7, 7), 以费米能级(垂直虚线)作为能量参考零点Figure3. The energy band structures of pristine graphene supperlattices with lattice vector extending from (1, 1) to (7, 7). Fermi energy level is referenced as energy zero indicated by horizontal dot line.
在计算的石墨烯纳米网的能带结构中都有一条几乎平行的能量色散曲线, 在图2(a)中标识为σ*态. 为了分析其属性, 在图2(b)中绘制出了G60(12, 12)纳米网的σ*态电子密度在空间的分布, 其能级为0.2—0.4 eV(以费米能级作为能量参考零点). 电子密度的空间分布表明此σ*态是网孔边缘碳-碳σ键的反键态. G60(12, 12)纳米网的网孔边缘碳原子投影能态密度计算结果如图2(c)所示, 证明σ*能带来源于网孔边缘碳原子. 石墨烯纳米网能带带隙的形成也与网孔边缘的局域应变有关, 因此需要分析网孔边缘碳-碳原子距离随纳米网超晶格胞尺寸大小的变化(图4). 石墨烯纳米网超晶格胞尺寸越大, 网孔边缘碳-碳原子间距越大, 因而来源于边缘碳-碳原子的反键态σ*能级越低; 并且当G60的超胞尺寸N = 3n (n为整数)时, 形成开口带隙, 导致σ*能级突然升高(如图4(b)所示).
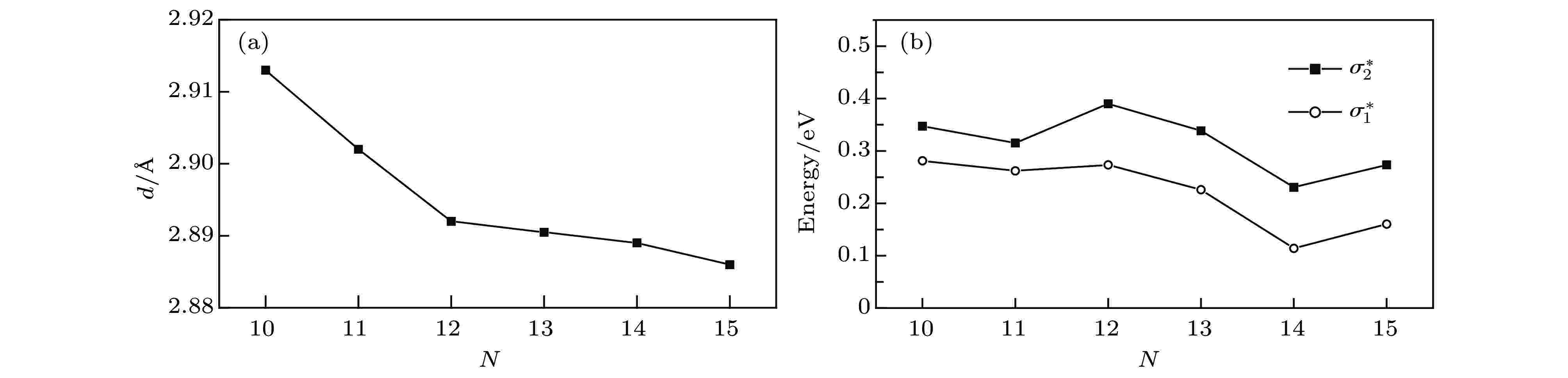图 4 G60 (N, N)石墨烯纳米网的网孔边缘碳-碳原子间距d (a)以及σ*态的K点能级(b)随超晶格胞尺寸N的变化, 费米能级作为参考能量零点Figure4. Carbon-carbon atomic distance d at hole edge (a) and energy level of the σ* state at K point (b) as a function of supperlattice cell size N for the G60 (N, N) graphene nanomeshes, with Fermi energy level referenced as energy zero.
2
3.3.磁性石墨烯纳米网
由于磁性石墨烯纳米网含有反铁磁耦合的MA或MC网孔, 对体系的整体对称性增加了一项量子条件, 也就是说, 除了原子排列对称性还要包括电子自旋形成磁有序相的对称性. 此外磁耦合也导致石墨烯纳米网的网孔边缘碳原子产生轻微的变化, 因此磁性石墨烯纳米网失去了反演对称性. 含有反铁磁耦合的MA和MC网孔的石墨烯纳米网的能带结构计算结果如图5所示, 反铁磁耦合破坏了石墨烯纳米网的反演对称性, 导致能带结构产生带隙. 为了探究磁相互作用是否也会导致能带带隙的形成, 对相应的石墨烯纳米网铁磁耦合态进行了电子结构的计算, 结果表明: (10, 10)和(11, 11)胞尺寸的石墨烯纳米网铁磁耦合态没有形成能带带隙, 因为铁磁耦合仍然使体系保持反演对称性; 而铁磁耦合态(12, 12)石墨烯纳米网的能带结构中产生了带隙, 这是由于简并微扰使四重简并态发生分裂所导致, 如图5上图所示. 铁磁耦合态(10, 10)和(11, 11)石墨烯纳米网不存在能带带隙, 证明磁相互作用不会使能带结构产生带隙. 当网孔边缘碳原子被氢钝化以后, MA和MC石墨烯纳米网转变为非磁性体, 其能带结构的计算结果如图5中下图所示: 反演对称性仍然使(10, 10)和(11, 11)石墨烯纳米网保持无带隙的金属能带结构特征, 而(12, 12)石墨烯纳米网因简并微扰在布里渊区中心Γ点产生能带带隙.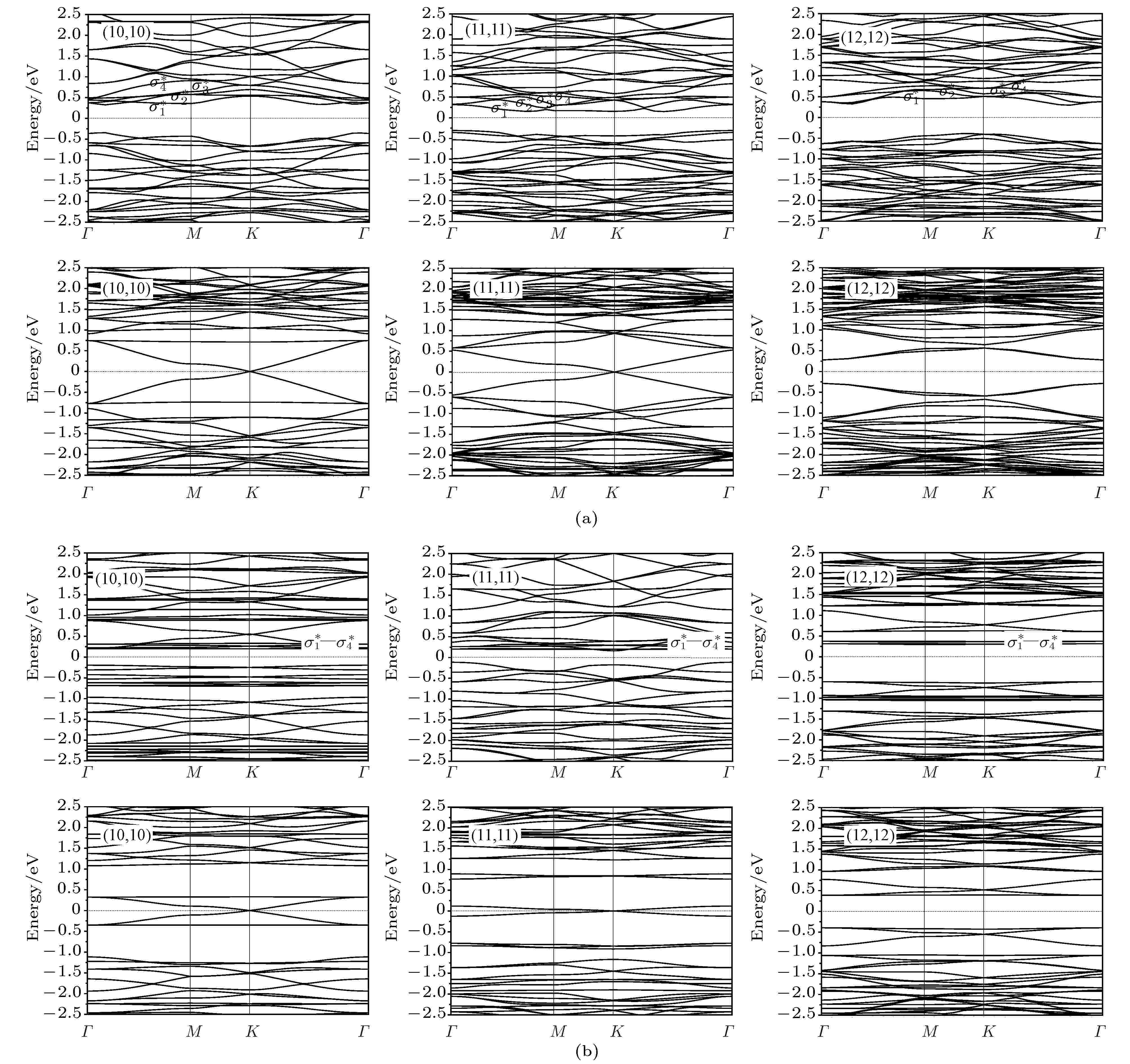
图 5 (a) MA (G42)和(b) MC (G84)型网孔石墨烯纳米网的能带结构, 上下两行能带结构图分别对应网孔边缘碳原子无氢钝化和氢钝化的石墨烯纳米网Figure5. Energy band structures of the graphene nanomeshes with (a) MA (G42) and (b) MC (G84) patterned holes, respectively. The up and down panels represent nanomeshes without and with hydrogen passivation at hole edge, respectively.
类似于非磁性石墨烯纳米网, MA和MC磁性石墨烯纳米网的能带结构中也出现了能量几乎不随波矢发生色散的σ*能级(平行能带), 但是该平行能带却由于有序的磁相互作用而出现明显的能量色散(形成较窄的导带边能带)和分裂. 如图6(a)中所示的G42石墨烯纳米网能带结构, 分裂的σ*能带分别由σ1*, σ2*, σ3*和σ4*标识. 尽管网孔结构参数dp几乎保持相同(7.18—7.23 ?), 但是(10, 10), (11, 11)和(12, 12)石墨烯纳米网的Y形交叉结点上的磁性原子(团簇)的距离dj差别很大, 分别为12.17, 14.64和17.28 ?. 网孔间隔越大(即Y形交叉结点尺寸dj越大), 各个磁性原子(团簇)在网孔交叉结点上的磁相互作用强度越小, 因而σ*能带色散有所减弱并且能带σ1*与σ2*以及σ3*与σ4*之间的分裂越小; 同时σ1*-σ2*和σ3*-σ4*两组能带之间的分裂以及能量色散程度还依赖于dp大小, 对于相同dp的石墨烯纳米网, 两组σ*能带之间的分裂带隙相同(包括非磁性石墨烯纳米网, 如图4下图对于G60的计算结果所示). G84磁性石墨烯纳米网(dp为9.9 ?)能带结构的计算结果表明: σ1*-σ2*和σ3*-σ4*两组能带之间的分裂及其能量色散随dp显著减小, 对于G84几乎可以忽略不计; 当超胞尺寸超过(12, 12)以后, σ*能级不发生能量色散且σ1*与σ2*以及σ3*与σ4*能级简并.
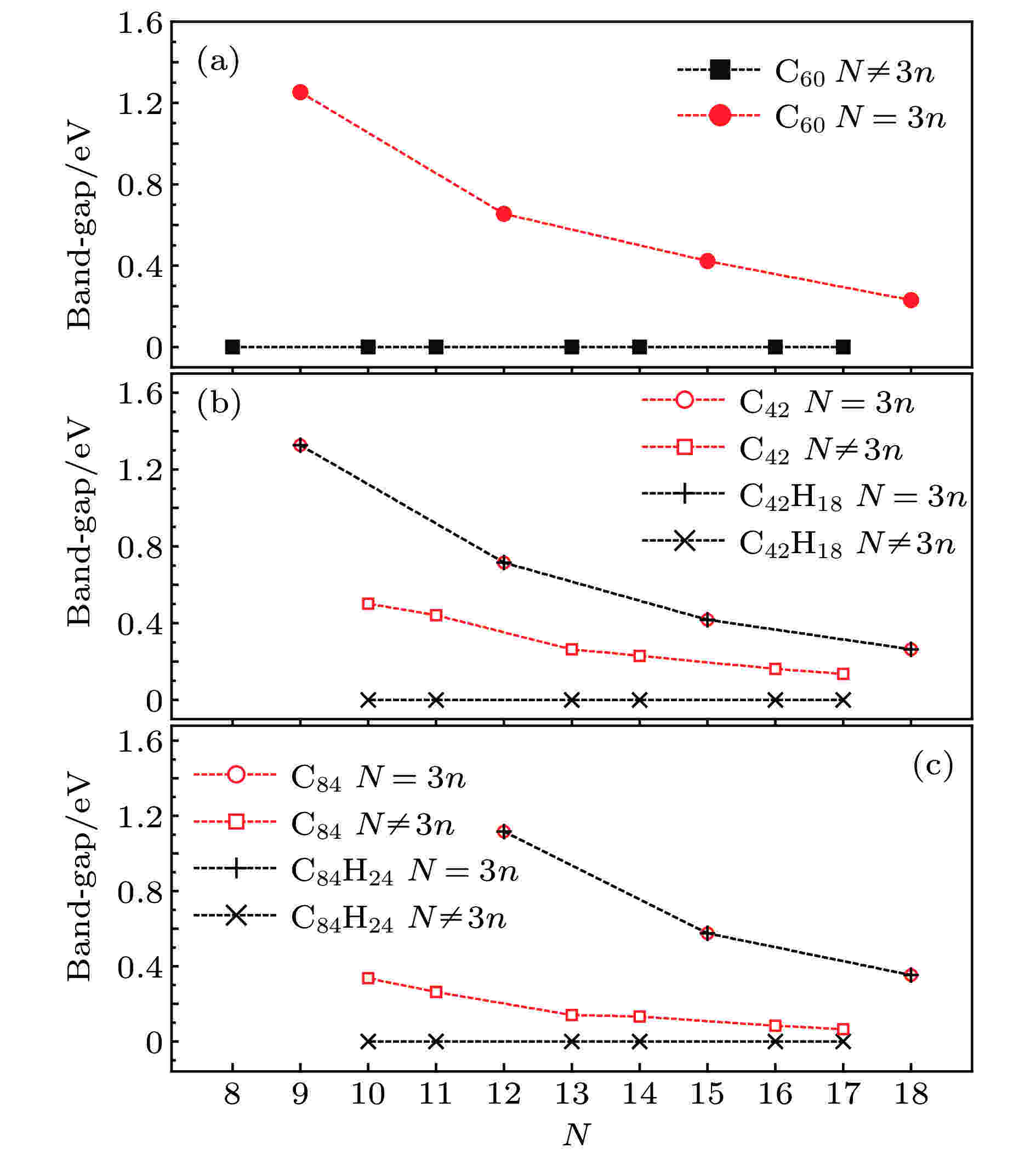图 6 (a) NM 网孔G60, (b) MA网孔G42和(c) MC网孔G84石墨烯纳米网的能带带隙随超晶格胞尺寸(N, N)的变化Figure6. Bandgap width varying with cell size (N, N) of (a) G60, (b) G42 and (c) G84 graphene nanomeshes with NM, MC and MA vacancy holes respectively.
已经报道的实验研究表明, 网孔边缘很容易被实验制备过程中存在的其它原子或功能团钝化, 如氢原子和羟基等, 故很难制备出纯的石墨烯纳米网. 因此, 本文用氢原子钝化磁性纳米网孔边缘的未饱和碳原子以后再进行同样的第一原理计算并进行比较. 在网孔边缘由氢原子钝化以后, MA和MC网孔转变为非磁性, 石墨烯纳米网也恢复了仅由超晶格原子排列决定的反演对称性. 只有(3m, 3n)(m和n都是整数)超晶格的石墨烯纳米网的能带结构中出现了带隙, 是由于在布里渊区中心Γ点费米能级处四重简并能级发生分裂, 与通过打破反演对称性来产生能带带隙的机理不同; 而其他网孔边缘氢钝化石墨烯纳米网超晶格能带结构不存在带隙, 是因为保持了反演对称性并不存在狄拉克锥点的简并分裂. 由此, 对石墨烯纳米网能带带隙形成机理有了更进一步的认识, 并证明石墨烯超晶格的能带带隙可以通过超晶格尺寸来调节, 为实验研究提供了理论依据和数据预测.
2
