摘要:具有良好可重构性、良好缺陷兼容性及紧凑型的声学拓扑结构可能成为声学发展中一个有前景的方向. 本文设计了一种可调谐、应用于空气声的二维宽带复合蜂窝形晶格结构, 其元胞拥有两个变量: 一个是中心圆的缩放参数s, 另一个是“花瓣”图案围绕其质心的旋转角度θ. 研究发现当s为1.2, θ为±33°时, 在结构的布里渊区中心点出现四重简并态. 在±33°两侧, 能带会发生反转, 体系经历拓扑相变; 同时, 结构的相对带隙宽带逐渐增加, 其中θ为0°和60°时, 相对带宽分别为0.39和0.33. 本研究还计算了由这两种转角的声子晶体组成的拼合结构的投影能带, 发现在其体带隙中存在着边界态并验证了此拓扑边界的缺陷免疫特性. 最后通过变化s, 构建了一种非周期性双狄拉克锥型的声拓扑绝缘体并验证了其缺陷免疫性. 本研究的体系相对带宽显著超过已知体系, 将为利用声拓扑边界的声波器件微型化打下良好的基础.
关键词: 拓扑相变/
宽带结构/
非周期双狄拉克锥拓扑绝缘体

English Abstract

全文HTML

--> --> -->

量子霍尔效应^[1-4]与量子自旋霍尔效应^[5-8]的发现引起了凝聚态物理研究的新高潮, 同时也将数学中的“拓扑”概念引入到物理研究当中. 2016年的诺贝尔物理学奖被授予“理论发现拓扑相变和拓扑相物质”方向^[9,10], 显示出拓扑这一概念在当今物理学中的重要性. 具有拓扑性质的材料有很多新颖的性质^[11-14], 比如边界的背散射抑制与无损传输等使得其在电子学、声学以及机械系统等领域存在巨大的应用潜力.
拓扑边界态首先发现于电子系统中, 此后通过与电子类比, ****发现此类现象也会出现于光子系统^[15-24]. 声系统属于玻色子系统, 其在本质上不同于电磁系统. 所以对于声学系统, 无法通过磁场来打破时间反演对称性. 有****通过引入旋转的气流或者引入声学赝自旋的方式来模拟声学系统中的“磁场”打破系统的对称性, 进而形成声学边界态^[25-27]. Ni等^[25]提出了一种声学拓扑结构, 它通过在设计的声环谐振器中使用循环流动的空气为声音创建有效的测量磁场, 从而实现拓扑声波晶体. Chen和Wu^[27]提出了一种正方形声子晶体, 然后同时打破结构的时间反转对称性和单位晶胞的几何尺寸形成了可以调节的拓扑能带. 也有****利用调节超耦合环的耦合强度来实现受到拓扑保护的边界态^[28-30]. Peng等^[29]利用改进性能的Floquet拓扑绝缘体实现了声波的低损耗、宽带、单向传播. 此后, Peng等^[30]通过调整波导晶格中的耦合强度来触发拓扑相变, 进而利用不同拓扑相的结构构建了受保护的边界态. 此外, 有****构造具有C_3v对称性声学系统, 从而在布里渊区的角点形成简并的狄拉克锥, 然后通过旋转散射体^[31-34]或者调整共振空腔的尺寸^[35,36], 降低结构的对称性至C₃, 发现此时狄拉克锥会打开形成带隙, 进而利用不同谷陈数的结构实现了拓扑谷边界. 也有****通过类比于电子系统中的石墨烯系统, 构造声学系统中具有C_6v对称性的二维结构, 从而在布里渊区的中心点形成四重简并的狄拉克锥, 然后改变散射体的转角、直径等方式打开简并态, 最后构建具有拓扑保护的边界^[37-43]. Zhang等^[37]在一个简单的无流动对称破碎的超材料晶格中实现了声赝自旋多极态, 通过简单地收缩或扩展超分子来调节分子间偶联的强度可以诱导赝自旋偶极子和四极子之间的带内转换效应来引发拓扑相变. Deng等^[38]增加或减少中心原子的半径, 同时保留结构整体的C_6v对称性来实现布里渊区中心点处四重简并态的打开与拓扑相变的发生. Zhang等^[39]改变结构的半径和旋转角度以实现赝自旋状态之间的频带反转. Zhang等^[40]通过将散射体从普通的三角形结构调节到“三腿”结构, 使带宽大约增加到以前的1.5倍. 接着作者利用此结构构建了宽带的声延迟线. Xia等^[41]首次提出了基于蜂窝状声子晶体可编程声拓扑绝缘体概念, 通过改变单元圆柱的直径实现了声子晶体的能带反转, 并将拓扑平庸与非平庸声子晶体分别定义为数字单元“0”和“1”. 与传统的声拓扑绝缘体不同, 通过变换可编程声拓扑绝缘体的编码, 可以灵活地实时调控拓扑绝缘体中的声传播路径. 最近, Han等^[44]构造了由两个或多个不同形状的原始单元组成的各种配置, 显示了非周期谷拓扑绝缘体的实现, 为声拓扑绝缘体的实现提供了更多的可能性. 然而现有的声学拓扑结构的相对带隙宽度还有提高的空间, 这对于设计对制造缺陷具有良好兼容性、紧凑型的声学拓扑结构比较重要; 同时也没有****研究基于蜂窝结构的, 在布里渊区中心具有四重简并态的非周期双狄拉克锥型拓扑绝缘体结构.
基于此, 本文设计了一种二维的应用于空气声的复合蜂窝形晶格结构(CHL), 其元胞具有缩放参数s (x方向扩大为原来的$\sqrt s $倍, y方向缩小为原来的$1/\sqrt s $倍)与位于晶格顶点的散射体围绕形心的转角θ两个变量. 首先研究s = 1.2、相对带宽(带隙宽度与带隙中间频率之比)为0.33的一种由不同θ的CHL拼接组成的宽带拓扑绝缘体的性质, 然后使用s为0.8, 1.0, 1.2的三种CHL构造了一个由“45 × 5”个混合声子晶体构成的非周期声拓扑绝缘体, 研究了这种混合边界的拓扑性质. 研究发现s为1.2时, 转角θ为0°与60°两种声子晶体构成的边界对直角、“Z”形角、乱序、缺失等缺陷有很好的鲁棒性; s为0.8, 1.0, 1.2的三种结构的混合边界依然是受到拓扑保护的, 入射声波能绕过乱序、缺失这些缺陷继续无反射地传播.

2

-->

2.1.体系的设计

CHL的元胞如图1(a)所示, 其最简布里渊区如图1(b)中的绿色区域Γ-M-K所示. 晶格常数a = 43 mm, 晶格基矢a₁ = ai, ${{{a}}_2} = - 1/2 ai + \sqrt 3 /2 aj$. 本文首先构建一个六角形基本结构, 然后在晶格中心取一半径r₁ = 6 mm的圆, 再将此圆进行s = 1.2的缩放, 即形成一个椭圆结构. 然后将椭圆绕着自己的中心旋转30°使得椭圆的水平轴指向六角形的一个角点b. 再将此旋转后的椭圆沿着顶点b与六角形中心o的连线移动, 移动距离为ob线段长度的0.8倍. 由于移动的距离没有达到ob的长度, 因此椭圆的中心并没有与b点重合. 再将椭圆绕着b点旋转120°, 240°, 将三个相交的椭圆组合成一个整体, 形成一个“类三角”的花瓣图形. 然后将“花瓣”绕着o点旋转到六边形的六个顶点. 然后在o点重新放置一个半径r₂ = 10 mm的圆, 即可得到本体系的晶格元胞. 此元胞“花瓣”的顶点朝向均与晶格的高对称方向重合, 结构整体具有C_6v对称性. 元胞中的“花瓣”形与位于中心的圆柱形结构使用的是硬质散射体, 其与空气的阻抗失配很大, 因此在使用有限元软件Comsol进行模拟仿真的时候可以忽略结构中剪切波的影响, 研究结构中的纵波传播特性.
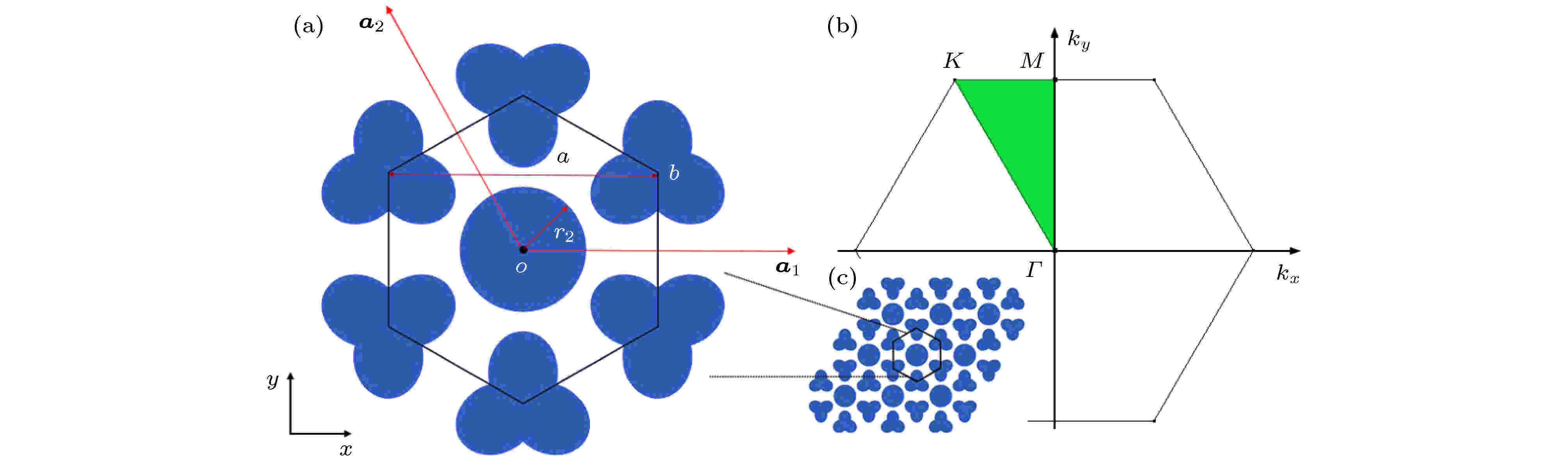图 1 (a)正六边形表示晶格的元胞, 其中a₁, a₂是晶格基矢. 在六边形顶点的蓝色“花瓣”形结构与位于中心的圆形结构表示位于空气中的硬质散射体; (b)晶格的最简布里渊区Γ-M-K; (c)晶格结构的示意图
Figure1. (a) The hexagon represents the cell of the lattice, where a₁, a₂ is the lattice basis vector, the blue “petal” shape at the apex of the hexagon and the circular structure at the center represent the hard scatterers surrounded by air; (b) the irreducible Brillouin zone Γ-M-K; (c) schematic diagram of crystal structure.

2 -->

2.2.能带反转

根据量子系统中的规则, 对于具有C_6v对称性的晶格结构, 在布里渊区的中心Γ点的本征态有2个二维不可约表示: ${E_1}$和${E_2}$. 二重简并的偶极子态, 对应于${E_1}$不可约表示, 具有奇宇称, 简称为p态, 如图2(a)中上面两个插图所示. 二重简并的四极子态, 对应于${E_2}$不可约表示, 具有偶宇称, 简称为d态, 如图2(a)中下面两个插图所示. 对于本文的声子晶体, 通过将每个“花瓣”绕着自己的中心旋转一定的角度θ, 发现在θ为±33°时Γ处的第2—5能带发生简并, 形成一个四重简并态, 即此时p态与d态形成简并. 改变θ发现p态与d态在特定角度会发生反转, 如图2(c)所示. 体系的p态与d态只是在θ为±33°时偶然地发生简并. 其他角度时p态与d态分开, 但是p态与d态仍然保持为双重简并的状态. 在0—33°(–33°—0)的范围内d态所对应的频率低(高)于p态所对应的频率. 在33°—60° (–60°—–33°)的范围内d态所对应的频率高(低)于p态所对应的频率. 也就是说体系在±33°两侧, 经历了p, d态互换的能带反转过程. 这种能带反转现象意味着拓扑相变的发生.
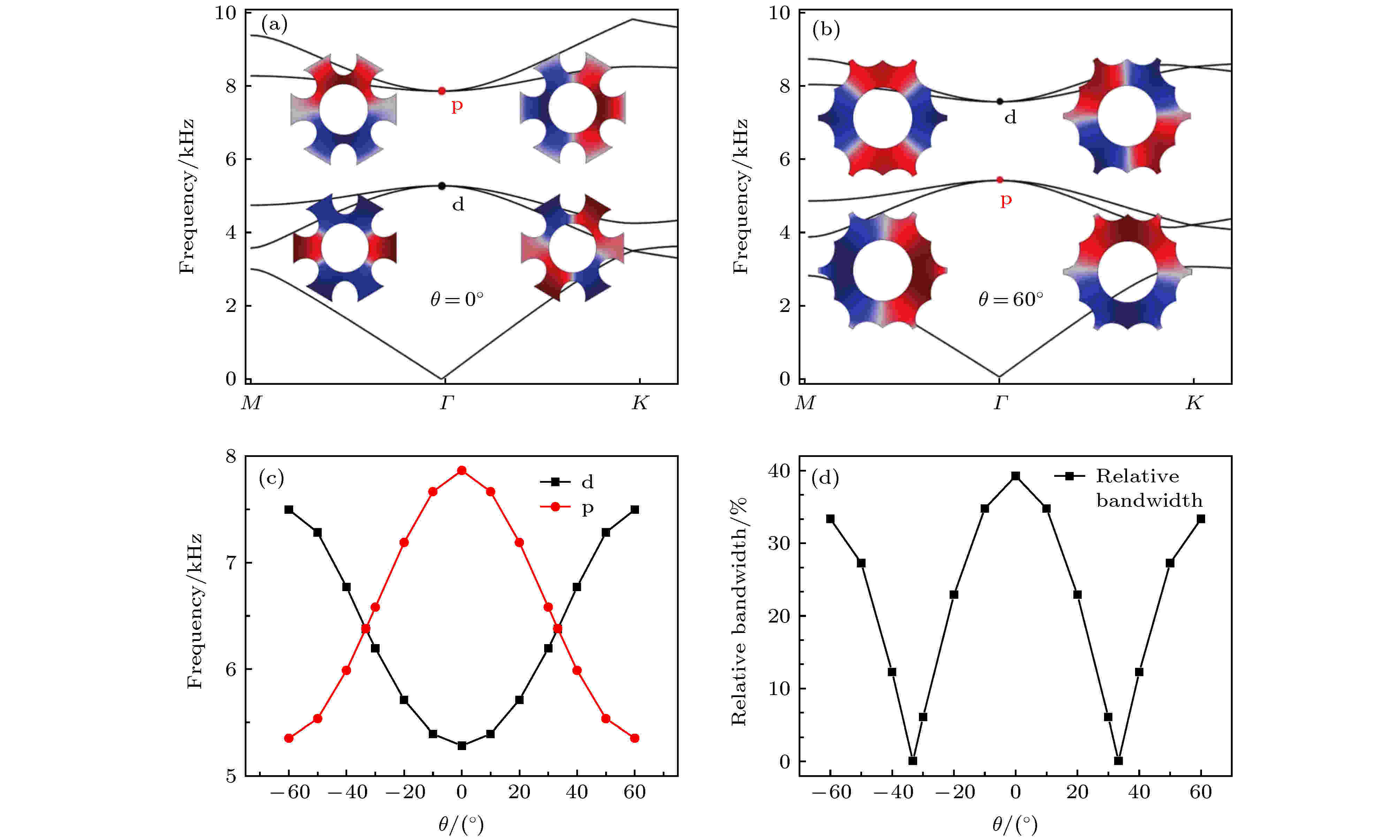图 2 CHL不同转角时的频带图与其拓扑相变　(a) θ = 0°, 其中下面两幅插图表示d态的声压场分布, 上面两幅插图表示p态的声压场分布; (b) θ = 60°, 插图表示p, d态的声压场分布; (c)结构的拓扑相图, 表示随着转角变化, 频带发生反转; (d)不同转角下带隙的相对带宽
Figure2. The band structures with different θ and its topological phase transition of the CHL: (a) θ = 0°, in which the lower two illustrations show the sound pressure field distribution of the d state, and the upper two illustrations show the sound pressure field distribution of the p state; (b) θ = 60°, in which the upper and lower illustrations show the sound pressure field distribution of the d and p states, respectively; (c) the topological phase diagram of the structure, indicating that the frequency band is reversed as the rotation angle changes; (d) the relative bandwidth of the band gap at different θ.

2 -->

2.3.宽带边界态的选择与构建

对于CHL, 当转角位于0—33°时, d态的频率位于p态的频率之下(f_d < f_p), 导致(f_d – f_p)/2 = M < 0, $C_s = \pm [{\rm sgn} (M) + {\rm sgn} (B)]/2 = \pm 1$(B来自体系有效哈密顿量的二阶微扰项的对角项, 且小于零^[42]), 属于非平庸拓扑带隙^[13]; 当转角位于33°—60°时, d态频率位于p态频率之上(f_d > f_p), 导致M > 0, C_s = 0, 属于平庸拓扑带隙. 从结构的拓扑相图图2(c)可知, 转角变化时结构的带隙宽带也在变化, 通过计算可以得到不同转角所对应的相对带宽如图2(d)所示. 其中, θ = 0°时, Γ点存在两个二重简并态, 而且在它们之间存在很宽的带隙(5284—7866 Hz), 相对带宽为39.3%. 从图2(a)的声压场分布图中可以看出, 位于较低频率处的是双重简并的d态, 较高频率的是p态, 因此这个带隙是非平庸的. 分析θ = 60°时元胞的声压场图2(b)发现, 位于较低频率处的是双重简并的p态, 较高频率的是d态, 因此这个带隙是平庸的, 其相对带宽为33.4%. 本文选择相对带宽为39.3%、θ = 60°的CHL与相对带宽为33.4%、θ = 0°的CHL两种声子晶体构成的边界进行研究.
2 -->

2.4.自旋依赖的拓扑边界态

选择θ = 60°的5层平庸型声子晶体与θ = 0°的5层非平庸型声子晶体沿着k_y方向拼接起来, 将其构成的边界称为Ⅰ型边界, 并计算了该结构沿k_x的投影带结构, 如图3(a)所示; 选择θ = 60°的10层平庸型声子晶体与θ = 0°的10层非平庸型声子晶体沿着k_x方向拼接起来, 将其构成的边界称为Ⅱ型边界, 如图3(b)所示. 从两个不同方向的投影能带图中都发现了存在于体带隙范围内的边界态, 而且从边界处的能流分布中可以发现其存在“自旋与动量锁定”的特性. 从边界态中可以看出: 1)由于边界上C_6v对称性被破坏, 导致边界态并没有完全占据体态的带隙范围, Ⅰ型边界中6278—6448 Hz范围依然存在禁带, Ⅱ型边界中6181—6612 Hz是禁带; 2)图中青色箭头大小和方向代表声波能流的大小和方向(黑色箭头是能流方向的示意图), 可以看出对于Ⅰ型边界在k_x为–0.04π/a的位置低频点处的能流是逆时针向右传播的, 高频点处的能流是顺时针向左传播的. 而其能流的方向与0.04π/a处的能流的方向刚好相反. 对于Ⅱ型边界, 在k_y为$ - 0.04{\text{π}}/\left( {a\sqrt 3 } \right)$的位置低频点处的能流是顺时针向左传播, 高频点处的能流是逆时针向右传播, 与$0.04{\text{π}}/\left( {a\sqrt 3 } \right)$处的能流的方向刚好相反. 所以, 本研究利用不同转角的CHL构造了一种类似于电子系统中QSHE的螺旋边界态. 而且, 由于此两种声子晶体具有较大的相对宽带, 所以使用较少的本体系即可观察到受到拓扑保护的边界态.
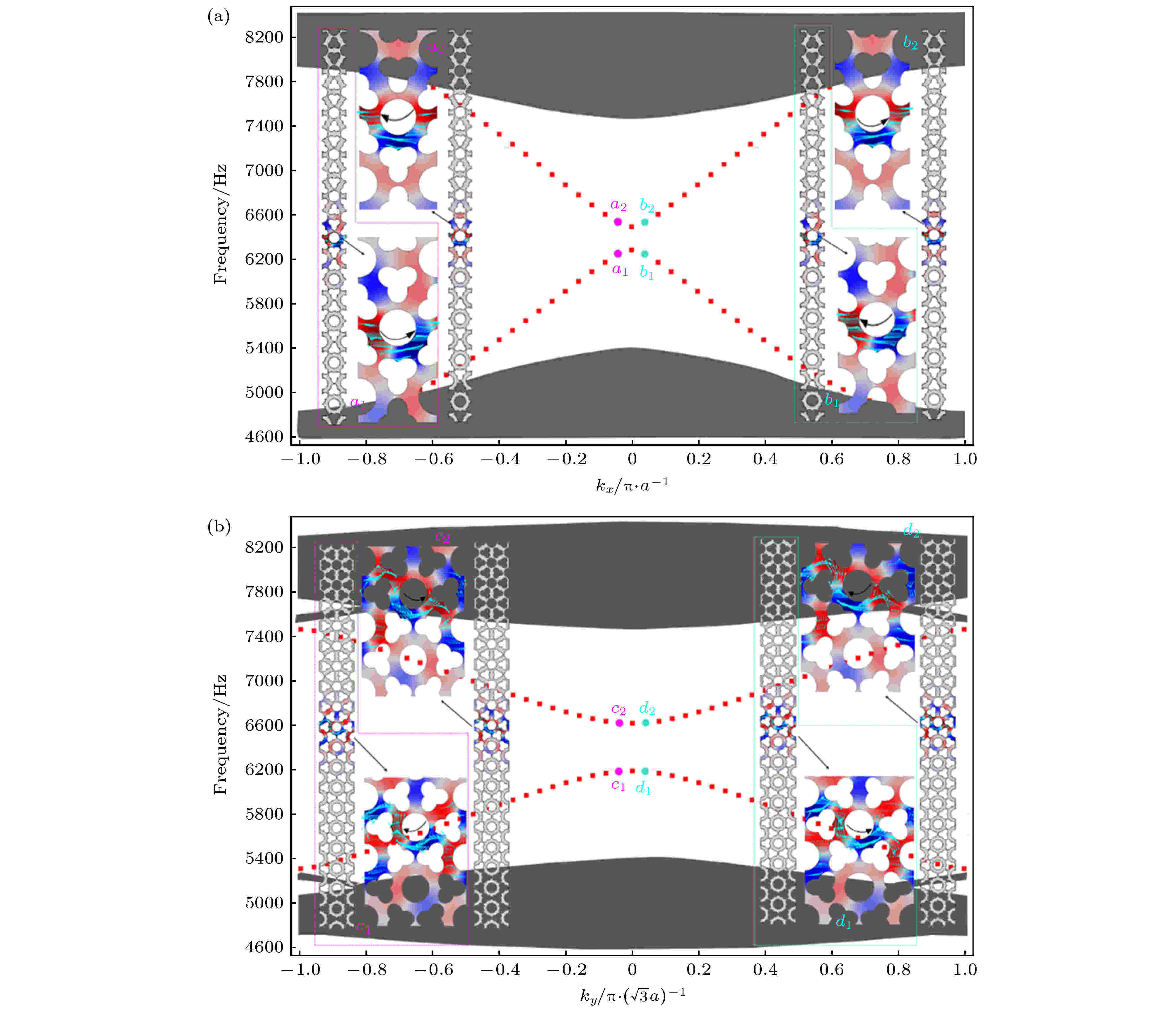图 3 (a) Ⅰ型边界沿k_x方向的投影带结构, 图中的灰色区域表示体态, 红色点线表示边界态, 两侧插图表示θ = 60°的5层平庸型声子晶体与θ = 0°的5层非平庸型声子晶体沿着k_y方向拼接起来, 构成的超胞及a₁, a₂, b₁, b₂点的声压分布; (b) Ⅱ型边界沿k_y方向的投影带结构, 两侧插图表示θ = 60°的10层平庸型声子晶体与θ = 0°的10层非平庸型声子晶体沿着k_x方向拼接起来, 构成的超胞及c₁, c₂, d₁, d₂点的声压分布, 插图中的黑色弧形箭头表示边界处的能流方向
Figure3. (a) The projection band structure of the type I edge along the k_x direction. The gray area in the figure represents the bulk state, and the red dotted line represents the edge state. The illustrations on both sides indicate that the five-layer trivial phononic crystal with θ = 60° and the five-layer nontrivial phononic crystal with θ = 0° are spliced along the k_y direction to form the supercell and the sound pressure distribution at a₁, a_2, b₁, b₂; (b) the projection band structure of the type II edge along the k_y direction. The illustrations on both sides indicate that a 10-layer trivial phononic crystal with θ = 60° and a 10-layer nontrivial phononic crystal with θ = 0° are spliced together in the k_x direction to form the supercell and the sound pressure distribution at points c_1, c₂, d₁, d₂. The black curved arrow in the illustration indicates the energy flow direction at the edge.

2 -->

2.5.拓扑边界的免疫缺陷特性

拓扑边界的一个重要特点就是其对缺陷具有免疫性. 拓扑边界对直角、“Z”形角与存在于边界的缺失、乱序等具有免疫性, 使得受到拓扑保护的边界态能绕过这些缺陷几乎没有反射地进行传播. 图4(a)模拟的是使用幅值为1、f = 6900 Hz的平面波从左侧入射到一个具有直角与Z形角的边界上的情况, 从声压分布图中发现声波能沿着θ = 60°与θ = 0°的声子晶体构成的边界顺利地传播过去. 图4(b)接着在图4(a)的传播路径上引入乱序与缺失的缺陷, 发现声波也可以绕过这这些缺陷继续向下传播. 图4(c)是对比实验, 其表示的是声波入射到单独由θ = 60°的声子晶体构成的与图4(a)、图4(b)相同大小的结构上时, 声压的分布情况. 图4(d)是图4(a)和图4(c)结构的声强透射谱. 声强的探测位置选在边界的出口附近, 如图4(b)中黄色区域内黑线(output)所示, 具体位置为灰色区域下0.081a, 宽度为1.5a. 从图4(d)可以看出: 对于图4(c)结构, 其声强透射率在体态与带隙范围相差比较大, 特别是在其带隙内声能几乎不能透过去; 在图4(a)和图4(b)中, 声波依然能够沿着边界传播到出口; 不同频率的透射声波能量略有不同. 由于图4(a)和图4(b)中的缺陷不同, 导致两者的透射率存在差异. 本文所设计的边界态是具有相对带宽33.4%的宽带结构, 所以边界态十分稳定, 能够免疫文中的那些缺陷. 这种宽带结构无论是在声波隔离还是在声波操控方面都具有很大的优势, 为实现声波的灵活控制打下了良好的基础.
图 4 幅值为1, f = 6900 Hz的平面波从左侧入时结构的声压分布及透射谱　(a)由θ = 60°与θ = 0°的声子晶体的拼接结构组成的混合声子晶体, 两种声子晶体的相接触的边界称为拓扑边界, 左侧的青色箭头表示平面波入射, 从图中声压分布可以看出: 声波能够绕过直角与Z形角沿着边界进行传播; (b)在图(a)的基础上继续引入乱序与缺失的缺陷, 声波依然能够绕过这些缺陷传播; (c)由θ = 60°声子晶体单独构成的结构, 声波不能传播; (d)图(a)—图(c)结构的声强透射谱
Figure4. The sound pressure distribution and transmission spectrum of the structure when a plane wave is incident from the left side with amplitude 1 Pa and f = 6900 Hz: (a) A mixed phononic crystal composed of a spliced structure of phononic crystals with θ = 60° and θ = 0°, and the edge between the two phononic crystals is called the topological edge. The cyan arrow on the left side indicates the plane wave incidence. It can be seen from the sound pressure distribution that the sound wave can propagate around the right angle and the Z-angle along the edge; (b) introduce disorder and cavity on the basis of Fig. (a), sound waves can still propagate around these defects; (c) a structure consisted of phononic crystals with θ = 60° alone where sound waves cannot propagate; (d) sound intensity transmission spectra of the structures of Fig. (a)—Fig. (c).

2 -->

2.6.非周期双狄拉克锥型拓扑绝缘体

保持“花瓣”形整体结构不变, 改变r₁ = 6 mm圆的缩放参数s, 并使用不同s的结构构造非周期双狄拉克锥型拓扑绝缘体. 首先研究在保持角度θ = 0°不变, s从0.7增加到1.7的情况下, 元胞布里渊区中心点Γ处d, p态的频率变化, 结果如图5(a)所示. 随着s的增加d, p态之间的带隙宽度逐渐增加, 并且没有相变发生. 此时, 计算可知, s为1.5, 1.6时, 相对带宽达到了0.52, 0.56, 超过了0.5. 然后保持s不变, 改变θ, 发现这些结构在θ为±33°两侧发生相变, 与s = 1.2时的拓扑变化相似. s = 0.8与s = 1.0的相图如图5(b)和图5(c)所示.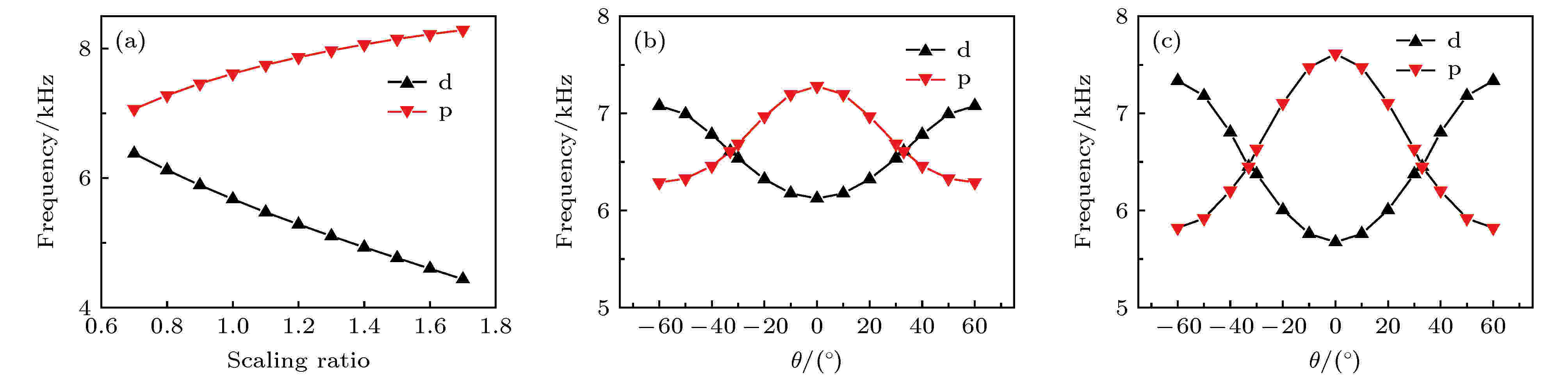
图 5 (a) Γ处d, p态对应的频率值随s的变化情况; (b) s = 0.8时结构的拓扑相图; (c) s = 1.2时结构的拓扑相图
Figure5. (a) The frequency corresponding to the d and p states with the changes of the parameter s at Γ; (b) the topological phase diagram of the structure at s = 0.8; (c) the topological phase diagram of the structure at s = 1.2.

使用s为0.8, 1.0, 1.2三种结构构造一个由“45 × 5”个混合声子晶体构成的非周期声拓扑绝缘体. 其结构如图6(a)所示, 右下角的插图表示组成, 其中A, B, C分别表示s为0.8, 1.0, 1.2三种不同的声子晶体, 数字1, 2分别代表θ为0°, 60°两种不同的转角. 研究中使用f = 6900 Hz的平面波从右侧入射, 图6(a)表示声压幅值的分布, 从图中可以看出声压主要分布在不同s参数声子晶体的水平拼接位置附近, 离开此位置声压迅速衰减, 这点从图6(b)中也能得到. 由此得出此处构造的非周期性结构能够限制特定频率的声波沿着边界传播; 图6(b)表示x = 20a处沿着y方向的声压幅值分布, 其值经过最大值归一化; 图6(c)是在图6(a)的基础上进一步引入缺失与乱序的缺陷时结构声压幅值的分布, 从中可以看出声波能够绕过缺陷继续向前传播. 在先前的工作中, 由于使用相同原始单位单元的限制, 并未实现非周期双狄拉克锥型拓扑绝缘体的构建. 本节使用不同s参数这种灵活简便、易于设计的方式实现了非周期的声拓扑绝缘体的设计, 为声拓扑绝缘体的构建提供了新颖、多变的“原材料”.
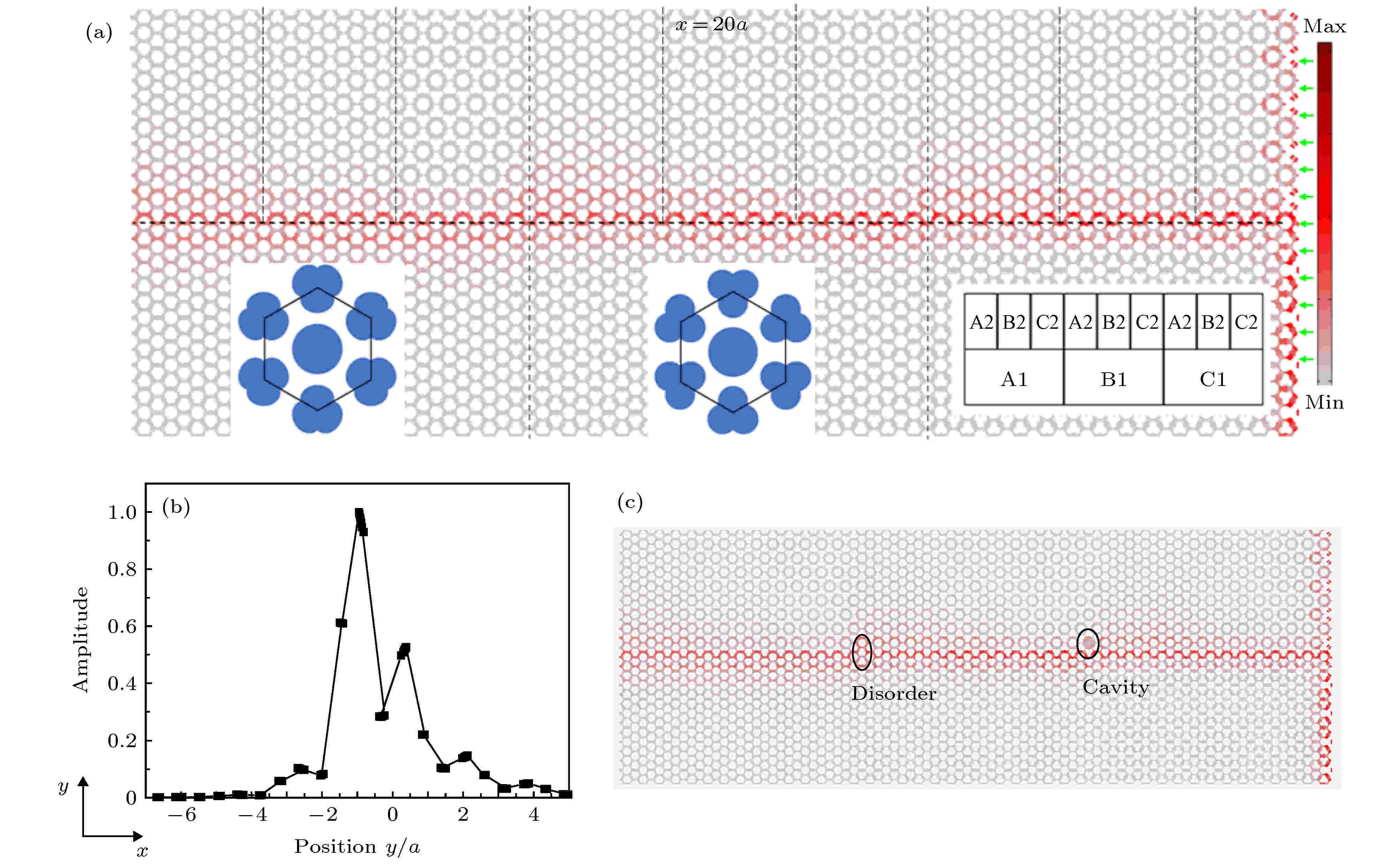图 6 非周期拓扑绝缘体结构的声压分布　(a)为由s为0.8, 1.0, 1.2三种声子晶体构造的非周期声拓扑绝缘体组成及其在右侧f = 6900 Hz声波入射下的声压幅值分布. 中间的横虚线表示水平拼接位置, 竖虚线表示竖直拼接位置, 第一、二幅插图代表θ为0°, s为0.8, 1.0时, 晶格的元胞. 三种声子晶体的具体位置如第三幅插图所示, 其中A, B, C分别表示s为0.8, 1.0, 1.2三种结构, 数字1, 2分别代表θ为0°, 60°两种不同的转角, 右侧的青色箭头代表平面波入射; (b)表示x = 20a处沿着y方向的声压幅值分布, 其值经过最大值归一化; (c)在图(a)的基础上进一步引入乱序与缺失的缺陷时结构声压幅值的分布
Figure6. Sound pressure distribution of aperiodic topological insulator structure: (a) A periodic acoustic topological insulator composed of three phononic crystal structures with s = 0.8, 1.0, and 1.2 and its sound pressure amplitude distribution when sound wave with f = 6900 Hz is incident from the right side. The horizontal dashed line in the middle indicates the horizontal stitching position, and the vertical dashed line indicates the vertical stitching position. The first and second insets represent the lattice cells with θ = 0° and s of 0.8 and 1.0, respectively. The specific positions of the three phononic crystals are shown in the third illustration, where A, B, and C respectively represent s = 0.8, 1.0, and 1.2, and the numbers 1 and 2 represent θ = 0° and 60°, respectively. The cyan arrow on the right indicates the incident plane wave; (b) the sound pressure amplitude distribution along the y direction at x = 20a, and its value is normalized by the maximum value; (c) the distribution of the sound pressure amplitude when introducing disorder and cavity on the basis of Fig. (a).

设计了可以应用于空气声的复合、宽带蜂窝形周期声拓扑绝缘体及非周期双狄拉克锥型拓扑绝缘体. 此结构可以调节的参数为半径r₁ = 6 mm的圆的缩放参数s与位于六边形顶点的散射体的转角θ. 首先固定s为1.2, 改变散射体的旋转角度θ进行研究. 通过计算发现θ为±33°时, 在结构的最简布里渊区中心点Γ点出现四重简并态; 在此θ两侧, 能带会发生p, d态的反转, 体系经历拓扑相变. 研究发现体系的相对带宽在±33°两侧从0逐渐增大, 其中θ为0°与60°时, 相对带宽分别为0.39与0.33. 接着使用θ为0°的非平庸型声子晶体与60°的平庸型声子晶体构建了两种边界, 并计算了它们的投影带结构. 研究发现在体带隙的频率范围内存在自旋-动量锁定的单向传输边界态, 而且此种边界具有对直角、乱序、缺失等缺陷的鲁棒性. 接着本文改变s, 发现元胞布里渊区中心点Γ处d, p态的频率随着s的增大逐渐增加, s增加到1.5时带宽达到了0.52. 接着使用s为0.8, 1.0, 1.2三种结构构造了一个由“45 × 5”个混合声子晶体构成的非周期双狄拉克锥型拓扑绝缘体, 并发现其对乱序、缺失具有免疫性. 综上所述, 本文在仿真时使用的是相对于空气声的硬质散射体, 其与空气具有较大的阻抗失配, 所以在选材方面比较宽泛. 同时本体系具有宽带、结构简单、易于设计的优点, 使用较少的CHL即可观察到受到拓扑保护的边界态, 为利用声拓扑边界的声波器件的小型化提供了一种方便、灵活的选择.