摘要: 从微观角度上讲, 单个极端异常波事件可视为可积模型方程的时空局域有理函数解. 本文主要讨论了三类典型的可积谐振相互作用模型(即长波短波谐振方程, 三波谐振相互作用方程, 非线性薛定谔和麦克斯韦-布洛赫方程)的基阶Peregrine异常波解及其相关研究进展; 明确指出了这些基阶异常波解形式具有普适性, 可推广应用到多分量或更高阶的可积模型中; 借助数值模拟, 还展示了共存异常波、互补异常波、以及自感应透明Peregrine孤子等新颖动力学.
关键词: 异常波 /
长波短波谐振 /
三波谐振相互作用 /
麦克斯韦–布洛赫方程 English Abstract Recent developments of extreme wave events in integrable resonant systems Pan Chang-Chang 1 ,Baronio Fabio 2 ,Chen Shi-Hua 1 1.School of Physics, Southeast University, Nanjing 211189, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11474051, 11974075)Received Date: 19 August 2019Accepted Date: 28 October 2019Available Online: 05 December 2019Published Online: 05 January 2020Abstract: From a microscopic perspective, the single extreme rogue wave event can be thought of as the spatiotemporally localized rational solutions of the underlying integrable model. A typical example is the fundamental Peregrine rogue wave, who in general entails a three-fold peak amplitude, while making its peak position arbitrary on a finite continuous-wave background. This kind of bizarre wave structure agrees well with the fleeting nature of realistic rogue waves and has been confirmed experimentally, first in nonlinear fibers, then in water wave tanks and plasmas, and recently in an irregular oceanic sea state. In this review, with a brief overview of the current state of the art of the concepts, methods, and research trends related to rogue wave events, we mainly discuss the fundamental Peregrine rogue wave solutions as well as their recent progress, intended for three typical integrable models, namely, the long-wave short-wave resonant equation, the three-wave resonant interaction equation, and the nonlinear Schr?dinger and Maxwell–Bloch equation. Basically, while the first two models can describe the resonant interaction among optical waves, the latter governs the interaction between the optical waves and the resonant medium. For each integrable model, we present explicitly its Lax pair, Darboux transformation formulas, and fundamental Peregrine rogue wave solutions, in a self-consistent way. We confirm by convincing examples that these fundamental rogue wave solutions exhibit universality and can be applied to the multi-component or the higher-order versions of the current integrable models. By means of numerical simulations, we demonstrate as well several novel rogue wave dynamics such as coexisting rogue waves, complementary rogue waves, and Peregrine solitons of self-induced transparency.Keywords: rogue wave /long-wave short-wave resonance /three-wave resonant interaction /Maxwell–Bloch equation 全文HTML --> --> --> 1.引 言 疯狗浪(rogue wave, RW), 又称畸波(freak wave)、怪波(monster wave)、极端波(extreme wave)、异常波(abnormal wave)、杀人波(killer wave)、水墙(walls of water)等, 最初专指海洋上发生的一类稀有的且破坏力极大的暂态巨浪事件[1 -3 ] . 它不期而至出现在某个地方, 掀起滔天巨浪, 然后消失得无影无踪, 因此获得了“深海怪兽”的绰号(the real monsters of the deep)[4 ] . 二三十年前, 这种神秘的疯狗浪事件还只是老水手之间的传说. 现在, 实时的卫星观测, 辅以先进的理论和实验研究, 已经确切证实了这种怪浪真的存在, 而且经常发生. 最为典型的例子是1995年元旦在北海德劳普纳(Draupner)海上平台检测到的时称“万年一遇”巨浪, 后来称之为“新年浪”, 其掀起的水墙就有26 m之高[1 ] .[3 ,5 -7 ] , 即使在称呼上, 也是五花八门. 鉴于此类极端波事件研究已扩展至多个学科, 如非线性光学[8 ] 、流体动力学[9 ] 、等离子体物理[10 ,11 ] 、声学[12 ] 、玻色-爱因斯坦凝聚[13 -16 ] 、甚至金融学[17 ] , 再沿用“疯狗浪”的称呼将变得不合时宜. 因此, 本文将采用更中性的术语“异常波”(RW)来统称这类极端波事件.[5 ] , 其中包括: 1)具有巨大的峰振幅, 通常是有效波高的2倍以上(在海洋学里面, 有效波高是指某片海域内最高的三分之一海浪的平均高度)[9 ,18 ] ; 2)不可预测性, 从某种意义讲, 异常波似乎来无影去无踪[19 ] ; 3)具有L型的波振幅统计规律, 即异常波的出现概率比常规高斯或瑞利统计所预测的要更频繁[20 ,21 ] . 上述三个基本特征目前已广泛用于异常波现象的学术定义、分析和讨论. 这也决定了异常波的科学研究存在“微观”和“宏观”两种方式.[9 ,22 ,23 ] . 特别地, 一个偏微分方程的解具有如下特征时可以视为基阶(或一阶)异常波[23 ,24 ] : 1)该解的模可用有理函数来表示, 且在时间和空间上都是局域的; 2)该解在时空上通常表现为一个3倍背景振幅的波峰, 并伴有两个侧洞形成. 典型的例子就是Peregrine孤子, 其由Peregrine教授[25 ] 于1983年首次提出, 当时作为标准非线性薛定谔(nonlinear Schr?dinger, NLS)方程的基阶有理函数解. 由于该概念能很好地解释实验上观测到的单个极端波事件, 因此Peregrine孤子被普遍认为是最简单的异常波原型[26 ] , 并相继在非线性光纤[27 ] 、水波池[18 ] 、等离子体[28 ] 以及不规则的海洋波态[29 ] 中观测到. 但另一方面, 在很多情形下, 各种色散波会相互作用, 产生极端复杂的湍流行为, 继而产生异常波[30 ,31 ] . 很自然, 由于湍流背景涉及大量的自由度, 这时人们需要用统计(即宏观)的方法来研究其中的异常波行为[32 ] . 在探索极端波事件本质特征上, 这两种研究方式相辅相成, 相得益彰[8 ,9 ] .[23 ] , 而不仅仅是简单的NLS方程. 下面列举几个光学方面的理由. 首先, 在很多光学晶体中, 主导非线性效应的是二次非线性系数, 而不是三次(或Kerr)非线性项 [33 ,34 ] . 其次, 对于飞秒激光脉冲, 基本方程模型还必须考虑进高阶色散和高阶非线性项, 以便能更准确地描述其传播动力学[35 ] . 对于色散管理或非线性管理光学系统(如色散渐减光纤), 人们还需要考虑变系数非线性模型[36 ,37 ] . 此外, 相互作用光场的矢量特性与传播介质的多维度特性也要求我们考虑一些耦合的或者高维的数学模型, 例如, 当考虑双折射光纤的脉冲传播[38 ,39 ] 或者光学晶体的光波相互作用[40 ] 时. 最后, 对于一些耗散系统如锁模光纤激光器[41 ,42 ] , 还需要额外考虑进耗散项(如增益[43 ] ), 尽管此时该模型方程(通常为复数Ginzburg-Landau方程[44 ,45 ] )将不再可积. 所有这些现实要求造就了众多的可积(或近可积)数学模型, 并持续推动理论工作者从事此类模型的求解工作[46 -49 ] .[23 ] , Kadomtsev-Petviashvili II 方程[50 ] 等)外. 这其中比较著名的可积模型包含有NLS方程[51 ] 、Hirota方程[52 ] 、Sasa-Satsuma方程[53 ,54 ] 、Chen-Lee-Liu方程[55 ,56 ] 、Fokas-Lenells方程[57 -59 ] 、复数modified KdV方程[60 -62 ] 、广义NLS方程[63 -66 ] 等, 它们的基阶和高阶异常波解均已获得. 相应地, 耦合或矢量可积模型也得到了广泛的关注, 如Manakov系统[67 -69 ] 及其推广[70 -72 ] 、Davey-Stewartson方程[73 ,74 ] 等. 数学上, 对于可积模型而言, 这些异常波解可以借助逆散射变换[75 ] 、达布(Darboux)变换[76 ] 、Hirota双线性方法[77 ] 、Riemann-Hilbert方法[78 ,79 ] 、或同宿波尝试法(homoclinic test method)[80 ] 来求解得到. 至于非可积模型, 人们可以用微扰论[81 ,82 ] 或者变分法[83 ] 来近似求解.[84 ,85 ] . 特别是最近几年, 各种异常波新现象、新特性被预测或观测到. 例如, 继2016年观测到光学暗异常波后[86 ] , Baronio等[87 ] 又成功在通信光纤上观测到了暗三姊妹异常波, 其演化动力学与Chen等[38 ] 在2014年所做的解析预测完全一致. 2017年, Peregrine孤子的普适性得到了实验验证[88 ] , 次年, 周期背景Peregrine孤子[89 ] 以及反常Peregrine孤子[90 ] 等概念又相继提出. 此外, 在异常波机制阐释上, 调制不稳定性(modulation instability, MI)和可积湍流是两个长期存在的话题, 得到了持续的关注[8 ,91 ] . 值得一提的是, 2016年Soto-Crespo等[32 ] 揭示了孤子湍流在异常波产生上扮演了一个常被忽视的重要角色. 所有这些新发现均加深了人们对异常波本质的理解.[92 ] , 三波谐振相互作用(three-wave resonant interaction, TWRI)方程[40 ,93 ] , 和非线性薛定谔和麦克斯韦-布洛赫(NLS and Maxwell-Bloch, NLS-MB)方程[94 ,95 ] . 前两个可积模型可描述光波之间的谐振相互作用, 后一个模型则描述光波与谐振介质之间的相互作用. 对于每一个可积谐振系统, 文中将给出其Lax对、达布变换、基阶Peregrine RW解, 以及数值模拟验证, 并展示其新颖的异常波动力学. 当然, 还有其他可积谐振方程, 如AB模型[96 ] 、MTM(massive Thirring model)方程[97 ,98 ] 等, 它们也存在异常波解, 但由于篇幅关系, 这里不一一叙述.1 节为引言部分, 给出了异常波的背景知识和最新研究动态. 第2 节讨论了LWSW方程的基阶异常波解, 数值展示了共存异常波概念. 第3 节讨论了TWRI方程的基阶异常波解, 分析了互补型异常波的动力学. 第4 节讨论了NLS-MB方程的基阶异常波解, 演示了自感应透明的光学Peregrine孤子和时空互补的物质波异常波动力学. 第5 节为全文总结.2.长波短波谐振系统 在耦合波动力学中, 长波短波(LWSW)谐振是一个典型的参量谐振过程, 通常发生于高频短波的群速度与低频长波的相速度匹配之时. 早在1972年, Zakharov[99 ] 在研究等离子体物理中的非线性朗缪尔波坍缩时就引入了LWSW谐振机制 , 五年后, Benney[100 ] 给出了LWSW相互作用方程. 作为一个重要的物理机制, LWSW谐振现象迅速在物理的各个分支得到了广泛的研究, 如流体动力学中重力波与毛细波之间的相互作用[101 ] , 负折射率光学介质中的简并基频波与差频波的三波混频过程[102 ] 等. 特别地, 2010年, Shats等[103 ] 在实验上直接观测到了毛细波异常波事件, 这一事实推动了人们对LWSW谐振介质中各类异常波事件的研究[104 ,105 ] .[102 ] $ u(z, t) $ 和$ \phi(z, t) $ 分别表示短波和长波分量, z 和t 为空间和时间变量, 下标则表示偏导数. 该可积方程可等价转变为一个$ 3\times3 $ 线性本征值问题:$ \lambda $ 为任意谱参数, ${{{U}}_{\rm{0}}} = {\rm{diag}}({\rm{2}}{\rm i}, {\rm{0}}, {\rm{ - 2}}{\rm i})$ , ${{{V}}_{\rm{0}}} = $ ${\rm{diag}}({\rm{ - 2}}{\rm i}{\rm{/3}}, {\rm{4}}{\rm i}{\rm{/3}}, {\rm{ - 2}}{\rm i}{\rm{/3}})$ ,$ (z, t) $ 变量已省略掉. 据此可以构造出正确的达布变换式[106 ] :$ (u_{0}, \; \phi_{0}) $ 和$ (u, \; \phi) $ 分别表示方程(1 )的种子解和新解, $ \rm{Im} $ 表示取虚部,$ \lambda $ 为某个给定的谱参数值, ${\sigma _1}$ 为第一个泡利算符的$ 3\times3 $ 版形式, 星号*表示复共轭, 剑号$ \dagger $ 表示复共轭转置. 这里已经假设$ s(-\lambda) = s(\lambda) $ 和$ w(-\lambda) = w(\lambda) $ , 但$ r(-\lambda) = r(\lambda)+ $ $2\lambda w(\lambda) $ . 因此, 容易发现, $ \alpha $ , $ \beta $ 和$ \gamma $ 满足$ \alpha+\beta = \gamma+\beta^{*} $ 和$ \lambda(\alpha-\beta^{*})+\lambda^{*}(\alpha+\beta) = 0 $ [106 ] .2 )式以及达布变换(3 )式和(4 )式, 人们可以求出LWSW方程(1 )的各类RW解. 具体推导过程可参看文献[92 ,106 ,107 ]. 这里仅提供其基阶RW解, 如下:$ u_{0}(z, t) = a\exp\left({\rm i}\omega t-{\rm i}k z\right) $ 为初始的平面波解, $ k =\omega^{2}/2-b $ 为其色散关系式, 实数b 为长波分量的背景高度(通常可设其值为0). 这里实数m 和n 由下面两个代数方程确定:5 )式和(6 )式展示了丰富的异常波动力学, 如黑异常波[92 ,107 ] (注: 所谓“黑异常波”是指振幅中心下陷至零的一类有限背景双局域波包结构). 特别地, 在文献[92 ]中, 作者借助解析预测和数值模拟, 分析了LWSW模型背景场的调制不稳定性(MI), 指出了上述基阶RW波的参数存在区间, 即$ \omega\leqslant3\omega_n/2 =3(2 a^2)^{1/3} /2$ , 其恰好位于MI图的基带(baseband)区, 参看文献[92 ]图5. 此后, Baronio等[68 ,108 ] 明确提出了MI的基带理论, 即异常波只能存在于MI的基带区, 而不是通频带(passband)区. 现在已证明, 这一理论可用于解析确定可积甚至非可积非线性系统的异常波解参数存在区间[23 ] .5 )式和(6 )式是可以推广到多分量LWSW方程中去的. 例如, 对于两短波分量LWSW方程[109 ] :u 和$ \phi $ 分量依然用(5 )式和(6 )式来表示, v 短波分量可类似表示为$ v_{0}(z, t) = A\exp\left({\rm i}\varOmega t-{\rm i}K z\right) $ 表示v 分量的初始平面波解 (相应色散关系为$K = \varOmega^{2}/2-b $ ). 同时, 确定实数m 和n 的两个代数方程变为:v 场消失时(即$ A = 0 $ ), 两短波分量LWSW方程(9 )约化为基本LWSW方程(1 ). 相应地, 其基阶解将变回(5 )式和(6 )式的形式, 同时代数方程(11 )和(12 )也变回方程(7 )和(8 )的形式.$ a = A = 1 $ , $ \omega = 0 $ , 和$ \varOmega \!=\! -1.2469 $ 时, 方程(11 )和(12 )将给出两组有效值$ (m, n) \!=\! (-1.3514, 0.7803) $ 和(–0.4287,0.6442). 很显然, 把每组$ (m, n) $ 值代入(5 )式, (6 )式和(10 )式中将得到基于相同背景参数的两种基阶RW解. 图1 左列和中列给出了这两类RW解在初始白噪声微扰情况下的数值模拟结果. 很显然, 在足够的距离里, 它们各自均能完美展开, 尽管这时候MI已然发挥作用.图 1 数值模拟验证初始白噪声微扰下的基阶RW解(5 )式, (6 )式和 (10 )式的稳定性, 左列图对应$(m, n) =(-1.3514, ~0.7803)$ , 中列图对应$(m, n) =(- 0.4287, ~0.6442)$ . 右列图显示这两类RW结构在同一背景场中的数值激发. 图改编自文献[109 ]Figure1. Simulations confirm the stability of the fundamental RW solutions (5 ), (6 ), and (10 ) against initial white noise perturbations. Left column: $(m, n) =(-1.3514, ~0.7803)$ ; Middle column: $(m, n) =(- 0.4287, ~0.6442)$ . The right column shows the numerical excitation of such two rogue wave families from the same background field. Figure adapted from Ref. [109 ].[109 ] 做了广泛的数值激发实验. 具体上, 选取$ z = 0 $ 的平面波解作为u 和v 的初始条件, 并令$ \phi = 0.4\cos(2{\text{π}} t/40)\times $ ${\rm sech}[(t-2)/8] $ , 然后利用分步傅里叶算法数值积分模型方程(9 ), 计算结果如图1 右列所示(图中已去掉前五个单位距离的波演化轮廓图, 因为初始阶段MI引起的波结构不是很明显). 可以清晰地看到, 在$ z = 10 $ 附近, 同一背景中同时出现了两种明显不同的异常波结构, 它们均和方程(9 )的解析解完全一致. 随后, 由于MI不断增强, 背景场中将出现多异常波动力学, 但所有这些动力学都是上述两种异常波类型的组合.3.三波谐振相互作用系统 众所周知, 三波谐振相互作用(TWRI)在非线性科学中扮演着重要的角色[110 ] . 例如, 在非线性光学中, TWRI可描述不同的光学过程, 如参量放大[111 ] 、频率转换[112 ] 、受激拉曼散射[113 ] 、受激发布里渊散射[114 ] 等. 此外, TWRI还可用来实现光脉冲的群速度控制[115 ] 、超短脉冲列产生[116 ] 、参量三波孤子产生[117 ] 以及激光-等离子体相互作用[118 ] 等. 早在20世纪70年代, 人们就建立了TWRI控制方程的可积性, 并给出了其孤子解[110 ] . 不同于大家所熟悉的二次孤子情形[119 ] , 此类相干孤子主要产生于由非线性效应引起的能量交换与由群速度不匹配所引起的对流之间的平衡[40 ] . 它们最终能以一个共同的(锁定的)速度传播, 尽管其三个波分量在相互捕获之前的群速度可以互不相同[120 ] . 这种特性使得这类TWRI孤子在应用中相当诱人, 这是因为由群速度不匹配而引起的走散效应(walk-off)此时能被非线性耦合抵消掉.[110 ] :$ u_{1, 2, 3}(z, t) $ 是三个光场的慢变复包络函数, $ V_{1, 2, 3} $ 为其相应的群速度常数. 下面不妨假定$ V_{3} = 0 $ , 此即意味着模型(13 )是建立在随$ u_{3} $ 场运动的参照系上. 一般地, 当$ V_1>V_2 $ 时, 该TWRI模型将允许孤子交换(soliton exchange)动力学(在非线性光学语境中, 又称为参量三波混频过程)得以存在, 但当$ V_1<V_2 $ 时, 其将展示有趣的受激背散射(stimulated backscattering)动力学[110 ] .[110 ] , 因此具有下面的Lax对形式:$ \lambda $ 为任意谱参数, ${{{U}}_{\rm{0}}} = {\rm{diag}}({\rm{ - 2}}{\rm i, i, i})$ , $ {{{V}}_{\rm{0}}} = $ ${\rm{diag}}({\rm{0}}, {\rm{1/}}{V_{\rm{1}}}, {\rm{1/}}{V_{\rm{2}}})$ ,[121 ] :$ u_{n0} $ 和${u_n}\left( {n = 1, 2, 3} \right)$ 分别表示方程(13 )的种子解和新解, $ \lambda $ 为某个任意给定的谱参数值, $ \sigma_{3} = \mathrm{diag}(1, \varGamma_1, \varGamma_2) $ , ${\varGamma _j} = {V_j}/({V_1} - {V_2})\left( {j = 1, 2} \right)$ .$ k_{1} = \dfrac{\omega_{1}}{V_{1}}+\dfrac{a_{2}^{2}}{\delta V_{1}} $ , $ k_{2} = \dfrac{\omega_{2}}{V_{2}}+\dfrac{a_{1}^{2}}{\delta V_{2}} $ , $ a_{3} = \dfrac{a_{1}a_{2}}{\delta} $ . 这里$ a_{1, 2, 3} $ 表示三波各自的背景高度, $ \delta = \omega_{1}-\omega_{2} $ (不失一般性, 下面假设$ \delta>0 $ ).14 )式和达布变换(15 )式, 很容易得到TWRI方程的基阶RW解[93 ] (借助达布变换求解基阶或高阶异常波解的详细过程可参看我们近期发表的论文[64 ,67 ,72 ]):$ \xi = t+\dfrac{z}{V_{1}-V_{2}}\left (\dfrac{a_{1}^{2}}{\alpha_{1}^{2}}+\dfrac{a_{2}^{2}}{\alpha_{2}^{2}}\right) $ , $ \alpha_{j} = \mu_{0}+\lambda_{0}- $ $(-1)^{j}\delta/2 $ , ${\theta _j} = \xi -{\rm i}/{\alpha _j}\left( {j = 1, 2} \right)$ . 这里, $ \mu_{0} $ 是立方代数方程$ \mu^3-3\sigma\mu+2\rho = 0 $ 的一个等根(可实可复), $ \lambda_{0} $ 是等根判别式$ \varDelta = \sigma^{3}-\rho^{2} = 0 $ 的一个复根(虚部不为0), 式中$ \sigma \!=\! \lambda_{0}^2+\delta^{2}/12\!+\!\dfrac{1}{3}( \varGamma_{1}a_{1}^{2}\!+\!\varGamma_{2}a_{2}^{2}) $ , $ \rho = \dfrac{1}{4}[\delta^{2}-2(\varGamma_{1}a_{1}^{2}+\varGamma_{2}a_{2}^{2})]\lambda_{0}\!-\!\lambda_{0}^3+\dfrac{1}{4}\delta (\varGamma_{1}a_{1}^{2}\!-\!\varGamma_{2}a_{2}^{2}) $ . 可以证明, 不管是三波混频($ V_1>V_2 $ )还是受激背散射($ V_1<V_2 $ )过程, 在特定参数条件下, 解(17 )式均能展示出标准的Peregrine孤子形式[93 ] .$ V_1 = V_2 = V $ )是否存在RW解呢? 这似乎很难从上面的达布变换式寻求答案, 因为在这种情形下, Lax对(14 )式将变得无意义. 但显然, 简并TWRI方程依然是可积的, 因此其RW解是可能存在的. 最近, 文献[122 ]采用另一个策略来回答这个问题, 也就是, 对广义解(17 )式取如下极限: $ V_2\rightarrow V_1 = V $ , 成功得到了简并TWRI方程的基阶RW解:$ A = a_{1}^{2}+a_{2}^{2} $ , $ \theta = \delta^{2}(Vt-z) -(a_{1}^{2}-a_{2}^{2})z $ . 容易证明:$ u_1 $ 分量和$ u_2 $ 分量的强度和总是不变的, 不管它们各自的时空结构如何变化. 换句话说, 它们是时空互补的, 因此称为互补异常波[122 ] .122 ]给出了互补型异常波的数值模拟结果, 见图2 . 具体来说, 作者将三个场分量的实部和虚部分别乘以因子$ [1+ \varepsilon r_i(z)] $ (这里, $ i = 1, \cdots, 6 $ , $ r_i $ 为均值为0、方差为1的随机分布函数, $ \varepsilon $ 为噪声强度参数), 然后采用分步Fourier算法对TWRI模型进行数值积分. 图2 左列为未添加白噪声($ \varepsilon = 0 $ )的模拟结果, 右列为添加了白噪声($ \varepsilon = $ 10–8 )的模拟结果. 可以看到, 在微小的扰动下, 所有三个异常波分量依然可以在相当长的时间内稳定传播, 直到连续波背景的MI显著增长为止.图 2 互补型基阶RW解(18 )式的数值模拟结果. 左列图: 未微扰情形; 右列图: 白噪声微扰情形. 图摘自文献[122 ]Figure2. Simulation results of the complementary fundamental rogue wave solutions (18 ). Left column: unperturbed; Right column: perturbed by initial white noises. Figure adapted from Ref. [122 ].[123 ] ; 在这种情况下, 泵浦光和斯托克斯(Stokes)光的群速度几乎相同, 而相比之下, 声波的速度可近似为零, 三者满足简并TWRI方程所需要的模间耦合条件, 从而出现上面提到的双色互补型异常波动力学[122 ] .4.非线性薛定谔-麦克斯韦布洛赫方程 另一方面, 光波与非线性谐振介质的相互作用也是一个经久不衰的光学研究话题(注意区分上面讲的LWSW, TWRI过程, 其通常发生在非谐振介质的两波或三波谐振相互作用)[124 ] . 而这其中最有名的莫过于光脉冲与两能级原子或离子的相互作用, 即所谓的麦克斯韦-布拉赫(MB)耦合[125 ] . 正是由于这种谐振相互作用, 原本不透明(或吸收)的介质在超短激光脉冲照射下将变得完全透明, 此即大家所熟知的自感应透明现象[126 ] . 除了自感应透明现象外, MB方程还可以产生面积为$ 2{\text{π}} $ 的基本sech型孤子[124 ] . 后来, 一些****对MB系统做了推广, 研究了掺铒光纤中的脉冲传播动力学[127 ] . 在慢变包络近似和旋波近似下, 该系统可用非线性薛定谔-麦克斯韦布洛赫(NLS-MB)方程来描述. 下面就来讨论这一有趣的可积模型及其基阶RW解.[94 ,95 ] :$ u(z, t) $ 表示光波复振幅, M 和F 表示物质波的特征函数(具体讲, M 由谐振介质密度矩阵的离对角元$ \rho_{12} $ 来确定, 为复函数; F 表示上下能级的布居差, 为实函数, 二者满足$ |M|^2+F^2 = 1 $ [95 ] ), $ \phi $ 为去谐频率常数.$ 2\times2 $ 线性本征值问题(Lax对):[128 ] :$ \varDelta = ( 2\lambda-\phi) |r|^2+(2\lambda^{*}-\phi)|s|^2 $ , $ \lambda $ 为某个给定的谱参数值, $ (u_0, M_0, F_0) $ 和$ (u, M, F) $ 分别表示NLS-MB方程(20 )的旧解和新解.64 ,67 ,72 ]的做法, 可以很容易推得 NLS-MB方程(20 )的基阶RW解[95 ] :$ \kappa = \omega- \phi $ , $ \vartheta = 4 {\rm i}\eta z+1 $ , $ \theta = t-\chi z $ , 以及$ u_{0}(z, t) $ , $ M_{0}(z, t) $ 和$ F_{0}(z, t) $ 可定义为F 和M 的时空分布满足$F{(z, t)^2} + |M(z, t){|^2} = \left( {\dfrac{{{\kappa ^2}}}{{4{a^2}}} + 1} \right){b^2}$ . 这表明物质波组分具有与简并TWRI系统相似的互补异常波特性[122 ] . 尽管上述RW解适用于任意b 值, 但考虑到概率守恒条件$ F^2 + |M|^2 = 1 $ , 可令 b = $2 a/\sqrt{\kappa^{2}+4 a^{2}} $ , 其值取决于参数a 和$ \kappa $ 的取值.图3(a) 展示了这些解析解的时空分布图, 其初始参数为$ a = 1.5 $ , $ \phi = 1/2 $ , $ \omega = 0 $ . 可以看出, 光场分量显示为一个标准的Peregrine孤子结构; 比较而言, 物质波分量M 和F 展示出更复杂的时空结构, 但二者满足$ F^2 + |M|^2 = 1 $ , 即时空互补性. 此外, 为了评估异常波动力学及其稳定性, Chen等[95 ] 采用指数时间差分Crank-Nicolson (ETDCN)算法对模型方程(20 )执行了数值模拟, 结果如图3(b) 所示. 这里使用$ u(z = -1, t) $ 作为光场分量的初始条件, 而让物质波分量M 和F 分别取$ M_0(z = -1, t) $ 和$ F_0 $ 作为其初始值. 这些初始条件对应于对解析解(23 )式的强烈扰动. 结果表明, 尽管自发性MI的发生呈指数增长, 并且倾向于干扰局域解的尾部部分, 但是异常波结构, 特别是对于光场分量, 均可以在相当长的距离上展开而不失真. 进一步地, 为了验证这类RW结构能否在真实条件下产生, 他们把光场的初始条件也换成平面波输入, 考察此类RW解的数值激发情况. 图3(c) 为其数值模拟结果, 清晰显示了这些典型的RW结构是可以激发产生的, 见图中黑圈标出部分. 这些数值结果充分预示了实验观测的可行性, 具体实验方案可参看文献[95 ].图 3 NLS–MB方程的基阶RW解(23 )的时空演化, 其中(a)列图对应解析解的3D曲面和轮廓图; (b)列图为数值模拟结果, 初始条件已文中给出; (c)列图显示这类异常波结构在背景场中的数值激发产生, 已黑线圈出. 图改编自文献[95 ]Figure3. Spatiotemporal evolution of the fundamental rogue wave solutions (23 ) of the NLS–MB equation. Column (a): Analytical solutions, given by 3D surface and contour plots; Column (b) the numerical results, with initial conditions being specified in the text; The column (c) shows the numerical excitation of the rogue waves, indicated by the black circles, from the background field. Figure adapted from Ref. [95 ].23 )式具有普适性, 可以推广应用到高阶NLS-MB方程中去. 例如, 对于下面的Hirota-MB 方程[129 ] :23 )式依然可以作为其基阶RW解, 只需要把(24 )式和(26 )式定义的k , $ \eta $ , 和$ \chi $ 参数换成如下形式即可:g 和h 为任意实常数. 不难看出, 当$ h = 0 $ 和$ g = 1 $ 时, 上述 Hirota-MB方程及其RW解就回到了NLS-MB情形.5.结 论 本文系统综述了LWSW谐振方程, TWRI方程和NLS-MB方程这三类典型可积谐振模型的新颖异常波动力学及其研究进展. 首先, 对于LWSW谐振系统, 提供了其基阶RW解的一般形式, 指出长波和短波之间的谐振相互作用能导致黑异常波的产生. 特别地, 该基阶RW解推广到多分量LWSW系统时, 可以产生有趣的共存异常波现象, 并得到了数值模拟验证. 其次, 在TWRI系统中, 给出了该可积模型的基阶RW解, 指出该解可以适用三波混频($ V_1>V_2 $ )和受激背散射($ V_1<V_2 $ )两种情形. 特别地, 对于简并TWRI情形(V 1 = V 2 = V ), 也提供了其精确基阶RW解, 并数值展示了其互补异常波动力学. 最后, 在NLS-MB方程框架内, 讨论了光场与低温光纤中的两能级掺杂离子的谐振相互作用, 给出了光学和物质波的基阶RW解一般形式, 数值展示了它们的新颖异常波动力学. 特别地, 指出上述基阶RW解可以推广应用到更高阶的NLS-MB耦合系统(如Hirota-MB系统), 展示了该解的普适性.[130 ] , 而后者与其他可积谐振模型如AB模型、MTM方程也有类似的转换关系[131 ,132 ] . 因此可以预测, 本文呈现的基阶Peregrine RW解对其他可积谐振系统的异常波动力学研究也将有参考借鉴作用. 



































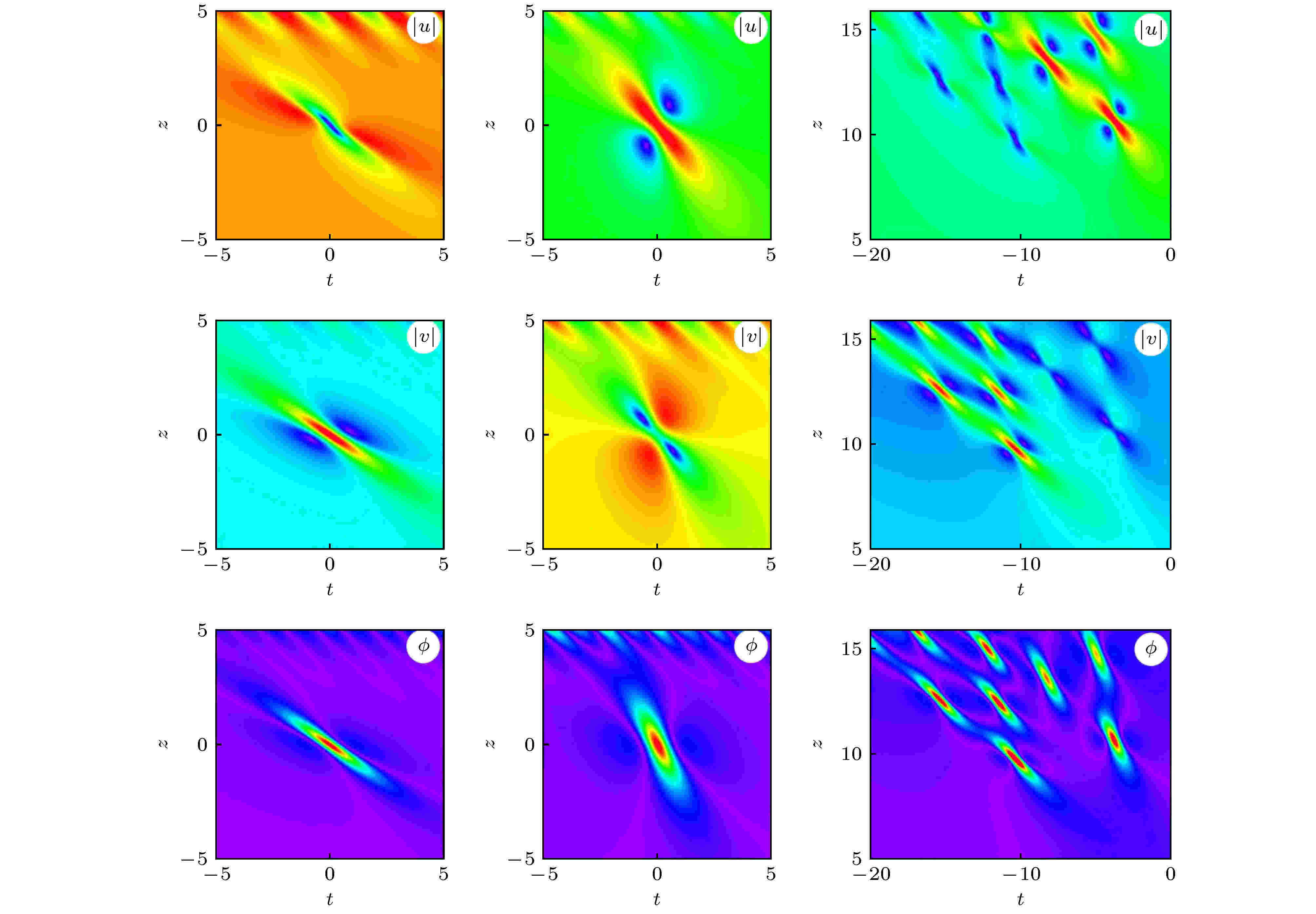 图 1 数值模拟验证初始白噪声微扰下的基阶RW解(5)式, (6)式和 (10)式的稳定性, 左列图对应
图 1 数值模拟验证初始白噪声微扰下的基阶RW解(5)式, (6)式和 (10)式的稳定性, 左列图对应




















































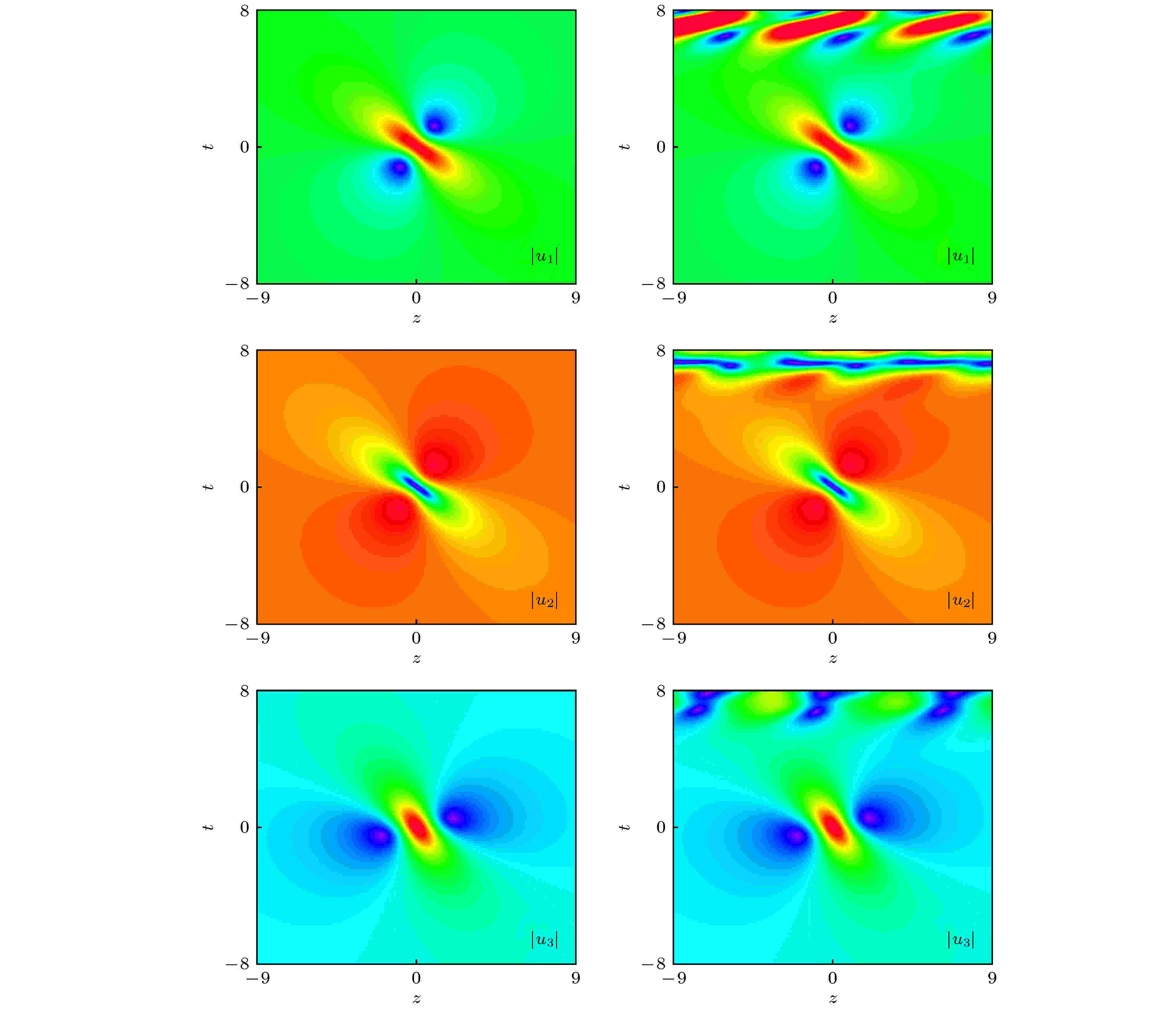 图 2 互补型基阶RW解(18)式的数值模拟结果. 左列图: 未微扰情形; 右列图: 白噪声微扰情形. 图摘自文献[122]
图 2 互补型基阶RW解(18)式的数值模拟结果. 左列图: 未微扰情形; 右列图: 白噪声微扰情形. 图摘自文献[122]


























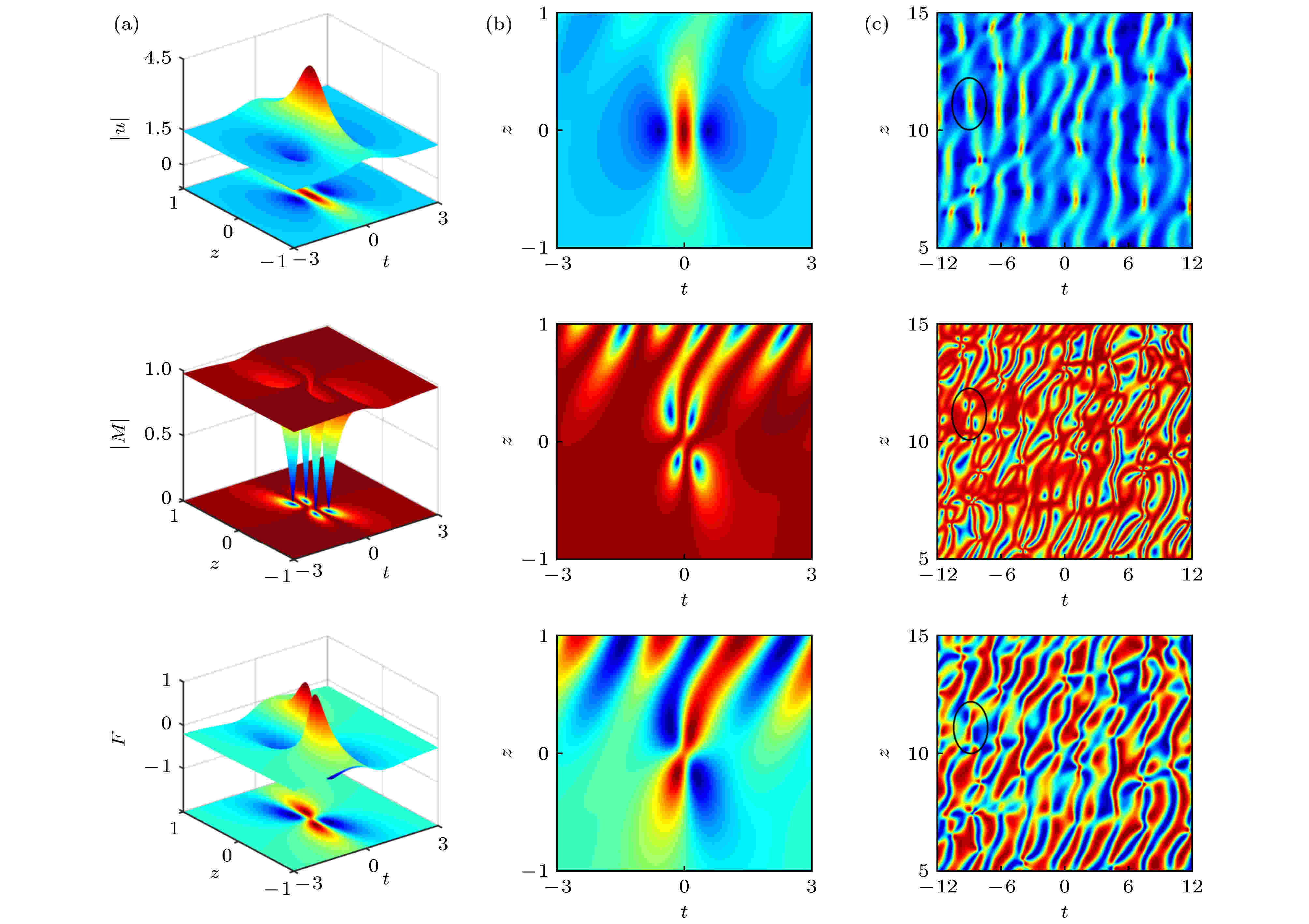 图 3 NLS–MB方程的基阶RW解(23)的时空演化, 其中(a)列图对应解析解的3D曲面和轮廓图; (b)列图为数值模拟结果, 初始条件已文中给出; (c)列图显示这类异常波结构在背景场中的数值激发产生, 已黑线圈出. 图改编自文献[95]
图 3 NLS–MB方程的基阶RW解(23)的时空演化, 其中(a)列图对应解析解的3D曲面和轮廓图; (b)列图为数值模拟结果, 初始条件已文中给出; (c)列图显示这类异常波结构在背景场中的数值激发产生, 已黑线圈出. 图改编自文献[95]





