摘要:采用DNS方法对隔板对流装置进行模拟计算, 研究系统中热流特性以及热量输入与传递特性. 讨论了热流的纵向和横向输运特性, 在此基础上对传热通道和狭缝区域的热通量以及对应底板外界输入热通量进行了定量化分析. 研究结果表明, 通道中低温流体向下冲击底板而后转入水平运动, 流入狭缝区域并不断被加热, 只进行水平的热量输运. 流出狭缝后的高温流体在传热通道中汇聚形成向上喷流, 进行热量传递. 水平热量输运的区域对应的底板外界输入的热通量很大, 占总输入热通量的92%, 狭缝区域底板外界输入热通量占总量的64%, 纵向热量传递区域对应底板外界输入热通量很小. 不同几何参数隔板对流系统都具有增强传热效果, 狭缝高度较小时对应的增强效果较强. 隔板数n = 11及狭缝高度d = 0.01时系统传热Nu数值最大, 是无隔板时的3倍以上.
关键词: 隔板对流系统/
热流/
热通量/
热量输运与传递/
增强传热

English Abstract

全文HTML

--> --> -->

热对流现象在自然科学和工程科学中广泛存在, 湍流热对流特性的研究具有重大意义^[1-2]. Rayleigh-Bénard (RB)热对流是热对流研究领域中最典型的流动物理模型之一^[3]. RB热对流系统存在丰富而复杂的流动和热输运现象, 一直受到国内外****的关注和研究. 已有大量关于RB热对流的研究成果^[4-9].
增强对流装置的传热效率始终是这一研究领域的重要目标之一. 非传统RB热对流是近年来增强传热研究的热点. 例如旋转RB对流, 在特定参数下热羽流由于Ekman pumping效应被拉伸成柱状涡流, 从而可以高效的抽吸温度边界层中流体, 达到显著增强系统传热的效果^[10-14]. 具有粗糙导热板的RB对流系统在一定参数范围内, 粗糙单元能够有效的提高羽流从温度边界层中脱落的频率, 起到增强系统传热效率的作用^[15-17]. 不加入外界能量的被动方式可以增强的传热效率大多在1倍以内, 对于安全要求较高的系统, 被动方式的增强传热则非常重要.
Bao等^[18]在宽高比为5的对流槽内等距加入竖直隔板并在隔板顶端与底板间留有狭缝, 实验中选取隔板数n的范围为0 ≤ n ≤ 6, 3.5 × 10⁷ ≤ Ra ≤ 8.3 × 10⁸, 数值模拟选取0 ≤ n ≤ 35, Ra = 10⁸, 结果发现随着隔板数的增加, 数值模拟与实验数据得出Nu一致, 并且当隔板数增加到28时传热Nu数存在着最大幅度的上升, 增强传热最高能达到无隔板时的2.3倍. 这种加入隔板的热对流系统并不需要外界能量输入, 而是由于热流的对称破缺自组织产生了绕隔板的单向热流, 使得隔板对流系统能产生高效增强传热. 包芸等^[19]进一步的数值模拟研究发现, 通过调整狭缝高度, 系统传热Nu数可达无隔板时的3.1倍. 他们对隔板对流系统展开系统深入地研究, 发现当隔板间的通道宽度b和狭缝高度d满足b ≥ 4d时, 狭缝尺寸d是控制系统流动和温度分布特性的关键几何参数^[20]; 隔板对流系统的压力特性为狭缝中的流动由水平压力驱动, 传热通道中纵向压力差与浮力基本相等, 纵向流动通过水平狭缝流动的连续性保持^[21]; 狭缝高度d决定热通道中的温度漂移特性, 传热通道宽度b的变化对单个通道的温度漂移特性和传热特性影响很小, 但较小的通道宽度会增加系统的传热通道个数, 进而影响系统的整体传热效率^[22]; 同时还研究了系统传热Nu数随几何参数和Ra数的变化规律^[23]. 此外, Bao等^[24]还发现狭缝高度与边界层厚度间存在着较强的相关关系.
本文基于隔板对流系统的数值计算结果, 对系统的热量输运过程进行分析, 研究讨论系统中热流这个与传热直接相关的物理量在不同区域的流动特性, 并通过局部区域热通量定量化分析, 探讨隔板对流系统中的高效增强传热机制.

已有的隔板对流系统计算研究工作表明, 在隔板数较多的层流状态下系统流动及其物理特性具有很好的二维性^[17]. 因此本文采用二维计算, 讨论隔板数较多时具有单向层流流动的系统中热流输运特性以及增强传热机制.
基于Oberbeck-Boussinesq近似, 无量纲化的二维RB热对流方程为:

$ \begin{aligned} & \nabla \cdot {{V}} = 0, \\ & \frac{{\partial {{V}}}}{{\partial t}} + ({{V}} \cdot \nabla ){{V}} = - \nabla P + \frac{1}{{\sqrt {Ra/\Pr } }}{\nabla ^2}{{V}} + \theta {{k}}, \\ & \frac{{\partial \theta }}{{\partial t}} + ({{V}} \cdot \nabla )\theta = \frac{1}{{\sqrt {Ra \cdot Pr } }}{\nabla ^2}\theta, \end{aligned} $

其中, V为速度, P为压力, θ为温度, k表示纵向的单位向量. 计算边界条件为下底板加热, θ = 0.5; 上底板冷却, θ = – 0.5. 速度边界条件为无滑移边界, 左右侧壁以及隔板壁面均为绝热条件. 采用常用的交错网格, 时间方向采用一阶精度, 空间采用二阶精度离散格式. 系统中的控制参数包括$Ra = g\beta \Delta \theta {H^3}/\upsilon \kappa $和$Pr = \upsilon /\kappa $, $\beta $为热膨胀系数, g为重力加速度, $\Delta \theta $为上下壁面温差, H为系统装置的高度, 本文取Ra =10⁸, Pr = 5.3, Ra数大小在实验所选的参数范围内, Pr数代表工作介质为水, 参数选取与实验保持一致^[18].
首先选取几何参数宽高比Γ = 2, 隔板厚度l = 0.12, 狭缝高度d = 0.015, 隔板数n = 9 (对应通道宽度b = 0.092)的系统作为典型研究模型进行数值计算, 讨论隔板对流系统的温度和流动特性.
图1给出的是系统温度场和流线分布. 明显可见, 传热通道中向上流动形成单向的红色表示高温流体, 向下流动形成单向的蓝色表示低温流体, 使得两种通道都形成单纯的正向热量传递过程, 产生了惊人的成倍增强传热效果^[18]. 图中围绕隔板的流线显示, 相邻通道间存在封闭的绕隔板环流结构, 使得向下冷通道的低温流体在冲击高温下底板并流经狭缝的过程中被不断加热, 产生高温流体随后进入向上热通道并将热量传递到低温上底板, 经过上底板冷却后低温流体再一次向下流动. 这种绕隔板流体被加热和冷却的闭合环具有很高的热量输运和传递效率.
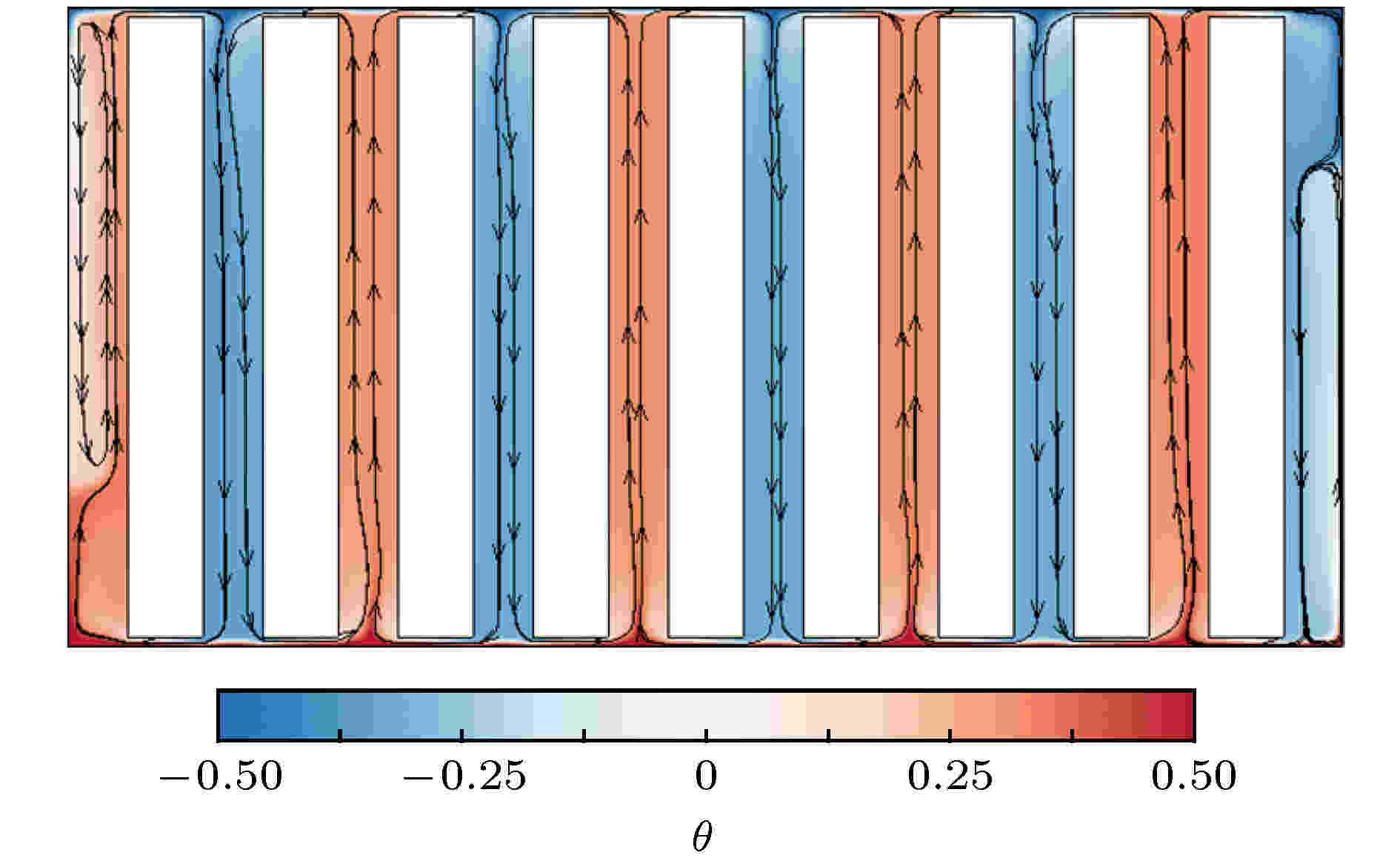图 1 对流系统中的温度场和流线图
Figure1. Temperature field and streamline of partitioned convection system

为了深入研究隔板对流系统中热量输运和传递过程, 本文将探讨和分析系统中与传热直接相关的物理量—热流的特性及其对热量输运和传递机制的影响.

在热对流系统中, 影响传热的热通量包括两个部分, 一个是通过流体运动产生的对流传热, 另一个是由流体间温差引起的热传导传热. 与通常的湍流热对流中冷热羽流混杂运动完全不同, 本文的隔板对流系统所产生的单向层流流动较为特殊, 传热通道中的单向流动携带温度形成单纯的向上高温热流和向下低温热流, 因此通道中的热流运动特性可以很好地反映系统的对流传热特性.
2

-->

3.1.隔板对流系统中传热通道热通量分布

首先研究系统中每个传热通道中的热通量分布情况. 由于热通量在离开狭缝区域的整个隔板间传热通道中是守恒量, 因此只需计算系统纵向中部位置的热通量. 对每个传热通道进行横向积分, 单通道的热通量计算公式为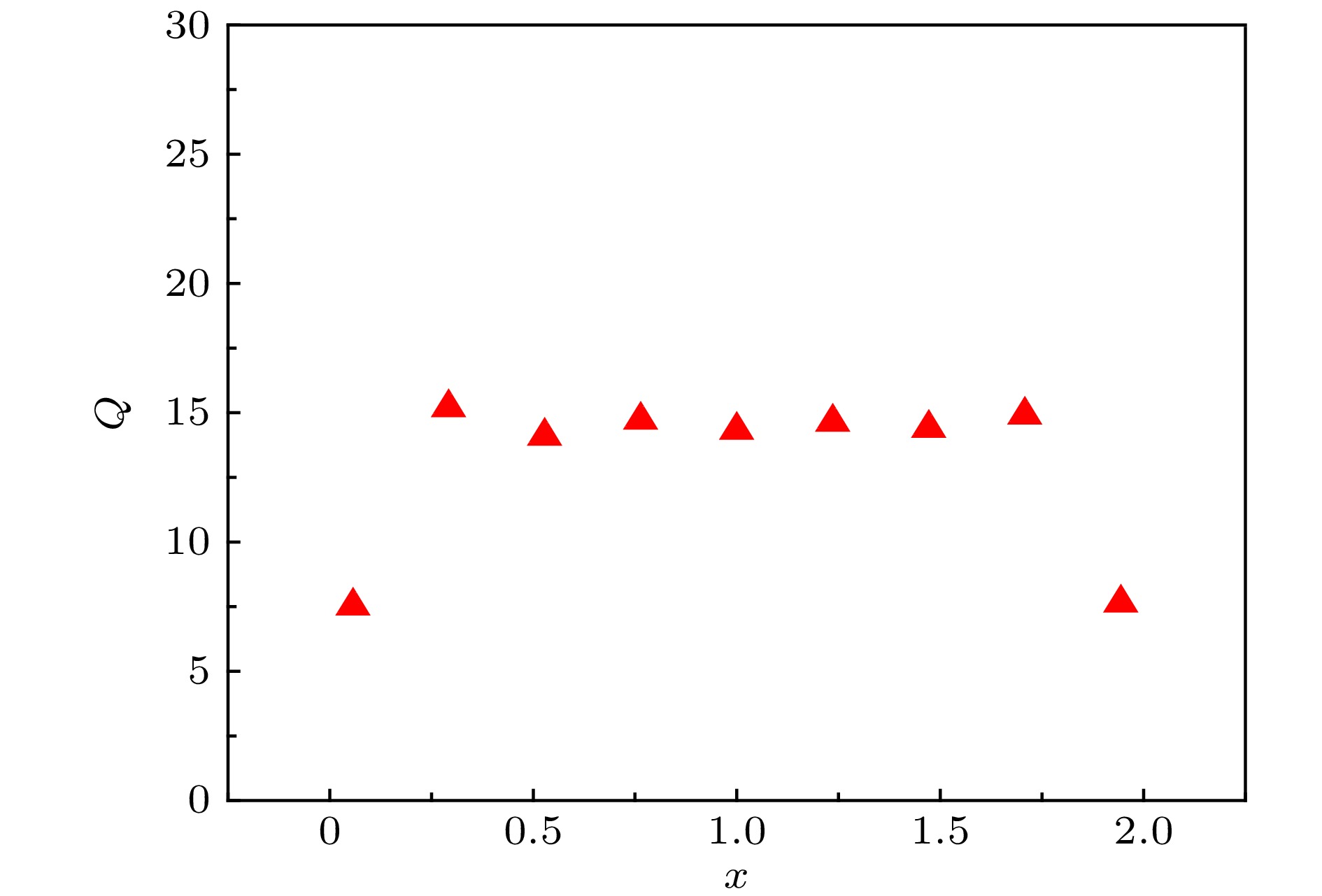

$Q = \displaystyle\int_b {\left( {\sqrt {RaPr} v\theta - \dfrac{{\partial \theta }}{{\partial y}}} \right){\rm{d}}x},$

其中x, y分别表示横向和纵向位置. 计算结果为无量纲的热通量, 结果如图2所示.
图 2 隔板对流系统中不同传热通道的热通量
Figure2. The heat flux of different heat transfer channels in partitioned convection system.

图2给出宽高比Γ = 2下隔板数n = 9和狭缝高度d = 0.015时隔板对流系统传热通道的热通量分布. 可以见到, 除靠近系统侧壁的两个通道外, 系统内部各个传热通道中的热通量基本相等. 系统侧边通道由于仅有一侧狭缝相连, 通过流量守恒由狭缝输入热通道中流量只有一半, 所以热通量也大致只有一半.
图2中的结果表明, 系统内部与热流特性相关的各个传热通道热通量具有一致性, 故在隔板对流系统的热流特性以及底板热量输入特性的研究中, 只需探讨单通道的特性.
2 -->

3.2.传热通道及其连接区域狭缝中的热流特性

热流的大小等于速度与温度的乘积, 直接反映流体对流过程中带动热量的情况. 在远离温度边界层的大部分区域由热流导致的对流传热占主要作用, 热传导引起的热量传递很小. 而在狭缝中虽然存在较大纵向温度梯度, 但不影响水平热流输运过程. 因此, 本文重点研究隔板对流系统中对增强传热起主导作用的热流特性.
文献[21,22]在研究隔板对流系统的压力特性和温度特性时, 仅对主导传热效率的传热通道中的压力和温度特性进行了讨论. 在讨论隔板对流系统的热流特性及底板输入热量特性时, 由于流动的连续性以及隔板顶端狭缝区域对应的底板输入热量作用很大, 因此本文的研究区域包括狭缝以及其连接的左右传热通道, 探讨整个系统中流动带动热量输运的完整特性.
隔板对流系统由于隔板的加入, 在几何上将空间分割为水平狭缝和纵向传热通道两个部分. 由于绕隔板的流动存在一定的对称周期性, 选取系统局部区域对流场和热流特性进行详细研究, 研究区域包括向上流动和向下流动的两个相邻通道的下部分和连接两者的狭缝区域. 由于热流为矢量, 本文将隔板对流系统中的热流分解为纵向热流和横向热流分别讨论, 其中纵向热流直接影响传热效率, 而水平横向热流对系统纵向传热没有作用, 仅起到水平热量输运的作用. 本文无量纲的局部纵向热流计算式为vθ, 横向热流计算式为uθ.
图3给出了纵向热流分布及对应的速度场. 在图3显示的纵向热流中, 由于隔板对流系统的流动特性, 通道中低温流体向下运动如蓝色箭头, 高温流体向上运动如红色箭头, 但对于热流均为向上输运热量, 因此纵向热流均为正值. 图中颜色深浅代表热流分布的数值大小.
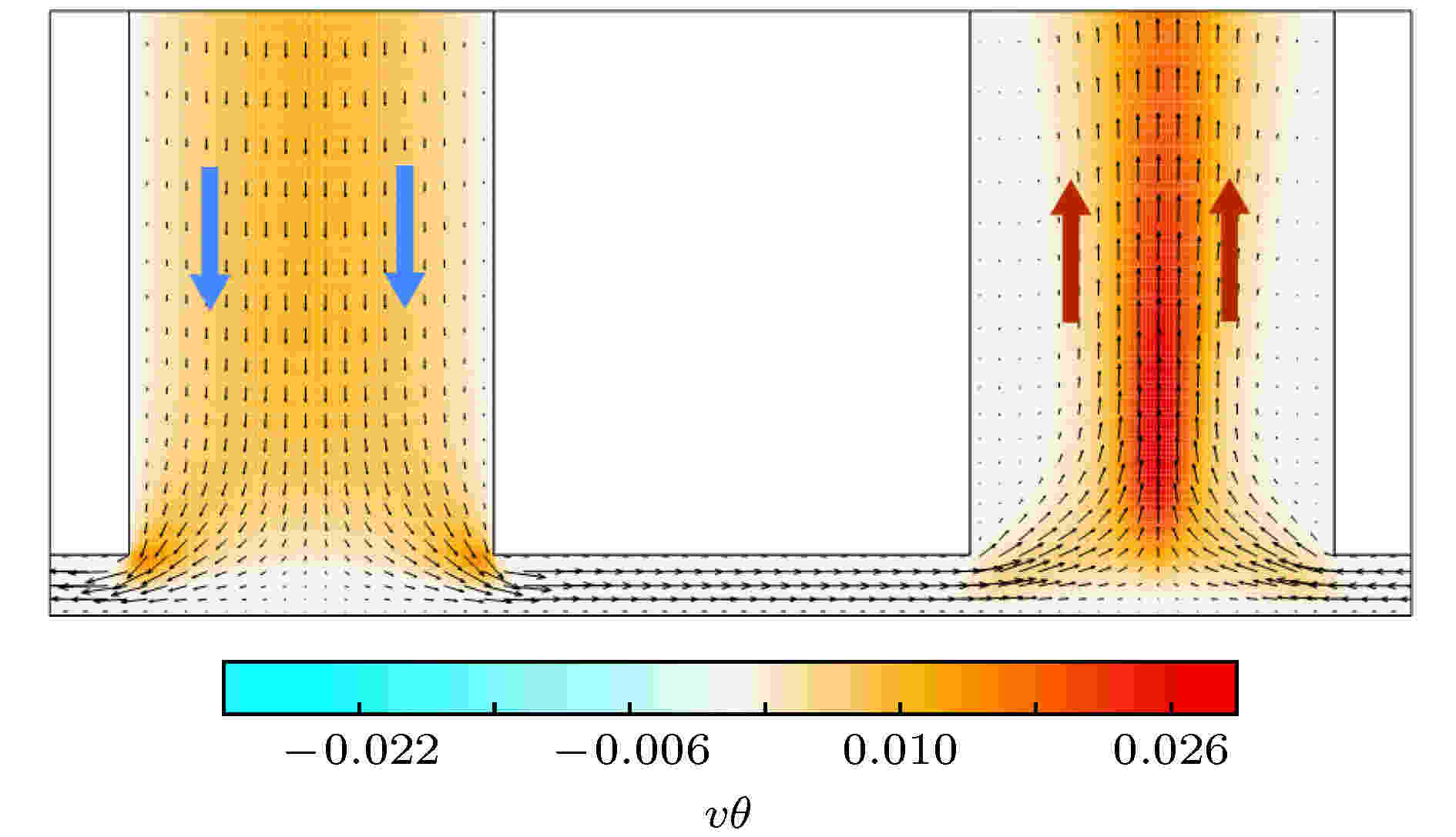图 3 隔板对流系统局部区域纵向热流分布特性
Figure3. An enlarged portion of the vertical heat flow field in partitioned convection system, the arrows represent the direction of the flow.

图3中可以看到, 左侧向下流动通道中的纵向热流, 在远离底板时除靠近隔板壁面区域外基本均匀, 近隔板壁的热流较小则是由于近壁面速度很小造成的. 随着冷流体进一步向下运动并冲击底板, 流体分别向两侧狭缝流动, 速度逐渐转为水平方向, 在狭缝中仅存在水平槽道流动^[20], 纵向热流消失. 此时狭缝中没有纵向热流, 也就是说狭缝中对传热效率的贡献为零.
流体从狭缝中流出进入右侧向上流动的热流通道, 来自两侧狭缝的射流在通道中部汇聚, 并形成向上的集中喷流. 喷流中带有较高的温度热流, 在喷流区域形成了强热流, 其左右两侧热流值很小, 同时高温也意味局部浮力较强, 使得喷流具有向上的加速流动. 随着高度逐渐增加, 由于温度场的扩散作用, 通道中的高温喷流逐渐向两侧扩展, 纵向热流也趋于均匀. 由于热流的对称性, 向上热通道的上部与图中左侧的冷通道中热流分布对称.
图4为隔板对流系统局部区域的横向热流分布特性及对应速度场, 蓝色为负热流, 红色为正热流. 其中横向热流的正负值定义为: 在图4的局部区域中由底板加热产生的高温(θ > 0)横向热流为正热流, 冷通道向下输运的低温(θ < 0)流体转向产生的低温横向热流为负热流.
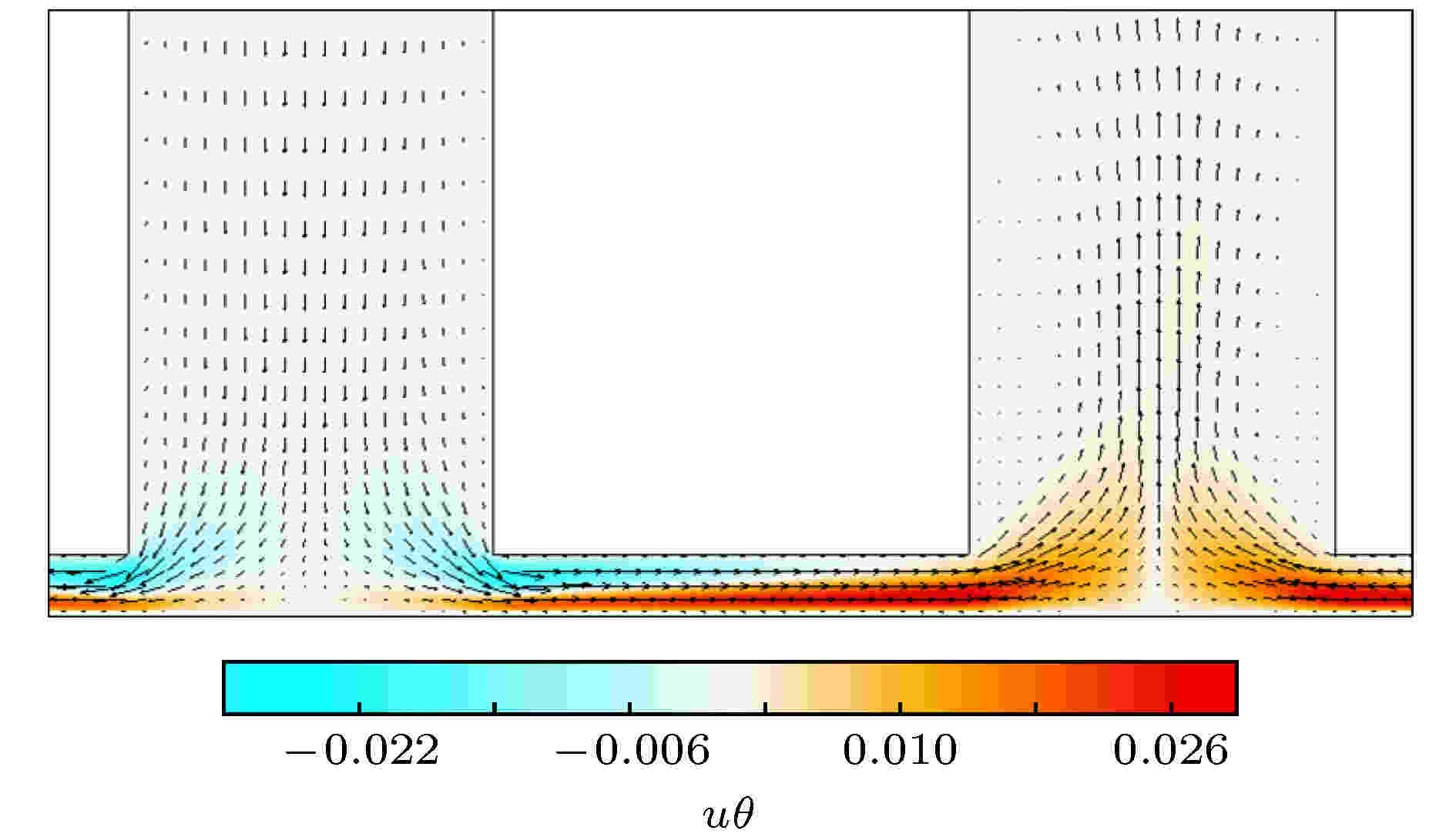图 4 隔板对流系统局部区域横向热流分布特性
Figure4. An enlarged portion of the horizontal heat flow field in partitioned convection system.

从图4中可见, 冷通道中的低温流体冲击底板并被高温底板加热, 和尚未被加热的冷流体一起流入狭缝, 在狭缝中形成上部为低温冷流和下部为高温热流的状况, 且在高温底板的持续加热作用下, 高温热流不断增长. 当流体流出狭缝时, 已基本上变为高温热流, 进入热通道后高温横向热流区迅速增大, 对应热流数值变小, 并与对面另一个狭缝的高温热流汇聚, 使得流动转向. 随着高度的增加, 通道中的横向热流逐渐消失, 由守恒关系知横向热流全部转化为向上的纵向热流.
在传热通道的正中靠近底板处, 无论是冷通道的冲击点还是热通道底部两射流的汇聚点, 均为流动的驻点, 而紧邻底板边界处, 温度虽然较高但速度为零, 因此热流为零.
2 -->

3.3.传热通道和狭缝不同区域热通量定量化分析

本文通过计算传热通道和狭缝两个不同几何区域的热通量定量分析局部热流变化, 并计算不同区域从恒温底板外界输入流体的热通量, 进而探讨不同区域对增强传热效率的贡献.
在远离狭缝的位置对传热通道的热流进行水平积分, 计算传热通道中的纵向热通量, 此时可以忽略温度梯度对热通量的影响. 在狭缝的入口和出口, 仅对水平热流进行纵向积分, 计算出流入狭缝和流出狭缝的热通量, 此时边界层温度梯度虽然很大但对水平热通量没有贡献. 由于存在底板加热过程, 狭缝流入和流出的热通量值不相等. 同时, 可以通过对底板边界处温度梯度的积分, 计算不同区域由底板传入流体的热通量. 以上热通量均为无量纲值.
在定量化热流特性分析中, 由于传热通道中热流的对称性及系统流动的守恒性, 分别只计算半个冷通道和热通道的热通量, 便于分析流体热量传递和与其保持一致的底板外界热量输入. 图5为系统局部区域传热过程定量化分析图, 研究区域包括半个冷通道下部、半个热通道下部以及连接二者的狭缝. 图中蓝色箭头为低温冷流, 红色箭头为高温热流, 数字表示相应位置热通量. 红色底板上的数字是流体在不同区域的热通量, 底板下方的数字是3个区域及总体从高温底板外界输入流体的热通量. 可以看见, 从冷通道和热通道向上输运的热通量总和与从高温底板外界输入流体的热通量总和均为14.64, 两者相等.
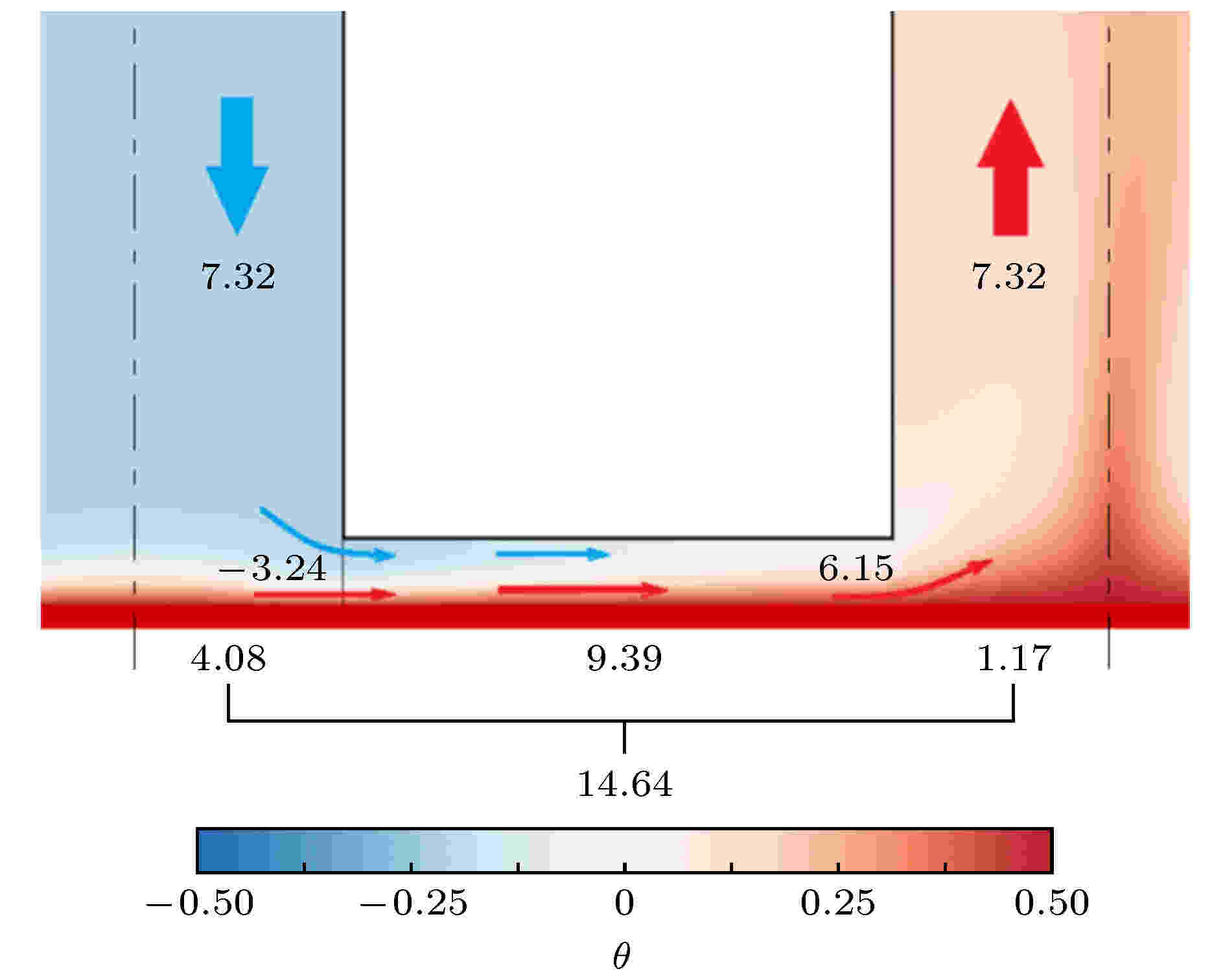图 5 系统局部区域热流热通量变化及底板传热特性定量表示
Figure5. Change of heat flux and heat flow in partial area of the system and quantitative representation of the heat transfer on the bottom plate.

图中箭头所示的热流流动特性在上节定性分析中已经讨论, 这里对各个区域的热通量进行定量分析. 数字的正值表示对系统传热是正贡献, 负值表示为负贡献. 左侧半个低温流体向下流动的热通量为7.32, 冲击热底板后对应底板区域输入热通量为4.08, 随后包含低温和加热的流体流入狭缝, 在狭缝入口处输入的水平热通量为–3.24, 即该区域底板加热流体的能力不够, 使得流入狭缝的流体热流对整体传热的贡献为负. 在狭缝区域, 流体流经时不断被高温底板加热, 此时底板输入热通量为9.39, 到狭缝出口时热通量变为6.15. 转入右侧高温热通道后, 该区域底板仍对流体有加热作用, 但流体以射流流出狭缝再转向上的过程中, 温度较高导致底板处的温度梯度值较小, 底板输入热通量仅为1.17, 最终半个向上输运热通道的热通量为7.32. 根据对称性, 高温通道中流向顶板的流体, 将在顶板通过狭缝进一步冷却, 并再次形成向下流动的低温流体. 通过这一循环过程, 实现了隔板对流系统中只出现单向层流流动的增强传热特性.
上述的热流运动过程中可以看到, 由隔板分割成的3个区域的热量输运流入和流出都是守恒的. 从高温底板输入热通量的分布看, 在冷通道底部由于冷流的冲击输入的热通量值为4.08, 但这部分被加热的流体不能进行向上传量传递, 只能随剩余低温冷流横向流入狭缝. 本文讨论的厚隔板使得狭缝长度足够长, 由此狭缝区域底板输入热通量值为9.39. 由于这两个区域的热流没有向上的流动, 所以只能进行水平的热量输运而不能进行向上热量传递. 到热通道, 流动逐渐转变为向上的单向流动, 所有的热流最终在热通道中进行热量传递. 由于两个相向的狭缝射流汇集形成向上的热喷流, 反而造成此处的温度边界层很厚, 底板热量输入仅为1.2. 前两个区域由底板传入的热通量占整体底板传入热通量的(4.08 + 9.39)/(4.08 + 9.39 + 1.17) = 0.92, 即只有横向水平热量输运的区域通过底板从外界输入流体的热通量占92%, 而厚隔板形成的狭缝区从外界输入的热通量值最大, 占外界输入热通量的64%.
从以上热流特性的定量分析可以看到, 由于隔板分割成的3个区域限定了流动方向, 可以分别讨论系统内部热流进行水平热量输运和纵向热量传递的特性, 以及对应区域底板外界输入热通量. 分析结果显示, 只有水平热量输运的区域其底板从外界输入的热通量很大, 而在向上热流传热通道中, 热流向上传递区域对应的外界输入热通量却很小. 隔板对流系统的不同几何区域的热流流动特性以及从底板外界输入热通量能力特性表明, 底板外界输入热量的主要区域和流体内部热量传递的主要区域是不相同的.
隔板对流系统的热流输运特性及底板输入热通量特性, 对探讨进一步提高系统的传热能力具有指导意义.

由于隔板的加入, 隔板对流系统的几何参数数量较多, 不利于讨论和优化. 研究表明, 厚隔板系统中狭缝高度是关键几何参数^[20], 可以决定单个传热通道中温度、压力和速度特性. 因此, 在研究几何参数对热流特性以及底板输入热量特性的影响时, 只需要讨论狭缝高度的变化对单个传热通道物理量的影响, 以及隔板数量变化对整个系统的传热效率的影响.
图6给出的是隔板对流系统局部区域温度场以及不同区域由底板外界输入的热通量. 如图6(a)和图6(b) 所示, 当狭缝高度d = 0.015时, 11块隔板相比于9块隔板传热通道宽度变窄, 但并不影响通道中的温度漂移TD数的大小^[22], 温度分布变化基本类似. 从底板外界输入的热通量发现, 占比最大的狭缝区域的输入热通量相等, 均为9.4, 表明此时不同隔板数情况下, 同样狭缝高度的狭缝中水平流动和热量输运状态是相同的. 由此可见, 厚隔板系统在狭缝中水平流动具有基本一致的速度^[20]、压力分布^[21]、温度漂移量^[22]以及本文讨论的输入热通量等物理量, 因此狭缝高度几何参数成为关键的决定参数. 隔板数增加导致单通道总体的输入热通量减少, 从9块隔板的14.7减到了11块隔板的13.3. 但由于隔板数增加, 所以整个系统的传热效率是增加的.
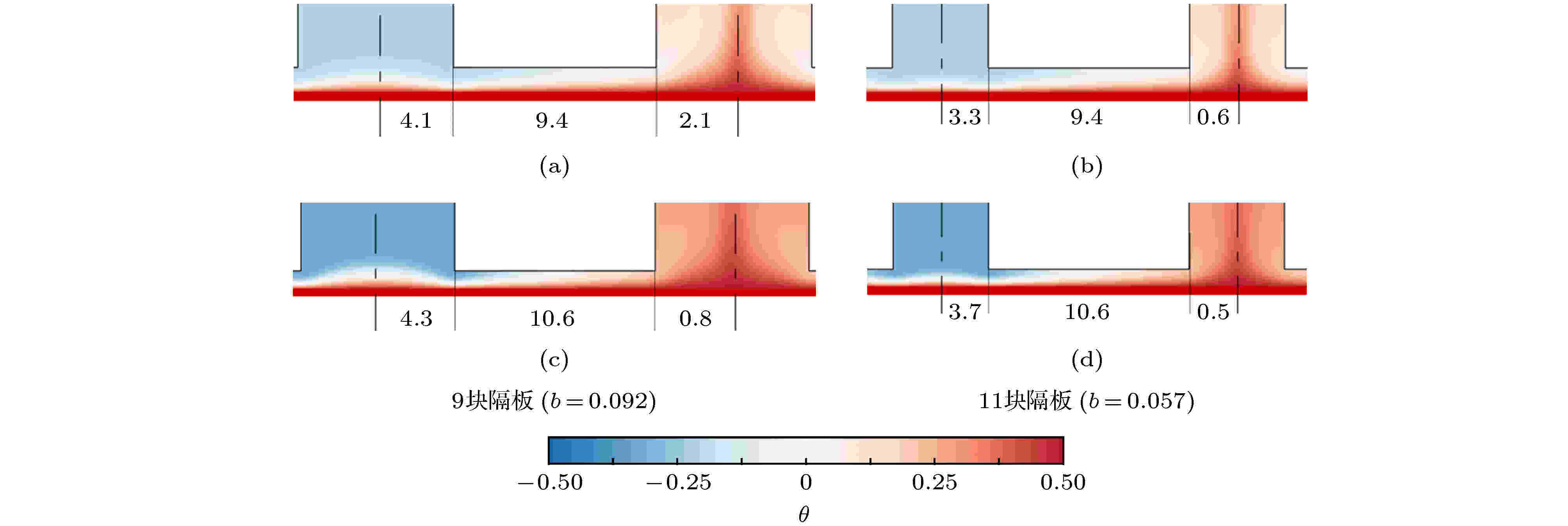图 6 狭缝高度d = 0.015时隔板数n = 9 (a), n = 11 (b)及d = 0.01时隔板数n = 9 (c), n = 11 (d)的局部温度场和局部传热大小
Figure6. Partial temperature field and magnitude of local heat flux under different number of partitions n = 9 (a) and n = 11 (b) when the height of gap is d = 0.015 and n = 9 (c) and n = 11 (d) when the height of gap is d = 0.01

图6(c)和图6(d)是狭缝高度d = 0.01时9块隔板和11块隔板的局部区域温度分布和外界输入热通量, 物理量特性基本特征与图6(a)和图6(b)中的结果相似. 由于狭缝高度变小, 流过狭缝的流动产生了更薄的温度边界层, 使得在狭缝区域底板外界输入热通量增大, 流出狭缝的流体具有更高的温度, 传热通道中的温度漂移TD数增高. 同样, 隔板数变化导致传热通道宽度不同, 但狭缝区域底板外界输入热通量不变, 增加隔板数会使单通道总体的输入热通量值略有减少. 从底板外界输入的总热通量, 9块隔板的输入热通量为15.7, 11块隔板的为14.3, 均大于图6(a)和图6(b)中对应的较大狭缝高度d = 0.015时的输入热通量值.
图6的显示了宽高比为2的对流系统中加入不同隔板数和变化狭缝高度情况下底板外界输入热通量的变化特征. 结果表明厚隔板造成的狭缝高度不但是关键几何参数且具有同样的流动特征, 在同样狭缝高度时还具有相同的底板外界输入热通量, 并在单通道底板输入的总热通量中占比达63%以上.
本文最终研究目的是隔板对流系统的增强传热特性, 因此接下来探讨隔板对流系统整体传热效率的增强效果. 系统的传热效率由传热Nu数表示, 无量纲的Nu数计算公式为

$Nu = \sqrt {RaPr} {\left\langle {v\theta } \right\rangle _{\rm{A}}} - {\left\langle {\partial \theta /\partial y} \right\rangle _{\rm{A}}}$

其中, ${\left\langle \cdots \right\rangle _{\rm{A}}}$表示横向平均值, Nu数值越大表示系统的对流传热效率越强. Nu_d表示来自狭缝区域的传热贡献, 即所有狭缝底部从外界输入的热通量总和.
图7给出了宽高比为2的对流系统中加入7块至11块隔板以及对应3个狭缝高度d = 0.01、d = 0.015和d = 0.02的系统传热Nu数及狭缝传热占比Nu_d/Nu变化情况. 在这个计算条件范围内可保证传热通道中的流动是单向层流流动, 并且满足狭缝高度是决定流动状态的单一几何参数^[20]. 在本文的研究范围内, 随着隔板数目的增加3个狭缝高度的系统传热Nu数都近乎线性增加. 究其原因, 可从单通道热通量分析中看到, 隔板顶端狭缝区域底板外界输入量占比很大, 由此造成多一块隔板近乎就多一份热量输入. 如图7所示, 狭缝传热贡献Nu_d/Nu随隔板数增加同样近乎线性增加. 相较于无隔板系统传热Nu数如图中红色虚线所示, 本文研究的所有隔板对流系统都具有增强传热效果, 狭缝高度较小时对应的增强传热较强. 在隔板数n = 11及狭缝高度d = 0.01时系统传热Nu数值最大(Nu = 82), 表明系统的增强传热效果最好, 是无隔板时Nu = 25.6的3倍以上.
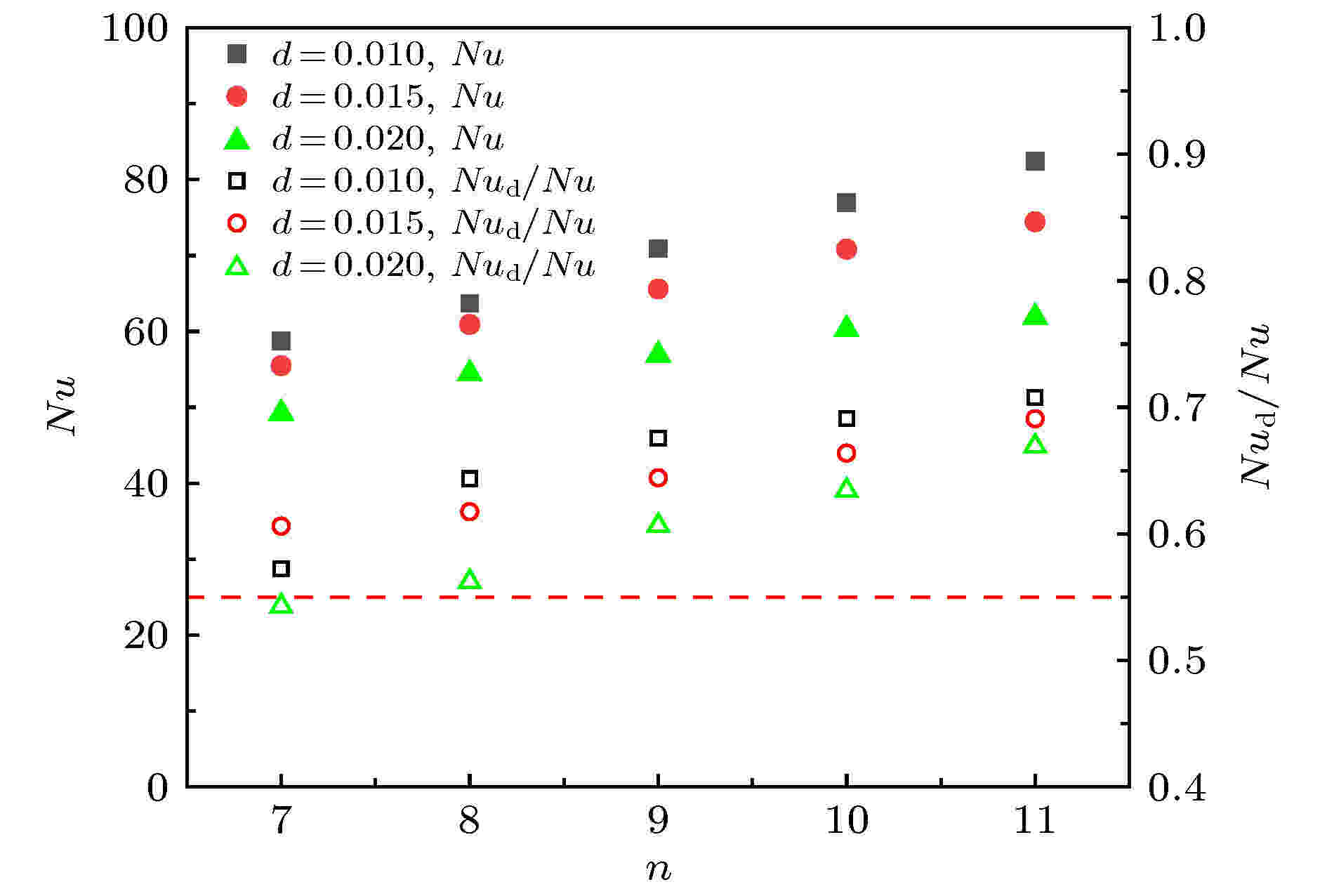图 7 不同狭缝高度下传热Nu数与Nu_d/Nu随隔板数的变化, 红色线表示无隔板时系统的传热
Figure7. Nu and Nu_d/Nu with the change of the partition number n under different height of gaps, the horizontal red dashed line represents the system without partitions.

Bao 等^[18,23]认为隔板对流系统中自组织形成了的环绕隔板的环流结构, 在狭缝两端形成水平压力梯度, 推动狭缝的喷流, 使得壁面边界层受到剪切作用, 从而提高系统的传热效率. 本文采用DNS方法对隔板对流装置进行模拟计算, 细致讨论与传热直接相关的物理量——热流的纵向和横向传输特性, 水平横向热流只有热量输运特性, 纵向热流才具有热量传递特性. 对传热通道和狭缝区域的热通量以及对应底板外界输入热通量进行了定量化分析, 探讨在隔板对流系统中热量输运和传递特性. 研究结果表明:
1)向下通道低温流体冲击底板并与高温底板进行热交换, 而后转入水平运动流入狭缝区域并不断被加热, 由于没有纵向热流存在, 狭缝中只进行水平的热量输运, 流出狭缝后的高温流体在传热通道中汇聚形成向上喷流. 此时在高温通道中热量向上传递, 到达低温上底板被冷却, 并通过狭缝进行绕隔板的往复循环流动和传热过程.
2)量化分析向下冷通道、狭缝和向上热通道的热通量变化, 并计算3个区域底板外界输入热通量, 结果表明在这3个区域中外界输入热通量和流体输运热通量守恒.
3)只有水平热量输运的区域对应的底板外界输入的热通量很大, 占总输入热通量的92%. 狭缝区域底板外界输入热通量占总量的64%以上, 纵向热量传递区域对应底板外界输入热通量很小. 外界输入热通量大的区域与系统内部流体进行热量向上传递的区域存在错位, 即底板输入热量大的区域对应的系统内部流体基本无法进行向上的热量传递, 而流体进行向上热量传递的区域对应底板外界输入热量很小.
4)在本文讨论的几何参数变化范围内, 不同参数隔板对流系统都具有增强传热效果. 隔板数目与系统传热Nu数呈近乎线性增加关系. 狭缝高度较小时对应的增强传热较强. 隔板数n = 11及狭缝高度d = 0.01时系统传热Nu数值最大, 是无隔板时的3倍以上.