全文HTML
--> --> -->自Al Balushi等[16]采用外延石墨烯, 通过迁移增强的封装生长法(migration-enhanced encapsulated growth, MEEG)首次成功合成二维GaN材料以来, 二维GaN为自旋电子学器件领域提供了新的材料选择, 而研究重点是如何通过掺杂获得稳定的本征铁磁性, 并提高材料的居里温度(Curie temperature, TC)至室温以上. Dietl等[17]从理论上预测GaN基稀磁半导体(diluted magnetic semiconductors, DMS)的TC可以达到室温以上, 这一理论预测引发了许多关于过渡金属掺杂GaN等宽带隙半导体的实验和理论研究. 随后, Overberg等[18]和Sasaki等[19]相继报道了Mn掺杂GaN的TC在800—900 K. Liu等[20]从实验上观察到Cr掺杂GaN的TC超过900 K. Wu等[21]利用第一性原理研究了Cu掺杂的GaN, Cu浓度为6.25%, 并预测TC可达到350 K. 尽管这些研究显示过渡金属掺杂二维GaN材料可实现高TC的铁磁性, 但传统过渡金属原子掺杂的低维材料会被磁性第二相与磁性团簇等不利于实用的问题所困扰[22,23]. 而d0铁磁性[24,25]的出现, 为这类问题的解决提供了可能, 不同于传统过渡金属原子磁性来源于部分填充的3d或4f轨道[26], 由于d0铁磁性的掺杂原子或离子本身是非磁性的, 其磁性来源于掺杂引起的自旋极化空穴[27-30]或是本征缺陷所带来的未配对电子[31-33], 所以即使是形成了磁性团簇或者磁性第二相也不会对宏观磁性有影响[34]. 近来, Hou等[35]利用第一性原理研究了Al掺杂和空位对ZnO磁性的影响. Huang等[36]通过实验与理论相结合研究了Al掺杂6H-SiC的磁性. d0铁磁性不但在理论上为非磁性材料的磁性起源提供了新的机理, 同时也为制备磁性半导体材料提供了一个新思路.
为了进一步寻找提高TC的途径, 同时探究d0的铁磁性起源机理, 本文采用基于密度泛函(density functional theory, DFT)的第一性原理方法对碱金属(Li, Na, K和Rb)和碱土金属(Be, Mg和Sr)等七种不同元素掺杂二维GaN单层体系的结构、电子、磁性进行了系统研究. 发现在富N条件下更易实现掺杂; 讨论了双原子掺杂系统的磁性耦合机制; 根据掺杂体系的电子态结构, 确定了四种碱金属原子掺杂体系是磁性半导体, 三种碱土金属掺杂体系呈半金属性; 预测了Li, Be, Mg和Sr掺杂二维GaN材料的居里温度均高于室温, 其结论为低维磁性半导体材料在自旋电子中应用提供了有意义的理论参考.
原始的二维GaN单层是从纤锌矿结构GaN的(
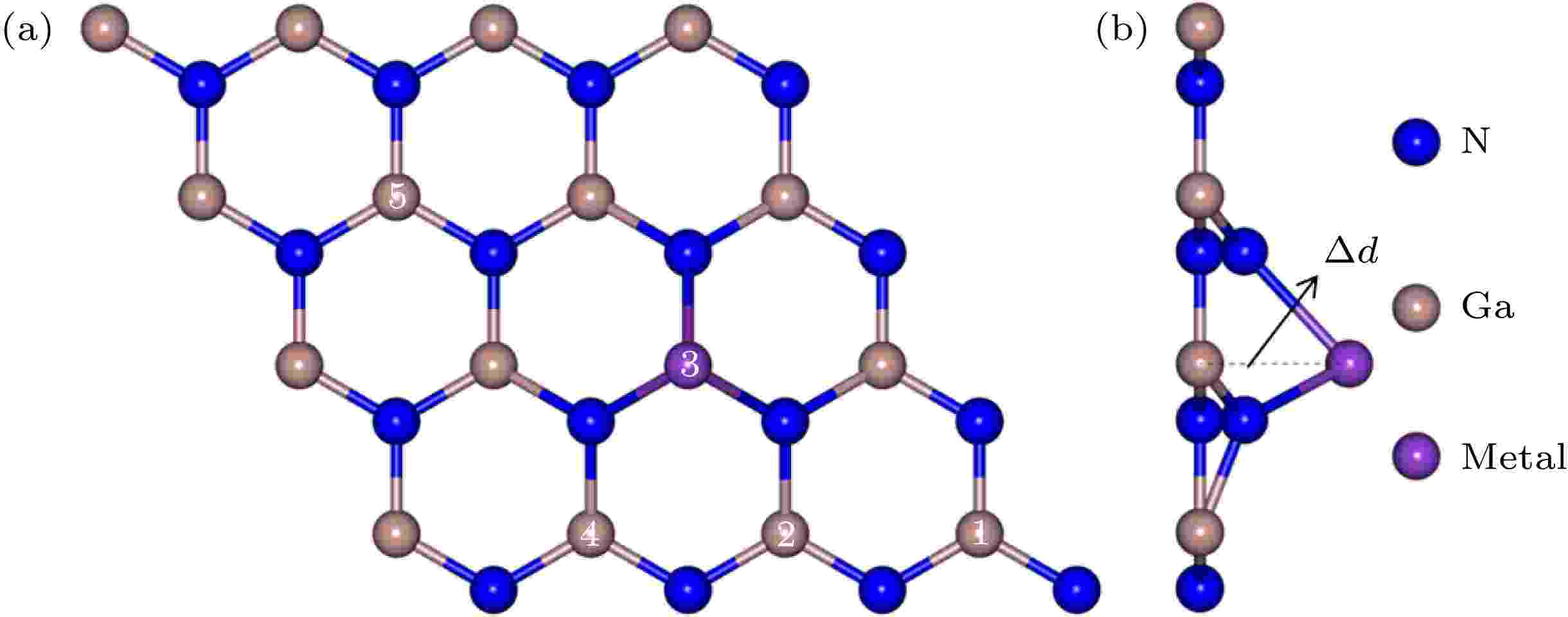图 1 碱金属和碱土金属掺杂GaN单层结构图 (a) 俯视图; (b) 侧视图Figure1. Geometry of alkali and alkali-earth metals doped GaN monolayer: (a) Top view; (b) side view.
3.1.单掺杂体系结构和稳定性分析
为简单起见, 约定以M原子代表碱金属(Li, Na, K和Rb)和碱土金属(Be, Mg和Sr)原子. 如图1(a)所示, 标记为3的Ga原子被一个M原子取代. 首先为了确定稳定的几何结构, 本文采用了两种替位掺杂模式: 1) M原子位于GaN单层平面内, 记为Pin; 2) M原子略微隆起, 高于GaN单层平面, 记为Pout. 对Pin掺杂模式, 结构优化后掺杂原子在非周期方向坐标不会发生变化, 也就是说掺杂原子仍然位于GaN单层平面内. 经过结构优化, 除Be原子掺杂外, 其余Pout掺杂模式的M原子均未回到GaN单层平面内, 因此, 对比这两种模式的能量来判断两种替位掺杂结构的稳定性. 表1列出了Pin和Pout这两种掺杂模式的能量差
| Metals | $\Delta E$/eV | $\Delta d$/? | dM—N/? | ${E_{{\rm{form}}}}$/eV | ${M_{\rm{N}}}/{\mu _{\rm{B}}}$ | ${M_{{\rm{tot}}}}/{\mu _{\rm{B}}}$ | |
| Ga-rich | N-rich | ||||||
| Li | 0.295 | 1.127 | 1.972 | 3.522 | 3.303 | 0.543 | 2 |
| Na | 1.202 | 1.874 | 2.305 | 4.224 | 4.005 | 0.521 | 2 |
| K | 2.436 | 2.482 | 2.657 | 3.734 | 3.515 | 0.531 | 2 |
| Rb | 3.076 | 2.675 | 2.796 | 3.370 | 3.151 | 0.525 | 2 |
| Be | 0.000 | 0.000 | 1.679 | 0.582 | 0.363 | 0.218 | 1 |
| Mg | 0.089 | 0.766 | 1.957 | 3.821 | 3.602 | 0.198 | 1 |
| Sr | 1.956 | 2.031 | 2.382 | 1.324 | 1.105 | 0.239 | 1 |
表1两种掺杂模式的能量差
Table1.Energy difference
通过结构优化研究了M原子掺杂GaN单层的几何结构和局域结构特征. 表1列出了结构优化之后的M—N键长分别为1.972, 2.305, 2.657, 2.796, 1.679, 1.957和2.382 ?. 掺杂原子到GaN平面的距离分别为1.127, 1.874, 2.482, 2.675, 0.000, 0.766和2.031 ?. 通过数据可以看出, 对于同一族元素, 随着掺杂原子半径增大, M—N键长度增加且局域结构畸变程度变大. 这些变化降低了原子间的静电斥力, 使掺杂系统的能量更低.
为了分析掺杂的难易程度, 本文计算了M原子掺杂GaN单层的形成能
2
3.2.掺杂体系磁性和自旋电荷密度分析
为了分析掺杂体系磁性, 本文计算了7种M原子掺杂GaN单层体系的总磁矩和M原子3个最近邻N原子的局域磁矩, 计算结果列于表1, 其中碱金属和碱土金属原子掺杂体系总磁矩分别为2μB和1μB. 由于碱金属和碱土金属相比于Ga原子而言, 价电子分别减少2个和1个, 而每减少一个价电子就会为掺杂体系带来一个空穴, 导致1μB磁矩的产生, 理论预测与计算结果一致. 7种掺杂体系掺杂原子周围三个最近邻N原子磁矩分别为0.543μB, 0.521μB, 0.531μB, 0.525μB, 0.218μB, 0.198μB和0.239μB, 三个N原子总磁矩与体系总磁矩相差非常小.M原子掺杂GaN单层的自旋电荷密度分布(即自旋向上与自旋向下之差)如图2所示, 通过分析自旋电荷密度分布可以了解掺杂体系磁性起源. 从图2可以看出, 掺杂体系的总磁矩主要由掺杂原子最近邻的3个N原子提供, 超晶胞中剩余的其他N原子也有少量贡献, 但掺杂的7种M原子几乎对掺杂体系总磁矩没有任何贡献. 表1中N原子磁矩和图2所示的自旋电荷密度分布均呈现一个很明显的现象, 即自旋电荷密度分布存在局域性和扩展性. 首先, 整个掺杂体系绝大部分自旋电荷密度集中在掺杂原子最近邻的3个N原子上, 而掺杂体系所形成的自旋极化基态和局域磁矩正是这种强局域性导致的. 其次, 除了掺杂原子最近邻的3个N原子以外, 整个体系中剩余的N原子上几乎均有自旋电荷密度分布, 尽管都较微弱, 但也扩展到了整个超晶胞中, 而局域磁矩之间的长程磁性耦合可能是依靠这种扩展到整个超晶胞的自旋极化态来调节的[33,48,49].
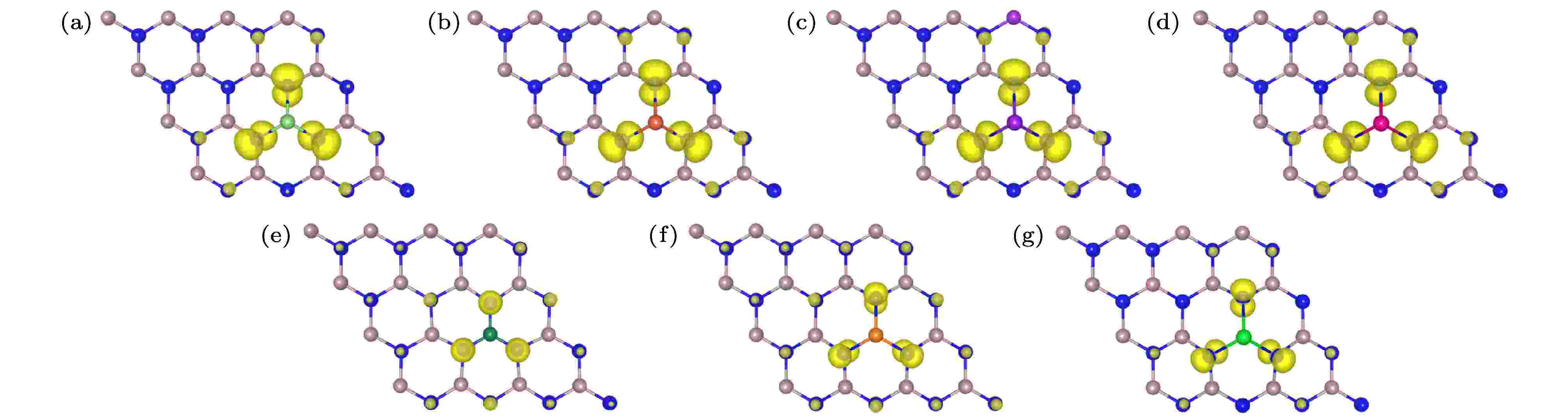图 2 单原子掺杂GaN单层的自旋电荷密度分布图, 等值面为0.004 eV/? (a) Li掺杂; (b) Na掺杂; (c) K掺杂; (d) Rb掺杂; (e) Be掺杂; (f) Mg掺杂; (g) Sr掺杂Figure2. Spin charge density distributions of single atom doped GaN monolayer, isosurface is 0.004 eV/?: (a) Li doping; (b) Na doping; (c) K doping; (d) Rb doping; (e) Be doping; (f) Mg doping; (g) Sr doping.
2
3.3.掺杂体系电子结构分析
为了进一步在电子结构上解释图2中的自旋电荷密度分布并了解掺杂体系的电子结构, 计算了7种掺杂体系的总态密度(density of states, DOS)和分波态密度(partial density of states, PDOS), 结果如图3所示. 图3(a)中未掺杂GaN单层DOS的自旋向上态和自旋向下态是对称的, 因此纯GaN单层是非磁性的. 而对于图3(b)—(h)中M原子掺杂GaN单层DOS的自旋向上态和自旋向下态是非对称的, 在费米能级附近呈现自旋劈裂, 这意味着自旋简并性被打破, 表明了一种净磁化现象的存在. 其中图3(b)—(e)中碱金属原子掺杂体系DOS的自旋向上态和自旋向下态均没有穿过费米面, 掺杂体系呈现磁性半导体性质. 图3(f)—(h)中碱土金属原子掺杂体系DOS的自旋向下态穿过费米面, 掺杂体系呈现半金属性质. 从图3中还发现, 在费米能级附近DOS都是由N原子贡献, 掺杂原子几乎没有贡献, 也验证了分析图2得出的结论.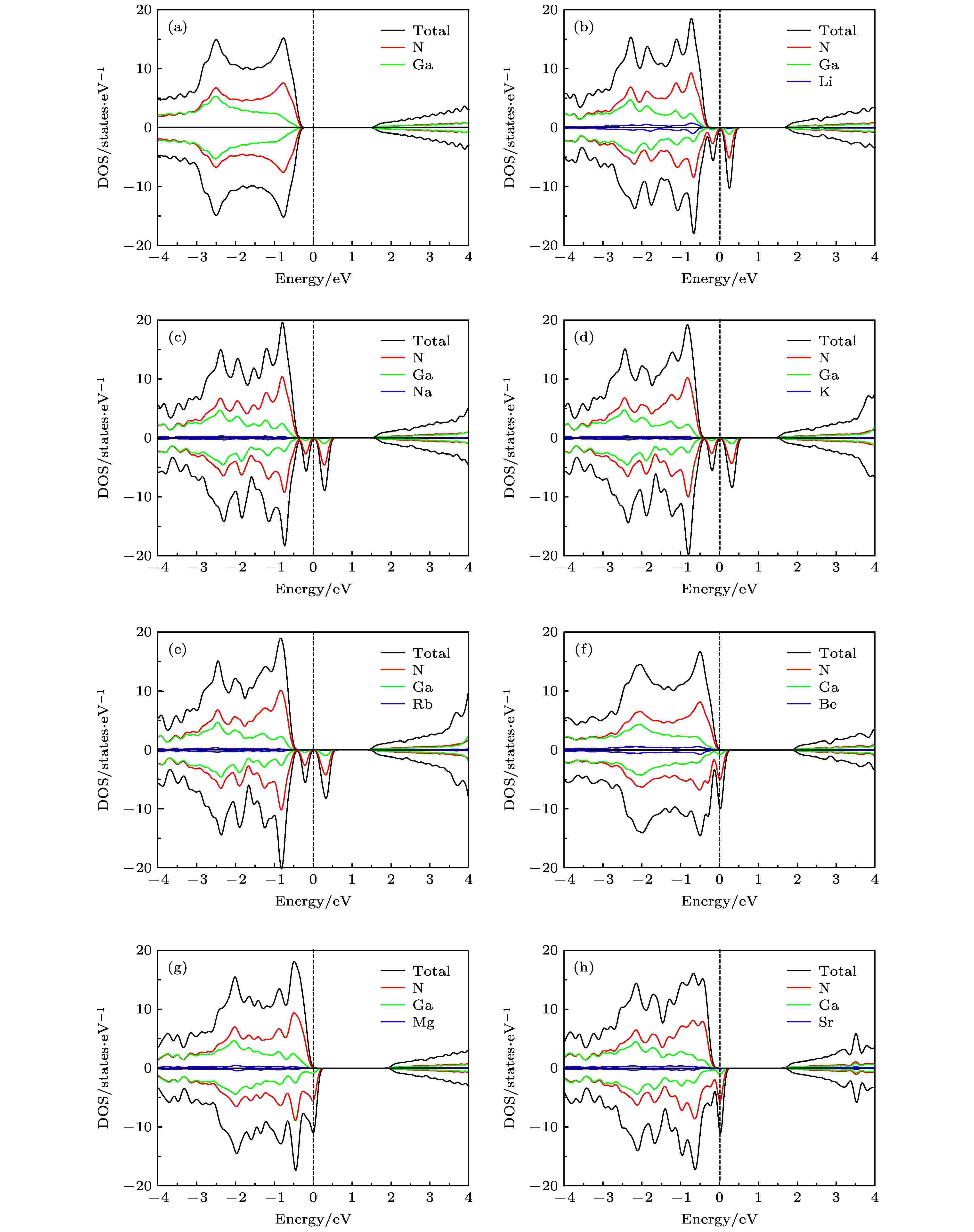
图 3 单原子掺杂GaN单层的自旋DOS和PDOS图 (a) 未掺杂; (b) Li掺杂; (c) Na掺杂; (d) K掺杂; (e) Rb掺杂; (f) Be掺杂; (g) Mg掺杂; (h) Sr掺杂Figure3. Spin resolved total DOS and PDOS of GaN monolayer doped single-atom: (a) Pristine; (b) Li doping; (c) Na doping; (d) K doping; (e) Rb doping; (f) Be doping; (g) Mg doping; (h) Sr doping.
下面将结合能带结构, 进一步分析掺杂体系的电子性质. 图4(a)中未掺杂GaN能带结构的自旋向上和向下对称, 因此纯GaN单层是非磁性的. 图4(b)—(h)显示上文所述的因掺杂原子引入而产生空穴导致掺杂体系引入了受主能级, 受主能级处于禁带中, 从而使掺杂体系比未掺杂之前能带隙减小, 显然这样的变化会影响材料的光学、电学和磁学特性. 从图4(b)—(h)中可以清楚地发现, 受主能级均只出现在自旋向下部分中, 其中图4(b)—(e)显示, 在自旋向下电子态中, 受主能级并没有穿过费米能级, 表明Li, Na, K和Rb掺杂的GaN单层由非磁性半导体变为了磁性半导体; 图4(f)—(h)显示, 在自旋向下态中, 受主能级穿过了费米能级, 表明Be, Mg和Sr掺杂体系都呈现出具有100%自旋极化的半金属特性, 这些掺杂体系可作为自旋电子学器件备选材料.
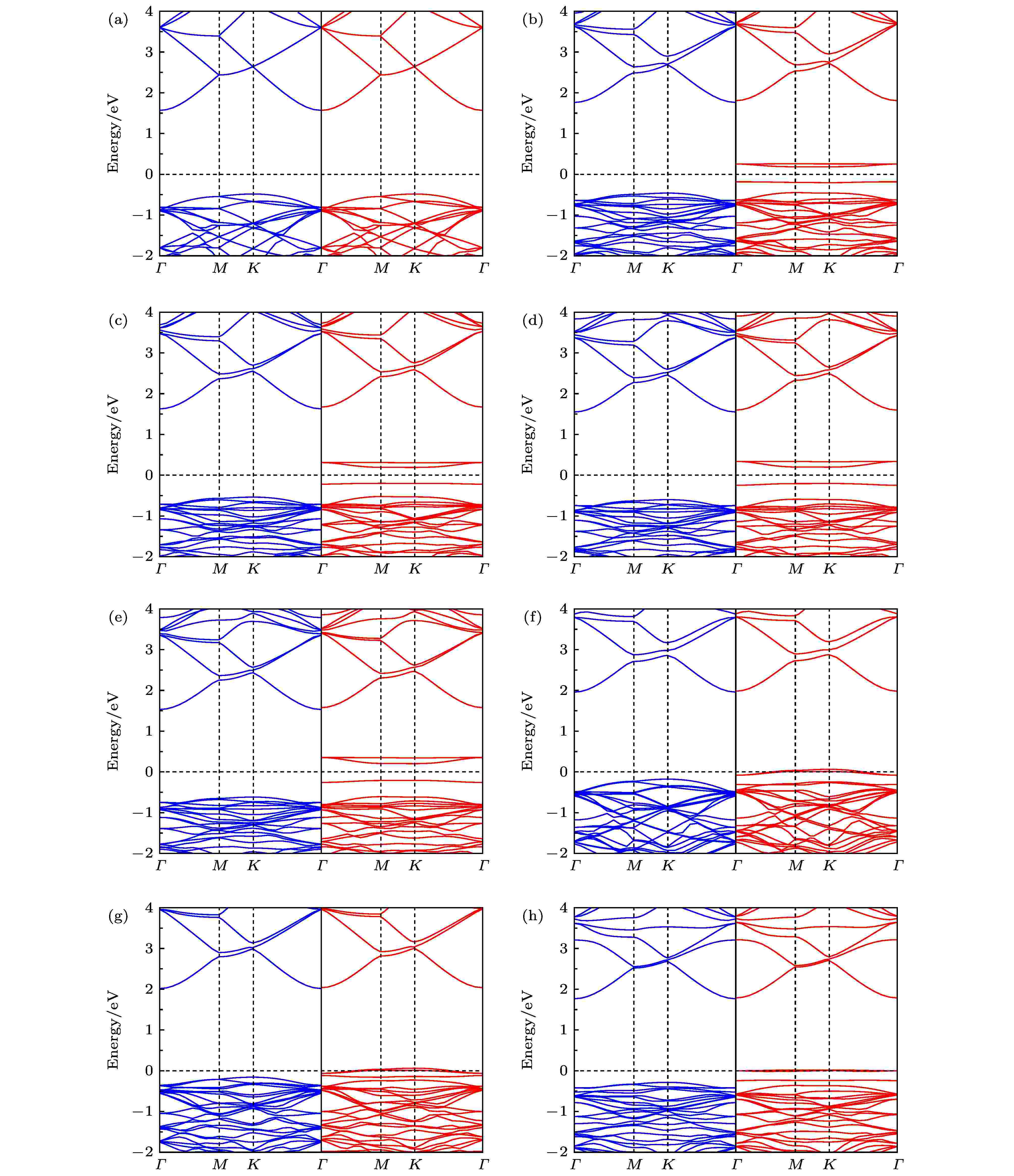图 4 单原子掺杂GaN单层的能带结构, 图中蓝与红分别代表自旋向上与向下 (a) 未掺杂; (b) Li掺杂; (c) Na掺杂; (d) K掺杂; (e) Rb掺杂; (f) Be掺杂; (g) Mg掺杂; (h) Sr掺杂Figure4. Band structures for single atom doped GaN monolayer, the blue and the red respectively represent the spin up and the spin down: (a) Pristine; (b) Li doping; (c) Na doping; (d) K doping; (e) Rb doping; (f) Be doping; (g) Mg doping; (h) Sr doping.
2
3.4.掺杂体系磁性机理分析
对于Be原子掺杂体系, 掺杂原子处于GaN单层平面内, 以Be原子为中心与周围最近邻3个N原子形成D3h对称结构. 对于除Be以外的原子掺杂体系, 掺杂原子隆起于GaN单层平面, 导致其周围最近邻N原子也凸出平面, 如图5(a)中虚线标记的三角形区域所示, N原子与周围原子几乎处于同一平面内, 也可以近似看作D3h对称结构. 严格来说, 由于M原子掺杂导致局部畸变破坏了这种对称性, 但是以N原子为中心的局部结构始终处于同一平面, 结构畸变只是使N原子与其周围三个原子所成键的键长不同, 对结构破坏微小, 因此, 文中针对两种掺杂模式中掺杂原子最近邻N原子均采用D3h对称性来定性分析其磁性来源. 在这种晶场对称性下, N-2p态由三重简并态劈裂为一个高能量的单重态a2 (pz)和一个低能量的双重简并态 exy (px和py)[50]. 上文中提到碱金属和碱土金属原子取代Ga原子导致所贡献价电子减少, 为掺杂体系分别带来2个和1个空穴, 而体系总磁矩来源于N-2p态未被占据的自旋极化空穴. 掺杂原子最近邻3个N原子磁矩相等, 因此N-2p态为部分填充. 碱金属的1个价电子分别填充了周围3个N原子pz轨道的1/3, 导致每个N原子pz轨道有2/3未被填充, 即掺杂体系的总磁矩为2μB (图5(b)). 同理, 碱土金属的2个价电子分别填充了周围3个N原子pz轨道的2/3, 即掺杂体系的总磁矩为1μB. 同时, 利用Bader电荷分析[51,52]计算了M原子最近邻N原子的电荷转移情况, 其中碱金属(Li, Na, K和Rb)与碱土金属(Be, Mg和Sr)掺杂体系中掺杂原子最近邻N原子分别得到2.34e, 2.32e, 2.32e和2.32e以及2.71e, 2.69e, 2.65e的电荷, 由于N原子2p轨道已被3e占据, 得到的电子填充剩余未被占据轨道, 由此得到pz轨道分别有近似2/3和1/3未被填充, 与上文中N原子pz轨道填充分析一致.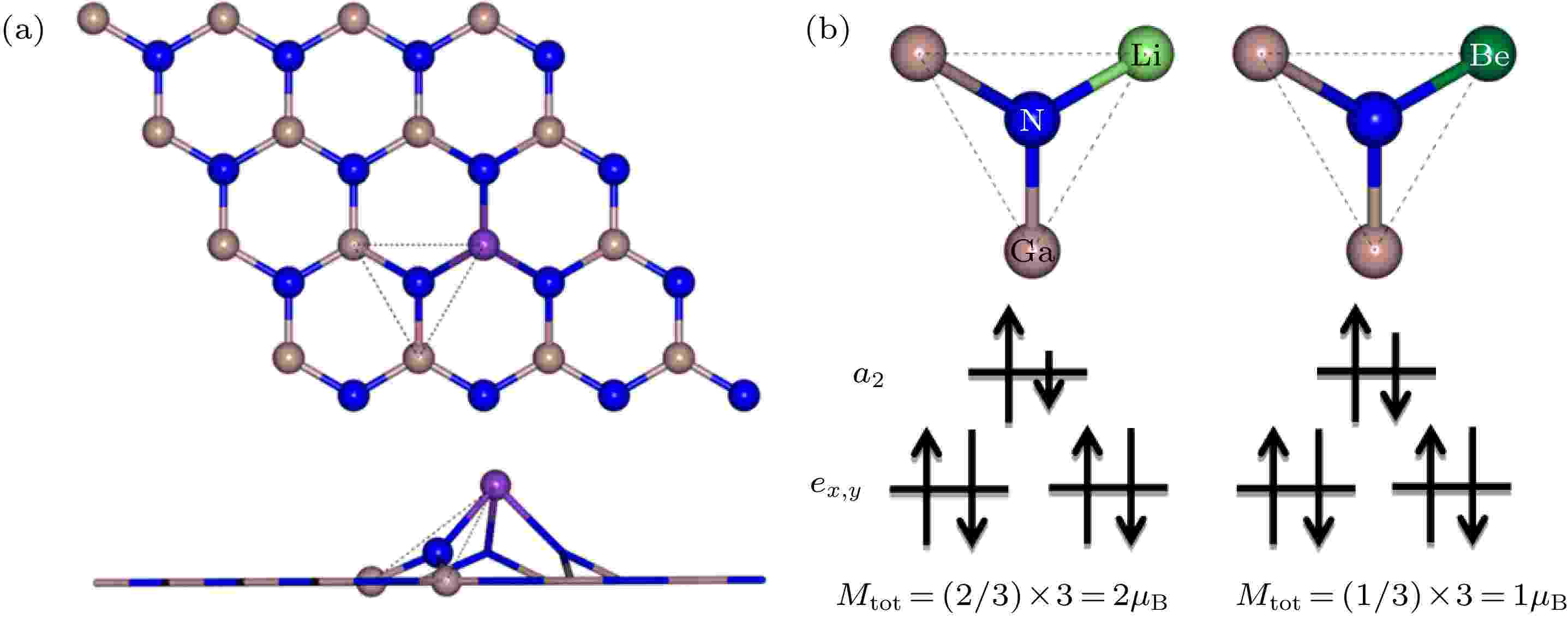
图 5 (a) 掺杂原子最近邻N原子为中心的局部结构俯视图和侧视图; (b) Li, Be掺杂原子最近邻N原子能级劈裂及电子填充示意图Figure5. (a) Top and side views of a local structure centered on the nearest neighboring N atom of the doped atom; (b) schematic diagram of the energy-level splitting and electron filling of the nearest N atom of the Li, Be-doped atom.
尽管前文中针对两种掺杂模式中掺杂原子最近邻N原子都近似采用D3h对称性来具体分析其磁性来源, 但是二者仍然存在差异, 接下来将进一步对掺杂原子3个最近邻N原子的p轨道进行分析, 其p轨道态密度如图6所示. 从图6可以看出, Be原子掺杂体系在费米能级附近的态密度主要由pz轨道贡献, px和py轨道几乎与图6(a)中未掺杂体系N原子一致, 这也表明以最近邻N原子为中心的局部结构受到结构畸变的影响很小, 与上文分析相符合. 对于除Be以外的原子掺杂体系, 则px, py和pz轨道均有贡献, 这是因为掺杂原子隆起于GaN单层平面, 并导致其周围最近邻N原子也凸出平面(图5(a)), 这将导致N原子的pz也会随之倾斜, 与GaN单层平面产生一定夹角, 图2中也显示其电子云的倾斜, 由于各掺杂体系变形程度不同, 从而产生不同的px, py和pz分量.
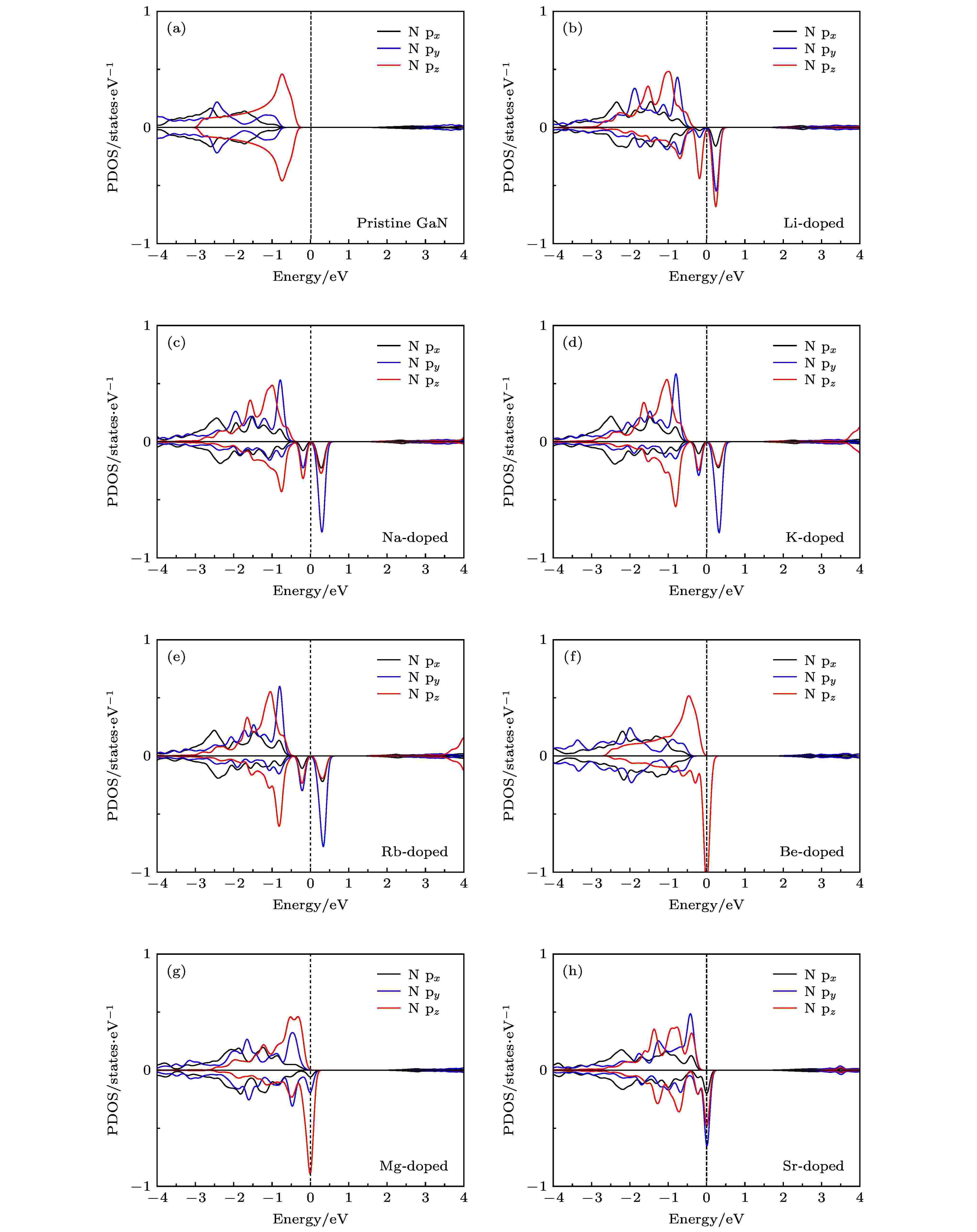图 6 掺杂原子最近邻N原子的p轨道态密度图 (a) 未掺杂; (b) Li掺杂; (c) Na掺杂; (d) K掺杂; (e) Rb掺杂; (f) Be掺杂; (g) Mg掺杂; (h) Sr掺杂Figure6. The p-orbital DOSs of the nearest neighbor N atom of doped atom: (a) Pristine; (b) Li doping; (c) Na doping; (d) K doping; (e) Rb doping; (f) Be doping; (g) Mg doping; (h) Sr doping.
2
3.5.双M原子掺杂GaN单层的磁性耦合分析
材料在自旋电子器件的实际应用中, 存在室温及室温以上的宏观铁磁性是关键, 然而局部磁矩的存在并不一定会产生宏观磁性. 为了确认室温及室温以上的宏观铁磁性是否存在于碱金属和碱土金属原子掺杂的GaN单层中, 设计了4种构型计算磁性耦合, 掺杂浓度为6.25%. 如图1(a)所示, 由两个相同的M原子分别取代1和2, 1和3, 1和4, 1和5位置的Ga原子, 这4种不同构型M原子间距逐渐增大, 分别记为C1, C2, C3, C4. 文中分别计算了4种掺杂构型的反铁磁耦合态(antiferro magnetism, AFM)和铁磁耦合态(ferro magnetism, FM)能量差, 通过比较二者能量高低判断哪种磁耦合态更稳定. 对双M原子掺杂体系计算依然考虑Pin和Pout两种模式, 经过结构优化后, 除Be双原子掺杂以外, 其余Pout掺杂模式的双M原子均未回到GaN单层平面内, 优化结果与单M原子掺杂GaN单层一致. 结构优化后的两个M原子的距离
| Metals | Configurations | ${d_{{\rm{M}} - {\rm{M}}}}$/? | ${E_{{\rm{RS}}}}$/eV | $\Delta E$/eV | ${M_{ {\rm{tot} } } }/{\mu _{\rm B}}$ | Coupling |
| Li | C1 (1, 2) | 3.315 | 0.000 | 0.313 | 4 | FM |
| C2 (1, 3) | 5.663 | 0.318 | 0.049 | 4 | FM | |
| C3 (1, 4) | 6.475 | 0.222 | 0.596 | 4 | FM | |
| C4 (1, 5) | 11.215 | 0.222 | 0.034 | 4 | FM | |
| Na | C1 (1, 2) | 3.662 | 0.000 | 0.308 | 4 | FM |
| C2 (1, 3) | 5.706 | 0.329 | 0.033 | 4 | FM | |
| C3 (1, 4) | 6.475 | 0.216 | 0.481 | 4 | FM | |
| C4 (1, 5) | 11.215 | 0.216 | 0.014 | 4 | FM | |
| K | C1 (1, 2) | 4.147 | 0.000 | 0.318 | 4 | FM |
| C2 (1, 3) | 5.789 | 0.276 | 0.032 | 4 | FM | |
| C3 (1, 4) | 6.475 | 0.142 | 0.239 | 4 | FM | |
| C4 (1, 5) | 11.215 | 0.142 | 0.022 | 4 | FM | |
| Rb | C1 (1, 2) | 4.326 | 0.000 | 0.322 | 4 | FM |
| C2 (1, 3) | 5.842 | 0.272 | 0.096 | 4 | FM | |
| C3 (1, 4) | 6.475 | 0.137 | 0.240 | 4 | FM | |
| C4 (1, 5) | 11.215 | 0.137 | 0.019 | 4 | FM | |
| Be | C1 (1, 2) | 3.168 | 0.068 | 0.289 | 2 | FM |
| C2 (1, 3) | 5.597 | 0.000 | 0.000 | 2 | FM | |
| C3 (1, 4) | 6.475 | 0.100 | 0.148 | 2 | FM | |
| C4 (1, 5) | 11.215 | 0.100 | 0.119 | 2 | FM | |
| Mg | C1 (1, 2) | 3.359 | 0.000 | 0.241 | 2 | FM |
| C2 (1, 3) | 5.651 | 0.035 | –0.003 | 2 | FM | |
| C3 (1, 4) | 6.475 | 0.080 | 0.068 | 2 | FM | |
| C4 (1, 5) | 11.215 | 0.079 | 0.168 | 2 | FM | |
| Sr | C1 (1, 2) | 4.092 | 0.049 | 0.194 | 2 | FM |
| C2 (1, 3) | 5.868 | 0.124 | 0.076 | 2 | FM | |
| C3 (1, 4) | 6.475 | 0.000 | –0.002 | 0 | AFM | |
| C4 (1, 5) | 11.215 | 0.002 | 0.352 | 2 | FM |
表2结构优化后两掺杂原子的距离
Table2.Distance between the two doped atoms after structural optimization
采用基于平均场近似理论的海森伯模型简单估算掺杂体系的TC,
为进一步研究宏观铁磁性起源, 图7(a)和(b)分别给出了Mg掺杂C4构型的自旋电荷密度图和Mg原子及其近邻N原子(由近及远分别标记为1 N, 2 N, 3 N)的PDOS. 在Mg掺杂的C4构型中, 两个掺杂原子的距离为11.215 ?, 很明显这种掺杂体系的铁磁耦合是长程的, 而长程磁耦合是在低浓度下掺杂实现高温铁磁性的关键[54]. 从图7(b)可以看出, Mg-2p态自旋向上和向下是对称的并没有发生劈裂, 而三个N原子N-2p态在费米能级处均发生自旋极化且有明显的重叠, 表明三个N原子之间存在p-p杂化相互作用[48,55]. 同时, 还可以看出最近邻N原子自旋极化非常强烈, 随着远离掺杂原子, 2N-2p和3N-2p态自旋极化越来越弱, 验证了上文所述的强局域性和扩展性. 这种强局域性削弱了局域之间的直接耦合, 而正是掺杂原子波函数缓慢衰减的扩展尾部诱导了掺杂引起的局域磁矩之间的长程磁耦合[33,48]. 从图7(a)可以看出, 扩展到整个体系的自旋极化空穴在p-p杂化相互作用的影响下呈现相同的自旋取向, 从而导致了体系的长程铁磁耦合. 也就是说, 因掺杂引入的空穴扩展到整个体系且受p-p杂化相互作用影响呈现相同的自旋极化方向, 从而促成了体系的长程铁磁耦合.
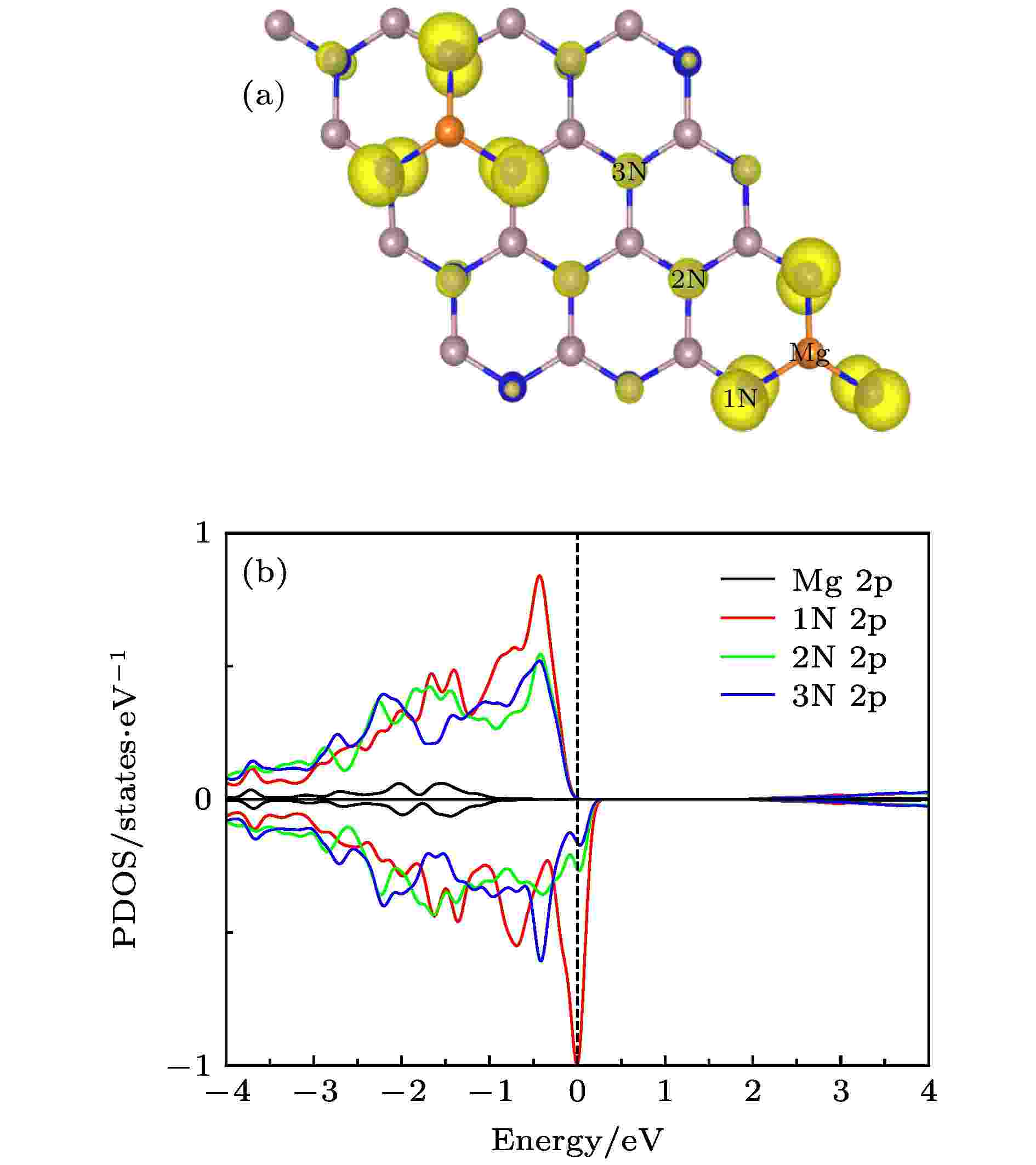图 7 (a) Mg掺杂C4构型的自旋电荷密度分布图, 等值面为0.02 eV/?; (b) Mg掺杂C4构型中Mg-2p, 1N-2p, 2N-2p和3N-2p的PDOSFigure7. (a) Spin charge density distribution of the Mg-doped C4 configuration, the isosurface is 0.02 eV/?; (b) PDOS of Mg-2p, 1N-2p, 2N-2p and 3N-2p in the Mg-doped C4 configuration.
