全文HTML
--> --> -->由拓扑体系中的铁磁或反铁磁长程序构造的磁性拓扑材料一直是吸引理论和实验研究的一个重要方向. 在磁性拓扑材料中, 时间反演对称性的缺失带来了崭新的物理现象. 例如当铁磁序被引入到三维拓扑绝缘体中时, 原本相交于一点的狄拉克锥拓扑表面态将打开一个磁性能隙, 当费米面恰好位于磁性能隙之中时, 量子反常霍尔效应就能够被实现. 这正是文献[31-36]发现量子反常霍尔效应时采取的技术路线. 又例如在具有反铁磁基态的拓扑体系中, 即使时间反演对称性和某些空间平移对称性本身破缺, 但其乘积可以成为一个新的Z2拓扑不变量, 支持无能隙的狄拉克锥拓扑表面态[37]. 目前磁性拓扑体系的研究仍方兴未艾, 可以预见, 磁性拓扑体系将是未来数年间拓扑材料研究的主要着力点和突破口.
角分辨光电子能谱 (angle-resolved photoemission spectroscopy, ARPES) 是固态物理学最成功的实验手段之一. 它独特的k空间分辨的单电子探测能力以及简单易明的数据形式使它受到理论和实验工作者的一致青睐. 从高温超导、拓扑不寻常体系等基础研究的热点, 到太阳能电池、自旋电子学等应用研究的前沿, ARPES技术在物理机理的探究和新材料的实验证实方面都扮演了重要的角色. 在拓扑不寻常体系的课题中, ARPES更一直是研究的中坚力量. 它能够直接观测到晶体材料的体能带和表面能带结构, 以非常直观的方式证明某一材料是不是拓扑材料, 以及是哪一类拓扑材料. 因此, ARPES技术往往是继理论预言和单晶生长之后, 实验研究首先使用的技术, 几乎所有种类的拓扑材料都是由ARPES技术首先发现的[9-12,14,16,20,21,38-51]. 本文试从材料分类的角度对2008年以来拓扑绝缘体的部分ARPES研究进展作一综述, 侧重于通过案例研究归纳出每一系列拓扑绝缘体的实验能带特征, 以及利用ARPES研究此系列材料的一般方法和过程. 限于篇幅, 本文仅讨论强三维拓扑绝缘体和磁性拓扑绝缘体的ARPES研究进展, 不涉及 TCI, TKI, 弱三维拓扑绝缘体、拓扑超导体和基于拓扑绝缘体的异质结构等.
本文的结构安排如下. 第2章介绍ARPES的基本原理, 着重介绍自旋分辨ARPES、时间分辨ARPES等较新的ARPES实验手段, 以及解释光电效应的常用理论(三步模型和一步模型). 第3章讨论各类强三维拓扑绝缘体的ARPES研究, 以Bi2Se3系列为重点. 第4章讨论各类磁性拓扑绝缘体的ARPES研究, 以MnBi2Te4系列为重点. 第5章对本文内容作一小结.
本文假定读者具有ARPES的基本知识, 因此对普通ARPES的原理不做详细讨论, 而着重介绍几种新型的ARPES实验手段, 以及光电子能谱学中的三步模型和一步模型的发展. 对ARPES基础概念不太熟悉的读者可以参阅文献[53-58] 以及文献[59] 的第2章内容. 本节的结构安排如下: 2.1节介绍圆二色性ARPES和自旋分辨ARPES的原理和基本的数据分析方法; 2.2节介绍时间分辨(泵浦)ARPES和双光子ARPES的原理和基本的数据分析方法; 2.3节粗略介绍一下三步模型; 2.4节对一步模型的核心内容作一简要介绍, 并尝试说明自旋分辨ARPES, 圆二色性ARPES和时间分辨ARPES的一步模型构建原则; 2.5节对时域能带结构, 即Floquet机制作一个粗略的介绍.
2
2.1.圆二色性ARPES和自旋分辨ARPES的基本原理
所谓圆二色性ARPES (circular dichroic ARPES, CD-ARPES), 指的是依次使用左旋圆偏振光 (σ+) 和右旋圆偏振光 (σ–) 作为入射光测量同一E-k平面的能带结构, 分别获得光电子强度 Iσ+ 和 Iσ-, 然后研究不同动量和束缚能下二者的差, 换算得圆二色性信号
自旋分辨ARPES (spin-resolved ARPES, SARPES)技术(见图1[58,71,72])利用安装在ARPES电子分析仪光电子成像端的自旋分析仪直接测量光电子的自旋, 即依次测量自旋分析仪对空间中沿j方向 (j = x, y, z) 的两个相反方向自旋(





 图 1 自旋分辨ARPES原理及示意图[58,71,72] (a) Mott自旋分析仪的原理示意图[58]; (b) Mott自旋分析仪的设计示意图[71]; (c) 加入两个互相垂直的VLEED自旋分析仪的一个ARPES系统(东京大学Shin-Kondo小组)[72], 其中VLEED的设计来自广岛大学Okuda小组
图 1 自旋分辨ARPES原理及示意图[58,71,72] (a) Mott自旋分析仪的原理示意图[58]; (b) Mott自旋分析仪的设计示意图[71]; (c) 加入两个互相垂直的VLEED自旋分析仪的一个ARPES系统(东京大学Shin-Kondo小组)[72], 其中VLEED的设计来自广岛大学Okuda小组Figure1. Principles and skematics of spin-resolved ARPES[58,71,72]: (a) Principle of the spin-selective exchange interaction used in a Mott spin detector[58]; (b) design skematics of a Mott spin detector[71]; (c) skematics of an ARPES system equipped with two parallelly arranged VLEED spin detectors[72], the design of which were adapted from Team of Okuda in Hiroshima University.
2
2.2.时间分辨ARPES和双光子ARPES的基本原理
普通的ARPES技术探测的是系统稳恒态时位于费米面以下的占据态电子学结构, 但不能探测系统的非占据态能带以及从激发态向稳恒态弛豫的过程. 时间分辨ARPES (time-resolved ARPES, trARPES)技术(图2[89,90])弥补了这个缺陷[68,69,72,77,78,88-96]. 它的原理是利用超快激光泵浦技术分别生成百飞秒 (100 fs) 级的激发光脉冲和探测光脉冲, 激发光把样品从基态激发到激发态, 而(通常能量比较高的)探测光则完成光电效应, 以普通ARPES方法记录不同动量、能量的光电流. 激发光和探测光到达样品的时间差由压电晶体等精确调节. 由于泵浦ARPES的时间尺度 Δt 和能量分辨率 ΔE 受海森伯不确定性原理


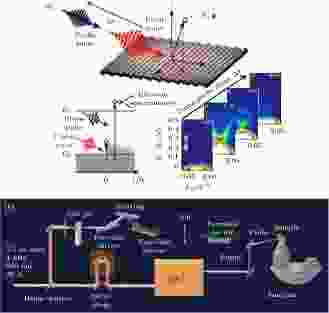 图 2 时间分辨ARPES原理及示意图[89,90] (a) 时间分辨ARPES原理图[89]; (b) 时间分辨ARPES的一种设计[90], 利用掺钛蓝宝石激光器发出的800 nm基频红外激光作为激发光, 再利用基于气体谐振腔的高次谐波发生器生成基频激光的高阶倍频光, 并以之作为探测光
图 2 时间分辨ARPES原理及示意图[89,90] (a) 时间分辨ARPES原理图[89]; (b) 时间分辨ARPES的一种设计[90], 利用掺钛蓝宝石激光器发出的800 nm基频红外激光作为激发光, 再利用基于气体谐振腔的高次谐波发生器生成基频激光的高阶倍频光, 并以之作为探测光Figure2. Principles and skematics of time-resolved ARPES[89,90]: (a) Principles of time-resolved ARPES[89]; (b) design example of a time-resolved ARPES system[90], using the 800 nm inferred radiation from a Ti:sapphire laser as the pump beam and its high hamonics produced by a gas jet as the probe beam.
与上述trARPES不同, 在时间-角分辨双光子光电效应 (time- and angle-resolved two-photon photoemission, TR & AR 2PPE) [55-58,97,98]中, 光电子在被发射前要吸收两个能量低于样品功函数的光子(γ1和γ2). 第一个光子(γ1)被低于样品费米能级EF的电子吸收并使其激发至中间态(该中间态可以是杂质能级等), 第二个光子 (γ2) 被位于中间态的同一个电子再次吸收并使其进一步激发到真空能级Evac之上, 继而发生光电子发射. 由此, 中间态的色散关系便可以通过测量这些光电子的动能和动量获得. 通过调节 γ1 和 γ2 之间的时间延迟, 也可以实现亚飞秒级的时间分辨率. 激发光 γ1 在样品中产生非平衡的电子分布, 延时的探测光γ2 监测中间态的弛豫动力学, 如粒子数衰减或载流子局域化等.
2
2.3.三步模型
Berglund 和 Spicer[99]在1964年提出了描述光电效应的第一个模型—三步模型 (three-step model), 把入射光激发固体中的电子、电子输运到晶体表面和电子透过表面势垒出射到真空看作三个接续的、可以分开描述的过程. 三步模型中用到的近似手段有费米黄金公式(Fermi’s golden rule)中的 δ 函数能级跃迁形式, 以及所谓的“瞬时近似 (sudden approximation)”, 即忽略光电子在晶体中输运的过程中晶格的弛豫以及光电子对晶格的影响. 根据三步模型, ARPES实际测得的光电子强度











光电效应矩阵元


2
2.4.一步模型
完整的光电效应过程涉及到不同能量、偏振的入射光对不同轨道、不同原子层的电子的复杂相互作用, 对它的理论理解实际上超出了三步模型的范畴, 而必须运用“一步模型(one-step model)”来解释. 一步模型把三步模型中的三个接续过程看成单一的量子相干过程, 并考虑所有的多重散射效应. 在一步模型里, 费米黄金公式和瞬时近似仍然有效. 模型的核心公式如下[100]:















为了直接求得光电流(即ARPES信号强度)














在激发光激发系统之前 (t = –∞), 系统处于由哈密顿量









受到哈密顿量为



















2
2.5.时域周期势场中的能带—Floquet机制
类似于空间周期性势场中电子形成的动量轴上的Bloch能带结构, 电子在遇到时间周期性势场时, 也会在能量轴上形成重复的本征态. Bloch机制告诉我们, 当哈密顿量满足














2
3.1.Bi1–xSbx和几种单质拓扑绝缘体
虽然Bi2Se3系列的拓扑绝缘体只在




 图 3 ARPES实验发现的第一类强三维拓扑绝缘体—Bi1-xSbx合金和Sb单晶[10] (a) Bi1–xSbx
图 3 ARPES实验发现的第一类强三维拓扑绝缘体—Bi1-xSbx合金和Sb单晶[10] (a) Bi1–xSbx



Figure3. The first 3 D topological insulators, Bi1-xSbx and Sb, discovered by ARPES[10]: (a) ARPES band structure along




文献[10] 也利用SARPES讨论了Sb单质(相当于x = 1)的能带和拓扑性, 指出其

也有不少文献研究单质拓扑绝缘体的单层或少层薄膜. 这些薄膜由分子束外延(molecular beam epitaxy, MBE) 等技术在不同的衬底上生长. 可以想象, 当体系的厚度越薄, 其上下表面的耦合就会变得越强, 最终使表面态打开能隙, 使体系产生拓扑相变而成为普通绝缘体(详见3.2.8节对Bi2Se3系列TI薄膜的讨论). 但在很多情况下, 用以生长薄膜的衬底对薄膜的影响不可忽略. 例如Bian等[118] 利用ARPES研究了在Si(111) 表面生长的8层(4个双层)Sb薄膜的拓扑性质, 发现表面态能隙并未打开, 和悬空的8层Sb的计算结果不符. 这表示硅衬底对这个样品的拓扑性质起了决定性的作用. Ohtsubo等[108] 和Takayama等[119] 分别对 α-Sn和双层Bi这两种单质拓扑绝缘体进行了普通ARPES和自旋分辨ARPES测量, 指出 α-Sn在层数在某个范围内(例如30层和34层)时才是TI, 太薄和太厚时均不是; 而Bi表面态的自旋极化P高度依赖于层数. 上海交通大学Miao等[120] 研究生长在Bi2Te3表面的双层Bi薄膜, 发现体系的狄拉克点在能量方向上有一定的拉长, 形成单粒子能带理论不允许的“无穷费米速度”的竖直色散关系, 并指出此现象来源于Bi2Te3衬底与双层Bi中狄拉克准粒子的耦合.
值得注意的是, 研究者还在岛状生长的拓扑绝缘体的边缘利用ARPES找到了纯一维的金属性边缘态的色散信号. Takayama等[121]在Si(111) 表面生长的, 面积小于ARPES入射光斑大小的Bi岛状结构的ARPES谱中, 在原本没有任何信号的位置发现了很弱的Rashba形的能带, 且这种能带在kx方向完全没有色散. 这项研究证实ARPES不仅对二维表面态敏感, 也具有一维边缘态的k空间分辨能力.
2
3.2.Bi2Se3系列拓扑绝缘体
真正典型的、满足TI最简模型且激发了爆炸式研究浪潮的强三维TI是Bi2Se3系列, 包括Bi2Se3, Bi2Te3和Sb2Te3这三种化合物(Sb2Se3是否为TI存在争议). 这些化合物都是以五个原子层 (quintuple layer) 为一个基本重复单元, 单元之间以极弱的范德瓦尔斯力结合的准二维层状材料, 非常适于ARPES, STM等表面物理技术的研究. 2009年, 斯坦福大学Chen等[11] 以及普林斯顿大学Xia等[12] 和Hsieh等[122,123] 几乎同时利用ARPES指出此类化合物的拓扑不寻常属性. 他们发现这一类化合物仅在
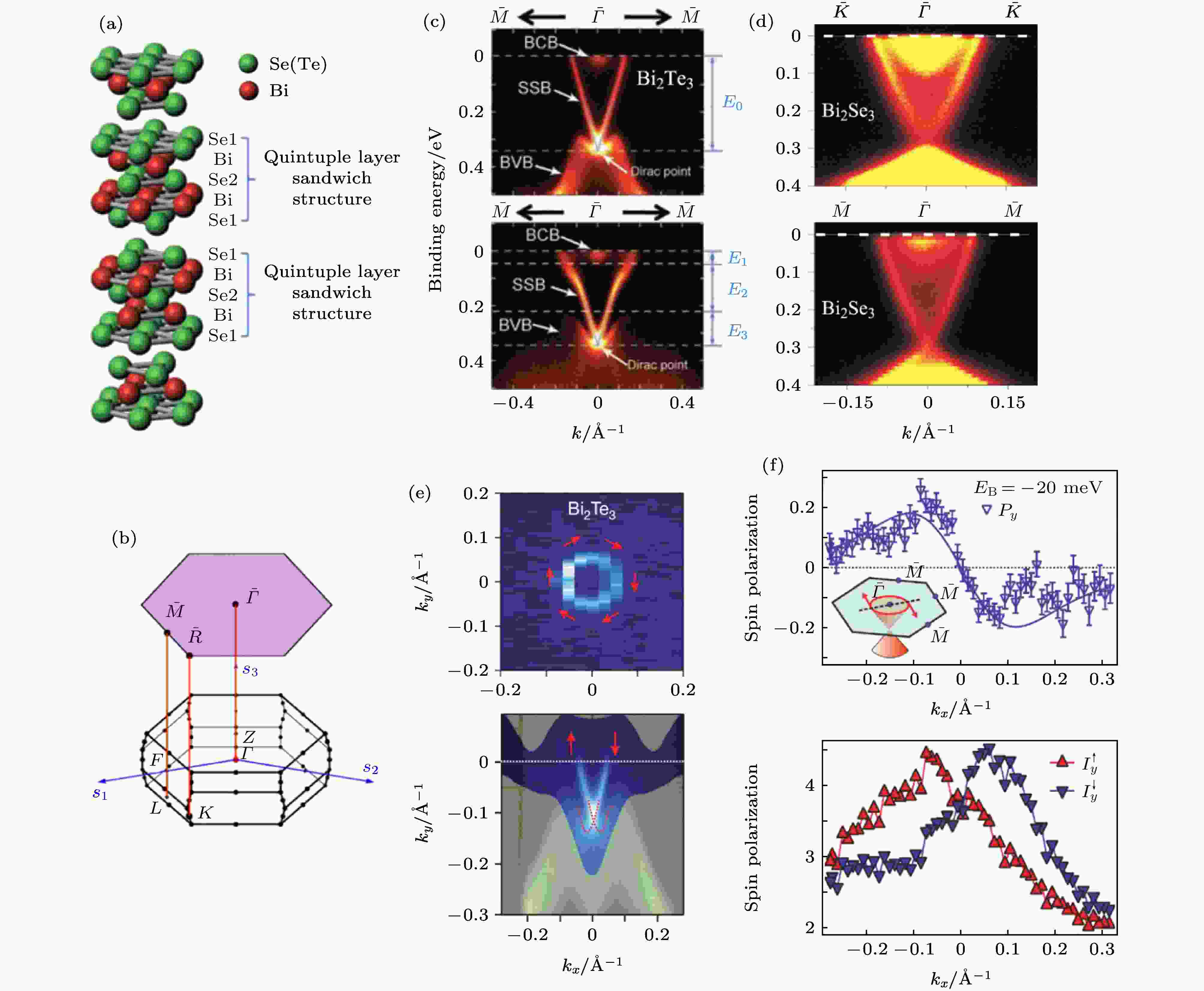 图 4 Bi2Se3和Bi2Te3单晶的最初几个ARPES研究[11,12,122] (a) Bi2Se3和Bi2Te3的晶体结构[11]; (b) Bi2Se3和Bi2Te3的体和表面布里渊区[124]; (c) Bi2Te3的狄拉克锥(沿两个高对称方向)[11]. SSB: 拓扑表面态; BCB: 体导带; BVB: 体价带; (d) Bi2Se3的狄拉克锥(沿两个高对称方向)[12]; (e) Bi2Te3狄拉克锥及其形成的费米面[122]; (f) 图 (e) 能带的自旋极化情况[122]
图 4 Bi2Se3和Bi2Te3单晶的最初几个ARPES研究[11,12,122] (a) Bi2Se3和Bi2Te3的晶体结构[11]; (b) Bi2Se3和Bi2Te3的体和表面布里渊区[124]; (c) Bi2Te3的狄拉克锥(沿两个高对称方向)[11]. SSB: 拓扑表面态; BCB: 体导带; BVB: 体价带; (d) Bi2Se3的狄拉克锥(沿两个高对称方向)[12]; (e) Bi2Te3狄拉克锥及其形成的费米面[122]; (f) 图 (e) 能带的自旋极化情况[122]Figure4. The first ARPES studies on Bi2Se3 and Bi2Te3 single crystals[11,12,122]: (a) Crystal structures of Bi2Se3 and Bi2Te3[11]; (b) bulk and surface Brillouin zone of Bi2Se3 and Bi2Te3[124]; (c) Dirac cone of Bi2Te3 (along two high symmetry directions)[11]. SSB: topological surface state; BCB: bulk conduction band; BVB: bulk valence band. (d) Dirac cone of Bi2Se3 (along two high symmetry directions)[12]; (e) the Fermi surface made by the Dirac cone of Bi2Te3[122]; (f) spin polarization of the bands in Fig.(e)[122].
确定了这些材料的拓扑性质以后, 科学家们利用ARPES对其电子学性质进行了极为详尽的探讨, 主要的研究方向有以下几个: 3.2.1节, 研究狄拉克锥在远离狄拉克点时因体能带的影响产生的变形; 3.2.2节, 对材料进行体掺杂或表面掺杂, 调控载流子浓度和费米面的位置; 3.2.3节, 对材料进行掺杂, 研究其拓扑性质的变化和对称性破缺带来的新颖物理现象, 例如类似量子阱的新狄拉克锥拓扑态和长程磁序导致的狄拉克锥能隙等; 3.2.4节, 精确测定狄拉克锥中每点的k-E位置和洛伦茨线型的宽度, 通过分析自能的实部和虚部研究狄拉克电子与声子的相互作用等; 3.2.5节, 利用CD-ARPES和SARPES研究狄拉克锥和体能态的自旋构型, 详细分析入射光子能量、入射光子偏振等对CD-ARPES和自旋信号的影响, 梳理出研究TI自旋构型的一般方法; 3.2.6节, 利用trARPES, 双光子ARPES (two photon angle resolved photoemission, 2PPE)等时域光电子能谱技术详细研究体系的非平衡态动力学弛豫过程; 3.2.7节, 利用trARPES技术研究TI在随时间周期变化的势场中的能带结构, 构造Floquet拓扑绝缘体; 3.2.8节, 通过MBE等方法生长TI的单层或少层薄膜, 研究其电子学性质和拓扑属性, 等等. 下面分述这几个方向的研究进展, 并在3.2.9节作一小结.
3
3.2.1.利用ARPES研究狄拉克锥远离$\bar \varGamma $
点时产生的变形
仔细观察文献[11, 122] 中Bi2Te3的费米面, 可以发现它的狄拉克锥的kx-ky横截面并不是一个完美的圆. 当等能面远离狄拉克点时, 圆形的横截面首先变成一个圆角的正六边形, 再进一步变化为雪花状的曲面. 2009年麻省理工学院的Fu[126]首先在理论上用k·p模型的高阶项解释了这一现象, 指出这个费米面的扭曲可以导致狄拉克能带z方向的自旋极化, 并且使各向同性条件下被禁止的背散射能够在一定程度上发生. 其后, ARPES接连观察到了Bi2Se3的费米面六角变形[127] 和狄拉克锥以120° 为周期的z方向自旋极化[128], 完美证实了k·p模型的正确性(图5[11,127-129]). 这种具有sin3θ 周期性的面外自旋在量子阱表面态(见3.2.3节)形成后仍能被观察到[129].
 图 5 Bi2Se3系列TI狄拉克锥的六角变形[11,127-129] (a) (Bi1-δSnδ)2Te3材料的雪花形费米面, 上图材料为Bi2Te3 (δ = 0), 下图材料为 δ = 0.67%[11]; (b) Bi2Se3的等能面形变, 上图位于费米面, 下图位于费米面以下150 meV[127]; (c) 利用CD-ARPES导出的费米面自旋极化sz分量. sin3θ 周期性清晰可见[128]; (d) 量子阱表面态存在时自旋极化的分布[129]
图 5 Bi2Se3系列TI狄拉克锥的六角变形[11,127-129] (a) (Bi1-δSnδ)2Te3材料的雪花形费米面, 上图材料为Bi2Te3 (δ = 0), 下图材料为 δ = 0.67%[11]; (b) Bi2Se3的等能面形变, 上图位于费米面, 下图位于费米面以下150 meV[127]; (c) 利用CD-ARPES导出的费米面自旋极化sz分量. sin3θ 周期性清晰可见[128]; (d) 量子阱表面态存在时自旋极化的分布[129]Figure5. Hexagongal warping of the Dirac cones in the Bi2Se3-class TIs[11,127-129]: (a) Snowflake-like Fermi surfaces of (Bi1-δSnδ)2Te3. Top: Bi2Te3(δ = 0); bottom: δ = 0.67%[11]; (b) constant energy contours of Bi2Se3. Top: E = EF; bottom: E = -150 meV[127]; (c) sz component of the spin polarization vector, extracted from CD-ARPES data. The sin3θ periodicity is clearly visible[128]; (d) distribution of the spin polarization vector in the presence of quantum well states[129].
3
3.2.2.利用体掺杂或表面掺杂调控Bi2Se3系列拓扑材料的费米面
由于Bi2Se3系列材料的天然费米面高于导带底, 这类拓扑材料的进一步应用要求利用体或表面的空穴掺杂把费米面移到体能隙中, 以实现特征的拓扑量子输运. 事实上, Bi2Se3系列材料的几篇开创性论文中对体掺杂和表面掺杂的材料已有讨论. 文献[11] 中利用ARPES研究了Sn体掺杂对Bi2Te3费米面的调控, 指出Sn是一种有效的空穴掺杂, 能使原来位于导带的费米面下移到体能隙中, 实现真正的体绝缘态. 文献[122] 指出Ca体掺杂也能使Bi2Te3的费米面下移, 使费米面位于狄拉克点或更低的位置, 实现全局的空穴掺杂. 除此以外, 对体掺杂TI的研究也有不少, 例如文献[123] 指出Mn可以实现Bi2Te3的空穴掺杂和体绝缘性, 文献[127] 指出1% 的Mg体掺杂可令Bi2Se3的费米面降至狄拉克点等. 文献[122] 同时提到了NO2对Bi2–xCaxSe3的表面掺杂可使费米面下移, 文献[130] 提到Te对Bi2Se3的体掺杂也有类似效果, 等等. Cu和Sr掺杂的Bi2Se3系列TI不但能调控费米面, 还能够实现超导. 这方面的研究有很多(例如文献[131,132] 等等), 但由于本文不涉及拓扑超导体的讨论, 这里先略过这些研究.3
3.2.3.利用掺杂研究Bi2Se3系列材料拓扑性质的变化和对称性破缺带来的新颖物理现象
除了有效调控费米面以外, TI的体掺杂和表面掺杂带来的物理现象非常丰富. 第一, 由于全局拓扑性质在微扰下不变, 杂质的引入不改变TI的拓扑不寻常性, 但会使材料的体能带呈现出类似量子阱的新狄拉克锥拓扑态. 文献[133] 是最早研究这一现象的论文之一. 文中指出Fe对Bi2Se3的表面掺杂令费米面升高, 使费米面更深入体导带中. 这时候, 体导带发生了新的变化, 一对或几对类似Rashba劈裂能带的新的表面态出现, 但总的拓扑不寻常的狄拉克锥数目维持为一, 两个TRIM点之间通过费米面的能带个数维持为奇数. 文献[129,134] 进一步指出K, CO, Rb等原子团对TI的表面掺杂, 甚至简单地把TI放置在超高真空环境中一段较长的时间, 也能导致同一现象. 这两篇论文对这个现象给出了一个简单的定量解释, 认为费米面在TI晶体表面发生了向下的弯曲, 弯曲处连同表面势垒构成了一个类似半导体表面p掺杂时出现的量子阱, 使Rashba分裂的电子形成二维电子气禁锢于其中[135], 于是形成了新的表面能带. 这些表面能带成对出现, 因此不影响体系的总体拓扑性(图6[129,133]). 这个现象充分说明了TI的全局拓扑性质不受杂质或扰动的影响. 后续的研究对这方面也有跟进, 例如中科院物理所Chen等[136] 把Bi2Se3系列TI在大气中放置一段可观的时间后进行ARPES测量, 发现TI表面态的拓扑性完全不受影响, 且观察到了Rashba表面态的形成. 文献[137] 利用水蒸气的表面覆盖模拟TI样品表面在大气中的退化, 也观察到了Rashba表面态的形成. 文献[138] 指出Cu, In, Mn等表面掺杂都会导致TI的费米面上升和二维电子气的产生, 但只有Mn掺杂到一定量时, TI的狄拉克锥重新变得清晰, 等等.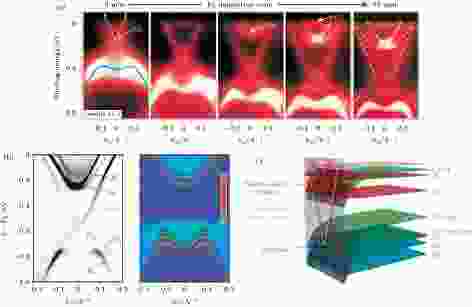 图 6 对Bi2Se3系列TI的表面掺杂引入新的量子阱表面能带[129,133] (a) 新表面能带的形成过程. 随着Fe掺杂原子的增加, 量子阱能带逐对生成. 每对新能带在两个TRIM点间增加两条通过费米面的能带[133]; (b) 钾掺杂Bi2Se3中观察到的同一现象, 及其定量计算解释[129]; (c) 解释此现象的物理图像[129]
图 6 对Bi2Se3系列TI的表面掺杂引入新的量子阱表面能带[129,133] (a) 新表面能带的形成过程. 随着Fe掺杂原子的增加, 量子阱能带逐对生成. 每对新能带在两个TRIM点间增加两条通过费米面的能带[133]; (b) 钾掺杂Bi2Se3中观察到的同一现象, 及其定量计算解释[129]; (c) 解释此现象的物理图像[129]Figure6. Introduction of quantum well surface states to the Bi2Se3-class TIs by surface deposition[129,133]: (a) Formation of the new surface bands[133]. Pairs of quantum well states are form progressively with increasing surface Fe dosage. Each pair of new states adds two Fermi-crossing bands between two TRIMs; (b) same phenomenon as (a) observed in K-doped Bi2Se3, compared with ab initio calculation results[129]; (c) physical explanation of this phenomenon[129].
第二, 由于TI的狄拉克点受时间反演对称性保护, 因此可以想象当破缺时间反演的磁性杂质在样品中引入长程磁序后, TI的拓扑性将被破坏, 表现在狄拉克点打开一个磁序造成的能隙, 使整个体系变成磁性拓扑绝缘体. 虽然引入磁性和非磁性的杂质都能使狄拉克锥打开能隙, 使无质量的狄拉克准粒子获得质量, 但只有磁性杂质破坏系统的时间反演对称性, 从而实现量子反常霍尔效应. 文献[139]系统地考察了稀释的磁性和非磁性杂质对Bi2Se3的费米面高度、Rashba二维电子气的形成和狄拉克锥的六角变形的影响, 指出磁性和非磁性杂质对狄拉克表面态的作用非常类似. 但是, 由于这份文献没有利用自旋分辨ARPES观测

3
3.2.4.通过分析自能的实部和虚部研究狄拉克电子的多体相互作用
根据光电效应三步模型(2.3节), ARPES单电子谱函数






文献[140] 是利用自能虚部研究TI拓扑表面态的准粒子耦合模式的第一份文献, 给出Bi2Se3的狄拉克电子如图7(a) 的自能虚部测量值, 并分析了不同的带间准粒子散射通道(如电子空穴对的生成、电子-声子耦合和杂质散射等)对自能虚部的贡献. 奇怪的是, 这份文献中的数据并未由后续的实验重复. 文献[141] 再次测量了Bi2Se3拓扑表面态的自能虚部, 得出如图7(b) 的数据. 与图7(a) 对比可见, 束缚能在0.17 eV附近的Σ''尖峰并未出现, 这可能是由于文献[141] 中拓扑表面态未受到体能态的干扰. 最重要的是, 图7(b) 中随着温度的上升, 能带的热展宽、过费米面能带的弯折和能量的重整化均观察不到, 这提示我们TI表面态中的电子-声子耦合非常微弱. 事实上文献[141] 对电声耦合系数


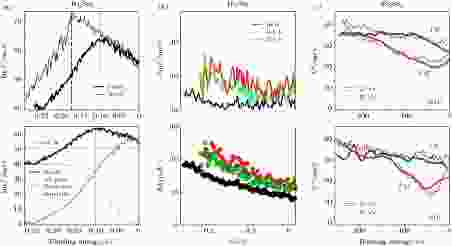 图 7 利用自能虚部研究TI中狄拉克电子的多体相互作用[140-142] (a) Bi2Se3狄拉克电子的自能虚部随束缚能的变化曲线(上), 以及可能的散射通道分析(下)[140]; (b) Bi2Se3狄拉克电子的自能虚部随束缚能的变化曲线(上), 以及MDC的半高全宽(下)[141]. (a) 和 (b) 中的拓扑表面态均沿
图 7 利用自能虚部研究TI中狄拉克电子的多体相互作用[140-142] (a) Bi2Se3狄拉克电子的自能虚部随束缚能的变化曲线(上), 以及可能的散射通道分析(下)[140]; (b) Bi2Se3狄拉克电子的自能虚部随束缚能的变化曲线(上), 以及MDC的半高全宽(下)[141]. (a) 和 (b) 中的拓扑表面态均沿
Figure7. Study of many-body interactions of the Dirac fermions in TIs by analyzing the imaginary part of the self energy[140-142]: (a) Results of Ref. [140]. Top: Imaginary part of the self energy (ImΣ) versus binding energy (Eb) for the topological surface state (TSS) of Bi2Se3. Bottom: Analysis of possible scattering channels; (b) results of Ref. [141]. Top: ImΣ vs. Eb for the TSS of Bi2Se3. Bottom: Full width half maximum (FWHM) of the momentum distribution curves (MDCs); (c) results of Ref. [142]. Top/bottom: ImΣ vs. Eb for the TSS of Bi2Te3, obtained from MDC/EDC analysis.
3
3.2.5.利用自旋分辨ARPES和圆二色性ARPES研究狄拉克锥和体能态的自旋构型
拓扑绝缘体其中一个最重要的物理性质是其狄拉克锥的自旋螺旋构型及其引致的严格背散射的缺失, 区别于例如石墨烯狄拉克锥的自旋简并性质. 拓扑绝缘体的一切可能的自旋电子学应用都由这种特殊的自旋纹理引致(严格地说, 在TI表面态中, 好量子数是赝自旋而非自旋本身, 但二者直接正比, 所以以下直接用“自旋”代称赝自旋). 所谓自旋螺旋构型(亦称“自旋-动量锁定”行为), 指的是形成狄拉克锥的两条线性能带的自旋都指向狄拉克锥在kx-ky面内的横截面的前切线方向. 换句话说, 在过狄拉克点的E-kx或E-ky能带图中, 两条准粒子群速度分别为正和负的狄拉克能带的自旋均垂直于E-k面, 且极化方向刚好相反[2-4]. 从ARPES角度讲, 如果不测量狄拉克能带的自旋, 则拓扑绝缘体和石墨烯类型的狄拉克锥是无法区分的, 因此要从实验上唯一确定某种材料是不是拓扑绝缘体, 对其狄拉克锥自旋的测量必不可少.利用ARPES测定能带自旋的方法大体有两种. 其一是利用安装在ARPES电子分析仪光电子成像端的自旋分析仪直接测量光电子的自旋(自旋分辨ARPES, SARPES), 即依次测量自旋分析仪对两个相反方向自旋敏感时同一E-k平面的能带结构, 分别获得光电子强度 I↑ 和 I↓, 换算得自旋极化强度


在Bi2Se3系列拓扑绝缘体研究的前期, ARPES实验工作通常直接利用一个或少数几个实验配置下的SARPES数据说明两条狄拉克能带的面内自旋方向相反, 从而证实拓扑绝缘体的自旋-动量锁定. 这种方法取得了巨大的成功, 它在实验上证实了三维拓扑绝缘体的存在, 从而开辟了人类物态认知的新纪元. 图3(f) 和图4(f) 给出了SARPES对拓扑绝缘体最早的几个测量[10,122], 证实了狄拉克锥的面内自旋螺旋纹理. 大阪大学Souma等[145]测量Bi2Se3狄拉克锥自旋的面外分量 (sz) 并与TlBiSe2(见3.3.3节)作对比, 指出自旋面外分量的成因是狄拉克锥的六角变形(3.2.1节). Bi2Se3系列TI的CD-ARPES数据出现得稍晚一些. Wang等[128] 利用基于飞行时间光电子能谱仪 (time-of-flight (TOF) spectrometer)的激光CD-ARPES(光子能量为6.2 eV)研究了Bi2Se3拓扑表面态的CD纹理. 其模型计算认为CD是拓扑表面态赝自旋






随着研究的深入, 人们发现事情并没有那么简单. Scholz 等[146] 在不同的入射光子能量下测量Bi2Te3的CD信号, 发现CD的正负在光子能量为20 —100 eV的区间中发生了几次似乎无规律的反转 (图8(b)). 很明显, CD反转来源于光电效应过程本身, 而非狄拉克电子的初态自旋. Jozwiak等[147]首先利用SARPES研究Bi2Se3的拓扑表面态, 发现不同的入射光子能量会令Bi芯能级 (core level) 的自旋极化率发生很大的变化, 且在同一光子能量下, 入射光的不同线偏振方向会使自旋极化信号发生反转; 继而利用其研制的自旋分辨激光ARPES仪器(光子能量为5.99 eV)发现不仅90° 的入射光偏振方向旋转(从p偏振变成s偏振)会导致自旋信号的完全反转, 而且45° 的偏振旋转会使测得的自旋方向沿着狄拉克锥横截面的径向 (图8(d)和图8(e)), 与TI表面态的自旋构型大相径庭[148]. 和CD-ARPES信号一样, 这些变化不可能来自狄拉克电子的初态, 而只能与矩阵元

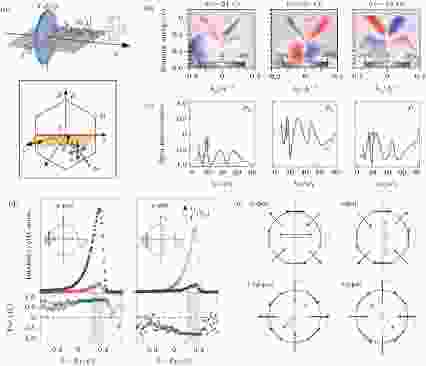 图 8 TI拓扑表面态圆二色性信号和自旋极化信号的复杂性[146,148,150] (a) 两份文献中CD-ARPES和SARPES的实验配置[148,150]. 图中p和 π(s和 σ)意义相同; (b) Bi2Te3狄拉克电子的CD信号[146]. 入射光子能量从21 到55 eV变化过程中, CD信号发生了两次反转; (c) Bi2Se3自旋极化信号的三个分量随光子能量的变化[150]; (d) Bi2Se3自旋极化信号在两种不同的线偏振入射光作用下方向完全相反[148]; (e) 自旋信号随入射光偏振变化的复杂响应[148]. ± sp-pol表示右(左)倾45° 的线偏振光
图 8 TI拓扑表面态圆二色性信号和自旋极化信号的复杂性[146,148,150] (a) 两份文献中CD-ARPES和SARPES的实验配置[148,150]. 图中p和 π(s和 σ)意义相同; (b) Bi2Te3狄拉克电子的CD信号[146]. 入射光子能量从21 到55 eV变化过程中, CD信号发生了两次反转; (c) Bi2Se3自旋极化信号的三个分量随光子能量的变化[150]; (d) Bi2Se3自旋极化信号在两种不同的线偏振入射光作用下方向完全相反[148]; (e) 自旋信号随入射光偏振变化的复杂响应[148]. ± sp-pol表示右(左)倾45° 的线偏振光Figure8. Complexity of the CD-ARPES and SARPES signals[146,148,150]: (a) Experimental geometries in Refs. [148,150]. p and π (s and σ) are the same; (b) CD-ARPES signal of the Dirac fermions in Bi2Te3[146]. The CD signal reverses sign for two times as the photon energy goes from 21 to 55 eV; (c) the three components of the spin polarization vector (Px, Py, Pz) vs. photon energy[150]; (d) sign reversal of P under two different linearly polarized incident lights[148]; (e) complex response of P as a function of light polarization[148]. ± sp-pol: 45° tilted linearly polarized light.
由于上述效应涉及到不同能量、偏振的入射光对TI不同轨道、不同原子层狄拉克电子的复杂相互作用, 对它的理论理解超出了光电子能谱学三步模型的范畴, 而必须运用一步模型(见2.4节)来解释. 在一步模型的框架下, SARPES信号正比于由相对论一步模型求得的自旋极化强度p, 而入射光偏振对ARPES信号的影响体现为矢量势A0的不同取值. 由于一步模型的复杂性, 不少研究组采用不同的简化模型来理解这一现象. 文献[128,143,149, 150] 均假定光电子末态是自旋简并的平面波, 即假定ARPES矩阵元

 图 9 虽然CD-ARPES和SARPES数据受多种参数影响, 利用SARPES研究TI表面态的自旋构型仍然是可能的[152] (a) 当入射光能量为50 eV时, 自旋信号不受入射光偏振的影响; (b) 当入射光能量为6 eV时, 自旋信号随入射光偏振的反转而反转
图 9 虽然CD-ARPES和SARPES数据受多种参数影响, 利用SARPES研究TI表面态的自旋构型仍然是可能的[152] (a) 当入射光能量为50 eV时, 自旋信号不受入射光偏振的影响; (b) 当入射光能量为6 eV时, 自旋信号随入射光偏振的反转而反转Figure9. Possibility for studying the initial state spin configuration despite the complexity of CD-ARPES and SARPES signals[152]: (a) When hν = 50 eV, the spin signal is unaffected by incident light polarization; (b) when hν = 6 eV, the spin signal changes sign as the light polarization reverses.
3
3.2.6.利用trARPES、2PPE等时域光电子能谱技术研究体系的非平衡态动力学过程
从实验上说, 并非每一类适于普通ARPES的材料都能够获得令人信服的trARPES、2PPE等时域光电子能谱信号. 幸运的是, Bi2Se3系列TI对此类技术十分友好, 且由于能带结构比较简单, 它们能够为时域ARPES提供一个研究拓扑表面态动力学过程的很好的平台. 文献中的研究内容主要有以下几类: A. 利用泵浦ARPES或2PPE把初态的电子激发到中间态或者激发态中, 研究位于费米面以上的非占据态能带结构; B. 精确控制激发光和探测光到达样品的时间差并测量每一时间差对应的能带结构, 详细研究系统从激发态到平衡态的动力学弛豫过程; C. 精确测定弛豫过程中的能带变化(能带的整体抖动), 研究TI中的准粒子耦合行为; D. 利用同时具有时间分辨和自旋分辨(或CD-ARPES)能力的ARPES仪器研究TI非平衡态的自旋纹理.利用trARPES和2PPE等技术, 我们首先获得的信息是TI非占据态的电子学结构. 其中比较有代表性的是Sobota等[153] 利用电子吸收两个6 eV光子的2PPE过程观察到的, 从费米面到真空能级的近6 eV内的非占据态能带结构(图10(b), 对应于图10(a)的 (i) 过程). 这个结果中最引人注目的特征是费米面以上1.3—2.4 eV之间, 交点位于1.7 eV的X型能带结构. 通过和理论计算的比对, 作者确认这是Bi2Se3的第二个拓扑表面态(狄拉克锥), 其零能隙和普通ARPES观察到的第一个狄拉克锥一样由时间反演对称性保护. 值得注意的是, 在利用1.5和6 eV两路激光共同激发的2PPE过程(图10(a)的 (ii) 过程)中, 也能够观察到很类似图10(b)的X形拓扑表面态, 但这个表面态是第一狄拉克锥在费米面上方形成的镜像, 不是第二狄拉克锥. 在第二狄拉克锥和第一狄拉克锥投影相交的地方, ARPES信号被共振增强(图10(c)[154]). 类似的现象也在Bi2Te3, Bi2Te2Se, Sb2Te3, Sb2Te2S等材料中被观察到[155-158], 其中文献[157,158] 利用能量为0.5 eV左右的红外激光作为激发光, 观察到表面态自身的泵浦过程, 发现狄拉克锥的两支信号强度有明显的不同, 也就是说这种过程诱发了热电子的自旋极化流. 利用红外激光作为激发光获得的最重要的结果是实现了电子在时域周期势场中的Floquet响应, 即发现了Floquet拓扑绝缘体. 这一点将在3.2.7节详述.
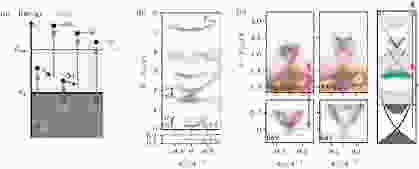 图 10 利用trARPES和2PPE ARPES研究Bi2Se3费米面以上的电子学结构[153,154] (a) 图中涉及的三种光电效应过程[154]: (i) 电子连续吸收两个6 eV光子后发射(对应于图(b)), (ii) 电子同时吸收一个1.5 eV和一个6 eV光子后发射(对应于图 (c) 的左上两图), (iii) 普通ARPES过程, 对应于图 (b) 和图(c) 的下方小图; (b) 由6 eV + 6 eV 2 PPE过程探测到的非占据态能带[153]; (c) 由1.5 eV + 6 eV 2PPE过程探测到的能带, 其中的X型狄拉克锥是费米面以下的拓扑表面态的投影, 并非第二狄拉克锥[154]
图 10 利用trARPES和2PPE ARPES研究Bi2Se3费米面以上的电子学结构[153,154] (a) 图中涉及的三种光电效应过程[154]: (i) 电子连续吸收两个6 eV光子后发射(对应于图(b)), (ii) 电子同时吸收一个1.5 eV和一个6 eV光子后发射(对应于图 (c) 的左上两图), (iii) 普通ARPES过程, 对应于图 (b) 和图(c) 的下方小图; (b) 由6 eV + 6 eV 2 PPE过程探测到的非占据态能带[153]; (c) 由1.5 eV + 6 eV 2PPE过程探测到的能带, 其中的X型狄拉克锥是费米面以下的拓扑表面态的投影, 并非第二狄拉克锥[154]Figure10. Studying the unoccupied electronic states of Bi2Se3 using trARPES and 2PPE ARPES[153,154]: (a) Three relavant processes of photoemission[154]. (i) An electron photoemits after absorbing two 6 eV photons consecutively (situation in Fig. (b)); (ii) An electron photoemits after simultaneously absorbing a 1.5 eV and a 6 eV photon [two upper left panels in Fig. (c)]; (iii) Normal photoemission (two lower panels in (b) and (c)); (b) unoccupied bands revealed by Process (i)[153]; (c) bands reveals by Process (ii)[154]. The X-shaped Dirac cone is a projection of the TSS below EF, not the 2nd TSS.
TI非平衡态到平衡态的动力学弛豫过程也是trARPES研究的重点内容. 利用基于1.5 eV激发光和6 eV探测光的泵浦ARPES, 几个研究组测量了两个光子到达样品的时间差不同的情况下非占据态电子学结构的演变. Sobota等[159] 使用的样品是空穴掺杂的Bi2Se3, 狄拉克点位于费米面以上(图11(a)和图11(b)). 他们发现Bi2Se3导带底的载流子寿命很长(10 ps量级), 使得导带底可以作为临时的电子库. 进一步的分析表明, 清空导带底载流子的时间常数和清空表面态电子的时间常数相同, 因此导带底通过弛豫向拓扑表面态提供电子, 使表面态在长时间内保持电子填充的状态. Wang等[160] 使用的样品是电子掺杂的Bi2Se3, 狄拉克点位于费米面以下. 他们没有观察到位于导带底的亚稳态(图11(c)), 但分析了不同晶格温度下电子温度随时间的弛豫过程, 认为在低晶格温度下声子辅助的表面态-体态耦合不明显, 而在高晶格温度下这类耦合很强.
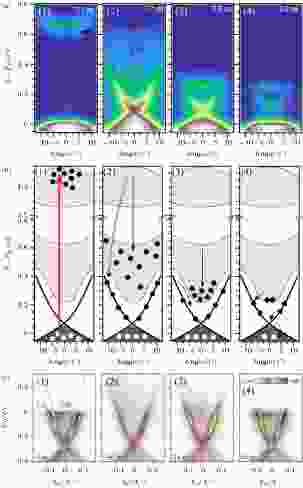 图 11 利用trARPES分析TI非稳恒态的动力学弛豫过程[159,160] (a), (b) 空穴掺杂Bi2Se3的动力学弛豫过程的 (a) 实验数据和 (b) 物理图像示意[159]. 在t ≈ 0 ps时, 激发光把电子激发到很高的非占据态中; 随着时间推移, 电子逐渐占据较低能的能带. 在t = 2.5—9.0 ps这段时间内, 导带底始终作为电子库向表面态供给电子; (c) 电子掺杂Bi2Se3的动力学弛豫过程[160]. 导带底在此实验中不可见
图 11 利用trARPES分析TI非稳恒态的动力学弛豫过程[159,160] (a), (b) 空穴掺杂Bi2Se3的动力学弛豫过程的 (a) 实验数据和 (b) 物理图像示意[159]. 在t ≈ 0 ps时, 激发光把电子激发到很高的非占据态中; 随着时间推移, 电子逐渐占据较低能的能带. 在t = 2.5—9.0 ps这段时间内, 导带底始终作为电子库向表面态供给电子; (c) 电子掺杂Bi2Se3的动力学弛豫过程[160]. 导带底在此实验中不可见Figure11. Studying the relaxation process of the excited state using trARPES[159,160]: (a), (b) The trARPES result ((a)) and skematics of physical process ((b)) of dynamic relaxation process of hole-doped Bi2Se3[159]; (c) dynamic relaxation process of electron-doped Bi2Se3[160].
假如对弛豫过程作高精度的分析, 会发现样品的整体能带结构(能带的位置)出现以时间为周期的规则抖动, 这现象由光电子和晶格声子的耦合引起. 分析这类抖动的频率可以探讨TI的电声耦合效应. 文献[161]利用这个方法分析了Bi2Se3表面态和体态的振动模式, 发现TI导带底(体态)的trARPES信号强度会以2.23 THz的频率作周期性变化, 这一变化被归因于体态与A1g声子模式的耦合. 另一方面, TI拓扑表面态的信号变化频率除了2.23 THz外, 还有2.05 THz的一个(因而信号出现差拍现象). 这被归因于表面层晶格相比于体晶格的微小差别造成的表面声子软化. 在Bi2Te3中, trARPES信号变化频率约为1.9 THz, 且由于狄拉克锥变形严重,


把时间分辨ARPES和CD-ARPES结合, 可以获得更深层次的非平衡态动力学信息. Soifer等[163] 利用3.02 eV的左旋或右旋圆偏振光作为激发光, 6 eV的s线偏光作为探测光, 观察到费米面以上的广大区域均有光电流产生(表现为+k和-k的信号强度不对称性), 且这种光电流在165 fs内弛豫消失. 更进一步, 作者对非平衡态能带图中每一个 (k, E) 点的信号上升时间(信号强度最大值对应的泵浦时间差)进行了细致的扫描, 结果显示费米面以下能带(占据态)加上激发光能量所对应的 (k, E) 位置的上升时间较短, 因而这些位置的非占据态信号主要由直接的光学跃迁形成. 通过这种分析, 我们可以标定特定时刻下光电子和光空穴对特定光学跃迁的贡献.
把时间分辨ARPES和自旋分辨ARPES结合, 可以获得非占据态的自旋极化信息. 由于被激发光激发的非占据态ARPES信号很弱, 且自旋分辨ARPES的效率远低于普通ARPES, 因而获取这种数据需要长时间的信号积累. 文献[164] 报道了一组自旋分辨的trARPES数据, 在泵浦时间差等于500 fs时测得费米面以上0.4 eV左右存在一个高自旋极化的区域. 在这个区域里, 两种自旋的电子的弛豫时间有较大差别. 利用完整的相对论一步模型数值计算(2.4节)并与实验比对, 作者指出这个自旋极化区来源于一个拓扑平庸的表面共振态. 进一步的数据表明, TI的表面态和体态甚至不能用同一个系综来表示, 而需要引入各自的电子有效温度. 因此TI中表面态和体态的耦合极弱.
3
3.2.7.利用trARPES构造和研究Floquet拓扑绝缘体
trARPES技术的本质, 是利用局域、相干的高强度激发光构建电磁波与晶体相互作用的场景, 继而利用探测光引起的光电效应观察这种相互作用对样品电子学结构的影响. 可以想象, 光与晶体中电子的相互作用不仅会使电子被激发到非占据态然后弛豫回稳恒态, 更有可能构造完全不同于稳恒态的新的物相. 把这一方法应用到Bi2Se3系列TI, 最重要的结果是发现了固体中的时域能带结构, 即Floquet-Bloch电子态.Floquet定理[165] 指出, 一个具有时间周期性的哈密顿量(例如波包形式的单色光)可以令固体中的电子形成以光子能量为周期的亚稳的本征态, 就像具有空间周期性的哈密顿量(例如晶体)可以令电子形成以晶格常数为周期的本征态(Bloch态)一样(见2.5节). 具体到Bi2Se3系列TI, 当激发光的光子能量小于TI的体能隙(约300 meV), 且激发光与探测光时间差很小(例如小于500 fs)时, 可以观察到TI的体态和拓扑表面态在能量轴上以光子能量为间隔重复出现. Wang 等[166]2013年首次观察到这个现象, 并在2016年以更高的数据质量重复了这一结果[167] (图12(b)和图12(c)). 除了探测到狄拉克锥的镜像以外, 还在特定的不同级镜像的交叉点观察到动力学能隙的打开, 从而把Floquet能带和图10(c)的狄拉克锥投影区别开来. 这种能隙的有无与入射光子的偏振和电子动量的方向有关, 特别是能隙的大小正比于入射光强度的开方. 此外, 文献[167] 详细研究了入射光的不同偏振对+kx和–kx两个相反动量方向上镜像能带强度的不对称性的影响(图12(d)), 指出除了热电子的自旋极化流[157,158]外, Volkov机制对Floquet能带的影响不可忽略. 所谓Volkov机制, 指的是入射光对光电子的末态(真空能级)的调制作用, 区别于Floquet机制中入射光对光电子的初态(就是通常的能带结构)的调制效应(图12(a)). 只有同时引入两个机制的理论计算才能定量解释实验测得的镜像能带强度的不对称性.
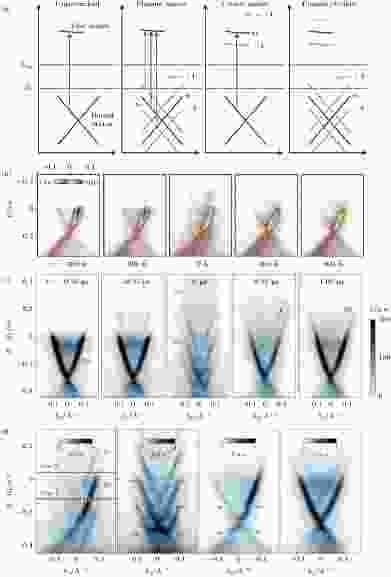 图 12 利用trARPES构造和研究Floquet拓扑绝缘体[166,167] (a) 时域能带结构的两种形成机制: Floquet机制和Volkov机制(见正文)[167]; (b) 对Floquet拓扑绝缘体的首次观测[166]; (c) 图 (b) 数据的高精度重复[167]; (d) p偏振(左二图)和s偏振(右二图)入射光对不同动量方向(一、三图为kx, 二、四图为ky)的Floquet能带的影响[167]. p偏振时ky方向能带产生Floquet能隙, 而s偏振时kx方向能带产生Floquet能隙(红色箭头标示能隙位置)
图 12 利用trARPES构造和研究Floquet拓扑绝缘体[166,167] (a) 时域能带结构的两种形成机制: Floquet机制和Volkov机制(见正文)[167]; (b) 对Floquet拓扑绝缘体的首次观测[166]; (c) 图 (b) 数据的高精度重复[167]; (d) p偏振(左二图)和s偏振(右二图)入射光对不同动量方向(一、三图为kx, 二、四图为ky)的Floquet能带的影响[167]. p偏振时ky方向能带产生Floquet能隙, 而s偏振时kx方向能带产生Floquet能隙(红色箭头标示能隙位置)Figure12. Realization of Floquet TI by trARPES[166,167]: (a) Skematics of the Floquet and Volkov mechanisms[167]; (b) the first experimental observation of a Floquet TI[166]; (c) a higher quality reproduction of data in Fig. (b)[167]; (d) influence on the Floquet bands at different momenta under differently polarized light[167]. Floquet gap (red arrows) appears along ky/kx under p/s-polarized light.
3
3.2.8.利用ARPES研究TI少层薄膜的电子学性质和拓扑属性
TI的单层或少层薄膜的物理性质和拓扑属性与TI单晶体材料有巨大的区别, 因此利用ARPES研究TI薄膜有特殊的意义. 这些薄膜可以生长在绝缘衬底上, 以模拟悬空 (free standing) 的少层TI的电子学行为, 也可以生长在各种不同功能材料的衬底上, 以研究其形成的异质结构的物理性质, 例如构造TI和超导体的异质结可用于研究拓扑超导体以及Majorana费米子等等. 由于篇幅所限, 本文仅介绍利用ARPES研究近似于悬空的TI薄膜的几个工作.首先, TI薄膜的厚度对其拓扑属性有重要的影响. 原则上, 当样品的厚度下降至只有数个原子层时, 本来互不相干的, 局域在样品上下表面的拓扑表面态波函数会发生可观的交叠, 形成电子隧穿的通路, 使拓扑表面态打开能隙, 从而使TI的拓扑性质发生全局的突变, 成为普通的能带绝缘体. 清华大学Zhang等[168]利用ARPES首先在Bi2Se3薄膜(生长于双层石墨烯覆盖的6 H-SiC(0001)衬底上)中观察到6层以下薄膜的能隙打开, 证实6层以下的Bi2Se3是拓扑平庸的体系(图13(a)), 继而在Sb2Te3薄膜(生长于Si(111)–7 × 7衬底上)中以同样方法证实5层以下的Sb2Te3是拓扑平庸的(图13(b))[169]. Neupane等[170] 利用自旋分辨ARPES指出Bi2Se3薄膜的拓扑能带的螺旋形面内自旋极化早在3层时便出现, 并随着层数的增加而增强. 在完整狄拉克锥最终形成时(6层), 自旋极化达到最大值. Landolt 等[171] 同样利用自旋分辨ARPES指出当厚度小于6层时, Bi2Se3薄膜带隙上方的能带是类似Rashba分裂的抛物线能带, 且其内外圈的自旋极化强度随层数有较大的变化.
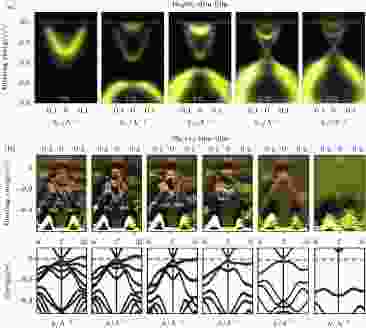 图 13 Bi2Se3系列TI少层薄膜的拓扑相变[168,169]. 从图中可以看到, 6 QL以下的Bi2Se3和5 QL以下的Sb2Te3是拓扑平庸的 (a) Bi2Se3少层薄膜的ARPES能带结构. 完整的狄拉克锥在6 QL样品中形成[168]; (b) Sb2Te3少层薄膜的二次微分ARPES能带结构(上)和第一性原理计算结果(下)[169]. 结合实验和理论, 可以看出完整的狄拉克锥在5 QL样品中形成
图 13 Bi2Se3系列TI少层薄膜的拓扑相变[168,169]. 从图中可以看到, 6 QL以下的Bi2Se3和5 QL以下的Sb2Te3是拓扑平庸的 (a) Bi2Se3少层薄膜的ARPES能带结构. 完整的狄拉克锥在6 QL样品中形成[168]; (b) Sb2Te3少层薄膜的二次微分ARPES能带结构(上)和第一性原理计算结果(下)[169]. 结合实验和理论, 可以看出完整的狄拉克锥在5 QL样品中形成Figure13. Topological phase transition on few-layer TI films[168,169]. Bi2Se3/Sb2Te3 films thinner than 6 QL/5 QL are topologically trivial: (a) ARPES band structure on few layer Bi2Se3 films. A well-defined Dirac cone is not present for films thinner than 6 QL[168]; (b) ARPES band structure (top) and first principles calculation results (bottom) on few layer Sb2Te3 films[169]. A Dirac cone forms in 5 QL and thicker samples.
第二, TI薄膜中的原子掺杂、衬底的性质等也对其电子学结构的调控起到关键作用. 在引入掺杂的前提下, TI薄膜的电子学结构能够被连续调节. 例如在 (Bi1–xSbx)2Te3薄膜中改变x的值可以在保持体系拓扑性质不变的基础上调控费米能和狄拉克点的位置[172,173]; 在Bi2Se3薄膜中引入铬 (Cr) 原子可以使狄拉克点打开非磁性能隙[174]; 在Bi2Se3薄膜中引入铟 (In) 原子能够使狄拉克锥从完全闭合连续调节到打开1.3 eV的大能隙[175]; 在Bi2Se3薄膜中引入碲 (Sb) 和铅 (Pb) 原子可以有效调节费米面的位置[176], 等等. 在不引入掺杂原子的情况下, 改变MBE生长的条件也能够方便地调控TI薄膜的能带结构. Wang等[177] 在不同温度的Si(111)–7 × 7衬底上生长Bi2Te3薄膜, 通过ARPES发现薄膜的费米面(正相关于电子浓度)随衬底温度的升高而单调下降. 当衬底温度足够高时, 电子型的Bi2Te3薄膜转变为空穴型.
3
3.2.9.小 结
Bi2Se3系列TI是迄今为止被研究得最多、最深入的拓扑材料. 仅仅利用ARPES这一实验工具, 人们就在这个系列的材料中获得了极为丰富的物理信息. 它们是TI中的“氢原子”, 拥有最简单的单个



2
3.3.其他含Bi的三元和四元拓扑绝缘体
虽然Bi2Se3系列TI是最简单的三维拓扑绝缘体, 在物理上极为重要, 但要在未来的电子学器件上直接应用它们, 仍然不太容易. 影响Bi2Se3系列TI应用前景的一个重要因素在于它们的体能隙不够大, 也就是说即使通过掺杂或者栅压使它们的费米能处于体导带和体价带之间, 成为真正的体绝缘体, 它们的体载流子浓度仍然过高, 绝缘性仍然不够好. 这样一来, 纯粹的表面态输运仍会受到体能态的影响, 使器件的性能降低. 于是, 自拓扑材料面世以来, 人们就致力于在230个空间群中, 在几万种已知和未知的材料中寻找TI, 力求改进Bi2Se3系列的固有缺陷, 引领拓扑材料的实用性研究. 在Bi2Se3系列TI被发现后不久, 人们就找到了一系列含Bi的三元或四元化合物, 具有与Bi2Se3类似的层状结构和不寻常的拓扑属性. 下面我们归纳一下利用ARPES研究这些TI的总体情况.3
3.3.1.Bi2Te2Se系列拓扑绝缘体
在含Bi的三元或四元TI中, 与Bi2Se3系列TI在晶体结构和电子学结构上最相似的是Bi2Te2Se系列拓扑绝缘体, 包括Bi2Te2Se, Bi2Se2Te等, 比较准确的通式是Bi2–xSbxTe3–ySey(Bi2Te2Se中x = 0, y = 1; Bi2Se2Te中x = 0, y = 2), 本文称之为Bi2Te2Se系列TI. 日本大阪大学Ren等[178]和Taskin 等[179]合成了这些材料并测量了它们的输运性质, 指出其低温纵向电阻率最高达到10 Ω·cm量级, 比Bi2Se3系列的 < 10 mΩ·cm[180] 高三个数量级. 同一小组的ARPES测量表明它们都是像Bi1Se3一样的单狄拉克锥TI, 而且其费米面位置随 (x, y) 值的变化而连续变化, 使良好的体绝缘性和能带的精细调控成为可能[181].普林斯顿大学Ji等[182]和Neupane 等[183]对这些化合物进行了比较系统的ARPES研究(图14), 同样发现它们是单狄拉克锥TI((Bi, Sb)2Te2S也是[184,185]), 而Bi2Se2S则是拓扑平庸的普通绝缘体. 其

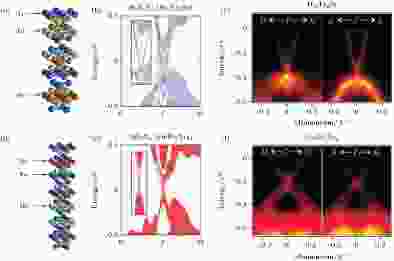 图 14 Bi2Te2Se与GeBi2Te4的ARPES能带图[183] (a)?(c) Bi2Te2Se的 (a) 晶体结构, (b) 第一性原理计算的体态和表面态, 以及 (c) 沿两个高对称方向的ARPES能带图; (d)?(f) 同 (a)?(c), 但体系为GeBi2Te4. 由图可见, Bi2Te2Se和GeBi2Te4都是具有
图 14 Bi2Te2Se与GeBi2Te4的ARPES能带图[183] (a)?(c) Bi2Te2Se的 (a) 晶体结构, (b) 第一性原理计算的体态和表面态, 以及 (c) 沿两个高对称方向的ARPES能带图; (d)?(f) 同 (a)?(c), 但体系为GeBi2Te4. 由图可见, Bi2Te2Se和GeBi2Te4都是具有
Figure14. ARPES band structure of Bi2Te2Se and GeBi2Te4[183]: (a) Crystal structure, (b) bulk and surface states by ab initio calculations, and (c) ARPES bands along two high symmetry directions, of Bi2Te2Se; (d)?(f) Same as (a)?(c) but for GeBi2Te4. It is clear that both compounds are 3 D TIs with a single Dirac cone at

除了能隙略大以外, Bi2Te2Se系列TI相比Bi2Se3系列也有其他的相同点与不同点. Shikin等[186]利用CD-ARPES和SARPES研究Bi2Te2.4Se0.6, 发现CD信号和自旋极化信号在狄拉克锥的两支上均相反, 和Bi2Se3系列一样. Neupane等[187]利用CD-ARPES研究Bi2Te2Se, 发现它的CD信号随着入射光子能量的变化发生正负交替, 也和Bi2Se3系列一样. 值得注意的是, Bi2Te2Se和其他TI对红外激发光的响应有很大的区别. Neupane等[188]利用1.47 eV的激发光和5.9 eV的探测光组成的泵浦ARPES研究几类TI的非平衡电子态, 发现其他TI(例如 (Bi1–xSbx)2Te3和GeBi2Te4)的弛豫过程在几个ps内即趋于结束, 表现为费米面以上的ARPES信号趋于消失; 但Bi2Te2Se的弛豫过程时长达到100 ps量级, 而且在激发光脉冲接触样品4 μs (= 4 × 106 ps) 后, 尽管弛豫已经完成, 但费米面以上100 meV以内的电子态仍然非常清晰. 也就是说, Bi2Te2Se的拓扑电子态的寿命比其他TI长六个数量级以上. 出现这种现象的原因, 文章认为是电子热扩散的维度不一样. 由于其他TI的绝缘性不够好, 电子的热扩散主要是三维的, 因此弛豫时间很短; Bi2Te2Se的绝缘性较好, 所以热扩散主要由表面态电子参与, 这一弛豫过程由于维度的限制而非常缓慢.
3
3.3.2.GeBi2Te4系列拓扑绝缘体
与Bi2Te2Se系列几乎同时被发现的Ge(Pb)Bi2Te4系列TI也被研究得比较多. 这一类TI的通式可以写成AB2X4, A2B2X5, AB4X7, AB6X10等 (A = Ge, Pb; B = Bi, Sb; X, X’ = Se, Te), 其中的AB2n+2X3n+4 (n = 0, 1, 2, …) 系列由AB2X4七重层和B2X3五重层这两种结构单元交替组成. 它们与下文将要详述的MnBi2Te4系列磁性TI(见4.2节)具有完全一样的晶体结构, 二者的主要区别有: 1) 本系列TI没有磁性原子Mn, 因而不具备磁性; 2) 本系列TI的2, 2, 5相、3, 2, 6相等单晶(如Ge2Bi2Te5)已被合成[189-192]; 3) 除了含Te的系统外, 含Se的PbBiSe系列化合物也已被合成. PbBi2Se4的少层薄膜可利用分子束外延方法生长[193], 但通过Bridgman方法生长的单晶并不形成PbBi2Se4七重层或Pb2Bi2Se5九重层之类, 而是形成通式为[(PbSe)5]n[(Bi2Se3)3]m的复杂结构 (n, m = 1, 2, …), 可以被看作一种天然的异质结构[194].理论计算(如文献[195])和ARPES测量均说明, 这个系列的绝大部分化合物是像Bi2Se3一样的单狄拉克锥TI. Neupane等[183]给出了真空解理和钾原子表面掺杂后GeBi2Te4的ARPES能带结构(图14(f)); 广岛大学Okamoto等[196]利用SARPES测量了它的能带自旋; Sterzi等[197]利用p和s线偏振入射光分别测量能带并把所得数据相减, 以此研究它的能带宇称反转, 所得结果均证实了GeBi2Te4的强三维TI属性. Muff等[198]利用ARPES和SARPES证实了GeBi4–xSbxTe7的拓扑属性并指出x值的变化会引起费米能(载流子浓度)的变化, 且在某一x值区间, 样品表面和体材料的载流子属性相反. Souma等[199]和Kuroda等[200]分别给出了Pb(Bi1–xSbx)2Te4为强三维TI的ARPES证据, 广岛大学Okuda等[201]利用ARPES和SARPES研究PbBi4Te7的能带结构和自旋纹理, 得出与Bi2Se3系列TI类似的结果. 不过由于PbBi4Te7具有两个不同的解理面, 而拓扑表面态的空间分布主要集中在PbBi2Te4层, 所以当样品在Bi2Te3层解理时, 表面态隐藏在一个五重层以下, 因而作者称之为“隐藏的拓扑表面态”. Shvets等[202]利用ARPES和SARPES指出Se掺杂的PbBi2Te4–xSex在x = 2, 2.6时也是TI. 根据文中的理论计算, Se含量越多, 体系的体能隙越大. PbBi2Se4(未成功生长)的体能隙可以达到约300 meV. Nakayama等[203]成功生长并利用ARPES研究了天然异质结构(PbSe)5[(Bi2Se3)3]m的其中两个成员 (m = 1, 2), 指出相比于Bi2Se3 (m = ∞) 来说, m = 2结构的狄拉克锥打开了一个100 meV量级的能隙, 而m = 1结构更是只有一个抛物线形的能带通过费米能. 这种变化规律和Bi2Se3系列TI的少层薄膜非常类似, 文章认为m值较小时PbSe和Bi2Se3的界面密度比较大, 所以由界面引致的有限尺寸效应比较明显. ARPES观察到的能隙正是来自不同结构单元形成的界面之间的耦合.
3
3.3.3.TlBiSe2系列拓扑绝缘体
对TI的大能隙和体绝缘性的追求也导致TlBiSe2系列拓扑绝缘体的发现. 这一系列的通式为TlBX2 (B = Bi, Sb; X = S, Se, Te), 其最小结构单元包含Tl-X-B-X四个二维的原子层, 而一个单胞包含三个最小结构单元. 以Sb取代Bi可以调节费米能的位置, 而变换X位原子可以调节体系的自旋轨道耦合强度. 这一类TI最大的特点是它们的狄拉克点几乎位于体能隙的中心, 有利于拓扑量子输运行为的探测. Kuroda等[204]、Sato等[205]和Chen等[206]分别通过ARPES测得其
因为TlBiSe2系列材料的自旋轨道耦合强度可以通过X元素的选择来方便地调节, 且在调节的过程中不会出现额外的结构相变, 因此这个材料是观测凝聚态体系从普通绝缘体到拓扑绝缘体的相变的最佳选择之一. 这种拓扑相变不同于结构相变或磁性相变, 其相变前后的空间群并不产生突变, 而是材料整体的拓扑不变量(如主拓扑数ν0)从普通绝缘体的零突变到TI的1, 伴随着正值体能隙的闭合和负值体能隙的打开. Xu等[209]利用ARPES和SARPES研究TlBi(S1–δSeδ)2的电子学结构, 在δ值变化时首次观察到拓扑相变的全过程, 并通过测量拓扑表面态在狄拉克点上下自旋螺旋方向的反转确认体系在 δ ≥ 0.6时为三维TI. 由图15可见, 当 δ 值从零开始增大(即自旋轨道耦合增大)时, 体系的体能隙开始减小. 到 δ = 0.6时, 体能隙完全闭合. 此时体系恰好位于普通绝缘体和TI的相变点, 体能态和拓扑表面态完全重合, 表现为体能态的两支亮度突然增强. 理论上, 这一相变点可以理解为一个相变区, 系统在相变区中依次经历狄拉克半金属-外尔半金属-狄拉克半金属的转变. 实际上, Neupane等[40]在讨论狄拉克半金属Cd3As2时 提到了TlBi(S1–δSeδ)2在δ ≈ 0.5时也是一个狄拉克半金属, 但文中没有给出这一结论的决定性证据—狄拉克型的线性面外色散. 当 δ > 0.6时, 导带进一步下降而价带进一步上升, 体能隙由于导带和价带的杂化而重新打开, 但其能量可定义为负值. 这体现在新形成的价带变成M形, 而新的导带变成W型(图15(c), 最右侧小图). 这个拓扑相变的过程伴随着能带自旋的变化, 由普通绝缘体的自旋简并变为TI的自旋螺旋纹理. 同一文献的SARPES数据表明这种自旋纹理在狄拉克点的上下是反向的, 这与理论预言相符[209].
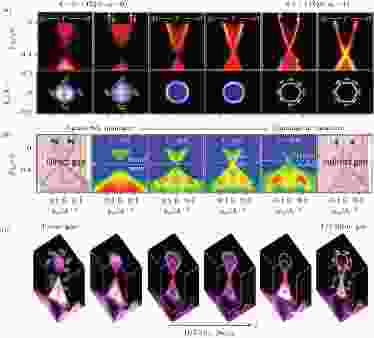 图 15 TlBi(S1-δSeδ)2体系中的拓扑相变[209] (a) 沿
图 15 TlBi(S1-δSeδ)2体系中的拓扑相变[209] (a) 沿
Figure15. Topological phase transition in TlBi(S1-δSeδ)2[209]: (a) ARPES k-E maps along

Ando小组对这一拓扑相变的后续测量揭示了更为丰富的物理图景. 文献[210] 证实了δ ≈ 0.5时的拓扑相变, 但在0.6 < δ < 0.9这个区间内, 作者观察到TlBi(S1–δSeδ)2虽然是个TI, 但其拓扑表面态实际上打开了一个达到100 meV量级的能隙, 且 δ越靠近0.5, 能隙越大. 对于这一点, 文章并未给出完整的解释, 只是提到它也许可以和高能物理中的Higgs质量形成机理类比. 文献[211] 对0.6 < δ < 1以及 δ = 0的样品作了系统的SARPES测量, 发现虽然狄拉克锥在0.6 < δ < 0.9区间中存在能隙, 但作为拓扑表面态特征的自旋动量锁定行为在这一区间仍然存在, 只是越靠近相变点, 自旋极化的程度越低.

3
3.3.4.小 结
Bi2Te2Se系列、GeBi2Te4系列、TlBiSe2系列等几类含Bi的拓扑绝缘体在晶体结构和电子结构上都与Bi2Se3系列比较相似. 它们都具有范德华力结合的层状结构, 其拓扑不寻常属性在能带上都表现为
2
3.4.HgTe
HgTe是个拓扑绝缘体, 这其实早就被大家所熟知. 因为HgTe与CdTe构成的异质结是第一种被理论提出并被输运实验证实的二维拓扑绝缘体(量子自旋霍尔绝缘体)[7,8], 所以说拓扑绝缘体的研究奠基于HgTe也不为过. 具体来说, 当HgTe-CdTe异质结中HgTe层的厚度在一个临界值 (dc = 6.35 nm) 以上时, HgTe的两个宇称不同的能带(Γ6和 Γ8的上半部分)会发生反转, 导致全局的拓扑相变[7]. 既然HgTe薄膜在比较厚的时候是拓扑的, 那么它的单晶肯定也是拓扑的. 实际上早期的理论工作也揭示了HgTe体材料的拓扑不寻常性质[212-214], 只不过人们一直致力于研究其异质结的二维拓扑性, 忽略了三维的情况而已. 相比于上文说到的几类含Bi的TI, HgTe有两个显著的不同点. 第一, 闪锌矿结构的HgTe(空间群为
利用ARPES研究HgTe体材料的文献比较少, 值得提及的有Brüne等[216]和Liu等[217]的工作(笔者是后一工作的主要完成人). Brüne等[216]的论文主要研究HgTe体材料的输运行为, 指出其拓扑表面态可以导致量子化的霍尔效应. 从文中唯一的ARPES k-E图可以看到, 在类似倒置抛物线的 Γ8能带下半部分内部存在一个










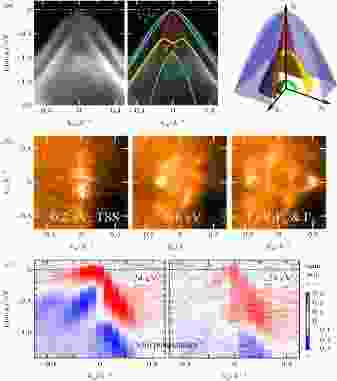 图 16 HgTe单晶的ARPES研究[217] (a) 过
图 16 HgTe单晶的ARPES研究[217] (a) 过
Figure16. ARPES on single crystal HgTe[217]: (a) ARPES k-E map (left) and guides-for-the-eye band dispersion (right). TSS: topological surface state (Dirac cone); (b) skematic kx–ky–E 3 D band dispersion; (c) kz dispersion of the TSS and the bulk states. TSS has no kz dispersion, while other bands show clear out-of-plane dispersive pattern; (d) spin polarization detected with SARPES, showing the spin-momentum lock behavior.
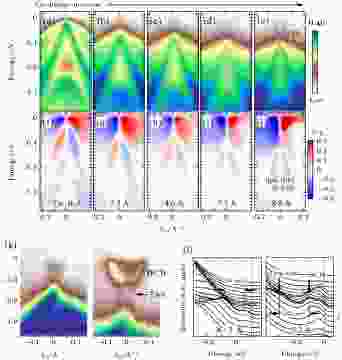 图 17 表面掺杂HgTe单晶的ARPES研究[217] (a)?(e) 碱金属Cs当量增加时能带的变化. 显然狄拉克锥的上半部分变得可见, 且Γ8能带上下两支之间存在能隙; (f)?(j) 对应的CD-ARPES信号, 表明锥的上半部分具有典型的拓扑表面态特征; (k) 碱金属K当量增加时能带的变化; (l) 图 (k) 的能量分布曲线, 显示体能隙从290 meV增加到392 meV
图 17 表面掺杂HgTe单晶的ARPES研究[217] (a)?(e) 碱金属Cs当量增加时能带的变化. 显然狄拉克锥的上半部分变得可见, 且Γ8能带上下两支之间存在能隙; (f)?(j) 对应的CD-ARPES信号, 表明锥的上半部分具有典型的拓扑表面态特征; (k) 碱金属K当量增加时能带的变化; (l) 图 (k) 的能量分布曲线, 显示体能隙从290 meV增加到392 meVFigure17. ARPES on surface-doped HgTe single crystals[217]: (a)?(e) Band evolution as Cs dosage increases. The upper half of the Dirac cone becomes visible, and a gap exists between the upper and the lower Γ8 band; (f)?(j) corresponding CD-ARPES signal, indicating the topological nature of the upper cone; (k) band evolution as K dosage increases; (l) EDCs of Fig. (k), showing an increase of the gap, from 290 to 392 meV.
2
3.5.半Heusler化合物拓扑绝缘体
半Heusler化合物拓扑绝缘体和HgTe是一脉相承的. 半Heusler化合物的通式为XYZ, 其结构可被看作利用第三元素填充间隙位置的闪锌矿晶格, 即用Xn+离子填充 (YZ)n- 闪锌矿亚晶格. 其中的X和Y原子具有阳离子特征, 而Z原子可被视为阴离子. 它们和HgTe具有相同的空间群 (

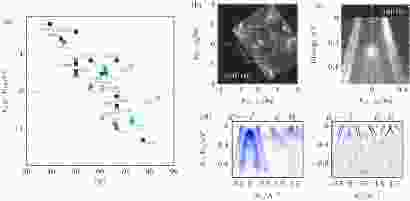 图 18 半Heusler拓扑绝缘体的ARPES研究[219,221,222] (a) 第一性原理计算给出的典型半Heusler化合物的体能隙 (EΓ6 – EΓ8) 大小与体系平均原子序数
图 18 半Heusler拓扑绝缘体的ARPES研究[219,221,222] (a) 第一性原理计算给出的典型半Heusler化合物的体能隙 (EΓ6 – EΓ8) 大小与体系平均原子序数







Figure18. ARPES on half Heusler TIs[219,221,222]: (a) Bulk band gap (EΓ6 – EΓ8) of typical half Heusler compounds as a function of the system’s average atomic number




半Heusler化合物TI的APRES研究也相对较少, 主要原因是技术性的: 由于半Heusler化合物是面心立方的闪锌矿结构, 不像含Bi的层状化合物那样具有天然的解理面, 所以它们的单晶在真空中的解理成功率很低. 半Heusler TI的第一份ARPES文献[221] 是笔者2011年时在Kaminski小组完成的, 文中给出了RPtBi (R = Lu, Dy, Gd) 的高分辨费米面扫描图和k-E图(图18(b) 和 图18(c)). 由数据可见, 实验得到的费米能在理论计算的费米能以下, 即体系具有本征的p型掺杂. 这些化合物有两对(四支)大致线性的能带通过费米面. 它们明显由同一能带自旋劈裂而成, 自旋相同的两支在费米能以上应该是分别接合的. 当时我们没有找到过费米面狄拉克能带为奇数的确实证据, 从而未能确定系统的拓扑性质. 2016年上海科技大学Liu 等[222]重新研究这个体系, 发现它在费米面以下约0.5 eV处有一对类似Rashba劈裂的能带(图18(d)). 通过与理论计算的比对以及CD-ARPES分析, 作者认为它就是半Heusler TI的狄拉克锥. 笔者基本认可这一观点, 只是觉得文中把这个狄拉克锥看作与其旁边的能带接合比较违反直觉, 毕竟狄拉克锥的每一支都必须分别与体导带和体价带接合, 而这种接合关系可能像单晶金[116] 一样是较难测量的.
研究半Heusler TI电子学结构的另一种方法是利用MBE生长其薄膜, 然后利用ARPES测量薄膜的能带. 当薄膜足够厚时, 它的能带和单晶的没有区别. Logan等[223]利用这个方法测量了LuPtSb的能带结构. 理论上, LuPtSb的体能隙非常接近零, 就是说它处在普通绝缘体和拓扑绝缘体的分界线附近. ARPES和SARPES实验结果表明它和LuPtBi一样具有狄拉克锥拓扑表面态, 也就是说它其实是一个TI而非普通绝缘体.
2
3.6.小 结
本章回顾了几类主要的强三维拓扑绝缘体的ARPES研究. 强三维拓扑绝缘体是近来层出不穷的拓扑材料中研究历史最长, 也最为人熟知的一类, 具有非常典型的狄拉克锥拓扑表面态和自旋螺旋纹理. 它的范围绝不仅限于文中介绍的几种. 最近完成的对所有已知或未知单晶材料的拓扑穷举[26-30] 表明, 拓扑绝缘体的种类极为繁多, 物理信息极为丰富. ARPES作为探测材料电子学结构, 特别是表面电子学结构的强大实验工具, 在拓扑绝缘体的研究中扮演着举足轻重的作用, 以至于人们在获得一个新材料的单晶, 进行简单输运测量以后, 会首先进行ARPES测量, 以确定材料的拓扑属性和基本的能带参数. 更细致的ARPES表征手段, 包括对时间、空间、自旋敏感的ARPES技术, 则被应用于探讨拓扑绝缘体的自旋构型、非平衡弛豫和电声耦合强度等物理信息. ARPES独一无二的k空间直接探测能力将帮助人们越来越深入地认识拓扑材料电子学结构, 并以此指导未来的拓扑自旋电子学和拓扑量子计算的研究和应用.与上述的总体研究脉络相似, 磁性拓扑绝缘体的ARPES研究也大致经历了两个阶段. 第一个阶段的研究对象主要是磁性掺杂的拓扑绝缘体, 即在三维TI中以体掺杂或表面掺杂的方式引入磁性杂质, 例如Fe, Cr, Mn原子等. 这些杂质有时会形成长程磁序, 使样品整体表现出例如磁滞回和面外自旋极化等磁性拓扑绝缘体的特征. 第二个阶段的研究对象是化学配比的本征的磁性拓扑绝缘体化合物, 以MnBi2Te4为代表. 这一族化合物的体材料是反铁磁的, 但其少层薄膜材料在层数为奇数时表现出铁磁性. 下面分别介绍这两个阶段的代表性ARPES研究.
2
4.1.磁性掺杂拓扑绝缘体的ARPES研究
由于预期能够实现QAHE, 磁性掺杂的三维TI从一开始就引起了研究者的莫大兴趣, 利用ARPES研究三维TI的几份最早的文献对磁性掺杂就有所提及. 2010年斯坦福大学Chen等[224]首次利用ARPES系统地研究了磁性掺杂TI的能带结构(图19). 他们发现在Bi2Se3中引入少量取代Bi位的铁磁杂质, 例如Fe和Mn, 能够令原来无能隙的拓扑表面态在狄拉克点打开能隙, 即令体系表面的狄拉克准粒子具有非零的有效质量. 这个磁性能隙的大小和杂质的浓度呈正相关. 更进一步, 由于Mn比Fe少一个电子, Mn掺杂在使狄拉克锥打开能隙的同时也能对Bi2Se3系统进行空穴掺杂. 当Mn浓度在1% 的时候, 系统的费米能刚好位于狄拉克点的能隙中, 实现了QAHE要求的体态和表面态的绝缘. 由于使用了体材料样品, 本文并未讨论由有限尺寸效应导致的能隙打开和时间反演破缺导致的磁性能隙的异同.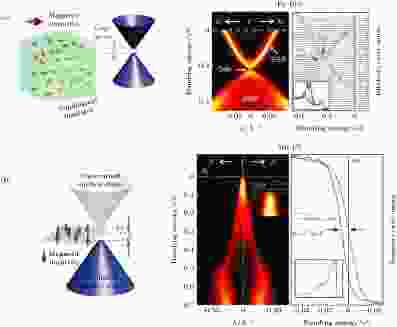 图 19 对磁性掺杂TI的首个ARPES研究[224] (a) 16% Fe体掺杂的Bi2Se3的能带. 由图可见, 狄拉克点打开了一个能隙; (b) 1% Mn体掺杂的Bi2Se3的能带. 不仅狄拉克点具有能隙, 而且样品的费米面被调节至狄拉克点中, 实现了表面态的绝缘相
图 19 对磁性掺杂TI的首个ARPES研究[224] (a) 16% Fe体掺杂的Bi2Se3的能带. 由图可见, 狄拉克点打开了一个能隙; (b) 1% Mn体掺杂的Bi2Se3的能带. 不仅狄拉克点具有能隙, 而且样品的费米面被调节至狄拉克点中, 实现了表面态的绝缘相Figure19. The first ARPES study on magnetic-doped TI[224]: (a) ARPES bands for 16% Fe bulk doped Bi2Se3. A gap is visible at the TSS; (b) ARPES bands for 1% Mn bulk doped Bi2Se3. The gap not only exist but also locates right at EF, realizing an insulating phase of the surface state.
2012年普林斯顿大学Xu等[225]利用自旋分辨ARPES进一步研究铁磁掺杂和普通掺杂的TI薄膜的能带属性, 揭示了磁性带隙的一个关键性质:









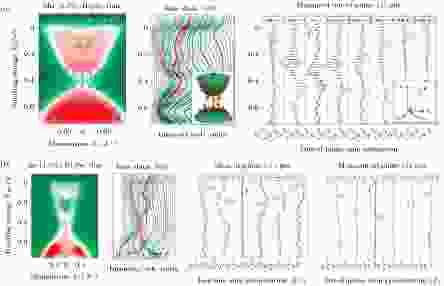 图 20 磁性掺杂和非磁掺杂的Bi2Se3薄膜的能带自旋分析[225] (a) Mn-Bi2Se3薄膜的能带自旋. 在这个铁磁掺杂的TI样品中,
图 20 磁性掺杂和非磁掺杂的Bi2Se3薄膜的能带自旋分析[225] (a) Mn-Bi2Se3薄膜的能带自旋. 在这个铁磁掺杂的TI样品中, 



Figure20. SARPES analysis on magnetic (Mn) and non-magnetic (Zn) doped Bi2Se3 films[225]: (a) Band spins in Mn-Bi2Se3 films. In this ferromagnetically doped TI, the large sz component at




由于磁性掺杂的TI表面存在原子磁矩, 一个微小的外磁场有可能使样品产生局部的磁化, 引起ARPES能谱的改变. Shikin等[227]在2018年指出, ARPES的线偏振和圆偏振入射光(来自同步辐射光源、激光光源等)会在磁性掺杂TI表面形成一个等效的磁场, 引起样品表面的磁化. 这种局域磁化在ARPES能谱上的有如下特征: 1) 不同偏振的入射光下, 狄拉克锥左右两支的ARPES信号强度有很大差别, 即产生了光电子的自旋极化流. 这在本文对CD-ARPES的讨论中已详述(见3.2.5节); 2) 不同偏振的入射光下, 狄拉克锥整体的面内k空间位置会有微小但可以测量的变化, 使狄拉克点不再正好位于

在TI的表面引入磁性原子也是一个有趣的研究方向. 清华大学Wang等[228] 和汉堡大学Schlenk等[229] 通过ARPES和STM测量指出, 不同于磁性杂质的体掺杂, 仅在Bi2Se3的表面沉积Cr和Fe原子并不能使狄拉克锥打开能隙, 而且通过对样品的升温退火, Fe原子会转移至表面层以下, 使表面掺杂程度下降.
2
4.2.本征磁性拓扑绝缘体的ARPES研究
虽然人们成功地在磁性掺杂的TI中实现了长程磁序, 继而在极低温下实现了QAHE, 但TI中的磁性杂质本质上是随机排列的, 并不形成有序的晶格结构, 这对提高QAHE的实现温度极为不利. 实际上, 研究者从一开始就意识到找到一种本征的、化学配比的磁性拓扑绝缘体对整个拓扑材料的研究具有基础性的意义, 但由于材料搜寻的难度, 这个方向的研究一直未有实质性进展. 在2013年, 韩国延世大学的Lee等[230]利用助溶剂方法第一次合成了MnBi2Te4的多晶粉末, 证实了这个相的存在. 2017年人们利用MBE生长MnSe与Bi2Se3构成的异质结构, 发现这个结构的拓扑表面态位于整个体系的表面, 而不像别的拓扑异质结构那样位于两种材料的分界处, 才意识到MnSe和Bi2Se3交替而成的层状结构是一种真正的单晶, MnBi2Se4, 而不是两种材料形成的异质结构[231,232]. 2018年, 人们进一步发现同样的MBE生长方法也适用于MnBi2Te4[233]. 紧接着, MnBi2Te4的单晶也被合成[234-236], 对这个体系的大规模实验研究的序幕由此揭开. MnBi2Te4的晶体结构和3.4节提及的GeBi2Te4系列TI完全相同, 它的一个最小结构单元由七个原子层组成, 自上往下分别是Te-Bi-Te-Mn-Te-Bi-Te, 称为“七重层 (septuple layer, SL)”, 区别于Bi2Te3的Te-Bi-Te-Bi-Te五重层 (quintuple layer, QL) (图21, 文献[234,237]), 相邻七重层之间以范德华力结合. Mn层位于七重层的正中, 是体系磁性的来源. 一个七重层的高度为1.37 nm, 而Bi2Te3五重层的高度约为1.0 nm. MnBi2Te4的原胞由3个七重层以ABC堆叠构成, 其c方向长度约为4.07 nm. 重要的是, 无论是理论预言或是中子衍射实验均指出, MnBi2Te4的基态磁结构是所谓A型的反铁磁相, 即一个Mn层内的每个磁矩均指向同一个面外方向(+z或-z), 而相邻Mn层的磁矩方向相反(图21(b)). 这一反铁磁结构的Neel温度TN(124) ≈ 24 K, 在此温度以上, 体系呈现顺磁性. 也就是说, MnBi2Te4是一个本征的反铁磁拓扑绝缘体.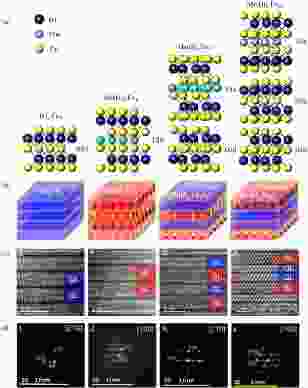 图 21 (MnBi2Te4)m(Bi2Te3)n (m = 1, n = 0, 1, 2, …) 系列磁性拓扑绝缘体以及普通拓扑绝缘体Bi2Te3的 (a) 晶体结构[234], (b) 理论预言的基态磁结构[237], (c) 扫描透射电子显微镜原子分辨HAADF STEM图样[237], 以及 (d) 选区电子衍射纹样[237]. 由图可见, 此系列化合物的构成单元是交替出现的Bi2Te3五重层(记为023层)和MnBi2Te4七重层(记为124层). Mn原子层位于124七重层的正中, 是体系磁性的来源. MnBi2Te4的体材料基态磁结构被中子衍射实验初步确定为面外磁矩的A型反铁磁
图 21 (MnBi2Te4)m(Bi2Te3)n (m = 1, n = 0, 1, 2, …) 系列磁性拓扑绝缘体以及普通拓扑绝缘体Bi2Te3的 (a) 晶体结构[234], (b) 理论预言的基态磁结构[237], (c) 扫描透射电子显微镜原子分辨HAADF STEM图样[237], 以及 (d) 选区电子衍射纹样[237]. 由图可见, 此系列化合物的构成单元是交替出现的Bi2Te3五重层(记为023层)和MnBi2Te4七重层(记为124层). Mn原子层位于124七重层的正中, 是体系磁性的来源. MnBi2Te4的体材料基态磁结构被中子衍射实验初步确定为面外磁矩的A型反铁磁Figure21. (a) Crystal structures[234], (b) predicted ground state magnetic structure[237], (c) Atomic resolution HAADF STEM images[237], and (d) Selected area electron diffraction (SAED) patterns[237], of magnetic TIs (MnBi2Te4)m(Bi2Te3)n (m = 1, n = 0, 1, 2, …) and 3 D TI Bi2Te3. This series of compounds consists of alternatively stacking Bi2Te3 QLs (023 layers) and MnBi2Te4 septuple layers (124 layers). The 0 K magnetic structure of bulk MnBi2Te4 is determined by neutron diffraction to be out-of-plane A-type antiferromagnetic.
有趣的是, 这样的磁性TI不止MnBi2Te4一种, 而是以MnBi2Te4(124相)为代表的一族化合物, 其通式可以用 (MnBi2Te4)m(Bi2Te3)n (m, n = 0, 1, 2, 3, …) 表示(图21). 这些化合物之中, 124相和MnBi4Te7 (147相)已被实验确定为磁性TI, MnBi6Te10 (1, 6, 10相)和MnBi8Te13 (1, 8, 13相)的单晶已被成功合成[237], 而m > 1的各种化合物, 以及每个最小结构单元包含多于一个Mn层的化合物(例如Mn2Bi2Te5, 225相), 应可利用MBE技术逐层生长而成, 但其是否为独立的化合物目前仍不确定. Bi2Te3, 124相和1, 6, 10相的空间点群为


MnBi2Te4等材料的基态A型反铁磁结构非常重要. 在反铁磁TI中可以定义一个新的







对MnBi2Te4, MnBi4Te7等的ARPES研究目前已有不少, 这些研究也可以分为两个阶段. 第一阶段大致从2018年中开始到2019年5月左右, 主要的结论是ARPES观察到了磁性引起的带有大能隙的拓扑表面态, 与理论和中子衍射实验得出的磁结构相符合. 第二阶段特指2019年7月(本文写作时), 4个研究组分别在arXiv上张贴文章, 各自独立发现MnBi2Te4的拓扑表面态能隙为零. 这一发现与理论和中子实验得出的体材料磁结构直接相悖, 引燃了对这类化合物的体材料磁结构和表面磁结构的又一次研究热潮. 下面讨论这些研究.
表1归纳了笔者所知的2019年7月22日之前对MnBi2Te4的所有ARPES研究. 从测得的能隙的有无上, 可以明显地看出研究的两个阶段. 第一阶段的ARPES数据如图22所示. 可以看到, 无论光子能量和测量温度是多少, 这些文献都观察到 约100 meV的

| 文献序号 | 样品形态 | 测量温度/K | 光子能量/eV | 能隙大小/meV | 备注 |
| [242] | 单晶 | 17/300 | 28/9 | 70 | |
| [243] | 单晶 | 30/300 | 未提及 | ~85/115 | |
| [235] | 单晶 | 18 | 21.5 | 100 | |
| [244] (v1, v2) | 单晶 | 18/40 | 7.25/9/11/13.75/15 | 50 | 在这篇arXiv文章的第三个版本(张贴于2019年7月9日)里, 作者加入了零能隙的数据. |
| [245] | 单晶 | 7/18/47/80 | 21.5/79 | 100 | |
| [246] | 薄膜 | 25 | 21.2 | 0 | 此文献观察到了零能隙, 但作者认为测量温度不够低, 测得的是无能隙的顺磁拓扑表面态. |
| [247] | 单晶 | 10/300 | 6.3/7-40 | 0 | 张贴于2019年7月8日 |
| [248] | 单晶 | 7.5 | 7/10-22 | 0 | 张贴于2019年7月11日 |
| [249] | 单晶 | 10/50 | 13.8/47/51 | 0 | 张贴于2019年7月15日 |
| [250] | 单晶 | 8/60 | 6.36/6.7 | 0 | 张贴于2019年7月22日 |
表1MnBi2Te4的ARPES研究小结(截至2019年7月22日). 表中“能隙大小”指的是每份文献各自认为的表面态中的

Table1.Summary of ARPES studies on MnBi2Te4 (as of 22 July 2019).
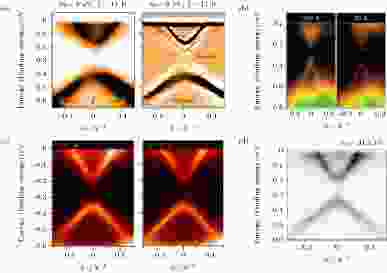 图 22 MnBi2Te4的早期ARPES数据, 观察到较大的表面态能隙. 图中数据的光子能量和测量温度分别为 (a) 9 eV, 17 K(右图为二次微分分析结果)[242]; (b) 30和300 K, 光子能量未标示[243]; (c) 21.5 eV, 7 K(左)和47 K(右)[244]; (d) 21.5 eV, 18 K[235]
图 22 MnBi2Te4的早期ARPES数据, 观察到较大的表面态能隙. 图中数据的光子能量和测量温度分别为 (a) 9 eV, 17 K(右图为二次微分分析结果)[242]; (b) 30和300 K, 光子能量未标示[243]; (c) 21.5 eV, 7 K(左)和47 K(右)[244]; (d) 21.5 eV, 18 K[235]Figure22. Early ARPES data on MnBi2Te4, observing sizable gaps at the surface state. The photon energies and measuring temperatures are (a) 9 eV, 17 K (right: 2nd derivative result)[242]; (b) 30 and 300 K, photon energy unmarked[243]; (c) 21.5 eV, 7 K (left) and 47 K (right)[245]; (d) 21.5 eV, 18 K[235].
自2019年7月起, 对MnBi2Te4的ARPES研究进入了一个新的阶段. 笔者所在的南方科技大学研究小组首先在arXiv上张贴论文[247], 利用激光ARPES (hν = 6.3 eV) 和基于低能同步辐射光 (hν = 7—40 eV) 的系统性的ARPES数据指出MnBi2Te4的拓扑表面态能隙为零. 原来以为的带有大能隙的表面态实际上是MnBi2Te4的体能态, 带有明显的kz方向色散(图23). 这个无能隙的拓扑表面态非常稳定, 无论在Neel温度以下还是以上, 甚至在300 K的室温下仍然保持其无能隙的特征. 即使在空气中解理样品, 气体分子和杂质也只令样品总体被空穴掺杂, 而拓扑表面态仍然是无能隙的(图24). 该文的数据质量非常高, 以无可辩驳的实验事实证明了无能隙表面态的存在. 在此文张贴于arXiv后的三周内, 又有三个各自独立的对MnBi2Te4的ARPES研究在arXiv上张贴出来[248-250] (分别来自牛津大学-清华大学陈宇林小组、中国科学院物理研究所钱天-丁洪小组和爱荷华州立大学Kaminski小组), 得到与其相同的实验结论.
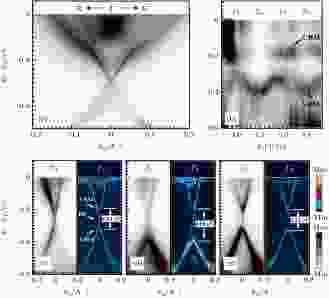 图 23 MnBi2Te4的最新ARPES数据, 观察到零能隙的表面态[247] (a) 一个典型的沿
图 23 MnBi2Te4的最新ARPES数据, 观察到零能隙的表面态[247] (a) 一个典型的沿


Figure23. Surface and bulk electronic structure of MnBi2Te4[247]: (a) A typical ARPES k-E map along



 图 24 MnBi2Te4无能隙狄拉克锥的稳定性[247]. 每一小图的左边为ARPES原始数据, 右边为二次微分后的数据. 所有数据均采自6.3 eV激光ARPES系统, 沿
图 24 MnBi2Te4无能隙狄拉克锥的稳定性[247]. 每一小图的左边为ARPES原始数据, 右边为二次微分后的数据. 所有数据均采自6.3 eV激光ARPES系统, 沿
Figure24. Robustness of the Dirac surface state[247]. The figure shows ARPES raw (left) and second derivative (right) k-E maps taken with 6.3 eV laser light along

由于ARPES实验观察到了无能隙的狄拉克锥形式的表面态, 而无能隙特性又与体态的A型反铁磁结构相悖, 所以接下来的研究重点便是寻找这个表面态的来源. 从图24看出, 这个表面态的稳定性和普通三维TI(例如Bi2Se3和Bi2Te3)的稳定性不相上下, 连空气解理也不能将其破坏. 因此这个表面态很有可能也是被拓扑保护的[247]. 同一份文献用细致的对称性分析和第一性原理计算提出该表面态有可能来源于和体材料A型反铁磁结构不同的的表面磁结构, 并讨论了每种表面磁结构的形成能以及从与实验比较中得出的形成该结构的可能性. 实验确定MnBi2Te4的表面磁结构对磁性拓扑绝缘体领域极为重要, 这将成为自旋分辨低能电子显微技术 (spin-polarized low energy electron microscopy, SP-LEEM)、磁圆二色性 (magnetic circular dichroism, MCD)、金刚石NV色心 (NV center) 或非线性光学等对表面磁性敏感的探测技术的一个很好的研究课题.
截止至2019年7月底, MnBi2Te4系列其他化合物(例如MnBi4Te7, MnBi6Te10等)的ARPES研究见于文献的并不多, 但许多研究小组已有尚未发表或张贴的数据, 或已把其列入最近的研究计划. 目前见于arXiv的MnBi4Te7 ARPES数据有两组, 分别来自科罗拉多大学Hu等[251] 和德国Vidal等[252]. 对比起MnBi2Te4, MnBi4Te7 (147相)结构的最大特点是其一个结构单元包含有两个相对独立的, 以范德瓦耳斯力相联系的部分, 分别是124层和Bi2Te3 (023) 层(即“147 = 124 + 023”). 因此当ARPES或STM测量在真空中解理样品时, 出现表面为124相和023相的概率大致相等. 这使147相具有两套截止面不同的能带结构(如此类推, 1, 6, 10相将有3套不同的能带结构, 等等). 上述的两篇文献均找到了这两套能带结构, 也都认为表面态存在较大的能隙, 但数据的动量分辨率并不算高, 因此其细致的能带尚不能分辨.
以MnBi2Te4为代表的磁性拓扑绝缘体无疑是磁性拓扑材料领域的一个新的热点和突破口. 由于其磁结构存在未曾料到的复杂性和表面-体材料不一致的情况, 对这一系列化合物中的每一个做高分辨率的系统性的ARPES研究是目前首要的任务. 这些研究将确定每一个化合物、每一种解理面的表面态能隙的有无和大小, 有助于理解这些体系的表面磁结构, 从而为下一步的研究(例如利用掺杂调控费米面, 进行输运测量等)提供依据. 由于ARPES在这一类材料中能够给出非常丰富的物理信息, 这一方向还是很有前景的.
2
4.3.小 结
本章回顾了目前为止利用ARPES对磁性拓扑绝缘体(包括磁性掺杂的TI和本征磁性TI)电子结构的研究. 凝聚态体系的磁性和拓扑性质的耦合与竞争一直是拓扑材料领域的一个重要的研究方向. 磁性拓扑材料特有的物理现象不仅包括QAHE, 也包括拓扑磁电效应、磁光学Faraday/Kerr效应等[239]. 这一方向的内涵不仅体现在磁性拓扑绝缘体中, 也体现在磁性拓扑半金属中, 例如磁性Weyl半金属的最小模型仅包括一对手性相反的Weyl点, 区别于空间反演破缺的Weyl半金属的两对Weyl点, 等等. 目前非磁拓扑体系已有相当完备的穷举性的材料预言, 而这种理论预言由于磁空间群的丰富性和确定磁基态的难度而很难被复制到磁性拓扑体系中. 因此实验数据, 特别是ARPES实验数据, 仍然是目前确定磁性拓扑材料性质的最佳手段. 可以预见, ARPES实验在较长的一段时间内仍将对磁性拓扑材料的研究起到引领作用.



强三维拓扑绝缘体和磁性拓扑绝缘体有非常特殊的能带特征, 其狄拉克准粒子只存在于样品的表面或界面, 因此ARPES是探测它们的首选实验方法. 利用ARPES, 人们不仅获得了强三维TI和磁性TI基本的表面电子态的色散关系, 证实了这些准粒子的存在, 还揭示了其自旋纹理、电声耦合和时域能谱等丰富的电子学信息. 在强三维TI领域, 对Bi, Au等单质的ARPES研究发现了第一类拓扑非平庸的三维材料, 也指出拓扑不寻常性在重金属单质中非常普遍; 对Bi2Se3系列TI的ARPES研究揭示了拓扑材料中最简单的单个

限于作者水平, 文中可能存在科学上、逻辑上和语句上的各种错误和含混之处, 且有许多重要的研究结果可能未被收录进本文中. 请各位读者批评指正.
