摘要:设计了一种含薄膜壁的Helmholtz型声子晶体, 该结构利用了空气和薄膜的耦合振动, 一方面将刚性壁转变为柔性壁, 降低了一阶振动时的等效刚度, 使第一带隙下限分别低于同参数下的普通Helmholtz型声子晶体和薄膜, 另一方面基于局域共振原理, 由于薄膜的出现和腔口空气通道长度的增加, 使得结构在低频范围内存在多个振动模态, 从而将原有一个带隙扩展为多个带隙. 将该结构带隙上下限分别等效为环形系统和串联系统, 用传递矩阵法和有限元法两种方法计算了其低频带隙范围, 两种方法结果吻合良好. 通过调整参数对带隙调控规律进行了进一步分析, 结果显示, 在低频范围内, 既可以通过改变与腔口空气通道或薄膜相关的参数, 在保证其中某些带隙变化不大的情况下, 单独调整其他带隙; 也可以通过调整内外腔体积, 对所有带隙进行调控.
关键词: Helmholtz共振腔/
低频带隙/
噪声控制/
声子晶体

English Abstract

全文HTML

--> --> -->

自声子晶体提出以来^[1], 其一直是声学领域国内外****研究重点之一^[2—7], 另一方面, Helmholtz共振腔这种声学器件在声学超材料中有着广泛的应用^[8—12]. 近年来, 利用Helmholtz共振原理构建的声子晶体及超材料已逐渐由简单叠加结构^[13,14]逐渐发展为长开口^[15]、多腔^[16]、多开口^[17,18]、嵌套^[19]、多层复合^[20]等结构.
由于空气密度的限制, 仅利用空气的振动往往无法进一步提升声子晶体的性能, 与此同时, 薄膜作为一种轻质材料, 其在低频方面也具有较好的隔声性能^[21—23]. 能否利用两种结构的耦合, 构建出低频隔声性能更好的声子晶体, 就成为值得探讨的问题. 实际上, 近年来已有关于含薄膜的Helmholtz腔仿真研究^[24,25], 腔体与薄膜耦合^[26—28]以及薄膜与穿孔板-腔耦合^[29]等结构的研究出现. 但薄膜与Helmholtz腔耦合结构的理论计算与声子晶体带隙研究仍较少.
本文在之前Helmholtz腔与固/固型声子晶体的耦合研究^[30]基础上, 设计了一种含薄膜壁的Helmholtz型声子晶体, 对其带隙机理进行了详细分析, 用传递矩阵法(transfer matrix method, TMM)和有限单元法(finite element method, FEM)计算了其低频带隙上下限. 该结构第一带隙下限分别低于同参数下的普通Helmholtz型声子晶体和薄膜, 且质量小于同尺寸传统Helmholtz型声子晶体, 进一步提高了Helmholtz腔在小尺寸、轻结构下控制大波长的能力, 提高了其在工程上的应用价值.

带薄膜壁的Helmholtz结构横截面如图1所示, 其晶格常数为a, 腔体框架边长为l, 腔壁厚度为b, 在腔右侧由悬臂梁形成“W”型开口, 其空气通道总长度为l₁ = n × (l – b) + b, 宽度为s, 其中n为悬臂梁的个数. 将腔体左侧壁更换为厚度为b_r的硅橡胶薄膜, 并在其上黏附有长h_s、厚b_s的铝制质量块, 薄膜受到y方向张力T的作用. 因框架材料一般为金属, 其声阻抗一般在空气的10⁵倍以上, 薄膜材料的10³倍以上, 对带隙的影响较小, 故将其设定为固定约束状态.
图 1 带薄膜壁的Helmholtz结构横截面
Figure1. Cross section of Helmholtz resonator structure with a membrane wall.

取a = 53 mm, l = 50 mm, b = 1 mm, n = 2 (l₁ = 99 mm), s = 1 mm, b_r = 1 mm, h_s = 5 mm, b_s = 1 mm, T = 1 × 10⁶ N/m², 先将其按照第一布里渊区进行扫描, 再将其沿纵向对3个元胞结构进行串联, 分别计算得出其在1700 Hz以下的结构能带图和隔声量曲线如图2所示. 从图2可以看出, 其在1700 Hz以下存在3个完全带隙(灰色区域), 分别为88.40—119.06 Hz, 302.09—533.03 Hz和772.31—891.44 Hz (各带隙起止点已在图中标出), 与此同时出现了多个平直带; 其对应隔声量曲线分别在各带隙下限处出现了40 dB以上的隔声峰. 若将薄膜也设定为固定约束状态, 则该结构变为普通二维Helmholtz结构, 用同样的方法计算得出的结构能带图和隔声量曲线如图3所示, 其在1700 Hz以下范围只存在1个完全带隙(116.60—318.34 Hz), 最大隔声峰为36 dB. 同时, 通过FEM计算得出其在相同条件下的薄膜基频为240.59 Hz.
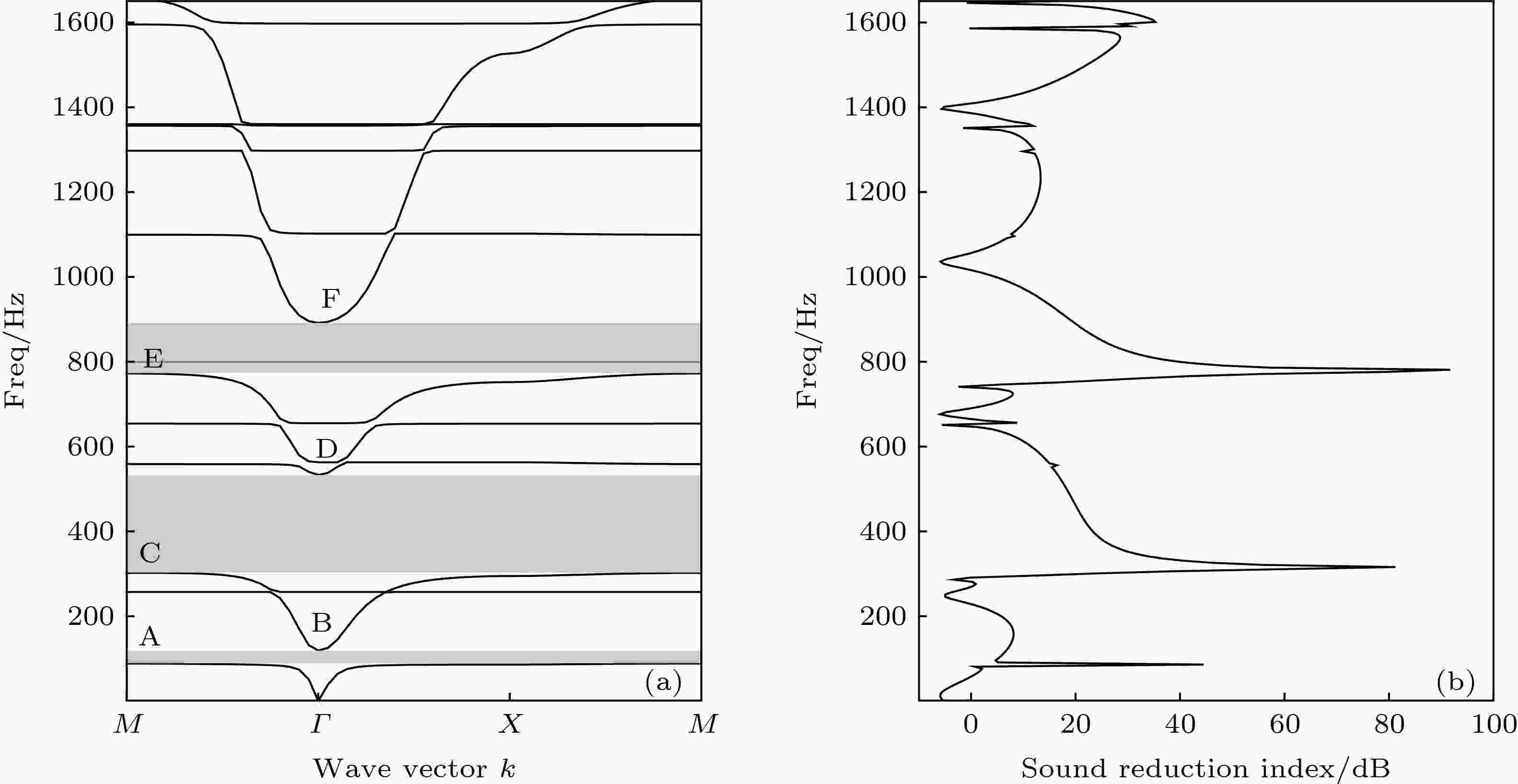图 2 带薄膜壁的Helmholtz结构　(a) 带隙图; (b) 隔声曲线
Figure2. Band diagram (a) and transmission spectrum (b) of the Helmholtz resonator structure with a membrane wall.

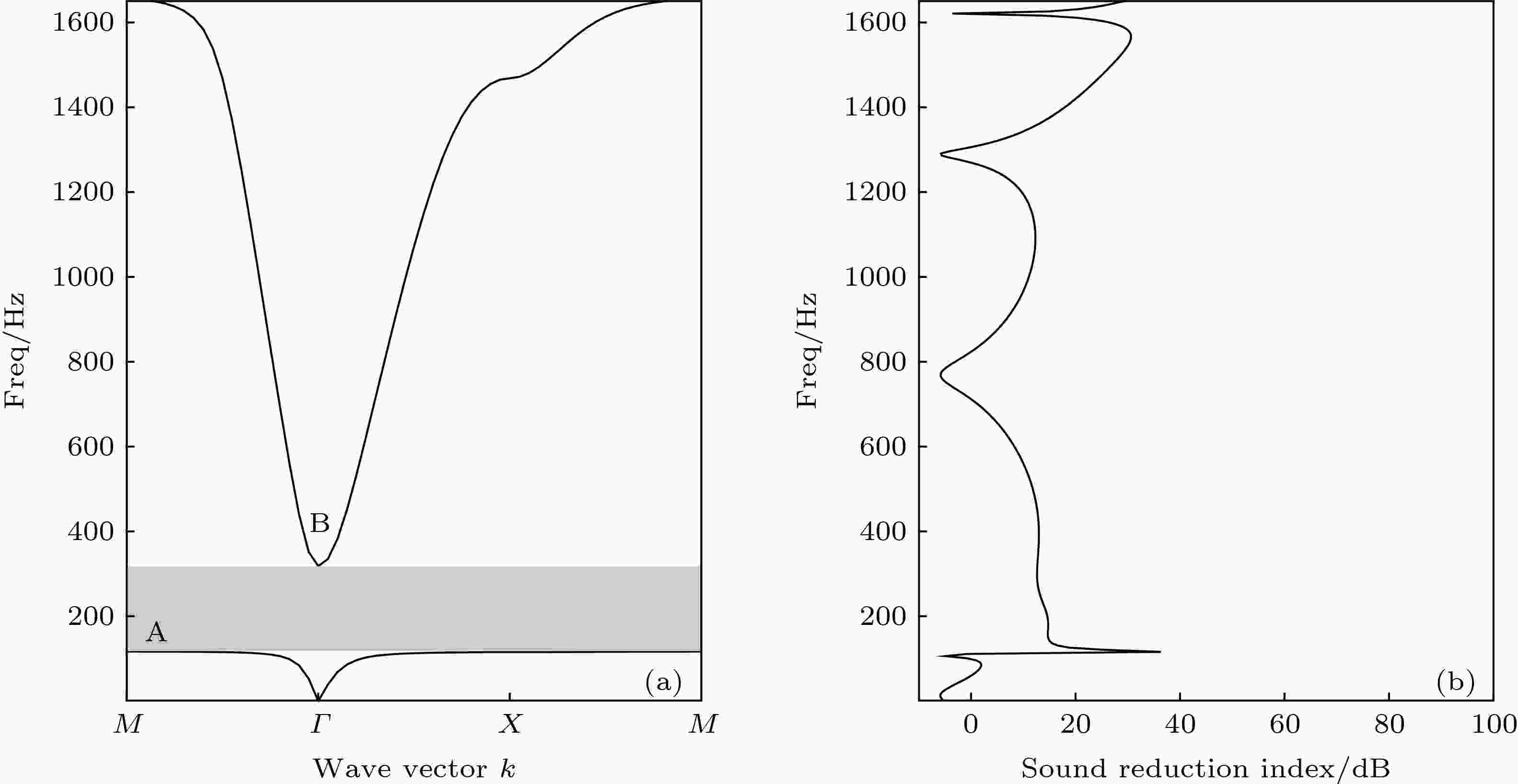图 3 普通Helmholtz结构的(a)带隙图和(b)隔声曲线
Figure3. Band diagram (a) and transmission spectrum (b) of the ordinary Helmholtz resonator structure.

通过以上分析可以发现, 将Helmholtz型声子晶体的一个刚性壁换为带分布质量的张紧膜后, 其低频隔声性能得到了提升. 具体表现为: 第一带隙下限得到进一步降低, 且同时低于同条件下的普通Helmholtz结构和薄膜结构; 出现了新的隔声峰, 且高度高于原有结构; 虽然第一带隙的宽度减小, 但在低频范围内出现了新的带隙, 使得总带隙宽度得到提升.

为研究薄膜与Helmholtz腔的耦合作用, 取该结构前3个带隙起止点处声压场和薄膜振型进行分析, 如图4所示, 其中纯灰色部分为薄膜振型(位移经放大), 右侧图例为声压场数值, 单位为Pa.
图 4 (a) 模态A (88.40 Hz)、(b) 模态B (119.06 Hz)、(c) 模态C (302.09 Hz)、(d) 模态D (533.03 Hz)、(e) 模态E (772.31 Hz)、(f) 模态F (891.44 Hz) 的薄膜振型和声场压力图
Figure4. Vibration mode of the membrane and sound pressure distribution diagrams of point A (88.40 Hz) (a), B (119.06 Hz) (b), C (302.09 Hz) (c), D (533.03 Hz) (d), E (772.31 Hz) (e), and F (891.44 Hz) (f).

从图4可以看出, 在模态A, C, E处, 结构声压场变化规律完全相同, 均为内腔声压最大, 并通过腔口空气通道逐渐过渡到外腔. 外腔左右两部分声压呈反对称分布, 其中薄膜侧为正, 腔口侧为负, 且这种差异随着带隙阶数的增大而增强, 但外腔声压和均为零. 此时声波被完全局域在内腔中, 振动与外腔无关, 与其对应于带隙下限相匹配. 而在模态B, D, F处, 结构声压场分布与前述相反, 内腔声压最小, 且为负值, 通过腔口空气通道过渡至外腔, 外腔声压最大. 此时振动与内腔外腔都有关, 声波可以在腔外传播, 对应于带隙上限.
由于膜的振动是各阶主振型叠加的结果, 通过振型图仅能推断某阶主振型占主要地位, 在后续分析中, 将占主要地位的某阶主振型称为其某阶振动. 从振型图可以看出, 随着频率的升高, 薄膜振动逐渐由低阶转向高阶, 但在带隙上下限处均没有发现反对称振型(该种振动模态下薄膜上下位移呈反对称分布, 平均位移为零)的参与.
对于出现多个平直带的原因, 与之前研究得出的结论相同^[30], 是由薄膜的反对称振型造成的, 这里不再进行讨论.
另外, 对于模态A, 可以看出膜与腔口空气做同向振动, 这样实际上减小了内腔空气弹簧刚度, 导致第一带隙下限下降; 与此类似, 模态B中内腔空气弹簧刚度增大, 外腔减小, 但由于两者体积变化比例不同, 其总体刚度是减小的, 导致其第一带隙上限也会下降.
经过以上分析可看出, 对于该结构在1700 Hz以下产生的多个带隙, 其不同带隙上限或下限处声压场分布规律均是相同的, 只是薄膜振动模态不同, 但各带隙上限和下限的声压场分布规律不同.
在此对上下限分别构建等效系统, 如图5所示, 其中X₁表示薄膜平均位移; X₂表示腔口通道内空气质心位移; N₁和N₂分别为内腔、外腔对薄膜的总压力, 采用TMM与连续体振动相结合的方法进行计算.
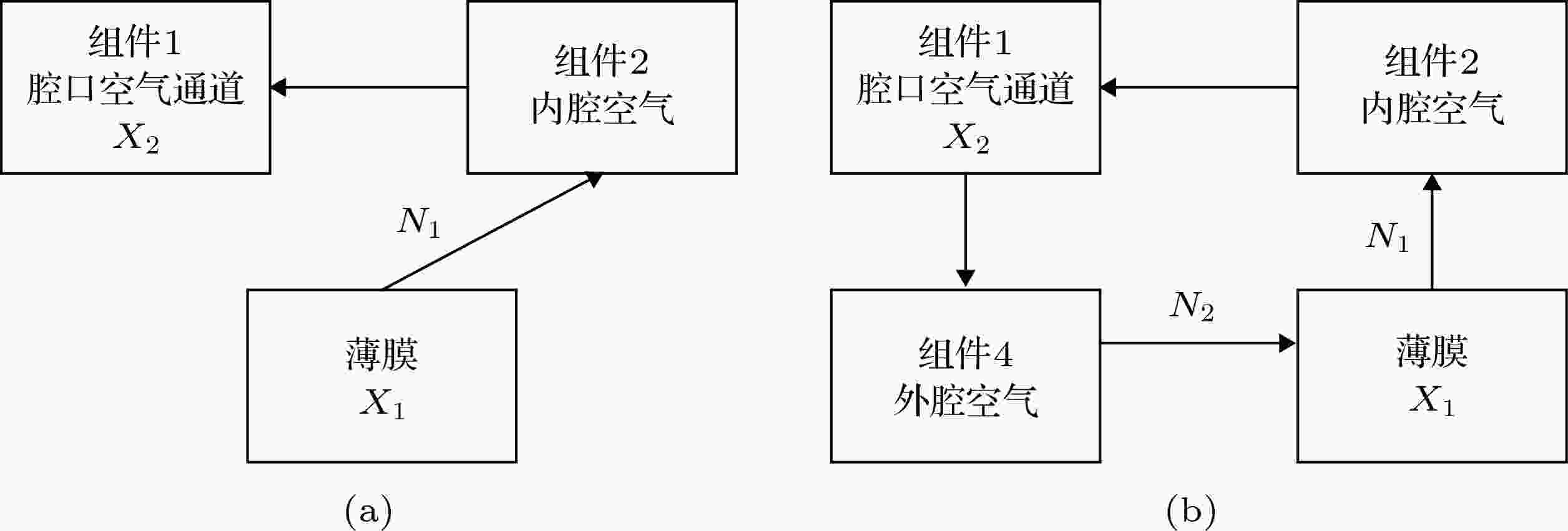图 5 (a) 带隙下限系统示意图; (b) 带隙上限系统示意图
Figure5. (a) System corresponding to starting frequency of band gaps; (b) system corresponding to cut-off frequency of band gaps.

将腔口通道内空气视为均质弹性杆, 其传递矩阵^[31]为

${{ U}_1} = \left[ {\begin{array}{*{20}{c}} {\cos \dfrac{\omega }{c}{l_1}}&{\dfrac{{ - \sin \dfrac{\omega }{c}{l_1}}}{{\omega c{\rho _{\rm{a}}}s}}} \\ {\omega c{\rho _{\rm{a}}}s\sin \dfrac{\omega }{c}{l_1}}&{\cos \dfrac{\omega }{c}{l_1}} \end{array}} \right],$

其中m₁ = sρ_al₁, ρ_a为空气密度, c为在空气中的声速, ω为角频率. 设内外腔内空气在振动过程中压强均匀, 则内腔空气传递矩阵为

${{ U}_2} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{l_{\rm{r}}}}}{s}}&{ - \dfrac{{{V_2}}}{{{\rho _{\rm{a}}}{c^2}s{l_{\rm{r}}}}}} \\ 0&{\dfrac{s}{{{l_{\rm{r}}}}}} \end{array}} \right],$

外腔空气的传递矩阵为

${{ U}_4} = \left[ {\begin{array}{*{20}{c}} {\dfrac{s}{{{l_{\rm{r}}}}}}&{ - \dfrac{{{V_4}}}{{{\rho _{\rm{a}}}{c^2}s{l_{\rm{r}}}}}} \\ 0&{\dfrac{{{l_{\rm{r}}}}}{s}} \end{array}} \right],$

其中V₂, V₄分别表示内腔和外腔体积; l _r = l – 2b, 为薄膜的长度.
对于薄膜的纵向振动, 采用Rayleigh-Ritz法^[32]求解, 同时考虑张力和弹性模量的影响, 其强迫振动方程为

${E_{\rm{r}}}{J_{\rm{r}}}\frac{{{\partial ^4}y}}{{\partial {x^4}}} + T\frac{{{\partial ^2}y}}{{\partial {x^2}}} + {\rho _{\rm{r}}}{b_{\rm{r}}}\frac{{{\partial ^2}y}}{{\partial {t^2}}} = p(x,t),$

其中E_r和ρ_r分别表示硅橡胶弹性模量和密度; J_r为截面对中性轴的惯性矩; p为薄膜收到的外力.
取基础函数为φ_i = 1 – cos(2πnx/l _r), 这种取法计算简便, 但舍弃了反共振振型, 故不能计算出平直带的振动频率. 考虑薄膜上质量块的分布作用, 此时其等效刚度矩阵和等效质量矩阵中各元素为

$\begin{split} {K_{ij}} \; &= {E_{\rm{r}}}{J_{\rm{r}}}\int_0^{{l_{\rm{r}}}} {{{\varphi }''_i}} {{\varphi}''_j}{\rm{d}}x + T{b_{\rm{r}}}\int_0^{{l_r}} {{{\varphi}'_i}{{\varphi}'_j}{\rm{d}}x} \\& = \left\{ {\begin{aligned}& {\frac{{8{E_{\rm{r}}}{J_{\rm{r}}}{i^4}{{\text{π}}^4}}}{{{l_{\rm{r}}}^3}} + \frac{{2T{b_{\rm{r}}}{i^2}{{\text{π }}^2}}}{{{l_{\rm{r}}}}},}\quad\quad\quad{i = j,} \\ & {0,}\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad {i \ne j,} \end{aligned}} \right. \end{split}$

${M_{ij}} = {\rho _{\rm{r}}}{b_{\rm{r}}}\int_0^{{l_{\rm{r}}}} {{\varphi _i}{\varphi _j}{\rm{d}}x} + {\rho _{\rm{s}}}{b_{\rm{s}}}\int_{\frac{{{l_{\rm{r}}} - {h_{\rm{s}}}}}{2}}^{\frac{{{l_{\rm{r}}} + {h_{\rm{s}}}}}{2}} {{\varphi _i}{\varphi _j}{\rm{d}}x},$

由此可解出特征值矩阵Λ和其对应的特征向量矩阵A.
振动时, 薄膜在空气的作用下, 相当于受到周期性均布激振力的作用, 设均布力为p sinωt, 则正则广义力为

${Q_i}\left( t \right) = p\sin \omega t\int_0^{{l_{\rm{r}}}} {{\varphi _i}{\rm{d}}x} = {l_{\rm{r}}}p\sin \omega t.$

此时方程(4)可写为

$\ddot \xi + {{\varLambda}} \xi = {{{A}}^{\rm{T}}}{{Q}}\left( t \right),$

其解为

${\xi _i} = \frac{1}{{{\varLambda _{ii}} - {\omega ^2}}}{B_i}p\sin \omega t,$

其中B_i是A^TQ(t)的第i个元素除以psinωt后的结果. 令η = Aξ, 则薄膜在空气作用下的稳态响应为

$y(x,t) = p\sin \omega t\sum\limits_{i = 1}^n {{\varphi _i}} {\eta _i},$

则其在振动过程中对空气造成的最大体积改变量为

$\begin{split} pV\left( \omega \right) \; &= p\int_0^{{l_{\rm{r}}}} {\sum\limits_{i = 1}^n {{\varphi _i}} {\eta _i}{\rm{d}}x} \\ &= p\sum\limits_{i = 1}^n {\left[ {\frac{1}{{{\varOmega _i}^2 - {\omega ^2}}}\sum\limits_{j = 1}^n {{{\left( {{\alpha _{ij}}{l_{\rm{r}}}} \right)}^2}} } \right]},\end{split}$

其中α_ij为A中各元素, Ω_i为矩阵Λ中对角线元素.
通过各传递矩阵及(11)式, 可分别对带隙上下限对应的系统进行求解.
对带隙下限, 设传递顺序为内腔-腔口, 则有

${{{U}}_{{\rm{down}}}} = {{ U}_1}{{ U}_2},$

$\left[ {\begin{array}{*{20}{c}} {{X_2}} \\ 0 \end{array}} \right] = {{{U}}_{{\rm{down}}}}\left[ {\begin{array}{*{20}{c}} {{X_1}} \\ {{N_1}} \end{array}} \right].$

并且, 根据薄膜平均位移在TMM和Rayleigh-Ritz法下计算结果应相同, 可得

${X_1}{l_{\rm{r}}} = \frac{{{N_1}}}{{{l_{\rm{r}}}}}V\left( \omega \right).$

联立(13)和(14)式可得

$\begin{split} & \left| {\begin{array}{*{20}{c}} {U_{{\rm{down}}}^{{\rm{1,1}}}}&{U_{{\rm{down}}}^{1,2}}&{ - 1} \\ {U_{{\rm{down}}}^{2,1}}&{U_{{\rm{down}}}^{{\rm{2,2}}}}&0 \\ { - {l_{\rm{r}}}}&{ - V\left( \omega \right)/{l_{\rm{r}}}}&0 \end{array}} \right|= \\ & \frac{{{V_2}\omega \sin \dfrac{{{l_1}\omega }}{c} + V(\omega ){c^2}{\rho _{\rm{a}}}\omega \sin \dfrac{{{l_1}\omega }}{c} - cs\cos \dfrac{{{l_1}\omega }}{c}}}{c}\\ & = 0,\end{split} $

其中$ U_{\rm down}^{i,j}$表示U_down中各元素.
同样, 对带隙上限, 设传递顺序为内腔-腔口-外腔, 则有

${{{U}}_{{\rm{up}}}} = {{ U}_4}{{ U}_1}{{ U}_2},$

$\left[ {\begin{array}{*{20}{c}} {{X_1}} \\ {{N_2}} \end{array}} \right] = {{{U}}_{{\rm{up}}}}\left[ {\begin{array}{*{20}{c}} {{X_1}} \\ {{N_1}} \end{array}} \right],$

${X_1}{l_{\rm{r}}} = \frac{{{N_2} - {N_1}}}{{{l_{\rm{r}}}}}V\left( \omega \right).$

联立(17)和(18)式可得

$\begin{split} & \left| {\begin{array}{*{20}{c}} {U_{{\rm{up}}}^{{\rm{1,1}}} - 1}&{U_{{\rm{up}}}^{{\rm{1,2}}}}&0 \\ {U_{{\rm{up}}}^{{\rm{2,1}}}}&{U_{{\rm{up}}}^{{\rm{2,2}}}}&{ - 1} \\ { - {l_{\rm{r}}}}&{ - V\left( \omega \right)/{l_{\rm{r}}}}&{V\left( \omega \right)/{l_{\rm{r}}}} \end{array}} \right|=0, \\ & {V_2}{V_4}{\omega ^2} + [\left( {{V_2} + {V_4}} \right)V(\omega ){c^2}{\rho _{\rm{a}}}{\omega ^2} - {c^2}{s^2}]\sin \frac{{{l_1}\omega }}{c} \\ & - \left[ {\left( {{V_2} + {V_4}} \right)cs\omega + 2V(\omega ){c^3}{\rho _{\rm{a}}}s\omega } \right]\cos \frac{{{l_1}\omega }}{c} \\ & + V(\omega ){c^3}{\rho _{\rm{a}}}s\omega \left( {{{\sin }^2}\frac{{{l_1}\omega }}{c} + {{\cos }^2}\frac{{{l_1}\omega }}{c}} \right) \\ &+ V(\omega ){c^3}{\rho _{\rm{a}}}s\omega = 0,\\[-17pt]\end{split} $

其中$ U_{\rm up}^{i,j}$ 表示U_up中各元素.
根据(15)与(19)式可分别计算出带隙下限与带隙上限的频率. 从这两式可以看出, 在低频范围内, 式子左端取得零值的主要因素有式中的V(ω)和其他含ω项, 其中V(ω)与薄膜的振动模态有关, 其他含ω项均来自于弹性杆传递矩阵. 这说明随着频率的增大, 每当薄膜或腔口空气的振动模态发生改变时, 都将出现一个新的带隙, 亦即产生了一种新的局域共振模态. 另外, 由于两者的耦合性及内外腔空气的作用, 带隙的上下限将不会出现在原固有频率处, 而是发生一定的偏移.

为验证理论计算方法的适用性, 并进一步研究带隙形成规律, 用FEM和TMM计算其带隙上下限频率随参数改变的变化情况, 并取其前三个带隙进行分析. 在此, 除研究的参数外, 其余参数与上文中相同. 从(15)和(19)式可以看出, 影响该结构带隙的主要参数有V₂, V₄, l₁, s以及与薄膜相关的函数V(ω), 在此仅有针对性的选取个别参数进行分析, 其中误差项是以FEM所得结果作为真实值计算得出.
从上文理论计算可发现, 薄膜受到张力T、重物质量及分布、薄膜长度l _r等因素会并且只会影响薄膜相关的函数V(ω), 在此首先选取了重物长度l _s作为变量进行分析, 结果如表1所列. 同时, 作为比较, 采用FEM计算了同条件下附加金属片薄膜的纵向振动固有频率(不含反共振频率), 结果如表2所列. 从表1和表2可以看出, 增大l _s, 薄膜一阶固有频率下降, 二阶固有频率增大, 而结构第二、第三带隙变化趋势与之完全相同, 变化幅度也很接近, 而结构第一带隙向低频方向移动, 但变化幅度较小. 该现象说明此结构在1700 Hz以下新出现的第二、三带隙分别是由于薄膜出现了前两阶振动模态引起的. 而第一带隙由于仍然对应于腔口空气的振动, 通过增大l _s的方式增加等效质量是一种间接的调控方式, 对于该带隙的优化效果并不理想.

l s/10–3 m	4	6	8	10	12	14
1阶固有频率	252.4	237.9	226.8	218.2	211.6	206.6
2阶固有频率	751.3	782.8	794.0	814.8	843.4	879.1

表2薄膜附加金属片长度l _s对薄膜固有频率的影响
Table2.Effect of the parameter l _s on natural frequency of membrane.

ls/10–3 m	第一带隙下限			第一带隙上限			第二带隙下限			第二带隙上限			第三带隙下限			第三带隙上限
	FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%
4	89.2	3.7		121.4	4.4		314.2	2.8		557.7	0.6		790.7	2.2		900.3	1.6
	92.5			126.7			323.0			561.2			808.3			914.7
6	88.9	3.6		120.1	4.2		297.7	1.8		526.8	–0.8		789.1	0.4		905.2	0.8
	92.2			125.1			303.1			522.8			792.4			912.2
8	88.7	3.5		118.9	3.9		285.1	0.9		508.3	–2.1		795.6	–1.1		916.1	–0.5
	91.9			123.5			287.6			497.5			786.8			912.0
10	88.6	3.4		117.9	3.5		275.6	–0.1		497.9	–3.5		815.9	–3.7		932.5	–2.3
	91.6			122.0			275.4			480.5			786.0			910.8
12	88.5	3.1		117.2	3.0		268.4	–1.0		492.6	–4.8		843.8	–6.9		953.9	–5.2
	91.3			120.7			265.6			469.1			785.3			904.4
14	88.5	2.8		116.7	2.3		262.9	–2.0		490.5	–5.9		878.5	–11		966.3	–8.2
	91.0			119.4			257.6			461.5			779.9			887.3

表1薄膜附加金属片长度l _s对低频带隙的影响
Table1.Effect of the parameter l _s on low-frequency band gaps.

另外, 当l _s较小时, 两种计算结果接近, 但当l _s > 10 × 10^–3 m后, 误差开始显著增大, 这是由于在用Rayleigh-Ritz法对薄膜进行处理时, 仅通过(6)式对分布质量进行了处理, 而忽略了附加金属片对薄膜等效刚度的影响. 随着l _s增大, 这种影响逐渐增大, 导致了误差不断增大.
表3显示的是薄膜张力对带隙的影响, 可以看出, 随着薄膜张力的增大, 其各带隙上下限均有增大的趋势, 但第二、三带隙的增长幅度大于第一带隙, 这与上文中所得出第二、三带隙对应于薄膜的振动模态产生和改变相一致. 对于第一带隙, 由于其对应的是腔口空气的振动模态, 可在分析时忽略薄膜质量的影响, 此时随着张力增大, 结构趋向于刚性壁, 其带隙上下限逐渐与无薄膜结构接近. 当张力增大到10⁸ N/m²后, 其第一带隙上下限已基本与无薄膜结构一致, 且1700 Hz以下已无其他完整带隙.

T/106 N·m–1	第一带隙下限			第一带隙上限			第二带隙下限			第二带隙上限			第三带隙下限			第三带隙上限
	FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%
0.5	74.3	3.4		89.3	2.8		259.2	0.7		440.3	–1.2		574.1	0.1		770.1	0.5
	76.8			91.8			261.0			434.9			574.4			774.3
1.5	96.3	3.4		143.1	4.6		345.5	3.2		589.6	0.2		952.1	2.2		1035.1	1.7
	99.6			149.7			356.7			591.0			973.0			1053.1
2.5	103.3	2.9		174.6	4.6		415.0	4.2		648.0	0.7		1217.4	2.8		1274.1	2.3
	106.4			182.7			432.6			652.4			1251.0			1303.2
3.5	106.8	2.7		196.4	4.4		474.9	4.8		691.4	1.1		1434.1	3.0		1478.6	2.5
	109.6			205.0			497.6			698.8			1477.6			1516.1
4.5	108.8	2.5		212.5	4.1		528.2	5.1		729.6	1.4		1621.6	3.2		1642.5	3.3
	111.5			221.3			555.2			740.1			1673.4			1696.5
10	113.0	2.1		257.8	3.0		757.3	5.9		907.9	2.7		1645.9	5.8		1741.8	3.1
	115.3			265.6			801.7			932.8			1740.6			1796.2
100	116.2	1.8		311.0	1.2		1654.1	5.2		1737.3	3.1		2270.8	9.0		2375.3	6.1
	118.3			314.9			1740.4			1791.6			2475.7			2520.3

表3薄膜张力T对低频带隙的影响
Table3.Effect of the parameter T on low-frequency band gaps.

腔口空气通道长度l₁对低频带隙的影响如表4所列, 可以看出, 随着l₁的增大, 第一带隙上下限均向低频方向移动, 而第二带隙下限变化不大, 这与上文提出的对应关系相符合.

l1/mm	第一带隙下限			第一带隙上限			第二带隙下限			第二带隙上限			第三带隙下限			第三带隙上限
	FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%
99	88.4	4.4		119.1	5.7		302.1	3.4		533.0	1.3		772.3	3.4		891.4	2.4
	92.3			125.9			312.5			540.0			798.6			912.9
148	74.5	3.4		101.5	5.1		301.2	3.5		513.3	1.1		772.6	3.4		873.7	2.4
	77.1			106.7			311.7			519.1			798.9			894.4
197	66.0	2.9		89.9	4.7		301.9	3.5		500.0	1.1		772.4	3.3		836.0	1.9
	67.9			94.1			312.5			505.3			798.2			851.8
246	60.1	2.6		81.4	4.5		303.2	3.5		488.5	1.0		697.6	1.2		734.1	0.9
	61.7			85.1			313.7			493.3			705.9			740.6
295	55.8	2.5		75.0	4.3		304.7	3.4		475.7	0.9		587.8	0.7		637.5	0.7
	57.2			78.2			315.2			479.9			591.9			642.3
344	52.5	2.4		69.8	4.2		306.3	3.4		458.4	0.7		507.5	0.6		558.9	3.1
	53.7			72.7			316.6			461.5			510.8			576.4

表4腔口空气通道长度l₁对低频带隙的影响
Table4.Effect of the parameter l₁ on low-frequency band gaps.

但第二带隙上限也不断下降, 特别是当l₁大于246 mm后, 第三带隙上下限急剧下降. 从带隙图分析发现, 腔口空气二阶振动对应的带隙(第四带隙)随着l₁的增大不断向低频方向移动, 压缩了第三带隙及第二带隙上限. 直至l₁ = 295 mm后, 腔口空气二阶振动对应的带隙下降到薄膜二阶振动对应带隙以下, 成为第三带隙, 如图6所示, 腔口空气表现为中间压强最大, 两端最小. 该现象说明随着l₁的增大, 腔口空气在1700 Hz以下范围内的振动模态增多, 固有频率下降. 实际上, 当l₁ = 344 mm时, 该结构在1700 Hz以下已有6个带隙, 其分别对应于腔口空气一阶振动、薄膜一阶振动、腔口空气二阶振动、薄膜二阶振动、腔口空气三阶振动和腔口空气四阶振动.
图 6 l₁ = 295 mm时(a) 第三带隙下限和(b) 第三带隙上限的声场压力图
Figure6. Sound pressure distribution diagrams at starting frequency (a) and cutoff frequency (b) of the 3th band gap when l₁ = 295 mm.

由(15)式可以看出, 外腔体积V₄不影响带隙下限, 而由(19)式可以看出, 对带隙上限, 内腔体积V₂与外腔体积V₄的作用完全相同, 故只对内腔体积V₂进行分析, 如表5所列. 从表5可以看出, 随着V₂的增大, 各带隙上下限均向低频方向移动, 这是由于腔体积增加会减小其等效刚度. 另外, 在此减小V₂的方式是在内腔中增加刚性填充物, 这种方法会使得内腔形状不规则, 腔内声压不均匀, 导致误差上升. 但即便刚性填充物占内腔比例达到66% (此时内腔体积为7.07 × 10^–4 m³), 最大误差仍较小, 说明本文采用的理论计算方法也适用于其他较为复杂结构.

V2/10–4 m3	第一带隙下限			第一带隙上限			第二带隙下限			第二带隙上限			第三带隙下限			第三带隙上限
	FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%		FEM TMM	误差/%
7.07	108.5	6.3		120.5	5.8		406.9	1.0		566.2	1.0		809.9	1.9		953.1	1.2
	115.3			127.6			411.0			571.8			825.3			964.2
10.57	103.3	4.8		121.1	4.8		361.4	1.6		558.3	–0.1		796.5	1.9		925.4	1.4
	108.3			126.8			367.2			557.8			811.4			938.7
14.07	98.0	4.2		121.0	4.4		335.0	1.9		550.0	–0.1		790.9	1.8		913.1	1.4
	102.2			126.4			341.3			549.4			804.9			925.8
17.57	93.3	3.9		120.9	4.3		317.7	2.1		544.4	–0.1		788.3	1.6		906.5	1.3
	96.9			126.1			324.4			543.9			801.1			918.1
19.32	91.1	3.8		120.8	4.3		311.1	2.2		542.3	–0.1		787.4	1.6		904.1	1.2
	94.5			126.0			317.9			541.8			799.7			915.3

表5内腔体积V₂对低频带隙的影响
Table5.Effect of the parameter V₂ on low-frequency band gaps.

从整体上看, 该种带薄膜壁的Helmholtz结构可变参数很多, 且各参数对不同带隙的影响程度不尽相同. 因此, 在低频范围内, 既可以通过改变与腔口空气通道或薄膜相关的参数, 在保证其中某些带隙变化不大的情况下, 单独调整其他带隙; 也可以通过调整内外腔体积, 对所有带隙进行调控.

本文设计了一种含薄膜壁的Helmholtz型声子晶体, 建立了系统等效模型, 通过研究发现: 1)该结构第一带隙下限分别低于同参数下的普通Helmholtz型声子晶体和薄膜, 且在1700 Hz以下范围内将原有一个带隙扩展为多个带隙; 2)利用TMM与Rayleigh-Ritz法相结合的方式可以较为精确地计算出其带隙上下限; 3)该结构的各带隙分别对应于腔口空气和薄膜的各阶振型, 因此可以通过改变与腔口空气通道或薄膜相关的参数, 在保证其中某些带隙变化不大的情况下, 单独调整其他带隙; 与此同时, 内外腔体积对所有带隙均有影响, 故可通过调整其体积对所有带隙进行调控. 这些结论对构建Helmholtz腔与薄膜耦合声学超材料具有指导意义, 有利于推动低频隔声技术的发展.