摘要:沃尔夫-拉叶(Wolf-Rayet stars, WR)星是一类非常特殊的恒星, 具有强烈的星风损失, 造成氢包层丢失, 仅具有裸露的氦核. WR 星被认为是Ib/Ic型超新星的前身星, 研究WR 星的形成及内部核合成具有重要意义. 根据转动恒星的角动量转移和元素扩散方程, 研究了影响WR星结构与演化的各种物理因素. 如恒星质量、初始转速、轨道周期、金属丰度等. 大质量、初始转速快和金属丰度高的单星模型, 星风物质损失率大, 易于形成WR星. 金属丰度低的恒星由于星风弱, 不容易丢失氢包层, 不容易形成WR星. 然而, 快速转动使低金属丰度恒星产生化学成分均匀的演化, 极大地增加了对流核的质量, 相应减小了氢包层厚度, 也可以产生WR星. 双星系统中发生洛希瓣物质交换, 将主星大量的氢包层物质转移到次星上, 也可使低金属丰度恒星产生WR星. 另外, 洛希瓣物质交换, 减少了氢包层的厚度以及对流核的温度和核反应速率, 主星表面的 ⁴He, ¹²C, ¹⁹F, ²²Ne, ²³Na, ²⁵Mg等元素的质量丰度高于相同初始条件的单星模型, 而¹H, ¹⁴N, ¹⁶O, ²⁰Ne 和²⁶Al等元素的质量丰度却低于单星模型. 总之, 大质量星、初始转速快、金属丰度高、短轨道周期双星系统是形成WR星的有利条件.
关键词: 密近双星/
演化/
转动/
潮汐

English Abstract

全文HTML

--> --> -->

沃尔夫-拉叶(Wolf-Rayet stars, WR)星是一种比较特殊的恒星, 1867年法国天文学家Wolf和Rayet^[1]发现该类恒星并命名. WR星与普通大质量恒星不同, 它的光谱中有强的发射线. 这些谱线是由氦、碳、氮等元素所发射的. 根据发射谱线的不同主要可以分为三大类型, 即含有大量氮元素发射线的WN型、含有大量碳元素发射线的WC型和含有大量氧元素发射线的WO型. 根据恒星的表面温度的不同, WN型、WC型WR星又可以细分为早型和晚型两种子类, Georgy等^[2] 详细给出了不同类型WR 星的判定标准(见表1). WR星的宽发射线是由多普勒展宽形成的, 并且在视线方向上WR星周围的气体运动速度约为300—2400 km/s. 这表明WR星正连续不断地将大量物质抛入星际空间, 形成高速运动的星云状包覆层. 由此WR星有相当高的星风损失率$ \dot{M} > 10^{-5} M_{\odot}/{\rm{yr}}$, 它的氢包层已被剥离, 认为是一种裸露的氦星. 在后期演化时, 它坍缩会形成Ib/Ic超新星, 甚至伽马射线暴^[3-5], 因而WR 星被认为是这些重要天体的前身星. 此外, WR 星会向星际空间抛射大量的核反应产物, 在高金属丰度条件下, 其星风含有大量的碳元素和²⁶Al元素, 由于处于基态的²⁶Al元素衰变成²⁶Mg (半衰期$ \tau_{{1}/{2}}\simeq 7.2\times 10^{5}\; {\rm{yr}}$), 释放出1.806 MeV的伽马暴射线, 可以在星系盘周围观测到的伽马暴射线辐射. 另外WC星风中含有大量的²²Ne, 常用来解释宇宙射线源物质中两种氖的同位素(²²Ne/²⁰Ne) 的比值. 因此, 研究WR 星的结构与演化对了解恒星内部核合成与星系化学演化有重要意义.

0.45 WR星的类型	判定依据
O型星	$\log (T_{\rm eff})>4.5$
WNL型星	$\log (T_{\rm eff})>4.0$ 和 $X_{\rm H} <0.3$
WNE型星	$X_{\rm H} <10^{-5}$ 和 $X_{\rm C}<X_{\rm N}$
WNC型星	$\dfrac{X_{\rm C}}{X_{\rm N}}>0.1$ 和 $\dfrac{X_{\rm C}}{X_{\rm N}}<10$
WC型星	$X_{\rm C}>X_{\rm N}$ 和 $\rm \dfrac{C+O}{He}<1$
WO型星	$X_{\rm C}>X_{\rm N}$ 和 $\rm \dfrac{C+O}{He}>1$
注: $T_{\rm eff}$是恒星的有效温度; ${X_{i} }/{X_{j} }$为恒星元素的质量丰度之比; $\rm ({C+O})/{He}$为数丰度之比.

表1WR星分类的判定依据
Table1.Criteria for classification of WR stars

此外, WR星也有可能是由于双星系统中的主星洛希瓣物质交换后产生的. 双星演化是形成WR星的另一重要途径. 双星系统由于两子星间的相互作用使得两子星的演化特征与单星有明显不同^[6-9]. 近年来人们逐渐认识到转动效应是影响双星结构和演化非常重要的物理因素^[10-14]. 转动使恒星内产生了新的物质运动形式—子午环流、剪切湍流和诸多不稳定. 这些物理过程引起恒星内的化学元素扩散和角动量的转移, 改变氦核的质量和恒星表面碳、氮、氧等元素的丰度, 这对WR 星形成和演化产生极其重要的影响.
在转动双星中两子星不但受到转动效应的影响 并且受到潮汐效应的影响. 潮汐力拉伸每颗子星产生沿两子星连线方向的隆起^[15-18]. 当子星的自转角速度与公转角速度不同时, 潮汐隆起形成潮汐转矩. 它使自转角速度与公转角速度趋向于一致, 称为潮汐同步和锁定^[19,20]. 在潮汐锁定的短周期系统, 快速转动引起化学元素的强烈转移和混合, 核反应区的氦元素将迅速进入外包层, 产生化学成分均匀演化^[21-23]. 这类恒星的演化与正常的恒星演化是完全不同的. 体现在恒星向高温和高光度的蓝段演化, 恒星半径膨胀得非常缓慢或几乎无变化. 双星间不进行洛希瓣物质交换, 两子星演化成氦星(或WR星), 另外, 快速转动单星也可以形成化学成分均匀的演化^[24-26], 这是形成WR 星的第三种重要途径.
本文将详细研究形成WR星的三种重要途径, 讨论恒星的初始转速、金属丰度、轨道周期等物理因素对WR星形成和演化的重要影响. 第2节给出了转动恒星的结构方程, 介绍角动量转移和元素扩散方程及边界条件和初始条件、星风物质损失等. 第3节用数值方法计算和讨论这几种物理因素对WR星结构与演化的影响. 第4节给出结论.

2

-->

2.1.转动恒星结构方程

假设恒星内压强为P的等压面包含的体积为$ V_{P} $, 表面积为$ S_{P} $, 等价的半径定义为$ r_{P} \!=\! \Big(\dfrac{3 V_{P}}{4{\text{π}} }\Big)^{1/3} $. 转动恒星结构方程可以表示为^[27]

$ \frac{{\rm d} P}{{\rm d} M_{P}}\Bigg| _{t} = -\frac{GM_P}{4{\text{π}} r_{P}^{4}}f_P, $

$ \frac{{\rm d} r_{P}}{{\rm d} M_P}\Bigg| _{t} = \frac{1}{4{\text{π}} r_{P}^{2}\bar{\varrho}}, $

$ \frac{{\rm d}L_P}{{\rm d} M_P}\Bigg| _{t} = \varepsilon_{\rm nucl}-\varepsilon_{\nu}+\varepsilon_{\rm grav}, $

$ \frac{{\rm d}\ln T}{{\rm d} M_P}\Bigg| _{t} = -\frac{GM_P}{4{\text{π}} r_{P}^{4}}f_P\min\left[ \nabla_{\rm ad}, \nabla_{\rm rad}\frac{f_T}{f_P} \right]. $

方程(1)—(4)中, $ G $, $ c $和$ a $分别为引力常量、光速和辐射常数; $ t $表示恒星演化的某一时刻; $ M_{P} $, $ \rho $, $ \bar{\rho} $和$ L_{P} $分别表示恒星等压面所包含的质量、 密度、平均密度和通过的能量流(光度); $ \varepsilon $, $ T $, $ P $和$ \kappa $分别为产能率、温度、压强和不透明度; $ f_{T} $和$ f_{P} $为转动的动力学效应影响恒星结构的两个修正因子, 可表示为

$\begin{split} & f_P = \frac{4{\text{π}} r_{P}^{4}}{GM_PS_P}\frac{1}{\left \langle g_{\rm eff}^{-1} \right \rangle}, \\ & f_T = \left( \frac{4{\text{π}} r_{P}^{2}}{S_P} \right)^2\frac{1}{\left \langle g_{\rm eff} \right \rangle \left \langle g_{\rm eff}^{-1} \right \rangle}. \end{split}$

重力加速度平均值和其倒数的平均值分别定义为

$ \begin{split} \langle g\rangle = \;& \frac{1}{S_{P}}\!\int_{P = \rm constant} g_{\rm eff} {\rm d} s, \\ \langle g^{-1}\rangle = \;& \frac{1}{S_{P}}\!\int_{P = \rm constant} {g_{\rm eff}}^{-1} {\rm d}s, \end{split}$

式中, $ S_{P} $表示等效半径为$ r $处的等压面面积, 体积为$ V_{P} $. 转动恒星的有效重力加速度可以表示为

$ { g}_{\rm eff} = \left[-\frac{GM}{r^2}+\varOmega^2r\sin^2\vartheta \right]{ e}_r+\left[ \varOmega^2 r\sin\vartheta\cos\vartheta \right]{ e}_\vartheta, $

式中, $ \vartheta $为余纬度, $ \varOmega $为自转角速度.
2 -->

2.2.元素扩散方程和各种不稳定性造成的元素扩散系数

恒星内部自转激发流体的各种不稳定性, 产生恒星内部的元素混合和角动量转移. Pinsonneault等^[12]以及Endal 和Sofia^[28]假定各种不稳定性产生的元素混合速率与角动量转移速率成正比, 给出各种不稳定性导致的各种化学元素在径向的扩散方程为

$\begin{split}\left( \frac{\partial X_n}{\partial t} \right)_m =\, & \left( \frac{\partial}{\partial m} \right)_t \left[ (4{\text{π}} r^2\rho)^2D \left( \frac{\partial X_n}{\partial m} \right)_t \right]\\ &+\left( \frac{{\rm d} X_n}{{\rm d} t} \right)_{\rm nuc},\end{split}$

式中, $ X_n $为某种元素$ X_n $的质量丰度; 右边第一项表示扩散效应对化学元素丰度的影响, 右边第二项表示核反应对化学元素丰度的影响. 方程(8)的初始条件是各种化学元素分别取它们在零龄主序的初始值. 相应的边界条件为

$ \left( \frac{\partial X_n}{\partial m} \right)_t \Bigg| _{\ m = 0} = 0 = \left( \frac{\partial X_n}{\partial m} \right)_t \Bigg| _{\ m = m(t)}, $

方程D为元素扩散系数, 包括对流和半对流及各种不稳定性对元素扩散的影响, 可以表示为

$\begin{split} D =\, & D_{\rm conv}+D_{\rm sem}+0.334 \big(D_{\rm SSI}+D_{\rm DSI} \\ & +D_{\rm SHI}+D_{\rm ES}+D_{\rm GSF}\big), \end{split}$

式中, $ D_{\rm conv} $为对流不稳定造成的元素扩散系数; $ D_{\rm sem} $为半对流不稳定产生的元素扩散系数; $ D_{\rm SSI} $为长期剪切不稳定产生的元素扩散系数; $ D_{\rm DSI} $为动力学剪切不稳定产生的元素扩散系数; $ D_{\rm SHI} $为Solberg-Hoiland不稳定产生的元素扩散系数; $ D_{\rm ES} $为子午环流产生的元素扩散系数. 由于转动造成恒星产生变形, 极区温度变高, 赤道区温度变低, 产生热不稳定, 恒星内部形成大尺度子午环流^[29], 是影响恒星内部角动量转移和元素扩散的主要因素; $ D_{\rm GSF} $为Goldreich-Schubert-Frike不稳定产生的元素扩散系数. 这些扩散系数的详细计算参见文献[30].
2 -->

2.3.角动量转移方程

由于转动恒星中产生上述不稳定, 造成恒星内部的角动量转移. 角动量转移方程可以写为^[30]

$\begin{split} \left( \frac{\partial \varOmega}{\partial t} \right)_m =\, & \frac{1}{i}\left( \frac{\partial}{\partial m} \right)_t \left[ (4{\text{π}} r^2\rho)^2iN\left(\frac{\partial \varOmega}{\partial m}\right)_t \right]\\ & -\frac{2\varOmega}{r}\left(\frac{\partial r}{\partial t}\right)_m \left( \frac{1}{2}\frac{{\rm d}\ln i}{{\rm d}\ln r} \right),\end{split}$

式中的$ i $是质量坐标为$ m $的单位壳层的转动惯量, 设其内半径为$ r_{\rm i} $, 外半径为$ r_{\rm o} $, 则$ i = 0.4(r_{\rm o}^{5}-r_{\rm i}^{5})/ $$(r_{\rm o}^{3}+r_{\rm i}^{3}) $. $ N $为湍动黏度, 可以写为

$ \begin{split} N ={}& D_{\rm conv}+D_{\rm sem}+D_{\rm SSI}+D_{\rm DSI} \\ & +D_{\rm SHI} +D_{\rm ES}+D_{\rm GSF}. \end{split}$

注意在双星系统中潮汐转矩已作用在恒星的外表面, 当作角动量转移方程的外边界条件.
2 -->

2.4.星风损失率的计算

按照辐射风理论^[31,32], 考虑到金属丰度和多重散射的影响, 他们给出的星风损失公式与恒星质量M (以$ M_{\odot} $为单位)、恒星光度L (以$ L_{\odot} $为单位)、有效温度$ T_{\rm eff} $、金属丰度Z以及星风的收尾速度和逃逸速度的比率$ {v_{\infty}}/{v_{\rm esc}} $有关, 铁原子电离度的变化对星风损失有重要影响. 铁原子电离度有两个转化温度: 第一有效温度近似为25000 K, 由电离度Fe Ⅳ转变为Fe Ⅲ; 第二个有效温度近似为15000 K, 由电离度Fe Ⅲ 转变为Fe Ⅱ, 因而形成双稳定性跳变(the bistability jumps), 具体为

$ \begin{split} \log \dot{M} =\, &-6.697+2.194\log \Big(\frac{L}{10^5}\Big)-1.313 \log\Big(\frac{M}{30}\Big) \\ & -1.226 \log\Big(\frac{ v_{\infty}/v_{\rm esc}}{2.0}\Big)+0.993\log \Big(\frac{T_{\rm eff}}{40000}\Big) \\ &-10.92{\Big[\log\Big(\frac{T_{\rm eff}}{40000}\Big)\Big]}^2+0.85 \log \Big(\frac{Z}{Z_{\odot}}\Big), \\ & T_{\rm eff} > 25000\; \rm K,\\[-15pt] \end{split} $

$ \begin{split} \log \dot{M} =\, & -6.688+2.210\log \Big(\frac{L}{10^5}\Big)-1.339\log \Big(\frac{M}{30}\Big) \\ & -1.601\log\Big(\frac{ v_{\infty}/v_{\rm esc} }{2.0}\Big)+1.07\log \Big(\frac{T_{\rm eff}}{40000}\Big) \\ & +0.85\log\Big(\frac{Z}{Z_{\odot}}\Big), \\ & 12500\; {\rm K}\! < \!T_{\rm eff}\! < \!22500\; \rm K, \\[-15pt]\end{split} $

$ \begin{split} \log \dot{M} =\, & -5.99+2.210\log \Big(\frac{L}{10^5}\Big)-1.339\log \Big(\frac{M}{30}\Big) \\ & -1.601\log \Big(\frac{ v_{\infty}/v_{\rm esc}}{2.0}\Big)+1.07\log \Big(\frac{T_{\rm eff}}{40000}\Big) \\ & +0.85\log \Big(\frac{Z}{Z_{\odot}}\Big), \quad T_{\rm eff} < 12500\; \rm K. \\[-15pt] \end{split} $

根据24颗WN型, 18颗WC型和2颗WO, 共44颗WR星的星风数据, 并考虑了星风的成团效应^[33], 给出WN型及WC和WO 型WR星的星风损失率公式. 对于WN型WR星:

$ \begin{split} \log \dot{M} =\, & -13.6+1.63\log(L)\\ &+2.22\log(Y)+0.85\log(Z_{\rm ini}). \end{split} $

对于WC型和WO型WR星:
当$ Z_{\rm ini} > 0.002 $时,

$\begin{split} \log \dot{M} =\, & -8.3+0.84\log(L)+2.04\log(Y)\\ &+1.04\log(Z)+x_{1}\log(Z_{\rm ini}); \end{split}$

当$ Z_{\rm ini} < 0.002 $时,

$\begin{split} \log\dot{M} =\, & -8.3+0.84\log(L)+2.04\log(Y)\\ &+1.04\log(Z)+x_{1}\log\Big(\frac {0.002}{Z_{\odot}}\Big)\\ &+x_{2}\log(Z_{\rm ini}).\end{split}$

其中L为恒星光度, Y为He的质量丰度, Z为金属质量分数, $ Z_{\rm ini} $为恒星的初始金属丰度(以$ Z_{\odot} $为单位), $ x_{1} $和$ x_{2} $取值来自文献[34].

采用Paxton等^[35-37]编写的MESA (Modules for Experiments in Stellar Astrophysics) 程序做数值计算. MESA包括恒星演化过程中所有涉及的核反应网络, 如PP-I链、CNO循环、Ne-Na循环等. 可以处理低质量恒星的He闪耀和大质量星的剧烈核反应等物理过程. 双星系统的洛希瓣物质交换和轨道演化计算见文献[37]. 主序阶段的星风公式采用文献[32]做计算, 而在WR星演化阶段采用Nugis等^[33]的星风公式做计算. 各种模型的初始参数列于表2中. 初始轨道周期为3.0 d的双星模型, 洛希瓣物质交换发生在主序阶段; 而初始轨道周期为40.0 d的双星模型, 洛希瓣物质交换发生在氦燃烧阶段. 目的是为了研究不同时期发生的洛希瓣物质交换对WR星结构与演化以及内部核合成的影响. 采用Geogry等^[2]研究者对WR星的判别和分类依据(见表1).

Models	$M_1/M_\odot$	$M_2/M_\odot$	$Z$	$\alpha$	$P_{\rm orb, ini}$/d	$V_{\rm ini, 1}$/km·s–1	$V_{\rm ini, 2}$/km·s–1
S1	60	—	0.014	0.0385	—	0	—
S2	60	—	0.014	0.0385	—	300	—
S3	60	—	0.014	0.0385	—	600	—
S4	40	—	0.014	0.0385	—	300	—
S5	60	—	0.0021	0.0385	—	300	—
S6	60	—	0.0021	0.0385	—	600	—
B1	60	40	0.014	0.0385	3.0	0	0
B2	60	40	0.014	0.0385	3.0	300	300
B3	60	40	0.014	0.0385	3.0	600	600
B4	60	40	0.014	0.0385	40.0	300	300
B5	60	40	0.0021	0.0385	3.0	300	300
注: B为双星系统, S为单星; $M_1$, $M_2$分别为主星和次星的质量(以太阳质量$M_{\odot}$为单位); Z为金属丰度; $\alpha$为对流超射系数; $P_{\rm orb, ini}$为双星初始轨道周期; $V_{\rm ini, 1}$, $V_{\rm ini, 2}$分别为主星和次星的初始自转赤道速度.

表2单星和双星理论模型的初始参数
Table2.Initial parameters for single stars and binaries

图1(a)给出了所有转动单星模型的赤道转动速度演化. 非转动模型S1在演化过程中赤道速度保持为零. 比较单星模型S2和S3 (或S5和S6), 发现在主序相同时间间隔内, 初速度快的恒星, 尽管具有较高的初始自转角动量, 但赤道速度下降较快, 这是因为快速转动恒星将损失较多的星风和自转角动量. 这说明快速转动恒星内部由子午环流和剪切湍流等过程由内向外传输的角动量速度也较快. 比较单星模型S2和S4, 发现初始质量大的恒星速度下降快, 这表明大质量恒星辐射驱动的星风较强, 携带的自转角动量较多. 比较模型S2和S5, 发现低金属丰度恒星在主序阶段速度较高, 这是因为大质量星的星风主要是由Fe原子吸收辐射后驱动的, 金属丰度低的恒星Fe原子含量少, 星风较弱. 主序后至中心氦开始燃烧, 所有单星模型转动速度小于40 km/s, 这是由于恒星在赫氏间歇期氢包层剧烈膨胀, 使恒星的转动惯量迅速增加, 因而表面转速降低. 但在中心碳燃烧开始前, 模型S4的赤道速度达到V_eq = 327 km/s, 这是因为该模型有较厚的表层对流区. 在对流表层厚度锐减的过程中, 自转角动量近似可保持不变, 但壳层转动惯量迅速减少, 自转角速度迅速变大.
图 1 (a)单星模型赤道转动速度随时间的变化; (b)双星模型赤道转动速度随时间的变化; 其中, 空心菱形为主序结束, 空心圆圈为中心氦开始燃烧, 实心圆圈为中心氦燃烧结束, 空心正方形为中心碳开始燃烧, 实心正方形是中心碳燃烧结束
Figure1. (a) Variations of equatorial velocity in single star models; (b) variations of equatorial velocity in binary star models. Hollow diamonds denote the end of main sequence; hollow circles stand for the beginning of helium burning; solid circles denote the end of helium burning; hollow squares represent the beginning of carbon burning; solid squares represent the end of carbon burning

图1(b)给出了所有转动双星模型中主星的赤道转动速度变化. 非转动模型B1在演化过程中赤道速度保持为零. 可以看出, 在双星系统同步过程中(演化年龄小于～0.2 Myr), 模型B2, B3和B5的转动速度均小于单星S2的转动速度. 原因是潮汐转矩对自转角速度大于轨道角速度的子星, 产生潮汐制动效应. 比较模型B2, B3和B5, 发现模型B2达到同步的时间最短, 而B3达到同步的时间最长. 原因是模型B3的初始角速度大, 潮汐转矩将更多的自转角动量转化为轨道角动量, 双星间距变宽, 潮汐转矩变弱, 因而达到同步的时间比较长. 这意味着这3个模型在达到同步时, B3模型的轨道周期最长. 模型B5达到同步的时间长于模型B2, 这是因为模型B5的金属丰度低, 恒星半径小, 潮汐同步时标与半径的7 次方成反比, 同步时标长. 模型B4的同步时间最长, 这是因为模型B4的初始轨道周期为40.0 d, 潮汐制动转矩非常小, 与不存在潮汐作用的单星S3演化类似. 模型B2同步后其速度缓慢增加至物质交换(t = 2.6314 Myr)前, 原因是达到同步后, 恒星半径逐渐增加. 对比模型B3和B5, 发现模型B3的轨道周期长, 洛希瓣半径大, 但比模型B5更早开始物质交换, 这是因为高金属丰度的恒星半径大, 演化过程膨胀较快达到洛希瓣. 洛希瓣物质交换过程, 造成主星自转角动量大量损失, 物质损失减速转矩大于潮汐加速转矩, 使其表面角速度低于轨道角速度. 物质交换停止后, 潮汐转矩使主星的自转角速度增加, 趋向与轨道角速度一致, 因而赤道速度增加. 在主序后, 恒星演化至WR星阶段, 星风损失加剧, 轨道间距增加, 潮汐作用减弱, 恒星损失大量的自转角动量, 其速度逐步减少.
图2(a)给出了所有转动单星模型的质量(实线)和对流核质量(同颜色的划线)的变化. 在零龄主序, 从图2(a)可看出质量小的模型S4对流核最小, 这说明低质量恒星辐射压小将形成低质量的WR 星. 同时比较模型S1, S2 和S3发现初始速度大的恒星, 对流核较小. 这是因为, 压强梯度和离心力的联合作用与重力平衡, 初始转动快的恒星离心力大, 实质上减小了恒星的有效质量, 对流区减小. 但随着演化发现初始速度大的模型, 质量减小得快, 对流核变大, 这是因为转动减小了重力加速度的约束, 使更多的物质可以逃脱恒星表面. 对流核变大的原因是因为快速转动产生迅速运动的子午环流, 增加了对流核边界元素的混合效率, 减弱了平均分子量梯度的形成, 使对流核边界向外扩大. 然而在主序临近结束时(TAMS), 发现模型S1的质量损失迅速变大 (见表3), 这是由于非转动模型S1经历双稳定性跳变, 引起质量损失大幅度增加. 在零龄主序, 比较模型S2和S5发现低金属模型S5的对流核较大, 这主要是因为低金属丰度模型S5中心温度较高造成的. 发现模型S6在主序的大部分时间内, 对流核质量不但不收缩, 反而增加. 这是因为快速转动形成化学成分均匀演化(见图3(c)). 因而快速转动是形成大质量WR星的重要途径. 低金属丰度恒星S5比高金属丰度恒星S2的主序寿命长(见表3), 这与低金属丰度恒星对流核大有密切关系.
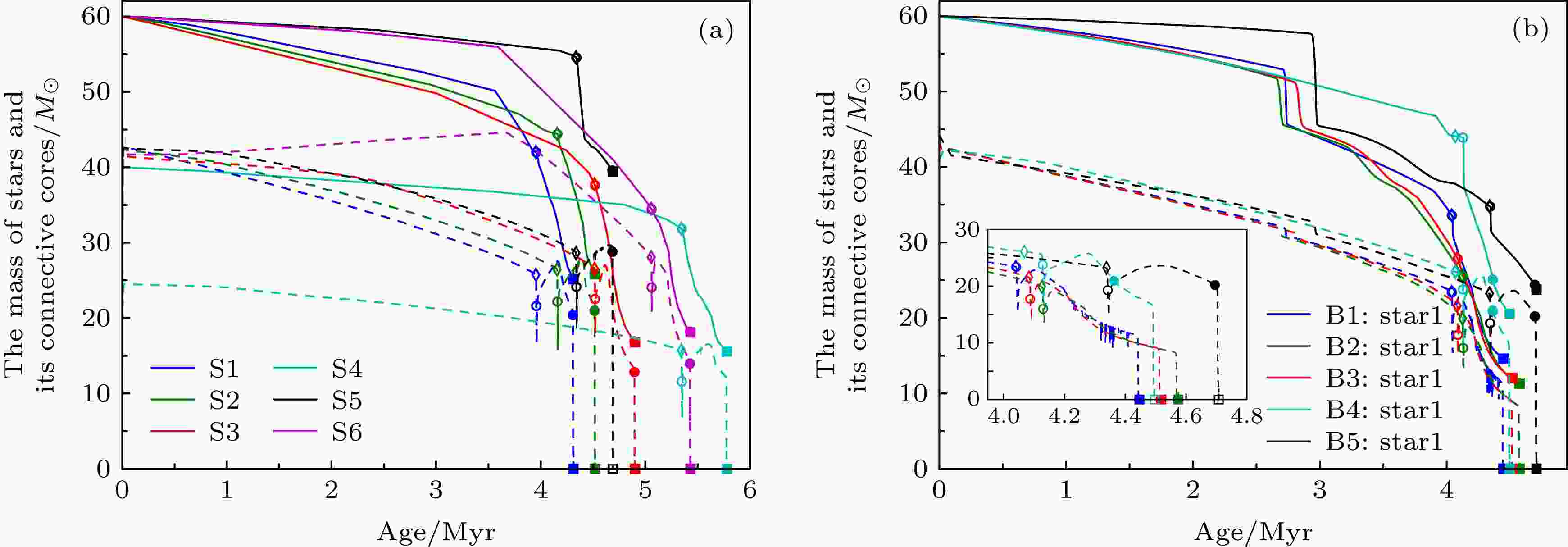图 2 (a) 各种单星模型的质量(实线)和其对应的对流核的质量(划线)随时间的变化; (b) 各种双星模型的质量(实线)和其对应的对流核的质量(划线)随时间的变化
Figure2. (a) Stellar mass and its mass of convective core vary with evolutionary time for the models of single star; (b) stellar mass and its mass of convective core vary with evolutionary time for the models of binary star

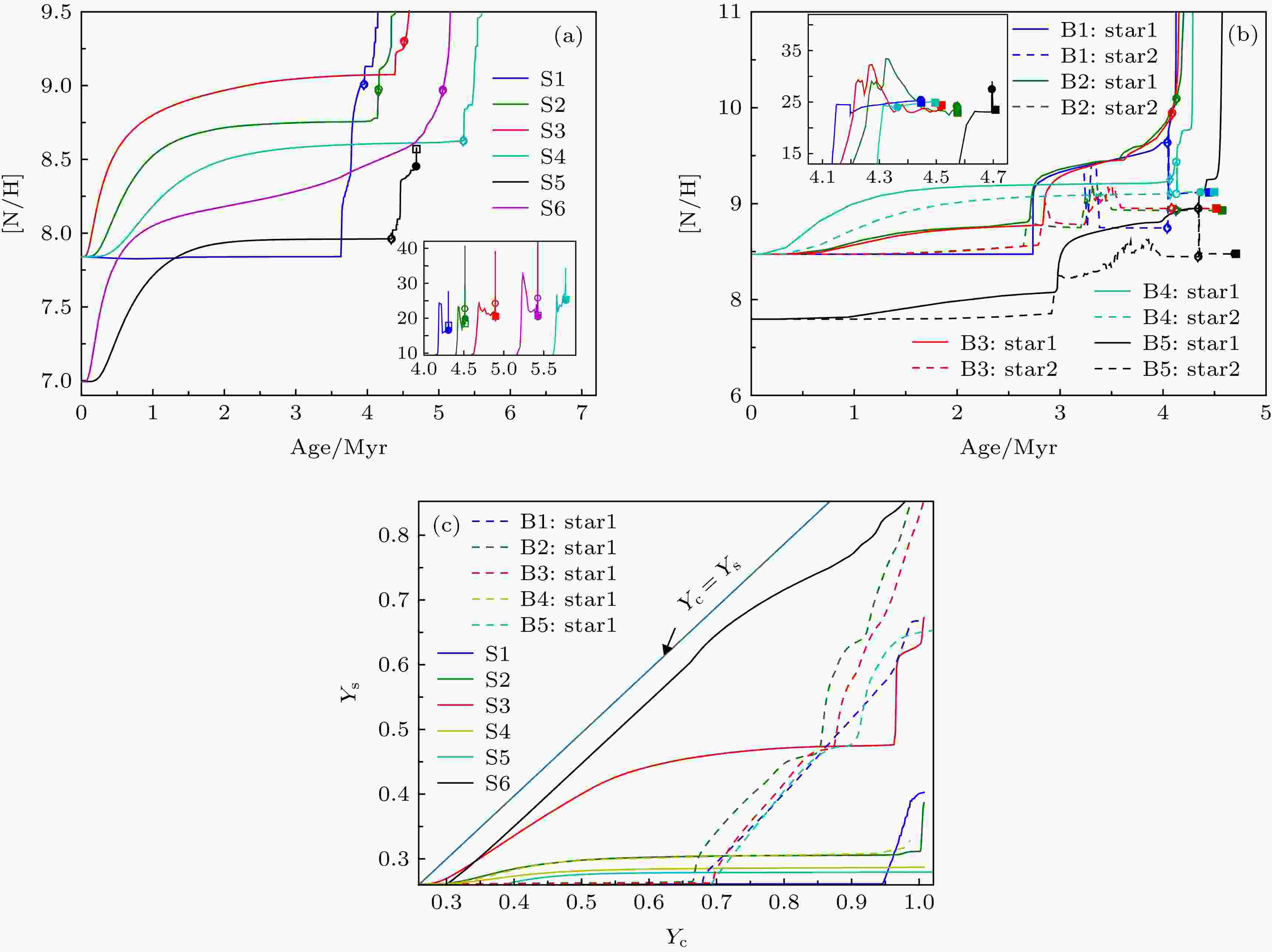图 3 (a)单星模型中恒星表面氮丰度随时间的演化; (b)双星模型中两子星表面氮丰度随时间的演化; (c) 主序阶段, 单星和双星模型的表面氦质量丰度随中心氦质量丰度的变化
Figure3. (a) Surface nitrogen abundance vary with evolutionary time for the models of single star; (b) surface nitrogen abundance vary with evolutionary time for the models of binary star; (c) surface helium abundance vary with central helium for the models of single stars and binary star

Sequence	Age/Myr	$M/M_{\odot}$	$\log T_{\rm eff}$	$\log ({L_{1}}/{L_{\odot}})$	$\rm [N/H]$	$V_{\rm eq}$/km·s–1	$\log T_{\rm c}$	$\log \rho_{\rm c}$
ZAMS
S1	0.0000	60.00	4.68	5.72	7.84	0.00	7.60	0.31
S2	0.0000	60.00	4.66	5.70	7.84	300.00	7.59	0.29
S3	0.0000	60.00	4.63	5.64	7.84	600.00	7.58	0.26
S4	0.0000	40.00	4.62	5.34	7.84	300.00	7.57	0.40
S5	0.0000	60.00	4.67	5.74	6.99	300.00	7.57	0.24
S6	0.0000	60.00	4.65	5.70	6.99	600.00	7.56	0.21
TAMS
S1	3.9511	42.02	4.42	5.98	9.01	0.00	7.81	0.91
S2	4.1537	44.42	4.46	6.00	8.96	18.07	7.81	0.90
S3	4.5124	37.75	4.69	5.98	9.29	18.66	7.81	0.92
S4	5.3408	31.87	4.22	5.70	8.63	1.42	7.79	1.00
S5	4.3346	54.56	4.29	6.05	7.96	7.21	7.87	1.05
S6	5.0531	34.52	4.88	5.99	8.96	25.65	7.86	1.10
BCHEB
S1	3.9550	42.01	4.46	6.00	9.01	0.00	7.98	1.43
S2	4.1574	44.40	4.51	6.02	8.98	19.75	7.98	1.42
S3	4.5162	37.62	4.77	6.01	9.30	25.72	7.98	1.45
S4	5.3453	31.83	4.25	5.72	8.63	1.37	7.96	1.51
S5	4.3383	54.53	4.31	6.06	7.96	7.28	8.03	1.55
S6	5.0570	34.44	4.96	6.02	8.97	36.78	8.03	1.60
ECHEB
S1	4.3054	25.27	5.21	5.99	23.45	0.00	8.53	3.13
S2	4.5120	25.94	5.21	6.00	23.02	158.64	8.53	3.13
S3	4.8924	16.90	5.20	5.74	24.64	76.49	8.51	3.22
S4	5.7771	15.57	5.35	5.79	25.17	327.58	8.88	4.59
S5	4.6825	39.56	4.45	6.19	8.45	5.98	8.54	3.07
S6	5.4231	18.20	5.21	5.79	28.82	49.92	8.52	3.21
BCCB
S1	4.3099	25.16	5.33	6.06	16.72	0.00	8.83	4.14
S2	4.5167	25.81	5.34	6.07	19.18	286.44	8.85	4.24
S3	4.8980	16.80	5.34	5.83	20.60	149.13	8.86	4.45
S4	5.7772	15.57	5.36	5.79	25.28	334.92	8.92	4.78
S5	4.6870	39.45	4.46	6.25	8.57	37.32	8.84	4.12
S6	5.4284	18.10	5.34	5.87	20.66	94.78	8.85	4.35
ECCB
S1	4.3100	25.15	5.42	6.09	18.59	0.00	9.07	5.25
S2	4.5167	25.81	5.42	6.10	18.47	313.57	9.06	5.19
S3	4.8981	16.80	5.41	5.86	20.55	157.94	9.06	5.40
S4	5.7772	15.57	5.40	5.81	25.43	367.73	9.03	5.33
S5	—	—	—	—	—	—	—	—
S6	5.4285	18.10	5.41	5.90	20.90	97.57	9.05	5.34
注: ZAMS为零龄主序; TAMS表示主序结束; BCHEB为中心氦核开始燃烧; ECHEB为中心氦核结束燃烧; BCCB 为中心碳核开始燃烧; CCB为中心碳核结束燃烧.

表3单星模型在各个演化阶段的参数
Table3.Parameters for single star at different evolutionary stages

图2(b)给出了所有转动双星模型的质量(实线)和对流核质量(划线)的变化. 结果表明, 在主星达到同步后和物质交换开始前, 比较模型B2和S2, 发现模型B2的质量较大, 这是因为潮汐同步过程减小了恒星的转速和离心力, 恒星可以损失较少的质量和角动量. 另外洛希瓣物质交换使恒星质量变小, 对流核也稍稍变小. 对比模型B2和B5, 发现低金属丰度双星模型B5, 因为弱的星风, 可以保持较高的质量和对流核. 由于长周期模型B4的演化与转动单星类似, 因有较高的转动速度, 物质交换又较晚(物质交换发生在中心氦燃烧阶段), 可以形成较大的氦核和WR星.
图3(a)给出了所有转动单星模型表面氮丰度随时间的变化(其中$ {\rm [N/H]} = \log( {n_{\rm N}}/{n_{\rm H}})+12 $, 为氮元素的相对数丰度). 在主序前阶段, 比较模型S1, S2和S3, 发现不转动的S1模型, 表面没有氮增丰. 初始速度越大的恒星, 氮丰度增丰越快, 这表明初始速度快的恒星, 子午环流造成的元素混合时标短. 在主序结束时(TAMS), 发现非转动模型S1的表面氮增丰超过转动模型S2 (见表3), 这是因为模型S1经历双稳定性跳变(见图2(a)), 大量物质被抛射, 氮元素暴露的缘故. 比较模型S2和S5, 发现初始金属丰度低的恒星, 在主序阶段, 恒星表面的氮较低. 这是因为初始金属丰度低的恒星, 经CNO循环由¹²C元素和¹⁶O元素转化为¹⁴N元素, 达到反应平衡时¹⁴N元素总量较少. 在氦燃烧阶段阶段, 除模型S5外, 尽管恒星转动速度较低, 所有单星模型的氮增丰非常快. 比如模型S2氮丰度由中心氦开始燃烧时的8.98 dex增加到氦结束燃烧时的23.02 dex, 这是因为WR星具有强烈的星风损失, 造成氢包层丢失, 逐渐将核反应区的氮暴露.
图3(b)给出了所有转动双星模型表面氮丰度随时间的变化. 实线表示双星系统的主星, 划线表示双星系统的次星¹⁴N的表面丰度. 在物质交换前, 比较模型S2和B2, 发现恒星在双星系统中氮增丰较小, 这是因为潮汐同步过程降低恒星的转动速度, 使子午环流速度减慢, 混合时标变长. 模型B4的氮增丰最显著, 因为它潮汐转矩小, 与转动模型S2类似. 对比模型B2的主星(实线)和次星(划线), 发现主星¹⁴N 表面氮增丰比次星显著, 这是因为子午环流的速度与辐射压成正比, 质量大的恒星子午环流较快. 在所有双星模型中, 物质交换开始后(见表4), 所有主星和次星表面的氮丰度增加. 这是因为洛希瓣物质交换, 逐渐暴露了主星核反应区产生的¹⁴N. 另外主星表面富氮元素物质转移到次星表面使次星表面氮元素增丰. 物质交换后, 星风继续丢失主星的氢包层, 使富含氮元素的物质不断暴露, 因而氮丰度逐渐升高. 而次星在物质交换后, 由于吸积物质的平均分子量高于底部, 热盐混合效应逐渐沉积表面的富氮物质, 使其表面氮丰度降低. 第二次物质交换也出现类似行为.

Sequence	Age /Myr	$P_{\rm orb}$ /d	$M_{1}/M_{\odot}$	$M_{2}/M_{\odot}$	$\log(T_{\rm eff, 1})$ /K	$\log \Big(\dfrac{L_{1}}{L_{\odot} }\Big)$	$\log(T_{\rm eff, 2})$ /K	$\log \Big(\dfrac{L_{2}}{L_{\odot} }\Big)$	$\Big[\rm \dfrac{N_{1}}{H}\Big]$	$\Big[\rm \dfrac{N_{2}}{H}\Big]$	$V_{\rm eq1}$/ km·s–1	$V_{\rm eq2}$/ km·s–1	$\log T_{\rm c}$/ K	$\log \rho_{\rm c}$/ g·cm–3
ZAMS
B1	0.0000	3.00	60.00	40.00	4.68	5.71	4.64	5.36	7.84	7.84	0.00	0.00	7.62	0.37
B2	0.0000	3.00	60.00	40.00	4.67	5.70	4.63	5.34	7.84	7.84	288.35	294.86	7.61	0.35
B3	0.0000	3.00	60.00	40.00	4.64	5.65	4.59	5.27	7.84	7.84	566.93	581.75	7.60	0.32
B4	0.0000	40.00	60.00	40.00	4.67	5.70	4.63	5.34	7.84	7.84	288.35	294.86	7.61	0.35
B5	0.0000	3.00	60.00	40.00	4.69	5.66	4.65	5.29	6.99	6.99	306.83	301.14	7.66	0.50
BTM1
B1	2.6862	3.60	53.01	38.15	4.59	5.84	4.59	5.48	7.84	7.84	0.00	0.00	7.64	0.39
B2	2.6314	3.63	51.90	38.00	4.59	5.82	4.59	5.47	8.25	7.94	250.24	162.73	7.63	0.39
B3	2.7810	4.12	51.34	37.86	4.57	5.83	4.59	5.48	8.22	7.96	238.80	146.79	7.64	0.40
B4	4.1328	63.17	43.82	35.94	4.23	6.02	4.49	5.56	9.05	8.69	35.18	120.39	8.24	2.26
B5	2.9131	3.25	57.69	39.46	4.60	5.86	4.61	5.47	7.34	7.07	270.95	164.95	7.68	0.52
ETM1
B1	3.8956	4.25	36.84	43.77	4.62	5.90	4.57	5.67	9.20	8.18	0.00	0.00	7.70	0.61
B2	2.7305	3.41	45.44	43.82	4.60	5.78	4.61	5.57	8.66	8.26	239.26	177.55	7.63	0.42
B3	2.9777	3.92	44.57	43.27	4.59	5.81	4.60	5.58	8.83	8.25	226.58	161.96	7.64	0.44
B4	4.1426	65.47	36.94	36.00	4.27	6.10	4.49	5.56	9.26	8.67	73.07	330.19	8.31	2.47
B5	3.9817	3.61	38.02	51.22	4.63	5.87	4.65	5.73	8.27	7.82	217.02	168.84	7.72	0.69
TAMS
B1	4.0397	4.65	33.60	43.48	4.68	5.91	4.56	5.68	9.30	8.18	0.00	0.00	7.81	0.95
B2	4.1254	5.13	25.57	43.47	4.83	5.79	4.53	5.69	9.86	8.41	20.52	193.13	7.80	0.99
B3	4.0832	5.43	27.93	43.40	4.81	5.84	4.54	5.68	9.66	8.44	19.99	174.17	7.80	0.97
B4	4.0693	62.61	44.06	36.03	4.41	5.97	4.54	5.56	8.82	8.63	6.63	68.60	7.72	0.65
B5	4.3382	3.81	34.79	50.91	4.68	5.92	4.63	5.75	8.44	7.81	169.76	181.54	7.86	1.10
BCHEB
B1	4.0409	4.65	33.57	43.48	4.69	5.91	4.56	5.68	9.30	8.18	0.00	0.00	7.82	0.99
B2	4.1297	5.15	25.44	43.46	4.92	5.82	4.53	5.69	9.87	8.41	30.07	192.49	7.97	1.52
B3	4.0874	5.45	27.80	43.39	4.90	5.87	4.54	5.68	9.68	8.44	29.48	173.40	7.98	1.50
B4	4.1281	63.03	43.88	35.95	4.48	5.99	4.53	5.56	9.04	8.63	4.75	60.68	7.91	1.21
B5	4.3422	3.82	34.74	50.91	4.75	5.94	4.63	5.76	8.44	7.81	149.04	181.17	8.02	1.60
BMT2
B1	4.0474	4.67	33.39	43.47	4.63	6.00	4.58	5.69	9.30	9.30	0.00	0.00	8.24	2.29
B2	3.1581	3.55	43.04	43.10	4.61	5.81	4.59	5.59	8.99	8.19	231.13	191.20	7.64	0.45
B3	3.1290	3.97	43.65	43.04	4.59	5.82	4.59	5.58	8.93	8.23	223.55	166.73	7.64	0.45
B4	—	—	—	—	—	—	—	—	—	—	—	—	—	—
B5	4.3460	3.84	34.70	50.90	4.66	5.99	4.63	5.76	8.44	7.81	187.54	180.93	8.26	2.34
EMT2
B1	4.0562	5.13	30.44	45.39	4.65	6.06	4.62	5.72	9.48	8.74	0.00	0.00	8.31	2.49
B2	3.5409	3.78	37.67	44.95	4.61	5.82	4.59	5.65	9.06	8.42	212.81	195.54	7.66	0.51
B3	3.6151	4.27	37.66	44.50	4.60	5.84	4.58	5.65	9.07	8.44	203.84	175.46	7.66	0.52
B4	—	—	—	—	—	—	—	—	—	—	—	—	—	—
B5	4.3517	4.25	31.33	51.54	4.67	6.05	4.64	5.77	8.60	7.91	174.27	292.23	8.31	2.49
ECHEB
B1	4.4454	8.50	14.60	44.32	5.30	5.71	4.57	5.75	25.43	8.65	0.00	0.00	8.74	3.96
B2	4.5716	8.31	11.27	42.40	5.27	5.52	4.45	5.73	24.26	8.41	58.94	181.80	8.70	3.93
B3	4.5155	9.20	12.05	42.46	5.27	5.56	4.47	5.71	24.15	8.44	52.74	142.55	8.68	3.83
B4	4.3645	94.44	25.01	35.66	5.14	5.92	4.50	5.58	24.02	8.65	0.32	127.17	8.37	2.68
B5	4.6953	5.16	24.36	51.19	5.18	5.95	4.61	5.80	27.78	7.85	6.01	149.71	8.48	2.99
BCCB
B1	4.4468	8.51	14.58	44.31	5.35	5.75	4.57	5.75	24.91	8.65	0.00	0.00	8.89	4.66
B2	4.5741	8.32	11.24	42.40	5.33	5.58	4.45	5.73	23.39	8.41	67.64	179.57	8.85	4.60
B3	4.5184	9.22	12.02	42.45	5.34	5.62	4.47	5.71	24.42	8.44	62.74	140.22	8.88	4.71
B4	4.4963	110.76	20.53	35.48	5.36	5.95	4.48	5.59	24.89	8.65	0.56	99.94	8.90	4.56
B5	4.7078	5.25	23.75	51.18	5.37	6.03	4.61	5.80	23.51	7.85	10.68	146.97	8.92	4.63
ECCB
B1	4.4469	8.51	14.58	44.31	5.41	5.77	4.57	5.75	24.88	8.65	0.00	0.00	9.04	5.38
B2	4.5743	8.32	11.24	42.40	5.37	5.60	4.45	5.73	22.95	8.41	66.77	173.97	9.01	5.44
B3	4.5185	9.22	12.01	42.45	5.38	5.64	4.47	5.71	24.41	8.44	63.39	136.75	9.01	5.41
B4	4.4963	110.77	20.53	35.48	5.42	5.97	4.48	5.59	24.88	8.65	0.67	98.21	9.05	5.22
B5	4.7078	5.25	23.75	51.18	5.42	6.04	4.61	5.80	23.50	7.85	12.57	144.92	9.05	5.18

表4双星模型在各个主要演化阶段的参数
Table4.Evolutionary parameters for binary star at different stages.

表4列出了所有双星模型在各个阶段的演化参数. 从零龄主序(ZAMS)到开始第一次物质交换(BTM1) 前. 比较模型B1, B2和B3的轨道周期变化, 发现快速自转使系统轨道周期变大, 这与潮汐同步过程造成的自转角动量转变为轨道角动量有关. 发现模型B4的轨道周期从40.0 d增加到63.17 d, 这主要因为星风物质损失使双星系统轨道间距变宽. 从第一、二次洛希瓣物质交换开始到物质交换结束, 模型B1, B2和B3主星表面的有效温度增加, 次星的光度增加. 这是因为洛希瓣物质交换逐渐暴露了主星表面的高温物质, 并将其转移到次星表面. 次星由于吸积富氦物质, 对流核变大, 不透明度减少, 显示高光度. 另外, 洛希瓣物质交换使主星的赤道速度变低, 次星的赤道速度变大, 这是因为物质交换减小了主星表面的自转角动量, 并且将一部分轨道角动量转变为次星的自转角动量. 另外, 两次洛希瓣物质交换均使主星中心温度和密度增加. 比较单星模型S1在主序结束的年龄(t = 3.95 Myr)和双星模型B1中的主星在主序结束的年龄(t = 4.04 Myr), 发现洛希瓣物质交换减小了中心温度, 却延长了恒星在主序的寿命. 在WR 星阶段, 强大的星风物质和洛希瓣物质交换的联合作用, 使模型B1, B2, B3的主星的氮丰度有强烈增丰(见表4). 在中心氦燃烧结束, 比较B2和B4两个模型, 发现低金属丰度恒星由于具有较高的质量(星风弱), 使中心温度和密度减小. 模型B5表面的氮增丰最大, 达到27.78 dex, 这主要是因为低金属丰度模型B5, 氦核和氢燃烧壳层间距窄. 由于潮汐锁定, 在中心氦燃烧阶段转动速度较高(平均速度约为100 km/s) 中心氦燃烧产生的碳元素, 通过转动混合进入氢燃烧壳层, 将碳元素转变为氮元素的缘故^[38].
图3(c)给出了所有单星和双星模型中的主星表面氦丰度随中心氦的变化趋势. 在主序前期单星模型S2的氮增丰比氦增丰显著, 这是因为CN循环进行得非常快, ¹⁴N元素产生迅速, 在恒星核和包层间形成较高的氮元素丰度梯度, 容易产生扩散. 可以看到模型S6的斜率接近于1, 这表明中心的氦和恒星表面的氦几乎一致. 原因是低金属丰度恒星, 星风非常弱, 损失非常少的自转角动量, 可以保持较高的转动速度. 快速转动使大质量星的元素混合时标短于核反应时标, 恒星内部不形成化学分子量梯度, 恒星内部核反应区产生的氦通过转动混合效应扩散至恒星表面, 同时包层的氢元素迅速进入核反应区, 使模型S6经历化学成分均匀演化. 这样的恒星膨胀非常缓慢, 如处在双星系统内将不经历洛希瓣物质交换. 主序后恒星半径反而收缩, 因而这是形成大质量氦星的另一主要途径. 可以看出, 双星模型B2和B3在中心氦质量丰度大于0.6时, 氦增丰迅速甚至超过同类型单星, 这是因为洛希瓣物质交换将氢包层除去, 氦元素暴露的缘故. 模型B4氦增丰明显低于其他双星模型, 这是因为洛希瓣物质交流发生在主序后.
图4给出了所有单星和双星模型中的主星表面各种元素的质量丰度随恒星质量的变化趋势. 对比模型S1和S6, 发现主序阶段快速转动对恒星表面的丰度改变比较明显, 模型S6表面的¹H, ¹²C, ¹⁶O, ²²Ne, ²⁵Mg和¹⁹F的质量丰度下降. 这说明子午环流将这些元素传输到核反应区, 使这些元素丰度下降(见表5). 在核反应区, ¹H, ¹²C和¹⁶O通过CNO循环转化成⁴He, ¹⁴N; ²²Ne, ²⁵Mg, ¹⁹F 等通过俘获质子分别变为²³Na, ²⁶Al, ¹⁶O. 核反应区的⁴He, ¹⁴N, ²³Na, ²⁶Al等元素通过转动混合效应传输到恒星表面, 使这些元素的表面丰度上升. 在WR星阶段, ¹H, ¹⁴N, ²⁶Al的质量丰度下降. ²⁶Al元素通过β (半衰期0.716 Myr)衰变放出1.806 MeV的γ射线, 因而²⁶Al的质量丰度下降(见表5); 另外, ²⁶Al的质量丰度下降的原因也可能是由于俘获²²Ne产生的中子变成²⁶Mg. 同时¹²C, ¹⁶O, ¹⁹F, ²²Ne等质量丰度增加. 这说明在氦燃烧阶段, 氦元素转成了¹²C和¹⁶O, ¹⁴N转化成¹⁹F和²²Ne. 氦燃烧只产生小部分的²⁰Ne, 大部分²⁰Ne是在中心碳燃烧产生的. ²⁰Ne丰度变化也表明在这个阶段产生了α族元素. 这些计算结果可以解释, WR星星风中含有较高的²⁶Al, ¹⁹F质量丰度, 较高的氖同位素比值²²Ne等观测事实.
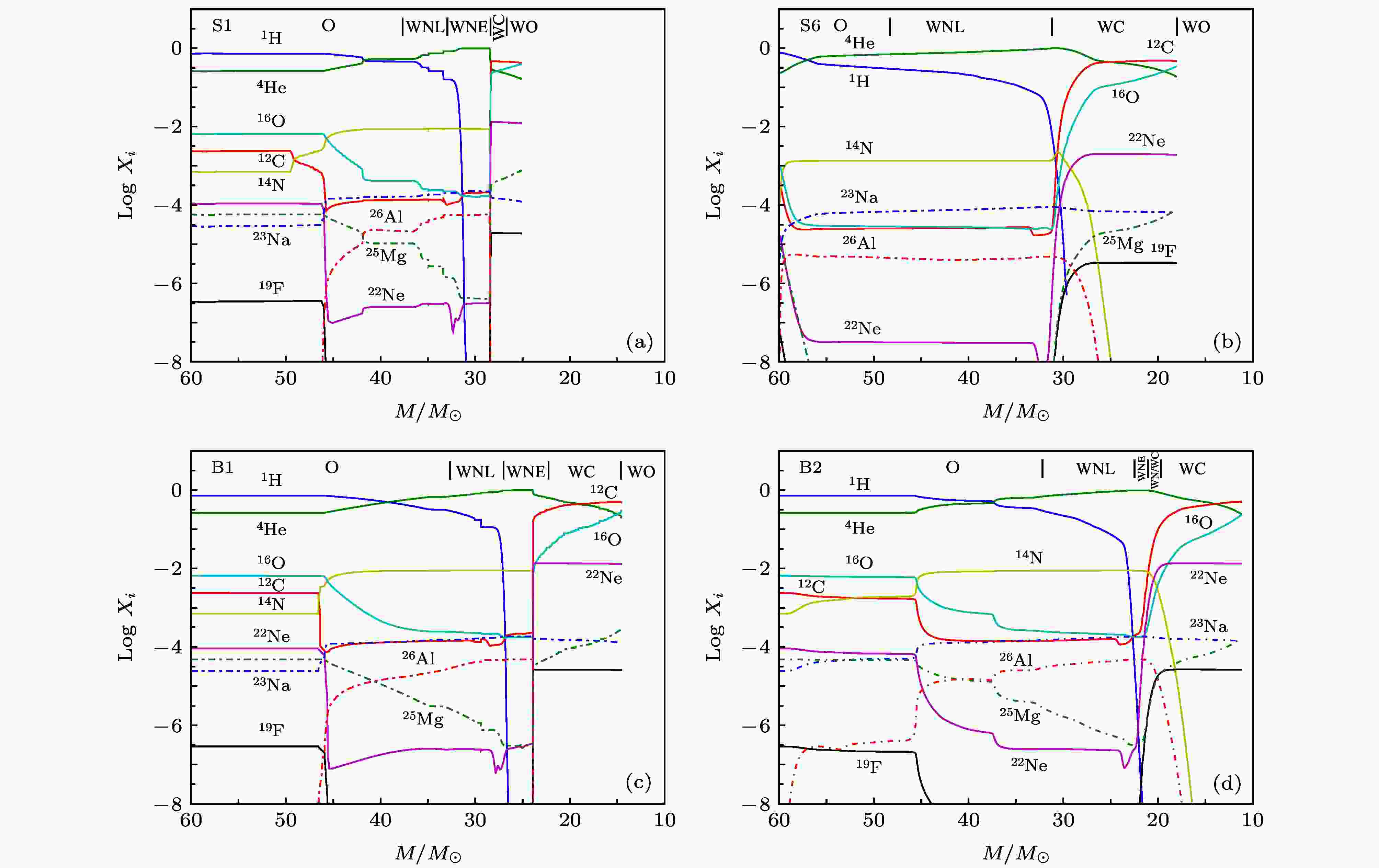图 4 (a) 单星非转动S1模型表面各种元素的质量丰度的对数值随时间的演化; (b) 单星转动S6模型表面各种元素的质量丰度的对数值随时间的演化; (c) 双星非转动B1模型中的主星表面各种元素的质量丰度的对数值随时间的演化; (d) 双星转动模型B2中的主星表面各种元素的质量丰度的对数值随时间的演化
Figure4. (a) Evolution as a function of the actual mass of the abundances (in mass fraction) of different elements at the surface of a non-rotating single model S1; (b) evolution as a function of the actual mass of the abundances (in mass fraction) of different elements at the surface of a rotating single model S6; (c) evolution as a function of the actual mass of the abundances (in mass fraction) of different elements at the surface of the primary star of model B1; (d) evolution as a function of the actual mass of the abundances (in mass fraction) of different elements at the surface of the primary star of model B2

Sequence	Age/Myr	$M_1/M_{\odot}$	log($X_{\rm ^{1}H}$)	log($X_{\rm ^{4}He}$)	log($X_{\rm ^{12}C}$)	log($X_{\rm ^{14}N}$)	log($X_{\rm ^{16}O}$)	log($X_{\rm ^{19}F}$)	log($X_{\rm ^{20}Ne}$)	log($X_{\rm ^{22}Ne}$)	$X_{\rm ^{26}Al}$
ZAMS
S1	0.0000	60.00	–0.14	–0.58	–2.62	–3.15	–2.18	–6.46	–2.87	–3.96	0
S2	0.0000	60.00	–0.14	–0.58	–2.62	–3.15	–2.18	–6.46	–2.87	–3.96	0
S6	0.0000	60.00	–0.12	–0.63	–3.45	–3.98	–3.01	–7.28	–3.69	–4.78	0
TAMS
S1	3.9511	42.02	–0.23	–0.40	–3.91	–2.08	–3.07	–9.23	–2.87	–6.77	9.77 × 10–6
S2	4.1537	44.42	–0.22	–0.42	–3.70	–2.11	–2.86	–7.86	–2.87	–5.37	4.57 × 10–6
S6	5.0531	34.52	–0.99	–0.05	–4.56	–2.88	–4.60	–10.46	–3.83	–7.51	4.36 × 10–6
BCHEB
S1	3.9550	42.01	–0.23	–0.40	–3.91	–2.08	–3.07	–9.23	–2.87	–6.77	9.77 × 10–6
S2	4.1574	44.40	–0.22	–0.41	–3.77	–2.10	–2.91	–8.07	–2.87	–5.58	4.89 × 10–6
S6	5.0570	34.44	–0.99	–0.05	–4.56	–2.88	–4.60	–10.46	–3.83	–7.51	4.36 × 10–6
WNL
S1	4.1147	34.94	–0.58	–0.14	–3.87	–2.06	–3.63	–9.72	–2.88	–6.53	4.16 × 10–5
S2	4.3343	36.29	–0.57	–0.14	–3.82	–2.06	–3.59	–9.67	–2.88	–6.45	3.54 × 10–5
S6	4.1796	48.34	–0.52	–0.16	–4.60	–2.88	–4.55	–10.50	–3.79	–7.50	4.46 × 10–6
WNE
S1	4.1801	31.26	–5.02	–0.01	–3.73	–2.05	–3.77	–9.61	–2.89	–6.56	5.62 × 10–5
S2	—	—	—	—	—	—	—	—	—	—	—
S6	—	—	—	—	—	—	—	—	—	—	—
WC
S1	4.2217	28.36	–21.87	–0.51	–0.34	–17.12	–0.68	–4.71	–2.80	–1.88	1.12 × 10–15
S2	4.4173	30.79	–5.22	–0.02	–1.50	–2.06	–2.05	–5.72	–2.89	–2.91	4.67 × 10–5
S6	5.2107	29.81	–5.80	–0.02	–1.37	–2.89	–2.52	–6.15	–3.84	–3.38	3.80 × 10–6
WO
S1	4.2569	26.70	–21.35	–0.65	–0.34	–16.95	–0.52	–4.72	–2.70	–1.89	2.57 × 10–15
S2	4.4302	28.58	–17.68	–0.71	–0.36	–5.17	–0.45	–4.72	–2.63	–1.91	4.16 × 10–8
S6	5.3898	18.84	–29.68	–0.64	–0.32	–17.99	–0.55	–5.48	–3.51	–2.71	8.51 × 10–17
ECHEB
S1	4.3054	25.27	–29.41	–0.77	–0.37	–16.81	–0.41	–4.72	–2.59	–1.91	5.01 × 10–15
S2	4.5120	25.94	–28.78	–0.82	–0.39	–16.61	–0.38	–4.72	–2.54	–1.93	7.07 × 10–15
S6	5.4231	18.20	–35.90	–0.71	–0.33	–17.93	–0.48	–5.48	–3.43	–2.72	1.14 × 10–16
BCCB
S1	4.3099	25.16	–22.67	–0.79	–0.37	–16.80	–0.40	–4.73	–2.58	–1.92	5.37 × 10–15
S2	4.5167	25.81	–24.97	–0.83	–0.40	–16.64	–0.37	–4.72	–2.52	–1.93	7.58 × 10–15
S6	5.4284	18.10	–27.74	–0.72	–0.33	–17.93	–0.47	–5.48	–3.41	–2.72	1.54 × 10–16
ECCB
S1	4.3100	25.15	–24.54	–0.79	–0.37	–16.80	–0.40	–4.73	–2.58	–1.92	5.37 × 10–15
S2	4.5167	25.81	–24.26	–0.83	–0.40	–16.64	–0.37	–4.72	–2.52	–1.93	7.76 × 10–15
S6	5.4285	18.10	–27.99	–0.72	–0.33	–17.93	–0.47	–5.48	–3.41	–2.72	1.54 × 10–16

表5单星模型S1, S2和S6在各个主要阶段恒星表面的各种元素的质量丰度
Table5.Mass fraction of various chemical elements at stellar surfaces at different stages in models S1, S2, and S6

表5和表6列出了本文典型模型恒星表面的各种元素丰度随时间的演化(主要是为方便比较图4的各元素质量丰度在恒星表面的值). 结果表明化学成分均匀演化模型S6 WNL阶段开始在氢燃烧结束前, 而模型S1和S2 WNL阶段开始在中心氦燃烧后. 说明化学均匀演化模型可以经历较长的WR星演化阶段. 转动模型S2和S6不经历WNE阶段, 因为当这两个模型表面氢的质量丰度小于$ 10^{-5} $时, 碳质量丰度已经大于氮质量丰度. 表6展示了双星模型B2的WNL阶段发生在主序阶段, 这与洛希瓣物质交换损失氢包层, 提前进入WR 阶段有关. 另外, 模型B2没有经历WO演化阶段, 这是因为该模型在WC后期恒星质量小(对比模型B1)、中心温度低、表面氦质量丰度高、氧质量丰度低造成的. 在中心氦燃烧结束, 比较模型S1和B1 (对比表5和表6), 发现双星模型的⁴He, ¹²C, ¹⁹F, ²²Ne, ²³Na, ²⁵Mg的质量丰度高于相同初始条件的单星模型, 而¹H, ¹⁴N, ¹⁶O, ²²Ne和²⁶Al质量丰度下降, 这与双星演化经历洛希瓣物质交换, 减小了恒星内部的温度和核反应速率有密切关系.

Sequence	Age/Myr	$M_1/M_{\odot}$	log($X_{\rm ^{1}H}$)	log($X_{\rm ^{4}He}$)	log($X_{\rm ^{12}C}$)	log($X_{\rm ^{14}N}$)	log($X_{\rm ^{16}O}$)	log($X_{\rm ^{19}F}$)	log($X_{\rm ^{20}Ne}$)	log($X_{\rm ^{22}Ne}$)	$X_{\rm ^{26}Al}$
ZAMS
B1	0.0000	60.00	–0.14	–0.58	–2.62	–3.15	–2.18	–6.46	–2.87	–3.96	0
B2	0.0000	60.00	–0.14	–0.58	–2.62	–3.15	–2.18	–6.46	–2.87	–3.96	0
BTM1
B1	2.6862	53.01	–0.14	–0.58	–2.62	–3.15	–2.18	–6.54	–2.95	–4.04	3.31 × 1021
B2	2.6314	51.90	–0.14	–0.58	–2.76	–2.74	–2.21	–6.66	–2.95	–4.16	3.38 × 10–7
ETM1
B1	3.8956	36.84	–0.40	–0.23	–3.87	–2.06	–3.56	–9.69	–2.96	–6.62	1.81 × 10–5
B2	2.7305	45.44	–0.16	–0.53	–3.02	–2.36	–2.38	–6.94	–2.95	–4.45	3.89 × 10–6
ECHB
B1	4.0397	33.60	–0.50	–0.18	–3.85	–2.05	–3.61	–9.72	–2.96	–6.61	2.45 × 10–5
B2	4.1254	25.57	–1.06	–0.05	–3.80	–2.05	–3.67	–9.68	–2.96	–6.63	4.16 × 10–5
BCHEB
B1	4.0409	33.57	–0.50	–0.18	–3.85	–2.05	–3.61	–9.72	–2.96	–6.61	2.45 × 10–5
B2	4.1297	25.44	–1.07	–0.05	–3.80	–2.05	–3.67	–9.68	–2.96	–6.63	4.16 × 10–5
BMT2
B1	4.0474	33.39	–0.50	–0.18	–3.85	–2.05	–3.61	–9.72	–2.96	–6.61	2.51 × 10–5
B2	3.1581	43.04	–0.24	–0.39	–3.80	–2.09	–2.95	–8.24	–2.95	–5.76	1.31 × 10–5
WNL
B1	4.0480	32.78	–0.52	–0.16	–3.85	–2.05	–3.61	–9.73	–2.96	–6.62	2.81 × 10–5
B2	3.8633	32.25	–0.52	–0.16	–3.85	–2.05	–3.61	–9.72	–2.96	–6.60	2.95 × 10–5
EMT2
B1	4.0562	30.44	–0.68	–0.11	–3.84	–2.05	–3.64	–9.72	–2.96	–6.60	3.89 × 10–5
B2	3.5409	37.67	–0.28	–0.34	–3.86	–2.07	–3.16	–8.72	–2.95	–6.19	1.41 × 10–5
WNE
B1	4.1344	26.76	–5.00	–0.01	–3.73	–2.05	–3.76	–9.59	–2.97	–6.65	4.78 × 10–5
B2	4.2129	22.30	–5.18	–0.01	–3.68	–2.06	–3.74	–9.45	–2.97	–6.52	4.78 × 10–5
WC
B1	4.1976	23.92	–28.45	–0.09	–0.80	–14.82	–2.17	–4.58	–2.97	–1.87	6.45 × 10–17
B2	4.2498	21.01	–10.94	–0.01	–2.05	–2.10	–3.40	–5.62	–2.97	–2.91	4.36 × 10–5
WO
B1	4.4339	14.75	–31.67	–0.64	–0.31	–17.28	–0.58	–4.59	–2.85	–1.88	5.62 × 10–5
B2	—	—	—	—	—	—	—	—	—	—	—
ECHEB
B1	4.4454	14.60	–31.77	–0.70	–0.31	–17.19	–0.53	–4.59	–2.82	–1.89	7.76 × 10–16
B2	4.5716	11.27	–30.86	–0.60	–0.30	–17.45	–0.65	–4.58	–2.90	–1.88	2.45 × 10–16
BCCB
B1	4.4468	14.58	–31.25	–0.70	–0.31	–17.19	–0.53	–4.59	–2.82	–1.89	7.76 × 10–16
B2	4.5741	11.24	–29.98	–0.61	–0.30	–17.44	–0.64	–4.58	–2.90	–1.88	2.51 × 10–16
ECCB
B1	4.4469	14.58	–31.22	–0.70	–0.31	–17.19	–0.53	–4.59	–2.82	–1.89	7.76 × 10–16
B2	4.5743	11.24	–29.54	–0.61	–0.30	–17.44	–0.64	–4.58	–2.90	–1.88	2.51 × 10–16

表6双星模型B1和B2在各个主要阶段主星表面的各种元素的质量丰度的对数值
Table6.Mass fraction of various chemical elements at the surfaces of the primary star at different stages in models B1 and B2

图5给出了所有双星模型中的洛希瓣物质交换速率恒星质量的变化趋势. 可以看出, 模型B2的物质交换最先开始, 这与模型B2中主星的半径首先达到洛希瓣半径有关. 由于转动的动力学效应, 模型B2的主星半径大于模型B1的主星半径, 物质交换先开始. 模型B3的初始速度大, 有更多的自转角动量转移到轨道角动量, 双星间距变得更宽, 洛希瓣半径大于模型B2, 物质交换延迟发生. 模型B5物质交换发生的时间较晚, 这是由于低金属丰度恒星半径小, 较晚达到洛希瓣半径. 并且模型B5进行了三次物质交换, 这与低金属丰度半径小, 损失较少的氢包层有关. 另外, 由于星风物质损失, 造成双星间距变宽. 所以低金属丰度模型, 相同条件下有较小洛希瓣半径, 较容易发生洛希瓣物质交换. 模型B4由于轨道周期最长, 只进行一次物质交换且发生在中心氦燃烧.
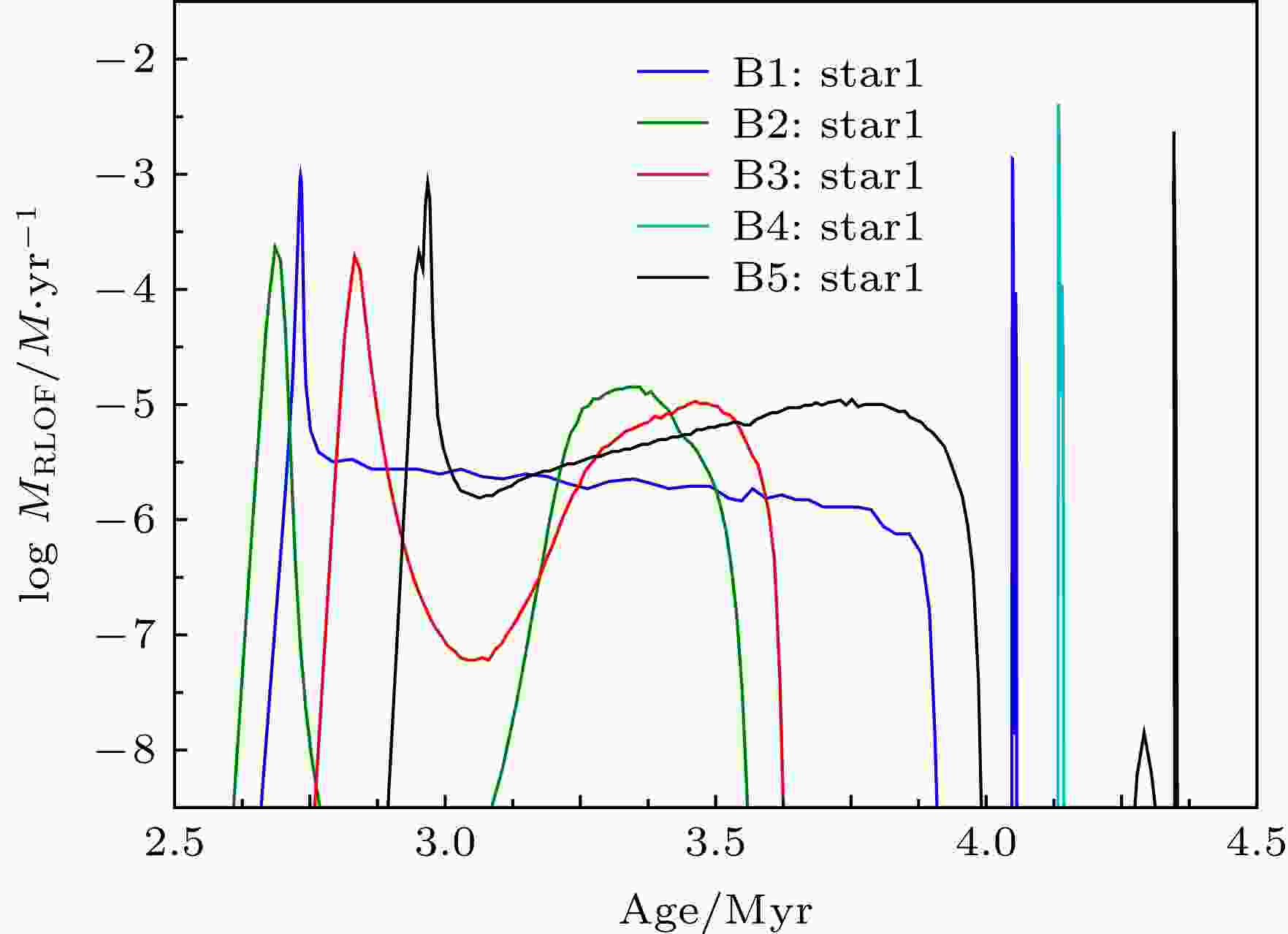图 5 双星模型洛希瓣物质交换率随时间的演化
Figure5. Rate of mass transfer during Roche lobe overflow vary with evolutionary time for the models of binary star

图6(a)给出了所有单星模型的赫罗图的演化轨迹. 在零龄主序, 比较S1, S2和S3, 发现快速转动趋向使恒星向低温和低光度端移动, 恒星中心温度和中心密度均变低(见表3). 这是因为离心力减小了恒星表面的重力加速度, 使恒星等效为较小质量星. 此时, 比较S1, S5, 发现低金属丰度模型S5具有较高的有效温度和光度. 这是因为: 1) 低金属丰度, 不透明度小, 包层变得透明, 恒星物质保持集聚; 2) 低金属恒星碳, 氮, 氧元素少, 核燃烧不得不部分依靠PP链, PP链对温度的依赖性远小于CNO循环. 零龄主序前, 为获得较高的中心温度, 低金属丰度恒星半径变小, 对流核变大, 有效温度和光度均变大. 模型S4的质量小于模型S2, 因而在ZAMS时中心温度和密度较低(见表3), 在演化后期形成低光度WR 星. 另外, 比较S1, S2在TAMS的演化时间(见表3)可以看出, 转动效应可以增加恒星在主序的演化时间. 同时, 恒星的有效温度和光度变大. 这主要有两方面原因, 一方面转动混合增加了对流核的大小(见图2(a)), 另一方面转动混合减小了包层的不透明度. 由于模型S5的金属丰度低, 星风损失少, 氢包层不容易去除, 在氦燃烧阶段并不形成WR星. 对比S4和S5, 这说明并不是质量越大的恒星就一定能形成WR 星, 金属丰度的影响甚于恒星质量的影响. 模型S6经历化学成分均匀演化, 尽管金属丰度低, 星风弱, 也形成了WR星. 比较模型S1和S2, 在主序后期模型S2的光度大. 实际上模型S2的半径反而比模型S1小, 这是因为转动效应使大量的氦混合到氢包层, 使包层不透明度变小造成的. 总之, 比较5个单星模型, 发现高金属丰度, 低速或不转动恒星易形成高光度WR星.
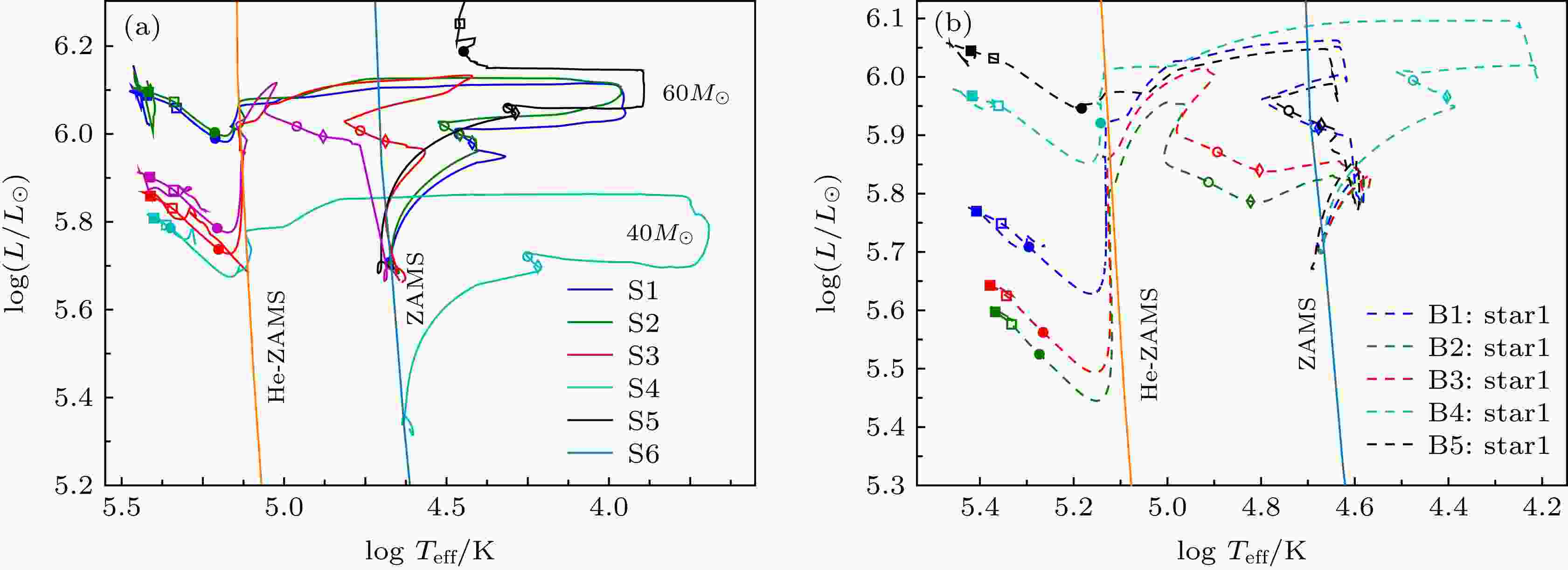图 6 (a) 单星模型在赫罗图中演化; (b) 双星模型中的主星在赫罗图中的演化; 双星模型的初始偏心率为0
Figure6. (a) Evolutionary tracks in HR diagram for single stars; (b) evolutionary tracks in HR diagram for binaries

图6(b)给出了所有双星模型的赫罗图的演化轨迹. 低金属丰度双星系统B5和初始大轨道周期的双星系统B4, 在主序后的演化可以产生高光度WR星. 比较模型B1和B2, 结果展示双星系统的转动效应产生低光度WR星, 这与主序阶段物质损失有关.
图7(a)给出了单星模型的表面氢的质量丰度随中心氦的质量丰度的变化. 图7(b)给出了单星模型表面有效温度随中心氦的质量丰度的变化. 在主序阶段, 比较模型S1, S2, S3 和S6, 发现快速转动恒星, 表面氢丰度下降快. 这主要有两方面的原因: 1) 由于转动混合造成氢元素向核反应区转移; 2) 更主要的原因是快速转动恒星造成氢包层逐渐快速丢失, 氦丰度增加迅速的缘故. 发现模型S5在中心氦消耗完, 表面氢丰度达到$ X_{\rm H} = 0.34 $, 这是由于该模型金属丰度低, 星风弱造成. 通常说表面氢丰度下降快, 意味着恒星丢失更多的氢包层, 表面有效温度变高, 恒星向蓝端移动(见图7(b)和图7(d)). 比较模型S2和S4, 发现低质量星氢丰度减小得慢. 这是因为低质量星星风损失较弱, 在主序阶段演化为黄超巨型(黄超巨型定义为: $ 3.68 < \log T_{\rm eff} < 3.88 $). 比较模型S1和S2在主序后的演化, 发现模型S1的表面氢在中心氦质量丰度高时消失, 这是因为模型S1的表面有效温度较高, 星风损失率高造成的. 实际上, 星风物质损失也与金属丰度有密切关系. 如模型S6虽然经历化学成分均匀演化, 表面温度比较高, 但是由于主序后模型S6金属丰度较低, 所以模型S6表面氢丰度下降的反而比模型S3较慢(见图7(a)).
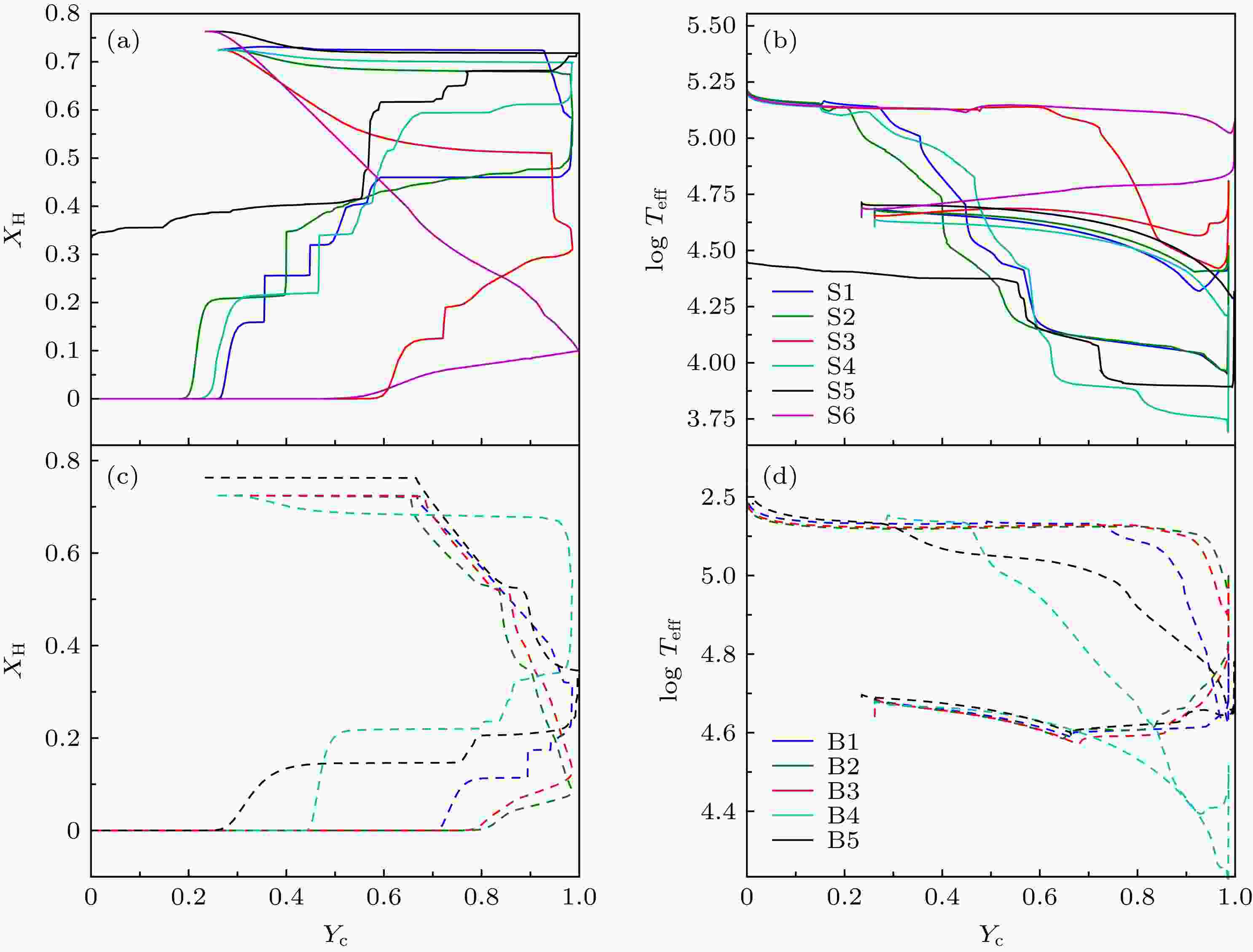图 7 (a) 单星模型表面氢的质量丰度随中心氦质量丰度的变化; (b) 单星模型表面有效温度随中心氦质量丰度的变化; (c) 双星模型表面氢的质量丰度随中心氦质量丰度的变化; (d) 双星模型表面有效温度随中心氦质量丰度的变化
Figure7. (a) Surface mass fraction of hydrogen varies with central helium mass fraction in models of single star; (b) surface effective temperature varies with central helium mass fraction in models of single star; (c) surface mass fraction of hydrogen varies with central helium mass fraction in models of binary star; (d) surface effective temperature varies with central helium mass fraction in models of of binary star

图7(c)给出了双星模型的表面氢的质量丰度随中心氦的质量丰度的变化. 图7(d)给出了双星模型表面有效温度随中心氦的质量丰度的变化. 比较模型S1和B1, 在主序阶段氢丰度在双星模型中下降得快, 这是因为双星系统洛希瓣物质交换除去氢包层造成的. 由于单星模型S4没有经历洛希瓣物质交换, 可以演化到黄巨星, 而所有双星模型在整个演化阶段始终为蓝超巨型($ \log T_{\rm eff} > 3.88 $). 另外, 双星模型B5表面氢丰度在中心氦最小时变为零. 这说明低金属丰度模型, 半径较小, 双星洛希瓣物质较困难, 仅除去了极少的氢包层, 所以在主序后($ 0.3 < \log Y_{\rm He, C} < 0.98 $), 模型B5的有效温度最低.

1) 星风物质损失、双星系统物质交换、化学成份均匀演化是形成WR星的3个非常重要的演化途径. WR星演化和内部核合成与恒星质量、初始转动速度、轨道周期、金属丰度等物理因素有密切关系. 单星模型的星风物质损失率越大, 越容易产生WR星. 因而恒星质量越大(恒星温度和光度大)、金属丰度越高(Fe原子含量高), 越容易形成WR星. 非转动大质量单星S1, 在主序后期发生双稳定性跳变, 丢失氢包层, 对形成WR星有重要影响.
2) 对WR星的形成, 金属丰度比恒星质量更重要. 金属丰度低的恒星由于星风弱, 不容易除去氢包层, 在WR星阶段有较低的有效温度. 因而单星模型S5尽管有较大的恒星质量, 由于金属丰度低, 并不产生WR星. 然而快速转动的低金属丰度的恒星, 元素混合时标短于核时标, 恒星内部不产生平均分子量栅栏, 氢包层和核反应区之间可以充分混合, 产生化学成分均匀演化(模型S6). 这样的模型对流核大, 氢包层比较薄, 反而容易形成WR星, 并且WR星阶段提前发生在主序阶段. 这说明快速转动可促使低金属丰度恒星形成WR星.
3) 对比低金属模型S5和B5, 发现恒星处在双星系统中可产生WR星. 这是因为双星系统发生洛希瓣物质交换, 将主星大量的氢包层物质转移到次星上. 双星系统的轨道周期对WR星的形成也有重要影响(对比模型B2和B4), 长轨道周期的双星系统B4, 洛希瓣半径大, 另外, 物质交换前星风物质损失也趋向使轨道间距变宽, 不容易发生洛希瓣物质交换, 这样氢包层除去少, 恒星的有效温度低. 短轨道周期的双星系统B2, 洛希瓣物质交换使WR阶段提前发生在主序阶段.
总之, 双星系统的洛希瓣物质交换和星风的联合作用使恒星趋向产生低光度的WR星. 研究发现双星模型的⁴He, ¹²C, ¹⁹F, ²²Ne, ²³Na, ²⁵Mg的质量丰度高于相同初始条件的单星模型, 而¹H, ¹⁴N, ¹⁶O, ²⁰Ne和²⁶Al质量丰度下降, 这说明洛希瓣物质交换减小了恒星内部的温度, 因而影响这些元素的核合成过程.
4) 非转动恒星氮增丰现象依赖星风物质损失和洛希瓣物质交换. 快速转动产生离心力, 增加星风损失量, 使恒星快速损失氢包层, 产生氦增丰. 另外转动效应产生元素混合和角动量转移, 使恒星表面氮元素增丰快, 减小包层的不透明度, 使恒星具有较高的光度. 双星系统中由于潮汐同步过程, 使初始转动速度大的子星, 转动变慢, 因而在主序阶段双星系统中氮元素增丰没有单星的氮元素超丰显著. 然而在主序后, 低金属丰度双星模型B5具有较厚的氢包层, 由于潮汐效应可以保持较高的转动速度, 中心氦燃烧生成的碳元素进入氢燃烧壳层, 产生氮元素强烈增丰, 这是氮增丰的重要机制. 总之, 大质量恒星, 初始转速快, 金属丰度高, 短轨道周期等物理条件, 容易除去氢包层, 产生裸露的氦核, 容易形成WR星.