摘要: 研究了含有非线性相互作用的腔机械系统中
N 个二能级原子在有限温度下的相变和相关的热力学性质, 采用虚时路径积分方法推导出系统的配分函数,求得系统的有效作用量. 通过对有效作用量进行变分得到系统的热力学平衡方程和原子布居数期待值的解析表达式, 重点研究了原子-场耦合强度、非线性原子-光相互作用、非线性声子-光子相互作用等影响下系统的相变, 发现除了会发生由正常相到超辐射相的二阶相变外, 还会出现正常相和亚稳的超辐射态共存的现象,同时会发现三相(正常相、超辐射相、亚稳的超辐射态)共存点. 有限温度的升高, 会使正常相到超辐射相的二阶相变点向原子-场耦合强度增大的方向移动; 当非线性原子-光相互作用(正或负)增强时, 相变点会向原子-场耦合强度弱的方向移动; 声子-光子相互作用会导致出现超辐射不稳定态; 有限温度下, 在正常相区熵为定值, 而在超辐射相区熵随原子-场耦合强度的增强迅速递减为零.
关键词: 有限温度 /
相变 /
虚时路径积分 /
非线性声子-光子相互作用 English Abstract Phase transition and thermodynamic properties of N two-level atoms in an optomechanical cavity at finite temperature Liu Ni Huang Shan Li Jun-Qi Liang Jiu-Qing State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute ofTheoretical Physics, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11772177, 61505100), the Natural Science Foundation of Shanxi Province, China (Grant No. 201701D221001), and the Fund for Shanxi "1331 Project" Key Subjects, ChinaReceived Date: 12 March 2019Accepted Date: 06 August 2019Available Online: 01 October 2019Published Online: 05 October 2019Abstract: Optomechanical cavity is a powerful connection between a nanomechanical oscillator and a quantized electromagnetic field. In this system, a novel photon-phonon nonlinear interaction arising from the nanomechanical oscillation is produced through the radiation pressure. Now this nonlinear photon-phonon interaction has become an important resource for implementing high-precision measurements and processing quantum information. Motivated by T. Esslinger group’s experiment, it is very meaningful to explore the exotic quantum phenomena when a ultra-cold BEC is trapped in an optomechanical cavity. In this paper, we mainly investigate phase transition and the finite-temperature thermodynamic properties of a Bose-Einstein condensate in an optomechanical cavity. It’s worth mentioning that at zero temperature many different mean-field approximate methods have been used to analyze the ground state properties of a Bose-Einstein condensate in an optomechanical cavity. Two common methods are Holstein-Primakoff transformation and spin coherent state variation. In this paper, an interesting imaginary-time path integral approach has been introduced to study finite temperature thermodynamic properties and phase transition of a Bose-Einstein condensate in an optomechanical cavity. First, we obtained system's partition function by taking imaginary-time path integration. Meanwhile, an effective action has been obtained by means of this method, which is the basic of the variation to get the numerical solution of photon number and the expression of the atomic number. At zero temperature, these results are consistent with what we have obtained by Holstein-Primakoff transformation or spin coherent state variational method. By adjusting the atom-field coupling strength and other parameters the second-order phase transition from the normal phase to the superradiant phase has been revealed. Meanwhile, a new unstable superradiant state was also found. And we found that in addition to the normal phase and superradiation phase, there exists an un-solution region of the mean photon number. Meanwhile, we find that the nonlinear photon-phonon interaction does not affect the normal phase. However, in the superradiant phase, the nonlinear photon-phonon interaction can enhance the macroscopic collective excitations. At the same time, the thermodynamic properties of the system are also discussed. According to the obtained distribution function, we can derive the analytical expression of the average energy and the free energy. Furthermore, the expression of entropy at finite temperature can also be obtained. we find the nonlinear photon-phonon interaction does not affect the average energy in the normal phase, but the average energy in the superradiant phase can deeply deviate in the large nonlinear photon-phonon interaction. It’s worth mentioning that the mean photon number and average energy in the finite-temperature tend to be consistent with the case in absolute zero temperature in the strong coupling region, while the entropy in the superradiant phase is rapidly reduced to zero as the atom-field coupling strength increases. In other words, strongly coupled collective excited states are highly ordered and are not affected by thermal fluctuations in the temperature range we are considering. The thermodynamic properties, such as the entropy and corresponding specific heat, characterize the Dicke phase transition.Keywords: quantum phase transition /imaginary-time path integral /superradiant phase /nonlinear ?photon-phonon interaction 全文HTML --> --> --> 1.引 言 腔光机械系统在探索经典系统和量子力学系统之间的界限发挥了重要作用[1 ] . 值得一提的是: 该混合系统中, 光腔模产生的光子和纳米机械振子产生的声子之间的新型非线性相互作用是通过辐射压诱导产生[2 ,3 ] . 目前, 这种非线性声子-光子相互作用是实现高精度测量和量子信息处理的一种重要资源[4 ] . 随着电磁自由度和机械自由度相干耦合技术的进步, 实验上实现了一种新的前沿量子领域: 腔光机械[5 ] . 光机械腔内可实现许多有趣的物理现象, 例如光学冷却[6 ] 、光学区域中的双稳态和光学非线性[7 ] 以及压缩[5 ] 等. 目前实验上将玻色-爱因斯坦凝聚体(BEC)与超精细光腔进行耦合, 并且在横向注入了泵浦光[8 ] , 这种将超冷原子系综与高精细腔模相互作用系统是典型的腔量子电动力学系统, 它在研究量子光学和冷原子物理领域具有重要的参考价值[9 ,10 ] . 基于此, 实验上还将BEC囚禁在光机械腔中, 这对于探索奇异的量子现象是非常有意义的.[11 ] . Dicke模型的量子相变就是最典型的例子, 它通过改变原子-场耦合强度产生由正常相(NP)到超辐射相(SP)的二阶相变. 该自旋玻色模型描述的是N 个二能级原子系综与单模量子化玻色场的耦合[12 ,13 ] . 从20世纪70年代开始, 虚时路径积分方法被用来研究有限温度下Dicke模型在热力学极限$N \to \infty $ 和弱耦合下的相变特性[14 ] .[15 —17 ] . 在$N \to \infty $ 极限下, 利用平均场近似方法(如: Holstein-Primakoff变换方法、自旋相干态变分方法)对零温下光学机械腔中囚禁的BEC的基态特性和相关量子相变(QPT)已进行了广泛的研究[15 ] . 现在我们采用虚时路径积分的方法来研究囚禁BEC的腔机械系统在有限温度下的相变和相关的热力学性质. 模型是光机械腔中囚禁BEC, 哈密顿量中引入了原子-光非线性相互作用. 用虚时路径积分方法可以方便地讨论热涨落起主导作用下, 温度对系统相变的影响, 而平均场近似下只能讨论零温极限下的量子相变. 本文用该虚时路径积分方法推导出系统的热力学平衡方程、原子布居数、平均光子数和平均能量、自由能的表达式, 并计算出熵的表达式, 并将得到的相图与零温下的量子相变等特性进行比较, 进而探讨温度对光机械系统的影响[15 ,18 ] . 我们发现: 原子-光非线性相互作用会使相变点移动, SP区域范围改变; 当原子-光非线性相互作用绝对值达到一定值时, SP区域会完全消失; 强的非线性声子-光子耦合强度可以出现超辐射不稳定态(NUS).2.模型以及哈密顿量 根据文献[19 ]中提出的实验装置, 我们考虑如图1 的冷原子系统: 四能级原子组被囚禁在频率为${\omega _{\rm{c}}}$ 的高精度光腔内, 且一束频率为${\omega _{\rm{p}}}$ 的横向泵浦光被垂直注入光腔; 通过辐射压力将高质量的机械振荡器与腔模进行耦合. 超冷原子将泵浦光相干地散射到与位置相关的腔模中. 通过泵浦激光器和腔模的光散射两种平衡拉曼通道, 在色散极限下, 原子的两个激发态能级可以绝热地消除进而来获得一个有效的二能级原子[2 ,20 ] . 相应的二次量子化的哈密顿量表示为(考虑自然单位$\hbar =1$ )图 1 将超冷原子囚禁在超精细的光腔内, 在z 方向注入一束泵浦光, 并且在x 方向外加一个与光腔发生相互作用的纳米机械振子Figure1. Experimental setup for an ultra-cold atoms trapped inside a high-finesse optical cavity driven by a pump laser in the z direction. While, a nanomechanical oscillator interacts with the optical cavity in the x direction.2 )中的哈密顿量是标准Dicke模型的哈密顿量[21 ,22 ] , 其中${a^\dagger }(a)$ 是有效光场的产生(湮灭)算符, ${b^\dagger }(b)$ 是声子的产生(湮灭)算符, ${\omega _0}$ 是原子的有效频率, ${\omega _0} = {\omega _{\rm{a}}} - {\omega _{\rm{p}}}$ 是有效的原子频率, ${\omega _{\rm{a}}}$ 是原子的共振频率, $\omega = {\Delta _{\rm{c}}} + 5U/2$ 是有效的腔频率, 其中${\Delta _{\rm{c}}} = {\omega _{\rm{c}}} - {\omega _{\rm{p}}}$ 是光腔的频率${\omega _{\rm{c}}}$ 和泵浦激光频率${\omega _{\rm{p}}}$ 之间的失谐(${\Delta _{\rm{c}}} > 0$ 为红失谐, ${\Delta _{\rm{c}}} < 0$ 为蓝失谐), $U = N{U_0}/4$ 代表的是原子-光非线性相互作用, 其中${U_0}=g_0^2({\omega _p} - {\omega _a})$ , ${g_0}$ 代表的是单个原子-场耦合强度, $g$ 代表原子-场集体耦合强度, $N$ 是原子数目. ${\omega _{\rm{b}}}$ 是纳米机械振子的频率, $\xi = \sqrt N {\xi _0}$ 是机械振子产生的声子和腔模产生的光子通过辐射压产生的非线性相互作用, 其中${\xi _0} = {{{\omega _{\rm{c}}}} / {l\sqrt {2M{\omega _{\rm{b}}}} }}$ , $l$ 是光腔的长度, $M$ 为纳米机械振子的质量. ${S_l} = \sum\limits_{i = 1}^N {{\sigma _{l,i}}} (l = x,y,z)$ 是原子集体赝自旋算符, ${S_ \pm } = ({S_x} \pm {\rm{i}}{S_y})$ 和${S_z}$ 满足角动量对易关系$[{S_ + },{S_ - }] = 2{S_z}$ 和$[{S_z},{S_ \pm }] = \pm {S_ \pm }$ . 值得一提的是: 在哈密顿量中我们忽略了三体相互作用项, 仅考虑两体(光子, 声子)辐射压相互作用[23 —25 ] . 引入两组费米算符, 定义费米算符的产生和湮灭算符为$\alpha _i^\dagger ,{\alpha _i}$ 和$\beta _i^\dagger ,{\beta _i}$ , 且费米算符满足反对易关系. 将赝自旋算符转换为双模费米子算符${\sigma _{z,i}} \to \alpha _i^\dagger {\alpha _i} - $ $\beta _i^\dagger {\beta _i}$ , ${\sigma _{ +,i}} \to \alpha _i^\dagger {\beta _i}$ , ${\sigma _{ -,i}} \to \beta _i^\dagger {\alpha _i}$ , 则我们可以得到哈密顿量(1 )的费米子算符形式:[26 ] . 系统的配分函数表示为$\beta = 1/\left( {{k_{\rm{B}}}T} \right)$ , ${k_{\rm{B}}}$ 是玻尔兹曼常数, $\left[ {{\rm{d}}\eta } \right]$ 是积分度量.$C = 1,c = - \dfrac{{\xi \sqrt \beta }}{{\sqrt {N{\omega _{\rm{b}}}} }}{a^*}a,z = \sqrt {\beta {\omega _{\rm{b}}}} b$ , 则可将配方函数式(6 )中的声子算符积分掉, 则${b^ * }(b)$ 变量去掉了, 只剩下变量${a^ * }(a)$ . 将(9 )式代入(5 )式, 则配分函数可以化简为$\tau = {\rm{i}}t$ 是虚时, ${{{\varPhi }}_i}$ $\varPhi _i^\dagger,$ $G(a(\tau ),{a^ * }(\tau ))$ 具体为以下形式:$ {\varPhi _i} = \begin{pmatrix}{{\alpha _i}(\tau )}\\{{\beta _i}(\tau )}\end{pmatrix},~ \varPhi _{i}^\dagger = \begin{pmatrix}{\beta _{_i}^ * (\tau )} & {\alpha _i^ * (\tau )}\end{pmatrix}, $ 13 )进行变分, 即$\dfrac{{{\rm{\delta }}{S_{{\rm{eff}}}}(a(\tau ),{a^ * }(\tau ))}}{{{\rm{\delta }}(a(\tau ))}} = \dfrac{{{\rm{\delta }}{S_{{\rm{eff}}}}(a(\tau ),{a^ * }(\tau ))}}{{{\rm{\delta }}({a^ * }(\tau ))}} = 0$ , 则我们最终可以得到热力学平衡方程$a(\tau )$ 和费米场${\varPhi _i}$ 进行傅里叶变换, 即${f_n} = 2{\text{π}}n/\beta $ ; 费米场满足反周期边界条件${g_n} = (2n + 1){\text{π}}/\beta $ , 其中$n$ 为整数, ${f_n}$ 和${g_n}$ 分别为玻色场和费米场的Matsubara频率. 采用定态位相微扰方法, 所有温度对稳态的影响可以忽略不计, 即$a$ 与虚时$\tau $ 无关, 则上式可以化简为${g_n}$ 求和, 也可以转化为复平面的环路积分. 得到的稳态解满足的热力学平衡方程为$\zeta = \sqrt {{{\left( {{\omega _0} + U\dfrac{{{a^*}a}}{N}} \right)}^2} + 16{g^2}\dfrac{{{a^*}a}}{N}} $ . 上式方程有一个平庸解${a^ * }\left( \tau \right) = a\left( \tau \right) = 0$ , 与之对应的光子数为零, 系统处于正常相; 如果存在非零解, 则满足的方程为${n_{\rm{p}}} = \left\langle {{a^ * }a} \right\rangle /N$ , $\varsigma =\sqrt {{{({\omega _0} + U{n_{\rm{p}}})}^2} + 16{g^2}{n_{\rm{p}}}} $ , 对应的光子数大于零, 系统处于超辐射相. 从方程(18 )我们可以得到温度为$T$ 的相变点为${g_{\rm{c}}}\left( T \right)= $ $\sqrt {\left( {2{\omega _0}\omega {\rm{/tanh}}\left( {\beta {\omega _0}{\rm{/4}}} \right) - U{\omega _0}} \right){\rm{/8}}} $ , 同时对应的原子布居数为3.温度对二阶相变点参数的影响 23.1.Dicke相变[26 ] 和平均光子数 3.1.Dicke相变[26 ] 和平均光子数 根据方程(18 ), 图2 给出了平均光子数随原子-场集体耦合强度变化的示意图. 给定的参数是${\omega _0}\;=\;0{\rm{.047}}\left( {{\rm{MHz}}} \right)$ , $\omega \; = \;{\omega _{\rm{b}}}\; = \;20\left( {{\rm{MHz}}} \right)$ .图 2 平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-场的集体耦合强度$g$ 变化的示意图Figure2. The average photon number$\left\langle {{a^\dagger }a} \right\rangle /N$ as a function of the atom-field coupling strength$g$ .图2 描述的是平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-场的集体耦合强度$g$ 变化的示意图. 图2(a) 是在原子-光非线性相互作用$U = 0\left( {{\rm{MHz}}} \right)$ 和光子-声子相互作用$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ 时, 温度影响下平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-场的集体耦合强度$g$ 变化的示意图, 温度分别为$T = 0\left( {{\rm{nK}}} \right)$ (黑线)、$T = 50\left( {{\rm{nK}}} \right)$ (红线)和$T = 140\left( {{\rm{nK}}} \right)$ (蓝线). 在温度为$T = 0\left( {{\rm{nK}}} \right)$ (黑线)的情况下系统退回到标准Dicke模型, 当原子-场集体耦合强度$g$ 增加到临界耦合强度${g_{\rm{c}}}=\;0.5$ 时, 系统会发生从NP到SP的二阶Dicke量子相变. 从图2(a) 可以看出: 温度的升高会使NP到SP的二阶相变发生推迟, 相变点${g_{\rm{c}}}$ 向原子-场耦合强度增强的方向移动; 当原子-场耦合强度$g$ 增大到一定值时, 有限温度下的平均光子数将会与零温时重合.图2(b) 给出有限温度$T = 140\left( {{\rm{nK}}} \right)$ 和声子-光子的耦合强度$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ (机械振子影响不存在)时, 在不同的原子-光场非线性相互作用影响($U = 0\left( {{\rm{MHz}}} \right)$ (黑线)、$U = - 20\left( {{\rm{MHz}}} \right)$ (红线)和$U = - 30\left( {{\rm{nK}}} \right)$ (蓝线))下平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-场集体耦合强度$g$ 变化的示意图. 我们发现: 原子-光场非线性相互作用会使NP到SP发生二阶相变的相变点移动. 同时当原子-光场非线性相互作用较大时, 当原子-场集体耦合强度$g$ 增加到一定值时, 平均光子数会显著增强($U = - 30\left( {{\rm{nK}}} \right)$ (蓝线)). 对照图2(a) 和图2(b) 中的黑线(零温和有限温度), 我们发现: 有限温度会导致NP到SP的二阶相变向原子-场耦合强度强的方向移动.图2(c) 是在原子-光场的非线性相互作用不存在、且给定有限温度$T = 140\left( {{\rm{nK}}} \right)$ 时, 不同的声子-光子非线性相互作用影响下平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-场集体耦合强度$g$ 变化的示意图, 分别给出了$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ (黑线)、$\xi \;=\;30\left( {{\rm{MHz}}} \right)$ (红线)和$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ (蓝线)三种情况. 该图主要体现: 给定温度下, 机械振子对Dicke相变的影响. 我们发现声子-光子耦合强度不会影响相变点, 对NP不会产生影响, 但会使平均光子数增大, 即增强宏观集体激发, 并且除了会发生从NP到SP的变化外, 还会在全区域出现NUS, 即图中的彩色点划线.图2(d) 是在给定有限温度$T = 140\left( {{\rm{nK}}} \right)$ 和负的原子-光场非线性相互作用$U = - 30\left( {{\rm{MHz}}} \right)$ 时, 在不同的非线性声子-光子相互作用$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ (黑线)、$\xi \;=\;30\left( {{\rm{MHz}}} \right)$ (红线)和$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ (蓝线)影响下平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-光场的集体耦合强度$g$ 变化的示意图. 与图2(c) 比较, 负的原子-光场非线性相互作用会导致二阶相变点向右移动, 仍然出现NUS. 图2(e) 是给定有限温度$T = 140\left( {{\rm{nK}}} \right)$ 和正的原子-光场非线性相互作用$U = 30\left( {{\rm{MHz}}} \right)$ 时, 在不同的非线性声子-光子相互作用$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ (黑线)、$\xi \;=\;30\left( {{\rm{MHz}}} \right)$ (红线)和$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ (蓝线)下平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-场集体耦合强度$g$ 变化的示意图. 与图2(c) 比较, 正的原子-光场非线性相互作用会导致相变点向左移动, 同时也出现了NUS. 图中的NUS对应的是不稳定的非零光子数解, 所谓的不稳指的是对应的能量二阶导数大于零.3.2.有限温度相图 -->3.2.有限温度相图 图3 给出不同的原子-光场非线性相互作用影响下, 平均光子数随原子-场集体耦合强度和温度变化的相图$(g - T)$ . 图3(c) 为有限温度影响下Dicke模型的相图, 温度会导致标准Dicke模型($T = 0\left( {{\rm{nK}}} \right)$ )的二阶相变的相变点向原子-场耦合强度增大方向平移. 将图3(a) 和图3(d) 与图3(c) 进行比较, 我们发现: 负的原子-光非线性相互作用((a)$U = - 30\left( {{\rm{MHz}}} \right)$ )会使相变点右移, SP区域减小; 而正的原子-光非线性相互作用((d)$U = 30\left( {{\rm{MHz}}} \right)$ )会使相变点左移, SP区域有所增大. 当原子-光非线性相互作用绝对值达到一定值时((b)$U = - 50\left( {{\rm{MHz}}} \right)$ 和(e)$U = 50\left( {{\rm{MHz}}} \right)$ ), SP区域会完全消失, 被NUS代替, 也就是由NP到SP二阶相变不再存在, 光子数没有稳定激发解. 虽然白色区域有非零光子数解, 但却不是稳定的超辐射态.图 3 原子-光场非线性相互作用影响下, 平均光子数随原子-场集体耦合强度和温度变化的相图$(g - T)$ , 其中声子-光子耦合强度$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ Figure3. The average photon number’s phase diagram of the atom-field collective coupling strength and the temperature for different atom-light nonlinear interaction strength with the disappeared phonon-photon coupling constant $\xi \;=\;0\left( {{\rm{MHz}}} \right)$ .3.3.机械振子影响下的相图 -->3.3.机械振子影响下的相图 图4 中(a1)—(c1)是零温($T\;=\;0\left( {{\rm{nK}}} \right)$ )时, 不同的原子-光非线性相互作用影响下, 平均光子数关于原子-场集体耦合强度和声子-光子非线性相互作用($g - \xi $ 平面)的相图. 对比图4(a1) 和图4(b1) 或图4(c1) 和图4(b1) , 我们发现: 原子-光非线性相互作用为负值($U = - 30\left( {{\rm{MHz}}} \right)$ )时, 相变点右移, NP到SP的二阶相变推迟, 且SP减小; 反之, 原子-光非线性相互作用为正值($U = 30\left( {{\rm{MHz}}} \right)$ )时, 相变点左移, NP到SP的二阶相变提前, 且SP区域增大. 同时我们发现: 当强的声子-光子非线性相互作用存在时, 除了会出现由NP到SP的二阶相变外, 还会出现NUS白色区域, 此区域没有稳定的光子数解. 同时我们发现弱的原子-光非线性相互作用会使NUS区域明显增大. 图4(a2) —(c2) 是有限温度($T = 140\left( {{\rm{nK}}} \right)$ )下, 在不同的原子-光非线性相互作用影响下, 平均光子数关于原子-场集体耦合强度和声子-光子非线性相互作用($(g - \xi )$ 平面)的相图. 将图4(1) 与图4(2) 进行对比可以发现: 零温时的SP区域比有限温度的区域要大, 这说明温度会使NP到SP的二阶相变发生推迟, 相变点右移.图 4 原子-光非线性相互作用影响下, 平均光子数关于原子-场耦合强度和声子-光子非线性相互作用强度$(g - \xi )$ 的相图, 其中有限温度分别为$T\;=\;0\left( {{\rm{nK}}} \right)$ (1)和$T\;=\;140\left( {{\rm{nK}}} \right)$ (2)Figure4. The phase diagram about the average photon number of atom-field collective coupling strength and the nonlinear photon-phonon interaction for different atoms-light nonlinear interaction strength with different finite temperature$T\;=\;0\left( {{\rm{nK}}} \right)$ (1) and$T=140\left( {{\rm{nK}}} \right)$ (2).3.4.温度和非线性原子-光相互作用影响的相变特性 -->3.4.温度和非线性原子-光相互作用影响的相变特性 通过对平均光子数进行数值求解, 图5 给出了($U - T$ )平面的相图. 对于给定的原子-场集体耦合强度$g = 0.7\left( {{\rm{MHz}}} \right)$ (a)和$g = 0.75\left( {{\rm{MHz}}} \right)$ (b)以及非线性声子-光子相互作用$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ 时, 我们比较不同参数下平均光子数随原子-光非线性相互作用$U$ 和温度$T$ 变化的相图. 我们发现: 当原子-场集体耦合强度较大($g = 0.75\left( {{\rm{MHz}}} \right)$ )时, 图中的NUS会增加, 此区域内没有稳定的非零光子数解. 将图5 与图4 相比较, 我们发现除了有NP和SP, 在NP和SP区域还有一个不稳定的非零解, 从图5 可以明显看到.图 5 在不同的原子-场集体耦合强度下, 平均光子数关于原子-光非线性相互作用和温度($U - T$ )的相图, 其中声子-光子非线性相互作用$\xi = 50\left( {{\rm{MHz}}} \right)$ Figure5. The phase diagram about the average photon number of the atoms-light nonlinear interaction and temperature for different atoms-field collective coupling strength, where the nonlinear photon-phonon interaction $\xi = 50\left( {{\rm{MHz}}} \right)$ .图5 黑线$T = 80\left( {{\rm{nK}}} \right)$ 所示, 图6 给出了温度为80(nK)时, 平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子与光子的非线性相互作用$U$ 变化的示意图. 其他给定的参数是: 非线性声子-光子相互作用$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ 和原子-场耦合强度$g = 0.7\left( {{\rm{MHz}}} \right)\left( {\rm{a}} \right){\rm{,0}}{\rm{.75}}\left( {{\rm{MHz}}} \right)$ (b). 随着非线性原子-光相互作用$U$ 的变化, 系统出现了丰富的平均光子数的解. 从图6(a) 可以发现: 除了出现正常相NP和超辐射相SP, 还出现一种新的超辐射不稳定态NUS. 该NUS态随能量变化的二阶导数是小于零的, 为能量极大值, 固不稳定. 图6(b) 中当原子-场耦合强度变大为g = $ 0.75\left( {{\rm{MHz}}} \right)$ 且非线性$U$ 达到一定值时还出现了光子数的无解区, 对应图5 中空白部分, 此时没有稳定的光子数解.图 6 平均光子数$\left\langle {{a^\dagger }a} \right\rangle /N$ 随原子-光非线性相互作用$U$ 变化的示意图, 给定的参数是: 原子-场耦合强度. (a)$g = 0.7\left( {{\rm{MHz}}} \right)$ 和(b)$g = 0.75\left( {{\rm{MHz}}} \right)$ , 温度$T = 80\left( {{\rm{nK}}} \right)$ 和光子-声子非线性耦合强度$\xi = 50\left( {{\rm{MHz}}} \right)$ Figure6. Variations of the average photon number $\left\langle {{a^\dagger }a} \right\rangle /N$ with respect to the atom-light nonlinear interaction$U$ . The given parameters are the atom-field coupling strength (a)$g = 0.7\left( {{\rm{MHz}}} \right)$ and (b)$g = 0.75\left( {{\rm{MHz}}} \right)$ , the temperature$T = 80\left( {{\rm{nK}}} \right)$ and the photon-phonon nonlinear coupling strength $\xi = 50\left( {{\rm{MHz}}} \right)$ .4.热力学性质 根据系统的配分函数, 我们得到平均能量的定义式$T = 0({\rm{nK}})$ 时, 正常相和超辐射相的平均能量为21 )式, 图7 刻画了平均能量随原子-场耦合强度的变化. 图7(a) 是给定有限温度$T = 140\left( {{\rm{nK}}} \right)$ 和原子-光非线性相互作用$U = - 30\left( {{\rm{MHz}}} \right)$ , 在不同声子-光子耦合强度影响下, 平均能量${E_{\rm{g}}}$ 随原子-场集体耦合强度$g$ 变化的示意图. 从图可见: 当声子-光子耦合强度$\xi \;=\;0\left( {{\rm{MHz}}} \right)$ (黑线)和$\xi \;=\;30\left( {{\rm{MHz}}} \right)$ (红线)时, 随着原子-场耦合强度的增大, 平均能量的曲线基本重合, 说明较小的声子-光子耦合强度作用不会影响平均能量; 但是当声子-光子耦合强度达到$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ (蓝线)时, 平均能量在原子-场耦合强度增大时会出现偏差. 可见, 无论声子-光子耦合强度和原子-场耦合强度如何变化都不会影响NP的平均能量, 而在原子-场强耦合下SP区有不明显的影响. 图7(b) 是给定声子-光子耦合强度$\xi \!=\! 50\left( {{\rm{MHz}}} \right)$ 和原子-光非线性相互作用$U \!=\! - 30 \left( {{\rm{MHz}}} \right)$ 时, 平均能量${E_{\rm{g}}}$ 在不同的温度影响下随原子-场集体耦合强度$g$ 变化的示意图. 我们发现: 当有限温度$T = 140\left( {{\rm{nK}}} \right)$ (蓝线)时, NP的平均能要高于较低的有限温度$T = 0\left( {{\rm{nK}}} \right)$ (黑线)和$T = 50\left( {{\rm{nK}}} \right)$ (红线)时的平均能量, 同时当原子-场集体耦合强度增大到一定值时, 有限温度下的平均能量都会和零温时的平均能量趋近于一致. 总之, 温度在NP区对能量影响明显, SP区也有显著影响; 但当原子-场耦合达到较大值时, 影响几乎为零.图 7 平均能量${E_{\rm{g}}}$ 随原子-场集体耦合强度$g$ 的变化Figure7. The average energy${E_{\rm{g}}}$ as a function of the atom-field collective coupling strength.$N \to \infty $ 下, 每个原子的自由能定义为$F = - \dfrac{1}{{N\beta }}\ln Z$ , 由此我们计算得到有限温度下NP和SP的自由能:$S = E - F/T$ 还可以求得熵的表达式为24 )式, 图8 给出了熵随原子-场耦合强度的变化.图 8 熵$S$ 随原子-场集体耦合强度$g$ 的变化Figure8. Entropy$S$ as a function of the atom-field coupling strength$g$ .图8 分别给出了蓝失谐((a)${\varDelta _{\rm{c}}} = - 20\left( {{\rm{MHz}}} \right)$ )、共振((b)$\varDelta \!=\! 0\left( {{\rm{MHz}}} \right)$ )和红失谐((c)${\varDelta _{\rm{c}}} \!=\! 20\left( {{\rm{MHz}}} \right)$ )时, 有限温度$T = 140\left( {{\rm{nK}}} \right)$ (红线)和$T = 100\left( {{\rm{nK}}} \right)$ (蓝线)下熵随原子-场集体耦合强度变化示意图. 其他给定参数是$\xi \;=\;50\left( {{\rm{MHz}}} \right)$ , ${\omega _0}\;=\;0{\rm{.047}}\left( {{\rm{MHz}}} \right)$ , $U = 20$ (MHz). 我们发现: 无论NP还是SP时, 有限温度高($T = 140\left( {{\rm{nK}}} \right)$ )时对应的熵值都要比温度低($T = 100\left( {{\rm{nK}}} \right)$ )时高, 并且在高的有限温度下相变会发生推迟. 同时随着原子-场耦合强度增大, 不同的有限温度下熵最后都会趋近于零, 这也说明强集体耦合激发态是高度有序的, 在我们考虑的温度范围内不受热涨落所影响, 但是从图8(c) 可看出, 蓝失谐下熵变趋于零会发生推迟.5.结 论 我们利用虚时路径积分方法讨论了含有原子-光非线性相互作用的BEC-腔光机械系统在有限温度下的相变和相关的热力学性质. 通过虚时路径积分方法计算出配分函数, 从而推导出系统的热力学平衡方程和原子布居数表达式. 根据热力学平衡方程, 我们对平均光子数进行数值求解并且进行稳定性分析, 最终发现: 随着不同非线性耦合强度的变化, 系统除了会发生由NP到SP的二阶相变外, 还会出现无稳定光子数解的NUS. 同时,本文也通过计算热力学熵讨论了系统的热力学性质, 发现: 温度越高, 熵越大; NP时熵为常数, 相变点之后随着原子-场耦合强度的增加, 熵迅速减为零. 我们还发现: 负的原子-光非线性相互作用会使二阶相变点向原子-场耦合强度$g$ 增大的方向移动, SP区域减小; 而正的原子-光非线性相互作用会使二阶相变点向原子-场耦合强度$g$ 减小的方向移动, SP域增大些. 当原子-光非线性相互作用绝对值达到一定值时, SP区域会完全消失, 也就是由NP到SP的二阶量子相变不再存在, 光子数没有稳定激发解. 虽然NUS有非零光子数解, 但却不是稳定的超辐射态. 强的非线性声子-光子耦合强度可诱导NUS. 




 图 1 将超冷原子囚禁在超精细的光腔内, 在z方向注入一束泵浦光, 并且在x方向外加一个与光腔发生相互作用的纳米机械振子
图 1 将超冷原子囚禁在超精细的光腔内, 在z方向注入一束泵浦光, 并且在x方向外加一个与光腔发生相互作用的纳米机械振子






























































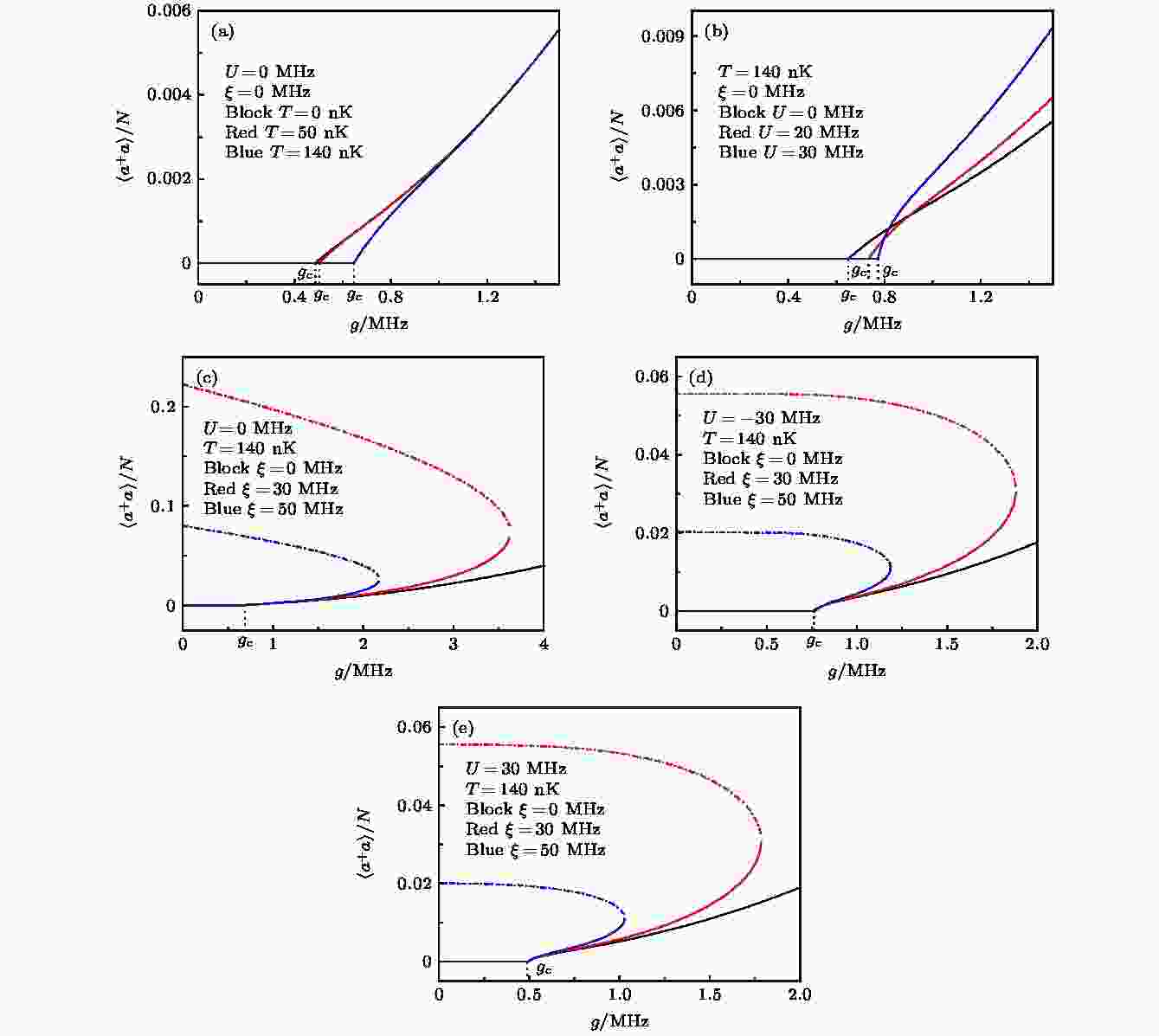 图 2 平均光子数
图 2 平均光子数




















































































 图 3 原子-光场非线性相互作用影响下, 平均光子数随原子-场集体耦合强度和温度变化的相图
图 3 原子-光场非线性相互作用影响下, 平均光子数随原子-场集体耦合强度和温度变化的相图








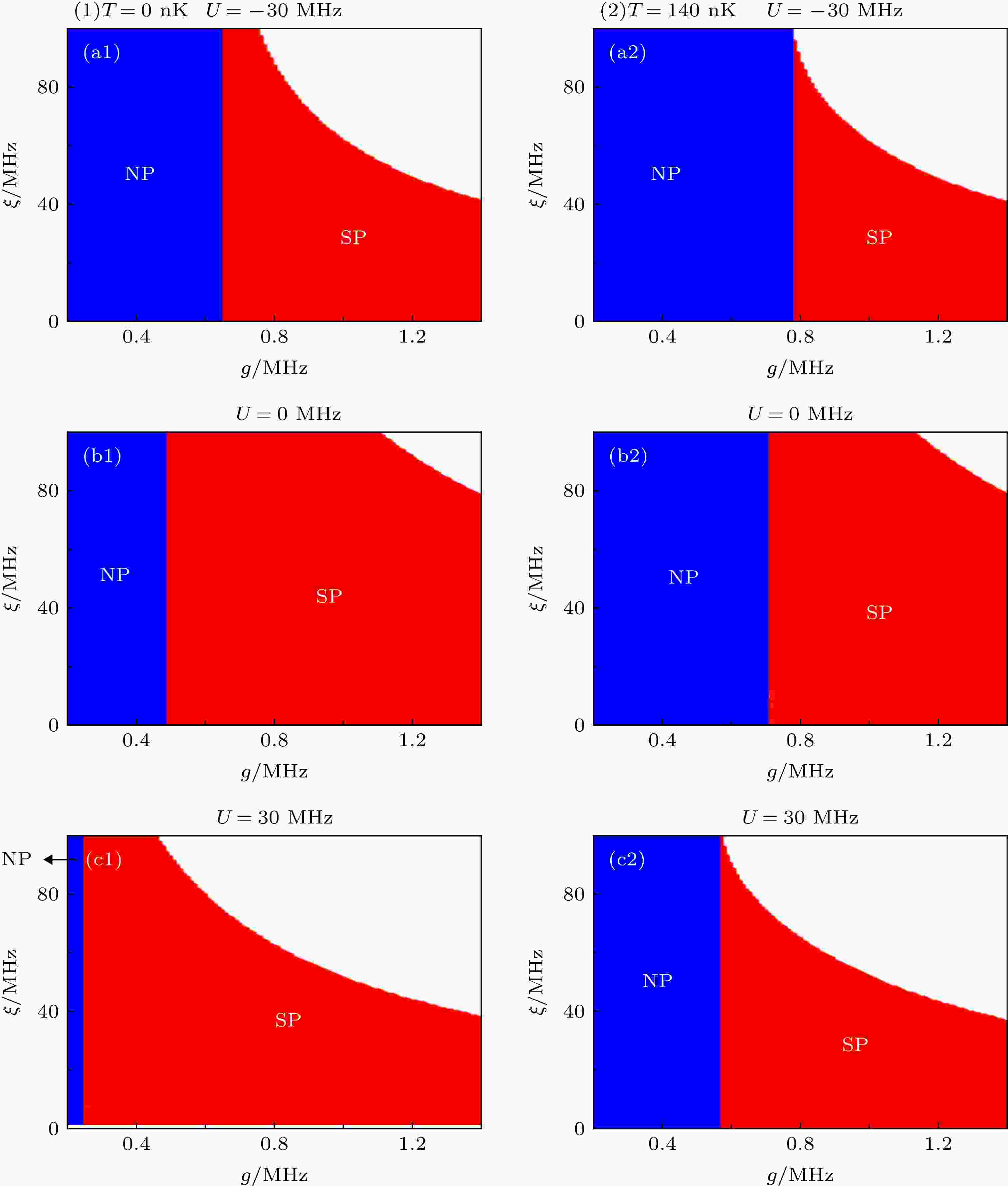 图 4 原子-光非线性相互作用影响下, 平均光子数关于原子-场耦合强度和声子-光子非线性相互作用强度
图 4 原子-光非线性相互作用影响下, 平均光子数关于原子-场耦合强度和声子-光子非线性相互作用强度













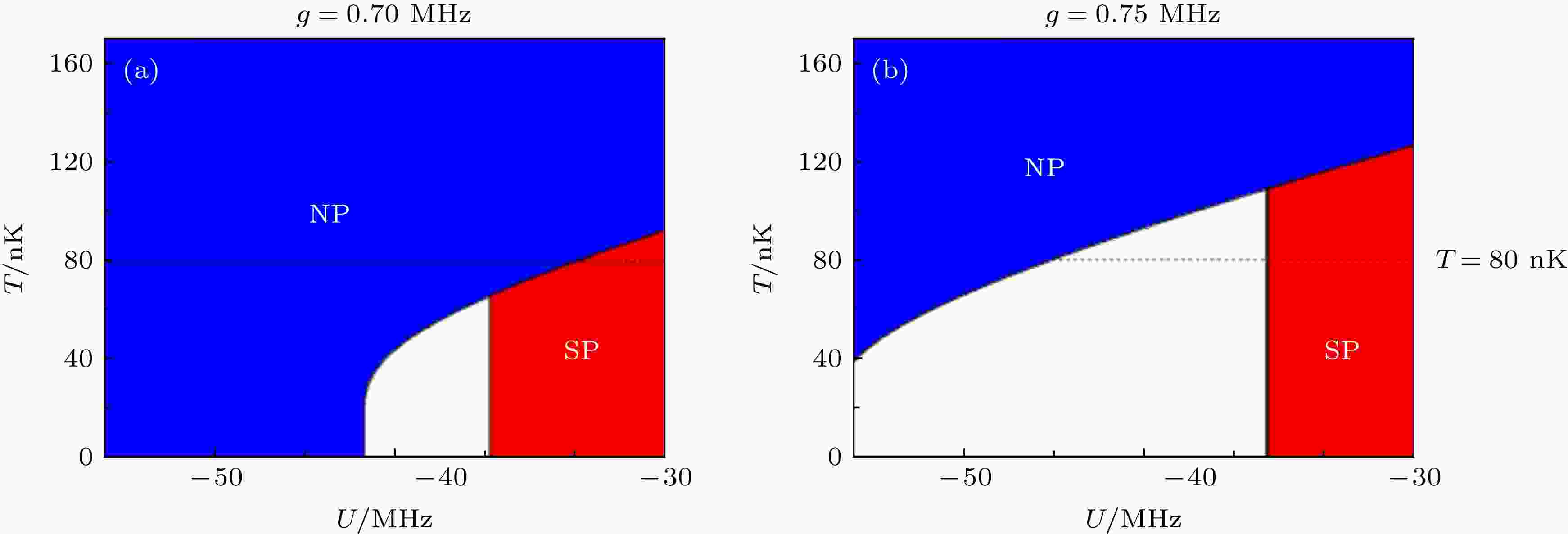 图 5 在不同的原子-场集体耦合强度下, 平均光子数关于原子-光非线性相互作用和温度(
图 5 在不同的原子-场集体耦合强度下, 平均光子数关于原子-光非线性相互作用和温度(
















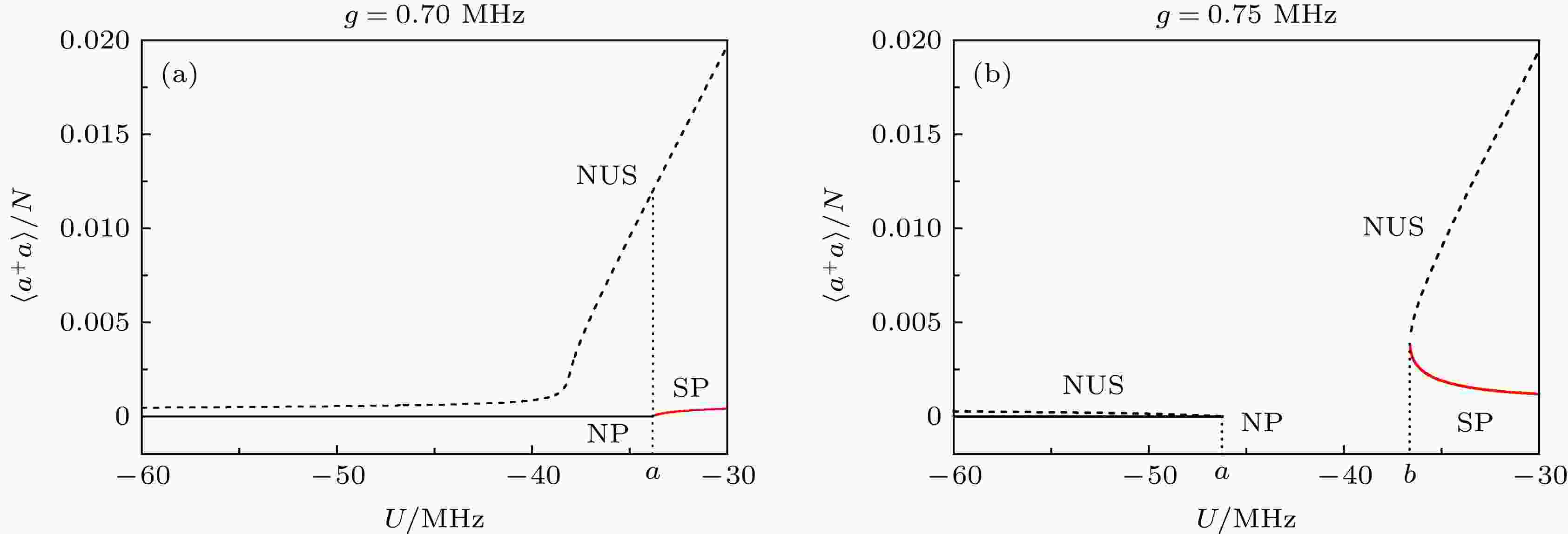 图 6 平均光子数
图 6 平均光子数
































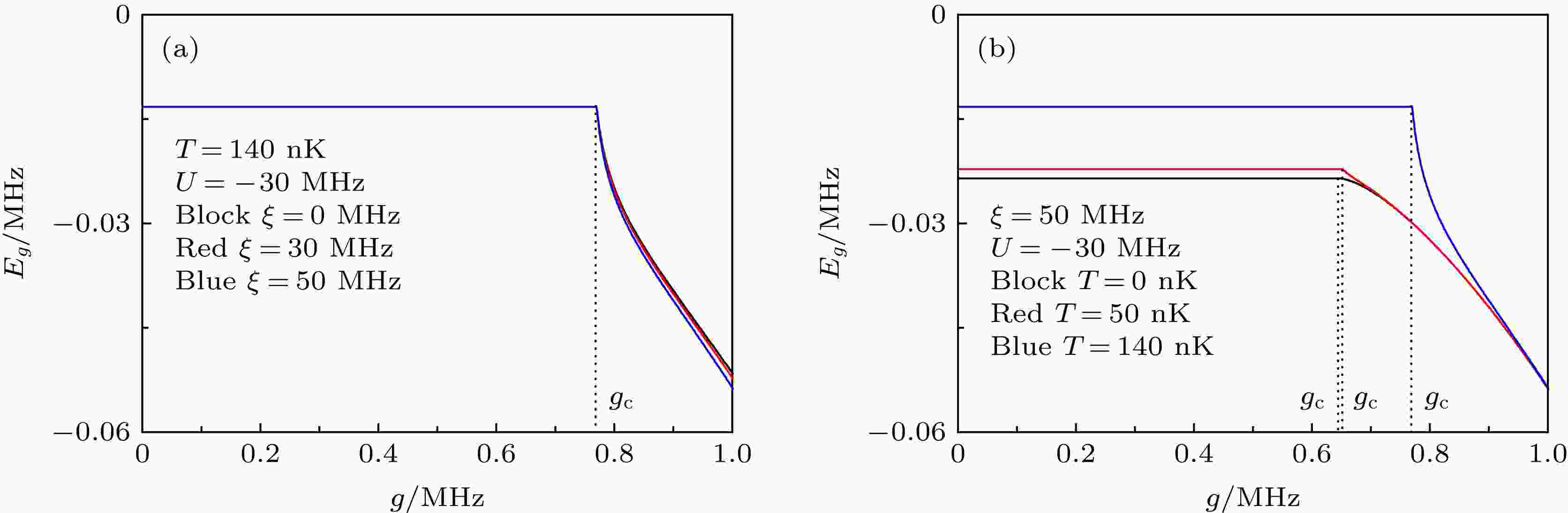 图 7 平均能量
图 7 平均能量





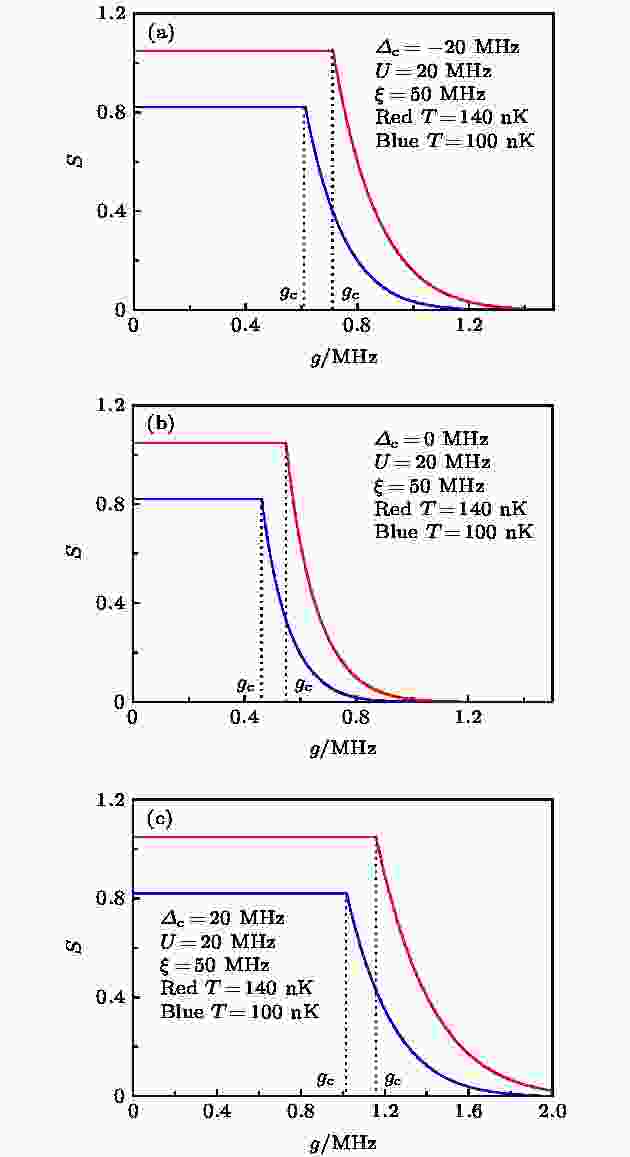 图 8 熵
图 8 熵





















