摘要:振动极大地影响着许多精密仪器的灵敏度和稳定性, 对于冷原子干涉重力仪尤其如此. 针对可移动的原子干涉仪建立了一套易于搬运的三维主动减振系统用来有效隔除地面的振动, 从而提高可移动原子干涉仪的测量灵敏度, 并能做到迅速部署迅速恢复工作. 通过实施我们设计的综合反馈算法, 本装置在三个维度的宽频带范围上实现了非常好的振动压制效果. 本系统取得了对地面竖直方向振动3个数量级, 对地面水平方向振动1个数量级的振动隔除效果. 在原子干涉仪敏感的10 Hz以下频段, 竖直方向的振动噪声被压制到了4.8 × 10^–9 m/s²/Hz^1/2, 水平方向的振动噪声被压制到了2.3 × 10^–7 m/s²/Hz^1/2. 振动噪声对干涉仪灵敏度的影响降至2 μGal/Hz^1/2以下, 比未放置减振系统的结果降低了2个数量级.
关键词: 三维主动减振/
反馈控制/
原子干涉仪

English Abstract

全文HTML

--> --> -->

对于许多精密测量实验和高精密的仪器而言, 振动会对其灵敏度和稳定性造成不可忽视的影响, 例如在引力波探测中, 要将关键元件的振动隔除到非常低的水平才能探测到微弱的引力波信号^[1-3]; 光钟实验中, 用来锁定激光频率的超稳腔也需要振动隔除^[4-6]; 对于精密的万有引力常数测量实验, 其测量结果会受地面振动的极大影响^[7,8]; 扫描隧道显微镜和扫描电子显微镜等仪器也对振动很敏感^[9]; 对于重力测量领域的绝对重力仪, 不论是经典的光学干涉重力仪还是冷原子干涉重力仪, 地面振动都是影响其测量灵敏度的重要因素^[10-15].
20世纪90年代初人们开始进行原子干涉仪的实验研究^[16], 到2001年时原子干涉仪测量灵敏度达到20 μGal/Hz^1/2[17] (1 μGal = 10^–8 m/s²). 2000年前后, 美国、欧洲、中国都相继开展了原子干涉仪相关的研究工作, 并且出现了固定式、可移动式等多种类型的原子干涉仪. 到现在, 固定式的原子干涉仪的尺度可高达10 m, 最高灵敏可以达到0.03 μGal/Hz^1/2[18]. 可搬运的原子干涉仪最高灵敏度可达9.6 μGal/Hz^1/2[19]. 国内的中国科学院武汉物理与数学研究所、华中科技大学、浙江大学、中国计量科学研究院和中国科学技术大学等单位先后开展了相关的研究并都参加了比对测量, 目前国内固定式的原子干涉仪的最高灵敏度可达4.2 μGal/Hz^1/2[20]的水平, 可移动式原子干涉仪的灵敏度在30—100 μGal/Hz^1/2的范围内^[21-23], 不确定度在几μGal到几十μGal的范围内, 还有很大的潜在进步空间. 通常来讲, 地面振动对原子干涉仪灵敏度的影响是最大的. 斯坦福大学将主动减振技术引入到原子干涉重力仪中^[24]. 洪堡大学利用Minus K公司的被动减振平台构建了主动减振系统^[13]. 中国科学院武汉物理与数学研究所利用被动减振平台研制了主动减振系统, 简化了体系结构并优化了装置性能, 他们的减振装置将竖直方向0.01—10 Hz频段的振动压制了300倍^[25]. 华中科技大学构建了应用于固定式原子干涉仪的三维主动减振系统并对其水平与竖直方向的耦合问题进行了研究^[26], 他们的减振装置将竖直方向0.2—2 Hz的振动噪声压制了50倍, 水平方向0.2—2 Hz的振动噪声压制了5倍.
本文针对可搬运的原子干涉仪研制了可移动的三维主动减振系统. 通过我们研制的综合反馈算法, 在地面振动噪声水平较高的中国科学技术大学上海研究院, 振动噪声对原子干涉仪灵敏度的影响被压制到了8.8 μGal/Hz^1/2, 约降低为地面上的1/1800. 在振动环境安静的中国计量科学研究院, 振动噪声对原子干涉仪灵敏度的影响被压制到了1.9 μGal/Hz^1/2, 约降低为地面上的1/60. 在0.5—2 Hz频段剩余振动已经到了高精度地震计的本底. 本装置在三个维度的宽频带范围上均取得了高的振动压制效果, 且极具可移动性, 经历了从上海到北京的多次搬运均能迅速恢复并稳定运行.

2

-->

2.1.硬件结构

本文搭建的主动减振系统的硬件结构如图1所示. 一个商用被动减振平台(Minus K, 50BM-4)对地面上的振动进行初步的振动隔除, 该商用减振平台的竖直本征频率可以调节到0.5 Hz, 水平本征频率也能调节到0.5 Hz 左右, 其最大承重为25 kg. 一个商用的高精度地震计(Guralp, 3ESPC)放置于减振平台上, 用来测量竖直方向(Z方向)和两个水平方向(X方向和Y方向)的振动信号. 图2所示的是地震计的幅频与相频响应曲线, 图中红色实线是理论值, 黑色的点则是使用该地震计的控制与采集器(Guralp, DM24)所测的幅频与相频响应数据, 两者基本一致. 从响应曲线中可以看到地震计0.1—10 Hz频段的振动信号几乎没有失真, 这使得我们能进一步抑制该频段的振动. 通过调节配重的质量以及被动减振平台主弹簧的刚度(stiffness), 被动减振平台的竖直与水平的本征频率降低到0.5 Hz附近. 对于振动敏感的干涉仪激光反射镜被直接固定在地震计上, 同时被动减震平台上还固定有一个高精度双轴倾角计用于实时记录倾角信号以便于修正减振平台的长期倾角漂移. 三组定制音圈电机(TMEC0001-004-01A)分别置于竖直的Z方向与水平的X, Y方向, 用于提供三个维度的反馈作用力. 音圈电机的推力常数为0.12 N/A, 峰值推力为0.55 N. 为了阻隔外界声音与气流对减振系统的干扰, 整个系统的外围包覆有隔音棉.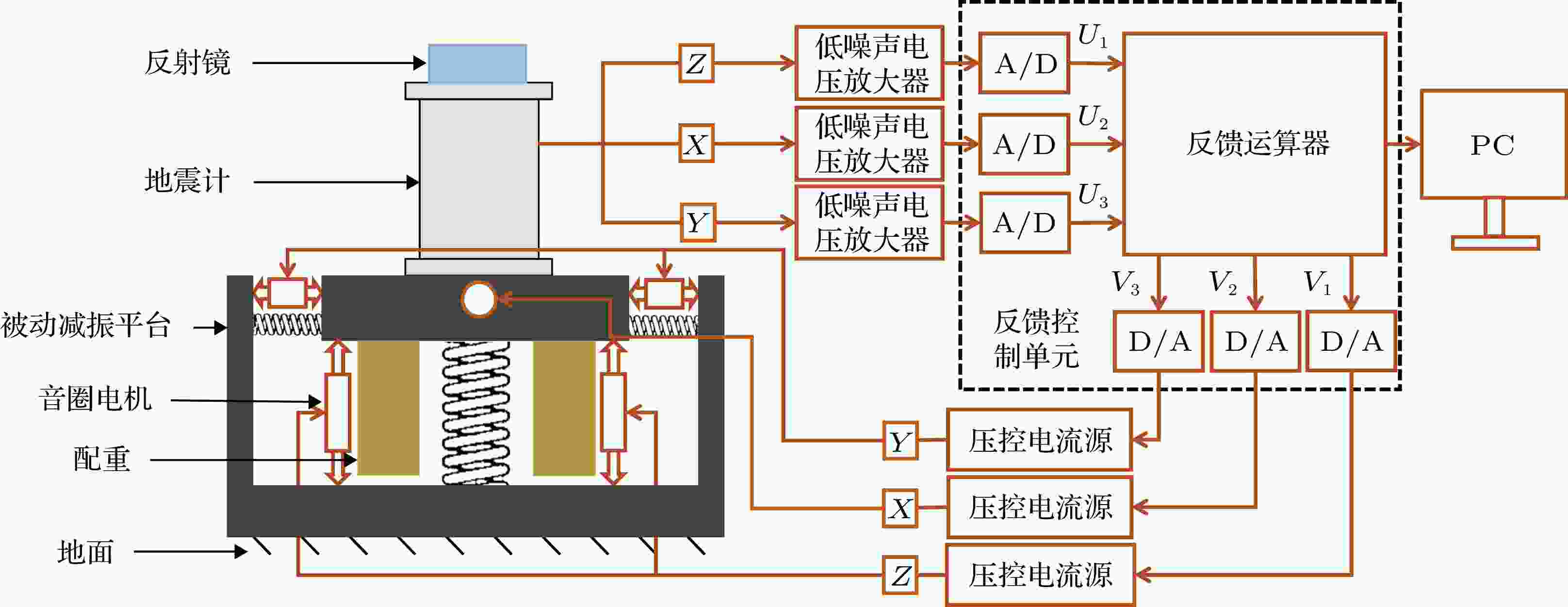
图 1 三维主动减振系统的结构示意图(地震计测量X, Y, Z三个方向的振动信号输出到低噪声电压放大器进行放大, 再经模数转换器转化为数字信号送入反馈运算器进行综合反馈运算; 得到的反馈信号经数模转换后通过压控电流源驱动音圈电机产生与平台运动方向相反的力从而抑制振动)
Figure1. Structrue of three-dimension active vibration isolator. Vibration signals measured in the X, Y, Z direction by the seismometer are amplified by a low-noise voltage amplifier, and then converted to digital signals by analog-to-digital converters and sent to a feedback unit for integrated feedback calculation. After passing digital-to-analog converters, the feedback signals drive voice coil actuators by voltage controlled current sources to generate a force opposite to movement direction of the platform to suppress vibration.

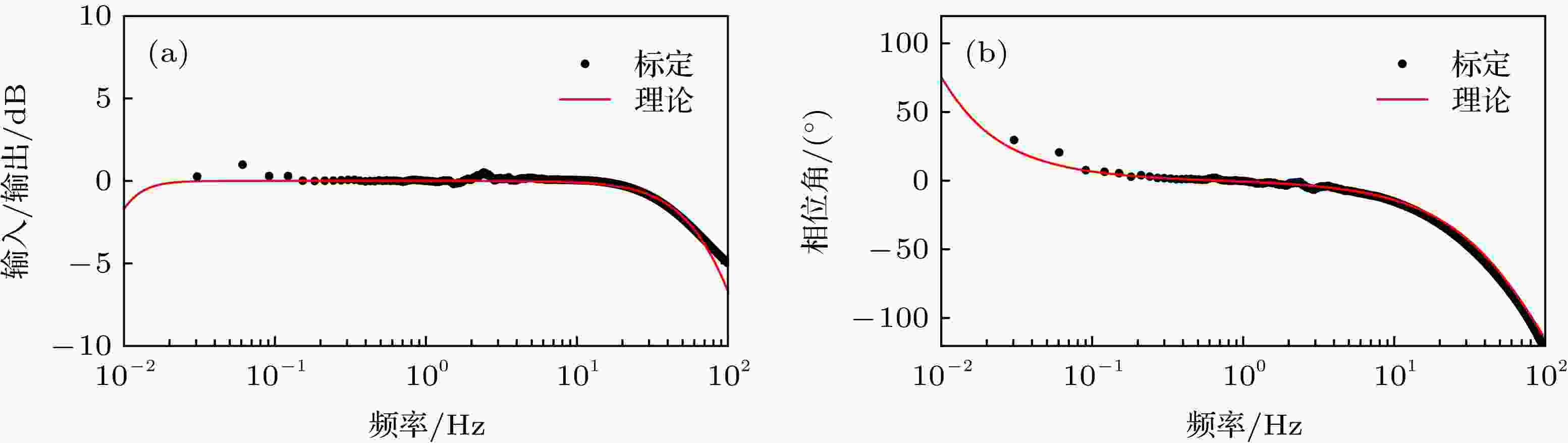图 2 地震计的频率响应曲线(红色实线是理论计算结果, 黑色实点是实验标定的结果)　(a)幅频响应; (b)相频响应
Figure2. Frequency response of the seismometer: (a) Amplitude response; (b) phase response. The red solid line is the theoretical calculation result, and the black solid dot is the experimental measurement result.

地震计测量X, Y, Z三方向的振动信号输出到低噪声电压放大器(Stanford Research Syetems, SR560)进行放大, 再分别经过一个24位的模数转换器A/D (National Instruments, NI 9239)转换为数字信号, 以实现数据采集. 一个可编程的反馈运算器(National Instruments, NI cRIO-9064) 接收到反馈信号并进行综合反馈运算生成三个方向的振动误差信号分别进行输出. 16位的数模转换器D/A (National Instruments, NI 9269)将数字误差信号转换为模拟信号, 通过压控电流源(Stanford Research Syetems CS580)驱动XYZ三个方向的音圈电机, 产生与平台运动方向相反的力来抑制振动. 其中反馈运算器还会实时将振动信号输出到电脑PC上, 通过电脑上记录的数据评估振动噪声并调节各项反馈参数.
2 -->

2.2.反馈控制算法

反馈控制算法的结构如图3所示, 其在图1中的反馈控制器中实施. 对于原子干涉仪而言, 只有竖直方向上的振动才会对测量结果造成影响, 所以我们构建主动减振系统的主要目的是抑制竖直方向上的振动. 因此首先将竖直方向(Z方向)的振动输入信号$ U_{1} $经高通滤波器$ H_{3} $滤除极低频成分, 再通过放大系数$ A_{2} $来反向并调节大小得到输出反馈信号, 用来抑制竖直方向上的振动. 为了更好地抑制竖直方向的振动, 尽量减小其对原子干涉仪的影响, 将输入信号$ U_{1} $同时经过一个带通滤波器来重点抑制该频段的振动噪声. 此带通滤波器由两个高通滤波器$ H_{1} $, $ H_{2} $和两个低通滤波器$ L_{1} $, $ L_{2} $联合组成. 此路信号乘以系数$ A_{1} $后被加入到原来的竖直信号中. 另外, 由于被动减振平台机械结构的原因, 竖直与水平方向的振动并不完全独立, 水平方向的振动也会耦合到竖直方向来. 为了解决这个问题, 需要采集水平方向的振动信号, 并将其处理之后反馈到竖直方向. 水平X方向振动信号$ U_{2} $和Y方向振动信号$ U_{3} $分别乘以耦合系数$ C_{1} $和$ C_{2} $后和竖直方向的振动信号$ U_{1} $加和. 利用前面已有的高通滤波器$ H_{3} $和放大系数$ A_{2} $来对这两个信号隔直和反向, 而利用耦合系数$ C_{1} $和$ C_{2} $来独立调节两者进入竖直反馈信号中的大小. 这样在水平方向的振动会被同时传入竖直方向的反馈回路, 压制水平振动与竖直振动的耦合从而保证了反馈系统的稳定. 最终竖直方向的反馈信号可以表达为
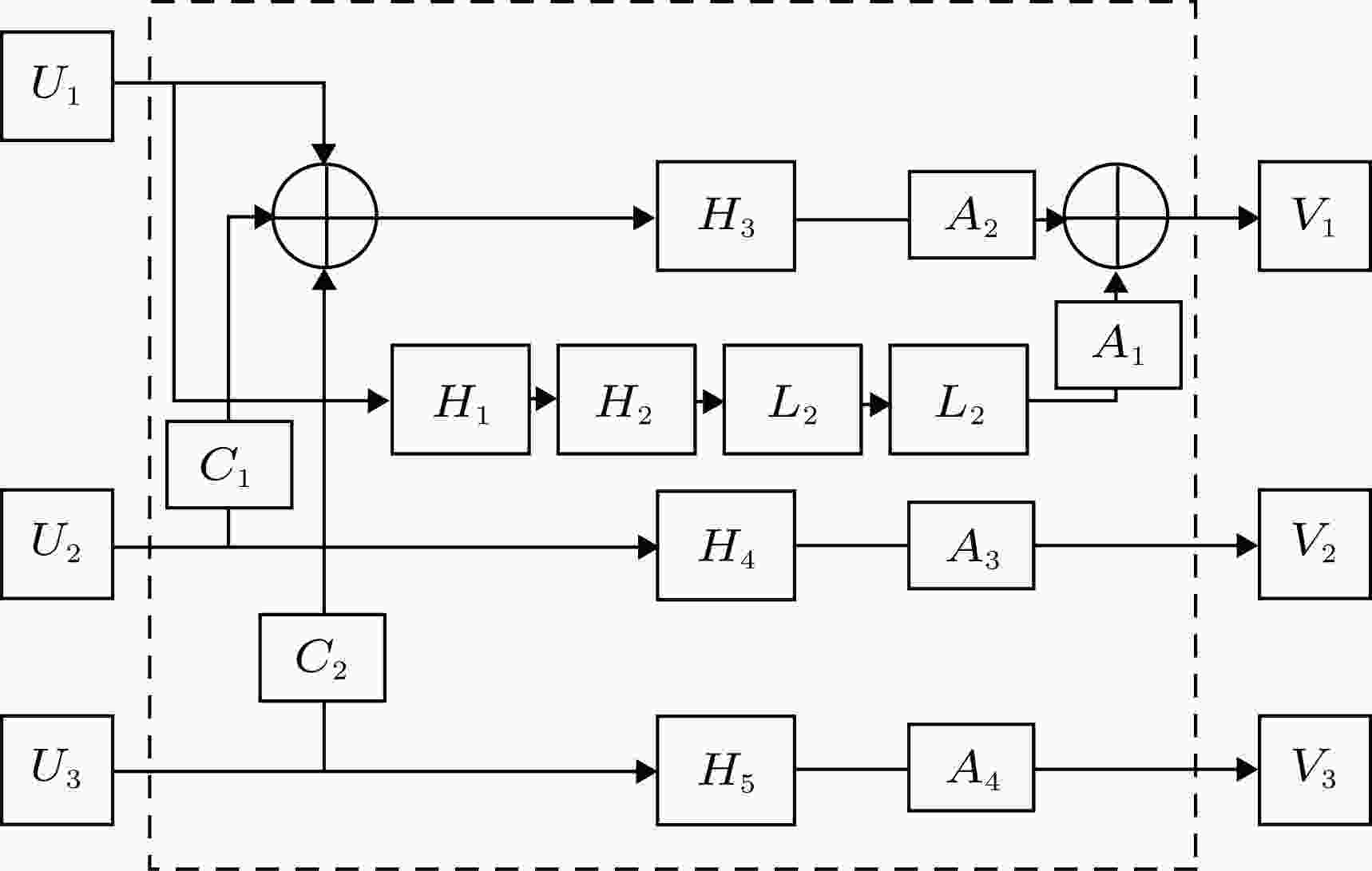图 3 反馈控制算法示意图($U_{1}$,$U_{2}$,$U_{3}$分别表示Z, X, Y方向数字化的输入振动信号; $H_{1}$—$H_{5}$表示高通滤波器; $L_{1}$,$L_{2}$表示低通滤波器; $C_{1}$,$C_{2}$表示水平耦合系数;$A_{1}$—$A_{4}$表示增益系数;$V_{1}$,$V_{2}$,$V_{3}$分别表示Z, X, Y方向数字化的输出反馈信号)
Figure3. Structure of feedback control algorithm. $U_{1}$,$U_{2}$,$U_{3}$ represent the digitized input vibration signals in Z, X and Y directions respectively. $H_{1}$?$H_{5}$ represent high-pass filters. $C_{1}$,$C_{2}$ represent horizontal coupling coefficient. $A_{1}$?$A_{4}$ represent gain coefficient. $V_{1}$,$V_{2}$,$V_{3}$ represent the digitized output feedback signals in Z, X and Y directions respectively.

$V_{1} = A_{2} H_{3} ( U_{1}+C_{1} U_{2}+C_{2} U_{3} )+A_{1} L_{2} L_{1} H_{2} H_{1} U_{1}.$

为了进一步减小水平振动对竖直振动的影响, 我们对水平方向的振动同时进行了反馈控制, 从而实现了三维的主动减振. 具体地, 将水平X方向的振动输入信号$ U_{2} $通过一个高通滤波器$ H_{4} $滤除极低频成分, 再乘以系数$ A_{3} $来反向并调节其大小, 最终得到水平X方向的输出反馈信号$ V_{2} = A_{3} H_{4} U_{2} $. 类似地, 将水平Y方向的振动输入信号$ U_{3} $通过一个高通滤波器$ H_{5} $滤除极低频成分, 再乘以系数$ A_{4} $来反向并调节其大小, 最终得到水平Y方向的输出反馈信号$ V_{3} = A_{4} H_{5} U_{3} $.
反馈算法中使用的均为一阶的高通与低通滤波器, 其中高通滤波器频域表达式为

$ H\left ( \omega \right ) = k\frac{{\rm i}\left ( \omega /\omega _{\rm c}\right )}{{\rm i}\left ( \omega /\omega _{\rm c}\right )+1}, $

低通滤波器频域表达式为

$ L\left ( \omega \right ) = k\frac{1}{{\rm i}\left ( \omega /\omega _{\rm c}\right )+1} , $

其中$ \omega $为振动角频率, $ \omega _{\rm c} $为滤波器的截止角频率, $ f _{\rm c} = \omega _{\rm c}/(2 {\text{π}}) $为滤波器的截止频率, k为滤波器的增益系数.
下面利用双线性变换法^[23]将模拟一阶高通和一阶低通波滤器转换为数字滤波器来实施反馈运算. 当模数转换器的采样时间间隔为T时, 利用双线性变换公式$ s = 2(z-1)/[T(z+1)] $, 其中$ s = {\rm i}\omega $, 将滤波器从s平面转换到z平面, 得到:

$ H\left ( z \right ) = \frac{k}{\left (\omega _{\rm c}T/2+1 \right )}\frac{1-z^{-1}}{1+\dfrac{\omega _{\rm c}T-2}{\omega _{\rm c}T+2}z^{-1}}, $

$ L\left ( z \right ) = k\dfrac{\dfrac{\omega _{\rm c}T}{\omega _{\rm c}T+2}\left (1+z^{-1} \right )}{1+\dfrac{\omega _{\rm c}T-2}{\omega _{\rm c}T+2}z^{-1}}. $

再利用逆z变换即可得, (1)式所示高通滤波器时域公式为

$\begin{split}u\left ( n \right ) = & \frac{k}{\omega _{\rm c}T/2+1}\left ( e\left ( n \right ) -e\left ( n-1 \right )\right )\\ & -\frac{\omega _{\rm c}T-2}{\omega _{\rm c}T+2}u\left ( n-1 \right ),\end{split}$

(2)式所示低通滤波器时域公式为

$ u\left ( n \right ) = \frac{k\omega _{\rm c}T}{\omega _{\rm c}T+2}\!\left ( e\!\left ( n \right ) +e\!\left ( n-1 \right )\right )-\frac{\omega _{\rm c}T-2}{\omega _{\rm c}T+2}u\!\left ( n-1 \right ) , $

其中$ e(n), n = 1,\;2,\;3,\;\cdots$代表输入的数字信号序列, 而$ u(n), n = 1,\;2,\;3,\;\cdots $代表输出的数字信号序列. 从(5)和(6)式可以看出设置k的效果与设置A₁—A₄的效果是一致的. 然而不同的是, k可以调节单个滤波器的输出信号大小, 使其接近输入信号的数量级, 这对于反馈算法在位数有限的处理设备上使用是非常有用的. 而我们使用的反馈运算器没有这个问题, 为了保持足够的通用性, 我们在算法中保留了这个参数, 并全部统一设定为$ k = 10$.

2

-->

3.1.振动噪声谱和传递函数

振动噪声对原子干涉重力仪灵敏度的影响可以用如下公式^[27]评估:

$ \sigma _{\rm g}^{2} = \int_{0}^{\infty }\left | H_{\rm a}\left ( \omega \right ) \right |^{2}S_{\rm a}\left ( \omega \right ){\rm d}\omega, $

式中, $ S_{\rm a}\left ( \omega \right ) $为竖直方向上的振动噪声功率谱密度, 从地震计测量的信号中可以得到; $ H_{\rm a}\left ( \omega \right ) $为振动噪声到原子干涉仪灵敏度的传递函数, 其表达式为

$ \left | H_{\rm a}\left ( \omega \right )\right |^{2} = [{4{\rm {sin}}^{2}\omega T/2}]/({\omega^{2}T^{2} }), $

其中$ \omega $为振动的角频率, T为干涉过程中原子在两个拉曼干涉光脉冲之间的自由演化时间. 我们的原子干涉重力仪在工作频率3 Hz, T = 80 ms的情况下, 相应的振动噪声传递函数如图4所示.
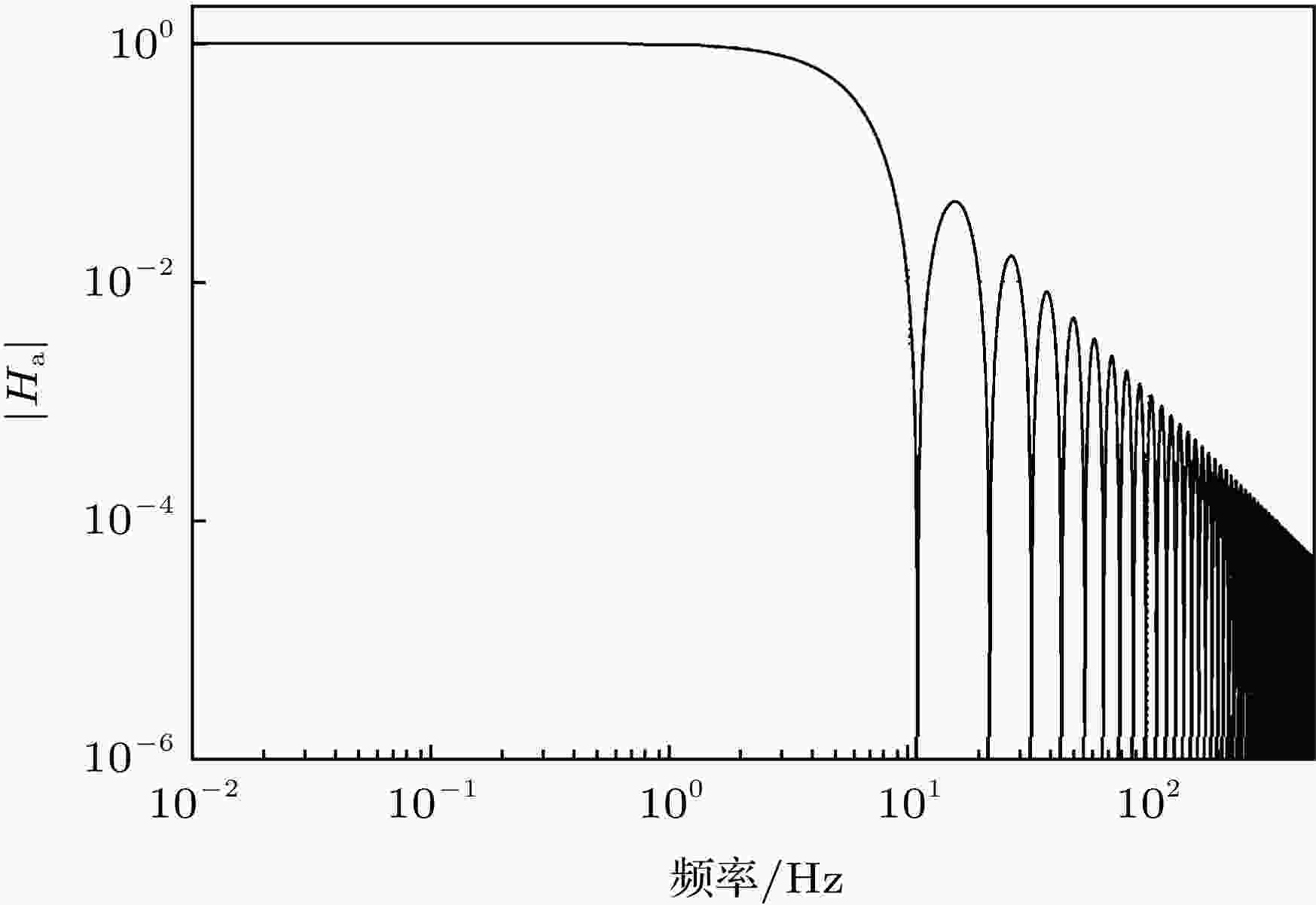图 4 T = 80 ms时, 振动噪声传递函数(随着振动频率的增大, 传递函数非常迅速地衰减)
Figure4. Transfor function of the vibration noise (T = 80 ms). The transfer function decays very rapidly as the vibration frequency increases.

2 -->

3.2.系统参数调试

在初次调节反馈算法时, 首先将放大系数$ A_{1} $, $ A_{2} $, $ A_{3} $和$ A_{4} $的初始值都设为0; 将用于滤除极低频成分的高通滤波器$ H_{3} $, $ H_{4} $, $ H_{5} $设定为0.016 Hz; 水平耦合系数$ C_{1} $与$ C_{2} $设定为0.01; 带通滤波中$ L_{1} $, $ L_{2} $的截止频率初始均设定为0.1 Hz; $ H_{1} $, $ H_{2} $的截止频率初始均设定为10 Hz. 接下来, 逐步增大$ A_{1} $, $ A_{3} $和$ A_{4} $, 并观察竖直方向(Z方向)以及水平方向(X方向和Y方向)振动信号的峰峰值, 直到峰峰值不再变小时, 得到$ A_{1} $, $ A_{3} $和$ A_{4} $的最佳值分别为0.11, 0.03和0.03. 再增大$ A_{2} $, 同时观察竖直方向振动信号的峰峰值, 当峰峰值不再变小时得到$ A_{2} $最佳值为9. 这样设定参数以后, 继续通过对$ L_{1} $, $ L_{2} $, $ C_{1} $, $ C_{2} $, $ H_{1} $—$ H_{5} $参数的细调来逐步优化振动噪声功率谱. 首先, 调节高通滤波器$ H_{3} $的截止频率并对比振动噪声功率谱, 使得在此振动下对干涉仪灵敏度的影响最小, 得到$ H_{3} $为0.001. 然后按照同样的方法分别调节带通滤波中$ L_{1} $, $ L_{2} $的截止频率和$ H_{1} $, $ H_{2} $的截止频率, 分别得到$ L_{1} $和$ L_{2} $的截止频率最优为6 Hz, $ H_{1} $和$ H_{2} $的截止频率最优为0.25 Hz. 然后分别调节$ H_{4} $和$ H_{5} $直至水平X方向与水平Y方向振动噪声谱最优, 得到$ H_{4} $和$ H_{5} $均为0.45 Hz. 最后调节$ C_{1} $和$ C_{2} $并对比竖直方向振动噪声功率谱, 使得在此振动下对干涉仪灵敏度的影响最小, 得到$ C_{1} $和$ C_{2} $均为0.01. 最后优化完毕得到的反馈参数如表1所列.

滤波器	截止频率 fc/Hz	反馈 系数	设定值	耦合 系数	设定值
$H_{1}$	0.25	$A_{1}$	0.11	$C_{1}$	0.01
$H_{2}$	0.25	$A_{2}$	9	$C_{2}$	0.01
$H_{3}$	0.001	$A_{3}$	0.03
$H_{4}$	0.45	$A_{4}$	0.03
$H_{5}$	0.45
$L_{1}$	6
$L_{2}$	6

表1反馈控制系统参数设定值
Table1.Parameters of the feedback control system

2 -->

3.3.振动抑制效果

当三维主动减振系统搭建完成后, 我们首先在中国科学技术大学上海研究院冷原子干涉仪研究室对其振动抑制效果进行了测试. 实验的地面未做任何的减振处理, 容易受到外界的地面振动的干扰. 最终测量得到的振动噪声谱如图5所示, 其中红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果. 利用图4的振动传递函数从测量数据中可以得到实验室地面上小于0.1 Hz频段的振动噪声为2.5 × 10^–7 m/s²/Hz^1/2, 0.1—1 Hz频段的振动噪声为2.6 × 10^–6 m/s²/Hz^1/2, 1—10 Hz频段的振动噪声为1.6 × 10^–4 m/s²/Hz^1/2, 大于10 Hz频段的振动噪声为2.5 × 10^–6 m/s²/Hz^1/2. 被动减振平台上小于0.1 Hz频段的振动噪声为1.6 × 10^–7 m/s²/Hz^1/2, 0.1—1 Hz频段的振动噪声为3.4 × 10^–6 m/s²/Hz^1/2, 1—10 Hz频段的振动噪声为4.4 × 10^–6 m/s²/Hz^1/2, 大于10 Hz频段的振动噪声为1.1 × 10^–7 m/s²/Hz^1/2. 在加上主动反馈减振以后, 小于0.1 Hz频段的振动噪声被压制到了1.4 × 10^–8 m/s²/Hz^1/2, 0.1—1 Hz频段的振动噪声被压制到了1.1 × 10^–8 m/s²/Hz^1/2, 1—10 Hz频段的振动噪声压制到了7.1 × 10^–8 m/s²/Hz^1/2, 大于10 Hz²/Hz^1/2, 大于10 Hz频段的振动噪声被压制到了4.8 × 10^–8 m/s²/Hz^1/2. 在原子干涉仪最敏感的小于10 Hz的频段, 其振动噪声被压制到了7.3 × 10^–8 m/s²/Hz^1/2, 约被压制为地面上的1/2200, 为被动减振平台上的1/75. 通过图5的振动噪声谱以及图4的振动传递函数, 计算得到中国科学技术大学上海研究院冷原子干涉仪研究室地面上的振动噪声对原子干涉仪灵敏度的影响为1.6 × 10⁴ μGal/Hz^1/2, 主动减振后为8.8 μGal/Hz^1/2, 约降低为地面上的1/1800. 即将振动噪声对冷原子重力仪灵敏度的影响降低了3个数量级.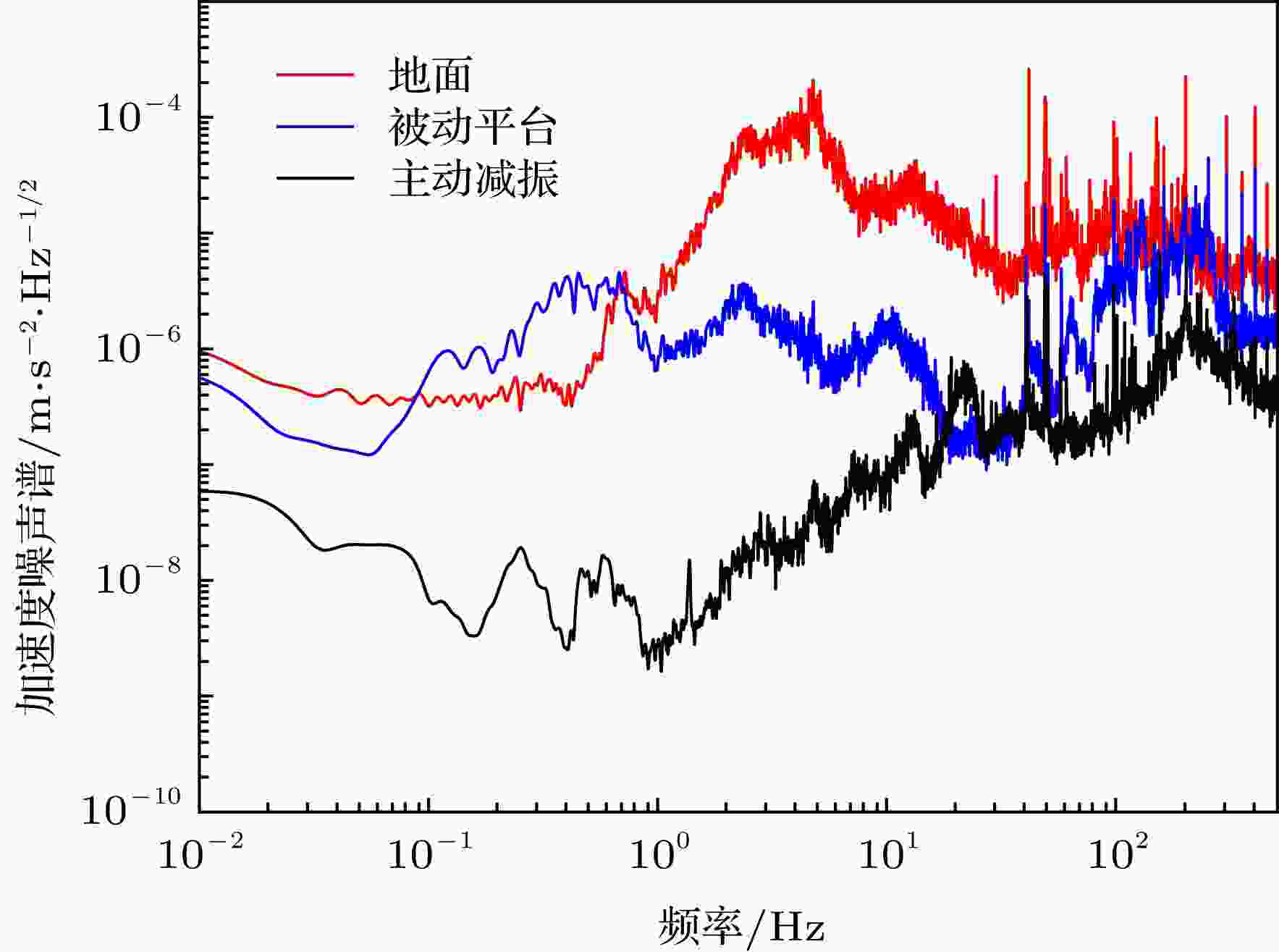
图 5 中国科学技术大学上海研究院冷原子干涉仪研究室测试的三维主动减振效果示意图(红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果)
Figure5. Performance of the three-dimension active vibration isolator at Shanghai branch, University of Science and Technology of China. The red solid line is the vibration acceleration noise spectrum of the laboratory ground, the bule soild line is the result of the passive isolator, the black solid line is the result of active vibration isolator.

我们将主动减振系统从上海搬运到北京, 在北京的中国计量院重力精测实验室(II)重力标定点位对主动减振系统的振动抑制效果进行了测试, 结果如图6所示. 其中红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果. 相对于我们在中国科学技术大学上海研究院冷原子干涉仪研究室而言, 中国计量院重力精测实验室的地面振动要小得多. 利用图4所示的传递函数从测量数据中可以得到实验室地面上小于0.1 Hz频段的振动噪声为1.1 × 10^–8 m/s²/Hz^1/2. 0.1—1 Hz频段的振动噪声为1.7 × 10^–7 m/s²/Hz^1/2, 而1—10 Hz频段的振动噪声为1.1 × 10^–6 m/s²/Hz^1/2, 大于10 Hz频段的振动噪声为1.9 × 10^–7 m/s²/Hz^1/2. 被动减振平台上小于0.1 Hz频段的振动噪声为1.3 × 10^–8 m/s²/Hz^1/2, 0.1—1 Hz频段的振动噪声为4.6 × 10^–7 m/s²/Hz^1/2, 1—10 Hz频段的振动噪声为8.1 × 10^–8 m/s²/Hz^1/2, 大于10 Hz频段的振动噪声为1.1 × 10^–8 m/s²/Hz^1/2. 在加上主动反馈减振后, 小于0.1 Hz频段的振动噪声为2.4 × 10^–9 m/s²/Hz^1/2, 0.1—1 Hz频段的振动噪声被压制到了2.4 × 10^–9 m/s²/Hz^1/2, 1—10 Hz频段的振动噪声压制到了3.4 × 10^–9 m/s²/Hz^1/2, 高于10 Hz频段的振动噪声为1.8 × 10^–8 m/s²/Hz^1/2. 在原子干涉仪最敏感的小于10 Hz的频段的振动噪声被压制到了4.8 × 10^–9 m/s²/Hz^1/2, 约被压制为地面上的1/230, 为被动减振平台上的1/100. 而在这里主动减振的压制效果没有上海的好, 是因为在0.5—2 Hz频段振动已经到达了高精度地震计的本底了. 从图4的传递函数可以看到10 Hz以后的振动对原子干涉仪灵敏度的影响在非常迅速地衰减, 超过50 Hz的高频段振动对原子干涉仪灵敏度的影响已很小. 利用图4所示的振动传递函数和图6所示的振动噪声谱, 计算得到在中国计量院重力精测实验室(II)地面上的振动噪声对原子干涉仪灵敏度的影响为113 μGal/Hz^1/2, 主动减振后为1.9 μGal/Hz^1/2, 即振动噪声约降低为地面上的1/60. 从评估结果来看, 我们的主动减振系统能将振动的噪声压制近2个数量级.
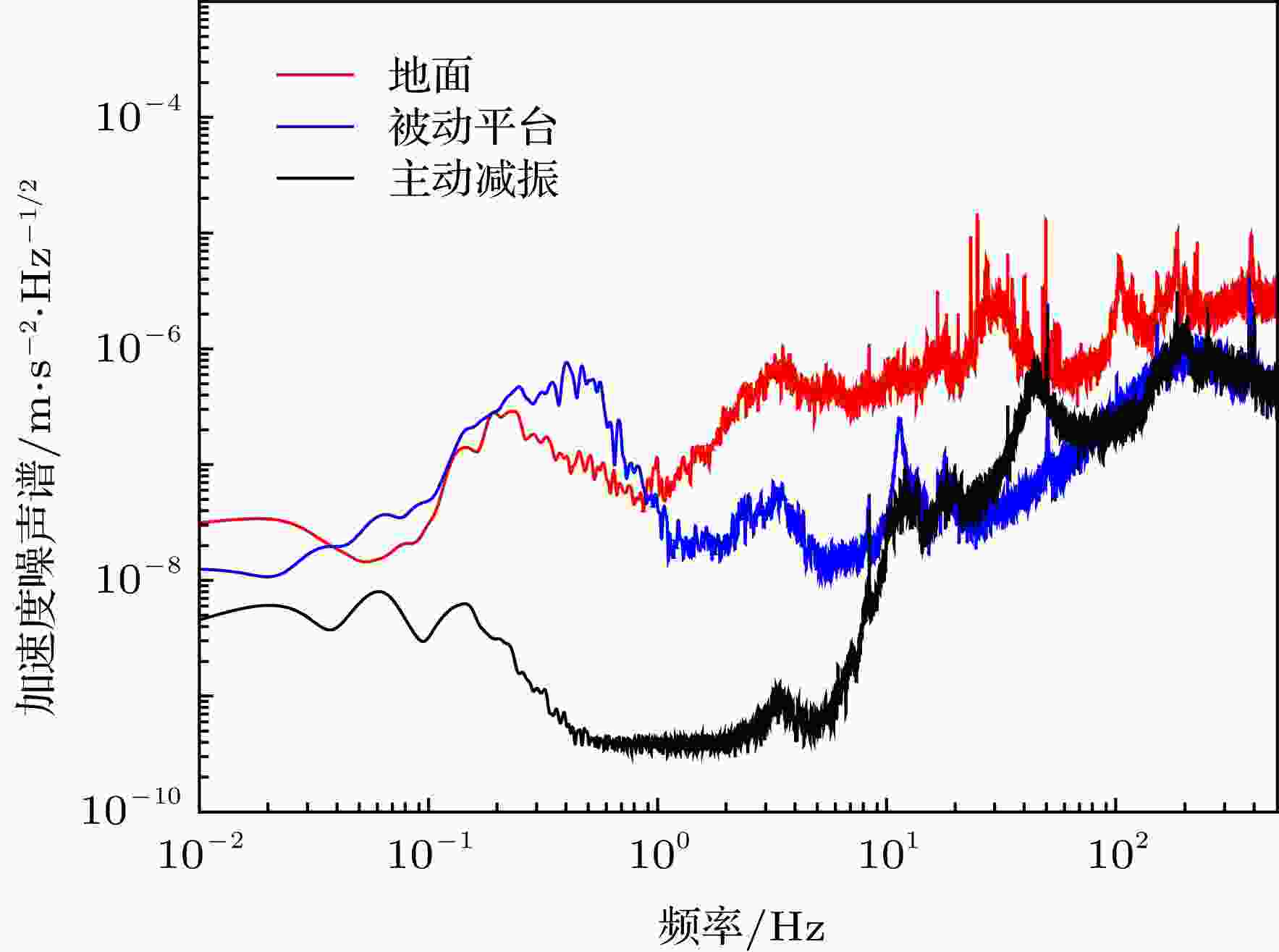图 6 中国计量院重力精测实验室(II)重力测量点位测试的三维主动减振效果图(红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果)
Figure6. Performance of the three-dimension active vibration isolator at Precision Measurement Laboratory II of Gravity, National Institute of Metrology, China. The red solid line is the vibration acceleration noise spectrum of the laboratory ground, the bule soild line is the result of the passive isolator, the black solid line is the result of active vibration isolator.

在中国计量院重力精测实验室(II)重力标定点位测得的主动减振平台X方向与Y方向的减振效果如图7(a)和图7(b)所示. 经过主动减振后小于10 Hz频段上的振动噪声被压制为地面上的1/6.
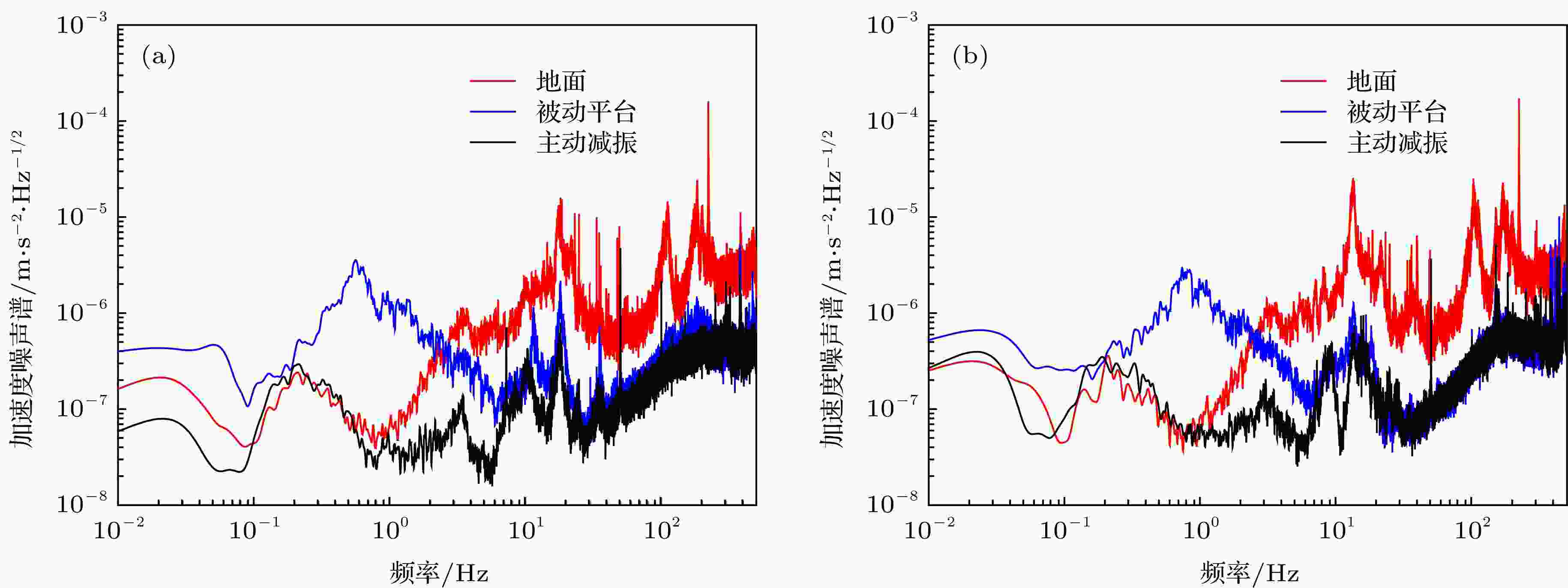图 7 水平X方向与Y方向的减振效果(红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果)　(a) X方向的减振效果; (b) Y方向的减振效果
Figure7. Performance of the three-dimension active vibration isolator in X and Y directions: (a) The performance in X direction; (b) the performance in Y direction. The red solid line is the vibration acceleration noise spectrum of the laboratory ground, the bule soild line is the result of the passive isolator, the black solid line is the result of active vibration isolator.

2 -->

3.4.应用于冷原子干涉仪

本文的冷原子干涉重力仪采用原子下落式的结构, 利用三束拉曼光$ ({\text{π}} /2\text{-} {\text{π}} \text{-} {\text{π}} /2) $对原子进行相干的分束、反射、合束操纵, 最后通过测量原子荧光提取出重力信息. 首先, 将干涉仪的探头直接放置于地面上进行重力测量, 图8(a)为在中国计量院重力精测实验室(II)重力标定点位直接放地面上连续21 h的重力加速度g值测量结果. 然后给干涉仪的探头换上主动减振系统后进行重力测量, 图8(b)为在相同的标定点位主动减振后连续7 h的重力加速度g值测量数据. 图8中每个黑色的点为一次g值的测量结果, 每次g值测量用时32 s. 可以看到图8中黑色的点所示的测量数据与红色实线所示的理论潮汐值趋势完全一致, 图中的残差(residue)是测量数据减去理论潮汐值后得到的差值, 可以看到在加上主动减振系统后残差明显地减小了.
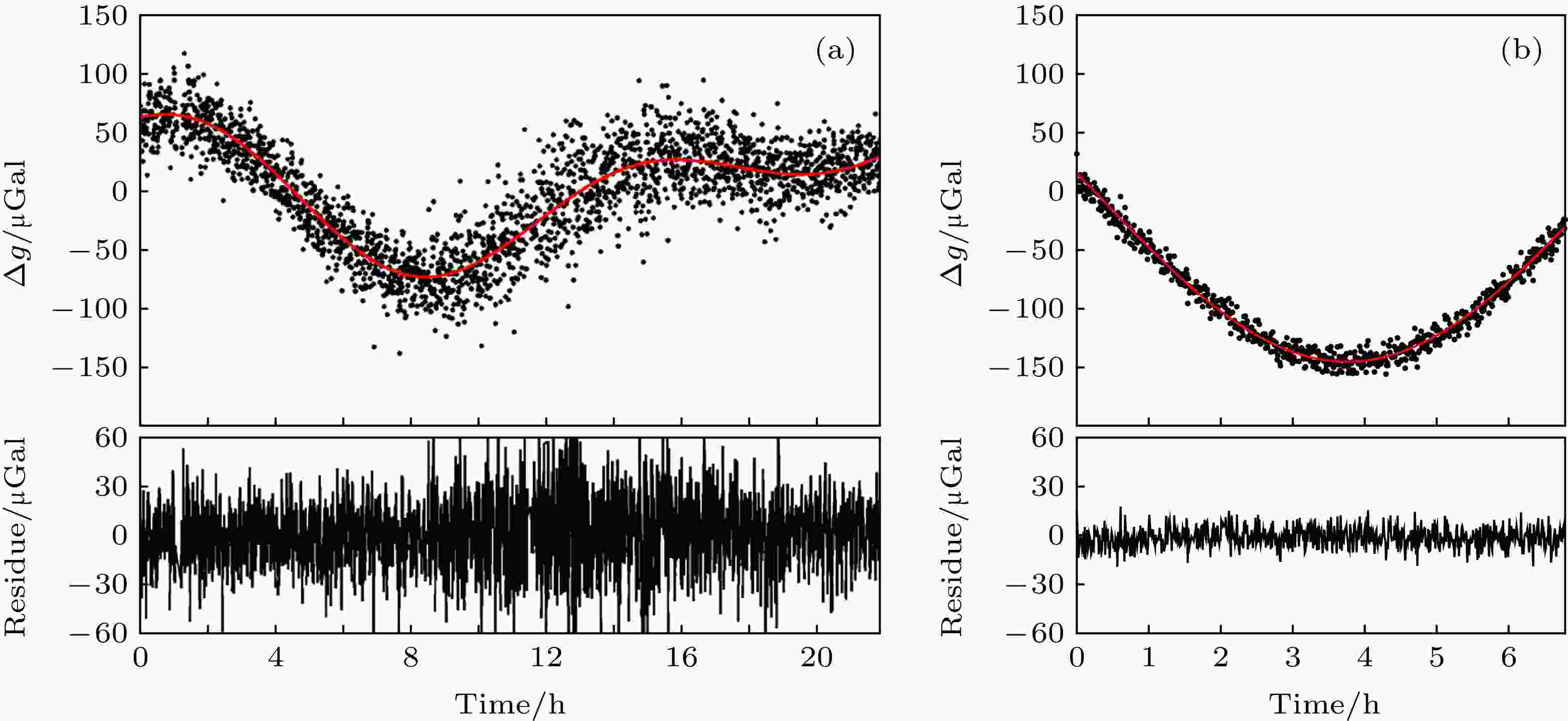图 8 重力加速度g值的测量结果及其与理论值的残差(黑色的点为实测的数据, 红色的实线为理论潮汐模型)　(a)将干涉仪探头直接放置于地面上测量得到的结果; (b)对干涉激光反射镜进行主动减振后测量得到的结果
Figure8. Measured and theoretical data of tidal signal and the difference between them: (a) The result obtained by placing the atom interferometry probe directly on the ground; (b) the result obtained by actively vibration isolating the interferometric laser reflector. The black dot is the measured data, and the red line is the theoretical tidal model.

利用Allan方差对g值的测量结果进行了进一步的评估. 图9中黑色实点为干涉仪探头直接放在地面上得到的残差(residue)的Allan方差评估结果, 评估结果显示其测量灵敏度为117 μGal/Hz^1/2. 红色实点为对干涉激光反射镜进行主动减振后得到的残差(residue)的Allan方差评估结果, 评估结果显示进行主动减振后原子重力仪测量灵敏度为35 μGal/Hz^1/2, 比直接放地面上的测量结果好了3倍以上. 目前, 原子干涉仪灵敏度主要受限于探测噪声. 从对比结果来看, 本文的主动减振系统实际应用时也有显著的效果, 使用主动减振系统后原子干涉仪测量灵敏度明显变好.
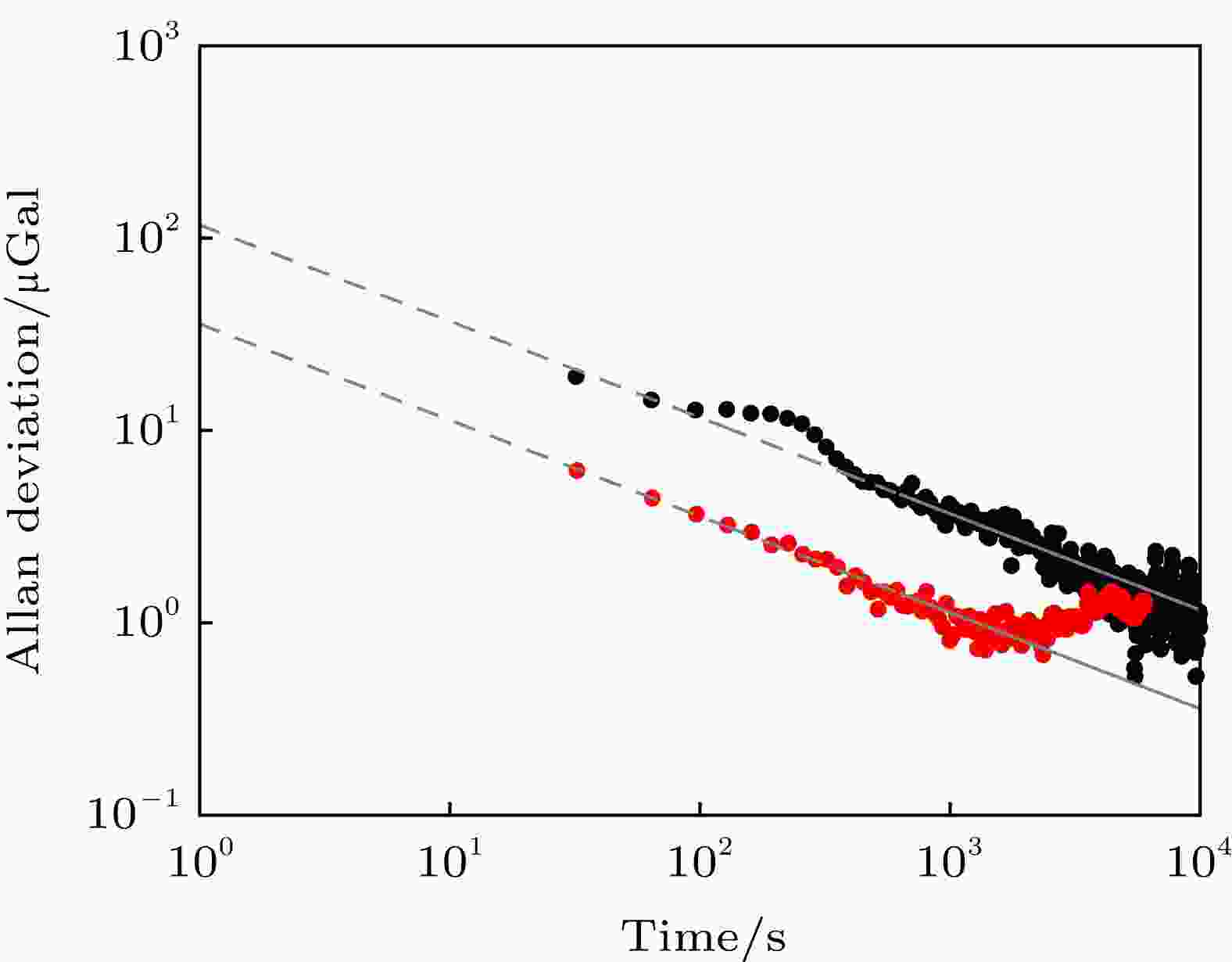图 9 Allan方差评估结果(黑色实点为干涉仪探头直接放地面上得到的残差(Residue)的Allan方差评估结果, 评估结果显示原子重力仪直接放地面上的测量灵敏度为117 μGal/Hz^1/2; 红色实点为对干涉激光反射镜进行主动减振后得到的残差(Residue)的Allan方差评估结果, 评估结果显示进行主动减振以后原子干涉仪测量灵敏度为35 μGal/Hz^1/2 )
Figure9. Allan deviations of the residual gravity accelerations. The black solid dot is the Allan deviation of the residual obtained by placing the atom interferometry probe directly on the ground. The result shows the sensitivity for the atom interferometry in this condition is 117 μGal/Hz^1/2. The red solid dot is the Allan deviation of the residual obtained by actively vibration isolating the interferometric laser reflector. The result shows the sensitivity for the atom interferometry in this condition is 35 μGal/Hz^1/2.

针对可移动原子干涉仪而设计研制了一套易于搬运的三维主动减振系统. 在经历了往返上海至北京的多次搬运后, 本套系统均能迅速恢复并能稳定运行. 通过实施设计的综合反馈算法, 在地面振动噪声水平较高的中国科学技术大学上海研究院, 振动噪声对原子干涉仪灵敏度的影响被压制到了8.8 μGal/Hz^1/2, 约降低为地面上的1/1800. 在原子干涉仪敏感的小于10 Hz的频段, 振动噪声被压制到了7.3 × 10^–8 m/s²/Hz^1/2, 约被压制为地面上的1/2200. 在振动环境安静的中国计量科学研究院, 振动噪声对原子干涉仪灵敏度的影响被压制到了1.9 μGal/Hz^1/2, 约降低为地面上的1/60. 在原子干涉仪敏感的小于10 Hz的频段, 振动噪声被压制到了4.8 × 10^–9 m/s²/Hz^1/2, 约被压制为地面上的1/230. 在0.5—2 Hz频段剩余振动已经到了高精度地震计的本底. 本装置在三个维度的宽频带范围上取得了好的振动压制效果, 振动噪声已不是限制干涉仪灵敏度的主要因素. 该隔振装置同样适用于精密激光干涉仪、原子钟、光钟等其他的精密测量装置.
感谢中国计量院吴书清博士、王启宇博士及重力标准测量团队提供测试场地, 以及在测量与标定过程中给予的大力协助.