摘要:提出一种新型的基于半导体光纤环形腔激光器(semiconductor fiber ring laser, SFRL)全光超宽带(ultra-wideband, UWB)信号源的方案, 该方案可以同时产生3路高斯脉冲一阶导数脉冲(monocycle) UWB信号. 建立了这种全光UWB信号源的宽带理论模型, 通过数值模拟的方法研究SFRL中的半导体光放大器(semiconductor optical amplifier, SOA)的注入电流、激射光波长、输入信号光功率和波长对monocycle信号性能的影响. 结果表明: SOA的注入电流在200—220 mA时可以获得对称性较好的monocycle脉冲; 输出monocycle脉冲平均功率和正、负脉冲振幅随激射光波长增加而增加; 较低的输入信号光功率可以获得性能较好的monocycle信号; 输入信号光波长对输出monocycle信号有一定的影响, 但影响很小.
关键词: 超宽带/
高斯脉冲一阶导数脉冲/
半导体光纤环形腔激光器/
交叉增益调制

English Abstract

全文HTML

--> --> -->

超宽带(ultra-wideband, UWB)射频技术是一种短距离无线传输技术, 具有高速率、低功耗和低成本的优点^[1], 但其发射功率受限制, 传输距离一般限制在几米到几十米. 为了克服这个不足, 人们提出了在光纤中传输UWB信号(UWB-over-fiber)的技术, 并开始研究光学产生UWB信号的技术.
高斯脉冲的一阶导数(monocycle)、二阶导数(doublet)及高阶导数因为没有直流分量, 只要在时域上选择合适的脉冲宽度就能得到符合美国联邦通信委员会(Federal Communications Commission, FCC)定义的UWB信号频谱. 利用调制出的极性相反、时间相对延迟的脉冲叠加, 形成高斯脉冲的导数, 从而获得UWB信号^[2-13], 文献[14]利用高斯脉冲在半导体光放大器(semiconductor optical amplifier, SOA)中传输峰值向前倾的特点, 两个极性相反的脉冲直接叠加不会全部抵消, 从而形成monocycle信号, 由于极性相反的脉冲由不同波长光承载, 传输一段距离后会因色散发生形变; 利用相位调制和频率鉴别器相结合, 通过选择合适的波长获得各种高斯脉冲的导数^[15-19]; 利用SOA的增益饱和效应, 负脉冲信号通过SOA放大, 并在脉冲的上升沿产生过冲(overshoot)形成一个正脉冲, 从而形成高斯脉冲导数波形^[6,20-23].
目前光学产生UWB方法主要产生的是单一信号源, 但对输出多路UWB信号源的研究少. 文献[24]利用光子晶体光纤中四波混频效应(four-wave mixing, FWM)同时产生4路monocycle信号, 但该方案需要输入3路光源, 且转换效率低. 本文提出一种基于半导体光纤环形腔激光器(semiconductor fiber ring laser, SFRL)的全光UWB信号源方案, 可以同时产生3路monocycle信号, 而只需要1束输入光信号, 结构简单且适合应用于广播式通信场景. 输出的3路monocycle信号均承载在一个波长上, 避免正、负脉冲由不同波长组成, 在光纤传输受到色散影响导致正、负脉冲产生相对时延导致变形. 本文建立了这种全光UWB信号源的宽带理论模型, 通过数值模拟的方法研究SFRL中的SOA的注入电流、激射光波长、输入信号光功率和波长对monocycle信号的影响.

图1为基于SFRL全光广播式UWB信号源的结构示意图. SFRL由 SOA、两个耦合器、偏振控制器、隔离器和梳状滤波器组成. SOA是SFRL的增益介质、偏振控制器对输入SOA的光进行偏振控制; 隔离器可以防止环中发生反向反射, 使SFRL工作在行波状态; 梳状滤波器具有许多间隔相同的通带和阻带, 是SFRL的选频元件. 基于SFRL全光广播式UWB信号源的工作原理: 当带有调制信号的信号光通过耦合器1输入到SFRL, 与SFRL的激射光一起输入到SOA中, 在SOA中发生交叉增益调制(cross-gain modulation, XGM), 激射光被调制成反相的高斯脉冲, 由于增益饱和效应, 反相高斯脉冲在SOA中传播产生一个过冲, 从而形成monocycle脉冲. 通过对梳状滤波器的波道数量设置, 可以实现多路monocycle信号产生.
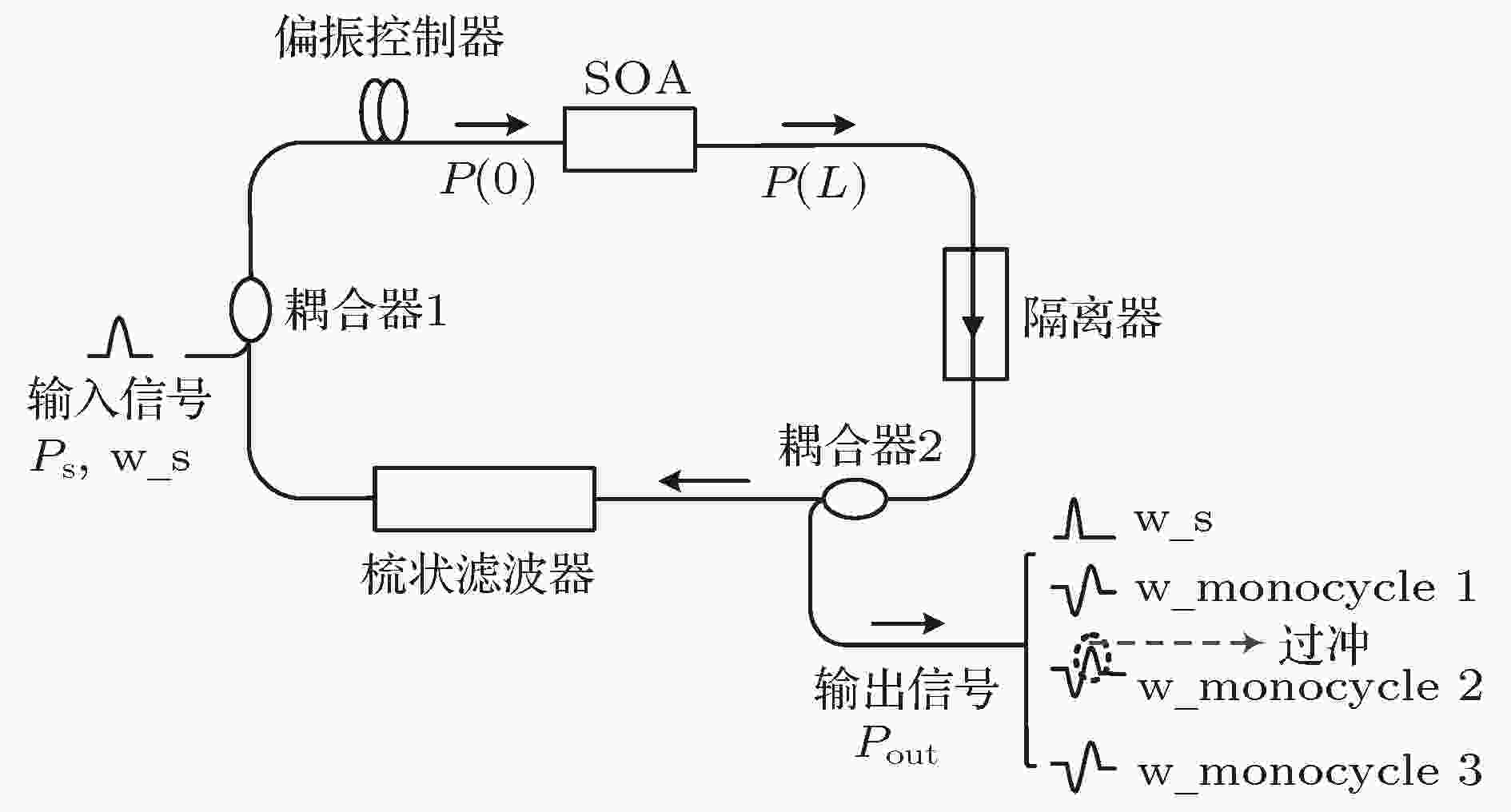图 1 基于SFRL全光广播UWB信号源的结构示意图
Figure1. The structure of all-optical UWB broadcast signal source based on SFRL.

2

-->

3.1.增益模型

SOA作为SFRL核心部件, 其材料增益系数$g(v,N)$和受激发射系数${R_{{\rm{st}}}}\left( {\nu ,N} \right)$可以表示为^[25-27]:

$\begin{split}g\left( {\nu ,N} \right) = & \frac{{{e^2}{{\left| M \right|}^2}}}{{4{{\text{π}}^{\rm{2}}}{\varepsilon _0}m_0^2c{n_{\rm{a}}}\nu }}{\left( {\frac{{8{{\text{π}}^{\rm{2}}}}}{{{h^2}}}} \right)^{\frac{3}{2}}}{\left( {h\nu - {E_{\rm{g}}}} \right)^{\frac{1}{2}}}\\& \times \left\{m_{{\rm{rh}}}^{\frac{3}{2}}\left[ {{f_{{\rm{ch}}}}\left( \nu \right) + {f_{{\rm{vh}}}}\left( \nu \right) - 1} \right] \right.\\& \left. \left.+ m_{{\rm{rl}}}^{\frac{3}{2}}\left[ {{f_{{\rm{cl}}}}\left( \nu \right) + {f_{{\rm{vl}}}}\left( \nu \right) - 1} \right] \right.\right\},\end{split}$

$\begin{split}{R_{{\rm{st}}}}\left( {\nu ,N} \right) = & \frac{{{e^2}{{\left| M \right|}^2}}}{{4{{\text{π}}^{\rm{2}}}{\varepsilon _0}m_0^2c{n_{\rm{a}}}\nu }}{\left( {\frac{{8{{\text{π}}^{\rm{2}}}}}{{{h^2}}}} \right)^{\frac{3}{2}}}{\left( {h\nu - {E_{\rm{g}}}} \right)^{\frac{1}{2}}}\\ &\times \left[ {m_{{\rm{rh}}}^{\frac{3}{2}}{f_{{\rm{ch}}}}\left( \nu \right){f_{{\rm{vh}}}}\left( \nu \right) + m_{{\rm{rl}}}^{\frac{3}{2}}{f_{{\rm{cl}}}}\left( \nu \right){f_{{\rm{vl}}}}\left( \nu \right)} \right],\end{split}$

${m_{{\rm{rh}}}} = \frac{{{m_{\rm{c}}}{m_{{\rm{hh}}}}}}{{{m_{\rm{c}}} + {m_{{\rm{hh}}}}}}, $

${m_{{\rm{rl}}}} = \frac{{{m_{\rm{c}}}{m_{{\rm{lh}}}}}}{{{m_{\rm{c}}} + {m_{{\rm{lh}}}}}}, $

其中$|{{M}}{|^2}$为动量矩阵, e为电子电荷量, h为普朗克常量, ${\varepsilon_0}$为真空中介电常数, ${m_0}$为自由电子质量, c为真空中的光速, ${f_{{\rm{ch}}}}\left( \nu \right)$和${f_{{\rm{vh}}}}\left( \nu \right)$分别为导带和价带中重空穴的狄拉克分布, ${f_{{\rm{cl}}}}\left( \nu \right)$和${f_{{\rm{vl}}}}\left( \nu \right)$分别为导带和价带中轻空穴的狄拉克分布, ${n_{\rm{a}}}$为折射率, ${E_{\rm{g}}}$为带隙能量, $ {m_{\rm{c}}} $为导带中电子有效质量, ${m_{{\rm{hh}}}}$为价带中重空穴有效质量, ${m_{{\rm{lh}}}}$为价带中轻空穴有效质量.
2 -->

3.2.光传输方程

在SFRL中, SOA作为非线性介质, 所以在数值模拟中主要研究光在SOA中的传输. 在建模过程中, 对SOA采用分段模型, 将整个SOA在沿着光传输方向分成n小段, 当n足够大时, 每小段的载流子浓度分布近似为均匀, 则在第i小段中, 信号光和第j束波长激射光的传输方程可以分别表示为:

$\frac{{{\rm{d}}{A_{{\rm s},i}}}}{{{\rm{d}}z}} = \frac{1}{2}\left[ {\frac{{\varGamma {g_{{\rm s},i}}}}{{1 + \frac{{{P_i}}}{{{P_{{\rm{sat}}}}}}}}\left( {1 - {\rm{i}}{\alpha _{{\rm s},i}}} \right) - {\alpha _{{\rm{int}}}}} \right]{A_{{\rm s},i}} + {\mu _{{\rm s},i}}\left( {z,t} \right), $

$\frac{{{\rm{d}}{A_{j,i}}}}{{{\rm{d}}z}} = \frac{1}{2}\left[ {\frac{{\varGamma {g_{j,i}}}}{{1 + \frac{{{P_i}}}{{{P_{{\rm{sat}}}}}}}}\left( {1 - {\rm{i}}{\alpha _{j,i}}} \right) - {\alpha _{{\rm{int}}}}} \right]{A_{j,i}} + {\mu _{j,i}}\left( {z,t} \right), $

式中A代表光场的慢幅变化, 下标i表示SOA的第i个子段; $\varGamma $为限制因子; ${\alpha _{{\rm{int}}}}$为SOA的内部损耗系数; ${g_{{\rm s},i}}$和${g_{j,i}}$ (j = p1, p2, p3)表示第i子段中光波的材料增益系数; ${\alpha _{{\rm s},i}}$和${\alpha _{i,j}}$是线宽增强因子, ${P_{{\rm{sat}}}}$为饱和功率.
放大自发辐射(amplifier spontaneous emission, ASE)噪声${\mu _{{\rm s},i}}(z,t)$和${\mu _{j,i}}(z,t)$ ($j = p1,p2,p3$)表示为两个统计学上的高斯随机分布过程, 自相关函数为:

$\begin{split} &\left\langle {{\mu _{{\rm s},i}}\left( {z,t} \right)\mu _{{\rm s},i}^*\left( {z',t'} \right)} \right\rangle \\ =\; & \beta \varGamma {R_{{\rm{sp}}}}\delta \left( {t - t'} \right)\delta \left( {z - z'} \right)\left( {{\nu _{\rm{g}}}{E_{\rm s}}{A_{{\rm{cross}}}}} \right),\end{split}$

$\begin{split} & \left\langle {{\mu _{j,i}}\left( {z,t} \right)\mu _{j,i}^*\left( {z',t'} \right)} \right\rangle\\ = & \beta \varGamma {R_{{\rm{sp}}}}\delta \left( {t - t'} \right)\delta \left( {z - z'} \right)\left( {{\nu _{\rm{g}}}{E_j}{A_{{\rm{cross}}}}} \right),\\ & \left( {j = p1,p2,p3} \right),\end{split}$

式中$\beta $为自发辐射耦合因子, R_sp为自发辐射率, ${\nu _{\rm{g}}}$为群速度, ${E_{\rm s}}$和${E_j}$为光子能量, A_cross为有源区的横截面积.
2 -->

3.3.载流子速率方程

载流子速率方程如下:

$\begin{split} \frac{{{\rm{d}}{N_i}}}{{{\rm{d}}t}} = & \frac{I}{{ewdL}} - \left( {{c_1}{N_i} + {c_2}N_i^2 + {c_3}N_i^3} \right)\\ & - {g_{{\rm s},i}}\frac{{{G_{{\rm s},i}} - 1}}{{\ln {G_{{\rm s},i}}}}\frac{{{{\left| {{A_{{\rm s},i}}} \right|}^2}{\lambda _{\rm s}}}}{{hcwd}} - {g_{j,i}}\frac{{{G_{j,i}} - 1}}{{\ln {G_{j,i}}}}\frac{{{{\left| {{A_{j,i}}} \right|}^2}{\lambda _j}}}{{hcwd}}, \\ & \left( {j = p1,p2,p3} \right),\end{split} $

式中I为SOA的注入电流; L, w和d分别为SOA有源区的长、宽和厚度; ${c_1}$, ${c_2}$, ${c_3}$分别为缺陷和俘获中心引起的非辐射复合系数、双分子复合系数和Auger复合系数; ${G_{j,i}}$为经过SOA第i子段获得的增益, 表示为

$\overline {{g_{j,i}}} = \varGamma \left( {{g_{j,i}} - {\alpha _{\rm a}}} \right) - \left( {1 - \varGamma } \right){\alpha _{\rm c}} - {\alpha _{{\rm{scat}}}},$

${G_{j,i}} = \exp (\overline {{g_{j,i}}} l).$

由于SFRL中隔离器的单向传输性, 因此边界条件为

${A_j}\left( 0 \right) = {A_j}\left( L \right){\varepsilon _1}{k_1}{k_2}, $

其中${\varepsilon _1}$, ${k_1}$, ${k_2}$分别为SFRL中不包括两个耦合器的耦合比的所有损耗, 耦合器1的耦合比和耦合器2的耦合比.

利用前面建立的宽带理论模型对这种全光广播UWB信号源进行数值模拟, 计算所用参数如表1所示. 输入信号波特率为10 GBd/s无啁啾理想归零高斯脉冲; 输入码元序列为周期性1000000000 (即码元“1”的重复频率为1 GHz); SOA的注入电流为200 mA; 通过设置梳状滤波器, 设置3路激射光的长分别为1538, 1540 nm和1542 nm; 输入信号光波长为1546 nm, 输入光功率为–7 dBm.

参量符号	取值
有源区长度L/10–4 m	5.5
有源区宽度w/10–6 m	3.3
有源区厚度d/10–7 m	1.5
非辐射符合系统${c_1}$/108 s–1	1.5
双分子复合系数${c_2}$/10–16 m3·s–1	2.5
Auger复合系数${c_3}$/10–40 m6·s–1	1.5
光限制因子Γ	0.3
折射率na	3.22
饱和功率${P_{{\rm{sat}}}}$/10–2 W	1.0
有源区损耗${\alpha _{{\rm{in}}}}$/104 m–1	1.4
涂覆层损耗${\alpha _{\rm{c}}}$/103 m–1	2.0
散射损耗${\alpha _{\rm{c}}}$/103 m–1	1.0
导带中电子有效质量mc/10–32 kg	4.1
价带中电子有效质量mhh/10–31 kg	4.19
价带中空穴有效质量mlh/10–33 kg	5.06
不包含两个耦合器耦合比的所有损耗${\varepsilon _1}$	0.4
耦合器1的耦合比${k_1}$	0.5
耦合器2的耦合比${k_2}$	0.5
ASE谱的起始波长${\lambda _1}$/10–6 m	1.40
ASE谱的结束波长${\lambda _{\rm{m}}}$/10–6 m	1.60
ASE谱的分段数m	10
SOA的分段数n	10
自发辐射因子β/10–5	2
群速度${\nu _{\rm{g}}}$/107 m·s–1	7.5

表1计算采用的参数值
Table1.Parameters used in the mode.

图2给出了3路输出monocycle信号的时域波形和功率谱, 可以看出输出monocycle信号时域波形对称性良好, 如图2(a)—(c)所示; 3路输出monocycle信号的中心频率(f_c)分别为6.5, 6.0和6.5 GHz, –10 dB带宽(band width, BW)分别为10, 11和10 GHz, 相对带宽(–10 dB频率带宽除以中心频率)分别为153.85%, 183.33%和153.85%, 均符合FCC对UWB信号的定义, 如图2(d)—(f)所示.
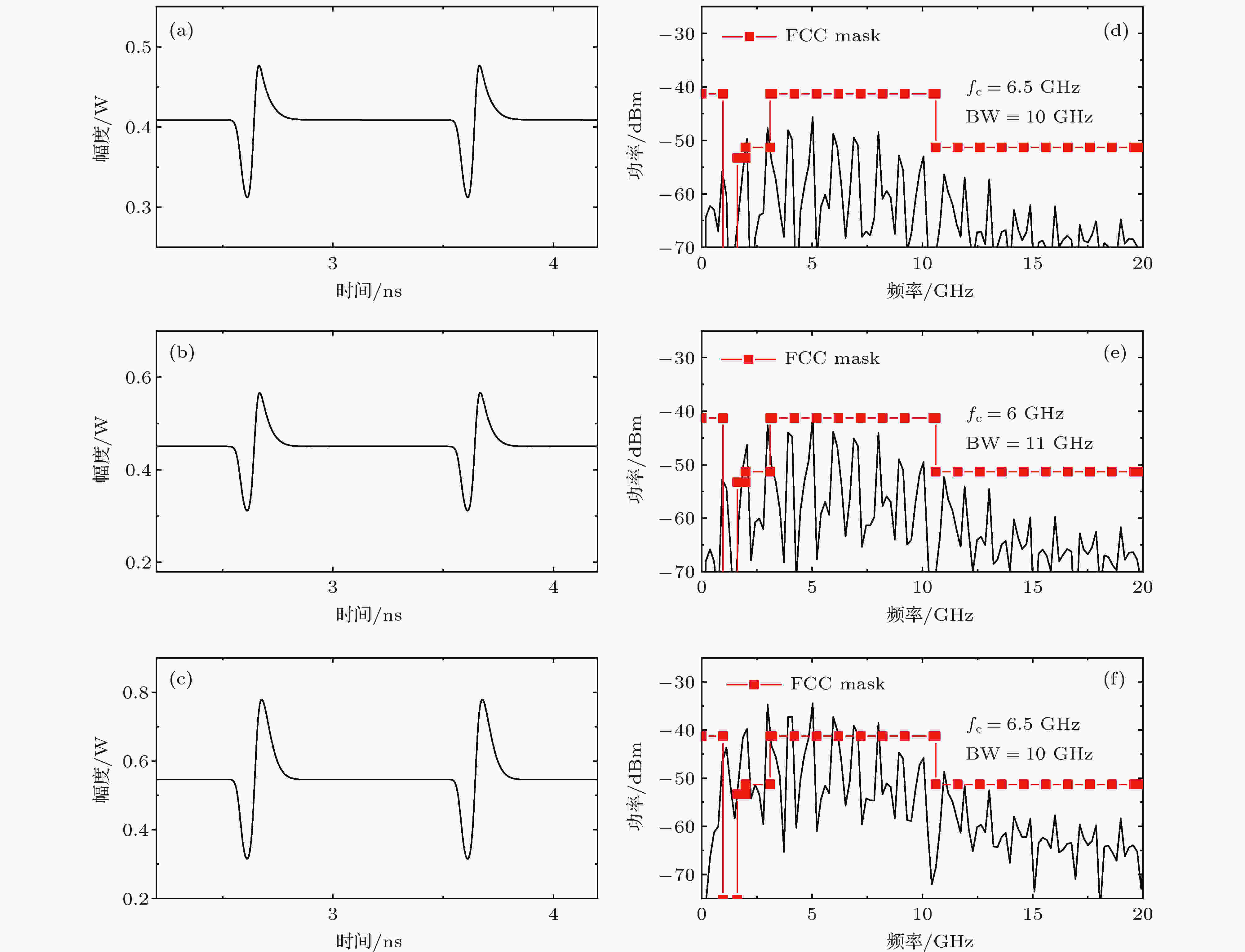图 2 基于SFRL全光广播式monocycle信号源的输出　(a), (b), (c) 激射光波长分别为1538, 1540, 1542 nm对应的时域波形; (d), (e), (f)激射光波长分别为 1538, 1540, 1542 nm对应的功率谱
Figure2. The output of all-optical broadcast monocycle signal source based on SFRL: The waveform of monocycle signals when the lasing light wavelength of 1538 nm (a), 1540 nm (b), 1542 nm (c); the power spectrum of monocycle signals when the lasing light wavelengthof 1538 nm (d), 1540 nm (e), 1542 nm (f).

另外, 从图2(a)—(c)还可以看出, 随着激射光波长增加, 输出monocycle信号的平均光功率和正、负脉冲幅值也逐渐增加, 这是由于SOA对不同波长放大增益不同. 当注入电流为200 mA时, SOA内部载流子形成稳态分布时, 不同波长的增益系数曲线如图3(a)所示, 此时峰值对应的波长为1549 nm, 由于信号光、激射光的波长均小于1549 nm, 因此, 增益系数随着波长的增大而增大; 在SOA输出端, 3路激射光增益-时间曲线如图3(b)所示, 此时增益系数随着激射光波长增加而增加, 说明信号光、激射光在SOA传输过程中虽然消耗了载流子, 但在SOA的输出端, 3路monocycle信号光的波长都小于增益-波长曲线的峰值波长, 因此输出monocycle信号的正、负脉冲幅度随着monocycle信号光的波长增加而增加.
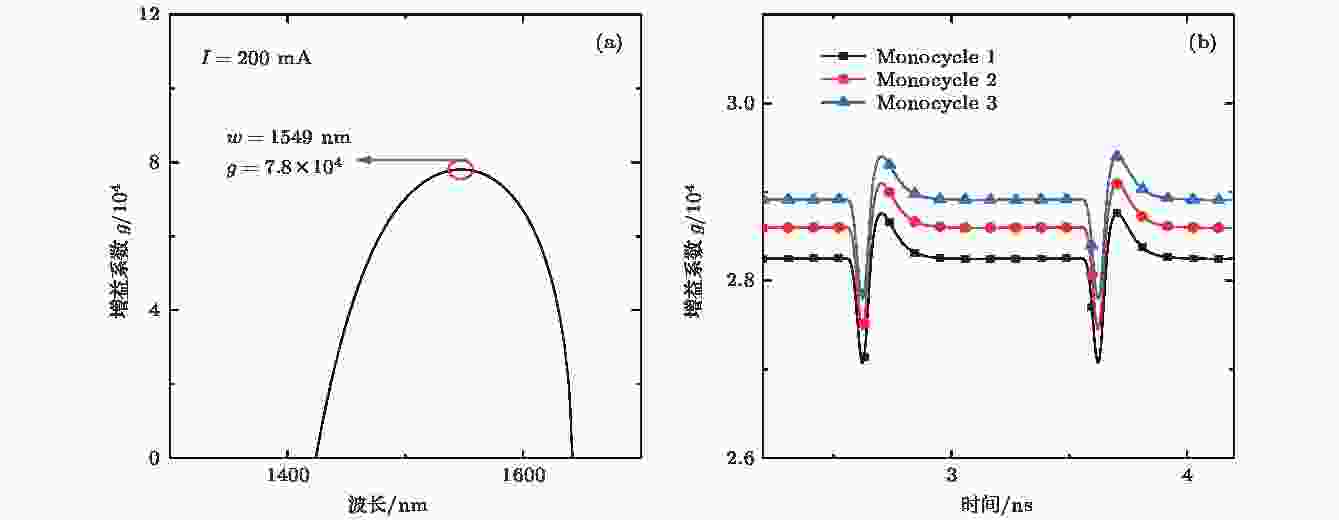图 3 (a)注入电流为200 mA时波长-增益系数曲线; (b)在SOA输出端激射光1?3路的增益-时间曲线
Figure3. (a) Wavelength-gain coefficient curve with 200 mA SOA bias current; (b) the gain-time curve of monocycle 1?3 at the SOA output.

保持其他参数不变, 分别设置SOA的注入电流为180, 210 mA和240 mA, 输出的monocycle信号时域波形和功率谱如图4所示. 当SOA的注入电流比较小时, 由于此时注入载流子浓度低, 增益饱和效果不明显, 产生过冲幅度很小, 如图4(a)所示; 随着SOA的注入电流增大, 过冲幅度慢慢增大, 并与负脉冲形成很好的对称性, 如图4(b)所示; 当注入电流继续增大, 由于载流子浓度过大, 正脉冲得到进一步放大, 导致正脉冲的幅度大于负脉冲的幅度, 输出信号对称性变差, 如图4(c)所示.
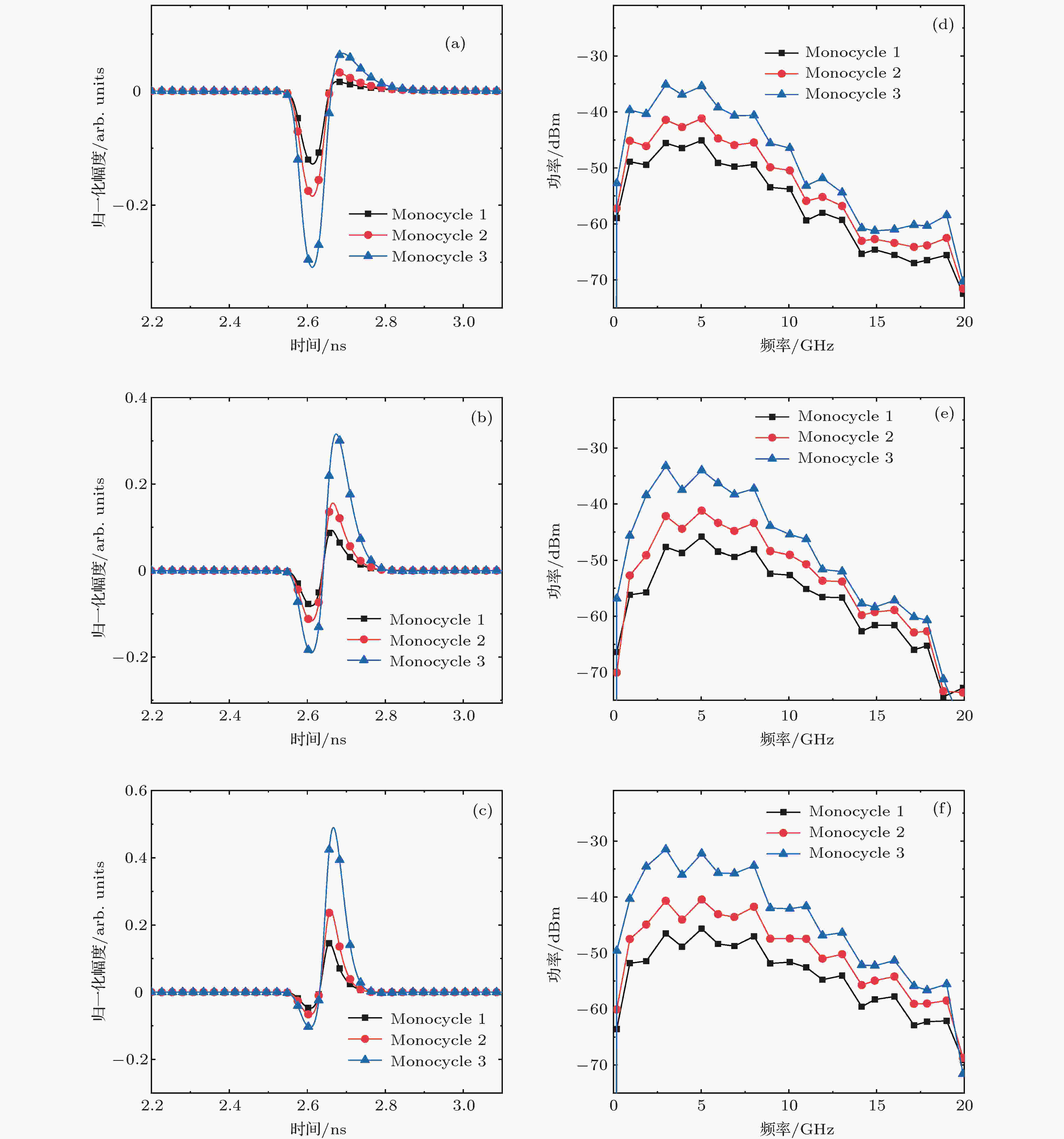图 4 不同SOA注入电流输出的monocycle波形和功率谱　(a) I = 180 mA, (b) I = 210 mA, (c) I = 240 mA输出的monocycle波形; (d) I = 180 mA, (e) I = 210 mA, (f) I = 240 mA输出的monocycle功率谱
Figure4. The waveform and the power spectrum of monocycle with different SOA bias current: The waveform when I = 180 mA (a), I = 210 mA (b), I = 240 mA (c); the power spectrum when I = 180 mA (d) I = 210 mA (e), I = 240 mA (f).

从频域上看, 当注入电流过小或过大时, 即时域波形对称性较差时, 功率谱密度在1—3 GHz频段功率高, 更加偏离FCC对UWB功率谱的定义, 如图4(d)和(f)所示; 如当注入电流为210 mA时, 时域波形对称性较好, 3路输出monocycle信号的–10 dB带宽和相对带宽均为6 GHz和166.67%, 符合FCC对于UWB功率谱的定义. 本方案SOA的注入电流为200—220 mA范围时, 获得较好的monocycle信号.
保持其他参数不变, 研究不同输入信号光功率情况下输出monocycle信号的特性. 图5(a)给出输出3路monocycle信号的中心频率、–10 dB频率带宽随输入信号光的功率变化曲线, 可以看出随着输入光功率的增加, 输出的3路monocycle信号的–10 dB带宽呈现下降趋势, 同时中心频率向低频移动. 这是由于在输入信号光功率低的情况下, 消耗的载流子较少, SOA对信号光和激射光都有着较高的增益系数, 正脉冲得到足够放大, 并且在高增益下, 下脉冲出现压缩, 可以获得对称性比较好的monocycle信号, 并且由于时域脉冲压缩, 对应的频谱变宽, 图5(b)和(c)给出的输入信号光功率为–10 dBm (即输入信号低功率情况) 输出的monocycle信号的时域波形和功率谱. 随着输入信号光的光功率增加, 信号光对载流子的消耗也在逐渐增加, SOA的增益系数下降, 过冲得不到足够放大, 而输入信号光功率较高的情况下, 对激射光的反相调制强度加强, 导致输出monocycle信号的正脉冲部分幅度减小而负脉冲部分幅度增加, 出现严重的不对称性. 图5(d)和(e)给出的输入信号光功率为–4 dBm (即输入信号高功率情况)输出的monocycle信号的时域波形和功率谱. 因此本方案采用较低的输入信号光功率可以获得性能较好的monocycle信号.
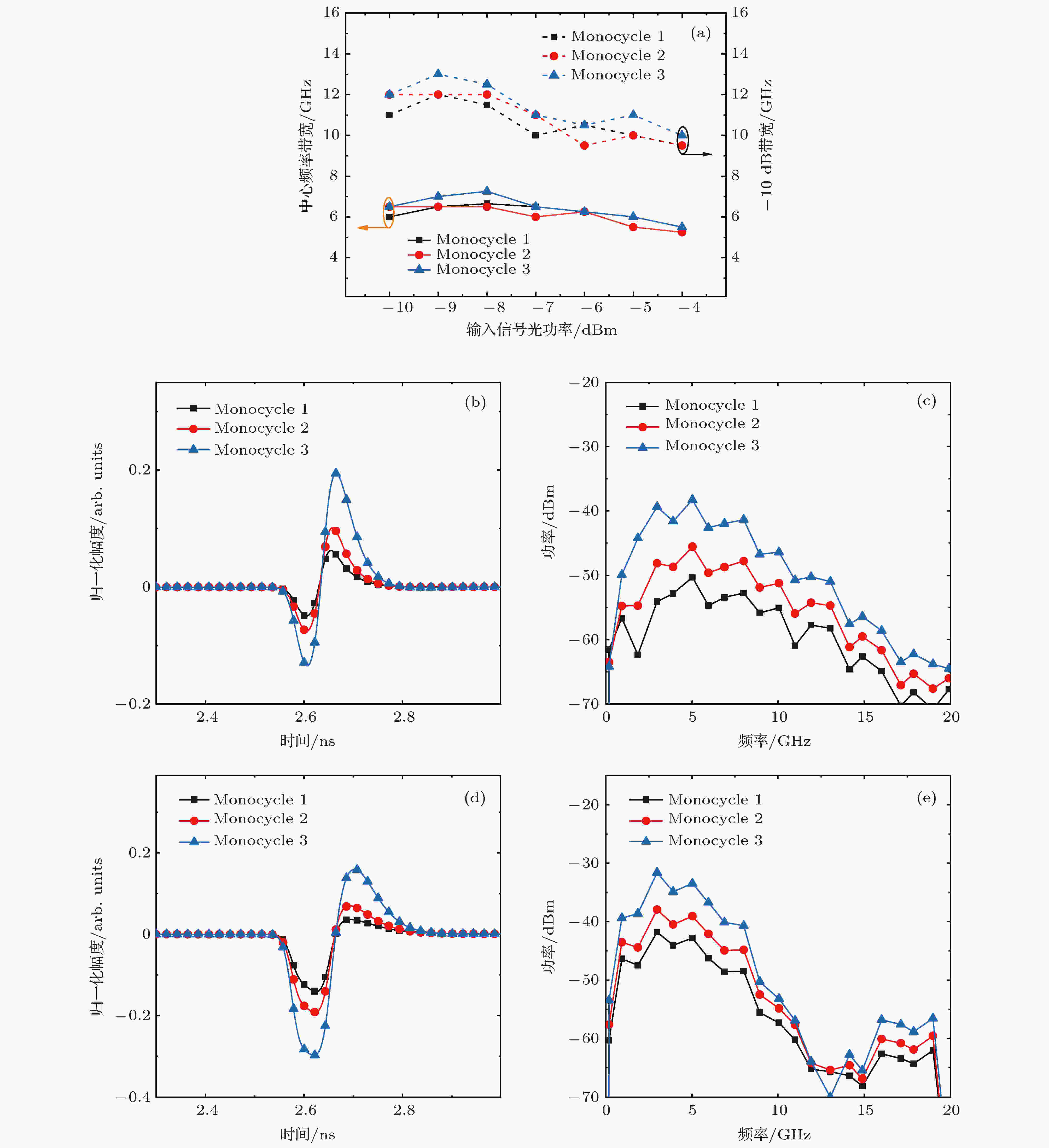图 5 输入信号功率对输出monocycles信号性能的影响　(a)不同输入信号功率情况下输出monocycle信号的中心频率和–10 dB频率带宽曲线; (b)输入功率为–10 dBm时输出的monocycle信号时域波形; (c)输入功率为–10 dBm时输出的monocycle信号功率谱; (d)输入光功率为–4 dBm时输出的monocycle信号时域波形; (e)输入光功率为–4 dBm时输出的monocycle信号功率谱
Figure5. The effect of input signal power on the performance of the output monocycle signals: (a) The curve of center frequency and –10 dB frequency bandwidth width different input signal powers; (b) the monocycle signal waveform when input signal power is –10 dBm; (c) the power spectrum when input signal power is –10 dBm; (d) the monocycle signal waveform when input signal power is –4 dBm; (e) the power spectrum when input signal power is –4 dBm.

保持其他参数不变, 研究不同输入信号光波长情况下输出monocycle信号的特性. 图6(a)给出3路输出monocycle信号的中心频率、–10 dB频率带宽随输入信号光波长变化的曲线图, 输出monocycle信号的中心频率和–10 dB带宽都随着输入信号光波长的变化出现小幅度的变化. 图6(b)和(c)给出输入信号光波长为 1530 nm (输入信号光波长较小的情况)输出的monocycle信号的时域波形和功率谱, 可以看出输出monocycle信号的时域波形对称性较差, 但功率谱满足FCC对于UWB的定义. 图6(d)和(e)给出输入信号光波长为 1550 nm (输入信号光波长较大的情况)输出的monocycle信号的时域波形和功率谱, 输出的monocycle信号时域对称性较好且功率谱同样满足FCC对于UWB的定义. 因此, 输入信号光波长对输出monocycle信号的带宽都有一定的影响, 当时影响比较小.
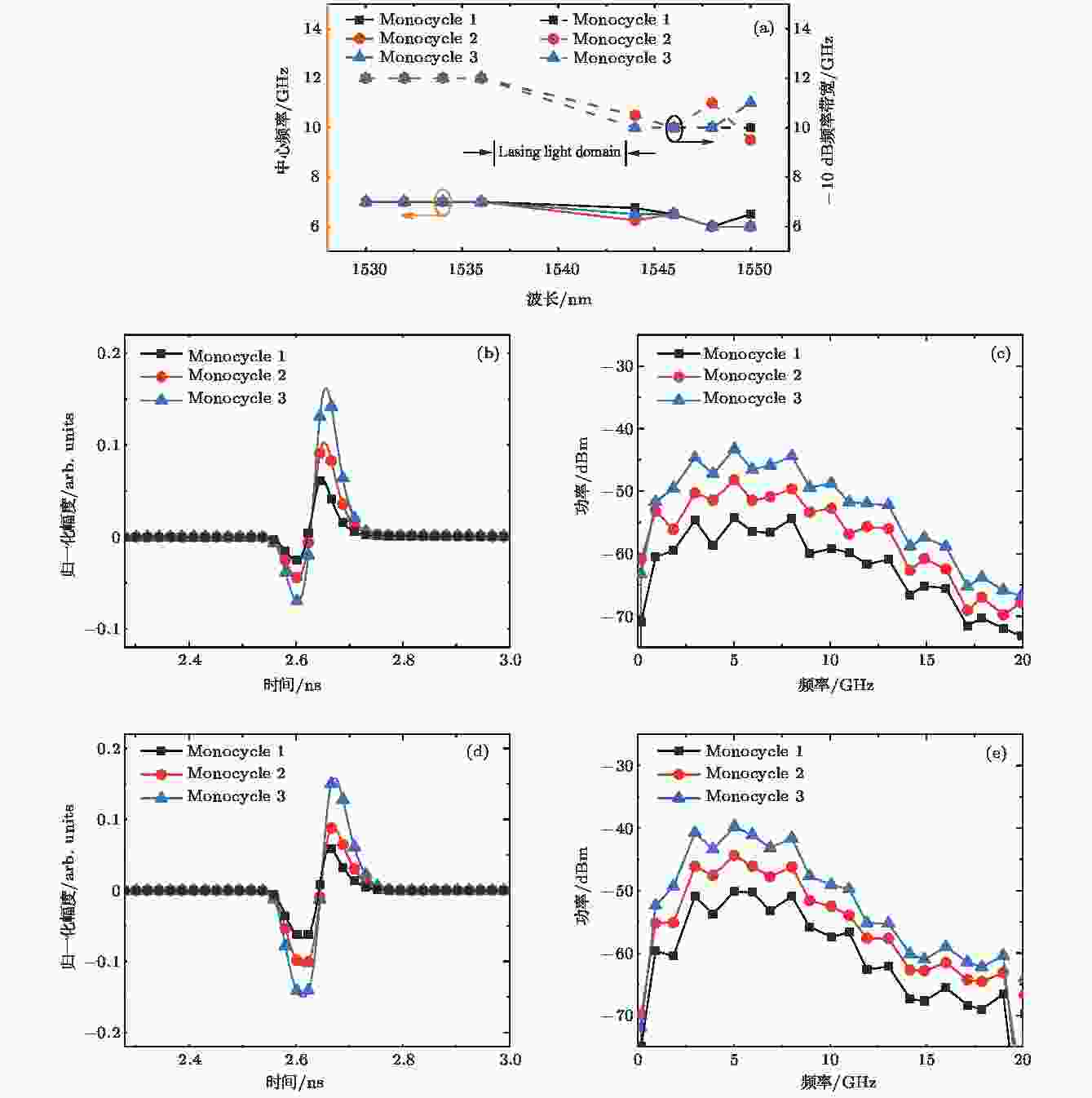图 6 (a)不同输入信号光波长情况下中心频率和–10 dB频率带宽曲线; (b)输入信号光波长1530 nm时输出的monocycle信号时域波形; (c)输入信号光波长1530 nm时输出的monocycle信号功率谱; (d)输入信号光波长为1550 nm时输出的monocycle信号时域波形; (e)输入信号光波长为1550 nm时输出的monocycle信号功率谱
Figure6. (a) Curve of center frequency and –10 dB frequency bandwidth width different input signal wavelength; (b) monocycle signal waveform when input signal wavelength is 1530 nm; (c) power spectrum when input signal wavelength is 1530 nm; (d) monocycle signal waveform when input signal wavelength is 1550 nm; (e) power spectrum when input signal wavelength is 1550 nm.

提出了一种基于SFRL的全光UWB信号源的方案. 该方案可以同时产生3路monocycle信号. 本文建立了这种信号源的宽带理论模型, 研究了SOA注入电流、激射波长、输入信号光功率和波长对输出monocycle脉冲性能的影响. 结果表明: SOA的注入电流在200—220 mA可以获得对称性较好的monocycle脉冲, 电流过高或过低都会使得输出monocycle脉冲对称性变差; 输出monocycle平均功率和正、负脉冲振幅随激射波长增加而增加; 输入信号光功率过高将导致monocycle信号对称性变差、频谱变窄, 因此本方案应采用低输入信号光功率; 输入信号光波长对monocycle信号有一定的影响, 但是影响很小.