摘要:耦合Duffing振子在检测强噪声中的微弱脉冲信号时具有可检测信噪比低等优点, 但目前检测模型还存在系统性能与初始状态有关、只能工作在倍周期分岔状态等缺陷. 为此本文构建了一种能克服上述缺点的新的微弱脉冲信号检测模型, 通过对两个Duffing振子同时施加较大的恢复力和阻尼力耦合, 可使振子间产生广义的“阱内失同步”现象, 基于这种现象可实现微弱脉冲信号的检测与恢复. 以信噪比改善和波形相似度为衡量指标, 研究了周期策动力幅值与周期、耦合系数、计算步长、阻尼系数等参量对模型信号检测与波形恢复效果的影响. 对方波、双指数脉冲和高斯导数脉冲进行检测和恢复的实验结果表明, 本文所构建的模型能够在较低信噪比条件下有效地检测并恢复出高斯白噪声背景中的微弱脉冲信号, 进而改善了现有的Duffing振子对非周期脉冲信号的检测能力并扩展了其应用领域.
关键词: 微弱脉冲信号/
强耦合Duffing振子/
信号检测/
参数估计

English Abstract

全文HTML

--> --> -->

在核爆炸电磁脉冲探测、闪电信号探测、电力系统局部放电探测、静电放电探测等信号被动探测研究领域, 信号通常具有单次、超宽带、低信噪比等特点, 当进行远距离探测时信号的强度将会非常微弱, 有可能淹没于强高斯噪声中, 此时采用常规探测手段进行信号提取和事件识别较为困难.
近年来, 随着现代信号处理技术的发展, 逐渐涌现出了一些适合微弱非周期脉冲信号探测的技术和方法, 例如: Power-Law检测法^[1]、小波变换^[2]、分数阶傅里叶变换^[3,4]、希尔伯特-黄变换^[5]、粒子滤波降噪^[6]、高阶累积量降噪^[7]等. 与这些方法相比, 混沌检测方法具有独特的优点, 例如可检测信噪比更低^[8,9]、适用范围更广^[10-14]等, 其原理是利用非线性系统对参数摄动的敏感性和对噪声的不敏感性, 通过系统相变或多个系统的耦合实现微弱信号探测^[15,16].
自1992年Birx首次将混沌振子用于微弱信号检测以来, 混沌振子检测理论得到了不断改进和发展. 2006年, 李月等^[17]首次提出了一种基于恢复力耦合的Duffing振子, 并应用该系统在高斯色噪声背景中检测周期方波信号, 取得了一定的效果. 2009年, Yuan等^[18]通过观测Duffing振子的混沌程度来探测脑电图, 首次将混沌振子的检测范围从周期信号扩展到非周期信号. 之后越来越多的****利用Duffing振子进行有关非周期脉冲信号检测的研究. 2011年, 吴勇峰等^{[19, 20]}发现脉冲信号能激励恢复力耦合混沌振子运动轨迹间出现瞬态同步突变现象, 并研究利用耦合Duffing振子从噪声背景中探测微弱局部放电信号^[21]. 2015年, 张悦等^[22]利用恢复力耦合Duffing振子对微弱电磁脉冲辐射信号进行远距离探测. 2015年, 曾喆昭等^[23]使用广义时间尺度变换扩展了微弱脉冲信号的探测频率范围. 2016年, 王晓东等^[24]提出了一种Duffing振子阻尼力耦合方法.
上述研究展现了混沌振子在微弱信号检测中广阔的应用前景, 但是总的来说基于混沌振子的时域微弱脉冲信号检测技术尚处于经验性的摸索阶段, 其实用性模型迄今鲜见报道, 工程应用尚属空白. 目前所提出的弱耦合Duffing振子具有明显的缺点, 如系统性能极大地依赖于系统初始状态、系统只能工作在倍周期分岔状态下、无法恢复被测信号的时域波形信息等. 为了解决这些问题, 本文对传统Duffing振子的耦合形式进行了改进, 通过对阻尼力和恢复力同时施加耦合, 构建了一个强相互作用的检测系统. 以信噪比改善和波形相似度为衡量指标, 研究了策动力幅值与周期、耦合系数、计算步长、阻尼系数等参量对模型信号检测与波形恢复效果的影响. 以强高斯白噪声背景中的方波、双指数脉冲、高斯导数脉冲为被测对象, 研究了强耦合系统的信噪比检测阈值与时域波形恢复效果. 实验结果表明该系统对初始状态不敏感, 可工作在任何相态, 信噪比改善(signal-to-noise ratio improvement, SNRI)可达20 dB, 对时域脉冲幅值和宽度的估计误差小于5%. 该方法在闪电信号探测、核爆炸电磁脉冲信号探测、局部放电探测、静电放电探测等被动信号探测研究领域具有重要的应用价值.

自1918年Duffing振子被应用于非线性动力学领域以来, 已逐渐成为众多混沌系统模型中研究和应用较为充分的模型之一, 其中Holmes型Duffing振子的动力学方程为

$\ddot x + \xi \dot x - x + {x^3} = F{\cos}\left( t \right), $

式中$\xi$为阻尼系数, $- x + {x^3}$为非线性恢复力, $F{\cos}\left( t \right)$为周期策动力, F为策动力幅值. (1)式是策动力角频率$\omega = 1$ rad/s时的情况, 为了方便对任意频率的信号进行检测, 通常对(1)式进行时间尺度变换, 在不改变其离散数值的情况下, 将其在时间尺度上进行压缩或放大, 方程性质并不改变^[24].
设$t = \omega \tau $, 则有$x\left( t \right) = x\left( {\omega \tau } \right)$, $\dot x\left( t \right) = \dfrac{{{\rm{d}}x\left( t \right)}}{{{\rm{d}}t}} =$$ \dfrac{1}{\omega }\dfrac{{{\rm{d}}x\left( {\omega \tau } \right)}}{{{\rm{d}}\tau }}, \;\ddot x\left( t \right) = \dfrac{1}{{{\omega ^2}}}\dfrac{{{{\rm{d}}^2}x\left( {w\tau } \right)}}{{{\rm{d}}{\tau ^2}}}$.
将广义时间变量$\tau$换为t, 代入方程(1)并整理, 得

$\ddot x + \omega \xi \dot x - {\omega ^2}\left( {x - {x^3}} \right) = {\omega ^2}F{\rm{cos}}\left( {\omega t} \right).$

经过时间尺度变换后方程(2)的激励角频率由1 rad/s变成了$\omega$, 因此可以适应外界不同频率的周期信号.
2011年, 吴勇峰等^[19]基于(1)式构造了一种恢复力耦合的Duffing振子,

$\left\{ {\begin{aligned}& {\ddot x_1} + \xi {{\dot x}_1} - k\left( {{x_1} - {x_2}} \right) - {x_1} + x_1^3 \\=\;& F\cos \left( {\omega t} \right) + s\left( t \right) + n\left( t \right),\\& {{\ddot x_2} + \xi {{\dot x}_2} - k\left( {{x_2} - {x_1}} \right) - {x_2} + x_2^3 = F\cos \left( {\omega t} \right), }\end{aligned}} \right.$

其中k为耦合系数, 其数值表示耦合强度, 在该系统中两振子的耦合强度保持一致; s(t)为待测脉冲信号; n(t)为高斯白噪声. 待测脉冲信号s(t)和噪声n(t)只加入到振子1中. 该模型检测机理为“阱间失同步”, 即微弱脉冲信号使处于倍周期振荡的振子1从某个势阱跃迁至另一个势阱, 由于耦合作用很小, 微弱脉冲信号对振子2几乎不起作用, 振子2保持原状, 依靠两振子的“阱间失同步”和混沌振子对噪声极强的免疫力检测微弱脉冲信号. 增大系统耦合系数后, 两振子产生同步的跃迁, 性能不但没有改善, 反而导致检测失败.
上述基于恢复力耦合的Duffing振子虽然可以实现–10 dB以下信噪比的微弱脉冲信号检测, 但检测原理决定了其存在以下的固有缺陷: 系统初始状态不同, 对正脉冲和负脉冲产生瞬态同步突变的能力不同; 系统只能工作在倍周期分岔状态下, 在混沌态和大尺度周期态时将会失效; 对微弱脉冲的幅值、宽度等信息不敏感, 无法恢复被测信号的时域波形. 由于其耦合系数较小, 本文称其为弱耦合Duffing振子.

2

-->

3.1.强耦合Duffing振子方程及其数值求解

为了解决上述弱耦合Duffing振子存在的各种问题, 本文结合时间尺度变换构造了一种新的强耦合Duffing振子模型:

$\left\{\begin{aligned}& {\ddot x_1} + \omega \xi {{\dot x}_1} + {\omega ^2}\xi k\left( {{x_1} - {x_2}} \right) \\ & +\omega k\left( {{{\dot x}_1} - {{\dot x}_2}} \right) - {\omega ^2}({x_1} - x_1^3)\\ =\; & {\omega ^2}\left[ {F\cos \left( {\omega t} \right) + s\left( t \right) + n\left( t \right)} \right],\\& {\ddot x_2} + \omega \xi {{\dot x}_2} + {\omega ^2}\xi k\left( {{x_2} - {x_1}} \right) \\ & + \omega k\left( {{{\dot x}_2} - {{\dot x}_1}} \right) - {\omega ^2}({x_2} - x_2^3)\\ = \; &{\omega ^2}F\cos \left( {\omega t} \right)\end{aligned}\right.$

式中$\left( {{x_1} - {x_2}} \right)$为恢复力耦合项; $\left( {{{\dot x}_1} - {{\dot x}_2}} \right)$为阻尼力耦合项; k为耦合系数, 即恢复力耦合系数和阻尼力耦合系数均为k; $\xi$与(1)式含义相同, 为阻尼系数.
非线性常微分方程(4)没有解析解, 常用的数值解法是龙格-库塔(Runge-Kutta, RK)法, 本文使用MATLAB中求解微分方程的函数ode45对其进行求解, 该函数是一种解决刚性问题的变步长数值解法, 采用四阶RK算法提供候选解, 五阶RK算法控制误差, 整体截断误差为h⁵, 求解过程中的步长h、相对误差、绝对误差等参量可以自行设定^[25].
2 -->

3.2.强耦合Duffing振子检测原理

强耦合Duffing振子检测原理为广义的“阱内失同步”, 即通过较大的“恢复力”和“阻尼力”的共同耦合, 使得脉冲对振子1的作用可以同时作用在振子2上, 并且使得两振子在脉冲作用下的“瞬时突变”方向不同, 这样通过比较两振子相轨迹的差异, 即可对脉冲进行检测. “阱内失同步”是指两振子在倍周期状态下处于同一势阱时的同步受到破坏; 广义的“阱内失同步”, 是指两个振子在倍周期、混沌、大尺度周期等各种状态下的同步受到破坏. 基于广义“阱内失同步”原理的强耦合Duffing振子从根本上克服了弱耦合模型“阱间失同步”检测方法的缺陷.
下面对强耦合Duffing振子的检测原理进行详细分析. 首先对单振子的动力学行为进行分析, 振子有1个鞍点(0, 0)和两个中心点(1, 0)和(–1, 0), 其阻尼系数$\xi$一般为正的常数. 当周期策动力为0时, Duffing振子相平面运动轨迹将在阻尼力的作用下以螺旋形式趋于两个中心点之一, 初始条件决定了趋于哪个中心点; 当周期策动力幅值F逐渐增大时, 其运动轨迹围绕某个中心点做线性振荡, 频率与策动力频率相同; 继续增大F值, 振荡运动出现分频, 频率为策动力频率的有理数倍, 轨迹出现倍周期分岔; 当F再增加超过某一阈值后, 轨迹将从原来的中心点进入到另一个中心点做倍周期振荡, 也可能从新的中心点跳回原中心点, 这种振荡和来回跃迁极难重复, 便称之为混沌; 当F进一步增加超过某一阈值后, Duffing振子被周期策动力所主导, 系统在外轨进行大尺度周期振荡.
在周期策动力上施加脉冲信号s(t)和噪声n(t)后, 将有可能打破系统原有的运动状态. 若脉冲信号s(t)在Duffing振子固有谐振频率处的能量足够大, 就能够使相轨迹发生改变. 文献[23]从频域对冲击信号能谱、谐振频率与相轨迹变化三者的关系进行了定量描述. 从时域角度看, 当脉冲信号的宽度与振荡的周期可比拟并且脉冲强度足够大时, 即可使振子轨迹发生较大的改变, 并且脉冲强度越大, 轨迹突变程度越大, 当脉冲信号s(t)消失后, 轨迹又能很快恢复初始状态. 一定强度下随机变化的噪声n(t)具有各个频率分量, 不同频率分量的扰动会使振子偏离共振态, 但在谐振频率处的能量不足以使状态发生跃迁或轨迹发生大的改变, 只能在轨迹上留下一些粗糙的痕迹. 因此, 通过构造两个同步的耦合振子, 并使得脉冲信号s(t)在振子中产生的轨迹“失同步”, 就可以通过检测这种“失同步”实现对s(t)的检测, 并通过失同步的程度估计s(t)的波形参数.
(4)式的强耦合Duffing振子即可满足这种要求, 下面通过数值计算对其检测原理做进一步说明. 在振子1内置周期策动力$F\cos \left( {\omega t} \right)$上叠加三角脉冲s(t)和零均值高斯白噪声n(t), 信噪比设为–10 dB, 如图1(a)所示, 三角脉冲的幅值为0.63, 上升沿与下降沿相等, 均为0.5 ${\text{μ}}{\rm s}$. 使用龙格-库塔法对强耦合Duffing振子微分方程进行求解, 从图1(c)和图1(d)振子1, 2的相图可以看出, 脉冲信号s(t)在两个相图中均引起了瞬时突变, 振子1的圆形振荡轨道向右上方突变, 振子2轨道向右下方突变. 这说明在脉冲信号s(t)的作用下, 系统变量x₁, x₂同时增大的瞬间, 变量${\dot x_1}, {\dot x_2}$一个增大, 一个减小. 从${\dot x_1}$与${\dot x_2}$的时域图1(e)和图1(f)也可以看出, ${\dot x_1}$在脉冲信号s(t)到来的时刻产生了叠加于由周期策动力$F\cos \left( {\omega t} \right)$产生的正弦波之上的正极性脉冲, ${\dot x_2}$在几乎同一时刻产生了负极性脉冲. 这样, 利用${\dot x_1}$和${\dot x_2}$的差值, 即可将相位相同的正弦波抵消, 检测出脉冲信号, 结果如图1(b)所示. 比较图1(b)的检测结果和图1(a)的输入信号可以看出, 强耦合Duffing振子在检测输入脉冲信号的同时, 较大程度上保留了信号的时域信息, 据此可以对输入信号的脉宽、幅值等参数进行估计.
图 1 强耦合Duffing振子检测微弱脉冲信号　(a)输入信号; (b)输出信号; (c)振子1相图; (d)振子2相图; (e)变量${\dot x_1}$时域图; (f)变量${\dot x_2}$时域图
Figure1. Detection of weak pulse signal using the strongly coupled Duffing oscillators: (a) Input signal; (b) output signal; (c) phase space of oscillator 1 and (d) oscillator 2; (e) time domain diagram of variable ${\dot x_1}$ and (f) ${\dot x_2}$

强耦合Duffing振子系统的参数取值、计算步长等对系统的检测效果均有可能产生影响, 本节通过对这些因素的分析, 为系统优化提供理论依据.
这里使用波形相似度与信噪比改善两个指标衡量系统探测效能. 波形相似度(也称皮尔逊相关系数)可以从时域反映两个波形的相似程度, 其定义为

$r = \dfrac{{\displaystyle\sum \nolimits_{i = 1}^n \left( {{x_i} - \bar x} \right)\left( {{y_i} - \bar y} \right)}}{{\sqrt {\displaystyle\sum \nolimits_{i = 1}^n {{\left( {{x_i} - \bar x} \right)}^2}\displaystyle\sum \nolimits_{i = 1}^n {{\left( {{y_i} - \bar y} \right)}^2}} }}, $

式中x_i为输入信号数列, y_i为输出信号数列, ${\bar x}$为数列x_i的均值, $\bar y$为数列y_i的均值, r为两个波形对应数列x和y的相关系数, 取值范围为[–1, 1], r越大表明正相关程度越高, r = 1时两个波形完全相似.
信噪比改善即检测系统输出信噪比与输入信噪比的差值,

${\rm{SNRI}} = {\rm{SN}}{{\rm{R}}_{\rm{o}}} - {\rm{SN}}{{\rm{R}}_{\rm{i}}}, $

式中SNR_o为输出信噪比, SNR_i为输入信噪比. 脉冲信号的信噪比定义为

${\rm{SNR}} = 10\log \left[ {{a^2}/\left( {4D} \right)} \right], $

式中a为脉冲信号s(t)的幅值, D为噪声方差. 系统变量初始值默认为${x_1} = {x_2} = 1.4$, ${y_1} = {y_2} = 4$, 初始值的选取原则是尽量减小检测结果开始阶段的振荡. 当对系统某个参数进行分析时, 该参数的取值位于某个区间内, 其他参数取默认值, 如表1所列.

参数	取值区间	默认值
F	[0, 2]	0.2
$\omega $/${\rm rad}\cdot {{\rm s}^{-1}} $	[1 × 105, 5 × 107]	5 × 106
k	[10–1, 103]	10
$\xi$	[10–2, 102]	0.7
计算步长/ns	[20, 1]	1

表1强耦合Duffing振子各参数取值区间与默认值
Table1.Values range and default values of parameters in strongly coupled Duffing oscillators

2

-->

4.1.周期驱动力幅值F (系统相态)

在使用固定计算步长并合理设置系统参数后, 通过逐步增加驱动力幅值F, 系统将出现周期振荡、分岔、混沌和大尺度周期等不同相态^[26]. 下面分析系统处于不同相态时的信噪比改善与波形相似度情况.
首先分析Duffing系统相态的变化区间, 当无被测信号时, 两振子完全同步. Duffing振子随参数F在区间[0, 2]内变化的分岔图如图2所示. 当F = 0时, 系统轨线将最终停在其中一个焦点; 当$0 < F < 0.467$时, 相点围绕其中一个焦点或另一个焦点做周期振荡; 当$0.467 < F < 0.504$时, 系统轨线将出现分岔, 相点围绕焦点做倍周期振荡; 当$0.505 < F < 1.142$时, 系统产生Smale马蹄意义下的混沌运动; 当$1.143 < F \leqslant 2$时, 系统进入大尺度周期运动状态. 系统相态在分界点处可能会存在小的过渡区间^[27], 这里暂不讨论. 其中混沌相态判别使用Lyapunov指数法, 当最大Lyapunov指数大于0, 且三个Lyapunov指数之和小于0时, 系统为混沌态. Lyapunov指数计算使用Jacobi算法^[28].
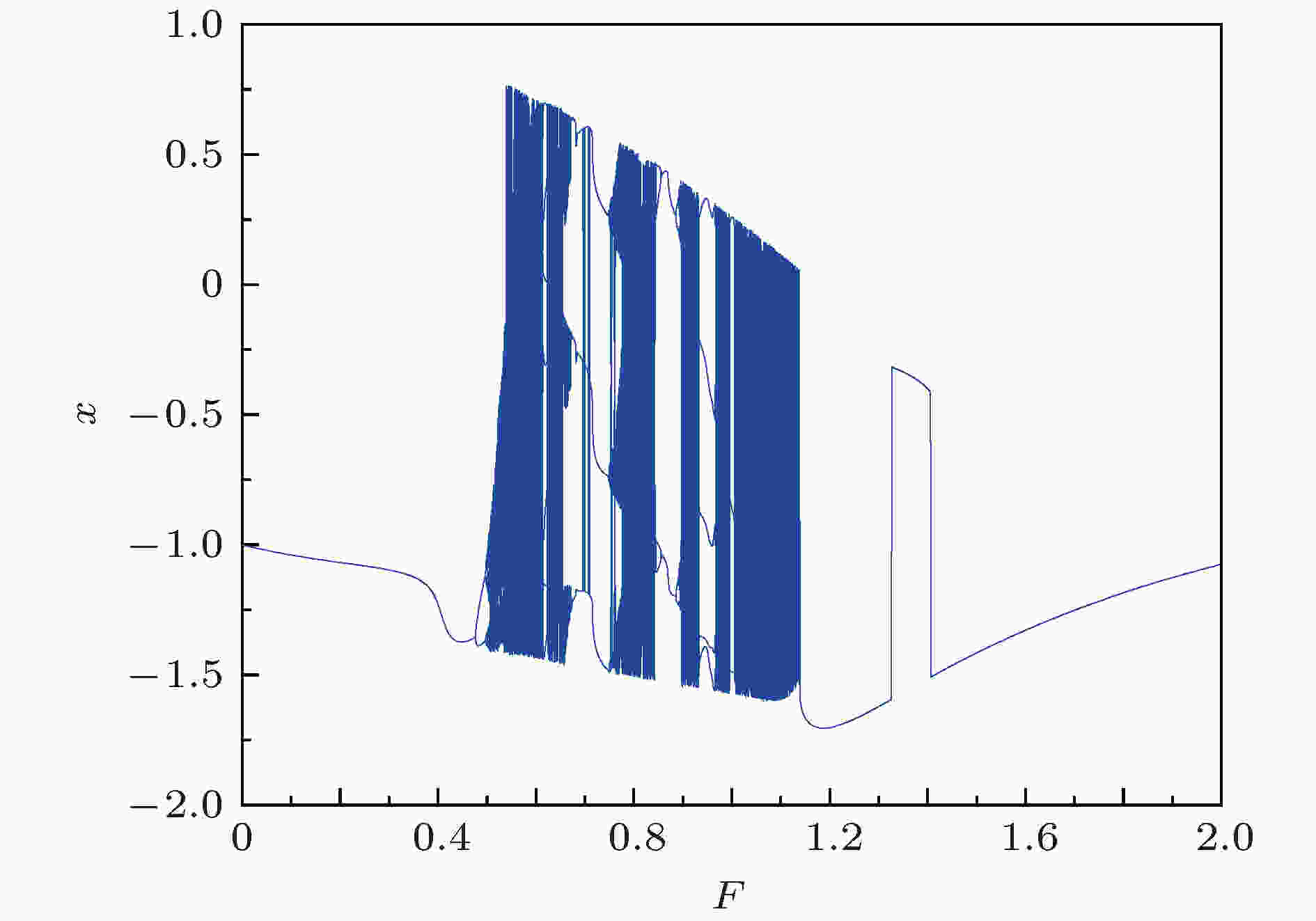图 2 Duffing振子随参数F变化的分岔图
Figure2. Bifurcation diagram of Duffing oscillator with parameter F

接下来观察强耦合Duffing振子在不同相态时检测微弱高斯脉冲信号的情况. 选取前沿5.5 ${\text{μs}}$, 半高宽5 ${\text{μs}}$的高斯脉冲作为被测信号:

$s\left( t \right) = A \cdot {{\rm{e}}^{ - {{\left( {\textstyle\frac{{t - b}}{c}} \right)}^2}}}, $

其中A = 0.632, b = 0, c = 3 × 10^–6. 设定噪声方差D = 0.1, Duffing系统输入信号信噪比为 0 dB, 主要原因是为了保证能检测出该信号, 方便研究Duffing振子参数与检测性能的关系, 从而为参数优化提供依据, 而非以检测为目的. 本节数值仿真实验均采用此信号作为被测信号.
100次实验的信噪比改善SNRI均值(及均方差)和波形相似度r均值与驱动力幅值F的关系如图3所示. 由图中可见SNRI在$0 \leqslant F \leqslant 2$的整个范围内均能达到19.2 dB以上且曲线较为平坦, 这表明Duffing振子相态的变化对微弱脉冲信号检测影响不大. 该特性对探测大动态范围的信号是非常有利的, 因为当输入信号的强度相对驱动力幅值变化较大时, 有可能会引起系统的相变, 若在不同相态时系统SNRI变化较大, 则会影响系统的稳定性. 检测系统处于不同相态时输出信号与被测信号s(t)的波形相似度均大于97%, 表明在系统的各个相态, 波形的时域特征恢复情况也是比较好的.
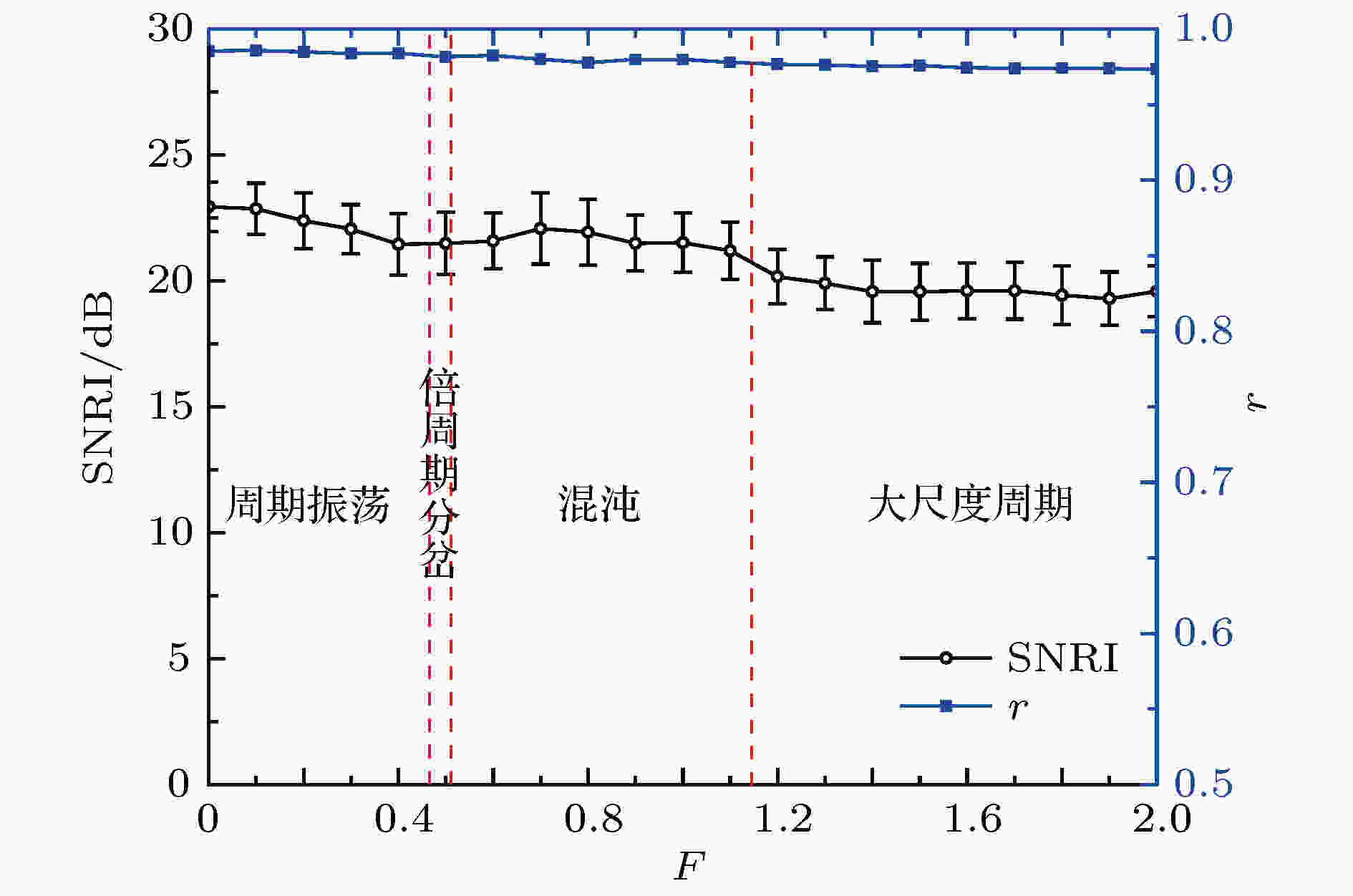图 3 SNRI和r与周期驱动力幅值F (相态)的关系
Figure3. SNRI and r versus the periodic driving force amplitude F (states of phase-space)

另外, 对系统初始值引起的相态变化也进行了研究, 得到的结果与上述结论相似, 这说明强耦合Duffing振子在实际使用时几乎不受初始值的限制.
2 -->

4.2.驱动力周期$\omega $

驱动力周期$\omega $是在Duffing方程时间尺度变换时引入的, 目的是为了便于检测各种不同频率的周期信号. 在检测具有宽带特性的脉冲信号时, 若仅凭对脉冲信号的频谱分析结果, 依据信号能量频率上限设置$\omega $, 检测结果往往不理想.
下面对该参数的设置进行分析, 首先设定系统其他参数与初始值为默认值. 计算$1 \times {10^5}\;{\rm{rad}}/{\rm{s}} \leqslant$$ \omega \leqslant 5 \times {10^7}\;{\rm{rad}}/{\rm{s}}$时系统的信噪比改善SNRI与波形相似度r, 统计结果如图4所示(实验次数100次). 可见SNRI最优的频点是1 × 10⁶ rad/s, 对应频率0.16 MHz, 这与信号能量频率上限相对应, 但波形相似度最优时的频率范围是$5 \times {10^6}\;{\rm{rad}}/{\rm{s}} \leqslant \omega \leqslant 9 \times {10^6}\;{\rm{rad}}/{\rm{s}}$. 时域信号检测系统往往更加注重波形相似度的要求, $\omega $的选择首先考虑提高波形相似度, 其次再考虑提高信噪比改善, 否则波形的畸变较为严重. 所以, 驱动力周期的设置需要根据不同信号的时域特性来决定. 仿真结果显示, 针对(8)式的高斯脉冲, 设置$\omega = 5 \times$$ {10^6}$ rad/s是较为合适的(大于信号能量频率上限).
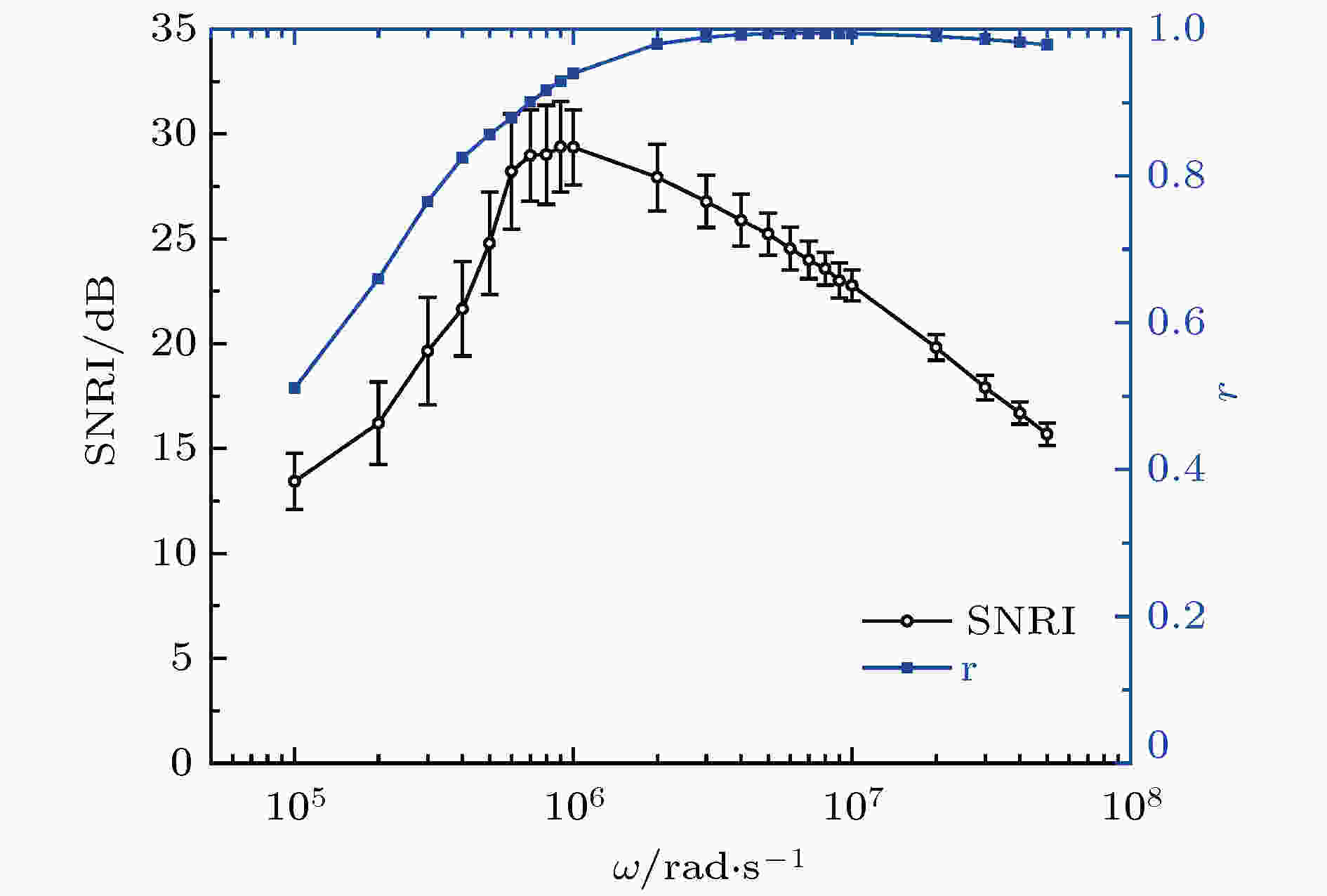图 4 SNRI和r与驱动力周期$\omega$的关系
Figure4. SNRI and r versus the driving force period $\omega$

2 -->

4.3.耦合系数k

耦合系数的作用在于将被测信号s(t)对振子1的作用耦合到振子2中去. 由该模型的检测机理可知, 耦合系数越大, 检测效果和波形恢复效果越好. 当耦合系数k = 0时, 两振子之间不存在耦合作用. 当0 < k < 1时, 两振子间的耦合属于弱耦合, 被测脉冲信号在振子1中引起的突变难以耦合到振子2中, 以至于变量差分后的结果几乎被噪声淹没, 检测失效; 当1 < k < 10时, 振子耦合强度逐渐增大, 振子2因s(t)产生的突变也逐步增大, 信噪比改善逐渐提高, 波形相似度也逐渐达到最优; 当k > 10时, 耦合系数的影响趋于固定. 设定系统其他参数与初始值, 在${10^{ - 1}} \leqslant k \leqslant {10^3}$的范围内, 系统的信噪比增益SNRI与波形相似度r在100次实验时的统计值如图5所示.
图 5 SNRI和r与耦合系数k的关系
Figure5. SNRI and r versus the coupling coefficient k

2 -->

4.4.阻尼系数$\xi$

设定系统其他参数与初始值, 对系统相图进行分析, 结果显示, 在小阻尼系数时$\left( {0 < \xi < 0.1} \right)$, 系统的相态会经历大尺度周期、混沌、分岔等不同状态的变化, 这时虽然系统对噪声的抑制能力较强, 但SNRI分散程度较大, 波形有所失真. 中等阻尼系数时$\left( {0.1 < \xi < 1} \right)$, 系统始终处于周期振荡状态, 脉冲引起的振子同步突变较为规则, 波形相似度很高, 同时信噪比改善也较好. 大阻尼系数时$\left( {\xi > 1} \right)$, 系统逐渐脱离周期振荡状态, 不再具有Duffing方程的属性, 波形检测失效. 信噪比改善SNRI和波形相似度r与阻尼系数$\xi$的关系如图6所示.
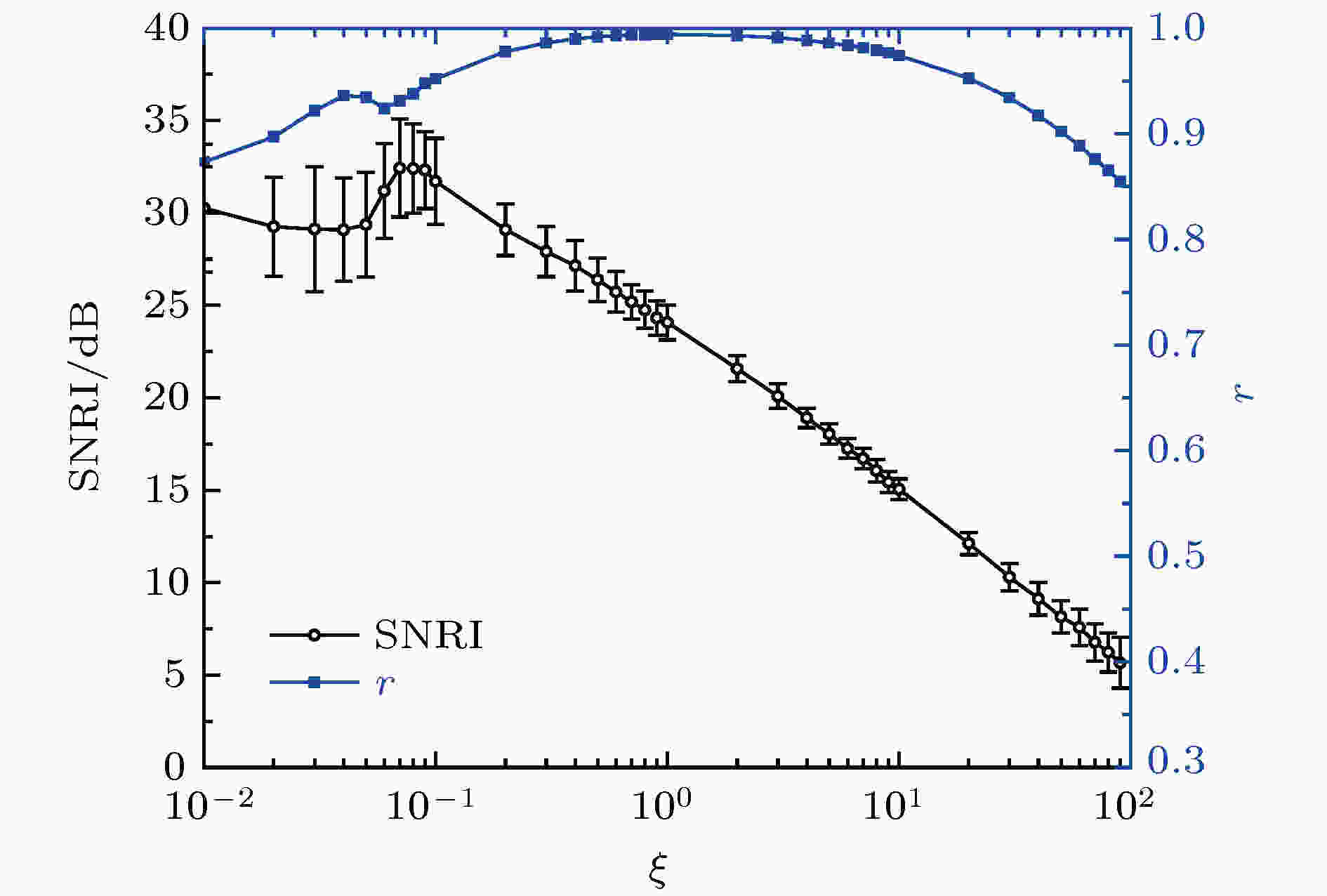图 6 SNRI和r与阻尼系数$\xi$的关系
Figure6. SNRI and r versus the damping coefficient $\xi$

2 -->

4.5.计算步长

计算步长在很大程度上决定了计算的精度, 计算步长越小计算精度越高, 但同时计算量越大. 下面利用不同的计算步长对Duffing方程进行求解, 以观察计算步长对检测效果的影响. 设定计算步长分别20, 10, 5, 2, 1 ns, 则输入信号采样率对应为50, 100, 200, 500, 1000 MHz. 100次实验检测结果的SNRI和波形相似度r统计值与计算步长的关系如图7所示, SNRI和r均随着计算步长减小而增加, 这与前面的分析一致. 所以在Duffing系统运算能力允许时, 应尽可能采用较小的计算步长(较高的采样率).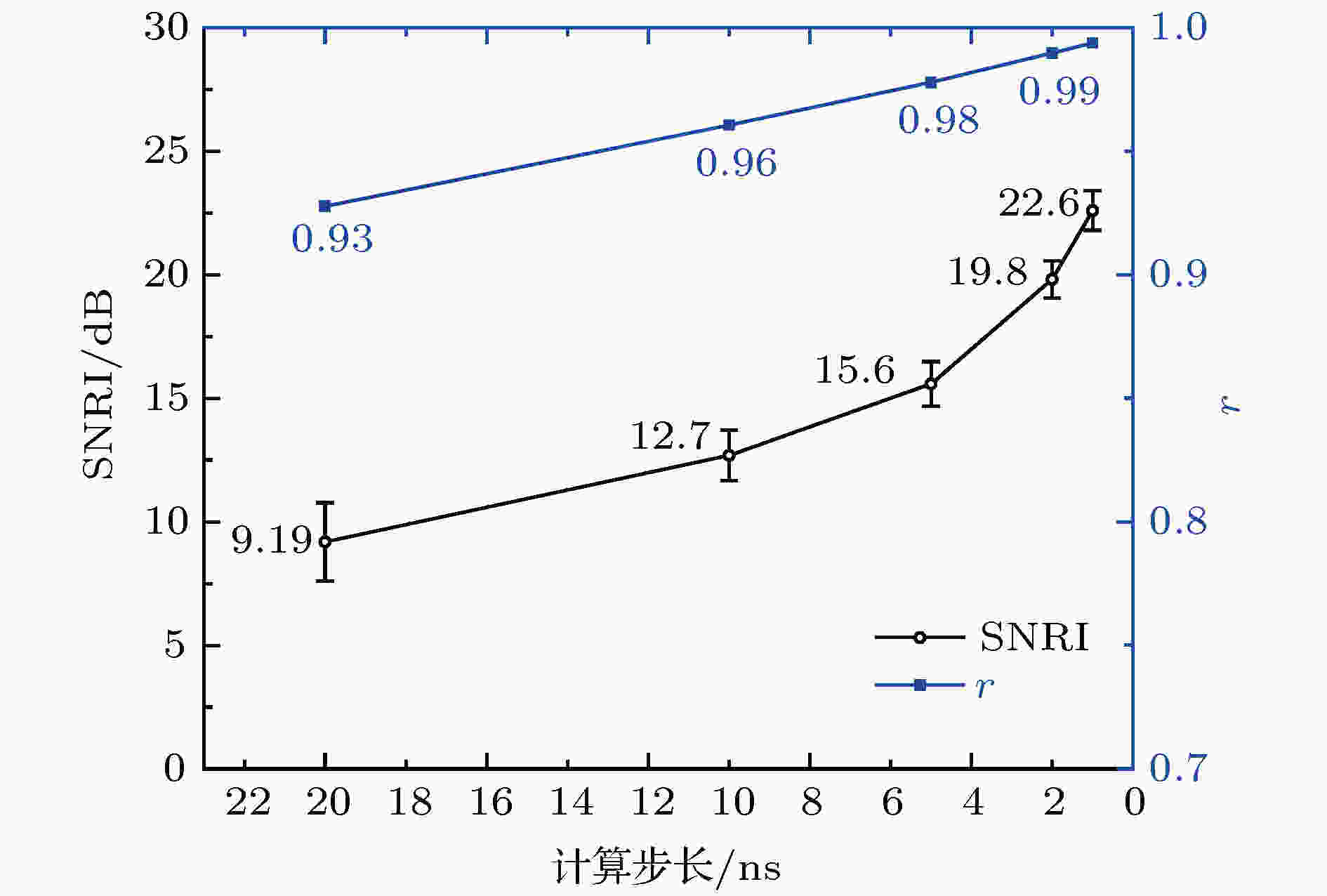
图 7 SNRI和r与不同计算步长的关系
Figure7. SNRI and r versus different calculation steps

2

-->

5.1.微弱脉冲信号检测

在前面强耦合Duffing振子原理与参数分析的过程中, 分别使用了三角脉冲和高斯脉冲作为被检测波形, 分析结果显示输出信噪比得到了有效改善, 波形相似度也很高. 下面利用强耦合Duffing振子对三种波形信号进行不同信噪比条件下的检测. 其中,
${\text{检测概率}} = \dfrac{{\text{检测成功的次数}}}{\text{总次数}} \times 100\% $.
检测成功的判据为: 输出信号脉冲幅度a大于5倍噪声均方差(输出信号信噪比大于7.96 dB). 设置该判据的原因在于, 在标准正态分布中, 样本大于5σ的概率为2.85 × 10^–6, 即一百万个数据点会有2.85个误判. 假设一次事件包含10⁴个数据点, 那么对事件的误判率将小于3%, 实践证明该判据用于脉冲检测是一种可靠的判据.
根据第4节的分析结果, 检测不同时域特征脉冲信号时需要设置不同的振子参数, 三种被测信号的波形特征及部分参数如表2所列, 其他参数取表1中默认值, 系统初始值同样取默认值.

脉冲类型	波形时域特征	Duffing振子参数
方波	上升时间0.1 ms	$\omega = 50$ rad/s
	半高宽1 s	计算步长0.1 ms
双指数脉冲	上升时间3 ${\text{μs}}$	$\omega = 5 \times {10^5}$ rad/s
	半高宽25 ${\text{μs}}$	计算步长10 ns
高斯导数脉冲	上升时间1.5 ${\text{μs}}$	$\omega = 4 \times {10^6}$ rad/s
	峰峰宽1.45 ${\text{μs}}$	计算步长1 ns

表2波形特征及部分振子参数
Table2.Waveform characteristics and partial oscillator parameters

背景固定为方差0.1的高斯白噪声, 通过调节脉冲信号幅度a, 将输入信噪比设置在区间[–20, –10] dB, 间隔1 dB, 100次实验的检测概率和波形相似度均值如表3所列. 可以看出, 三种波形的检测概率和波形相似度同时大于0.9的输入信噪比门限分别为–15, –12和–16 dB.

脉冲类型	输入信噪比/dB	–20	–19	–18	–17	–16	–15	–14	–13	–12	–11	–10
方波	检测概率/%	14.0	21.5	41.5	60.5	78.0	91.5	99.0	100	100	100	100
	波形相似度r	0.88	0.90	0.92	0.93	0.94	0.95	0.96	0.97	0.97	0.98	0.98
双指数脉冲	检测概率/%	0.5	4.5	5.5	10.0	23.5	51.0	67.5	87.5	95.5	100	100
	波形相似度r	0.67	0.71	0.74	0.78	0.81	0.84	0.86	0.88	0.90	0.91	0.92
高斯导数脉冲	检测概率/%	37.5	55.0	73.0	86.5	94.0	99.5	100	100	100	100	100
	波形相似度r	0.85	0.87	0.88	0.89	0.90	0.91	0.92	0.92	0.93	0.93	0.93

表3强耦合Duffing振子检测结果
Table3.Detection results of strongly coupled Duffing oscillators

2 -->

5.2.微弱脉冲信号参数估计

强耦合Duffing振子对目标信号的检测是基于时域的, 由于检测结果${s_{\rm{o}}}\left( t \right) = {\dot x_1} - {\dot x_2}$与目标信号s(t)在时域具有良好的波形相似度, 因此可通过直接测量${S_{\rm{o}}}\left( t \right)$来估计目标信号s(t)的时域特征. 以三种波形的检测概率和波形相似度同时大于0.9时的输入信噪比(即–15, –12, –16 dB)作为检测门限, 采用一阶矩估计法分别估计脉冲幅值和宽度的均值, 并计算估计值的误差和均方误差. 估计前先选取100个样本对模型进行训练, 随后对另100个测量样本进行参数估计. 估计结果列于表4和表5, 其中${\text{误差}} = \dfrac{{{\text{估计值}} - {\text{真实值}}}}{{\text{真实值}}} \times 100\% $, 均方误差(MSE)为

脉冲类型	输入信噪比/dB	–16	–15	–14	–13	–12	–11	–10
方波	真实值	—	0.1125	0.1262	0.1416	0.1589	0.1783	0.2000
	估计值	—	0.1114	0.1304	0.1375	0.1641	0.1761	0.1943
	误差/%	—	–0.98	3.34	–2.90	3.29	–1.24	–2.85
	MSE/10–4	—	1.26	1.43	0.75	2.04	1.23	2.49
双指数脉冲	真实值	—	—	—	—	0.1589	0.1783	0.2000
	估计值	—	—	—	—	0.1586	0.1773	0.2032
	误差/%	—	—	—	—	–0.16	–0.55	1.62
	MSE/10–4	—	—	—	—	2.79	6.43	5.03
高斯导数脉冲	真实值	0.1002	0.1125	0.1262	0.1416	0.1589	0.1783	0.2000
	估计值	0.1039	0.1180	0.1297	0.1423	0.1595	0.1807	0.1960
	误差/%	3.74	4.93	2.78	0.52	0.41	1.35	–2.02
	MSE/10–4	0.29	0.89	0.79	1.60	0.82	1.46	0.71

表4脉冲信号幅值估计结果
Table4.Estimation results of pulse signals amplitude

脉冲类型	输入信噪比/dB	–16	–15	–14	–13	–12	–11	–10
方波	真实值/s	—	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000
	估计值/s	—	1.0011	0.9988	0.9941	0.9984	0.9972	0.9986
	误差/%	—	0.11	–0.12	–0.59	–0.16	–0.28	–0.14
	MSE/10–4	—	1.40	1.11	0.57	0.13	0.56	0.45
双指数脉冲	真实值/${\text{μ}}{\rm s}$	—	—	—	—	25	25	25
	估计值/${\text{μ}}{\rm s}$	—	—	—	—	25.22	24.79	24.68
	误差/%	—	—	—	—	0.89	–0.84	–1.27
	MSE	—	—	—	—	15.8	3.8	7.7
高斯导数脉冲	真实值/${\text{μ}}{\rm s}$	1.45	1.45	1.45	1.45	1.45	1.45	1.45
	估计值/${\text{μ}}{\rm s}$	1.38	1.52	1.52	1.47	1.48	1.52	1.46
	误差/%	–5.02	4.99	4.61	1.43	2.37	4.49	0.34
	MSE	0.011	0.023	0.017	0.032	0.024	0.003	0.012

表5脉冲信号宽度估计结果
Table5.Estimation results of pulse signals width

${\rm{MSE}} = \dfrac{1}{N}\mathop \sum \nolimits_{t = 1}^N {\left( {{s_{\rm{o}}}\left( t \right) - \widehat {{s_{\rm{o}}}}\left( t \right)} \right)^2}, $

其中${s_{\rm{o}}}\left( t \right)$为检测结果的单次测量值, $\widehat {{s_{\rm{o}}}}\left( t \right)$为估计值, N为样本数量.
对脉冲幅值和宽度的估计结果表明, 在信噪比门限之上, 强耦合Duffing振子对脉冲波形的恢复效果较好, 误差基本在5%以内, MSE表明结果的一致性也很好. 图8、图9、图10分别为三种脉冲波形在各自信噪比检测门限处的恢复效果.
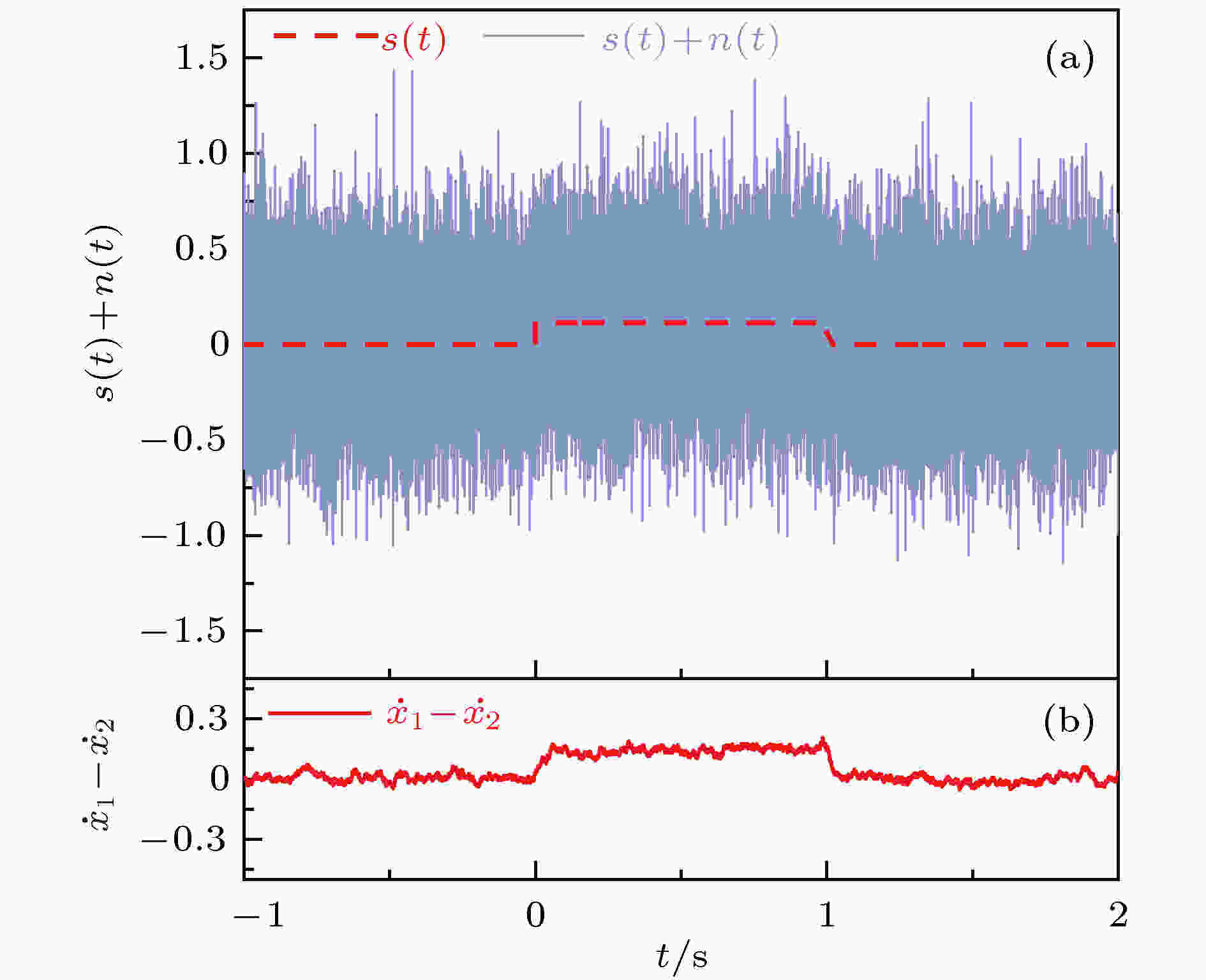图 8 检测信噪比–15 dB的方波信号　(a)输入信号; (b)输出信号
Figure8. Detection of square wave signal with SNR of –15 dB: (a) Input signal; (b) output signal

图 9 检测信噪比–12 dB的双指数脉冲　(a)输入信号; (b)输出信号
Figure9. Detection of double exponential pulse with SNR of –12 dB: (a)Input signal; (b) output signal

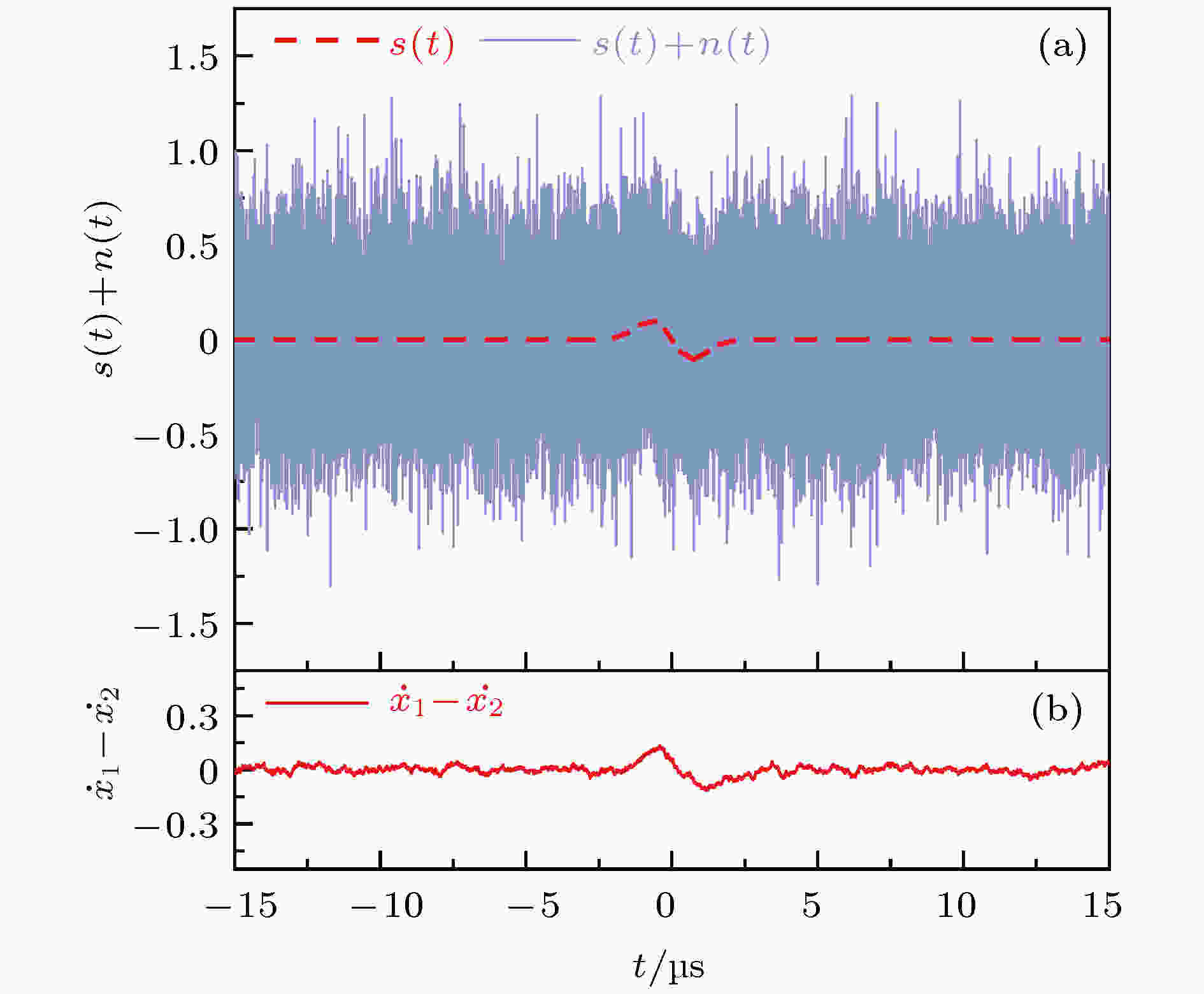图 10 检测信噪比–16 dB的高斯导数脉冲　(a)输入信号; (b)输出信号
Figure10. Detection of Gaussian derivative pulse with SNR –16 dB: (a) Input signal; (b) output signal

从三种波形的恢复效果可以看出: 噪声得到了很好的抑制, 波形整体畸变较小, 幅值、脉宽等时域信息均能在恢复结果中体现; 系统能够检测和恢复正负交替的脉冲信号; 方波虽然恢复波形在前后沿部分有所变缓, 但波形整体相似性较好, 尤其是平顶部分基本没有畸变; 通过时间尺度变换后系统可以检测和恢复从微秒级至秒级的脉冲信号, 表明系统不受时间尺度的限制.
2 -->

5.3.对比实验

下面对弱耦合Duffing振子和强耦合Duffing振子的信号检测和波形恢复情况进行对比. 输入信噪比–10, –12, –14和–16 dB的微弱高斯导数脉冲, 如图11(a)所示. 实验结果表明, 两种方法的信噪比检测门限都能达到–16 dB, 基本处于同一水平, 如图11(b)和图11(c)所示, 但强耦合Duffing振子对脉冲波形的恢复效果明显更好, 并且其稳定性、一致性等要优于弱耦合Duffing振子.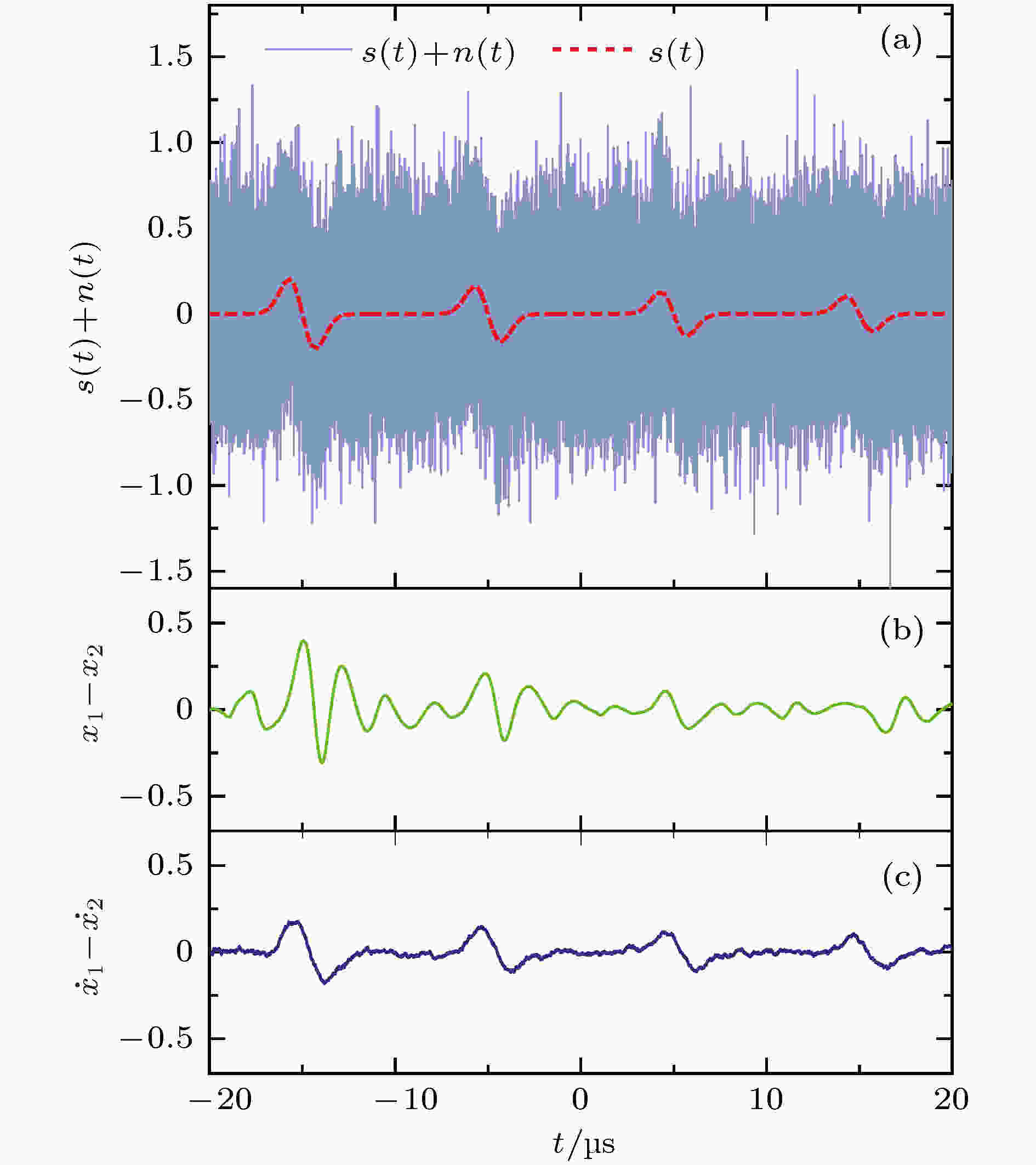
图 11 对比实验结果　(a)输入信号; (b)弱耦合Duffing振子输出信号; (c)强耦合Duffing振子输出信号
Figure11. Contrast experimental results: input signal (a); output signal of weakly coupled Duffing oscillators (b) and strongly coupled Duffing oscillators (c)

本文提出了一种强耦合Duffing振子的微弱脉冲信号时域检测方法, 解决了弱耦合情况下探测脉冲信号的一些固有缺陷. 该方法不仅能在高斯白噪声背景中判断微弱脉冲信号的有无, 还可恢复信号的一些时域信息. 本文工作的结论如下:
1)利用信噪比改善和波形相似度对强耦合Duffing振子参数进行分析, 结果表明优化后系统对微弱脉冲信号的信噪比增益可达20 dB以上;
2)强耦合Duffing振子处于任何相态时均可工作, 具有可检测脉冲强度变化范围大、可检测脉冲种类多、可检测正负交替的脉冲等特点;
3)该方法不受时间尺度的限制, 只需调节驱动力周期, 即可检测不同时间尺度的脉冲信号;
4)由于该方法对系统初始状态不敏感, 因此有利于执行分段并行计算, 这对脉冲信号的实时检测应用非常重要.
该方法受计算步长的影响较大, 对采样率的要求较高, 另外本文研究的背景噪声仅限高斯白噪声, 其他噪声对系统检测性能的影响有待进一步研究.