摘要: 导航地面验证是X射线脉冲星导航研究必不可少的环节. 针对导航算法验证需要真实连续的脉冲星信号的需求, 同时避免X射线调制及探测难度大、成本高的问题, 提出了一种基于可见光源的X射线脉冲星导航地面验证系统. 该系统利用太阳系质心处脉冲星信号模型和航天器轨道信息, 建立航天器处实时光子到达速率函数, 再通过硬件系统转换成电压信号, 利用该电压控制线性光源输出, 最后经衰减、探测及甄别后获得航天器处的实时光子到达时间序列. 该时间序列不仅具有导航脉冲星的轮廓特性、自转特性, 还包括空间传播时间效应及宇宙X射线背景. 本系统利用半物理装置对可见光进行调制及衰减, 实时判断轨道各位置处导航脉冲星的可见性, 实现X射线脉冲星信号传播过程的模拟. 该系统提供四路可控输出信号, 支持多种导航模式的验证. 仿真系统的性能分析和功能验证结果表明, 该系统具有良好的性能, 可提供真实便捷的地面验证环境.
关键词: X射线脉冲星导航 /
地面验证系统 /
多物理特性 /
信号模拟 English Abstract Ground verification system of X-ray pulsar navigation with multi-physical properties Fang Hai-Yan Cong Shao-Peng Sun Hai-Feng Li Xiao-Ping Su Jian-Yu Zhang Li Shen Li-Rong School of Aerospace Science and Technology, Xidian University, Xi’an 710126, China Received Date: 19 December 2018Accepted Date: 16 February 2019Available Online: 01 April 2019Published Online: 20 April 2019Abstract: Navigation ground verification is an essential part of X-ray pulsar navigation (XPNAV) research. Aiming at the need of real and continuous pulsar signals for navigation algorithm verification, and to avoid the difficulties and high costs of X-ray modulation and detection, we propose an XPNAV ground verification system based on visible light source. In this system, the pulsar signal model at the solar system barycenter and the orbit information are used to establish the real-time photon arrival rate function at a spacecraft, and then the rate function is digitized and converted into voltage signal by the designed hardware system to drive a linear light source. After the processes of light attenuation, signal detection and pulse discrimination are experienced, the real-time photon time of arrivals (TOAs) at a spacecraft can be achieved. These photon TOAs contain characteristics of the pulsar profiles and frequency, the time propagation effect in the solar system, and cosmic X-ray background. The system uses semi-physical devices to modulate and attenuate visible light, and judges whether the spacecraft can observe the navigation pulsar according to the real position, thereby realizing the simulation of X-ray propagation in space. At present, the detection method of pulsar observation with single detector include detection of single pulsar, time division detection of multiple pulsars, and simultaneous detection of multiple pulsars. The system has four channels, each of which has three output modes mentioned above, and can support the verification of multiple navigation modes. This system consists of signal simulator and controller, single photon generator and detector, single photon screening and time tagging, and navigation algorithm verification. This paper presents the testing results of the system characteristics, the authenticity of the simulated photon arrival time series and the navigation verification. Monte Carlo experiments show that the recording accuracy of photon arrival time is 10 ns and the delays of the four channels are (11 ± 2), (15 ± 4), (14 ± 3), and (16 ± 4) ${\text{μ}}{\rm{s}}$ , respectively. The multi-physical properties of simulated photon arrival time series are introduced in detail, including photon flux, shape of observation profile, pulsar frequency characteristics and Doppler shift. The position and velocity errors of autonomous navigation algorithm test are 13.587 km and 14.277 m·s–1 , respectively, with an orbital altitude 26610 km and within 10 h. The ground verification system adopts master-slave control mode, the master computer mainly implements parameter setting and navigation algorithm verification, and the slave computer mainly carry out pulsar signal simulation. The communication based on TCP/IP protocol is applied to realize parameter transmission and real-time control between the master and slave computers in navigation verification process. The results of performance and functional test show that the system is available to accomplish the simulation of photon TOAs of X-ray pulsars at a spacecraft in real time and implement the ground verification of XPNAV.Keywords: X-ray pulsar navigation /ground verification system /multi-physical properties /signal simulation 全文HTML --> --> --> 1.引 言 X射线脉冲星导航是一种新型的天文自主导航方式, 通过探测脉冲星辐射信号提取导航观测信息[1 ] . 由于大气中的氧原子与氮原子对X射线的强吸收, 地面设备难以探测X射线脉冲星信号, 导航实验要在稀薄的大气层或其外部进行. 因此需在地面完成验证后再开展空间实验,这就要求建立一套可靠有效的地面验证系统. X射线脉冲星导航地面验证系统的关键是具有多物理特性的脉冲星信号模拟及导航过程的模拟.[2 -4 ] 和半物理模拟两种方式, 其中半物理模拟又有机械转盘[5 , 6 ] 和电控光源[7 -12 ] 两种形式. 算法模拟中光子到达时间(time of arrival, TOA)序列是由计算机产生的伪随机序列, 半物理模拟通过对光信号的衰减, 得到真实的随机序列. 机械转盘的模拟方式结构较复杂, 脉冲星轮廓特性和频率特性的模拟精度相对较低, 且模拟不同的脉冲星信号需要更换形状不同的转盘, 灵活性较差. 而电控光源的方式, 可以解决上述问题, 根据采用的光源不同, 可以分为X射线光源[5 -8 , 12 ] 和可见光源[9 -11 ] 模拟. 由于脉冲星导航的观测量是光子到达时间序列, 该序列体现出的脉冲星的轮廓特性、频率特性及空间传播特性是导航验证必不可少的物理特性, 这些特性的模拟是导航算法地面验证中信号模拟的关键所在. X射线在不同能级上的轮廓特性有微小的差别, 导航选用的能级确定后其轮廓特性也是稳定的[13 ] , 虽然可见光与X射线在信号能量上具有较大差异, 但产生的光子时间序列能反映出相同的轮廓特性及其他所需的物理特性, 因此可用于X射线脉冲星导航信号的模拟[11 ] . X射线源的使用管理、调制及探测成本较高, 其优势在于对探测器和系统整体的验证; 而基于调制可见光的信号模拟结构简单且安全性高, 更便于导航算法的验证.6 , 8 ]采用了这种模式. 实时模拟则在导航验证过程中根据航天器的实际轨道、速度等信息, 实时产生航天器处具有多物理特性的各导航脉冲星的光子序列, 对导航进行验证. 实时模拟过程与航天器实际飞行过程一致, 模拟的真实度更高. 本文所提导航验证系统, 采用实时模拟.[14 ] 、XPNAV-1卫星[15 ] 和HXMT慧眼卫星[16 ] 均搭载有X射线探测器, 可开展定轨实验; 美国NASA利用SEXTANT完成世界首次X射线脉冲导航空间验证[17 ] . 我国已具有空间X射线探测的能力, 但在开展空间导航验证前, 利用具有多物理特性的地面系统进行验证都是必要的环节.2.地面验证系统结构 X射线脉冲星导航地面验证系统由信号模拟与控制、单光子产生与探测、单光子甄别与处理和导航算法验证四个单元组成, 如图1 所示. 针对目前脉冲星导航算法研究中涉及的航天器对脉冲星信号的不同探测方式: 单探测器同时探测多颗脉冲星、单探测器分时探测多颗脉冲星、单探测器探测单颗脉冲星, 本验证系统实现了四路可控独立输出, 每路均具有上述三种方式输出的功能, 提供所需模式的探测器信号, 支持多星导航、贯序导航等不同类型导航算法的验证.图 1 系统组成 (a)结构图; (b)实物图Figure1. Component of the system: (a) Structure diagram; (b) physical diagram.图2 所示.图 2 导航验证系统软件框架Figure2. Framework of navigation verification platform.3.航天器处光子序列实时模拟 航天器在轨飞行过程中接收到的光子序列不仅包含了脉冲星的物理特性、大尺度空间下的时间效应, 还体现了航天器的位置及速度等信息.3.1.航天器处光子速率函数 3.1.航天器处光子速率函数 航天器处X射线脉冲星光子到达时间可建模为强度是${\lambda _{{\rm{SC}}}}(t)$ 的非齐次泊松过程[18 ] , ${\lambda _{{\rm{SC}}}}(t)$ 即航天器处的光子速率函数, 可通过将脉冲星自转特性、航天器轨道信息等调制到太阳系质心(SSB)处的X射线脉冲星信号模型上获得.[1 , 18 ] ${N_{s, e}}$ 表示在观测时间段$(s, e)$ 内接收到的光子数; $\lambda (t)$ 表示光子到达的速率函数(单位为ph·s–1 ), 包含两部分${\lambda _{\rm{b}}}$ 和${\lambda _{\rm{s}}}$ 分别是宇宙背景流量和脉冲星源信号的光子流量; $h(\phi )$ 为$\phi \in [0, 1)$ 上的脉冲星标准轮廓[18 , 19 ] , 满足$\mathop {\min }\limits_\phi h(\phi ) = 0, \int_0^1 {h(\phi ){\rm{d}}\phi = 1} $ ; $\phi (t)$ 为脉冲星SSB处的计时模型, 表示为${\phi _0}$ 是脉冲星${t_0}$ 时刻在SSB处的相位, ${f^{(n - 1)}}$ 是脉冲星的频率项, ${f^{(0)}}$ (n = 1, 即$f$ )为脉冲星的自转频率, ${f^{(1)}}$ (n = 2, 即$\dot f$ )为频率一阶项, 依次类推, 高阶导数项反映了X射线脉冲星长期自转变慢的特性[20 , 21 ] , 通常取n = 3; $t$ 采用太阳系质心力学时(barycentric dynamic time, TDB).$t$ 时刻接收到的脉冲星信号的相位为${\phi _{{\rm{SC}}}}(t)$ , 则$\tau (t)$ 为时间转换项, 包括光子从航天器传播到SSB处的光行时和航天器固有时到TDB时间系统的转换. 时间转换采用RXTE平台里的实用简化公式:$c$ 为光速, ${\mu _{\rm{s}}}$ 为太阳引力常数, ${{n}}$ 为脉冲星在SSB坐标系下的单位方向矢量, ${{{r}}_{{\rm{SC/SSB}}}}$ 和${{{r}}_{{\rm{SC/E}}}}$ 分别为航天器相对于SSB和地球质心的位置矢量, ${{{v }}_{{\rm{E/SSB}}}}$ 为地球质心相对于SSB的速度矢量, $P$ 是地球时(terrestrial time, TT)到TDB的解析法转换公式中的周期校正项. 公式右侧第一项为几何延迟, 第二项为太阳Shapiro延迟, 第三和第四项为爱因斯坦延迟校正.[4 ] 3.2.航天器处光子序列产生与测量 -->3.2.航天器处光子序列产生与测量 为获得航天器处的光子序列, 首先利用太阳系质心处脉冲星信号模型和航天器轨道信息, 建立航天器处实时光子到达速率函数; 再通过硬件系统转换成电压信号, 利用该电压控制线性光源输出; 最后经衰减、探测及甄别后获得航天器处的光子序列, 原理如图3 所示. 基于本文的模拟原理, 将脉冲星宇宙背景流量的统计结果${\lambda _{\rm{b}}}$ 代入(6 )式中, 就可实现含有实际宇宙X射线背景的航天器处光子序列的模拟. 若在模拟时间内宇宙背景流量趋势性变化小, 可将${\lambda _{\rm{b}}}$ 设为常数.图 3 航天器处光子序列实时模拟原理图Figure3. Principle flow diagram of real-time simulation of photon TOA at the spacecraft.图4 所示, 首先计算出包含脉冲星自转特性及多普勒效应的航天器处${\lambda _{{\rm{SC}}}}(t)$ ; 然后经轮廓电压合成电路, 使用数/模转换电路(DAC)合成正比于${\lambda _{{\rm{SC}}}}(t)$ 的电压信号$U(t)$ , 由$U(t)$ 驱动线性光源LVS, 经衰减器得到单光子流, 即航天器处光子序列; 最后经过探测、甄别及电子学读出电路的处理, 获得每个光子的到达时间. 在物理上模拟该过程, 要求线性光源的瞬时发光功率$P(t)$ 与其衰减后的光子速率函数${\lambda _{{\rm{SC}}}}(t)$ 成正比线性关系[10 ] .图 4 航天器处光子序列实时模拟流程图Figure4. Flow diagram of simulation of photon TOA at the spacecraft.${\lambda _{{\rm{SC}}}}(t)$ 后, 以$\Delta t$ 为取样周期对其进行取样, 可获得离散化的轮廓$D(t)$ . $\Delta t$ 的取值取决于两个因素: X射线脉冲星信号的截止频率、DAC的零阶保持输出方式, 这种输出方式会对理论采样信号的频谱有一定的衰减作用. 为满足模拟要求, 采样率要尽可能高于信号的截止频率.$D(t)$ 转换成LVS的控制电压, 是由轮廓电压合成电路完成的. 这部分电路由数据流控制、DAC构成, 是在FPGA上开发的, 如图5 所示. 数据流控制电路的主要目的是高速接收从计算机传输的$D(t)$ , 并以一定的速率将接收到的数据写入DAC, 并产生启动信号和同步时钟信号. 本系统采用FIFO(first-in-first-out)来解决多比特数据跨时钟域传输问题, 实现数据的连续传输. 从计算机一次计算四颗脉冲星的${\lambda _{{\rm{SC}}}}(t)$ , 并且控制每次传入FIFO里$D(t)$ 的时间段一致, 解决了各通道仿真时间不一致的问题.图 5 电压合成电路组成Figure5. Diagram of the voltage synthesis which consists of a FPGA and a DAC.[11 ] . 光线经过衰减器衰减为光子流, 这些光子流拥有${\lambda _{{\rm{SC}}}}(t)$ 所包含的多种物理特性.4.系统测试 本文导航验证系统的测试主要从系统性能、航天器处光子序列模拟的真实性及导航验证等三方面进行论述.4.1.系统性能 4.1.系统性能 34.1.1.脉冲轮廓取样频率 -->4.1.1.脉冲轮廓取样频率 为获得离散化的轮廓$D(t)$ , 需要对${\lambda _{{\rm{SC}}}}(t)$ 进行取样, 取样频率f s 的选取直接影响模拟系统的工作性能和模拟获得的轮廓特性. 脉冲星轮廓的频谱具有收敛性[22 ] , 是频带有限信号. 但由于后续DAC电路采用零阶保持的方式对信号进行输出, 相当于理论采样信号卷积宽度为采样时间间隔的窄脉冲信号, 体现在频域上就是信号频谱乘以sinc函数, 会引起频谱上的衰减, 造成输出的轮廓失真, 因此仅由奈奎斯特取样定理确定取样频率是不够的.图6 所示(实验条件为采样时间间隔$\Delta t = 60\;{\text{μ}}{\rm{s}}$ , 对应的脉冲轮廓取样频率${f_{\rm{s}}}$ = 16.67 kHz). Crab脉冲星的周期约为33 ms, 经计算在频率为1.8 kHz时, 其标准脉冲轮廓幅频谱已达到–200 dB的衰减, 因此可将1.8 kHz作为Crab脉冲星的带宽. 当采样频率${f_{\rm{s}}}$ = 16.67 kHz时, 在1.8 kHz频率点处, sinc函数对理论频谱的衰减系数为0.977, 此时sinc函数对Crab脉冲星频谱的影响很小, 满足无失真恢复脉冲轮廓的要求.图 6 DAC输出信号频谱Figure6. Frequency spectrum analysis of the DAC output signal.4.1.2.系统的时间延迟 -->4.1.2.系统的时间延迟 本文的地面验证系统中采用了时钟同步来保证光子时间标记的一致性, 但由于信号经过硬件系统时存在延迟, 导致光子到达时间产生整体的偏移, 因此需要对系统的时间延迟进行测量, 从而实现光子到达时间的修正.图7 所示, 将具有确定周期$T$ 的信号替代脉冲星轮廓信号作为基准信号, 对系统产生的光子时间序列以周期$T$ 进行叠加, 获得观测信号, 然后利用基于最优频段的Taylor FFT算法[22 ] 计算观测信号与基准信号的时延, 所得结果即为系统的时间延迟. 根据该时延算法原理, 为提高估计精度, 本文采用具有丰富频率成分的周期矩形脉冲信号(如图7 所示)进行实验. 经蒙特卡罗实验, 本系统四个通道的时延分别为(11 ± 2), (15 ± 4), (14 ± 3)和(16 ± 4) ${\text{μ}}{\rm{s}}$ . 从统计结果看, 各通道的延迟不一致, 这主要是由线性光源引入的误差, 后期可改进光源响应性能来降低通道时延误差.图 7 系统时间延迟测量原理Figure7. Principle of system time delay measurement.4.2.系统模拟的真实性 -->4.2.系统模拟的真实性 34.2.1.脉冲星流量与轮廓 -->4.2.1.脉冲星流量与轮廓 本文模拟了5颗脉冲星, 模拟中设置的实际流量[20 ] 如表1 所示, 实际流量中包含宇宙背景流量, 模拟时长36000 s. 将所得光子数据分成500段, 光子流量统计结果见表1 , 实验结果表明, 模拟的X射线脉冲星信号光子流量与实际流量基本一致, 存在的微小偏差主要是由PMT暗计数和LVS热效应导致的.脉冲星 实际流量/–2 ·s–1 模拟流量/ph·m–2 ·s–1 ± B0531+21 15400 15410 ± 100 B1821–24 51.93 53 ± 6 B1937+21 50.499 51 ± 4 B1509–58 212 214 ± 10 B0833–45 65.9 66 ± 5
表1 脉冲星流量Table1. Flux of pulsars.5 )式和(6 )式转换到SSB处, 并对转换后的时间序列进行历元折叠, 可得到脉冲星的观测轮廓如图8 所示, 经计算, 与其标准轮廓的相关系数分别为0.9926, 0.9970和0.9982. 模拟时间越长, 观测轮廓的信噪比越高.图 8 面积归一化的观测轮廓Figure8. Observed profiles by area normalization.4.2.2.频率缓变特性与多普勒频移 -->4.2.2.频率缓变特性与多普勒频移 频率缓变特性是X射线脉冲星信号的重要物理特性, 对(3 )式求导可得到SSB处脉冲星信号频率${f_{\rm{p}}}$ 随时间的变化规律5 )式和(6 )式, 将所有时间序列转换到SSB处, 然后使用$Z_{\rm{m}}^2$ 方法[23 ] 进行频率搜索. 图9 给出了脉冲星频率缓变的理论值和模拟信号频率的实验值, 模拟值相对理论值的标准差分别为7.85 × 10–6 Hz (B1509–58)和5.25 × 10–6 Hz (B0531+21). 实验结果表明模拟的光子序列具有脉冲星的频率缓变特性.图 9 频率缓变特性模拟Figure9. Simulation of slow changing frequency characteristics.${f_{{\rm{sc}}}}$ 会受到多普勒效应的影响, 理论上会随航天器在轨周期运动而出现周期性变化:${f_{\rm{p}}}$ 是脉冲星在$t$ 时刻的频率.8 )式计算出理论的频率值, 再利用频率搜索方法获得模拟的光子序列的频率值, 比较两者的差异即可检验所模拟的光子序列. 设定系统的初始参考历元为MJD 49353.000696574074, 分别模拟了轨道高度约为450 km的航天器处B0531+21和B0833–45两颗脉冲星光子到达时间序列, 时长9360 s. 将模拟的光子到达时间序列均分成26段, 使用$Z_{\rm{m}}^2$ 法对每段数据进行频率搜索. 图10 给出了理论多普勒频移曲线和模拟信号的频率值, 模拟值相对理论值的标准差分别为1.04 × 10–5 Hz (B0531+21)和3.44 × 10–5 Hz (B0833–45). 实验结果表明模拟的光子序列的确具有航天器的多普勒效应.图 10 光子序列的多普勒频移Figure10. Doppler frequency of photon TOA at the spacecraft.4.3.导航算法验证测试 -->4.3.导航算法验证测试 34.3.1.验证流程 -->4.3.1.验证流程 X射线脉冲星导航中首先把航天器处光子到达时间序列校正到SSB处, 然后利用SSB处的计时模型进行历元折叠, 获得观测脉冲轮廓. 理论上当不存在定位误差时, 观测轮廓与标准轮廓的相位差为零. 当与标准轮廓存在相位差时, 该相位差反映了航天器的误差轨道与真实轨道在平均意义上的偏差. 以该相位差为观测量, 利用导航滤波算法校正航天器轨道, 可实现航天器自主导航[1 , 20 , 24 ] . 本系统实现导航算法验证的流程如图11 所示.图 11 导航算法验证流程图Figure11. Flow diagram of navigation algorithm verification.4.3.2.导航验证结果 -->4.3.2.导航验证结果 进行导航验证, 需要知道航天器的真实轨道, 选取的导航脉冲星及导航算法更新时间等参数, 更重要的是加载被测试的导航算法, 并进行导航结果的显示及评价. 而这些都可以通过主计算机的人机界面方便地进行设置和加载.表2 . 考虑地球和卫星的二体运动模型, 用数值积分生成航天器间隔为60 s的轨道文件, 将该轨道文件加载到导航工程中. 导航初始参考历元为MJD 49353.000696574074, 导航验证总时长37080 s, 导航算法的更新时间为360 s. 导航所选脉冲星见表3 , 流量参数同表1 . 表3 中RAJ与DECJ分别表示脉冲星在J2000坐标系下的赤经和赤纬, MJD是脉冲星参考历元的约化儒略日, Area表示航天器的有效探测面积.参数 航天器初始状态 状态初始估计值 X /m–13305111.403 –13305111.403 + 10000 Y /m13305111.403 13305111.403 + 10000 Z /m18816268.995 18816268.995 + 10000 V x –1 –2736.715 –5473.431 + 10 V y –1 –2736.715 –5473.431 + 10 V z –1 0 0 + 10 R /m26610222.806 26610222.806 + 17320.508 V /m·s–1 3870.299 3870.299 + 17.321
表2 航天器初始参数Table2. Initial parameters of spacecraft.Pulsar B1509–58 B0531+21 B0833–45 RAJ 15 13 55.598 5 34 31.972 8 35 20.591 DECJ –59 8 9.56 22 0 52.07 –45 10 35.35 MJD 49180.000000505 49368.000000239 49353.000000103 f (0) /s–1 6.6327493860874 29.9167641742573 11.1975539227276 f (1) /s–2 –6.75556 × 10–11 –3.76613 × 10–10 –1.55984 × 10–11 f (2) –3 1.96 × 10–21 4.28 × 10–21 1.72 × 10–22 Area/m2 1 1 1
表3 脉冲星参数Table3. Pulsars parameters.图1(b) ). 图12(a) 为主计算机导航算法评估部分界面截图, 显示了航天器三维位置偏差和速度误差曲线; 图12(b) 为利用导出数据绘制的相应曲线. 收敛后的位置和速度误差均值分别为13.587 km和14.277 m·s–1 .图 12 导航算法结果 (a)评估界面截图; (b)算法精度Figure12. Results of navigation algorithm: (a) Evaluation-interface screenshot; (b) algorithm precision.5.结 论 本文提出的导航验证系统实现了从光子仿真到导航算法验证的全过程. 系统模拟了X射线脉冲星信号在宇宙空间的衰减, 产生了具有轮廓、自转及空间传播等多物理特性的航天器处实时光子序列, 实现了导航算法的地面验证. 从光子到达时间标记精度、流量稳定度、观测轮廓形状、信号的周期缓变特性、多普勒现象和导航算法验证示例综合验证了平台的可靠性, 说明了模拟的航天器处光子到达时间序列更接近真实情况. 该地面验证系统利用可见光源, 便于实验室实现, 可有效支撑X射线脉冲星导航相关算法的研究.  图 1 系统组成 (a)结构图; (b)实物图
图 1 系统组成 (a)结构图; (b)实物图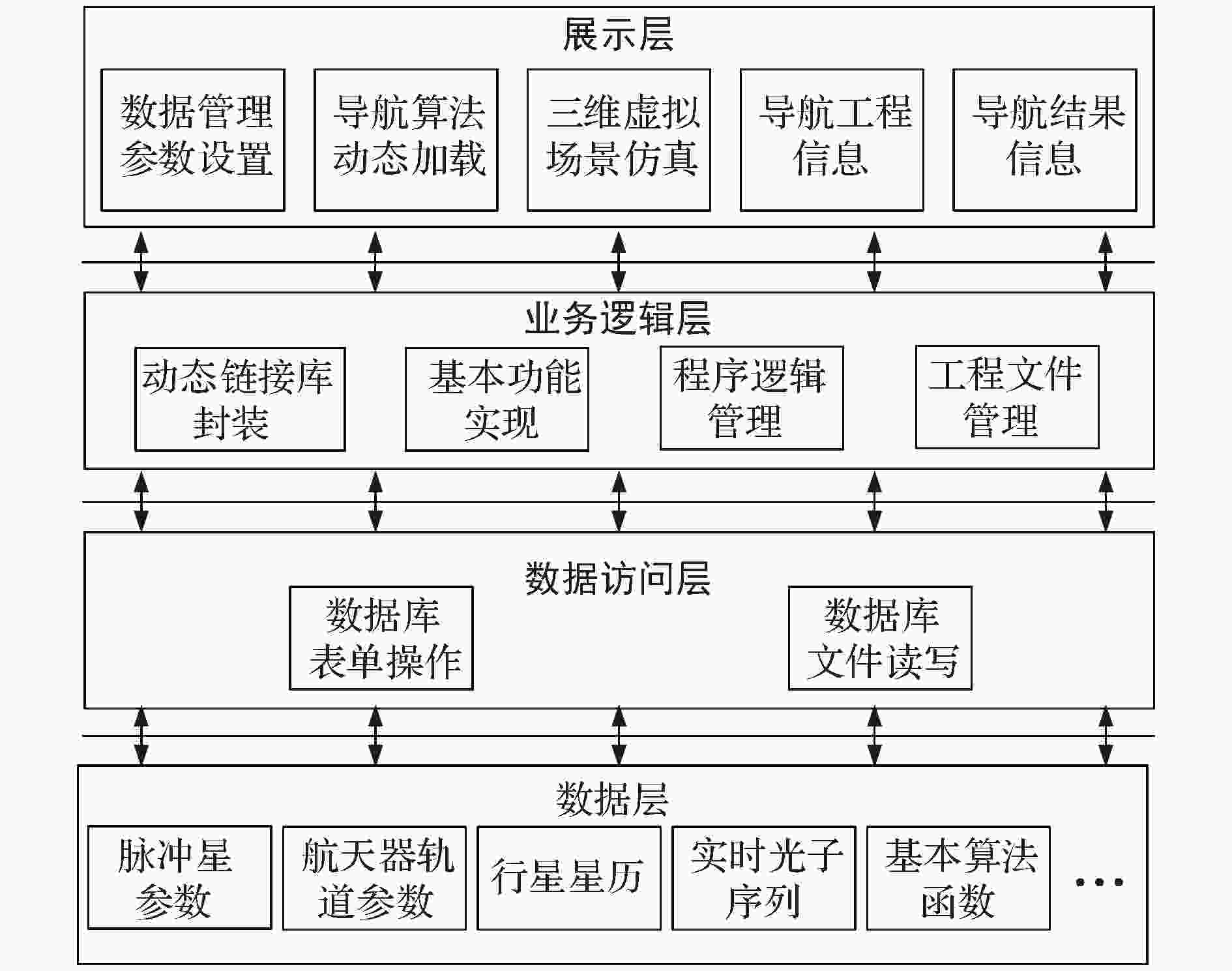 图 2 导航验证系统软件框架
图 2 导航验证系统软件框架


































 图 3 航天器处光子序列实时模拟原理图
图 3 航天器处光子序列实时模拟原理图













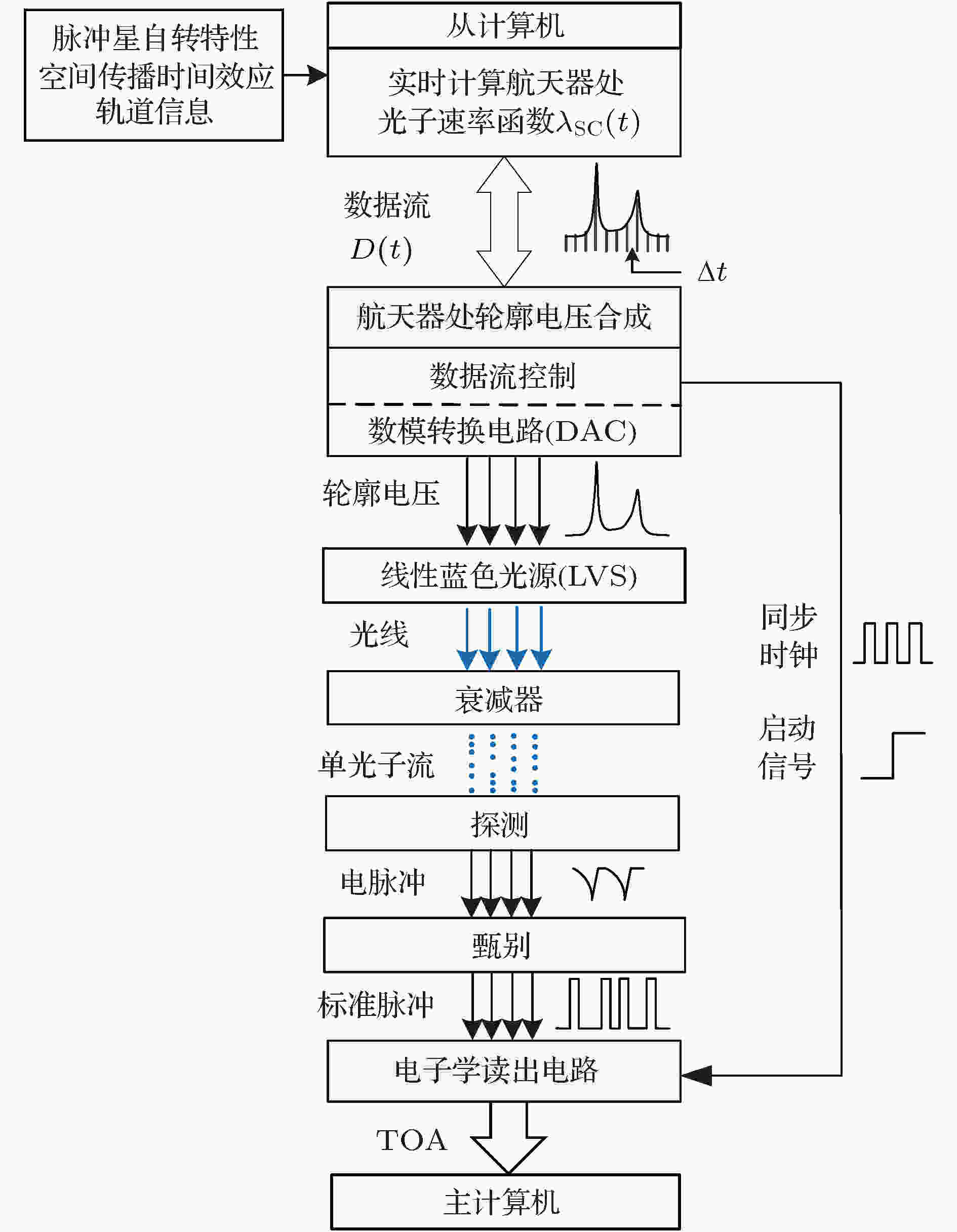 图 4 航天器处光子序列实时模拟流程图
图 4 航天器处光子序列实时模拟流程图















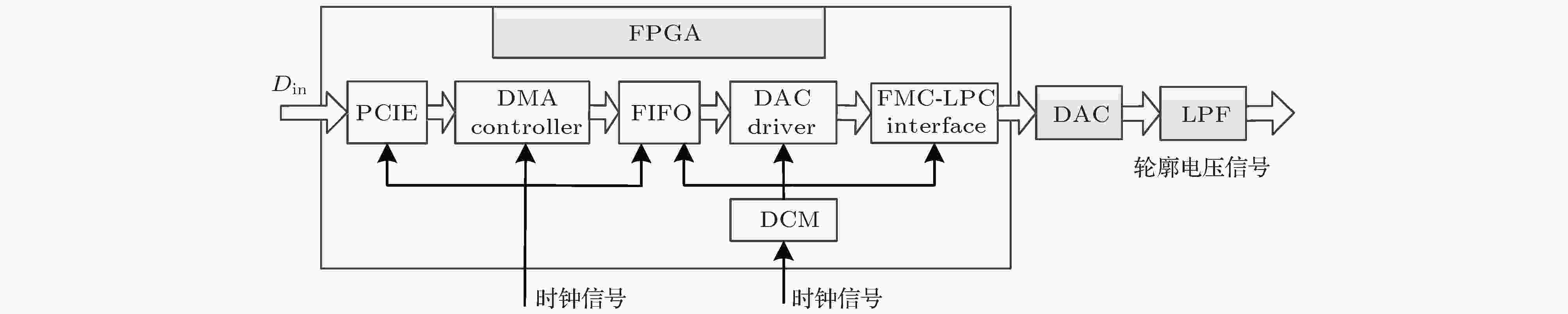 图 5 电压合成电路组成
图 5 电压合成电路组成







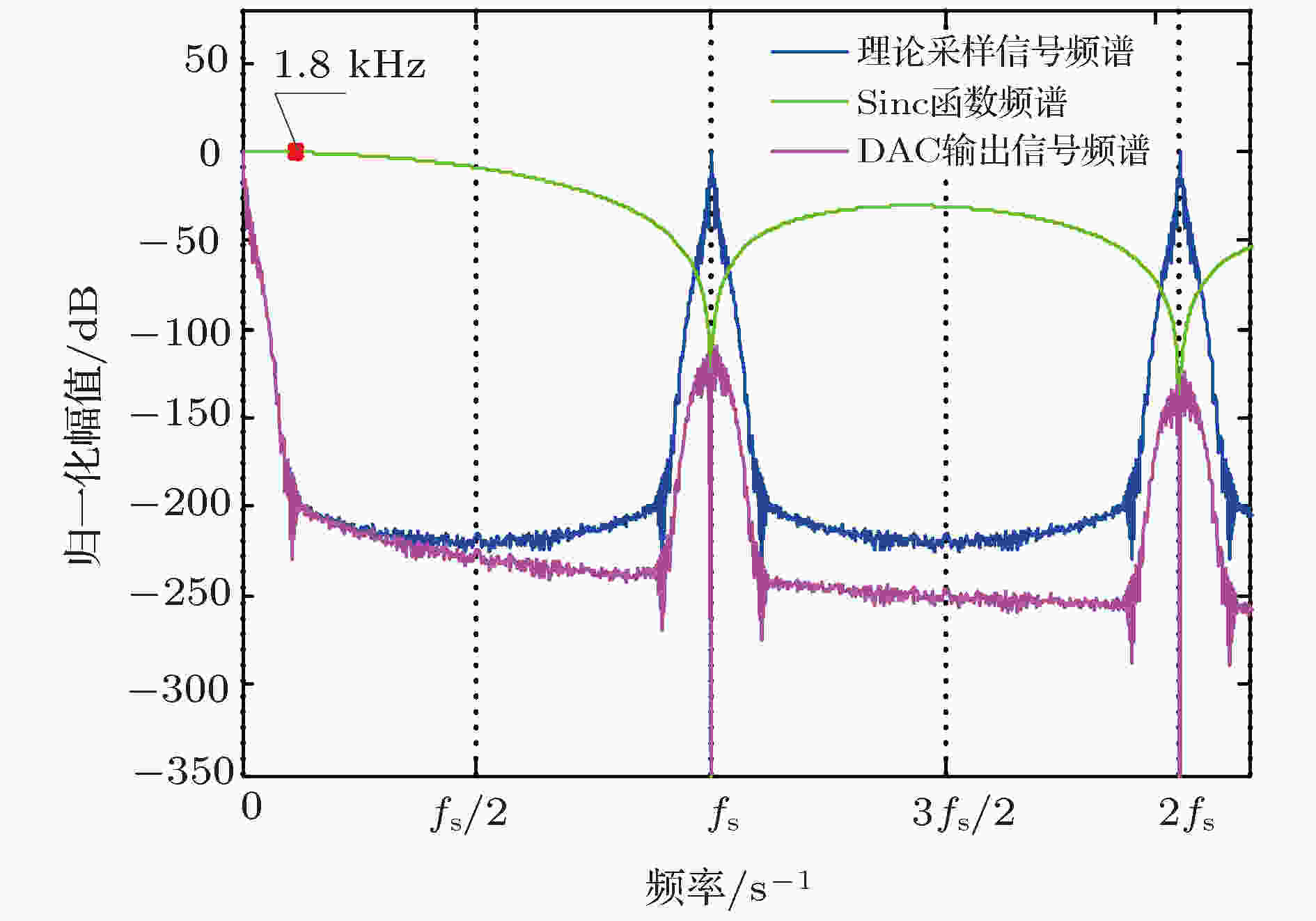 图 6 DAC输出信号频谱
图 6 DAC输出信号频谱




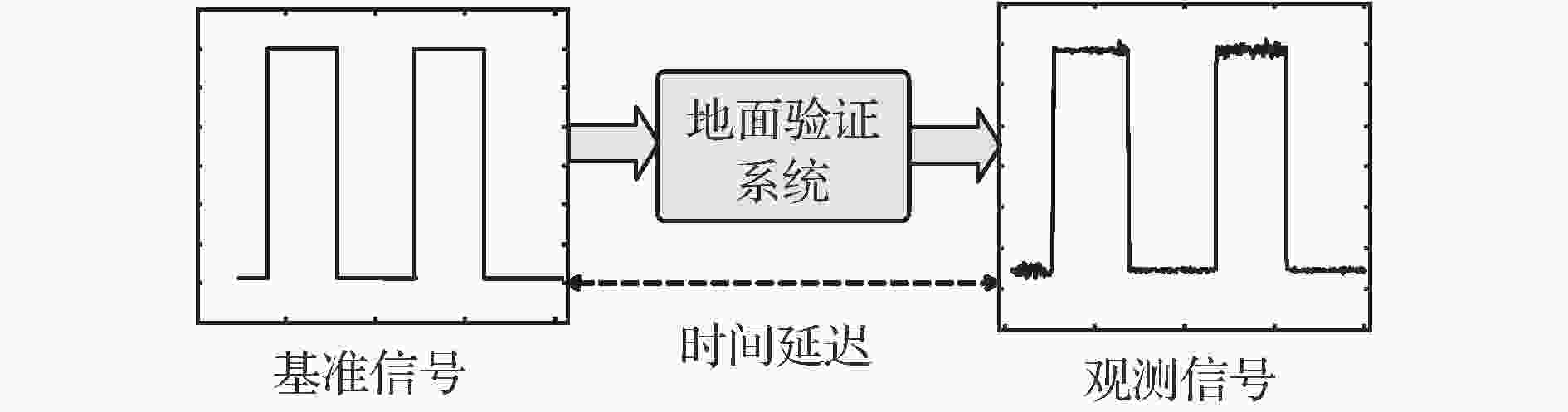 图 7 系统时间延迟测量原理
图 7 系统时间延迟测量原理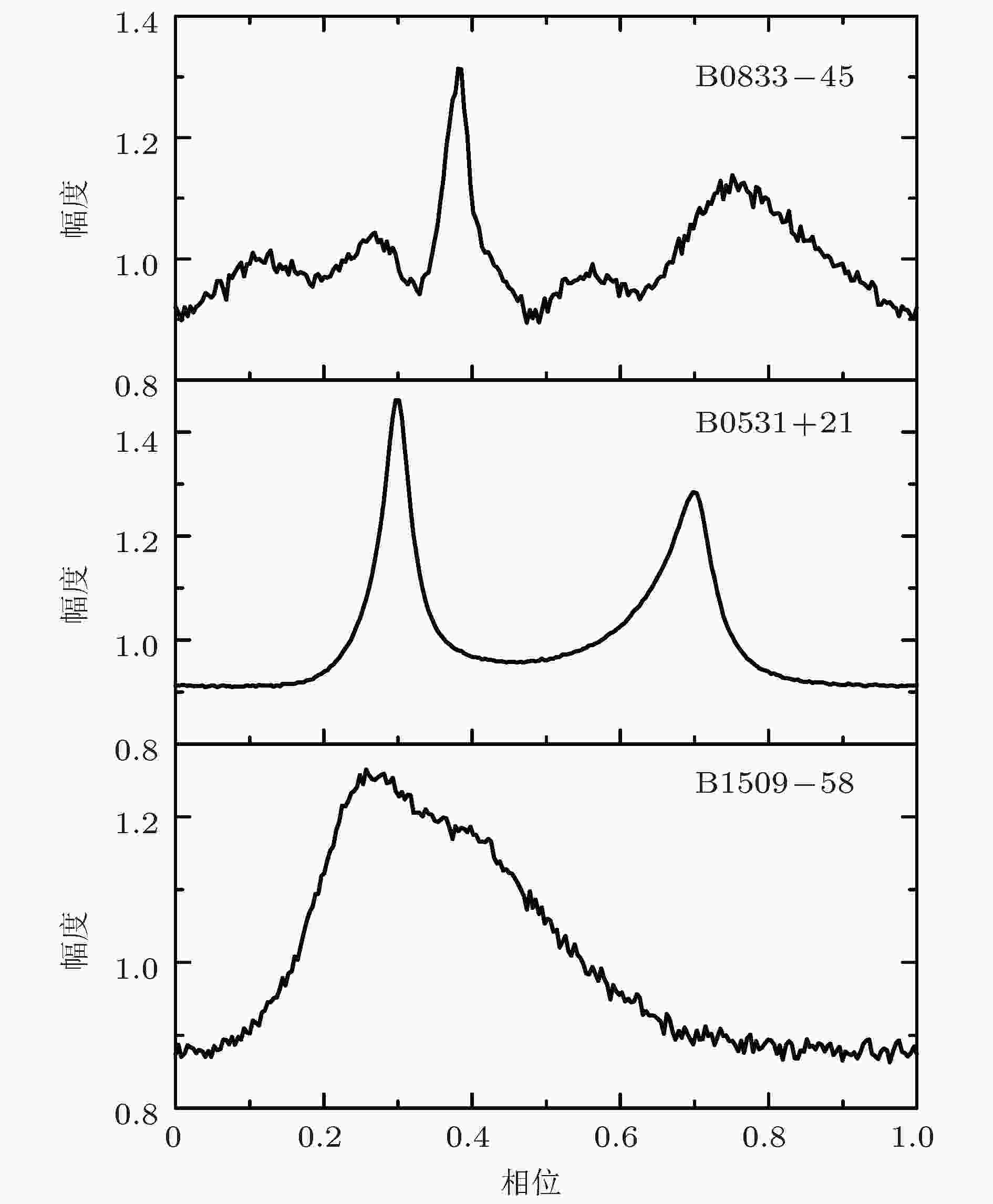 图 8 面积归一化的观测轮廓
图 8 面积归一化的观测轮廓

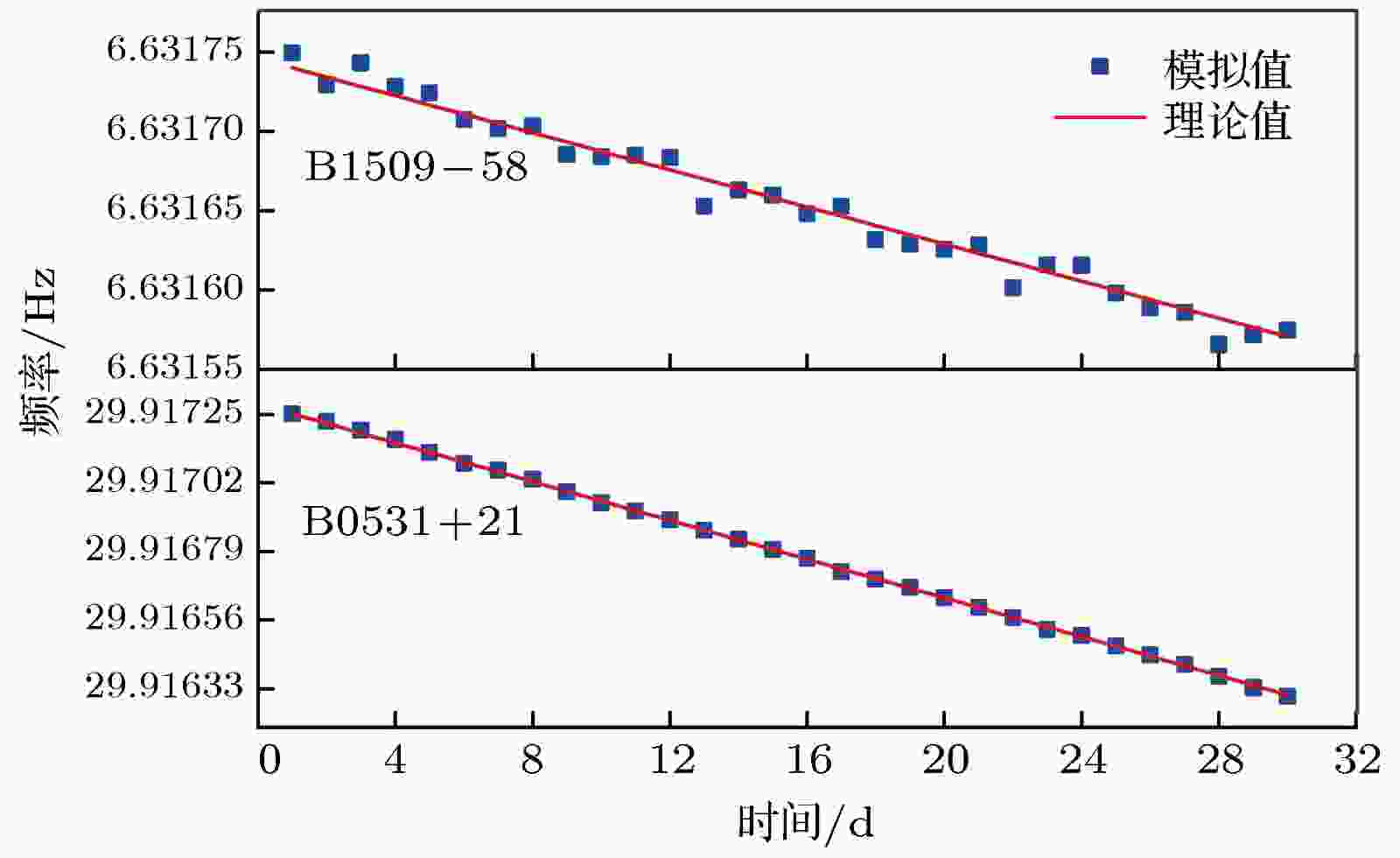 图 9 频率缓变特性模拟
图 9 频率缓变特性模拟



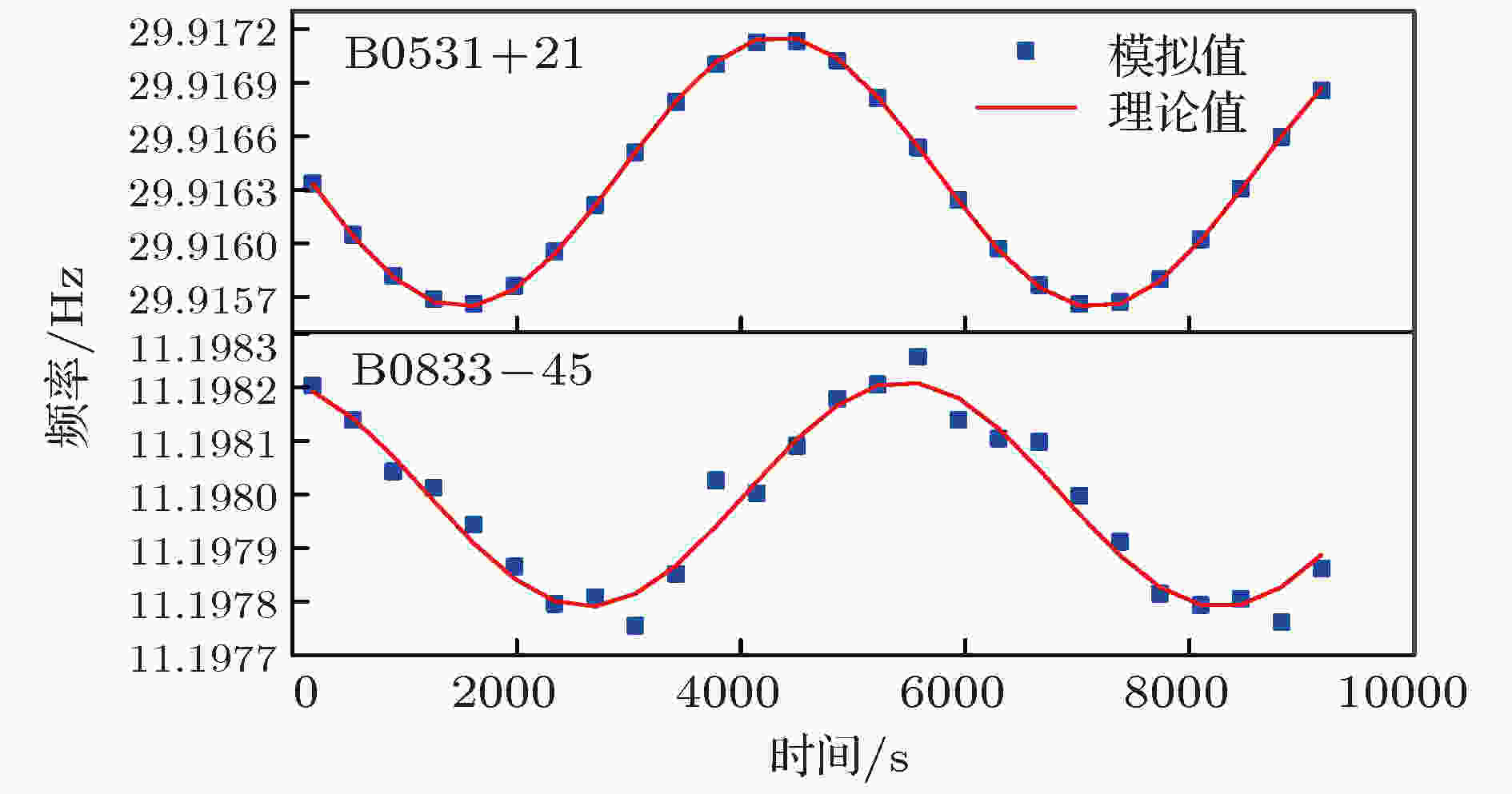 图 10 光子序列的多普勒频移
图 10 光子序列的多普勒频移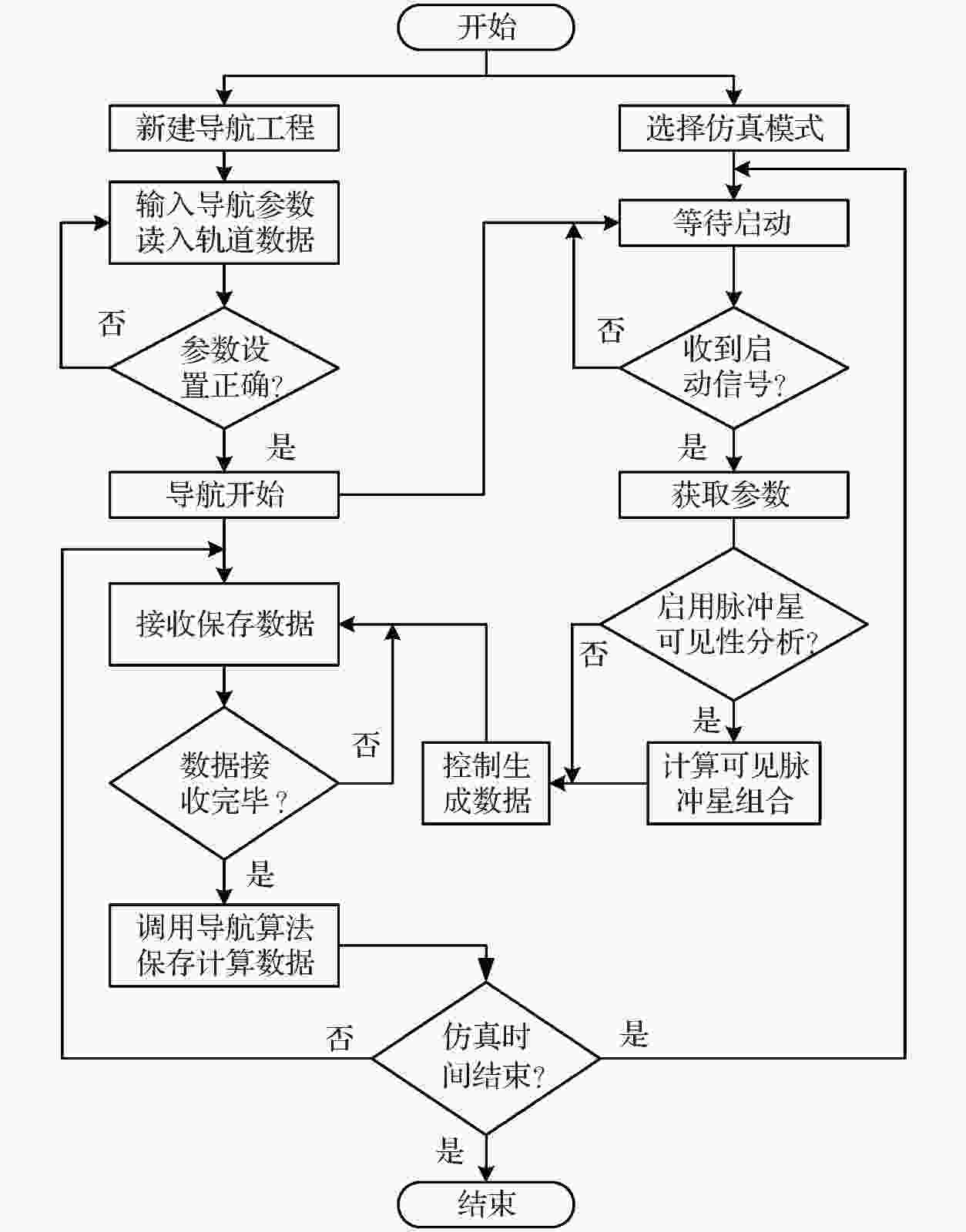 图 11 导航算法验证流程图
图 11 导航算法验证流程图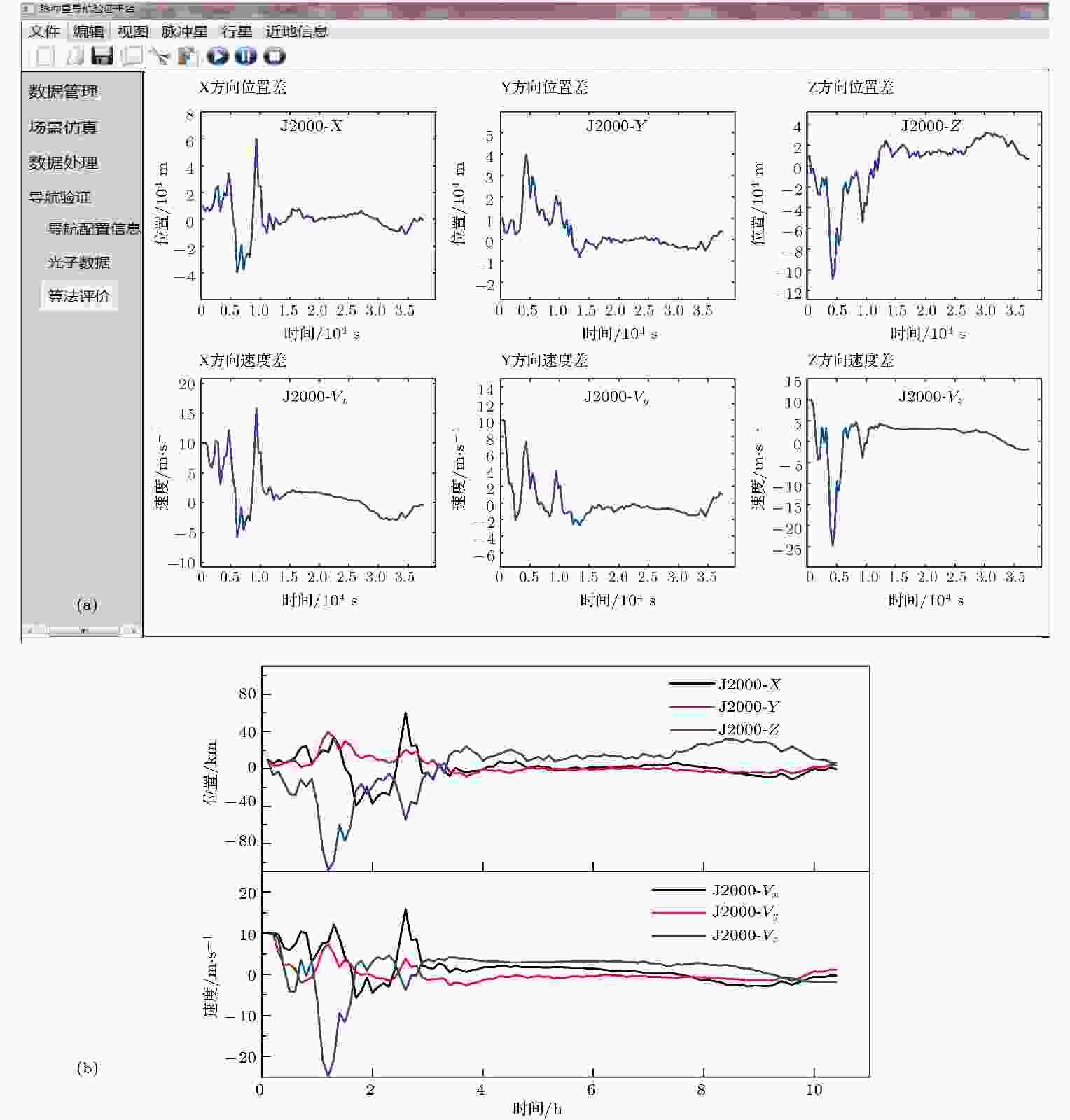 图 12 导航算法结果 (a)评估界面截图; (b)算法精度
图 12 导航算法结果 (a)评估界面截图; (b)算法精度
