摘要: 基于单模微腔与二能级原子系综(库)构成的混合动力学模型, 探索了非平衡库中量子关联相干(quantum correlated coherence, QCC) [Tan K C,
et al. 2016 Phys. Rev. A 94, 022329])对系统动力学的影响. 推导了量子关联相干库下系统演化的动力学方程. 借助于含QCC的类GHZ库及其对应的参考库, 清晰地揭示了非平衡库中QCC扮演着热力学资源的角色——能够有效辅助系统从库中提取更多能量. 同时, 结合解析与数值模拟方法研究了类GHZ库的有效温度和系统与库间的耦合参数对QCC能量效应的影响. 研究发现, QCC对腔场的能量贡献不仅依赖于库的有效温度, 而且也和系统与库间的耦合参数有关. 这与二能级原子构成的传统的热库的情况(腔场从热库中提取的能量仅仅依赖于库的有效温度即二能级原子的热布局)完全不同. 此外, 研究发现QCC可视作一类优质的热力学资源, 在特定条件下其对系统的能量贡献远大于原子热布局的贡献. 因此, QCC将是高输出功率或高效率量子热机设计中的一类重要燃料.
关键词: 量子纠缠 /
量子关联相干 /
能量提取 /
热力学资源 English Abstract Study on energy extraction assisted with quantum correlated coherence in bath Li Hai 1,2,3 ,Zou Jian 2 ,Shao Bin 2 ,Chen Yu 4 ,Hua Zhen 1 1.School of Information and Electronic Engineering, Shandong Technology and Business Universiy, Yantai 264000, China Fund Project: Project supported by the National Science Foundation of China (Grants Nos. 11547036, 11775019, 11375025, 61472227), the Education Department Foundation of Guizhou Province of China (Grants No. 090122), and the Ph.D. Research Startup Foundation of Shandong Technology and Business University, China (Grant No. BS201418).Received Date: 14 August 2018Accepted Date: 23 November 2018Available Online: 01 February 2019Published Online: 20 February 2019Abstract: Based on a hybrid model of a single-mode microcavity system plus an ensemble of two-level atoms (TLAs), we investigate the effect of quantum correlated coherence (QCC) [Tan K C, et al. 2016 Phys. Rev. A 94, 022329] of bath on the dynamic behaviors of system. The dynamic equations of system for a general bath with QCC have been derived. With the help of the GHZ-like state with QCC and its reference state, the role of QCC as a thermodynamic resource has been clearly shown where QCC could be used to enhance the system's energy. Meanwhile, combining with the analytical and numerical simulation methods, the influences of effective temperature of $ GHZ $ -like bath and the coupling strength between the system and the bath on the energy effect of QCC have been studied. We find that the energy contribution of QCC to the cavity field relies not only on the effective temperature of bath but also on the coupling strength. That is completely different from the case of traditional thermal bath where the energy captured by the cavity from the bath only depends on the bath temperature, i.e., the thermal distribution of TLAs. Moreover, several interesting phenomena, in the paper, have been shown: 1) the higher of the effective temperature of bath, the larger of the cavity's energy extracted from the QCC of bath; 2) under the fixed effective temperature of bath, the smaller of the coupling strength the larger of the maximal extractable energy from QCC of bath; 3) there exists the trade-off between the cavity's energy and the capability of cavity capturing the energy of TLAs entering the cavity, i.e., the cavity's energy extracted from each TLA crossing the cavity always decreases as the energy of cavity increases; 4) the energy contribution of QCC of bath to cavity is beyond the one of the thermal distribution of TLAs in bath, and it could become more prominent when the coupling strength is taken the smaller value, which also means that in the case of weak coupling strength it is the QCC of bath not the thermal distribution of bath dominating the cavity's energy. Thus, the QCC of bath could be viewed as a kind of high quality thermodynamic resource. It has the potential applications in the design of a quantum engine with high output power or efficiency, and the enhancement of charging speed of quantum battery. Our investigation is beneficial to the further understanding of quantum coherence in quantum thermodynamic regime.Keywords: quantum entanglement /quantum correlated coherence /energy extraction /thermodynamics resource 全文HTML --> --> --> 1.引 言 量子信息科学的快速发展使人们对量子资源, 如非定域性、纠缠和量子相干等的物理特性有了更加深入的认识[1 ] . 借助于这些量子资源, 科学家们可以实现经典物理中不可能完成的一些任务[2 ] . 随着激光技术以及微纳米制造工艺的不断提高, 人们正朝着操控越来越小器件的方向发展. 同时, 这也进一步促进众多研究者对微小器件中出现的量子效应的关注. 尤其是量子相干, 其作为核心的物理资源已参与到大多数量子现象之中并得以应用[3 ] . 近期, 德国物理学家Plenio课题组[4 ] 首次给出了量子相干度量的简洁的数学描述. 这一突破性研究激发了众多****对量子相干在量子信息中作为资源的相关理论的进一步探索[5 -20 ] . 例如, 关于量子关联和量子相干之间的联系方面, Streltsov课题组[14 ] 和Yao等[15 ] 的研究表明: 量子相干能够产生量子纠缠并可以被视作量子纠缠的源; 韩国科学家Tan等[16 ] 提出: 量子纠缠可以被认为是一种特殊的量子相干. 这种量子相干被称为量子关联相干(quantum correlated coherence, QCC), QCC指的是多体系统的各个子系统之间的量子纠缠或相干. 最近, Wang等[17 ] 给出了基于熵的QCC的度量方案, 并验证了量子失谐(discord)和量子纠缠能够用QCC有效刻画.[21 -43 ] . 他们在多种量子系统和模型中对量子相干的热力学特性进行了探索, 包括: 量子光学系统如微腔[21 -26 ] 、离子陷阱[27 ] 、光学晶格[28 ] 、光力学系统[29 ,30 ] 和生物系统[31 ,32 ] 等. 从研究角度上看, 量子效应的热力学探索包括两类: 一类是研究热循环中系统或量子工质携带的量子效应的热力学特性[19 ,37 ,44 -58 ] ; 另一类则考察量子非平衡库中量子效应的热力学特性, 如库中的热纠缠[59 ] 、 量子相干[22 -26 ] 和量子压缩[60 -63 ] . 特别地, 在量子光学实验中微腔是为数不多的可以被有效操控的微纳器件, 它为非平衡库中量子相干的热力学效应研究提供了重要的平台. 2003年, 物理学家Scully等[22 ] 借助于微腔系统开创性地研究了非平衡相干库中三能级原子内近简并能级间相干的热力学效应. 他们揭示了库中原子的量子相干能够有效促进微腔系统能量的提取并实现高输出功率的光子卡诺热机. 受此工作启发, ****们基于微腔系统对量子相干热力学特性开展了一系列有趣的研究工作. 比如: 2012年Liao等[23 ] 利用大量彼此独立且携带量子相干的二能级原子检验了原子相干在腔场热化中的作用; Türkpen?e等[24 ] 探索了多能级相干系统组成的非平衡库对实现高输出功率的量子热机的意义; Dillenschneider等[59 ] 研究了构成库的原子对中的热纠缠和量子失谐的能量效应; 近期, 文献[25 ]讨论了处于一般X型态下原子对的量子相干和量子关联对微腔系统做功能力的影响, 揭示了影响系统做功能力的较为本质的热力学源是量子相干而非量子关联. 这些研究使人们对非平衡库中量子相干或关联的热力学特性有了更加深入的认识.图1 所示). 为研究方便, 文中考虑了单个二能级原子为粒子单元顺次穿腔的情形. 借助于具体的库态—类GHZ态(携带QCC)和其对应的参考态(不含QCC), 我们清楚地展示了: 腔场从类GHZ库态中提取的能量总大于其从相应参考态的库中获得的能量, 并表明QCC与局域相干[22 -26 ] (单个粒子单元中携带的相干)类似, 能够扮演热力学资源的角色以提高系统的能量. 同时, 我们也讨论了库的有效温度以及系统与库间的耦合参数对QCC的能量效应的影响, 并揭示了QCC对腔场的能量贡献不仅依赖于库的有效温度而且与系统和库间的耦合参数有关. 特别是在弱耦合条件下, 类GHZ库中的QCC对腔场的能量贡献远大于库中原子热布局对腔场的能量贡献. 因此, 在特定条件下QCC可视为一种优质的热力学资源.图 1 单模微腔与一系列二能级原子组成的原子库相互作用示意图 (a)处于QCC库中的二能级原子顺次穿过微腔; (b)库中无QCC情况下, 二能级原子顺次穿过微腔Figure1. Schematic diagram of a single-mode microcavity interacting with a TLA-bath consisting of a series of two-level atoms: (a) The atoms of bath with QCC passing through the cavity one by one; (b) the atoms of bath without QCC crossing the cavity.2.腔量子电动力学(QED)模型 这里, 我们考虑由大量完全相同的二能级原子构成的非平衡库与一单模腔场相互作用QED模型[64 -68 ] (如图1 所示). 假设库中原子间无任何相互作用, 并让原子一个接一个随机地注入腔场. 当考虑任意时刻腔内至多保留一个原子, 且原子与腔场发生共振耦合即Jaynes-Cummings (JC)耦合时, 系统哈密顿可表示为$ \hat{H}_{at} = \hbar\omega\hat{\sigma}^{z} /2 $ , $ \hat{H}_{ca} = \hbar\omega \hat{a}^{\dagger}\hat{a} $ 且$ \hat{H} _{int} = g(\hat{a}\hat{\sigma}^{+}+$ $ \hat{\sigma}^{-}\hat{a}^{\dagger}) $ 分别代表进入腔场的原子, 单模腔场以及原子与腔相互作用的哈密顿; $ \hat{\sigma}^{\pm} = \dfrac{1}{2}( \hat{\sigma}^{x}\pm i \hat{\sigma}^{y}) $ 为原子的升(“+”)降(“-”)算符, 其中, $ \hat{\sigma}^{x, y, z} $ 为标准的泡利算符; $ \hat{a}^{\dagger} (\hat{a}) $ 代表单模腔场的产生(湮灭)算符; 参量$ \omega $ 和$ g $ 分别代表二能级原子能级间的跃迁频率以及原子与腔场的耦合强度. 在标准微激光假设条件(假设系统为无损耗的高品质腔体, 且考虑每个原子快速地穿过腔场即忽略原子的弛豫)下[69 ] , 二能级原子与腔场的动力学满足幺正演化. 在相互作用绘景下幺正算符可表示为:$ \tau $ 代表每个二能级原子穿过腔场时在腔内的驻留时间(单个原子与腔的作用时间); $ \xi = g\tau $ 称之为耦合参数. 上式给出了二能级原子能量本征基下腔场幺正演化算符的具体形式. 这里, 二能级原子能量本征基: $ \{|g\rangle, |e\rangle\}\rightarrow\{|1\rangle, |2\rangle\} $ 记为$ |g\rangle = \left( {\begin{array}{*{2}c} 0\\ 1 \end{array}} \right) $ , $ |e\rangle = \left( {\begin{array}{*{2}c} 1\\ 0 \end{array}} \right) $ . 在弱耦合极限下($ \xi\rightarrow 0 $ ), 利用近似关系: $ \cos \theta\approx 1-{\theta^{2}}/{2} $ 以及$ \sin \theta\approx\theta $ , 幺正演化算符$ \hat{U} (\tau) $ 可进一步化简为:$ \hat{\rho} _{ca}(0) $ 与$ \hat\rho_{bath}(0) $ 为腔场与原子库的初始态, 当任意的第$ k $ 原子穿过腔场时, 即在$ t_{k} = k\tau $ 时刻, 腔场的密度矩阵可表示为:$ \hat{U}_{k} = \prod_ {{m} = 1}^{k} {\hat I}^{ \otimes N-m}\otimes \hat{U}_{am} \otimes {\hat I}^{ \otimes m-1} $ 为第$ k $ 原子穿过腔场后的幺正演化算符; ${\hat I}$ 为二能级原子对应的单位阵; $ \hat{U}_{am} $ 代表第$ m $ 个原子与腔场作用的幺正算符. 由于库中的所有原子为全同粒子且与腔场的作用方式相同, 所以$ \hat{U}_{am} $ 的形式与方程(2 )和(3 )给出的完全相同. 方程(4 )给出了一般原子库下单个二能级原子依次穿过腔场时系统演化的密度矩阵表达形式. 实际上, 此表达式对于粒子单元为原子对或多个原子构成的原子团簇的情形也是适用的.3.非平衡QCC库 23.1.量子局域相干与QCC 3.1.量子局域相干与QCC 对于一个多粒子系统而言, 根据量子相干在其中存储形式的不同, 系统的态可划分为两种:局域相干的态和QCC态. 这里, 局域相干指的是体系中各个子系统之间相互独立即彼此间无任何的关联存在, 且相干仅仅出现于各个子系统之内; 而QCC则是指出现在各个子系统之间的量子关联或相干[16 ] . 为了清晰地对比两类态的特征, 下面给出任意$ N $ 体量子系统的局域相干的态和QCC态, 分别记为$ \hat\rho^{\rm loc} $ 和$ \hat\rho^{\rm qcc} $ , 的一般表达形式. 根据局域相干的态的特征, $ \hat\rho^{\rm loc} $ 可形式地表示为$ \hat{\rho}_{k} = R_k\hat{\rho}_{k}^{\rm coh}+(1-R_k){\hat I}_k^{ dia} $ , ($ 0\leqslant R_k\leqslant 1 $ ), 代表第$ k $ 个子系统的密度矩阵, 且$ \hat{\rho}_{k}^{\rm coh} ({\hat I}_k^{\rm dia}) $ 对应第$ k $ 个子系统纯的相干态(最大混合态); $ R_k $ 描述子系统中局域相干占据的组分大小. 而对于QCC态, 其密度矩阵的特征为在任意一套完备基下都不能分解为各子系统直积的形式. 因此, $ \hat\rho^{\rm qcc} $ 可表示为$ \hat{\rho}_{ii} = |i_{1, 2\!,\cdots , k,\cdots\!, N}\rangle\ \langle i_{1, 2,\cdots\!, k,\cdots , N}| $ (${\hat \rho _{ij}} = |{i_{1,2, \cdots\!,}}$ $k, \cdots\!, N \rangle \langle {j_{1,2, \cdots ,k, \cdots ,N}}|$ )和$ p_{ij} $ ($ p_{ij} $ , $ i\neq j $ )分别对应态中对角元(非对角元即QCC元)以及相应的权重; $ \{|i_{1, 2,\cdots , k, \cdots , N}\rangle\} $ 代表$ N $ 体量子系统的一套完备基.3.2.类GHZ态和参考态 -->3.2.类GHZ态和参考态 为了便于分析QCC的热力学效应, 我们构造一类非平衡QCC库态—类GHZ态及其对应的参考态进行研究. 在二能级原子本征基矢构造的非正交基下, 类GHZ库态表示为$ \{|+\rangle, |-\rangle\} $ 代表二能级原子的一组非正交基: $ |+\rangle = a|g\rangle+b|e\rangle $ , $ |-\rangle = a|g\rangle-b|e\rangle $ 且$ a = \sin\theta $ , $b =$ $ \cos\theta $ ; $ | {0}\rangle_{\rm GHZ} = |-\rangle^{\otimes N} $ , $ | {1}\rangle_{\rm GHZ} = |+\rangle^{\otimes N} $ , 且$ \gamma = 2+$ $2(a^2-b^2)^N $ 为类GHZ态的归一化系数. 类GHZ态的密度矩阵表示为$ {\hat{\rho}}_{jl}^{\rm GHZ} = | {j}\rangle_{\rm GHZ} \langle {l}| $ . 作为一个简单的例子, 当取库尺寸$ N = 2 $ 和$ N = 3 $ 时$ |\psi\rangle_{\rm GHZ} $ 可表示为:$ N = 2 $ 还是$ N = 3 $ , 类GHZ库态中总存在QCC. 当$ N $ 取较大值时, $ |\psi\rangle_{\rm GHZ} $ 则对应着较复杂的QCC态. 考虑到构成库的粒子为完全相同的二能级原子, 库中任意两原子(假设为$ A $ 和$ B $ )的密度矩阵$ \hat{\rho}_{\rm AB} $ 可表示为$ \alpha_{11} = 2{(1+{\varDelta})\cos{^{4}\theta/\gamma}} $ , $ \alpha_{22} = \alpha_{33} = \alpha_{23} = $ $ \alpha_{32} = {(1-{\varDelta})\sin{^{2}2\theta}/2{\gamma}} $ , $ \alpha_{14} = \alpha_{41} = (1+{\varDelta})\sin^2$ $ 2\theta/2{\gamma} $ , $ \alpha_{44} \!=\! 2{(1+{\varDelta}){\rm{Sin}}{^{4}}{\theta}/{\gamma}} $ , $ \varDelta \!=\! {\cos{^{N-2}({\text{π}}-2\theta)}} $ . 根据Wootter关于两体纠缠的定义[70 ] , 原子A和B间的纠缠度可以表示为$ C_{\rm AB} $ 的大小依赖于参数$ \theta $ 和库尺寸$ N $ . 特别地, 当类GHZ库尺寸为无穷大时任意两体间的纠缠度将趋于零, 即$ \lim_{N\rightarrow\infty}C_{\rm AB} = 0 $ .$ \hat{\rho}_{\rm ref} $ , 可以通过求迹掉类GHZ态中$ N-1 $ 个二能级原子的自由度所得的约化密度矩阵来构造, 并表示为$ {N\rightarrow\infty} $ 时$ p_{gg}^{\rm ref} = \sin^{2}\theta $ 且$ p_{ee}^{\rm ref} = \cos^{2}\theta $ . 对于一个由大量相同二能级原子构成的原子库, 其温度完全由单个二能级原子的布局及其能级差来确定:$ p_{gg} $ $ (p_{ee}) $ 为原子处于基态(激发态)上的概率; $ k_B $ 和$ \omega $ 分别代表玻尔兹曼常数和原子的能级差(能级跃迁频率). 不失一般性, 取$ k_B = \omega = 1 $ . 因此, 类GHZ库的有效温度与其参考库的温度相同并表示为:13 )可以看出: 对于一个确定大小的类GHZ库或参考库(库尺寸$ N $ 固定), 其有效温度仅与参数$ \theta $ 有关. 因此, 我们将$ \theta $ 称之为温度参数. 当库尺寸非常大即$ N\rightarrow \infty $ 时, 方程(13 )可进一步简化为$ \theta $ 成反比, 且为保证库温度为正$ \theta $ 需满足$ \theta\in({\text{π}}/4, {\text{π}}/2) $ . 此外, 需要解释的是: 在文中我们采用二能级原子的一组非正交基$ \{|+\rangle, |-\rangle\} $ 代替传统的正交基$ \{|e\rangle, |g\rangle\} $ 来构造非平衡库, 目的是使库有合适的有效温度对应. 对于由正交基$ \{|e\rangle, |g\rangle\} $ 所构造的传统的GHZ态, 我们容易检验其对应的有效温度趋于无穷大, 在腔场演化的过程中系统的能量将是发散的.4.非平衡库下的腔场动力学 24.1.局域相干库下腔场演化 4.1.局域相干库下腔场演化 这里, 我们将考虑腔场处于N 个独立的二能级原子构成的局域相干库下的腔场演化. 记$ \hat{\rho}_{\rm bath}^{\rm loc}(0) $ 为库的密度矩阵并表示为:${\rm a}k $ $ (k = 1, 2,\cdots, N) $ , 代表第k 个二能级原子; $ \hat{\rho}_{{\rm a}k} $ 为第k 个二能级原子在自然基($ \{|e\rangle, |g\rangle\} $ 记为$ \{|1\rangle, |2\rangle\} $ )下的密度矩阵, 可表示为: $ \hat{\rho} _{{\rm a}k} = \sum_{j, l = 1}^{2}{a} _{jl, k}\hat{\rho} _{jl} $ , 其中$ \hat{\rho} _{jl} = |j\rangle\langle l| $ 且$ {a} _{jl, k} $ 为相应的矩阵元. 这里, $ \hat{\rho} _{{\rm a}k} $ 是方程(5 )中$ \hat{\rho} _{k} $ 的一种等价形式, 非对角元$ {a} _{jl, k} $ ($ j\neq l $ )用于刻画库的局域相干. 在自然基下, 当非对角元不为零即$ {a} _{jl, k}\neq 0 $ ($ j\neq l $ )时, 表明原子态$ \hat{\rho}_{\rm bath}^{\rm loc}(0) $ 中拥有局域相干, 反之, 当$ {a} _{jl, k} = 0 $ ($ j\neq l $ )时, 则表明原子中没有相干存在. 考虑到局域相干态下的所有原子相互独立, 根据方程(4 ), 当第k 原子穿过腔即$ t_{k} = k\tau $ 时, 系统的密度矩阵可表示为$ \hat{U}_{{\rm a}k} = \hat{U}(\tau) $ 在方程(2 )中给出, ${\mathcal{D}} (\tau) $ 为超算符. 在Fock基下我们记$ t_{k-1} $ 时刻腔场的密度矩阵为$ \hat{\rho} _{\rm ca}(t_{k-1}) = \sum_{m, n = 0}\rho_{m, n}(t_{k-1})|m\rangle$ $\langle n|$ , 那么, 方程(16 )可进一步表示为17 ), 只要给出腔场的初始态, 便可求得任意第$ k $ 个原子穿过腔后腔场的密度矩阵. 这里, 假设原子随机穿过腔场, 且每次最多只有一个粒子以概率$ p $ 进入腔场(原子未进入腔的概率为$ 1-p $ ). 当考虑原子每次穿过腔的时间$ \tau $ 极短即$ \tau\rightarrow 0 $ 时, 腔场的主方程可表示为$ \mathcal{\hat{H}} _{\rm eff} $ 和$ \mathcal{\hat{J}} $ 分别为系统的有效哈密顿量和超算符, 且表示为18 )给出了腔场在局域相干库${\rho}^{\rm loc} _{\rm bath}(0) $ 下的演化的具体形式. 从方程(19b )可以看出: 穿腔原子的对角元即原子的布局$ \{{a} _{11, k}, {a} _{22, k}\} $ 直接刻画了腔场中单个光子的吸收与辐射率, 其决定系统的细致平衡; 然而, 原子的相干部分即非对角元$ {a} _{12, k} $ $ ({a} _{21, k}) $ 则出现在方程(19a )中, 不仅对腔场有能量贡献即当$ {a} _{12, k}\neq 0 $ 时$ \mathtt{Tr}[\mathcal{\hat{H}} _{\rm eff}\hat{\rho} _{\rm ca}(t_{k})]\neq 0 $ , 而且能够引起腔场相干的产生(对比第$ k $ 个原子穿腔前后腔场的态$ {\hat{\rho}}_{\rm ca}(t_{k-1}) $ 和$ {\hat{\rho}}_{\rm ca}(t_{k}) $ , 原子穿腔后腔中出现了新的非对角元). 这里, 需要指出的是: 作为刻画系统动力学演化的基本方程(17 )和(18 ), 在弱耦合极限下(即$ \xi\rightarrow 0 $ 时)它们是等价的. 从方程(18 )当库中所有原子均相同时, 通过求解$\langle \dot {n}\rangle^{loc}_{ss} =$ $ \mathtt{Tr}[(\dot{\hat\rho}^{loc}_{ca} (t_k)) \hat{a }^{\dagger}\hat{a}]|_{t_k\rightarrow\infty} = 0 $ , 我们可以解析地得到腔场达到非平衡稳态时的能量[23 ] :$ a _{11} $ $ (a _{22}) $ 和$ a _{12} $ 分别对应自然基下二能级原子激发(基)态的布局和相干元. 方程(20 )中的第一项和第二项分别代表二能级原子纯经典布局(热布局)和局域相干对腔场能量的贡献. 由于第二项总为正, 因此我们可以认为局域相干扮演了热力学源的角色. 然而, 在有限耦合参数$ \xi $ 下主方程(18 )将不再适用. 此时, 腔场演化的动力学行为可以借助于递归方程(17 )用数值方法来揭示.4.2.QCC库下腔场演化 -->4.2.QCC库下腔场演化 接下来, 我们考虑由$ N $ 个二能级原子构成的QCC库下腔场的演化. 记$ \hat{\rho}_{\rm bath}^{\rm qcc}(0) $ 为任意一携带QCC的非平衡库的密度矩阵. 根据前面QCC的定义, 在任意一组完备基下$ \hat{\rho}_{\rm bath}^{\rm qcc}(0) $ 总包含对角元和非零的非对角元两部分, 并表示为:$ \hat{\rho}_{{bv}}^{ loc} $ $ (v = 1, 2, ..., m) $ 和$ {p} _{{v}}\neq 0 $ 分别代表库态的组分及相应的非零权重. 在各个子系统构成的局域基下, 方程(21 )中的非对角元部分$ \sum_{i\neq j} p _{ij}\hat{\rho} _{ij} $ 刻画了相互关联的各子系统之间的QCC. 考虑到库态中的每一组分$ \hat{\rho}_{{bv}}^{loc} $ 均为$ N $ 个独立二能级原子构成的直积态, 我们可以通过执行类似于4.1节中局域相干库下腔场演化的推导来得到QCC库(库态$ \hat{\rho}_{\rm bath}^{\rm qcc}(0) $ )下腔场的演化:$ \hat{\rho}^{\rm loc}_{cv}(t_{k+1}) $ ($ \dot{\hat{\rho}}^{\rm loc}_{cv}(t_k) $ )对应方程(21 )中库态的组分$ \hat{\rho}^{\rm loc}_{bv} $ 下的腔场演化, 且$ \hat{\rho}^{\rm loc}_{cv}(t_{k+1}) $ 和$ \dot{\hat{\rho}}^{\rm loc}_{cv}(t_k) $ 的具体表达形式分别与方程(17 )中的$ \hat{\rho} _{\rm ca}(t_{k+1} $ )和方程(18 )中的$ \dot{\hat{\rho}} _{\rm ca}(t_k) $ 完全相同. 方程(22 )和(23 )给出了腔场在QCC库下演化的一般方程. 然而, 两方程的适用范围有所差异: 在弱耦合极限($ \xi\rightarrow 0 $ )下方程(22 )和(23 )完全等价; 在有限耦合参数下方程(23 )不再适用, 此时我们则需要采用方程(22 )来研究系统的动力学行为.4.3.类GHZ库态下QCC的能量效应 -->4.3.类GHZ库态下QCC的能量效应 这里, 我们将基于类GHZ库态来展示QCC的能量效应, 并讨论耦合参数$ \xi $ 以及库的有效温度参数$ \theta $ 对腔场从QCC中提取能量的影响. 为简便起见, 记$ \langle n(m, N)\rangle $ 和$ \langle n\rangle_{SS} $ 为库中$ m $ 个二能级原子($ m\leqslant N $ , $ N $ 为库尺寸即库中的总的原子数)穿过腔后腔场的能量以及腔场达到稳态时的能量. 假设腔场的初始态为真空态. 在弱耦合极限$ \xi\rightarrow 0 $ 下, 根据腔场演化主方程(18 )和(23 )可以分别求得参考库态$ \hat\rho_{ref} $ 和类GHZ库态$ \hat\rho _{\rm GHZ} $ 下腔场达到稳态时的能量:24 )中的二能级原子布局$ \{p_{gg}^{\rm ref}, p_{ee}^{\rm ref}\} $ 的具体表达式已在方程(11 )中给出. 上面方程(24 )和(25 )分别给出了腔场从局域参考库(库态为$ \hat\rho_{\rm ref} $ 的热库)和类GHZ库(库态为$ \hat\rho _{\rm GHZ} $ 的QCC库)中所提取的最大能量(腔场的稳态能). 对比两库($ \hat\rho _{\rm GHZ} $ 和$ \hat\rho_{\rm ref} $ )在局域上它们是完全相同的, 即两态中单个二能级原子的布局及相干完全相同; 但从全局看, 由于QCC的存在类GHZ态中所有原子都相互关联而参考态下的原子则相互独立. 因此, 在两种不同库态下腔场从库中获取的能量的差异主要由类GHZ态中的QCC引起. 我们可以将QCC对腔的能量贡献定义为腔场从类GHZ库和其参考库中提取能量的差: $ \langle n(m, N)\rangle^{\rm qcc} = \langle n(m, N)\rangle^{\rm GHZ}-$ $\langle n(m, N)\rangle^{\rm ref} $ . 根据方程(24 )和(25 ), 腔场在类GHZ库态下达到非平衡稳态时QCC对腔场的能量贡献为26 )式可以看到: $ \langle n\rangle^{\rm qcc}_{SS} $ 是变量$ \theta $ 和$ \xi $ 的函数, 即腔场从库中QCC所提取的能量依赖于库的有效温度以及腔场与原子耦合强度. 同时, 在有效温度参数$ \theta $ 取值范围: $ \theta\in({\text{π}}/4, {\text{π}}/2) $ 内, 腔场的能量$ \langle n\rangle^{\rm qcc}_{SS} $ 是关于温度参数$ \theta $ 的非线性单调递减函数, 即库温度越高(温度参数$ \theta $ 越小)腔场从QCC中提取的能量越多, 且在零温极限下腔场从QCC中提取的能量趋于零, 即$ \lim_{\theta\rightarrow {\text{π}}/2}\langle n\rangle^{\rm qcc}_{SS} = 0 $ (这一特征可以对(26 )式的简单数值模拟得以验证). 因此, 方程(26 )表明: 在耦合极限下库中QCC确实扮演了热力学源的角色, 能够有效增加系统的能量.$ \xi $ 下, 描述腔场的动力学主方程(24 )和(25 )将不再适用. 此时, 系统动力学将由递归演化方程(17 )和(22 )来刻画. 借助于方程(17 )和(22 ), 我们能够研究耦合参数$ \xi $ 和库的有效温度参数$ \theta $ 如何影响QCC对腔场能量的贡献. 原则上, 在给定腔场初始态的条件下, 基于递归演化方程(17 )和(22 )可解析地求得任意时刻腔场的能量以及QCC的贡献. 然而, 当库态中有相干存在时, 即使仅少数几个原子穿过腔场, 腔场的能量表达式也会变得非常复杂. 因此, 通过解析的方法来分析有限耦合参数下QCC的能量效应是比较困难的. 考虑到在有限耦合情形下腔场能量与耦合参数$ \xi $ 和库的有效温度参数$ \theta $ 存在较为复杂的关系, 为清楚两参数如何影响腔场能量的提取, 我们在下面的数值模拟中将采用固定其中一个参$\xi(\theta )$ 来研究另一个参量$\theta(\xi )$ 的办法, 分别就$ \xi $ 和$ \theta $ 对腔场能量提取以及动力学过程的影响进行分析.$ \theta $ 和$ N $ 取确定值)耦合参数$ \xi $ 对$ \langle n(m, N)\rangle^{qcc} $ (类$ GHZ $ 态的QCC对腔场能量贡献)的影响.图2(a) 和图2(b) 分别给出了$ \langle n(m, N)\rangle^{qcc} $ 和$ \langle n(m, N)\rangle^{ref} $ (参考态下腔场提取的能量)在不同耦合参数$ \xi $ : $ \xi = \{0.1, $ $0.3, 0.5\}$ 下随原子穿腔次数$ m $ , $ m\in[1, 2\times10^3] $ , 的变化. 其中, 其他参数$ \theta $ 和$ N $ 取: $ \theta = 3{\text{π}}/8 $ , $ N = 2 \times $ $10^3$ . 从图2(a) 可以看出:对于不同的耦合参数$ \xi $ , 库中QCC对腔场能量贡献$ \langle n(m, N)\rangle^{qcc} $ 总是随着原子穿腔次数$ m $ 的增加而增加, 并最终达到各自的稳定值. 同时, 耦合参数越小, 腔场从QCC中可提取的最大能量值($ \langle n(m, N)\rangle^{qcc} $ 对应的稳定值)越大. 这一特征完全不同于由独立二能级原子构成的传统热库的情况:系统从热库中可提取的最大能量(系统稳态下的能量)仅仅依赖于热库的有效温度, 而与系统与库间的耦合强度无关. 正如图2(b) (图2(b) 和2(a) 取完全相同的参数)所示:当库处于参考态(热态)时, 腔场从热库中可提取的最大能量与耦合参数$ \xi $ 无关, 即在不同$ \xi $ 下, 腔场从处于参考态的热库中可提取的最大能量(稳态能)相等. 同时, 从图2(a) 和2(b) 也展示了腔场演化的两个特征: 1)不论库处于类$ GHZ $ 态还是其参考态, 腔场到达其稳态所需的时间, 记为$ t_{ss} $ ($ t_{ss} = m_{ss}\tau $ , $ m_{ss} $ 为腔场到达稳态时穿过腔的粒子数), 依赖于耦合参数$ \xi $ , 且耦合参数越小腔场到达稳态所需时间越长, 如在类$ GHZ $ 态和其参考态下, 当$ \xi $ 取: $ \xi = $ $ \{0.1, 0.3, 0.5\} $ 时, 腔场稳态对应的粒子数$ m_{ss} $ 分别约为: $ m_{ss} = \{1200, 120, 40\} $ (图2(a) )和$ m_{ss} = \{780, $ $80, 30\}$ (图2(b) ); 2)腔场能量的增加抑制其从库中提取能量的能力(这里的“提取能量的能力”是指:腔场从完全相同的单个穿腔二能级原子中提取能量多少的能力), 这一特征由腔场能量随穿腔粒子数$ m $ 的变化曲线的斜率反映—斜率越大, 表明腔场从单个原子中提取的能量越多(腔的能量提取能力越强), 反之越少(腔的能量提取能力越弱). 如图2(a) 中$ \langle n(m, N)\rangle^{qcc} $ 和图2(b) 中$ \langle n(m, N)\rangle^{ref} $ 均随穿腔粒子数$ m $ 的增加而增加, 但是它们关于$ m $ 的变化率(曲线斜率)却逐渐减小直到为零(腔场达到稳态).图2(a) 和图2(b) 所展示的这两特征与我们的物理预期是吻合的. 前者($ \xi $ 越小$ m_{ss} $ ($ t_{ss} $ )越大)从物理上可理解为: 耦合参数$ \xi $ 的大小, 在一定程度上可视作穿腔原子与腔场相互作用强弱的反映; 当相互作用强度越弱时, 每个原子与腔场间的能量交换(原子能量向腔场传递)就越小, 腔场要从类$ GHZ $ 态(图2(a) ) (参考态下(图2(b) ))下提取较大(固定大小)的稳态能量所需时间就会变长; 对于后者(腔场能量与其提取能量的能力间存在竞争关系)可理解为: 腔场能量越高其对应的“有效温度”越高(这里“有效温度”反映腔场能量与实际有效温度正相关), 腔场与原子间的“温差”将变小, 从而使得其从完全相同的原子中提取能量减少. 同时, 特征2)也保证了腔场在演化过程中其能量的收敛性(即稳态的存在), 这与物理实际是一致的. 此外, 从图2(a) 的内插图中可以看到: 在腔场演化的短时间范围内, 即穿过腔场的原子数较少时如$ m\leqslant 15 $ , 耦合参数$ \xi $ 越大QCC对腔场的能量贡献$ \langle n(m, N)\rangle^{qcc} $ 越大; 但是随着演化时间的增加, 情况恰好相反, 即较小的耦合参数$ \xi $ 对应着较大的QCC对腔场的能量贡献$ \langle n(m, N)\rangle^{qcc} $ . 这一特征可从腔场演化的动力学机制上给出以下解释. 首先, 耦合参数$ \xi $ 越大, 腔场从进入腔的原子中所捕获的能量以及原子携带的QCC越多; 其次, 随着原子不断穿过腔场, 腔场从原子中获取的QCC一部分以相干的形式存储于腔场之中(即腔场不断产生新的非零的非对角元(见方程(17 )), 另一部分则参与到腔场布局中表现出QCC的能量效应(即腔场的对角元受到正向调制). 在不同的耦合参数$ \xi $ 下, 当腔场演化时间远小于其到达稳态时所需的时间(即少量原子穿过腔时, 如内插图中$ m\leqslant 15 $ 的范围), $ \xi $ 越大也就意味着有较多的相干参与到腔场布局之中, 从而导致QCC对腔场的能量贡献较大; 但是, 随着原子穿腔数目的增加, $ \xi $ 越大, 腔场到达稳态时间越短, 此时QCC对腔场能量的影响快速减弱, 从而展现出: $ m $ 处于较大值时, $ \xi $ 越小QCC对腔场的能量贡献越大.图 2 腔场在不同耦合参数 $\xi=0.1$ (蓝色点线), $\xi=0.3$ (红色点线)和$\xi=0.5$ (黑色点线)下, 从不同库态中提取的能量随穿腔原子数 ($m\in[1, 2\times10^3]$ ) 的变化 (a)腔场从类GHZ态下QCC中提取能量$\langle n(m, N)\rangle^{\rm qcc}$ 随$m$ 的变化; (b)腔场从参考态(热态)下原子布局中提取的能量$\langle n(m, N)\rangle^{\rm ref}$ 随$m$ 的变化; 其他参数取为 $\theta=3{\text{π}}/8$ , $N=2\times$ 103 ; 内插图为$m$ 在区间$[1, 120]$ 的图形Figure2. The variations of cavity's energy, $\langle n(m, N)\rangle^{\rm qcc}$ and $\langle n(m, N)\rangle^{\rm ref}$ , respectively captured from the QCC of GHZ-like state in (a) and the thermal distribution of reference state (thermal state) in (b) with the number of TLAs crossing the cavity $m$ ($m\in[1, 2\times10^3]$ ), with $\theta=3{\text{π}}/8$ and $N=2\times10^3$ for $\xi=0.1$ (blue dots), $\xi=0.3$ (red dots) and $\xi=0.5$ (black dots). In the inset $m\in[1, 120]$ .$ \xi $ 下, 库的有效温度参数$ \theta $ 对$ \langle n(m, N)\rangle^{\rm qcc} $ 及其系统动力学的影响. 图3(a) 和图3(b) 分别给出了$ \langle n(m, N)\rangle^{qcc} $ 和$ \langle n(m, N)\rangle^{ref} $ 在不同库温度参数$ \theta $ : $ \theta = \{3{\text{π}}/7, 3{\text{π}}/$ $8, {\text{π}}/3\} $ 下, 随原子穿腔次数$ m $ , $ m\in[1, 200]$ , 的变化. 这里, $ \xi = 0.3 $ , $ N = 200 $ . 从图3(a) 可以看到: 在固定耦合参数及库尺寸($ \xi = 0.3 $ , $ N = 200 $ )下, 不论温度参数$ \theta $ 取较大还是较小值, 库中QCC对腔场的能量贡献$ \langle n(m, N)\rangle^{qcc} $ 总是随原子穿腔次数$ m $ 的增加而单调递增, 并最终达到稳定值. 这是因为:腔场的初始态为真空态, 在原子穿腔的过程中其不断地将自身所携带的信息—反映原子能量的布局信息和携带的QCC信息, 传递给腔场, 从而导致腔场能量表现出单调递增的趋势. 但是, 由于在腔场演化过程中, 腔场能量的增高会抑制其能量提取能力, 因此腔场能量最终趋于稳定值(即稳态能). 此外, 图3(a) 也展示了类GHZ库的有效温度参数$ \theta $ 越小, 即库的有效温度$ T_{\rm eff} $ 越高($ \theta $ 与$ T_{\rm eff} $ 成反比), 腔场到达稳态的时间相对越长, 且腔场从QCC中可提取的能量越多, 即$ \langle n(m, N)\rangle^{qcc}|_{\theta = {\text{π}}/3}\!>\!\langle n(m, N)\rangle^{qcc}|_{\theta = 3{\text{π}}/8}\!> \!\langle n(m, N)\rangle^{qcc} $ $|_{\theta = 3{\text{π}}/7}$ . 这表明腔场从QCC中可提取的能量与库的有效温度正相关, 即库温度越高, 原子穿越腔场时传递给腔场的QCC越多, 相应地QCC对腔场的能量贡献也就越大. 此特征类似于腔场从传统热库中提取能量的情况—在传统热库(独立二能级原子构成的热库如这里的参考库)下, 库温度越高腔场被热化到达稳态的时间越长(即稳态对应的穿腔粒子数$ m_{ss} $ 越大), 且从库中获取的能量越多(即稳态能越高, 如图3(b) 所示: $\langle n(m, N)\rangle^{ref}|_{\theta = {\text{π}}/3}>$ $ \langle n(m, N)\rangle^{ref}|_{\theta = 3{\text{π}}/8}>\langle n(m, N)\rangle^{ref}|_{\theta = 3{\text{π}}/7} $ ). 这是符合物理直觉的. 如果从类$ GHZ $ 库中任意两原子间的纠缠角度看, 根据方程(9 ), 图3(a) 中不同的温度参数$ \theta $ 对应的纠缠度满足关系: $C_{AB}(\theta = 3{\text{π}}/7)> $ $ C_{AB}(\theta = 3{\text{π}}/8)>C_{AB}(\theta = {\text{π}}/3) $ , 即较高的库温度对应较小的两体纠缠. 直观上, 库中两体纠缠越大, 原子在穿腔过程中传递给腔场的QCC会越多, 对应的QCC对腔场的能量贡献也就越大. 而目前图3(a) 却展现出相反的结果, 这似乎是反直觉的. 事实上, 对于多体关联体系, 其两子系统间的量子纠缠尚不能有效反映整体的量子关联(相干), 如处于一般GHZ态下的二能级原子系统, 通过求迹可以发现: 原子对所对应的态为非纠缠态(纠缠度为零), 不能反映整个体系中的量子关联. 因此, 图3(a) 所显示的整体库的QCC对腔场能量贡献结果与库中原子对间纠缠的大小关系并不矛盾. 此外, 从作用方式看, 两种不同库态(类GHZ态和参考态)下腔场与库的作用方式是相同的—每次仅有单个原子穿过腔场. 但是, 从信息传输的角度看, 由于类GHZ态下所有原子相互关联, 类GHZ态下腔场与进入腔的单原子的作用等价于系统与整个库的全局作用(进入腔场的原子与腔外其他原子关联, 携带有QCC信息), 而参考态(各原子相互独立)下腔场与库的作用可看作是局域作用—腔场仅与进入腔的独立的原子进行信息交换, 与腔外其他原子无关. 对比类GHZ态下QCC和参考态下原子布局(与类GHZ态中原子布局相同)对腔场的能量贡献$ \langle n(m, N)\rangle^{\rm qcc} $ (图2(a) ,图3(a) 所示)和$ \langle n(m, N)\rangle^{\rm ref} $ (图2(b) ,图3(b) 所示), 可以发现: 类 GHZ态中QCC对腔场的能量贡献总大于其原子布局对腔场的能量贡献即$ \langle n(m, N)\rangle^{\rm qcc}>$ $\langle n(m, N)\rangle^{\rm ref} $ , 特别是当$ \xi $ 取较小值时QCC的优势更加明显. 这表明: 类GHZ态中的QCC可以视为是一类优质的热力学资源, 在腔场与原子弱耦合的条件下QCC主导了腔场的能量即库的QCC成为腔场能量的主要来源.图 3 腔场在不同有效温度参数 $\theta=3{\text{π}}/7$ (蓝色点线), $\theta=3{\text{π}}/8$ (红色点线)和$\theta={\text{π}}/3$ (黑色点线)下, 从不同库态中提取的能量随穿腔原子数$m$ ($m\in[1, 2\times10^3]$ ) 的变化 (a)腔场从类GHZ态下QCC中提取能量$\langle n(m, N)\rangle^{\rm qcc}$ 随$m$ 的变化; (b)腔场从参考态(热态)下原子布局中提取的能量$\langle n(m, N)\rangle^{ref}$ 随$m$ 的变化; 其他参数取为 $\xi$ = 0.3, $N$ = 200Figure3. The variations of cavity's energy, $\langle n(m, N)\rangle^{\rm qcc}$ and $\langle n(m, N)\rangle^{\rm ref}$ , respectively captured from the QCC of $GHZ$ -like state in (a) and the thermal distribution of reference state (thermal state) in (b) with the number of TLAs crossing the cavity $m$ ($m\in[1, 200]$ ) and $\xi$ = 0.3 and $N=200$ for $\theta=3{\text{π}}/7$ (blue dots), $\theta=3{\text{π}}/8$ (red dots) and $\theta={\text{π}}/3$ (black dots).5.结 论 本文基于原子穿腔模型研究了非平衡库中QCC的热力学特性, 给出了一般量子关联相干库下系统演化的动力学方程. 借助于类GHZ态及其相应的参考态清晰地展示了非平衡库中QCC的能量效应, 即库中QCC能够有效地辅助微腔系统获取更多的能量. 我们所揭示的QCC的这一热力学特征与近期Francica等[46 ] 的研究结果是一致的(文献[46 ]展示了两体间纠缠能够辅助系统从中提取更多的功, 而我们则展示了多体中的QCC可辅助系统获取更多的能量). 多体系统QCC所展现的这一热力学特性具有潜在的应用价值. 如将传统的热库替换为相应的非平衡QCC库, 来设计高输出功率或高效率的光量子热机[22 ,26 ,59 ,61 ] . 这可以看作是QCC作为热力学资源的一个直接应用. 再如, 随着激光技术以及微纳加工工艺的不断提高, 近年来量子电池[71 -74 ] (quantum battery)的设计和制造引起了科学家们极大兴趣. 最近的研究表明: 量子关联在提高电池充电速度以及电池能量存储方面扮演了重要的角色[75 -76 ] . 因此, 多体系统中QCC也可视为提高量子电池性能特性的重要资源. 此外, 本文也讨论了库的有效温度和耦合参数对QCC能量效应以及系统动力学的影响. 揭示了一些有趣的现象: 1)库的有效温度越高QCC对腔场的能量贡献越大, 这与传统热库下的情况(腔场从热库中可提取的能量与热库温度成正比)一致; 2) QCC对腔场的能量贡献与耦合参数$ \xi $ 有关, 且耦合参数越小腔场从QCC中可提取的能量(腔场达到稳态时的能量)越大, 这一特征完全不同于传统热库下的情况—腔场从传统热库中可提取的能量独立于耦合参数, 且仅与库的温度有关; 3)腔场能量的高低与其提取能量的能力存在竞争关系—随着腔场能量的增加, 其从相同原子中可提取的能量逐渐减少; 4)非平衡原子库中QCC对系统能量的贡献优于原子热布局的贡献, 特别是在较小的耦合参数下QCC的优势更加明显. 这展示了QCC可视作一类优质热力学资源的特性. 本研究工作进一步促进了我们对量子相干热力学特性的理解与认识. 未来如何结合信息几何[77 ] 理论来挖掘多体量子关联和相干中更加丰富、深刻的热力学特性是非常有趣并值得研究的课题.? 感谢北京理工大学物理学院魏永波博士以及郭丽莎博士的讨论. 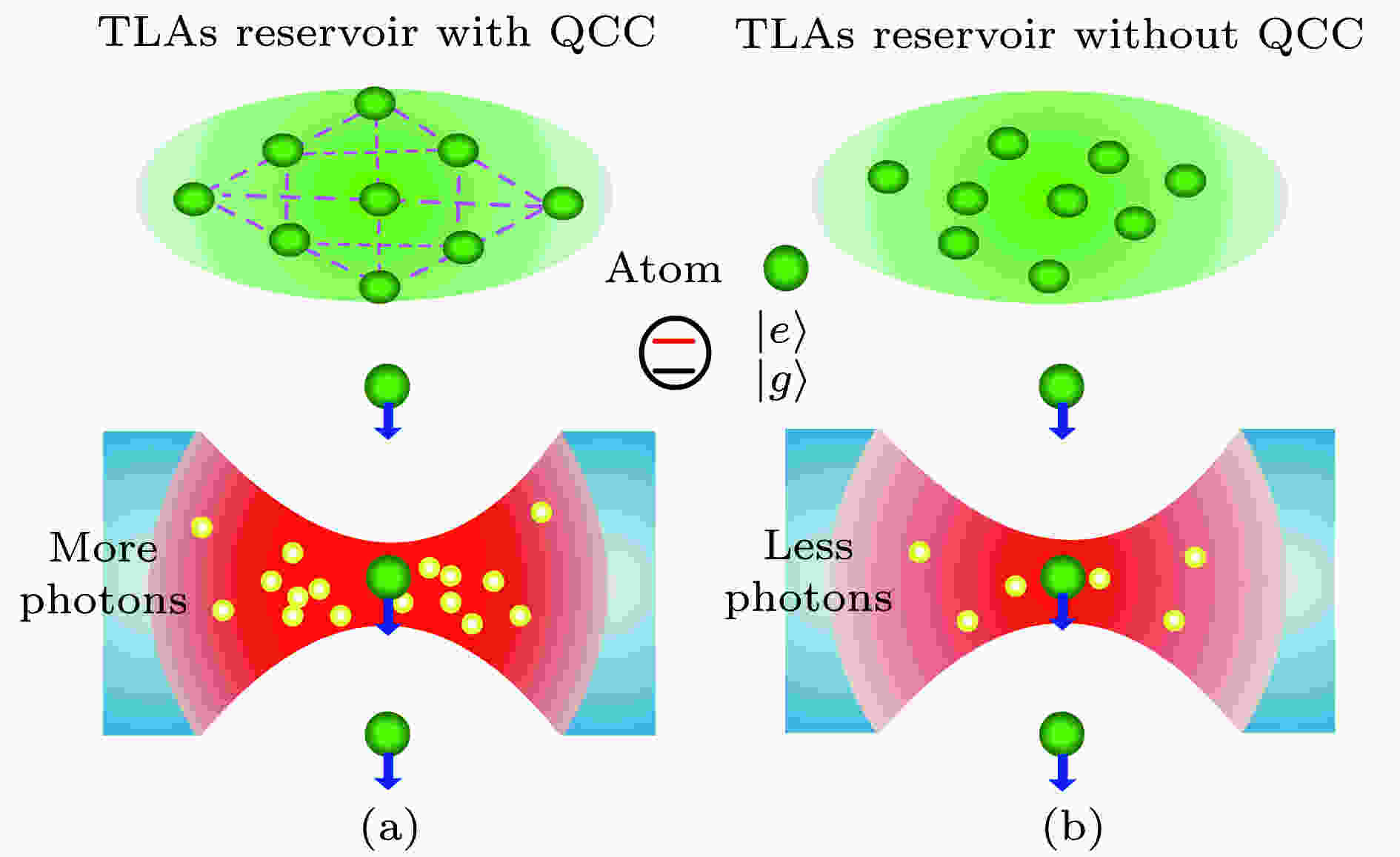 图 1 单模微腔与一系列二能级原子组成的原子库相互作用示意图 (a)处于QCC库中的二能级原子顺次穿过微腔; (b)库中无QCC情况下, 二能级原子顺次穿过微腔
图 1 单模微腔与一系列二能级原子组成的原子库相互作用示意图 (a)处于QCC库中的二能级原子顺次穿过微腔; (b)库中无QCC情况下, 二能级原子顺次穿过微腔




















































































































































































































































































































































































































































































































































































































































































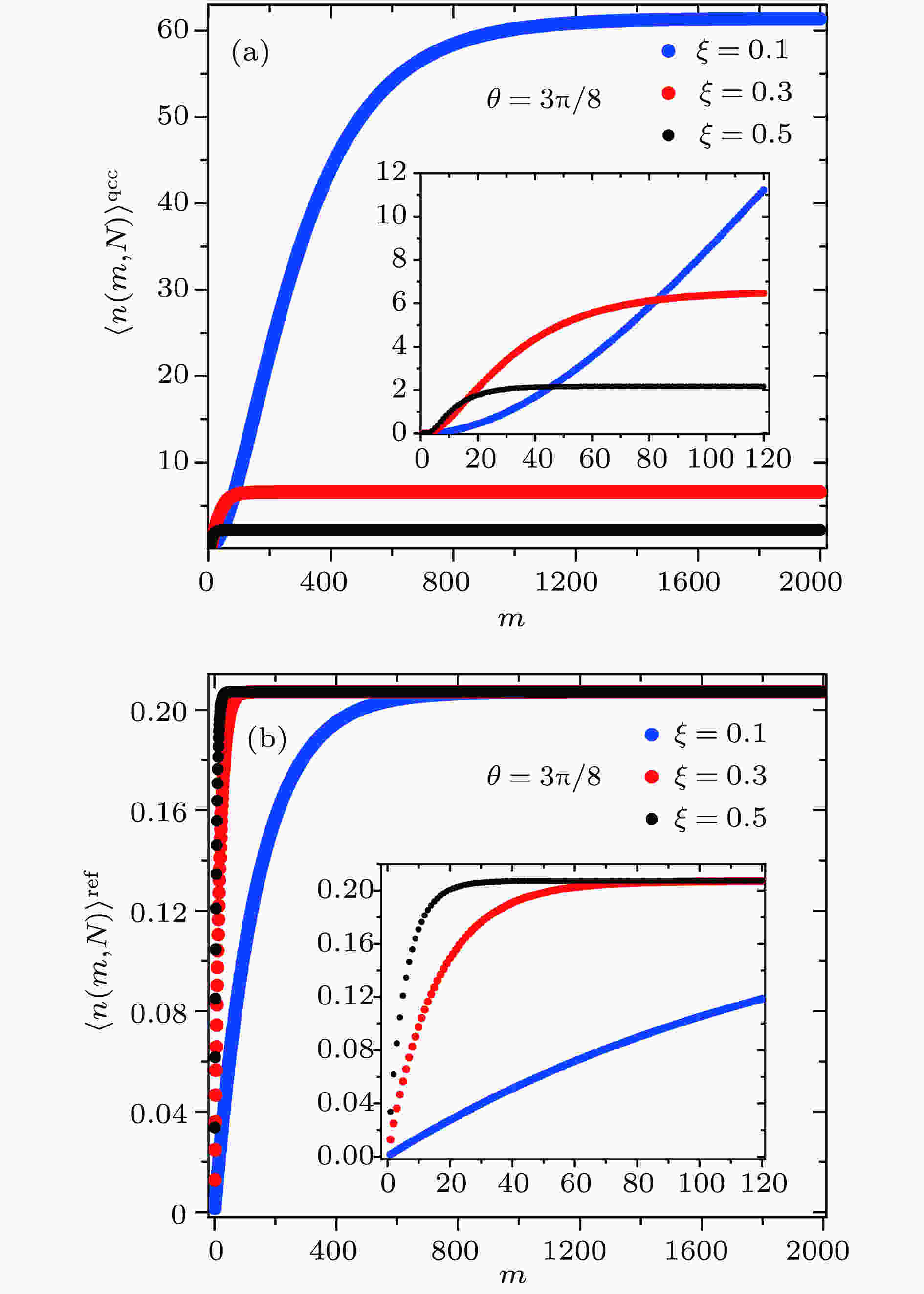 图 2 腔场在不同耦合参数
图 2 腔场在不同耦合参数 










































































































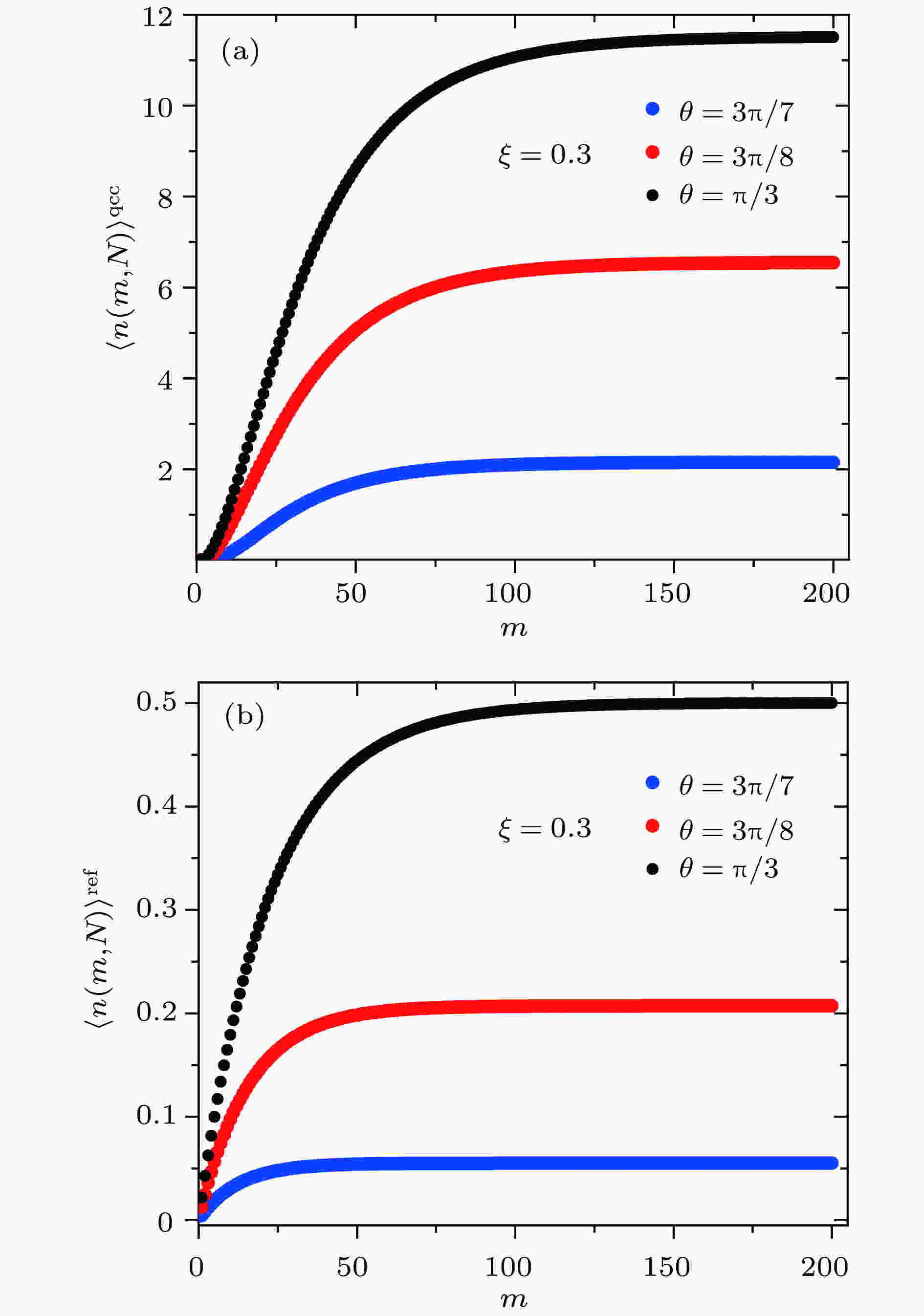 图 3 腔场在不同有效温度参数
图 3 腔场在不同有效温度参数 




























