摘要: 量子精密测量是基于量子力学的基本原理对特定物理量实施测量, 并利用量子效应提高测量精度的交叉科学. 随着超冷原子实验技术的发展, 超冷原子为量子精密测量提供了一个优异的研究平台. 利用发展成熟的量子调控技术, 人们可以基于超冷原子系综制备一些新奇的非高斯多粒子纠缠态. 基于多体量子干涉, 利用这些非高斯纠缠态作为输入, 可以实现超越标准量子极限的高精度测量. 本文简要综述这一研究领域的进展.
关键词: 量子精密测量 /
非高斯纠缠态 /
超冷原子系综 /
多体量子干涉 English Abstract Non-Gaussian entangled states and quantum metrology with ultracold atomic ensemble Lu Bo 1,2 ,Han Cheng-Yin 1,2 ,Zhuang Min 1,2 ,Ke Yong-Guan 1,2 ,Huang Jia-Hao 1,2 ,Lee Chao-Hong 1,2 1.Laboratory of Quantum Engineering and Quantum Metrology, School of Physics and Astronomy, Sun Yat-Sen University (Zhuhai Campus), Zhuhai 519082, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11874434, 11574405, 11704420).Received Date: 26 January 2019Accepted Date: 20 February 2019Available Online: 19 February 2019Published Online: 20 February 2019Abstract: Quantum metrology is the interdisciplinary of investigating how to utilize the principles of quantum mechanics to perform parameter estimation and improve the measurement precision by quantum effects. With the experimental developments of ultracold atoms, ultracold atomic ensemble provides an excellent platform for implementing quantum metrology. Attributed to well-developed techniques of quantum control, one can prepare several exotic non-Gaussian multi-particle entangled states in the ensembles of ultracold atoms. Based on many-body quanum interferometry, and using these non-Gaussian entangled states as probe, the high-precision measurement beyond the standard quantum limit can be realized. This article introduces the background and advancement of this field.Keywords: quantum metrology /non-Gaussian entangled states /ultracold atomic ensemble /many-body quanum interferometry 全文HTML --> --> --> 1.引 言 量子精密测量是量子物理学与精密测量科学相结合的学科[1 -4 ] . 其研究对探索基础科学问题、发展前沿技术都具有重要意义. 它不仅能提高基本物理学常数(如万有引力常数、精细结构常数、普朗克常数等)的测量精度, 在更高精度上检验物理学基本定律[5 -8 ] , 而且能应用于设计制造各种量子器件, 提高时间频率、磁场、重力加速度等参数测量的灵敏度[9 -16 ] .[1 -4 ] . 目前, 用于研究的物理体系主要包括超冷原子体系[17 ,18 ] 、囚禁离子体系[19 -21 ] 、光子体系[22 ,23 ] 、金刚石色心体系[24 ] 、核磁共振体系[25 -27 ] 、固态体系[28 ] 等. 其中, 超冷原子气体作为一种环境洁净且便于操控的多体量子系统而备受关注. 超冷原子体系具有稳固的量子相干性和高度的可控性. 利用磁光囚禁技术, 超冷原子气体几乎处于没有其他杂质存在的空间中, 体系与环境的相互作用可以忽略, 因而体系具有超长的量子相干时间. 超冷原子体系是原子层次的人造量子体系, 原子被囚禁在特定的空间范围之内, 原子的超精细态和原子之间的相互作用可以用电场、磁场、微波或激光等外场进行精确地操控. 这些特性使超冷原子气体成为研究多体量子物理的一个新平台, 尤其为基于超冷原子系综的量子精密测量提供了新的机遇.[29 ,30 ] . 基于量子力学的基本原理, 干涉结果可由每个粒子沿不同路径或内态的振幅相干叠加而得到. 不同路径或者内态受到待测参数的影响会积累一个相对相位$\phi $ . 根据干涉的结果可以测定这一相对相位$\phi $ , 从而得到待测参数的信息. 增加干涉仪中使用的粒子数目可以提高测量的信噪比. 如果用$N$ 个没有关联的独立粒子作为干涉仪的输入态, 这等同于对同一个粒子进行$N$ 次测量. 由中心极限定理可知, 其所能达到的测量精度最终将受限于标准量子极限: ${N^{ - 1/2}}$ , 也叫经典极限. 进一步, 如果引入多体量子效应, 利用粒子之间的量子关联, 将有可能突破这一经典极限. 例如, 把输入态制备成最大纠缠态, 在理想情况下可以把测量精度提高到${N^{ - 1}}$ . 此精度极限比标准量子极限提高了${N^{1/2}}$ 倍, 通常被称为海森伯极限.$\left| {\psi \left( \phi \right)} \right\rangle $ , 其所能达到的测量精度极限可用量子Fisher信息${F_{\rm{Q}}}$ 来计算[31 -33 ] . 待测相位$\phi $ 的标准偏差满足$\Delta \phi \geqslant \Delta {\phi _{{\rm{QCRB}}}} \equiv {\left( {\nu {F_{\rm{Q}}}} \right)^{ - 1/2}}$ , 其中$\nu $ 是测量的次数. 对于一个粒子数为$N$ 的无纠缠态, ${F_{\rm{Q}}} = N$ , 其相位测量极限为标准量子极限. 对于一个$N$ 粒子的纠缠态, 量子Fisher信息可能会增大, ${F_{\rm{Q}}} > N$ , 从而其相位测量精度极限可能突破标准量子极限. 因此, 寻找和制备合适的多粒子纠缠态是实现突破标准量子极限测量的一个核心问题.[13 ,17 ,18 ] . 由于自旋相干态和压缩态的概率分布可以用高斯统计来描述, 因而它们都是多粒子高斯态. 与之相反, 若概率分布不能用高斯统计来描述, 则这样的多粒子量子态属于非高斯态. 最大纠缠态、自旋猫态、双数态等都是典型的非高斯纠缠态. 最近, 这些非高斯纠缠态也逐步受到人们的关注, 在理论与实验上均取得了很大的突破[34 -38 ] .2.基于量子干涉的精密测量 一般的物理量测量过程可以分为如下3个步骤: 1)将探针制备到所需的输入态; 2)让探针经历一个与待测参数有依赖关系的动力学演化; 3)对探针含有待测参数信息的末态进行相应的测量, 选取合适的分析方法估算出参数的值.$\left| {{\psi _{{\rm{in}}}}} \right\rangle $ ; 在动力学演化过程中, 输入态在演化算符$ U(\theta ) $ 的作用下演化成含有$\theta $ 信息的末态$\left| {\psi (\theta )} \right\rangle {\rm{ = }}U(\theta )\left| {{\psi _{{\rm{in}}}}} \right\rangle $ ; 得到末态后, 再选取适当的可观测量$O$ , 并作用到$\left| {\psi (\theta )} \right\rangle $ 上得到相应的期望值. 要成功地提取出未知参数$\theta $ 的信息, 所选取的观测量$O$ 的期望值$\left\langle O \right\rangle $ 必须与$\theta $ 有一定的函数依赖关系. 如果对动力学演化过程有一定的先验知识, 而且能得到观测量期望值$\left\langle O \right\rangle $ 与未知参数$\theta $ 的函数依赖关系, 那么未知参数$\theta $ 的信息可以通过观测量$O$ 的测量结果提取出来. 同时, 估计未知参数$\theta $ 的误差也能相应得到. 根据误差传递公式, 可以得到估计未知参量的标准偏差$\Delta \phi = \dfrac{{\Delta O}}{{\left| {\partial \left\langle O \right\rangle /\partial \theta } \right|}}$ , 其中, $\Delta O$ 是观测量$O$ 的标准偏差, $\Delta O = \sqrt {\left\langle {{O^2}} \right\rangle - {{\left\langle O \right\rangle }^2}} $ , $\left\langle O \right\rangle = \left\langle {\psi (\theta )} \right|O\left| {\psi (\theta )} \right\rangle $ , $\left\langle {{O^2}} \right\rangle = \left\langle {\psi (\theta )} \right|{O^2}\left| {\psi (\theta )} \right\rangle $ .[31 -33 ] , 待测参数的测量精度极限由量子Fisher信息$ {F_{\rm{Q}}} =$ $ 4\left( {\left\langle {\psi '\left( \theta \right)|\psi '\left( \theta \right)} \right\rangle - {{\left| {\left\langle {\psi '\left( \theta \right){\rm{|}}\psi \left( \theta \right)} \right\rangle } \right|}^2}} \right)$ 决定, 即$ \Delta \theta \geqslant $ $ \Delta {\theta _{{\rm{QCRB}}}} \equiv {\left( {\nu {F_{\rm{Q}}}} \right)^{ - 1/2}} $ , 其中$\nu $ 是测量的次数, $\left| {\psi '\left( \theta \right)} \right\rangle $ 表示$\left| {\psi \left( \theta \right)} \right\rangle $ 对相位$\theta $ 求导数.${\text{π}}/2$ 脉冲和一个自由演化过程组成. Ramsey干涉类似于Mach-Zehnder干涉, Ramsey干涉的两个${\text{π}}/2$ 脉冲相当于Mach-Zehnder干涉的两个分束镜, 而自由演化过程对应于Mach-Zehnder干涉的相位积累过程.$\left| \downarrow \right\rangle $ 和$\left| \uparrow \right\rangle $ . 不失一般性, 假设基态与激发态对应的本征能量分别为$ - {\omega _0}/2$ 与$ + {\omega _0}/2$ . 这里, ${\omega _0}$ 就是待测参数. 假设初始态$\left| {{\psi _0}} \right\rangle $ 处于基态$\left| \downarrow \right\rangle $ , 运用第一个${\text{π}}/2$ 脉冲后, 得到输入态$\left| {{\psi _{{\rm{in}}}}} \right\rangle = \dfrac{1}{{\sqrt 2 }}\left( {\left| \downarrow \right\rangle + \left| \uparrow \right\rangle } \right)$ , 输入态为基态$\left| \downarrow \right\rangle $ 与激发态$\left| \uparrow \right\rangle $ 的等概率叠加态. 接着, 系统经历一个自由演化过程. 在此过程中, 基态$\left| \downarrow \right\rangle $ 积累一个正的相位$ + \phi /2$ , 激发态$\left| \uparrow \right\rangle $ 积累一个负的相位$ - \phi /2$ . 其中, $\phi = {\omega _0}T$ , $T$ 为相位积累时间. 这时, 自由演化后的输出态可以写成$\left| {\psi (\phi )} \right\rangle = $ $ \dfrac{1}{{\sqrt 2 }}\left( {{{\rm{e}}^{ - {\rm{i}}\phi /2}}\left| \uparrow \right\rangle + {{\rm{e}}^{ + {\rm{i}}\phi /2}}\left| \downarrow \right\rangle } \right)$ . 最后, 运用第二个${\text{π}}/2$ 脉冲, 并对末态进行布居数测量. 测得原子处在基态$\left| \downarrow \right\rangle $ 的概率为$p\left( { \downarrow |\phi } \right) = \dfrac{{1 + \cos \phi }}{2} = {\cos ^2}\dfrac{\phi }{2},$ 测得原子处在激发态$\left| \uparrow \right\rangle $ 的概率为$p\left( { \uparrow |\phi } \right) = \dfrac{{1 - \cos \phi }}{2} = $ $ {\sin ^2}\dfrac{\phi }{2}$ . 因此, 由布居数的测量即可得到$\phi $ 的信息.${F_{\rm{Q}}}\left( \phi \right) = 1$ . 由此可得, 相对相位的不确定度$\Delta \phi \geqslant \dfrac{1}{{\sqrt {{F_{\rm{Q}}}\left( \phi \right)} }} = 1$ . 于是, 只要知道相位积累时间$T$ , 就可以得到待测参数的不确定度$\Delta {\omega _0} \geqslant \dfrac{1}{T}$ . 对于$N$ 个独立单原子, 待测参数的不确定度则降低$\sqrt N $ 倍, 即$\Delta {\omega _0} \geqslant \dfrac{1}{{\sqrt N T}}$ . 假设$N$ 个原子是纠缠的, 待测参数的测量不确定度会进一步降低. 下面详细介绍量子多体纠缠态如何提高测量的精度.3.多粒子高斯态与精密测量 23.1.自旋相干态 3.1.自旋相干态 对于一个由$N$ 个二能级原子组成的超冷原子系综, 可以把每个原子看成全同的自旋1/2粒子. 这样, 整个系综就可以被描述成一个自旋长度为$J = N/2$ 的大自旋系统. 因此, 系综可以用集体自旋算符${\hat J_i} = \sum\limits_{l = 1}^N {\hat S_i^{(l)}} (i = x,y,z)$ 来刻画, 其中$\hat S_i^{(l)}(i = $ $x,y,z)$ 为第$l$ 个自旋1/2粒子的自旋算符. 当$N$ 个独立的、没有任何量子关联的自旋1/2粒子同时处在同一个单粒子态时, 就可以把这样的量子态叫作自旋相干态, 它是最接近经典态的一个多粒子态. 任意一个自旋相干态都可以写成$(\theta ,\varphi )$ 为自旋相干态的平均自旋方向. 自旋相干态在Dicke基矢下的一般形式可以写成${\left| {\theta ,\varphi } \right\rangle _{{\rm{SCS}}}} = $ $ \sum\limits_{m = - J}^J {{c_m}\left( \theta \right){{\rm{e}}^{ - {\rm{i}}\left( {J + m} \right)\varphi }}} \left| {J,m} \right\rangle ,$ 其系数${c_m}\left( \theta \right) = $ ${\left[ {\dfrac{{\left( {2J} \right)!}}{{\left( {J + m} \right)!\left( {J - m} \right)!}}} \right]^{\frac{1}{2}}}{\cos ^{J - m}}\left( {\theta /2} \right){\sin ^{J + m}}\left( {\theta /2} \right) $ .当粒子数$N$ 很大时, 其分布趋近标准的高斯正态分布[39 ] , 如图1 左边. 对于一个自旋相干态, 任意垂直于其平均自旋方向$\left( {\theta ,\varphi } \right)$ 的自旋分量的方差${\left( {\Delta {{\hat J}_ \bot }} \right)^2}$ 都相等. ${\left( {\Delta {{\hat J}_ \bot }} \right)^2}$ 就等于$N$ 个自旋1/2粒子的方差${\left( {\Delta {{\hat S}_ \bot }} \right)^2}$ 之和, 即${\left( {\Delta {{\hat J}_ \bot }} \right)^2} = N \times {\left( {\Delta {{\hat S}_ \bot }} \right)^2} =$ $ \dfrac{N}{4}$ . 自旋相干态满足海森伯不确定关系的极限条件, 即不等式取等号的情况. 利用自旋相干态进行Ramsey干涉, 计算其量子Fisher信息得到${F_{\rm{Q}}} = N$ , 可知其相位测量精度最多只能达到标准量子极限[33 ] .图 1 自旋相干态(左)与自旋压缩态(右)在广义Bloch球上的Husimi分布(摘自文献[39 ] )Figure1. The Husimi distribution of spin coherent state (left) and spin squeezed state (right) on the generalized Bloch sphere. Adapted from Ref. [39 ].3.2.自旋压缩态 -->3.2.自旋压缩态 自旋压缩的概念由两位日本物理学家Kitagawa和Ueda于1992年提出, 他们把量子光学的压缩定义推广到自旋算符中[40 ] . 对于无纠缠的自旋相干态, 在垂直于平均自旋方向上, 每个独立的自旋1/2粒子的涨落均为1/4. 假如可以在各个独立自旋间建立一定的关联, 就有可能抵消或者增加某个方向上的涨落. 类似于位置动量的量子压缩, 在不违背海森伯不确定关系的基础上, 一个自旋分量的涨落(方差)能以增大另一个共轭自旋分量的涨落(方差)为代价而降低. 对于自旋为J 的系统, 如果一个量子态沿某个自旋方向的涨落${\left( {\Delta {{\hat J}_ \bot }} \right)^2}$ 小于$\left| {\left\langle {{J_k}} \right\rangle } \right|/2$ ($k$ 为平均自旋方向), 这个量子态就可以被称为自旋压缩态. 自旋压缩的产生与粒子间的量子关联密切相关. 其相对粒子数差的概率分布也会从标准的高斯分布(自旋相干态)变为半高宽狭窄的高斯型分布[39 ] , 如图1 右边所示.$\xi _{\rm{H}}^2 = \dfrac{{2{{\left( {\Delta {{\hat J}_\alpha }} \right)}^2}}}{{\left| {\left\langle {{{\hat J}_\gamma }} \right\rangle } \right|}}, \alpha \ne \gamma \in$ $ (x,y,z)$ . 第二种压缩参数定义为垂直于平均自旋方向的自旋分量涨落的最小值与平均自旋长度的比值, 即$\xi _{\rm{S}}^2 = \dfrac{{\min {{\left( {\Delta {{\hat J}_{{{ n}_ \bot }}}} \right)}^2}}}{{J/2}} = \dfrac{{4\min {{\left( {\Delta {{\hat J}_{{{ n}_ \bot }}}} \right)}^2}}}{N}$ , 这里可以通过寻找垂直于平均自旋方向上所有可能的${ n_ \bot }$ 对应自旋分量的最小值, 来确定最佳的自旋压缩方向. 第三种压缩参数与精密光谱密切相关, 它是通过给定的量子态相位不确定度与一个参考的自旋相干态对应的相位不确定度的比值来定义, 具体写成$\xi _{\rm{R}}^2 = \dfrac{{\Delta \phi }}{{{{\left( {\Delta \phi } \right)}_{{\rm{SCS}}}}}} = \dfrac{{N{{\left( {\Delta {{\hat J}_{{{ n}_ \bot }}}} \right)}^2}}}{{{{\left| {\left\langle {\hat J} \right\rangle } \right|}^2}}}$ , 其中, $\left\langle {\hat J} \right\rangle $ 为平均自旋长度. 当压缩系数$\xi _\alpha ^2 < 1{\rm{ }}(\alpha = {\rm{H,S,R}})$ 时, 可知体系产生自旋压缩. 输入自旋压缩态进行Ramsey干涉, 其量子Fisher信息${F_{\rm{Q}}} > N$ , 因此测量精度能突破标准量子极限.[13 ,18 ,41 ] :$\chi $ 描述的是原子间的有效非线性相互作用强度. 实验上可以对原子之间的非线性相互作用进行调节, 利用时间演化制备自旋压缩态. 一方面, 可以在体系中外加一个控制磁场, 利用Feshbach共振技术, 调节原子间的s分波散射长度, 从而改变原子间的有效相互作用[18 ] . 另一方面, 可以通过调节原子物质波的空间密度分布来控制有效相互作用的大小. 在原子芯片上, 可以采用后一种方法, 通过微波操控波函数的交叠来调控原子间的非线性相互作用, 实现自旋压缩[13 ,17 ] . 在一个双势阱中绝热相干地劈裂一个玻色-爱因斯坦凝聚体, 利用劈裂后两个不同的外部空间模式同样可以实现自旋压缩[42 ,43 ] . 利用自旋压缩态, 可以实现突破标准量子极限的测量. 另外, 一种新型的非线性探测手段被提出, 并在自旋压缩态上实现了无需单粒子分辨的探测器也能突破标准量子极限的相位测量[44 -47 ] . 这类方案实际上是在可观测量探测前再进行一次非线性的动力学演化过程. 其实现与非线性动力学制备输入态类似, 实验可操作性强, 丰富了现有量子精密测量的探测手段.4.非高斯纠缠态与精密测量 24.1.最大纠缠态 4.1.最大纠缠态 在$J = N/2$ 的大自旋系统中, 所有N 个粒子同时处在$\left| \downarrow \right\rangle $ 与所有N个粒子同时处在$\left| \uparrow \right\rangle $ 的等概率叠加态, 被称为N 粒子的Greenberger-Horne-Zeilinger(GHZ)态, 有时也被称为最大纠缠态. N 粒子的GHZ态在Dicke基矢下可以写成$\gamma $ 代表一个任意相位. 在理想情况下, GHZ态被认为是提高测量精度的最优候选态.$\gamma = 0$ . 利用GHZ态来进行量子干涉, 输入态写成${\left| \varPsi \right\rangle _{i{\rm{n}}}} = \dfrac{1}{{\sqrt 2 }}\left( {\left| {\dfrac{N}{2},}\right.}\right.$ $\left.{\left.{ + \dfrac{N}{2}} \right\rangle + \left| {\dfrac{N}{2}, - \dfrac{N}{2}} \right\rangle } \right)$ . 在自由演化过程中, 每个处在$\left| \downarrow \right\rangle $ 的粒子都积累一个$ + \dfrac{\varphi }{2}$ 的相位, 而每个处在$\left| \uparrow \right\rangle $ 的粒子都积累一个$ - \dfrac{\varphi }{2}$ 的相位. 于是, 得到输出态$\left| \varPsi \right\rangle = \dfrac{1}{{\sqrt 2 }}\left( {{{\rm{e}}^{ - {\rm{i}}\frac{{N\varphi }}{2}}}\!\left| \!{\dfrac{N}{2}, \!+ \dfrac{N}{2}} \right\rangle \!+ \!{{\rm{e}}^{ + {\rm{i}}\frac{{N\varphi }}{2}}}\left| {\dfrac{N}{2}, - \dfrac{N}{2}} \!\right\rangle } \right)$ . 因此, 可以得到其量子Fisher信息为${F_{\rm{Q}}} = {N^2}$ , 其相位极限精度达到1/N . 对比没有量子关联的独立原子, 把原子制备成最大纠缠态, 理论上能使测量精度从标准量子极限提高到海森伯极限[48 -53 ] .$\chi t = \dfrac{{\text{π}}}{2}$ 的条件时[54 ] , 系统的态可以从自旋相干态演化为最大纠缠态. 然而, 要达到这一条件比较困难. 其一, 实验上可实现的有效相互作用较弱, 需要很长的演化时间, 体系难以长时间保持相干性; 其二, 演化的时间需要控制得非常精确, 制备具有很大的随机性. 另外, 最大纠缠态非常脆弱, 纠缠特性容易受粒子数损失、失相等环境效应影响而被破坏. 这些都是利用最大纠缠态来进行量子精密测量时亟待解决的问题.4.2.自旋猫态 -->4.2.自旋猫态 由于最大纠缠态极端脆弱且制备较为困难, 实验上能实现的并不多, 即使实现了, 其纠缠的粒子数也很少. 因此, 寻找对环境效应具有鲁棒性同时实验上又易于制备的多粒子态成为关键. 下面, 着重介绍另一种有潜力运用到量子精密测量中的非高斯多粒子纠缠态—自旋猫态. 首先, 简要阐述自旋猫态的基本特点, 然后讨论其制备的方案和在精密测量中的表现.[55 ] . 假设有两个不同的自旋相干态相干叠加, 对于这样形成的量子态, 可以由彼此正交的或非正交的自旋相干态叠加而成. 宏观自旋相干叠加态的形式可以写成${\left| {\varPsi \left( {\theta ,\varphi } \right)} \right\rangle _M} = {N_{\rm{C}}}\left( {{{\left| {\theta ,\varphi } \right\rangle }_{{\rm{SCS}}}} + {{\left| {{\text{π}} - \theta ,\varphi } \right\rangle }_{{\rm{SCS}}}}} \right)$ , 其中, ${N_{\rm{C}}}$ 代表量子态的归一化系数. ${\left| {\theta ,\varphi } \right\rangle _{{\rm{SCS}}}}$ 和${\left| {{\text{π}} - \theta ,\varphi } \right\rangle _{{\rm{SCS}}}}$ 为两个自旋相干态. 不失一般性, 假设径角$\varphi = 0$ , 这时, 在Dicke基矢下, 宏观自旋相干叠加态表示为$\theta = 0$ , ${\left| {\varPsi \left( 0 \right)} \right\rangle _M}$ 变为最大纠缠态. 当$\theta = {\text{π}}/2$ 时, ${\left| {\varPsi \left( {{\text{π}}/2} \right)} \right\rangle _M}$ 实际上是$\theta = {\text{π}}/2,\varphi = 0$ 的自旋相干态${\left| {{\text{π}}/2,0} \right\rangle _{{\rm{SCS}}}}$ . 在$0 \leqslant \theta \leqslant {\text{π}}/2$ 的区间内, ${\left| {\varPsi \left( \theta \right)} \right\rangle _M}$ 中的两个相干叠加态间的距离随着$\theta $ 的增大而减小. 在图2 上方, 给出了不同$\theta $ 对应的${\left| {\varPsi \left( \theta \right)} \right\rangle _M}$ 在广义Bloch球面上的Husimi分布. 从图上可以看到, 对于$0 \leqslant \theta < {\text{π}}/2$ , 每个Husimi分布会出现两个峰, 而这两个峰的距离会随着$\theta $ 的减小而增大. 特别地, 对于适中的$\theta $ 值, ${\left| {\varPsi \left( \theta \right)} \right\rangle _M}$ 会是两个准正交的自旋相干态的叠加态, 这种态可以看作是自旋猫态. 这里, 准正交指的是两个自旋相干态${\left| {\theta ,0} \right\rangle _{{\rm{SCS}}}}$ 与${\left| {{\text{π}} - \theta ,0} \right\rangle _{{\rm{SCS}}}}$ 波函数交叠的部分非常小. 当$0 \leqslant \theta \leqslant $ ${\theta _{\rm{C}}}$ , 交叠部分满足${\left| {_{{\rm{SCS}}}\left\langle {\theta ,0{{\left| {{\text{π}} - \theta ,0} \right\rangle }_{{\rm{SCS}}}}} \right.} \right|^2} < \varepsilon $ ($\varepsilon $ 是一个很小的参数)时, 就可以把${\left| {\varPsi \left( \theta \right)} \right\rangle _M}$ 看成是自旋猫态. 此时, 自旋猫态可以写成[56 ] :图 2 上图为不同自旋猫态在广义Bloch球上的Husimi分布; 下图为不同自旋猫态在有原子数损失($\eta $ 为原子的损失率)情况下的相位测量精度极限(摘自文献[55 ])Figure2. Top: The Husimi distribution of different spin cat states on the generalized Bloch sphere. Bottom: The ultimate phase measurement precision with different spin cat states under atomic loss ($\eta $ denotes the ratio of atom loss). Adapted from Ref. [55 ].$ {F_{\rm{Q}}} =$ $ {\left( {1 - \dfrac{{2{{\tan }^2}(\theta /2)}}{{1 + {{\tan }^2}(\theta /2)}}} \right)^2}{N^2}$ . 因此, 其相位测量精度满足$\Delta \phi \geqslant \Delta {\phi _{QCRB}}\; \equiv \;{\nu ^{ - 1/2}}\left( {1+ \dfrac{{2{{\tan }^2}(\theta /2)}}{{1 - {{\tan }^2}(\theta /2)}}} \right){N^{ - 1}}$ , 接近海森伯极限[56 ] .[55 ] . 通过与不同的输入态(尤其与最大纠缠态)做对比, 发现纠缠适中的自旋猫态对原子损失具有很强的鲁棒性, 其在耗散下所能达到的相位测量精度依然很高, 如图2 所示.[57 -71 ] . 在玻色-爱因斯坦凝聚体中可以利用原子碰撞引起的非线性Kerr效应来制备[57 ,58 ] . 也可以从自旋相干态出发利用非线性动力学来制备, 但制备的自旋猫态可能需要合适的旋转操作才能作为输入态[59 ] . 利用与热库的耦合[60 ,61 ] 、非破坏测量[62 -65 ] 、里德伯阻塞[66 ] 等手段都可以产生有效非线性, 从而制备自旋猫态. 引入一系列自旋测量操作也可以条件性地产生自旋猫态[67 -69 ] . 此外, 还有研究组在热原子体系中利用量子泽诺(Zeno)效应也能实现自旋猫态的制备[71 ] .[48 ,51 ,72 ] . 通过绝热改变系统的参数, 初态可以从一个非简并的基态逐渐演化到一个高度简并的纠缠态[72 ] . 这样的过程既实现了产生纠缠态的作用, 同时又发挥了分束的作用, 如图3 所示. 利用这样的方法可以在超冷原子系综上实现自旋猫态.图 3 基于量子相变和多体量子干涉的相位测量方案示意图( 摘自文献[61 ])Figure3. Schematic of precision phase measurement based on driving through quantum phase transitions and many-body quantum interferometry. Adapted from Ref. [61 ].[17 ,18 ,41 ,73 ] :$\varOmega $ 为Rabi频率(在下面的讨论中假设$\varOmega \geqslant 0$ ), $\delta $ 表示失谐量, $\chi $ 为有效非线性相互作用. 其中, $\chi \propto {g_{aa}} + {g_{bb}} - 2{g_{ab}}$ 与模内、模间的原子相互作用强度相关. 通过Feshbach共振调节原子模内或模间的散射长度就可以调节有效非线性相互作用$\chi $ .$\chi < 0$ )的基态特性[48 ,49 ] . 理论上, 对于$\chi < 0$ 的对称玻色-约瑟夫森结($\delta = 0$ ), 可以利用绝热制备的方法产生从自旋相干态到自旋猫态等各种纠缠态. 当$\chi < 0$ , $\delta = 0$ , 体系基态性质只由系数$\kappa = \varOmega /\chi $ 决定. 在强耦合极限下($\left| \kappa \right| \gg 1$ ), 其基态为自旋相干态. 当$\kappa $ 从$\kappa < - N$ 变到$ - N <$ $ \kappa < 0$ 时, 基态的布居数差概率分布会出现从单峰形态到双峰形态的转变. 这种双峰形态所对应的基态可以被看成是两个对称的自囚禁态的等概率宏观叠加, 与自旋猫态类似.$\varOmega $ , 使其从很大的数值缓慢降为0, 系统所处的态会绝热演化到最大纠缠态上. 在绝热演化过程中, 系统的态会经过一个从正常态到自囚禁态的分叉. 当$\varOmega $ 较小时, 由于宇称对称性的保护[48 ,74 ] , 系统演化的态会是两个自囚禁态的叠加态, 即自旋猫态. 而自旋猫态${\left| {\varPsi \left( \theta \right)} \right\rangle _{{\rm{CAT}}}}$ 中决定两个叠加自旋相干态“距离”的参数$\theta $ 只需要通过调节$\varOmega /\chi $ 来控制即可[51 ] . 相比动力学演化的方法, 利用基态的绝热制备, 得到的自旋猫态是确定性的.[75 ] 、绝热捷径[76 ] 等手段在玻色-约瑟夫森系统中产生自旋猫态, 其态制备时间能进一步缩短.[51 ] . 然而, 宇称测量需要分辨原子数的奇偶性, 实际需要单原子分辨率的探测器. 这是一个比较严苛的实验要求, 在实验中很难实现.图3 所示)作为合束器后, 就可以利用布居数之差的测量来提取相位信息, 从而不需要单原子分辨的探测器[61 ] . 另外, 在探测前引入非线性探测过程也可以实现. 非线性探测过程包括一个单轴压缩、两个${\text{π}}/2$ 脉冲和布居数测量, 均可用当前实验技术实现. 相比之前基于自旋压缩态的非线性探测方案, 改用自旋猫态, 其测量精度对探测噪声的鲁棒性大大增强[56 ] .4.3.双数态 -->4.3.双数态 双数态是两个模具有确定相等粒子数目的Fock直积态, 即$N$ 为偶数. 由于其两模的粒子数都是确定的, 相对粒子数的不确定度为零, 因此两模间的相对相位是完全不确定的[77 ] . 利用双数态作为输入, 可以实现达到海森伯极限的量子干涉测量. 首先, 双数态经过一个形式${\hat U_{{\rm{BS1}}}} = \exp \left[ {\dfrac{{\text{π}}}{4}\left( {{{\hat a}^\dagger }\hat b - {{\hat b}^\dagger }\hat a} \right)} \right]$ 的分束器会变成${\left| \Psi \right\rangle _{i{\rm{n}}}} = \sum\limits_{k = 0}^{N/2} {C_k^{N/2}{{\left| {2k} \right\rangle }_a}{{\left| {N - 2k} \right\rangle }_b}} $ , 其系数$C_k^{N/2}$ 的形式为$ {F_{\rm{Q}}} \!=\! N\left( {1 \!+\! N/2} \right)$ , 得知其相位测量精度极限满足$\Delta \varphi \geqslant \dfrac{1}{{\sqrt {{N^2}/2 + N} }}$ . 因此, 利用双数态进行相位测量, 理论上所能达到的最小相位不确定度几乎正比于总粒子数$N$ ($N \gg $ 1), 具有海森伯极限的标度[32 ] .$b$ 模上的宇称算符为${\hat \varPi _b} = \exp \left( {{\rm{i}}{\text{π}} {{\hat b}^\dagger }\hat b} \right)$ , 其对末态的期望值为$\left\langle {{{\hat \varPi }_b}} \right\rangle = {{\rm{P}}_{N/2}}\left[ {\cos \left( {2\varphi } \right)} \right]$ (其中${{\rm{P}}_{N/2}}\left[ {\cos \left( {2\varphi } \right)} \right]$ 为Legendre多项式)[78 ] . 根据误差传递公式$\Delta \varphi = \dfrac{{\Delta {{\hat \varPi }_b}}}{{\left| {\partial \left\langle {{{\hat \varPi }_b}} \right\rangle /\partial \varphi } \right|}}$ , 可以得到: 当$\varphi \to 0$ 时, 宇称测量的相位不确定度与总粒子数$N$ 成反比关系, 即$\Delta \varphi \propto \dfrac{1}{N}$ . 最近, 国内外在基于超冷原子系综的双数态制备及其相位估计方面取得了巨大的实验突破.[34 ] . 若将原子制备在mF = 0的初始态, 两个mF = 0原子通过自旋交换碰撞就可以产生一对自旋向上和向下(mF = ±1)的原子. Klempt等[34 ] 利用自旋交换动力学成功制备了双数态, 他们的实验利用旋量为2的87 Rb凝聚体, 通过选择合适的磁场强度(1.23 G)和演化时间(15 ms), 制备了原子数可多达104 的双数态, 并利用双数态得到低于散粒噪声$1.61_{ - 1.1}^{ + 0.98}$ dB的干涉灵敏度. 然而, 利用旋量BEC中的自旋动力学产生的双数态总原子数存在很大的涨落, 因此在利用双数态展示突破标准量子极限的测量时需要对样本总原子数进行后选择, 大大降低了双数态的实用性.87 Rb凝聚体自旋混合过程, 实现连续发生两次量子相变, 可以在实验中确定性地制备约11000个原子的双数态[35 ] . 在这个实验中, 旋量BEC的自旋动力学哈密顿量可以描述为$ H = \dfrac{{{c_2}}}{{2{N_{\rm{t}}}}}\left[ {2\left( {\hat a_1^\dagger \hat a_{ - 1}^\dagger {{\hat a}_0}{{\hat a}_0} + {\rm{h}}.{\rm{c}}.} \right) +}\right.$ $\left.{ \left( {2{{\hat N}_0} - 1} \right)\left( {{N_{\rm{t}}} - {{\hat N}_0}} \right)} \right] - q{\hat N_0}$ , 其中$\hat a_{{m_F}}^\dagger \left( {{{\hat a}_{{m_F}}}} \right)$ 与${\hat N_{{m_F}}}$ 分别代表mF 磁子能级原子产生(湮灭)和粒子数算符, Nt = N +1 + N –1 + N 0 为总粒子数. 第一项代表与自旋相关的相互作用, 包括自旋交换相互作用, 参数|c 2 |表示自旋交换发生的平均速率;第二项代表二阶塞曼效应对系统的影响, 实验上通过磁场或者微波可以调控q . 对于该哈密顿量, 在q = ±2|c 2 |处有两个量子相变点, 如图4(a) 所示, 对于$q \gg 2\left| {{c_2}} \right|$ , 所有基态为polar(P)相; 对于$q \ll - 2\left| {{c_2}} \right|$ , 基态变成双数相, 产生相等数目的mF = ±1态; –2|c 2 | < q < 2|c 2 |对应broken-axis symmetry相, 在该区域内BEC中的原子容易发生自旋交换碰撞, 产生双数态. 他们在实验中设计q 的扫描曲线, 让q 尽量慢地穿过量子相变点, 使相变点的激发大为减少, 从而确定性地制备双数态. 在扫描结束后, 有(96 ± 2)%的mF = 0的原子(共约11000个原子)转换为双数态. 另外, 利用类似的方法, 他们还成功制备了三模的balanced spin-1 Dicke态, 并实现了超越三模标准量子极限的干涉精度(达到$2.42_{ - 1.29}^{ + 1.76}$ dB)[36 ] . 这些成果为研究超越标准量子极限的量子精密测量指引了新的方向.图 4 (a)旋量BEC的基态由单原子内态的二阶塞曼效应和BEC中自旋交换作用强度的大小决定, 会出现两个相变点, 将相图分为三个区域, 分别为P, BA和TF相; (b)线性扫描q 时, 通过吸收成像观察到的BEC在各个内态上的分布随时间的变化(摘自文献[35 ])Figure4. (a) The thick black solid line denotes the gap $\Delta $ between the first excited and the ground state of Hamiltonian, which together with the two minima at q = ±2|c 2 | defines three quantum phases, illustrated by their atom distributions in the three spin components, the first-order Zeeman shifts are not shown because they are inconsequential for a system with zero magnetization; (b) absorption images of atoms in the three spin components after Stern-Gerlach separation, showing efficient conversion of a condensate from a polar state into a TFS by sweeping q linearly from 3|c 2 | to –3|c 2 | in 3 s. Adapted from Ref. [35 ].4.4.精密测量中的应用 -->4.4.精密测量中的应用 基于上述非高斯纠缠态, 通过多体量子干涉可实现对物理参数的高精度测量. 第一, 利用多粒子GHZ态的Sagnac干涉来提高旋转频率的测量精度[51 ] . 利用态依赖的旋转势, 两态的玻色原子系综在一个环内移动. 其中, 不同内态的原子沿不同方向运动. 然后, 原子通过Ramsey脉冲进行复合干涉. 相位积累的时间由态依赖的旋转势的形式确定. 只要原子的内态存在纠缠(把原子制备在GHZ态上), 其旋转频率的精度极限将有可能达到海森伯极限. 第二, 基于玻色凝聚铷原子气体, 耦合不同Zeeman能级并调控原子之间的相互作用强度[13 ] , 制备磁敏感非高斯纠缠态(自旋猫态、双数态等)并实施Ramsey干涉, 再选取恰当的可观测量提取磁场信号, 可实现超越传统测量极限的精密磁场测量. 第三, 利用旋量玻色凝聚原子, 可利用多模的多体量子干涉实现线性与非线性Zeeman系数的同时测量[52 ] . 把原子制备在多模的GHZ态上, 两个系数的测量精度有可能同时达到海森伯极限.[79 ] 、磁力计[80 ] 、陀螺仪[81 ,82 ] 、纠缠原子钟[83 -85 ] 等. 虽然这些工作目前仍处于实验研发阶段, 但是已显现出巨大的实用前景和研究价值.5.总结与展望 综上所述, 基于非高斯纠缠态的量子精密测量是一个正在稳步发展的研究方向. 其中, 基于超冷原子系综的绝热量子相变与多体量子干涉实施量子精密测量是一种有广泛应用前景的探索. 利用跨越量子相变临界点的绝热过程可成功制备超冷原子系综的非高斯纠缠态(如自旋猫态和GHZ态). 基于多体量子干涉, 输入所制备的非高斯纠缠态, 可实现超越标准量子极限的高精度测量. 这些都为基于超冷原子系综实施超越标准量子极限的精密测量给出了一条可行的新途径. 当然, 在实际应用中还面临许多挑战, 如实验中各个过程都可能存在退相干效应, 非高斯纠缠态在环境中会变得脆弱, 对最终测量精度产生影响; 针对不同的非高斯输入态, 需要设计合适的探测过程等. 针对这些挑战, 还需要进行更深入的理论分析与实验探索. 
图 1 自旋相干态(左)与自旋压缩态(右)在广义Bloch球上的Husimi分布(摘自文献[39])
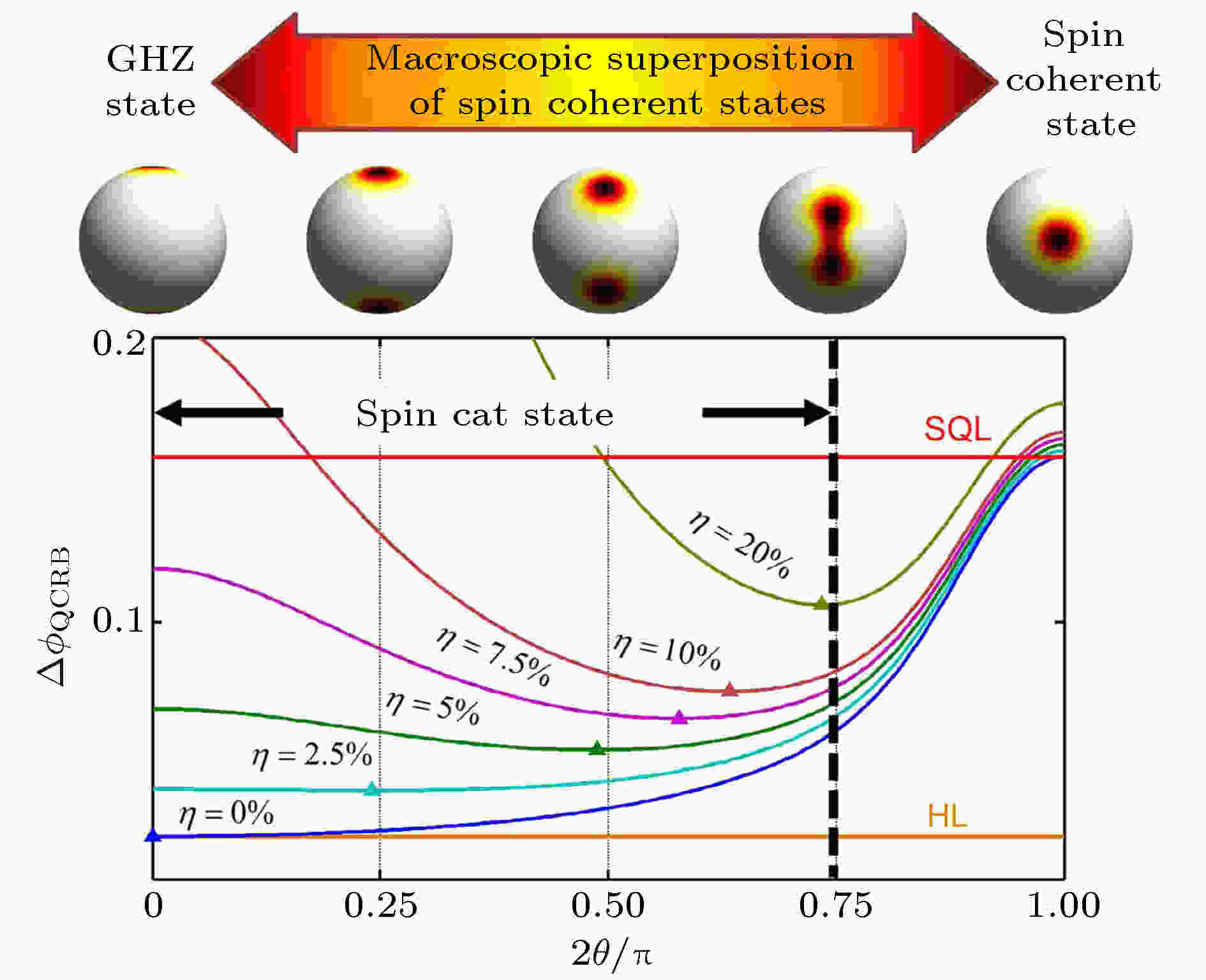图 2 上图为不同自旋猫态在广义Bloch球上的Husimi分布; 下图为不同自旋猫态在有原子数损失(
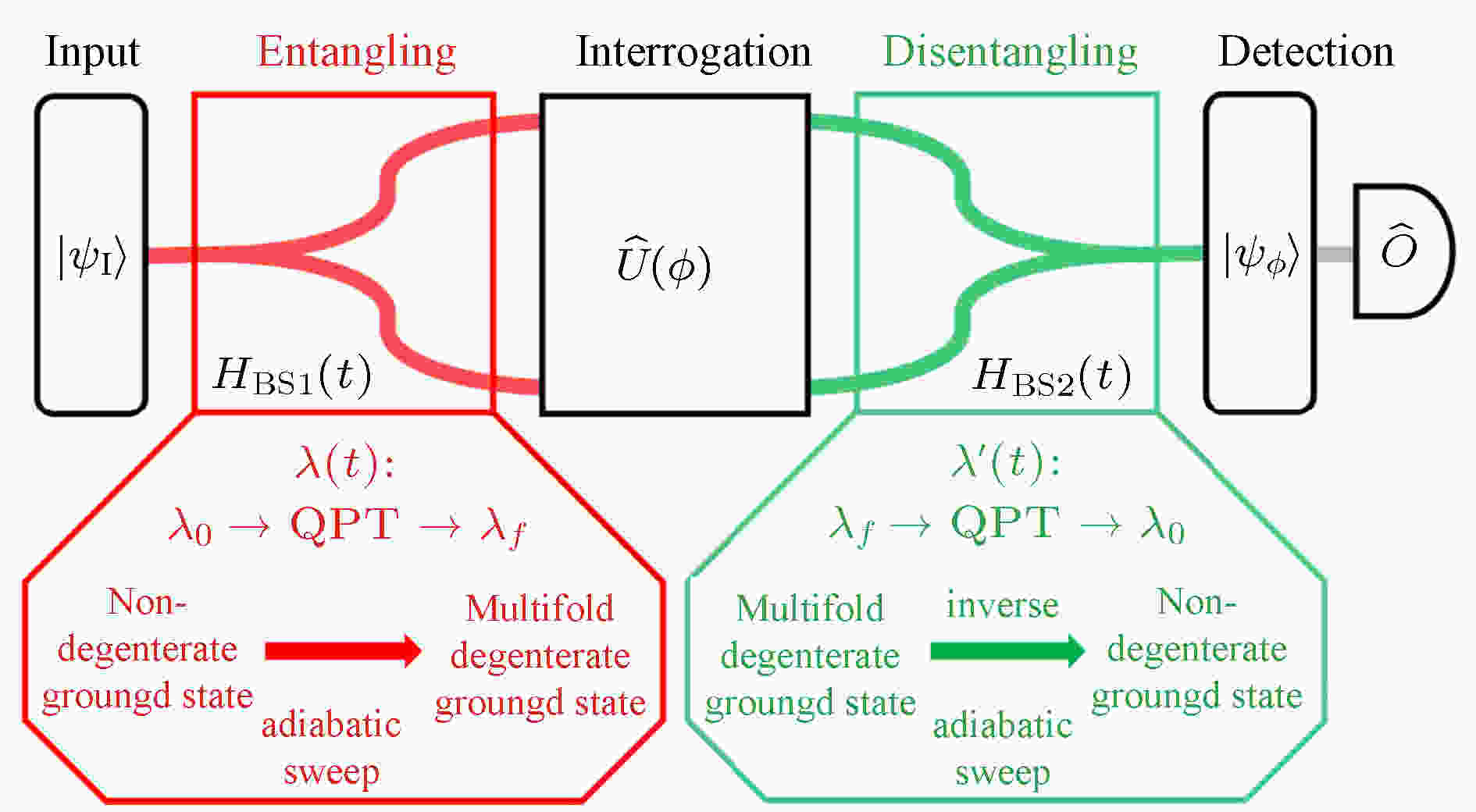图 3 基于量子相变和多体量子干涉的相位测量方案示意图( 摘自文献[61])
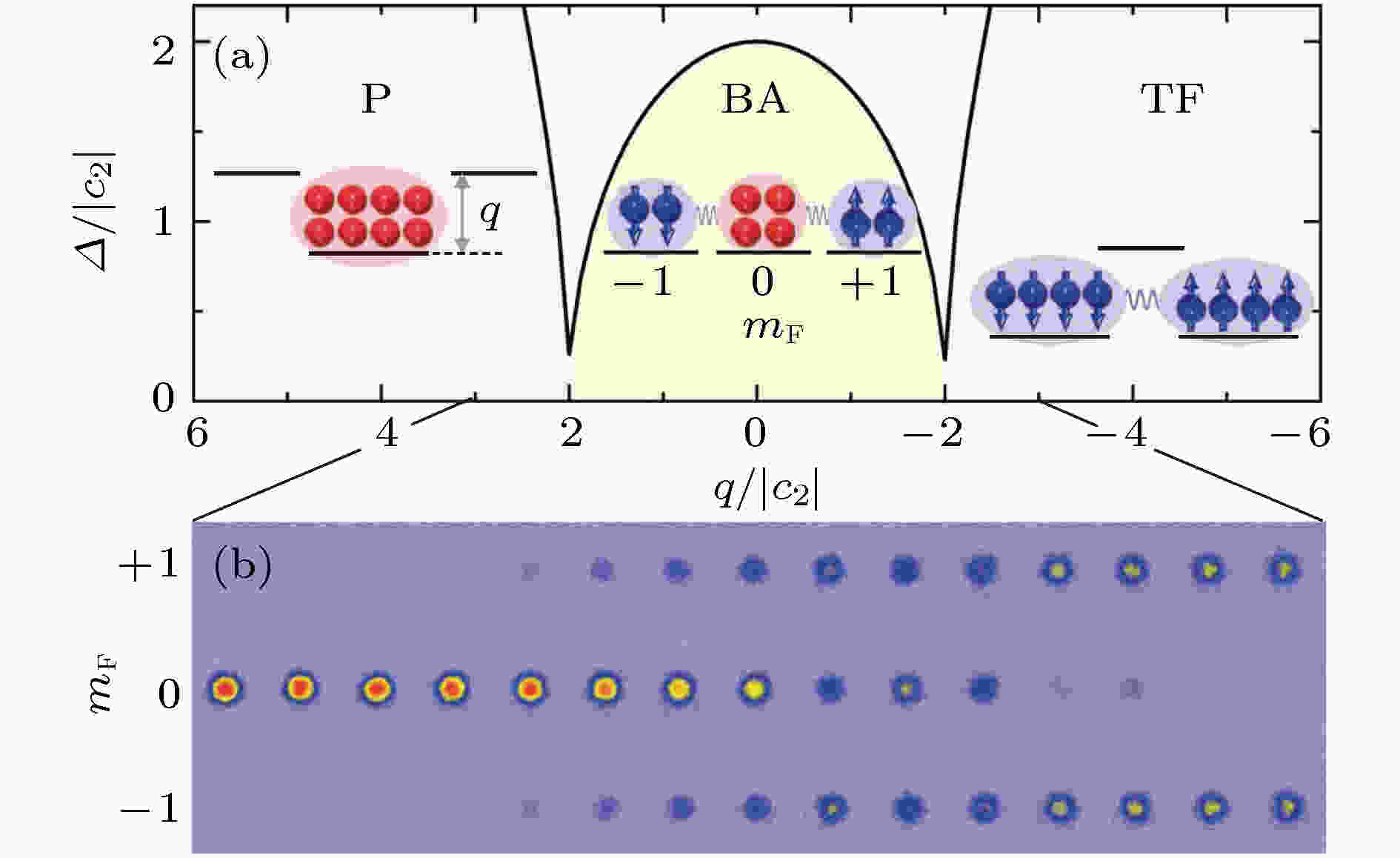图 4 (a)旋量BEC的基态由单原子内态的二阶塞曼效应和BEC中自旋交换作用强度的大小决定, 会出现两个相变点, 将相图分为三个区域, 分别为P, BA和TF相; (b)线性扫描q时, 通过吸收成像观察到的BEC在各个内态上的分布随时间的变化(摘自文献[35])
