摘要: 相互作用可控、相干时间较长的中性单原子体系具备在1 mm
2 的面积上提供成千上万个量子比特的规模化集成的优势, 是进行量子模拟、实现量子计算的有力候选者. 近几年中性单原子体系在实验上取得了快速的发展, 完成了包括50个单原子的确定性装载、二维和三维阵列中单个原子的寻址和操控、量子比特相干时间的延长、基于里德伯态的两比特量子门的实现和原子态的高效读出等, 这些工作极大地推动了该体系在量子模拟和量子计算方面的应用. 本文综述了该体系在量子计算方面的研究进展, 并介绍了我们在其中所做的两个贡献: 一是实现了“魔幻强度光阱”, 克服了光阱中原子退相干的首要因素, 将原子相干时间提高了百倍, 使得相干时间与比特操作时间的比值高达10
5 ; 二是利用异核原子共振频率的差异建立了低串扰的异核单原子体系, 并利用里德伯阻塞效应首次实现了异核两原子的量子受控非门和量子纠缠, 将量子计算的实验研究拓展至异核领域. 最后, 分析了中性单原子体系在量子模拟和量子计算方面进一步发展面临的挑战与瓶颈.
关键词: 里德伯态 /
中性单原子 /
量子纠缠 /
相干时间 English Abstract Experimental progress of quantum computation based on trapped single neutral atoms Xu Peng 1,2 ,He Xiao-Dong 1,2 ,Liu Min 1,2 ,Wang Jin 1,2 ,Zhan Ming-Sheng 1,2 1.State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China Fund Project: Project supported by the National Key Research and Development Program of China (Grant Nos. 2016YFA0302800, 2017YFA0304501), the Strategic Priority Research Program of the Chinese Academy of Sciences, China (Grant No. XDB21010100), and the National Natural Science Foundation of China (Grant Nos. 11674361, 11774389).Received Date: 04 December 2018Accepted Date: 24 December 2018Available Online: 01 February 2019Published Online: 05 February 2019Abstract: As an important candidate for quantum simulation and quantum computation, a microscopic array of single atoms confined in optical dipole traps is advantageous in controlled interaction, long coherence time, and scalability of providing thousands of qubits in a small footprint of less than 1 mm2 . Recently, several breakthroughs have greatly advanced the applications of neutral atom system in quantum simulation and quantum computation, such as atom-by-atom assembling of defect-free arbitrary atomic arrays, single qubit addressing and manipulating in two-dimensional and three-dimensional arrays, extending coherence time of atomic qubits, controlled-NOT (C-NOT) gate based on Rydberg interactions, high fidelity readout, etc.In this paper, the experimental progress of quantum computation based on trapped single neutral atoms is reviewed, along with two contributions done by single atom group in Wuhan Institute of Physics and Mathematics of Chinese Academy of Sciences. First, a magic-intensity trapping technique is developed and used to mitigate the detrimental decoherence effects which are induced by light shift and substantially enhance the coherence time to 225 ms which is 100 times as large as our previous coherence time thus amplifying the ratio between coherence time and single qubit operation time to 105 . Second, the difference in resonant frequency between the two atoms of different isotopes is used to avoid crosstalking between individually addressing and manipulating nearby atoms. Based on this heteronuclear single atom system, the heteronuclear C-NOT quantum gate and entanglement of an Rb-85 atom and an Rb-87 atom are demonstrated via Rydberg blockade for the first time. These results will trigger the quests for new protocols and schemes to use the double species for quantum computation with neutral atoms. In the end, the challenge and outlook for further developing the neutral atom system in quantum simulation and quantum computation are also reviewed.Keywords: Rydberg state /single neutral atom /quantum entanglement /coherence time 全文HTML --> --> --> 1.引 言 量子计算是指以量子态作为信息载体, 利用量子态的线性叠加和量子纠缠等量子力学基本原理进行信息并行计算的方案; 以量子计算为基础的信息处理技术的发展有望引发新的技术革命, 为密码学、催化化学反应计算、新材料设计、药物合成等诸多领域的研究提供前所未有的强力手段, 对未来社会的科技、经济、金融, 以及国防安全等产生革命性的影响[1 ] . 当前各国政府和大公司纷纷投入巨资开展量子计算的研究, 探索实现量子计算机的各种可能体系, 包括离子阱中囚禁的离子[2 ] 、超导线路[3 ] 、线性光学中的光子[4 ] 、量子点[5 ] 、金刚石NV色心[6 ] 、光阱中的中性原子[7 ] 等. 但由于不同量子体系的操控技术难度和发展应用前景不同[8 ] , 面临的挑战也不一样, 目前哪种体系是最优体系还没有尘埃落定. 其中, 相互作用可控、相干时间较长且具备扩展优势的中性原子体系是实现量子计算机的有力候选者之一.图1 所示, 高数值孔径透镜将原子比特操控所需的Raman光、里德伯激发光、态制备光等聚焦到单个原子上, 形成对阵列中量子比特的操控. 同时透镜也收集原子的荧光并传输到电子倍增型相机(EMCCD)上实现量子态的探测. 根据收集到的信息和实验的需要, 通过传统计算机上的数据采集和时序产生系统, 实时控制原子的冷却、转移以及相应的磁场、电场和光场来完成量子算法的执行. 在进行量子计算时, 中性原子体系将根据不同的量子算法, 采用优化后所需逻辑操作数最少的原子阵列构型, 执行一系列高保真的单比特门和两比特受控非门.图 1 中性单原子量子计算的概念架构Figure1. Conceptual architecture for a neutral atom quantum computer.[9 ] , 相比于原子量子比特操控需要的微秒量级时间, 比率达到$ 10^7 $ , 这一指标超过了目前大多数量子计算的候选体系. 2) 具备可控的相互作用. 相互作用的大小不仅决定了两比特相位门的操作时间, 而且作用强度的控制对于减少量子算法执行过程中的退相, 提高操作的保真度具有重要的作用. 基于里德伯态原子的偶极-偶极相互作用是一个长程的、强度比基态相互作用大12个量级的相互作用[7 ] , 由此可以将两比特逻辑门的操控时间控制到微秒以内, 而且该作用可以通过相干激发到里德伯态或从里德伯态相干退激发进行开关, 也可以通过电场、磁场和原子的空间排列来调整大小. 在相互作用可开关的各种量子计算候选体系中, 对于相干时间与两比特相互作用强度的比值, 主量子数大于50的里德伯态比其他体系更具优势[10 ] . 3) 具备很好的扩展性, 且原子阵列的构型灵活可变. 量子计算在编码逻辑比特执行纠错算法和进行复杂量子算法时, 对于物理比特数目的要求通常达到数千以上. 目前已报道的量子计算体系中最多的物理比特数目大多集中在50—100个, 对于大多数体系来说, 进一步扩展物理比特数目而不影响操作的保真度都具有很大的挑战. 中性单原子体系不仅可以通过光晶格实现1 mm2 的面积上集成数千个单原子[11 ] , 或者在光偶极阱阵列中实现包含72个单原子且构型可变的阵列[12 ] , 而且这种灵活可变的中性原子阵列构型, 结合里德伯态原子的多比特逻辑门, 将会有效优化并提高算法的适应性.[13 ,14 ] 、二维(2D)和三维(3D)阵列中单个原子的寻址和操控[15 ,16 ] 、量子比特相干时间的延长[17 ,18 ] 、基于里德伯态的两比特量子门的实现[19 ,20 ] 和原子态的高效读出[21 ,22 ] 等一系列重要的工作, 这些工作极大地推动了该体系在量子模拟和量子计算方面的应用, 使得基于里德伯态相互作用的中性原子体系在量子计算的候选体系中得到了越来越多的关注和认可. 本文将介绍该体系量子计算方面的国内外研究进展, 以及我们团队为该体系的发展所做的两个贡献, 即单比特相干时间的延长[17 ] 和异核两原子纠缠的实现[20 ] , 并对该体系的进一步发展进行了总结和展望.2.中性原子量子计算研究进展 DiVincenzo[23 ] 总结了一个量子力学系统作为量子计算的候选者必须满足的5个主要条件, 即DiVincenzo判据, 该判据被认为是实现量子计算机的基本条件. 中性原子体系经过近20年的技术积累和发展, 在可扩展的量子比特(qubit)系统、量子比特初始化、量子比特相干性、通用逻辑门组和量子比特测量方面都已满足判据的要求.2.1.实现了可扩展的量子比特的系统 2.1.实现了可扩展的量子比特的系统 中性原子体系通常采用一个碱金属原子(如铷原子和铯原子)基态超精细能级的磁子能级作为一个量子比特的0态和1态. 这样的量子态具备纯净和易操控的特点, 是理想的量子比特. 单个原子捕获和囚禁则一般用光阱来实现, 主要有两种方法, 一是在光晶格中, 利用Mott绝缘态在每个格点制备一个原子[24 ] , 但由于冷原子云和光场的空间不均匀性, 只有光晶格中心的部分会均匀地装载; 二是利用碰撞阻塞效应, 当一个光镊型光偶极阱足够小时, 阱中两个以上的原子在共振光的作用下会很快损失掉, 只有一个原子能保存在阱中, 从而获得单个原子[25 ] , 如图2 所示. 但该装载是随机的, 扩展到多个原子阵列时, 无法实现确定性的制备. 2016年, 法国Barredo等[13 ] 发展了一种用可移动光阱实现单原子逐个装配的技术. 他们在2D包含100个光偶极阱的阵列中采用碰撞阻塞的原理随机装载单原子, 随后对光阱阵列进行成像, 判断出哪些阱中有原子, 然后用一个可移动的光阱将单原子逐个转移到所需要的光阱中, 从而确定性地制备包含了50个单原子的不同构型的单原子阵列, 随后他们还演示了包含72个单原子的任意3D构型的确定性制备[12 ] . 类似的工作还包括美国Endres等[14 ] 在一维(1D)包含50个单原子的阵列中制备演示, 韩国Kim等[26 ] 在2D阵列中通过对转移算法的优化和对格点中单原子的实时反馈装载来提高制备效率, Kumar等[27 ] 展示了3D光晶格中利用态依赖的光晶格重排原子得到了$ 5\times5\times2 $ 和$ 4\times4\times3 $ 的单原子阵列. 采用单原子装载后重新排列的方案理论上可以扩展到包含更多单原子的阵列的确定性制备, 从而基本解决了中性原子体系扩展性的问题.图 2 远红失谐光聚焦形成的偶极阱和偶极阱中收集的单原子荧光信号Figure2. The optical dipole trap formed by strongly focusing far red-detuned laser. The fluorescence of single atoms trapped by the dipole trap.2.2.实现了高精度的态初始化 -->2.2.实现了高精度的态初始化 利用成熟的光泵技术将原子制备到量子比特的$ |0\rangle $ 态或$ |1\rangle $ 态, 效率可以达到99.9%以上[28 ] . 例如, 将铷原子制备到编码量子比特的$ |1\rangle $ 态的$ F=2, $ $ m_F=0 $ 态时(如图3 所示), 一般采用高斯量级的磁场将不同的磁子能级区分开, 然后用${\text{π}}$ 偏振的$ F=2 $ 到$ F'=2 $ 的共振光配合$ F=1 $ 到$ F'=2 $ 的回泵光, 由于跃迁选择定则, $ F=2 $ , $ m_F=0 $ 是暗态, 经过一段时间的激光作用后, 原子会全部布居到暗态上. 而且由于相同种类的原子能级结构都是一致的, 因此采用同样的光泵光可以同时实现阵列中所有原子的态初始化.图 3 $ ^{87}{\rm Rb} $ 原子能级和相关的冷却光$ I_{\rm cool} $ 、回泵光$ I_{\rm rep} $ 、态制备光$ I_{\rm pum} $ 和态探测光$ I_{\rm prob} $ 对应的跃迁(量子比特的$ |0\rangle $ 态和$ |1\rangle $ 态编码在 $ F=1 $ ,$ m_F $ = 0和$ F=2 $ , $ m_F=0 $ 上)Figure3. The energy levels and lasers used for cooling, repumpiup ng, optical pumpiup ng, and state detection of $ ^{87}{\rm Rb} $ . The ground hyperfine states of $ F=1 $ , $ m_F=0 $ and $ F=2 $ , $ m_F=0 $ are used for encoding the qubit.2.3.实现了足够长的量子比特相干时间 -->2.3.实现了足够长的量子比特相干时间 要实现量子纠错, DiVincenzo提出: 量子比特的相干时间需要达到基本量子门操作时间的$ 10^4 $ 倍以上[23 ] . 在中性原子体系中, 量子比特的相干时间主要由如下三个因素决定[29 ] . 一是原子在光阱中的囚禁时间, 由于光阱的束缚无法达到离子阱中的势阱深度, 一般只有毫开量级, 室温条件下, 背景气体的碰撞会导致原子的直接损失, 因此即使不考虑光阱本身功率起伏和散射造成的加热, 原子在光阱的寿命也只有百秒量级. 二是量子比特反转时间(T $ _1 $ ), 主要是由囚禁原子的偶极光引起的拉曼散射造成的, 散射率正比于原子所感受到的光强, 反比于失谐的平方. 对于Rb原子, 1 mK阱深的830 nm光阱中, T $ _1 $ 在秒量级. 三是两基态相对相位丢失时间(T $ _2 $ ), 任何改变两基态能级间隔的因素都会对T $ _2 $ 造成影响, 包括原子的热分布、偶极阱功率的起伏、偶极阱位置的抖动、磁场的起伏等. 德国Kuhr等[29 ] 对光阱中原子退相的三个因素进行了详细的研究, 在40 $ {\text{μ}}{\rm K}$ 阱深下没有加任何回波脉冲时, 获得了相干时间为20 ms的单原子和少原子. Li等[18 ] 建立了中空的蓝失谐光阱, 将单个原子囚禁在光强最弱的地方, 从而避免了偶极光引起的退相干, 在没有回波脉冲作用时, 单个原子的相干时间达到了43 ms. 国内Yang等[17 ] 对单原子的相干时间进行了更深入的研究, 获得了微型光偶极阱中无回波脉冲条件下目前最长的相干时间, 达到了225 ms. 相对于单原子为微秒量级的操作时间, 其比值也达到了$10^5 $ 倍, 满足了判据对相干时间的要求. Wang等[30 ] 在3D光晶格中获得了无回波脉冲时26 ms的相干时间, 施加回波后, 相干时间达到7 s以上, 在将原子进一步冷却到振动基态后, 施加回波得到的相干时间达到12.6 s[9 ] .2.4.实现了单量子比特门操作和两量子比特受控非门的操作 -->2.4.实现了单量子比特门操作和两量子比特受控非门的操作 中性原子体系中, 单量子比特门操作一般利用与0态和1态能级间隔共振的微波[29 ] 或者一对拉曼光[31 ] 进行操控, 通过控制作用的时间和相位分别控制量子态的布居和相位. 对于单独一个原子的操控可以简单地采用上述方案进行, 对于原子阵列, 则需要保证对其中一个原子的操控不会影响到其他原子. 2004年, 德国的Schrader等[32 ] 在1D光晶格中, 利用梯度为15 G/cm (1 G = 10?4 T)的磁场产生位置依赖的频率移动, 从而用不同频率的微波脉冲实现了每个格点中单原子的寻址和操控. 在2D光晶格中, 美国的Bake等[33 ] , 德国的Sherson等[34 ] 和英国的Haller等[35 ] 分别采用超高数值孔径的透镜组(NA > 0.68)实现了光晶格中单个格点的分辨. Weitenberg等[36 ] 用该透镜组将远失谐的光聚焦到单个格点从而诱导该格点原子的能级发生偏移, 进而用微波脉冲对该原子进行操控而不影响周围的原子. Xia等[16 ] 在2D的$ 7\times7 $ 的单原子阵列中, 采用类似的方法实现了单量子比特的寻址和操控, 并使用随机基准测试(randomized benchmarking)[37 ] 的方法详细研究并优化了操控的保真度, 实现了原子阵列中任意一个原子单量子比特操控的保真度达到0.99以上, 而且平均串扰只有0.002(9). 美国的Wang等[30 ] 进一步将该方法扩展到3D光晶格, 采用两束交叉的寻址光来使目标原子的能级发生偏移, 然后用共振的微波来操作, 操作的串扰小于0.003. 随后, Wang等[15 ] 采用类似的寻址光, 并利用寻址光累积的相位结合一系列微波脉冲, 实现了一种对寻址光的不稳定非常不敏感并且具备很低串扰的新的寻址和操作方法, 操作的保真度达到0.9962(16), 串扰小于0.002.[38 ] 将单原子激发后, 利用自发辐射, 实现辐射单光子的偏振与单原子磁子能级的纠缠, 在此基础上制备两组纠缠的单光子和单原子, 然后对两个光子进行贝尔态测量, 获得纠缠光子对的同时通过纠缠交换实现两个原子的纠缠[39 ] . 该方法产生纠缠的过程不可控且效率较低, 并不适合作为量子计算中的逻辑门. 第二种是基于原子基态受控碰撞的方案[40 ,41 ] , 通过调节同一个阱中两个原子的振动态、电子态, 或者通过精确调制两个阱的间距来控制隧穿进而控制两个原子自旋碰撞交换相互作用, 实现两量子比特纠缠门. 目前已经在光晶格中实现了两团原子间基于碰撞的纠缠和受控相位门[42 ,43 ] . 对于两个原子间的纠缠, 美国的Kaufman等[44 ] 和美国的Thompson等[45 ] 分别在强聚焦光偶极阱中, 通过Raman边带冷却将原子冷却到振动基态, 随后Kaufman等[46 ] 精确控制两阱的相对位置, 基于自旋交换实现了保真度为0.44的两原子纠缠, 扣除原子损失后, 纠缠的保真度达到0.63. 该实验受限于原子在光阱中三个维度的冷却效率和对两原子间距的控制精度, 进一步提高保真度面临很大的挑战. 第三种方案是基于原子里德伯态的偶极-偶极相互作用实现受控非门, 包括采用里德伯阻塞形成受控相位门[47 ] , 利用共振的偶极-偶极相互作用形成的两原子暗态进行绝热演化[48 ] , 利用里德伯缀饰形成受控相位门[49 ] 等. 实验上, 美国的Urban等[50 ] 在相距8 ${\text{μ}}{\rm m}$ 的两个微型光偶极阱中分别囚禁了单个铷原子, 然后将其中一个原子相干激发到97D的里德伯态, 此时另一个原子的里德伯能级由于偶极-偶极相互作用发生偏移, 从而无法实现里德伯的激发. 利用该效应, Isenhowe等[19 ] 首次实现了两个中性原子间的受控非门, 保真度达到0.73, 并进一步实现了两原子纠缠, 纠正原子损失后保真度为0.58. 法国的Ga?tan等[51 ] 和Wilk等[52 ] , 将单原子囚禁在两个相距4 ${\text{μ}}{\rm m}$ 的偶极阱中, 将两个铷原子的初始态制备为$|1\rangle $ 态, 在58D的里德伯态激发光的作用下, 利用相同的里德伯态相互作用实现里德伯阻塞, 则只有一个原子被激发, 于是两原子被制备到基于里德伯态的两原子纠缠, 随后施加一个将里德伯原子耦合到激发光, 相干转移到基态, 获得基态两原子的最大纠缠态, 保真度在纠正原子损失后达到0.75. 采用原子里德伯态偶极-偶极相互作用实现两量子比特纠缠门对于原子热运动并不敏感, 而且门操作时间在微秒量级, 是目前最适合中性原子体系的两量子比特门方案. Zhang等[53 ] 和Maller等[54 ] 从理论上对该方案进行了细致的分析和模拟, 并在实验上对相关技术噪声进行了进一步的优化, 目前得到的保真度为0.82, 但距离实现纠错的0.99的阈值还有很大差距, 需要进一步研究和优化.2.5.实现了量子态的测量与读出 -->2.5.实现了量子态的测量与读出 为获取量子计算的结果或执行纠错算法, 必须对量子态进行方便而快速的测量. 中性原子体系对原子0态和1态的测量普遍采用的方法是用共振激光将1态的原子加热从而在阱中损失掉, 如图3 中的探测光. 由于加热所需的散射光子数依赖于阱深, 因此可以通过降低阱深减少散射的光子, 从而避免在探测过程中由于共振光的拉曼跃迁改变原子的状态, 提高探测的保真度[55 ] . 该方法的缺陷在于每次探测导致原子损失, 需要重新装载单原子, 不利于提高实验速率. 随后, 法国的Fuhrmanek等[56 ] 和美国的Gibbons等[57 ] 同时用高数值孔径透镜提高原子荧光收集效率, 并仔细优化探测光频率与闭合跃迁能级的共振来抑制拉曼跃迁, 实现了95%以上的态探测效率, 同时原子的损失只有1%. 美国的Kwon等[21 ] 和德国的Martinez-Dorantes等[22 ] 进一步将该方法拓展到2D原子阵列, 用共振光同时激发原子阵列中所有原子, 并用电子倍增型相机收集荧光进行态的探测, 态的探测效率都大于97%, 且原子损失小于2%.[58 ] 在偶极阱中实现了捕获时间为130 s的单个铯原子, 并开展了两方面与量子计算相关的研究工作, 一是利用单原子制备单光子源; 二是研究单原子与高细度微腔的耦合. 中国科技大学Dai等[59 ] 采用光晶格来囚禁和操控铷原子的BEC, 利用光极化势形成了有效磁场梯度, 来调控原子间相互作用, 进而开展拓扑量子计算方面的研究工作. 詹明生等[60 ,61 ] 自2009年利用强聚焦光偶极阱实现了单个铷原子的囚禁以来, 围绕中性原子量子计算, 克服了单原子量子比特的精确操控、两原子量子比特相互作用的有效调控和多量子比特阵列的制备等一系列关键物理问题和技术难题, 在中国科学院武汉物理与数学研究所初步建立了满足DiVincenzo判据的中性单原子量子计算平台; 在此基础上, 发展了“魔幻强度光阱”的方法和低串扰的异核单原子阵列, 实现了中性单原子体系在相干时间和原子阵列中串扰抑制方面的突破, 并开展了异核原子碰撞和量子纠缠的工作, 将该体系量子计算的实验研究进一步拓展到了异核领域. 以下将详细介绍单量子比特相干时间的延长和异核两原子纠缠的实现.3.魔幻强度光阱延长量子比特的相干时间 如前所述, 中性原子量子比特的相干时间主要受限于基态相对相位丢失时间T $ _2 $ . 实验研究表明, 用于编码量子比特的超精细能级劈裂通常有几个GHz大小, 由此导致光阱中的量子比特的0态和1态光频移不同, 即微分光频移, 这是导致$ T_2 $ 减小的主要因素. 例如, 由于热分布, 原子在偶极阱中的不同位置所感受到的光强不同, 从而导致微分光频移的大小不同, 所以原子的共振频率会被原子的热运动展宽(通常在100 Hz的量级), 该展宽会直接导致原子量子比特的非均匀退相. 虽然在静态偶极阱中该非均匀退相可以被动力学退耦的办法(如自旋回波或CPMG脉冲序列)有效地抑制[62 ] , 但是实验上发现, 动力学退耦的方法很难抵消单原子量子比特转移中的相干性丢失. 这是由于在用移动光镊将原子从某个偶极阱转移到另外一个偶极阱的过程中, 光场是动态变化的. 移动光镊的指向起伏以及原子加热所导致的退相都是频率较高的均匀退相, 通常的动力学退耦的方法很难压制[63 ] . 另外一个方面的问题是, 量子比特的能级展宽也会造成单量子比特的操控误差[15 ,16 ] . 因此, 降低微分光频移对相干时间的影响可以更好地提高原子量子比特的质量, 并突破相干时间对大规模中性原子量子信息处理平台实现与应用的限制.3.1.魔幻强度光阱的构建和相干时间的延长 3.1.魔幻强度光阱的构建和相干时间的延长 2010年, Derevianko[64 ] 以及Lundblad等[65 ] 提出和演示了可以利用矢量光频移抵消微分光频移的方案. 为了诱导矢量极化率, 即等效磁场, 基本的实验方案是, 将囚禁光场从原来的线偏振改为圆偏振, 同时将光的偏振矢量的方向与量子化轴的磁场方向设为一致. 由此得到微分光频移为$ \text{δ}\nu(B, U_{\rm a})=\beta_1 U_{\rm a}+\beta_2 B U_{\rm a}+\beta_4 U_{\rm a}^2 $ , 其中B 为量子化轴磁场, $ \beta_1 $ 为标量光频移系数, $ \beta_2 $ 为矢量极化率与塞曼相互作用导致的3阶交叉项的系数, $ \beta_4 $ 为基态超极化率系数, $ U_{\rm a} $ 为偶极阱的阱深. 他们发现, 在弱场极限条件下, 光场诱导的原子的4阶超极化率$ \beta_4 $ 可以忽略, 从而可以得到一个“魔幻磁场”囚禁条件, 即在一个特定的磁场下(通常需要几个高斯), 微分光频移能够被矢量极化率与塞曼相互作用导致的3阶交叉项所抵消. 但是实验上为了囚禁温度为十几微开的单原子量子比特, 光镊所需的光场较强, 这时光场诱导的等效磁场达到高斯量级, 与外加磁场可比拟, 因而弱场近似不成立, 高阶项即超极化率不可忽略. 而且由于超极化率的贡献, 光频移是势阱深度的二次函数. 实验上, 考虑到$ \beta_2 $ 和$ \beta_4 $ 也依赖于偶极光的圆偏振度, 为简单起见, 我们采用完全相同的圆偏振光, 测量了不同阱深和磁场下原子所感受到的微分光频移, 结果如图4(a) 所示. 采用圆偏振阱中$ \beta_{1}\approx3.47\times$ $ 10^{-4} $ 去拟合, 得到$ \beta_2 $ 为$-0.99(3) \times 10^{-4}\ {\rm G}^{-1} $ , 并且首次测量了$ ^{87}{\rm Rb} $ 原子的超极化率$ \beta_4 $ = 4.6(2) $ \times $ $ 10^{-12} $ $ {\rm Hz}^{-1} $ . 该结果与理论计算结果$\beta_{2}=$ $ -1.03\times 10^{-4}\;{\rm G}^{-1} $ 和$ \beta_{4}=4.64\times10^{-12}\;{\rm Hz}^{-1} $ 相符合.图 4 (a)超极化率不可忽略情况下, 原子量子比特的微分光频移在不同磁场下随偶极阱势深的变化; (b)原子量子比特相干时间在不同偶极阱势深下的实验值, 蓝色实线为理论值; 内插图显示了阱深为$ U_{\rm M} $ 时, 通过拟合Ramsey条纹的对比度得到相干时间为$ \tau= (225 \pm 21) $ ms[17 ] Figure4. (a) In the presence of hyperpolarizability, the differential light shift (DLS) of a qubit in the circularly polarized trap is measured as a function of trap depths at various magnetic field strengths; (b) coherence time $ \tau $ and its dependence on normalized ratios $ U/U_{\rm M} $ obtained from experiment. The solid blue line is the theoretical curve. A coherence time is extracted from a decay time of the envelope of Ramsey visibility, as shown as in the inset. At $ U_a= U_{\rm M} $ , $ \tau= (225 \pm 21) $ ms[17 ] .$ U_{\rm M}={-(\beta_1+\beta_2 B)}{(2\beta_4)^{-1}} $ , 展宽最小, 因而是魔幻光强点. 在该偶极阱阱深附近, 原子的微分光频移对于势深起伏的敏感性降到二阶. 在特定磁场($ B \rightarrow-{\beta_1}/{\beta_2}\approx 3.51 $ G)下, $ U_{\rm M} $ 趋近于0, 此时阱深太浅不利于原子的囚禁, 因此一般选用更小的磁场和稍大一点的阱深进行实验. 在综合考虑微分光频移和偶极光散射引起的退相的因素后, 实验上选取的磁场强度为3.115 G, 通过测量Ramsey条纹的衰减时间随势阱深度的变化曲线, 发现相干时间最长的地方就在微分光频移的极值点附近, 如图4(b) 所示. 最长的Ramsey条纹的衰减时间达到$(225 \pm 21)$ ms, 而在线偏振偶极阱中是(1.4 $\pm$ $ 0.1) $ ms[62 ] , 相干时间提高了百倍. 相比于Li等[18 ] 在中空的蓝失谐光阱中获得的铯原子43 ms的Ramsey相干时间, 我们的结果提高了5倍. 需要强调的是, 红失谐魔幻光强偶极阱比中空的蓝失谐光阱更加便于扩展到较大规模的魔幻偶极阱阵列. 这是由于红失谐的单阱所需功率只需毫瓦量级, 而中空的蓝失谐光阱的功率要到达百毫瓦量级.3.2.相干转移的实现 -->3.2.相干转移的实现 在大规模的单原子阵列里, 受限于中性原子间微弱的相互作用, 要实现任意两个原子间的量子算法进而实现量子计算和量子模拟, 需要将单原子相干地转移到相互作用区. 我们提出了一种简单易行的深阱转移方案, 实现了单原子在光阱阵列中的高效转移(约95%), 但在转移过程中, 即使采用动态退耦的方法也无法保持量子比特的相干性, 主要原因在于偶极光引起的微分光频移[63 ] . 运用魔幻光强偶极阱技术(图5 所示), 首先在其中一个魔幻光强偶极阱中(trap 2)制备一个量子比特, 通过微波制备到相干叠加态上, 之后通过一个移动魔幻阱(trap 1)将目标量子比特提取出来转移到5 $ {\text{μ}}{\rm m} $ 的地方后再送回原来的偶极阱, 而后分析量子比特的相干性. 结果发现无转移和被转移的量子比特的Ramsey相干时间几乎一致, 因此在实验的测量精度内, 没有观测到原子的相干性在进行转移操作后有明显的损失, 即使转移后原子的温度从8 ${\text{μ}}{\rm K}$ 升到16 ${\text{μ}}{\rm K}$ . 因此, 实验上证明了用魔幻光强偶极阱转移原子量子比特的过程中, 指向涨落、加热等退相因素变得很小. 然而线偏振阱中这些退相机制是占主导的. 由此解决了中性单原子大规模阵列中单原子相干转移的问题, 极大地提高了原子量子比特间的互联性, 该方法与原子量子比特阵列灵活的构型互相结合, 将有效地降低中性原子量子计算算法的复杂性.图 5 (a)原子量子比特相干转移的实验装置示意图(Trap 1是可移动阱, 其在焦平面上的位置由2D声光偏转器控制; Trap 2是静止阱; 两阱的偏振可以通过液晶相位片(Thorlabs LCR-1-NIR)实时控制); (b) 原子量子比特在两阱中不转移(黑色方块)和转移(红色圆点)时的Ramsey条纹(实验数据中每个点是100多次实验的平均值; 通过衰减的正弦函数拟合(实线部分), 可以得到静止量子比特和转移量子比特的相干时间分别是(206 $ \pm $ 69) ms和(205 $ \pm $ 74) ms[17 ] Figure5. (a) Experimental setup for coherent transfer of atomic qubit. Trap 1 is a movable trap which can be shiftted in two orthogonal diretions by an AOD. Trap 2 is a static one. Both of their polarizations can be actively controlled by a liquid crystal retarder (LCR). (b) Measured Ramsey signals for single static qubits (black squares) and single mobile qubits (red dots) at $ B = 3.115 $ G. Every point is an average over 100 experimental runs. The solid curves are fits to the damped sinusoidal function, with coherence times of static qubits and mobile qubits are (206 $ \pm $ 69) ms and (205 $ \pm $ 74) ms, respectively[17 ] .3.3.魔幻光强偶极阱中原子退相的主要因素 -->3.3.魔幻光强偶极阱中原子退相的主要因素 由原子结构以及光和原子作用参数决定, 构建魔幻光强偶极阱需要3.2 G的磁场, 导致量子比特对磁场噪声变得敏感. 通过对磁场的监视和对自旋回波的实验测量, 我们详细分析了魔幻光强偶极阱中量子比特相干时间的影响因素, 如表1 所列. 从中发现相干时间主要受限于磁场的噪声. 为了压制磁场噪声, 可以搭建磁屏蔽来消除背景的磁场噪声, 但更有科学价值的是寻找磁场的魔幻条件, 使得量子比特对于磁场噪声的敏感性降到2阶. Carr和Saffman[66 ] 提出一个理论方案, 利用双色光场实现更低的磁场噪声敏感度来提高铯原子的相干时间. 目前还未有实验演示中性原子体系中的双魔幻囚禁, 即同时将量子比特对于势深以及磁场噪声的敏感性降到2阶. 这样的实验具有挑战性, 但对于中性原子量子比特来说是非常重要的.87 Rb 退相干机制 参数 无转移时$T_2 $ 转移后$T_2 $ 均匀退相时间$T'_{2} $ 磁场起伏 $ \sigma_B=0.019 $% 300 ms 300 ms 偶极光功率起伏 $ \sigma_I=0.0015 $ 200 s 200 s 偶极光重合及指向抖动 $ \sigma_{\rm{point}}=0.06 $ — 30 s 微波频率起伏 $ \sigma_{\rm MW} < 1 $ mHz $ > 300 $ s $ > 300 $ s 原子加热 2 μK/s 34 s 34 s 非均匀退相时间$T^{*}_{2} $ 原子热运动 约8 μK 2 s — 转移引起的加热 $ < 10\;{\text{μ}}{\rm K} $ — $ > 1.2 $ s 自旋翻转时间$T_{1} $ 偶极光引起的自旋翻转 0.66 $ {\rm s}\cdot {\rm mK}$ 4 s 4 s 总的退相干时间T $ T=1/(1/T_{1}+1/T^{*}_{2}+1/T^{'}_{2}) $ — 约242 ms 约222 ms 实验值 约200 ms 约200 ms
表1 魔幻光强偶极阱中的退相干机制Table1. The mechanisms of decoherence in magic intensity optical trap.4.基于里德伯阻塞的异核两原子受控非门与量子纠缠的实现 正如Saffman[11 ] 在基于里德伯态原子相互作用的中性单原子量子计算综述中指出的, 中性原子体系距离实现量子计算机还有诸多难题, 目前面临的主要挑战包括更高保真度的纠缠门操作、原子的再装载、原子态的无损读出、量子比特间距在微米量级的阵列中低串扰的测量和初始化以及表面附近电场噪声的控制. 其中, 针对原子态的无损读出、量子比特间距在微米量级的阵列中低串扰的测量问题, Beterov和 Saffman[67 ] 提出了建立异核单原子体系, 利用异核原子共振频率的差别来避免串扰, 并利用异核原子间的纠缠来解决无损探测的方案. 相比于同核体系, 异核单原子体系中不同种类的原子可以用于执行量子计算中不同的任务, 如 Auger等[68 ] 提出采用一种原子量子比特作为纠错码中的校验子, 另一种原子作为数据量子比特, 可以有效地执行纠错并避免串扰. 类似地, 在囚禁离子体系中, 也有两个异核离子间的受控非门的实验, 并且展望了两种离子分别作为量子存储和光接口以及在量子非破坏性测量中的应用[69 ,70 ] . 在量子模拟中, 异核体系提供了额外的操控自由度, 为多组分多自旋体系的模拟提供了必备的条件, 如Weimer等[71 ] 提出利用异核单原子作为辅助量子比特, 来克服量子态操作时的串扰, 以模拟带耗散的量子自旋体系的相干演化; 华东师范大学Qian等[72 ] 提出在1D异核原子阵列中研究丰富的动态相位演化等. 由此可见, 基于里德伯阻塞的异核原子的受控非门和量子纠缠在量子模拟、量子计算和量子精密测量等领域都有广泛的应用.4.1.里德伯态的原子及其相互作用 4.1.里德伯态的原子及其相互作用 里德伯态原子是指原子中的一个电子被激发到主量子数较高的轨道时的原子. 由于电子远离原子核, 里德伯态的寿命相对于低激发态的寿命要长很多, 对电场也更加敏感等. 里德伯阻塞是利用里德伯态原子间强烈的偶极-偶极相互作用或范德瓦耳斯相互作用, 使得一定区域内一群原子同时激发时, 只有一个原子能被激发到里德伯态, 而其余原子由于相互作用导致能级发生偏移, 因而失谐于激发光, 无法被激发.$ {\text{μ}}{\rm m}$ , 远小于原子间的普遍间距$ R $ (3 $ {\text{μ}}{\rm m}$ 以上), 因此两个里德伯原子A和B之间的相互作用可近似为 $ V_{\rm dd}=\dfrac{e^2}{R} ({ a}\cdot{ b}-3{ a}\cdot \hat{{ R}}\hat{{ R}}\cdot { b}) $ , 其中$ { a} $ 和$ { b} $ 分别是两个里德伯电子距离各自原子核的位置. 在两原子间距R 比较大时, 原子间的相互作用$ V_{\rm dd} $ 可视为微扰, 相应的能级移动$ \Delta E_n $ 可采用二阶微扰计算得到为$ C_6(n)/R^6 $ , 其中$ C_6\simeq\dfrac{1}{(4{\text{π}}\varepsilon_0)^2}\dfrac{e^4 a_0^4 n^{*11}}{2 R_y} $ , 此时的相互作用与$ {R^6} $ 成反比, 对应经典的范德瓦耳斯相互作用; 而当R 较小, 原子相互作用大到足以导致原子邻近能级混合时, 即$ V_{\rm dd}\geqslant \delta $ 时, 其中$ \delta=E(n_{\rm a}l_{\rm a}j_{\rm a})+E(n_{\rm b}l_{\rm b}j_{\rm b})-2E(njl) $ 为邻近里德伯能级组合与原里德伯能级的差, 两原子体系的哈密顿量需要选择新的基矢重新对角化, 其相互作用导致的能级移动将变为$ \Delta E_n\approx-{\rm sgn}(\delta)C_3/R^3 $ , 此时的相互作用与$ R{^3} $ 成反比, 对应于共振的偶极-偶极相互作用[7 ] . 针对实验中采用的${}^{85}{\rm{Rb}} $ 和${}^{87}{\rm{Rb}} $ 异核原子的里德伯态的相互作用, 考虑到两种原子里德伯态能级的差别, 由量子数$|n_{\rm a}, l_{\rm a}, j_{\rm a}, $ $ m_{\rm a};n_{\rm b}, l_{\rm b}, j_{\rm b}, m_{\rm b}\rangle $ 决定的双原子态在主量子数为79D时有436个组态, 将相互作用的哈密顿量在两原子态构成的子空间展开并求解里德伯阻塞的能级移动. 并进一步考虑到实验中单原子在偶极阱中的热分布, 由此得到$ T_{87}= 8\; {\text{μ}}{\rm K}$ , $ T_{85}=9\; {\text{μ}}{\rm K} $ , 且偶极阱束腰为2.1 $ {\text{μ}}{\rm m}$ , 两阱间距3.8 $ {\text{μ}}{\rm m}$ , 阱深为0.1 mK时, 异核两原子间典型的相互作用强度为200 MHz, 两原子同时激发到里德伯态的概率约为1.3%.4.2.单原子里德伯态的相干激发 -->4.2.单原子里德伯态的相干激发 实现原子从基态到里德伯态的相干激发是实验的第一步. 由于里德伯态的主量子数很高, 使用单光子将原子从基态激发到里德伯态需要短波长的激光. 对于铷原子, 单光子激发波长在297 nm左右, 对于铯原子, 需要318 nm的激光. 国内山西大学Wang等[73 ] 采用和频加倍频的方案产生了2.26 W的318 nm激光, 而且该激光波长可调范围覆盖了铯原子从$ n=70 $ 到电离态的所有能级. 我们在实验中采用 780 nm + 480 nm的双光子激发方案, 780 nm激光由普通的半导体激光器产生, 而480 nm激光由960 nm激光倍频获得(Toptica SHG). 相对于单光子激发, 双光子激发所需的激光波长和激光功率比较容易实现, 而且采用对射的激发方案可以有效地减少激发过程引起的多普勒展宽, 但双光子激发也会引起中间能级的布居形成自发辐射损失, 造成激发效率的降低. 因此在实验中, 双光子激发需要考虑对中间能级的失谐和激发光的光强, 来平衡基态到里德伯态的激发速度与中间态布居引起的自发辐射损失.[74 ] . 简单地估算, 用$ {\text{π}}$ 脉冲将原子从基态相干地激发到里德伯态时, 激发效率的损失正比于$ \varDelta^2/\varOmega^2 $ , 其中$ \varDelta $ 是双光子失谐, $ \varOmega $ 是基态到里德伯态的有效Rabi频率. 当Rabi频率为$ 2{\text{π}} \times1 $ MHz, 且激发效率的损失小于$ 10^{-4} $ 时, 则要求$ \varDelta/2{\text{π}} $ 小于10 kHz. 由此可见, 实现高效率的里德伯态的激发不仅需要将激发光的线宽和频率的长漂控制到10 kHz量级, 同时也要控制背景电场和磁场, 避免里德伯态能级的移动超过10 kHz.[75 ] 小组用超稳腔将铯原子的里德伯激发光线宽压窄到260 Hz, 但激光频率的长漂为86 kHz/d. 为避免激光频率的长漂, 我们定制了一个可调节腔长的高细度传输腔(Stable Laser Systems公司)进行稳频. 该腔在780, 960和1064 nm的细度分别是9.1万、5.9万和8.7万, 同时腔长变化一个1.5 GHz的自由光谱程可以通过在腔镜的PZT上施加0—75 V的电压实现. 先将传输腔的腔长锁定到一个商用的碘稳激光器(Innonlight, Coherent)上, 这个激光器的线宽约为1 kHz, 长漂在1 kHz/0.5 $ {}^\circ{\rm C} $ . 然后将里德伯态的激发光780和960 nm (480 nm 的种子光)通过Pound-Drever-Hal (PDH)频率稳定的方法锁定到腔长稳定的超腔上. 锁定后, 通过延时自拍频的方法标定780和480 nm激光的线宽分别是12.6和10.8 kHz, 并通过里德伯态的吸收峰得到两个激发光频率之和的长漂小于33 kHz/10 h[76 ] .$2{\text{π}}\times 3 $ MHz. 激光功率不进行稳定时, 功率的长漂在10%左右, 这个值对应的原子基态能级的变化达到2${\text{π}} \times 3 $ 00 kHz. 因此我们采用类似Noise eater的方案将480和780 nm激发光的功率进行稳定, 长时间功率漂移控制到0.1%以内以满足实验需求. 此外, 里德伯态原子的极化率正比于$ n^7 $ , 因此其能级对外电场非常敏感. 例如, 处于$ 79{\rm D}_{5/2}, m_j= $ 5/2态的铷原子, 当外电场为0.1 V/cm时, 其能级偏移约为27 MHz. 因此当里德伯态的原子距离真空腔或透镜表面只有几个毫米, 许多实验小组在介质表面镀ITO的导电膜来屏蔽外电场的干扰[77 ,78 ] , 并减少铷原子吸附在介质表面时产生的电场的干扰[79 ] . 实验系统中原子囚禁的位置距离真空腔达到12 mm, 而且由于系统一直使用铷原子的释放剂作为铷源, 导致整个真空系统内壁镀一层铷原子薄膜, 对外电场有很好的屏蔽作用. 在我们的实验中, 即使外电场从0变化到26 mV/cm, 都没有看到$ {79\rm D}_{5/2}, m_j=5/2 $ 的里德伯能级有显著移动.${\text{μ}}{\rm W} $ 的$ \sigma^{+} $ 偏振的780 nm激发光聚焦到约8 $ {\text{μ}}{\rm m}$ , 51 mW的$ \sigma^{+} $ 偏振的480 nm激发光聚焦到约12.8 ${\text{μ}}{\rm m}$ , 获得的单个$ {}^{87}{\rm Rb} $ 原子从基态5$ {\rm S}_{1/2} $ , $ F=2 $ , $ m_F=0 $ 到里德伯态79$ {\rm D}_{5/2}, m_j=5/2 $ 的Rabi振荡如图6 所示. 激发过程中, 480 nm的激发光始终打开, 通过控制780 nm激发光的作用时间控制里德伯态的激发. 里德伯态的探测则是利用里德伯态原子在偶极阱中的损失来探测, 其损失来源于830 nm的偶极阱对于里德伯原子的排斥和偶极光对里德伯态原子的电离. 原子激发到里德伯态的效率通过详细分析将原子全部转移到里德伯态后剩余原子的内态布居得到, 可以得到激发效率约为96%, 由此对应的里德伯态的探测效率约为90%.图 6 (a) $ ^{85}{\rm Rb} $ 和$ ^{87}{\rm Rb} $ 的能级及相应的激光; (b) 实验光路示意图; (c)$ ^{87}{\rm Rb} $ 原子在$ |\!\!\uparrow\rangle $ 和$ |r\rangle $ 态间的相干Rabi振荡; 里德伯态激发光同时作用到$ ^{85} {\rm Rb}$ , 由于频率的差别, $ ^{85}{\rm Rb} $ 没有任何激发, 两原子间操作的串扰可忽略[20 ] Figure6. (a) Energy levels and lasers of $ ^{85}{\rm Rb} $ and $ ^{87}{\rm Rb} $ ; (b) experimental setup; (c) the coherent Rabi oscillation between $ |\!\!\uparrow\rangle $ and $ |r\rangle $ of $ ^{87}{\rm Rb} $ , there is no excitation of $ ^{85}{\rm Rb} $ although the Rydberg excitation lasers also act on it which shows negligible crosstalk between two atoms[20 ] .4.3.异核受控非门 -->4.3.异核受控非门 从单个原子的里德伯态相干激发扩展到两个不同原子的里德伯态间的相互作用, 首先需要构建两个异核原子的阵列. 我们采用类似图5(a) 的设置, 利用两束830 nm的激光建立了两个偶极阱, 分别装载单个$ ^{87}{\rm Rb} $ 原子和单个$ ^{85}{\rm Rb} $ 原子. 由于光偶极阱中单原子的装载是一个随机过程, 需要等待单原子进入偶极阱来实现单原子的囚禁, 因此先打开阱1装载$ ^{87}{\rm Rb} $ , 然后打开阱2装载$ ^{85}{\rm Rb} $ , 再利用后选择的方案, 确保装载完成后异核单原子位于对应的光阱中[80 ] . 异核体系最大的优势在于异核原子共振频率的不同, 可以有效地避免操作的串扰, 并且可以利用激光频率的差别实现两原子的独立寻址. 我们的实验装置中, 所有的激光同时覆盖两个异核原子, 对两个异核原子的单独操控是利用不同频率的激光完成的. 如图6 所示, 对于$ ^{87}{\rm Rb} $ 和$ ^{85}{\rm Rb} $ 原子, 其基态能级的频率差最小为1.1 GHz左右, 利用该频率差别, 进行$ ^{87}{\rm Rb} $ 的里德伯态相干激发时, 对$ ^{85}{\rm Rb} $ 原子的串扰可以忽略, $ ^{85}{\rm Rb} $ 原子几乎没有任何激发.$ {\text{π}} $ 脉冲将${}^{87}{\rm Rb} $ 原子从基态激发到79D里德伯态, 然后等待0.3 $ {\text{μ}}{\rm s} $ , 再测量${}^{85}{\rm Rb} $ 原子的基态到里德伯态Rabi振荡. 由于79D里德伯态的寿命达到180 $ {\text{μ}}{\rm s}$ , 可以提供足够长的相互作用时间, 而且实验中仅记录时序完成后${}^{87}{\rm Rb} $ 不在阱1中的事件, 由此排除${}^{87}{\rm Rb} $ 没有激发到里德伯态的事件. 如图7 所示, 我们在实验上首次展示了异核里德伯阻塞, 当阱1中没有${}^{87}{\rm Rb} $ 原子时, 阱2中的$ {}^{85}{\rm Rb} $ 展示了很好的基态到里德伯态相干Rabi振荡; 而阱1中的${}^{87}{\rm Rb} $ 激发到里德伯态后, 阱2中的${}^{85}{\rm Rb} $ 里德伯激发被极强地抑制了, 激发效率只有约3%, 与理论预期相符合. ${}^{85}{\rm Rb} $ 的里德伯激发没有被完全抑制, 主要原因是实验中阱1的${}^{87}{\rm Rb} $ 原子由于其他原因造成的损失被计入到有效阻塞事件中引起的误差.图 7 (a) 异核里德伯阻塞的时序; (b) 异核里德伯阻塞. 没有$ ^{87}{\rm Rb} $ 时, $ ^{85}{\rm Rb} $ 展示了很好的基态到里德伯态的相干Rabi振荡, 当$ ^{87}{\rm Rb} $ 激发到里德伯态时, 由于异核里德伯阻塞, $ ^{85}{\rm Rb} $ 几乎没有Rabi振荡[20 ] Figure7. (a) Time sequence for heteronuclear Rydberg blockade; (b) Rabi oscillations between the $ ^{85}{\rm Rb} $ $ {\rm 5S_{1/2}}, F=3, m_F=0 $ and $ {\rm 79D_{5/2}}, m_j=5/2 $ states with and without $ ^{87}{\rm Rb} $ in Rydberg state[20 ] .${\text{μ}}{\rm m}$ , 相互作用换算成频率在$10^{-3} $ Hz量级. 当其中一个原子激发到里德伯态后, 相互作用主要是基态与里德伯态的二阶偶极-偶极相互作用, 间距约4 $ {\text{μ}}{\rm m}$ 时强度约为$10^{-3} $ Hz量级[28 ] . 而当两个原子同时激发到里德伯态后, 由于里德伯态具备的巨大的电偶极矩, 他们之间的相互作用达到共振的偶极-偶极相互作用的极限, 其强度将得到量级上的提升, 可以达到100 MHz以上. 因此可以通过如下步骤形成受控的相位门: 1)将“控制”原子用$ {\text{π}} $ 脉冲激发从$ |1\rangle $ 态激发到$ |r\rangle $ , 处在$ |1\rangle $ 态的原子将变成$ -{\rm i}|r\rangle $ 态; 2)在“目标”原子上施加2$ {\text{π}} $ 脉冲激发$ |1\rangle $ 态和$ |r\rangle $ , 没有里德伯阻塞时, 处在$ |1\rangle $ 态的目标原子将变成$ -|1\rangle $ 态, 有里德伯阻塞时, 态不变; 3)将“控制”原子用$ {\text{π}}$ 脉冲激发从$ |r\rangle $ 态退激发到$ |1\rangle $ , 处在$ -{\rm i}|r\rangle $ 态的控制原子将变成$ -|1\rangle $ . 因此在$ |00\rangle $ , $ |01\rangle $ , $ |10\rangle $ , $ |11\rangle $ 的两原子基矢下, 可以得到受控相位门$ Cz={\rm diag}(1, -1, -1, -1) $ [28 ] . 再结合两个Hadamard门, 即可将受控相位门转变为受控非门.$ ^{87}{\rm Rb} $ 原子的5$ \rm S_ {1/2} $ , $ F=2 $ , $ m_F=0 $ 和5$ \rm S_ {1/2} $ , $ F=1 $ , $ m_F=0 $ 作为控制量子比特$ |\!\!\uparrow\rangle $ 和$ |\!\!\downarrow\rangle $ 态, $ ^{85}{\rm Rb} $ 原子的5$ \rm S_ {1/2} $ , $ F=3 $ , $ m_F=0 $ 和5$ {\rm S_ {1/2}}, F=2, m_F=0 $ 作为目标量子比特$ |\!\!\Uparrow\rangle $ 和$ |\!\!\Downarrow\rangle $ 态. 如图8(b) 所示, 得到输出态的布居随着两个Hadamard门的相对相位的振荡, 体现了C-NOT门操作的内在相干性. 当设定相对相位为$ \text{π} $ 时, $ ^{87}{\rm Rb} $ 处于$ |\!\!\uparrow\rangle $ 态, C-NOT操作会翻转$ ^{85}{\rm Rb} $ 的态. 通过测量C-NOT门的真值表, 得到异核C-NOT门操作的保真度为0.73(1). 该保真度主要受限于里德伯态的激发效率和初态制备的效率. 实验中里德伯态的激发效率只有96%, 主要原因在于里德伯态激发光锁定到超高细度FP腔时, 为了压窄线宽, 激发光高频部分的相位噪声有所增加, 从而导致了基态到里德伯态Rabi振荡的退相[81 ] , 降低了里德伯态的激发效率. Levine等[82 ] 最近展示了利用超高细度FP腔过滤激发光的高频相位噪声, 实现了高效的里德伯态激发和保真度达到0.97的里德伯态原子的纠缠. 这也是我们在实验上下一步需要进行的工作. 异核C-NOT保真度的另一限制因素是初态的制备效率只有0.91 (如图8(c) ), 主要原因在于基态Raman光功率起伏造成跃迁效率的变化和实验过程中背景气体以及原子在两阱间的转移造成的损失. 这一部分损失将通过改进实验条件加以抑制.图 8 (a) 异核C-NOT门的时序; (b) 不同输入态$ |\!\!\downarrow\Uparrow\rangle $ (黑色方块)和$ |\!\!\uparrow\Uparrow\rangle $ (红色圆点)时, 输出态的布居随两个Raman $ {\text{π}}/2 $ 脉冲的振荡; 用正弦函数拟合后, 两个振荡间的相位差为$ (0.94 \pm 0.01) {\text{π}} $ ; (c) 初态制备的真值表; (d) 两个Raman $ {\text{π}}/2 $ 脉冲的相对相位设为0时, 测得的H-Cz型的C-NOT门的真值表[20 ] Figure8. (a) Experimental time sequence of H-Cz C-NOT gate; (b) output states as a function of the relative phase between the Raman $ {\text{π}}/2 $ pulses, for the initial states $ |\!\!\downarrow\Uparrow\rangle $ (black squares) and $ |\!\!\uparrow\Uparrow\rangle $ (red circles). The solid curves are sinusoidal fits yielding the phase difference of $ (0.94 \pm 0.01){\text{π}}$ between the two signals; (c) truth table matrix for the initial state preparation; (d) set the relative phase to be 0, the measured truth table matrix for H-Cz C-NOT gate[20 ]. .4.4.异核两原子纠缠 -->4.4.异核两原子纠缠 异核受控非门可用于确定性地实现异核两原子的纠缠态. 当用基态$ \text{π} $ /2的Raman脉冲作用到$ ^{87}{\rm Rb} $ 原子上, 就可以制备$ (|\!\!\uparrow\rangle+\rm i|\!\!\downarrow\rangle)|\!\!\Downarrow\rangle/\sqrt{2} $ 或者$ (|\!\!\uparrow\rangle+\rm i|\!\!\downarrow\rangle)|\!\!\Uparrow\rangle/\sqrt{2} $ 的初态, 然后执行异核C-NOT门, 就可以得到两种Bell纠缠态$ (|\!\!\uparrow\Uparrow\rangle+|\!\!\downarrow\Downarrow\rangle)/\sqrt{2} $ 或者$ (|\!\!\uparrow\Downarrow\rangle+|\!\!\downarrow\Uparrow\rangle)/\sqrt{2} $ . 为确定实验得到的是纠缠态, 一般通过测量宇称信号$ P=P_{\uparrow\Uparrow} +P_{\downarrow\Downarrow} -P_{\uparrow\Downarrow}-$ $ P_{\downarrow\Uparrow} $ 来获取纠缠的保真度. 实验上, 首先制备$ (|\!\!\uparrow\Uparrow\rangle+|\!\!\downarrow\Downarrow\rangle)/\sqrt{2} $ , 然后对两个原子分别施加基态${\text{π}}$ /2的Raman脉冲, 但这两个脉冲相对于初始化时的基态Raman脉冲有$ \phi_1 $ 的相位变化, 然后可以测得宇称信号P 随$ \phi_1 $ 的振荡$P=2\Re(C_{2})- $ $ 2|C_{1}|\cos(2\phi_{1}+\xi) $ , 其中$ C_1 $ 代表了$ |\!\!\uparrow\Uparrow\rangle $ 和$ |\!\!\downarrow\Downarrow\rangle $ 相干性. 如图9 所示, 通过拟合宇称信号的振荡, 得到$ C_1 = 0.16 \pm 0.01 $ , 结合纠缠态的布居$ P_{\uparrow\Uparrow}=0.41 $ 和$ P_{\downarrow\Downarrow}=0.44 $ , 得到纠缠态的保真度为$ F=$ $ (P_{\uparrow\Uparrow}+P_{\downarrow\Downarrow})/2 +|C_1|= 0.59\pm $ 0.03. 该保真度已经超过纠缠的判定阈值0.5, 因此可以确认异核纠缠的存在.图 9 (a) 制备和测量异核两原子纠缠的时序; (b) 纠缠态的布居; (c) 宇称信号随测量脉冲相对相位的振荡, 拟合得到$ |C_{1}|= 0.16 \pm 0.01 $ [20 ] Figure9. (a) Time sequence for generating and verifying entanglement of two heteronuclear atoms; (b) measured probabilities for the entangled state; (c) the parity signal $ P $ ; the solid curve is a sinusoidal fit with $ |C_{1}|= 0.16 \pm 0.01 $ [20 ] .$ T_{87} = 8\;{\text{μ}}{\rm K} $ , 控制量子比特的两个里德伯$ {\text{π}}$ 脉冲的时间间隔是$ \text{δ} t = 3.6 \;{\text{μ}}{\rm s} $ , 在此期间, 由于原子的热运动累积的随机相位为$ \langle {\rm{e}}^{{\rm{i}}\varphi}\rangle = {\rm{e}}^{-\langle \varphi^2\rangle/2} = {\rm{e}}^{-{ k}^2 (\Delta v)^2 (\text{δ} t)^2/2}=0.78 $ , 其中$ { k} $ 为对射的480和780 nm里德伯激发光的波矢, $ \Delta v= \sqrt{2 k_{\rm B} T_{87}/m_{87}} $ . 由此得到随机相位对纠缠保真度的限制为$ F_{\langle {\rm{e}}^{{\rm{i}}\varphi}\rangle}=0.89 $ , 结合受控非门的保真度, 纠缠保真度的上限应为$ F_{\rm{en{\text -}max}}=0.65 \pm $ 0.03, 与实验结果比较符合. 下一步实验将优化实验条件, 目标是降低原子的温度到4 $ {\text{μ}}{\rm K}$ , 并提高里德伯激发光强从而减少两个里德伯$ {\text{π}}$ 脉冲的时间间隔到1.5 $ {\text{μ}}{\rm s} $ , 从而可以将原子热运动导致的纠缠保真度限制提高到$ F^{\prime}_{\langle {\rm{e}}^{{\rm{i}}\varphi}\rangle}=0.99 $ .5.总结与展望 在科学界持续而深入地对量子计算的实现条件、计算能力进行研究的过程中, 清晰地确定并展示量子计算机相对于传统设备的优势将是量子计算研究领域中一个具有里程碑意义的目标. 如“量子霸权”(quantum supremacy)[83 ] , 认为对某些特定的问题, 并不需要量子编码过程, 只需要50个物理量子比特量子计算机(准确地说是专为解决具体问题而构建的量子模拟器, 而不是普适的量子计算机)就可以超越现在的超级计算机的能力. 随后这一数目的要求通过优化经典算法, 又进一步提高到64位[84 ] . 但单单提高量子比特数目, 而使用较差保真度的量子逻辑门, 并不会有效提高体系的量子计算能力, 因此IBM的科学家进一步提出了“量子容积”的概念. 近期, Bravyi等[85 ] 首次证明了求解特定线性代数问题时量子算法的优势, 并行量子电路需要的计算步骤和问题规模无关, 而类似的经典电路需要的计算步数随着问题规模的增长而对数式增加. 由此可见, 明确量子计算相对于传统设备的优势, 针对现有传统计算难以克服的问题提出新的量子计算的优势方案将是未来量子计算理论方面的主要研究内容. 而在实验上, 提高物理量子比特的数目、提高逻辑门操作保真度、进而实现优化的特定目的量子算法将是下一阶段量子计算实验体系追求的主要目标.[86 ] ; 在两量子比特逻辑门保真度方面, 在Levine等[82 ] 通过高细度FP腔过滤里德伯激发光相位噪声并实现了保真度达到0.97的两原子纠缠态后, 通过更为严格和精确地操控实验条件, 包括对背景电场和磁场的屏蔽和控制、亚微秒量级激光脉冲波形和频率的同步精确调制技术、对偶极光光强的精确控制、激发光相位的保持等, 将非常有希望实现两量子比特逻辑门的保真度突破0.99. 同时在态探测方面, Wu等[9 ] 在3D阵列中实现了约160个量子比特态无损探测, 并且保真度达到0.9994, 这是目前4个量子比特以上量子计算体系中最高的态探测效率. 进一步实现纠错操作时, 考虑到现有探测方案中荧光的串扰, 采用异核单原子阵列配合异核两原子量子受控非门进行量子态探测的方案[67 ] 将是一个很好的选择. 其中异核单原子阵列可以采用现有的单原子装载后重新排列的技术, 逐次对每种原子进行排列, 对于排列完成后异核阵列中可能出现的缺陷可以再次进行成像并予以补充.[87 –89 ] , 基于中性原子阵列与光学腔耦合并通过里德伯阻塞效应实现光子-原子量子逻辑门等[90 –92 ] . 长期来看, 通用量子计算需要面对的将是成千上万的量子比特, 由此带来的更复杂的系统操控将是一个需要花费数年乃至数十年不断研究的长期课题, 并且最终方案极有可能采用混合体系, 综合各个体系的优势并避免各自的不足, 实现可靠性、容错性和纠错性于一体的量子计算机, 并开展适用于量子计算机的接口及网络技术、研究并发展量子算法和量子协议、将处于实验室阶段的关于量子系统的控制和测量技术转化到工业化生产, 以期获得工业上的兴趣及支持来推广发展量子系统等工作. 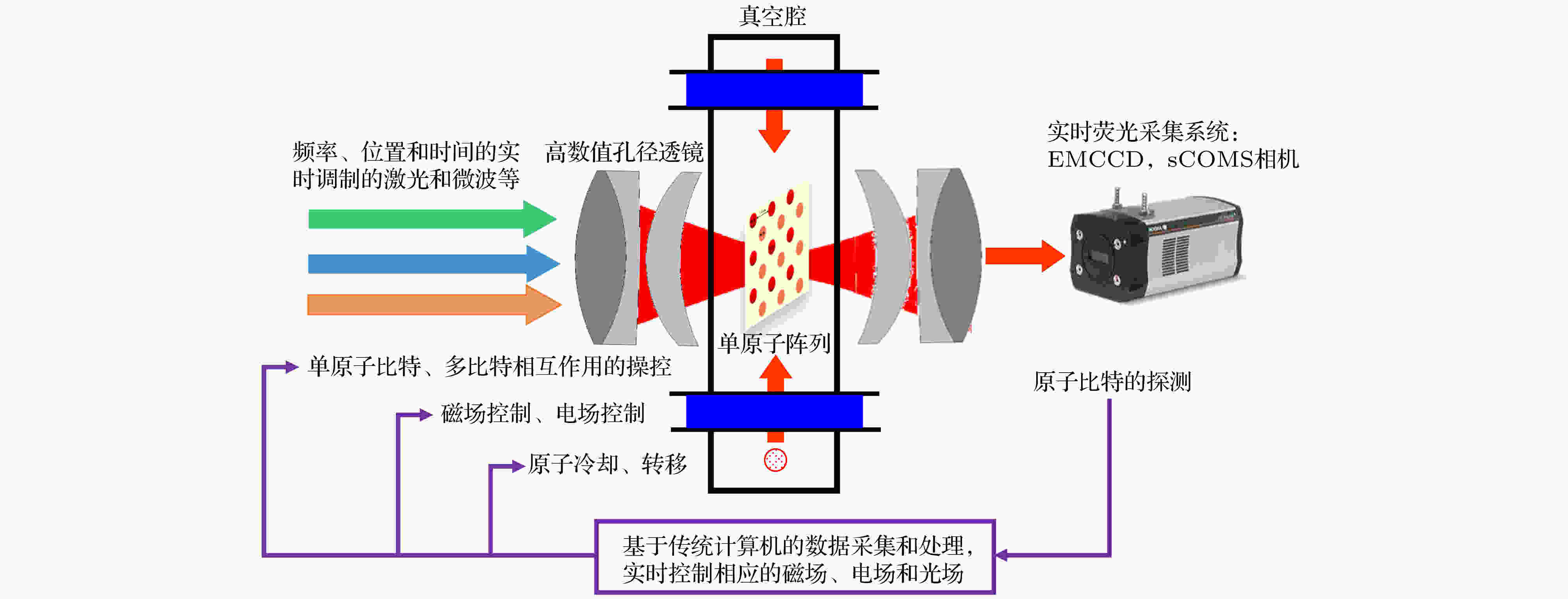 图 1 中性单原子量子计算的概念架构
图 1 中性单原子量子计算的概念架构


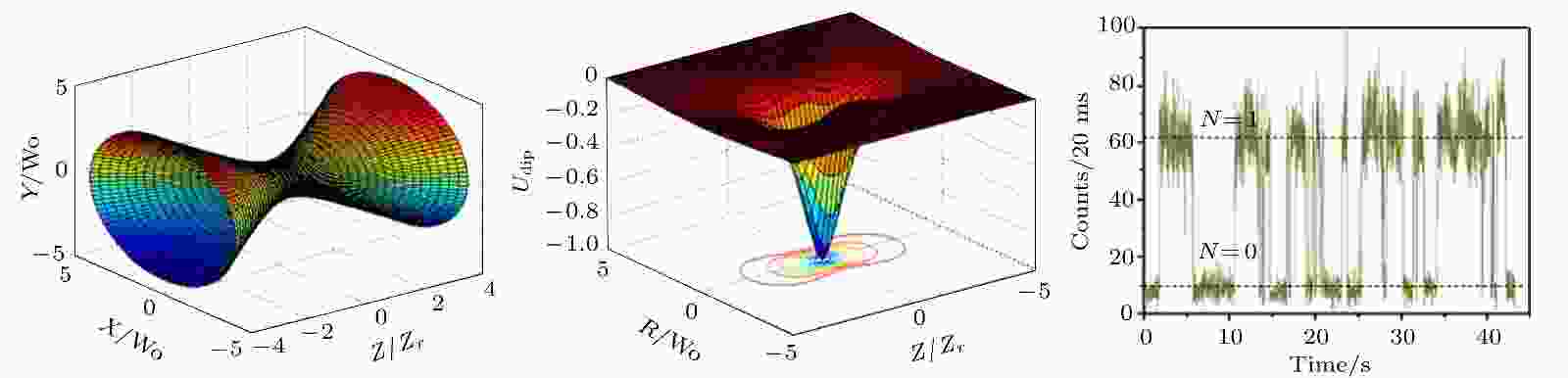 图 2 远红失谐光聚焦形成的偶极阱和偶极阱中收集的单原子荧光信号
图 2 远红失谐光聚焦形成的偶极阱和偶极阱中收集的单原子荧光信号



















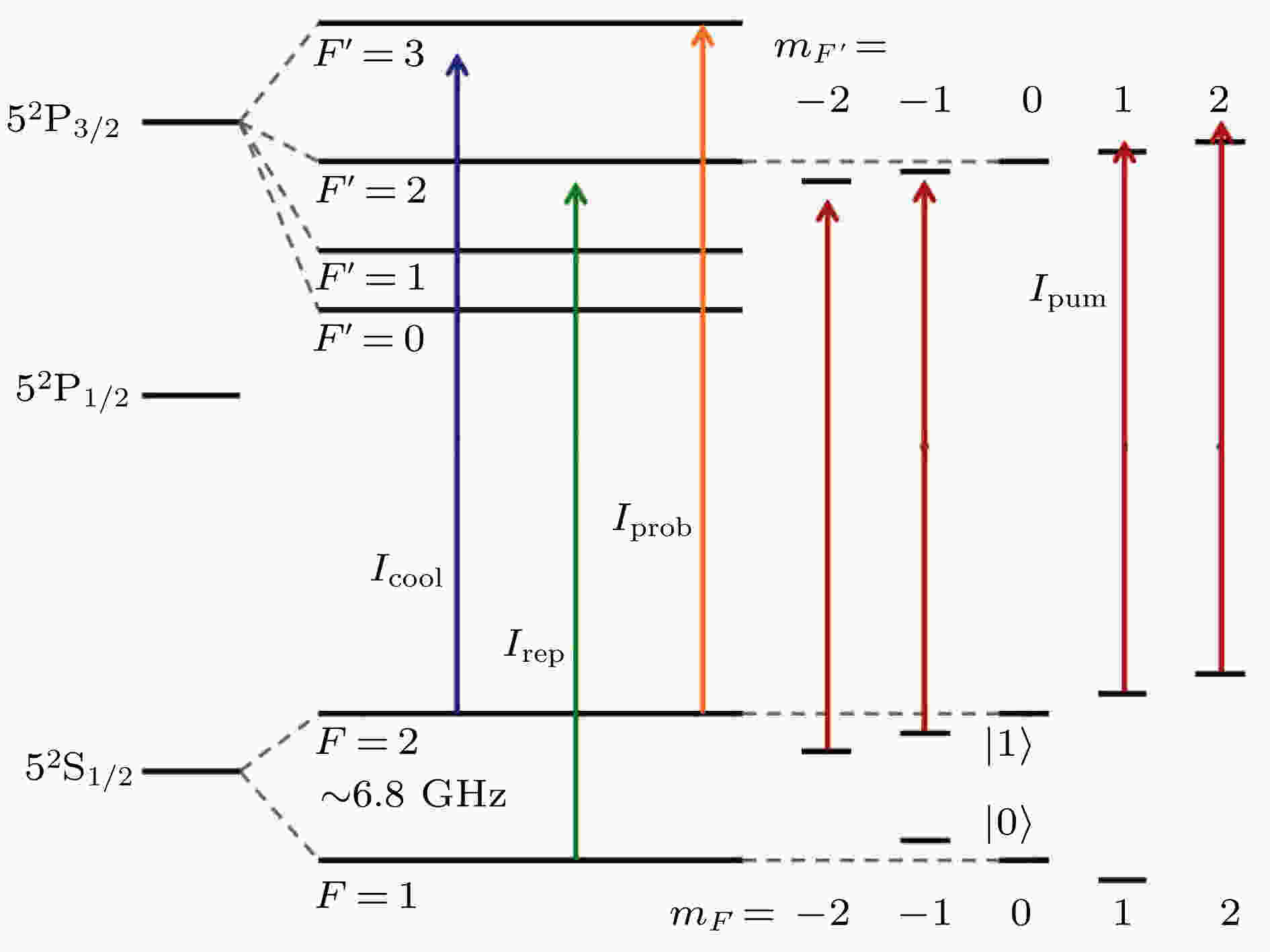 图 3
图 3 










































































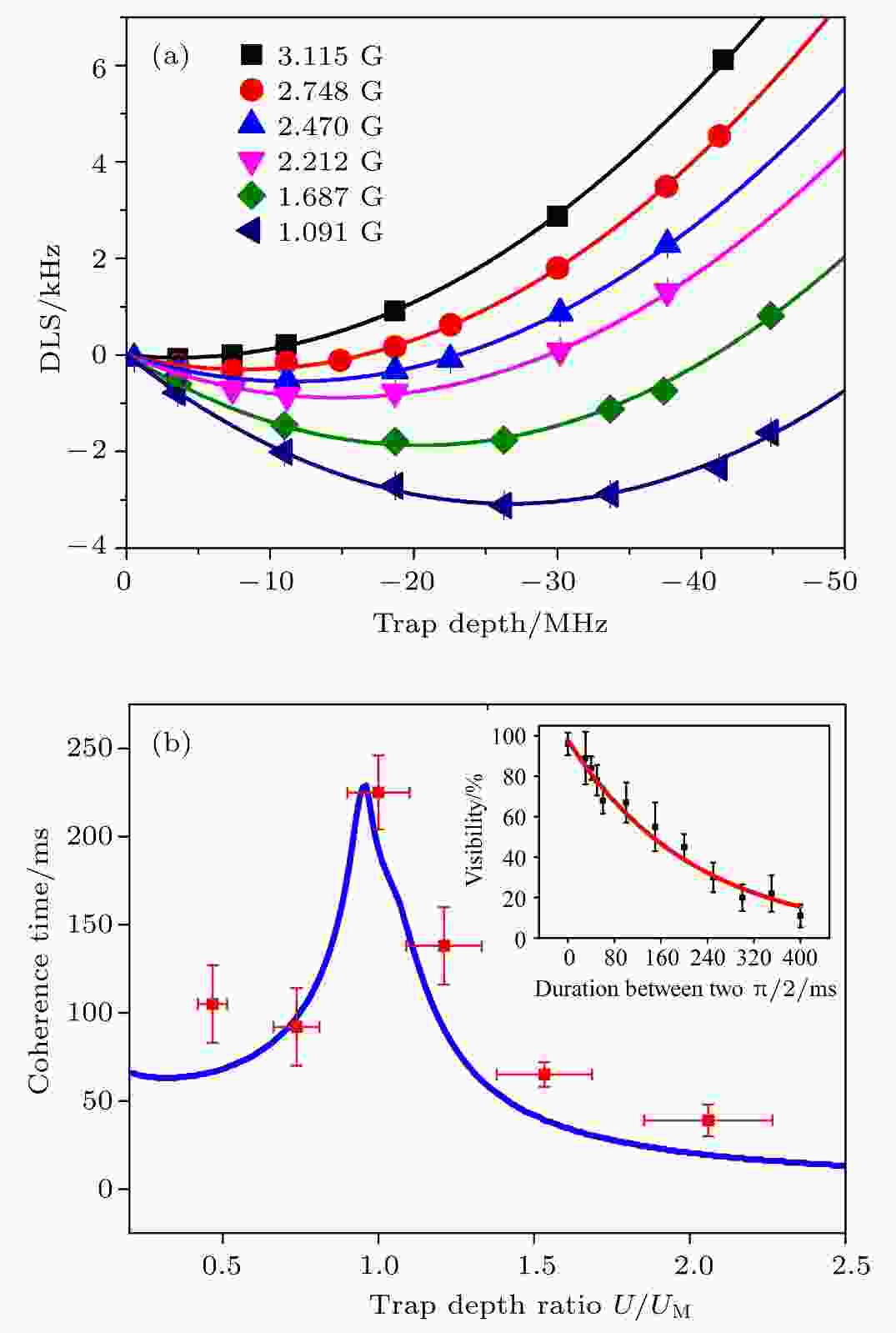 图 4 (a)超极化率不可忽略情况下, 原子量子比特的微分光频移在不同磁场下随偶极阱势深的变化; (b)原子量子比特相干时间在不同偶极阱势深下的实验值, 蓝色实线为理论值; 内插图显示了阱深为
图 4 (a)超极化率不可忽略情况下, 原子量子比特的微分光频移在不同磁场下随偶极阱势深的变化; (b)原子量子比特相干时间在不同偶极阱势深下的实验值, 蓝色实线为理论值; 内插图显示了阱深为
















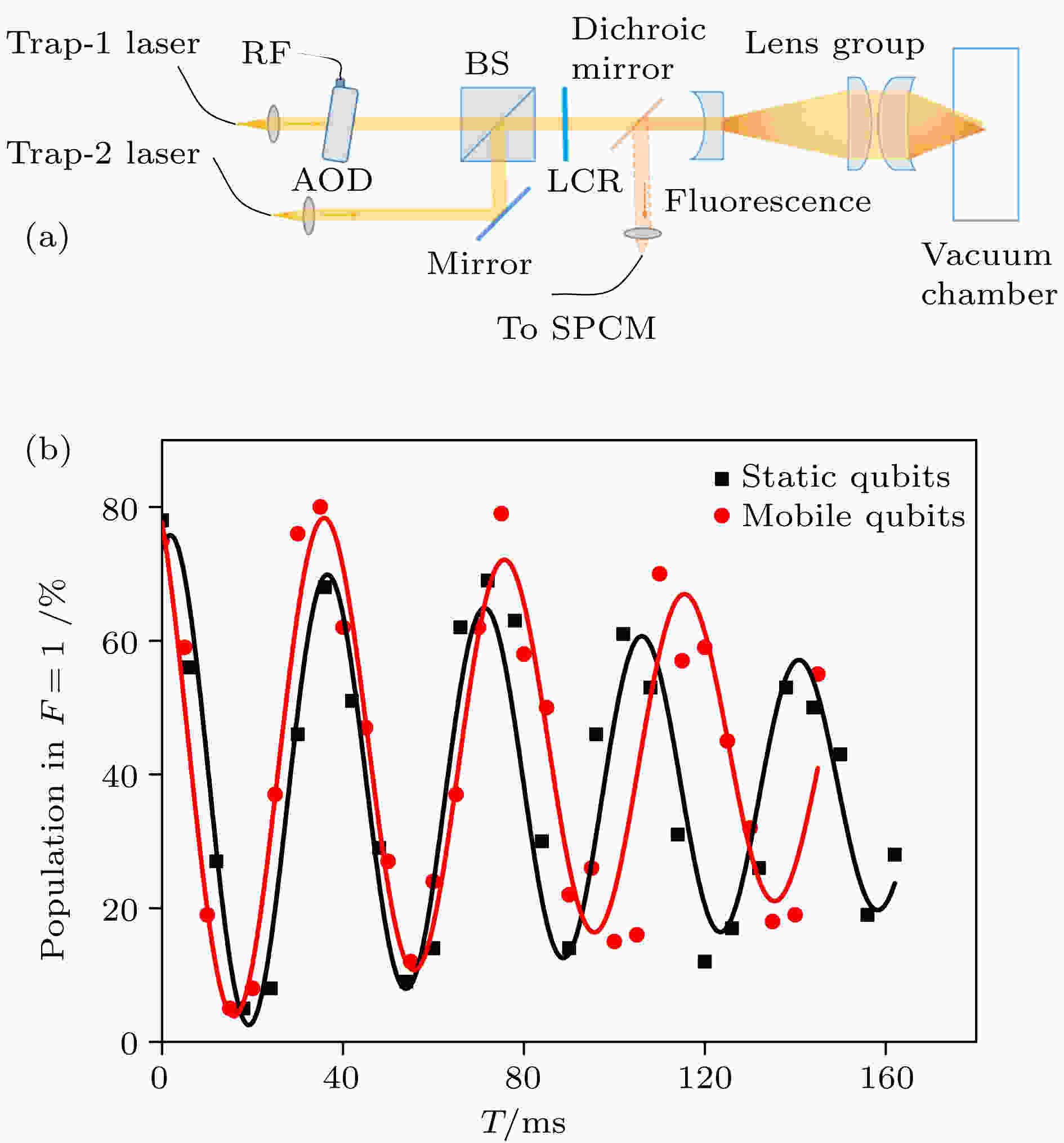 图 5 (a)原子量子比特相干转移的实验装置示意图(Trap 1是可移动阱, 其在焦平面上的位置由2D声光偏转器控制; Trap 2是静止阱; 两阱的偏振可以通过液晶相位片(Thorlabs LCR-1-NIR)实时控制); (b) 原子量子比特在两阱中不转移(黑色方块)和转移(红色圆点)时的Ramsey条纹(实验数据中每个点是100多次实验的平均值; 通过衰减的正弦函数拟合(实线部分), 可以得到静止量子比特和转移量子比特的相干时间分别是(206
图 5 (a)原子量子比特相干转移的实验装置示意图(Trap 1是可移动阱, 其在焦平面上的位置由2D声光偏转器控制; Trap 2是静止阱; 两阱的偏振可以通过液晶相位片(Thorlabs LCR-1-NIR)实时控制); (b) 原子量子比特在两阱中不转移(黑色方块)和转移(红色圆点)时的Ramsey条纹(实验数据中每个点是100多次实验的平均值; 通过衰减的正弦函数拟合(实线部分), 可以得到静止量子比特和转移量子比特的相干时间分别是(206 





































































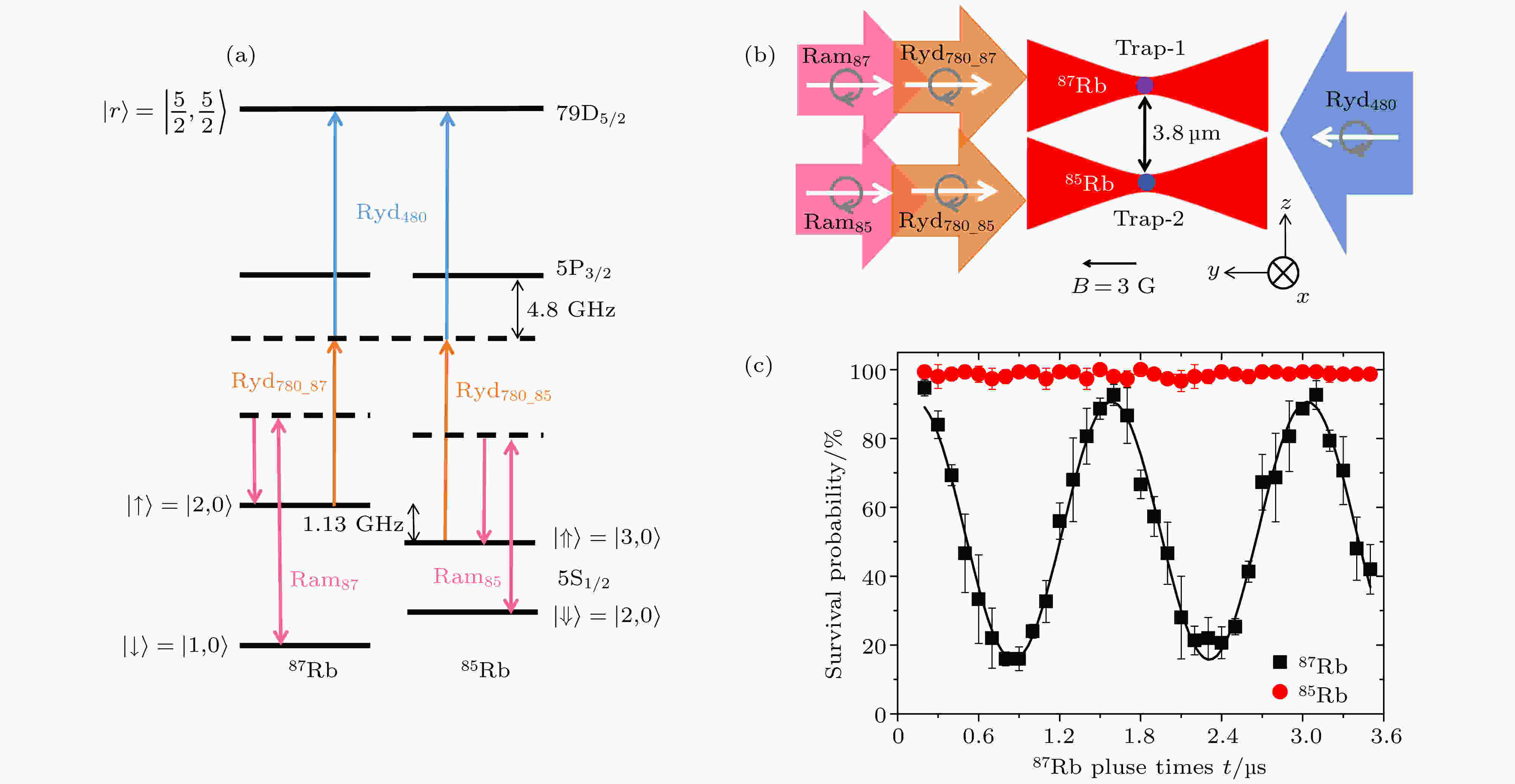 图 6 (a)
图 6 (a) 














































































































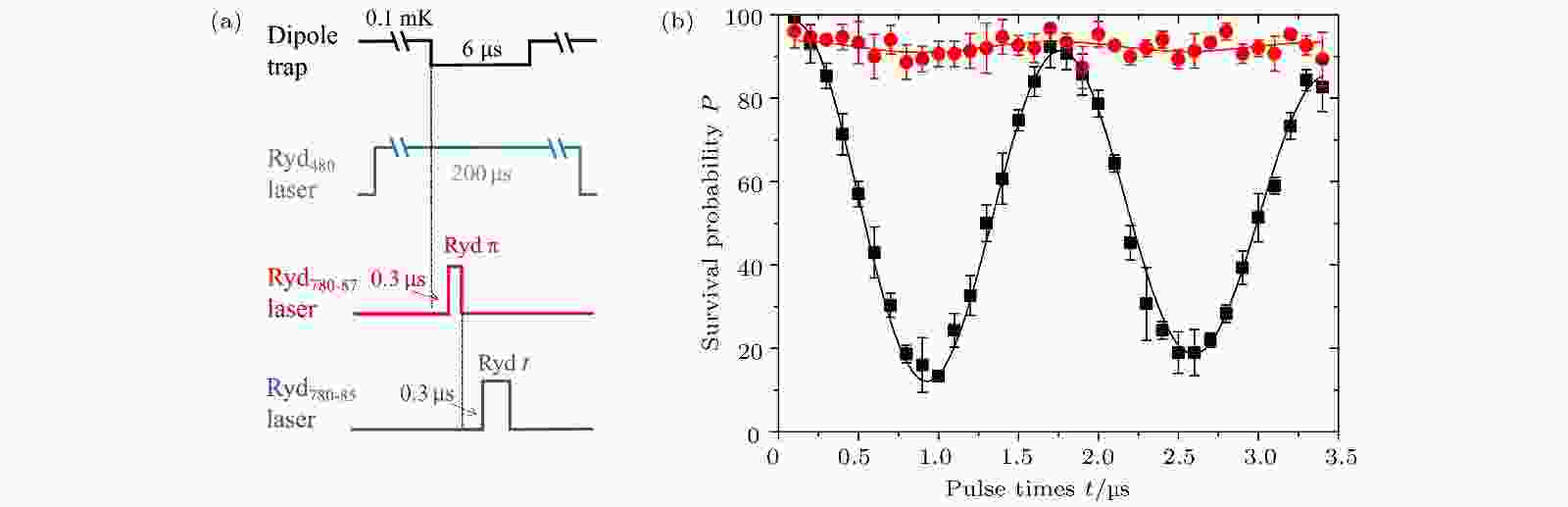 图 7 (a) 异核里德伯阻塞的时序; (b) 异核里德伯阻塞. 没有
图 7 (a) 异核里德伯阻塞的时序; (b) 异核里德伯阻塞. 没有











































































































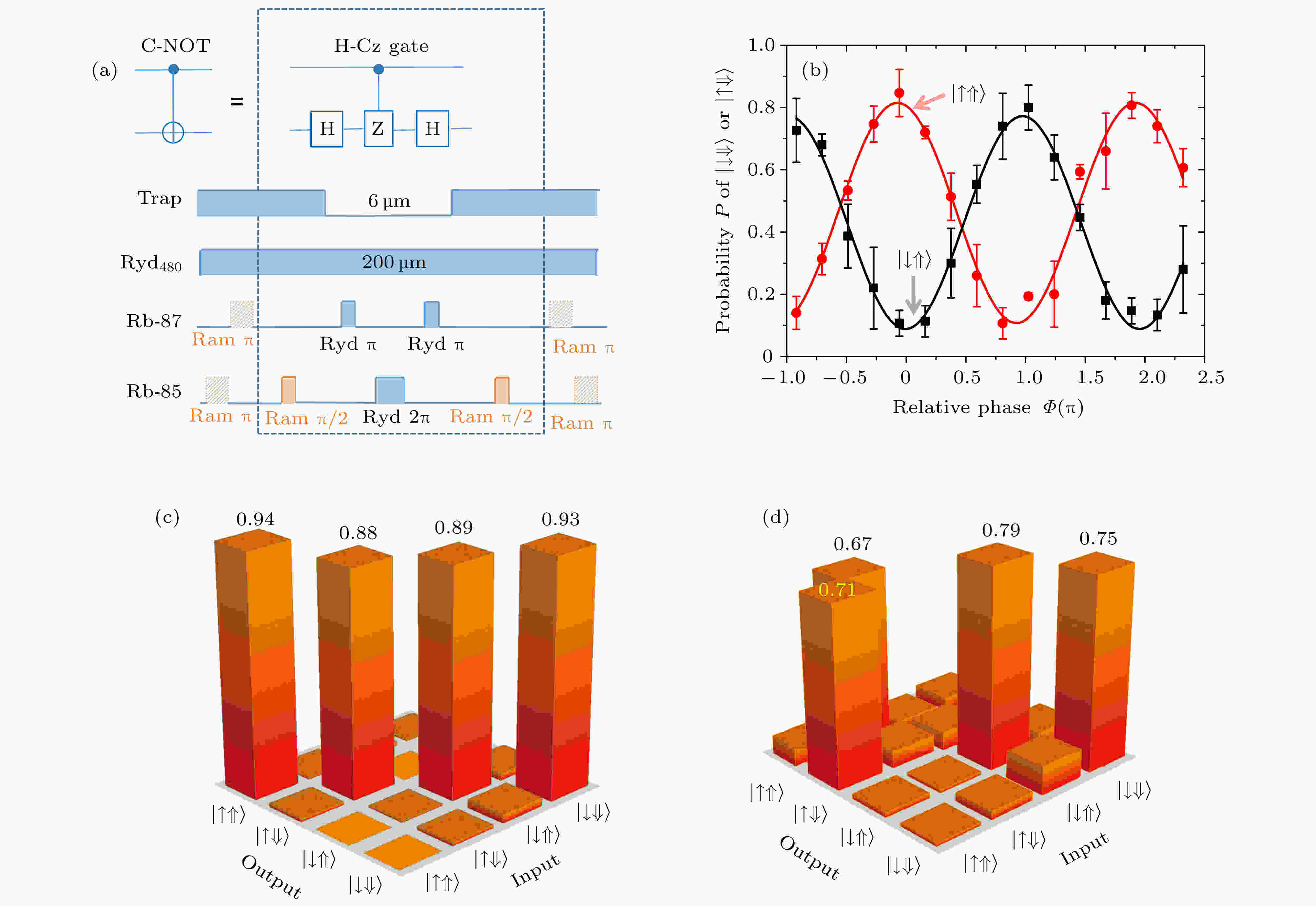 图 8 (a) 异核C-NOT门的时序; (b) 不同输入态
图 8 (a) 异核C-NOT门的时序; (b) 不同输入态




































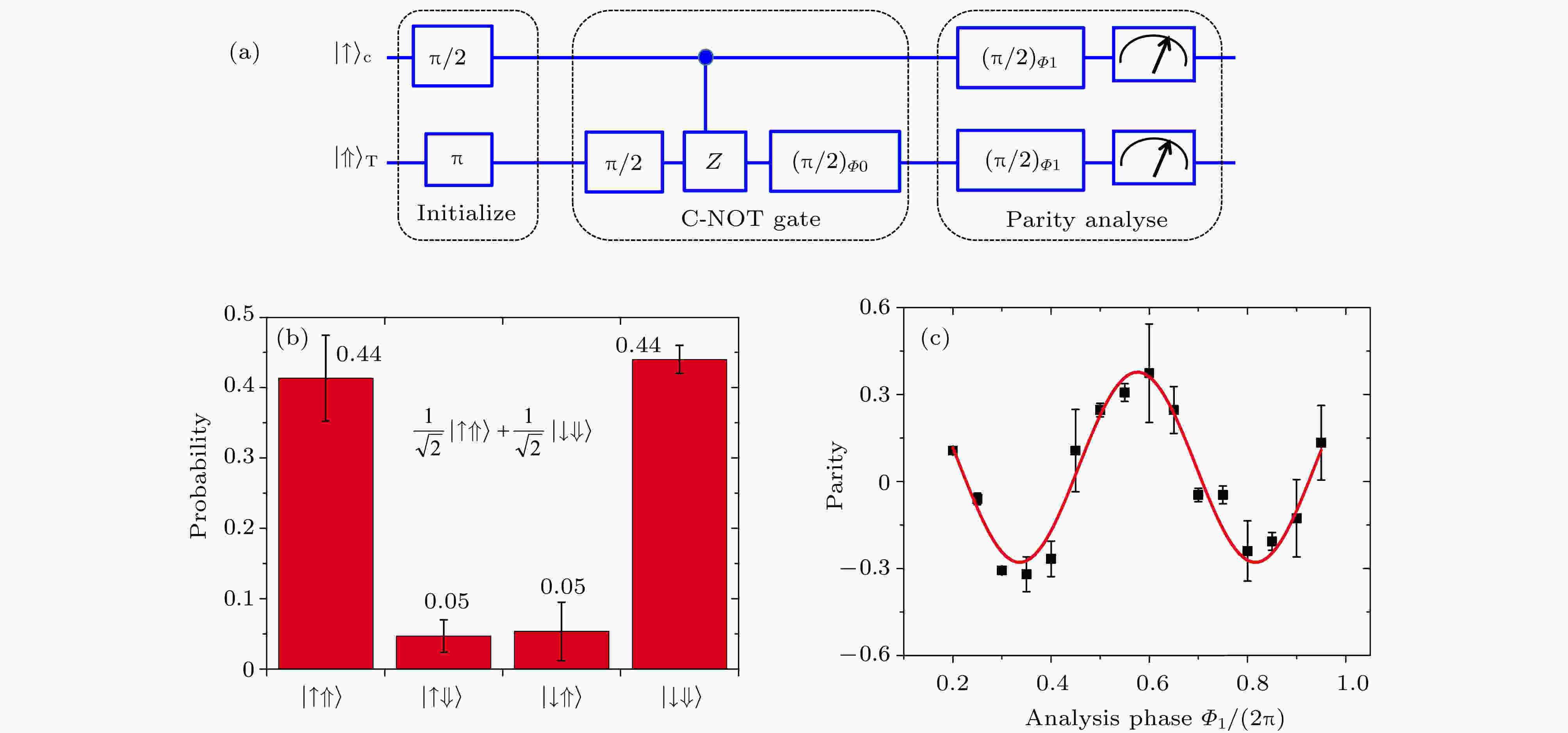 图 9 (a) 制备和测量异核两原子纠缠的时序; (b) 纠缠态的布居; (c) 宇称信号随测量脉冲相对相位的振荡, 拟合得到
图 9 (a) 制备和测量异核两原子纠缠的时序; (b) 纠缠态的布居; (c) 宇称信号随测量脉冲相对相位的振荡, 拟合得到














