摘要: 作为构成量子多体系统的基本单元, 一维少体系统的研究不仅可以在理论上为多体系统的量子关联及动力学等性质提供更为基本的理解, 也可以为实验上制备多体系统提供更加方便和功能更加全面的方法. 本文回顾了冷原子物理中一维少体系统最新的实验和理论进展. 首先介绍了少体实验中实现的谐振子势阱中确定原子数的精确制备, 亚稳态势阱和双阱系统中原子的隧穿, 以及强相互作用下等效自旋链的实验结果. 然后深度解析了理论研究方面, 特别是基于精确可解模型的一些重要结果, 包括亚稳态势阱中相互作用原子的隧穿概率, 以及相应实验上常见势阱的能谱分析、密度分布、隧穿动力学以及强相互作用极限下的有效自旋链模型等.
关键词: 冷原子物理 /
一维系统 /
少体问题 /
精确可解模型 English Abstract Review of one-dimensional few-body systems in ultracold atomic physics Liu Yan-Xia 1,2 ,Zhang Yun-Bo 1 1.Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11674201, 11474189).Received Date: 09 November 2018Accepted Date: 07 January 2019Available Online: 01 February 2019Published Online: 20 February 2019Abstract: We review some recent theoretical and experimental developments of one-dimensional few-body problems in ultracold atomic system. The experiments have so far realized the deterministic loading of few atoms in the ground state of a potential well, the observation of tunneling dynamics out of the metastable trap controlled by a magnetic gradient for a repulsively or attractively interacting system, the preparation of two fermionic atoms in an isolated double-well potential with a full control over the quantum state of the system, the formation of a Fermi sea by studying quasi-one-dimensional systems of ultracold atoms consisting of a single impurity interacting with an increasing number of identical fermions, and the deterministic preparation of antiferromagnetic Heisenberg spin chains consisting of up to four fermionic atoms in a one-dimensional trap. These achievements make the ultracold atoms an ideal platform to study many-body physics in a bottom-up approach, i.e., one starts from the fundamental building block of the system and observes the emergence of many-body effects by adding atoms one by one into the system. Corresponding theoretical models have been developed to explain the experimental data, to tackle the crossover boundary between few and many particles, and even explore the solvability and integrability of the models, especially the energy spectrum of interacting few atoms such as two atoms in a harmonic trap, two heteronuclear atoms of unequal mass in a ring trap, and two atoms in a $\delta$ -barrier split double well potential. After a brief review of Bethe-Ansatz method, a theory for the tunneling of one atom out of a trap containing two interacting cold atoms is developed based on the calculation of the quasiparticle wave function, and the tunneling dynamics of two atoms starting from the NOON state is explored from the exactly solved model of $\delta$ -barrier split double well based on a Bethe ansatz type hypothesis of the wave functions. It was shown that the spectroscopy and spin dynamics for strongly interacting few atoms of spin-1/2 and spin-1 can be described by effective spin chain Hamiltonians, which serves as a useful and efficient tool to study the quantum magnetism with clod atoms.Keywords: ultracold atom physics /one dimensioanl system /few-body problem /exactly solvable model 全文HTML --> --> --> 1.引 言 少体物理几乎在所有的物理分支中都起着重要作用, 比如天体力学中的三体开普勒问题以及量子力学中把氦原子中的核子看做是质点的三体问题, 一般情况下三体问题很难退化到一个有效的单体问题. 这里简单介绍一些囚禁在势阱中的玻色子或费米子的少体问题, 这些都是研究少体物理的理想模型. 这些系统中有很多是可以解析处理的, 尽管存在很强的相互作用和很多的自由度, 但是在某些情况下, 可以转换成单体问题来求解.$ r_0 $ 远小于德布罗意波长$ \lambda_{\rm {dB}} $ 时, 原子间的相互作用主要是以各向同性的s波碰撞为主. s波碰撞的效应可以通过s波散射长度$ a_{\rm s} $ 描述, 在很多情况下$ a_{\rm s} $ 成为用来描述系统的唯一微观参数[1 ,2 ] . 一个经典的例子就是平均场Gross-Pitaevskii 方程[3 -6 ] 只依赖于粒子数N 和s波散射长度$ a_{\rm s} $ . Gross-Pitaevskii方程将多体问题转换成一个有效的单体问题, 可以非常准确地描述弱相互作用稀薄玻色凝聚体的特性. 除了碱金属原子, 实验上也可以实现价电子结构更复杂的原子的凝聚, 如Ca, He, Cr, Yb, Sr. 例如两个Cr 原子间的碰撞是各向异性和长程的[7 ,8 ] . 这些特性会引起超出s波的物理, 两原子间的相互作用除了依赖s波散射长度外还依赖偶极相互作用的强度.[9 ] . 一系列的少体系统可以通过将多个原子囚禁在很深的光晶格中来实现, 其中不同格点间的隧穿被抑制, 近邻相互作用可以忽略[10 ,11 ] . 对于冷原子系统, 原子间的相互作用可以通过外磁场在Feshbach共振附近调节[12 ] . 超冷碱金属原子间的Feshbach共振现象可以用两通道模型解释. 两个原子最外面的两个电子的相互作用可以由一个比较浅的电子自旋三重态和一个比较深的单重态的Born-Oppenheimer 势能曲线来描述. 超精细相互作用将单态和三重态的势能耦合, 形成一个闭通道和一个开通道. 当闭通道的束缚能量和开通道入口处的能量相同时就发生Feshbach 共振, 散射长度趋于发散, 1998年首次在超冷原子气体中观察到Feshbach共振[13 -15 ] , 为理论和实验对比铺平了道路.[16 ,17 ] 就发现在无穷大s-波散射长度时, 自由空间的两体系统只存在一个零能束缚态, 没有其他弱的束缚态. 但是当加入第三个粒子以后, 就会出现令人惊讶的结果, 相应的三体系统会出现无穷多个弱的束缚三体态, 且束缚能有分立标度不变性[18 ,19 ] (这里假设只有两体相互作用). Efimov 效应激发了很多理论和实验的研究[20 ] , 直到现在仍然是少体物理中的重要研究课题. 在氦的三聚物、核物理、还有其他系统中都有三体Efimov 效应和关联的Efimov共振的研究. 然而, 它的第一个实验验证是2006年由Kraemer等[21 ] 在铯原子气体中完成的. 从更广的范围看, Efimov 态是Borromean 环的一种, 这一类物态的标志特征是只有三个粒子会形成束缚态环链, 而其中任意两个都不互相束缚. 这是一个纯粹由量子力学导致的效应, 有丰富而深刻的物理内涵. 自从Efimov 效应提出以后, 推广到大系统已经有很多进展, 但这仍然是一个开放问题. 在自由空间或者有外势的情况下N 体系统(N > 3)的能谱如何依赖于三体参数, 四体、五体和更多体系统的研究可能会给出答案.[22 ,23 ] . 海德堡Zürn等首先将两个费米子囚禁在光势阱中, 研究了强相互作用下费米子的费米化, 通过施加一个磁场梯度, 在排斥相互作用下研究了单粒子的隧穿[24 ] , 在吸引相互作用下研究了配对粒子的隧穿[25 ] . 然后通过精确地逐个增加原子个数, 测量单个杂质粒子与背景气体的相互作用可以用来研究从少体到多体的跨越, 观察到了费米海的形成[26 ] . 该实验组接着实现了两个原子在双势阱间的量子隧穿, 得到相互作用强度对双势阱的本征态以及占据概率的影响[27 ] , 在一维的谐振子势阱中准确制备由自旋1/2 费米子构成的反铁磁海森堡自旋链[28 ] . Kaufman等[29 ] 用光镊子将单个原子冷却到它的振动基态, 随后扩展实验技术将两个原子冷却到双阱的基态, 通过两个粒子的干涉观察粒子的统计效应[30 ] .2.一维冷原子少体实验 目前超冷气体的研究大部分关注的是多体系统的性质, 在热力学极限下粒子数的涨落和散粒噪声一样, 不会明显改变热力学量, 例如温度、压强等. 与此相反, 少体系统非常依赖于粒子的数目. 目前的实验技术已经可以很精确地控制少体系统中粒子的个数. 海德堡Jochim实验小组从2011年开始对一维冷原子物理中的少体问题做了一系列关键实验, 包括相互作用原子在亚稳态和双阱模型中的隧穿[24 -28 ] , 从少体到多体的转变, 以及一维自旋链的量子磁学. 他们用光偶极阱和磁场梯度将少数6 Li费米原子制备到基态, 精确度可以达到93 ± 2%. 粒子囚禁在纵横比为1:10的三维雪茄状的势阱中, 各方向可近似认为是谐振子势阱, 此系统可以作为一维系统来处理. 文献[31 ]中给出的解析解可以很好地描述这种势阱中两个相互作用原子的基态. 一维光势阱加上梯度磁场可以将势阱的一边打开而形成一个亚稳态势阱, 是研究隧穿动力学的重要模型之一. 原子间的相互作用可以通过Feshbach共振[12 ] 和束缚诱导共振[32 ] 来调节. 一维的耦合常数g 可以通过三维散射长度$ a_{3\rm D} $ 和横向谐振子势的特征长度$ a_\perp=\sqrt{\hbar/\mu \omega_\perp} $ 来确定, 这里$ \hbar $ 是普朗克常数, $ \mu=m/2 $ 是两个质量为m 的原子的约化质量. 耦合常数为$ C=\zeta(1/2)\simeq 1.46 $ , $ \zeta $ 是Riemann zeta函数. 当$ a_{3\rm D}=a_\perp/C $ 时发生所谓的束缚诱导共振, 一维耦合常数发散, 这样三维散射长度为有限值时就可以表现出共振散射的特点.2.1.原子的费米化及单粒子隧穿 2.1.原子的费米化及单粒子隧穿 当相互作用强度趋于无穷时, 两个可区分的粒子的能量和波函数的模平方与两个无相互作用的全同费米子相同, 这被称为原子的费米化. 实验上通过直接比较强相互作用极限的两种可区分费米子和相同势阱中的两个全同费米子来观察这种现象. 文献[24 ]将两个6 Li费米原子制备到最低的两个Zeeman子能级的超精细态$ \left\vert F=1/2,\right.$ $ \left. m_F=\pm 1/2\right\rangle $ , 分别标记为$ \left\vert \uparrow \right\rangle $ 和$ \left\vert \downarrow \right\rangle $ . 对于可区分粒子系统和全同系统分别用和$ \left\vert \uparrow \uparrow \right\rangle $ 和$ \left\vert \uparrow \downarrow \right\rangle $ 表示. 由于费米子的反对称性, 全同系统感受不到s波相互作用, 对于可区分粒子系统的相互作用则可以通过磁Feshbach共振来调节. 实验上可以测量其中一个原子隧穿出势阱的时间随相互作用强度g 的变化规律, 通过拟合留在阱中的平均粒子数可定义一个隧穿时间常数$ \tau $ . 实验发现随着磁场的增加,两个可区分原子的$ \tau $ 减少了两个数量级, 而全同费米子的$ \tau $ 保持为常数, 二者在CIR处相交. 对6 Li原子, 该CIR共振发生在磁场为(783.4 ± 0.4)G($ 1\rm G=10^{-4}\rm T $ )处. 也就是说在相互作用强度$ g\rightarrow \infty $ 时, $ \left\vert \uparrow \uparrow \right\rangle $ 态和$ \left\vert \downarrow \downarrow \right\rangle $ 态的能量, 波函数密度分布及隧穿时间常数$ \tau $ 都是相同的. 文献[33 ]通过WKB(Wenzel-Kramers-Brillouin)近似给出了隧穿的准粒子理论, 很好地解释了实验的数据点, 揭示了波函数在束缚诱导共振点处的费米化特点.2.2.原子的配对隧穿 -->2.2.原子的配对隧穿 原子费米化的研究是将两个可区分的原子制备到排斥相互作用区域, 该区域系统中的粒子只会出现单粒子隧穿. 当原子处在吸引相互作用区域时, 会发生两个原子同时隧穿的现象[25 ] . 测量过程如下: 首先将两个原子制备到基态, 一个原子处在$ \left\vert \uparrow \right\rangle $ 态, 另一个处在$ \left\vert \downarrow \right\rangle $ 态, 然后突然加上磁场梯度, 使势阱的一边倾斜形成势垒, 这时粒子会跑出去, 在某个固定的时间迅速去掉磁场梯度, 将势阱恢复, 然后测量势阱里面的原子个数, 重复多次, 计算某一时刻的势阱出现两个原子、单个原子、以及零个原子的概率$ P_2(t), P_1(t), P_0(t) $ . 通过这些概率可以得到平均粒子数$ \bar N(t)=2P_2(t)+P_1(t) $ 随时间的演化.图1 所示. 对于两个原子的隧穿有两个过程: 一个过程是配对隧穿, 即两个原子同时离开势阱, 发生这个过程的速率记为$ \gamma_{\rm p} $ . 另一个过程是原子按次序离开势阱, 第一个粒子先离开势阱, 第二个粒子处在势阱的非微扰基态, 这个过程第一个粒子隧穿的速率记成$ \gamma_{\rm s} $ . 这个速率主要由隧穿势垒的高度决定, 同时依赖于两个原子的相互作用能. 对于第二个原子, 没有相互作用的影响, 因此离开势阱的速率是无相互作用系统的$ \gamma_{s_0} $ . 考虑实验上有限的准备精确度以及通过改变磁场调节相互作用强度会影响原子自旋的取向, 隧穿速率可以修正成为一个依赖于自旋的结果. 实验结果表明在相互作用强度g > –0.59时是没有配对隧穿的. 在强吸引相互作用区域g < –0.64, 粒子配对隧穿占主导地位, 单粒子的隧穿速率很小, 可以认为两个粒子绑在一起形成了束缚态, 相互作用可看做是其内部的自由度. 文献[33 ,34 ]通过WKB近似理论计算给出了隧穿率和其随相互作用强度的变化.图 1 双原子的两种隧穿过程: 单原子次序隧穿及两原子配对隧穿. 本图摘自参考文献[25 ]Figure1. The loss processes include two tunneling processes of two atoms out of a metastable potential: subsequent single-particle tunneling and direct pair tunneling (Reproduced with permission from Ref. [25 ]).2.3.双阱中的两个费米子 -->2.3.双阱中的两个费米子 实验上双阱可以由两束激光通过高分辨率的物镜聚焦产生, 通过声光偏转器独立地控制两束激光的强度和位置, 可以调节双阱的隧穿耦合系数J 和两阱之间的偏差$ \varDelta $ . 双阱是构成光晶格的基本单元, 文献[27 ]介绍了半满填充时Fermi-Hubbard模型的基本构建块的实现, 即在双阱中$ \left\vert \uparrow \right\rangle $ 态和$ \left\vert \downarrow \right\rangle $ 态原子形成的自旋单态. 在Hubbard模型体系, 两个粒子的空间波函数可以由基矢$ \left\vert LL \right\rangle, \left\vert LR \right\rangle,$ $ \left\vert RL \right\rangle, \left\vert RR \right\rangle $ 展开, 其中$ \left\vert L \right\rangle $ 和$ \left\vert R \right\rangle $ 分别表示单粒子在左阱和右阱的基态. 通过对角化对称双阱在双模近似下的哈密顿量, 可以得到四个本征态$ a, b, c, d $ , 其本征能量分别是$ 2 A_- J, U, 2A_+ J, 0 $ , 这里$A_\pm = $ $ \dfrac 14 \left( U/J \pm \sqrt {16 + (U/J)^2}\right) $ . 基态a 和第二激发态c 是依赖隧穿能J 和相互作用强度U 的, 并且这两个态都是满足交换对称的. 文献[27 ]给出了实验结果: 基态a 的双占据概率随着排斥相互作用的增加而增加, 第二激发态c 则相反, 双占据几率随着相互作用的增加而减小. b 和d 这两个态的占据概率则不依赖于相互作用强度. d 是交换反对称的态, 其占据概率不随相互作用强度改变. 但是b 是交换对称的态, 实验中并没有给出这个态的占据概率随相互作用强度的改变. 另一方面, 从这几个态的宇称对称性来看, a 和c 是偶宇称态, b 和d 是奇宇称态. 双模近似下b 是一个两粒子的NOON态, 是量子力学两体的最大纠缠态.$ \left\vert LL \right\rangle $ 态, 然后迅速将势垒降低到可以使原子在双阱中来回隧穿. 为了观察动力学的结果, 在演化的不同时刻, 迅速增加势垒的高度使原子在双阱中的空间分布锁定, 然后通过荧光谱测量每个阱中原子的个数, 重复测量多次得到每一时刻的占据概率. 实验可以给出不同参数下占据概率随时间的振荡图像, 也可以将原子制备到系统的本征态, 如基态、激发态, 探测两个粒子在不同阱的概率和两个粒子在同一个阱的概率, 得到相互作用强度对双势阱的本征态以及占据概率的影响.2.4.少体到多体: 观察费米海的形成 -->2.4.少体到多体: 观察费米海的形成 知道一个物理体系什么时候可以具有宏观特性并且可以用多体理论很好地描述是非常困难的. 一维冷原子的少体实验[26 ] 通过精确控制单杂质系统中全同费米子的数目来研究从少体到多体的跨越. 首先制备一个N + 1个粒子的系统, 其中1个杂质粒子和N 个囚禁在细长光偶极阱基态的全同粒子之间存在排斥相互作用. 实验上将超冷费米子原子制备到两个精细态来实现这样的系统, 这里杂质粒子处在$ \left\vert \downarrow \right\rangle $ 态, 全同粒子都处在$ \left\vert \uparrow \right\rangle $ 态. 为了探测这个系统, 实验上主要测量杂质和全同粒子间的相互作用能$ \Delta E=E(N, N_\downarrow =1)-E(N, N_\downarrow =0) $ 随多数粒子数的变化. 相互作用能的测量可以通过RF(radio frequency)脉冲改变杂质粒子的内态来实现. 如果没有全同粒子的存在, 转变发生在频率$ \nu_0 $ , 对应杂质粒子初末态超精细能级差. 对于有N 个全同粒子存在的情况, 杂质粒子和全同粒子之间的相互作用引起一个$ \Delta \nu (N) $ 的频率移动. 对于给定的相互作用强度, 相互作用能为$ E=\hbar \Delta \nu (N) $ .$ \Delta E \propto \sqrt{N} $ . 当$ N \rightarrow \infty $ 时, $ \Delta E $ 是发散的. 因此, 通过自然能量标度重新定义相互作用能, 无量纲的相互作用能为$ E=\Delta E/E_{\rm F} $ , 这里$ E_{\rm F} $ 是全同原子的费米能. 由于只考虑相互作用能, 因此忽略零点动能, 这意味着对于谐振子的情况$ E_{\rm F}=N\hbar \omega $ . 为了补偿由于增加粒子引起的密度改变, 引入无量纲的排斥相互作用参数$ \gamma $ > 0. 为了判断系统是否达到多体极限, 实验的数据要和两种极限情况比较, 一种是N = 1的情况, 另一种是$ N \rightarrow \infty $ 的情况. 前一种情况的相互作用能可以通过两相互作用原子的精确解得到, 后一种情况是多粒子极限, 即单个杂质粒子浸入到无穷多个粒子形成的费米海中. 对于$ \gamma $ = 0, 相互作用能为0. 对于$ \gamma \rightarrow \infty $ , 系统达到费米化极限, 杂质粒子和N 个全同费米子相互作用的能量与N + 1个没有相互作用的全同粒子的能量相同, 因此这种情况的相互作用能与费米能量$ E_{\rm F} $ 是相同的. N = 1和$ N \rightarrow \infty $ 两种极限情况在$ \gamma \rightarrow \infty $ 时结果是一致的. 比较理论和实验的结果, 可以发现$ N \geqslant 4 $ 时的相互作用能和无穷多个粒子情况符合很好, 也就是说, $ N \geqslant 4 $ 就已经体现了多体的特性.2.5.一维势阱中的反铁磁Heisenberg自旋链 -->2.5.一维势阱中的反铁磁Heisenberg自旋链 实验[28 ] 报导了$ N_\uparrow $ 个自旋向上的粒子和$ N_\downarrow $ 个自旋向下的粒子在一维势阱中如何实现Heisenberg自旋链. 实验中研究的系统有$(N_\uparrow, N_\downarrow)= $ $ (2, 1), (3, 1), (2, 2) $ . 这些体系的基态在强相互作用区域都表现出反铁磁态的特征. 实验上通过两个独立的测量来判断系统是否处于反铁磁态: 利用隧穿技术探测自旋链最外边粒子自旋的方向, 以及利用波函数在单粒子能级的投影探测自旋向下粒子在体系中的空间波函数.$ \left \vert {\rm {AFM}}_3\right\rangle \propto \left( \left\vert \uparrow \uparrow \downarrow \right\rangle-2 \left\vert \uparrow \downarrow \uparrow \right\rangle + \left\vert \downarrow \uparrow \uparrow \right\rangle \right) $ , 自旋向下粒子隧穿出去的概率为$ P_\downarrow = \left \vert \left \langle \uparrow \uparrow \downarrow \right \vert {\rm {AFM}}_3\rangle \right \vert ^2 $ . 在实验中由于要加磁场梯度, 因此实验结果要考虑外加磁场梯度使外势不对称引起的变化. 通过以上的测量计算就可以判断是否处在反铁磁态. 对于强相互作用系统, 相对坐标在杂质处会产生一个尖峰, 这个尖峰会导致更高能量的能级占据. 一个态空间波函数越对称, 尖峰就会越多. 因此单粒子能级占据数的分布直接反应了系统自旋的结构. 不引入外势的情况下, 两分量间的强相互作用就可以使自旋链达到稳定, 这使得在非格点模型中制备自旋链成为可能, 也为磁学性质的研究提供了一个新的平台.3.一维冷原子少体可解模型 量子力学中只有屈指可数的几个问题是可以严格求解的, 其中应用最广的例子之一是谐振子势阱中的单个粒子. 考虑相互作用的两体问题可精确求解的则更少, 特别地, 氢原子中由于库仑相互作用只和相对坐标有关, 引入相对坐标和质心坐标可将动能部分分离变量, 描述质心运动的方程是一个自由粒子的能量本征方程, 而描述相对运动部分的方程形式上与单体波动方程完全一样, 两体问题于是简化为单体问题. 实验上使用激光冷却和蒸发冷却技术实现的简并原子气体需要将原子囚禁于外势场中, 这些囚禁系统中的相互作用所起的作用与自由空间中的超冷碰撞不同. 在自由空间中, 通过微分散射截面和碰撞相移因子来探测两原子间的相互作用, 而在存在囚禁势的情况下这些物理量都没有了意义, 因为囚禁系统中无法构造入射态和出射态的渐进行为. 相反, 在囚禁势中相互有作用的多原子系统的特征在于其离散能谱以及能级间的跃迁矩阵元. 下面简单介绍几种一维囚禁势阱中严格可解的相互作用少原子体系的离散能谱及相关的动力学结果, 该体系的哈密顿量为$ x_i $ 为原子的坐标, $ m_i $ 为原子的质量, N 为粒子数, $ V(x_i) $ 为囚禁势阱, 原子间为接触相互作用, 相互作用强度g 可以通过Feshbach共振从弱相互作用到强相互作用很大范围内进行调节.3.1.Bethe Ansatz方法简介 3.1.Bethe Ansatz方法简介 对于相互作用的多体均匀系统, 哈密顿量(2 )式中$ V(x_i)=0 $ , Bethe ansatz (BA)[35 ] 提供了一种行之有效的方法, 在特定的边界条件下可以给出某些一维系统的精确结果. 该方法最早由Bethe[35 ] 在1931年提出并成功求解了一维各向同性的铁磁Heisenberg自旋链. 1963年, Lieb和Liniger[36 ] 将这个方法应用到一维排斥性相互作用无自旋的均匀玻色子系统中. 随后, McGuire[37 ] , Gaudin[38 ] , Yang等[39 ] 和Baxter[40 ] 将该方法推广到了多分量费米子、玻色子以及玻色费米混合系统中. Lieb和Wu[41 ] 将该方法应用到Hubbard模型, 得到了基态能量、波函数以及化学势. BA方法在凝聚态物理、强关联体系、以及数学领域中都有很广泛的应用[42 -46 ] . 近年来, 冷原子实验技术的精确可控性促进了理论上进一步更细致准确地研究基础模型的原理和性质, 其中一个方面就是可积模型的研究, 包括各种可积模型BA方程的数值求解其基态[47 -53 ] , 一维可积模型的热力学及临界现象[54 -63 ] 等. 例如, 在2004年和2009年实验上分别实现了Tonk-Girardeau(TG)气体[64 ,65 ] 和超TG(sTG)气体[66 ,67 ] , 很快就有理论小组通过BA严格解给出了关于TG气体和超TG(sTG)气体的联系, 同时也解释了sTG气体实现的物理机理[68 -71 ] . 近期有实验利用光晶格实现Lieb-Liniger模型, 并通过测量得到的高精度密度分布来提取热力学量, 验证了量子临界现象和Tomonaga-Lutinger Liquid理论等[72 ,73 ] . 下面主要介绍BA方法的基本思路.$\psi(\cdots, x_j= $ $0, \cdots)= \psi(\cdots, x_j=L, \cdots) $ , 系统的波函数可以假设成平面波叠加的形式$ Q=(Q_1, Q_2, \cdots, Q_N) $ 和$ P=(P_1, P_2, \cdots, P_N) $ 是$ (1, 2, \cdots, N) $ 的两个排序, $ k_i $ 是准动量, $ \theta $ 是阶梯函数, 当$ x_{Q_1} < \cdots < x_{Q_N} $ 时等于1, 否则为0, A 是系数. 根据波函数在$ x_i-x_j=0 $ 的连续性和其一阶导数的不连续性可以得到散射矩阵S S c 数, 再结合周期性边界条件就可以得到BA方程, 形如${\rm e}^{{\rm i}k_jL}= $ $ \prod_{l\neq j}^N S_{lj} (k_j-k_l) $ . 在描述单分量玻色子的Lieb-Liniger模型中$S_{lj} (k_j-k_l)=(k_j-k_l+{\rm i}c)/(k_j- $ $k_l- {\rm i}c) $ , c 为粒子间的相互作用强度.S [39 ] 和Baxter[40 ] 在研究一维$ \delta $ 势相互作用费米气体模型和二维格子统计模型时分别提出的. 其含义是系统从初态$ (a, b, c) $ 到末态$ (c, b, a) $ 有两种途径, 这两种散射过程是等价的. (4 )式是周期性边界条件系统可积的条件. 根据Yang-Baxter方程, 得到转移矩阵$\rm t(u)= {\rm {tr}}L_{1}(u)L_{2}(u)$ $ \cdots L_{N}(u) $ , 这里Lax算符形式与散射矩阵相同:$ u_j\!=\!k_j/c $ , $ b(x)\!=\!-x/(-x\!+\!{\rm i}) $ , $ c(x)\!=\!i/(-x\!+\!{\rm i}) $ , $ P_{\sigma_j \tau} $ 是自旋交换算符, $ \tau $ 代表辅助空间的自旋. 系统的哈密顿量与转移矩阵$ t(u) $ 是对易的, 通过转移矩阵的本征值和本征态, 就可以得到相应的哈密顿量的本征值和本征态. 将转移矩阵作用到本征态上结合周期性边界条件就可以得到$ t(u_j) \left\vert \psi \right\rangle= $ $ {\rm e}^{{\rm i}k_jL} \left\vert \psi \right\rangle $ , 其中$ \psi $ 是转移矩阵的本征态. 这个方程可通过代数BA方法计算, 从而得到BA方程. 对于两分量费米子的Gaudin-Yang模型, BA方程为$ j=1, \cdots, N, \alpha =1, \cdots, M $ , $ \varLambda $ 是自旋快度, M 是数量较少分量的粒子数目. 这就是BA方法的基本思路.3.2.谐振子势阱中的两粒子问题 -->3.2.谐振子势阱中的两粒子问题 1998年Busch等[31 ] 给出了两个冷原子在谐振子势中的精确波函数和解析解. 为了避免处理真实原子间相互作用的困难, 在稀薄原子气体中通常采用零程的点状势将原子间相互作用近似为接触相互作用, 一维系统中只含有简单的$ \delta(x) $ 项. 质量为m 的两个原子在频率为$ \omega $ 的一维谐振子势中的运动由(2 )式中描述的哈密顿量, 其中$ \hat H \psi(x_1, x_2)=E \psi(x_1, x_2) $ , 这里$ \psi(x_1, x_2) $ 为两粒子波函数, E 为本征能量. 由于动能项和势能项都是二次函数的形式, 引入质心坐标$ X=(x_1+x_2)/2 $ 和相对坐标$ x=x_1-x_2 $ , 可将本征函数分离变量$ \psi(x_1, x_2)=\varPsi_{\rm {CM}}(X) \varphi(x) $ , 哈密顿量(8 )式可以分解为质心部分和相对运动部分, $ \hat H =\hat H_{\rm {CM}}+\hat H_{\rm {rel}} $ , 可以看出质心运动的本征函数就是质量为$ M=2m $ 的单粒子谐振子态$\varPsi_{\rm {CM}, n}(X)\propto $ $ {\rm e}^{- a^2X^2}H_n\left(\sqrt{2}a X\right) $ , 其中$ a=\sqrt{m\omega/\hbar} $ , $ H_n(x) $ 为$ n $ 阶厄米多项式, 其本征能量为$ {\cal{E}}_n=(n+1/2)\hbar \omega $ , 这里$ n=0, 1, 2, \cdots $ . 而相对运动部分的薛定谔方程可以看作质量为$ \mu=m/2 $ 的粒子在谐振子势阱加一个$ \delta $ 势阱中的运动.31 ]给出了该哈密顿量的精确解, 其波函数分为奇宇称和偶宇称两部分: 1)奇宇称的波函数(即满足粒子交换反对称)为$\varphi_j(x)\propto $ $ {\rm e}^{-a^2x^2/4}H_j\left(\sqrt{2}a x/2\right) $ , 本征能量不依赖于相互作用强度$ \varepsilon_j=(j+1/2)\hbar \omega $ , 这里$ j=1, 3, 5, \cdots $ ; 2)偶宇称波函数满足粒子交换对称, 依赖相互作用强度, 其形式为[31 ,74 ] $\varphi_j(x)\propto {\rm e}^{- a^2x^2/4} \varGamma(-v_j)U$ $ \left(-v_j, \dfrac 12, \dfrac 12 a^2x^2\right) $ , 相应的本征能量为$ \varepsilon_j=(2v_j+$ . $ 1/2)\hbar \omega $ , 其中$ \varGamma $ 为伽马函数, $ U $ 是合流超几何函数, $ v_j $ 是主量子数的非整数类似量. 具体来说, 将相对运动部分的波函数$ \varphi_j(x) $ 按照谐振子波函数$ \phi_n(x) $ 展开, 根据正交归一性可得到展开系数$A_n= $ $ C\dfrac{\phi_n^*(0)}{n-2v_j} $ , 这里$ C=-g \varphi_j(0)/\hbar \omega $ . 通过波函数的积分表示可以确认$ \varphi_j(x) $ 具有合流超几何函数的形式, 而其在零点的取值$ \varphi_j(0) $ 则是贝特函数, 后者可以用伽马函数表示. 由此可以得到$ v_j $ 满足下面的关系式:g 是以$ \sqrt{\hbar^3\omega/\mu} $ 为单位的重新标度过的相互作用强度, $ j=0, 2, 4, \cdots $ . 给定一个相互作用强度g 的值, $ v_j $ 有无数多个解. 以上可以看出相互作用只对交换对称的偶宇称波函数有影响, 而奇宇称的波函数因其在x = 0处取值为零是感受不到相互作用势的. 系统的总能量为$ E_{n, j}={\cal{E}}_n+\varepsilon_j $ , 总的波函数为$ \psi_{n, j}(x_1, x_2)\propto \varPsi_{\rm {CM}, n}(X) \varphi_j(x) $ , 图2(a) 展示了n = 0情况下总能量E 随相互作用变化的趋势.图 2 三种相互作用的两原子系统的能量E 与相互作用强度g 的关系: (a)谐振子势阱中的两原子, 黑实线和红虚线分别表示相对运动奇宇称和偶宇称波函数所对应的能量; (b)周期边界条件下两异核原子, 黑实线和红虚线分别表示质量相等两原子和质量比为2.175情况下对应的能量; (c)双势阱中相互作用两原子的奇宇称态, 一维无限深方势阱中心为一个强度为d = 0.5的$ \delta $ 势垒劈开, 黑实线和红虚线分别表示准动量为实数的原子本征态和准动量为复数的分子态对应的能量. 这里能量的单位分别是$ \hbar \omega, 8\hbar^2 /m_1 L^2, 2\hbar^2 /m L^2 $ , 相互作用强度g 的单位分别是$ \sqrt{\hbar^3\omega/\mu}, 8\hbar^2 /m_1 L, 2\hbar^2 /m L $ Figure2. Energy spectrum of three types of interacting two-atom system: (a)Two atoms in a harmonic oscillator potential. Black solid lines and red dashed lines are odd parity and even parity energy level respectively; (b)two heteronuclear atoms in a ring trap. Black solid lines and red dashed lines are energy levels for equal mass and mass ratio $\alpha $ = 2.175 respectively; (c) two atoms in a $\delta $ -split hard-wall double well. Five lowest odd parity levels for barrier height d = 0.5. Black solid lines and red dashed lines are the bound states for atoms with real-valued quasimomentum and the molecule states with complex-valued quasimomentum respectively.[75 ] 用变分法对一维谐振子势阱中两相互作用费米子的基态波函数进行了研究, 但其试探波函数存在缺陷, 即在边界处一阶导数不连续, Liu等[76 ] 改进了该变分法方案得到了关于动量的一个限制条件, 该条件类似于Bethe ansatz方程, 但是与边界条件无关, 结合变分法和波函数及其一阶导数的连续性条件得到的基态能量和精确结果符合, 给出了更为合理的基态波函数, 可以作为两原子亚稳态隧穿的初始波函数.3.3.周期边界条件下两异核原子的解析解 -->3.3.周期边界条件下两异核原子的解析解 冷原子混合物体系是不同质量原子的混合, 实验上已经成功制备了40 K-6 Li, 40 K-87 Rb, 6 Li-23 Na等异核系统[77 -79 ] . 异核费米子的超流性质、配对机制以及异核分子的形成等新现象得到广泛研究[80 -82 ] . 在异核系统中, 一个新的自由度——质量比表征了原子混合物体系的特性, 诱导了异核模型中新的物理效应. 这里介绍一种精确求解周期边界条件下两体相互作用异核系统的精确求解方法[83 ] , 其关键在于较为普适的波函数假设.2 )式中取$\psi(x_1+L, x_2)= $ $ \psi(x_1, x_2+L)=\psi(x_1, x_2) $ , 其中L 是一维系统的长度或环状势的周长. 异核系统质心坐标应当定义为$ X=\left( m_1 x_1 +m_2 x_2 \right)/\left( m_1+m_2\right) $ , 约化质量则为$ \mu=m_1m_2/(m_1+m_2) $ . 形式上质心和相对部分的运动仍然可以分离变量, 波函数可写为$ \psi(x_1, x_2)= $ ${\rm e}^{{\rm i}KX}\varphi(x) $ , 这里$ {\rm e}^{{\rm i}KX} $ 是质心运动为自由粒子情况下的平面波解, $ K=k_1+k_2 $ 为总动量, 而相对运动部分的波函数有如下形式$ A_{\pm} $ 和$ B_{\pm} $ 为待定系数, $ \theta(x) $ 为阶跃函数. 然而相对部分的动量$ k=(m_2k_1-m_1k_2)/(m_1+m_2) $ 并不是独立的, 事实上由于周期边界条件的影响它总是与质心部分的总动量$ K $ 耦合在一起. 将波函数(11 )式写回到$ x_1 $ 和$ x_2 $ 坐标空间, 利用周期边界条件可以得到$ {\rm e}^{{\rm i}KL}=1 $ , 这意味着$ KL=2\text{π} n $ , n 为整数. 相对动量满足$ c=gm_1/\hbar^2, \alpha=m_2/m_1 $ 为质量比, 显然k 与K 是耦合在一起的. 令$ \hbar^{2}/2m_{1}=1 $ , 异核系统的能量表示为$ E=\dfrac{1}{1+\alpha}K^{2}+\left(1+\dfrac{1}{\alpha}\right)k^{2} $ . 由于系统总动量守恒, 可以用K 来标记能谱. K = 0对应系统的基态, $ K=\pm 2\text{π}/L $ 则对应两个简并的激发态. 数值求解上述方程得到异核系统的本征能谱和本征波函数, 可以研究系统的密度分布和动量分布等. 在实际的异核系统40 K-87 Rb中质量比为$ \alpha= $ 2.175, 图2(b) 对比了异核两原子和两玻色原子的无量纲能谱. 结果表明不等质量情况下的能谱总是低于等质量情况. 在吸引相互作用c < 0时, 发现仅当吸引相互作用足够强, 超过一定阈值$ c_{\rm t} $ 时才能够形成束缚态, 阈值$ c=c_{\rm t} $ 表示为$c_{\rm t}=\left(1+\alpha\right)\times $ $ \left[\cos\left(KL/(1+\alpha\right)-1\right]/\alpha L $ . 对于总动量$ K=0 $ 的情况, 阈值$ c_{\rm t}=0 $ , 束缚态可以在任意小的相互作用下形成. 当总动量$ K\neq 0 $ , 则有$ c_{\rm t} $ < 0, 仅当吸引作用足够大$ |c|>|c_{\rm t}| $ 时, 两体异核系统才能形成束缚态.$ \alpha=2.175 $ 时的动量分布表明[83 ] , 对于全同粒子系统, 每个粒子的动量分布相同, 动量位于$ \pm2\text{π}/L $ 或者0的概率相同; 对于异核系统, 质量大的粒子以$ \pm2\text{π}/L $ 为中心, 质量小的粒子则集中在0处, 从而保证总体能量更低.3.4.双原子在亚稳态势阱的隧穿 -->3.4.双原子在亚稳态势阱的隧穿 冷原子少体实验的准确制备使得在少体系统中研究隧穿问题成为可能. 隧穿理论的两个主要模型包括亚稳态势阱和双势阱. 在这两种势阱中研究隧穿已有很长的历史, 最新进展包括隧穿的干涉效应以及共振隧穿等[24 ,25 ,84 ] . 亚稳态势阱的量子隧穿衰变是早已熟知的量子现象, 如核衰变、量子成核等, 这些模型都是在单粒子图像上建立的. 这里主要介绍相互作用的双原子体系在亚稳态势阱的隧穿问题, 哈密顿量中的外势场如下$ V_0 $ 是光势阱的初始深度, $ p $ 是以初始光阱深度为单位的光阱深度, $ x_{r} $ 是光势阱光波的Rayleigh长度, $ \mu_{\rm m} $ 是原子磁矩, $ B' $ 是磁场梯度的强度. 不考虑两个原子在势阱外的相互作用, 文献[33 ]建立了一个原子从含有两个相互作用的冷原子的阱中隧穿的理论, 通过与势阱中的伴随原子相互作用而缀饰的准粒子波函数取代了隧穿矩阵元中的无相互作用的轨道. 计算出的两个6 Li原子的衰减时间与最近的实验结果一致. 双原子在这样一个外势中的运动可分为三个区域: 势阱I, 势垒II和真空III. 边界是依赖于能量的经典折返点$ x_a $ 和$ x_b $ , 因此区域II的范围是$ x_a < x < x_b $ . 这里有两种单粒子态: (i)真空区域的波函数可以看作在势垒的地方反射, 能量为$ \varepsilon $ 的平面波$ \chi_\varepsilon(x) $ 在势垒区域以指数衰减; (ii)势阱区域在低能时可以看作是谐振子波函数$ \phi_n(x) $ , 并且在势垒有一个尾巴, 在真空区域光滑地消失. 这两种态都不能很好地描述整个区域, 但是这两个态可以近似认为是正交的.$ \varPsi_0(x_1, x_2) $ 是2.1节介绍过的能量为$ W_0 $ 的两个相互作用原子在谐振子势阱中的波函数, $ \varPsi_{m, \varepsilon}(x_1, x_2) $ 是一个原子留在势阱的轨道$ \phi_m(x) $ , 另一个原子隧穿出去处在真空态$ \chi_\varepsilon(x) $ , 且与原子无相互作用, 能量为$ W_{m, \varepsilon} $ 的波函数. 根据隧穿理论, 量子隧穿过程可以看做是从$ \Psi_0(x_1, x_2) $ 到末态$ \Psi_{m, \varepsilon}(x_1, x_2) $ 的跃迁过程, 其跃迁矩阵元为$ M_{m, \varepsilon} $ , 当能量守恒时$ W_0 \simeq W_{m, \varepsilon} $ , Bardeen[85 ] 证明$ M_{m, \varepsilon}=$ $ -\hbar^2 J_{m, \varepsilon}/2m $ , 这里$ J_{m, \varepsilon} $ 正比于几率流密度算符的矩阵元. 衰变率可以通过量子跃迁的费米黄金规则估算, $ 1/\tau =\dfrac{2\text{π}}{\hbar} \displaystyle\sum_{m, \varepsilon} \left\vert M_{m, \varepsilon} \right\vert^2 \delta(W_0- W_{m, \varepsilon}) $ .$ \left\vert \uparrow \uparrow\right\rangle $ 的情况是很容易计算的. 势阱的初态就是n = 0和n = 1的史莱特行列式, 所有可能的末态中, 概率最大的一种是n = 0, $ \varepsilon=3\hbar \omega/2 $ 的组合. 对于两个可区分费米子的情况, $ \left\vert \uparrow \downarrow\right\rangle $ 不再平庸. 初态不能写成简单的史莱特行列式的形式, 事实上在3.1节, 已经给出了质心坐标波函数$ \varPsi_{\rm {CM}}(X) $ 和相对运动波函数$ \varphi(x) $ 的具体形式, 这里可以简单记为$ \psi_{\uparrow \downarrow} $ . 末态仍然是一个自旋单态, 一个原子在势阱最低的能态, 另一个在真空态$ \chi_\varepsilon $ , 这里的共振能量$ \varepsilon $ 由能量守恒来确定, 与相互作用强度g 有关. 经过计算得到以下关于跃迁矩阵元的重要结果$ x_{{\rm {bar}}} $ 是势垒区域II的任意一点, $ \varphi^*_{ {QP}} $ 是准粒子的波函数, 其定义为$ 1/\tau \simeq A_{ {QP}}/\tau_0 $ , 其中$ A_{ {QP}}=\int {\rm d}x \left\vert \varphi_{ {QP}}(x)\right\vert^2 $ . 图3 给出了单粒子的衰减时间$ \tau $ 随磁场的变化. 如黑色实线所示, 加上修正以后明显与实验结果符合得更好. 由于势阱部分并不是一个好的谐振子势阱, 在求解势阱部分的波函数时可以把非谐部分看作微扰, 来计算其波函数和能量, 得到一个更准确的准粒子波函数, 进而给$ A_{ {QP}} $ 一个修正, 使隧穿率的计算结果更准确, 隧穿的时间依赖于相互作用强度, 如图3 中绿线所示. 隧穿的准粒子理论为少体冷原子的亚稳态隧穿实验给出一个很好的解释.图 3 (a)衰减时间随磁场的变化. 黑色虚线和实线分别是WKB和考虑准粒子波动方程的修正的结果. 绿色线表示通过微扰论考虑非谐项贡献的结果; (b)相互作用强度和隧穿能量随磁场的变化.本图摘自参考文献[33 ]Figure3. (a) Decay time $ \tau $ vs magnetic field B . The points with error bars are the experimental data[24 ] , the dashed and solid lines are, respectively, the WKB $ (\tau_0) $ and QPWF predictions. The green light gray lines include the perturbation theory correction to the tunneling energy $ \varepsilon $ ; (b) interaction strength (red gray curve) and tunneling energy (black and green light gray curve) vs B (Reproduced with permission from Ref. [33 ]).3.5.双阱中少体玻色系统的基态性质及隧穿动力学 -->3.5.双阱中少体玻色系统的基态性质及隧穿动力学 双阱是研究超导比特Josephson振荡[86 ] 和玻色爱因斯坦凝聚中自囚禁现象[87 -89 ] 的典型模型. 受实验启发, 对于双阱的研究, 目前大部分的工作都是基于双模近似[90 ,91 ] , 或者是数值求解[92 ,93 ,94 ] , 没有严格解的结果. Murphy等[95 ] 研究中间带有$ \delta $ 势垒的一维简谐势阱中一对超冷玻色原子的基态和低能激发态性质. 通过计算约化单粒子密度矩阵、动量分布和双粒子纠缠来完整表征基态性质, 得到了无限排斥相互作用Tonks-Girardeau极限的几个解析表达式, 并通过数值解处理了有限粒子间的相互作用, 这里空间坐标的离散化是通过分立变量表象(DVR)做到的. 双阱中的对相互作用形成了周期势中多体系统的基本构件, 势垒的添加使得系统变得不平庸, 由于中间势垒的存在, 势垒两边的粒子可以发生隧穿, 人们在双阱中发现了约瑟夫森振荡和自束缚现象等. 文献[96 ]研究了束缚在中间带有势垒的无限深方势阱中的少体玻色气体的基态性质. 利用玻色子与费米子的对应关系构建了Tonks-Girardeau气体的基态波函数, 研究了势垒两边的关联特性以及这种特性和粒子数目宇称的关系, 并且运用精确对角化方法计算了在任意势垒高度和原子间相互作用强度下系统基态的密度分布、占据数分布、动量分布等. 计算表明动量次峰峰值随着势垒的升高而增大, 随着原子间相互作用强度的增大而减小. 该模型甚至可以被推广到玻色费米混合物系统[97 ] , 在动量分布中次峰的出现显示了势垒两边有着显著的关联.[98 ] 给出了双阱中的BA严格解, 在严格解的基础上研究了其隧穿动力学问题. 考虑N 个质量为m 的玻色子在中间加$ \delta $ 势垒的一维无限深方势阱中运动, (2 )式的系统哈密顿量中d > 0是势垒的强度, $ V_{\rm S} $ 为宽度为L 的无限深方势阱, 可以等价为开边界条件$\psi(x_i= $ $ \pm L/2)=0 $ . 由于系统是反射对称的, 可以定义宇称算符$ P\psi(x_1, x_2, \cdots)=\psi(-x_1, -x_2, \cdots) $ , 将本征态分成偶宇称和奇宇称两部分. 文献[98 ]只得到了奇宇称部分的严格解, 主要原因是不考虑两个粒子同时与势垒的散射, 正如在Lieb-Liniger模型中忽略三体相互作用一样. 波函数可以由如下的Bethe假设给出:3 )式中的BA波函数, 这里引入额外的求和指标n , 其物理意义为位于势垒左边的原子个数. 用下标n 来标记这一块(block)区域, (17 )式中对n 的求和包含所有可能的N + 1个块. 另外$ \epsilon_{\rm P}=\pm 1 $ 表示粒子向右或向左运动, 在势垒处粒子发生反射. 因此对于固定的块区域n , 开边界条件对于左边界和右边界是不同的, 在左阱的粒子($ i=1, 2, \cdots, n $ )只能感受到左边的边界条件$ \psi(x_{Q_i}\!=\!-L/2)\!=\!0 $ , 在右阱的粒子($i\!=\!n+1, n+2, $ $\cdots\!, N $ )只能感受到右边的边界条件$ \psi(x_{Q_i}\!=\!L/2)\!= $ 0. 于是存在两个反射矩阵$ { R}(P_1) $ 和$ { R}(P_N) $ 分别在左右边界上反射.$ S_{\epsilon_{P_i}P_i, \epsilon_{P_j}P_j} $ . 根据位于中心处势垒的阶跃条件连接块区域$ n-1 $ 和n , 可以得到第n 个粒子和$ \delta $ 势垒的散射矩阵$ S_{d, P_n}(n) $ . 存在势垒时准动量满足的BA类型的方程为$ R_{n-1}(P_n) $ 表示在块区域$ n-1 $ 改变$ P_n $ 符号$ \epsilon_P $ 的两个系数$ A $ 的比值. 一系列散射加反射会改变第n 个粒子的动量方向, 即$ P_n $ 反号: 在块区域$ n-1 $ , 首先应该和右边最邻近的粒子依次散射$ N-n $ 次, 直到没有粒子可以散射到达最右端, 然后和边界反射改变符号, 再向左边依次散射, 回到原先位置. 两个粒子在散射过程中尽管会改变内部状态, 但仍然满足动量守恒. 自封闭条件要求粒子间的碰撞顺序不影响最后的结果, 这给出如下的Yang-Baxter类型的方程$ (d, P_n, P_{n+1}) $ 到$ (P_{n+1}, P_n, d) $ 的两个等价过程: 左边表示块区域$ n-1 $ 的两个粒子先碰撞, 然后依次和势垒碰撞, 右边表示两个邻近的粒子先后和势垒碰撞, 然后这两个粒子再碰撞. 作为量子反散射方法中最基础的代数结构, Yang-Baxter方程是判断系统可积的重要依据. (19 )式不同于常规的Yang-Baxter方程, 这里存在两种不同形式的散射矩阵, 一种是描述两个粒子之间的散射, 另一种描述粒子和势垒间的散射. 极限情况下, 当d = 0时(18 )式将变成熟知的开边界条件下Lieb-Liniger模型的BA方程[35 ] , 在无相互作用, 即g = 0时则简化为单粒子的结果.18 )式和(19 ) 两式, 通过数值求解得到N = 2即两粒子在双阱中的能谱图. 图2(c) 展示了d = 0和2的能谱随着相互作用强度g 的变化. 在无势垒的情况下奇宇称和偶宇称的解析解都存在, 除g = 0外该方法只找到了奇宇称的解. 对于g > 0的情况, 准动量的解都是实数, 对于g < 0的情况, 准动量有两种解, 实数解对应亚稳态, 互为共轭的复数解对应分子态.d = 300), 然后将势垒的强度突然降低到d = 0.5, 原子在两阱间隧穿. 图4 给出了两个原子在同一个阱中的占据概率随时间的演化. 随着排斥相互作用强度从弱到强, 双占据概率振荡过程的振幅逐渐增强. 强排斥相互作用使得振荡不再完整, 双占据概率不能再100%回到初始NOON态. 图4(b) 展示了相互作用强度分别为g = 1.5和20的两体密度分布在一个周期内的变化.图 4 (a)两个原子在同一个阱中的占据概率随时间的演化图. 黑实线, 蓝虚线, 红点线分别表示不同的相互作用强度g = 0.5, 1.5, 20. 在t = 0时刻势垒高度突然从d = 300降到d =0.5. (b)g = 1.5和20时一个周期里不同时刻的密度分布图, 这里坐标 $ x_1 $ 和 $ x_2 $ 的单位是 $ L/2 $ . 本图摘自参考文献[98 ]Figure4. (a) Tunneling dynamics of the occupation probability $ P_2(t) $ of finding both atoms in the same well for g = 0.5 (black solid line), g = 1.5 (blue dashed line), and g = 20 (red dotted line). The $ \delta $ barrier is abruptly lowered from a height d = 300 to 0.5 at time t = 0. (b) the two-body density functions $ \rho (x_1, x_2, t) $ at different times t , for g = 1.5 and 20, respectively. Here the coordinates $ x_1 $ and $ x_2 $ are in units of $ L/2 $ (Reproduced with permission from Ref. [98 ]).3.6.强相互作用系统的等效自旋链 -->3.6.强相互作用系统的等效自旋链 强相互作用系统有很丰富的物理, 但通常情况下求解是非常困难的. 然而有一种情况除外, 即相互作用趋于无穷大时. 对于无穷大相互作用极限的情况, 不论是玻色子还是费米子都表现出无自旋费米子的行为, 每个粒子占据不同的位置, 不可穿透, 也就是说具有了费米化的特点, 因此相互作用趋于无穷时的系统是容易处理的. 对于强相互作用区域, 相互作用强度为有限值的连续系统可以等效成自旋链模型, 在实验上通过自旋1/2的费米子系统已经实现了海森堡自旋链. 一个重要的区别在于外势的不同会导致格点间的耦合强度的非均匀性. 比如对强相互作用极限下的自旋1/2系统, 无穷大相互作用附近的微扰计算可以将连续模型的哈密顿量等效为一个自旋链模型$ E_{\rm F} $ 是系统的费米能, $ P_{i, i+1} $ 是两个粒子自旋的置换算符, $ J_{i} $ 是格点间的耦合强度, 外势的不均匀会导致不同格点间的耦合强度依赖格点位置, ±分别对应玻色子和费米子. 近年来, 很多理论小组在不同的体系, 如仅考虑s波的两分量系统[99 ,100 -111 ] 、同时考虑s波和p波的系统[112 -114 ] 、玻色费米混合系统[115 ,116 ] 、不等质量系统[117 ] 和多组分的系统[118 ,119 ] 都给出了等效自旋链模型, 并且研究了系统的能谱、磁学性质、密度分布、动量分布以及相变. 对于接触相互作用且外势不依赖自旋的连续模型, 系统有很多守恒量, 比如总自旋守恒、总自旋的z 分量守恒、宇称守恒等等. 通过这些守恒量可以给出体系能级排布的规律, 例如对于自旋1/2的系统, 具有SU(2)对称性, 在强相互作用区域, 能量关于相互作用的倒数1/g 成线性关系, 在g > 0时, 能量随总自旋的增加而增加. 多组分系统, 如果具有SU(N )对称性, 可以借助杨图来排布能级[118 ] , 如果不具有SU(N )对称性, 则情况比较复杂, 但是也有规律可循, 文献[119 ]列出了自旋为1的系统能级排布的规律.4.结 论 量子少体问题是当前研究的一个热点问题. 少体系统的研究对于理解微观现象有很大的帮助, 也为研究多体系统奠定了基础. 随着冷原子实验迅速发展, 实验上的精确操控, 少体系统的研究成为目前关注的热点. 本文简单介绍了实验和理论两方面的进展. 由于目前冷原子实验的精确操控, 少体实验可以准确地观察到一些重要的物理现象, 比如强相互作用时的费米化, 格点模型中的量子相变, 以及少体到多体转变等等. 这些基本物理现象在少体实验中的实现让我们看到了少体研究的重要性. 对于少体的理论研究不同于多体物理, 基于精确可解模型的一些重要结果, 包括亚稳态势阱中相互作用原子的衰减率以及双势阱中的相互作用原子的隧穿动力学研究, 使得该研究领域富有挑战性又对理解单体到多体系统的物理性质提供了过渡. 




















































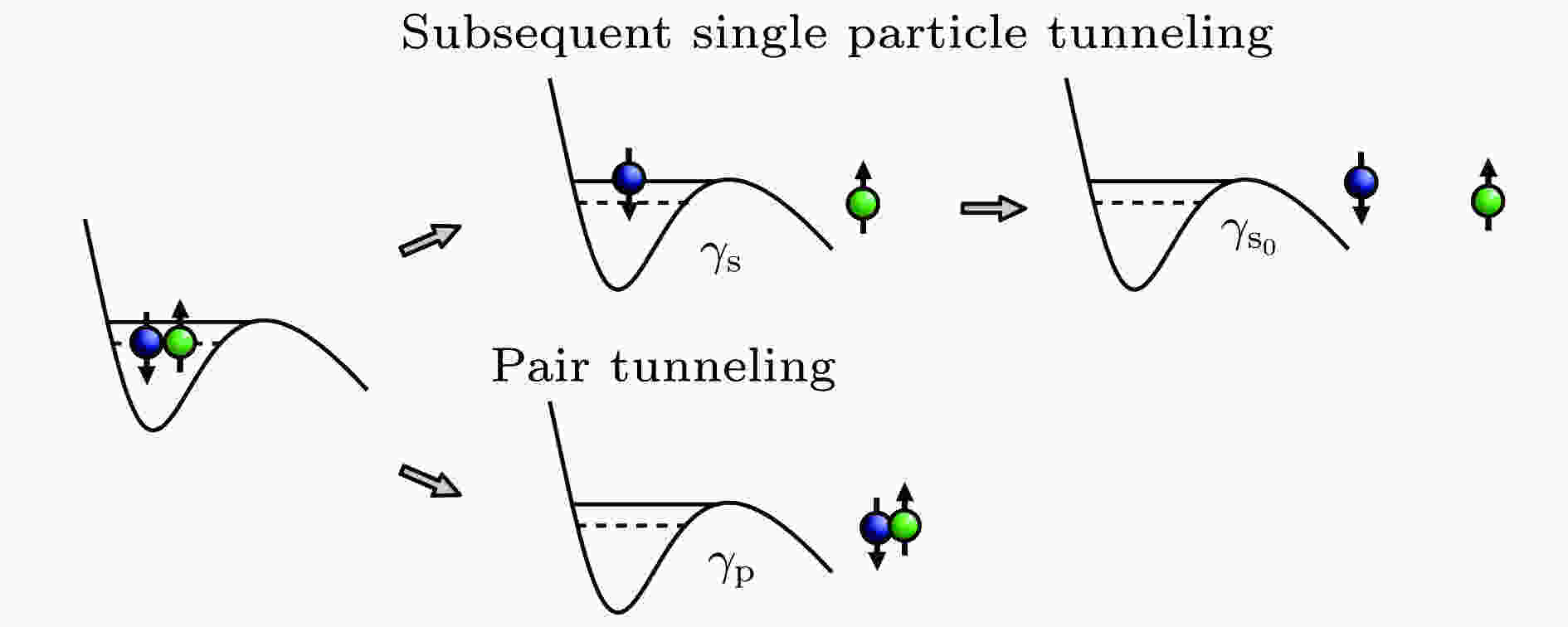 图 1 双原子的两种隧穿过程: 单原子次序隧穿及两原子配对隧穿. 本图摘自参考文献[25]
图 1 双原子的两种隧穿过程: 单原子次序隧穿及两原子配对隧穿. 本图摘自参考文献[25]



































































































































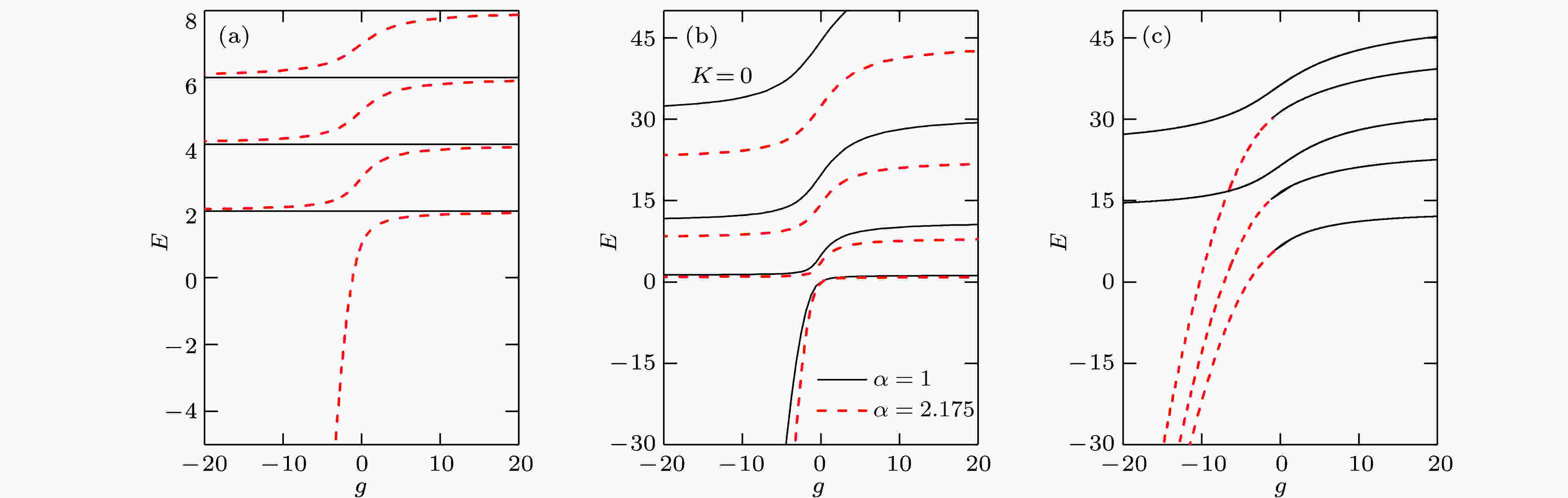 图 2 三种相互作用的两原子系统的能量E与相互作用强度g的关系: (a)谐振子势阱中的两原子, 黑实线和红虚线分别表示相对运动奇宇称和偶宇称波函数所对应的能量; (b)周期边界条件下两异核原子, 黑实线和红虚线分别表示质量相等两原子和质量比为2.175情况下对应的能量; (c)双势阱中相互作用两原子的奇宇称态, 一维无限深方势阱中心为一个强度为d = 0.5的
图 2 三种相互作用的两原子系统的能量E与相互作用强度g的关系: (a)谐振子势阱中的两原子, 黑实线和红虚线分别表示相对运动奇宇称和偶宇称波函数所对应的能量; (b)周期边界条件下两异核原子, 黑实线和红虚线分别表示质量相等两原子和质量比为2.175情况下对应的能量; (c)双势阱中相互作用两原子的奇宇称态, 一维无限深方势阱中心为一个强度为d = 0.5的

















































































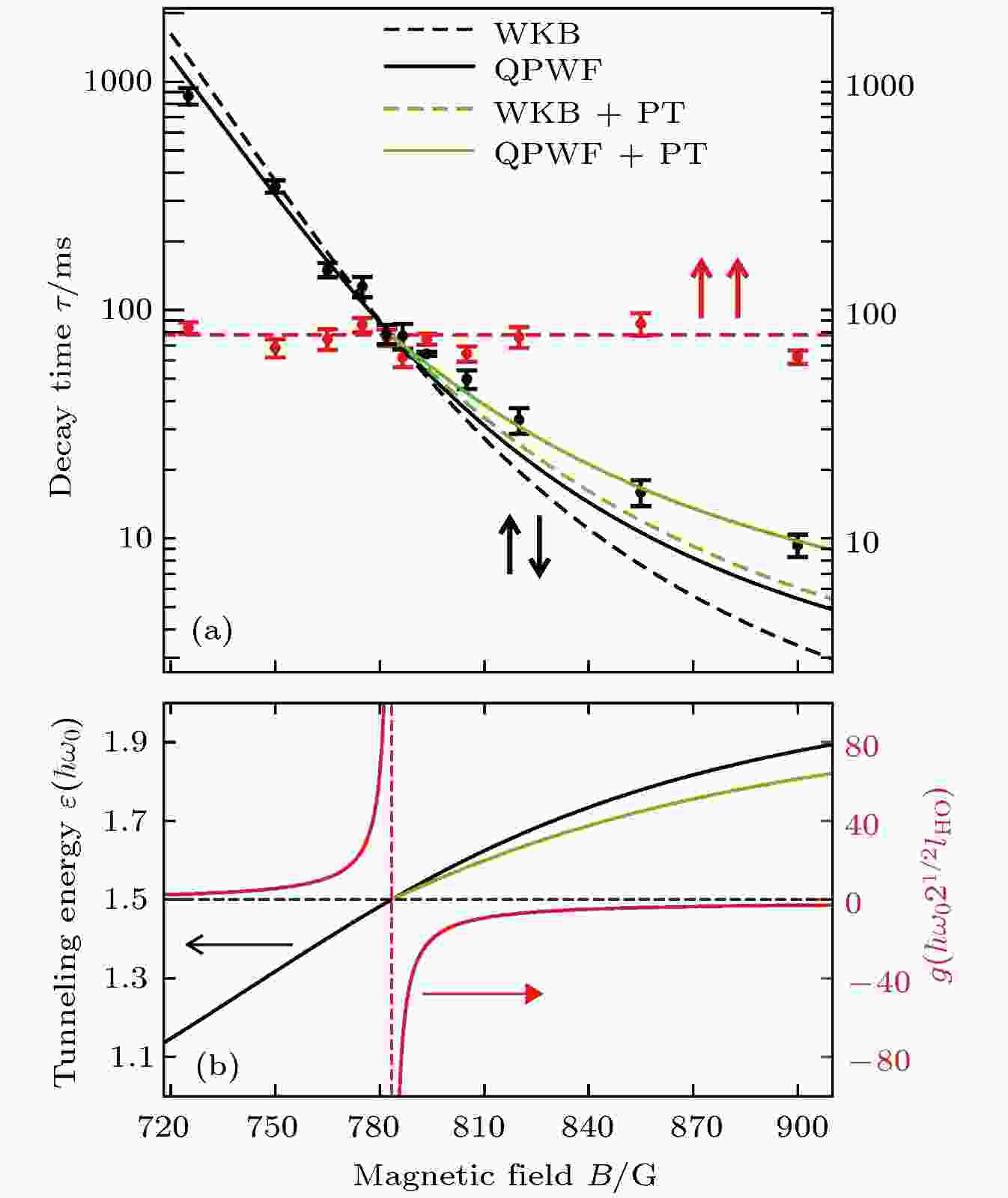 图 3 (a)衰减时间随磁场的变化. 黑色虚线和实线分别是WKB和考虑准粒子波动方程的修正的结果. 绿色线表示通过微扰论考虑非谐项贡献的结果; (b)相互作用强度和隧穿能量随磁场的变化.本图摘自参考文献[33]
图 3 (a)衰减时间随磁场的变化. 黑色虚线和实线分别是WKB和考虑准粒子波动方程的修正的结果. 绿色线表示通过微扰论考虑非谐项贡献的结果; (b)相互作用强度和隧穿能量随磁场的变化.本图摘自参考文献[33]



































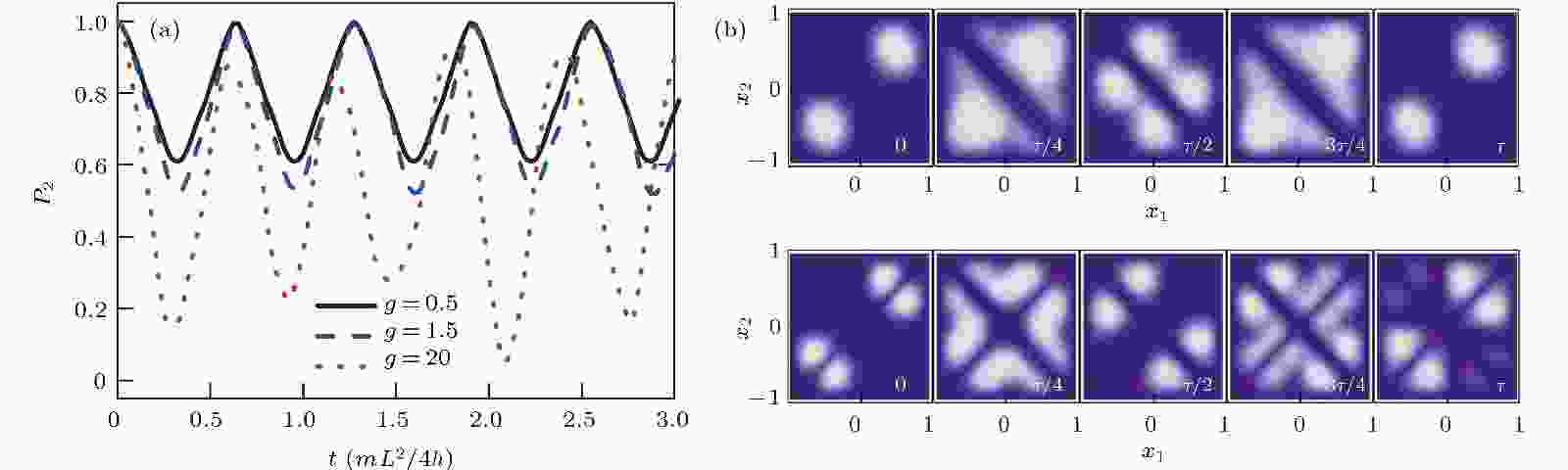 图 4 (a)两个原子在同一个阱中的占据概率随时间的演化图. 黑实线, 蓝虚线, 红点线分别表示不同的相互作用强度g = 0.5, 1.5, 20. 在t = 0时刻势垒高度突然从d = 300降到d =0.5. (b)g = 1.5和20时一个周期里不同时刻的密度分布图, 这里坐标
图 4 (a)两个原子在同一个阱中的占据概率随时间的演化图. 黑实线, 蓝虚线, 红点线分别表示不同的相互作用强度g = 0.5, 1.5, 20. 在t = 0时刻势垒高度突然从d = 300降到d =0.5. (b)g = 1.5和20时一个周期里不同时刻的密度分布图, 这里坐标 












