摘要: 近年来, 碱土金属原子和类碱土金属原子体系的研究成为冷原子物理的研究热点之一. 特别是最近在
173 Yb原子中发现的轨道Feshbach共振, 使得研究有强相互作用的碱土金属和类碱土金属原子系统成为可能, 极大扩展了此类原子体系的研究范围. 本文介绍了
173 Yb费米气体在轨道Feshbach共振附近的杂质态问题. 在此问题中, 位于
$ ^{3}{\rm P}_0 $ 态的杂质原子与处于基态的背景费米海相互作用, 并在费米海表面产生分子态或极化子态. 本文使用试探波函数的研究方法, 首先对分子态和吸引极化子态进行介绍, 并重点描述了分子态与吸引极化子态间的转变. 其次归纳总结了排斥极化子态的相关性质, 如有效质量、衰变率等. 然后考虑双费米面情况, 介绍在闭通道中引入另外一个费米面对系统产生的影响. 最后简要介绍二维
173 Yb费米气体中的杂质态问题.
关键词: 类碱土金属原子 /
轨道Feshbach共振 /
分子态 /
极化子态 English Abstract Impurity problem of alkaline-earth-like atoms near an orbital Feshbach resonance Shi Yue-Ran 1 ,Lu Zhuo-Cheng 1 ,Wang Jing-Kun 1,2 ,Zhang Wei 1,2 1.Department of Physics, Renmin University of China, Beijing 100872, China Fund Project: Project supported by the National Key R&D Program of China (Grant No. 2018YFA0306501), the National Natural Science Foundation of China (Grant Nos. 11434011, 11522436, 11774425), and the Research Funds of Renmin University of China (Grant Nos. 16XNLQ03, 18XNLQ15).Received Date: 31 October 2018Accepted Date: 29 December 2018Available Online: 01 February 2019Published Online: 20 February 2019Abstract: In recent years, alkaline-earth and alkaline-earth-like atoms have attracted much research interest in the field of ultracold atom. Especially, the recently discovered orbital Feshbach resonance makes it possible to investigate a strongly interacting gas of alkaline-earth or alkaline-earth-like atoms, which has greatly enriched the scope of quantum simulation in these systems. This paper focuses on the impurity problem in a Fermi gas of 173 Yb atoms near orbital Feshbach resonance. In this problem, the impurity atom in 3 P 0 state will interact with the background Fermi sea in the ground state and the molecule or polaron state will be produced out of the Fermi sea. By using the Chevy-like ansatz, we investigate the properties of the molecule and attractive polaron states firstly and a transition between these two states will be found. Then, some properties of the repulsive polaron state will be introduced, such as the effective mass and the decay rate. Furthermore, the effect of an additional Fermi sea will be considered in this system. Finally, we will discuss the impurity problem in a two-dimensional system.Keywords: alkaline-earth-like atom /orbital Feshbach resonance /the molecule state /the polaron state 全文HTML --> --> --> 1.引 言 由于存在两个最外层价电子, 碱土金属原子和类碱土金属原子拥有一些特殊性质, 例如存在长寿命的原子激发态, 以及可实现核自旋与电子自旋分离等, 这使该类原子成为近年来的一个研究热点, 并且已被广泛应用于精密测量[1 -3 ] 、量子信息和量子模拟[4 -9 ] 等领域的研究中. 然而, 由于类碱土金属原子的电子总自旋角动量为零, 无法在此类原子体系中应用磁Feshbach共振技术. 尽管已有实验利用光Feshbach共振技术来调控该类原子间相互作用, 但这种手段会造成大量的原子损失[10 -12 ] .173 Yb原子中实现的轨道Feshbach共振 (orbital Feshbach resonance, OFR), 成功解决了上述难题, 并极大扩展了在碱土金属和类碱土金属原子系统中进行量子模拟的研究范围[13 -15 ] . 与碱金属中的磁Feshbach共振技术类似[16 ] , OFR同样由开通道和闭通道间的共振散射引起, 例如在173 Yb原子中, 开通道对应的是分别占据在$ | g \downarrow \rangle $ 态和$ | e \uparrow \rangle $ 态的两个原子, 其中$ | g \rangle $ 和$ | e \rangle $ 态分别与电子轨道态$ ^{1}{\rm S}_0 $ 和$ ^{3}{\rm P}_0 $ 对应, $ | \downarrow \rangle $ 和$ | \uparrow \rangle $ 代表不同的核自旋态. 闭通道则对应于分别占据$ | g \uparrow \rangle $ 态和$ | e \downarrow \rangle $ 态的两个原子. 值得注意的是, 由于电子总自旋角动量J = 0, 核自旋和电子自旋不耦合, 体系中的短程两体相互作用可以发生在轨道单态通道: $ | - \rangle \equiv \dfrac{1}{2}(| ge \rangle-| eg \rangle)\otimes(| \downarrow\uparrow \rangle+| \uparrow\downarrow \rangle) $ 或轨道三态通道: $ | + \rangle \equiv \dfrac{1}{2}(| ge \rangle+| eg \rangle)\otimes(| \downarrow\uparrow \rangle-| \uparrow\downarrow \rangle) $ [7 -9 ] . 因此, 短程相互作用以开通道和闭通道为基时是非对角化的, 并且可以将这两个通道以轨道间核自旋交换相互作用的形式耦合起来. 此外, 当存在磁场时, 利用$ | g \rangle $ 态和$ | e \rangle $ 态间塞曼移动的不同, 可以调节开通道和闭通道间的能量差[13 ,17 ,18 ] . 因此, 当闭通道中的浅束缚态能量被调节至开通道两体散射阈值时, 便会发生散射共振. 2015年, 在理论研究中首次提出OFR方法[13 ] , 紧接着在173 Yb原子中实验实现了该技术. 之后对OFR的进一步研究表明: 从普适性的角度来看, OFR是窄共振, 而从磁场角度来看, OFR则是一个宽共振[19 ] , 后者决定了OFR在173 Yb原子中易于实现.[20 -30 ] . 这其中, 在OFR附近的杂质态问题是一个很重要的研究方向. 在碱金属原子体系中, 磁Feshbach共振中的杂质态问题, 也就是极化子问题, 近年来已被广泛研究[31 -42 ] , 这是由于: 第一, 可以利用简单的理论模型来对此多体系统进行精确描述; 第二, 利用对碱金属原子体系中杂质态问题的研究, 可以模拟研究有强相互作用的量子混合系统中的相图, 例如, 利用极化子问题可以对巡游铁磁进行研究. 在之前对杂质态问题的研究中, Landau[43 ] 和Pekar[44 ] 提出, 对电介质中传导电子的性质可以用极化子理论来解释. 这个开创性的想法后来被Fr?hlich等[45 ,46 ] 和Feynman[47 ] 进一步推导, 他们将离子晶体和极性半导体看作由声子组成的背景粒子体系. 其他还有一些著名的研究, 例如在氦-4原子背景体系下, 研究氦-3原子作为杂质粒子的杂质态问题[48 ] , 以及在金属中研究局域磁性杂质引起的Kondo效应[49 ] .[50 -53 ] 和费米子[31 -33 ] 的系统均已实现. 在玻色系统中的杂质态问题可以看作是对Fr?hlich极化子的模拟[54 -56 ] . 系统中杂质粒子动态性质的改变由其与玻色激发相互作用决定, 在玻色凝聚中的激发为Bogoliubov粒子, 而在热玻色气体中的激发为单粒子. 当背景粒子为低温费米气体时, 产生的费米极化子是Landau准粒子基本概念的典型再现. 在冷原子系统中, 可以在强相互作用区域内, 用一个十分简单的理论模型来精确描述极化子的性质, 这为增进对强关联系统的认识和理解提供了便利. 进一步研究发现, 在冷原子中, 对只存在一个杂质粒子的系统进行研究, 就能够得到有强相互作用的极化气体的精确信息. 在这样的背景下, 科研工作者在冷原子系统中针对杂质态问题进行了一系列的研究, 例如: 在有两种不同自旋轨道耦合的二维费米气体中研究杂质态问题[57 ] ; 在玻色极化子系统中研究Efimov态[58 ] ; 在有拓扑p波超流的一维准周期费米系统中研究极化子态[59 ] ; 研究非零温和杂质粒子数密度为有限值对吸引极化子性质的影响[60 ] 等. 这些理论和实验研究揭示了强极化条件下多体系统中的物理性质. 在有OFR的系统中, 科研工作者们自然希望通过类似的研究得到此系统中的少体和多体性质.$ | e\uparrow \rangle $ 的杂质原子与处于基态的费米海间的相互作用. 当存在一个有限强度的磁场时, 利用OFR技术可以调节杂质原子与费米海中原子间的相互作用. 在此过程中, 在不同参数情况下, 杂质原子可能与背景费米海结合形成极化子, 也可能形成紧束缚分子态. 因此, 当调节粒子间相互作用强度时, 会出现所谓的吸引极化子态到分子态的转变. 研究发现, 转变点位置在OFR附近, 且与系统的粒子数密度有关. 由于OFR中存在轨道间自旋交换相互作用, 极化子态和分子态的形成都会经历自旋翻转的过程, 例如, 一个位于$ | g\downarrow \rangle $ 态的粒子和一个位于$ | e\uparrow \rangle $ 态的粒子会被散射到$ | g\uparrow \rangle $ 态和$ | e\downarrow \rangle $ 态. 由此产生的结果是, 对于极化子, 除了传统自旋守恒的激发, 也存在自旋翻转激发, 在这类激发中, 原来空着的超精细态将被占据, 研究发现这种自旋翻转过程十分重要. 接下来, 对排斥极化子态的性质进行介绍, 包括谱函数、本征能量、准粒子残余、有效质量、衰变率等. 然后考虑双费米面情况, 介绍引入另一个费米面对系统性质的影响. 最后介绍二维173 Yb费米气体中的分子态和极化子态性质.2.体系简介 本文关注由类碱土金属原子组成的费米气体. 在此体系中, 开通道$ |o\rangle $ 和闭通道$ |c\rangle $ 由两个核自旋态和两个轨道能级组成, 分别为: $|o\rangle= \dfrac{1}{\sqrt{2}}(|g{\downarrow};e{\uparrow}\rangle-$ $\!|e{\uparrow};g{\downarrow}\rangle) $ 和$ |c\rangle=\dfrac{1}{\sqrt{2}}(|g{\uparrow};e{\downarrow}\rangle- $ $|e{\downarrow};g{\uparrow}\rangle) $ , 通道间的相对能量可以通过磁场进行调节. 体系的哈密顿量可以表示为[13 ,19 ] $ a_{{ k} p \sigma}^\dagger $ 和$ a_{{ k} p \sigma} $ ($ p=e, g $ , $ \sigma=\uparrow, \downarrow $ )是与动量$ k $ 有关的费米算符. 由于轨道态$ |g\rangle $ 和$ |e\rangle $ 中的朗德因子不同, 两个超精细能级间的塞曼移动$ \delta_g $ 和$ \delta_e $ 不相等, 如图1 所示. 通过调节磁场, 可以控制两个通道间的塞曼移动差$ \delta=\delta_e-\delta_g $ . 这里需要注意的是, 为了将系统哈密顿量写为(1 )式所示的对称形式, 将$ |g\uparrow\rangle $ 和$ |e\downarrow\rangle $ 设为零能参考点, 同时设定$ |g\downarrow\rangle $ 和$ |e\uparrow\rangle $ 均移动$ \delta/2 $ .图 1 类碱土金属原子中的OFR能级图. 杂质原子处于$ | e\uparrow \rangle $ 态, 费米海处于$ | g\downarrow \rangle $ 态. 通过相互作用, 杂质原子和费米海中原子会被散射到闭通道的两个态上. $ \delta_g $ 和$ \delta_e $ 是两个能级的塞曼移动Figure1. Level diagram of an OFR. An impurity atom in the $ |e\uparrow\rangle $ state is immersed in a Fermi gas of alkaline-earth-like atoms in the $ |g\downarrow\rangle $ state. $ \delta_g $ and $ \delta_e $ are the Zeeman shifts of the $ |g\rangle $ and $ |e\rangle $ manifolds, respectively.${\text{可以写为}} $ $ g_{\pm} $ 可以通过公式 $1/g_{\pm}=1/g_{\pm}^{p}- $ $ \displaystyle\sum\limits_{ k}1/(2\varepsilon_{ k}) $ 和$ g_{\pm}^{p}=4\text{π}\hbar^{2}a_{\pm}/m $ 与$ {\rm s} $ 波散射长度$ a_{\pm} $ 联系起来, 其中$ m $ 为原子质量. 在接下来的章节中, 将介绍利用Chevy试探波函数来研究体系中分子态和极化子态的性质[61 ,62 ] .3.分子态的研究 分子态中, 处于$ |e\uparrow\rangle $ 态的杂质原子会从处于$ |g\downarrow\rangle $ 态由$ N $ 个原子形成的费米海中散射出一个原子, 并且二者形成束缚态. 分子态的试探波函数可以写为$ Q $ 为质心动量, $ |g{\downarrow}\rangle_{N-1} $ 代表余下的$ N-1 $ 个原子组成的费米海. 值得注意的是, 这里形成的分子态可以在开通道中, 也可以在闭通道中, 与之对应的系数分别为$ \alpha_{ k} $ 和$ \beta_{ k} $ .4 )对应的薛定谔方程:$ \widetilde{E}_{\rm M}({ Q}) $ 为本征能量. 将试探波函数方程代入哈密顿量(1 )式中, 在舍弃掉一些高阶项后, 可以得到一系列关于系数$ \alpha_{ k} $ 和$ \beta_{ k} $ 的线性方程. 在将系数$ \alpha_{ k} $ 和$ \beta_{ k} $ 作为变分参数时, 这些线性方程也可以通过计算期望值$ {_{ Q}}\langle M | H-{\tilde E}_{\rm M}({ Q}) |M\rangle_{ Q} $ 来获得. 系数方程可整合为如下形式:$E_{\rm M} = {\tilde E}- $ $ \displaystyle\sum\limits_{|{ k}|>k_{\downarrow {\rm F}}}(\varepsilon_{ k}+ $ $ \delta/2)$ . 在此能量参考点下, 位于$ | e\uparrow \rangle $ 态的杂质粒子的阈值能量为$ E_{\rm {th}}=E_{\downarrow {\rm F}}+\delta $ . 从(6 )式中可以得到关于分子态本征能量的重整化方程为$ \varLambda_c\equiv\displaystyle\sum\limits_{ k}1/(2\varepsilon_{ k}) $ .$ { Q}=0 $ 时分子态的性质. 通过对(8 )式进行数值求解, 可以得到能量$ E_{\rm M} $ 的两个解: 一个解为浅束缚态, 即能量接近阈值能量$ |E_{\rm M}-E_{\rm {th}}| \sim E_{\downarrow {\rm F}} $ , 另一个解为深束缚态, 即能量远高于阈值能量$ |E_{\rm M}-E_{\rm {th}}| \gg E_{\downarrow {\rm F}} $ . 本文关注的是由173 Yb原子组成的系统, 系统参数为: 粒子数密度$ n=2\times 10^{13} $ cm–3 , 取$ m=1/2 $ , $ \hbar=1 $ , $ k_{\downarrow {\rm F}}=1 $ , $ E_{\downarrow {\rm F}} $ 为能量单位, 散射长度$ a_{+}=1900a_0 $ 和$a_{-}= $ $ 200a_0 $ , 其中$ a_0 $ 是玻尔半径[15 ,19 ] . 在此参数取值下, 深束缚态能量约为常数$ 160E_{\downarrow {\rm F}} $ , 远远大于费米能$ E_{\downarrow {\rm F}} $ , 所以只考虑浅束缚态能量, 即$|E_{\rm M}-E_{\rm {th}}| \sim $ $ E_{\downarrow {\rm F}} $ 的情况. 图2(a) 和图2(b) 分别展示了本征能量$ E_{\rm M}-E_{\rm {th}} $ 随$ \delta $ 和$ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ 的变化情况, 其中, $ {\rm s} $ 波散射长度满足如下关系式[19 ] :图 2 (a), (b) 分子态的能量随$ \delta $ 和$ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ 的变化; (c) 分子态的波函数分布情况; (d) $ E_{\rm M} $ 接近阈值能量$ E_{\rm F} $ 的分子态, 在$ { Q}\neq 0 $ 时的有效质量. 引自参考文献[23 ]Figure2. (a), (b) The eigenenergy in the molecular state varies with $ \delta $ and $ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ ; (c) the wave functions' distribution in the open and closed channels; (d) the effective mass for the molecular state whose energy is closed to the threshold energy when $ { Q}\neq 0 $ . Reproduced from Ref. [23 ].$ a_{{\rm s}0}=(a_{+}+a_{-})/2 $ , $ a_{{\rm s}1}=(a_{-}-a_{+})/2 $ .4 )式中的系数. 图2(c) 描述了浅束缚态中波函数的分布情况. 其中, 闭通道部分$ \displaystyle\sum\limits_{ k}|\beta_{ k}|^2 $ 随$ \delta $ 的增大而变大, 并且在$ \delta $ 较大时成为波函数的主要部分, 而波函数中的开通道部分$ \displaystyle\sum\limits_{ k}|\alpha_{ k}|^2 $ 呈现出与闭通道部分相反的变化趋势. 此现象可解释为, 当$ \delta $ 为一个较大的正值时, 开通道在闭通道之上有很大的失谐, 如图1 所示, 这导致开通道的部分可以被忽略.$ { Q}\neq 0 $ 的情况. 可以计算当$ Q $ 略微背离零值时, 分子态的有效质量. 如图2(d) 所示, 在深BEC (Bose-Einstein condensate)极限下, 分子有效质量从一个有限值开始增大, 此时分子本质上是一个质量为有限值, 且无固定结构的玻色子. 在BCS (Bardeen-Copper-Schrieffer)一侧时, 有效质量变为负值. 有效质量将会在$ \delta/E_{\downarrow {\rm F}} \approx -6.6 $ 处发散, 此发散点位于共振的BCS一侧. 此发散行为,也表明OFR是一个窄共振, 因为在宽共振中, 有效质量的发散点通常位于共振的BEC一侧.4.吸引极化子态的研究 极化子态的试探波函数可写为11 )式和对应的系数方程, 可以得到极化子态的相关性质. 与分子态相似, 在极化子态中, 也存在两个低于阈值的能量解: 一个解接近阈值能量, 另一个解满足$ |E_{\rm P}-E_{\rm {th}}|\gg E_{\downarrow {\rm F}} $ . 其中, 前者为浅吸引极化子态, 后者为深吸引极化子态. 本节关注浅吸引极化子态的性质.图(3) 中, 描绘了吸引极化子态能量、波函数分布以及质心动量$ { Q} \neq 0 $ 时有效质量的变化情况. 从图中可以发现, 在BCS极限下, 即$ \delta $ 是一个较大负值时, 波函数主要是由裸粒子态部分$ |\gamma|^2 $ 组成, 而在BEC极限下, 闭通道部分$ \displaystyle\sum\limits_{{ k}, |{ q}| < k_{\downarrow {\rm F}}}|\beta_{ {kq}}|^2 $ 成为主要组成部分. 开通道部分$ \displaystyle\sum\limits_{|{ k}|>k_{\downarrow {\rm F}}, |{ q}| < k_{\downarrow {\rm F}}}|\alpha_{ {kq}}|^2 $ 在共振点处, 与闭通道部分相当, 但随着$ \delta $ 的增大会降低.图 3 (a), (b) 吸引极化子态的能量随$ \delta $ 和$ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ 的变化; (c) 吸引极化子态的波函数分布情况; (d) 吸引极化子态在$ { Q}\neq 0 $ 时的有效质量, 图中发散点为$ \delta/E_{\downarrow {\rm F}}\approx -0.35 $ , 对应于$ 1/(k_{\downarrow {\rm F}}a_{\rm s})\approx 1.40 $ . 图中参数与图2 中一致. 引自参考文献[23 ]Figure3. (a), (b) The eigenenergy in the attractive polaron state varies with $ \delta $ and $ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ ; (c) the wave functions' distribution in the open and closed channels; (d) the effective mass for the attractive polaron state when $ { Q}\neq 0 $ . Parameters here are the same as those in Fig. 2 . Reproduced from Ref. [23 ].$ { Q}\neq 0 $ 的情况. 与研究分子态时相似, 计算当${ Q}$ 偏离零值很小时, 吸引极化子态的有效质量. 从图3(d) 中可以发现, 在BCS极限下, 吸引极化子的有效质量趋近于有限值1/2, 此时系统变为一个未受扰动的费米海, 同时费米海表面存在一个质量为1/2的杂质粒子. 当向共振点移动时, 有效质量变大, 并且会呈现出与分子态类似的发散行为. 发散点位于$ \delta/E_{\downarrow {\rm F}}\approx -0.35 $ 处, 位于共振的BEC一侧.5.吸引极化子态到分子态的转变 前面两节分别介绍了分子态和吸引极化子态的性质. 将计算得到的两个态的能量放在同一张图中, 如图4(a) 和图4(b) 所示, 可以清晰地看到, 存在吸引极化子态到分子态的转变, 且转变点$ \delta_{\rm c}/E_{\downarrow {\rm F}} \approx -2.3 $ , $ 1/(k_{\downarrow {\rm F}} a_{\rm c})\approx 0.81 $ . 当$ \delta < \delta_{\rm c} $ 时, 系统的基态为质心动量为零的吸引极化子态. 另一方面, 当$ \delta>\delta_{\rm c} $ 时, 系统基态变为质心动量为零的分子态. 图4(c) 中, 描绘了转变点$ \delta_{\rm c} $ 随粒子数密度的变化情况. 从图中可以发现, $ \delta_{\rm c} $ 随粒子数密度的增大而变大, 这清楚表明, 系统在共振点附近表现出的性质不具有普适性, 体现出窄共振的特点.图 4 (a), (b) 分子态(黑色实线)和吸引极化子态(蓝色虚线)的本征能量随$ \delta $ 和$ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ 的变化, 吸引极化子态到分子态的转变发生在$ \delta_{\rm c}/E_{\downarrow {\rm F}} \approx -2.3 $ 和$ 1/(k_{\downarrow {\rm F}} a_{\rm c})\approx 0.81 $ 处; (c) 转变点$ \delta_{\rm c} $ (黑色实线)和对应的转变能量$ E_{\rm c} $ (红色实线)随粒子数密度的变化. 引自参考文献[23 ]Figure4. (a), (b) The eigenenergy of the molecule (black solid) and polaron (blue dashed) states vary with $ \delta $ and $ 1/(k_{\downarrow {\rm F}}a_{\rm s}) $ . The transition point is around $ \delta_c/E_{\downarrow {\rm F}} \approx -2.3 $ and $ 1/(k_{\downarrow {\rm F}} a_{\rm c})\approx 0.81 $ ; (c) the transition point $ \delta_{\rm c} $ (black solid) and the corresponding energy $ E_{\rm c} $ (red solid) vary with particle density. Reproduced from Ref. [23 ].6.排斥极化子态的研究 本节中将对能量$ E_{\rm P} $ 高于阈值能量$ E_{\rm {th}} $ 的排斥极化子态进行研究. 该体系的自能可以表示为[63 ,64 ] $ \varGamma'_{ {Qq}} $ 和$ \varGamma_{ {Qq}} $ 在(12 )式中给出定义. 谱函数方程可写为如下形式:$ \varepsilon_{ Q}+\delta/2 $ 是质心动量为$ Q $ 的杂质粒子的能量.图(5) 描绘了质心动量$ { Q}=0 $ 时, 谱函数在$ \delta-E $ 平面中的变化情况. 从图中可以看出, 谱函数存在两支峰值, 且满足关系:$ E_{{\rm P}-}-E_{\rm {th}} < 0 $ , 对应于前面讨论的吸引极化子态. 当$ \delta/E_{\downarrow {\rm F}}\lesssim-2.3 $ 时, 吸引极化子态是系统的稳定基态. 当$ \delta/E_{\downarrow {\rm F}} $ >–2.3时, 吸引极化子态变得不稳定, 可以衰减为一个分子和一个空穴, 或者一个分子、两个空穴和一个费米子, 或者一个分子和其他粒子-空穴激发, 并在$ \delta / E_{\downarrow {\rm F}} $ 大于零时与粒子-空穴连续区域汇合, 这与图(5) 中吸引极化子态分支上面的浅黄色部分对应. 图(5) 中位于上面的一支峰值$ E_{{\rm P}+}-E_{\rm {th}}>0 $ , 与排斥极化子态相对应. 在$ \delta/E_{\downarrow {\rm F}}\lesssim-4.0 $ 区域, 排斥极化子态与粒子-空穴连续区域重叠. 当$-4.0\lesssim $ $ \delta/E_{\downarrow {\rm F}}\lesssim0 $ 时, 排斥极化子是一个界限清晰的准粒子态. 当$ \delta/E_{\downarrow F}\gtrsim0 $ 时, 排斥极化子态分支的峰值变得模糊, 这是由于排斥极化子态和闭通道中的散射态发生耦合造成的[65 ] .图 5 极化子态的谱函数$ A({ Q}=0, E_{\rm P}) $ 随$ \delta $ 和能量变化的彩色图. 图中红色实线表示分子态能量, 由(8 )式计算得到. 黑色点划线为吸引极化子态能量, 由(11 )式计算得到. 两条线相交于$ \delta_{\rm c}/E_{\downarrow {\rm F}}\approx -2.3 $ 处. 图中蓝色虚线代表排斥极化子能量, 由(15 )式得到. 当$ \delta $ 为较大负值时, 排斥极化子与图中由浅黄色区域代表的粒子-空穴连续区域重合. 当$ \delta $ 大于零时, 由于存在闭通道散射, 排斥极化子分支会变得模糊. 引自参考文献[30 ]Figure5. The spectral function of the polaron state as a function of $ \delta $ and energy for $ { Q}=0 $ . The red solid line represents the energy of molecule state, which is given by Eq. (8 ), and the black dashed-dotted line is the energy of attractive polaron state given by Eq. (11 ). The value of the crossing point for these two lines is $ \delta_{\rm c}/E_{\downarrow {\rm F}}\approx -2.3 $ . The blue dashed line denotes the repulsive polaron energy given by Eq. (15 ). At large negative $ \delta $ , the branch of repulsive polaron merges into the molecule-hole continuum, which is represented by the broad light yellow area. When $ \delta $ is a positive value, because of the closed channel scattering continuum, the repulsive polaron branch will be blurred. Reproduced from Ref. [30 ].[66 ] $ [66 ] [63 -66 ] :$ Z_+ $ 是排斥极化子的准粒子残余, $ \tilde{\varSigma} $ 为:$ \tilde{\varSigma} $ 的表达式中, 与(13 )式相比, 已将$ (\varGamma'_{ {Qq}} -\varLambda) $ 替换为$(1 - Z_+)(\varGamma'_{ {Qq}} -\varLambda) $ , 这是为了便于确定衰变后的终态.图6(a) 和图6(b) 中描绘了排斥极化子态的准粒子残余和有效质量, 为了便于比较, 在图中同时画出了吸引极化子态的准粒子残余和有效质量. 从图中可以看出, 当$ \delta $ 变大时, $ Z_{+} $ 变大, $ m_{P+} $ 变小, 这与碱金属原子体系情况一致. 但不同的是, 在本文研究的体系中, 排斥极化子态的准粒子残余和有效质量都会出现明显的非解析行为. 这种非解析行为的出现, 可定性解释为由类似于共振散射的行为引起. 其中, 由于杂质原子和费米海中原子相互作用, 在失谐满足能量和动量守恒条件下, 一个通道中的原子可能被共振散射到另一个通道中[65 ] . 图6(c) 展示了从(18 )式中计算得到的衰变率$ \varGamma $ . 当$ \delta $ 在大于零或小于但较接近零的区域中, 开通道失谐在闭通道之上, 排斥极化子的衰变主要由闭通道决定. 当$ \delta $ 向着较大正值不断趋近时, 衰变率会变大. 另一方面, 当$ \delta $ 在小于零或者大于但较接近零的区域时, 衰变通道主要由开通道决定, 并随着$ \delta $ 减小而变大. 衰变率$ \varGamma $ 的非单调变化, 是由两个通道间的竞争导致的, 当两个通道简并时, 衰变率处于最小值处. 当$ \delta $ 趋近于较大的负值时$ \varGamma $ 开始下降, 这是由准粒子残留$ Z_+ $ 的降低造成的. 如图(5) 所示, 当排斥极化子分支最终与粒子-空穴连续区域重合时, 排斥极化子将不再是一个定义较好的准粒子, 所以本文不对此区域中的衰变率进行讨论.图 6 (a), (b) 极化子态的准粒子残余和有效质量随$ \delta $ 的变化, 其中红色实线对应排斥极化子态, 蓝色虚线对应吸引极化子态; (c) 排斥极化子态的衰变率随$ \delta $ 的变化. 引自参考文献[65 ]Figure6. (a), (b) Quasiparticle residues $ Z_\pm $ and effective masses for the attractive (blue dashed) and repulsive (red solid) polarons as functions of $ \delta $ ; (c) the decay rate $ \varGamma $ varies with $ \delta $ . Reproduced from Ref. [65 ].7.双费米面情况下系统性质的研究 本节将介绍双费米面情况下系统的性质. 此时体系如图7 所示, 处于激发态$ | e\uparrow \rangle $ 的杂质粒子与处于$ | g\uparrow \rangle $ 和$ | g\downarrow \rangle $ 态的费米海相互作用. 同样利用轨道单态和三态作基, 系统相互作用哈密顿量可以写为图 7 双费米面情况下, 类碱土金属原子的OFR能级图. 杂质原子处于$ | e\uparrow \rangle $ 态, 费米海处于$ | g\downarrow \rangle $ 态和$ | g\uparrow \rangle $ 态. 通过相互作用, 杂质原子和费米海中原子会被散射到闭通道的两个态上. $ \delta_g $ 和$ \delta_e $ 是两个能级的塞曼移动Figure7. Level diagram of an OFR, which has two fermi seas. An impurity atom in the $ |e\uparrow\rangle $ state is immersed in a Fermi gas of alkaline-earth-like atoms in the $ |g\downarrow\rangle $ and $ | g\uparrow \rangle $ states. $ \delta_g $ and $ \delta_e $ are the Zeeman shifts of the $ |g\rangle $ and $ |e\rangle $ manifolds, respectively.7.1.分子态与吸引极化子态 7.1.分子态与吸引极化子态 图8(a) —图8(c) 描绘了质心动量$ { Q}=0 $ 时, 分子态和吸引极化子态的能量在$ k_{\uparrow {\rm F}} $ 等于不同值时的变化情况. 从图中可以看出, 在$ k_{\uparrow {\rm F}} $ 为不同值的所有情况中, 当$ \delta $ 为较大负值时, 系统的基态为吸引极化子态, 而伴随着$ \delta $ 的增大并超过转变点$ \delta_{\rm c} $ 时, 分子态成为系统的基态. 同时可以发现, 对于图8 中三种不同$ k_{\uparrow {\rm F}} $ 的情况, 转变点均处于OFR的BEC一侧, 分别为(a) $ \delta_{\rm c}=-2.28 $ $1/(k_{\downarrow {\rm F}}a_{\rm c})\approx $ , $ 0.81 $ ; (b) $ \delta_{\rm c}=-1.50 $ , $ 1/(k_{\downarrow {\rm F}}a_{\rm c})\approx 1.01 $ ; (c) $\delta_{\rm c}= 2.02 $ , $ 1/(k_{\downarrow {\rm F}}a_{\rm c})\approx 0.87 $ . 为进一步阐明在闭通道中引进另一个费米面对系统产生的影响, 在图8(d) 中画出了转变点$ \delta_{\rm c} $ 随$ k_{\uparrow {\rm F}} $ 的变化情况. 从图中可以看出, 转变点$ \delta_{\rm c} $ 会随着费米能级$ k_{\uparrow {\rm F}} $ 的变大而单调上升, 这说明$ | g\uparrow \rangle $ 态上的费米面占据了费米能$ E_{\uparrow {\rm F}} $ 以下的所有态, 等效于提高了闭通道能量$ \delta_g $ . 相应地, 开通道能量$ \delta_{\rm c} $ 也需要升高相同的能量来抵消闭通道中能量的移动. 从图8(d) 中也可以看出, 在$ k_{\uparrow {\rm F}} $ 不是很大时, 利用费米能$ E_{\uparrow {\rm F}} $ 能够近似估算出转变点$ \delta_{\rm c} $ , 而当$ k_{\uparrow {\rm F}} $ 较大时, 二者的偏离是由费米面附近相互作用引起的涨落引起的.图 8 质心动量为零, $ k_{\uparrow {\rm F}}=0 $ ((a)), $ k_{\uparrow {\rm F}}=1 $ ((b)), $ k_{\uparrow {\rm F}}=2 $ ((c))时, 分子态和吸引极化子态的本征能量随$ \delta $ 的变化; (d) 吸引极化子态到分子态的转变点随$ k_{\uparrow {\rm F}} $ 的变化, 其中, 黑色实线为计算得到的转变点, 红色点划线为费米能级$ E_{\uparrow {\rm F}}=k_{\uparrow {\rm F}}^2 $ . 引自参考文献[30 ]Figure8. The eigen energies of molecule and attractive polaron states vary with $ \delta $ when $ { Q}=0 $ and (a) $ k_{\uparrow {\rm F}}=0 $ , (b) $ k_{\uparrow {\rm F}}=1 $ , (c) $ k_{\uparrow {\rm F}}=2 $ ; (d) the transition point $ \delta_{\rm c} $ varies with $ k_{\uparrow {\rm F}} $ , where the black solid line represents $ \delta_{\rm c} $ and the red dashed-dotted line is the Fermi level $ E_{\uparrow F}=k_{\uparrow {\rm F}}^2 $ . Reproduced from Ref. [30 ].图9 中$ k_{\uparrow {\rm F}}=1 $ 和$ k_{\uparrow {\rm F}}=2 $ 的情况可以发现, 除了存在能量移动, 波函数的整体结构都十分类似. 从图中可以看出, 在分子态和吸引极化子态中, 在$ \delta $ 小于零的区域, 开通道部分为波函数的主要组成, 但在$ \delta $ 大于零的区域, 闭通道部分占据主导. 另外也可以发现, 在吸引极化子态中, 当开通道失谐较大时, 裸杂质态部分$ |\gamma|^2 $ 消失. 这些发现与前几节讨论的单费米面情况相似.图 9 (a), (c) 分子态的波函数分布情况; (b), (d) 吸引极化子态的波函数分布, 此时质心动量为零. (a)和(b)中, $ k_{\uparrow {\rm F}}=1 $ , (c)和(d)中, $ k_{\uparrow {\rm F}}=2 $ . 引自参考文献[30 ]Figure9. The fractions of wave functions for molecule ((a), (c)) and attractive polaron states ((b), (d)) with zero center-of-mass momentum. The parameter in this figure is $ k_{\uparrow {\rm F}}=1 $ for (a) and (b), $ k_{\uparrow {\rm F}}=2 $ for (c) and (d). Reproduced from Ref. [30 ].7.2.排斥极化子态 -->7.2.排斥极化子态 接下来讨论双费米面体系中排斥极化子态的各项性质. 图10 描绘了在$ k_{\uparrow {\rm F}} $ 等于不同值时排斥极化子态的准粒子残余、有效质量和衰变率随$ \delta $ 的变化情况. 从图10(a) 中的准粒子残余和图10(b) 中的有效质量曲线可以发现, 随着$ \delta $ 的不断增大, 排斥极化子态的准粒子残余$ Z_+ $ 和有效质量$ m_{{\rm P}+} $ 均趋于一个定值, 这意味着随着$ \delta $ 的不断增大, 排斥极化子态将变为一个满足$ Z_{+}\rightarrow 1 $ 和$ m_{{\rm P}+}\rightarrow 1/2 $ 的裸杂质粒子态, 且杂质粒子与费米海相互作用极弱. 此外也发现, 在单费米面, 即$ k_{\uparrow {\rm F}}=0 $ 时出现的非解析行为, 将随着闭通道中费米面的出现而变得模糊并最终消失. 在单费米面时已经介绍过, 这种非解析行为的出现由类似共振行为引起. 当失谐满足能量-动量守恒时, 一个通道中的原子会被共振散射到另外一个通道中. 当闭通道为空,即$ k_{\uparrow {\rm F}}=0 $ 时, 这种共振现象最为显著. 当闭通道中存在另外一个费米面时, 这种非解析行为会发生移动, 以此来抵消闭通道中引入费米面后带来的能量移动. 同时由于存在相互作用, 费米面以下的态不再被完全禁戒, 最终导致非解析行为变得模糊, 进而消失. 图10(c) 描绘了在$ k_{\uparrow {\rm F}} $ 等于不同值时衰变率$ \varGamma $ 随$ \delta $ 的变化情况. 从图中可以看出, 对于$ k_{\uparrow {\rm F}} $ 等于不同值的情况, 除了另一个费米面所带来的能量移动, 衰变率$ \varGamma $ 的整体变化行为都十分相似, 且与单费米面时性质定性相同.图 10 (a), (b) 在$ k_{\uparrow {\rm F}} $ 等于不同值时, 排斥极化子态的准粒子残余和有效质量随$ \delta $ 的变化情况. 图(a)中的插图描绘了吸引极化子态的准粒子残余随$ \delta $ 的变化情况. 图中, 当$ k_{\uparrow {\rm F}}=0 $ 时出现的非解析行为发生在$ \delta/E_{\downarrow {\rm F}}=-0.87 $ 处; (c) 排斥极化子态的衰变率$ \varGamma $ 在$ k_{\uparrow {\rm F}} $ 等于不同值时随$ \delta $ 的变化情况. 引自参考文献[30 ]Figure10. (a), (b) The quasiparticle residue $ Z_+ $ and the effective mass $ m_{{\rm P}+} $ vary with $ \delta $ for different values of $ k_{\uparrow {\rm F}} $ . The obvious kink structure when $ k_{\uparrow {\rm F}}=0 $ appears near $ \delta/E_{\downarrow {\rm F}}=-0.87 $ . The inset of (a) is the residues for attractive polarons; (c) the decay rates vary with $ \delta $ for different values of $ k_{\uparrow {\rm F}} $ . Reproduced from Ref. [30 ].8.二维系统中杂质态问题的研究 本节将介绍二维173 Yb费米气体中的杂质态问题. 实验上, 一般通过在$ x $ -$ y $ 平面添加频率较弱的简谐束缚势阱, 同时在$ z $ 轴方向施加强束缚来实现二维体系[67 ] . 为了与实验研究有可比性, 在二维系统杂质态问题的计算中, 设定$ z $ 轴方向的束缚频率满足$ \hbar\omega_{z}= 10 \gg E_{\downarrow {\rm F}} $ , 其他参数与前面讨论的三维体系相同. 利用与研究三维系统相同的方法, 可以得到二维173 Yb费米气体中分子态和极化子态的性质, 以及外加费米面对体系的影响.图11(a) —图11(c) 描绘了二维系统中质心动量$ { Q}=0 $ 时, 分子态和吸引极化子态的能量在$ k_{\uparrow {\rm F}} $ 等于不同值时随$ \delta $ 的变化情况. 从图中可以看出, 与三维体系性质相同, 当$\delta $ 为较小值时, 系统基态为吸引极化子态, 而当$ \delta $ 值较大时, 分子态成为系统的基态, 这中间存在吸引极化子态到分子态的转变. 图11(d) 描绘了转变点$ \delta_{\rm c} $ 随$ k_{\uparrow {\rm F}} $ 的变化情况. 从图中可以看出, 转变点$ \delta_{\rm c} $ 会随着费米能级$ k_{\uparrow {\rm F}} $ 的变大而单调上升, 这说明二维系统中$ | g\uparrow \rangle $ 态上的费米面同样有提高闭通道能量$ \delta_g $ 的作用. 但与三维系统不同的是, 即使在$ k_{\uparrow {\rm F}} $ 较小的情况下, 转变点$ \delta_{\rm c} $ 的变化也会显著偏离费米能$ E_{\uparrow {\rm F}} $ . 这说明在二维时, 另一个费米面的存在不仅仅提供了一个能量偏置, 而且费米面附近的涨落会产生更加显著的多体效应.图 11 (a)-(c) 二维系统中, 质心动量为零,$ k_{\uparrow {\rm F}}=0 $ ((a)), $ k_{\uparrow {\rm F}}=1 $ ((b)), $ k_{\uparrow {\rm F}}=2 $ ((c))时, 分子态和吸引极化子态的本征能量随$ \delta $ 的变化; (d) 吸引极化子态到分子态的转变点随$ k_{\uparrow {\rm F}} $ 的变化, 其中黑色实线为计算得到的转变点, 红色虚线为费米能级$ E_{\uparrow {\rm F}}=k_{\uparrow {\rm F}}^2 $ Figure11. The eigen energies of molecule and attractive polaron states vary with $ \delta $ when $ { Q}=0 $ in a two-dimensional system and (a) $ k_{\uparrow {\rm F}}=0 $ , (b) $ k_{\uparrow {\rm F}}=1 $ , (c) $ k_{\uparrow {\rm F}}=2 $ ; (d) the transition point $ \delta_{\rm c} $ varies with $ k_{\uparrow {\rm F}} $ , where the black solid line represents $ \delta_{\rm c} $ and the red dashed line is the Fermi level $ E_{\uparrow {\rm F}}=k_{\uparrow {\rm F}}^2 $ .图12 描绘了二维系统中, 在$ k_{\uparrow {\rm F}} $ 等于不同值时排斥极化子态的衰变率$ \varGamma $ 随$ \delta $ 的变化情况. 从图中可以看出, 与三维系统情况类似, 由于存在开通道与闭通道间的竞争, 衰变率$ \varGamma $ 随$ \delta $ 的变化是非单调的, 且当两个通道简并时, 衰变率处于最低点处. 同时可以发现, 在二维系统中引入另一个费米面, 同样会引起能量的移动.图 12 二维系统中$ k_{\uparrow {\rm F}} $ 等于不同值时排斥极化子态的衰变率$ \varGamma $ 随$ \delta $ 的变化情况Figure12. The decay rates of the repulsive polaron state in a a two-dimentional system vary with $ \delta $ for different values of $ k_{\uparrow {\rm F}} $ .9.结 论 本文介绍了利用试探波函数的方法来研究由类碱土金属原子173 Yb组成的费米气体在轨道Feshbach共振附近的杂质态问题.$ { Q}=0 $ 时, 分子态的本征能量和波函数分布随失谐$ \delta $ 的变化. 研究发现, 分子态的本征能量存在两个解: $ |E_{\rm M}-E_{\rm {th}}| \gg E_{\downarrow {\rm F}} $ 和$ |E_{\rm M}-E_{\rm {th}}| \sim E_{\downarrow {\rm F}} $ , 其中前者为深束缚态且束缚能约为常数, 所以只讨论后者的情况. 在分子态的波函数分布中, 发现当$ \delta $ 为较大正值时, 开通道相对于闭通道有很大失谐, 此时波函数中开通道的部分可以被忽略, 而随着$ \delta $ 不断减小, 开通道将变为波函数中的主要组成. 然后介绍了质心动量$ Q $ 略微背离零值时分子态的有效质量, 发现在共振的BCS一侧, 有效质量存在发散行为.$ { Q}=0 $ 时, 系统中吸引极化子态的本征能量和波函数分布随失谐$ \delta $ 的变化. 从计算结果中可以发现, 吸引极化子态同样存在深浅两个分支. 其中浅吸引极化子态的波函数分布在BCS极限下主要由裸粒子态部分构成; 在BEC极限下主要由闭通道部分构成; 而在共振点处, 开通道与闭通道占比相当. 同时, 质心动量$ Q $ 略微背离零值时, 吸引极化子态的有效质量会在BEC一侧存在发散.$ \delta $ 的变化, 系统中存在由吸引极化子态到分子态的转变. 当$ \delta $ 小于转变点$ \delta_{\rm c} $ 时, 系统的基态为吸引极化子态, 而当$ \delta $ 大于$ \delta_{\rm c} $ 时, 系统基态变为分子态. 同时研究发现, $ \delta_{\rm c} $ 会随着系统粒子数密度的增大而变大. 这一普适性的缺失说明OFR是一个窄共振.$ \delta $ 的变化, 排斥极化子态会与其他态发生耦合. 在排斥极化子态的准粒子残余和有效质量中均存在明显的非解析行为, 这可以定性解释为由类似于共振散射行为引起. 同时, 研究发现当开通道与闭通道近简并时, 排斥极化子态的衰变率最小.$ | g\uparrow \rangle $ 态中另外引入一个费米面, 此时体系变为双费米面情况. 通过对比单费米面和双费米面两种情况中分子态、吸引极化子态和排斥极化子态的各项性质可以发现, 在闭通道中引入费米海等效于对闭通道基态的移动, 这使分子态到吸引极化子态的转变点和其他特征量都向着$ \delta $ 较大的方向移动. 闭通道中由于自旋交换相互作用引起的费米面附近的涨落, 会使排斥极化子态中类共振行为及其他非解析结构变得模糊并最终消失.173 Yb费米气体中的杂质态问题. 通过对比发现, 二维体系中分子态和极化子态的性质与三维系统类似, 例如存在吸引极化子态到分子态的转变, 排斥极化子态的衰变率在两个通道简并时存在最小值点, 以及引入另一个费米面会引起能量移动等. 但与三维系统不同的是, 二维系统中费米面附近的涨落较大, 会产生更为显著的多体效应. 













































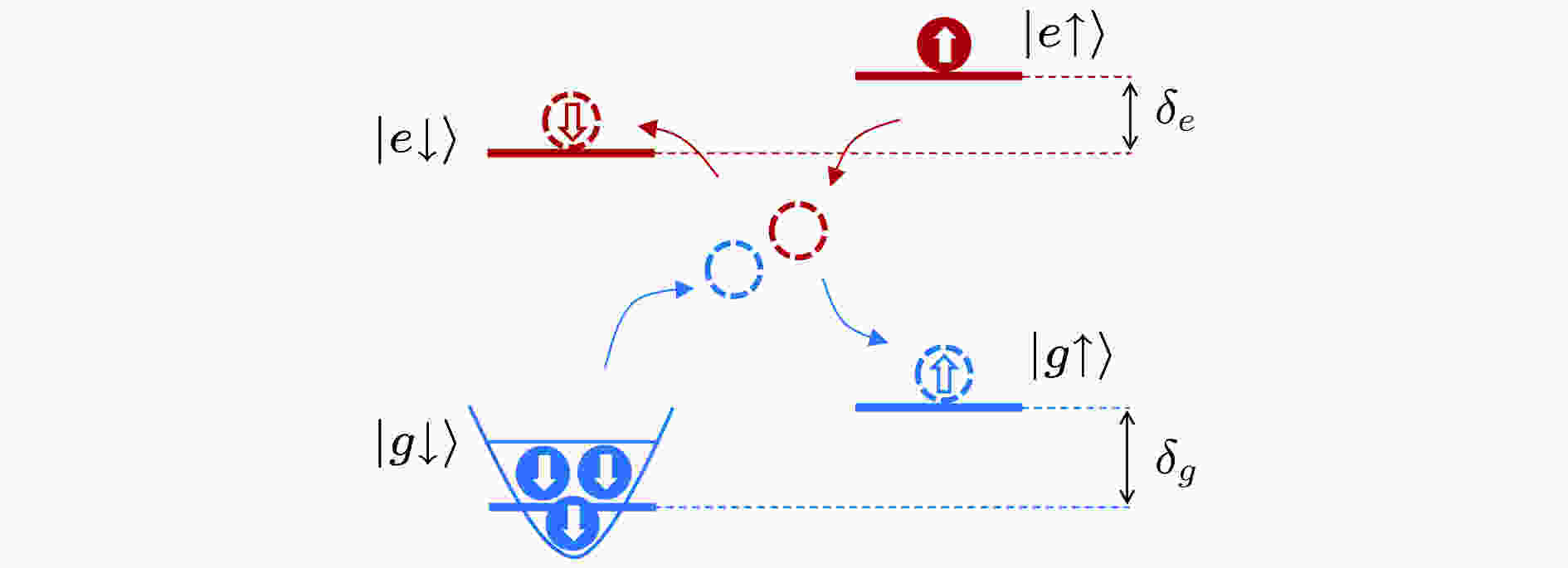 图 1 类碱土金属原子中的OFR能级图. 杂质原子处于
图 1 类碱土金属原子中的OFR能级图. 杂质原子处于
































































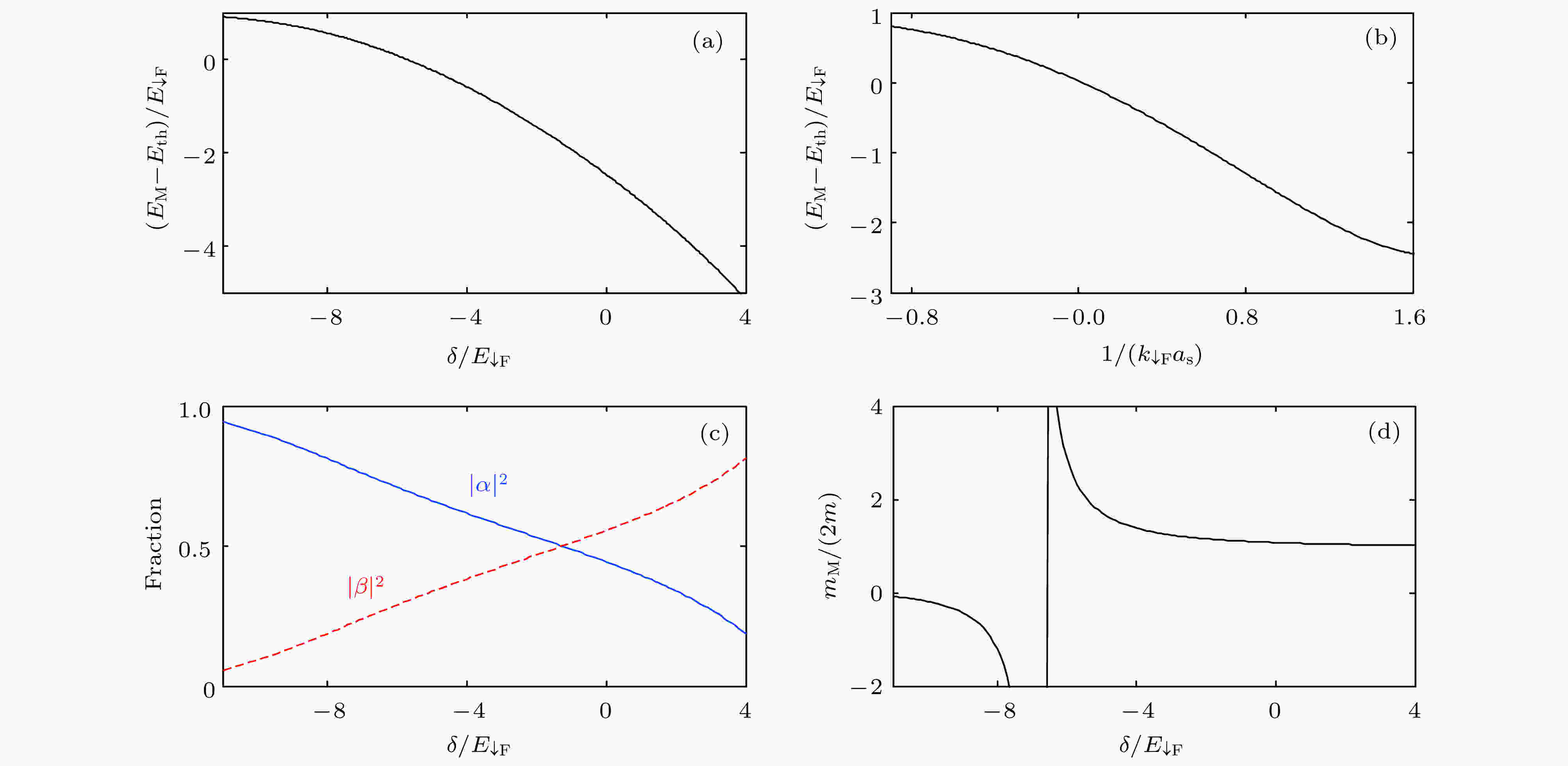 图 2 (a), (b) 分子态的能量随
图 2 (a), (b) 分子态的能量随
































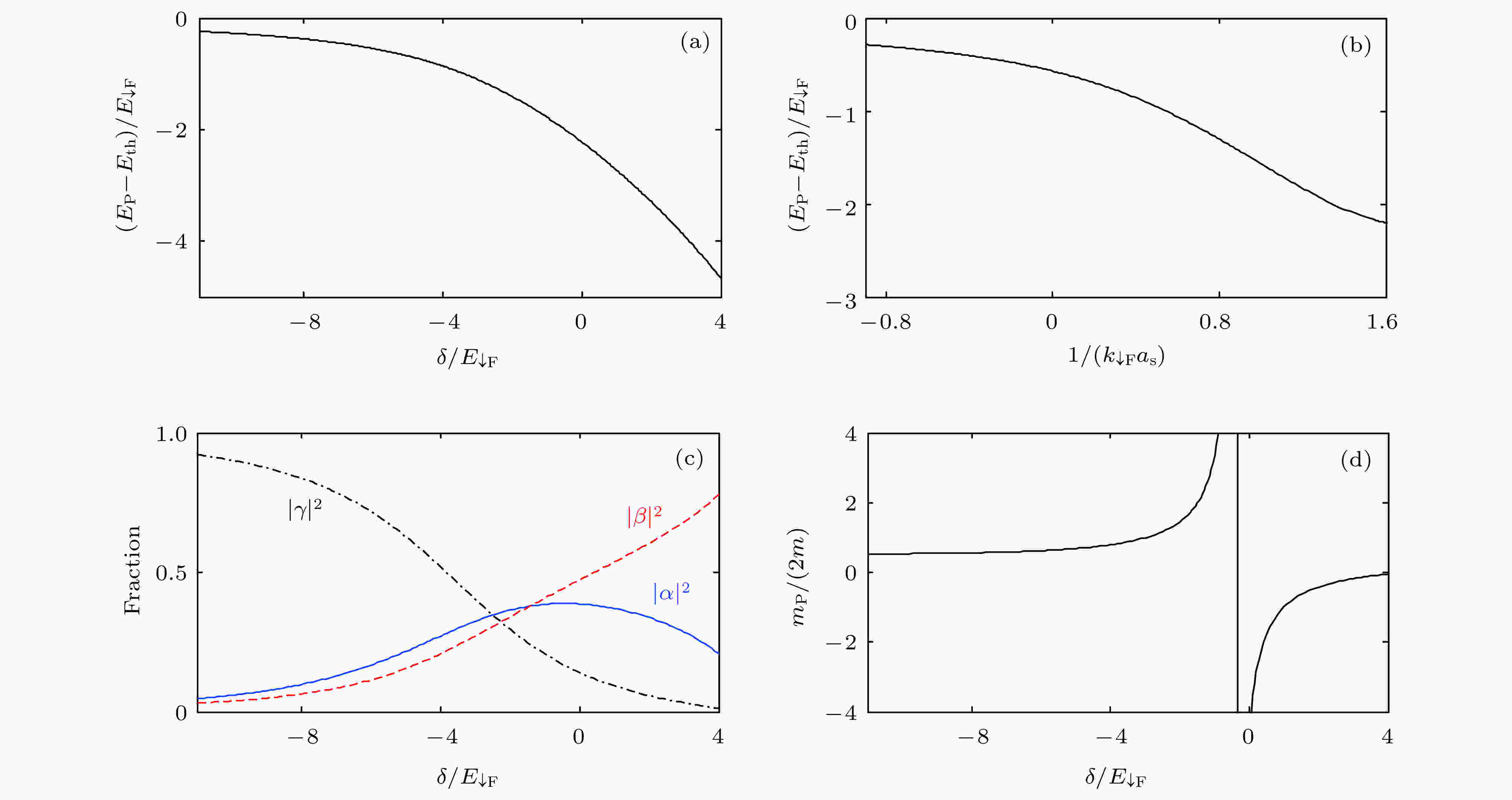 图 3 (a), (b) 吸引极化子态的能量随
图 3 (a), (b) 吸引极化子态的能量随


















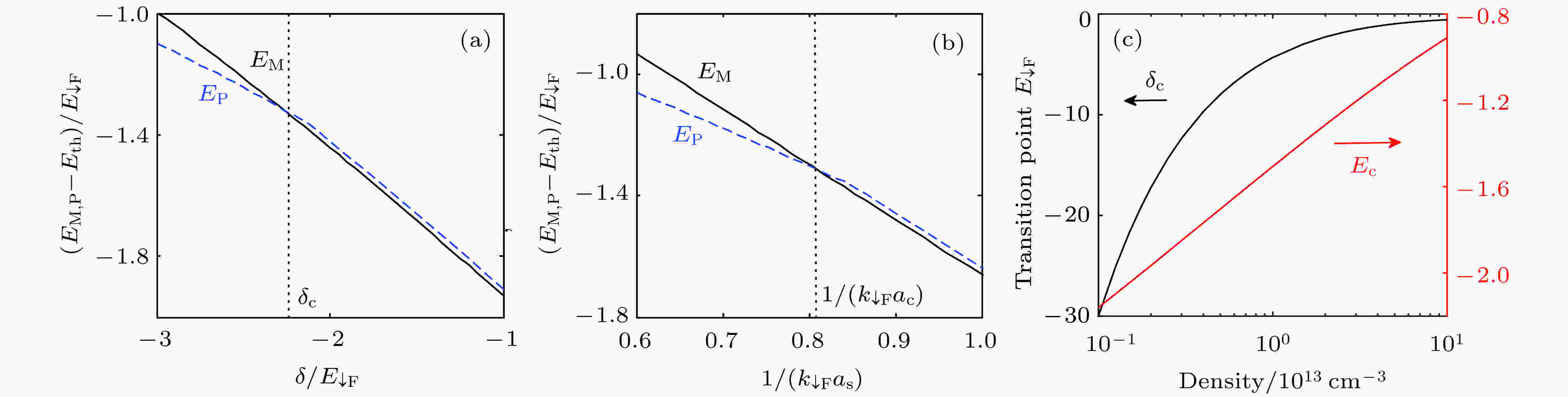 图 4 (a), (b) 分子态(黑色实线)和吸引极化子态(蓝色虚线)的本征能量随
图 4 (a), (b) 分子态(黑色实线)和吸引极化子态(蓝色虚线)的本征能量随




























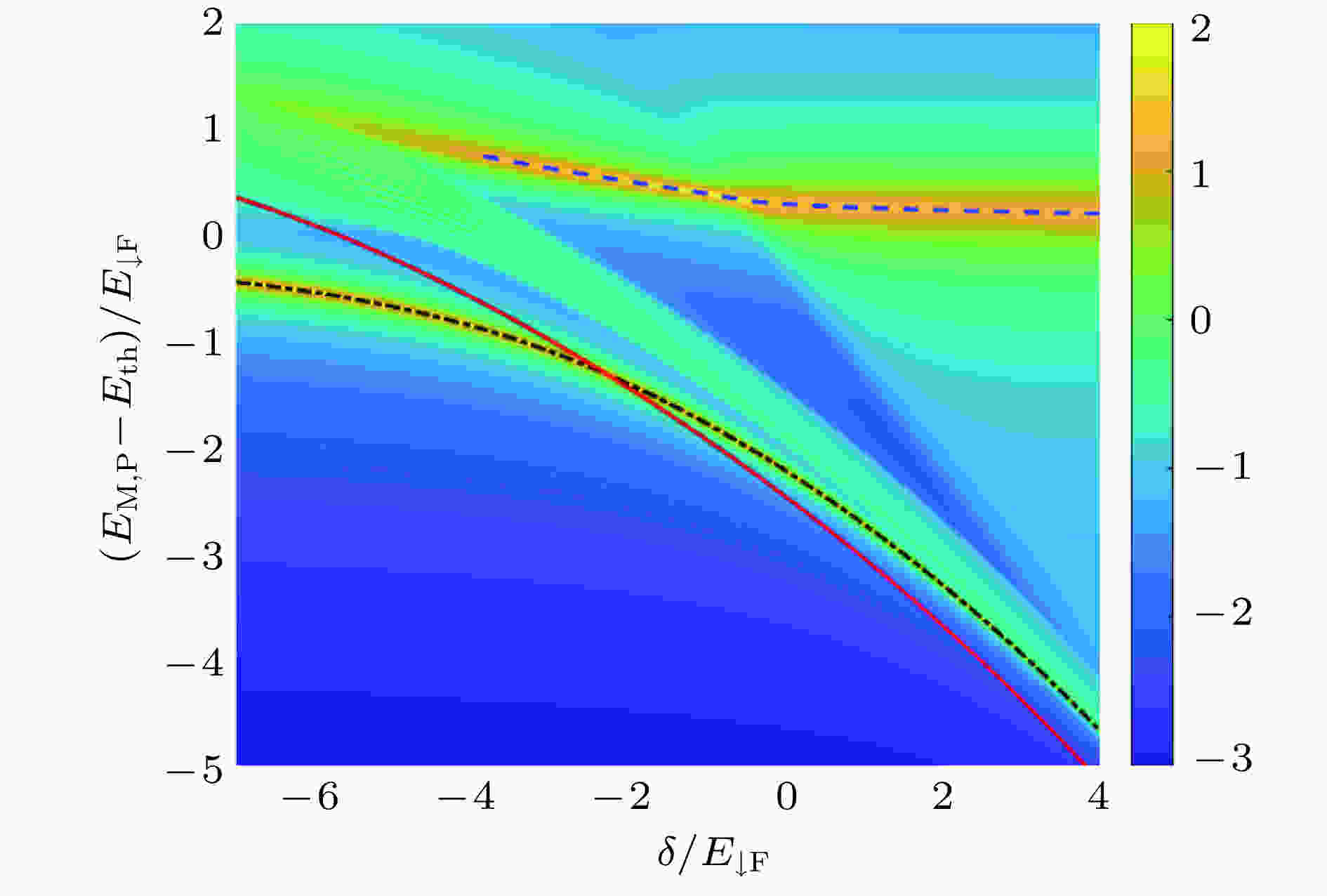 图 5 极化子态的谱函数
图 5 极化子态的谱函数











































































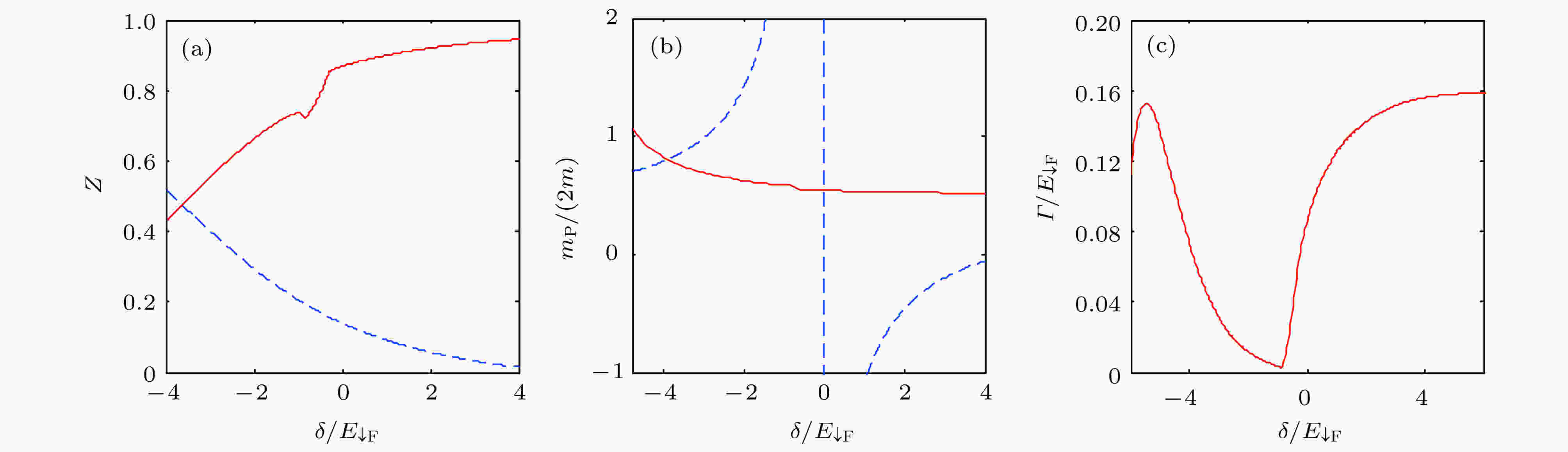 图 6 (a), (b) 极化子态的准粒子残余和有效质量随
图 6 (a), (b) 极化子态的准粒子残余和有效质量随












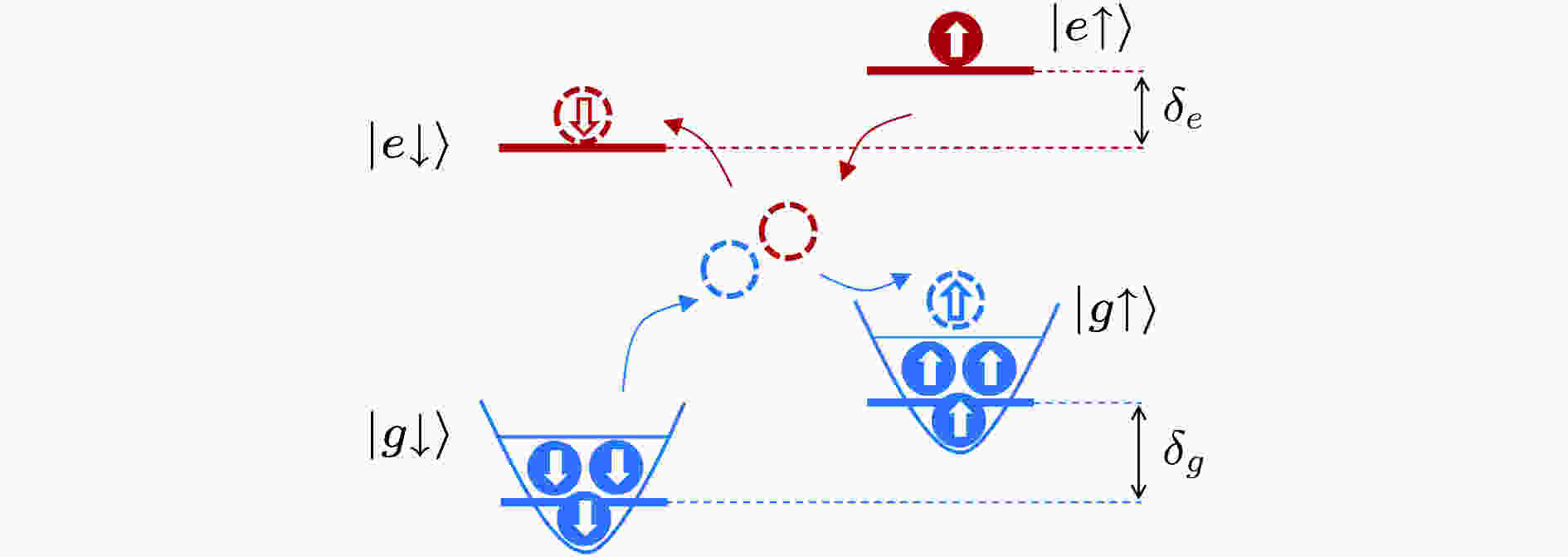 图 7 双费米面情况下, 类碱土金属原子的OFR能级图. 杂质原子处于
图 7 双费米面情况下, 类碱土金属原子的OFR能级图. 杂质原子处于







































































































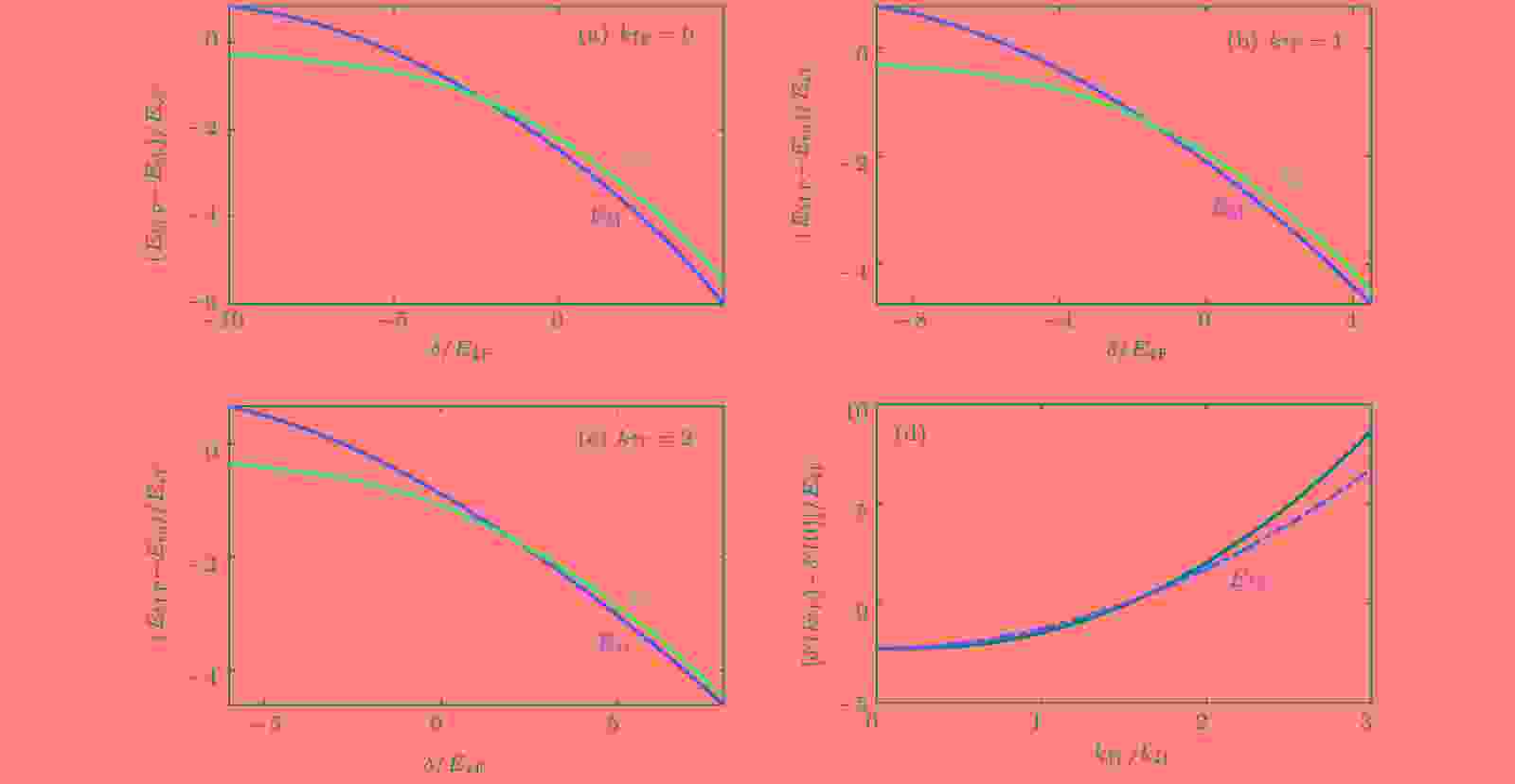 图 8 质心动量为零,
图 8 质心动量为零, 























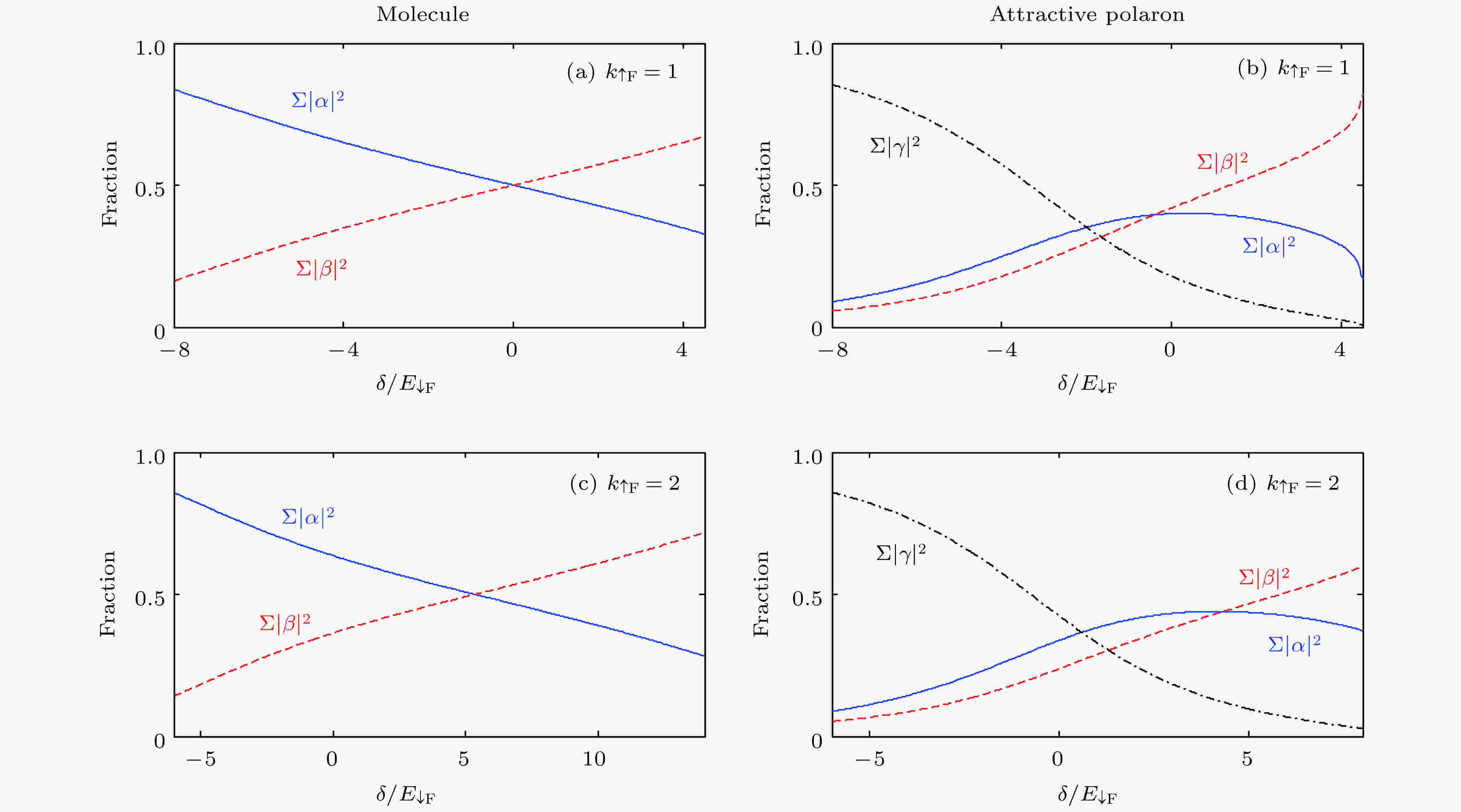 图 9 (a), (c) 分子态的波函数分布情况; (b), (d) 吸引极化子态的波函数分布, 此时质心动量为零. (a)和(b)中,
图 9 (a), (c) 分子态的波函数分布情况; (b), (d) 吸引极化子态的波函数分布, 此时质心动量为零. (a)和(b)中, 








































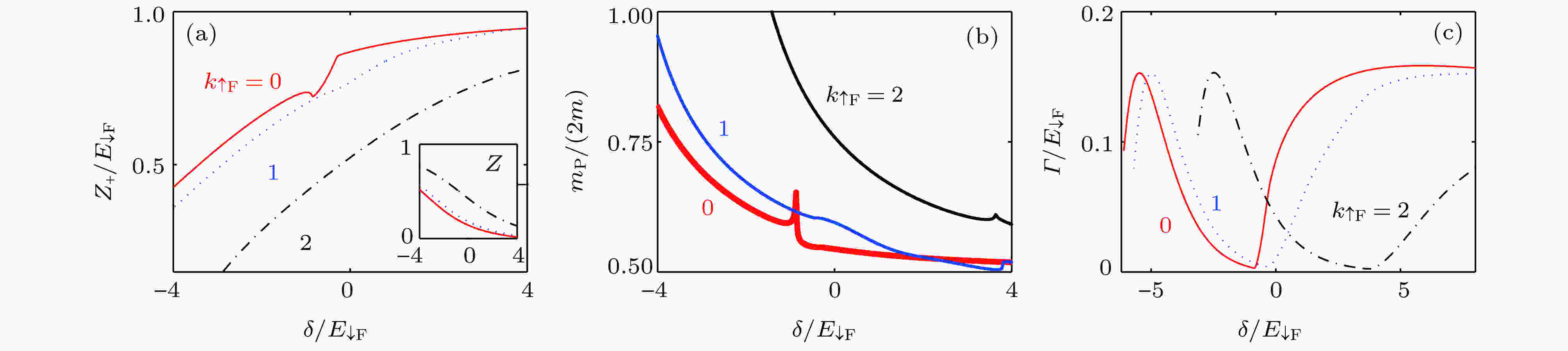 图 10 (a), (b) 在
图 10 (a), (b) 在




































































 图 11 (a)-(c) 二维系统中, 质心动量为零,
图 11 (a)-(c) 二维系统中, 质心动量为零,

























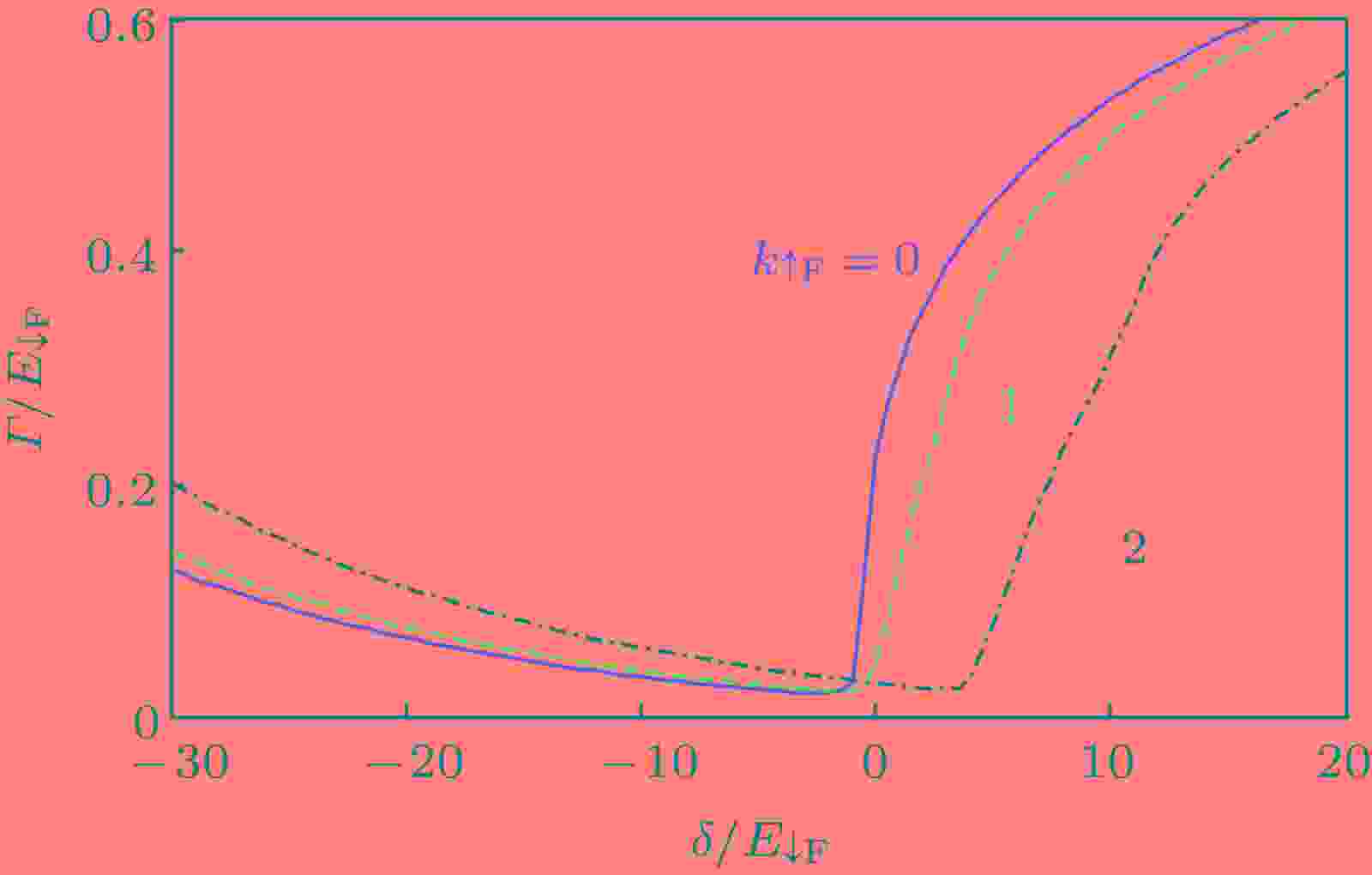 图 12 二维系统中
图 12 二维系统中










































