摘要: 随着纳米科技以及半导体技术的迅猛发展, 光力诱导透明、快慢光和光存储以及其他在光力系统中发现的量子光学和非线性光学效应成为人们目前研究的热点. 本文将薄膜腔光力系统同被束缚在腔中的二能级冷原子系综相耦合, 通过直接在薄膜振子上引入弱辅助驱动场来研究该原子辅助光力系统中原子和相位对量子相干性质及其快慢光的调控. 经过分析发现, 通过改变辅助驱动场的强度可直接实现对光力诱导透明窗口深度的调控, 通过改变辅助场与探测场之间的相位差, 可实现输出的探测场在“吸收”、“透明”和“增益”之间相互转换, 进而对弱探测场进行动态调控实现光开关. 与此同时, 还发现系统的群延迟时间随相位差的改变呈周期性变化. 通过调节相位差及原子数, 不但可以改变群延迟时间, 还可实现快慢光之间的相互转换.
关键词: 光力学 /
光力诱导透明 /
快慢光 English Abstract Quantum control of fast/slow light in atom-assisted optomechanical cavity Gu Kai-Hui 1,2 ,Yan Dong 3 ,Zhang Meng-Long 3 ,Yin Jing-Zhi 1 ,Fu Chang-Bao 4 1.College of Electronic Science and Engineering, Jilin University, Changchun 130012, China Fund Project: Project supported by the “Spring Sunshine” Plan Foundation of Ministry of Education of China (Grant No. Z2017030) and the Natural Science Foundation of Jilin Province, China (Grant Nos. 2016286, GH16102).Received Date: 25 July 2018Accepted Date: 23 October 2018Available Online: 01 March 2019Published Online: 05 March 2019Abstract: In recent years, due to the rapid development of nano science and advanced semiconductor technology, one is able to observe more significant quantum optomechanical effects as optomechanical system turns smaller in size. Optomechanically induced transparency, fast and slow light, optical storage as well as other quantum optical and nonlinear optical effects have become the focus of research. On the other hand, the optomechanical systems coupled to other small subsystems (such as atoms, quantum dots, single electron transistors, etc.) also attract great attention in research. This is because the coupling system has not only provided more degrees of freedom for quantum manipulation, but also opened up more channels for classical and quantum information transfer. In this paper we study the optomechanically induced transparency and fast/slow light phase control in atom-assisted optomechanical cavity. Unlike the traditional systems, in this model the mechanical resonator is directly driven by a weak auxiliary driving field. We therefore find that with the change of amplitude ratio and phase difference between the auxiliary driving field and the probe field, the absorption and dispersion properties of the whole system and the group delay time vary accordingly. In the absence of auxiliary field, we observe the spectral features of the hybrid electromagnetically induced transparency and optomechanically induced transparency (OMIT) in an atom-cavity-oscillator tripartite optomechanical system. When there exists no phase difference between the auxiliary field and the probe field, we find that the membrane resonance absorption is enhanced with the increase of auxiliary field strength at resonance, causing the the optomechanically induced transparency to be suppressed, and therefore we can modify the amplitude of auxiliary field to control the depth of the OMIT window. When keeping amplitude ratio between the auxiliary field and the probe field unchanged, the modification of the phase difference between the auxiliary field and the probe field directly affects the we can not only realize the manipulation of OMIT window depth, but also control the transformation of tunable optical switch among "absorption", "transparent" and "gain" of the system. Therefore, through changing the phase of auxiliary field and probe field, we can not only realize the manipulation of OMIT window depth, but also control the transformation of tunable optical switch among "absorption" , "transparent" and "gain". In the meantime, we find that the system’s group delay time varies periodically with the change of phase difference. It is worth noting that by adjusting the phase difference and the atomic number, we can not only change the magnitude of the group delay, but also realize the conversion between slow light and fast light effect.Keywords: optomechanics /optomechanically induced transparency /fast and slow light 全文HTML --> --> --> 1.引 言 随着纳米技术和半导体工艺的迅猛发展, 人们越来越关注光力学这个新领域, 它为人们在高精密测量、量子信息处理以及量子基本原理的验证等方面打开了一扇大门. 近年来, 光力系统实现了一些经典的量子光学现象, 例如Agarwal和Huang[1 ] 在Fabry-Perot (FP) 腔光力系统中发现了类似原子的电磁诱导透明现象(electromagnetically induced transparency, EIT), 即光力诱导透明现象(optomechanically induced transparency, OMIT), 同原子中的电磁诱导透明一样, 光力诱导透明效应不仅促进了量子光学的发展, 同时也在快慢光[2 -7 ] 、光存储[8 -11 ] 和光开关[12 ,13 ] 等量子信息处理方面有着广泛的应用. 此外, 在光力系统中人们还实现了机械振子的基态冷却[14 ,15 ] , 在宏观物体上观察到相干态[16 ] 、压缩态[17 ,18 ] 和纠缠态[19 -23 ] 等量子现象. 然而, 目前大部分典型腔光力学系统仍然只涉及两个自由度之间的耦合, 超过两个自由度耦合的多元光力学系统较少受到研究者关注.[24 ] 、声子诱导透明[25 ] 、相干完美吸收及相干完美透射[13 ,26 ,27 ] 等, 这些研究成果在量子信息处理方面有着潜在的应用价值, 因此成为当前光力学的一个研究趋势. 同时在原子辅助光力系统中, Chang等[28 ] 、Fu等[29 ] 和韩明等[30 ] 发现了电磁诱导透明的多稳现象, Yan等[31 ] 则在与FP腔耦合的具有偶极-偶极相互作用的里德伯超级原子系综中发现了双稳现象, 另外还观察到了EPR (Einstein-Podolsky-Rosen)态的产生[32 ] 以及基态冷却[33 -35 ] 等量子现象. 但是在原子辅助光力系统中通过相位调控快慢光的研究则较少见. 很明显这种杂化光力学系统中, 原子-腔-薄膜振子三模耦合, 原子作为辅助物质扮演着一个非常重要的角色, 它同光力系统的相互作用通过腔模联系起来, 控制原子可改变光力学腔中的腔场, 进而影响整个杂化光力系统的量子相干性, 从而实现对快慢光的量子调控, 因此原子辅助光力系统比常见的光力系统表现出了更多的量子操控自由度.2.物理模型与计算 考虑如图1 所示的原子辅助光力系统, 它由线性耦合的薄膜腔光力系统和被束缚在其中频率为${\omega _{\rm{a}}}$ 的$N$ 个全同二能级87 Rb超冷原子系综构成, 其中二能级的量子态$\left| 0 \right\rangle $ 和$\left| 1 \right\rangle $ 分别对应87 Rb原子的$D1$ 线的量子态$\left| {5{S_{1/2}}} \right\rangle $ 和$\left| {5{P_{1/2}}} \right\rangle $ . 选择的薄膜振子的本征频率为${\omega _{\rm{m}}}$ , 弛豫速率为${\gamma _{\rm{m}}}$ , 其力学品质因子为$Q=\omega_{\rm{m}} /\gamma_{\rm{m}}$ . 如图1 , 整个系统由外加的一个频率为${\omega _{\rm{d}}}$ 的强驱动场和一个频率为${\omega _{\rm{p}}}$ 的弱探测场驱动, 而薄膜振子则是直接由弱辅助驱动场${\varepsilon _{\rm{f}}}$ 驱动, 这三个外加相干场之间的频率假设满足${\omega _{\rm{p}}} - {\omega _{\rm{d}}} = {\omega _{\rm{f}}}$ 关系.图 1 由单模FP腔以及束缚在其中的N 个全同二能级87 Rb冷原子系综和中间由弱辅助驱动场${\varepsilon _{\rm{f}}}$ 驱动的振动频率为${\omega _{\rm{m}}}$ 的薄膜振子构成的光力学系统, 该系统的探测场和驱动场分别为${\varepsilon _{\rm{p}}}$ 和${\varepsilon _{\rm{d}}}$ Figure1. Schematic diagram of an optomechanical cavity containing N identical two-level cold 87 Rb atoms with two fixed-end mirrors of equal reflectivity, which is driven by a strong coupling field ${\varepsilon _{\rm{d}}}$ , a weak auxiliary drive field ${\varepsilon _{\rm{f}}}$ and probed by a weak field ${\varepsilon _{\rm{p}}}$ .${H_0}$ 为系统的自由哈密顿量${\omega _{\rm{c}}}$ 为单模腔场的本征频率, $c$ 和${c^\dagger }$ 分别表示腔中光子的湮灭和产生算符, 它们之间满足对易关系$[ c, {c^\dagger }] = 1$ . ${\omega _{\rm{a}}}$ 表示原子在能级$\left| 0 \right\rangle $ 和$\left| 1 \right\rangle $ 之间的跃迁频率, 在弱激发及原子数$N \gg 1$ 条件下, $a = {1 / {\sqrt N }}\Sigma _{i = 1}^N|0{\rangle _{ii}}\langle 1|$ 表示集体跃迁算符[28 ,29 ] , 满足对易关系$[a, {a^\dagger }] = 1$ . 由于中间的薄膜振子在其平衡位置做微小振动, 所以可用量子谐振子模型来描述其量子性质, 写成声子产生算符($b^\dagger$ )和湮灭算符($b$ )的形式, 满足对易关系$[b,b^\dagger]=1$ . 第二项${H_{\rm{i}}}$ 为原子-腔和腔-薄膜振子相互作用哈密顿量${g_{{\rm{ac}}}} = \mu \sqrt {{\omega _{\rm{c}}}/(2\hbar V{\varepsilon _0})} $ 表示腔场与原子之间相互作用的耦合系数, $\mu $ 表示原子跃迁的电偶极矩, $V$ 表示腔的体积, ${\varepsilon _0}$ 表示真空介电常数. 光力耦合系数用${g_{{\rm{mc}}}}{{ = }}{{{\omega _{\rm{c}}}} / l}\sqrt {{\hbar / {(2m{\omega _{\rm{m}}})}}} $ 表示. (1 )式中的第三项${H_{\rm{d}}}$ 为三个外加输入场与腔场和薄膜振子相互作用哈密顿量${\varepsilon _{\rm{d}}} = \sqrt {2\kappa {P_{\rm{d}}}/(\hbar {\omega _{\rm{d}}})} $ , $\left| {{\varepsilon _{\rm{p}}}} \right| = \sqrt {2\kappa {P_{\rm{p}}}/(\hbar {\omega _{\rm{p}}})} $ 和$\left| {{\varepsilon _{\rm{f}}}} \right| = \sqrt {2\kappa {P_{\rm{f}}}/(\hbar {\omega _{\rm{f}}})} $ 分别代表驱动场、探测场和辅助驱动场的输入振幅, ${P_{\rm{d}}}$ , ${P_{\rm{p}}}$ 和${P_{\rm{f}}}$ 分别代表驱动场、探测场和辅助驱动场的输入功率.$\delta = {\omega _{\rm{p}}} - {\omega _{\rm{d}}} = {\omega _{\rm{f}}}$ 是探测场与驱动场之间的失谐, ${\gamma _{\rm{a}}}$ 为原子的弛豫速率, $\gamma_{\rm{m}}$ 为薄膜振子的弛豫速率, $\kappa $ 为腔场的弛豫速率. ${a_{{\rm{in}}}}$ 为作用在原子上的平均值为零的量子噪声, ${b_{{\rm{in}}}}$ 为作用在可移动薄膜振子上平均值为零的热噪声, ${c _{\rm{in}}}$ 为由输入场引入的平均值为零的量子真空噪声. 即$\left\langle {{c^\dagger }c} \right\rangle = \left\langle {{c^\dagger }} \right\rangle \left\langle c \right\rangle $ , $\left\langle {{b^\dagger }c} \right\rangle = \left\langle {{b^\dagger }} \right\rangle $ $\left\langle c \right\rangle$ 和$\left\langle {bc} \right\rangle = \left\langle b \right\rangle \left\langle c \right\rangle $ , 则在稳态情况下, 算符在平均值附近涨落的关联与相应算符平均值乘积之比可忽略.${\varDelta _{\rm{a}}} = {\omega _{\rm{a}}} - {\omega _{\rm{d}}}$ 表示原子与驱动场之间的失谐, ${\varDelta _0} = {\omega _c} - {\omega _{\rm{d}}}$ 表示腔场与驱动场之间的失谐. 当不考虑含时间因子的探测场和辅助驱动场时, 令(7a )—(7c )式左侧为零, 可以得出系统相关算符的稳态平均值:$\left| {{\varepsilon _{\rm{p}}}} \right| \ll \left| {{\varepsilon _{\rm{d}}}} \right|, \left| {{\varepsilon _{\rm{f}}}} \right| \ll \left| {{\varepsilon _{\rm{d}}}} \right|$ 情况下, 把系统算符写成各自平均值及其微小涨落的和:9 )式代入(7 )式中, 并且只保留线性项, 忽略非线性项$\delta {c^\dagger }\delta c$ , $\delta b\delta c$ , $\delta {b^\dagger }\delta c$ 和平均值为零的量子热噪声项, 可得涨落算符平均值满足的方程为:10 )式, 可以假设其解具有如下形式:$s = a, b, c$ . 把(11 )式代入(10 )式, 比较等式两边含${\varepsilon _{\rm{p}}}{{\rm{e}}^{ - {\rm{i}}\delta t}}$ 与$\varepsilon _{\rm{p}}^{\rm{*}}{{\rm{e}}^{ - {\rm{i}}\delta t}}$ 项的系数可得:$Y$ 为辅助驱动场同探测场振幅大小之比, $\varPhi $ 为它们之间的相位差. 由(12b )式$\delta {c_ + }$ 的表达式可以看出, 第一项主要体现原子对光力学系统的影响, 第二项主要体现辅助驱动场对原子辅助光力学系统的影响.${\varepsilon _{\rm{T}}}$ 和反射场${\varepsilon _{\rm{R}}}$ 的表达式也写成与(11 )式相同的形式,14a )式和(14b )式中的${\varepsilon _{\rm{T}}}$ 和${\varepsilon _{\rm{R}}}$ 表述的是输出场对探测场${\omega _{\rm{p}}}$ 的响应, 而${\varepsilon _{{\rm{T}} - }}$ 和${\varepsilon _{{\rm{R}} - }}$ 描述的则是输出场对非线性四波混频过程产生的新频率$2{\omega _{\rm{d}}} - {\omega _{\rm{p}}}$ 的响应.[36 ] ${\varepsilon _{\rm{T}}} = 2\kappa \delta {c_ + }$ 和${\varepsilon _{\rm{R}}} = 2\kappa {\rm{\delta}} {c_ + } - 1$ 是因为本文只关心输出场对探测场的响应. 这里${\varepsilon _{\rm{T}}}$ 的实部和虚部分别描述透射的探测场的吸收和色散性质, ${\varepsilon _{\rm{R}}}$ 的实部和虚部则分别描述反射的探测场的吸收和色散性质.17 )式可得到群延迟时间[7 ] 为:3.讨 论 以下主要讨论原子辅助光力学腔中相位对OMIT及快慢光现象的影响. 本文采用的是实验上真实可行的实验参数[29 ,33 ] , 并满足劳斯-胡尔维茨稳态判定准则[36 ] , 确保系统稳态的稳定性. 各参数具体值为: $l \!=\! 1$ mm, $m \!=\! 10$ ng, ${\omega _{\rm{m}}}/(2{\text{π}}) \!=\! 10$ MHz, ${\gamma _{\rm{m}}}/(2{\text{π}}) = 100$ Hz, $\kappa = {\omega _{\rm{m}}}/10$ , ${\varDelta _{\rm{a}}} = {\omega _{\rm{m}}}$ , ${P_{\rm{d}}} = 1$ mW, $\lambda \! = \! 2{\text{π}}c/{\omega _{\rm{d}}} \! = \! 794.98$ nm, ${\gamma _{\rm{a}}}/2{\text{π}} \! = \! 2.875$ MHz, ${g_{{\rm{ac}}}}\sqrt N \!= $ $3 \times 2{\text{π}}$ MHz.图2 所示为当考虑外加辅助场与探测场同相位时($\varPhi = 0$ ), 振幅比$Y$ 对杂化系统吸收和色散性质的影响. 如图2(a) 所示, 在没有辅助驱动场的情况下($Y = 0$ 或${\varepsilon _{\rm{f}}} = 0$ 时), 在共振$\delta = {\omega _{\rm{m}}}$ 处观察到了由原子-腔-薄膜振子三模耦合形成的杂化的EIT和OMIT. 如图2(b) 所示, 当辅助场与机械振子耦合时($Y = 0.05$ ), 在共振$\delta = {\omega _{\rm{m}}}$ 处OMIT窗口的深度变浅, 这是因为外加辅助场对薄膜振子直接激发, 而辅助场的频率与薄膜振子频率共振${\omega _{\rm{f}}} = {\omega _{\rm{m}}} = \delta $ , 使得薄膜振子在$\delta = {\omega _{\rm m}}$ 处发生共振吸收, 部分抵消了OMIT现象, 从而使得OMIT窗口深度变浅. 在图2(c) 中发现, 随着$Y$ 的增加, OMIT窗口逐渐消失并形成了吸收峰, 这是因为随着辅助场强度的增加, 薄膜振子的共振吸收也随之增强, 从而导致光力效应被完全抵消掉, 产生吸收峰. 由以上的分析可知, 在辅助场与探测场同相位时, 改变辅助场同探测场振幅比$Y$ 可直接影响系统光力耦合效果, 从而实现对OMIT窗口深度的调控.图 2 $\operatorname{Re} ({\varepsilon _{\rm{T}}})$ (黑色实线)和${\rm{Im}}({\varepsilon _{\rm{T}}})$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线 (a) $Y = 0$ ; $\varPhi = 0$ ; (b) $Y = 0.05$ ; $\varPhi = 0$ ; (c) $Y = 0.2$ ; $\varPhi = 0$ ; 其他参数值见文中第4部分Figure2. The real (black line) and the imaginary (red dotted line) parts of ${\varepsilon _{\rm{T}}}$ as a function of $\delta /{\omega _{\rm{m}}}$ with (a) $Y = 0$ ; $\varPhi = 0$ ; (b) $Y = 0.05$ ; $\varPhi = 0$ ; (c) $Y = 0.2$ ; $\varPhi = 0$ . Relevant parameters are the same as those in Sec. 4.图3 所示为外加辅助场与探测场振幅比$Y = 0.2$ 时, 相位差$\varPhi $ 对系统吸收和色散性质的影响. 如图3(a) 所示, 辅助场与探测场同相位, 即$\varPhi = 0$ 时, 在共振$\delta = {\omega _{\rm{m}}}$ 处OMIT消失形成了吸收峰. 但是随着相位差增加到$\varPhi = {\text{π}}/4$ (图3(b) ), 却发现在共振处出现了吸收为零的现象. 随着相位差进一步增加到$\varPhi = {\text{π}}/2$ 和$\varPhi = 3{\text{π}}/4$ 时(如图3(c) 和图3(d) 所示), 在共振$\delta = {\omega _{\rm{m}}}$ 处则出现了吸收增益现象. 随着相位差$\varPhi $ 的再增加(如图3(e) —图3(h) 所示), 也发现了由“增益”到“透明”再到“吸收”的过程, 图3(e) —图3(h) 的趋势与图3(a) —图3(d) 的趋势相同, 呈现一定的周期性变化. 实际上, 从(12a )式就可以看出, $\varPhi $ 的取值直接影响$\delta b_+$ 的大小, 也就是说辅助场与探测场的相位差直接影响着系统的光力耦合效应, 使得通过调节相位可以实现输出探测场在“吸收”、“透明”和“增益”之间相互转换, 从而改变整个系统的吸收和色散性质.图 3 $Y = 0.2$ 时$\operatorname{Re} ({\varepsilon _{\rm{T}}})$ (黑色实线)和${\rm{Im}}({\varepsilon _{\rm{T}}})$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线 (a) $\varPhi = 0$ ; (b) $\varPhi = {\text{π}}/4$ ; (c) $\varPhi = {\text{π}}/2$ ; (d) $\varPhi = 3{\text{π}}/4$ ; (e) $\varPhi = {\text{π}}$ ; (f) $\varPhi = 5{\text{π}} /4$ ; (g) $\varPhi = 6{\text{π}}/4$ ; (h) $\varPhi = 7{\text{π}}/4$ ; 其他参数值见文中第4部分Figure3. The real (black line) and the imaginary (red dotted line) parts of ${\varepsilon _{\rm{T}}}$ as a function of $\delta /{\omega _{\rm{m}}}$ with $Y = 0.2$ : (a) $\varPhi = 0$ ; (b) $\varPhi = {\text{π}}/4$ ; (c) $\varPhi = {\text{π}}/2$ ; (d) $\varPhi = 3{\text{π}}/4$ ; (e) $\varPhi = {\text{π}} $ ; (f) $\varPhi = 5{\text{π}}/4$ ; (g) $\varPhi = 6{\text{π}}/4$ ; (h) $\varPhi = 7{\text{π}}/4$ . Other parameters are the same as those in Sec. 4.图4 所示为辅助驱动场存在时, 原子数$N$ 对系统吸收和色散性质的影响. 在图4(a) —图4(c) 中, 令振幅比$Y = 0.2$ , 相位差$\varPhi = {\text{π}}/4$ , 可观察到随着原子数$N$ 的增加, 系统的吸收增益也随之增大. 相反, 在图4(e) —图4(f) 中, 令$Y = 0.2$ , $\varPhi = 6{\text{π}}/4$ , 可以观察到随着原子数$N$ 的增加, 系统的吸收增益反而逐渐减小. 也就是说在不同的相位下, 原子对系统吸收和色散性质的影响不同. 由此可知, 除了可通过相位$\varPhi $ 来操控系统的“吸收”、“透明”和“增益”以外, 还可通过改变原子数$N$ 来调控整个系统的吸收和色散性质.图 4 $Y = 0.2$ 时$\operatorname{Re} ({\varepsilon _{\rm{T}}})$ (黑色实线)和${\rm{Im}}({\varepsilon _{\rm{T}}})$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线 (a) $\varPhi = {\text{π}}/4$ , $g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b) $\varPhi = {\text{π}}/4$ , $g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c) $\varPhi = {\text{π}}/4$ , $g\sqrt N = 9 \times 2{\text{π}}$ MHz; (d) $\varPhi = 6{\text{π}}/4$ , $g\sqrt N = 3 \times 2{\text{π}}$ MHz; (e) $\varPhi = 6{\text{π}}/4$ , $g\sqrt N = 6 \times 2{\text{π}}$ MHz; (f) $\varPhi = 6{\text{π}}/4$ , $g\sqrt N = 9 \times 2{\text{π}}$ MHz; 其他参数值见文中第4部分Figure4. The real (black line) and the imaginary (red dotted line) parts of ${\varepsilon _{\rm{T}}}$ as a function of $\delta /{\omega _{\rm m}}$ with $Y = 0.2$ : (a) $\varPhi = {\text{π}}/4$ , $g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b) $\varPhi = {\text{π}}/4$ , $g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c) $\varPhi = {\text{π}}/4$ , $g\sqrt N = 9 \times 2{\text{π}}$ MHz; (d) $\varPhi = 6{\text{π}}/4$ , $g\sqrt N = 3 \times 2{\text{π}}$ MHz; (e) $\varPhi = 6{\text{π}}/4$ , $g\sqrt N = 6 \times {{2{\text{π}} }}$ MHz; (f) $\varPhi = 6{\text{π}}/4$ , $g\sqrt N = 9 \times {{2{\text{π}} }}$ MHz. Other parameters are the same as those in Sec. 4.图5 所示为辅助驱动场与探测场相位差$\varPhi $ 对与色散性质紧密相关的群延迟时间的影响, 其中黑色实线对应透射的群延迟时间${\tau _{\rm{T}}}$ , 红色虚线对应反射的群延迟时间${\tau _{\rm{R}}}$ . 如图5(a) —图5(h) 所示, 透射群延迟时间${\tau _{\rm{T}}}$ 和反射群延迟时间${\tau _{\rm{R}}}$ 随着相位差$\varPhi $ 的增加, 出现了大于零及小于零的情况, 这意味着输出场包含着慢光和快光传播, 并伴有一定的周期性规律. 同时在$\varPhi = {\text{π}}/4$ 和$\varPhi = 5{\text{π}}/4$ 时还观察到了快慢光同时存在的现象. 从前面的分析可知, 相位差$\varPhi $ 的取值影响整个系统的吸收和色散性质, 从而直接影响群延迟时间${\tau _{\rm{T}}}$ 和${\tau _{\rm{R}}}$ 的取值. 因而, 通过调节相位差$\varPhi $ 可使原子辅助光力系统表现出慢光或快光效应, 并可实现快慢光之间的转换.图 5 ${\tau _{\rm{T}}}$ (黑色实线)和${\tau _{\rm{R}}}$ (红色虚线)随频率失谐$\delta /{\omega _{\rm{m}}}$ 的变化曲线: (a) $\varPhi = 0$ ; (b) $\varPhi = {\text{π}}/4$ ; (c) $\varPhi = {\text{π}}/2$ ; (d) $\varPhi = 3{\text{π}}/4$ ; (e) $\varPhi = {\text{π}}$ ; (f) $\varPhi = 5{\text{π}} /4$ ; (g) $\varPhi = 6{\text{π}}/4$ ; (h) $\varPhi = 7{{{\text{π}} }}/4$ ; 其他参数取值同图3 Figure5. The ${\tau _{\rm{T}}}$ (black line) and the ${\tau _{\rm{R}}}$ (red dotted line) as a function of $\delta /{\omega _{\rm{m}}}$ with (a) $\varPhi = 0$ ; (b) $\varPhi = {\text{π}}/4$ ; (c) $\varPhi = {\text{π}}/2$ ; (d) $\varPhi = 3{\text{π}}/4$ ; (e) $\varPhi = {\text{π}}$ ; (f) $\varPhi = 5{\text{π}}/4$ ; (g) $\varPhi = {{6{\text{π}} /}}4$ ; (h) $\varPhi = 7{\text{π}}/4$ . Other parameters are the same as those in Fig.3 .图6(a) —图6(c) 中, 给出了在共振处$\delta = {\omega _{\rm{m}}}$ , 随着原子数$N$ 的增加, 透射的群延迟时间${\tau _{\rm{T}}}$ 和反射的群延迟时间${\tau _{\rm{R}}}$ 随相位差$\varPhi /{\text{π}}$ 的变化情况. 可以看出, 黑色实线对应的${\tau _{\rm{T}}}$ 和红色虚线对应的${\tau _{\rm{R}}}$ 随相位差$\varPhi /{\text{π}}$ 呈周期性变化. 在图6(a) 中反射和透射群延迟时间全部大于零, 表现出明显的慢光效应, 但随着原子数$N$ 的增加, 在图6(b) 和图6(c) 中可以看出${\tau _{\rm{T}}}$ 和${\tau _{\rm{R}}}$ 的取值逐渐减小, 其中${\tau _{\rm{R}}}$ 还出现了负值, 即表现出了快光现象. 出现这种情况的原因是原子数的增加, 改变了光力学腔中的腔场以及耦合强度, 进而影响了整个杂化光力系统的光学特性, 从而能够改变群延迟时间. 通过上述分析发现, 除了可以通过相位$\varPhi $ 对快慢光进行周期性调制外, 还可以通过控制原子数$N$ 来实现快慢光之间的转换.图 6 $\delta = {\omega _{\rm{m}}}$ 时${\tau _{\rm{T}}}$ (黑色实线)和${\tau _{\rm{R}}}$ (红色虚线)随相位差$\varPhi /{\text{π}}$ 和振幅比$Y$ 的变化曲线: (a) $Y = 0.2$ , $g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b) $Y = 0.2$ , $g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c) $Y = 0.2$ , $g\sqrt N = 9 \times 2{\text{π}}$ MHz; 其他参数取值见文中第4部分Figure6. The ${\tau _{\rm{T}}}$ (black line) and the ${\tau _{\rm{R}}}$ (red dotted line) as a function of $\varPhi /{\text{π}}$ and Y with $\delta = {\omega _{\rm{m}}}$ : (a) $Y = 0.2$ , $g\sqrt N = 3 \times 2{\text{π}}$ MHz; (b) $Y = 0.2$ , $g\sqrt N = 6 \times 2{\text{π}}$ MHz; (c) $Y = 0.2$ , $g\sqrt N = 9 \times 2{\text{π}}$ MHz. Other parameters are the same as those in Sec. IV.4.结 论 本文主要研究了在薄膜振子上耦合弱辅助场的原子辅助光力系统中相位对OMIT及快慢光的调控. 当没有辅助场与薄膜振子耦合时, 在原子-腔-薄膜振子三模耦合的光力系统中观察到了杂化EIT和OMIT. 当辅助场直接激发薄膜振子且与探测场同相位时发现, 在共振处辅助场使薄膜振子产生共振吸收, 从而抑制了OMIT. 所以本文通过改变辅助场同探测场的相对振幅比, 直接影响了腔场与薄膜振子的光力耦合效果, 从而实现了对OMIT窗口深度的调控. 当保持辅助场与探测场振幅比不变, 只改变它们之间的相位差时发现, 相位差的取值也直接影响着系统的光力耦合效应, 使得仅通过调节相位就可以实现输出的探测场在“吸收”、“透明”和“增益”之间相互转换, 从而改变整个系统的吸收和色散性质. 与此同时, 发现群延迟时间随相位差的改变呈周期性变化. 通过调节相位差及原子数, 可以改变群延迟时间, 使其表现出慢光或快光效应以及快慢光之间的转换. 利用该系统不但可以通过相位的调节来操控光在“吸收”和“透明”之间相互转换从而实现全光开关, 同时还可以通过光在“吸收”、“透明”和“增益”之间相互转换实现光电倍增, 因而该系统在量子光学器件方面有着潜在的应用价值. 













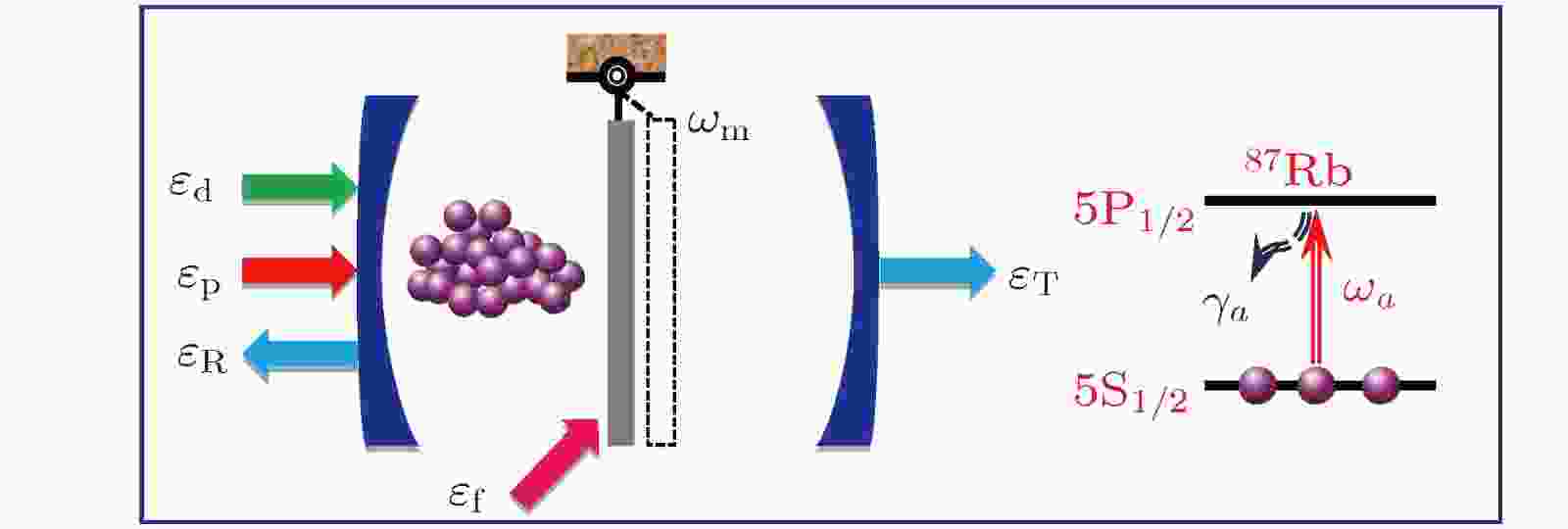 图 1 由单模FP腔以及束缚在其中的N个全同二能级87Rb冷原子系综和中间由弱辅助驱动场
图 1 由单模FP腔以及束缚在其中的N个全同二能级87Rb冷原子系综和中间由弱辅助驱动场


































































































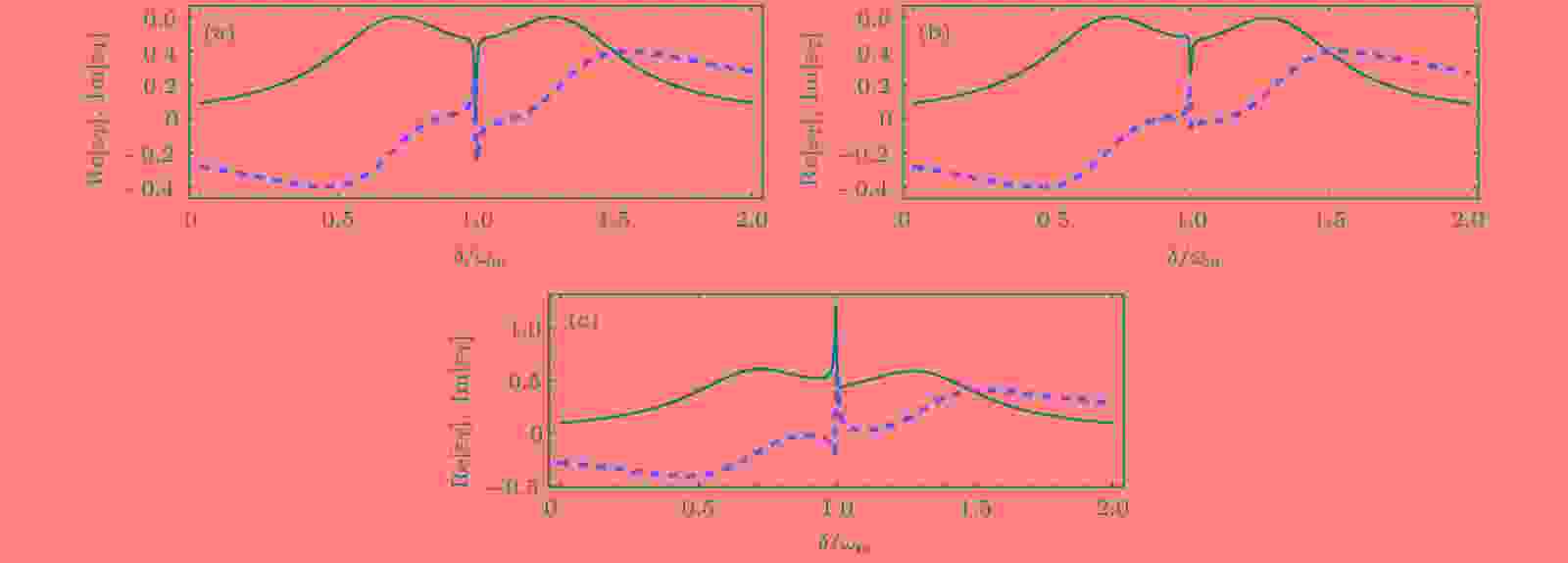 图 2
图 2 















































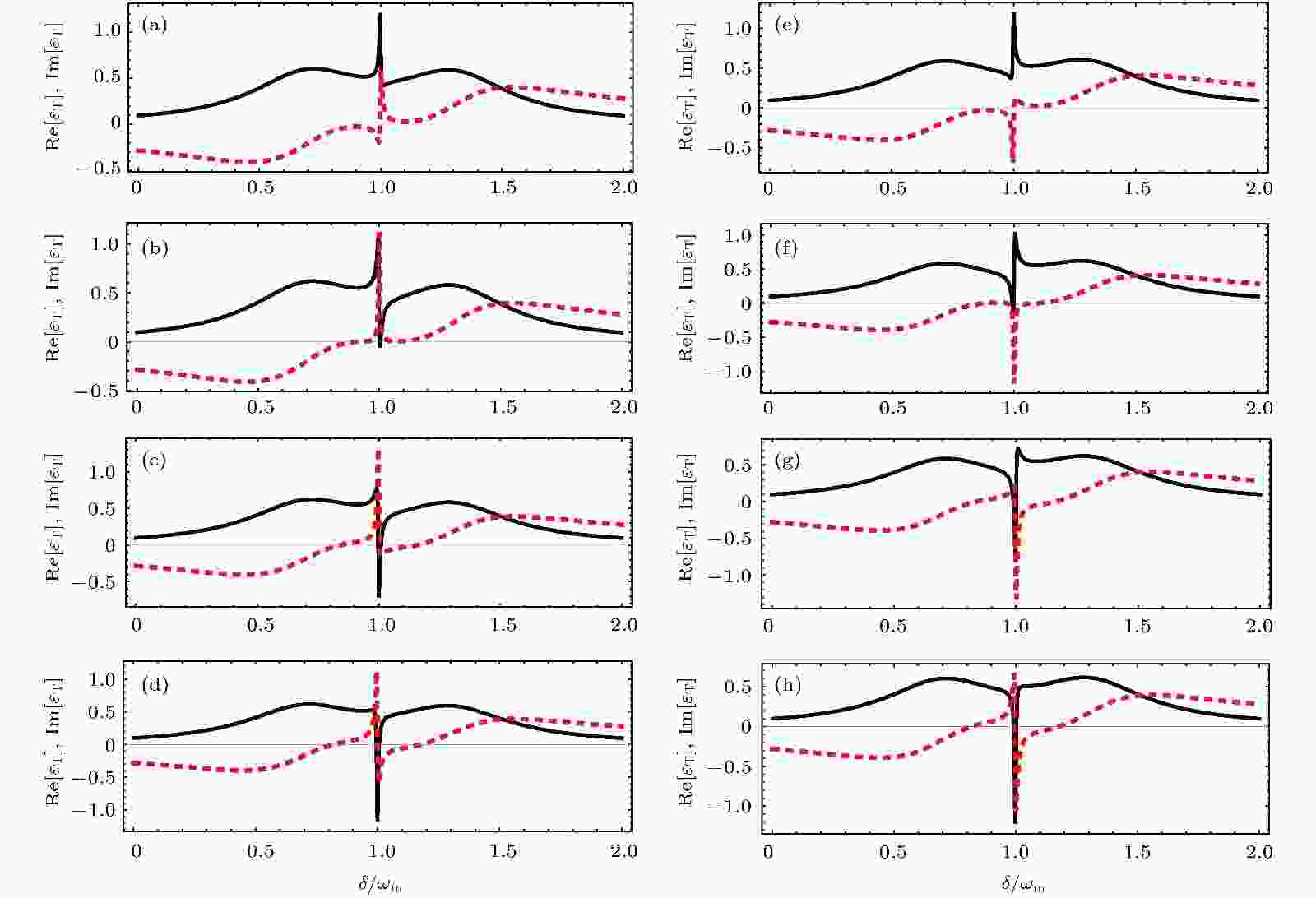 图 3
图 3 













































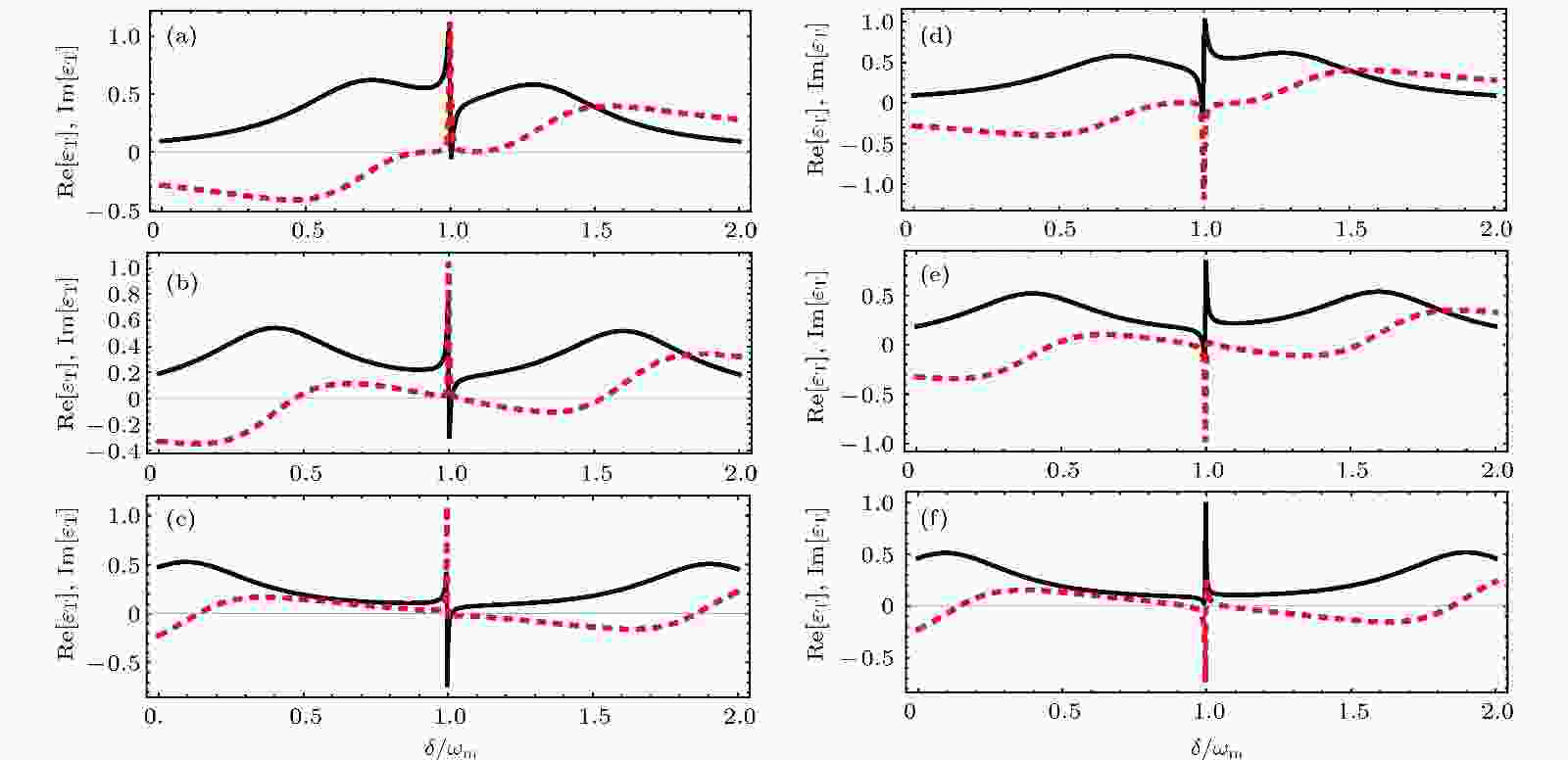 图 4
图 4 


































































































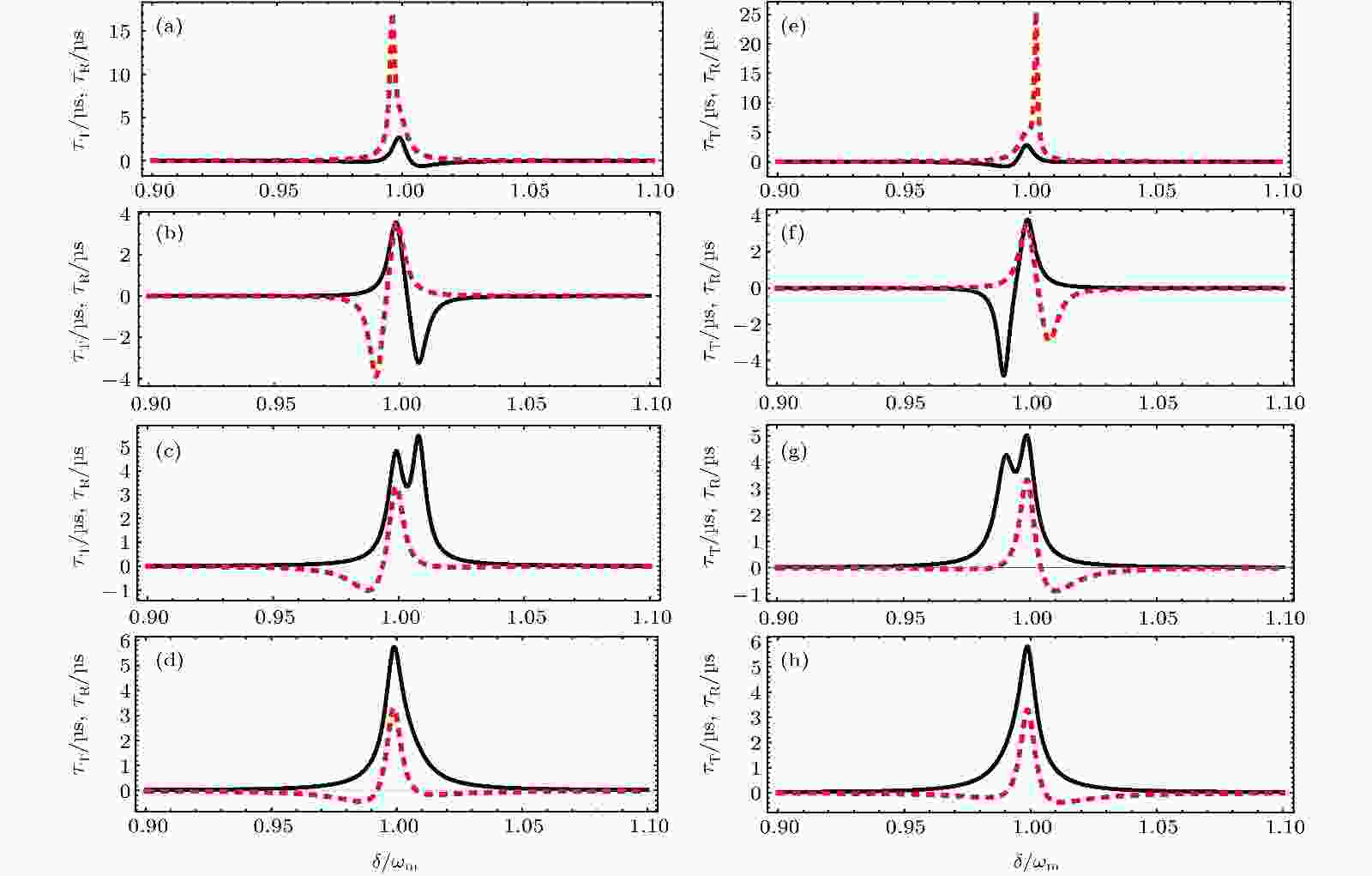 图 5
图 5 





























































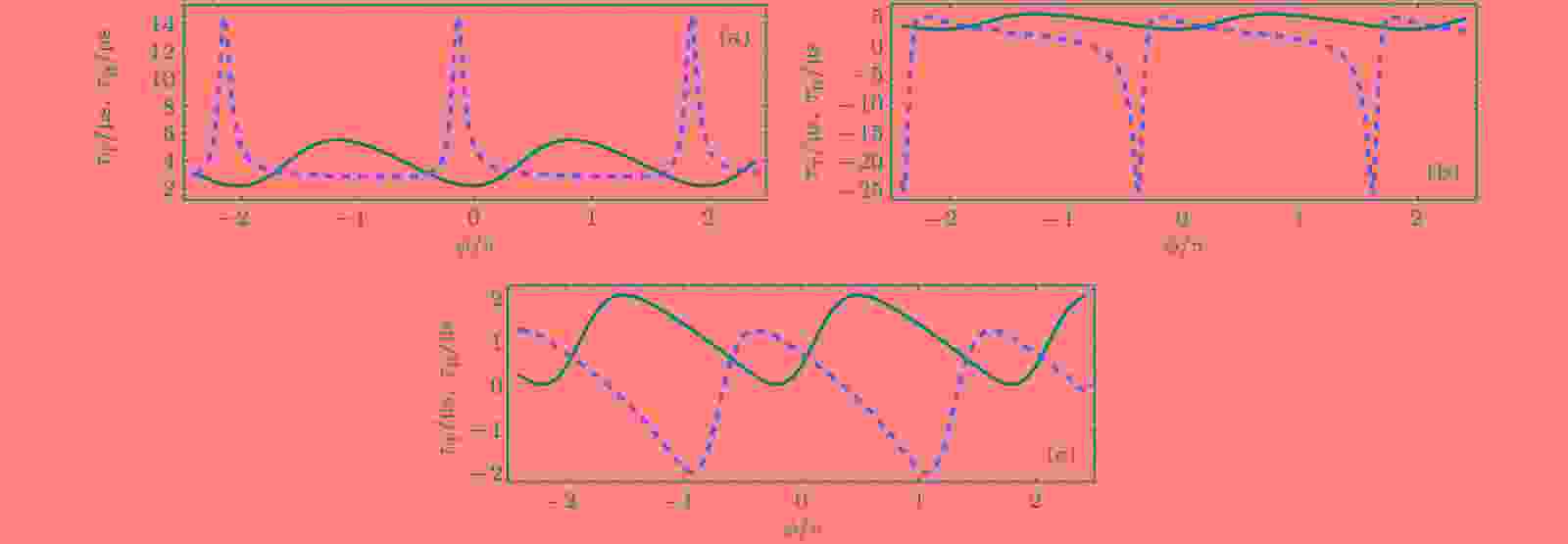 图 6
图 6 
































