摘要: 本文对近两年来有关淬火动力学过程中拓扑现象的研究做简要综述. 这些动力学拓扑现象被动力学过程中的衍生拓扑不变量保护, 与淬火前后体系的拓扑性质有密切关系. 基于人工量子模拟平台的高度可控性, 已在诸如超冷原子、超导量子比特、核磁共振、线性光学等众多物理体系中, 通过对人工拓扑体系动力学过程的调控, 观测到如动力学涡旋、动量-时间域的Hopf映射及环绕数、拓扑保护的自旋环结构、动力学量子相变、动量-时间斯格明子等诸多动力学拓扑现象. 其中某些拓扑结构还可以在非幺正动力学淬火过程中稳定存在. 这些研究将人们对拓扑物相的认识和研究从平衡态推广到非平衡动力学领域, 具有重要的科学价值.
关键词: 拓扑相 /
淬火动力学 /
动力学拓扑不变量 /
超冷原子 English Abstract Fixed points and dynamic topological phenomena in quench dynamics Deng Tian-Shu Yi Wei Key Laboratory of Quantum Information, University of Science and Technology of China, CAS, Hefei 230026, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 15522545).Received Date: 30 October 2018Accepted Date: 27 December 2018Available Online: 01 February 2019Published Online: 20 February 2019Abstract: In this review, we discuss the recent progress on the study of dynamic topological phenomena in quench dynamics. In particular, we focus on dynamic quantum phase transition and dynamic topological invariant, both of which are hinged upon the existence of fixed points in the dynamics. Further, the existence of these fixed points are topologically protected, in the sense that their existence are closely related to static topological invariants of pre- and post-quench Hamiltonians. We also discuss under what condition these dynamic topological phenomena are robust in non-unitary quench dynamics governed by non-Hermitian Hamiltonians. So far, dynamic topological phenomena have been experimentally observed in synthetic systems such as cold atomic gases, superconducting qubits, and linear optics. These studies extend our understanding of topological matter to the non-equilibrium regime.Keywords: topological phase /quench dynamics /dynamic topological invariant /ultracold atoms 全文HTML --> --> --> 1.引 言 对拓扑相与相变的研究是现代物理的重要方向之一. 在传统的金斯堡-朗道相变中, 量子相与体系的对称性有深刻的关系, 量子相变由局域序参量刻画, 同时伴随着对称性的破缺. 拓扑相和相变与此截然不同: 拓扑相变一般不伴随对称性的破缺, 拓扑相则与体系基态波函数在希尔伯特空间的几何性质相关并由拓扑不变量刻画[1 ,2 ] . 从人们发现量子霍尔效应至今已有三十余年了, 此间人们对无相互作用体系中拓扑相的理解和分类日趋完善, 对有相互作用体系中拓扑相的认识也有了长足进展. 近年来拓扑物态研究领域的一个新兴方向是在凝聚态物质之外的体系中寻找、刻画拓扑相及与拓扑相关的现象. 随着超冷原子、线性光学等量子模拟平台的蓬勃发展, 具有拓扑能带及拓扑特性的人工拓扑体系相继在这些平台上得以实现[3 -11 ] . 此外, 人工拓扑体系的高度可控性使对动力学过程及非厄米体系中拓扑现象的实验研究成为可能[7 -11 ] , 而这也驱动了相关领域的理论研究[12 -16 ] . 值得强调的是, 动力学过程及非厄米体系中的拓扑现象在传统凝聚态体系中一般很难被实现. 因此各量子模拟平台上的人工拓扑体系具有重要的价值.$ H^i $ 的本征态出发, 在末态哈密顿量$ H^f$ 作用下演化的动力学过程. 对于拓扑体系, 一个重要的问题是该体系的淬火动力学过程中是否也会出现受拓扑保护的拓扑现象? 更进一步, 如果初态和末态哈密顿量具有不同拓扑性质的能带, 体系淬火过程中的拓扑现象是由初态还是末态哈密顿量的拓扑性质决定? 对这些问题, 一个最直接的回答来自于对体系瞬时波函数几何性质的刻画. 文献[17 ,18 ]研究了几种简单拓扑体系在淬火过程中瞬时波函数的拓扑不变量, 结果表明瞬时波函数的拓扑不变量不随时间变化, 即淬火过程的拓扑性质完全由初始哈密顿量决定. 由于这些工作中考虑的体系都是无相互作用(或者平均场意义下无相互作用)的厄米体系, 淬火动力学时间演化相当于对初始态做局域幺正变换. 此时, 由于局域幺正变换不破坏保护拓扑性质的对称性, 瞬时态的拓扑不变量必然不变. 然而, 人们发现在淬火过程中会出现衍生的动力学拓扑现象, 这些拓扑现象或与初态和末态哈密顿量的拓扑性质相关, 或由衍生的动力学拓扑数保护, 并在动力学过程中表现出可观测效应[19 -31 ] . 有趣的是, 即使基于同一淬火过程中观测到的拓扑现象, 也可以构造不同的衍生拓扑结构加以解释. 这一方面说明了淬火动力学过程中丰富的物理内涵, 另一方面也会引发关于动力学拓扑现象普适描述的思考.[24 ] . 此后, 清华大学的研究组从理论上研究了淬火动力学过程中的衍生拓扑结构, 利用Hopf映射和环绕数重新解释了汉堡实验, 并把环绕数与淬火前后哈密顿量的静态拓扑性质联系了起来[19 ] . 这一理论随后被汉堡大学研究组的另一实验所证实[25 ] . 与此同时, 来自中国科学技术大学和北京大学的研究组在对拉曼晶格上的冷原子气体进行淬火时发现了动力学过程中原子自旋分布中的环形结构, 并通过能带反转面的理论把环的出现与静态哈密顿量的陈数联系了起来[22 ,23 ,26 ] . 这些实验充分反映了淬火动力学中衍生拓扑现象的普遍性和丰富性. 除冷原子气体之外, 淬火过程中的动力学拓扑现象也在超导量子比特、单光子量子行走等量子模拟平台上被实验观测. 目前这些模拟平台都还是通过操控单量子比特模拟费米体系拓扑模型的淬火过程, 其优势是更易于进行实验操控和态重构, 以及可以方便的实现耗散以研究非幺正动力学淬火过程.2.动力学量子相变及动力学拓扑序参量 我们首先介绍动力学量子相变及其与拓扑保护不动点的关系. 先回顾动力学过程中Loschmidt回波的定义. Loschmidt回波是量子体系动力学演化中的一个重要可观测量, 它描述体系初态在演化过程中的重现行为. 如体系的时间演化由$ H^f $ 决定, 则Loschmidt回波$ L $ 可表示为$ |\psi^i\rangle $ 为体系初态, $ G(t) $ 为Loschmidt振幅. 如果对(1 )式中的时间作Wick转动, 即取虚时$ t=-i\beta $ , Loschmidt振幅$ G(\beta) $ 的形式会非常类似于热力学中的正则系综配分函数$ \beta=1/k_{\rm B} T $ , $ k_{\rm B} $ 为玻尔兹曼常数, $ T $ 为体系温度.[32 -36 ] . 在热力学中, 热力学相变发生在体系自由能$ F=-\dfrac{1}{V}\lim_{V\rightarrow \infty} \ln Z $ ($ V $ 为体系体积)非解析处, 此时$ Z $ 过零点. 相应的, Heyl等人认为, 当$ G(t) $ 过零点时, 动力学演化过程中也存在动力学量子相变. 相应的动力学自由能$ g(t) $ 可定义为[35 ] . 在这个意义上, 动力学量子相变可以看作是动力学过程中的衍生拓扑现象. 动力学序参量的定义与所谓的Pancharatnam几何相位有密切联系. Pancharatnam相位是Loschmidt振幅$ G $ 的辐角中与动力学相位无关的部分, 源于体系动力学演化过程中的几何性质. 以无相互作用的半满晶格模型为例, 由于晶格平移对称性, 不同晶格动量子空间的动力学演化解耦. 此时, Pancharatnam几何相位写做$ \phi_{k}^{G}(t)=\phi_{k}(t)-\phi_{k}^{\rm{dyn}}(t) $ , 其中$ G=\prod_k G_k $ , 而$ \phi_{k}(t) $ 为$ G_{k} $ 的辐角. 体系的动力学相位为$ \phi_{k}^{\rm{dyn}}(t)=-\int_{0}^{t}\langle\psi_k(t')|H^f_k|\psi_k(t')\rangle dt' $ , 其中$ H^f_k $ 为末态的Bloch哈密顿量(假设$ H^f_k $ 不含时).$ \phi_k^G $ 在任意时刻都消失的不动点$ \{k_m\} $ ($ m=1,2,... $ ). 而在拓扑体系的淬火过程里, 不动点的存在性与淬火前后哈密顿量的拓扑性质有一定关系[37 ,38 ] . 举例来说, 对于一维两能带拓扑体系, 只要淬火前后的能带具有不同的拓扑数, 则不动点一定成对出现. 对于二维的两能带陈绝缘体, 如淬火前后哈密顿量能带的陈数绝对值不同, 则不动点也会成对出现. 其他诸如高维、多能带、不同拓扑分类的情况不动点原则上也会存在, 但规律会比较复杂[39 ,40 ] . 除此之外, 淬火过程中也可能出现一些与拓扑完全无关的不动点. 这里, 我们主要考虑与淬火前后体系拓扑特性相关的不动点, 即拓扑不动点.$ \phi_k^G $ 在不动点上消失, $ \nu^D $ 为从$ k\in(k_m,k_n) $ 到$ e^{i\phi^G_k} $ 的$ S^1\rightarrow S^1 $ 映射度, 因此只能取整数. 同时, 在动力学量子相变发生时$ G_k(t)=0 $ , $ \phi^G_k $ 无法定义, 所以$ \nu^D $ 只能在临界点处跳变. 在二维体系中, 动力学序参量的定义更为复杂. 这是因为动力学量子相变的临界点$ k_c $ 会随时间在布里渊区内产生、移动、消失. 文献中目前存在两种不同的定义二维动力学拓扑序参量的方式, 其出发点均基于动力学量子相变的几何结构. 因此, 动力学拓扑序参量的重要性在于提供了一个从动力学衍生拓扑不变量的角度理解动力学量子相变的途径. 目前, 动力学量子相变已在离子阱, 超冷原子, 单光子量子行走, 以及核磁共振等多个人工量子模拟平台上被观测到, 动力学量子相变和Pancharatnam几何相及动力学拓扑序的关系也相继被实验证实 [24 ,27 -30 ] .3.动力学拓扑不变量 我们在第2节讨论了拓扑体系淬火过程中的拓扑不动点. 在拓扑不动点上, Pancharatnam相位在时间演化过程中恒为零. 相位在拓扑不动点消失的本质原因在于这些不动点同时也是动力学不动点, 即在这些参数点上体系的态不随时间演化. 基于这一认识, 人们发现可以基于不动点在动量-时间的二维参数空间里定义衍生动力学拓扑不变量[20 ,21 ,27 ,28 ,31 ] . 这些动力学拓扑不变量跟同样基于不动点的动力学量子相变、动力学拓扑序参量以及淬火前后哈密顿量的拓扑性质等紧密关联. 目前文献里这方面的工作主要集中在一维两能带拓扑体系的淬火过程, 我们也将具体介绍这类体系中的不动点结构和动力学拓扑不变量. 高维多带体系的动力学淬火过程中的拓扑结构会更加丰富, 但仍有待进一步研究.$ H^i_k $ 由$ {h}_k^i $ 刻画; 末态的哈密顿量$ H^f_k $ 由$ {h}_k^f $ 刻画. 同时, 选择体系初态为$ H^i_k $ 的基态. 对于而能带体系, 体系的初态和任意时刻的瞬时态都可以表示在同一个Bloch球上.图1 所示, 淬火动力学过程可以形象的表示为瞬时态矢量从初态出发, 在Bloch球面上绕$ {h}^f $ 轴的转动. 这里有两种值得注意的特殊情况.图 1 Bloch球上的动力学演化 (a) 态矢量在Bloch球上绕$ {h}^f $ 运动; (b) 动力学不动点对应于$ {h}^i\cdot {h}^f=\pm 1 $ ; (c) 临界点对应于$ {h} ^i\cdot {h}^f=0 $ . 实线代表$ {h}^i $ (绿色)与$ {h}^f $ (红色), 虚线代表态矢量; 假设初态处于$ H_k $ 基态上, 即$ t=0 $ 时态矢量与$ {h}^i $ 方向相反Figure1. Visualizing dynamics on the Bloch sphere: (a) State vector revolving around the $ {h}^f $ axis; (b) illustration of fixed points when $ {h}^i\cdot {h}^f=\pm 1 $ ; (c) illustration of critical points with $ {h} ^i\cdot {h}^f=0 $ .$ {h}^i $ 和$ {h}^f $ 平行或反平行. 此时只有瞬时态的相位随时间演化, 瞬时态在Bloch球上的矢量位置不变. 这种情况对应着前述的不动点. 我们定义$ {h}^i\cdot {h}^f_k=\pm 1 $ 为两种不同类型的不动点. 可以证明, 当初始哈密顿量和末态哈密顿量基态拓扑数不一样时, 不同类型的不动点一定成对出现. 对于二维两能带拓扑体系, 不同类型不动点出现的充分不必要条件变为初始哈密顿量和末态哈密顿量对应的陈数绝对值不同. 我们把这种与体系静态拓扑性质相关的不动点叫做拓扑保护的不动点.$ {h}^i_k $ 和$ {h}^f_k $ 垂直. 此时, 瞬时态在Bloch球上演化半个周期后会与初态正交. 按照前一节的定义, 在相应的临界动量和时间处会发生动力学量子相变. 由于$ {h}^i\cdot {h}^f_k $ 是$ k $ 的连续函数, 可以证明两个不同类型的不动点间一定存在至少一个临界动量$ k_c $ 满足$ {h}^i_k\cdot {h}^f_k=0 $ . 这样的临界点称为拓扑临界点.$ {h}(k,t) $ 为动量$ k $ 上瞬时态在时刻$ t $ 对应的矢量, $ k_{m,n} $ 为不动点, $ t_k $ 为动量$ k $ 上的演化周期. 可以证明, 动力学陈数不为零的条件是$ k_m $ 和$ k_n $ 是不同类型的不动点. 考虑到前述静态哈密顿量拓扑性质和动力学不动点之间的关系, 我们可以证明淬火前后静态哈密顿量具有不同拓扑数是存在非零动力学拓扑不变量的充分非必要条件.$ {h}(k,t) $ 于动量-时间衍生空间内的自旋结构上. 如图2 所示, 当淬火前后哈密顿量具有不同拓扑数时, $ {h}(k,t) $ 在动量-时间空间表现出斯格明子结构. 由于前述的不动点和动力学量子相变临界点的关系, 我们发现动力学量子相变就发生在斯格明子的极点上. 这一结构已在实验上被直接观测到[27 ,31 ] . 同时, 如文献[21 ]所示, 动力学拓扑不变量的存在, 也体现在体系的纠缠谱中.图 2 淬火前后哈密顿量具有不同拓扑数时的典型斯格明子结构. 黑色箭头为自旋在平面内方向, 背景颜色对应自旋在与平面垂直方向上的分量大小, 蓝色对应向内, 黄色对应向外. 竖直虚线为不动点位置, 红色实线表示不同动量$ k $ 点的周期Figure2. Momentum-time skyrmions when pre- and post-quench Hamiltonians possess different winding numbers.4.非厄米体系中的非幺正淬火过程 前述的动力学拓扑结构也存在于非厄米体系的非幺正淬火过程中, 前提是体系的动力学演化仍然是相干的[41 ] . 这一前提满足的条件体系具有宇称-时间对称性. 一般而言, 非厄米哈密顿量的本征值不是实数. 但如果该哈密顿量有宇称-时间对称性, 即$ \mathcal{PT}H(\mathcal{PT})^{-1}=H $ , 且本征态也为$ \cal{PT} $ 算符的本征态时, 该本征态对应的哈密顿量本征值为实数[42 -44 ] . 这里$ \cal{P} $ 为宇称算符, $ \cal{T} $ 为时间反演算符. 如果宇称-时间守恒的哈密顿量所有本征值均为实数, 则体系处于宇称-时间对称守恒相; 反之, 如哈密顿量某些本征值非实数, 体系处于宇称-时间对称自发破缺相.[45 ,46 ] .图3(a) 所示, 该模型与标准SSH模型的区别在每个格点上均存在增益或损耗项. 体系的Bloch哈密顿量仍然可记为$ H_k={h}_k\cdot{\sigma} $ , 其中$h_x=$ $ w\cos k+v $ , $ h_y=w\sin k $ , and $ h_z=iu $ . 体系的拓扑数可由全局贝里相$ \varphi_B $ 对应的绕数刻画图 3 非厄米SSH模型及其拓扑相图 (a) 非厄米SSH模型. 在厄米SSH模型的基础上, 每个格点上均有增益或损耗; (b) 体系拓扑相图. 实线为拓扑边界, 虚线为宇称-时间对称与对称破缺区域的边界. $ v $ , $ w $ 为SSH模型的跃迁系数, $ u $ 为增益损耗系数, $ \nu $ 为绕数Figure3. Non-Hermitian SSH model and its topological phase diagram: (a) Non-Hermitian SSH model; (b) topological phase diagram.$ |\chi_{\mu}\rangle $ 和$ |\psi_{\mu}\rangle $ ($ \mu=+,- $ )分别是$ H_k $ 的左、右本征矢, 即$ H_k|\psi_\mu\rangle=\epsilon_\mu|\psi_\mu\rangle $ ,$ H_k^{\dagger}|\chi_{\mu}\rangle=\epsilon^*_{\mu}|\chi_{\mu}\rangle $ . 这里$ \epsilon_{\mu} $ 是体系本征谱. 体系的拓扑相图如图3 (b)所示. 我们注意到拓扑相变界周围是宇称-时间对称性自发破缺区域.[41 ,47 ,48 ] $ {\tau}=(\tau_1,\tau_2,\tau_3) $ , 并且$ \tau_\gamma=\sum_{\mu,\nu=\pm}|\psi_{\mu}^{f}\rangle\sigma^{\mu\nu}_\gamma\langle\chi_{\nu}^{f}| $ ($ \gamma=0,1,2,3 $ ). 引入${\tau}$ 矩阵的好处是, 虽然密度矩阵是非厄米的, $ {d}(k,t) $ 是模为1的实矢量. 这一点至关重要, 因为我们又可以在Bloch球上表示体系演化的轨迹了.图4 所示, 此时动力学量子相变的发生会存在多个周期, 同时也会存在多个对应的动力学拓扑序参量.图 4 非厄密SSH模型淬火中的典型动力学自由能$ g(t) $ 与动力学拓扑序参量$ \nu^D(t) $ (a) 动力学自由能$ g(t) $ ; (b) 动力学拓扑序参量$ \nu^D(t) $ . 在非厄米淬火过程中存在两个临界时间尺度及两个动力学拓扑序参量Figure4. Dynamic free energy $ g(t) $ and dynamic topological order parameter $ \nu^D(t) $ in the quench dynamics of non-Hermitian SSH model: (a) Dynamic free energy $ g(t) $ ; (b) dynamic topological order parameter $ \nu^D(t) $ .[49 ,50 ] . 被动宇称-时间守恒非厄米体系虽然不会有纯实数的本征谱, 但体系的能谱及动力学性质可以方便地映射到基于损耗-增益的主动宇称-时间守恒非厄米体系上. 最近, 动力学量子相变、动力学拓扑序参量、动力学拓扑不变量等衍生动力学拓扑现象已经在具有被动宇称-时间守恒性质的单光子非幺正量子行走实验里被探测到[31 ] .5.总结与展望 本文集中讨论了几种基于拓扑保护动力学不动点的动力学拓扑结构的构造和关联. 由于相关动力学拓扑不变量的定义都基于不同类拓扑不动点的存在, 而后者又与静态哈密顿量的拓扑性质密切相关, 拓扑保护的动力学不动点成为有机联系各种动力学衍生拓扑现象及平衡态拓扑相的核心要素. 目前对于动力学拓扑现象的讨论多数集中在低维(一维或者二维)两能带五相互作用体系的突变淬火过程. 高维多能带拓扑系统淬火过程中会出现更丰富的拓扑结构, 如何系统的刻画它们是今后研究的一个方向.除本文讨论的衍生拓扑现象以外, 其他已知的动力学拓扑结构如Hopf映射、环绕数、基于能带反转面的拓扑环等与动力学不动点及动力学量子相变临界点的关系则需要进一步研究讨论. 因此, 关于动力学拓扑结构的更普适的描述是个亟待解决的问题. 















































 图 1 Bloch球上的动力学演化 (a) 态矢量在Bloch球上绕
图 1 Bloch球上的动力学演化 (a) 态矢量在Bloch球上绕





































 图 2 淬火前后哈密顿量具有不同拓扑数时的典型斯格明子结构. 黑色箭头为自旋在平面内方向, 背景颜色对应自旋在与平面垂直方向上的分量大小, 蓝色对应向内, 黄色对应向外. 竖直虚线为不动点位置, 红色实线表示不同动量
图 2 淬火前后哈密顿量具有不同拓扑数时的典型斯格明子结构. 黑色箭头为自旋在平面内方向, 背景颜色对应自旋在与平面垂直方向上的分量大小, 蓝色对应向内, 黄色对应向外. 竖直虚线为不动点位置, 红色实线表示不同动量










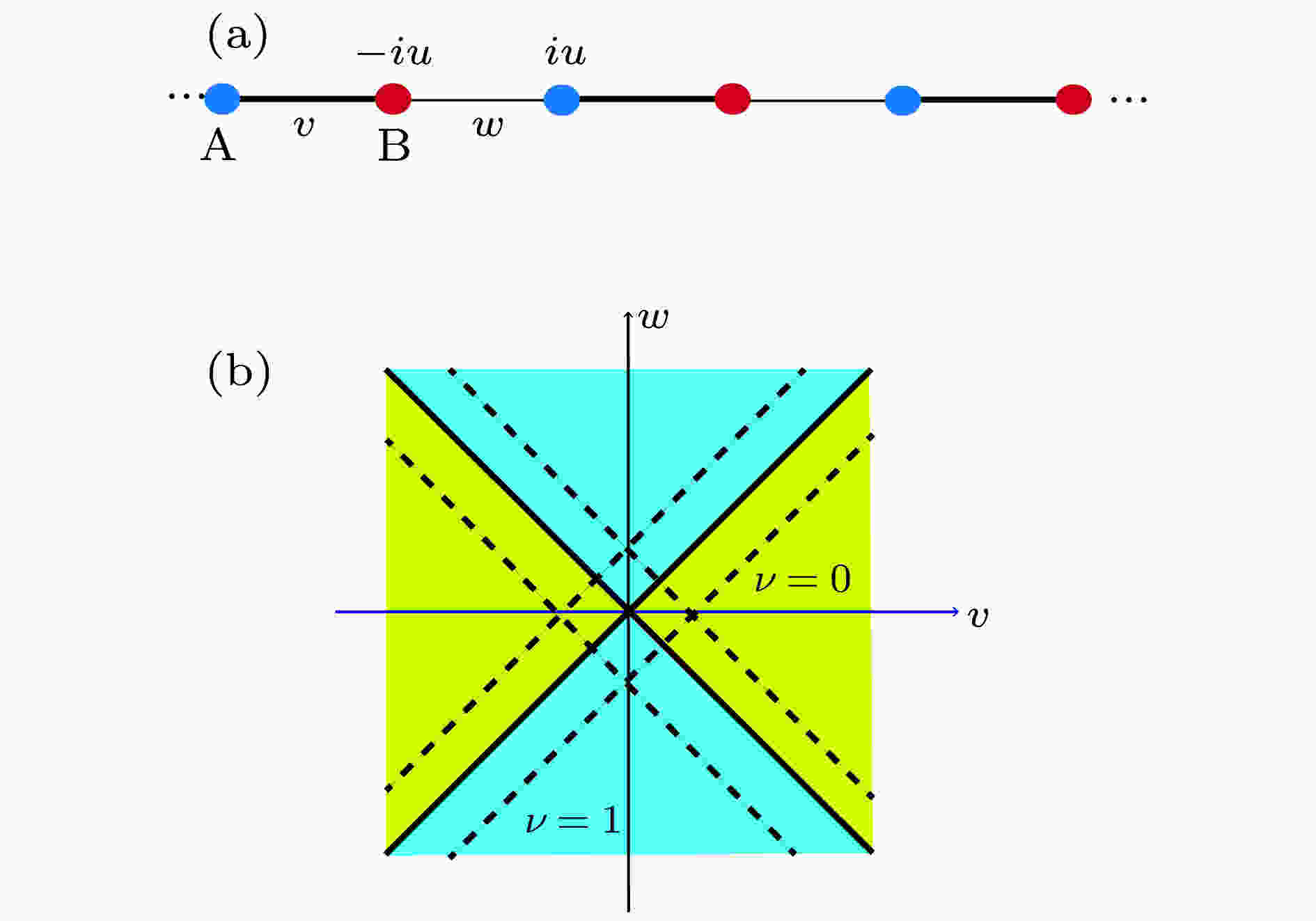 图 3 非厄米SSH模型及其拓扑相图 (a) 非厄米SSH模型. 在厄米SSH模型的基础上, 每个格点上均有增益或损耗; (b) 体系拓扑相图. 实线为拓扑边界, 虚线为宇称-时间对称与对称破缺区域的边界.
图 3 非厄米SSH模型及其拓扑相图 (a) 非厄米SSH模型. 在厄米SSH模型的基础上, 每个格点上均有增益或损耗; (b) 体系拓扑相图. 实线为拓扑边界, 虚线为宇称-时间对称与对称破缺区域的边界. 















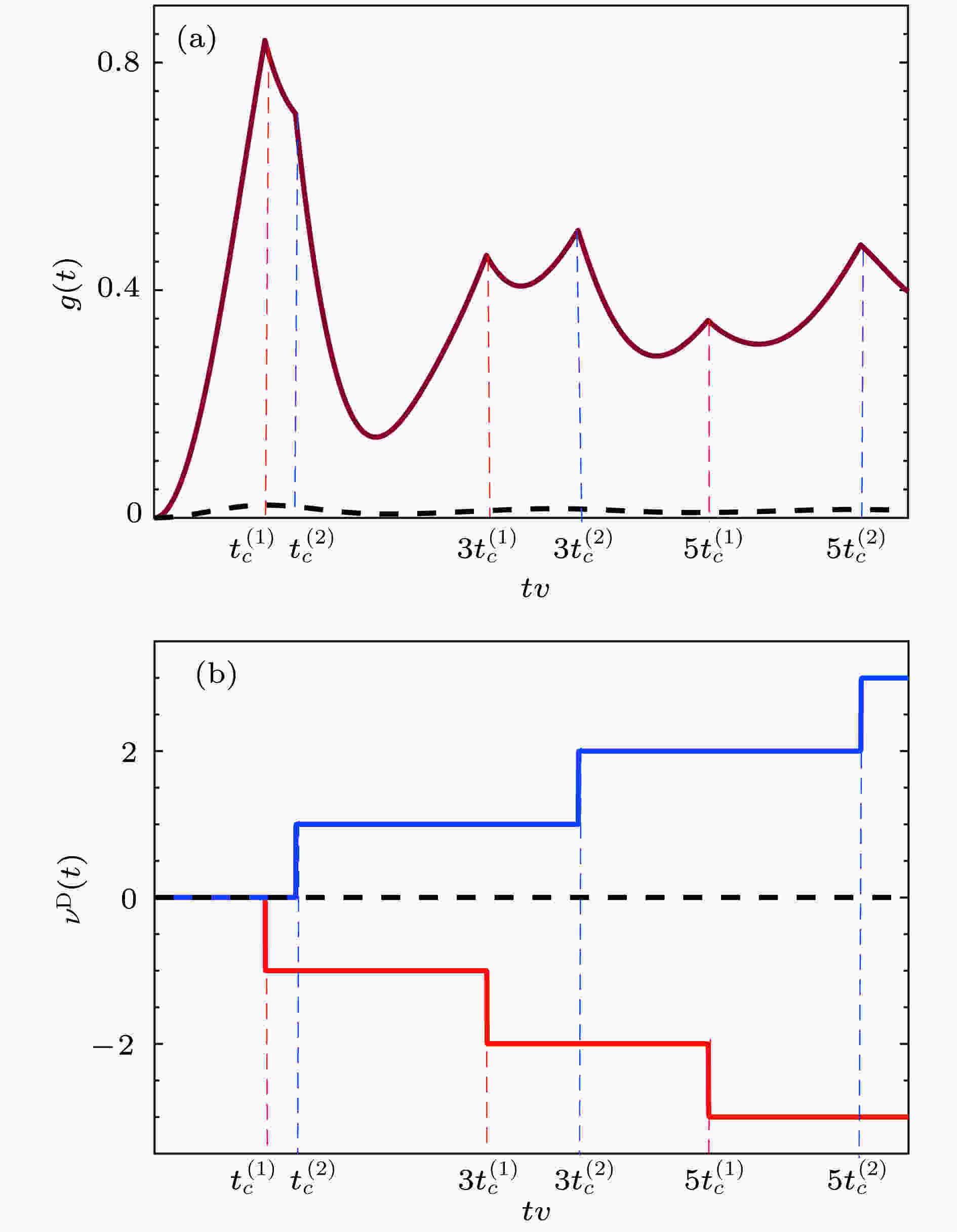 图 4 非厄密SSH模型淬火中的典型动力学自由能
图 4 非厄密SSH模型淬火中的典型动力学自由能















