摘要:多体系统的非平衡动力学演化是当前物理学中最具挑战性的问题之一. 超冷量子费米原子气体具有较强的可控性, 是研究多体非平衡动力学的理想系统, 可以用来模拟和理解大爆炸后的早期宇宙、重离子碰撞中产生的夸克-胶子以及核物理等动力学. 一般多体系统演化是非常复杂的, 往往需要利用对称性来研究. 利用Feshbach共振可以制备标度不变的费米原子气体: 无相互作用和幺正费米量子气体. 当远离平衡态时, 可利用普适的指数和函数来刻画, 其动力学可以通过对系统的时空演化进行标度变换来识别. 本文主要介绍近年来强相互作用超冷费米气体的膨胀动力学研究进展, 包括原子气体的各向异性展开、标度动力学和Efimovian膨胀动力学.
关键词: 强相互作用超冷费米气体/
Feshbach共振/
各向异性展开/
标度不变性/
Efimovian膨胀动力学

English Abstract

全文HTML

--> --> -->

自从1999年简并费米气体(DFG)在实验中被实现以来^[1], 费米原子气体具有的量子统计规律和稳定可控的相互作用使得其迅速成为了研究热点, 近二十年来得到了迅猛发展. 相较于玻色气体, 费米气体遵从不同的量子统计规律, 在无相互作用下费米原子气体从经典气体到量子气体趋于平滑过渡, 超流相变过程只会在原子间存在相互作用的情况下才能出现. 费米气体初期的研究内容主要集中在超冷费米气体的超流特性上, 比如强相互作用超冷费米气体的流体动力学展开^[2]和集体激发振荡^[3,4]、分子的玻色爱因斯坦凝聚(BEC)和原子对的BCS (Bardeen-Cooper-Schri effer) 超流的渡越物理(BEC-BCS crossover)^[5-7]、强相互作用费米气体量子化涡旋的实现^[8]、自旋极化的费米气体^[9]、孤子的产生和传播^[10]、Mott绝缘态^[11]以及反铁磁态^[12,13]的超流相变等, 最近几年超冷费米气体的自旋轨道耦合^[14]、Bragg谱^[15]、新奇非平衡动力学^[16]以及具有长程偶极相互作用的超冷磁性原子气体^[17,18]等也取得了较大的进展.
膨胀动力学是超冷费米气体非常重要的研究方向. 在超冷费米气体中, Feshbach共振技术的使用可以精确调控原子间的相互作用, 当原子间$ \rm s $波散射长度调至0时, 原子气体为无散射碰撞的无相互作用费米气体; 而在Feshbach共振点处, 原子间$ \rm s $波散射长度远超原子间距, 系统的相互作用能占主导, 形成幺正费米气体. 在幺正费米气体中, 原子间距成为了系统唯一的长度单位, 系统可以表现出许多普适性的物理规律^[19-21].
无论无相互作用费米气体还是幺正费米气体, 系统中均存在标度不变动力学对称性, 在这种动力学对称性下, 超冷费米量子气体的局域关联函数在演化过程中是自相似的, 因此其热力学流体性质可以通过一个简单的坐标含时标量因子变换来描述, 极大地简化了多体非平衡系统动力学的复杂性. 在超冷费米气体膨胀动力学的研究中, 可以通过快速精确调控原子间相互作用以及外加势来构成一个测试基本的少体和多体物理的理想系统, 探索强相互作用费米气体许多新奇的非平衡特性, 理解复杂少体和多体量子系统动力学过程.
本文主要介绍超冷费米气体中膨胀动力学的研究进展. 首先介绍强相互作用超冷费米气体各向异性膨胀动力学, 这一动力学膨胀行为直接反映了超冷费米气体的超流特性; 其次是超冷费米气体的标度不变性及其对称性破缺, 介绍了幺正费米气体和无相互作用费米气体的标度不变展开动力学, 以及在有限散射长度情形下原子气体系统的标度不变性不再能够维持而产生的标度不变对称性破缺动力学行为; 最后是标度不变费米气体的Efimovian 膨胀动力学的观测, 分别讲述了超冷费米气体的Efimovian 膨胀动力学的实验结果和普适的动力学特性, 并且对超冷费米气体超级Efimovian 膨胀动力学原子团大小以及能量的双对数标度振荡行为展开了讨论和分析.本综述以强相互作用费米气体为研究主体, 介绍了最近强相互作用超冷费米气体膨胀动力学的最新研究进展, 主要对超冷费米气体在少体和多体动力学研究、 新奇非平衡动力学探究等方面展开了深入讨论.

2

-->

2.1.强相互作用超冷费米气体的各向异性展开

类似超冷费米气体存在高温超导特性, 超流体也是超冷费米气体具有的一大特性. 在超冷费米气体接近零温的情况下, 流体中存在的量子黏度越来越小, 费米流体越来越接近超流体, 通过对超流体所具有的流体力学性质^[2,22]、量子化涡旋^[8]、原子成对效应^[23,24]等进行深入探索研究, 可以进一步提高人们对超流体性质的深入认知.
2002年, 美国杜克大学的 O'Hara等^[2]利用全光俘获的方法获取了强相互作用的⁶Li超冷费米气体, 并且首次观测了强相互作用费米气体的各向异性膨胀过程. 在实验中, 他们使用外加磁场来进行原子的Feshbach共振, 使三维“雪茄型”费米气体处于强相互作用区域, 当快速关掉光阱使原子气体自由地在三维空间飞行膨胀时, 发现其膨胀过程展现出图1(a)中所示的情形, 原子气体的纵横比很快发生颠倒, 体现为各向异性的动力学膨胀, 这是由于原子间强烈的散射碰撞导致的. 对于稀释的原子气体而言, 原子间间距相对较大, 原子间短程相互作用长度一般会远小于原子间距, 利用Feshbach共振技术可以将超冷原子将s波散射长度调至远大于原子间距, 此时原子间的散射碰撞将占据主导作用, 费米原子气体也因此展现出各向异性的“椭圆流动”行为^[2]. 而对于无相互作用的费米气体, 由于原子气体间没有散射碰撞, 在足够长的时间后原子的动量分布将趋向于各向同性, 最终在空间中原子气体将形成趋向于球形. 因此这种各向异性膨胀过程不会发生在无相互作用的费米气体中, 无相互作用原子气体的纵横比不会超过1, 如图1(c)所示.
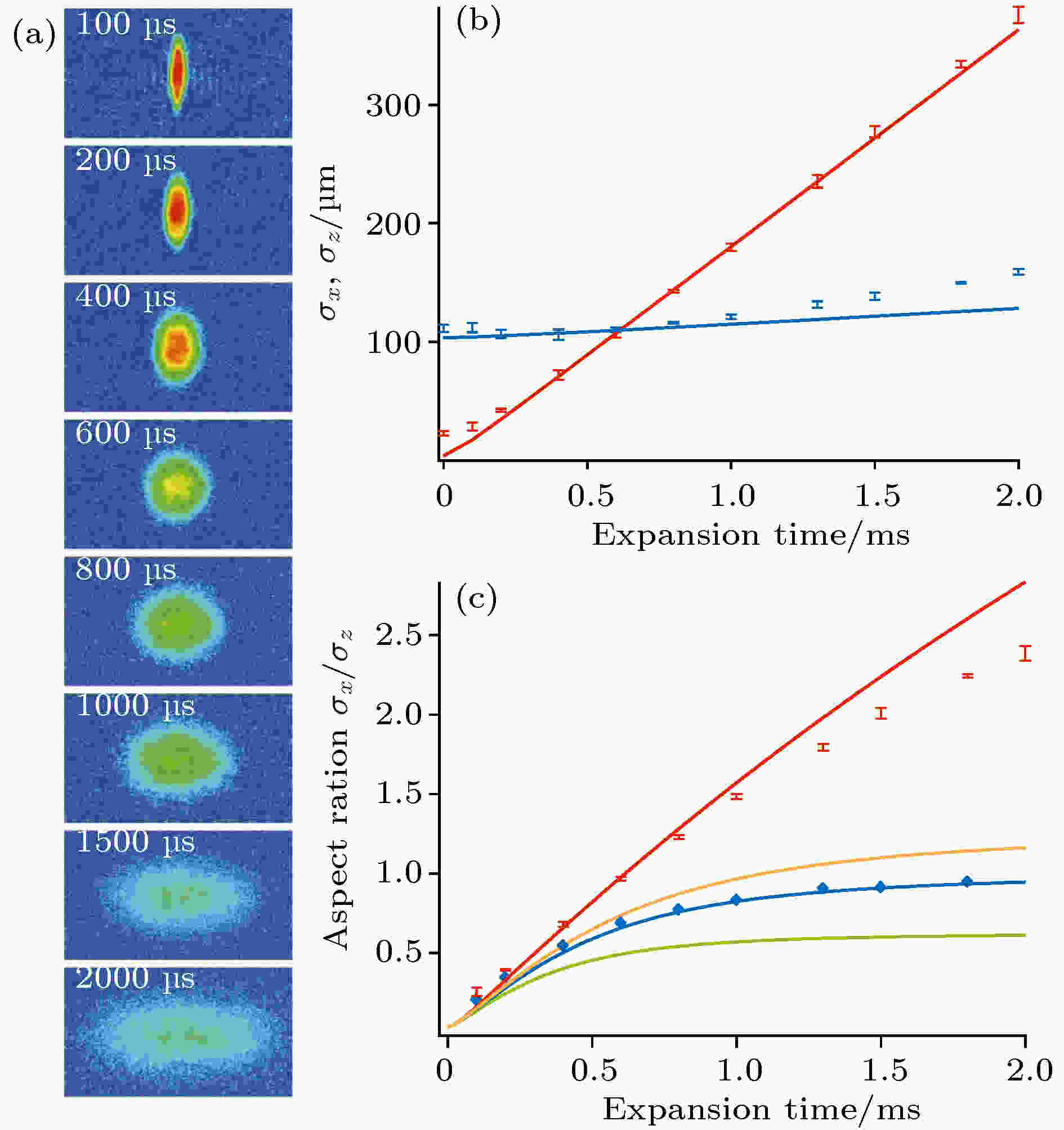图 1 (a)强相互作用超冷费米气体的各向异性膨胀吸收成像图; (b)原子团不同方向的非平衡动力学膨胀行为; (c)不同相互作用下原子团的纵横比大小演化图^[2]
Figure1. (a)The absorption image of the anisotropic expansion dynamics in strongly interacting Fermi gas; (b) the non-equilibrium dynamical expansion behavior in different directions; (c) the evolution for the aspect ratio of the atomic cloud under different interaction regime^[2].

强相互作用超冷费米气体各向异性的动力学膨胀行为是超冷费米气体原子间超强相互作用最直观的体现, 曾一度作为费米超流体的有力证据. 不仅如此, 强相互作用超冷费米气体的各向异性膨胀还与系统中存在的量子黏度^[25]有着紧密的联系. 当系统中量子黏度增大时, 原子气体的动量分布将从快速膨胀的径向方向流向缓慢膨胀的轴向方向, 进而使得原子气体的纵横比逐步缩小, 这一特性还可以用于测量费米流体中的量子黏度系数以及熵^[3,20,25,26].
在理论方面, 2002年意大利特伦托大学的Menotti等^[27]做出了重要的贡献. 在研究中, 从平衡态超流费米气体的流体力学出发, 研究了系统的连续性方程和欧拉流体方程, 利用Landau-Vlasov方程以及标量变换方程^[28], 成功推导了三维谐振子阱中强相互作用费米气体的动力学方程, 较为完备地描述了超流态强相互作用费米气体BEC-BCS渡越区域的飞行时间动力膨胀行为. 研究结果可以用以下方程来表示:

$n(x, y, z, t)=(b_xb_yb_z)^{-1}n_0\left(\dfrac{x}{b_x}, \dfrac{y}{b_y}, \dfrac{z}{b_z}, t\right), $

$\ddot{b}+\dfrac{\omega^2_i}{(b_xb_yb_z)^\gamma}=0,$

其中$ n $为原子气体的密度, $ b $为标量参数, $ \omega $表征系统的谐振子阱, $ \gamma $表征原子间相互作用强度, 在相互作用强度趋于无穷大的Feshbach共振点处, $ \gamma $值为2/3. 此动力学方程具有很大的普适性, 不仅可以用来描述超冷费米气体的BEC-BCS渡越, 还可以用来描述其他系统, 比如相互作用的玻色系统中$ \gamma=1 $^[29,30].
2 -->

2.2.超冷费米气体的标度不变性及其对称性破缺

标度不变物理系统有一个鲜明的特征, 系统中缺乏有效特征长度标度, 使得连接不同物理领域的重大进展成为可能. 在超冷费米气体中, 原子气体间的s波散射占据主导作用, 超冷原子间相互作用可以通过Feshbach 共振技术来调节, 在原子间相互作用趋于0时可以形成无相互作用费米气体, 而原子间散射长度趋于无穷大时会形成幺正费米气体. 对于无相互作用费米气体, 原子间散射长度为0, 幺正费米气体中原子散射长度趋于无穷, 更是远大于原子间距, 因此对于这两种特殊情形, 系统中原子间距成为了唯一标度, 都将体现出标度不变的动力学对称特性. 在标度不变动力学对称性下, 超冷费米量子气体的局域关联函数在演化过程中是自相似的, 因此其热力学流体性质可以通过一个简单的坐标含时标量因子变换来描述, 极大地简化了多体非平衡系统动力学的复杂性, 可以激发许多少体和多体动力学的研究, 在热力学和流体力学方面产生许多普适的动力学规律^[19,31-33].
超冷原子气体从谐振子阱中自由展开时, 在强相互作用区域原子气体不仅仅体现出“椭圆流动”的行为, 其均方原子团大小$ \langle{{r}}^2\rangle=\langle x^2+y^2+z^2\rangle $也呈现出标量动力学特征^[34]. 这一标量动力学展开行为被Elliott 等^[34]在实验上证实, 如图2所示, 他们发现当标度不变的费米气体在飞行时间展开时, 原子气体的均方原子团大小$ \langle{{r}}^2\rangle $有着普适的飞行时间$ t^2 $标量关系, 无论是无相互作用费米气体还是幺正费米气体均遵从这一规律.
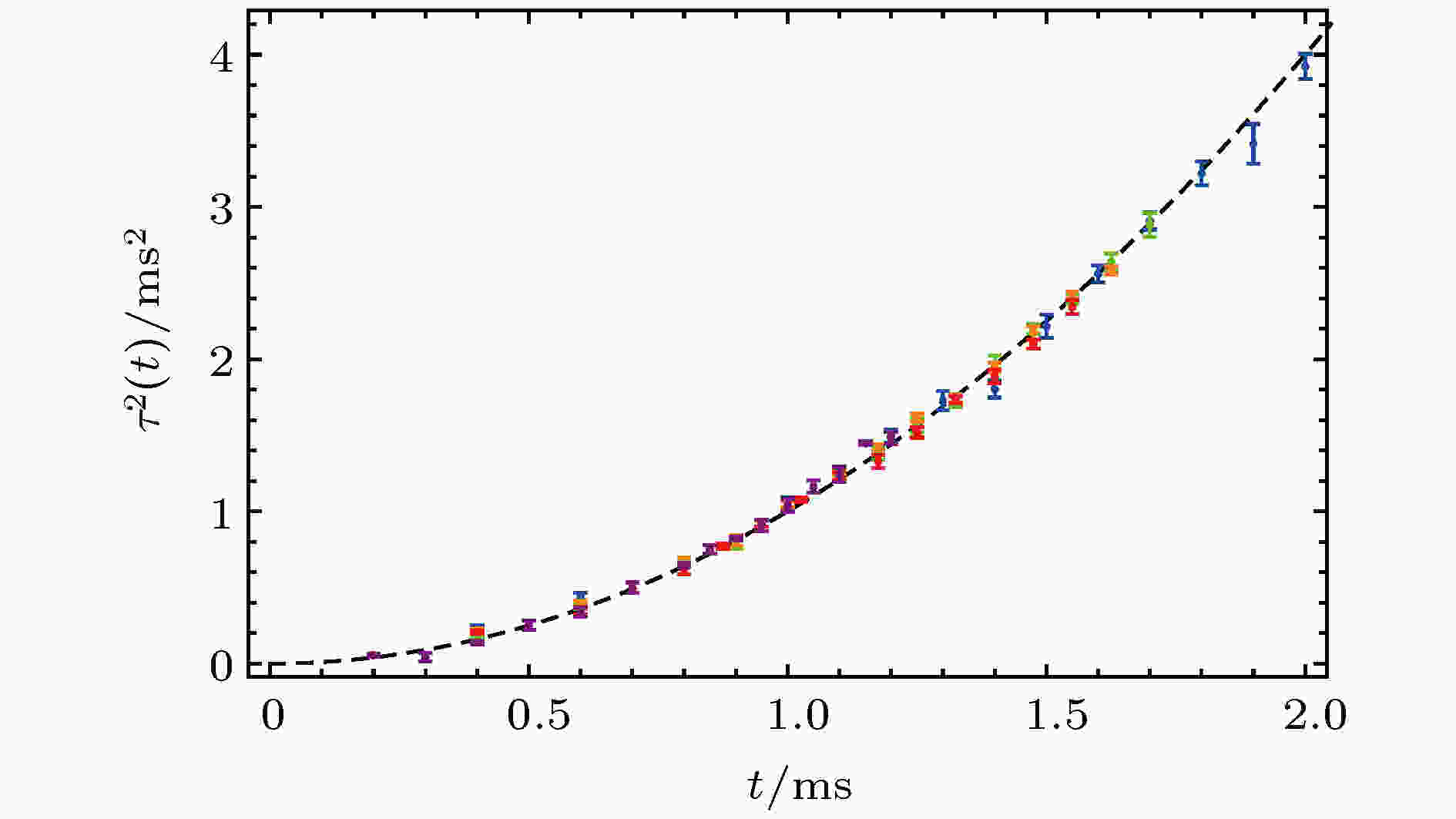图 2 幺正费米气体和无相互作用费米气体的标度不变展开动力学^[34]
Figure2. Scale invariant expansion of a resonantly interacting Fermi gas compared with the non-interacting Fermi gas^[34].

在强相互作用幺正区域, 当原子气体从偶极阱中自由展开时, 由于原子气体间的体黏滞阻力和局域非平衡态带来的压力对原子气体的自由膨胀过程影响较小, 尽管原子气体有着各向异性的动力学膨胀行为, 原子气体的整体均方原子团大小$ \langle{{r}}^2\rangle=\langle x^2+y^2+z^2\rangle $仍旧维持着飞行时间$ t^2 $标量关系. 而当散射长度有限时, 系统的标度不变对称性得到破坏, 费米量子流体中的体黏滞阻力加大, 并且出现了由标度对称性破缺所产生的费米压力, 这些阻力与原子间的散射长度有着相同的符号, 致使在散射长度为正的BEC区域阻碍原子气体的自由展开, 在散射长度为负的BCS区域使得原子气体的膨胀速度加快, 因此呈现出如图3所示的动力学情形.
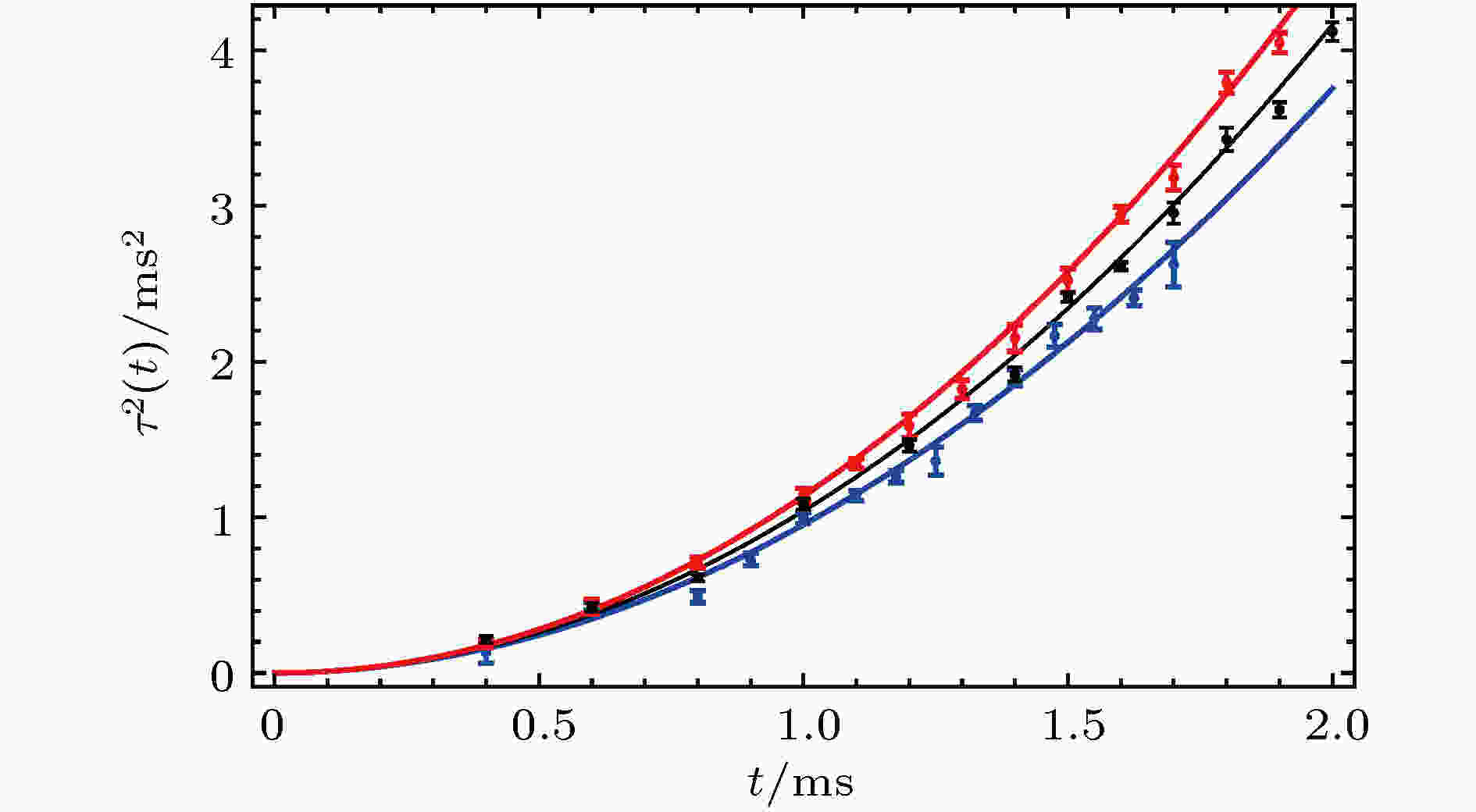图 3 Feshbach共振点附近费米气体膨胀动力学的对称性破缺行为, 从上到下依次为BCS区域、幺正区域和BEC区域^[34]
Figure3. Conformal symmetry breaking in the expansion for a Fermi gas near a Feshbach resonance. Top: BCS region; Center: unitary region; Bottom: BEC region^[34].

这一实验结果证实了两个问题: 首先, 在强相互作用超冷费米气体的各向异性膨胀过程, 费米气体仍然维持着标度不变对称性; 其次, 在流体力学膨胀中费米压强$ P $与能量密度$ \varepsilon $之间存在着定量的依靠关系$ P=\dfrac{2}{3}\varepsilon $. 在有限散射长度的情形下, 系统的标度不变性将不再能够维持, 原子气体中也会产生由标度对称性破缺所产生的费米压强差.
2 -->

2.3.超冷费米气体的Efimovian新奇膨胀动力学

3 -->

2.3.1.超冷费米气体的Efimovian动力学

Efimovian膨胀动力学^[16]是近年来超冷费米气体膨胀动力学研究中一个非常重要的研究内容, 在标度不变性对称性下, 当超冷费米气体所处谐振子阱的频率按照$ 1/t $关系连续变化时, 原子团的膨胀过程将会随着时间变化出现一系列分离的平台结构, 在每一个平台附近费米气体几乎停止膨胀, 平台的位置和大小构成了一个等比数列, 呈现出指数周期式分布. 这种新奇的动力学膨胀过程和三体物理中的Efimov效应^[35-38]有着类似的数学表达式, 是由量子费米原子气体所具有的对称性决定的, 只有在空间和时间上同时具有标度不变性的时候才会出现. 而当超冷费米气体原子间相互作用为有限值时, 标度不变对称性遭到破坏, 此时系统的量子化平台结构也不再能够维持^[39].
在Efimovian 膨胀动力学的实验中, 华东师范大学的武海斌研究组利用两束交叉光偶极阱构成原子气体的谐振子阱, 利用磁场Feshbach的技术来调控原子气体间的相互作用强度, 分别在无相互作用费米气体和幺正费米气体中进行了实验观察, 结果如图4(d)和图4(e)所示. 当谐振子频率按照$ 1/\sqrt{\lambda}t $变化且$ \lambda $<4时, 原子气体的膨胀过程会出现一系列的量子化平台结构, 且每个量子化平台所处的时间和原子团的大小均呈现出周期式的离散化指数规律. 随着无量纲因子$ \lambda $的逐渐变大, 系统的平台结构数目逐步减少且平台间距逐渐加大, 最终在$ \lambda $=4 的时候达到阈值点, 趋近于连续分布. 而在图4(d)和图4(e)中大于4的左侧灰色区域, 原子气体膨胀过程不存在量子化平台结构, 原子气体表现出连续的对称性.
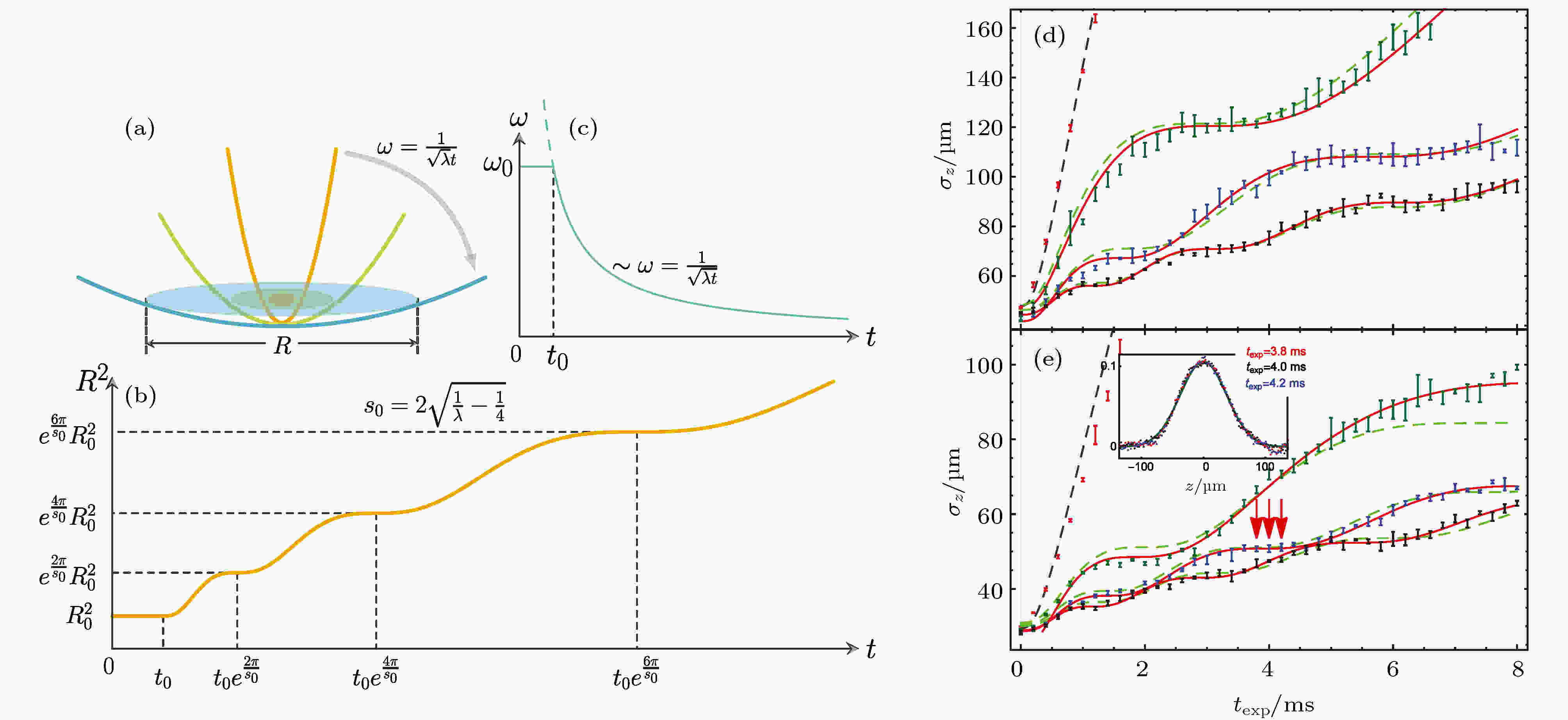图 4 Efimovian膨胀动力学示意图　(a), (b)原子气体所处谐振子阱频率的变化过程; (c)Efimovian 膨胀动力学的理论预测; (d), (e)分别代表无相互作用费米气体和强相互作用费米气体的Efimovian 膨胀动力学的实验观测结果^[16]
Figure4. The Efimovian expansion dynamics: (a) and (b) are the evolution of the harmonic trap frequency; (c) the prediction of the Efimovian expansion dynamics; (d) and (e) are the experimental observation of the Efimovian expansion in non-interacting Fermi gas and unitary Fermi gas respectively^[16].

类似于在超冷原子气体中观测的Efimov 三体束缚态的离散化束缚能^[36], Efimovian动力学膨胀过程也受因子$ s_0 $控制, 其动力学膨胀行为可以用数学表达式描述如下:

$\dfrac{\langle\hat{R}\rangle^2(t)}{R_{0}^2}=\dfrac{t}{t_{0}\sin^2\varphi}[1-\cos\varphi\cos{(s_0\ln{\dfrac{t}{t_{0}}}+\varphi)}], $

其中$ s_0=\omega_{\rm b}\gamma $, $ \gamma=\sqrt{1/\lambda-1/4} $, $ \varphi=-\arctan{s_{0}} $. 如图5(a)所示, $ \omega_{\rm b} $与原子气体的集体激发模有关, 在无相互作用费米气体中数值为2, 在幺正费米气体中实验结果接近$ \sqrt{12/5} $, 与三维幺正费米气体长轴的集体激发模式有着相同的因子^[40-42]. 图5(b)表明, 费米气体在量子简并附近, $ s_0 $随$ \gamma $呈线性变化且比值与原子的集体激发频率因子相同, 在一定范围内原子数目的多少以及温度的高低不影响Efimovian膨胀动力学.
图 5 Efimovian膨胀动力学的普适性　(a) Efimovian 膨胀动力学与原子间相互作用的关系; (b) Efimovian 膨胀动力学与原子数目、温度间的关系; (c), (d)无量纲化后的普适Efimovian 动力学膨胀图^[16]
Figure5. The universality of the Efimovian expansion dynamics: (a) The Efimovian expansion with different interaction regime; (b) the Efimovian expansion with different atoms' number and temperature; (c) and (d) are the universal dimensionless Efimovian expansions^[16].

对比在不同相互作用下的超冷费米气体的Efimovian膨胀动力学行为, 研究发现当$ s_0 $相同时, 幺正费米气体和无相互作用费米气体有着相同的动力学膨胀规律, 方程(3)可重新表示为

$\bar{R}_z^2=\dfrac{\bar{t}}{\sin^2{\varphi}}[1-\cos{\varphi}\cos{(s_0\ln{\bar{t}}+\varphi)}], $

其中$ \bar{R}_z=R_z(t)/R_z(0) $为原子气体的膨胀率, $\bar{t}= $$ (t_{\rm {exp}}+t_0)/t_0 $为无量纲相对时间, $ \bar{R}_z $只与$ \bar{t} $和$ s_0 $相关, Efimov膨胀动力学对无相互作用费米气体和幺正费米气体是普适的. 图5(c)和图5(d)共同展示了不同相互作用下标度不变费米气体在相同$ s_0 $情况下的膨胀动力学, $ s_{0} $取值分别为10.53和5.88. 该研究结果表明, Efimovian膨胀动力学是普适的物理规律, 适用于所有的标度不变系统.
在偏离Feshbach共振点、散射长度有限的BEC和BCS区域, 超冷费米气体的Efimovian膨胀动力学的量子化台阶显然也将不再能够维持, 原子气体中存在的体黏滞阻力和对称性破缺所带来的压强差会阻碍或者加速原子气体的动力学膨胀行为, 进而使得量子化平台结构发生破坏和偏离. 可以想像的是, 随着台阶数目的增加, 标度不变对称性破缺带来的影响会逐步增加, 量子化平台结构的破坏也会变得愈加严重.
3 -->

2.3.2.超冷费米气体的超级Efimovian膨胀

基于超冷费米气体的标度不变性, 在谐振子频率按照$ 1/\sqrt{\lambda}t $变化时, 原子气体呈现出可控的时间-空间离散的Efimovian动力学膨胀行为, 这与三体物理中著名的Efimov效应十分相像. Efimov 效应是基于三个相互作用的玻色子在三维空间s波相互作用下形成的, 在一定的情况下, 三个玻色子可以形成无限多离散的三体束缚态. 近期有理论研究发现, 三个费米子在二维空间p波相互作用下也可以形成类似的三体束缚态, 被称为超级Efimov效应^[43]. 超级Efimov效应的能量本征值不再是简单的指数依靠关系, 而是呈现出双指数的标量行为, $ E_n=E_0 {\rm e}^{-2{\rm e}^{{\text{π}} n/\bar{s}_0+\theta_0}} $($ \bar{s}_0=4/3 $, $ \theta_0 $是短程相互作用参数). 然而较大的标量因子以及双指数依靠关系的存在使得三体束缚态间的能量比值变得非常巨大, 即便有理论证明可以通过采用不同质量的原子种类来缩小这一差值^[44,45], 超级Efimov效应目前在实验中仍旧难以观测.
近期有理论提出可以在标度不变费米气体中开展动力学超级Efimov效应的研究^[46], 并且很快就被实验证实^[42]. 当超冷费米气体的频率按照$ \sqrt{1/4t^2+1/t^2\lambda\log^2(t/t_*)} $变化并且$ \lambda < 4 $时, 原子气体的膨胀动力学方程可以表述为

$\langle R^2\rangle=At\log(t/t_*)\{{1+B\cos[s_0\log{(\log{t/t_*})}+\varphi]}\}. $

实验结果如图6所示, 在时间和空间坐标下超冷费米气体无论是在无相互作用下(图6(c))下还是处于幺正区域(图6(a))均呈现出与Efimov效应类似的时间空间离散结构, 而将其转化到双对数坐标下(图6(b)和图6(d))原子团大小清晰地展现出正弦振荡的行为, 表征出原子气体膨胀过程中所显现的双对数依赖关系.
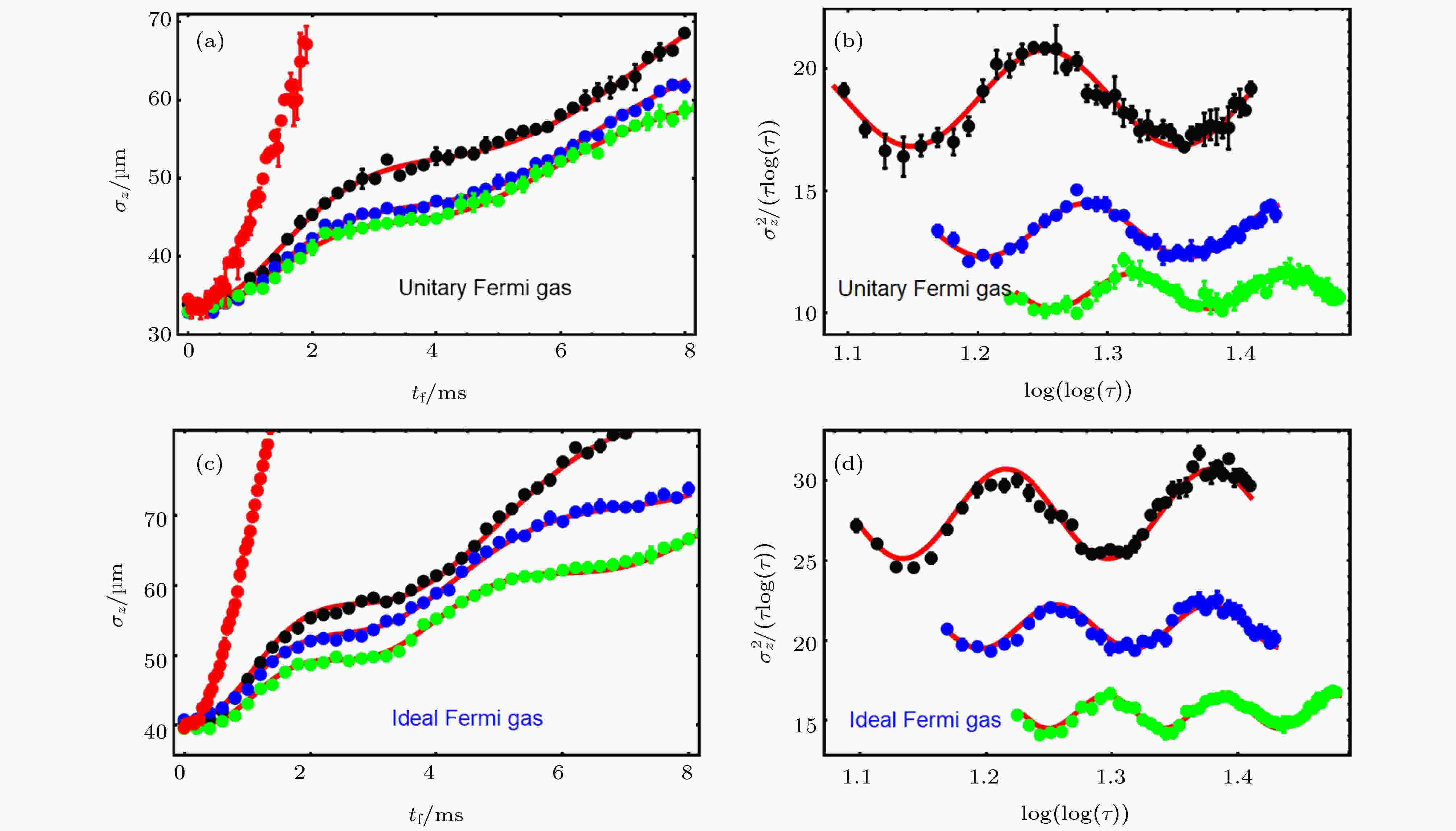图 6 超级Efimovian 膨胀动力学实验结果　(a)和(c)分别表示幺正费米气体和无相互作用费米气体的超级Efimov 动力学效应; (b)和(d)表示在时间双对数标度下相应原子团大小的振荡行为^[42]
Figure6. The experimental observation of dynamical super Efimovian expansion. (a), (b) and (c), (d) are the mean axial cloud size versus the expansion time and the dimensionless axial mean square cloud size versus the dimensionless time in the unitary Fermi gas and ideal Fermi gas, respectively^[42].

值得一提的是, 超级Efimovian动力学膨胀过程中不仅原子团大小呈现双对数依赖关系, 其能量本征值也符合双对数标量关系. 谐振子阱中的量子气体的能量可以认为势能和内能之和, 内能包括原子气体的动能和相互作用能. 如图7所示, 在无相互作用费米气体中, 由于相互作用能为零, 系统可以简单地认为只存在势能和动能, 随着超级Efimovian动力学膨胀行为的进行, 原子气体的内能和势能同步减少, 且内能和势能存在很大程度的周期式交换过程, 其能量交换的周期刚好和超级Efimovian动力学效应的振荡周期相同. 超级Efimovian动力学过程中内能和势能均符合双对数指数标度关系, 且振荡周期相同, 相位相差$ {\text{π}} $.
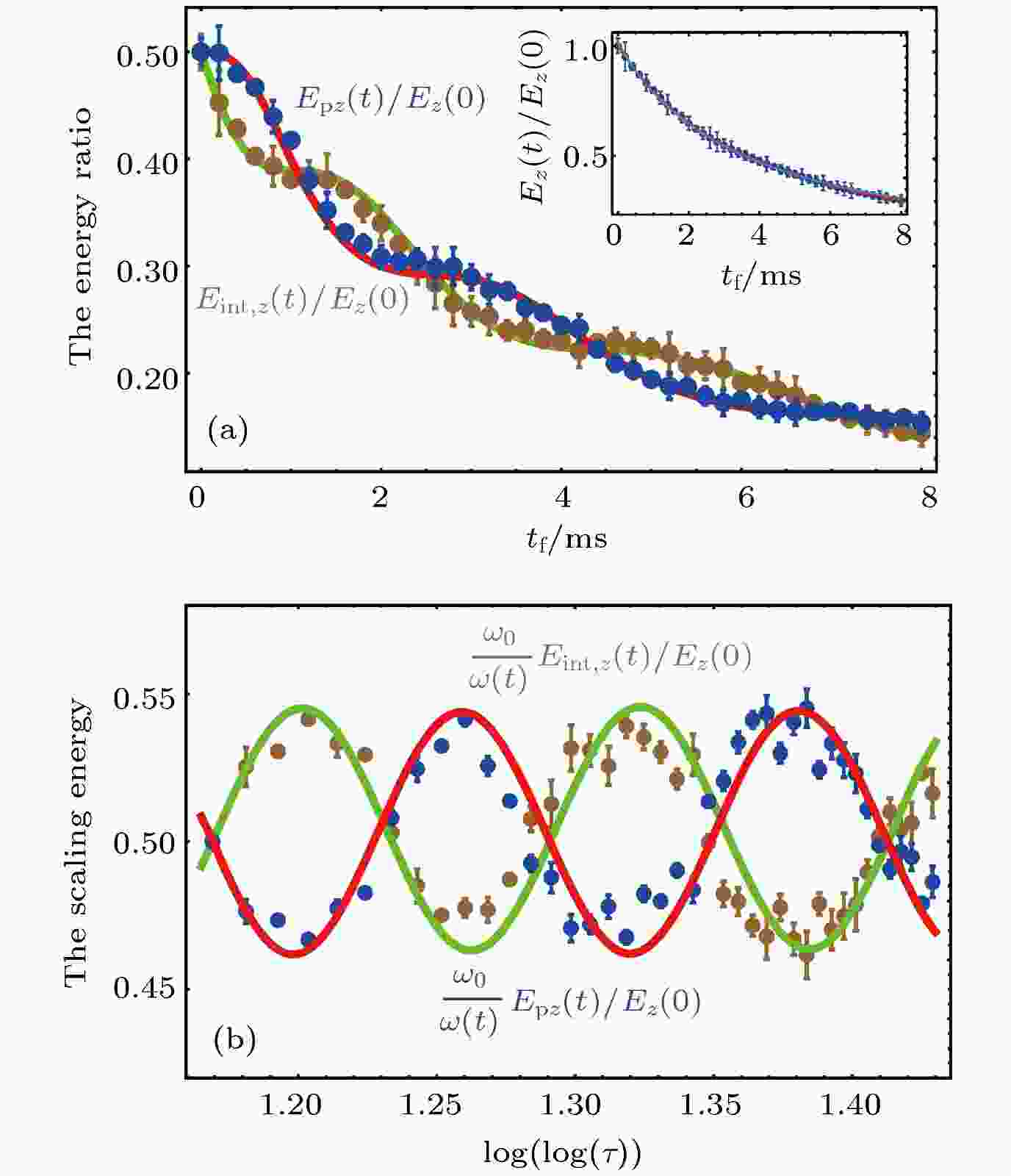图 7 超级Efimovian 膨胀过程中的内能和势能在时间(a)及其双对数标度(b)下的变化示意图^[42]
Figure7. The axial potential (internal) energy ratio versus expansion time (a) and the axial energy scaling versus dimensionless time (b) for the super Efimovian expansion^[42].

近期河海大学的Zhang等^[47]用标度理论对不同构型、不同相互作用情形的动力学超级Efimov效应开展了拓展研究, 研究发现在对称性破缺的情形下超级Efimov动力学行为仍旧可以呈现出双对数周期振荡的行为, 但是在BEC区域振荡行为将表现为偏离中心向下振荡, 而相应的BCS区域则表现为偏离中心向上振荡, 这种行为可以用来区分不同类型的超流特性.

超冷费米气体的研究是当前冷原子分子物理的重要研究方向之一, 强相互作用超冷费米气体的膨胀动力学更是有着非常重要的研究意义. 当费米气体处于强相互作用幺正区域时, 超冷的费米气体原子间散射长度趋于无穷, 费米多体系统除原子间的距离外不再具有特征长度, 表现出普适的热力学特性, 具有标度不变性的对称性. 重要的是这一膨胀动力学行为是普适的行为, 可以拓展至其他标度不变的系统中, 比如一维Tonk气体和二维弱相互作用量子气体等, 这些系统中的行为需要进行进一步的实验验证.
本文介绍的工作均是在标度不变系统中进行的研究工作, 此时的超冷费米气体为无相互作用或者散射共振状态. 然而当系统偏离散射共振时, 散射长度变为具体有限的大小, 系统的标度不变性将遭到破坏, 相应的膨胀动力学也将发生改变甚至原有的特性都会被破坏. 研究散射长度从零变为无穷大过程中原子气体的膨胀动力学有助于人们更加清晰地认知少体和多体物理, 以及理解碰撞散射过程的机理. 对于某些鲜明的动力学特征如Efimovian膨胀动力学的离散周期特性是否能够保持仍旧需要探索, 相应周期长度之间的关系还需要进一步的研究.
可以预见的是, 强相互作用超冷费米气体的非平衡动力学是未来比较前沿的研究课题, 有许多新奇的非平衡动力学课题还未解决. 比如低温原子气体散射长度突然改变时多体系统的膨胀动力学如何改变, 以及在此变化条件下如何探索量子气体中原子对能带间隙的大振幅和低振动频率的振荡的集体行为, 这对于研究孤立强相互作用费米气体的准热化、热化和热平衡过程有较大意义.
总的来说, 研究强相互作用超冷费米气体的膨胀动力学意义深远, 在这样的超冷超强相互作用的标度不变费米气体中, 通过精确调控外加俘获势和原子间相互作用强度, 构成了一个基本的测试少体和多体物理的理想系统, 对于新奇非平衡动力学操控和探测有着深远的影响.
感谢清华大学翟荟教授、中山大学俞振华教授、中国人民大学齐燃副教授, 以及美国Adolfo Del Campo教授的合作与讨论.