摘要:利用多物理场耦合有限元法对结构和流体适应性强、抛物方程声场计算高效准确的特点, 提出了三维浅海波导下弹性结构声振特性研究的有限元-抛物方程法. 该方法采用多物理场耦合有限元理论建立浅海下结构近场声辐射模型, 计算局域波导下结构声振信息, 并提取深度方向上复声压值作为抛物方程初始值; 然后采用隐式差分法求解抛物方程以步进计算结构辐射声场. 重点介绍了该方法对浅海下结构声辐射计算的准确性、高效性以及快速收敛性后, 对Pekeris波导中有限长弹性圆柱壳的声振特性进行了分析. 研究得出, 当圆柱壳靠近海面(海底)时, 其耦合频率比自由场下的要高(低), 当潜深达到一定范围时, 与自由场耦合频率基本趋于一致; 在低频远场, 结构辐射场与同强度点源声场具有一定的等效性, 且等效距离随着频率增加而增加; 由于辐射声场受结构振动模态、几何尺寸和简正波模式影响, 结构辐射场传播的衰减规律按近场声影响区、球面波衰减区、介于球面波和柱面波衰减区、柱面波衰减区四个扩展区依次进行.
关键词: 浅海波导/
弹性圆柱壳/
有限元-抛物方程法/
声振特性

English Abstract

全文HTML

--> --> -->

弹性圆柱壳作为水下潜器、运输管道和海洋技术仪器等典型的简化结构, 对其声振特性研究也一直是国内外研究者关注的重点. 弹性结构在水下振动时, 会产生结构与周围流体介质声的耦合作用即流固耦合, 已有大量****对这种单一耦合作用下典型弹性圆柱壳声振特性进行了深入研究, 为后续开展板壳振动与声辐射的深入研究奠定了理论基础^[1?3]. 然而, 在实际工程中, 流体域往往存在一个或多个边界, 对于具有一个边界的半空间下结构声辐射的研究相对较早, 国内外****相继提出了多种方法^[4?11], 并取得了一定的研究成果.
对于具有上下边界的浅海下弹性结构声辐射的研究, 因涉及流-固耦合、辐射声与边界耦合、反射声与结构耦合等多个物理场耦合, 加上受海底地形多变、底质复杂、声学参数多等因素的限制, 具有较大难度. 早期的研究工作集中于理想浅海波导(海面软边界、海底硬边界)下典型结构声辐射研究, 如Soni等^[12]通过薄壳理论、伯努利方程以及上下边界条件建立浅水域下平板的声振理论模型; Ergin等^[13]分别采用实验法和三维声弹性理论模型研究了自由界面和刚性界面对浸没圆柱壳声辐射特性的影响; 白振国等^[14]采用虚源法分析了波导下圆柱壳远场辐射声场的衰减规律; 为了掌握上下边界对结构声振特性的影响规律, Wang等^[15]采用镜像法结合模态附连水质量法得出了浅海上下边界对结构耦合振动频率的影响规律. 为了提高研究方法对复杂结构和浅海环境的适应性, Sarkissian^[16] 、商德江等^[17]分别采用波叠加法(CWSM)进行了浅海波导下弹性结构的声散射、声辐射的有效计算; 同时, Zou等^[18]、Jiang等^[19]根据三维声弹性理论, 提出了可调整格林函数结合声场积分的方法, 进行了浅海水域下舰船辐射噪声的研究. 虽然波叠加和三维声弹性理论均可通过调整格林函数进行不同浅海下结构辐射声场计算, 为解决复杂浅海波导下任意结构声辐射问题提供了新思路, 但两种方法均需在结构内部(或表面)布放若干个虚拟源, 涉及大量虚拟源的优化配置和反向求解, 其研究过程的简便性和高效性有待提高. 这就需要探索一种适应性更强、具有可操作性和效率更高的新方法.
浅海波导下弹性结构声辐射研究需要结合海洋声传播相关理论来重点考虑结构辐射场的传播问题, 针对简谐点源的声传播问题, 各国****主要采用抛物方程法、简正波法、波数积分法以及耦合简正波抛物法等多种方法进行海洋声传播、海洋声反演和声场测量、预报等领域的研究^[20?22]. 其中抛物方程(PE)法是目前较为简便且高效的波动理论方法, 该方法的优点在于其构成了距离初始问题, 只要给定初始距离上沿深度方向分布的源场, 便可按距离步进的数值技术进行求解, 其计算过程简单、效率高、对浅海环境适应性好. 目前已有大量的研究不断提高了PE计算的精度、速度和适应性^[23], 使得PE已能够解决楔形的液-液^[24]、固-固^[25]和液-固^[26]交界面以及无限大边界^[27]等复杂边界下的声传播问题, 并由标准二维PE拓展为三维PE声场问题^[28], 不断完善了PE在不同海洋环境下的理论模型, 使其应用范围更加广泛.
浅海波导下弹性结构声辐射研究还要需要重点关注三维结构源的声振特性, 而对于目前多边界耦合影响下的结构声振问题, 解析法难以建立理论模型, 实验法代价大且周期长. 有限元法(FEM)对弹性结构和周围流体环境适应性强, 能方便地解决多边界耦合环境下结构的声振问题, 已成功应用于浅海波导下弹性结构的声辐射研究^[29]. 但因涉及有限元网格划分, 其计算能力受到分析频率、结构尺寸以及声场计算距离的严重限制，所以一般采用有限元法建立近场局域流体下的结构中低频声辐射模型, 计算获取近场声场信息, 然后再结合其他方法进行远程声场计算, 如有限元/波叠加法^[17]、有限元/声弹性理论^[19]、有限元/边界元法^[30]等, 以有效地进行浅海下弹性结构声辐射研究.
综上, 为了高效准确地研究浅海波导下弹性结构声振特性和辐射场传播问题, 本文利用FEM对结构、流体环境适应性强和PE法对声场计算快速准确的优点, 提出了浅海波导下弹性结构声辐射快速计算的有限元-抛物方程法(FEM-PE). 该方法首先通过多物理场耦合FEM理论建立三维浅海波导下近场低频声辐射模型, 计算获取结构在近场的声振特性; 最后, 采用N个二维 (2D)的PE进行三维浅海波导下弹性结构远场声辐射的快速预报. 并从声场计算的准确性、收敛性和高效性三个方面重点说明了该方法对浅海波导下结构辐射场计算的优势后, 对Pekeris波导下有限长圆柱壳的振动特性和辐射场传播进行了研究分析, 得出了浅海波导上、下边界对三维弹性结构耦合模态频率、辐射声场传播以及衰减特性的影响规律, 为后续开展复杂浅海波导环境下结构声辐射预报、声学测量和声源识别等领域的研究提供了一种新途径.

如图1所示, 建立三维浅海波导下的弹性结构声辐射预报的FEM-PE理论模型. 该理论模型主要由两部分组成: 多物理场耦合FEM近场声场计算域, 即采用多物理场耦合FEM理论建立三维浅海波导下复杂弹性结构(潜深为$h$)近场声辐射模型, 计算获取距结构中心一定距离${r_0}$处的声场信息; PE声场计算域, 即采用FEM在深度方向上已求解的复声场信息作为FEM与PE的耦合条件, 即PE初始声场, 采用分段三次Hermite插值法对FEM计算结果与PE初始场进行空间格点匹配后, 采用隐式的有限差分法求解PE, 以计算距离结构r处的声场P.
图 1 浅海波导下结构声辐射FEM-PE计算原理图
Figure1. Principle of FEM-PE in shallow water.

2

-->

2.1.多物理场耦合FEM理论

由理论模型可知, FEM计算结果作为PE声场计算的初始条件, 所以FEM理论建模部分变得尤为重要, 其计算准确性直接影响到PE声场计算的精度和整个研究过程的可靠性, 需要采用合适的FEM理论建立浅海波导下结构声辐射的准确模型. 不同于其他流体环境下结构声振问题, 浅海波导下结构声振特性将受上下界面的重要影响, 且还受海底类型多、声参数复杂、地形多变等因素的限制, 声振数值建模难度大大增加. 传统FEM难以建立这种复杂流体环境下的结构声辐射准确模型, 本文采用多物理场耦合FEM理论联立求解多个耦合子系统及控制方程, 计算多个物理场共同耦合作用下结构声振信息. 浅海波导下弹性结构声辐射问题涉及流-固耦合、声边界耦合和无限大边界等声学耦合边界处理, 多物理场耦合FEM可建立声学波动方程、无限远边界和上下边界相互之间的耦合作用和连续条件^[17].
在结构表面与外部流体接触的耦合面上, 满足的结构表面法向振动速度与外部流体介质的振动速度相同, 可写出结构与流体的耦合方程为

$\begin{split}&\left( {\left[ {\begin{array}{*{20}{c}} {{K_{\rm s}}}& {{K_{\rm \tau} }} \\ 0& {{K_{\rm w}}} \end{array}} \right] + {\rm j}\omega \left[ {\begin{array}{*{20}{c}} {{C_{\rm s}}}& 0 \\ 0& {{C_{\rm w}}} \end{array}} \right] }\right.\\&-\left.{{\omega ^2}\left[ {\begin{array}{*{20}{c}} {{M_{\rm s}}}& 0 \\ { - {\rho _0}K_{\rm \tau} ^{\rm T}}& {{M_{\rm w}}} \end{array}} \right]} \right)\left[ \begin{gathered} {u_i} \\ {p_i} \\ \end{gathered} \right]=\left[ \begin{gathered} {F_{{\rm st}}} \\ {F_{{\rm wt}}} \\ \end{gathered} \right]\end{split},$

其中刚度矩阵${{ K}_{ij}}$和阻尼矩阵${{ C}_{ij}}$、质量矩阵${{ M}_{ij}}$均为$n \times n$阶矩阵, 下标w, s和${\rm \tau} $分别表示声学矩阵、力学结构矩阵和耦合矩阵. 定义耦合矩阵${{ K}_{\rm \tau} }$,${{ M}_{\rm \tau} }$为

$\begin{split}&{{ K}_{\rm \tau} }=\sum\limits_{e=1}^{{n_{_{{\rm s}e}}}} {\left( {\int_{{\varOmega _{{\rm s}e}}} {(N_s^{\rm T}\left\{ {{n^e}} \right\}{N_{\rm w}}){\rm d}\varOmega } } \right)},\\ &{{ M}_{\rm \tau} }=\sum\limits_{e=1}^{{n_{_{se}}}} {\left( {\int_{{\varOmega _{{\rm s}e}}} {({\rho _0}N_{\rm w}^{\rm T}\left\{ {{n^e}} \right\}{N_{\rm s}}){\rm d}\varOmega } } \right)}, \end{split}$

且${ M}_{\rm \tau} ^{\rm T}=- {\rho _0}{ K}_{\rm \tau} ^{\rm T}$, ${n_{_{{\rm s}e}}}$为结构与流体接触的结构网格数量, $\left\{ {{{ n}^e}} \right\}$为结构网格的法向向量; $\omega=2{\text{π}} f$为角频率, $f$为频率(Hz), ${\rho _0}$为海水密度; ${u_i}$, ${p_i}$为位移和声压幅值; ${F_{{\rm st}}}$, ${F_{{\rm wt}}}$分别为结构、流体介质声的耦合激励载荷^[31].
浅海波导的海面边界通常为Dirichlet边界, 在界面上满足声压为零, 即

${p_{\rm a}}(x, y, z)\left| {_{z=0}} \right.=0,$

其中 下标a和b分别表示海水流体层和海底层.
FEM模型与PE理论在建模环境上需要一致, 且PE主要涉及标准PE和弹性PE两种类型, 相应地, FEM理论需要建立两种典型海底交界面上连续方程. 在液态海底上满足的边界条件为声压$p(x, y, z)$连续, 法向振速$v(x, y, z)$连续,

${p_{\rm a}}(x, y, z)={p_{\rm b}}(x, y, z),$

$\frac{1}{{{\rho _{\rm a}}}}\frac{{\partial {p_{\rm a}}(x, y, z)}}{{\partial z}}=\frac{1}{{{\rho _{\rm b}}}}\frac{{\partial {p_{\rm b}}(x, y, z)}}{{\partial z}}.$

在各向同性弹性海底法向上满足位移连续和应力连续, 切向的应力为零,

$\frac{\partial }{{\partial z}}\left( {{\lambda _{\rm a}}{\varDelta _{\rm a}}} \right) + {\rho _{\rm a}}{\omega ^2}{w_{\rm b}}=0,$

${\lambda _{\rm a}}{\varDelta _{\rm a}}={\lambda _{\rm b}}{u_{r{\rm b}}} + \left( {{\lambda _{\rm b}} + 2{\mu _{\rm b}}} \right)\frac{{\partial {w_{\rm b}}}}{{\partial z}},$

$\frac{\partial }{{\partial z}}\left( {{\lambda _{\rm b}}{u_{r{\rm b}b}}} \right) + \frac{\partial }{{\partial z}}\left( {\left( {{\lambda _{\rm b}} + 2{\mu _{\rm b}}} \right)\frac{{\partial {w_{\rm b}}}}{{\partial z}}} \right) + {\rho _{\rm b}}{\omega ^2}{w_{\rm b}}=0,$

其中 u为弹性体中的水平位移; w为弹性体中的垂直位移; $\rho $为介质密度; $\lambda $, $\mu $为拉梅常数; 定义$\varDelta $为$\varDelta=\displaystyle\frac{{\partial u}}{{\partial r}} + \displaystyle\frac{{\partial w}}{{\partial z}}$.
均匀浅海环境的四周边界为声场无限远边界, 在FEM中采用完全匹配层 (PML)技术模拟, PML通过在波动方程中增加吸收系数转换为PML吸收层的控制方程, 令$x$轴为${x_1}$轴、$y$轴为${x_2}$轴, 利用分离变量可写出PML方程为

${k^2}p + \sum\limits_{i=1}^2 {\frac{{{\rm j}\omega }}{{{\sigma _i} \!-\! {\rm j}\omega }}\frac{\partial }{{\partial {x_i}}}} \left(\frac{{{\rm j}\omega }}{{{\sigma _i} \!-\!{\rm j}\omega }}\frac{{\partial {p_i}}}{{\partial {x_i}}}\right)\!=\!0,\;\;\; i\!=\!1, 2, \cdots, $

其中 ${\sigma _i}$为吸收系数; ${v_i}$, ${p_i}$分别为匹配层域的速度和声压幅值.
采用PML处理边界后, 使在边界层上满足Smerfield远场熄灭条件, 使得边界没有反射声以模拟波导四周的无限大空间, 即

$p(x, y, z)\left| {_{r=\infty }} \right.=0.$

通过流-固耦合方程、声边界耦合方程和PML技术建立浅海下结构声辐射FEM模型, 联立求解耦合系统计算获取结构表面的振动特性和近场声场信息. 但由于FEM网格划分类型和疏密程度与PE网格划分不一致, 且FEM网格划分尺寸比PE空间格点间隔小, 导致FEM在深度方向提取的离散点数比PE初始场的格点数要多, 所以FEM计算的空间声场节点信息难以完美匹配PE初始场的空间格点, 使PE声场计算不准确, 需采用合适的插值法从FEM计算复声压信息中近似求解有限个场点信息. 为了使在每个小区间上取得较好的近似结果以避免插值造成的龙格现象, 可采用收敛性强、光滑度高的分段三次Hermite法对复声压插值处理后, 再匹配PE初始场空间格点, 使PE声场计算更加精确.
为了使初始场以及PE计算声场能够更好地表征声源的源信息和辐射信息, 即FEM计算初始场包含了结构近场声能量耦合信息、PE步进计算域远离近场声影响区, 这里要求初始场距源中心的距离${r_o}$为大于最大波长(${r_o} \geqslant {\lambda _{\max }}$). 根据FEM在深度方向提取声场结果${P_{\rm f}}$, 可在建立起深度坐标${z_{\rm f}}$与声压${P_{\rm f}}$的线性关系, 则在深度方向上每个深度格点$({r_0}, z)$声场可通过以下方程获取:

$\begin{split} \psi _0^0({r_0}, z)=&{\left( {\frac{{z - {z_{k + 1}}}}{{{z_k} - {z_{k + 1}}}}} \right)^2}\left( {1 + 2\frac{{z - {z_k}}}{{{z_{k + 1}} - {z_k}}}} \right){P_{{\rm f}, k}}\\ &+{\left( {\frac{{z - {z_k}}}{{{z_{k + 1}} - {z_k}}}} \right)^2}\left( {1 + 2\frac{{z - {z_{k + 1}}}}{{{z_k} - {z_{k + 1}}}}} \right) \\& \times{P_{{\rm f}, (k + 1)}}+{\left( {\frac{{z - {z_{k + 1}}}}{{{z_k} - {z_{k + 1}}}}} \right)^2}\left( {z - {z_k}} \right)P_{{\rm f}, k}'\\& +{\left( {\frac{{z - {z_k}}}{{{z_{k + 1}} - {z_k}}}} \right)^2}\left( {z - {z_{k + 1}}} \right)P_{{\rm f}, (k + 1)}' , \end{split}$

其中${z_p}$为最小区间$\left[ {{z_k}, {z_{k + 1}}} \right]$上一点, $P_{{\rm f}, k}'$为有限元提取结果函数在节点${z_k}$处的导数值, $k=0, 1, $$2, 3, \cdot \cdot \cdot, n$, $n$为FEM提取计算结果的离散个数.
通过(10)式匹配PE初始场上各个格点的声场值$\psi _0^0({r_0}, z)$, 作为PE法声场快速计算的初始条件$\psi _0^0$， 即FEM-PE耦合条件, 然后采用PE进行声场的步进计算.
2 -->

2.2.波导下PE理论及有限差分解

采用Pappert^[32]的分离变量法, 可把轴对称坐标系下简谐源的亥姆霍兹方程简化为椭圆形波动方程^[20]

$\frac{{{\partial ^2}\psi }}{{\partial {r^2}}} + 2i{k_0}\frac{{\partial \psi }}{{\partial r}} + \frac{{{\partial ^2}\psi }}{{\partial {z^2}}} + k_0^2\left[ {{n^2}\left( {r, z} \right) - 1} \right]\psi=0,$

其中 ${k_0}$为参考波数, $n\left( {r, z} \right)={c_0}/c\left( {r, z} \right)$, ${c_0}$为参考声速.
声场$\psi $在一个波长内随距离的变化是缓慢的, 即满足$\displaystyle\frac{{{\partial ^2}\psi }}{{\partial {r^2}}} \ll 2{\rm i}{k_0}\displaystyle\frac{{\partial \psi }}{{\partial r}}$ 的“近轴近似”条件, 可得到标准抛物型方程

$2{\rm i}{k_0}\frac{{\partial \psi }}{{\partial r}} + \frac{{{\partial ^2}\psi }}{{\partial {z^2}}} + k_0^2\left[ {{n^2}\left( {r, z} \right) - 1} \right]\psi=0.$

在海水介质中声场${\psi _{\rm a}}$需满足抛物型方程, 利用泰勒级数展开可把抛物型方程(12)式变换为

$\begin{split}\frac{{\partial {\psi _{\rm a}}}}{{\partial z}}=&- \frac{{\Delta z}}{2}\left[ {\frac{{{\partial ^2}{\psi _{\rm a}}}}{{\partial {r^2}}} + 2{\rm i}{k_0}\frac{{\partial {\psi _{\rm a}}}}{{\partial r}} }\right.\\&+\left.{k_0^2(n_a^2 - 1){\psi _{\rm a}} - \frac{2}{{{{(\Delta z)}^2}}}({\psi _{\rm a}} - \psi _{j - 1}^m)} \right]\end{split}.$

同理, 在液态海底中声场${\psi _b}$满足的方程为

$\begin{split}\frac{{\partial {\psi _{\rm b}}}}{{\partial z}}=&\frac{{\Delta z}}{2}\left[ {\frac{{{\partial ^2}{\psi _{\rm b}}}}{{\partial {r^2}}} + 2{\rm i}{k_0}\frac{{\partial {\psi _{\rm b}}}}{{\partial r}} + k_0^2(n_{\rm b}^2 - 1){\psi _{\rm b}} \!\!\!\!\!\!\!\!\!}\right.\\&+\left.{\frac{2}{{{{(\Delta z)}^2}}}(\psi _{j + 1}^m - {\psi _{\rm b}})} \right].\end{split}$

通过在界面满足的边界条件((3)式、(4)式), 可建立两介质中声场关系为

$\frac{{{\partial ^2}\psi }}{{\partial {r^2}}} + 2{\rm i}{k_0}\frac{{\partial \psi }}{{\partial r}} + G\psi=0,$

其中, $G=k_0^2\upsilon + \varGamma $, $\upsilon=\displaystyle\frac{{{\rho _b}}}{{{\rho _a} + {\rho _b}}}(n_a^2 + \displaystyle\frac{{\rho _a^2}}{{\rho _b^2}}n_b^2) - 1$, $\varGamma \psi\!=\!\displaystyle\frac{2}{{{{(\Delta z)}^2}}}\displaystyle\frac{{{\rho _b}}}{{{\rho _a} + {\rho _b}}}\left( {\psi _{j - 1}^m - \displaystyle\frac{{{\rho _a} + {\rho _b}}}{{{\rho _b}}}\psi _j^m \!+\! \displaystyle\frac{{{\rho _a}}}{{{\rho _b}}}\psi _{j + 1}^m} \right)$.
如果将G写成$G\!=\!k_0^2\left( {{n^2} \!-\! 1} \right) \!+\! \displaystyle\frac{{{\partial ^2}}}{{\partial {z^2}}}$, 则(15)式与(11)式一致, 选择声场的输出分量可得到单向的波动方程^[20]

$\begin{split}\frac{{\partial \psi }}{{\partial r}}&={\rm i}{k_0}\left( {\sqrt {{n^2} + \frac{1}{{k_0^2}}\frac{\partial }{{\partial {z^2}}}} - 1} \right)\psi\\&={\rm i}{k_0}\left( {Q - 1} \right)\psi={\rm i}{k_0}(\sqrt {1 + q} - 1)\psi \end{split},$

其中, $P=\displaystyle\frac{\partial }{{\partial r}}$, $Q=\sqrt {{n^2} + \displaystyle\frac{1}{{k_0^2}}\displaystyle\frac{{{\partial ^2}}}{{\partial {z^2}}}} $, $q=\eta + \mu $, $\eta={n^2} - 1$, $\mu=\displaystyle\frac{1}{{k_0^2}}\displaystyle\frac{{{\partial ^2}}}{{\partial {z^2}}}$.
求解(16)式方法主要有分离?步进傅里叶技术和有限差分/有限元技术, 其中隐式有限差分(IFDM)能够完全适用于小角度和大角度抛物型波动方程, 该方法极大地提高了计算精确度和稳定性, 而且通过改进的初始场可有效处理各种边界条件^[33]. 各个方向的离散步距需满足$\Delta z \leqslant {\lambda /4}$, $\Delta r=$(2—5)$ \Delta z$, 如图2所示, 其中${z_j}=\ell \Delta z, $$ \ell=1, 2, 3, \cdots, N$; ${r_m}= $$m\Delta r, m=1, 2, 3, \cdot \cdot \cdot, n$. 为了推导方便, 空间各点$({r_m}, {z_j})$的声场$\psi ({x_m}, {z_j})$简写为$\psi _j^m$.
图 2 Crank-Nicolson有限差分法示意图
Figure2. Schematic diagram of IFDM used Crank-Nicolson.

为了用点${r_{m + 1}}$的场信息表示点${r_m}$的场信息, 考虑两点中点

$\frac{{\partial {\psi ^\xi }}}{{\partial r}}=\frac{{{\psi ^{m + 1}} - {\psi ^m}}}{{\Delta r}}, {\psi ^\xi }=\frac{{{\psi ^{m + 1}} + {\psi ^m}}}{2}.$

通过Crank-Nicolson有限差分法求解(16)式, 即

$\frac{{\psi _{}^{m + 1} - \psi _{}^m}}{{\Delta r}}={\rm i}{k_0}(\sqrt {1 + q} - 1)\frac{{\psi _{}^m + \psi _{}^{m + 1}}}{2},$

导出如下隐式表达式

$\begin{split}&\left[ {1 - \frac{{{\rm i}{k_0}\Delta r}}{2}(\sqrt {1 + q} - 1)} \right]\psi _{}^{m + 1}\\&\quad=\left[ {1 + \frac{{{\rm i}{k_0}\Delta r}}{2}(\sqrt {1 + q} - 1)} \right]\psi _{}^m\end{split}.$

对(19)式平方根算子可采用不同的近似处理方式, 如Tappert, Claerbout, Greene和Pade等近似方法, 不同近似方法得到不同角度范围、计算量和计算精度, 接下来引入较为通用的算子近似表达式

$\sqrt {1 + q}=\frac{{{a_0} + {a_1}q}}{{{b_0} + {b_1}q}}.$

a, b取不同值, 便可得到处理算子的Tappert, Claerbout, Greene的近似法. 为了减小上述三种近似方法带来的相位误差和对角度的限制, Collins^[34]采用一种基于帕德级数法展开算子, 可得到

$\sqrt {1 + q}=1 + \sum\limits_{j=1}^\infty {\frac{{{a_{j, m}}q}}{{1 + {b_{j, m}}q}}} + O({q^{2m + 1}}),$

其中
${a_{j, m}}=\displaystyle\frac{2}{{2m + 1}}{\sin ^2}\left(\displaystyle\frac{{{\rm j{\text{π}} }}}{{2m + 1}}\right)$, ${b_{j, m}}={\cos ^2}\left(\displaystyle\frac{{{\rm j{\text{π}}} }}{{2m + 1}}\right) $,
m为展开式中的项数.
通过在(21)式中保留更多的Pade项, 开角几乎达到了90°, 但同时计算量也大幅度增加. 为了避免级数求和带来的计算效率问题, 结合不同近似方法在Pekeris波导下性能测试结果, 当相位误差取0.002时, 大角度的Greene近似法的最大开角可达45°, 且声场计算精度与FFP计算的基准值一致, 且不涉及级数求, 计算效率较高^[20]. 所以选用Greene近似法, 则(20)式可写为

$\sqrt {1 + q}=\frac{{0.99987 + 0.79624q}}{{1 + 0.30102q}}.$

代入(19)式后结合(15)式对各项重新组合, 便可得到如下的向量表达式:

$\left[ {1, u, v} \right]\left[ \begin{gathered} \psi _{j - 1}^{m + 1} \\ \psi _j^{m + 1} \\ \psi _{j + 1}^{m + 1} \\\end{gathered} \right]=\frac{{{\hbar _ + }}}{{{\hbar _ - }}}\left[ {1, {u^*}, v} \right]\left[ \begin{gathered} \psi _{j - 1}^m \\ \psi _j^m \\ \psi _{j + 1}^m\end{gathered} \right].$

(23)式中, 各参数的定义如下:

$\left\{ \begin{split}& u=\frac{{{\rho _{\rm{a}}} + {\rho _{\rm{b}}}}}{{{\rho _{\rm{b}}}}}\left[ {\frac{{k_0^2{{(\Delta z)}^2}}}{2}\left( {\frac{{{ \lambda _ - }}}{{{\hbar _ - }}}} \right) - 1} \right] + \frac{{k_0^2{{(\Delta z)}^2}}}{2}\left[ {n_{\rm{a}}^2 - 1 + \frac{{{\rho _{\rm{a}}}}}{{{\rho _b}}}\left( {n_{\rm{b}}^2 - 1} \right)} \right], \\& {u^*}=\frac{{{\rho _{\rm{a}}} + {\rho _{\rm{b}}}}}{{{\rho _{\rm{b}}}}}\left[ {\frac{{k_0^2{{(\Delta z)}^2}}}{2}\left( {\frac{{{ \lambda _ + }}}{{{\hbar _ + }}}} \right) - 1} \right] + \frac{{k_0^2{{(\Delta z)}^2}}}{2}\left[ {n_{\rm{a}}^2 - 1 + \frac{{{\rho _{\rm{a}}}}}{{{\rho _{\rm{b}}}}}\left( {n_{\rm{b}}^2 - 1} \right)} \right] ,\\& v=\frac{{{\rho _{\rm{a}}}}}{{{\rho _{\rm{b}}}}} ,\\& {\hbar _ \pm }={b_1} \pm \frac{{{\rm{i}}{k_0}\Delta r}}{2}({a_1} - {b_1}) ,\\& { \lambda _ \pm }={b_0} \pm \frac{{{\rm{i}}{k_0}\Delta r}}{2}({a_0} - {b_0}) ,\\& {a_0}=0.99987, {b_0}=1, {a_1}=0.79624, {b_1}=0.30102 .\end{split} \right.$

把PE声场按IFDM的步进表示, (23)式写为深度N个格点的全局矩阵解:

$\begin{split}&\left[ {\begin{array} {*{10}{c}} {{u_1}}& {{v_1}}& {}& {}& {}& {}& {} \\ 1& {{u_2}}& {{v_2}}& {}& {}& {}& {} \\ {}& 1& {u{ _3}}& {{v_3}}& {}& {}& {} \\ {}& {}& \ddots & \ddots & \ddots & {}& {} \\ {}& {}& {}& 1& {{u_{N - 2}}}& {{v_{N - 2}}}& {} \\ {}& {}& {}& {}& 1& {{u_{N - 1}}}& {{v_{N - 1}}} \\ {}& {}& {}& {}& {}& 1& {{u_N}} \end{array}} \right]{\left[ \begin{gathered} {\psi _1} \\ {\psi _2} \\ {\psi _3} \\ \vdots \\ {\psi _{N - 2}} \\ {\psi _{N - 1}} \\ {\psi _N} \\ \end{gathered} \right]^{m + 1}}\\&\quad=\left( {\frac{{{\hbar _ + }}}{{{\hbar _ - }}}} \right)\left[ {\begin{array}{*{20}{c}} {u_1^*}& {{v_1}}& {}& {}& {}& {}& {} \\ 1& {u_2^*}& {{v_2}}& {}& {}& {}& {} \\ {}& 1& {u_3^*}& {{v_3}}& {}& {}& {} \\ {}& {}& \ddots & \ddots & \ddots & {}& {} \\ {}& {}& {}& 1& {u_{N - 2}^*}& {v_{N - 2}^{}}& {} \\ {}& {}& {}& {}& 1& {u_{N - 1}^*}& {{v_{N - 1}}} \\ {}& {}& {}& {}& {}& 1& {u_N^*} \end{array}} \right]{\left[ \begin{gathered} {\psi _1} \\ {\psi _2} \\ {\psi _3} \\ \vdots \\ {\psi _{N - 2}} \\ {\psi _{N - 1}} \\ {\psi _N}\end{gathered} \right]^m}. \end{split}$

可知, 基于有限差分法的PE是进一步推进求解的过程, 通过在各层介质中分别满足(15)式所示的椭圆型波动方程, 在海水与海底的液-液交界面$z={z_j}$上满足(3)式和(4)式的边界条件, 便可由前一个场信息${\left[ {\psi _1^m, \psi _2^m, \psi _3^m, \ldots, \psi _N^m} \right]^{\rm T}}$求解下一个m+1处的${\left[ {\psi _1^{m + 1}, \psi _2^{m + 1}, \psi _3^{m + 1}, \ldots, \psi _N^{m + 1}} \right]^{\rm T}}$场信息. 同样, 在PE边界设置中, 海面自由表面采用声场软边界处理, 在表面满足$\psi (r, 0)=0$. 海底为半无限均匀液态空间, 对于深海, 人工吸收层的厚度为海面到海底下边界距离的1/3; 对于复杂的浅海环境下海底延续部分, 则需通过厚度为几个波长的人工吸收层来设定^[20].
本文采用2.1节多物理场耦合FEM理论建立了波导下结构声辐射的准确模型, 提取了${r_0}$处准确的初始场信息, 并按(10)式进行PE初始场空间格点匹配后, 按照(25)式进行了结构辐射声场N 个 2D的PE步进计算. 在实际工程中也可通过试验法(垂直线列阵)测得结构某距离处在深度方向上的矢量声场, 然后采用PE实时快速计算辐射声场, 实现浅海水域下结构辐射噪声的在线监测预报.

2

-->

3.1.FEM-PE法准确性验证

建立如图3所示的轴对称坐标下Pekeris波导下点源声传播模型, 点源深度为${z_0}=100 $ m. 采用FEM理论计算并提取距点源最大波长${r_0}=50$ m处、在整个波导深度方向上的复声压值作为PE初始场以进行远场声场的IFDM步进计算.
如图4所示, 计算了30 Hz和300 Hz下点源的声压级(SPL, ${\rm SPL}=20\lg \displaystyle\frac{{{p_{\rm e}}}}{{{p_{{\rm ref}}}}}$ (dB), ${p_{\rm e}}$为总声压的有效值, ${p_{{\rm ref}}}$为在水中取的参考值, ${p_{{\rm ref}}}=1 \times $$10^{-6}$ Pa)随距离的变化曲线, 并与相同条件下FFP计算结果进行了对比, 声压参考级为$1 \times {10^{ - 6}}$ Pa, 各场点深度为50 m. 可以看出, 在低频和较高频率下FEM-PE计算结果与FFP计算结果符合得很好, 验证了该方法计算的准确性. 虽然在远距离存在一固定相位误差, 但从整体声场计算来看, 该误差对计算精度影响较小, 整体精度满足计算要求.
图 3 浅海波导下点源声传播模型
Figure3. Acoustic propagation model of point source in shallow water.

图 4 点源的FEM-PE理论验证　(a) f = 30 Hz; (b) f = 300 Hz
Figure4. Verification of point source used FEM-PE: (a) f = 30 Hz; (b) f = 300 Hz.

为了验证该方法对三维浅海下弹性结构声辐射计算的可靠性, 建立如图5所示的浅海下受激弹性球壳FEM模型. 同时, 为了减小网格计算量, 建立了轴对称坐标下受激弹性球壳的二维声辐射FEM-PE模型, 球壳中心位于对称轴深度方向上100 m处, 在其顶端施加垂直向下的简谐点激励${F_{\rm s}}=1000$ N. 球壳半径20 m, 厚度0.1 m, 材料为4340型钢, 波导环境参数、分析频率和场点选取与上述验证模型相同. 采用该方法计算了弹性球壳在浅海下的辐射声场, 并与FEM直接计算的声压级进行了对比, 如图6所示. 可以看出, 该方法计算结果与相同情况下有限元计算结果符合得很好, 验证了该方法对浅海下弹性结构辐射声场计算的准确性.
图 5 浅海下弹性球壳声辐射有限元模型示意图
Figure5. FEM model diagram of elastic spherical shell in shallow water.

图 6 弹性球壳的FEM-PE理论验证　(a) f = 30 Hz; (b) f = 300 Hz
Figure6. Verification of elastic sphere used FEM-PE: (a) f = 30 Hz; (b) f = 300 Hz.

通过Pekeris波导下点源和弹性结构辐射声场的验证结果可看出, 该方法计算结果与FFP, FEM计算结果吻合得很好. 虽然因该方法采用(22)式的Greene近似, 在远场声场时存在较小的固定相位误差, 但从声场整体计算精度来看, 该方法的计算精度是满足要求的, 且该方法操作过程简单、计算高效, 能够快速准确地进行浅海波导下复杂结构源辐射声场计算.
2 -->

3.2.FEM-PE法收敛性分析

因为FEM计算结果作为PE计算的初始条件, 所以FEM计算精度对方法整个计算过程的影响尤为重要; 且在PE计算过程中采用了有限差分法, 即使有限元计算精度满足要求, 但PE网格划分不恰当也会对整个计算精度的影响, 所以很有必要同时掌握该方法中FEM和PE网格划分对计算精度、效率的影响规律. 为了分析该方法在整个计算距离上的计算精度, 定义平均相对误差为

$\varpi=\frac{1}{N}\sum\limits_{n=1}^N {\eta (n)},\;\eta (n)=\frac{{\left| {{p_w}(n) - {p_{\rm t}}(n)} \right|}}{{\left| {{p_{\rm t}}(n)} \right|}} \times 100 {\fzssfont\text{%}}, $

其中 ${p_{\rm w}}(n)$为FEM-PE计算结果, ${p_{\rm t}}(n)$为采用FFP理论解计算结果, $\eta (n)$为在各场点上声场计算的相对误差, n为场点离散数, N为离散场点总数; 该算例中在 50—2000 m范围每隔5 m选取一场点, 即N = 391点.
表1为FEM和PE在不同网格划分下该方法计算的相对误差、计算自由度(DOF)、计算时间(t)以及计算机占用内存(RAM). 测试模型为3.1节验证模型即轴对称Pekeris波导下点源声传播模型, 频率为30 Hz, 解析解采用波数积分法的FFP程序计算. 有限元模型采用软件COMSOL multiphysics建立, PE计算程序采用Matlab编译, 所有计算均在 Intel(R) Core(TM) i7-4790 CPU 3.60 GHz 上运行, 内存16 GB. 可看出, 当把PE网格大小设为${d_z}={\lambda / 8}$, ${d_r}={\lambda / 4}$后, 计算精度随着FEM网格质量的提高而增加, 但FEM网格减小到${\lambda / 6}$后, 计算精度可达到3％左右且趋于稳定; 继续增加网格密度不仅没有大幅度提高精度, 反而增加计算时间, 建议FEM网格大小选为${\lambda / 6}$. 当把有限元网格设定为${\lambda / 6}$后, 把竖直z方向的网格大小${d_z}$从$\lambda $变为$\lambda /16$, 且r方向的网格大小${d_r}$始终保持${d_r}=2{d_z}$的关系, 当${d_z}$减小为$\lambda /4$后, 平均相对误差降到10％以内. 类似地, 当${d_z} \geqslant \lambda /8$后, 该方法计算的平均相对误差为3.34％左右且趋于稳定. 综上, 为了达到较高的计算精度和计算效率, 建议该方法的网格划分方式为: ${d_{\rm FEM}}=\lambda /6$, ${d_z}=\lambda /8$及${d_r}=\lambda /4$, 本文后续计算均采用这一网格划分方式.

FEM	$\scriptstyle {d_{\rm FEM}}$		$\scriptstyle \lambda $	$\frac{\lambda }{2}$	$\frac{\lambda }{4}$	$\frac{\lambda }{6}$	$\frac{\lambda }{8}$	$\frac{\lambda }{{10}}$		$\frac{\lambda }{6}$
PE	$\scriptstyle {d_z}$		$\frac{\lambda }{8}$							$\scriptstyle \lambda $	$\frac{\lambda }{2}$	$\frac{\lambda }{4}$	$\frac{\lambda }{8}$	$\frac{\lambda }{{16}}$
	$\scriptstyle {d_r}=2{d_z}$		$\frac{\lambda }{4}$							$\scriptstyle 2\lambda $	$\scriptstyle \lambda $	$\frac{\lambda }{2}$	$\frac{\lambda }{4}$	$\frac{\lambda }{8}$
$\scriptstyle \varpi $/％			11.6	6.8	4.2	3.3	3.4	3.5		13.8	11.2	7.8	3.3	3.5
DOF/$\scriptstyle \times {10^4}$			2.2	3.4	7.2	13.1	20.9	40.9		11.5	11.6	11.9	13.1	17. 7
RAM/GB			1.9	2.0	1.9	2.0	2.2	2.5		2.0	2.0	2.0	2.0	2.1
t/s			2.3	4.5	7.5	12.4	17.3	21.9		11.5	11.6	11. 7	12.4	14.1

表1方法收敛性分析
Table1.Convergence analysis of the method.

2 -->

3.3.FEM-PE法高效性分析

针对于浅海波导下弹性结构声辐射研究, 目前主要的研究方法有镜像法、三维声弹性理论和联合波叠加法等. 但由于镜像法对其他复杂结构和浅海海底时涉及一定的计算效率和适应性问题, 虽然三维声弹性理论和联合波叠加法避免了这些问题, 但均涉及大量虚拟源的优化配置和声学反问题等数值求解问题, 特别是当结构增大频率增加时, 虚拟源数目增加, 在工程应用上的效率有待继续提高. 为了说明该方法不仅避免了上述研究方法涉及的问题, 且在计算效率和计算过程简化性上具有一定优势, 以下进行了该方法与联合波叠加法在相同情况下的计算时间对比分析, 计算模型与文献[17]一致.
图7为相同计算模型下该方法与CWSM计算结果对比验证. 可看出, 该方法与CWSM计算结果具有较好的一致性, 再次证明该方法声场计算的正确性. 然后, 进行了该方法和联合波叠加法在不同距离范围(l)和频率(f)下对浅海波导下大型结构辐射声场计算的时间测试分析, 如表2所列.
图 7 60 Hz频率下FEM-PE与CWSM计算结果对比
Figure7. Contrast between method of FEM-PE and CWSM at 60 Hz.

可看出, 随着频率的增加, FEM-PE法计算优势在逐渐降低, 因为频率增加FEM计算网格大幅度增加, 这时FEM的对效率占主要影响, 导致整体效率降低; 但随着距离增加, FEM-PE计算优势较为明显, 因为远场采用PE计算, PE的高效性提高了整个远场声场计算效率. 从时间比值上来看, FEM-PE法对浅海波导下弹性结构声辐射计算效率更高, 最高的计算效率超出了CWSM的17倍, 最低效率倍数也达到了8倍, 整体计算效率比联合波叠加法提高了一个数量级. 特别是针对波导下结构低频远距离声场计算, 该方法计算效率优势更为突出.

l/km		$\scriptstyle \lambda-5$					$\scriptstyle \lambda-1$	$\scriptstyle \lambda-10$	$\scriptstyle \lambda-50$	$\scriptstyle \lambda-100$
f/Hz		30	60	90	100		60
t	CWSM	24.62	40.47	62.00	68.78		27.97	98.98	189.57	276.68
	FEM-PE	2.20	4.18	7.21	9.45		2.17	5.98	11.60	18.76
	$\textstyle {\eta _{\rm CWSM/FEM {\text{-}} PE}}$	11 : 1	10 : 1	9 : 1	8 : 1		14 : 1	17 : 1	16 : 1	14 : 1
注: $\textstyle {\eta _{\rm CWSM/FEM{\text{-}}PE}}$为两种方法时间比值, FEM-PE网格为$\scriptstyle {d_{\rm FEM}}=\lambda /6$, $\scriptstyle {d_z}=\lambda /8$及$\scriptstyle {d_r}=\lambda /4$.

表2运行时间对比测试 (单位: min)
Table2.The contrast test of runtime between FEM-PE and CWSM (unit: min).

如图8所示, 通过该方法建立三维Pekeris波导下有限长弹性圆柱壳声辐射理论模型. 其中, 海水深度H_water = 30 m, 海底深度为H_seabed = 60 m, 海底PML深度H_PML = 100 m, 圆柱壳长为l =10 m, 厚度d = 0.01 m, 材料为4340型钢 ($\rho_{\rm s}$, E_s 和 u_s 分别为材料密度、杨氏模量和泊松比). 由图可知该理论模型主要由多物理场耦合FEM计算域和声场PE计算域两部分组成, 半无限液态海底底部采用较厚的PML模拟无反射边界, 远场采用较薄的PML.
图 8 浅海波导下圆柱壳声辐射FEM-PE预报模型
Figure8. Model of cylindrical sound radiation used FEM-PE in shallow water.

2

-->

4.1.FEM-PE法的三维结构声源特性分析

由于浅海海面海底对结构源的影响主要表现为上下边界反射声会反作用于结构表面, 使结构的激励条件和周围流体环境发生改变, 最终影响结构源自身的振动特性. 为了研究浅海上下边界对结构振动特性的影响规律, 对不同流体环境下圆柱壳的耦合模态频率进行了对比分析.
表3计算了不同流体环境下弹性圆柱壳各阶模态振型(m, n)所对应的耦合频率, 其中, m和n分别表示周向和轴向的模态数目. 圆柱壳潜深h为半径的两倍, 即$h=2$ m, 自由场流体域四周满足Smerfield远场熄灭条件, 半空间上边界为Dirichlet边界, 其他边界满足Smerfield条件. 可看出, 相对于自由场, 半空间流体域下由于Dirichlet边界存在, 边界反射声使结构表面附连水质量减少, 导致结构各阶振动耦合模态频率较高^[15]; 而浅海波导下相对于半空间多了海底界面, 且海底边界使得结构附连水质量增加, 结构耦合频率降低, 但由于圆柱壳靠近海面远离海底, 海底影响较小, 而海面边界影响起主要作用, 各阶振动耦合模态频率比半空间环境下耦合频率略低, 比自由场环境下耦合频率大.

Environment	(4, 1)	(4, 2)	(6, 1)	(6, 2)	(6, 3)	(6, 4)
Free field	7.72	27.18	9.75	18. 19	35.12	57.63
Half-space	7.83	27.53	9.87	18.41	35.62	58.18
Pekeris	7.80	27.42	9.80	18.26	35.26	57.71

表3不同流体环境下圆柱壳耦合模态频率(单位: Hz)
Table3.Comparison of coupled modal frequency in different fluid environments (unit: Hz).

为了显示浅海海面和海底对圆柱壳振动特性的影响规律, 图9计算了Pekeris波导下圆柱壳各阶耦合模态频率随潜深的变化曲线, 并与自由场下的耦合频率进行对比. 可看出, 当圆柱壳靠近海面(海底)时, 其耦合频率比自由场下要高(低), 当潜深达到一定距离范围后, 浅海波导下圆柱壳耦合频率与自由场耦合频率基本趋于一致, 且在该距离范围内, 随着频率增加, 波导下耦合频率围绕自由场耦合频率上下波动的细节增加. 当海底为液态半空间时, 相对于绝对硬边界, 浅海海底边界对结构振动的影响作用距离减小. 在文献[15]中, 具有硬海底的理想浅海环境下耦合频率与自由场耦合频率的一致距离区间为海面海底均大于4倍半径, 即$4r \leqslant h \leqslant H - 4r$; 而Pekeris波导下为距海面距离大于4倍半径且距液态海底大于2倍半径, 即$4r \leqslant h $$ \leqslant H - 2r$. 可看出, 液态海底对结构耦合频率的影响距离减小, 因为在Pekeris波导下, 弹性圆柱壳近场辐射声场透射到下方液态海底的入射角度较小, 在临界角内液态海底的界面反射系数并非1, 圆柱壳一部分辐射声能量从海底界面透射到无限大液态海底, 所以液态海底边界反射声相对于绝对反射(反射系数为1)硬海底的反射声较弱, 较小的液态海底反射声与结构的耦合作用减小, 海底边界对圆柱壳耦合频率的影响距离减小.
图 9 耦合模态随潜深的变化曲线　(a) (4, 1); (b) (4, 2); (c) (6, 1); (d) (6, 2); (e) (6, 3); (f) (6, 4)
Figure9. Curves of coupled modal frequency changed with diving depth: (a) Modal (4, 1); (b) modal (4, 2); (c) modal (6, 1); (d) modal (6, 2); (e) modal (6, 3); (f) modal (6, 4).

2 -->

4.2.FEM-PE法的声场特性分析

在Pekeris波导下, 各阶简正波声传播频率可表示为^[35]

${f_n}=\frac{{\left( {2n - 1} \right){\text{π}}{c_a}{c_b}}}{{4H\sqrt {c_b^2 - c_a^2} }}, n=1, 2, 3, \cdot \cdot \cdot. $

根据(27)式以及Pekeris波导环境参数计算了该波导中1—6阶的简正频率, 如表4所列. 可看出第一阶简正频率即截止频率为35.52 Hz, 虽然在低于截止频率下结构也会产生辐射声场, 但这些辐射声场为非均匀波, 即随着距离成指数衰减而无法远距离传播, 所以为了进行波导下弹性圆柱壳远场声辐射分析, 计算频率须高于35.52 Hz.

n	1	2	3	4	5	6
f/Hz	35.52	106.56	177.60	248.65	319.69	390.73

表4Pekeris波导中各阶简正波频率
Table4.Normal mode frequencies in Pekeris waveguide.

为了清楚地看出Pekeris波导中弹性圆柱壳辐射声场的整体分布情况, 图10采用该方法分别计算了50, 100, 150 和200 Hz频率下圆柱壳在波导二维截面上的辐射场传播伪彩图, 截面为圆柱壳轴线方向, 圆柱壳潜深为15 m.
图 10 不同频率下结构声场传播伪彩图　(a) f = 50 Hz; (b) f = 100 Hz; (c) f=150 Hz; (d) f = 200 Hz
Figure10. Colour maps of structural sound propagation at different frequencies: (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz.

结合表4可看出, 当频率为50 Hz时, 波导中只包含了一个简正波模式的声传播, 辐射场在二维截面上的分布只出现了一个辐射状云图, 并随着距离按一定规律衰减. 随着频率的增加, Pekeris波导中包含的简正波模式也在增加, 各阶简正波模式相互干涉叠加, 加大了波导中圆柱壳结构辐射声场干涉结构的复杂性.
虽然Pekeris波导中圆柱壳辐射声场整体分布与点源声场分布具有一定的相似性, 但也存在一定的区别. 如图11所示, 在进行点源(强度)与结构声功率等效处理之后, 进行了不同频率下结构辐射声场与点源声场的对比. 结构潜深与点源深度均为15 m, 各场点深度为15 m, 场点连线方向为圆柱壳轴线方向. 结合表3 和表4的计算结果, 在频率为50 Hz的低频段时, 因为在近场, 辐射声场空间分布主要受结构辐射直达声的影响, 海面海底反射声对结构振动和辐射声场的影响较小. 且在该频率下, 结构具有(4, 1), (4, 2), (6, 1), (6, 2)和(6, 3)阶等少量振动模态, 该频率下结构近场辐射声场空间分布曲线的有较小的波动. 达到一定距离(如500 m左右), 结构本身对辐射声场的影响减小, 上下界面反射声对声场叠加的影响占主要部分, 而该频率下包含一个简正波模式, 总声场无不同模态辐射声与简正模式的干涉叠加影响, 辐射曲线出现平滑衰减, 衰减规律与相同强度下点源产生声场分布是一致的. 但随着频率的增加, 结构振动模态数增加, 各阶模态激励出的辐射场对总声场的干涉影响加大, 且随着频率的增加, 相对于低频, 频率较高时需要达到更远的距离才能降低结构自身对声场的影响作用, 从而使波导中上下边界的影响(或上下边界束缚的简正波)起主导作用, 才会与点源产生声场相似的分布规律. 因为总声场是由结构各阶不同强度模态声场经过波导上下边界干涉叠加而来的, 所以, 波导中结构辐射总声场与相同强度下点源声场在幅值上有一定差异, 这与文献[17]得出的结论是一致的. 对于结构声源和点源相似性条件的判据公式, 可以用$\displaystyle\frac{a}{\lambda } \ll 1$(a为结构最大尺寸)近似表示^[36].
图 11 不同频率下结构辐射声场与点源声场对比　(a) f = 50 Hz; (b) f = 100 Hz; (c)f = 150 Hz; (d) f = 200 Hz
Figure11. Acoustic propagation contrast between structure and point souce at different frequencies: (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz.

分析声场衰减规律能够更好地掌握浅海波导下声传播特性, 典型点源在具有声吸收的均匀浅海声传播过程中, 平均声强的衰减规律由三部分构成, 即声强随距离按$-2 $次方的球面波衰减区、介于球面波和柱面之间的$-3/2 $次方规律衰减区和$ -1$次方的柱面波衰减区, 并通过海洋声传播理论推导了各个衰减区的距离判据以及传播损失的分段表达式和半经验式^[35].
同样, 本文对弹性圆柱壳辐射声场在Pekeris波导中的传播特性进行了研究. 如图12所示, 分别为圆柱壳在不同潜深下的声压级随距离的变化曲线, 各场点深度为15 m, 场点连线方向为圆柱壳的轴线方向. 可看出, 在近场, 因为总声场主要由不同振动模态结构辐射的直达声组成, 浅海边界的影响很小, 声场干涉复杂而并非出现类似点源的近场球面波衰减规律, 而是在圆柱壳轴线方向上出现了受结构自身振动和几何尺寸共同影响的近场声影响区. 随着距离的进一步增加, 虽然上下界面反射声已对声场产生了一定程度影响, 但由结构辐射的直达波仍然还是总声场的主要贡献者, 只是随着距离的增加, 结构的几何尺寸对声场的影响减小, 即声场指向性分布减弱, 导致辐射场传播按球面波衰减规律进行^[36]. 当场点距离位于“介于球面波和柱面波”衰减区时, 此时 结构不同模态的辐射声和上下边界束缚的简正波模式共同干涉叠加形成总声场, 总声场的波动变化规律较为复杂, 难以给出规律性的描述. 当传播距离足够远以后, 结构的几何尺寸和模态辐射声场对总声场的影响很小, 声场主要由波导上下边界限制的有限阶数简正波干涉叠加构成, 各阶简正波均按柱面扩展规律$1/\sqrt r $衰减, 当频率为50 Hz时, 只有一阶简正波, 所以其在柱面波衰减区的辐射曲线是平滑的, 随着频率的增加, 总声场由各阶简正波干涉叠加构成, 增加了结构辐射曲线的波动细节, 但辐射曲线的包络面(或声场幅值)仍然按照柱面$1/\sqrt r $的规律进行衰减, 即传播距离每增加一倍, 声压级降低3 dB.
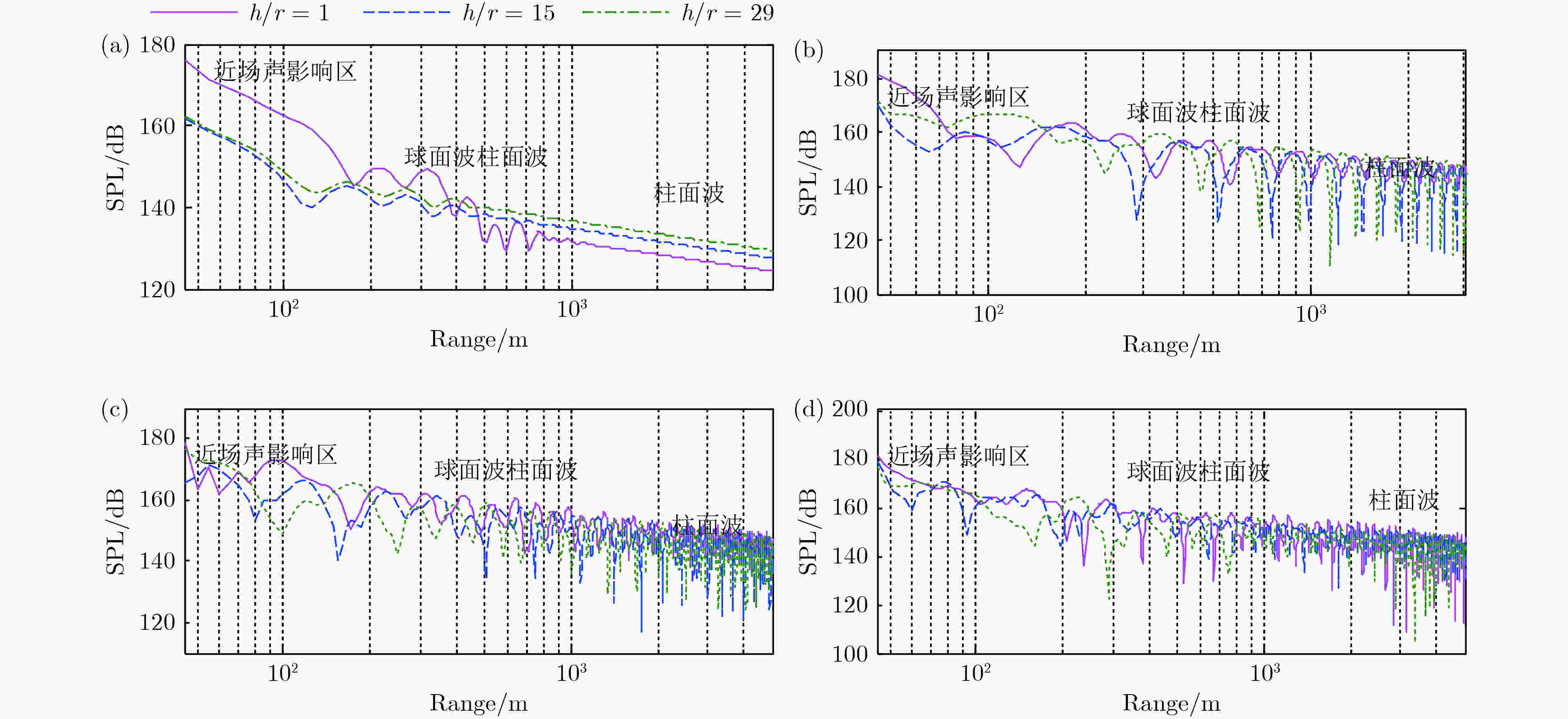图 12 不同频率下结构辐射场传播特性分析　(a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz
Figure12. Analysis of structural sound propagation at different frequencies: (a) f = 50 Hz; (b) f = 100 Hz; (c) f = 150 Hz; (d) f = 200 Hz.

以多物理场耦合FEM理论和声场计算的PE法为理论基础, 提出了三维浅海波导中弹性结构辐射声场以及振动特性研究的FEM-PE法, 建立了三维Pekeris波导下弹性结构辐射声场和耦合振动的理论模型. 并分别从方法的准确性、收敛性和高效性三个方面重点介绍了该方法进行Pekeris波导中声辐射以及声传播问题研究的优势后, 进行了三维Pekeris波导中大型弹性圆柱壳的耦合振动和辐射声场分析, 主要结论如下.
1)本文提出的FEM-PE法, 通过提取距源中心r_o处的初始场信息, 便可对三维均匀浅海下任意大型弹性结构中低频振动声场的N个2D进行预报研究, 该方法对结构和浅海环境适应性强, 中低频段下声场计算效率和精度较高.
2)浅海下结构振动特性受到了周围流体和上下边界反射声的耦合影响, 当圆柱壳靠近海面(海底)时, 其耦合频率比自由场环境下要高(低), 当潜深达到一定距离范围$4r \leqslant h \leqslant H - 2r$后, 浅海下圆柱壳耦合频率与自由场耦合频率趋于一致, 且随频率增加, 浅海下耦合频率围绕自由场耦合频率上下波动细节增加.
3)弹性结构源在浅海波导下的辐射场(声压级)随距离的变化曲线与相同功率下点源产生声场的波动曲线在近场区域相差较大, 该区域内不可进行结构源和点源的等效; 达到一定距离后, 圆柱壳辐射声场在波导中的传播曲线与点源声传播曲线可近似等效.
4)Pekeris波导中弹性圆柱壳辐射场的衰减规律由“近场声影响区”、“球面波衰减区”、“介于球面波和柱面波的衰减区”和“柱面波衰减区”四个区域构成. 在近场区域, 主要来自于结构振动产生的直达声的干涉声场; 随着距离的增加, 声场的特征主要体现为直达波按球面波规律衰减; 之后, 是结构直达波和上下边界反射声共同干涉叠加的“介于球面波和柱面波之间”的衰减区; 最后, 声场特征表现为 “柱面波衰减区”.
这些结论为以后方便有效地开展波导环境下弹性结构, 如声场预报、声学测量和减振降噪等领域的研究提供了一些新参考, 同时也说明了该方法能够有效地解决在研究浅海波导下大型弹性结构远程声辐射特性时所涉及的计算量大、耦合物理场多和波导环境复杂等问题, 为开展复杂环境下的任意弹性结构声辐射的研究提供了一种新思路.
特别感谢宾夕法尼亚大学David Bradley教授、哈尔滨工程大学水声学院黄益旺教授、张海刚副教授对论文提出的宝贵意见.