摘要:采用三维多相流格子玻尔兹曼方法(lattice Boltzmann method, LBM), 对纳米结构超疏水表面液滴的冷凝行为进行模拟研究. 通过Laplace定律和光滑表面的本征接触角理论对三维LBM模型进行定量验证. 模拟分析了超疏水表面纳米阵列的几何尺寸和润湿性的局部不均匀性对冷凝液滴形核位置和最终润湿状态的影响规律. 结果表明, 较高的纳米阵列使液滴在纳米结构间隙的上部侧面和底部优先形核长大, 通过采用上下不均匀的间隙可避免液滴在底部形核长大, 而在上部侧面形核的冷凝液滴在生长过程中向上运动, 其润湿状态由Wenzel态转变为Cassie态; 较低的纳米阵列使液滴在纳米结构底部优先形核长大, 液滴的最终润湿状态为Wenzel态; 润湿性不均匀的纳米结构表面使液滴在阵列顶端亲水位置处优先形核长大, 成为Cassie态. 冷凝液滴在不同几何尺寸的纳米结构表面上的最终润湿状态的模拟结果与文献报道的实验结果符合良好. 通过模拟还发现, 冷凝液滴在生长过程中的运动行为与液滴统计平均作用力的变化有关. 本文的LBM模拟再现了三维空间中液滴的形核、长大和润湿状态转变等物理现象.
关键词: 纳米结构/
冷凝/
超疏水/
格子玻尔兹曼方法

English Abstract

全文HTML

--> --> -->

随着人们对自然界中微纳尺度下的生物表面形貌观察的不断深入, 发现许多看似光滑的生物表面实际上具有形状各异的粗糙微纳结构, 这些结构对其表面性能有重要影响. 例如, 近年来研究者们发现荷叶表面的超疏水性能与其表面的纳米结构有着密切联系, 启发人们在材料表面制备一层纳米结构, 使原来的普通表面具备某些特殊的性能. 这些仿生材料在不同领域具有广泛的应用. 通过大量研究发现, 纳米结构仿生超疏水材料具有优异的表面自清洁、防雾、防结冰、抗结露和抗结霜等性能, 这些性能与冷凝液滴在纳米结构表面的润湿行为密切相关^[1-4]. 研究表明, 固体表面能和表面粗糙度是影响材料表面润湿性能的两个主要因素^[5]. 固体表面能决定了液滴在固体表面的本征接触角, 即液滴在光滑固体表面所形成的接触角^[6]. 人们通常用经典的Young氏方程分析液滴在光滑表面的润湿行为^[7]. 而对于纳米结构粗糙表面的润湿性能, 除了材料的物性, 还受到纳米结构几何参数的重要影响. 超疏水表面纳米结构对冷凝液滴润湿现象的影响规律是近年来表面润湿性能研究领域的热点问题之一^[8-11].
研究者们建立了描述预测表观接触角(液滴在粗糙表面形成的接触角)的相关理论模型, 其中有Wenzel和Cassie-Baxter等描述粗糙表面润湿性的经典理论模型. 在Wenzel和Cassie-Baxter理论模型中, 液滴在粗糙表面上的表观接触角与液滴的本征接触角和表面粗糙度有关. 对于处于粗糙表面上的液滴, 当有液体填充于凸起结构之间的凹槽处时, 其润湿状态被称为Wenzel态; 当液滴完全处于凸起结构的顶端时, 其润湿状态被称为Cassie态^[12,13].
在理论研究的基础上, ****们对潮湿环境下液滴在粗糙表面的形核、长大以及润湿状态的转变开展了大量的实验研究^[14-17]. Narhe和Beysens^[14,15]在微米结构超疏水表面上进行了冷凝实验, 发现冷凝液滴长大后在粗糙表面处于Wenzel态, 即原来表面的超疏水性能遭到破坏. Rykaczewski^[16]和Lau等^[17]采用环境扫描电子显微镜(environmental scanning electron microscopy, ESEM)对液滴在纳米结构超疏水表面上的冷凝现象进行了实验观察, 发现冷凝液滴的最终润湿状态为Cassie态, 表明纳米结构超疏水表面具有较好的抗冷凝性能. 但是, 用ESEM实时观察液滴冷凝过程采用的分辨率一般在亚微米尺度, 而低温下冷凝液滴的形核尺寸在纳米量级. 因此, 采用ESEM只能够观察到冷凝液滴的生长过程和最终的润湿状态, 却无法直接观察到冷凝液滴的形核过程.
随着数值计算技术和计算机技术的快速发展, 数值模拟已成为研究流体行为的有效方法. 在各种数值模拟技术中, 以微观分子动力学模型和介观的动理学模型为基础的格子玻尔兹曼方法(lattice Boltzmann method, LBM)被广泛应用于科学研究的众多领域^[18]. LBM是一种介于流体的微观分子动力学和宏观连续方法之间的介观模型, 非常适合模拟复杂系统中的多相流体行为. 近年来, 在材料表面的润湿性能研究领域, 人们采用LBM多相流模型模拟液滴在粗糙表面的冷凝过程^[19-25]. 张博^[19]通过理论能量分析和LBM模拟研究了液滴在冷凝过程中的润湿性转变现象. Kusumaatmaja等^[20,21]采用LBM模型模拟了液滴在具有疏水和亲水条纹的表面上的迁移过程. Cui等^[22]采用LBM模型模拟了液滴在粗糙疏水表面的移动过程, 发现液滴移动的阻力相对于在平界面上有所减少. Liu等^[23]采用LBM模型模拟了液滴在粗糙表面合并后的弹跳现象, 讨论了液滴弹跳速率与液滴半径以及接触角大小的相互关系. Zhang等^[24,25]采用二维多相流伪势LBM模型, 通过液滴的临界形核尺寸将无量纲LBM的格子尺寸与实际空间的尺度相关联, 模拟研究了不同尺寸的纳米结构和润湿性的不均匀性对冷凝液滴形核位置和润湿状态转变过程的影响, 发现纳米结构的几何尺寸和局部润湿性会显著影响液滴在粗糙表面上的形核位置和最终的润湿状态.
目前, 应用三维LBM模型对纳米结构粗糙表面冷凝液滴形核阶段的模拟研究较少, 尤其是纳米结构的几何尺寸和局部润湿性等因素对液滴冷凝行为的影响规律, 尚未见三维LBM模拟研究的相关报道. 本文采用三维多相流伪势LBM模型, 针对不同的纳米结构几何尺寸和局部润湿性不均匀条件下, 液滴在粗糙表面的冷凝现象进行模拟研究, 并将三维模拟结果与前期的二维模拟结果^[24,25]进行对比分析.

本文采用D3Q19格式多相流伪势LBM模型^[26]对固相表面的润湿现象进行模拟研究. 图1给出了D3Q19格式的离散速度示意图^[27]. LBM演化方程可表示为
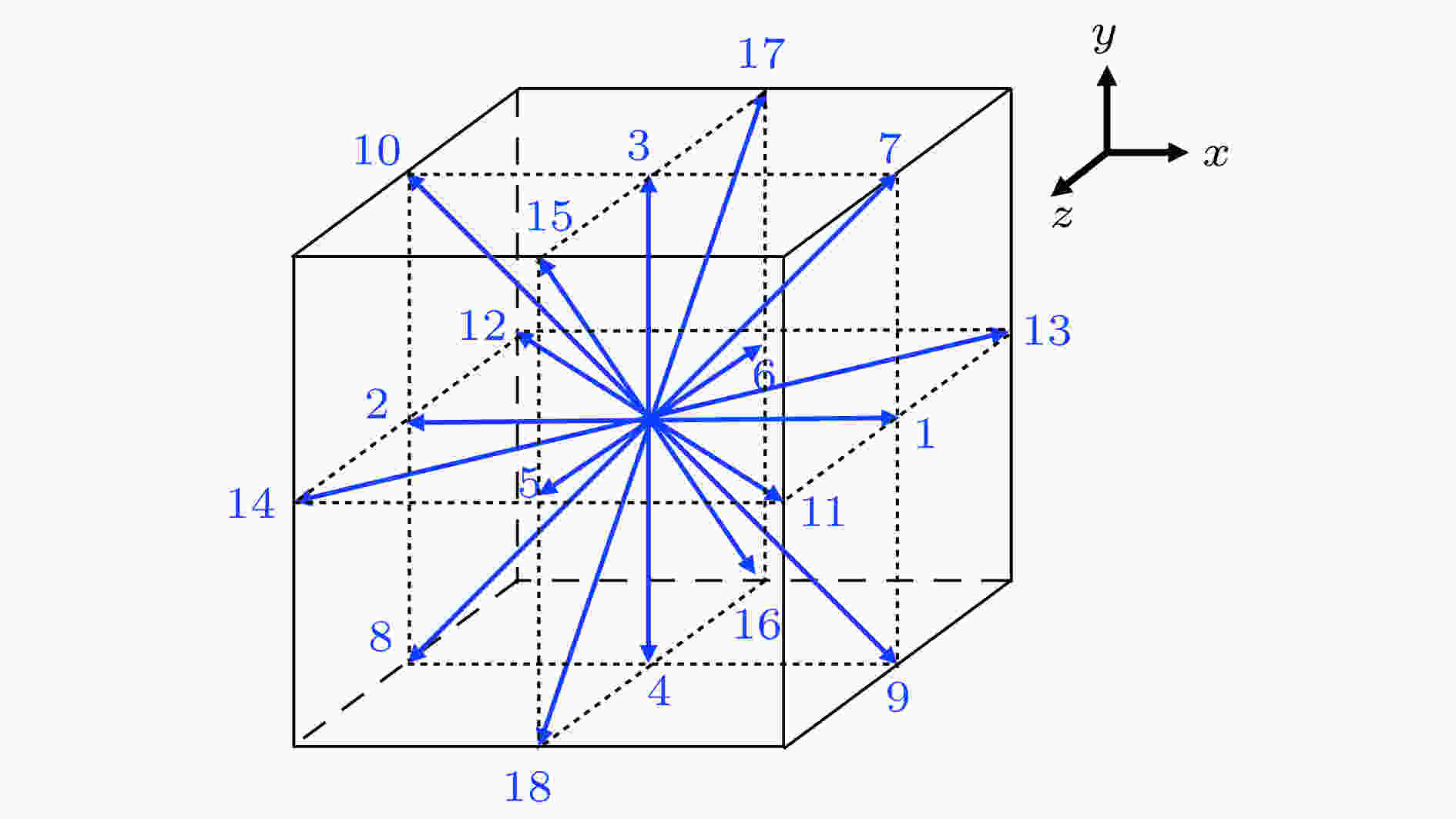图 1 D3Q19 LBM模型离散速度示意图^[27]
Figure1. Schematic sketch of LBM discrete velocities in the D3Q19 scheme^[27].

$\begin{split} & {f_i}({{x}} + {{{e}}_i}\Delta t,t + \Delta t) - {f_i}({{x}},t) \\= & - \frac{1}{\tau }[{f_i}({{x}},t) - {f_i}^{{\rm{eq}}}({{x}},t)] + {\omega _i}E, \\ & i = 0, 1, \cdots {\rm{,}}18,\; \end{split} $

式中f_i(x, t)为i方向上的粒子分布函数; $\tau $为无量纲松弛时间; $\Delta t$为时间步长; e_i为粒子的离散速度; E为作用于计算区域上边界的源项, 其大小会影响冷凝液滴的形核生长. 采用均匀正方网格剖分计算空间, e_i的矩阵表达式为

$\begin{gathered} [{{{e}}_0},{{{e}}_1},{{{e}}_2},{{{e}}_3},{{{e}}_4},{{{e}}_5},{{{e}}_6},{{{e}}_7},{{{e}}_8},{{{e}}_9},{{{e}}_{10}},{{{e}}_{11}},{{{e}}_{12}},{{{e}}_{13}},{{{e}}_{14}},{{{e}}_{15}},{{{e}}_{16}},{{{e}}_{17}},{{{e}}_{18}}] \\ = c \cdot \left[ {\begin{array}{*{20}{c}} 0&1&{ - 1}&0&0&0&0&1&{ - 1}&1&{ - 1}&1&{ - 1}&{ - 1}&1&0&0&0&0 \\ 0&0&0&1&{ - 1}&0&0&1&{ - 1}&{ - 1}&1&0&0&0&0&1&{ - 1}&1&{ - 1} \\ 0&0&0&0&0&1&{ - 1}&0&0&0&0&1&{ - 1}&1&{ - 1}&1&{ - 1}&{ - 1}&1 \end{array}} \right] \\ \end{gathered} , $

式中c 为格子速度, $c=\Delta x/\Delta t $, 其中$ \Delta x$为空间步长.
(1)式中$f_i^{\left( {{\rm{eq}}} \right)}\left( {{x},t} \right)$是流体粒子的平衡态分布函数, 通过下面的公式进行计算:

$\begin{split} & f_i^{({\rm{eq}})}({{x}},t) = {\omega _i}\rho ({{x}},t) \\ & \quad\times \left[1 + \frac{{{{{e}}_i} \cdot {{u}}({{x}},t)}}{{c_{\rm{s}}^{\rm{2}}}} + \frac{{{{({{{e}}_i} \cdot {{u}}({{x}},t))}^2}}}{{2c_{\rm{s}}^{\rm{4}}}} - \frac{{{{({{u}}({{x}},t))}^2}}}{{2c_{\rm{s}}^{\rm{2}}}}\right], \end{split}$

其中c_s为格子声速, 在直角坐标系下的取值为c_s = 1/$\sqrt 3 $^[18,27]; $\omega_i$为权重系数, 对于D3Q19格式, $\omega_i$的取值为

${\omega _i} = \left\{ {\begin{aligned}& {1/3,\;i = 0,} \\ & {1/18,\;i = 1—6,} \\ & {1/36,\;i = 7—18.} \end{aligned}} \right.$

在(3)式中, $\rho $(x, t)和u(x, t)分别为流体的宏观密度和速度, 计算公式分别为

$\rho ({{x}},t) = \sum\limits_{i = 0}^{18} {{f_i}({{x}},t)} , $

${{u}}({{x}},t) = \frac{{\sum\limits_{i = 0}^{18} {{{{e}}_i}{f_i}({{x}},t)} }}{{\rho ({{x}},t)}} + \frac{{\tau F({{x}},t)}}{{\rho ({{x}},t)}}, $

其中F(x, t)为流体粒子所受的作用力, 主要包括流-流作用力F_c(x, t)和流-固作用力F_ads(x, t). 流-流作用力的计算公式为

${F_{\rm{c}}}({{x}},t) = - {G_{\rm{c}}}\psi ({{x}},t)\sum\limits_{i = 0}^{18} {{\omega _i}\psi ({{x}} + {{{e}}_i}\Delta t,t){{{e}}_i}}, $

式中G_c为流-流作用系数, 控制液相和气相的分离过程和气-液界面的表面张力大小; $\psi $(x, t)为伪势函数, 是流体密度的函数, 在本模型中的计算公式为

$\psi ({{x}},t) = 1 - \exp [ - \rho ({{x}},t)].$

当体系中存在固相时, 流体粒子与固相之间的流-固作用力的计算公式为

${F_{{\rm{ads}}}}({{x}},t) = - {G_{{\rm{ads}}}}\psi ({{x}},t)\sum\limits_{i = 0}^{18} {{\omega _i}s({{x}} + {{{e}}_i}\Delta t,t){{{e}}_i}} ,$

式中G_ads为流-固作用系数, 是流体粒子与固相之间的作用力强度, G_c和G_ads共同决定了液滴固相表面的本征接触角; $ s({ x}+{ e}_i \Delta t, t)$为标示函数, 当格点为固相时其值取1, 为流体相时其值取0.
流体所受到的压力P(x, t)可由状态方程求得, 其计算公式为

$P({{x}},t) = \frac{{\rho ({{x}},t)}}{3} + \frac{{{G_{\rm{c}}}}}{6}{\psi ^2}({{x}},t).$

2

-->

3.1.模型验证

首先采用Laplace定律对所采用的三维多相流LBM模型进行验证. Laplace定律描述弯曲气-液界面的附加压力和液滴表面张力以及液滴半径之间的关系. 在三维空间下, Laplace定律的表达式为

$\Delta P = {P_{{\rm{in}}}} - {P_{{\rm{out}}}} = \frac{{2\gamma }}{R}, $

式中P_in和P_out分别为液滴内、外的压力; $ \Delta P $为液滴内外压力差; $\gamma $为液滴的表面张力; R为液滴曲率半径.
设置计算区域为120 lu × 120 lu × 120 lu (lu为格子单位), 计算区域下边界设置为固相; 其他边界均采用周期性边界条件, 固体壁面采用反弹边界条件. 在区域正中心预置1个初始液滴, 在每次计算前改变初始液滴的半径R. 图2为分别设置流-流作用系数G_c = ?6.0, ?6.5和?7.0时, 三维多相流LBM模型模拟得到的液滴内外压力差$ \Delta P$与液滴曲率1/R之间的关系曲线. 由图2可见, 每条线的截距很小, 基本通过坐标原点, 与(11)式的形式相符, 表明本研究中采用的三维多相流LBM模型的模拟结果与Laplace定律预测结果符合良好.
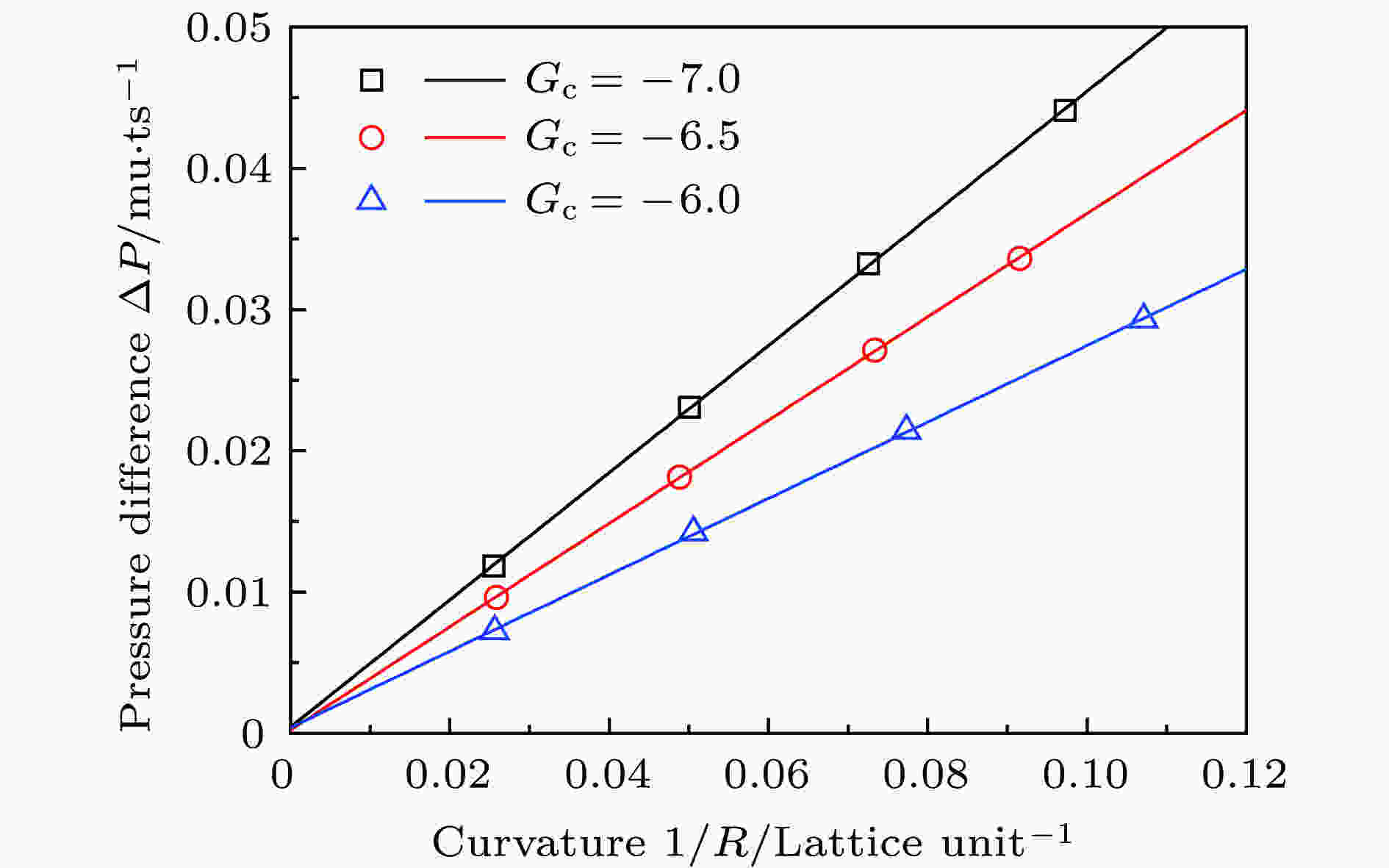图 2 模拟的液滴内外压力差与液滴曲率的关系(符号, 模拟值; 直线, 线性拟合)
Figure2. Simulated pressure difference between inside and outside of a spherical droplet as a function of droplet curvature (symbols, simulated data; lines, linear fitting).

随后, 对光滑固体表面的本征接触角进行模拟验证. 固定流-流作用系数为G_c = ?6.5, 改变流-固作用系数G_ads, 对液滴在具有不同亲疏水性的固相表面的本征接触角$\theta_{\rm c} $进行模拟. 设置计算区域为128 lu × 128 lu × 64 lu, 在区域正中心预置一个半径为20 lu的初始液滴, 区域下边界设置为固相, 其他边界均采用周期性边界条件, 固体壁面采用反弹边界条件. 在模拟过程中, 液滴接触角$\theta _{\rm{c}} $的测量公式为^[28]

$\tan {\theta _{\rm{c}}} = \frac{L}{{2(R - H)}}, $

式中H为液滴球冠的高度; L为液滴底部的长度, 取值为液滴与固相表面接触面积的等效直径; R为液滴达到稳态时的半径, 计算公式为^[28]

$R = \frac{{4{H^2} + {L^2}}}{{8H}}.$

对于本征接触角分别为0°, 90°和180°的情况, 通过固-液-气三相接触线的受力分析和(8)式, 可以得到流-固作用系数G_ads的计算公式分别为^[29]

$0{\rm{^\circ }}\!\!:{G_{{\rm{ads}}}} = {G_{\rm{c}}}{\psi _{\rm{l}}} = {G_{\rm{c}}}(1 - {{\rm{e}}^{ - {\rho _{\rm{l}}}}}),\tag{14a}$

$90{\rm{^\circ }}\!\!:{G_{{\rm{ads}}}} = {G_{\rm{c}}}\bar \psi \!=\! {G_{\rm{c}}}\frac{{({\psi _{\rm{l}}} + {\psi _{\rm{g}}})}}{2} \!=\! {G_{\rm{c}}}\!\!\left(\!1 - \frac{{{{\rm{e}}^{ \!-\! {\rho _{\rm{l}}}}} \!+\! {{\rm{e}}^{ - {\rho _{\rm{g}}}}}}}{2}\!\right)\!,\tag{14b}$

$180{\rm{^\circ }}\!\!:{G_{{\rm{ads}}}} = {G_{\rm{c}}}{\psi _{\rm{g}}} = {G_{\rm{c}}}\left(1 - {{\rm{e}}^{ - {\rho _{\rm{g}}}}}\right),\tag{14c}$

式中$\psi $_l和$\psi $_g分别为液相和气相的伪势函数; $\rho $_l和$\rho $_g分别为模拟得到的液相和气相的宏观密度.
利用(14)式得到0°, 90°和180°时G_ads的计算值, 再将其代入到程序代码中计算得到相应的本征接触角. 计算上述三种情况下本征接触角的模拟值$\theta_{\rm c1} $和设定值$\theta_{\rm c0} $的相对误差, 结果如表1所列. 可以看出, 三维LBM模拟得到的固相表面本征接触角$\theta_{\rm c1} $与设定值$\theta_{\rm c0} $符合良好, 表明所采用的三维多相流LBM模型能够合理描述固体表面的润湿现象.

Gads	$\theta_{\rm c0} $	$\theta_{\rm c1} $	$\operatorname{Re} {\rm{lative \;error = }}\dfrac{{{\theta _{{\rm{c}}1}} - {\theta _{{\rm{c0}}}}}}{{{\theta _{{\rm{c}}0}}}}$/%
?5.68	0°	0°	0
?3.33	90°	90.13°	0.14
?0.39	180°	180°	0

表1取G_c = ?6.5时液滴本征接触角设定值与模拟值对比
Table1.Comparison of intrinsic contact angles between the targeted data and the simulated results (G_c = ?6.5).

上述的Laplace定律和接触角模拟验证了本文采用的三维LBM模型对于表面润湿性模拟的合理性和程序代码的正确性.
图3为G_c = ?6.5时, 应用三维的LBM模型模拟得到的液滴的本征接触角$\theta_{\rm c} $随流-固作用系数G_ads的变化关系. 可以看出, 液滴的本征接触角随流-固作用系数G_ads的增大而增大.
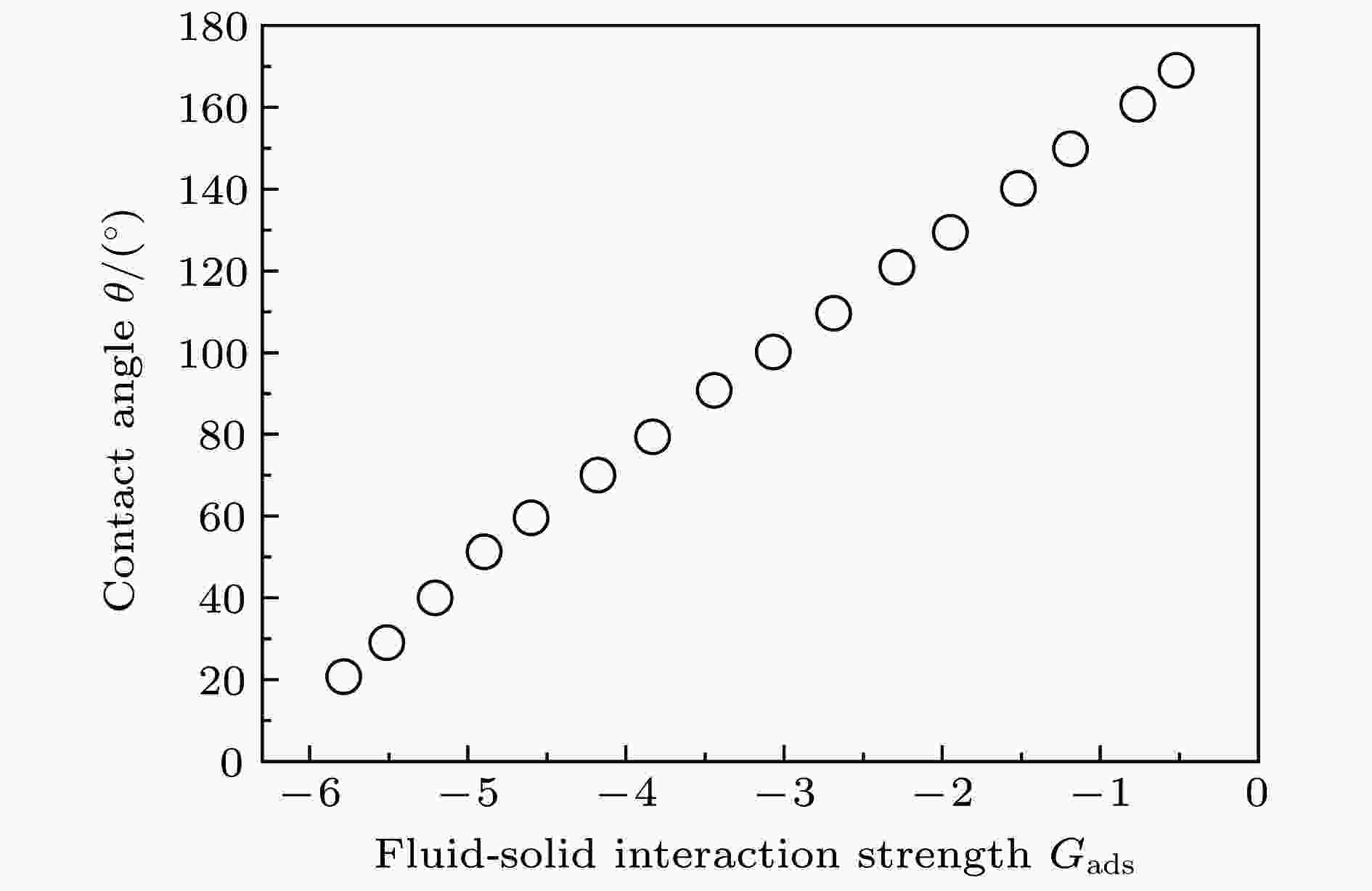图 3 取G_c = ?6.5时模拟的液滴本征接触角随流-固作用系数的变化
Figure3. Simulated intrinsic contact angle as a function of the fluid-solid interaction strength at G_c = ?6.5.

2 -->

3.2.纳米结构几何尺寸对粗糙表面液滴冷凝过程的影响

采用三维多相流LBM模型对不同几何尺寸纳米结构表面的液滴冷凝现象进行模拟研究. 图4为液滴冷凝的三维模拟区域示意图. 固相基底表面上分布了一定几何尺寸的纳米阵列, 用宽度(W)、间隙(S)和高度(H)进行表征. 在模拟液滴冷凝过程时, (1)式中的源项E作用在区域的上边界, 本文模拟中将参数E取为5 × 10^?4; 计算区域下边界设置为固相, 固体壁面采用反弹边界条件; 其他边界均采用周期性边界条件. 在开展纳米结构表面液滴冷凝的实验时, 为了降低材料的表面能, 研究者们通常在纳米结构表面涂覆一层聚四氟乙烯(poly tetra fluoroethylene, PTFE). 经试验测定, 液滴在涂覆PTFE的表面上的本征接触角约为110°^[17,30]. 为了使模拟的固体表面与实验材料具有相似的润湿性能, 根据图3的模拟结果, 本文模拟中将流-固作用系数设置为G_ads = ?2.7. 使液滴在固体表面的本征接触角为$\theta $_c = 110°. 模拟区域中水蒸气的初始含量为0.07 mu·lu^?2. 模拟开始后, 水蒸气从上边界进入计算区域, 由于固相与水蒸气之间的相互作用, 水蒸气粒子在纳米结构固相表面吸附和聚集. 随着吸附过程的不断进行, 水蒸气在某些固相表面达到过饱和, 液滴会在该位置形核析出. 随着冷凝过程的进行, 液滴继续长大并发生润湿状态转变.
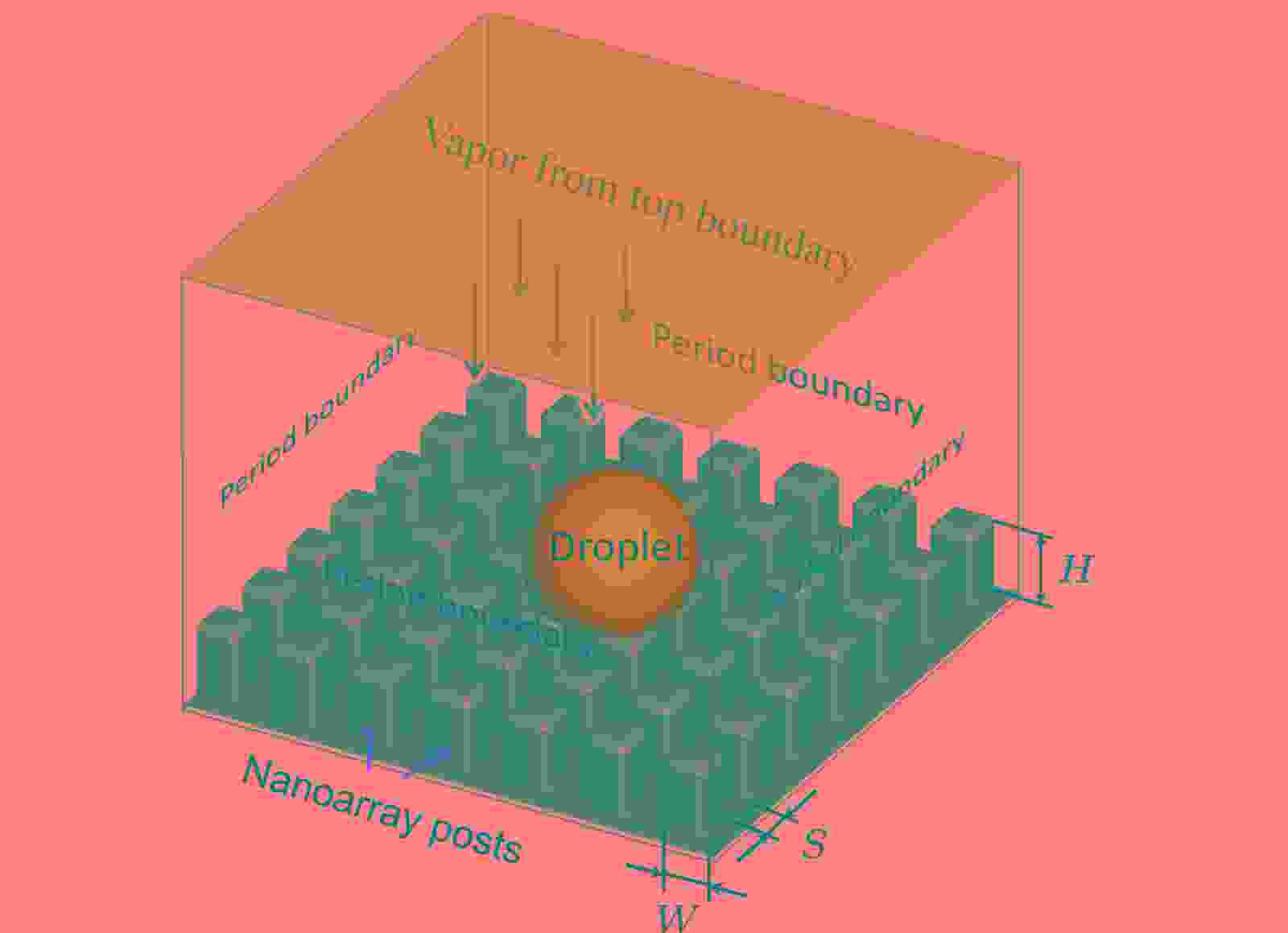图 4 液滴冷凝的三维模拟区域示意图
Figure4. Schematic of the three-dimensional domain for the simulation of droplet condensation.

设置计算区域大小为123 lu × 123 lu × 200 lu, 纳米阵列的宽度、高度和间隙为W = 5 lu × 5 lu, H = 100 lu和S = 4 lu × 4 lu. 根据前期的二维模拟结果, 如果采用完全均匀的纳米结构几何尺寸, 冷凝的液相不是以液滴的形式而是以液膜的形式在纳米阵列上均匀析出^[24]. 此外, 考虑到实际中纳米结构会有局部不均匀性, 因此在本模拟中, 在中部区域取较窄的间隙S = 3 lu × 3 lu. 在初始时刻, 模拟区域内充满密度均匀的水蒸气. 当LBM计算开始后, 由于模型上边界不断供应的水蒸气, 模拟区域内水蒸气的密度不断升高. 水蒸气粒子与固相表面产生流-固作用力使得水蒸气在纳米阵列的间隙处富集, 并在过饱和区域形核析出液滴. 图5为液滴在纳米结构粗糙表面上侧面和底部同时形核和生长过程的模拟结果. 约在21200 ts时, 水蒸气在较窄间隙上部和底部达到过饱和状态而形核. 由于阵列间隙上端的液滴更靠近上边界处的水蒸气来源, 其长大速度快于底部形核生长的液滴. 随后, 液滴吸收周围区域的水蒸气粒子, 位于上部的液滴同时向上和向下生长. 如图5所示, 大约到22000 ts时, 液滴上端从间隙中溢出并与周围相邻液滴合并. 之后, 位于间隙上部的液相随纳米阵列上方液相的生长而向上运动, 直到液滴完全位于纳米阵列的上方呈现Cassie态并继续长大, 即液滴的润湿状态由Wenzel态逐渐转变为Cassie态. 然而, 处于间隙底部的液相生长速度较慢, 并始终与间隙底部接触而呈现Wenzel态．
图 5 模拟的液滴在纳米阵列上部侧面和底部同时形核、生长及合并演化过程
Figure5. Simulated evolution of droplet nucleation, growth, and coalescence for the droplets that nucleate simultaneously in the upside space and the bottom corners between the posts of nanoarrays.

Zhang等^[24,25]采用二维多相流LBM模型对液滴冷凝现象的模拟研究中, 当冷凝液滴在纳米阵列的侧面形核时, 没有观察到在阵列底部出现液滴核心．关于二维和三维模拟结果的这一差别, 我们分析认为三维模拟得到纳米阵列上部侧面和底部同时出现液滴核心这一现象与三维空间中的阵列间隙相互连通有关, 水蒸气粒子可在间隙的底部聚集并形核长大．根据水蒸气易在较窄的纳米阵列间隙聚集形核的现象, 为了避免液滴在底部形核, 将模拟区域中部较窄的纳米阵列间隙值进行重新设置: 当0 ≤ H < 20 lu时, 阵列间隙尺寸取为4 lu × 4 lu; 当20 lu ≤ H ≤ 100 lu时, 中部阵列间隙尺寸仍保持3 lu × 3 lu. 其他模拟条件与图5一致. 图6为液滴在上述尺寸的纳米结构表面上部侧面形核和生长过程的模拟结果. 可以看出, 改变纳米阵列的几何尺寸后, 阵列底部没有发生液滴的形核. 而上部侧面液滴的冷凝过程与图5中的相似: 水蒸气在中部上侧面间隙处聚集、形核、长大、合并, 间隙中的液相向上运动使其润湿状态发生改变, 即从Wenzel态逐渐转变为Cassie态. 将图6中在36000 ts时的冷凝液滴形貌与Lau等^[17]在液滴冷凝实验中观察到的液滴形貌进行对比, 可以看出模拟得到的液滴的最终润湿状态与实验结果符合良好.
图 6 液滴在纳米阵列上部侧面形核、生长及合并演化过程的LBM模拟结果和实验结果^[17]对比
Figure6. Comparison of LBM simulation and experiment^[17] regarding the evolution of droplet nucleation, growth, and coalescence for the droplets that nucleate in the upside space between the posts of nanoarrays.

对比图5和图6的模拟结果可以看出, 在三维模拟中增大纳米阵列底部的间隙, 可以避免液滴在底部形核. 从这一现象我们可以得到一些启发: 在设计纳米结构超疏水抗冷凝表面时, 适当增大纳米阵列底部的间隙, 有利于提高纳米结构的超疏水性能. 此外, 本文针对单个液滴的形核生长, 在模拟中发现, 计算区域大小对模拟的液滴形核和开始聚集合并的时间略有影响, 但冷凝液滴在纳米结构表面上的形核和生长演化规律基本一致.
为了分析图6中纳米结构间隙处的冷凝液滴从Wenzel态向Cassie态转变的机理, 对图6中位于间隙中的液相进行受力分析, 用下式计算冷凝过程中间隙中的液相在竖直方向(z方向)所受的统计平均作用力:

$ {{{\bar{ F}}_z}} = {{\sum\limits_{{x} \in S} {{{F}_z}\left( {{x},t} \right) \cdot \rho \left( {{x},t} \right)} }\Big{/}{\sum\limits_{{x} \in S} {\rho \left( {{x},t} \right)} }}, $

式中F_z(x, t)为液滴内每个流体粒子受到的竖直方向的作用力, 其值为(7)和(9)式计算得到粒子所受流-流作用力和流-固作用力在z方向的矢量和; 式中求和符号$\displaystyle\sum $的下标${x} \in S$表示统计平均作用力的计算只针对液滴内部的流体粒子. 由(15)式计算得到的${{{\bar{ F}}_z}} $为矢量, 正值和负值分别表示液滴所受到的统计平均作用力方向为向上和向下.
图7为图6中位于上部间隙的液相在21200—36000 ts所受到的统计平均作用力, 图7中标号c, d, e, f, g分别对应图6中的不同时间步. 可以发现, 在上述润湿状态转变时段, 液相所受的统计平均作用力的方向均向上, 使得间隙上部的液相向上运动直至液滴完全位于纳米阵列的上方, 完成由Wenzel态向Cassie态的转变. 图7的统计平均作用力曲线开始均呈缓慢增大趋势, 此时位于间隙上部的液相向上运动缓慢; 随着位于纳米阵列上方的液滴不断长大, 在约30800 ts时统计平均作用力开始急剧增大, 此时位于纳米阵列顶端的液相发生合并, 间隙中的液相加速向上运动完成润湿状态的转变, 使液滴呈现Cassie态并继续长大.
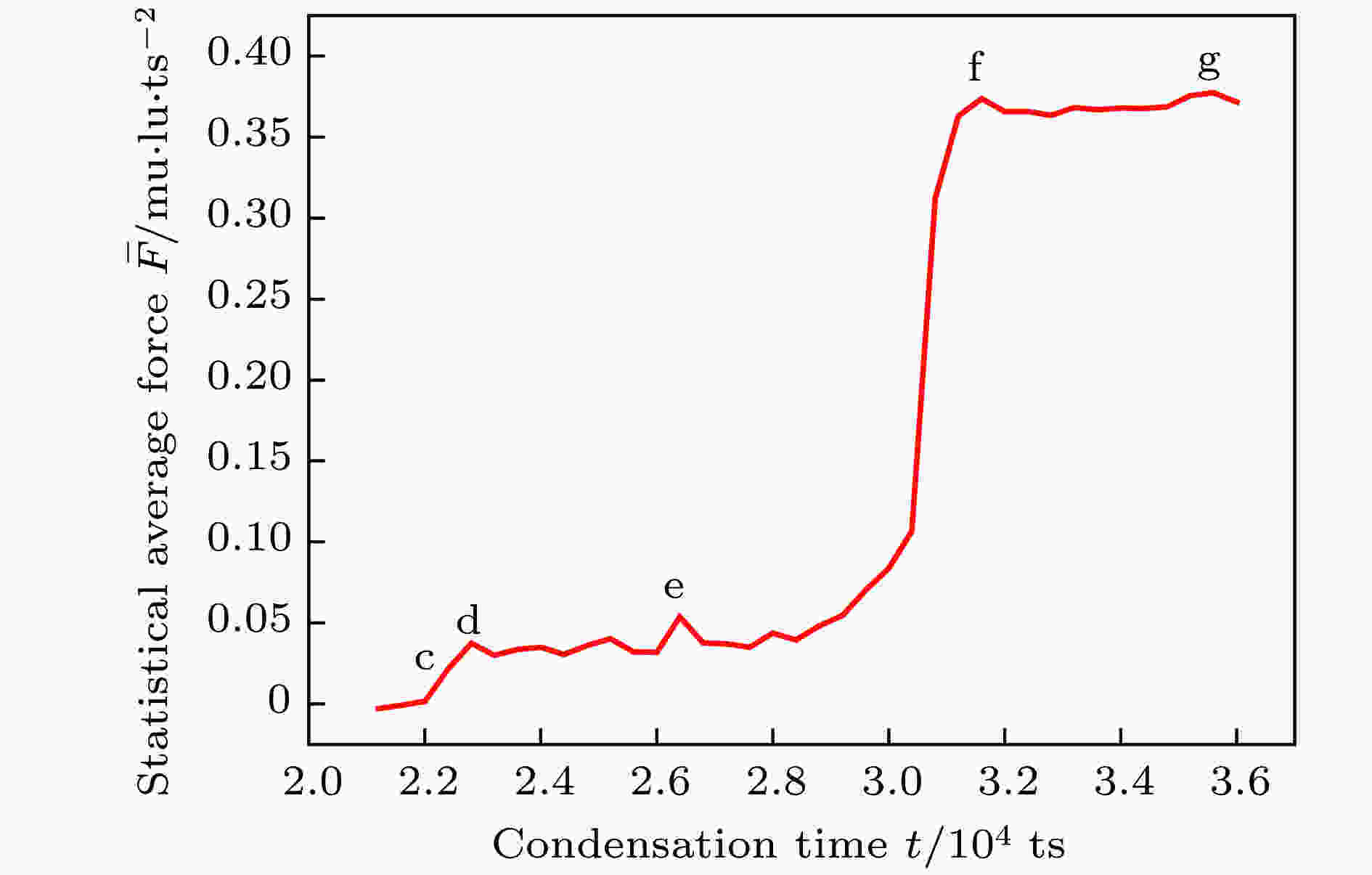图 7 对应于图6中间隙上部的液相在润湿状态转变阶段所受的统计平均作用力随时间的变化
Figure7. Statistical average force of the condensate liquid in the upside space between the posts of nanoarrays in Fig. 6 during wetting state transition as a function of time.

随后, 对冷凝液滴在纳米阵列底端形核和生长过程进行模拟研究. 设置计算区域大小为144 lu × 144 lu × 100 lu, 纳米阵列的宽度、高度和间隙为W = 5 lu × 5 lu, H = 21 lu和S = 7 lu × 7 lu, 但中部区域纳米阵列的间隙设为S = 3 lu × 3 lu. 其他模拟条件与图5相同. 图8为液滴在纳米结构表面底部形核和生长过程的模拟结果. 从图8可见, 在冷凝初期, 水蒸气在相邻纳米阵列的间隙处富集. 约在6800 ts, 液滴在较窄的间隙底部优先形核. 随着液滴的不断长大, 相邻小液滴在底部开始合并. 随后, 小液滴吸收周围区域的水蒸气粒子沿纵向和横向生长, 横向生长方向受相邻液滴合并前“竞争生长”的显著影响. 大约到8400 ts时, 液滴从纳米阵列上端溢出. 之后, 随着液滴的生长, 相邻液滴间相互接触而发生多次合并. 约在20000 ts, 所有小液滴合并成一个大液滴, 随后继续长大. 同时, 在冷凝初期向周围间隙处横向生长的液相逐渐向液滴下方处汇聚, 形成一个稳定的Wenzel态液滴并继续长大. 将图8中液滴在冷凝过程中的演化形貌与Chen等^[30]在液滴冷凝实验中观察到的液滴形貌进行对比, 可以看出模拟得到的液滴最终润湿状态与实验结果符合良好.
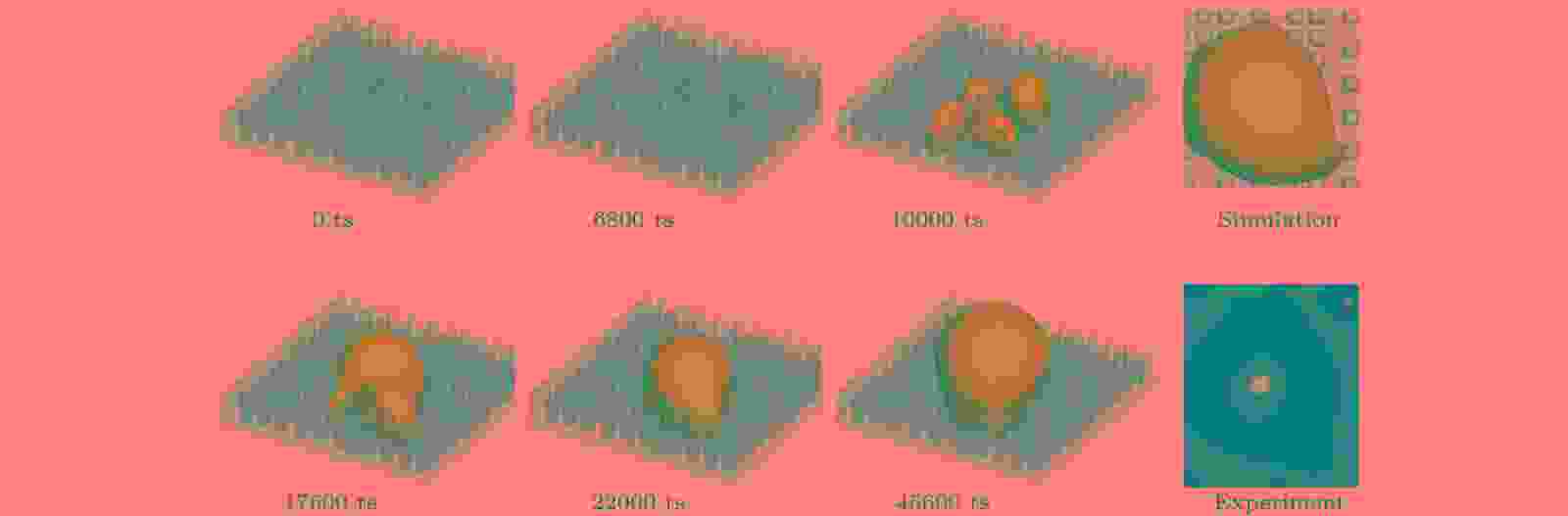图 8 液滴在纳米阵列底部形核、生长及合并演化过程的LBM模拟结果和实验结果^[30]对比
Figure8. Comparison of LBM simulation and experiment^[30] regarding the evolution of droplet nucleation, growth, and coalescence for the droplets that nucleate in the bottom corners between the posts of nanoarrays.

上述模拟结果显示, 不同尺寸的纳米结构会显著影响冷凝过程中液滴的形核位置和最终润湿状态. 较高的纳米阵列使冷凝液滴在阵列间隙的上部侧面和底部优先形核和生长, 通过采用“上密下疏”的不均匀间隙可避免液滴在底部形核, 在间隙上部侧面形核的液滴在长大过程中会发生润湿状态转变, 最终呈现Cassie态; 而较低的纳米阵列使冷凝液滴在阵列底部优先形核和生长, 液滴在长大过程中始终处于Wenzel态. 模拟得到的液滴最终润湿状态与实验观察结果^[17,30]符合良好.
2 -->

3.3.纳米结构表面局部润湿性对液滴冷凝过程的影响

本节采用三维多相流LBM模型模拟纳米结构表面局部润湿性对液滴冷凝过程的影响. 模拟区域和纳米阵列的几何尺寸与图8相同, 将中部区域16根纳米柱顶端设置为亲水($\theta_{\rm c} $ = 60°), 其余位置保持为疏水($\theta_{\rm c} $ = 110°). 图9为三维模型模拟得到的液滴在具有不均匀润湿性的纳米阵列顶端形核和生长的过程. 图9第一张图片中绿色区域表示设置为亲水的纳米结构顶端. 模拟中发现, 约在4800 ts后, 水蒸气在亲水纳米阵列顶端有少量富集. 约在5600 ts, 液滴在亲水纳米阵列顶端形核. 随后, 小液滴吸收周围区域的水蒸气粒子而迅速长大. 随着冷凝过程的进行, 不断生长的相邻液滴之间会逐渐合并, 约在7200 ts, 液滴合并成一个大液滴, 并保持Cassie态继续生长.
图 9 模拟的液滴在具有不均匀润湿性的纳米阵列顶端形核、生长及合并演化过程
Figure9. Simulated evolution of droplet nucleation, growth, and coalescence on the nanoarrays non-uniformly patterned with hydrophilic and hydrophobic regions on the top of nanoarrays.

对比图8和图9的模拟结果发现, 纳米阵列顶端的不均匀润湿性使得冷凝液滴的形核位置由阵列底部转变为阵列顶端, 液滴的最终润湿状态也由完全润湿的Wenzel态转变为不润湿的Cassie态. 因此, 纳米结构几何尺寸相同的条件下, 纳米结构的局部润湿性会显著影响冷凝过程中液滴的形核位置和最终的润湿状态.
将上述采用三维多相流LBM模型模拟得到的结果与Zhang等^[24,25]采用二维多相流LBM模型模拟得到的结果进行对比分析, 发现冷凝液滴在二维和三维空间下的形核和生长过程的规律基本一致, 但也存在一些差异, 归纳如下.
1) 相同点. 关于在纳米阵列间隙底部和亲水纳米阵列顶端形核的冷凝液滴, 在二维和三维空间中, 形核位置相同, 生长合并后呈现相同的润湿状态: 在纳米阵列上部间隙处形核的冷凝液滴呈现Cassie态; 在纳米阵列间隙底部形核长大的液滴均呈现Wenzel态; 在亲水纳米阵列顶端形核长大的液滴均呈现Cassie态.
2) 不同点. 关于纳米阵列间隙处形核的冷凝液滴, 在二维空间中, 液滴仅在纳米阵列间隙的上部侧面形核^[24,25], 而在三维空间中, 液滴可同时在纳米阵列上部和底部间隙处形核. 这是由于二维空间中纳米阵列间隙底部相互隔离, 水蒸气粒子无法在间隙底部自由传输. 而在三维空间中, 纳米阵列间隙空间相互连通, 水蒸气粒子在间隙底部可自由扩散、聚集至过饱和, 从而也可在间隙底部析出液滴核心.

本文采用三维多相流LBM模型对纳米结构表面的液滴冷凝现象进行了模拟研究, 将模拟结果与文献报道的实验结果进行了对比, 二者符合良好. 本文的模拟工作再现了冷凝液滴在纳米结构表面的形核长大过程, 阐释了纳米结构几何尺寸和材料表面局部润湿性对冷凝液滴形核和生长过程的影响规律. 得到如下结论.
1) 模拟的液滴内外压力差$\Delta P $和液滴半径的倒数1/R呈线性正比关系, 符合Laplace定律. 在不同流-流作用系数G_c下, 拟合直线的斜率随着|G_c|的增大而增大, 直线斜率反映液滴的表面张力$\gamma $, 说明表面张力$\gamma $和|G_c|成正比.
2) 模拟的液滴在光滑表面本征接触角$\theta $_c随流-固作用系数G_ads的增大而增大. 模拟结果与相关理论公式的计算结果符合良好.
3) 当纳米阵列较高时, 液滴在纳米阵列的上部和底部间隙处同时形核, 在上部间隙处形核的液滴合并、长大、并向上运动, 使液滴的润湿状态由Wenzel态转变为Cassie态. 而在间隙底部形核会损坏纳米结构表面的超疏水性, 通过设计“上密下疏”的不均匀间隙可避免液滴在间隙底部形核.
4) 当纳米阵列较低时, 液滴在纳米阵列的底部形核, 在合并、长大过程中始终呈现Wenzel态; 保持相同几何尺寸的纳米结构, 在纳米阵列顶端设置不均匀的亲、疏水区域, 液滴会在亲水的阵列顶端优先形核, 使液滴由底部形核长大转变为在顶端形核长大, 最终的润湿状态为Cassie态.
5) 将三维模拟结果与前期的二维模拟结果对比发现, 二维与三维的模拟结果基本一致, 但对于较高尺寸的纳米结构也存在一些差异; 在三维空间下纳米阵列间隙之间相互连通是造成二维和三维模拟结果差异的主要原因.