摘要:采用基于密度泛函理论加U的计算方法, 研究了Ce和O空位单(共)掺杂锐钛矿相TiO₂的电子结构和光吸收性质. 计算结果表明, Ce和O空位共掺杂TiO₂的带隙中出现了杂质能级, 且带隙窄化为2.67 eV, 明显比纯TiO₂和Ce, O空位单掺杂TiO₂的要小, 因而可提高TiO₂对可见光的响应能力, 使TiO₂的光吸收范围增加. 光吸收谱显示, 掺杂后TiO₂的光吸收边发生了显著红移; 在400.0—677.1 nm的可见光区, 共掺杂体系的光吸收强度显著高于纯TiO₂和Ce单掺杂TiO₂, 而略低于O空位单掺杂TiO₂. 此外, Ce掺杂TiO₂中引入O空位后, TiO₂的导带边从?0.27 eV变化为?0.32 eV, 这表明TiO₂的导带边的还原能力得到了加强. 计算结果为Ce和O空位共掺杂TiO₂在可见光光解水方面的进一步研究提供了有力的理论依据.
关键词: Ce掺杂/
O空位/
锐钛矿相TiO₂/
电子结构/
第一性原理

English Abstract

全文HTML

--> --> -->

1972年, Fujishima和Honda^[1]首次报道了在紫外光的照射下TiO₂可以使水发生水解, 从而掀起了对TiO₂光催化性能的研究热潮. 最近几十年来, 人们从光解水^[1,2]、太阳能电池^[3]、自清洁^[4]、污染物降解^[5]等方面对TiO₂的应用进行了广泛而深入的研究. 这些研究表明, TiO₂具有高氧化能力、良好的化学稳定性及无毒、廉价等优异性能^[6,7], 是一种较理想的光催化半导体, 在环保和能源等领域极具应用潜力. 然而, TiO₂在光催化和能量转换应用过程中仍存在两大亟待解决的瓶颈^[8]: 一是, 由于TiO₂的本征带隙较宽(约3.0 eV), 纯TiO₂只能吸收占太阳光谱约5%、波长小于387.5 nm的紫外光, 却不能响应占太阳光约43%的可见光; 二是, TiO₂材料中光生载流子的复合率较高, 光生电子-空穴对难以有效分离, 致使TiO₂的光量子产率偏低. 为此, 人们利用离子掺杂、贵金属沉积、半导体复合、染料敏化, 以及基于能带工程设计的异质结等方法和技术^[9,10]来提高TiO₂材料对太阳光能的利用率与光催化活性.
最近, 许多实验和理论研究均发现镧系离子在裁剪TiO₂的能带结构和增强TiO₂的光催化活性方面具有特殊的作用. 如, Mazierski等^[11]利用电化学方法制备了一系列的Er-, Yb-, Ho-, Gd-, Pr-掺杂的TiO₂纳米管, 发现这些镧系离子掺杂均能增强TiO₂的光催化活性. 在可见光解降甲苯的过程中, Ho掺杂TiO₂的效率尤为显著; 进一步的理论计算表明, 能带中新出现的Ho-f能级和表面缺陷态可能是TiO₂可见光催化能力增强的主要原因. Du等^[12]报道Ce掺杂TiO₂体系不但展现出优异的可见光吸收活性, 而且显示出良好的热稳定性. Nasir等^[13]认为这种光催化活性增强的原因之一在于TiO₂中形成了氧化还原电荷对(即Ce³⁺/Ce⁴⁺, 其中Ce³⁺具有4f¹5d⁰电子构型, 而Ce⁴⁺具有4f⁰5d⁰电子构型), 因而在光生载流子的过程中Ce³⁺/Ce⁴⁺充当了“清道夫”的作用, 有效促进了电子-空穴对的分离, 提高了TiO₂的光催化活性. Li等^[14]发现, 当TiO₂表面的Ce/Ti原子的比率为2.0%时, 在可见光照射下Ce-TiO₂显示出优良的光催化活性. Xiao等^[15]指出随着Ce掺杂浓度的提高, TiO₂纳米纤维的光吸收边从450.0 nm大幅红移至739.0 nm, 当Ce/Ti的摩尔比增加到0.03后, 其可见光的吸收能力又逐渐变小. 而Fu等^[16]通过第一性原理计算则发现, 随着Ce掺杂浓度的增加, Ti 3d轨道电子在导带底的态密度不断减弱, 从而使TiO₂在180.0—600.0 nm之间的光吸收强度逐渐降低. 可见, 有关Ce掺杂TiO₂的光吸收性能的理论研究与实验研究之间仍存在一定的差距. 这些差距的形成与多方面原因密切相关. 例如, 实验制备的掺杂体系, 不可避免地会产生一些缺陷(如氧空位(O_V)、间隙掺杂、异种原子置换掺杂等缺陷), 而理论计算中常常却忽略了某些缺陷, 因而计算结果与实验观测之间有一定的差距. 对于金属氧化物而言, O_V是一种常见的缺陷, 对金属氧化物的电子结构和物化性能可产生重要影响^[17]. 最近, 占昌朝等^[18]报道La³⁺置换TiO₂中的Ti⁴⁺后形成了O_V, 从而引起刃型位错, 他们认为这些位错缺陷为光催化反应活性位点提供了可能, 十分有利于增强TiO₂的光催化活性. 再如, 最近Yang等^[19]研究发现: 当氢原子占据O_V, 形成新型的O_VH缺陷时, 锐钛矿相TiO₂的能带中出现了新的亚能级, 从而有效提高了TiO₂的可见光吸收能力; 利用可见光辐射含O_VH缺陷的TiO₂光阳极, 可以把水完全裂解.
综上所述, 离子掺杂和空位缺陷均对氧化物半导体的能带结构、光吸收性能以及光催化活性具有重要的调控与影响作用. 鉴于Ce与O_V共掺杂TiO₂的理论和实验研究鲜有报道, 本文对Ce/O_V共掺杂锐钛矿相TiO₂的电子结构和光学性质进行理论计算和研究.

锐钛矿型TiO₂晶体结构属四方晶系, 空间群为I4₁/amd, 每个晶胞内包含12个原子, 由4个TiO₂基本单元构成. 其中, Ti原子处于由邻近6个O原子所围成的八面体中心, Ti原子的配位数为6, O原子配位数为3, 而且O原子的位置只与一个内坐标u有关, Ti和O两种原子的坐标分别为Ti(0, 0, 0)和O(0, 0, u). 已有诸多理论研究^[8,16,20,21]表明采用2 × 2 × 1的锐钛矿相TiO₂超胞结构进行周期性计算, 可获得可靠的计算结果, 此时相邻超胞中掺杂原子间的相互作用可以忽略. 另一方面, 采用2 × 2 × 1超胞结构, 掺杂浓度可调控到与最近许多实验和理论研究中相近的掺杂浓度^[12-14,20]. 考虑到以上两个因素, 本研究各计算模型均采用2 × 2 × 1的超胞结构(各超胞模型的原子和缺陷位置如图1所示). 其中, 纯锐钛矿相TiO₂, Ce掺杂TiO₂, 含O_V的TiO₂, 以及Ce与O_V共掺杂TiO₂的结构模型分别命名为: pure TiO₂, Ce-TiO₂, O_V-TiO₂, Ce/O_V-TiO₂.
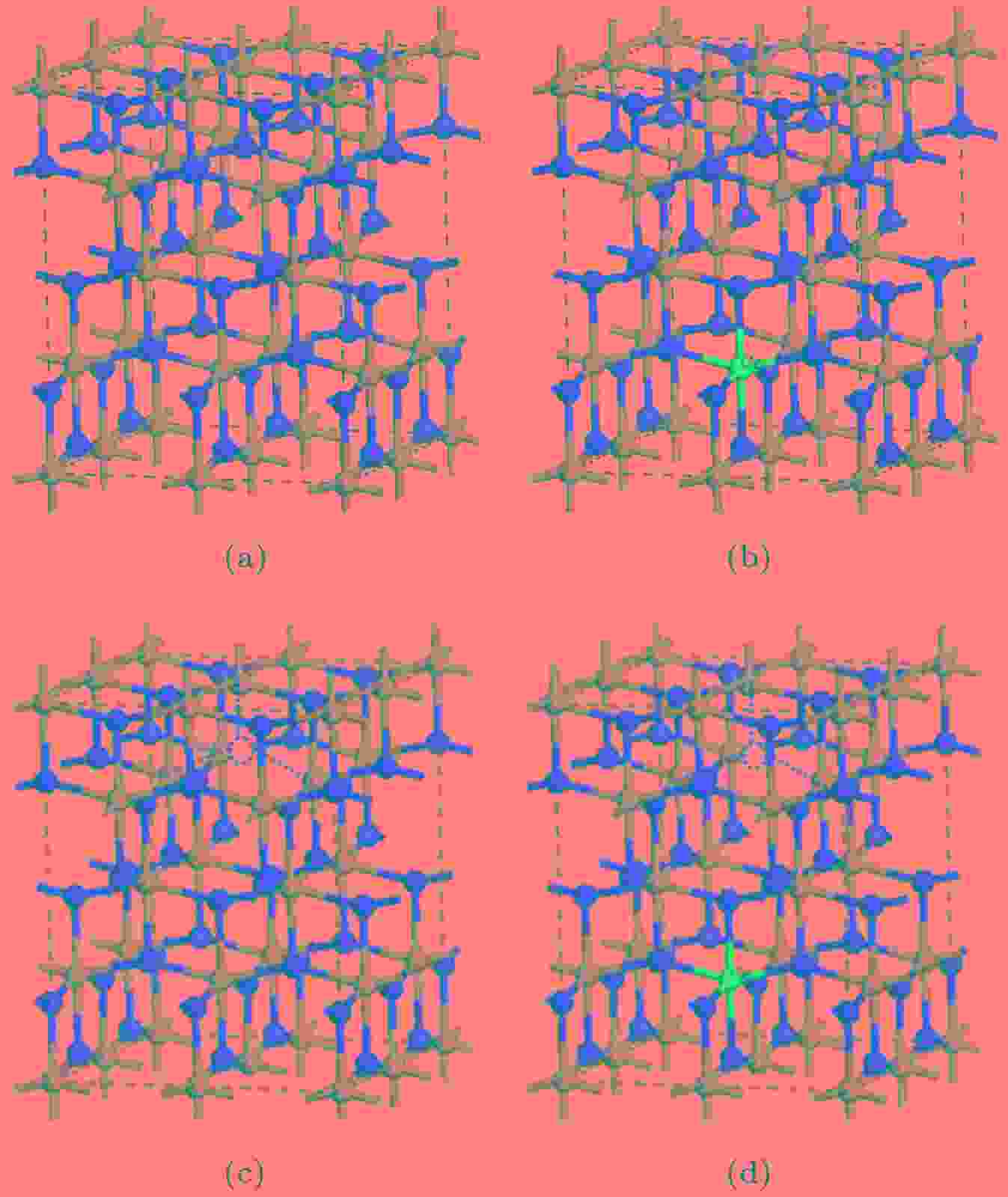图 1 2 × 2 × 1的超胞结构图(红色球为O, 灰色球为Ti, 蓝色球表示Ce原子的掺杂位置, 红色虚圆圈表示O_V的位置)　(a) Pure TiO₂; (b) Ce-TiO₂; (c) O_V-TiO₂; (d) Ce/O_V-TiO₂
Figure1. The 2 × 2 × 1 supercell structure of various supercell models (the red, grey and blue balls represent O, Ti and Ce atoms, respectively; the imaginary red circle shows the position of oxygen vacancy): (a) Pure anatase TiO₂; (b) Ce-TiO₂; (c) O_V-TiO₂; (d) Ce/O_V-TiO₂.

本文采用Materials Studio软件中基于密度泛函理论(density functional theory, DFT)的平面波超软赝势法的CASTEP程序包进行计算. 考虑到计算体系含有强关联性的局域性Ti 3d和Ce 4f电子, 采用标准的DFT计算难以获得满意的电子结构和光学性质. 因此, 计算过程中交换关联泛函采用局域密度近似(local density approximation, LDA), 并对具有强关联作用的Ti 3d和Ce 4f电子用$U$值修正. $ U$值修正^[22]是指对强定域性的电子(如d, f轨道电子), 引入一个在位(on-site)的库仑排斥项$U$, 从而修正交换关联泛函对强关联电子局域性的低估, 以达到合理的结果. 基于文献[16, 21]提供的$U$值, 并通过对TiO₂和CeO₂的带隙与$U$之间的关系测试发现: 当取$U$_{Ti 3d} = $ U$_{Ce 4f} = 8.0 eV时, TiO₂和CeO₂的带隙值分别为3.12和2.78 eV. 此测试结果与采用相同$U$值的理论计算结果^[16,23]吻合极好; 与实验测量值^[24,25]也非常接近; 且测试过程中, TiO₂和CeO₂晶格参数相对于初始的参数变化均小于2.0%, 计算得到的电子能带结构也可靠合理. 因此, 计算中Ti 3d和Ce 4f轨道的$U$值均设为8.0 eV.
计算中平面波截断动能设置为620 eV, 采取6 × 6 × 5的Monkhorst-Pack格点取样. 自洽场运算中应用Pulay密度混合法, 能量收敛标准为1.0 × 10^?5 eV/atom (1 eV/atom = 9.6485 × 10⁴ J/mol), 最大公差为0.0002 nm, 晶体内应力收敛标准为0.05 GPa, 每个原子间相互作用力小于0.2 eV/nm. 计算电子能带结构和光学性质之前, 计算所用的超胞结构先采用BFGS (Broyden-Flecher-Goldfarb-Shanno)方法进行几何优化, 然后再对优化后的模型结构进行单点能计算. 参与计算的价电子的构型分别为O: 2s²2p⁴, Ti: 3s²3p⁶3d²4s², Ce: 4f¹5s²5p⁶5d¹6s². 为保证计算结果的可比性, 各模型的计算均在倒易空间中进行, 其参数的设置均与上述设置相同.
为便于和实验测量结果比较, 光吸收性质计算中运用了非极化多晶模型, 并利用剪刀算符修正带隙值. 考虑到纯TiO₂的实验带隙值为3.23 eV, 而本计算的值为3.12 eV, 两者间相差0.11 eV. 因此, 剪刀算符设为0.11 eV. 在能带带边的计算中亦使用0.11 eV对各体系的带隙宽度进行修正.

2

-->

3.1.结构优化结果

表1为采用广义密度梯度近似(generalized gradient approximation, GGA), GGA + U, LDA及LDA + U方法, 对纯TiO₂进行结构优化及能带结构计算得到的晶格参数和带隙值. 其中, 采用LDA + U计算得到的纯TiO₂的晶格常数和内坐标参数(a, b, c, u) (u = d_ap/c)的计算误差均小于2.0%, 与实验和理论计算值^{[16,20,21,24,26-30]}均吻合良好. 表2为采用LDA + U方法, 对Ce/O_V单(共)掺杂TiO₂的超晶胞结构几何优化后, 折合成单晶胞的结构参数.

参量	GGA	GGA + U	LDA	LDA + U	Experiment	Theory	Error%
a/nm	0.3791	0.3897	0.3745	0.3806	0.3785[26]	0.3831[29]	0.5548
b/nm	0.3791	0.3897	0.3745	0.3806	0.3785[26]	0.3831[29]	0.5548
c/nm	0.9805	0.9925	0.9447	0.9674	0.9514[26]	0.9631[29]	1.6817
c/a	2.5860	2.5470	2.5230	2.5410	2.5140[26]	2.5140[29]	1.0739
u	0.2050	0.2050	0.2080	0.2070	—	0.2050[29]	—
dap/nm	0.2011	0.2031	0.1966	0.2005	0.1980[27]	0.1973[29]	1.2626
deq/nm	0.1946	0.2000	0.1914	0.1948	0.1934[28]	0.1930[29]	0.7238
Eg/eV	2.18	3.18	2.16	3.12	3.32[24]	3.23[29]	—
注: dap, deq分别表示Ti—O长键和短键的键长; 误差指LDA + U方法相对于实验值的误差.

表1采用GGA, GGA + U, LDA及LDA + U方法计算得到的纯锐钛矿相TiO₂的晶格参数和带隙宽度
Table1.Lattice parameters and band gap width of pure anatase TiO₂ calculated at the GGA, GGA + U, LDA and LDA + U levels of theory.

参量	Ce-TiO2				OV-TiO2		Ce/OV-TiO2
	This work	Experiment	Other theory		This work		This work
a/nm	0.3822	0.3789[25]	0.3980[31]		0.3789		0.3827
b/nm	0.3833	—	0.3980[31]		0.3793		0.3798
c/nm	0.9956	0.9509[25]	0.9757[31]		0.9824		1.0090
dap/nm	0.2225	—	0.2273[32]		0.2012		0.2233
deq/nm	0.2183	—	0.2119[32]		0.1946		0.2252
注: dap, deq分别表示Ce-TiO2, Ce/OV-TiO2中Ce—O长键和短键的键长, 对于OV-TiO2则表示Ti—O长键和短键的平均键长.

表2Ce/O_V单(共)掺杂锐钛矿相TiO₂弛豫后的晶胞参数
Table2.Lattice parameters of Ce/O_V single and co-doped anatase TiO₂ after the structure relaxation.

表2数据表明, 掺杂体系的晶格参数均发生了不同程度的畸变. 由晶体场理论可知^[11]: 晶格畸变可导致TiO₂中八面体单元的正负电荷中心分离, 从而在晶体中形成局域内建电场. 由于产生了内建电场, TiO₂中光生电子-空穴对的分离和迁移变得更加容易, 十分有利于增强TiO₂的光催化活性. 这种内建电场的强弱, 可以用八面体单元的电偶极矩来度量. 表3列出了掺杂体系的平均电偶极矩的计算值.

Model	Ef/eV			q/e			p/Debye
	Ti-rich	O-rich		O	Ti	Ce
Pure TiO2	—	—		?0.720	1.440	—	0.0000
Ce-TiO2	10.42	1.16		?0.719	1.405	1.920	0.0168
OV-TiO2	1.02	5.65		?0.727	1.412	—	0.0668
Ce/OV-TiO2	?15.84	?20.48		?0.725	1.373	1.920	0.0251

表3Ce/O_V掺杂锐钛矿相TiO₂的缺陷形成能(E_f)、平均净电荷(q)和平均偶极矩(p)
Table3.Defect formation energy, average net charges and average dipole moment of Ce/O_V doped TiO₂ supercell after the structure relaxation.

表3中平均偶极矩的计算结果表明: O_V可显著提高TiO₂中八面体结构的平均偶极矩; Ce掺杂TiO₂中引入O_V后, 八面体结构单元的平均电偶极矩的大小明显增加. 可见, 形成一定浓度的O_V, 有利于增强TiO₂的光催化活性. 后文中的电子能带结构、态密度和光吸收谱的计算结果均进一步印证了这一结论.
2 -->

3.2.缺陷形成能

为评估掺杂原子嵌入TiO₂晶格与空位形成的相对难易程度, 以及确定掺杂体系的稳定性, 这里采用缺陷形成能来表征^[20,29]. 缺陷形成能(E_f)的计算公式如下:

${E_ {\rm{f}}} = {E_ {\rm{doped}}} - {E_ {\rm{pure}}} - m{\mu _ {\rm{Ce}}} + n{\mu _ {\rm{O}}} + l{\mu _ {\rm{Ti}}}, $

其中, E_doped与E_pure分别代表掺杂(缺陷)模型与纯TiO₂超胞模型的总能量; ${\mu _{{\rm{Ce}}}}$, ${\mu _{{\rm{O}}}}$, ${\mu _{{\rm{Ti}}}}$分别表示Ce原子、O原子、Ti原子的化学势; m, n, l分别表示掺杂进入TiO₂的Ce原子的个数, 以及从TiO₂中移除的O原子和Ti原子的个数. 对于Ce-TiO₂模型, m = 1, n = 0, l = 1; 类似地, O_V-TiO₂模型, m = 0, n = 1, l = 0; Ce/O_V-TiO₂模型, m = 1, n = 1, l = 1. 众所周知, 材料的缺陷形成能与其生长制备条件密切相关. 因此, 本文只计算富氧(O-rich)和富钛(Ti-rich)条件下的形成能.
在富氧条件下, 显然, ${\mu _{\rm{O}}} = {{{\mu _{{{\rm{O}}_2}}}} / 2}$(${{\mu _{{{\rm{O}}_2}}}}$为氧气分子的总能); 此时, ${\mu _{{\rm{Ti}}}}$的大小则由关系式${\mu _{{\rm{Ti}}{{\rm{O}}_{\rm{2}}}}} = $${\mu _{{\rm{Ti}}}} + 2{\mu _{\rm{O}}}$得出. 在富钛条件下, ${\mu _{{\rm{Ti}}}}$的大小取自密排六方相(hcp) $\alpha$-Ti金属中单个原子的能量; 此时, ${\mu _{{\rm{O}}}}$由 $2{\mu _{\rm{O}}} = {\mu _{{\rm{Ti}}{{\rm{O}}_{\rm{2}}}}} - {\mu _{{\rm{Ti}}}}$决定. Ce的化学势由关系式${\mu _{{\rm{Ce}}}} = {\mu _{{\rm{Ce}}{{\rm{O}}_{\rm{2}}}}} - {\mu _{{{\rm{O}}_{\rm{2}}}}}$获得. 各掺杂体系在富氧和富钛条件下的形成能的计算结果列于表3. 结果表明, O_V-TiO₂在富氧和富钛条件下的形成能的大小分别与Wu等^[33]在富氧和富钛条件下的计算值1.00和5.30 eV极其接近. 比较共掺杂与单掺杂体系的形成能大小可知: Ce/O_V共掺杂TiO₂的缺陷形成能显著低于单掺杂TiO₂的形成能, 负的形成能说明Ce/O_V共掺杂体系具有良好的稳定性.
2 -->

3.3.能带结构和态密度

基于DFT + U的计算方法, 对优化后的纯锐钛矿相TiO₂和掺杂与缺陷体系的能带结构和态密度进行了计算. 为方便比较, 各体系的能带图均选取费米能级在能量零点来观察TiO₂晶体沿布里渊区高对称方向的能带结构(如图2所示). TiO₂掺杂前后各体系对应的总态密度(total density of states, TDOS)和分态密度(partial density of states, PDOS)图(如图3所示)中的费米能级也取为能量零点.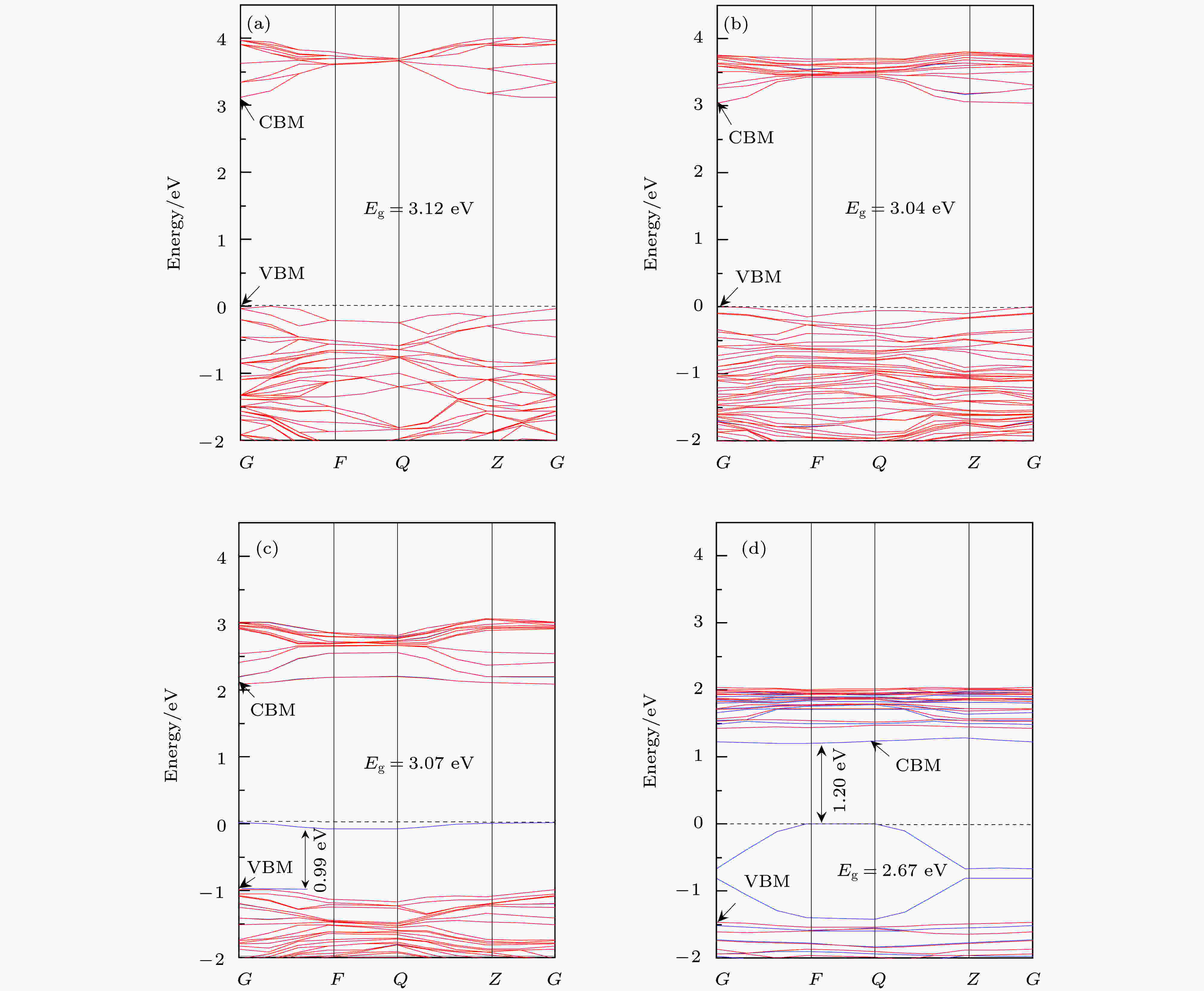
图 2 纯TiO₂和Ce/O_V掺杂TiO₂的能带结构图(图中虚线代表费米能级E_F)　(a) Pure TiO₂; (b) Ce-TiO₂; (c) O_V-TiO₂; (d) Ce/O_V-TiO₂
Figure2. Band structure of anatase TiO₂ before and after doping (the dashed lines represent the Fermi level, E_F): (a) Pure TiO₂; (b) Ce-doped TiO₂; (c) O_V-TiO₂; (d) Ce/O_V-TiO₂.

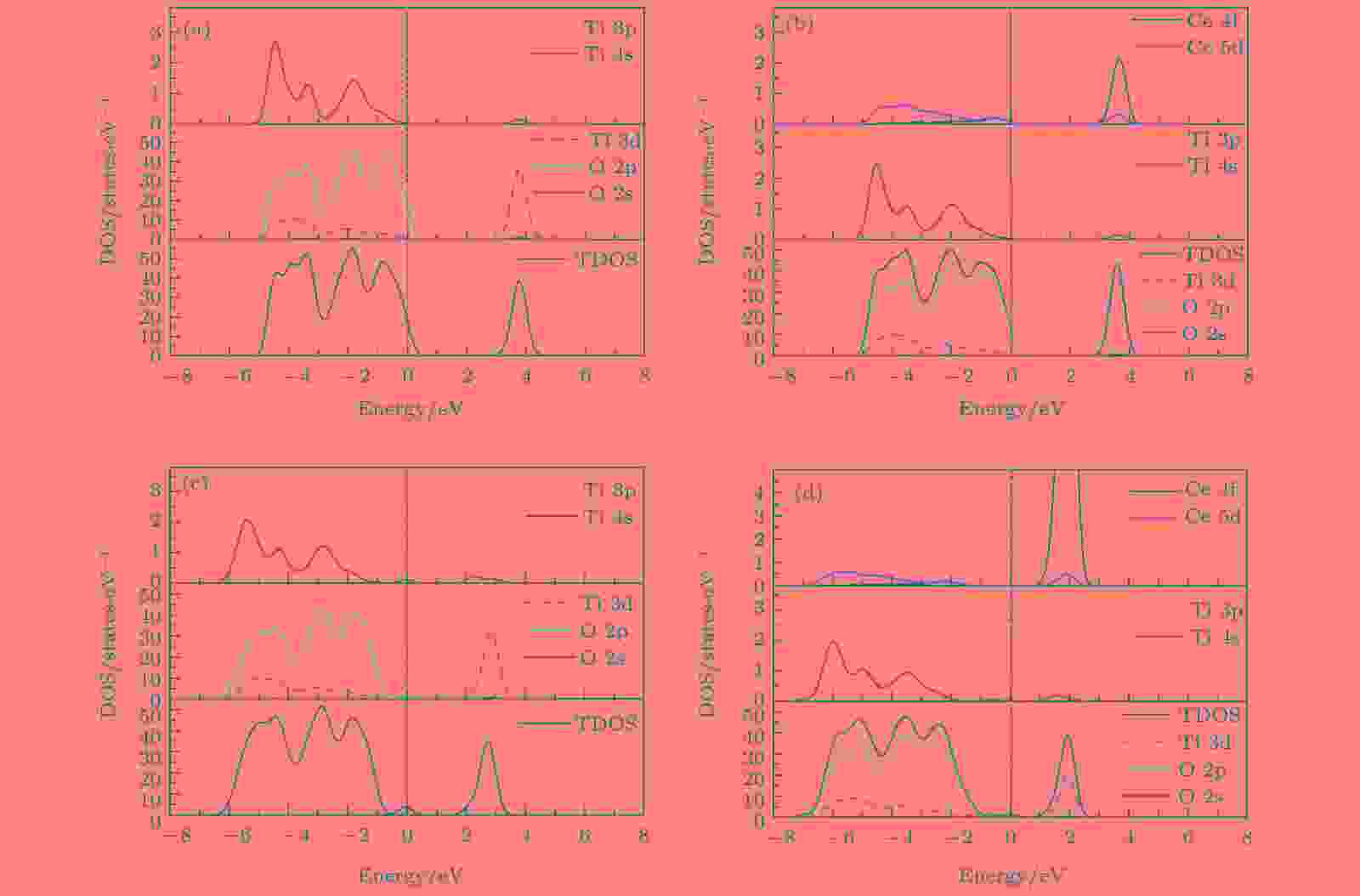图 3 纯TiO₂和Ce/O_V掺杂TiO₂的态密度图(图中虚线代表费米能级E_F)　(a) Pure TiO₂; (b) Ce-TiO₂; (c) O_V-TiO₂; (d) Ce/O_V-TiO₂
Figure3. Comparison of partial density of states of anatase TiO₂ before and after doping (the dashed lines represent the Fermi level, E_F): (a) Pure TiO₂; (b) Ce-doped TiO₂; (c) O_V-TiO₂; (d) Ce/O_V-TiO₂.

由图2(a)可知, 在高对称点G处纯锐钛矿相TiO₂几乎为直接带隙, 其带隙宽度为3.12 eV, 与实验测量值3.23 eV十分接近. 对应的态密度图3(a)显示, 纯TiO₂的价带(valence band, VB)和价带顶(valence band maximum, VBM)的态密度主要由O 2p轨道电子贡献, 其导带(conduction band, CB)和导带底(conduction band minimum, CBM)的态密度则主要由Ti 3d轨道电子贡献. 由此可知, 纯锐钛矿相TiO₂的光吸收主要起源于电子在O 2p轨道与Ti 3d轨道之间的跃迁. 另一方面, 图3(a)表明纯TiO₂的VB和CB中都含有O 2p和Ti 3d轨道电子, 这表明O原子与Ti原子之间具有部分共价键成分, 这一特性与文献[16, 33]的报道一致.
图2(b)为Ce单掺杂TiO₂的能带图. 由图2(b)可知, 相对于纯TiO₂而言, Ce-TiO₂的VBM几乎没有移动, 而其CB整体朝低能方向发生了的移动, 从而导致Ce掺杂后TiO₂的带隙宽度窄化为3.04 eV. 结合图3(b)可知, 这种变化的主要原因可归于CBM附近的Ce 4f, Ce 5d, Ti 3d及O 2p轨道之间充分混合, 致使反键峰的位置相对于未掺杂前反键峰的位置明显下移, 从而导致TiO₂的CB下移、带隙收缩. 显然, 带隙窄化可引起半导体的光吸收谱发生红移. 与之相吻合是, 后文中计算所得的光吸收谱和相关理论和实验研究^[16,25,34]中均观测到了这一红移现象.
如图2(c)所示, O_V-TiO₂的禁带宽度相对于纯TiO₂发生了微小的收缩, 并且在费米能级附近出现了杂质能级. 态密度图3(c)显示, O 2p, Ti 3d, Ti 3p, Ti 4s轨道之间充分叠加耦合, 在费米能级附近形成成键峰, 从而导致O_V-TiO₂的费米能级下方出现了具有占据态特性的受主能级. 这一结果与Zhang等^[35]采用GGA + U方法计算得到的结果完全一致. 图2(c)显示该杂质能级与VBM相距0.99 eV, 这一能量差值与Rumaiz等^[36]在实验中观测的结果极其相近. 他们观测到含O_V的TiO₂带隙中的杂质能级比VBM高1.0 eV. 此外, 对比图3(c)与图3(a)容易发现O_V-TiO₂的价带宽度明显发生了宽化. 这预示着电子具有更强的离域性, 十分有利于增强载流子的移迁能力.
比较图2(d)与图2(b)可知, Ce/O_V共掺杂TiO₂的禁带宽度(2.67 eV)相对于Ce掺杂TiO₂的禁带宽度(3.04 eV)显著窄化. 由此可见Ce掺杂TiO₂中进一步引入O_V, 可有效诱导Ce/O_V-TiO₂的带隙收缩. 态密度图3(d)显示Ce 4f和Ce 5d进入CBM, 并且与Ti 3d轨道充分混合, 致使反键峰所在位置明显向低能方向移动, 从而导致Ce/O_V-TiO₂的导带整体向低能方向大幅移动(如图3(b)所示); 同时, 在价带区Ce 5d, Ti 3p, Ti 4s与O 2p轨道电子之间的成键峰的位置均较单掺杂时的成键峰的位置向价带低端能移动, 从而引起TiO₂的价带整体向低能明显移动. 因此, Ce与O_V协同作用下可导致TiO₂的带隙显著收缩. 另一方面, 能带图2(d)显示, Ce/O_V-TiO₂的禁带中形成了极浅的受主能级. 这些杂质能级处于费米能级下方(与CBM相距1.20 eV), 并且与VBM充分交叠, 有利于电子从VBM跃迁至CBM. 这一效果与直接减小带隙宽度相似, 极大地提高了TiO₂对可见光的响应能力.
比较图3(d)与图3(b), 可观测到相对于Ce-TiO₂的价带和导带而言, Ce/O_V-TiO₂的价带和导带区的TDOS均向价带低能端下移和延伸, 且峰形降低, 变得更为平滑和宽化. 这种价带宽化与Ce 5d, Ti 4s与O 2p轨道电子在价带低能区相互叠加引起电子的分布更为宽广密切相关; 类似地, 图3(c)中也观测到价带发生了宽化, 且其价带宽化幅度略小于Ce/O_V-TiO₂. 事实上, 这种价带宽化现象, 是掺杂致使晶体的对称性降低, 导致电子分布的非局域性增强而形成的. 此时, 态密度曲线的峰形降低、变得更为平滑和宽化^[29,37]. 显然, O_V-TiO₂和Ce/O_V-TiO₂中电子的非局域性的增强, 对提高光生载流子的迁移能力和TiO₂的光催化活性十分有益.
2 -->

3.4.带边位置

为探索掺杂前后半导体的导带边和价带边的还原氧化能力的变化, 可采用如下公式^[38]: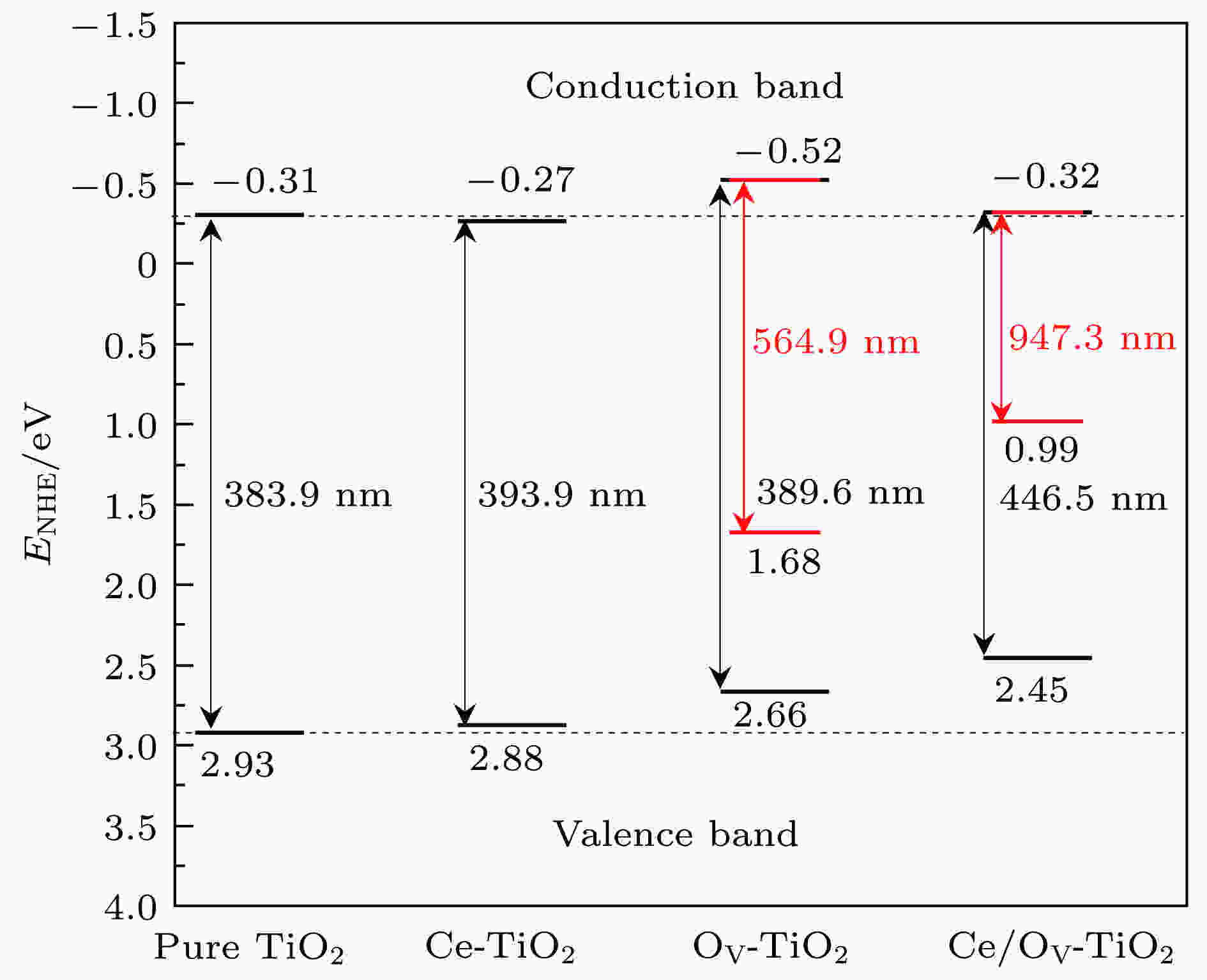

${E_{{\rm{CB}}}} = X - {E_{\rm{e}}} - \frac{1}{2}{E_{\rm{g}}}, $

${E_ {\rm{VB}}} = {E_ {\rm{CB}}} + {E_ {\rm{g}}}.$

(2)和(3)式中, 导带边的还原电势用E_CB表示, 组成体系各原子的电负性的几何平均值用X表示, 自由电子的电势值E_e以标准氢电极(normal hydrogen electrode, NHE)为参照(～4.5 eV). 经计算纯TiO₂的导带边和价带边的电势分别为?0.31和2.93 eV, 与实验观测值^[39]极为相近. 图4为Ce/O_V掺杂锐钛矿相TiO₂的能带带边位置的示意图.
图 4 Ce/O_V掺杂锐钛矿相TiO₂的能带带边位置示意图(图中各带边位置的电位均以NHE的电位为参考零点, 粗黑线代表忽略杂质能级时的带边位置, 细红线代表考虑杂质能级时的带边位置)
Figure4. Calculated band energy positions of pure TiO₂, Ce-TiO₂, O_V-TiO₂, Ce/O_V-TiO₂ (the energy scale is indicated by the normal hydrogen electrode in electron volts as a reference; the short thick lines and fine red lines represent the band energy positions of TiO₂ by neglecting and considering the impurity levels, respectively).

如图4所示, 相对于纯TiO₂的导带边和价带边的位置而言, Ce-TiO₂ (Ce掺杂浓度为2.08%)对应的带边位置分别向下和向上移动了0.035和0.047 eV. Ce-TiO₂的带边位置移动方向与Lenka等^[25]报道的掺杂浓度为0.28%和3.0%的Ce/TiO₂样品的带边位置的移动方向一致. 但此两种掺杂浓度的Ce/TiO₂的带边移动幅度明显大于本研究中Ce-TiO₂的带边移动幅度. 究其原因除了与掺杂浓度不同这个因素有关外, 更重要的在于实验制备中会形成CeO₂, 因而可在TiO₂的能带中产生新的能级, 对半导体的带边电势产生重要的影响. 显然, Ce-TiO₂的价带边的氧化能力因其价带边上移而有所削弱, 但2.88 eV的价带边电势, 相对于氧化剂H₂O₂和O₃的氧化电势1.77和2.07 eV而言, 可认为Ce-TiO₂的价带边仍具有良好的氧化能力. 另一方面, Ce-TiO₂的导带边的还原能力却因其导带边电势位置下移, 而略有减弱. 值得指出的是, O_V-TiO₂的导带带边显著向上移动, 这表明TiO₂中引入O_V可明显提高其导带边的光催化还原能力. Liu等^[40]通过光致发光光谱(photoluminescence spectra, PL)检测到TiO₂样品中形成了O_V. 这些O_V的存在可导致Ti⁴⁺向Ti³⁺转化, 有利于降低光生电子-空穴对的复合^[13]. 类似地, 图4显示, Ce/O_V共掺杂TiO₂的导带边的电势位置略高于纯TiO₂和Ce单掺杂的导带边的电势位置, 这说明其导带边的还原能力高于纯TiO₂和Ce单掺杂的情形.
根据光解水的基本条件^[41]: 光催化剂的导带边的电势应低于H⁺/H₂的还原电势(0 eV vs. NHE); 另一方面, 光催化剂的价带边的电势应高于O₂/H₂O的氧化电势(1.23 eV vs NHE). 结合图2和图4可知, Ce/O_V-TiO₂的基本带隙明显窄化, 对可见光具有良好的响应能力, 且其带边电势可满足上述光解水的基本要求. 因此, Ce/O_V-TiO₂可能是一种良好的适合于可见光光解水的光催化材料.
另一方面, 图4显示Ce/O_V单(共)掺杂TiO₂的光吸收阈值相对于纯TiO₂的光吸收阈值均向长波方向增长. 特别是, Ce/O_V-TiO₂的基本带隙的光吸收响应明显增长到可见光区域. 若考虑杂质能级的作用, O_V-TiO₂和Ce/O_V-TiO₂的光吸收能力分别拓展到可见光长波区域和红外光区.
2 -->

3.5.光吸收谱

半导体的光学性质的计算基本原理是基于直接带间传输的介电函数的虚部公式^[42]:

$ \begin{split}{\varepsilon _2}\left( \omega \right) = &\frac{A}{{{\omega ^2}}}\sum\limits_{{\rm{C, V}}} {\int\limits_{{\rm{BZ}}} {\frac{{\rm{2}}}{{{{\left( {{\rm{2}}{\text{π}} } \right)}^3}}}} } {\left| {{M_{{\rm{CV}}}}\left( {{K}} \right)} \right|^2} \\ &\cdot\delta \left( {E_{\rm{k}}^{\rm{C}} - E_{\rm{k}}^{\rm{V}} - h\omega } \right){{\rm{d}}^3}{{K}}, \end{split}$

式中C, V, BZ和K分别表示导带、价带、第一布里渊区和倒格矢; ${\left| {{M_ {\rm{CV}}}({{K}})} \right|^2}$为动量跃迁矩阵元; A为与允许直接跃迁吸收系数有关的常数; $\omega $为声子频率; E_k^C和E_k^V分别为导带和价带上的本征能级. 进一步由Kramers-Kroning变换关系^[43], 可导出介电函数的实部${\varepsilon _1}$. 最终便可计算出材料的光吸收谱. 图5为Ce/O_V掺杂锐钛矿TiO₂的光吸收谱.
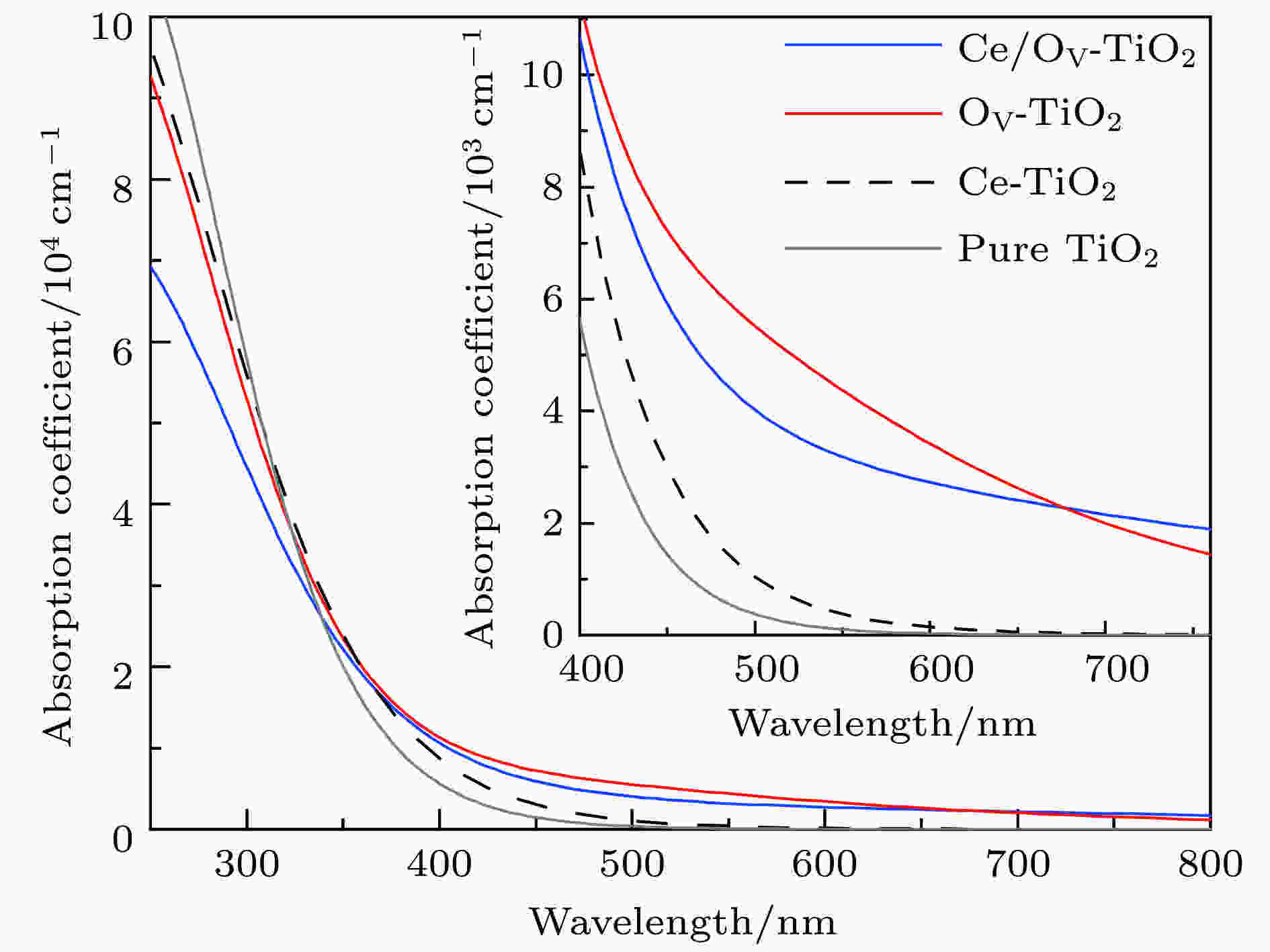图 5 Ce/O_V掺杂锐钛矿TiO₂的光吸收谱(插图为可见光区光吸收谱的放大图)
Figure5. Absorption spectra of pure and different doping TiO₂ models (inset is the expanded absorption spectra in the visible region).

图5显示, 各掺杂体系的光吸收谱均发生了明显的红移, 且其在可见光区和更长波段区域的光吸收系数均高于纯锐钛矿相TiO₂的光吸收系数. 其中, O_V-TiO₂和Ce/O_V-TiO₂在可见光区的吸收系数明显大于Ce-TiO₂的可见光光吸收系数, 且前者在大部分的可见光区的光吸收系数均高于后者. 由此可见, Ce-TiO₂中引入O_V, 可有效增强TiO₂对可见光的响应能力.
仔细比较Ce/O_V-TiO₂与O_V-TiO₂的光吸收谱, 可发现在400.0—677.1 nm之间, 前者比后者的光吸收系数略弱一些. 究其原因, 主要可归因于如下两个方面. 一是, 由图3(c)和图3(d)可发现, O_V-TiO₂与Ce/O_V-TiO₂在其费米能级附近的杂质能级上的电子态密度的大小存在较大差距, 前者明显高于后者. 这预示着, 相对于Ce/O_V-TiO₂而言, O_V-TiO₂中杂质能级上的电子吸收光能向导带跃迁的概率要大. 二是, 由图4可知, Ce/O_V-TiO₂在可见光区域的光吸收阈值约为446.5 nm, 而O_V-TiO₂由于杂质能级的作用, 其光吸收阈值约为564.9 nm. 这就是说, 前者对可见光的响应在一定区域内要弱于后者. 另一方面, 图5显示在波长大于677.1 nm的区域, Ce/O_V-TiO₂的光吸收系数略高于O_V-TiO₂的光吸收系数. 这一现象可以从图2(d)和图4得到解释. 图2(d)和图4显示, Ce/O_V-TiO₂的受主能级对更长波长的吸收响应能力显著强于O_V-TiO₂中的杂质能级对更长波长的吸收响应能力, 因而导致在更长波段中Ce/O_V-TiO₂的光吸收系数略高于O_V-TiO₂.
最近, 许多实验研究^[25,34,44]报道, Ce掺杂TiO₂可引起半导体的光吸收谱发生红移, 并显示出优良的光催化活性. 例如, Yan等^[44]实验发现Ce掺杂浓度为1.0 mol%的Ce/TiO₂的光吸收边的红移约为50.0 nm, 但掺杂浓度进一步增加时, TiO₂的光吸收边的红移却不再增加; 而Lenka等^[25]在实验中却观测到了Ce掺杂浓度增至10 mol%时, TiO₂的光吸收边的红移约为81.0 nm. 相比于Yan等^[44]和Lenka等^[25]的实验结果, 本文研究的Ce/O_V-TiO₂的光吸收边的红移约为62.0 nm. 可见, 本研究的Ce/O_V-TiO₂的红移幅度与实验研究的Ce/TiO₂的红移幅度相近. 这是因为实验制备的Ce掺杂TiO₂不可避免地会产生一定浓度的O_V, 本计算已考虑了这一因素, 因而计算结果与实验相近; 若计算中不考虑O_V的作用, 本研究发现Ce-TiO₂的红移幅度仅约为10.0 nm. 另一方面, 尽管本研究的Ce/O_V-TiO₂的红移幅度与实验结果相近, 但仍然存在明显差距. 究其原因有: 实验中TiO₂样品的表面可形成CeO₂, 因而O_V和Ce的4f轨道在TiO₂的能带中形成了新的能级, 从而促进了TiO₂对可见光的响应能力. 此外, 实验制备中因Ce离子氧化不充分, Ce⁴⁺和Ce³⁺可以同时存在, 从而形成氧化还原电对Ce³⁺/Ce^4+[25,44], 因而十分有利于提高光生电子-空穴对的迁移率和光量子产率^[13]. 因此, 实验中观测到的Ce掺杂TiO₂表现出了更优异的可见光光催化活性.

本文运用第一性原理LDA + U方法, 计算了Ce和O_V单(共)掺杂锐钛矿相TiO₂的晶格参数、缺陷形成能、电子结构和光吸收性质. 由计算结果可得到如下结论.
1) 在Ce/O_V共掺杂TiO₂的导带区Ce 4f, Ce 5d, Ti 3d轨道之间充分混合, 致使反键峰的位置和导带整体下移; 同时, 价带区的Ce 5d, Ti 3p, Ti 4s, Ti 3d, O 2p轨道电子之间交叠耦合, 引起成键态峰位朝低能方向移动. 最终, 共掺杂TiO₂的价带明显宽化, 在费米能级附近形成受主能级, 带隙窄化为2.67 eV, 明显小于纯的和单掺杂TiO₂的带隙宽度. 因此, Ce/O_V共掺杂可有效提高TiO₂对可见光的响应能力和增加其光吸收范围.
2) Ce/O_V共掺杂使TiO₂的晶格畸变, 并在其八面体单元中诱生出显著的电偶极矩, 从而可有效提高光生电子-空穴对的迁移能力和半导体的光催化活性; 另一方面, Ce掺杂TiO₂中引入O_V可增强导带边的还原能力, 共掺杂后TiO₂的能带边的电势位置满足光解水的基本条件, 且在可见光区的光吸收强度明显高于纯TiO₂和Ce单掺杂TiO₂.
综上所述, Ce/O_V共掺杂TiO₂的能带结构可满足可见光光解水的基本要求. 本文的研究为相关理论和实验的进一步研究提供了良好的理论基础.